Developed on the basis of mathematical simulation of the relaxation-recovery process of polymer textile materials for technical purposes, the method for determining the functional-useful relaxation-recovery properties of these materials [1,2,3] makes it possible to assess their qualitative characteristics by relaxation-recovery parameters.

Let us consider a mathematical model of the relaxation-recovery process of polymer textile materials for technical purposes [4, 5]:

$$ {E}_{\varepsilon t}={E}_0-\left({E}_0-{E}_{\infty}\right){\upvarphi}_{\varepsilon t}, $$
(1)

where the function of the normalized arctangent of the logarithm (NAL) is chosen as the relaxation function φεt. It characterizes the integral Cauchy distribution [6]:

$$ {\upvarphi}_{\upvarepsilon t}=\frac{1}{2}+\frac{1}{\uppi}\mathrm{arctg}\left(\frac{1}{b_{n\upvarepsilon}}\ln \frac{1}{\uptau_{\upvarepsilon}}\right). $$
(2)

Here: τε is the average relaxation time; bnε is the relaxation rate; σt is the stress, changing in time t under the action of deformation.

Viscoelastic modulus

$$ {E}_{\infty }=\underset{t\to \infty }{\lim }{E}_{\upvarepsilon t}, $$
(3)

and elastic modulus

$$ {E}_0=\underset{t\to 0}{\lim }{E}_{\upvarepsilon t}, $$
(4)

are the two asymptotic values of the relaxation modulus

$$ {E}_{\upvarepsilon t}=\frac{\upsigma_t}{\upvarepsilon}. $$

To assess the relaxation-recovery properties of polymeric textile materials for technical purposes, several developed criteria are proposed that can be combined into a single integrated criterion due to the fact that all relaxation-recovery parameters for assessing the properties of these materials are subject to probabilistic Cauchy law and include an assessment of their quality [7,8,9].

To assess the relaxation-recovery properties of polymeric textile materials for technical purposes, the following criteria are proposed:

– the criterion of the material recovery intensity after operation;

– the criterion of the material recoverability degree after operation;

– the criterion of the possibility of the material repeated recovery during operation;

– the time-based recovery criterion of the functional-useful properties of the material after operation;

– the criterion of the material resistance to repeated recovery after operation.

A quantitative assessment of the parameters within the framework of the proposed criteria for the relaxationrecovery properties of polymer textile materials for technical purposes is proposed to be carried out in dimensionless units, which can be described as follows [10,11,12].

1. Criterion of the material recovery intensity after operation.

Let us denote by

$$ {\upalpha}_1={b}_{n\upvarepsilon} $$
(5)

a dimensionless variable characterizing the value of the material recovery intensity after operation, which is numerically equal to the intensity of the relaxation process responsible for the recovery of the functional-useful properties of the material under consideration. In this case, α1 can take any non-negative values (α1 ≥ 0). The lower the value of α1, the faster is the process of material recovery after operation [13].

2. Criterion of the material recoverability degree after operation.

Let us denote by

$$ {\upalpha}_2=\frac{E_{\infty }}{E_0+{E}_{\infty }} $$
(6)

a dimensionless variable characterizing the material recoverability degree after operation. In this case, α2 takes nonnegative values (α2 ≥ 0). The lower the value of α2, the higher is the material recovery degree after operation. The higher the value of the parameter α2, the less is the possibility of the material recovery [14].

3. Criterion of the possibility of the material repeated recovery during operation.

Let us denote by

$$ {\upalpha}_3=\frac{100\%}{\upvarepsilon_p} $$
(7)

a dimensionless variable characterizing the possibility of the material repeated recovery during operation, where εp is the ruptural deformation (in %). In this case, α3 can take any non-negative values (α3 ≥ 0). The lower the value of α3, the higher is the possibility of material repeated recovery. The value α3 = 0 corresponds to a material possessing the property of complete repeated recovery [15].

4. Time-based recovery criterion of the functional-useful properties of the material after operation.

Let us denote by

$$ {\upalpha}_4=\frac{{\overline{\uptau}}_{\upvarepsilon}}{t_1} $$
(8)

a dimensionless variable characterizing the ability of the material to recover in time the functional-useful properties after operation, where t1 is some value of the base time, for example, t1 = 60 s; \( {\overline{\uptau}}_{\varepsilon } \) is the average relaxation time, determined by the formula

$$ {\overline{\uptau}}_{\upvarepsilon}=\frac{1}{\upvarepsilon_2-{\upvarepsilon}_1}\cdot \underset{\upvarepsilon_1}{\overset{\upvarepsilon_2}{\int }}{\uptau}_{\upvarepsilon}\cdot d\upvarepsilon, $$
(9)

where ε1 is the lowest value from the range of the investigated deformations, ε2 is the highest value from the range of the investigated deformations [16,17,18].

In this case, α4 can take any non-negative values (α4 ≥ 0). The lower the value of α4, the faster is the material recovery after operation.

5. Criterion of the material resistance to repeated recovery after operation.

Let us denote by

$$ {\upalpha}_5=\frac{E_{\infty }}{E_0-{E}_{\infty }} $$
(10)

a dimensionless variable characterizing the material resistance to repeated recovery after operation. In this case, α5 can take any non-negative values (α5 ≥ 0). The lower the value of α5, the higher is the material resistance to repeated recovery after operation. The value α5 = 0 corresponds to the condition of complete material resistance to repeated recovery after operation.

Since the relaxation characteristics E0, E∞, bnε and τε are obtained using the mathematical simulation of relaxationrecovery properties based on the Cauchy probability distribution, the integral distribution function of which is the NAL function, all the variables α1, α2, α3, α4, α5 also obey the Cauchy probability distribution due to the additivity of this law [19, 20].

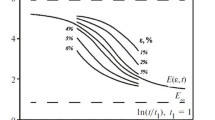
The Cauchy probability distribution is quite close to the normal distribution, differing from it in some properties, for example, the slower convergence of the integral function to its asymptotic values (Fig. 1). This property of the Cauchy distribution makes it possible to process statistical samples with higher reliability, since it possesses a significant degree of scattering, which is just specific for the set samples of relaxation-recovery characteristics of polymer textile materials for technical purposes.

Fig. 1.
figure 1

NAL, PI, HT, and KF integral distribution functions, which are the foundations of mathematical models of relaxation-recovery processes of polymer textile materials for technical purposes.

Full size image

According to the above, it should be noted that the probability relaxation characteristic εp is also subject to the Cauchy law.

As integral functions of probability distributions in the study of relaxation, deformation and other properties of polymer textile materials for technical purposes, in addition to the normal distribution with the “probability integral” (PI) function and the Cauchy distribution with the NAL function, sometimes the “hyperbolic tangent” (HT) function and the “Kohlrausch function” (KF) are used [21, 22], graphs of which are shown in Fig. 1.

6. Integrated criterion for relaxation-recovery properties. Since all introduced probabilistic characteristics α1, α2, α3, α4, α5 are distributed according to the Cauchy law, it is advisable to consider a new relaxation-recovery parameter

$$ {A}_p={\upalpha}_1+{\upalpha}_2+{\upalpha}_3+{\upalpha}_4+{\upalpha}_5 $$
(11)

also distributed according to the Cauchy law.

According to the properties of the terms α1, α2, α3, α4, α5, the parameter Ap can take any non-negative values (Ap ≥ 0), and the relaxation-recovery properties of polymer textile materials for technical purposes will be the better, the lower the value of relaxation-recovery parameter Ap.

In the ideal case, those materials of textile and consumer goods industry for which Ap = 0 will have the best functional-useful relaxation-recovery characteristics, from the point of view of the materials quality. However, in practice, it cannot be achieved [23,24,25].

Thus, the criterion for optimizing the relaxation-recovery properties of polymeric textile materials for technical purposes can be formulated as follows:

$$ \frac{\sum \limits_{k=1}^N{A}_{pk}}{t_1}=\frac{\sum \limits_{k=1}^N\left({\upalpha}_{1k}+{\upalpha}_{2k}+{\upalpha}_{3k}+{\upalpha}_{4k}+{\upalpha}_{5k}\right)}{N}={\overline{A}}_p\to \min, $$
(12)

where N is the number of material samples under study (sample size), \( {\overline{A}}_p \) is the average value of the relaxation-recovery parameter.

As noted above, the developed criterion for optimizing the relaxation-recovery properties of polymer textile materials for technical purposes is of an integrated nature and includes optimization according to five partial criteria of relaxation-recovery properties, namely: the criterion of the recovery intensity; the criterion of the recoverability degree; the criterion for the possibility of repeated recovery; the time-based recovery criterion of the functional-useful properties of the material after operation; the criterion of the material resistance to repeated recovery after operation.

Thus, on the basis of mathematical simulation of relaxation-recovery processes of polymer textile materials for technical purposes, five local criteria for qualitative assessment of the relaxation and recovery properties of these materials have been developed. On the basis of local criteria for the qualitative assessment of the relaxation and recovery properties of polymer textile materials for technical purposes and taking into account the additivity of the Cauchy probability distribution, a complex integrated criterion for assessing the relaxation-recovery properties of these materials has been developed. The developed five local and one integrated criterion for the qualitative assessment of the relaxation and recovery properties of polymeric textile materials for technical purposes serve as an instrument of comparative analysis and technological selection of the indicated materials with specified functional properties.