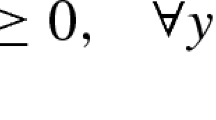1 Introduction

Bilevel programming is a powerful modeling tool that is widely used in many fields (see e.g. [6,7,8, 11, 40]). We focus on the general case in which the lower level problem may have multiple solutions. From that respect, we take the so-called optimistic point of view (for the pessimistic counterpart see, e.g. [24]) that leads us to consider the Standard optimistic Bilevel programming Problem (SBP), as commonly done in the literature (for further details, we refer the interested reader to [23, 42]). The latter problem is structurally nonconvex and nonsmooth; furthermore, it is hard to define suitable Constraint Qualification (CQ) conditions for it, see, e.g. [41]. In fact, the study of provably convergent and practically implementable algorithms for its solution is still in its infancy (see, e.g. the references in [8, 23]), as also witnessed by the scarcity of results in the literature. To date, the most studied and promising approaches rely on either the KKT or the optimal value one-level reformulations. Replacing the lower level problem by its KKT conditions, thus obtaining a Mathematical Program with Complementarity Constraints (MPCC), can be done only when the lower level problem is convex and such that Slater’s constraint qualification holds. However, even in this case, the set of local optima for the SBP is only a (often strict) subset of (the projection of) the set of local optima for the MPCC, which is what one actually craves to compute (since the MPCC is nonconvex) (see Sect. 2 and, in particular, Example 2). On the other hand, the optimal value reformulation is obtained by replacing the lower level solution set by its description via the optimal value function; in this case, while the resulting mathematical program is still a nonconvex, nonsmooth, implicitly defined optimization problem for which standard CQs are not readily at hand, the resulting reformulation and the original SBP lead to the same global and local solutions. There exist few recent solution procedures (e.g. [10, 27]) that leverage the optimal value reformulation but they are viable only for small dimensional problems.

Motivated by common situations in real-world applications (see Sect. 5), we address the nontrivial and wide class of fully convex lower level SBPs whose feasible set does not depend on the upper level variables (see Definition 1 and Example 1) by relying on the value function approach and suitably relaxing the optimal value function constraint.

In Sect. 3, we show that stationary points of the relaxed SBP can be obtained by computing equilibria of a suitably defined Generalized Nash Equilibrium Problem (GNEP). Such a GNEP is convex, explicitly defined and with a nonempty solution set. It should be remarked that the GNEP introduced in Sect. 3 is profoundly different from the one presented in [23], see “Appendix C”. In fact, while [23] is intended to provide a theoretical analysis of the relations between optimistic bilevel problems and Nash games in terms of their optimal points, the distinctive properties of the GNEP proposed here, which is tailored to address stationary solutions of the bilevel problem, pave the way to algorithmic developments. In Sect. 4 we present a simple algorithmic scheme to compute equilibria of the GNEP and, hence, stationary points of the relaxed SBP. This procedure turns out to be provably convergent, easily implementable and numerically viable also for big dimensional problems. In Sect. 5 we propose an application in economics involving a problem with two decision levels; under suitable conditions, this mathematical program is proven to belong to the class of fully convex lower level SBPs. Our numerical results show that the points provided by our procedure are not only stationary for the relaxed SBP but, in most cases, good approximations of global optima for the original SBP.

For the sake of presentation, we first describe our method not in its full generality. In fact, in order to better highlight the core simple idea underlying the approach, we defer to the appendix important theoretical results that widen the scope of applicability of the procedure. Specifically, “Appendix A” is devoted to the study of the behavior of the solutions for the relaxed SBP as the relaxation parameter vanishes, while “Appendix B” extends the convergence results of our algorithm whenever the upper level objective is nonconvex and the upper level feasible set is unbounded.

In the paper we employ standard notation. However, for the reader’s convenience, we remark that, considering \(h: {{\mathbb {R}}}^{n_0} \times {{\mathbb {R}}}^{n_1} \rightarrow {{\mathbb {R}}}\), we denote by \(\nabla _1 h(x,y)\) the gradient of \(h(\bullet , y)\) evaluated at x, while by \(\nabla _2 h(x,y)\) the gradient of \(h(x, \bullet )\) evaluated at y. Furthermore, with C convex set and \(z \in C\), \(N_C(z)\) is the classical normal cone (to C at z) of convex analysis (see e.g. [32, Chapter 6]). As for the definitions of semicontinuity and other properties of single and set-valued mappings such as lower semicontinuity, outer and inner semicontinuity, and local boundedness, we refer the reader to [32]: in particular, for outer and inner semicontinuity, see [32, Definition 5.4].

2 A class of standard optimistic bilevel problems

Let us consider the Standard optimistic Bilevel programming Problem (SBP)

$$\begin{aligned} \begin{array}{ll} \underset{x,y}{\text{ minimize }} & F(x,y) \\ \text{ s.t. } & x \in X\\ & y \in S(x), \end{array} \end{aligned}$$
(1)

where \(F: {{\mathbb {R}}}^{n_0} \times {\mathbb {R}}^{n_1} \rightarrow {\mathbb {R}}\) is continuously differentiable, \(X \subseteq {\mathbb {R}}^{n_0}\) is a compact nonempty set, and the set-valued mapping \(S: {\mathbb {R}}^{n_0} \rightrightarrows {\mathbb {R}}^{n_1}\) is defined (implicitly) as the solution set of the following lower level parametric optimization problem:

$$\begin{aligned} \begin{array}{cl} \underset{w}{\text{ minimize }} & f(x,w)\\ \text{ s.t. } & w \in U, \end{array} \end{aligned}$$
(2)

where \(f: {\mathbb {R}}^{n_0} \times {\mathbb {R}}^{n_1} \rightarrow {\mathbb {R}}\) is continuously differentiable and \(U \subseteq {\mathbb {R}}^{n_1}\) is a compact nonempty set.

We address the case in which the lower level’s parameter dependence only stems from its parametric objective function: thus, problem (1) is a so-called Stackelberg game (see [23]). Moreover, in view of the continuity of function f and the compactness of set U, S(x) turns out to be nonempty for every choice of \(x \in X\) and may contain infinitely many points.

We make the following blanket assumptions:

  • X and U are convex nonempty compact sets;

  • F is convex on \(X \times U\);

  • the lower level problem (2) is convex, e.g. when \(f(x,\bullet )\) is convex for each \(x \in X\).

We remark that, while the assumption on F, as long as the boundedness of X, can be removed at the price of a more convoluted analysis (see “Appendix B”), the other conditions are quite standard and often invoked when bilevel problems are investigated.

In this paper we focus on the class of the so-called fully convex lower level bilevel programming problems (see e.g. [10]).

Definition 1

An instance of (1) is called fully convex lower level SBP if f is fully convex, that is \(f(\bullet , \bullet )\) is convex on \(O \times U\), where O is an open convex set containing X.

From now on, problem (1) is assumed to be a lower level fully convex SBP. We observe that the introduction of the open set O in Definition 1 is instrumental to obtain useful differentiability properties, see the developments in Proposition 1.

On the one hand, despite all the previous convexity conditions seem reassuring, in general problem (1) is, anyway, nonconvex (see, e.g. [7, 23] and the references therein) and implicitly defined. On the other hand, the requirement of a (fully) convex f may appear strong; nonetheless, in Example 1 we show that, under additional assumptions, one can always make the lower level objective fully convex. This can be done by adding a (sufficiently) strongly convex term that, depending only on x, does not influence the lower level solution set mapping S. Thus, as witnessed by the procedure in the following example and by the application in Sect. 5, the class of fully convex lower level SBPs is sufficiently broad and encompasses many important real-world problems.

Example 1

Assume

$$\begin{aligned} f(x, w) = f_1(x, w^1) + f_2(w^2) + \frac{\beta }{2} x^{\scriptscriptstyle T}x, \qquad w = \begin{pmatrix} w^1\\ w^2\end{pmatrix} \in {\mathbb {R}}^{n_{1,1}+n_{1,2}} \end{aligned}$$

where \(f_1: {\mathbb {R}}^{n_0} \times {\mathbb {R}}^{n_{1,1}} \rightarrow {\mathbb {R}}\), \(f_2: {\mathbb {R}}^{n_{1,2}} \rightarrow {\mathbb {R}}\) are twice continuously differentiable and \(n_1 = n_{1,1} + n_{1,2}\), \(\beta \in {\mathbb {R}}\). Note that the lower level solution set S(x) does not depend on the value of \(\beta \). Thus, we can freely fix \(\beta \) in order to obtain a fully convex f. In fact, supposing that \(f_1(\bullet , w^1)\) is convex for every \(w^1\), \(f_1(x, \bullet )\) is uniformly strongly convex with constant \(\tau > 0\) (independent of x) for every x and \(f_2\) is convex, then, choosing

$$\begin{aligned} \beta \ge \frac{1}{\tau } \Vert \nabla ^2_{1,2} f_1(x, w^1)\Vert _2^2, \qquad \forall (x,w^1,w^2) \in X \times U, \end{aligned}$$
(3)

where \(\nabla ^2_{1,2} f_1(x, w^1)\) is the transposed Jacobian of \(\nabla _2 f_1(\bullet ,w^1)\) evaluated at x, we obtain a convex f and, in turn we have an instance of fully convex lower level SBP. We have

$$\begin{aligned} \nabla ^2 f(x, w) = \begin{pmatrix} \nabla ^2_{1,1} f_1(x, w^1) + \beta I \quad & \nabla ^2_{1,2} f_1(x, w^1) & 0\\ \nabla ^2_{2,1} f_1(x, w^1) & \nabla ^2_{2,2} f_1(x, w^1) & 0\\ 0 & 0 & \quad \nabla ^2 f_2(w^2) \end{pmatrix} \end{aligned}$$

where \(\nabla ^2_{1,1} f_1(x, w^1)\) is the Hessian of \(f_1(\bullet , w^1)\) evaluated at x, \(\nabla ^2_{2,2} f_1(x, w^1)\) is the Hessian of \(f_1(x, \bullet )\) evaluated at \(w^1\), \(\nabla ^2 f_2(w^2)\) is the Hessian of \(f_2(\bullet )\) evaluated at \(w^2\), and \(\nabla ^2_{2,1} f_1(x, y) = [\nabla ^2_{1,2} f_1(x, y)]^{\scriptscriptstyle T}\). For every \(z \in {\mathbb {R}}^{n_0}\),

$$\begin{aligned} \begin{array}{l} z^{\scriptscriptstyle T}[\nabla ^2_{1,1} f_1(x, w^1) + \beta I] z - z^{\scriptscriptstyle T}[ \nabla ^2_{1,2} f_1(x, w^1)] [ \nabla ^2_{2,2} f_1(x, w^1)]^{-1} [\nabla ^2_{2,1} f_1(x, w^1)] z\\ \ge \beta \Vert z\Vert ^2 - \frac{1}{\tau } z^{\scriptscriptstyle T}[ \nabla ^2_{1,2} f_1(x, w^1)] [\nabla ^2_{2,1} f_1(x, w^1)] z \ge 0, \end{array} \end{aligned}$$

where the first inequality holds by the convexity of \(f_1(\bullet , w^1)\) and since \(f_1(x, \bullet )\) is (uniformly) strongly convex, while the second relation is due to (3). In turn, \(\nabla ^2 f(x,w) \succeq 0\) by the Schur-complement Theorem and thanks to the convexity of \(f_2\), thus proving the claim.

It goes without saying that, if the original lower level objective does not incorporate the quadratic term \(\beta /2 \; x^{\scriptscriptstyle T}x\), i.e. \(f(x, w) = f_1(x, w^1) + f_2(w^2)\), one can simply add it in order to suitably convexify the function.

We remark that in this case, in view of the presence of the convex term \(f_2\) in f, S(x) does not necessarily reduce to a singleton.

Finally, we also observe that the requirement of a convex \(f_1(\bullet , w^1)\) can be relaxed at the price of sufficiently increasing the value of \(\beta \) in order to, roughly speaking, compensate for the degree of nonconvexity of \(f_1\). \(\square \)

We recall that, to date, the most studied reformulations of the SBP are the optimal value and the KKT ones (see [11] and the references therein). As for the KKT reformulation, it should be remarked that the SBP has often be considered as a special case of Mathematical Program with Complementarity Constraints (MPCC) (see [28]). Actually, this is not the case, as shown in [9]. Indeed, in general, one can provably recast the SBP as an MPCC only when the lower level problem is convex and such that Slater’s constraint qualification holds for all x. More interestingly, even in this case, a local solution of the MPCC, which is what one can expect to compute (since the MPCC is nonconvex), may happen not to lead to a local optimal solution of the corresponding SBP. This problematic aspect occurs even when, as in our framework, one deals with fully convex lower level SBPs: the following very simple example makes this critical issue of the MPCC reformulation apparent.

Example 2

Consider the following standard optimistic bilevel problem:

$$\begin{aligned} \begin{array}{cl} \underset{x,y}{\text{ minimize }} & x\\ \text{ s.t. } & x \in [-1, 1]\\ & y \in S(x), \end{array} \end{aligned}$$
(4)

where the set-valued mapping \(S: {\mathbb {R}}\rightrightarrows {\mathbb {R}}^{2}\) is defined as the solution set of the following lower level parametric optimization problem:

$$\begin{aligned} \begin{array}{cl} \underset{y_1, y_2}{\text{ minimize }} & (y_1 - x)^2 + (y_2 + 1)^2\\ \text{ s.t. } & y_1^3 - y_2 \le 0\\ & - y_2 \le 0. \end{array} \end{aligned}$$
(5)

Problem (4) is an instance of fully convex lower level SBPs: the lower level objective is fully convex on \({\mathbb {R}} \times {\mathbb {R}}^2\) and \(U = \left\{ (y_1, y_2) \in {\mathbb {R}}^2 \, | \, y_1^3 - y_2 \le 0, -y_2 \le 0 \right\} \) is a convex set. The point \((-1, -1, 0)\) is the unique local (and also global) solution of (4). Moreover, since the Mangasarian-Fromovitz constraint qualification is easily seen to hold for the lower level problem (5) at every feasible \((y_1, y_2)\), we also have [32, Theorem 6.12]

$$\begin{aligned} N_U(y_1, y_2) = \left\{ \begin{pmatrix}3 \lambda _1 y_1^2\\ -\lambda _1 - \lambda _2\end{pmatrix} \, \biggr | \, (\lambda _1, \lambda _2) \in N_{{\mathbb {R}}^2_-}(y_1^3 - y_2, -y_2)\right\} . \end{aligned}$$

Taking into account the latter relation and recalling that, for any fixed \(x \in [-1, 1]\), condition \(0 \in \nabla _2 f(x, y) + N_U(y)\) is necessary and sufficient for the feasible solution \(y = (y_1, y_2)\) to be (global) optimal for (5), one can suitably introduce the following MPCC reformulation of (4):

$$\begin{aligned} \begin{array}{cl} \underset{x,y_1,y_2,\lambda _1,\lambda _2}{\text{ minimize }} & x\\ \text{ s.t. } & x \in [-1, 1]\\ & 2(y_1 - x) + 3 \lambda _1 y_1^2 = 0\\ & 2(y_2 + 1) - \lambda _1 - \lambda _2 = 0\\ & 0 \le \lambda _1 \perp (y_1^3 - y_2) \le 0\\ & 0 \le \lambda _2 \perp -y_2 \le 0. \end{array} \end{aligned}$$
(6)

We remark that the point \((-1, -1, 0, 0, 2)\) is globally optimal for problem (6). However, the feasible solution (0, 0, 0, 1, 1) is a local optimum: in fact, considering an open neighborhood of the latter point, we have \(\lambda _1, \, \lambda _2 > 0\) and, in turn, the corresponding constraints are active, implying that \(y_1 = y_2 = 0\). By the first equality constraint, we also obtain \(x = 0\) and, thus, a locally flat upper level objective function. But point (0, 0, 0), that is the projection of (0, 0, 0, 1, 1) on the \((x, y_1, y_2)\)-space, is just a “non promising” feasible point for (4). To the best of our knowledge, it is still an open question whether the illustrated effect of additional local minima in the MPCC reformulation would persist under stronger assumptions such as requiring the lower level feasible to be described by smooth convex functions satisfying the Slater condition. \(\square \)

In view of the considerations above, in order to deal with problem (1), we refer to the optimal value reformulation (see [29]), that is

$$\begin{aligned} \begin{array}{cl} \underset{x,y}{\text{ minimize }} & F(x,y) \\ \text{ s.t. } & x \in X, \, y \in U\\ & f(x, y) \le \varphi (x), \end{array} \end{aligned}$$
(SBP)

where

$$\begin{aligned} \varphi (x) \triangleq \min _w \{f(x, w) \, : \, w \in U\} \end{aligned}$$

is the value function. Also, we denote by \(W \triangleq \left\{ (x, y) \in X \times U \, | \, f(x,y) \le \varphi (x)\right\} \) the feasible set of (SBP). Preliminarily, we observe that, under the initial assumptions, the value function enjoys the following nice properties.

Proposition 1

Function\(\varphi \)is convex and continuously differentiable on the open convex setOfrom Definition1. Moreover, for any\(x \in O\), the set\(\{\nabla _{1} f(x, w) \, |\)\(w \in S(x)\}\)is a singleton and, for any\(w \in S(x)\),

$$\begin{aligned} \nabla \varphi (x) = \nabla _{1} f(x, w). \end{aligned}$$
(7)

Proof

Problem (2) can be equivalently reformulated as an unconstrained program employing the so-called indicator function \(\delta _U(w)\), where \(\delta _U(w) = 0\) if \(w \in U\) and \(\delta _U(w) = \infty \) if \(w \notin U\). Since, by our assumptions, function \(\delta _U\) turns out to be lower semicontinuous and convex, then the convexity of \(\varphi \) follows from [32, Corollary 3.32], being f fully convex (see Definition 1).

In order to show that \(\varphi \) is continuously differentiable on O, leveraging [32, Corollary 9.19], by the convexity of \(\varphi \), suffice it to prove that the set of subgradients \(\partial \varphi (x)\) is single-valued for every \(x \in O\). For this to be done, one can rely on, e.g. [39]. However, to maintain the paper self-contained, we show that, for every \(x \in O\) and any \(w \in S(x)\),

$$\begin{aligned} \partial \varphi (x) = \{\nabla _1 f(x, w)\}. \end{aligned}$$

Let us consider a generic \(v \in \partial \varphi (x)\). By the convexity of \(\varphi \), we have for every \(u \in O\)

$$\begin{aligned} f(u,w) \ge \varphi (u) \ge \varphi (x) + v ^{\scriptscriptstyle T}(u - x) = f(x,w) + v ^{\scriptscriptstyle T}(u - x), \end{aligned}$$

where the last equality holds since \(w \in S(x)\). It follows that

$$\begin{aligned} x \in \arg \min _{u \in O} f(u,w) - v ^{\scriptscriptstyle T}u. \end{aligned}$$

This, due to the convexity of the problem, is equivalent to \(0 = \nabla _1 f(x, w) - v\). The claim is a consequence of the arbitrariness of \(w \in S(x)\) and \(v \in \partial \varphi (x)\). \(\square \)

We remark again that (SBP) is a nonconvex and implicitly defined problem for which standard constraint qualifications are not readily at hand (see, e.g, [7, 11]). For this reason, following a well-established path in the literature (see, e.g. [26, 27]), one is naturally led to consider the following perturbed version of (SBP):

$$\begin{aligned} \begin{array}{cl} \underset{x,y}{\text{ minimize }} & F(x,y) \\ \text{ s.t. } & x \in X, \, y \in U\\ & f(x, y) \le \varphi (x) + \varepsilon , \end{array}\qquad \qquad (\text{SBP}_\varepsilon) \end{aligned}$$

where \(\varepsilon > 0\) could be interpreted as a reasonable tolerance on the optimal value of the follower’s problem. Furthermore, we indicate with \(W_\varepsilon \triangleq \left\{ (x,y) \in X \times U \, | \, f(x, y) \le \varphi (x) + \varepsilon \right\} \) the feasible set of (\(\text{SBP}_\varepsilon \)).

Problem (\(\text{SBP}_\varepsilon \)) is still nonconvex and implicitly defined. However, while, as suggested above, the Mangasarian-Fromovitz Constraint Qualification (MFCQ) does not hold on W, on the contrary, it is verified on \(W_\varepsilon \). Here, for the reader’s convenience, we recall the definition of the MFCQ.

Definition 2

(MFCQ) Let \((x, y) \in W_\varepsilon \). We say that the MFCQ holds at (x, y) if the relations

$$\begin{aligned} \begin{array}{l} 0 \in \lambda _1 \nabla _1 f(x, y) - \lambda _1 \nabla \varphi (x) + N_X(x)\\ 0 \in \lambda _1 \nabla _2 f(x, y) + N_U(y)\\ \lambda _1 \in N_{{\mathbb {R}}_-}(f(x, y) - \varphi (x) - \varepsilon ) \end{array} \end{aligned}$$
(8)

imply \(\lambda _1 = 0\).

In order to show that the MFCQ is satisfied everywhere on \(W_\varepsilon \), suffice it to observe that for \(\lambda _1\) to be positive, we must have \(f(x, y) - \varphi (x) - \varepsilon = 0\), and thus \(f(x, y) = \varphi (x) + \varepsilon > \varphi (x)\). In turn, by the convexity of the lower level problem, \(0 \notin \nabla _2 f(x,y) + N_U(y)\) that contradicts the second inclusion in (8).

A further motivation to introduce the parameter \(\varepsilon \) is given in Sect. 5, where a real-world application is considered. Finally, in “Appendix A”, we analyze the “behavior” of (\(\text{SBP}_\varepsilon \)) with vanishing values of the perturbation, i.e. for \( \varepsilon{\downarrow} 0 \).

For the sake of clarity, we specify the definition of stationary points for (\(\text{SBP}_\varepsilon \)).

Definition 3

(Stationary point) Let (x, y) be feasible for (\(\text{SBP}_\varepsilon \)). We say that (x, y) is a stationary point for (\(\text{SBP}_\varepsilon \)) if a multiplier \(\lambda _1\) exists such that:

$$\begin{aligned} \begin{array}{l} 0 \in \nabla _{1} F(x, y) + \lambda _1 \nabla _1 f(x, y) - \lambda _1 \nabla \varphi (x) + N_X(x)\\ 0 \in \nabla _{2} F(x, y) + \lambda _1 \nabla _2 f(x, y) + N_U(y)\\ \lambda _1 \in N_{{\mathbb {R}}_-}(f(x, y) - \varphi (x) - \varepsilon ). \end{array} \end{aligned}$$
(9)

If (x, y) solves (\(\text{SBP}_\varepsilon \)), since it satisfies the MFCQ (8), then it is a stationary point for (\(\text{SBP}_\varepsilon \)). Hence, as standard in nonconvex optimization (see, just as a matter of example in this context, [27]), the aim of our method is to compute a stationary point of (\(\text{SBP}_\varepsilon \)). In particular, in Sect. 3 we show that calculating a stationary point of (\(\text{SBP}_\varepsilon \)) can be accomplished by finding an equilibrium of a suitable Nash equilibrium problem and vice versa. In Sect. 4 we provide a simple scheme to compute such a point with global convergence guarantees.

We observe that, when more general assumptions are considered, e.g. whenever the lower level feasible set depends parametrically on x, some difficulties arise. In particular, the value function \(\varphi \) can no more be expected to be smooth (as opposed to the picture analyzed in Proposition 1). However, even in this more general framework, something can be said, but considering criticality conditions that are more general (usually less sharp) than (9).

3 An equilibrium problem reformulation

We introduce the following Generalized Nash Equilibrium Problem (GNEP) with two players, namely player 1 and player 2:

$$\begin{aligned} \begin{array}{clccl} \underset{x, y}{\text{ minimize }} & \; F(x,y) & & \underset{u, w}{\text{ minimize }} & f(x,w) + \frac{1}{2} \Vert u - x\Vert ^2\\ \text{ s.t. } & x \in X, \, y \in U & & \text{ s.t. } & u \in X, \, w \in U,\\ & f(x, y) \le f(u, w) & & & \\ & \qquad \qquad + \nabla _1 f(u, w)^{\scriptscriptstyle T}(x - u) + \varepsilon & & & \end{array}\qquad \qquad (\text{GNEP}_{\varepsilon }) \end{aligned}$$

where \(\varepsilon \) is a positive parameter. Note that the quadratic term in the optimization problem of player 2 is introduced with the only purpose of constraining u to be equal to x; thus, \(1/2 \; \Vert u - x\Vert ^2\) is not a proximal term.

We call equilibrium of (\(\text{GNEP}_{\varepsilon }\)) a feasible solution (x, y, u, w) from which no player has incentives to deviate unilaterally (see [14], to which we refer for all the fundamental definitions and tools regarding GNEPs). Here, for the sake of clarity, we recall the Karush–Kuhn–Tucker (KKT) conditions for (\(\text{GNEP}_{\varepsilon }\)).

Definition 4

(KKT point) Let (x, y, u, w) be feasible for (\(\text{GNEP}_{\varepsilon }\)). We say that (x, y, u, w) is a KKT point for (\(\text{GNEP}_{\varepsilon }\)), if a multiplier \(\lambda _1\) exists such that:

$$\begin{aligned}&\begin{array}{l} 0 \in \nabla _{1} F(x, y) + \lambda _1 \nabla _1 f(x, y) - \lambda _1 \nabla _1 f(u, w) + N_X(x)\\ 0 \in \nabla _{2} F(x, y) + \lambda _1 \nabla _2 f(x, y) + N_U(y)\\ \lambda _1 \in N_{{\mathbb {R}}_-}(f(x, y) - f(u,w) - \nabla _1 f(u,w)^{\scriptscriptstyle T}(x - u) - \varepsilon ), \end{array} \end{aligned}$$
(10)
$$\begin{aligned}&\begin{array}{l} 0 = u - x\\ 0 \in \nabla _{2} f(x, w) + N_U(w).\\ \end{array} \end{aligned}$$
(11)

We propose to rely on (\(\text{GNEP}_{\varepsilon }\)) as an instrument to find stationary points of (\(\text{SBP}_\varepsilon \)). In fact, (\(\text{GNEP}_{\varepsilon }\)), while being tightly related to (\(\text{SBP}_\varepsilon \)) (see the following developments), as opposed to (\(\text{SBP}_\varepsilon \)), is convex, that is each player solves a convex (parametric) optimization problem, and, among the constraints, no implicitly defined functions (as \(\varphi \) in (\(\text{SBP}_\varepsilon \))) appear.

Remark 1

Under our assumptions, (\(\text{GNEP}_{\varepsilon }\)) satisfies all the conditions in the Ichiishi Theorem (see, e.g. [14, Theorem 4.1]) and, thus, is such that an equilibrium always exists. In particular,

  1. (i)

    any feasible point (x, y, u, w) is such that \((x,y) \in X \times U\) and \((u,w) \in X \times U\), where \(X \times U\) is a compact set;

  2. (ii)

    (\(\text{GNEP}_{\varepsilon }\)) is convex, that is each player solves a convex (parametric) optimization problem, given the strategy of the rival;

  3. (iii)

    since \(X \times U\) is nonempty, then the feasible set of player 2 is nonempty for every choice (x, y) of player 1. At the same time, for any strategy (u, w) of player 2, the point \((x,y) = (u,w)\) always belongs to the feasible set of player 1;

  4. (iv)

    since \(f(\bullet , \bullet )\) is continuously differentiable and the Slater constraint qualification holds on the feasible set of player 1 for any choice of \((u,w) \in X \times U\), then the feasible set of player 1, considered as set-valued mapping, is continuous relative to \(X \times U\) at every point in \(X \times U\) (see [2, Theorems 3.1.1 and 3.1.6]).

We also observe that point (x, y, u, w) is an equilibrium of (\(\text{GNEP}_{\varepsilon }\)) if and only if it is a KKT point for (\(\text{GNEP}_{\varepsilon }\)): on the one hand, the necessity holds since the Slater constraint qualification is valid on the feasible set of player 1 for any choice \((u,w) \in X \times U\); on the other hand, the sufficiency is due to the convexity of the game.

In the light of the previous considerations, quite naturally one can recover a stationary point of (\(\text{SBP}_\varepsilon \)) by computing a KKT solution, i.e. an equilibrium (that certainly exists), of (\(\text{GNEP}_{\varepsilon }\)).

Theorem 3.1

The following claims hold:

  1. (i)

    any KKT point (x, y, u, w) of (\(\text{GNEP}_{\varepsilon }\)) is such that (x, y) is stationary for (\(\text{SBP}_\varepsilon \));

  2. (ii)

    any stationary point (x, y) for (\(\text{SBP}_\varepsilon \)) is such that (x, y, x, w) is a KKT point of (\(\text{GNEP}_{\varepsilon }\)) for any\(w \in S(x)\).

Proof

The claims follow observing that (10) and (11) imply (9) with \(w \in S(x)\), and vice versa. This is true thanks to Proposition 1 and observing that \(f(u,w) = \varphi (x)\). \(\square \)

The previous result proves that the link between (\(\text{GNEP}_{\varepsilon }\)) and (\(\text{SBP}_\varepsilon \)) is strong: any stationary point of (\(\text{SBP}_\varepsilon \)) can be recovered by computing equilibria of (\(\text{GNEP}_{\varepsilon }\)). Thus, since one can obtain any stationary point of (\(\text{SBP}_\varepsilon \)) passing through the “well-behaved” (\(\text{GNEP}_{\varepsilon }\)), Theorem 3.1 paves the way to the algorithmic developments of the next section.

Example 3

Let us go back to Example 2, where we showed that the point \((x, y_1, y_2) = (0, 0, 0)\) is nothing more than a “non promising” feasible solution for the SBP, while resulting from a futile local optimum for the MPCC reformulation. Now we illustrate how, for any \(\varepsilon \), no KKT points \((x, y_1, y_2, u, w_1, w_2)\) of (\(\text{GNEP}_{\varepsilon }\)) exist such that \(x = 0\). It is easy to see that, if \(x = 0\), then (11) implies \(u = 0\), \(w_1 = 0\) and \(w_2 = 0\). By (10), since \(N_{[-1,1]}(0) = {0}\), we obtain

$$\begin{aligned} 0 = 1 - 2 \lambda _1 y_1,\quad 0 = 2 \lambda _1 y_1 + 3 \lambda _2 y_1^2, \quad \lambda _2 \ge 0, \end{aligned}$$

that is an inconsistent system of relations. Even more importantly, reasoning similarly and after some calculations, one can prove that, for any \(\varepsilon \), no KKT points of (\(\text{GNEP}_{\varepsilon }\)) exist such that \(x \ne -1\). Thus, our reformulation, for any \(\varepsilon \), leads to the correct optimal value of the upper level objective of the SBP (4), that is \(-1\). Moreover, any KKT solution of (\(\text{GNEP}_{\varepsilon }\)) is of the type \((-1, y_1, y_2, -1, -1, 0)\) with \(y_1^3 \le 0,\)\(-y_2 \le 0\) and \((y_1 + 1)^2 + (y_2 + 1)^2 - 1 - \varepsilon \le 0\); in turn, the projection of any such point on the \((x, y_1, y_2)\)-space, for \(\varepsilon \) sufficiently small, is an accurate approximation of the global solution for the original SBP (4). \(\square \)

Some connections between (optimistic) bilevel problems and a class of Nash games, different from the one proposed here, have been investigated in the recent paper [23]. As shown in “Appendix C”, (\(\text{GNEP}_{\varepsilon }\)) and the Nash game introduced in [23] are different models and, having peculiar relations with the bilevel problem, serve different purposes.

4 A simple convergent scheme for (\(\text{SBP}_\varepsilon \))

Leveraging the results in Sect. 3, one can find a stationary point of (\(\text{SBP}_\varepsilon \)) by computing an equilibrium of (\(\text{GNEP}_{\varepsilon }\)). Hence, in principle, under further conditions, one can resort to many numerical methods for solving GNEPs (see, e.g. [1, 12,13,14,15,16,17, 20, 22, 25, 30, 31, 37]). Here, exploiting the peculiar structure of (\(\text{GNEP}_{\varepsilon }\)), and without requiring any additional assumption, we propose a new simple Gauss–Seidel-like procedure to calculate one of its equilibria, which in turn is stationary for (\(\text{SBP}_\varepsilon \)). We remark that, as highlighted in e.g. [14], without such special structures, which consist in the sequential optimization of the single players’ problems, do not work properly for GNEPs.

Given the current iterate \((x^k, y^k, w^k)\), the core steps of the scheme consist in computing successively \((x^{k+1}, y^{k+1})\) by solving the strongly convex program

$$\begin{aligned} \begin{array}{cl} \underset{x,y}{\text{ minimize }} & F(x,y) + \frac{\tau }{2} \Vert (x, y) - (x^k, y^k)\Vert ^2 \\ \text{ s.t. } & x \in X, \, y \in U\\ & f(x, y) \le f(x^k, w^k) + \nabla _1 f(x^k, w^k)^{\scriptscriptstyle T}(x - x^k) + \varepsilon , \end{array}\qquad \qquad (\text{P1}_\varepsilon (x^k,y^k,w^k)) \end{aligned}$$

where \(\tau \) is a positive constant, and, then, in calculating \(w^{k+1}\) addressing the convex optimization problem

$$\begin{aligned} \begin{array}{cl} \underset{w}{\text{ minimize }} & f(x^{k+1},w) \\ \text{ s.t. } & w \in U. \end{array}\qquad \qquad (\text{ P2 }(x^{k+1})) \end{aligned}$$

Of course, requiring \(w^{k + 1}\) to be a solution of (\(\text{ P2 }(x^{k+1})\)) is equivalent to say \(w^{k + 1} \in S(x^{k+1})\). The detailed description of the method is given in the scheme of Algorithm 1.

figure a

First, we observe that \((x^{k+1},y^{k+1}) = (x^k, y^k)\) is equivalent to say that \((x^k, y^k)\) is the solution of (\(\text{ P1 }_\varepsilon (x^k,y^k,w^k)\)).

Proposition 2

A point\((\bar{x}, \bar{y})\)solves(P1\(_\varepsilon (\bar{x}, \bar{y}, \bar{w})\)), with\(\bar{w} \in S(\bar{x})\), if and only if\((\bar{x}, \bar{y}, \bar{x}, \bar{w})\)is an equilibrium of (\(\text{GNEP}_{\varepsilon }\)). In turn, \((\bar{x}, \bar{y})\)is stationary for (\(\text{SBP}_\varepsilon \)).

Proof

In view of the convexity of the game (see (ii) in Remark 1), \((\bar{x}, \bar{y}, \bar{x}, \bar{w})\) is an equilibrium of (\(\text{GNEP}_{\varepsilon }\)) if and only if

$$\begin{aligned} \nabla F(\bar{x}, \bar{y})^{\scriptscriptstyle T}((x, y) - (\bar{x}, \bar{y})) \ge 0, \qquad \nabla _2 f(\bar{x}, \bar{w})^{\scriptscriptstyle T}(w - \bar{w}) \ge 0 \end{aligned}$$

for every \((x, y, w) \in X \times U \times U\) such that \(f(x, y) \le f(\bar{x}, \bar{w}) + \nabla _1 f(\bar{x}, \bar{w})^{\scriptscriptstyle T}(x - \bar{x}) + \varepsilon \). In turn, thanks to the convexity of problems (P1\(_\varepsilon (\bar{x}, \bar{y}, \bar{w})\)) and (P2\((\bar{x})\)), the previous relations are equivalent to requiring that \((\bar{x}, \bar{y})\) is the unique solution of problem (\(\hbox {P1}_\varepsilon (\bar{x}, \bar{y}, \bar{w})\)) and \(\bar{w}\) is a solution of (\(\hbox {P2}(\bar{x})\)), that is \(\bar{w} \in S(\bar{x})\) and the claim readily follows.

The last assertion follows by Theorem 3.1. \(\square \)

The convergence properties of the scheme are summarized in Theorem 4.1.

Theorem 4.1

Let\((\bar{x}, \bar{y}, \bar{w})\)be a cluster point of the sequence\(\{(x^k, y^k, w^k)\}\)generated by Algorithm 1. Then, \((\bar{x}, \bar{y}, \bar{x}, \bar{w})\)is an equilibrium for (\(\text{GNEP}_{\varepsilon }\)) and, in turn\((\bar{x}, \bar{y})\)is stationary for (\(\text{SBP}_\varepsilon \)).

Proof

Preliminarily, we show that, for every \(k \ge 1\), \((x^k, y^k)\) is feasible for (P1\(_\varepsilon (x^k, y^k, w^k)\)). In view of step (S.1), \((x^k,y^k)\) is a solution, and a fortiori feasible, for P1\(_\varepsilon (x^{k-1},y^{k-1},w^{k-1})\), that is,

$$\begin{aligned} f(x^k,y^k) \le f(x^{k-1},w^{k-1}) + \nabla _1 f(x^{k-1},w^{k-1})^{\scriptscriptstyle T}(x^k - x^{k-1}) + \varepsilon . \end{aligned}$$
(12)

The convexity of \(\varphi \) (see Proposition 1) entails \(\varphi (x^{k-1}) + \nabla \varphi (x^{k-1})^{\scriptscriptstyle T}(x^k - x^{k-1}) \le \varphi (x^k)\). Since \(w^{k - 1} \in S(x^{k - 1})\), we get \( \varphi (x^{k - 1}) = f(x^{k - 1}, w^{k - 1})\) and \(\nabla _1 f(x^{k-1}, w^{k - 1})\)\(= \nabla \varphi (x^{k-1})\), by (7). Moreover, since \(w^k \in S(x^k)\), we have \(\varphi (x^k) = f(x^k, w^k)\). In turn,

$$\begin{aligned} f(x^{k-1}, w^{k-1}) + \nabla _1 f(x^{k - 1}, w^{k - 1})^{\scriptscriptstyle T}(x^k - x^{k - 1}) \le f(x^k, w^k). \end{aligned}$$

Combining the latter inequality with (12), we obtain

$$\begin{aligned} f(x^k,y^k) \le f(x^k,w^k) + \varepsilon = f(x^k,w^k) + \nabla _1 f(x^k,w^k)^{\scriptscriptstyle T}(x^k - x^k) + \varepsilon , \end{aligned}$$

and thus \((x^k, y^k)\) is feasible for (P1\(_\varepsilon (x^k, y^k, w^k)\)). This fact, since \((x^{k+1}, y^{k+1})\) is the optimal solution for problem (P1\(_\varepsilon (x^k, y^k, w^k)\)), implies

$$\begin{aligned} F(x^{k+1}, y^{k+1}) - F(x^k, y^k) \le -\frac{\tau }{2} \Vert (x^{k + 1}, y^{k + 1}) - (x^{k}, y^{k})\Vert ^2. \end{aligned}$$
(13)

Observing that F is bounded from below on the compact set \(X \times U\), the sequence \(\{F(x^k, y^k)\}\) converges and, thus,

$$\begin{aligned} \Vert (x^{k + 1}, y^{k + 1}) - (x^{k}, y^{k})\Vert \rightarrow 0. \end{aligned}$$
(14)

Consider the infinite set of indices \({\mathcal {K}}\) such that \((x^k,y^k,w^k) \underset{\mathcal {K}}{\rightarrow } (\bar{x}, \bar{y}, \bar{w})\). By (14), we have

$$\begin{aligned} \lim _{{\mathcal {K}} \ni k \rightarrow \infty }(x^{k + 1}, y^{k + 1}) = (\bar{x}, \bar{y}). \end{aligned}$$
(15)

Relying on Proposition 2, we are left to show that \((\bar{x}, \bar{y})\) solves (P1\(_\varepsilon (\bar{x}, \bar{y}, \bar{w})\)) and \(\bar{w} \in S(\bar{x})\). In order to do so, leveraging (15), we need to prove that the solution set-valued mapping of (P1\(_\varepsilon \)) and S are outer semicontinuous. In fact, in view of the continuity of the functions involved, the feasible set of (P1\(_\varepsilon \)), considered as the set-valued mapping \((X \times U) \cap \{(x,y) \in {\mathbb {R}}^{n_0} \times {\mathbb {R}}^{n_1} \, | \, f(x,y) \le f(\bullet , \bullet ) + \nabla _1 f(\bullet , \bullet )^{\scriptscriptstyle T}(x - \bullet ) + \varepsilon \}\), is [2, Theorem 3.1.1] outer semicontinuous and, thanks to the convexity assumption and since the Slater’s constraint qualification always holds on \(X \times U \times U\), [2, Theorem 3.1.6] inner semicontinuous relative to \(X \times U \times U\) at any point in \(X \times U \times U\): hence, it is continuous relative to \(X \times U \times U\) at any point in \(X \times U \times U\) (see the introduction for references about outer and inner semicontinuity). Then, in view of [2, Theorems 4.3.3 and 3.1.1] and [32, Corollary 5.20], the (single-valued) solution set mapping of (P1\(_\varepsilon \)) is continuous relative to \(X \times U \times U\) at any point in \(X \times U \times U\). Reasoning similarly, the set-valued mapping S is outer semicontinuous relative to X at any point in X. \(\square \)

The developments in the proof of Theorem 4.1, see in particular (14), and Proposition 2 suggest a possible stopping criterion for Algorithm 1: namely, the procedure can be stopped whenever the measure \(\Vert (x^{k + 1}, y^{k + 1}) - (x^{k}, y^{k})\Vert \) is sufficiently small (see the numerical results in Sect. 5.1).

5 Applications in economics

Bilevel programs are widely and fruitfully used to model many real-world problems in economics (see, e.g. [7]). Here we propose an application in economics involving a problem with two decision levels. Under suitable conditions, this mathematical program is proven to belong to the class of fully convex lower level SBPs.

Let us consider a market in which N firms produce the same n goods. Moreover, an independent regulator sets the selling prices of the first \(n_1\) goods, while the remaining \(n_2 = n - n_1\) ones have a fixed price. Any firm \(\nu \in \{1, \ldots , N\}\) produces the quantities \(q^\nu \in {\mathbb {R}}^{n_1}\), \(\overline{q}^\nu \in {\mathbb {R}}^{n_2}\) of the goods, with \((q^\nu , \; \overline{q}^\nu )\in [l^\nu , u^\nu ]\), where \(l^\nu \) and \(u^\nu \) are suitable bounds. On the other hand, the regulator decides the prices \(p \in {\mathbb {R}}^{n_1}\), while the fixed prices are denoted by \(\overline{p} \in {\mathbb {R}}^{n_2}\). Any firm \(\nu \) has quadratic production costs:

$$\begin{aligned} \text {Cost}_\nu (q^\nu ) \triangleq (q^\nu )^{\scriptscriptstyle T}c^\nu + \frac{1}{2} (q^\nu )^{\scriptscriptstyle T}M^\nu q^\nu + (\overline{q}^\nu )^{\scriptscriptstyle T}\overline{c}^\nu \end{aligned}$$

where \(c^\nu \in {\mathbb {R}}^{n_1}\) and \(\overline{c}^\nu \in {\mathbb {R}}^{n_2}\) are positive parameters and \(M^\nu \) is a \(n_1 \times n_1\) real symmetric positive definite matrix whose minimum (positive) eigenvalue is denoted by \(\sigma _\nu \). Assuming the presence of some shared constraints on the production levels, each firm, trying to minimize its own loss function, addresses the following optimization problem:

$$\begin{aligned} \begin{array}{cl} \underset{q^\nu , \overline{q}^\nu }{\text{ minimize }} & (q^\nu )^{\scriptscriptstyle T}(c^\nu - p) + \frac{1}{2} (q^\nu )^{\scriptscriptstyle T}M^\nu q^\nu + (\overline{q}^\nu )^{\scriptscriptstyle T}(\overline{c}^\nu - \overline{p})\\ \text{ s.t. } & g(q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) \le 0 \\ & l^\nu \le (q^\nu , \; \overline{q}^\nu ) \le u^\nu , \end{array} \end{aligned}$$
(16)

where \(g : {\mathbb {R}}^{nN} \rightarrow {\mathbb {R}}^m\) is a convex function that models the shared constraints.

We consider the case in which the firms do not cooperate and play simultaneously and rationally. In this case, given any prices p, we model the game played by the firms as a GNEP. In particular, the GNEP defined by (16) is a generalized potential game, see e.g. [21, 33]. It is well known that, given p, any solution of the following convex optimization problem

$$\begin{aligned} \begin{array}{cl} \underset{q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N}{\text{ minimize }} & \displaystyle \sum _{\nu = 1}^N \left( (q^\nu )^{\scriptscriptstyle T}(c^\nu - p) + \frac{1}{2} (q^\nu )^{\scriptscriptstyle T}M^\nu q^\nu + (\overline{q}^\nu )^{\scriptscriptstyle T}(\overline{c}^\nu - \overline{p}) \right) + v(p) \\ \text{ s.t. } & g(q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) \le 0 \\ & l^\nu \le (q^\nu , \; \overline{q}^\nu ) \le u^\nu , \quad \nu = 1, \ldots , N, \end{array} \end{aligned}$$
(17)

for any function \(v : {\mathbb {R}}^{n_1} \rightarrow {\mathbb {R}}\) that depends only on p, is an equilibrium of GNEP (16). Note that the additional term v(p) is introduced in (17) in order to have a fully convex objective function in the same spirit of Example 1; see the forthcoming discussion on how to explicitly choose v(p).

The aim of the regulator is to set the prices \(p \in [\bar{l}, \bar{u}]\) to pursue two different targets:

obj1:

maintaining p as close as possible to its lower bounds \(\bar{l}\);

obj2:

entailing the production quantities of the firms (\(q^1, \ldots , q^N\)) that satisfy the most the customers’ demand \(d \in {\mathbb {R}}^{n_1}\) (obj2).

By resorting to classical techniques for multi-objective programming, the regulator minimizes the loss function

$$\begin{aligned} \displaystyle \kappa \left\| p-\bar{l}\right\| ^2 + (1 - \kappa ) \left\| \sum _{\nu = 1}^N q^\nu - d\right\| ^2, \end{aligned}$$

where \(\kappa \in [0, 1]\) is a parameter that suitably weights the two objectives. Assuming an optimistic point of view, the regulator solves the following SBP:

$$\begin{aligned} \begin{array}{cl} \underset{p, q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N}{\text{ minimize }} & \displaystyle \kappa \left\| p-\bar{l}\right\| ^2 + (1 - \kappa ) \left\| \sum _{\nu = 1}^N q^\nu - d\right\| ^2\\ \text{ s.t. } & \bar{l} \le p \le \bar{u} \\ & g(q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) \le 0 \\ & l^\nu \le (q^\nu , \; \overline{q}^\nu ) \le u^\nu , \quad \nu = 1, \ldots , N \\ & \sum _{\nu = 1}^N \left( (q^\nu )^{\scriptscriptstyle T}(c^\nu - p) + \frac{1}{2} (q^\nu )^{\scriptscriptstyle T}M^\nu q^\nu + (\overline{q}^\nu )^{\scriptscriptstyle T}(\overline{c}^\nu - \overline{p}) \right) + v(p) \le \varphi (p), \end{array} \end{aligned}$$
(18)

where \(\varphi \) is the value function of problem (17). We note that problem (18) is an instance of the general framework (SBP), where

  • \(x = p\), \(y = (q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N)\)

  • \(F(p, q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) = \kappa \left\| p-\bar{l}\right\| ^2 + (1 - \kappa ) \left\| \sum _{\nu = 1}^N q^\nu - d\right\| ^2\)

  • \(X = [\bar{l}, \bar{u}]\), \(U = \left\{ (q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) \, | \, g(q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) \le 0,\right. \)

    \(\left. (q^\nu , \overline{q}^\nu ) \in [l^\nu , u^\nu ],\right. \)\(\left. \nu = 1, \ldots , N \right\} \)

  • \(f(p, q^1, \ldots , q^N, \overline{q}^1, \ldots , \overline{q}^N) = \sum _{\nu = 1}^N \left( (q^\nu )^{\scriptscriptstyle T}(c^\nu - p) + \frac{1}{2} (q^\nu )^{\scriptscriptstyle T}M^\nu q^\nu \right) \)

    \(+ (\overline{q}^\nu )^{\scriptscriptstyle T}(\overline{c}^\nu - \overline{p}) + v(p)\).

We observe that function v is most useful (see Example 1). On the one hand, its presence does not alter in any way the problem since v is not depending on the quantities \((q^\nu , \overline{q}^\nu )_{\nu = 1}^N\). On the other hand, it allows us to have a fully convex lower level objective. In fact, by choosing \(v(p) \triangleq \frac{\beta }{2} p^{\scriptscriptstyle T}p\), and setting \(\beta \ge \frac{N}{\min _{\nu \in \{1, \ldots , N\}}\{\sigma _\nu \}}\), we obtain (see (3) in Example 1) \(\nabla ^2 f(p, q^1, \ldots , q^N,\overline{q}^1, \ldots , \overline{q}^N) \succeq 0\), that is, a fully convex f. Thus, problem (18) is a fully convex lower level SBP. Finally, we note that the lower level problem (17), for any fixed p, has in general a non unique optimal solution. From this respect, we recall that in this paper we take the so-called optimistic point of view, as a major departure from the pessimistic robust counterpart (see, e.g. [24]) where the leader wishes to hedge against the worst possible response of the follower.

5.1 Numerical experiments

The numerical results reported here show that the points provided by our method, when applied to problem (18), are not only stationary for its relaxed version but, in most cases, good approximations of its global optima.

All the experiments were carried out on an Intel Core i7-4702MQ CPU @ 2.20GHz x 8 with Ubuntu 14.04 LTS 64-bit and by using AMPL. As optimization solver we used SNOPT 7.2-8 with default options.

At the lower level, as far as the potential game is concerned, we consider a market with \(N = 3\) firms, each producing a total amount of \(n_1 = 20\) (10 of low quality (LQ) and 10 of high quality (HQ)) and \(n_2 = 10\) goods (5 of low quality (LQ) and 5 of high quality (HQ)).

Data were randomly generated by using the uniform distribution according to Table 1: consistently, we considered three different instances A, B and C.

Table 1 Problem data
Full size table

We remark that in our test problems \(M^\nu \) is assumed to be diagonal.

The lower level affine constraints \(g: {\mathbb {R}}^{90} \rightarrow {\mathbb {R}}^4\) model the following requirements: on the one hand, the total amount of HQ goods (qHQ) must be, at least, \(33\%\) of the goods produced by the industry (qtot). On the other hand, the total amount of goods produced by each firm (q1, q2, q3) must not exceed a threshold of \(40\%\) of the quantity of goods produced by the industry (qtot).

We remark that, to take into account the different scale between the objectives, we multiply (obj1) \(\Vert p - \bar{l}\Vert ^2\) by 1e+3. Also, we set \(\alpha = 10\) and \(\beta = \frac{N}{\min _{\nu \in \{1, \ldots , N\}}\{\sigma _\nu \}}\). We consider \(\varepsilon =\) 1e-2: this amounts to having a tolerance (in the approximated problem (\(\text{SBP}_\varepsilon \))) less than one cent with respect to total profits ranging from 1e+4 to 1e+5 of the currency (see profit1, profit2, profit3 in Tables 2, 3 and 4).

Taking in to account the theoretical results in Sect. 4, we stop the algorithm iterations when the distance \(\Vert (x^{k+1}, y^{k+1}) - (x^k, y^k)\Vert _{\infty }\) is less than 1e-3. Finally, we adopt \((x^0, y^0) = (\bar{l}, w^0)\) as starting point of our procedure; we make this choice in order to start from a point that achieves the first objective (obj1) of the regulator, that is setting the prices as low as possible.

Concerning Tables 2, 3 and 4, we consider three different values for \(\kappa \):

  • \(\kappa =\) 1e–4, which corresponds to having the regulator mainly interested in satisfying the customers’ demand (obj2);

  • \(\kappa = 1 -\) 1e–4, which corresponds to having the regulator mainly interested in maintaining p as close as possible to \(\bar{l}\) (obj1);

  • \(\kappa = 0.5\), which corresponds to having equally-weighted preferences.

We report the total number of iterations (iter) and the CPU time in seconds (time) needed by Algorithm 1 in order to meet the stopping criterion. The numerical results show that, in each instance of the problem that we have considered and for \(\kappa =\) 1e–4 and \(1-1\)e–4, the point provided by our procedure is not only stationary for (\(\text{SBP}_\varepsilon \)) but also a good approximation of a global optimum for problem (18), since the optimal value for obj1, when \(\kappa = 1-1\)e–4, and for obj2, when \(\kappa =\)1e–4, is clearly 0.

Table 2 Numerical results for instance A
Full size table
Table 3 Numerical results for instance B
Full size table
Table 4 Numerical results for instance C
Full size table

6 Conclusions

We identify a nontrivial and broad class of SBPs that turns out to be numerically tractable. As witnessed by Sect. 5, this class of problems is of practical interest since it can be employed to model complicated multi-agent hierarchical real-world situations. More specifically, we introduce a novel GNEP reformulation of the original bilevel problem. We remark that this reformulation is completely different from the model presented in [23], as shown in “Appendix C”. In fact, among other things, as a major departure from [23], here, leveraging the distinctive properties of the novel GNEP reformulation, we are able to devise one of the first (as far as we are aware) efficient algorithmic procedures for SBPs.

As further developments, we aim at extending our approach to multi-leader-follower games. In fact, when applied to these more complicated contexts, our one-level GNEP reformulation technique allows one to put at the same level all the agents (leaders and followers) in order to practically tackle these problems.