Solving quasi-variational inequalities via their KKT conditions

Abstract

We propose to solve a general quasi-variational inequality by using its Karush–Kuhn–Tucker conditions. To this end we use a globally convergent algorithm based on a potential reduction approach. We establish global convergence results for many interesting instances of quasi-variational inequalities, vastly broadening the class of problems that can be solved with theoretical guarantees. Our numerical testings are very promising and show the practical viability of the approach.

1 Introduction

We propose and analyze a globally convergent algorithm for the solution of a finite-dimensional quasi-variational inequality (QVI), which is the problem of finding a point $x^* \in K(x^*)$ such that

$$\begin{aligned} F(x^*)^{\scriptscriptstyle T}(y-x^*) \ge 0, \qquad \forall y \in K(x^*), \end{aligned}$$

(1)

where $F:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^n$ is a (point-to-point) mapping and $K:{\mathbb{R }}^n \rightrightarrows {\mathbb{R }}^n$ is a point-to-set mapping with closed and convex images.

QVIs were introduced by Bensoussan and Lions in a series of papers [4–6] in connection with the study of impulse control problems and soon they turned out to be a powerful modeling tool capable of describing complex equilibrium situations that can appear in such different fields as generalized Nash games (see e.g. [3, 24, 27, 44]), mechanics (see e.g. [2, 7, 25, 29, 38, 39]), economics (see e.g. [27, 48]), statistics (see e.g. [28]), transportation (see e.g. [8, 11]), and biology (see e.g. [23]). We refer the reader to the monographs of Mosco [33] and Baiocchi and Capelo [2] for a more compehensive analysis of QVIs.

In spite of their modeling power, relatively few studies have been devoted to the numerical solution of finite-dimensional QVIs; a topic which, beside being of great interest in its own, also forms the backbone of solution methods for infinite-dimensional QVIs. Motivated by earlier research on the implicit complementarity problem [33, 41, 42], Chan and Pang introduced in [9] what is probably the first globally convergent algorithm for a QVI. In this seminal paper, the authors use a fixed point argument to prove convergence of a projection-type algorithm in the case in which $K(x) = c(x) + Q$, where $Q$ is a closed convex set and $c:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^n$ a mapping satisfying certain conditions. It is safe to say that practically all subsequent papers, where globally convergent algorithms are analyzed, consider variants or extensions of the basic setting proposed in [9] and also follow the fixed point approach, see e.g. [34, 35, 45, 45, 47] and references therein. In a departure from this setting, Pang and Fukushima [44] proposed a sequential penalty approach to general QVIs. The method in [44] reduces the solution of a QVI to the solution of a sequence of variational inequalities (VIs); however, even if this approach is very interesting and promising, its global convergence properties are in jeopardy since they ultimately hinge of the capability of solving a sequence of possibly very challenging VIs. More recently, Fukushima [20] studied a class of gap functions for QVIs, reducing the solution of a QVI to the global minimization of a nondifferentiable gap function, but no algorithms are explicitly proposed in [20] (see [30] for a further and more detailed application of this approach in a specialized game setting). This essentially completes the picture of globally convergent proposals for the solution of QVIs. We also mention that Outrata and co-workers studied some interesting local Newton methods, see [38–40], but the globalization of these methods is not discussed.

In this paper we propose a totally different approach to the solution of a QVI. Assuming that the feasible set mapping $K(\cdot )$ is described by a finite number of parametric inequalities, we consider the Karush–Kuhn–Tucker (KKT) conditions of the QVI, reformulate them as a system of constrained equations and then apply an interior-point method. It turns out that the convergence properties of the resulting algorithm depend essentially on the nonsingularity of a certain Jacobian matrix $J\!H$. Our main contributions are therefore:

• An in-depth analysis of the nonsingularity of $J\!H$, showing that global convergence of the proposed method can be obtained in the case in which $K(x) = c(x) + Q$, but also in many other situations covering a wide array of new and significant settings, thus enlarging considerably the range of QVIs that it is possible to solve with theoretical guarantees;

• A discussion of the boundedness of the sequence generated by the algorithm;

• A numerical testing on a set of test problems demonstrating the effectiveness of the new method and its robustness even if compared to the PATH solver [19]. We remark that our set of test problems is by far the largest in the literature and includes problems with up to 4,900 variables and 4,900 constraints.

The approach we consider in this paper is based on an interior-point-like framework introduced in [32] and it can be viewed as a generalization of the method proposed in [14] for the solution of Generalized Nash Equilibrium Problems (GNEPs). Indeed, it is well-known that, under mild conditions, GNEPs can be reformulated as QVIs, so that the extension might appear quite natural. But we remark that the technical issues that we must deal with when facing a QVI are considerably different from those encountered in the analysis of GNEPs. This forced us to take a quite different path from that used in [14] and, as a consequence, the results in this paper are considerably deeper than those in [14], and the analysis is more sophisticated. This is shown also by the fact that, when we specialize some of the results in this paper to the GNEP setting, we improve on the results of [14].

The paper is organized as follows. In the next section, we first describe in detail our setting and then, based on the general framework introduced in [32], introduce the interior-point algorithm along with its main convergence properties. In Sect. 3, we identify several classes of QVIs for which the nonsingularity of $J\!H$ can be established. Section 4 deals with the boundedness of the sequence generated by our algorithm while in Sect. 5 we report the results of our numerical experimentation. Some definitions and auxiliary results are discussed and proved in the “Appendix”.

Notation

${\mathbb{R }}_+$ denotes the set of nonnegative numbers, while ${\mathbb{R }}_{++}$ is the set of positive numbers. The symbol $\Vert v\Vert$ denotes the Euclidean norm of a vector $v \in {\mathbb{R }}^n$. Similarly, given a matrix $M \in {\mathbb{R }}^{m\times n} , \,\Vert M\Vert$ is the spectral norm, i.e. the norm induced by the Euclidean vector norm. We recall that $\Vert M\Vert = \max \{ \sqrt{\lambda } \mid \lambda$ is an eigenvalue of $M^{\scriptscriptstyle T}M\}$. The spectral norm is compatible with the Euclidean norm in the sense that $\Vert M v\Vert \le \Vert M\Vert \Vert v\Vert$. For a differentiable mapping $F: {\mathbb{R }}^n \rightarrow {\mathbb{R }}^m$, we denote its Jacobian at $x$ by $J\!F(x)$, whereas $\nabla F(x)$ is the transposed Jacobian. Similarly, when $F: {\mathbb{R }}^n \times {\mathbb{R }}^n \rightarrow {\mathbb{R }}^m$ depends on two sets of variables $(y,x)$, the notation $J_y F(y,x)$ and $\nabla _y F(y,x)$ denote the corresponding partial Jacobian and its transpose, respectively, where the derivatives are taken only with respect to $y$. A matrix $A \in {\mathbb{R }}^{n \times n}$ (not necessarily symmetric) is positive semidefinite (definite) if $x^{\scriptscriptstyle T}A x \ge 0$ holds for all $x \in {\mathbb{R }}^n$ ($x^{\scriptscriptstyle T}A x > 0$ for all $x \in {\mathbb{R }}^n \setminus \{ 0 \}$), whereas $A \in {\mathbb{R }}^{n \times n}$ is a $P_0$-matrix ($P$-matrix) if, for each $x \ne 0$, there exists an index $j \in \{ 1, \ldots , n \}$ such that $x_j \ne 0$ and $x_j [Ax]_j \ge 0$ ($x_j [Ax]_j > 0$). Note that every positive semidefinite (definite) matrix is a $P_0$-matrix ($P$-matrix). For more details, we refer to [18]. The symbol $\mu _m(A)$ denotes the minimum eigenvalue of a square, symmetric matrix $A$, whereas $\mu _m^+(A)$ denotes its minimum positive eigenvalue. Similarly, $\mu _m^s(A)$ indicates the minimum eigenvalue of the symmetric part of the square matrix $A$, that is the minimum eigenvalue of the matrix $\frac{1}{2}(A^{\scriptscriptstyle T}+ A)$. Finally, given two vectors $x, y \in {\mathbb{R }}^n$, we denote by $x \circ y := ( x_i y_i )_{i=1}^n \in {\mathbb{R }}^n$ their Hadamard (componentwise) product, by $x^{-1}$ its componentwise inverse vector $\big ( \frac{1}{x_1}, \ldots , \frac{1}{x_n} \big )$ and by $y/x := y \circ x^{-1}$ the componentwise quotient of two vectors (provided that $x_i \ne 0$ for all $i$).

2 Problem definition and interior-point algorithm

Let $F:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^n$ be a (point-to-point) continuous mapping and $K:{\mathbb{R }}^n \rightrightarrows {\mathbb{R }}^n$ a point-to-set mapping with closed and convex images. The Quasi-Variational Inequality QVI $(K,F)$ is the problem of finding a point $x^* \in K(x^*)$ such that (1) holds. For sake of simplicity, we always assume that all functions involved are defined over ${\mathbb{R }}^n$, even if this request could easily be weakened. A particularly well known and studied case occurs when $K(x)$ is actually independent of $x$, so that, for all $x, \,K(x) = K$ for some closed convex set $K$. In this case, the QVI becomes the Variational Inequality VI $(K,F)$, that is the problem of finding $x^* \in K$ such that $F(x^*)^{\scriptscriptstyle T}(y-x^*) \ge 0, \, \forall y \in K.$ For this latter problem, an extensive theory exists, see for example [18].

In most practical settings, the point-to-set mapping $K$ is defined through a parametric set of inequality constraints:

$$\begin{aligned} K(x) := \{ y \in {\mathbb{R }}^n \mid g(y,x) \le 0 \}, \end{aligned}$$

(2)

where $g: \mathbb R ^n \times \mathbb R ^n \rightarrow \mathbb R ^m$. We will use the following assumption.

Assumption 1

$g_i(\cdot , x)$ is convex and continuously differentiable on ${\mathbb{R }}^n$, for each $x\in {\mathbb{R }}^n$ and for each $i=1, \ldots , m$.

The convexity of $g_i(\cdot , x)$ is obviously needed in order to guarantee that $K(x)$ be convex, while we require the differentiability assumption to be able to write down the KKT conditions of the QVI. We say that a point $x\in {\mathbb{R }}^n$ satisfies the KKT conditions if multipliers $\lambda \in {\mathbb{R }}^m$ exist such that

$$\begin{aligned} \begin{array}{l} F(x) + \nabla _y g(x,x) \lambda \,=\, 0, \\ 0 \,\le \, \lambda \,\perp \, g(x,x) \!\le \! 0. \end{array} \end{aligned}$$

(3)

Note that $g(x,x) \le 0$ means that $x\in K(x)$ and recall that $\nabla _y g(x,x)$ indicates the partial transposed Jacobian of $g(y,x)$ with respect to $y$ evaluated at $y=x$. These KKT conditions parallel the classical KKT conditions for a VI, see [18], and it is quite easy to show the following result, whose proof we omit.

Theorem 1

Suppose Assumption 1 holds. If a point $x$, together with a suitable vector $\lambda \in {\mathbb{R }}^m$ of multipliers, satisfies the KKT system (3), then $x$ is a solution of the QVI $(K,F)$. Vice versa, if $x$ is a solution of the QVI $(K,F)$ and the constraints $g(\cdot , x)$ satisfy any standard constraint qualification, then multipliers $\lambda \in {\mathbb{R }}^m$ exist such that the pair $(x, \lambda )$ satisfies the KKT conditions (3).

In the theorem above, by “any standard constraint qualification” we mean any classical optimization constraint qualification for $g(\cdot , x)$ at $y=x$ such as the linear independence of the active constraints, the Mangasarian–Fromovitz constraint qualification, Slater’s one and so on.

The KKT conditions (3) are central to our approach as our solution algorithm aims at finding KKT points of the QVI $(K,F)$. In view of Theorem 1, the solution of these KKT conditions is essentially equivalent to the solution of the underlying QVI and, in any case whenever we can find a solution of the KKT conditions, we are sure that the corresponding $x$-part solves the QVI itself.

As we already mentioned, we propose to solve the KKT conditions (3) by an interior-point method designed to solve constrained systems of equations. In order to reformulate system (3) as a constrained system of equations (CE for short), we introduce slack variables $w\in {\mathbb{R }}^m$ and consider the CE system

$$\begin{aligned} H(z) = 0, \quad z = (x, \lambda , w ) \in Z \end{aligned}$$

(4)

with

$$\begin{aligned} H(x,\lambda ,w) := \left( \begin{array}{c} L(x,\lambda ) \\ h(x) + w \\ \lambda \circ w \end{array} \right) \end{aligned}$$

and where

$$\begin{aligned} L(x,\lambda ) := F(x) + \nabla _y g(x,x) \lambda , \qquad h(x) := g(x,x) \end{aligned}$$

(5)

and

$$\begin{aligned} Z := \{ z = (x, \lambda , w) \mid x \in {\mathbb{R }}^n, \lambda \in \mathbb R ^m_+, w \in \mathbb R ^m_+\}. \end{aligned}$$

It is clear that the couple $(x, \lambda )$ solves system (3) if and only if $(x, \lambda )$, together with a suitable $w$, solves the CE (4). From now on, we will aim at solving the CE (4) by the interior-point method described next.

Let $p:{\mathbb{R }}^{n} \times {\mathbb{R }}^{m}_{++}\times {\mathbb{R }}^m_{++} \rightarrow {\mathbb{R }}$ be the function

$$\begin{aligned}&p (u,v) := \zeta \log (\Vert u\Vert ^2 \, + \, \Vert v\Vert ^2) - \sum _{i=1}^{2m} \log (v_i),\\&( u, v ) \in {\mathbb{R }}^{n} \times {\mathbb{R }}^{m}_{++}\times {\mathbb{R }}^m_{++}, \quad \zeta > m, \end{aligned}$$

and let

$$\begin{aligned} {\varvec{\psi }}(z) := p(H(z)) \end{aligned}$$

be the potential function of the CE, which is defined for all

$$\begin{aligned} z \in Z_I:= H^{-1}({\mathbb{R }}^{n} \times {\mathbb{R }}^{m}_{++}\times {\mathbb{R }}^m_{++}) \cap \mathrm{int}\, Z, \end{aligned}$$

where $\mathrm{int}Z$ denotes the interior of the set $Z$. In order to be able to define our potential reduction interior-point method we need some further differentiability conditions.

Assumption 2

$F(x), \,h(x)$ and $\nabla _yg(x,x)$ are continuously differentiable on ${\mathbb{R }}^n$.

The following algorithm is precisely the interior-point method from [32]; see also [18] for further discussion and [14] for an inexact version.

Algorithm 1 is well-defined as long as the Jacobians $J\!H(z^k)$ in (6) are nonsingular. Actually, the following theorem, which can be found in [32] and [18], shows that this condition also guarantees that every limit point of the sequence generated by the algorithm is a solution.

Theorem 2

Suppose that Assumptions 1 and 2 hold. Assume that $J\!H(z)$ is nonsingular for all $z \in Z_I$, and that the sequence $\{ \rho _k \}$ from (S.2) of Algorithm 1 satisfies the condition $\limsup _{k \rightarrow \infty } \rho _k < 1$. Let $\{ z^k \}$ be any sequence generated by Algorithm 1. Then the following statements hold:

• (a) the sequence $\{ H(z^k) \}$ is bounded;

• (b) any accumulation point of $\{ z^k \}$ is a solution of CE (4).

In view of Theorem 2, the main question we must answer in order to make our approach viable is: for which classes of QVIs can we guarantee that the Jacobian matrices $J\!H(z)$ are nonsingular for all $z \in Z_I$? A related, albeit practically less crucial, question is whether we can guarantee that the sequence $\{ z^k \}$ generated by Algorithm 1 is bounded. This obviously would guarantee that the algorithm actually has at least a limit point and therefore that a solution is certainly found. The first question will be answered in detail in the next section, whereas the second question will be dealt with in Sect. 4.

3 Nonsingularity conditions

As noted before, the main topic in order to guarantee global convergence of Algorithm 1 to a solution of CE (4) is the nonsingularity of $J\!H(z)$. The structure of this Jacobian is given by

$$\begin{aligned} J\!H(x,\lambda ,w)=\left(\begin{array}{ccc} J_x L(x,\lambda )&\quad \nabla _y g(x,x)&\quad 0 \\ J_x h(x)&\quad 0&\quad I \\ 0&\quad \mathop {\mathrm{diag}}(w)&\quad \mathop {\mathrm{diag}}(\lambda ) \end{array}\right). \end{aligned}$$

This section is devoted entirely to the study of QVI classes for which the nonsingularity of $J\!H$ can be established. It is not too difficult to give conditions that guarantee the nonsingularity of $J\!H$; what is less obvious is how we can establish sensible and significant conditions for interesting classes of QVIs. This we achieve in two stages: in the next subsection we give several sufficient or necessary and sufficient conditions for the nonsingularity of $J\!H$ which are then used in the following subsections to analyze various QVI classes. In particular, we will discuss and establish nonsingularity results for the following QVI classes:

• Problems where $K(x) = c(x) + Q$ (the so called “moving set” case, already mentioned in the introduction);

• Problems where $K(x)$ is defined by a linear system of inequalities with a variable right-hand side;

• Problems where $K(x)$ is defined by box constraints with parametric upper and lower bounds;

• Problems where $K(x)$ is defined by “binary constraints”, i.e. parametric inequalities $g(x, y) \le 0$ with each $g_i$ actually depending only on two variables: $x_j$ and $y_j$;

• Problems where $K(x)$ is defined by bilinear constraints.

While we refer the reader to the following subsections for a more accurate description of the problem classes, we underline that, as far as we are aware of and with the exception of the moving set case, these problem classes are all new and we can establish here for the first time convergence results, according to Theorem 2.

3.1 General nonsingularity conditions

The results in this subsection do not make explicit reference to a specific structure of the QVI and, in particular, of the feasible set mapping $K$. However, they are instrumental in proving the more specific results in the following subsections. The first result we present is a necessary and sufficient condition for the nonsingularity of $J\!H$.

Theorem 3

Suppose that Assumptions 1 and 2 hold. Let $(x, \lambda , w ) \in {\mathbb{R }}^n \times {\mathbb{R }}^m_{++} \times {\mathbb{R }}^m_{++}$ be given. Then the matrix

$$\begin{aligned} N(x,\lambda ,w) := J_xL(x,\lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x) \end{aligned}$$

(8)

is nonsingular if and only if $J\!H (x,\lambda ,w)$ is nonsingular.

Proof

We first prove the only-if-part. Let $q = \big ( q^{(1)}, q^{(2)}, q^{(3)} \big )$ be a suitably partitioned vector such that $J\!H(x,\lambda ,w) q = 0$. This equation can be rewritten in partitioned form as

$$\begin{aligned} J_x L(x, \lambda ) q^{(1)} + \nabla _y g(x,x) q^{(2)}&= 0, \end{aligned}$$

(9)

$$\begin{aligned} J_x h(x) q^{(1)} + q^{(3)}&= 0, \end{aligned}$$

(10)

$$\begin{aligned} \mathop {\mathrm{diag}}(w) q^{(2)} + \mathop {\mathrm{diag}}(\lambda ) q^{(3)}&= 0. \end{aligned}$$

(11)

Solving (11) for $q^{(3)}$ gives

$$\begin{aligned} q^{(3)} = - \mathop {\mathrm{diag}}\big ( \lambda ^{-1} \circ w \big ) q^{(2)}. \end{aligned}$$

(12)

Inserting this expression into (10) yields

$$\begin{aligned} J_x h(x) q^{(1)} - \mathop {\mathrm{diag}}\big ( \lambda ^{-1} \circ w \big ) q^{(2)} = 0 \end{aligned}$$

which, in turn, gives

$$\begin{aligned} q^{(2)} = \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x) q^{(1)}. \end{aligned}$$

(13)

Substituting this expression into (9) finally yields

$$\begin{aligned} \left[ J_x L(x, \lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x) \right] q^{(1)} = 0. \end{aligned}$$

However, the matrix in brackets is precisely the matrix $N(x, \lambda , w)$ from (8) and, therefore, nonsingular. Hence, it follows that $q^{(1)} = 0$ which then also implies $q^{(2)} = 0$ and $q^{(3)} = 0$.

Now, to prove the if-part, we show that if $N(x,\lambda ,w)$ is singular, then $J\!H(x,\lambda ,w)$ is singular, too. If $N(x,\lambda ,w)$ is singular, there exists a nonzero vector $q^{(1)}$ such that

$$\begin{aligned} \left[ J_x L(x, \lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x) \right] q^{(1)} = 0. \end{aligned}$$

Now, let $q^{(2)}$ and $q^{(3)}$ be vectors defined by (13) and (12), respectively. Then (9)–(11) hold, and hence $J\!H(x,\lambda ,w) q = 0$ for $q = \big ( q^{(1)}, q^{(2)}, q^{(3)} \big ) \ne 0$. This shows that $J\!H(x,\lambda ,w)$ is singular and, therefore, completes the proof. $\square$

We next state a simple consequence of Theorem 3.

Corollary 1

Suppose that Assumptions 1 and 2 hold and let $(x, \lambda , w ) \in {\mathbb{R }}^n \times {\mathbb{R }}^m_{++} \times {\mathbb{R }}^m_{++}$ be given. Suppose that $J_x L(x, \lambda )$ is positive definite and one of the following conditions holds:

• (a) $\nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x)$ is positive semidefinite, or

• (b) $\nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x g(x,x)$ is positive semidefinite.

Then $J\!H(x, \lambda , w)$ is nonsingular.

Proof

In view of Theorem 3, it suffices to show that the matrix $N(x, \lambda , w)$ from (8) is nonsingular. Since $J_x L(x, \lambda )$ is positive definite by assumption, the statement is trivially satisfied under condition (a). Hence, suppose that (b) holds. Since $h(x) = g(x,x)$, we have $J_xh(x) = J_y g(x,x) + J_x g(x,x)$. This implies

$$\begin{aligned} N(x, \lambda , w)&= J_x L(x,\lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}\big (w^{-1} \circ \lambda \big ) J_x h(x) \\&= J_x L(x, \lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_y g(x,x) \\&+\, \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x g(x,x). \end{aligned}$$

Now, the first term $J_x L(x, \lambda )$ in the last expression is positive definite by assumption, the second term is obviously positive semidefinite since $\lambda , w > 0$, and the third term is positive semidefinite by condition (b). Consequently, $N(x, \lambda , w)$ is positive definite, hence nonsingular. $\square$

Note that the previous proof actually shows that condition (b) from Corollary 1 implies condition (a) which, therefore, is a weaker assumption in general, whereas condition (b) might be easier to verify in some situations.

We now state another consequence of Theorem 3.

Corollary 2

Suppose that Assumptions 1 and 2 hold and let $(x, \lambda , w) \in {\mathbb{R }}^n \times {\mathbb{R }}^m_{++} \times {\mathbb{R }}^m_{++}$ be given. Suppose that $J_x L(x,\lambda )$ is nonsingular and

$$\begin{aligned} M(x,\lambda ) := J_x h(x) J_x L(x,\lambda )^{-1} \nabla _y g(x,x) \end{aligned}$$

is a P$_0$-matrix. Then $J\!H(x, \lambda , w)$ is nonsingular.

Proof

For notational simplicity, let us write

$$\begin{aligned} A(x,\lambda ,w) := J_x L(x,\lambda )^{-1} \nabla _y g(x,x) \mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big ) J_x h(x). \end{aligned}$$

We note that $\mathop {\mathrm{diag}}\big ( w^{-1} \circ \lambda \big )$ is a positive definite diagonal matrix and can therefore be written as a product $D D$, where $D$ is another positive definite diagonal matrix.

We have that the matrix $N(x,\lambda ,w)$ is nonsingular if and only if $I + A(x,\lambda ,w)$ is nonsingular. In turn, recalling that $\mu$ is an eigenvalue of $A(x,\lambda ,w)$ if and only if $1 + \mu$ is an eigenvalue of $I + A(x,\lambda ,w)$, we see that $N(x,\lambda ,w)$ is surely nonsingular if $A(x,\lambda ,w)$ has all real eigenvalues nonnegative. But it is well known that, given two square matrices $A, B$, the matrix product $AB$ has the same eigenvalues as the matrix product $BA$, see [26, Theorem 1.3.20], hence it follows that $A(x,\lambda ,w)$ has the same eigenvalues as $D J_x h(x) J_x L(x,\lambda )^{-1} \nabla _y g(x,x) D$ which is exactly the matrix $D M(x,\lambda ) D$. By assumption, we have that $M(x,\lambda )$ is a $P_0$ matrix, hence $D M(x,\lambda ) D$ is also a $P_0$ matrix since $D$ is diagonal and positive definite, and then it has all real eigenvalues nonnegative, see [10, Theorem 3.4.2]. This completes the proof.$\square$

The remaining part of this section specializes the previous results to deal with specific constraint structures.

3.2 The moving set case

As we mentioned in the Introduction, this is the most studied class of problems in the literature and (variants and generalizations apart) essentially the only class of problems for which clear convergence conditions are available. In this class of problems, the feasible mapping $K(\cdot )$ is defined by a closed convex set $Q \subseteq {\mathbb{R }}^n$ and a “trajectory” described by $c:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^n$ according to:

$$\begin{aligned}K(x) = c(x) + Q. \end{aligned}$$

In order to proceed in our analysis, we suppose that $Q$ is defined by a set of convex inequalities:

$$\begin{aligned} Q\, =\, \{x\in {\mathbb{R }}^n | q(x) \le 0\}, \end{aligned}$$

where $q:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^m$ and each $q_i$ is convex on ${\mathbb{R }}^n$. It is easy to see that, in this setting, we have

$$\begin{aligned} K(x) = \{ y \in \mathbb R ^n \mid q(y - c(x)) \le 0 \}. \end{aligned}$$

(14)

By exploiting this structure, we can prove the following theorem.

Theorem 4

Let $K(x)$ be defined as in (14), with $q_i$ convex for every $i=1, \ldots , m$. Let a point $x\in {\mathbb{R }}^n$ be given and assume that around $x$ it holds that $F$ and $c$ are $C^1$ and $q$ is $C^2$. Suppose further that $J\!F(x)$ is nonsingular and that

$$\begin{aligned} \Vert J\!c(x) \Vert \, \le \,\frac{ \,\mu _m^s (J\!F(x)^{-1})\,}{\Vert J\!F(x)^{-1}\Vert }. \end{aligned}$$

(15)

Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

Proof

We are going to show that the conditions from Theorem 3 are satisfied. First of all note that the hypotheses imply Assumptions 1 and 2. Taking into account (14), we have, using the notation in (2) and (5),

$$\begin{aligned} g(y,x) = q(y - c(x)), \quad h(x) = q(x - c(x)) \end{aligned}$$

and, hence,

$$\begin{aligned} \nabla _y g(x,x)\,=\, \nabla q (x - c(x)),\qquad J_x h(x) \,=\, J q(x-c(x))(I-J c(x)). \end{aligned}$$

Therefore we can write

$$\begin{aligned} N(x,\lambda ,w) \,=\, J\!F(x) + \bar{S}(I-J c(x)), \end{aligned}$$

where

$$\begin{aligned} \bar{S}\,=\, \sum _{i=1}^m \lambda _i \nabla ^2 q_i(x-c(x)) + \nabla q (x - c(x)) \mathop {\mathrm{diag}}(w^{-1} \circ \lambda ) J q(x-c(x)). \end{aligned}$$

Note that, for any positive $\lambda$ and $w, \,\bar{S}$ is positive semidefinite and symmetric. Therefore, we can write $\bar{S} = S S^{\scriptscriptstyle T}$ for some suitable square matrix $S$. Recalling that $J\!F(x)$ is nonsingular by assumption, we have that the matrix $N(x,\lambda ,w)$ is nonsingular if and only if

$$\begin{aligned} I + J\!F(x)^{-1} SS^{\scriptscriptstyle T}(I-J c(x)) \end{aligned}$$

is nonsingular. In turn, since $\mu$ is an eigenvalue of $J\!F(x)^{-1} SS^{\scriptscriptstyle T}(I-J c(x))$ if and only if $1 + \mu$ is an eigenvalue of $I + J\!F(x)^{-1} SS^{\scriptscriptstyle T}(I-J c(x))$, we see that $N(x,\lambda ,w)$ is surely nonsingular if $J\!F(x)^{-1} SS^{\scriptscriptstyle T}(I-J c(x))$ has all real eigenvalues nonnegative. But, similar to the proof of Corollary 2, it follows that $J\!F(x)^{-1} SS^{\scriptscriptstyle T}(I-J c(x))$ has the same eigenvalues as $S^{\scriptscriptstyle T}(I-J c(x))J\!F(x)^{-1} S$. If we can show that $(I-J c(x))J\!F(x)^{-1}$ is positive semidefinite, we obviously also have that $S^{\scriptscriptstyle T}(I-J c(x)) J\!F(x)^{-1} S$ is positive semidefinite and, therefore, has all the real eigenvalues (if any) nonnegative. Hence, to complete the proof, we only need to show that (15) implies that $(I-J c(x))J\!F(x)^{-1}$ is positive semidefinite. In order to see this, it is sufficient to observe that for any $v\in {\mathbb{R }}^n$ we can write

$$\begin{aligned} v^{\scriptscriptstyle T}J c(x)J\!F(x)^{-1} v&\le \Vert J c(x)\Vert \Vert J\!F(x)^{-1}\Vert \Vert v\Vert ^2\, \le \, \mu _m^s(J\!F(x)^{-1}) \Vert v\Vert ^2\\&\le v^{\scriptscriptstyle T}J\!F(x)^{-1} v, \end{aligned}$$

where the second inequality follows from (15). From this chain of inequalities the positive semidefiniteness of $(I-J c(x))J\!F(x)^{-1}$ follows readily and this concludes the proof.$\square$

Note that (15) is a condition purely in terms of $F$ and $c$, neither $q$ nor the values of $\lambda$ and $w$ are involved. The fact that $q$ is not involved simply indicates that the nonsingularity of $N$ is not related to the “shape” of the set $Q$, but only to the trajectory the moving set follows. More precisely, as will also become more clear in the following corollary, (15) requires the trajectory described by $c$ to be not “too steep”, where the exact meaning of “too steep” is given by (15). The following corollary shades some further light on this condition.

Remark 1

In part (d) of the following Corollary, and in the rest of this section we freely use some notation and definitions for Lipschitz and monotonicity constants that are fully explained and discussed at length in the “Appendix”.

Corollary 3

Assume the setting of Theorem 4 and consider the following conditions:

• (a) The matrix $N(x, \lambda , w)$ is nonsingular on ${\mathbb{R }}^n \times {\mathbb{R }}^m_{++}\times {\mathbb{R }}^m_{++}$;

• (b) Condition (15) holds for all $x\in {\mathbb{R }}^n$;

• (c) It holds that

  $$\begin{aligned} \sup _{x\in {\mathbb{R }}^n} \Vert Jc(x) \Vert \, \le \, \inf _{x\in {\mathbb{R }}^n} \frac{ \,\mu _m^s (J\!F(x)^{-1})\,}{\Vert J\!F(x)^{-1}\Vert }; \end{aligned}$$

• (d) $c$ is Lipschitz continuous on ${\mathbb{R }}^n$ with Lipschitz modulus $\alpha , \,F$ is Lipschitz continuous on ${\mathbb{R }}^n$ and strongly monotone on ${\mathbb{R }}^n$, the moduli of Lipschitz continuity and strong monotonicity of $F^{-1}$ are $L_{-1}$ and $\sigma _{-1}$, respectively, and

  $$\begin{aligned} \alpha \, \le \, \frac{\sigma _{-1}}{L_{-1}}. \end{aligned}$$

  (16)

Then it holds that

$$\begin{aligned} (d) \; \Longrightarrow \; (c) \; \Longrightarrow \; (b) \; \Longrightarrow \; (a). \end{aligned}$$

Proof

The only implication that needs a proof is $(d) \Longrightarrow (c)$. By Proposition 3(a) in the “Appendix”, we have $\alpha = \sup _{x\in {\mathbb{R }}^n} \Vert Jc(x) \Vert$. We now recall that since $F$ is strongly monotone on ${\mathbb{R }}^n$, its range is ${\mathbb{R }}^n$, see [37, Theorem 5.4.5]. Therefore, by Proposition 3 in the “Appendix” and taking into account that $J\!F^{-1}(F(x)) = J\!F(x)^{-1}$, we can write

$$\begin{aligned} \frac{\sigma _{-1}}{L_{-1}} \, = \, \frac{\inf _{y\in {\mathbb{R }}^n} \mu _m^s(J\!F^{-1}(y))}{\sup _{y\in {\mathbb{R }}^n} \Vert J\!F^{-1}(y)\Vert } \, = \, \frac{\inf _{x\in {\mathbb{R }}^n} \mu _m^s(J\!F(x)^{-1})}{\sup _{x\in {\mathbb{R }}^n} \Vert J\!F(x)^{-1}\Vert } \, \le \, \inf _{x\in {\mathbb{R }}^n} \frac{ \,\mu _m^s (J\!F(x)^{-1})\,}{\Vert J\!F(x)^{-1}\Vert }. \end{aligned}$$

This completes the proof. $\square$

Although the sufficient condition (16) is the strongest one among those we analyzed, it gives a clear geometric picture of the kind of conditions we need in order to guarantee nonsingularity. Note that Lipschitz continuity and strong monotonicity of $F$ imply that also the inverse of $F$ enjoys the same properties, see Proposition 5 in the “Appendix”, so that $L_{-1}$ and $\sigma _{-1}$ are well defined. Furthermore, observe that $(\sigma _{-1}/L_{-1})\le 1$ (this is obvious from the very definition of these constants, see “Appendix”). Therefore (16) stipulates that $c(x)$ is rather “flat” and consequently, $K(x)$ varies “slowly”, in some sense.

Remark 2

Reference [34] is one of the most interesting papers where the moving set structure has been used in order to show convergence of some algorithm for QVIs. It is shown in [34] that if $\alpha \le \frac{\sigma }{L}$, where $\alpha$ and $L$ are the Lipschitz moduli of $c$ and $F$, respectively, and $\sigma$ is the strong monotonicity modulus of $F$, then a certain gradient projection type method converges to the unique solution of the QVI. It is then of interest to contrast this condition to our condition $\alpha \le \frac{\sigma _{-1}}{L_{-1}}$ in Corollary 3 (d) (which is the strongest among the conditions we considered). If the function $F$ is a gradient mapping, then Proposition 6 in the “Appendix” implies that $\sigma /L=\sigma _{-1}/L_{-1}$, so that our condition and that in [34] are exactly the same. However, in general $\sigma _{-1}/L_{-1} < \sigma /L$ and $\sigma _{-1}/L_{-1} > \sigma /L$ can both occur. In fact, consider the function

$$\begin{aligned} F(x) = \left(\begin{array}{ccc} 1&\quad 0 &\quad 1 \\ 0&\quad 1&\quad 0 \\ 0&\quad 1&\quad 1 \end{array}\right) x. \end{aligned}$$

It is easy to see that $\sigma ({\mathbb{R }}^n,F) = 1-\frac{1}{\sqrt{2}}$ and $L({\mathbb{R }}^n,F) \simeq 1.8019$. Moreover, we have

$$\begin{aligned} F^{-1}(x) = \left(\begin{array}{ccc} 1&\quad \;\;\,1&\quad -1 \\ 0&\quad \;\;\,1&\quad \;\;\,0 \\ 0&\quad -1&\quad \;\;\,1 \end{array}\right) x. \end{aligned}$$

Again, it is easy to see that $\sigma ({\mathbb{R }}^n,F^{-1}) = \frac{1}{2}$ and $L({\mathbb{R }}^n,F^{-1}) \simeq 2.2470$. Therefore, we have

$$\begin{aligned} \frac{\sigma ({\mathbb{R }}^n,F)}{L({\mathbb{R }}^n,F)} \simeq 0.1625 < 0.2225 \simeq \frac{\sigma ({\mathbb{R }}^n,F^{-1})}{L({\mathbb{R }}^n,F^{-1})}, \end{aligned}$$

and then for this function our condition is less restrictive than that in [34]. But it is sufficient to switch the function with its inverse to get exactly the opposite. Therefore there is no one condition that dominates the other one in general. $\square$

The following example shows how condition (c) in Corollary 3 simplifies in certain situations and the way it can be used (i) to show how interesting classes of problems can be analyzed and (ii) to easily check whether this condition is actually satisfied in a concrete situation.

Example 1

The discretization of many (elliptic) infinite-dimensional QVIs involving suitable partial differential operators often leads to linear mappings of the form $F(x) = Ax + b$ for some positive definite matrix $A$, see e.g. [21, 22]. Furthermore, in many applications in mechanics an implicit-obstacle-type constraint described by the set $K(x) := \{ y \mid y \le c(x) \}$ for some smooth mapping $c$ is present, see [29]. In these cases $K(x)$ belongs to the class of moving sets with $q$ being the identity mapping in (14). Taking into account that $J\!F(x) =A$, we can easily calculate $\frac{\mu _m^s (J\!F(x)^{-1})}{\Vert J\!F(x)^{-1} \Vert }$ which is obviously a positive constant. It actually turns out that there are interesting applications where $A$ is symmetric. Furthermore the minimum and maximum eigenvalues of $A$, here denoted by $\lambda _{\min } (A)$ and $\lambda _{\max } (A)$ respectively, are even known analytically in some cases, e.g., if $A$ corresponds to a standard finite difference-discretization of the two-dimensional Laplace operator on the unit square $(0,1) \times (0,1)$. In this setting we can write

$$\begin{aligned} \frac{\mu _m^s (J\!F(x)^{-1})}{\Vert J\!F(x)^{-1} \Vert } = \frac{\lambda _{\min } (A^{-1})}{\Vert A^{-1} \Vert } = \frac{1/\lambda _{\max }(A)}{1/\lambda _{\min }(A)} = \frac{\lambda _{\min }(A)}{\lambda _{\max } (A)} > 0. \end{aligned}$$

Hence condition (c) in Corollary 3 holds provided that $\Vert Jc(x) \Vert$ is less or equal to this positive constant, i.e. provided that $c$ is Lipschitz continuous with a sufficiently small Lipschitz constant. $\square$

3.3 Linear constraints with variable right-hand side

We now pass to consider the case in which the feasible set $K(x)$ is given by

$$\begin{aligned} K(x) \, =\, \{ y\in {\mathbb{R }}^n \mid g(y,x) := E y - b - c(x) \le 0\}, \end{aligned}$$

(17)

where $E \in {\mathbb{R }}^{m \times n}$ is a given matrix, $c:{\mathbb{R }}^n \rightarrow {\mathbb{R }}^m$ and $b \in {\mathbb{R }}^m$. In this class of QVIs, the feasible set is defined by linear inequalities in which the right-hand side depends on $x$.

Theorem 5

Let $g$ be defined as in (17), let $x\in {\mathbb{R }}^n$ be a given point, and assume that $F$ and $c$ are $C^1$ around $x$. Suppose further that $J\!F(x)$ is positive definite and that

$$\begin{aligned} \Vert Jc(x) \Vert \, \le \,\frac{ \, \mu _m^+(x) \,}{\Vert J\!F(x)^{-1}\Vert \Vert E\Vert }, \end{aligned}$$

(18)

where

$$\begin{aligned} \mu ^+_m(x) \!=\! \min \{\mu ^+_m(A) \mid A \text{ is} \text{ a} \text{ principal} \text{ submatrix} \text{ of} \frac{1}{2} E (J\!F(x)^{-1} \!+\! J\!F(x)^{-T}) E^{\scriptscriptstyle T}\}, \end{aligned}$$

$\mu ^+_m(A)$ denotes the minimum positive eigenvalue of the matrix $A$, and $A^{-T}$ is the transpose of the inverse of $A$. Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

Proof

We will show that the assumptions from Corollary 2 hold. First of all note that the hypotheses imply Assumptions 1 and 2. Taking into account (17), we have $\nabla _y g(x,x)\,=\, E^{\scriptscriptstyle T}$ and $J_x h(x) \,=\, E - Jc(x)$. Since $J\!F(x)$ is nonsingular by assumption, we can write

$$\begin{aligned} M := M(x,\lambda ) \,=\, (E - Jc(x)) J\!F(x)^{-1} E^{\scriptscriptstyle T}. \end{aligned}$$

In view of Corollary 2, we need to show that $M$ is a $P_0$ matrix.

To this end, we first observe that the rank of $M$ is obviously less or equal to $n$ (the rank of $J\!F(x)$). Hence each principal minor of $M$ with dimension greater than $n$ is equal to zero. Therefore, it suffices to show that each principal minor of $M$ with size less or equal to $n$ is nonnegative.

A generic principal submatrix of $M$ with dimension $s \le n$ is defined by

$$\begin{aligned} (E_{i*} - Jc(x)_{i*})_{i \in I_s} J\!F(x)^{-1} (E_{i*})_{i \in I_s}^{\scriptscriptstyle T}\end{aligned}$$

where $I_s$ is a subset of $\{1, \ldots , m\}$ with cardinality equal to $s$. Therefore, each of these subsets of indices defines a principal submatrix of $M$. Now we have two cases: $E_{I_s} := (E_{i*})_{i \in I_s}$ has full row rank or not. If not, the principal minor corresponding to $I_s$ is equal to zero. Otherwise, if $E_{I_s}$ has full row rank, then we can prove that the principal submatrix corresponding to $I_s$ is positive semidefinite. In fact, we can write

$$\begin{aligned} v^{\scriptscriptstyle T}E_{I_s} J\!F(x)^{-1} E_{I_s}^{\scriptscriptstyle T}v&\ge \mu _m^+(x) \Vert v \Vert ^2 \\&\stackrel{(18)}{\ge } \Vert Jc(x) \Vert \, \Vert J\!F(x)^{-1}\Vert \, \Vert E \Vert \, \Vert v \Vert ^2 \\&\ge \Vert Jc(x)_{I_s} \Vert \, \Vert J\!F(x)^{-1}\Vert \, \Vert E_{I_s} \Vert \, \Vert v \Vert ^2 \\&\ge v^{\scriptscriptstyle T}Jc(x)_{I_s} J\!F(x)^{-1} E_{I_s} v, \quad \forall v \in {\mathbb{R }}^n, \end{aligned}$$

where the third inequality follows from the fact that the spectral norm of a submatrix is less or equal to the spectral norm of the matrix itself. Then we have

$$\begin{aligned} v^{\scriptscriptstyle T}(E_{I_s} - Jc(x)_{I_s}) J\!F(x)^{-1} E_{I_s}^{\scriptscriptstyle T}v \ge 0, \quad \forall v \in {\mathbb{R }}^n. \end{aligned}$$

Hence $M$ is a $P_0$ matrix, and using Corollary 2, we have the thesis. $\square$

By the inclusion principle (see, for example, [26, Theorem 4.3.15]) and recalling condition (18), it is clear that if the matrix $E$ has full row rank, then we have

$$\begin{aligned} \mu _m^+(x) = \mu _m^s(EJ\!F(x)^{-1} E^{\scriptscriptstyle T}). \end{aligned}$$

This allows us to state the following immediate corollary.

Corollary 4

Let $g$ be defined as in (17), let $x\in {\mathbb{R }}^n$ be a given point, and assume that $F$ and $c$ are $C^1$ around $x$. Moreover, suppose that $E$ has full row rank. Suppose that $J\!F(x)$ is positive definite and that

$$\begin{aligned} \Vert Jc(x) \Vert \, \le \,\frac{ \, \mu _m^s(EJ\!F(x)^{-1} E^{\scriptscriptstyle T}) \,}{\Vert J\!F(x)^{-1}\Vert \Vert E\Vert }. \end{aligned}$$

Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

Technicalities apart, the meaning of Theorem 5 is that $c(x)$ should not vary “too quickly”. Note, however, that, in contrast to the case from the previous section, this does not immediately imply that $K(x)$ changes “slowly” with $x$, since a polyhedron can have abrupt changes even when the right-hand side changes only slightly.

The following result parallels Corollary 3 and gives stronger, but more expressive conditions for the nonsingularity of $J\!H$.

Corollary 5

Assume the same setting as in Theorem 5 and consider the following conditions:

• (a) The matrix $N(x, \lambda ,w)$ is nonsingular on ${\mathbb{R }}^n \times {\mathbb{R }}^m_{++}$;

• (b) For all $x \in \mathbb R ^n , \, J\!F(x)$ is positive definite and condition (18) holds;

• (c) For all $x, \, J\!F(x)$ is positive definite and it holds that

  $$\begin{aligned} \Vert Jc(x) \Vert \, \le \,\frac{ \,\mu _m^s (J\!F(x)^{-1})\,}{\Vert J\!F(x)^{-1}\Vert } \frac{\mu ^+_m}{\Vert E\Vert }, \end{aligned}$$

  where $\mu ^+_m = \min \{\mu ^+_m(A) \mid A$ is a principal submatrix of $EE^{\scriptscriptstyle T}\}$;

• (d) The Jacobian $J\!F(x)$ is positive definite for all $x \in \mathbb R ^n$, and it holds that

  $$\begin{aligned} \sup _{x\in {\mathbb{R }}^n} \Vert Jc(x) \Vert \, \le \, \inf _{x\in {\mathbb{R }}^n} \frac{ \, \mu _m^s (J\!F(x)^{-1})\,}{\Vert J\!F(x)^{-1}\Vert } \frac{\mu ^+_m}{\Vert E\Vert }; \end{aligned}$$

• (e) $c$ is Lipschitz continuous on ${\mathbb{R }}^n$ with Lipschitz modulus $\alpha , \,F$ is Lipschitz continuous on ${\mathbb{R }}^n$ and strongly monotone on ${\mathbb{R }}^n$, the moduli of Lipschitz continuity and strong monotonicity of $F^{-1}$ are $L_{-1}$ and $\sigma _{-1}$, respectively, and

  $$\begin{aligned} \alpha \, \le \, \frac{\sigma _{-1}}{L_{-1}} \frac{\mu ^+_m}{\Vert E\Vert }, \end{aligned}$$

  where $\mu _m^+$ is defined as before.

Then the following implications hold:

$$\begin{aligned} (e) \; \Longrightarrow \; (d) \; \Longrightarrow \; (c) \; \Longrightarrow \; (b) \; \Longrightarrow \; (a). \end{aligned}$$

Proof

We only prove the implication $(c) \Longrightarrow (b)$, the other ones are very similar to those of Corollary 3, hence they are left to the reader.

In order to verify the implication $(c) \Longrightarrow (b)$, we have to show that

$$\begin{aligned} \mu _m^+(x) \ge \mu _m^s (J\!F(x)^{-1}) \mu _m^+, \quad \forall x \in \mathbb R ^n \end{aligned}$$

(19)

holds. Take an arbitrary $x$, and let $I_s^*$ be a set of indices such that $\frac{1}{2} E_{I_s^*} (J\!F(x)^{-1} + J\!F(x)^{-T}) E_{I_s^*}^{\scriptscriptstyle T}$ is a submatrix of $\frac{1}{2} E (J\!F(x)^{-1} + J\!F(x)^{-T}) E^{\scriptscriptstyle T}$ for which one obtains the minimum positive eigenvalue $\mu _m^+(x)$ for the given $x$. Let $\bar{v}$ be an eigenvector of the matrix $\frac{1}{2} E_{I_s^*} (J\!F(x)^{-1} + J\!F(x)^{-T}) E_{I_s^*}^{\scriptscriptstyle T}$ associated to $\mu _m^+(x)$; we may assume without loss of generality that $\Vert \bar{v} \Vert = 1$. Then we have

$$\begin{aligned} \bar{v}^{\scriptscriptstyle T}E_{I_s^*} J\!F(x)^{-1} E_{I_s^*}^{\scriptscriptstyle T}\bar{v} = \frac{1}{2} \bar{v}^{\scriptscriptstyle T}E_{I_s^*} (J\!F(x)^{-1} \!+\! J\!F(x)^{-T}) E_{I_s^*}^{\scriptscriptstyle T}\bar{v} \nonumber \\ =\mu _m^+(x) \Vert \bar{v} \Vert ^2 \!=\! \mu _m^+(x). \end{aligned}$$

(20)

Since the eigenvectors corresponding to different eigenvalues of a symmetric matrix are orthogonal to each other, we have $\bar{v} \perp \text{ null} \big ( \frac{1}{2} E_{I_s^*} (J\!F(x)^{-1} + J\!F(x)^{-T}) E_{I_s^*}^{\scriptscriptstyle T}\big )$. However, it is easy to see that, for any positive definite (not necessarily symmetric) matrix $A$, the two matrices $E_{I_s^*} A E_{I_s^*}^{\scriptscriptstyle T}$ and $E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}$ have the same null space. Hence we also have $\bar{v} \perp \text{ null} \big ( E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}\big )$. Now, assuming that $E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}$ is an $s \times s$-matrix, let $E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}= Q D Q^{\scriptscriptstyle T}$ with $Q \in \mathbb R ^{s \times s}$ orthogonal and $D = \text{ diag} ( \lambda _1, \ldots , \lambda _s )$ be the spectral decomposition of $E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}$, i.e. $\lambda _i$ are the eigenvalues with corresponding eigenvectors $v_i$ being the $i$-th column of $Q$. Suppose further that the null space of this matrix has dimension $r \le s$ and that the eigenvalues are ordered such that $\lambda _1 \le \cdots \le \lambda _s$. Then $\lambda _1 = \cdots = \lambda _r = 0$ (and $\lambda _{r+1} \ge \mu _m^+$ in our notation) and the eigenvectors $v_1, \ldots , v_r$ form a basis of the null space of $E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}$. We therefore have $\bar{v}^{\scriptscriptstyle T}v_i = 0$ for all $i = 1, \ldots , r$. Consequently, $w_i = 0$ for all $i = 1, \ldots , r$, where $w := Q^{\scriptscriptstyle T}\bar{v}$. It therefore follows that

$$\begin{aligned} \bar{v}^{\scriptscriptstyle T}E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}\bar{v}&= \bar{v}^{\scriptscriptstyle T}Q D Q^{\scriptscriptstyle T}\bar{v} = w^{\scriptscriptstyle T}D w = \sum _{i=1}^s \lambda _i w_i^2 \\&= \sum _{i=r+1}^s \lambda _i w_i^2 \ge \mu _m^+ \sum _{i=r+1}^s w_i^2 = \mu _m^+ \sum _{i=1}^s w_i^2 = \mu _m^+ \Vert w \Vert ^2\\&= \mu _m^+ \Vert \bar{v} \Vert ^2 = \mu _m^+. \end{aligned}$$

Combining this inequality with (20), we obtain

$$\begin{aligned} \mu _m^+ (x) = \bar{v}^{\scriptscriptstyle T}E_{I_s^*} J\!F(x)^{-1} E_{I_s^*}^{\scriptscriptstyle T}\bar{v} \ge \mu _m^s (J\!F(x)^{-1}) \bar{v}^{\scriptscriptstyle T}E_{I_s^*} E_{I_s^*}^{\scriptscriptstyle T}\bar{v} \ge \mu _m^s (J\!F(x)^{-1}) \mu _m^+, \end{aligned}$$

and this shows that (19) holds. $\square$

We illustrate the previous result by the following example which comes from a realistic model described in [39], and which is also used as a test problem in Sect. 5 (test problems OutKZ31 and OutKZ41).

Example 2

Consider the problem of an elastic body in contrast to a rigid obstacle. In particular assume that Coulomb friction is present. After discretization, this class of QVIs is characterized by a linear function $F(x) := Bx - g$ with a positive definite matrix $B$, and by the following constraints:

$$\begin{aligned} a_i - y_i&\le 0, \quad a_i = \left\{ \begin{array}{l@{\qquad }l} \quad \quad l,&\,\, \text{ if} i \in \{ 1, \ldots , n\} \text{ is} \text{ even},\\ \; \phi \, x_{i+1},&\,\,\text{ if} i \in \{ 1, \ldots , n\} \text{ is} \text{ odd,}\end{array}\right. \\ y_i - b_i&\le 0, \quad b_i = \left\{ \begin{array}{l@{\qquad }l} \quad \quad u,&\text{ if} i \in \{ 1, \ldots , n\} \text{ is} \text{ even},\\ -\phi \, x_{i+1},&\text{ if} i \in \{ 1, \ldots , n\} \text{ is} \text{ odd,}\end{array}\right. \end{aligned}$$

with $l < u\le 0$ and where $\phi \in {\mathbb{R }}$ is the friction coefficient. Let $x^* \in {\mathbb{R }}^n$ be a solution of the described QVI, then odd elements of $x^*$ are interpreted as tangential stress components on the rigid obstacle in different points of such obstacle, while even elements are interpreted as outer normal stress components. This example fits into the framework of this subsection with

$$\begin{aligned} E&:= \left( \begin{array}{c}-I \\ I\end{array} \right), \quad \Vert Jc(x)\Vert = \sqrt{2} \phi , \quad \Vert E\Vert = \sqrt{2},\\ \mu _m^+&= \min \left\{ \mu _m^+ (A): \; A \text{ is} \text{ a} \text{ principal} \text{ submatrix} \text{ of} \left(\begin{array}{c@{\quad }c} I&-I \\ -I&I \end{array}\right) \right\} = 1. \end{aligned}$$

According to Corollary 5 (c)$\rightarrow$(a), we can say that if

$$\begin{aligned} \phi \le \frac{1}{\sqrt{2}} \frac{\mu _m^s(B^{-1})}{\Vert B^{-1}\Vert } \frac{\mu _m^+}{\Vert E\Vert } = \frac{1}{\sqrt{2}} \frac{\mu _m^s(B^{-1})}{\Vert B^{-1}\Vert } \frac{1}{\sqrt{2}} \left( \le \frac{1}{2} \right), \end{aligned}$$

then we are sure that $J\!H(x,\lambda ,w)$ is nonsingular for all $\lambda$ and $w$ positive. Note that this condition holds for all sufficiently small friction coefficients $\phi$. $\square$

So far, in this subsection we have considered only QVIs that are linear in the $y$-part. This restriction has allowed us to give conditions that do not depend on the multipliers $\lambda$. However, we can extend the results we have obtained to the more general setting in which

$$\begin{aligned} K(x) \, =\, \{y\in {\mathbb{R }}^n \, | \, g(y,x) := q(y) - c(x) \le 0\}, \end{aligned}$$

(21)

where both $q$ and $c$ are functions from ${\mathbb{R }}^n$ to ${\mathbb{R }}^m$. We can prove the following theorem, in which nonsingularity conditions now also depend on the Lagrange multiplier $\lambda$. The proof follows lines identical to those of Theorem 5 and is therefore omitted.

Theorem 6

Let $g$ be defined as in (21), let a point $(x,\lambda )\in {\mathbb{R }}^n \times {\mathbb{R }}^m_{++}$ be given and assume that $F$ and $c$ are $C^1$ while $q$ is $C^2$ around $x$. Suppose further that $J_x L(x,\lambda )$ is positive definite and that

$$\begin{aligned} \Vert Jc(x) \Vert \, \le \,\frac{ \, \mu _m^+(x,\lambda ) \,}{\Vert J_xL(x, \lambda )^{-1}\Vert \Vert Jq(x)\Vert }, \end{aligned}$$

where $\mu ^+_m(x,\lambda ) = \min \{\mu ^+_m(A) \mid A$ is a principal submatrix of $\frac{1}{2} Jq(x) (J_xL(x,\lambda )^{-1} + J_xL(x,\lambda )^{-T})\, Jq(x)^{\scriptscriptstyle T}\}$ and $\mu ^+_m(A)$ denotes once again the minimum positive eigenvalue of a symmetric matrix $A$. Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $w$.

We conclude by considering a particular structure of the constraints of the QVI that is a subclass of that studied in this section. Suppose that

$$\begin{aligned} g(y,x) := \left(\begin{array}{c} l - y \\ y - u \\ I^{\pm } \left( y - c(x) \right) \end{array}\right) \le 0, \end{aligned}$$

(22)

where $I^{\pm }$ is a diagonal matrix with elements equal to 1 or $-1$, that is there are box constraints for $y$ with lower bounds $l$ and upper bounds $u$, and $n$ special linear constraints with variable right-hand side.

Theorem 7

Let $g$ be defined as in (22), let a point $x\in {\mathbb{R }}^n$ be given and assume that around $x$ it holds that $F$ and $c$ are $C^1$. Suppose that $J\!F(x)$ and $I - Jc(x)$ are row diagonally dominant with positive diagonal entries. Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

Proof

Let

$$\begin{aligned} D := \left(\begin{array}{ccc} D_1&\quad 0&\quad 0\\ 0&\quad D_2&\quad 0 \\ 0&\quad 0&\quad D_3 \end{array}\right) := \mathop {\mathrm{diag}}(w^{-1} \circ \lambda ), \end{aligned}$$

where $D_1, D_2, D_3 \in {\mathbb{R }}^{n\times n}$ and $w = (w^1, w^2, w^3), \lambda = ( \lambda ^1, \lambda ^2, \lambda ^3 )$ denote the slack variables and Lagrange multipliers corresponding to the three blocks in the definition of the inequality constraints from (22), respectively. Then we can write

$$\begin{aligned} N(x,\lambda ,w)&= J\!F(x) + \left(\begin{array}{ccc} -I& I &I^{\pm } \end{array}\right) D \left(\begin{array}{c} -I\\ I\\ I^{\pm } (I - Jc(x)) \end{array}\right) \\&= J\!F(x) + D_1 + D_2 + D_3 \left(I - Jc(x) \right). \end{aligned}$$

Note that $D_3 \left(I - Jc(x) \right)$ is a row diagonally dominant matrix with positive diagonal entries for all $\lambda$ and $w$ positive. Hence $N(x,\lambda ,w)$ is a strictly row diagonally dominant matrix for all $\lambda$ and $w$ positive since it is the sum of two row diagonally dominant matrices with positive diagonal entries ($J\!F(x)$ and $D_3 \left(I - Jc(x) \right)$) and two strictly row diagonally dominant matrices with positive diagonal entries ($D_1$ and $D_2$). Recalling that every strictly row diagonally dominant matrix is nonsingular, we obtain the thesis. $\square$

It is possible to generalize constraints (22) by imposing that lower or upper bounds may not exist for every variable and that the number of special linear constraints with variable right-hand side may be less or greater than $n$:

$$\begin{aligned} g(y,x) := \left(\begin{array}{c} (l_i - y_i)_{i \in L} \\ (y_i - u_i)_{i \in U} \\ [.3em] \left( y_i - c_i^{j}(x) \right)_{i \in S_+}^{j \in C(i)} \\ [.5em] \left( - y_i + d_i^{j}(x) \right)_{i \in S_-}^{j \in D(i)} \end{array}\right) \le 0, \end{aligned}$$

(23)

where $L, U, S_-, S_+ \subseteq \{1,\ldots ,n\}$ and for any $i\in S_+, \,C(i) \subseteq \{1,2,\ldots \}$ and for any $i\in S_-, \,D(i) \subseteq \{1,2,\ldots \}$. For QVIs with these constraints a result similar to Theorem 7 can be given. The proof of this theorem is akin to that of Theorem 7 and hence it is left to the reader.

Theorem 8

Let $g$ be defined as in (23), let a point $x\in {\mathbb{R }}^n$ be given and assume that around $x$ it holds that $F, \,c$ and $d$ are continuously differentiable. Suppose that $J\!F(x)$ is row diagonally dominant with positive diagonal entries and such that for every $i \notin L \cup U$ it holds that $J\!F(x)_{ii} > \sum _{k=1,\ldots ,n, \, k \ne i} |J\!F(x)_{ik}|$. Suppose further that for all $i \in S_+$ and all $j \in C(i)$ it holds that

$$\begin{aligned} 1 - \frac{\partial c_i^j(x)}{\partial x_i} \,\ge \displaystyle \sum _{k=1,\ldots ,n, \, k \ne i} \left| \frac{\partial c_i^j(x)}{\partial x_k}\right|, \end{aligned}$$

and that for all $i \in S_-$ and all $j \in D(i)$ it holds that

$$\begin{aligned} 1-\frac{\partial d_i^j(x)}{\partial x_i}\, \ge \displaystyle \sum _{k=1,\ldots ,n, \, k \ne i} \left| \frac{\partial d_i^j(x)}{\partial x_k}\right|. \end{aligned}$$

Then $J\!H(x,\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

3.3.1 Generalized Nash equilibrium problems

As we mentioned in Sect. 1, the approach used in this paper is motivated by some recent results obtained in [14] for the case of Generalized Nash Equilibrium Problems (GNEPs). In this subsection, we consider GNEPs, reformulate them as QVIs and show that our new results improve on the specialized ones in [14]. For more background material on GNEPs, we refer the interested reader to the survey paper [16].

We consider GNEPs where each player solves a problem whose feasible set is defined by a system of linear inequalities with variable right-hand side, i.e., player $\nu \; ( \nu = 1, \ldots , N )$ controls $x^\nu \in {\mathbb{R }}^{n_\nu }$ and tries to solve the optimization problem

$$\begin{aligned} \min _{x^\nu } \; \theta _\nu (x^\nu , x^{-\nu }) \quad \text{ s.t.} \quad E^\nu x^\nu - b^\nu - c^\nu (x^{-\nu }) \le 0 \end{aligned}$$

(24)

with given $\theta _\nu : \mathbb R ^n \rightarrow \mathbb R , \,E^\nu \in {\mathbb{R }}^{m_\nu \times n_\nu }$ and $c^\nu : \mathbb R ^{n - n_{\nu }} \rightarrow \mathbb R ^{m_\nu } , \, b^\nu \in \mathbb R ^{m_{\nu }}$. Here, $n := n_1 + \cdots + n_N$ denotes the total number of variables, $m := m_1 + \cdots + m_N$ will be the total number of (inequality) constraints, and $( x^\nu , x^{-\nu } )$ is a short-hand notation for the full vector $\mathbf{x}:= ( x^1, x^2, \ldots , x^N )$, so that $x^{-\nu }$ subsumes all the block vectors $x^\mu$ with $\mu \ne \nu$. In what follows, we assume that $\theta _\nu (\cdot , x^{-\nu })$ is convex for every $x^{-\nu }$, and for every $\nu =1, \ldots , N$. Moreover, we assume that $\theta _\nu$ are $C^1$ functions for every $\nu =1, \ldots , N$.

It is well known that a solution of the GNEP (24) can be computed by solving the following QVI:

$$\begin{aligned}&\text{ Find} \bar{\mathbf{x}}\in \{\mathbf{x}\in {\mathbb{R }}^n: E^\nu x^\nu - b^\nu - c^\nu (x^{-\nu }) \le 0, \nu =1,\ldots ,N\} \; \text{ such} \text{ that} \nonumber \\&{\left( \nabla _{x^\nu } \theta _\nu (\bar{\mathbf{x}}) \right)_{\nu \!=\! 1}^N}^{\scriptscriptstyle T}(\mathbf{y}\!-\! \bar{\mathbf{x}}) \ge 0, \quad \forall \mathbf{y}\in {\mathbb{R }}^n : E^\nu y^\nu \!-\! b^\nu \!-\! c^\nu (\bar{x}^{-\nu }) \!\le \! 0, \; \nu =1,\ldots ,N.\nonumber \\ \end{aligned}$$

(25)

To simplify the notation, we write

$$\begin{aligned} F(\mathbf{x}) := \left( \nabla _{x^\nu } \theta _\nu (\mathbf{x}) \right)_{\nu = 1}^N, \quad E := \left(\begin{array}{ccc} E^1&\,&0\\&\ddots&\\ 0&\,&E^N \end{array}\right), \quad c(\mathbf{x}) := \left(\begin{array}{c} c^1(x^{-1}) \\ \vdots \\ c^N(x^{-N}) \end{array}\right). \end{aligned}$$

(26)

Note that the QVI (25) belongs to the class of QVIs whose constraints are defined by (17). This fact allows us to rewrite Theorem 5 for the GNEP (24).

Theorem 9

Consider a GNEP in which each player tries to solve (24). Recalling the notation in (26), let a point $\mathbf{x}\in {\mathbb{R }}^n$ be given and assume that $F$ and $c$ are $C^1$ around $x$. Suppose further that $J\!F(\mathbf{x})$ is positive definite and that

$$\begin{aligned} \Vert Jc(\mathbf{x}) \Vert \, \le \,\frac{ \, \mu _m^+(\mathbf{x}) \,}{\Vert J\!F(\mathbf{x})^{-1}\Vert \Vert E\Vert }, \end{aligned}$$

(27)

where $\mu ^+_m(\mathbf{x}) = \min \{\mu ^+_m(A) \mid A$ is a principal submatrix of $\frac{1}{2} E (J\!F(\mathbf{x})^{-1} + J\!F(\mathbf{x})^{-T}) E^{\scriptscriptstyle T}\}$, and $\mu ^+_m(A)$ is again the minimum positive eigenvalue of the matrix $A$. Then $J\!H(\mathbf{x},\lambda , w)$ is nonsingular for all positive $\lambda$ and $w$.

Note that a similar result is stated in [14]. In particular, Theorem 4.7 in [14] gives

$$\begin{aligned} J\!F(\mathbf{x}) \text{ positive} \text{ definite} \text{ and} \Vert Jc(\mathbf{x}) \Vert \, \le \, \frac{ \, \mu _m^s(EJ\!F(\mathbf{x})^{-1} E^{\scriptscriptstyle T}) \,}{\Vert J\!F(\mathbf{x})^{-1}\Vert \Vert E\Vert }, \end{aligned}$$

(28)

as a sufficient condition for the nonsingularity of the Jacobian of $H$ for all $\lambda$ and $w$ positive, in the case of the QVI (25). However, Theorem 9 gives better conditions, in fact it is clear that

$$\begin{aligned} \mu _m^s(EJ\!F(\mathbf{x})^{-1} E^{\scriptscriptstyle T}) \le \mu _m^+(\mathbf{x}) \end{aligned}$$

and then conditions (28) imply those of Theorem 9. The following example describes a GNEP that satisfies the conditions of Theorem 9, but violates those from (28) for all $\mathbf{x}$.

Example 3

Consider a GNEP in which there are two players controlling one variable each one, $x^1$ and $x^2$ respectively. The optimization problems of the players are the following:

$$\begin{aligned} \begin{array}{ll|} \displaystyle \min _{x^1}&(x^1 - 2)^2 \\ \text{ s.t.}&x^1 + \frac{1}{2} x^2 \le 1, \qquad \quad \\&x^1 \ge 0, \end{array} \qquad \qquad \begin{array}{ll} \displaystyle \min _{x^2}&(x^2 - 2)^2 \\ \text{ s.t.}&x^2 + \frac{1}{2} x^1 \le 1, \\&x^2 \ge 0. \end{array} \end{aligned}$$

This GNEP has only one equilibrium in $(\frac{2}{3}, \frac{2}{3})$. Referring to the notation in (26), we write

$$\begin{aligned} F(\mathbf{x}) = \left(\begin{array}{c} 2x^1 -4\\ 2x^2 -4 \end{array} \right), \quad E = \left(\begin{array}{cc} \;\;\;1&\quad \;\;\;0\\ -1&\quad \;\;\;0\\ \;\;\;0&\quad \;\;\;1\\ \;\;\;0&\quad -1 \end{array}\right), \quad c(\mathbf{x}) = \left(\begin{array}{c} - \frac{1}{2}x^2 \\ 0 \\ - \frac{1}{2}x^1 \\ 0 \end{array}\right). \end{aligned}$$

Then

$$\begin{aligned} J\!F (x) = \left(\begin{array}{cc} 2 & 0\\ 0 & 2 \end{array} \right) \succ 0, \quad J\!F(x)^{-1} = \left(\begin{array}{cc} \frac{1}{2} & 0\\ 0 & \frac{1}{2} \end{array} \right), \quad Jc(x) = \left(\begin{array}{cc} \;\;\;0&\quad - \frac{1}{2} \\ \;\;\;0&\quad \;\;\;0 \\ - \frac{1}{2}&\quad \;\;\;0 \\ \;\;\;0&\quad \;\;\;0 \end{array}\right). \end{aligned}$$

Since $\Vert J\!F(x)^{-1} \Vert = \frac{1}{2}, \,\Vert E\Vert = \sqrt{2}, \,\Vert Jc(x)\Vert = \frac{1}{2}$, and

$$\begin{aligned} E\!J\!F(x)^{-1} E^{\scriptscriptstyle T}= \frac{1}{2} \left(\begin{array}{cccc} \;\;\;1&-1&\;\;\;0&\;\;\;0\\ -1&\;\;\;1&\;\;\;0&\;\;\;0\\ \;\;\;0&\;\;\;0&\;\;\;1&-1\\ \;\;\;0&\;\;\;0&-1&\;\;\;1 \end{array}\right), \end{aligned}$$

conditions (28) do not hold since $\mu _m^s (E J\!F^{-1} E^{\scriptscriptstyle T}) = 0$ and therefore $\frac{1}{2} \not \le 0$. However, condition (27) holds because, recalling the notation of Theorem 9, $\mu _m^+(\mathbf{x}) = \frac{1}{2}$, and then we have $\frac{1}{2} < \frac{\frac{1}{2}}{\frac{1}{2} \sqrt{2}} = \frac{1}{\sqrt{2}}$.$\square$

Remark 3

In the previous development we concentrate our attention on games whose feasible region is defined by a system of linear inequalities with variable right-hand side, see (24), because we wanted to compare to the results in [14], which are among the few in the literature about GNEPs where convergence can be guaranteed. However we can consider games with totally different structure and still get convergence results. In particular we can consider GNEPs that can be reformulated as QVIs with moving sets (see Sect. 3.2). Suppose that each player $\nu$ has to solve the following optimization problem

$$\begin{aligned} \min _{x^\nu } \; \theta _\nu (x^\nu , x^{-\nu }) \quad \text{ s.t.} \quad q^\nu ( x^\nu - c^\nu (x^{-\nu }) ) \le 0 \end{aligned}$$

with given $\theta _\nu : \mathbb R ^n \rightarrow \mathbb R , \,q^\nu : \mathbb R ^{n_\nu } \rightarrow \mathbb R ^{m_\nu }$ and $c^\nu : \mathbb R ^{n - n_{\nu }} \rightarrow \mathbb R ^{n_\nu }$. Here, $n := n_1 + \cdots + n_N$ denotes the total number of variables, $m := m_1 + \cdots + m_N$ will be the total number of (inequality) constraints. The feasible region of player $\nu$ is therefore a “moving set” whose position depends on the variables of all other players. The GNEP can be reformulated as a QVI($F,K$) with

$$\begin{aligned} F(\mathbf{x})&:= \left( \nabla _{x^\nu } \theta _\nu (\mathbf{x}) \right)_{\nu = 1}^N, \quad K(\mathbf{x}) := c(\mathbf{x}) + Q, \\ c(\mathbf{x})&:= \left(\begin{array}{c} c^1(x^{-1}) \\ \vdots \\ c^N(x^{-N}) \end{array}\right), \quad Q:=\prod _{\nu =1}^N \left\{ y^\nu \in {\mathbb{R }}^{n_\nu } \, | \; q^\nu (y^\nu ) \le 0 \right\} , \end{aligned}$$

that is a QVI with a moving set to which the nonsingularity results in Sect. 3.2 can readily be applied.

3.4 Box constraints and “binary constraints”

We now consider the situation where each component $g_i$ of the constraint function from (2) depends only on a single pair $(y_j, x_j)$ for some index $j \in \{ 1, \ldots , n \}$. In particular, this includes the case of bounds having parametric bound constraints. We use the terminology “binary constraints” for this class of problems. The following result shows how the nonsingularity Theorem 3 can be applied.

Theorem 10

Let $x \in \mathbb R ^n$ and $\lambda > 0$ be given. Suppose that each constraint $g_i ( \cdot , \cdot ) \ (i = 1, \ldots , m)$ depends only on a single couple $(y_{j(i)},x_{j(i)})$ for some $j(i) \in \{ 1, \ldots , n \}$ and that Assumptions 1 and 2 hold. Assume further that one of the following conditions holds:

• (a) $J_x L(x, \lambda )$ is a $P$-matrix and $\nabla _{y_{j(i)}} g_i (x_{j(i)},x_{j(i)}) \nabla _{x_{j(i)}} h_i (x_{j(i)}) \ge 0$ for all $i$, or

• (b) $J_x L(x, \lambda )$ is a $P_0$-matrix and $\nabla _{y_{j(i)}} g_i (x_{j(i)},x_{j(i)}) \nabla _{x_{j(i)}} h_i (x_{j(i)}) > 0$ for all $i$.

Then $J\!H(x,\lambda ,w)$ is nonsingular for all positive $w$.

Proof

We verify the statement under condition (a) since the proof under (b) is essentially identical.

We assume without loss of generality that the constraints $g$ are ordered in such a way that the first $m_1$ constraints depend on the pair $(y_1,x_1)$ only, the next $m_2$ constraints depend on the couple $(y_2,x_2)$ only, and so on, with the last $m_n$ constraints depending on $(y_n,x_n)$ only. Note that $m_i$ might be equal to zero for some of the indices $i \in \{ 1, \ldots , n \}$, and that we have $m_1 + m_2 + \cdots + m_n = m$. Taking this ordering into account, it is not difficult to see that

$$\begin{aligned} J_x h(x) = \left( \begin{array}{cccc} \nabla _{x_1} h_1 (x_1)&\quad 0&\quad \cdots&\quad 0 \\ \nabla _{x_1} h_2 (x_1)&\quad 0&\quad \cdots&\quad 0 \\ \vdots&\quad \vdots&\quad&\quad \vdots \\ \nabla _{x_1} h_{m_1} (x_1)&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad \nabla _{x_2} h_{m_1+1} (x_2)&\quad&\quad 0 \\ \vdots&\quad \vdots&\quad&\quad \vdots \\ 0&\quad \nabla _{x_2} h_{m_1+m_2} (x_2)&\quad&\quad 0 \\ 0&\quad 0&\quad \ddots&\quad 0 \\ \vdots&\quad \vdots&\quad&\quad \vdots \\ \vdots&\quad \vdots&\quad 0&\quad \nabla _{x_n} h_{m-m_n+1} (x_n) \\ \vdots&\quad \vdots&\quad \vdots&\quad \vdots \\ 0&\quad 0&\quad 0&\quad \nabla _{x_n} h_{m} (x_n) \end{array} \right), \end{aligned}$$

whereas $\nabla _y g(x,x)$ is given by

$$\begin{aligned} \left( \begin{array}{ccccccc} \nabla _{y_1} g_1 (x_1,x_1)&\quad \cdots&\quad \nabla _{y_1} g_{m_1} (x_1,x_1)&\quad 0&\quad \cdots&\quad \cdots&\quad 0 \\ 0&\quad \cdots&\quad 0&\quad \ddots&\quad 0&\quad \cdots&\quad 0 \\ 0&\quad \cdots&\quad \cdots&\quad 0&\quad \nabla _{y_n} g_{m-m_n+1} (x_n,x_n)&\quad \cdots&\quad \nabla _{y_n} g_m (x_n,x_n) \end{array} \right). \end{aligned}$$

Then, an easy calculation shows that the matrix $N(x, \lambda , w)$ from (8) is given by

$$\begin{aligned} N(x,\lambda ,w) = J_x L(x, \lambda ) + D \end{aligned}$$

with the diagonal matrix

$$\begin{aligned} D := \left( \begin{array}{ccc} \sum _{i=1}^{m_1} \frac{\lambda _i}{w_i} \nabla _{y_1} g_i (x_1,x_1) \nabla _{x_1} h_i (x_1)&\quad&\quad 0 \\&\quad \ddots&\quad \\ 0&\quad&\quad \sum _{i=m-m_n+1}^{m} \frac{\lambda _i}{w_i} \nabla _{y_n} g_i (x_n,x_n) \nabla _{x_n} h_i (x_n) \end{array} \right). \end{aligned}$$

In view of assumption (a) together with $\lambda , w > 0$, it follows that $J_x L(x, \lambda )$ is a $P$-matrix and the diagonal matrix $D$ is positive semidefinite. This implies that $N(x,\lambda , w)$ is nonsingular for all positive $w$, and then from Theorem 3 we obtain the thesis. $\square$

We give below a specialization which deals with the most important case of Theorem 10: the case in which the constraints are bound constraints of the type

$$\begin{aligned} u_i (y_i,x_i)&:= y_i - a_i x_i \le c_i \quad \forall i = 1, \ldots , n \quad \text{ and} \end{aligned}$$

(29)

$$\begin{aligned} l_i (y_i,x_i)&:= - y_i + b_i x_i \le d_i \quad \forall i = 1, \ldots , n. \end{aligned}$$

(30)

For this class of QVIs, Theorem 10 easily gives the following corollary.

Corollary 6

Let $x \in \mathbb R ^n$ be given, and consider a QVI whose feasible set is defined by the constraints (29) and (30) and suppose that $F$ is $C^1$ around $x$. Assume that one of the following conditions hold:

• (a) $J F(x)$ is a $P_0$-matrix and $a_i < 1, b_i < 1$ for all $i = 1, \ldots , n$, or

• (b) $J F(x)$ is a $P$-matrix and $a_i \le 1, b_i \le 1$ for all $i = 1, \ldots , n$.

Then $J\!H(x,\lambda ,w)$ is nonsingular for all positive $\lambda$ and $w$.

In principle, QVIs with box constraints can be viewed as a subclass of QVIs with linear constraints and variable right-hand sides, see (23). However, the conditions we got here are somewhat weaker. Note in particular that the conditions in Theorem 8 require $J\!F$ to be diagonally dominant with positive diagonal elements, which implies that $J\!F$ must be $P_0$, while a $P_0$ matrix is not necessarily diagonally dominant.

3.5 Bilinear constraints

We conclude this section on nonsingularity results for $J\!H$ by considering the case of bilinear constraints which can be considered as a natural variant of the case of (linear) constraints with variable right-hand side in which the right-hand sides are fixed, but the coefficients of the linear part vary. Specifically, we consider a QVI in which the feasible set is defined by some convex “private” constraints $q_i(y) \le 0$ (that depend only on $y$) and some bilinear constraints of the form

$$\begin{aligned} x^{\scriptscriptstyle T}Q_i y - c_i \le 0 \end{aligned}$$

in which each matrix $Q_i$ is symmetric and positive semidefinite. Hence we consider constraints of the form

$$\begin{aligned} g(y,x) := \left(\begin{array}{c} q_1(y)\\ \vdots \\ q_p(y) \\ x^{\scriptscriptstyle T}Q_1 y - c_1\\ \vdots \\ x^{\scriptscriptstyle T}Q_b y - c_b \end{array}\right) \le 0. \end{aligned}$$

(31)

In order to deal with these constraints we give a preliminary result on QVIs in which the feasible set satisfies the condition

$$\begin{aligned} \nabla _x h(x) = \nabla _y g(x,x) \, D_+, \end{aligned}$$

(32)

where $D_+$ is a diagonal matrix with nonnegative entries. Although this is a technical result, it is the key to the analysis of QVIs with bilinear constraints.

Theorem 11

Suppose that Assumptions 1 and 2 hold. Let $x \in \mathbb R ^n$ and $\lambda > 0$ be given. Assume that $g$ and $h$ satisfy Eq. (32) in $x$, and that $J_x L(x, \lambda )$ is a positive definite matrix. Then $J\!H(x,\lambda ,w)$ is nonsingular for all positive $w$.

Proof

It is easy to see that the matrix $M$ from Corollary is given by

$$\begin{aligned} M(x,\lambda ) = D_+ \, \nabla _y g(x,x)^{\scriptscriptstyle T}J_x L(x, \lambda )^{-1} \nabla _y g(x,x), \end{aligned}$$

which is the product of a diagonal matrix with nonnegative entries and a positive semidefinite matrix. It is well known that a matrix with this form is $P_0$, and then by Corollary 2 the thesis holds. $\square$

Now, it is not difficult to see that the constraints (31) satisfy condition (32) with $D_+$ having the first $p$ entries equal to 1 and the last $b$ entries equal to 2. Therefore, the nonsingularity of $J\!H$ follows immediately from Theorem 11.

Corollary 7

Consider the constraints (31), with each $q_i, \,i=1, \ldots , p$, convex and $C^2$ and each $Q_j, \,j=1,\ldots ,b$, positive semidefinite and symmetric and suppose that $F$ is $C^1$. Let $x \in \mathbb R ^n$ and $\lambda > 0$ be given and assume that $J_x L(x, \lambda )$ is a positive definite matrix. Then $J\!H(x,\lambda ,w)$ is nonsingular for all positive $w$.

Note that $J_x L(x, \lambda )$ is certainly positive definite if either $F$ is strongly monotone, or at least one $q_i$ is strongly convex or at least one $Q_j$ is positive definite.

4 Boundedness

In this section, we consider conditions guaranteeing that a sequence generated by Algorithm 1 is bounded and, therefore, has an accumulation point. We first discuss a general result and then its application to the moving set case. Application of the general result to the remaining settings considered before does not require any specific investigation, so we conclude the section with a few more examples and general considerations.

4.1 General boundedness conditions

We begin with a general result that shows that under a sort of coercivity condition [(a1) below] and constraint qualification [(a2) below] we can guarantee boundedness of the sequence generated by Algorithm 1. We recall that we assume that $K(x)$ is defined by (2) and that $h(x) := g(x,x)$.

Theorem 12

Let the setting and the assumptions of Theorem 2 be satisfied and suppose, in addition, that

• (a1) $\displaystyle \lim \nolimits _{\Vert x \Vert \rightarrow \infty } \left\Vert \max \{0, h(x)\} \right\Vert = \infty$,

• (a2) for all $x \in {\mathbb{R }}^n$ there exist a $d$ such that $\nabla _yg_i(x,x) ^{\scriptscriptstyle T}d < 0$ for all $i\in \{ i: h_i(x) \ge 0\}$.

Then any sequence generated by Algorithm 1 remains bounded, and any accumulation point is a solution of the QVI.

Proof

By Theorem 2(a), it is enough to show that $\Vert H (x, \lambda , w)\Vert$ has bounded level sets over $Z_I$. To this end, suppose that a sequence $\{ (x^k, \lambda ^k, w^k) \} \subseteq Z_I$ exists such that $\lim _{k \rightarrow \infty } \,\Vert (x^k, \lambda ^k, w^k) \Vert = \infty$. We will show that $\Vert H(x^k, \lambda ^k, w^k) \Vert \rightarrow \infty$ as $k \rightarrow \infty$.

We first claim that the sequence $\{ x^k \}$ is bounded. Assume we have $\Vert x^k\Vert \rightarrow \infty$. Then condition (a1) would imply $\Vert \max \{0,h(x^k)\}\Vert \rightarrow \infty$. Hence there would exist an index $j \in \{1,\ldots ,m\}$ such that, on a suitable subsequence, $h_j(x^k) \rightarrow +\infty$, and therefore also $\Vert h(x^k) + w^k \Vert \rightarrow \infty$ since $w^k > 0$. But this would imply $\Vert H (x^k, \lambda ^k, w^k ) \Vert \rightarrow \infty$ and gives the desired contradiction. Hence it remains to consider the case in which $\Vert (\lambda ^k, w^k)\Vert \rightarrow \infty$ and $\{x^k\}$ is bounded.

Suppose that $\Vert w^k \Vert \rightarrow \infty$ and $\{x^k\}$ is bounded. Then $\{ h(x^k) \}$ is also bounded due to the continuity of $h$. We therefore obtain $\Vert h(x^k) + w^k \Vert \rightarrow \infty$. This, in turn, implies $\Vert H(x^k, \lambda ^k, w^k) \Vert \rightarrow \infty$ which, again, is a contradiction. Thus we have to consider only the case where $\Vert \lambda ^k\Vert \rightarrow \infty$ and $\{(x^k, w^k)\}$ is bounded.

For $\Vert \lambda ^k \Vert \rightarrow \infty$, let $J_\lambda$ be the set of indices such that $\{ \lambda ^k_j \} \rightarrow \infty$, whereas, subsequencing if necessary, we may assume that the remaining components stay bounded. Without loss of generality, we may also assume that $x^k \rightarrow \bar{x}$ and $w^k \rightarrow \bar{w}$. If, for some $j \in J_\lambda$, we have $\bar{w}_j > 0$, it follows that $\lambda ^k_j w^k_j \rightarrow + \infty$ and, therefore, again $\Vert H(x^k, \lambda ^k, w^k) \Vert \rightarrow \infty$. Consequently, it remains to consider the case where $\bar{w}_j = 0$ for all $j \in J_\lambda$.

Since $(x^k, \lambda ^k, w^k)$ belongs to $Z_I$, we have $h_j (x^k) + w^k_j > 0$ which implies $h_j (\bar{x}) \ge 0$ for all $j \in J_\lambda$. Hence we can apply condition (a2) and obtain a vector $d$ such that $\nabla _y g_j(\bar{x},\bar{x}) ^{\scriptscriptstyle T}d < 0, \, \forall j \in J_\lambda .$ This implies

$$\begin{aligned} \lim _{k \rightarrow \infty } L(x^k, \lambda ^k) ^{\scriptscriptstyle T}d&= \lim _{k \rightarrow \infty } \left( F(x^k)^{\scriptscriptstyle T}d + \sum _{j \not \in J_\lambda } \lambda ^k_j \nabla _y g_j(x^k,x^k)^{\scriptscriptstyle T}d\right) \\&+ \lim _{k \rightarrow \infty } \left( \sum _{j \in J_\lambda } \lambda ^k_j \nabla _y g_j(x^k,x^k)^{\scriptscriptstyle T}d \right) = - \infty \end{aligned}$$

since the first term is bounded (because $\{ x^k \} \rightarrow \bar{x}$ and the functions $F$ and $\nabla _y g$ are continuous, and because all sequences $\{\lambda ^k_j\}$ for $j \not \in J_\lambda$ are bounded by definition of the index set $J_\lambda$), whereas the second term is unbounded since $\lambda ^k_j \rightarrow + \infty$ and $\nabla _y g_j(\bar{x}, \bar{x} )^{\scriptscriptstyle T}d < 0$ for all $j \in J_\lambda$. Using the Cauchy–Schwarz inequality, we therefore obtain

$$\begin{aligned} \Vert L (x^k, \lambda ^k) \Vert \, \Vert d \Vert \ge | L (x^k, \lambda ^k) ^{\scriptscriptstyle T}d | \rightarrow \infty \end{aligned}$$

for $k \rightarrow \infty$. Since $d$ is a fixed vector, this implies $\Vert L (x^k, \lambda ^k) \Vert \rightarrow \infty$ which, in turn, implies $\Vert H(x^k, \lambda ^k, w^k) \Vert \rightarrow \infty$ for $k \rightarrow \infty$. This contradiction, together with Theorems 1 and 2, completes the proof. $\square$

Note that condition (a1) in Theorem 12 guarantees boundedness of the $x$- and $w$-parts, whereas (a2) is needed for the $\lambda$-part. In principle, if we knew an upper bound for the multipliers value, we could add this bound to the constrained equation reformulation of the KKT system and dispense with assumption (a2) altogether; we do not elaborate further on this idea for lack of space.

Condition (a1) is a mild coercivity condition that implies neither the boundedness of $K(x)$ for any $x$ nor the existence of a compact set $K$ such that $K(x) \subseteq K$ for all $x$, as one might think at first sight.

Example 4

Consider a problem with $K(x) = \{ y \in {\mathbb{R }} \, | \, y + x^2 \le 1\}$. In this case, for every $x$, the set $K(x)$ is unbounded and yet (a1) is easily seen to hold, since $h(x) = x+x^2 -1$.

Example 5

Consider a problem with $K(x) = \{ y \in {\mathbb{R }}^2 \, | \, \Vert y + x\Vert ^2 \le 1\}$. In this case, for every $x$, the set $K(x)$ is a ball of radius 1 and center in $-x$. We have $\cup _{x\in {\mathbb{R }}^n} K(x) = {\mathbb{R }}^n$. But $h(x) = 4\Vert x\Vert ^2 -1$ and so (a1) holds.

However, uniform boundedness of $K(x)$ does imply (a1) if some, very common and natural, further structure is assumed. So suppose $K(x) = K \cap K^{\prime }(x)$, i.e. suppose that $K(x)$ is given by the intersection of a fixed set $K$ and a point to set mapping $K^{\prime }$. Analytically, this simply means that if $K(x) = \{ y\in {\mathbb{R }}^n \, | \, g(x,y) \le 0 \}$, then some of the $g_i$ actually only depend on $y$. Obviously, if $K$ is bounded, $K(x)$ is uniformly bounded when $x$ varies. In the proposition below we assume for simplicity that $K$ is a bounded polyhedron (a quite common case, but see the remark following the proposition for a simple generalization).

Proposition 1

Let $K(x)$ be defined by (2) with $g$ continuous and convex in $y$ for every $x\in {\mathbb{R }}^n$. Suppose that the first $p$ inequalities of $g$ are of the form $Ay \le b$ and that the polyhedron defined by these inequalities is bounded. Then (a1) in Theorem 12 holds.

Proof

Denote by $K$ the bounded polyhedron defined by the inequalities $Ay \le b$. By Hoffman’s error bound, we know there exists a positive constant $c$ such that for every $x\in {\mathbb{R }}^n$ we have $\mathrm{dist}(x, K) \le c\, \Vert \max \{0, Ax-b\}\Vert$. Since $K$ is bounded, this shows that $\lim _{\Vert x \Vert \rightarrow \infty } \left\Vert \max \{0, Ax-b\} \right\Vert = \infty$. But then (a1) in Theorem 12 follows readily.

Remark 4

It is clear that the polyhedrality of the set $K$ is only used to deduce that an error bound holds. Therefore, it is straightforward to generalize the above result in the following way: Suppose that the first inequalities of $g$ define a bounded set $K = \{ g_i(y) \le 0, i = 1, \ldots , p\}$ and that an error bound holds for this system of $p$ inequalities. Then (a1) in Theorem 12 holds. The literature on error bounds is vast and there are many conditions that ensure the error bound condition, polyhedrality is just one of them. We refer the interested reader to [18, 43].

Condition (a2) in Theorem 12 is a very mild constraint qualification. It is related to the well-known extended Mangasarian–Fromovitz constraint qualification (EMFCQ) for a system of inequalities.

Definition 1

We say that a system of continuously differentiable inequalities $f(x)\le 0$, with $f:{\mathbb{R }}^n\rightarrow {\mathbb{R }}^m$, satisfies the EMFCQ if, for all $x \in \mathbb R ^n$, there exists a vector $d \in \mathbb R ^{n}$ such that $\nabla f_i(x)^{\scriptscriptstyle T}d < 0$, for all $i$ such that $f_i(x) \ge 0$.

For each given $x$, the set $K(x)$ is defined by the system of inequalities $g(y,x) \le 0$. It is then clear that condition (a2) is the requirement that an EMFCQ-like conditions holds just at the point $y=x$ and that this is a much weaker requirement than requiring the EMFCQ to hold for the system $g(y,x) \le 0$. We give an example to clarify this point.

Example 6

Consider a problem with $K(x) = \{ y \in {\mathbb{R }} \mid y^2 + x^2 -1 \le 0\}$. We have $\nabla _yg(x,x) = 2x$. It is clear that we can find a $d\in {\mathbb{R }}$ such tht $2xd <0$ at any point except at $x=0$. Therefore, (a2) holds because we have $h(0) < 0$. The EMFCQ, instead, is not satisfied for the set $K(1)$. In fact $\nabla _yg(y,1) = 2y$ and for $y=0$ it is immediate to verify that the EMFCQ fails. It is interesting to observe that for this problem also (a1) clearly holds.

Furthermore, if $x$ is greater than 1, we have $K(x) = \varnothing$, hence this simple example also shows that (a1) and (a2) together do not imply $K(x) \ne \varnothing$ for all $x$. The latter is a condition often encountered in papers dealing with algorithms for the solution of QVIs.

Armed with the developments so far, we can now study the applicability of Theorem 12 to the moving set case, which is the only setting, among those considered in the previous section, for which an additional analysis is useful.

4.2 The moving set case

Consider the QVI structure defined in Sect. 3.2:

$$\begin{aligned} K(x) := c(x) + Q = \{y \in {\mathbb{R }}^n \, | \, q(y - c(x)) \le 0\}, \quad Q := \{y \in {\mathbb{R }}^n \, | \, q(y) \le 0\}. \end{aligned}$$

We recall that, in the previous section, we have given sufficient conditions for nonsingularity of $J\!H$. Such conditions presuppose that $\Vert Jc(x)\Vert \le 1$ for all $x \in {\mathbb{R }}^n$. In the next proposition, we show that if the constraints $q(x) \le 0$ define a full-dimensional bounded set and $\Vert Jc(x)\Vert$ is uniformly bounded away from 1, then conditions (a1) and (a2) of Theorem 12 hold.

Proposition 2

In the setting described above, assume that $c$ and $q$ are continuously differentiable. Suppose that:

• (b1) $\Vert Jc(x)\Vert \le \alpha < 1$ for all $x \in {\mathbb{R }}^n$;

• (b2) $Q$ is compact and the system $q(y) \le 0$ satisfies Slater’s condition, i.e. there exists $\bar{y}$ such that $q(\bar{y}) < 0$.

Then conditions (a1) and (a2) of Theorem 12 hold.

Proof

Since $\Vert Jc(x)\Vert \le \alpha$ for all $x \in {\mathbb{R }}^n$, the Cauchy–Schwarz inequality implies $y^{\scriptscriptstyle T}Jc(x) y \le \alpha \Vert y\Vert ^2$ for all $x, y \in {\mathbb{R }}^n$. Therefore, $y^{\scriptscriptstyle T}(I - Jc(x)) y \ge (1 - \alpha ) \Vert y\Vert ^2$ for all $x, y \in {\mathbb{R }}^n$, hence the function $x-c(x)$ is strongly monotone on ${\mathbb{R }}^n$ and, consequently, $\lim _{\Vert x\Vert \rightarrow \infty } \Vert x- c(x) \Vert = \infty$. Now, since $q_i$ is convex for all components $i$, it follows that $\max \{ 0, q_i \}$ and, therefore, also $\Vert \max \{ 0, q (z) \} \Vert$ is convex. Hence, the corresponding level sets are bounded for all levels if and only if at least one level set is bounded. But the level set with level zero is precisely the set $Q$ which was assumed to be compact. It therefore follows that all level sets of the function $z \mapsto \Vert \max \{ 0, q (z) \} \Vert$ are bounded. But then $\lim _{\Vert x\Vert \rightarrow \infty } \Vert x- c(x) \Vert = \infty$ implies $\lim _{\Vert x\Vert \rightarrow \infty } \Vert \max \{ 0, q (x - c(x)) \} \Vert = \infty$, hence condition (a1) holds.

To show that also (a2) is satisfied, we first note that $\nabla _y g(x,x) = \nabla q(x-c(x))$. Therefore, taking $d := \bar{y} - (x- c(x))$, with $\bar{y}$ being the Slater point from assumption (b2), the convexity of $q_i$ implies

$$\begin{aligned} 0 > q ( \bar{y} ) \ge q_i ( x - c(x)) + \nabla q_i (x - c(x))^{\scriptscriptstyle T}\big ( \bar{y} - (x - c(x) \big ) \end{aligned}$$

for all components $i$ such that $h_i (x) = q_i ( x - c(x) ) \ge 0$. But this immediately gives $\nabla _y g_i(x,x) ^{\scriptscriptstyle T}d < 0$ for all $i$ with $h_i(x) \ge 0$. $\square$

4.3 Final examples and comments

We complete our discussion by giving a few additional examples on which we apply the results of both this and the previous section in order to show the ability of our algorithm to solve problems that are not solvable by other methods. This will also give us the opportunity to discuss very briefly some existence implications of the results obtained so far.

An often used assumption in the analysis of algorithms and also in many existence proofs is that either $K(x)$ is nonempty for all $x\in {\mathbb{R }}^n$ or that there exists a convex compact set $T\subset {\mathbb{R }}^n$ such that $K(T) \subseteq T$ and $K(x)$ is nonempty for all $x\in T$. The following example shows that this assumption is not implied by our conditions.

Example 7

Consider a one dimensional QVI with $F(x) = x^3$ and $K(x) = \{y \in {\mathbb{R }}^n \, | \, y^2 + x^2 + x^4 - 1 \le 0\}$. First of all note that $K(x) = \varnothing$ if $x\not \in [-a,a]$, where $a\approx 0.7862$ is the only positive root of the equation $x^2 + x^4 =1$. Furthermore, it is not difficult to see that there cannot exist a convex compact set $T$ (which would be a closed interval in our case) such that $K(T) \subseteq T$ holds and $K(x)$ is nonempty for all $x\in T$. In fact, it should be $T\subseteq [-a, a]$ since otherwise $K(x)$ is empty for some $x\in T$. Furthermore, $0$ can not belong to $T$, otherwise $K(0) = [-1,1] \not \subseteq T$. Then $T$ should be an interval of either all negative or all positive numbers. But if nonempty, $K(x)$ always contains both positive and negative points.

Nevertheless, we can show that the conditions of Theorem (a) are satisfied. We have $h(x) = 2x^2 + x^4 -1$, so that $\nabla _y g(x,x) \nabla _x h(x) = (2x) (4x+4x^3) = 8(x^2 + x^4) \ge 0$. Furthermore $J_xL(x, \lambda ) = 3x^2 + 2\lambda$ which, for every $x$ and positive $\lambda$, is positive. So Theorem (a) tells us that $J\!H(x, \lambda , w)$ is nonsingular for any $x$ and positive $\lambda$ and $w$.

We next verify that also the assumptions of Theorem 12 are met. Condition (a1) is obvious from the expression of $h(x)$, so we consider (a2). We have $\nabla _yg(x,x) = 2x$, and if $x\ne 0$, it is sufficient to take $d=-x$ to have $\nabla _yg(x,x) d <0$. If $x=0$, this is not possible, but in this case we also have $h(x) <0$ so that (a2) is satisfied. We can then conclude that every sequence generated by our interior-point method will be bounded and that every limit point is a solution of the QVI. Note that this also gives an algorithmic proof of the existence of a solution. We do not know any method that could provably solve this example. Also proving existence by using other known results seems not obvious.

As far as we are aware of, all methods for which convergence to a solution can be proved make assumptions that imply the existence of a (at least locally) unique solution and require the function $F$ to be strongly monotone. In the following example, we present a problem with a monotone, but not strongly monotone $F$, that has infinitely many solutions and for which we can prove convergence of our method.

Example 8

Consider again a one dimensional problem with

$$\begin{aligned} F(x)\, =\, \left\{ \begin{array}{lll} -(x+1)^4&\qquad \text{ if}&\quad x \le -1, \\ 0&\qquad \text{ if}&\quad x \in [-1,0], \\ x^4&\qquad \text{ if}&\quad x \ge 0 \end{array}\right. \end{aligned}$$

and $K(x)=\{ y \in {\mathbb{R }} \, | \, -10 \le y \le -2x \}$. The function $F$ is monotone, but not strongly monotone, and the solutions of the problem are all points in $[-1,0]$. The assumptions of Corollary 6 are easily checked to be satisfied; in fact $a_1 = -2, \,b_1 = 0$ and since $F$ is monotone, its Jacobian is positive semidefinite. Also condition (a1) in Theorem 12 holds trivially. Consider then (a2) in the same theorem. We have $h(x) = (-x -10, 3x)^{\scriptscriptstyle T}$, so that it is clear that at most one component of $h$ can be positive at any point, a fact that easily permits to check that also (a2) is satisfied. We conclude that the interior-point method is able to find a solution of this problem which admits infinitely many solutions.

We remarked already several times that, when it comes to algorithms, the most studied QVIs are those with a moving set type of constraints. One of the most interesting papers in this category is [34] where, among other things, a wider class of problems is studied under a condition, subsequently used also by other authors, which is implied by the moving set structure (which actually constitutes the main case in which the condition below can be verified). This condition is

$$\begin{aligned} \Vert \varPi _{K(x)}(z) - \varPi _{K(y)}(z)\Vert \le \alpha \Vert x - y\Vert , \quad \alpha < 1, \quad \forall x,y,z \in {\mathbb{R }}^n, \end{aligned}$$

(33)

where $\varPi _K$ denotes the Euclidean projector on $K$ and $\alpha$ is a positive constant whose exact definition is immaterial here. Roughly speaking, condition (33) is a strenghtening of a contraction property of the point-to-set mapping $K(\cdot )$. The following example shows that our assumptions do not imply condition (33).

Example 9

Consider the same problem as in the previous example and, in particular, its feasible set mapping $K(x)=\{ y \in {\mathbb{R }} \, | \, -10 \le y \le -2x \}$. Then

$$\begin{aligned} \Vert \varPi _{K(0)}(1) - \varPi _{K(1)}(1)\Vert = \Vert 0 - (-2) \Vert = 2 \le \alpha \Vert 0 - 1\Vert = \alpha \end{aligned}$$

implies $\alpha \ge 2$, so that condition (33) does not hold, whereas we have already mentioned in Example 8 that our method provably solves this example.

5 Numerical results

In this section we report the results obtained by a preliminary implementation of the method analyzed so far on a reasonably varied set of test problems. These results are intended to show the viability of our approach and to give the reader a concrete feel for the practical behavior of the interior-point method on QVI problems. All the computations in this paper were done using Matlab 7.6.0 on an Ubuntu 10.04 64 bits PC with Intel(R) Core(TM) i7 CPU 870 and 7.8 GiB of RAM. A larger set of experiments and a more detailed analysis, with comparisons, is currently being performed and will be reported elsewhere.

5.1 Implementation details

The implemented algorithm corresponds exactly to the theoretical scheme given in Algorithm 1. In what follows we give some implementation details.

At step (S.2), Algorithm 1 calls for the solution of an $n+2m$ square linear system in order to determine the search direction $d^k$. However, this system is very structured and some simple manipulations permit to reduce its solution to that of a linear system of dimension $n$. More precisely, we must find a solution $(\bar{d}_1, \bar{d}_2, \bar{d}_3)$ of the following linear system of dimension $n+2m$

$$\begin{aligned} \left(\begin{array}{ccc} J_x L(x,\lambda )&\quad \nabla _y g(x,x)&\quad 0 \\ J_x h(x)&\quad 0&\quad I \\ 0&\quad \mathop {\mathrm{diag}}(w)&\quad \mathop {\mathrm{diag}}(\lambda ) \end{array}\right) \left(\begin{array}{c} d_1 \\ d_2 \\ d_3 \end{array}\right) = \left(\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\right), \end{aligned}$$

(34)

where all the quantities involved are defined in detail in Sect. 2. It is easy to verify, by substitution and by the fact that $w > 0$, that if we compute $\bar{d}_1$ as solution of

$$\begin{aligned}&\left( J_x L(x,\lambda ) + \nabla _y g(x,x) \mathop {\mathrm{diag}}(w^{-1} \circ \lambda ) J_x h(x) \right) d_1 \\&\quad = b_1 - \nabla _y g(x,x) \mathop {\mathrm{diag}}(w)^{-1} b_3 + \nabla _y g(x,x) \mathop {\mathrm{diag}}(w^{-1} \circ \lambda ) b_2 \end{aligned}$$

and $\bar{d}_2, \,\bar{d}_3$ by $\bar{d}_3 = b_2 - J_x h(x) \bar{d}_1$ and $\bar{d}_2 = \mathop {\mathrm{diag}}(w)^{-1} b_3 - \mathop {\mathrm{diag}}(w^{-1} \circ \lambda ) \bar{d}_3$, respectively, this is indeed a solution of (34). This shows clearly that the main computational burden in solving the linear system (34) is actually the solution of an $n \times n$ square linear system. In order to perform the linear algebra involved, we used Matlab’s linear system solver mldivide. The procedure just described has the advantage of reducing the dimension of the system as much as possible; however this might not always be the best strategy, since sparsity patterns could be lost. For example it might be more convenient, from this point of view, to eliminate just the $\lambda$ variables and then solve the resulting $n+m$ system in $x$ and $w$. Or solve directly the original $n + 2m$ system and leave to the solver the task of exploiting sparsity. This, as well as the choice of the most suitable linear solver, along with numerical procedures to deal with singularities, are very important issues that can have huge practical impact. We are currently investigating on these topics and will report on this research elsewhere.

In the line search at step (S.3) of Algorithm 1, we take $\beta = 0.5, \,\gamma = 10^{-2}$ and $\xi = 2m$. In order to stay in $Z_I$ we preliminarily rescale $d^k= (d^k_x, d^k_\lambda , d^k_w)$. First we analytically compute a positive constant $\alpha$ such that $\lambda ^k + \alpha d^k_\lambda$ and $w^k + \alpha d^k_w$ are greater than $10^{-10}$. This ensures that the last two blocks in $z^k + \alpha d^k$ are in the interior of ${\mathbb{R }}^{2m}_+$. Then, if necessary, we further reduce this $\alpha$ until $h(x^k + \alpha d^k_x) + w^k + \alpha d^k_w \ge 10^{-10}$ thus finally guaranteeing that $z^k + \alpha d^k$ belongs to $Z_I$. In this latter phase, an evaluation of $h$ is needed for each bisection. At the end of this process, we set $d^k \leftarrow \alpha d^k$ and then perform the Armijo line-search.

The value of $\rho ^k$ is set to $0.1$. This is only changed, and increased by $0.1$, if in the previous iteration the step size $t_k$ is smaller than $0.1$. Should $\rho ^k$ reach the value of $0.9$, it is reset to $0.1$ in the following iteration.

The stopping criterion is based on an equation reformulation of the KKT conditions which uses the Fischer-Burmeister function that, we recall, is defined by $\phi (a,b) = \sqrt{a^2 + b^2} - (a+b)$ and has the property that $\phi (a,b) = 0$ if and only if $a\ge 0, b\ge 0, ab =0$. The equation reformulation is then defined by

$$\begin{aligned} V(x, \lambda )\,=\, \left( \begin{array}{c} L(x, \lambda )\\ (\phi (\lambda _i, - g_i(x,x)))_{i=1}^m \end{array} \right). \end{aligned}$$

The main termination criterion is $\Vert V(x^k, \lambda ^k)\Vert _\infty \, \le \, 10^{-4}$. The iterations are also stopped if the number of iterations exceeds 1,000 or the running time exceeds 1 h.

5.2 Test problems and numerical results

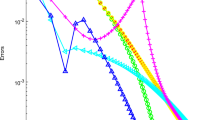
We solved several test problems whose detailed description can be found in [17] and in addition also Example 3 in Sect. 3, and Examples 7 and 8 in Sect. 4. Here we report a few details to make the presentation as self-contained as possible; nevertheless, for lack of space, we refer the interested reader to [17] for a complete description. In Table 1 we report, for each problem,

• the number $n$ of variables;

• the number $m$ of the constraints defining the feasible set $K(x)$ and, among these,

• the number $m_c$ of constraints that depend on $x$;

• the source of the problem.

The functions of the QVIs are always linear, except for Wal2, Wal5, Box2, Box3, Ex7, Ex8, which are non linear. The constraints of the QVIs are as follows:

• OutZ40, OutZ41, OutZ43, OutKZ1 (all), Scrim22, Box (all), MovSet4 (all), RHS2B1, Ex3, Ex8 : linear (in $x$ and $y$)

• OutZ42, OutZ44, KunR (all), Wal (all), MovSet3 (all) , RHS1A1, Ex7 : non linear (in at least $x$ or $y$).

Problems OutZ (all), MovSet (all), Box (all) and RHS (all) are purely academic problems, while the remaining problems correspond to some kind of engineering or economic models. A few more details on the test problems are given below.

Table 1 Problems, dimensions, and sources

• OutZ40, OutZ41, OutZ42, OutZ43, OutZ44: small academic problems from [40], where they were used to test a Newton type method;

• OutKZ31, OutKZ41: QVI model of an elastic body in contrast to a rigid obstacle with Coulomb friction (friction coefficient = 10), taken from Example 11.1 in [39]; the two problems differ in the fragmentation degree of the obstacle in identical segments (in OutKZ31 the obstacle is divided into 30 segments, in OutKZ41 the obstacle is divided into 40 segments);

• Scrim22: dynamic competition on networks QVI model taken from [46], with time instants $\{0, \ldots , 1200\}$;

• KunR11, KunR12, Kun21, KunR22, Kun31, KunR32: discretization of an infinite dimensional QVI formulation of the Stefan problem (described in (3.4), (3.5) in [31], with $p = 2, \; \varOmega = \big \{ (z^1, z^2) \in \mathbb R ^2 \mid 0 < z^1, z^2 < 1 \big \}, \; j_c (t) := t^2$); the discretization is performed by using forward finite differences; the six problems differ in the discretization degree $N$ and in the boundary function $u_1$ used (in KunR11, KunR21, KunR31: $N=50$; in KunR12, KunR22, KunR32: $N=70$; in KunR11, KunR12: $u_1(x,y):=x+y+1$; in KunR21, KunR22: $u_1(x,y):=1-0.1(\sin (2\pi x) + \cos (2\pi y))$; in KunR31, KunR32: $u_1(x,y):=e^{x+y}$);

• Wal2, Wal3, Wal5: QVI reformulation of a Walrasian pure exchange economy with utility function without production from [13]; the three problems differ in the number of agents, the number of exchanged goods, the utility functions and the initial endowments (these are taken from Example A.10 in [15]);

• MovSet3 (all) MovSet4 (all): problems with the structure analyzed in Sect. 3.2, see [17] for the details;

• Box2A, Box2B, Box3A, Box3B: problems with the structure analyzed in Sect. 3.4, see [17] for the details;

• RHS1A1, RHS1B1, RHS2A1, RHS2B1: problems with the structure analyzed in Sect. 3.3, see [17] for the details.

Finally, the following is a list of problems for which the key nonsingularity assumption of JH can be guaranteed based on the results in Sect. 3:

• OutZ43, MovSet3A1, MovSet3A2, MovSet4A1, MovSet4A2,

• Box2A, Box3A, RHS1A1, Ex3, Ex7, Ex8.

Note that the structure of problems OutKZ31 and OutKZ41 is the one analyzed in Example 2 and therefore these problems are nonsingular if the friction coefficient $\phi$ is small. However in the test problem we used, we took the friction coefficient large to make the problems more difficult. More in general, we included many problems whose nonsingularity is not guaranteed (i.e. we actually do not know whether nonsingularity is satisfied or not) in order to test the robustness of the method.

In Table 2 we report the numerical results of our algorithm on the test problems described above. For each problem we list

• the $x$-part of the starting point (the number reported is the value of all components of the $x$-part of the starting point);

• the number of iterations, which is equal to the number of evaluations of $J\!H$;

• the number of evaluations of the constraints vector $g$;

• the number of evaluations of $F$, which is equal to the number of evaluations of the gradients of the constraints vector $\nabla g$;

• the value of the $KKT$ violation measure $V(x, \lambda )$ at termination.

Note that for the $(\lambda ,w)$-part of the starting vector, we always used $\lambda ^0=5$ and further set $w^0=\max (5, 5 - h(x^0))$, so as to ensure that the starting point is “well inside” $Z_I$.

Table 2 Potential reduction algorithm numerical results for QVIs

We see that overall the algorithm seems efficient and reliable and able to solve a wide array of different problems. The four failures deserve a few more comments. The failures on KunR31 and KunR32 are due to the limit on computing time (3,600 s), but the algorithm actually appears to be converging in both cases. In fact, the value of $V(x, \lambda )$ at the last iteration is $1.1\times 10^{-3}$ and $1.3\times 10^{-3}$, respectively. In the case of Box3A and Box3B instead, difficulties arise because of an almost singularity of the linear system giving the search direction; this leads to a failure due to the inability of the algorithm to find a step-size satisfying the acceptance criterion (7).

In order to better gauge the robustness of our algorithm we also solved all the problems using a C version of the PATH solver with a Matlab interface downloaded from http://pages.cs.wisc.edu/~ferris/path/ and whose detailed description can be found in [12, 19]. PATH is a well-established and mature software implementing a stabilized Josephy–Newton method for the solution of Mixed Complementarity Problems and it can be used to solve the KKT conditions of a QVI, although with no theoretical guarantee of convergence in our setting. We used the same $x$-part for the starting point as we used in the testing of our method. For the $\lambda$ part, we considered two options. In the first we took $\lambda ^0=5$, therefore using exactly the same starting point we used in the testing of the interior-point algorithm. In the second option we set $\lambda ^0=0$; this latter alternative was considered because the choice of $\lambda ^0=5$ is geared towards our interior-point method, while $\lambda ^0=0$ seems more natural for PATH. It might be useful to remark that we run PATH with its default settings and the stopping criterions using by PRA and PATH are marginally different. In spite of this, the precision at the computed solution, measured in terms of $V(x, \lambda )$, is consistently comparable. In both the tested cases, PATH was not able to solve 4 problems (the failures are given in Table 3, where under the heading PATH (5) we report the timings for PATH with $\lambda ^0=5$ and analogously under PATH (0) we have the timings for PATH with $\lambda ^0=0$). These results seem to indicate that our method has the potential to become a very robust solver for the solution of the KKT conditions arising from QVIs.

Table 3 CPU times in seconds and failures (F)

The comparison of CPU times is somewhat more problematic. In fact one should take into account that, although the main computational burden in our algorithm is given by the solution of linear systems, a task very efficiently performed by the Matlab built-in function mldivide, we did use Matlab, an interpreted language, and furthermore, what we implemented is a straightforward version of our algorithm, with none of all those crash and recover techniques that are to be found in a well developed software as PATH. In spite of this, Sven Leyffer kindly suggested that having current CPU times would still be of interest, and so we report them in Table 3. Note that we do not report major, minor and crash iterations for PATH. In fact PRA and PATH are very unlike, and the meaning of “iteration” is so different in the two methods that we feel that, besides the number of failures, CPU time is the only other meaningful parameter to compare. These results show that even the current prototypical Matlab implementation of the interior-point method compares well to PATH, also in terms of computing times. The development of a more sophisticated C version of our method, fully exploiting its potential for parallelism, is currently under the way and more extended and detailed numerical results, along with more accurate comparisons, will be reported elsewhere.

6 Conclusions

We presented a detailed convergence theory for an interior-point method for the solution of the KKT conditions of a general QVI. We could establish convergence for a wide array of different classes of problems including QVIs with the feasible set given by “moving sets”, linear systems with variable right-hand sides, box constraints with variable bounds, and bilinear constraints. These results surpass by far existing convergence analyses, the latter all having a somewhat limited scope. In our view, the results in this paper constitute an important step towards the development of theoretically reliable and numerically efficient methods for the solution of QVIs.

A Appendix on monotonicity and Lipschitz properties

In this appendix we recall some well-known definitions and discuss some related results. Although the latter are also mostly well-known, in some cases we could not find in the literature the exact versions we needed. Therefore, for completeness we also report the proofs of these results.

We begin by recalling the definitions of several classes of functions.

Definition 2

Let $D \subseteq {\mathbb{R }}^n$ and $F: D \rightarrow {\mathbb{R }}^n$ be a given function. Then

• (a) $F$ is strongly monotone on $D$ with constant $\sigma$ if $\sigma >0$ and

  $$\begin{aligned} (x - y)^{\scriptscriptstyle T}\big ( F(x) - F(y) \big ) \,\ge \, \sigma \Vert x - y\Vert ^2, \quad \forall x, y \in D; \end{aligned}$$

  The largest $\sigma$ for which such a relation holds is termed the monotonicity modulus of $F$ on $D$:

  $$\begin{aligned} \sigma (D,F) \, :=\, \inf _{x\ne y, x,y \in D}\frac{(x - y)^{\scriptscriptstyle T}\big ( F(x) - F(y) \big )}{\Vert x-y\Vert ^2}. \end{aligned}$$

• (b) $F$ is co-coercive on $D$ with constant $\xi$ if $\xi >0$ and

  $$\begin{aligned} (x - y)^{\scriptscriptstyle T}\big ( F(x) - F(y) \big ) \,\ge \, \xi \Vert F(x) - F(y)\Vert ^2, \quad \forall x, y \in D; \end{aligned}$$

• (c) $F$ is Lipschitz continuous on $D$ with constant $L \ge 0$ if

  $$\begin{aligned} \Vert F(x) - F(y)\Vert \, \le \, L \Vert x - y\Vert , \quad \forall x, y \in D. \end{aligned}$$

  The smallest $L$ for which such relation holds is termed the Lipschitz modulus of $F$ on $D$:

  $$\begin{aligned} L(D,F) \, :=\, \sup _{x\ne y, x,y \in D} \frac{\Vert F(x) - F(y)\Vert }{\Vert x-y\Vert }. \end{aligned}$$

• (d) $F$ is a homeomorphism of $D$ onto $F(D)$ if $F$ is one-to-one on $D$ (that is $F(x) \ne F(y)$ whenever $x,y \in D, x \ne y$, or, in other words, $F$ has a single-valued inverse $F^{-1}$ defined on $F(D)$), and $F$ and $F^{-1}$ are continuous on $D$ and $F(D)$, respectively. $\square$

Characterizations of the Lipschitz and strong monotonicity moduli are given in the following result.

Proposition 3

Let $D \subseteq {\mathbb{R }}^n$ be an open, convex subset of ${\mathbb{R }}^n$ and let $F: D \rightarrow {\mathbb{R }}^n$ be a continuously differentiable function. Then the following statements hold:

• (a) $F$ is Lipschitz continuous on $D$ with constant $L$ if and only if $\Vert J\!F(x)\Vert \le L$ for all $x \in D$; consequently

  $$\begin{aligned} L(D,F) \, =\, \sup _{x\in D}\Vert J\!F(x)\Vert , \end{aligned}$$

  provided the $\sup$ on the right hand side is finite.

• (b) $F$ is strongly monotone on $D$ with constant $\sigma$ if and only if $h^{\scriptscriptstyle T}J\!F(x) h \ge \sigma \Vert h\Vert ^2$ for all $x \in D , \, h \in {\mathbb{R }}^n$; consequently

  $$\begin{aligned} \sigma (D,F) \, =\, \inf _{x\in D}\mu _m^s(J\!F(x)), \end{aligned}$$

  provided the $\inf$ on the right hand side is positive.

Proof

• (a) From Theorem 3.2.3 in [37], if $\Vert J\!F(x)\Vert \le L$ then $L$ is a Lipschitz constant for $F$ on $D$. Conversely, assume that

  $$\begin{aligned} \big \Vert F(x) - F(y) \big \Vert \le L \Vert x - y \Vert , \quad \forall x, y \in D \end{aligned}$$

  (35)

  holds. Applying the differential mean value theorem to each component function $F_i$ of $F$, it follows that, for any given $x, y \in D$, we can find suitable points $\xi ^{(i)} \in (x,y)$ such that

  $$\begin{aligned} F_i(x) - F_i (y) = \nabla F_i (\xi ^{(i)})^T (x-y) \quad \forall i = 1, \ldots , n. \end{aligned}$$

  Setting

  $$\begin{aligned} G(\xi ) := \left( \begin{array}{ccc}&\nabla F_1 (\xi ^{(1)})^T&\\&\vdots&\\&\nabla F_n (\xi ^{(n)})^T&\end{array} \right) \in {\mathbb{R }}^{n \times n}, \end{aligned}$$

  this can be rewritten in a compact way as

  $$\begin{aligned} F(x) - F(y) = G(\xi ) (x-y). \end{aligned}$$

  (36)

  Now, let $x \in D$ be fixed, and note that

  $$\begin{aligned} G( \xi ) \rightarrow J\!F (x) \end{aligned}$$

  (37)

  for any sequence $y \rightarrow x$ in view of the continuous differentiability of $F$. We now consider a particular sequence $y = x + td$ with a fixed (but arbitrary) vector $d \in {\mathbb{R }}^n \setminus \{ 0 \}$ and a sequence $t \downarrow 0$. Then (35) and (36) together imply

  $$\begin{aligned} \big \Vert G(\xi ) t d \big \Vert = \big \Vert F(x) - F(x + td) \big \Vert \le L \Vert t d \Vert . \end{aligned}$$

  Dividing by $t$ and subsequently letting $t \downarrow 0$ (note that $\xi$ still depends on $t$), we obtain

  $$\begin{aligned} \big \Vert J\!F(x) d \big \Vert \le L \Vert d \Vert \end{aligned}$$

  in view of (37). Since $d$ was taken arbitrarily, this implies $\Vert J\!F(x) \Vert \le L$, and this inequality is true for any vector $x \in D$.

• (b) See [37, Theorem 5.4.3]. $\square$

The following result gives a relation between the Lipschitz constants etc. of a given mapping $F$ and its inverse $F^{-1}$.

Proposition 4

Let a function $F: D\rightarrow {\mathbb{R }}^n$ be given where $D$ is an open subset of ${\mathbb{R }}^n$. Assume that two positive constants $\ell$ and $L$ exist such that

$$\begin{aligned} \ell \Vert x -y\Vert \le \Vert F(x) - F(y) \Vert \le L \Vert x-y\Vert , \quad \forall x, y \in D. \end{aligned}$$

(38)

Then $F$ is a homeomorphism from $D$ to $F(D)$ (which is an open set) and

$$\begin{aligned} \frac{1}{L}\Vert a-b\Vert \le \Vert F^{-1}(a) - F^{-1}(b) \Vert \le \frac{1}{\ell } \Vert a-b\Vert , \quad \forall a, b \in F(D), \end{aligned}$$

(39)

in particular, $F$ and $F^{-1}$ are Lipschitz continuous on $D$ and $F(D)$, respectively.

Proof

The first inequality from (38) implies that $F$ is one-to-one on $D$ (therefore the inverse $F^{-1}$ exists on $F(D)$), and that, setting $a = F (x)$ and $b = F (y)$, the second inequality in (39) holds. In particular, this implies that $F^{-1}$ is Lipschitz continuous on $F(D)$, hence continuous, so that $F(D) = (F^{-1})^{-1} (D)$, being the pre-image of a continuous map of the open set $D$, is also an open set. Finally, let $a, b \in F(D)$ be arbitrarily given. Setting $x = F^{-1} (a),y = F^{-1} (b)$, we obtain from the second inequality in (38) that

$$\begin{aligned} \Vert F^{-1} (a) - F^{-1} (b) \Vert = \Vert x - y \Vert \ge \frac{1}{L} \Vert F(x) - F(y) \Vert = \frac{1}{L} \Vert a - b \Vert , \end{aligned}$$

and this completes the proof. $\square$

The next result considers a strongly monotone and Lipschitz continuous mapping and provides suitable bounds for the moduli of Lipschitz continuity and strong monotonicity of the corresponding inverse function. We stress, however, that the constant of strong monotonicity of the inverse function provided by this result is really just an estimate and typically not exact. It seems difficult to find a stronger bound in the general context discussed here. In a more specialized situation, much better results can be obtained, see Proposition 6 below.

Proposition 5

Let $D \subseteq {\mathbb{R }}^n$ be an open set and $F: D \rightarrow {\mathbb{R }}^n$ be strongly monotone with modulus $\sigma$ and Lipschitz continuous with modulus $L$ on $D$. Then $F$ is co-coercive with constant $\frac{\sigma }{L^2}$. Furthermore, it holds that the inverse $F^{-1}$ exists on $F(D)$, is Lipschitz with constant $\frac{1}{\sigma }$ and strongly monotone with constant $\frac{\sigma }{L^2}$.

Proof

We can write

$$\begin{aligned} \big ( F(x) - F(y) \big )^{\scriptscriptstyle T}(x-y) \ge \sigma \Vert x - y \Vert ^2, \quad \forall x, y \in D \end{aligned}$$

and

$$\begin{aligned} \Vert F(x) - F(y) \Vert ^2 \le L^2 \Vert x - y \Vert ^2, \quad \forall x, y \in D \end{aligned}$$

by assumption. A combination of these two inequalities yields

$$\begin{aligned} \Vert F(x) - F(y) \Vert ^2 \le L^2 \Vert x \!-\! y \Vert ^2 \le \frac{L^2}{\sigma } \big ( F(x) \!-\! F(y) \big )^{\scriptscriptstyle T}(x-y), \quad \forall x, y \in D.\qquad \end{aligned}$$

(40)

Hence $F$ is co-coercive with constant $\frac{\sigma }{L^2}$.

By Proposition 4 we know that $F$ is a homeomorphism from $D$ to $F(D)$ and $F^{-1}$ is Lipschitz continuous with constant $\frac{1}{\sigma }$. Finally writing $a=F(x), b=F(y)$ in (40) gives

$$\begin{aligned} \big ( F^{-1}(a) - F^{-1}(b) \big )^{\scriptscriptstyle T}(a-b) \ge \frac{\sigma }{L^2} \Vert a - b \Vert ^2, \quad \forall a, b \in F(D). \end{aligned}$$

This completes the proof. $\square$

The following result gives an exact estimate of the Lipschitz and strong monotonicity moduli of the inverse of a function under the assumption that the mapping $F$ itself is a gradient mapping, i.e. that $F = \nabla f$ for a differentiable real-valued function $f$.

Proposition 6

Let $D \subseteq {\mathbb{R }}^n$ be an open convex set and $F: D\rightarrow {\mathbb{R }}^n$ be a gradient mapping. Assume that $F$ is strongly monotone with modulus $\sigma$ and Lipschitz continuous with modulus $L$ on $D$. Then the inverse function $F^{-1}$ exists on $F(D)$, is Lipschitz with modulus $\frac{1}{\sigma }$ and strongly monotone with modulus $\frac{1}{L}$.

Proof

The result can easily be derived from the Baillon–Haddad Theorem, see [1], when $D={\mathbb{R }}^n$. We give here a direct proof which is valid also when $D \ne {\mathbb{R }}^n$. In view of Proposition 5, we only have to verify the statement that $F^{-1}$ is strongly monotone with constant $\frac{1}{L}$.

To this end, first consider a symmetric positive definite matrix $A \in {\mathbb{R }}^{n \times n}$, let $A^{1/2}$ be the corresponding (unique) symmetric positive definite square root of $A$ so that $A^{1/2} A^{1/2} = A$, and let $A^{-1/2}$ be the inverse of $A^{1/2}$. Then the symmetry of $A^{1/2}$ together with the Cauchy–Schwarz inequality implies

$$\begin{aligned} \Vert d \Vert ^2 = d^{\scriptscriptstyle T}d = d^{\scriptscriptstyle T}A^{1/2} A^{-1/2} d \le \Vert A^{1/2} d \Vert \cdot \Vert A^{-1/2} d \Vert , \quad \forall d \in {\mathbb{R }}^n. \end{aligned}$$

Squaring both sides shows that

$$\begin{aligned} \Vert d \Vert ^4 \le \big ( d^{\scriptscriptstyle T}A d \big ) \big ( d^{\scriptscriptstyle T}A^{-1} d \big ), \quad \forall d \in {\mathbb{R }}^n \end{aligned}$$

(41)

holds. Since $F$ is strongly monotone, the Jacobian $J\!F(x)$ is positive definite for all $x \in D$; furthermore, since $F$ is a gradient mapping, this Jacobian is also symmetric. Hence we can apply inequality (41) to the matrix $A := J\!F(x)$ and obtain

$$\begin{aligned} \Vert d \Vert ^4&\le \big ( d^{\scriptscriptstyle T}J\!F(x) d \big ) \big ( d^{\scriptscriptstyle T}J\!F(x)^{-1} d \big ) \\&\le \big ( d^{\scriptscriptstyle T}J\!F(x)^{-1} d \big ) \Vert d \Vert ^2 \Vert J\!F(x) \Vert \\&\le \big ( d^{\scriptscriptstyle T}J\!F(x)^{-1} d \big ) L \Vert d \Vert ^2, \qquad \forall d \in {\mathbb{R }}^n, \end{aligned}$$

where the second inequality uses the Cauchy–Schwarz inequality once again, and the third inequality takes into account Proposition 3. This implies

$$\begin{aligned} \frac{1}{L} d^{\scriptscriptstyle T}d = \frac{1}{L} \Vert d \Vert ^2 \le \big ( d^{\scriptscriptstyle T}J\!F(x)^{-1} d \big ), \quad \forall d \in {\mathbb{R }}^n \forall x \in D. \end{aligned}$$

Since $J\!F(x)^{-1} = J\!F^{-1}(y)$ for $y = F(x)$ by the Inverse Function Theorem, this gives

$$\begin{aligned} \frac{1}{L} d^{\scriptscriptstyle T}d \le d^{\scriptscriptstyle T}J\!F^{-1}(y) d, \quad \forall d \in {\mathbb{R }}^n \forall y \in F(D). \end{aligned}$$

By a well-known result, see [37, Theorem 5.4.3] this is equivalent to saying that $F^{-1}$ is strongly monotone on $F(D)$ with constant $1/L$. $\square$

The sharper result from Proposition 6 regarding the modulus of strong monotonicity does, in general, not hold for non-gradient mappings, see the corresponding discussion and (counter-) example at the end of Sect. 3.2.