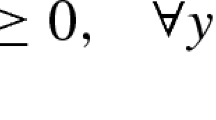Keywords

1 Introduction

Bilevel optimization problems model situations in which a sequential set of decisions are made: the leader chooses a decision to optimize its objective function, anticipating the response of the follower, who optimizes its objective function given the leader’s decision. Mathematically, we have the following optimization problem:

(12.1.1)

where f and g are the objectives for the leader and follower, respectively, c(x, y) ≥ 0 is a joint feasibility constraint, and d(x, y) ≥ 0 defines the feasible actions the follower can take. Throughout this survey, we assume all functions are at least continuously differentiable in all their arguments.

Our survey focuses on optimistic bilevel optimization. Under this assumption, if the solution set to the lower-level optimization problem is not a singleton, then the leader chooses the element of the solution set that benefits it the most.

1.1 Applications and Illustrative Example

Applications of bilevel optimization problems arise in economics and engineering domains; see [10, 24, 27,28,29, 78, 92, 111, 116] and the references therein. As an example bilevel optimization problem, we consider the moral-hazard problem in economics [72, 101] that models a contract between a principal and an agent who works on a project for the principal. The agent exerts effort on the project by taking an action \(a \in \mathcal {A}\) that maximizes its utility, where \(\mathcal {A} = \{ a | d(a) \geq 0\}\) is a convex set, resulting in output value o q with given probability p q(a) > 0, where \(q \in \mathcal {Q}\) and \(\mathcal {Q}\) is a finite set. The principal observes only the output o q and compensates the agent with c q defined in the contract. The principal wants to design an optimal contract consisting of a compensation schedule \(\{c_q\}_{q \in \mathcal {Q}}\) and a recommended action \(a \in \mathcal {A}\) to maximize its expected utility.

Since the agent’s action is assumed to be neither observable nor forcible by the principal, feasibility of the contract needs to be defined in order to guarantee the desired behavior of the agent. Two types of constraints are specified: a participation constraint and an incentive-compatibility constraint. The participation constraint says that the agent’s expected utility from accepting the contract must be at least as good as the utility U it could receive by choosing a different activity. The incentive-compatibility constraint states that the recommended action should provide enough incentive, such as maximizing its utility, so that the agent chooses it.

Mathematically, the problem is defined as follows:

where w(⋅) and u(⋅, ⋅) are the utility functions of the principal and the agent, respectively. The first constraint is the participation constraint, while the second constraint is the incentive-compatibility constraint. This problem is a bilevel optimization problem with a joint feasibility constraint.

1.2 Bilevel Optimization Reformulation as an MPEC

We assume throughout that the lower-level problem is convex with a nonempty, compact feasible region and that it satisfies a constraint qualification for all feasible upper-level decisions, x. Under these conditions, the Karush-Kuhn-Tucker (KKT) conditions for the lower-level optimization problem are both necessary and sufficient, and we can replace the lower-level problem with its KKT conditions to obtain a mathematical program with equilibrium constraints (MPEC) [82, 90, 98]:

$$\displaystyle \begin{aligned}{}[2] & \operatorname*{\mbox{minimize}}_{x,y,\lambda} && f(x,y) & \\ & \operatorname{\mbox{subject to}} && c(x,y) \geq 0 & \\ & && \nabla_y g(x,y) - \nabla_y d(x,y) \lambda = 0 & \\ & && 0 \leq \lambda \; \perp \; d(x,y) \geq 0, \end{aligned} $$
(12.1.2)

where ⊥ indicates complementarity, in other words, that either λ i = 0 or d i(x, y) = 0 for all i.

This MPEC reformulation is attractive because it results in a single-level optimization problem, and we show in the subsequent sections that this class of problems can be solved successfully. We note that when the lower-level problem is nonconvex, a solution of the MPEC may be infeasible for the bilevel problem [94, Example 1.1]. Thus, we consider only the case where the lower-level problem is convex when using the MPEC formulation.

In the convex case, the relationship between the original bilevel optimization problem (12.1.1) and the MPEC formulation (12.1.2) is nontrivial, as demonstrated in [30, 32] for smooth functions and [33] for nonsmooth functions. These papers show that a global (local) solution to the bilevel optimization problem (12.1.1) corresponds to a global (local) solution to the MPEC (12.1.2) if the Slater constraint qualification is satisfied by the lower-level optimization problem. Under the Slater constraint qualification, a global solution to the MPEC (12.1.2) corresponds to a global solution to the bilevel optimization problem (12.1.1). A local solution to the MPEC (12.1.2) may not correspond to a local solution to the bilevel optimization problem (12.1.1) unless stronger assumptions guaranteeing the uniqueness of multipliers are made, such as MPEC-LICQ, which is described in Sect. 12.2.2; see [30, 32] for details.

By using the Fritz-John conditions, rather than assuming a constraint qualification and applying the KKT conditions, we can ostensibly weaken the requirements to produce an MPEC reformulation [2]. However, this approach has similar theoretical difficulties with the correspondences between local solutions [31], and we have observed computational difficulties when applying MPEC algorithms to solve the Fritz-John reformulation.

1.3 MPEC Problems

Generically, we write MPECs such as (12.1.2) as

$$\displaystyle \begin{aligned}{}[2] & \operatorname*{\mbox{minimize}}_{z} && f(z) & \\ & \operatorname{\mbox{subject to}} && c(z) \geq 0 && \\ & && 0 \leq G(z) \; \perp \; H(z) \geq 0, \end{aligned} $$
(12.1.3)

where z = (x, y, λ) and where we summarize all nonlinear equality and inequality constraints generically as c(z) ≥ 0.

MPECs are a challenging class of problem because of the presence of the complementarity constraint. The complementarity constraint can be written equivalently as the nonlinear constraint G(z)TH(z) ≤ 0, in which case (12.1.3) becomes a standard nonlinear program (NLP). Unfortunately, the resulting problem violates the Mangasarian-Fromowitz constraint qualification (MFCQ) at any feasible point [108]. Alternatively, we can reformulate the complementarity constraint as a disjunction. Unfortunately, the resulting mixed-integer formulation has very weak relaxations, resulting in large search trees [99].

This survey focuses on practical theory and methods for solving MPECs. In the next section, we discuss the stationarity concepts and constraint qualifications for MPECs. In Sect. 12.3, we discuss algorithms for solving MPECs. In Sect. 12.4, we focus on software environments for specifying and solving bilevel optimization problems and mathematical programs with equilibrium constraints, before providing pointers in Sect. 12.5 to related topics we do not cover in this survey.

2 MPEC Theory

We now survey stationarity conditions, constraint qualifications, and regularity for the MPEC (12.1.3). The standard concepts for nonlinear programs need to be rethought because of the complementarity constraint 0 ≤ G(z)  ⊥ H(z) ≥ 0, especially when the solution to (12.1.3) has a nonempty biactive set, that is, when both G j(z ∗) = H j(z ∗) = 0 for some indices j at the solution z ∗.

We assume that the functions in the MPEC are at least continuously differentiable. When the functions are nonsmooth, enhanced M-stationarity conditions and alternative constraint qualifications have been proposed [119].

2.1 Stationarity Conditions

In this section, we define first-order optimality conditions for a local minimizer of an MPEC and several stationarity concepts. The stationarity concepts may involve dual variables, and they collapse to a single stationarity condition when a local minimizer has an empty biactive set. Unlike standard nonlinear programming, these concepts may not correspond to the first-order optimality of the MPEC when there is a nonempty biactive set.

One derivation of stationarity conditions for MPECs is to replace the complementarity condition with a set of nonlinear inequalities, such as G j(z)H j(z) ≤ 0, and then produce the stationarity conditions for the equivalent nonlinear program:

$$\displaystyle \begin{aligned} & \operatorname*{\mbox{minimize}}_{z} && f(z)\\ & \operatorname{\mbox{subject to}} && c_i(z) \geq 0 &&\forall i =1,\ldots,m\\ &&& G_j(z) \ge 0, H_j(z) \ge 0, G_j(z)H_j(z) \le 0 &&\forall j=1,\dots,p, {} \end{aligned} $$
(12.2.1)

where \(z \in \mathbb {R}^n\). An alternative formulation as an NLP is obtained by replacing G j(z)H j(z) ≤ 0 by G(z)TH(z) ≤ 0. Unfortunately, (12.2.1) violates the MFCQ at any feasible point [108] because the constraint G j(z)H j(z) ≤ 0 does not have an interior. Hence, the KKT conditions may not be directly applicable to (12.2.1).

Instead, stationarity concepts are derived from several different approaches: local analysis of the NLPs associated with an MPEC [90, 108]; Clarke’s nonsmooth analysis to the complementarity constraints by replacing them with the \(\min \) function [23, 108]; and Mordukhovich’s generalized differential calculus applied to the generalized normal cone [97]. The first method results in B-, weak-, and strong-stationarity concepts. The second and the third lead to C- and M-stationarity, respectively. These stationarity concepts coincide with each other when the solution has an empty biactive set.

We begin by defining the biactive index set \(\mathcal {D}\) (or denoted by \(\mathcal {D}(z)\) to emphasize its dependency on z) and its partition \(\mathcal {D}_{01}\) and \(\mathcal {D}_{10}\) such that

$$\displaystyle \begin{aligned} \mathcal{D} := \{ j \mid G_j(z)=H_j(z)=0\},\,\, \mathcal{D} = \mathcal{D}_{01} \cup \mathcal{D}_{10}, \mathcal{D}_{01} \cap \mathcal{D}_{10} = \emptyset. {} \end{aligned} $$
(12.2.2)

If we define an \(\text{NLP}_{\mathcal {D}_{01},\mathcal {D}_{10}}\)

$$\displaystyle \begin{aligned} &\operatorname*{\mbox{minimize}}_{z} && f(z)\\ & \operatorname{\mbox{subject to}} && c_i(z) \ge 0 &&\forall i=1,\dots,m\\ &&& G_j(z) = 0 && \forall j: G_j(z)=0, H_j(z)>0\\ &&& H_j(z) = 0 && \forall j: G_j(z)>0, H_j(z)=0\\ &&& G_j(z) = 0, H_j(z) \ge 0 &&\forall j \in \mathcal{D}_{01}\\ &&& G_j(z) \ge 0, H_j(z) = 0 &&\forall j \in \mathcal{D}_{10},\\ \end{aligned} $$
(12.2.3)

then z ∗ is a local solution to the MPEC if and only if z ∗ is a local solution for all the associated NLPs indexed by \((\mathcal {D}_{01},\mathcal {D}_{10})\). The number of NLPs that need to be checked is exponential in the number of biactive indices, which can be computationally intractable.

Like many other mathematical programs, the geometric first-order optimality conditions are defined in terms of the tangent cone. A feasible point z ∗ is called a geometric Bouligand- or B-stationary point if \(\nabla f(z^*)^Td \ge 0, \forall d \in \mathcal {T}_{\text{MPEC}}(z^*)\), where the tangent cone \(\mathcal {T}(z^*)\) to a feasible region \(\mathcal {F}\) at \(z^* \in \mathcal {F}\) is defined as

$$\displaystyle \begin{aligned} \mathcal{T}(z^*) := \left\{d \mid d = \lim_{t_k \downarrow 0} \frac{z^k - z^*}{t_k} \text{ for some } \{z^k\}, z^k \rightarrow z^*, z^k \in \mathcal{F}, \forall k\right\}. \end{aligned} $$
(12.2.4)

To facilitate the analysis of the tangent cone \(\mathcal {T}_{\text{MPEC}}(z)\) at \(z \in \mathcal {F}_{\text{MPEC}}\), we subdivide it into a set of tangent cones of the associated NLPs:

$$\displaystyle \begin{aligned} \mathcal{T}_{\text{MPEC}}(z) := \bigcup_{(\mathcal{D}_{01},\mathcal{D}_{10})}\mathcal{T}_{\text{NLP}_{\mathcal{D}_{01},\mathcal{D}_{10}}}(z). {} \end{aligned} $$
(12.2.5)

Therefore, z ∗ is a geometric B-stationary point if and only if it is a geometric B-stationary point for all of its associated NLPs indexed by \((\mathcal {D}_{01},\mathcal {D}_{10})\).

Additionally, two more NLPs, tightened [108] and relaxed [48, 108] NLPs, are defined by replacing the last two conditions of (12.2.3) with a single condition: tightened NLP (TNLP) is defined by setting G j(z) = H j(z) = 0 for all \(j \in \mathcal {D}\), whereas relaxed NLP (RNLP) relaxes the feasible region by defining G j(z) ≥ 0, H j(z) ≥ 0 for all \(j \in \mathcal {D}\). These NLPs provide a foundation to define constraint qualifications for MPECs and strong stationarity.

Figure 12.1 depicts the feasible regions of the NLPs associated with a complementarity constraint 0 ≤ G j(z) ⊥ H j(z) ≥ 0 for \(j \in \mathcal {D}\). One can easily verify that

$$\displaystyle \begin{aligned} \mathcal{T}_{\text{TNLP}}(z) \subseteq \mathcal{T}_{\text{MPEC}}(z) \subseteq \mathcal{T}_{\text{RNLP}}(z). {} \end{aligned} $$
(12.2.6)

When \(\mathcal {D} = \emptyset \), the equality holds throughout (12.2.6), and lower-level strict complementarity [104] holds. From (12.2.6), if z ∗ is a local minimizer of RNLP(z ∗), then z ∗ is a local minimizer of the MPEC, but not vice versa [108].

Fig. 12.1
figure 1

Feasible regions of the NLPs associated with a complementarity constraint 0 ≤ G j(z) ⊥ H j(z) ≥ 0 for \(j \in \mathcal {D}\). (a) Tightened NLP. (b) \(\text{NLP}_{\mathcal {D}_{01}}\). (c) \(\text{NLP}_{\mathcal {D}_{10}}\). (d) Relaxed NLP

Full size image

Algebraically, B-stationarity is defined by using a linear program with equilibrium constraints (LPEC), an MPEC with all the functions being linear, over a linearized cone. For a feasible z ∗, if d = 0 is a solution to the following LPEC, then z ∗ is called a B-stationary (or an algebraic B-stationary) point:

$$\displaystyle \begin{aligned} & \operatorname*{\mbox{minimize}}_z && \nabla f(z^*)^Td\\ & \operatorname{\mbox{subject to}} && d \in \mathcal{T}_{\text{MPEC}}^{\text{lin}}(z^*), \end{aligned} $$
(12.2.7)

where

$$\displaystyle \begin{aligned} \mathcal{T}_{\text{MPEC}}^{\text{lin}}(z^*) &:= \big\{d \mid && \nabla c_i(z^*)^Td \ge 0, \,\,\forall i: c_i(z^*)=0,\\ & && \nabla G_j(z^*)^Td = 0, \,\, \forall j: G_j(z^*)=0, H_j(z^*) > 0,\\ & && \nabla H_j(z^*)^Td = 0, \,\, \forall j: G_j(z^*)>0, H_j(z^*) = 0,\\ & && 0 \le \nabla G_j(z^*)^Td \perp \nabla H_j(z^*)^Td \ge 0, \,\, \forall j \in \mathcal{D}(z^*) \big\}. {} \end{aligned} $$
(12.2.8)

As with geometric B-stationarity, B-stationarity is difficult to check because it involves the solution of an LPEC that may require the solution of an exponential number of linear programs, unless all these linear programs share a common multiplier vector. Such a common multiplier vector exists if MPEC-LICQ holds, which we define in Sect. 12.2.2.

Since \(\mathcal {T}_{\text{MPEC}}(z^*) \subseteq \mathcal {T}_{\text{MPEC}}^{\text{lin}}(z^*)\) [42], B-stationarity implies geometric B-stationarity, but not vice versa. A similar equivalence (12.2.5) and inclusion relationship (12.2.6) hold between the linearized cones of its associated NLPs [42].

The next important stationarity concept is strong stationarity.

Definition 12.2.1

A point z ∗ is called strongly stationary if there exist multipliers satisfying the stationarity of the RNLP. △

Note that if \(\hat {\nu }_{1j}\) and \(\hat {\nu }_{2j}\) are multipliers for G j(z ∗) and H j(z ∗), respectively, then \(\hat {\nu }_{1j},\hat {\nu }_{2j} \ge 0\) for \(j \in \mathcal {D}(z^*)\). Strong stationarity implies B-stationarity due to (12.2.6) and the inclusion relationship between the tangent and linearized cones. Equivalence of stationarity between (12.2.1) and the RNLP was shown in [5, 48, 103].

Other stationarity conditions differ from strong stationarity in that the conditions on the sign of the multipliers, \(\hat {\nu }_{1j}\) and \(\hat {\nu }_{2j}\), are relaxed when G j(z ∗) = H j(z ∗) = 0. One can easily associate these stationarity concepts with the stationarity conditions for one of its associated NLPs. If we define the biactive set \(\mathcal {D}^* := \mathcal {D}(z^*)\), we can state these “stationarity” concepts by replacing the sign of the multipliers in the set \(\mathcal {D}^*\) as follows:

  • z ∗ is called weak stationary if there are no sign restrictions on \(\hat {\nu }_{1j}\) and \(\hat {\nu }_{2j}, \forall j \in \mathcal {D}^*\).

  • z ∗ is called A-stationary if \(\hat {\nu }_{1j} \ge 0\) or \(\hat {\nu }_{2j} \ge 0, \forall j \in \mathcal {D}^*\).

  • z ∗ is called C-stationary if \(\hat {\nu }_{1j}\hat {\nu }_{2j} \ge 0, \forall j \in \mathcal {D}^*\).

  • z ∗ is called M-stationary if either \(\hat {\nu }_{1j} > 0\) and \(\hat {\nu }_{2j} > 0\) or \(\hat {\nu }_{1j}\hat {\nu }_{2j}=0, \forall j \in \mathcal {D}^*\).

Of particular note is M-stationarity, which implies that if z ∗ is M-stationary, then z ∗ satisfies the first-order optimality conditions for at least one of the nonlinear programs (12.2.3). This condition seems to be the best one can achieve without exploring the combinatorial number of possible partitions for the biactive constraints. The extended M-stationarity in [56] extends the notion of M-stationarity in a way that it holds at z ∗ when M-stationarity is satisfied for each critical direction d defined by \(d \in \mathcal {T}^{\text{lin}}_{\text{MPEC}}(z^*)\) and ∇f(z ∗)Td ≤ 0, possibly with different multipliers. Thus, if z ∗ is extended M-stationary, then z ∗ satisfies the first-order optimality conditions for all the associated NLPs. Hence it is also B-stationary. When a constraint qualification is satisfied, B-stationarity implies extended M-stationarity. Figure 12.2 summarizes relationships between stationarity concepts.

Fig. 12.2
figure 2

Relationships between stationarity concepts where M-stationarity is the intersection of C- and A-stationarity

Full size image

As in the stationarity concepts, the second-order sufficient conditions (SOSCs) of an MPEC are defined in terms of the associated NLPs. In particular, SOSC is defined at a strongly stationary point so its multipliers work for all the associated NLPs. Depending on the underlying critical cone, we have two different SOSCs: RNLP-SOSC and MPEC-SOSC. In Definition 12.2.2, the Lagrangian \(\mathcal {L}\) and the critical cone for the RNLP are defined as follows:

$$\displaystyle \begin{aligned} \mathcal{L}(z,\lambda,\hat{\nu}_1,\hat{\nu}_2) &:= f(z) &&- \sum_{i \in \mathcal{E}\cup\mathcal{I}} c_i(z)\lambda_i - \sum_{j=1}^p G_j(z)\hat{\nu}_{1j} - \sum_{j=1}^p H_j(z)\hat{\nu}_{2j},\\ \mathcal{C}_{\text{RNLP}}(z^*) &:= \{d \mid && \nabla c_i(z^*)^Td = 0, \,\,\forall i: \lambda_i^* > 0,\\ &&& \nabla c_i(z^*)^Td \ge 0, \,\,\forall i: c_i(z^*)=0, \lambda_i^*=0,\\ &&& \nabla G_j(z^*)^Td = 0, \,\,\forall j: G_j(z^*)=0, H_j(z^*) > 0,\\ &&& \nabla H_j(z^*)^Td = 0, \,\,\forall j: G_j(z^*)>0, H_j(z^*) = 0,\\ &&& \nabla G_j(z^*)^Td = 0, \,\, \forall j \in D(z^*), \hat{\nu}^*_{1j}>0,\\ &&& \nabla G_j(z^*)^Td \ge 0, \,\, \forall j \in D(z^*), \hat{\nu}^*_{1j}=0,\\ &&& \nabla H_j(z^*)^Td = 0, \,\, \forall j \in D(z^*), \hat{\nu}^*_{2j}>0,\\ &&& \nabla H_j(z^*)^Td \ge 0, \,\, \forall j \in D(z^*), \hat{\nu}^*_{2j}=0 \big \}. \end{aligned} $$
(12.2.9)

Definition 12.2.2

RNLP-SOSC is satisfied at a strongly stationary point z ∗ with its multipliers \((\lambda ^*,\hat {\nu }^*_1,\hat {\nu }^*_2)\) if there exists a constant ω > 0 such that

$$\displaystyle \begin{aligned}d^T\nabla_{zz}^2\mathcal{L}(z^*,\lambda^*,\hat{\nu}^*_1,\hat{\nu}^*_2)d \ge \omega \mathrm{ for all} d \neq 0, d \in \mathcal{C}_{\text{RNLP}}(z^*).\end{aligned}$$

If the conditions hold for \(\mathcal {C}_{\text{MPEC}}(z^*)\) instead of \(\mathcal {C}_{\text{RNLP}}(z^*)\), where \(\mathcal {C}_{\text{MPEC}}(z^*) := \mathcal {C}_{\text{RNLP}}(z^*) \cap \{ d \mid \min (\nabla G_j(z^*)^Td,\nabla H_j(z^*)^Td)=0, \forall j \in \mathcal {D}(z^*), \hat {\nu }^*_{1j}=\hat {\nu }^*_{2j}=0\}\), then we say that MPEC-SOSC is satisfied. △

We note that \(d \in \mathcal {C}_{\text{MPEC}}(z^*)\) if and only if it is a critical direction of any of the \(\text{NLP}_{\mathcal {D}_{01},\mathcal {D}_{10}}(z^*)\)’s at z ∗ [104, 108]. Thus, MPEC-SOSC holds at z ∗ if and only if SOSC is satisfied at z ∗ for all of its associated NLPs, which leads to the conclusion that z ∗ is a strict local minimizer of the MPEC.

In a similar fashion, we define strong SOSC (SSOSC) for RNLPs. Using RNLP-SSOSC, we can obtain stability results of MPECs by applying the stability theory of nonlinear programs [77, 105] to the RNLP. The stability property can be used to show the uniqueness of a solution of regularized NLPs to solve the MPEC as in Sect. 12.3. A critical cone \(\mathcal {C}_{\text{RNLP}}^{\text{S}}(z^*)\) is used instead of \(\mathcal {C}_{\text{RNLP}}(z^*)\), which expands it by removing the feasible directions for inequalities associated with zero multipliers:

$$\displaystyle \begin{aligned} \mathcal{C}^{\text{S}}_{\text{RNLP}}(z^*) &:= \big \{d \mid && \nabla c_i(z^*)^Td = 0, \,\,\forall i: \lambda_i^* > 0,\\ &&& \nabla G_j(z^*)^Td = 0, \,\,\forall j: \hat{\nu}^*_{1j} \neq 0,\\ &&& \nabla H_j(z^*)^Td = 0, \,\,\forall j: \hat{\nu}^*_{2j} \neq 0 \big \}. \end{aligned} $$
(12.2.10)

Definition 12.2.3

RNLP-SSOSC is satisfied at a strongly stationary point z ∗ with its multipliers \((\lambda ^*,\hat {\nu }^*_1,\hat {\nu }^*_2)\) if there exists a constant ω > 0 such that

$$\displaystyle \begin{aligned}d^T\nabla_{zz}^2\mathcal{L}(z^*,\lambda^*,\hat{\nu}^*_1,\hat{\nu}^*_2)d \ge \omega \mathrm{ for all} d \neq 0, d \in \mathcal{C}^{\text{S}}_{\text{RNLP}}(z^*).\end{aligned}$$

△

By definition, we have an inclusion relationship between SOSCs: RNLP-SSOSC ⇒ RNLP-SOSC ⇒ MPEC-SOSC. Reverse directions do not hold in general; an example was presented in [108] showing that MPEC-SOSC \(\nRightarrow \) RNLP-SOSC.

2.2 Constraint Qualifications and Regularity Assumptions

Constraint qualifications (CQs) for MPECs guarantee the existence of multipliers for the stationarity conditions to hold. They are an extension of the corresponding CQs for the tightened NLP. Among many CQs in the literature, we have selected five. Three of them are frequently assumed in proving stationarity properties of a limit point of algorithms for solving MPECs described in Sect. 12.3. The remaining two are conceptual and much weaker than the first ones, but they can be used to prove that every local minimizer is at least M-stationary.

We start with the first three CQs. Because of the space limit, we do not specify the definition of the CQs in the context of NLPs. In Definition 12.2.4, LICQ denotes the linear independence constraint qualification, and CPLD represents constant positive linear dependence [102].

Definition 12.2.4

An MPEC (12.1.2) is said to satisfy MPEC-LICQ (MPEC-MFCQ, MPEC-CPLD) at a feasible point z if the corresponding tightened NLP satisfies LICQ (MFCQ, CPLD) at z. △

We note that MPEC-LICQ holds at a feasible point z if and only if all of its associated NLPs satisfy LICQ at z. This statement is true because active constraints at any feasible point do not change between the associated NLPs. For example, MPEC-LICQ holds if and only if LICQ holds for the relaxed NLP.

Under MPEC-LICQ, B-stationarity is equivalent to strong stationarity [108] since the multipliers are unique, thus having the same nonnegative signs for a biactive set among the associated NLPs.

The above CQs provide sufficient conditions for the following much weaker CQs to hold. These CQs are in general difficult to verify but provide insight into what stationarity we can expect for a local minimizer. In the following definition, ACQ and GCQ denote Abadie and Guignard constraint qualification, respectively, and for a cone C its polar is defined by C ∘ := {y∣〈y, x〉≤ 0, ∀x ∈ C}.

Definition 12.2.5

The MPEC (12.1.3) is said to satisfy MPEC-ACQ (MPEC-GCQ) at a feasible point z if \(\mathcal {T}_{\text{MPEC}}(z)=\mathcal {T}_{\text{MPEC}}^{\text{lin}}(z)\) (\(\mathcal {T}_{\text{MPEC}}(z)^\circ = \mathcal {T}^{\text{lin}}_{\text{MPEC}}(z)^\circ \)). △

Although MPEC-ACQ or MPEC-GCQ holds, we cannot directly apply the Farkas lemma to show the existence of multipliers because the linearized cone may not be a polyhedral convex set. However, M-stationarity is shown to hold for each local minimizer under MPEC-GCQ by using the limiting normal cones and separating the complementarity constraints from other constraints [43, 56].

Local preservation of constraint qualifications has been studied in [20], which shows that for many MPEC constraint qualifications, if z ∗ satisfies an MPEC constraint qualification, then all feasible points in a neighborhood of z ∗ also satisfy that MPEC constraint qualification.

As with standard nonlinear programming, a similar implication holds between CQs for MPECs: MPEC-LICQ ⇒ MPEC-MFCQ ⇒ MPEC-CPLD ⇒ MPEC-ACQ ⇒ MPEC-GCQ.

3 Solution Approaches

In this section, we classify and outline solution methods for MPECs and summarize their convergence results. Solution methods for MPECs such as (12.1.3) can be categorized into three broad classes:

  1. 1.

    Nonlinear programming methods that rewrite the complementarity constraint in (12.1.3) as a nonlinear set of inequalities, such as

    $$\displaystyle \begin{aligned} G(z) \geq 0, \; H(z) \geq 0, \; \mbox{ and }\; G(z)^TH(z) \leq 0,\end{aligned} $$
    (12.3.1)

    and then apply NLP techniques; see, for example, [26, 45, 74, 87, 103, 104, 109]. Unfortunately, convergence properties are generally weak for this class of methods, typically resulting in C-stationary limits unless strong assumptions are made on the limit point.

  2. 2.

    Combinatorial methods that tackle the combinatorial nature of the disjunctive complementarity constraint directly. Popular approaches include pivoting methods [40], branch-and-cut methods [8, 9, 11], and active-set methods [57, 84, 88]. This class of methods has the strongest convergence properties.

  3. 3.

    Implicit methods that assume that the complementarity constraint has a unique solution for every upper-level choice of variables. For example, if we assume that the lower-level problem has a unique solution, then we can express the lower-level variables y = y(x) in (12.1.2), and use the KKT conditions to eliminate (y(x), λ(x)), resulting in a reduced nonsmooth problem

    $$\displaystyle \begin{aligned} \operatorname*{\mbox{minimize}}_x \; f(x,y(x)) \quad \operatorname{\mbox{subject to}} \; c(x,y(x)) \geq 0\end{aligned} $$

    that can be solved by using methods for nonsmooth optimization. See the monograph [98] and the references [63, 118] for more details.

In this survey, we do not discuss implicit methods further and instead concentrate on the first two classes of methods.

3.1 NLP Methods for MPECs

NLP methods are attractive because they allow us to leverage powerful numerical solvers. Unfortunately, the system (12.3.1) violates a standard stability assumption for NLP at any feasible point. In [108], the authors show that (12.3.1) violates MFCQ at any feasible point. Other nonlinear reformulations of the complementarity constraint (12.3.1) are possible. In [46, 83], the authors experiment with a range of reformulations using different nonlinear complementarity functions, but they observe that the formulation (12.3.1) is the most efficient format in the context of sequential quadratic programming (SQP) methods. We also note that reformulations that use nonlinear equality constraints such as G(z)TH(z) = 0 are not as efficient, because the redundant lower bound can slow convergence.

Because traditional analyses of NLP solvers rely heavily on a constraint qualification, it is remarkable that convergence results can still be proved. Here, we briefly review how SQP methods can be shown to converge quadratically for MPECs, provided that we reformulate the nonlinear complementarity constraint (12.3.1) using slacks as

$$\displaystyle \begin{aligned} s_1 = G(z) , \; s_2 = H(z) \geq 0, \; s_1 \geq 0, \; s_2 \geq 0, \mbox{ and }\; s_1^Ts_2 \leq 0 . \end{aligned} $$
(12.3.2)

One can show that close to a strongly stationary point that satisfies MPEC-LICQ and RNLP-SOSC, an SQP method applied to this reformulation converges quadratically to a strongly stationary point, provided that all QP approximations remain feasible. The authors [48] show that these assumptions are difficult to relax, and they give a counterexample that shows that the slacks are necessary for convergence. One undesirable assumption is that all QP approximations must remain feasible, but one can show that this assumption holds if the lower-level problem satisfies a certain mixed-P property; see, for example, [90]. In practice [45], a simple heuristic is implemented that relaxes the linearization of the complementarity constraint.

In general, the failure of MFCQ motivates the use of regularizations within NLP methods, such as penalization or relaxation of the complementarity constraint, and these two classes of methods are discussed next.

3.1.1 Relaxation-Based NLP Methods

An attractive way to solve MPECs is to relax the complementarity constraint in (12.3.1) by using a positive relaxation parameter, t > 0:

$$\displaystyle \begin{aligned} & \operatorname*{\mbox{minimize}}_{z,u,v} && f(z)\\ & \operatorname{\mbox{subject to}} && c_i(z) \ge 0 && \\ &&& G_j(z) \geq 0, H_j(z) \geq 0, G_j(z) H_j(z) \leq t &&\forall j=1,\dots,p . {} \end{aligned} $$
(12.3.3)

This NLP then generally satisfies MFCQ for any t > 0, and the main idea is to (approximately) solve these NLPs for a sequence of regularization parameters, . This approach has been studied from a theoretical perspective in [104, 109]. Under the unpractical assumption that each regularized NLP is solved exactly, the authors show convergence to C-stationary points.

More recently, interior-point methods based on the relaxation (12.3.3) have been proposed [87, 103] in which the parameter t is chosen to be proportional to the barrier parameter and is updated at the end of each (approximate) barrier subproblem solve. Numerical difficulties may arise when the relaxation parameter becomes small, because the limiting feasible set of the regularized NLP (12.3.3) has no strict interior.

An alternative regularization scheme is proposed in [74], based on the reformulation of (12.3.1) as

$$\displaystyle \begin{aligned} G_j(z) \geq 0, \; H_j(z) \geq 0, \; \mbox{ and }\; \phi(G_j(z),H_j(z),t) \leq 0, \end{aligned} $$
(12.3.4)

where

$$\displaystyle \begin{aligned} \phi(a,b,t) = \left\{\begin{array}{ll} a b & \text{if } a + b \geq t \\ -\frac{1}{2}(a^2+b^2) & \text{if } a + b < t. \end{array}\right. \end{aligned}$$

In [74], convergence properties are proved when the nonlinear program is solved inexactly, as one would find in practice. The authors show that typically, but not always, methods converge to M-stationary points with exact NLP solves but converge to only C-stationary points with inexact NLP solves. Other regularization methods have been proposed, and a good theoretical and numerical comparison can be found in [64], with later methods in [73]. Under suitable conditions, these methods can be shown to find M- or C-stationary points for the MPEC when the nonlinear program is solved exactly.

An interesting two-sided relaxation scheme is proposed in [26]. The scheme is motivated by the observation that the complementarity constraint in the slack formulation (12.3.2) can be interpreted as a pair of bounds, s ij ≥ 0, or, s ij ≤ 0, and strong stationarity requires a multiplier for at most one of these bounds in each pair. The authors propose a strictly feasible two-sided relaxation of the form

$$\displaystyle \begin{aligned} s_{1j} \geq - \delta_{1j} , \; s_{2j} \geq - \delta_{2j} , \; s_{1j} s_{2j} \leq \delta_{cj} .\end{aligned}$$

By using the multiplier information from inexact subproblem solves, the authors decide which parameter δ 1, δ 2, or δ c needs to be driven to zero for each complementarity pair. The authors propose an interior-point algorithm and show convergence to C-stationary points, local superlinear convergence, and identification of the optimal active set under MPEC-LICQ and RNLP-SOSC conditions.

3.1.2 Penalization-Based NLP Methods

An alternative regularization approach is based on penalty methods. Both exact penalty functions and augmented Lagrangian methods have been proposed for solving MPECs. The penalty approach for MPECs dates back to [41] and penalizes the complementarity constraint in the objective function, after introducing slacks:

$$\displaystyle \begin{aligned} & \operatorname*{\mbox{minimize}}_{z,u,v} && f(z) + \pi s_1^T s_2 \\ & \operatorname{\mbox{subject to}} && c_i(z) \ge 0 &&\forall i=1,\ldots,m\\ &&& G_j(z) - s_{1j} = 0, H_j(z) - s_{2j} = 0&&\forall j=1,\dots,p \\ &&& s_2 \geq 0, s_1 \geq 0 {} \end{aligned} $$
(12.3.5)

for positive penalty parameter π. If π is chosen large enough, the solution of the MPEC can be recast as the minimization of a single penalty function problem. The appropriate value of π is unknown in advance, however, and must be estimated during the course of the minimization. In general, if limit points are only B-stationary and not strongly stationary, then the penalty parameter, π, must diverge to infinity, and this penalization is not exact.

This approach was first studied by [3] in the context of active-set SQP methods, although it had been used before to solve engineering problems [41]. It has been adopted as a heuristic to solve MPECs with interior-point methods in loqo by [15], who present very good numerical results. A more general class of exact penalty functions was analyzed by [66], who derive global convergence results for a sequence of penalty problems that are solved exactly, while the author in [4] derives similar global results in the context of inexact subproblem solves.

In [85], the authors study a general interior-point method for solving (12.3.5). Each barrier subproblem is solved approximately to a tolerance 𝜖 k that is related to the barrier parameter, μ k. Under strict complementarity, MPEC-LICQ, and RNLP-SOSC, the authors show convergence to C-stationary points that are strongly stationary if the product of MPEC-multipliers and primal variables remains bounded. Superlinear convergence can be shown, provided that the tolerance and barrier parameter satisfy the conditions

$$\displaystyle \begin{aligned} \frac{(\epsilon+\mu)^2}{\epsilon} \to 0, \; \frac{(\epsilon+\mu)^2}{\mu} \to 0, \; \text{and} \; \frac{\mu}{\epsilon} \to 0. \end{aligned}$$

A related approach to penalty functions is the elastic mode that is implemented in SNOPT [58, 59]. The elastic approach [6] combines both a relaxation of the constraints and penalization of the complementarity conditions to solve a sequence of optimization problems

$$\displaystyle \begin{aligned} &\operatorname*{\mbox{minimize}}_{z,u,v,t} && f(z) + \pi (t + s_1^Ts_2) \\ & \operatorname{\mbox{subject to}} && c_i(z) \ge -t &&\forall i =1,\ldots.m\\ &&& -t \leq G_j(z) - s_{1j} \leq t, -t \leq H_j(z) - s_{2j} \leq t &&\forall j=1,\dots,p \\ &&& s_1 \geq 0, s_2 \geq 0, 0 \leq t \leq \bar{t}, {} \end{aligned}$$

where t is a variable with upper bound \(\bar {t}\) that relaxes some of the constraints and π is the penalty term on both the constraint relaxation and the complementarity conditions. This problem can be interpreted as a mixture of ℓ ∞ and ℓ 1 penalties. The problem is solved for a sequence of π that may need to converge to infinity. Under suitable conditions such as MPEC-LICQ, the method is shown to converge to M-stationary points, even with inexact NLP solves.

An alternative to the ℓ 1 penalty-function approaches presented above are augmented Lagrangian approaches, which have been adapted to MPECs [51, 69]. These approaches are related to stabilized SQP methods and work by imposing an artificial upper bound on the multiplier. Under MPEC-LICQ one can show that if the sequence of multipliers has a bounded subsequence, then the limit point is strongly stationary. Otherwise, it is only C-stationary.

Remark 12.3.1

NLP methods for MPECs currently provide the most practical approach to solving MPECs, and form the basis for the most efficient and robust software packages; see Sect. 12.4. In general, however, NLP methods may converge only slowly to a solution or fail to converge if the limit point is not strongly stationary. △

The result in [74] seems to show that the best we can hope for from NLP solvers is convergence to C-stationary points. Unfortunately, these points may include limit points at which first-order strict descent directions exist, and which do not correspond to stationary points in the classical sense. To the best of our knowledge, the only way around this issue is to tackle the combinatorial nature of the complementarity constraint directly, and in the next section we describe methods that do so.

3.2 Combinatorial Methods for MPECs

Despite the success of NLP solvers in tackling a wide range of MPECs, for some classes of problems these solvers still fail. In particular, problems whose stationary points are B-stationary but not strongly stationary can cause NLP solvers to either fail or exhibit slow convergence. Unfortunately, this behavior also occurs when other pathological situations occur (such as convergence to C- or M-stationary points that are not strongly stationary), and it is not easily diagnosed or remedied.

This observation motivates the development of more robust methods for MPECs that guarantee convergence to B-stationary points. Methods with this property must resolve the combinatorial complexity of the complementarity constraint, and we discuss these methods here.

Specialized methods for solving linear programs with linear equilibrium constraints (LPECs), in which all the functions, f(z), c(z), G(z), and H(z), are linear, include methods based on disjunction for computing global solutions [11, 60, 67, 68], pivot-based methods for computing B-stationary points [40], and penalty methods based on a difference of convex functions formulation [70]. Global optimization methods for problems with a convex quadratic objective function and linear complementarity constraints are found in [8]. Algorithms for problems with a nonlinear objective function and linear complementarity constraints include combinatorial [9], active-set [52], sequential quadratic programming [88], and sequential linear programming [57] methods.

One early general method for obtaining B-stationary points is the branch-and-bound method proposed in [11]. It starts by solving a relaxation of (12.1.3) obtained by relaxing the complementarity between G(z) and H(z). If the solution satisfies G(z)TH(z) = 0, then it is a B-stationary point. Otherwise, there exists an index j such that G j(z)H j(z) > 0, and we branch on this disjunction by creating two new child problems that set G j(z) = 0 and H j(z) = 0, respectively. This process is then repeated, creating a branch-and-bound tree. A branch-and-cut approach is described in [67] for solving LPECs. The algorithm is based on equivalent mixed-integer reformulations and the application of Benders decomposition [14] with linear programming (LP) relaxations. In contrast, the authors in [40] generalize LP pivoting techniques to locally solve LPECs. The authors prove convergence to a B-stationary point, but unlike [67] do not obtain globally optimal solutions.

The SQPEC approach extends SQP methods by taking special care of the complementarity constraint [110]. This method minimizes a quadratic approximation of the Lagrangian subject to a linearized feasible set and a linearized form of the complementarity constraint. Unfortunately, this method can converge to M-stationary points, rather than the desired B-stationary points, as the following counterexample shows [84]:

$$\displaystyle \begin{aligned} \operatorname*{\mbox{minimize}}_{x,y} \; (x-1)^2 + y^3 + y^2 \quad \operatorname{\mbox{subject to}} \; 0 \leq x \; \perp \; y \geq 0. \end{aligned} $$
(12.3.6)

Starting from (x 0, y 0) = (0, t) for 0 < t < 1, SQPEC generates iterates

$$\displaystyle \begin{aligned} (x^{(k+1)},y^{(k+1)}) = \left(0,\frac{3 y^{(k)^2}}{6 y^{(k)} + 2}\right) \end{aligned}$$

that converge quadratically to the M-stationary point (0, 0), at which we can easily find a descent direction (1, 0) and which is hence not B-stationary.

An alternative class of methods to SQPEC methods that provide convergence to B-stationary points is extensions of SLQP methods to MPECs; see, for example, [16, 17, 21, 47]. The method is motivated by considering the linearized tangent cone, \(\mathcal {T}_{\text{MPEC}}^{\text{lin}}(z^*)\) in (12.2.8) as a direction-finding problem. This method solves a sequence of LPECs inside a trust region [84] with radius Δ around the current point z:

$$\displaystyle \begin{aligned} \mbox{LPEC}(z,\Delta) \left\{ \begin{array}{ll} \displaystyle \operatorname*{\mbox{minimize}}_d & \nabla f(z)^T d \\ \operatorname{\mbox{subject to}} & c(z) + \nabla c(z)^T d \geq 0, \\ & 0 \leq G(z) + \nabla G(z)^T d \; \perp \; H(z) + \nabla H(z)^T d \geq 0, \\ & \| d \| \leq \Delta . \end{array} \right. \end{aligned}$$

The LPEC need be solved only locally, and the pivoting method of [40] is a practical and efficient method of solving the LPEC. Given a solution d ≠ 0, we find the active sets that are predicted by the LPEC,

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{A}_c(z+d) &\displaystyle := &\displaystyle \big\{ i : c_i(z) + \nabla c_i(z)^T d = 0 \big\} \end{array} \end{aligned} $$
(12.3.7)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{A}_G(z+d) &\displaystyle := &\displaystyle \big\{ j : G_j(z) + \nabla G_j(z)^T d = 0 \big\} \end{array} \end{aligned} $$
(12.3.8)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathcal{A}_H(z+d) &\displaystyle := &\displaystyle \big\{ j : H_j(z) + \nabla H_j(z)^T d = 0 \big\}, \end{array} \end{aligned} $$
(12.3.9)

and solve the corresponding equality-constrained quadratic program (EQP):

$$\displaystyle \begin{aligned} \mbox{EQP}(z+d) \left\{ \begin{array}{lrl} \displaystyle \operatorname*{\mbox{minimize}}_d & \nabla f(z)^T d + \frac{1}{2} d^T \nabla^2 \mathcal{L}(z) d & \\ \operatorname{\mbox{subject to}} & c_i(z) + a_i(z)^T d = 0, \; & \forall i \in \mathcal{A}_c(z+d) \\ & G_j(z) + \nabla G_j(z)^T d = 0, \; & \forall j \in \mathcal{A}_G(z+d) \\ & H_j(z) + \nabla H_j(z)^T d = 0, \; & \forall j \in \mathcal{A}_H(z+d) . \end{array} \right. \end{aligned}$$

We note that EQP(z + d) can be solved as a linear system of equations. The goal of the EQP step is to provide fast convergence near a local minimum. Global convergence is promoted through the use of a three-dimensional filter that separates the complementarity error and the nonlinear infeasibility.

The SLPEC-EQP method has an important advantage over NLP reformulations: the solution of the LPEC matches exactly the definition of B-stationarity, and we therefore always work with the correct tangent cone. In particular, if the zero vector solves the LPEC, then we can conclude that the current point is B-stationary. To our knowledge, this algorithm is the only one that guarantees global convergence to B-stationary points.

3.3 Globally Optimal Methods for MPECs

The methods discussed above typically guarantee convergence to a stationary point at best. They do not guarantee convergence to a global minimum, even if the problem functions, f, c, G, and H are convex, because the feasible set of even the simplest complementarity constraint, 0 ≤ x 1 ⊥ x 2 ≥ 0, is nonconvex.

Here, we briefly summarize existing results for obtaining global solutions to certain classes of MPECs. We limit our discussion to cases where the lower-level follower’s problems is convex. One approach to obtaining global solutions would be to simply apply global optimization techniques to the nonlinear program (12.2.1). However, state-of-the-art solvers such as BARON [107, 115] or Couenne [12] require finite bounds on all variables to construct valid underestimators, and it is not clear that such bounds are easy to obtain on the multipliers. If we assume that such bounds exist, then we can apply BARON and Couenne. Unfortunately, the effectiveness of these solvers is limited to a few dozen variables at most.

If the MPEC has some special structure, then we can employ formulations and methods that guarantee convergence to a global minimum. One example are LPECs (or QPECs), when f(z) is a linear (or a convex quadratic function), c(z) = Az − b is an affine function, and the complementarity constraint is affine, i.e. 0 ≤ G(z) = Mz − c  ⊥ Nz − d = H(z) ≥ 0. Then it is possible to model the complementarity condition using binary variables, y ∈{0, 1}p, as

$$\displaystyle \begin{aligned} \Theta y \geq M z - c \geq 0 \; \text{and} \; (1-\Theta) y \geq N z - d \geq 0 ,\end{aligned}$$

where Θ > 0 is an upper bound on Mz − c and Nz − d that can be computed by solving an LP. Unfortunately, the resulting mixed-integer linear program often has a very weak continuous relaxation, resulting in massive branch-and-cut trees. Moreover, numerical issues can cause both Mz − c and Nz − d to be positive. In [8, 67], the authors extend a logical Benders decomposition technique [65] to this class of MPECs that avoids these pitfalls. The approach is based on a minimax principle and derives valid inequalities from LP relaxations. These approaches easily generalize to MPECs with more general (convex) f(x) and c(x).

4 Software Environments

Several modeling languages and solvers support bilevel optimization problems and MPECs. Table 12.1 presents a list of them. GAMS/EMP [53] and Pyomo [62] directly support bilevel optimization problems—they provide constructs that allow users to formulate bilevel optimization problems in their natural algebraic form (12.1.1) without applying any reformulations. GAMS introduced an extended mathematical programming (EMP) framework in which users can annotate the variables, functions, and constraints of a model to specify to which level, either upper or lower, they belong. In this case, a single monolithic model is defined, and annotations are provided via a separate text file, called the empinfo file. Pyomo takes a different approach by requiring users to define the lower-level problem explicitly as a model using their Submodel( ) construct and to link it to the upper-level model. In this way, not only bilevel optimization problems, but also multilevel problems [92] can be specified by defining submodels recursively and linking them together.

Table 12.1 Modeling languages and solvers that support bilevel or MPECs
Full size table

In contrast to bilevel optimization problems, most modeling languages support MPECs by providing a dedicated construct to take complementarity constraints in their natural form. AMPL [50] and Julia [79] provide complements and @complements keywords, respectively, GAMS [55] has a dot . construct, AIMMS [106] defines ComplementarityVariables, and Pyomo [61] defines Complementarity along with a complements expression. All these constructs enable complementarity constraints to be written as first-class expressions so that users can seamlessly use them in their models.

Regarding solvers, to the best of our knowledge, no dedicated, robust, and large-scale solvers are available for bilevel optimization problems at this time. The aforementioned modeling languages for bilevel optimization problems transform these problems into a computationally tractable formulation as an MPEC or generalized disjunctive program and call the associated solvers. Bilevel-specific features, such as optimal value functions, are not exploited in these solution procedures.

Although there are some recent efforts [75, 76, 94] exploiting the value function to globally solve the bilevel problem (12.1.1) using a branch-and-bound scheme, even in the case when the lower-level problem is nonconvex, these methods require repeated global solutions of nonconvex subproblems to compute the lower bounds. This requirement makes these methods unsuitable for large-scale bilevel problems. In particular, the requirement for global optimality may not be relaxed easily as discussed in [75].

In the case of MPECs, a few solvers are available. Most reformulate the MPECs into nonlinear or mixed-integer programming problems by applying relaxation, penalization, or disjunction techniques to the complementarity constraints. FilterMPEC [44] and KNITRO [7] transform the given problem into an NLP and solve it using their own algorithms by taking special care with the complementarity constraints. NLPEC [55] and Pyomo [61] are metasolvers that apply a reformulation and invoke an NLP solver, rather than supplying their own NLP solver. In contrast to the NLP-based approaches, Pyomo additionally provides a disjunctive programming method that formulates the MPEC as a mixed-integer nonlinear program. We believe that a combination of modeling languages for bilevel programs and MPEC solvers is the most promising and viable approach for quickly prototyping and solving bilevel problems when the lower-level problem is convex.

A number of bilevel optimization problems and MPECs are available online. The GAMS/EMP library [54] contains examples of bilevel optimization problems written by using the EMP framework. GAMS also provides MPEC examples [38]. The MacMPEC collection [81] is a set of MPEC examples written in AMPL that are frequently used to test performance of MPEC algorithms. QPECgen [71] generates MPEC examples with quadratic objectives and affine variational inequality constraints for lower-level problems.

5 Extensions

Our focus in this survey is on the optimistic bilevel optimization problem where the lower-level optimization problem is convex for all upper-level decisions. This approach contrasts with the pessimistic bilevel optimization problem [34, 35, 89, 117] where the leader plans for the worst by choosing an element of the solution set leading to the worst outcome and results in a problem of the form

$$\displaystyle \begin{aligned}{}[3] & \operatorname*{\mbox{minimize}}_{x, \theta} && \theta \\ & \operatorname{\mbox{subject to}} && f(x,y) \leq \theta && \forall\; y \in Y(x) \\ & && c(x,y) \geq 0 && \forall\; y \in Y(x), \end{aligned} $$
(12.5.1)

where Y (x) is the solution set of the lower-level optimization problem parameterized by x. This formulation is consistent with robust optimization problems [13] with a complicated uncertainty set Y (x). The two robustness constraints determine the worst objective function value and guarantee satisfaction of the joint feasibility constraint, respectively.

If the lower-level optimization problem is nonconvex, then the global solution of the bilevel optimization problem (12.1.1) may not even be a stationary point for the MPEC reformulation (12.1.2) because the MPEC reformulation is a relaxation of (12.1.1) in these cases; see [93, Example 1]. In the nonconvex case, special algorithms can be devised by a two-layer bounding scheme: bounding the optimal value function of the lower-level problem and computing lower and upper bounds of the upper-level problem, see [75, 76, 94]. These bounds need to be refined as the algorithm progresses, to ensure convergence to a global solution.

Many other extensions of bilevel optimization problems were not covered in this survey, including problems with lower-level second-order cone programs [18, 19], stochastic bilevel optimization [1, 22], discrete bilevel optimization with integer variables in both the upper- and lower-level decisions [36, 96], multiobjective bilevel optimization [25, 39, 91, 100], and multilevel optimization problems [80, 86, 92, 116]. Alternatives to the MPEC reformulations also exist that we did not cover in this survey; see [37, 49, 95, 112,113,114] for semi-infinite reformulations and [32, 120] for nonsmooth reformulations based on the value function.