A search for triple collision orbits inside the domain of the free-fall three-body problem

Abstract

We look for triple collision orbits which are collisionless before triple collision. We developed a procedure of fixing the positions of these orbits inside the initial condition plane of the free-fall three-body problem as a natural consequence of the use of symbol sequences. Before looking for these orbits, an error regarding the relation between triple collision points and binary collision curves is corrected, that is, we confirmed that the intersections of binary collision curves of different generations (see the text for definition) are not the initial points of triple collision orbits but of the orbits with plural binary collisions along their trajectories. Then, we numerically established that a triple collision point (i.e., a point of the initial condition plane whose orbit ends at triple collision) can be found as an intersection of three cylinders of the same generation. We do not obtain triple collision orbits with symbol sequences shorter than eight digits. We obtained 11 triple collision points inside the initial condition plane. The orbits starting from these points have finite lengths in the future and in the past since the problem is free fall. These orbits start at triple collision, expand the size until the free-fall states, and go back to triple collision. Thus, these are time symmetric with respect to the time of free fall. Two types of triple collision orbits are identified. One type of orbits starts with a positive triangle formed with three bodies and ends at triple collision also with a positive triangle. The other type starts with a positive triangle and ends with a negative triangle.

1 Introduction and motivation

The free-fall three-body problem is a forum of the three-body problem in which the systematic numerical studies have been done for various kinds of orbits including periodic orbits, escape orbits, triple collisions, oscillatory orbits, and so on. As for the free-fall problem itself, the celebrated paper by Agekyan and Anosova (1967) has done a small number of numerical integrations of the initial condition plane. So, no discussion on the global and local structures of the plane was possible. Anosova continued the numerical investigation of the problem (Anosova 1986; Anosova et al. 1994). Tanikawa et al. (1995) started systematic integrations of orbits in the initial condition plane of the free-fall problem with a fast computer focusing on the search for collision orbits. The number of integrated orbits amounted to a million. The number was more than a million in Tanikawa (2000). Then gradually, some of the structure of the phase space of the free-fall problem became known. Of course, the structure turned out extremely complicated so that it becomes evident that to go farther, the survey of the network of intermediate objects bridging the global and local structures is necessary. These objects are periodic orbits, binary collision orbits, triple collision orbits, and escape orbits.

Recently, searches for periodic orbits are popular (Rose and Dullin 2013; Iasko and Orlov 2014; Dmitras̆inović and S̆uvakov 2015; Rose 2015; Tanikawa 2016; Li and Liao 2017) and lots of them are found. On the other hand, search for collision orbits requires rather special numerical techniques equipped with efficient regularizations (Tanikawa et al. 1995). Triple collision requires more severe conditions because the dimensionality of the triple collision is small compared with binary collision, that is, binary collisions form curves in a certain section of the phase space, while triple collisions form points in the same section. In addition, a numerical difficulty of orbit integrations with respect to triple collision requires regularization of more efficient kind.

In the present paper, we overcome the above two difficulties and obtain triple collision orbits by using symbol sequences (Tanikawa and Mikkola 2008, 2015) and by using our regularizing techniques (Mikkola and Tanikawa 1999, 2013b). So far, we obtained triple collision orbits with symmetry. Thus, Tanikawa and Mikkola (2000a, b, 2015) obtained triple collision orbits in the collinear three-body problem, and Tanikawa and Umehara (1998), Umehara and Tanikawa (2000), and Tanikawa and Mikkola (2015) obtained isosceles and collinear triple collision orbits. This time, we obtain triple collision orbits of general starting triangles.

The authors made mistakes in the former publications saying “the cross points of the binary collision curves of different types are triple collision points” (Tanikawa 2000, Fig. 4). In fact, crosses inside the initial condition plane are not necessarily triple collision points, but they are collision points whose orbits have plural binary collisions along their trajectories. We correct this error in Sect. 4.1.

2 Equations of motion and the algorithmic regularization

The algorithmic regularization is a result of the marriage of symplectic integration and regularization. In general, a symplectic integration assumes a constant time step, whereas the regularization requires the time-step shortening when the gravitational attraction is large and the velocity changes are large. This marriage was almost simultaneously carried out in two articles (Mikkola and Tanikawa 1999; Preto and Tremaine 1999). The method has later been implemented (Mikkola and Tanikawa 2013a, b).

The idea of symplectic integration is to consider the evolution of solution in time of the equations of motion as the canonical transformation of the coordinates and momenta at some time t to a later time $t'$. The symplectic method then uses a series of canonical transformations to propagate the system forward in time. This means the integration is accurate compared with those not taking into account the symplecticity. The idea of regularization is to keep the same accuracy even in the close approach of gravitating bodies. In the N-body problem, close approaches of bodies frequently take place. The integration scheme of regularization comprises the coordinate transformation and shortening of the step size of integration. The symplectic integration does not like the step-size change, whereas the regularization needs step-size changes.

The algorithmic integration, to begin with, extends the phase space and introduces a new Hamiltonian in this space. Let $\mathbf{p}$ be the momenta of the coordinates $\mathbf{q}$. Let further $T(\mathbf{p})$ be the kinetic energy and $U(\mathbf{q}, t)$ the force function such that the Hamiltonian is $H = T - U$. If the time t is also considered to be a coordinate and the corresponding momentum is B, then for this system the function

$$\begin{aligned} \Lambda = \log (T + B) - \log (U) \end{aligned}$$

can be used as a Hamiltonian in the extended phase space. The equations of motion derived from $\Lambda$ are

$$\begin{aligned} \mathbf{p}' = U_\mathbf{q}/U,\quad \mathbf{q}' = T_\mathbf{p}/(T+B),~~B'= U_t/U,\quad t' = 1/(T+B), \end{aligned}$$

(1)

where the prime denotes differentiation with respect to the new independent variable s and partial derivatives are denoted by subscripts. U is the potential with

$$\begin{aligned} U = G \left( \frac{m_2m_3}{r_{23}} + \frac{m_1m_3}{r_{13}} + \frac{m_1m_2}{r_{12}} \right) . \end{aligned}$$

(2)

We use interparticle vectors for the labeling of the relative coordinates

$$\begin{aligned} \mathbf{R}_1=\mathbf{r}_3-\mathbf{r}_2;\quad \mathbf{R}_2=\mathbf{r}_1-\mathbf{r}_3;\quad \mathbf{R}_3=\mathbf{r}_2-\mathbf{r}_1, \end{aligned}$$

(3)

as new coordinates and the velocities are $\mathbf{V}_k=\dot{\mathbf{R}}_k$. Denoting $R_i = |\mathbf{R}_i|$ and taking units so that $G = 1$, we have the potential

$$\begin{aligned} U=m_2m_3/R_1+m_1m_3/R_2+m_1m_2/R_3 \end{aligned}$$

(4)

and the kinetic energy

$$\begin{aligned} T=\frac{1}{2M}\left( m_2m_3 |\mathbf{V}_1|^2+m_1m_3 |\mathbf{V}_2|^2 + m_1m_2 |\mathbf{V}_3|^2\right) . \end{aligned}$$

(5)

One obtains the following

$$\begin{aligned} \dot{\mathbf{R}}_k=\mathbf{V}_k; \quad \dot{\mathbf{V}}_k=-M\frac{\mathbf{R}_k}{|\mathbf{R}_k|^3} +m_k\sum _\nu \frac{\mathbf{R}_\nu }{|\mathbf{R}_\nu |^3}, \end{aligned}$$

(6)

with $M=m_1+m_2+m_3$. Then, Eq. (1) becomes

$$\begin{aligned} t'=1/(T+B);\quad \mathbf{R}_k'=\mathbf{V}_k/(T+B);\quad \mathbf{V}_k'=\dot{\mathbf{V}}_k/U, \end{aligned}$$

(7)

since $B=U-T$ is a constant. This form is suitable for the leapfrog algorithm. Time and coordinates move with the ‘subroutine’ X(h):

$$\begin{aligned} \mathrm{d}t= & {} h/(T+B), \end{aligned}$$

(8)

$$\begin{aligned} t\rightarrow & {} t+\mathrm{d}t, \end{aligned}$$

(9)

$$\begin{aligned} \mathbf{R}_k\rightarrow & {} \mathbf{R}_k+\mathrm{d}t \mathbf{V}_k~~(k=1,2,3), \end{aligned}$$

(10)

and velocities with the ‘subroutine’ V(h):

$$\begin{aligned} \mathbf{S}= & {} \sum _k \mathbf{R}_k/|\mathbf{R}_k|^3, \end{aligned}$$

(11)

$$\begin{aligned} \delta t= & {} h/U, \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{V}_k\rightarrow & {} \mathbf{V}_k + \delta t(-M \mathbf{R}_k/|\mathbf{R}_k|^3+m_k \mathbf{S}) \quad (k=1,2,3). \end{aligned}$$

(13)

It is possible to write the final leapfrog algorithm over n steps, so that the total “macro” step has the length $=n\, h$. Then, we obtain the leapfrog over long intervals in the form

$$\begin{aligned} \mathbf{X}(h/2) [\mathbf{V}(h) \mathbf{X}(h)]^{n-1}{} \mathbf{V}(h)\mathbf{X}(h/2), \end{aligned}$$

(14)

where the power ($n-1$) means repetition of the operations. These leapfrogs, with many values of the step size h, can be used in the Bulirsch and Stoer (1966) extrapolation algorithm. The above leapfrog is regular even in point mass collisions and gives correct trajectories for two-body problems.

3 Definition of the free-fall problem

We consider the free-fall problem with equal masses. The problem belongs to the class of the planar three bodies with zero angular momentum. The triple systems of this problem are considered most unstable compared with the systems with nonzero angular momentum because of the existence of triple collisions. In particular, the equal mass case may be the most unstable among other combinations of masses. There is no proof for this statement. However, there is evidence. In fact, the problem reduces to the restricted three-body problem if the mass of one of the bodies tends to zero, in which problem there are so many stable periodic orbits. If two of the masses tend to zero, the problem reduces to the superposition of two two-body problems and is integrable; hence, orbits are stable.

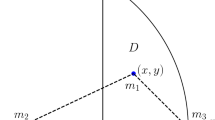
The definition of the problem is simple (see, e.g., Agekyan and Anosova 1967; Tanikawa et al. 1995). We put body 2 of mass $m_2$ at $A(-0.5,0)$ and body 3 of mass $m_3$ at B(0.5, 0) both on the x-axis of the (x, y)-plane. We put body 1 of mass $m_1$ at any place P in

$$\begin{aligned} D=\left\{ (x,y)~:~ x \ge 0; y \ge 0; (x+0.5)^2+y^2 \le 1 \right\} . \end{aligned}$$

Then, in the triangle formed by the three bodies, always ${\overline{AB}}$ is the longest, ${\overline{PA}}$ the second longest, and ${\overline{PB}}$ the shortest. We consider the equal mass case, i.e., $m_1= m_2 = m_3 = 1$. Then, the triangles exhaust all possible form of triangles if P moves in D (Fig. 1a). This initial condition region is sometimes called Anosova’s region. More generally, suppose that three masses are different. In this case, Anosova’s region does not exhaust the form of triangles. We need larger areas (see Fig. 1b). In this figure, $D_{11}$ corresponds to Anosova’s region. The other regions represent different forms of triangles. As an example, in region $D_{12}$, edge lengths satisfy ${\overline{PA}} \ge {\overline{AB}} \ge {\overline{PB}}$, and triple systems correspond to different initial conditions from those of $D_{11}$. The plane formed with $D_{ij}$ is called the shape plane. We obtain the shape sphere if we glue $D_{13},D_{43},D_{23}$, and $D_{33}$ at infinity (Moeckel et al. 2012; Montgomery 1996; Kuwabara and Tanikawa 2010).

We integrate equations of motion with the AR (algorithmic regularization) code (Mikkola and Tanikawa 1999, 2013b).

Fig. 1

The geometry of the free-fall problem. a The initial condition plane. b The shape space. $D_{11}$ corresponds to the D-shaped domain in Fig. 1a. The other $D_{ij}$ are obtained by reflections. As examples, $D_{21}$ is the mirror image of $D_{11}$ with respect to the y-axis; $D_{12}$ is the mirror image of $D_{11}$ with respect to their boundary circle (cf. Tanikawa and Mikkola 2015)

3.1 Symbols and symbol sequences

Let us define symbols and symbol sequences (Tanikawa and Mikkola 2008, 2015; Montgomery 1998). In the planar three-body problem, three bodies generally form a triangle (two-dimensional simplex, or 2-simplex), and occasionally they form a collinear configuration (one-dimensional simplex, or 1-simplex). Montgomery (2007) proved that all solutions to the zero angular momentum, negative energy Newtonian three-body problem admit a collinear configuration (syzygy) except for the Lagrange homothetic solutions. There will be an infinite sequence of collinear configurations unless the orbit ends in triple collision. Considering this property of the three-body problem, we give a symbol to an orbit each time when three bodies form a 1-simplex, or become a syzygy state.

We give the orientations to the simplex (triangle) so that it is positive when three bodies 1, 2, and 3 are arranged counterclockwise around their gravity center, while it is negative when clockwise (Tanikawa and Mikkola 2015). We sometime call the triangle itself positive or negative.

Until the preceding paper, the authors defined the symbols and symbol sequences as follows: We give symbol 1 if a positive 2-simplex degenerates into a 1-simplex with body 1 at center, symbol 2 if a positive 2-simplex into a 1-simplex with body 2 at center, and symbol 3 if a positive 2-simplex into a 1-simplex with body 3 at center. We give symbols 4, 5, and 6 if a negative 2-simplex degenerates into a 1-simplex, respectively, with center at bodies 1, 2, and 3.

In this stage, the authors did not take into account the resulting symbolic dynamics. This time, Richard Montgomery kindly read our manuscript and suggested that the number of symbols should be not six but three. Six symbols are redundant. The authors are convinced. The authors have experience of an elementary symbolic dynamics in the case of collinear three-body problem (Tanikawa and Mikkola 2000b). There the authors introduced two symbols and effectively treated the symbols sequences, and discussed elementary symbolic dynamics.

Now we introduce three symbols 1, 2, and 3. The redundancy came with the introduction of the front and back sides of triangles and with the consideration of the discrimination of the syzygy crossings from the front and back sides. However, these two crossings can be identified in the symbol sequences at either even or odd digits because two different crossings alternate.

Now neglecting the difference of crossings from the frontside and backside, we give symbol 1 when a 2-simplex degenerates into a 1-simplex with body 1 at center, symbol 2 when a 2-simplex into a 1-simplex with body 2 at center, and symbol 3 when a 2-simplex into a 1-simplex with body 3 at center.

We denote a symbol sequence s by

$$\begin{aligned} s = \ldots s_{-3}s_{-2}{s_{-1}}_\bullet s_1s_2s_3 \ldots , \end{aligned}$$

(15)

where $s_i$ is either 1, 2, or 3. As time goes on, positive and negative 2-simplexes alternate. In our setting, symbols $s_1, s_3, s_5, \ldots , s_{-2}, s_{-4}, s_{-6}, \ldots$ correspond to the syzygy crossings from the front to back sides, whereas symbols $s_2, s_4, s_6$, $\ldots , s_{-1}, s_{-3},s_{-5}, \ldots$ correspond to the syzygy crossings from the back to front sides. The period ($_{\bullet }$) separates the past and future. The part of the sequence to its right represents the future sequence, while the sequence to its left represents the past sequence. $s_1$ is the symbol for the present. We integrate the orbits to the future. So, we as a rule consider the future symbol sequence:

$$\begin{aligned} s = _\bullet s_1s_2s_3 \ldots . \end{aligned}$$

(16)

A finite sequence of symbols is called a word. The word is called a k -word if the length of the word is k. The set of symbol sequences which contain a k-word in a fixed position is called a k -cylinder. In the present paper, we consider the k-cylinder which contains its k-word at the initial k-digits, i.e.,

$$\begin{aligned} s = _\bullet s_1s_2s_3 \ldots s_k ***, \end{aligned}$$

(17)

where *** represents an arbitrary (infinite) sequence of symbols.

3.2 Division of the initial condition plane

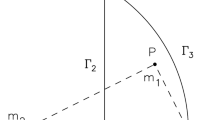
By abuse of notation, we will also say that an initial condition is in a particular k-cylinder if its symbol sequence lies in that cylinder. The k-cylinders then form open sets of the initial condition plane, which, together with their boundaries, partition the initial condition plane for a fixed k. As we will soon see, these boundaries are curves separating one cylinder from another and correspond to initial conditions having binary collisions. For example, the 3-cylinders 123 and 121 are separated from each other by initial conditions lying in the 2-cylinder 12 which have, at their third collinearity, a 1–3 binary collision. These domains, and the bounding curves, cover all of the initial condition plane with the exception of the triple collision initial conditions which will lie at intersections of some binary collision curves. The reason all of the plane is so partitioned, for a given k, is that the only initial condition having the empty symbol sequence is the Lagrange orbit corresponding to the point C in Fig. 1.

For illustration, we show in Fig. 2 two divisions of Anosova’s region by the set of 3-cylinders (Fig. 2a) and 4-cylinders (Fig. 2b). For conciseness sake, we denote a cylinder, say, $_\bullet s_1s_2s_3s_4 \ldots$ simply by $s_1s_2s_3s_4$. As shown in the figure, the set of 3-cylinders divide Anosova’s region into two and the set of 4-cylinders into five. $T_1$ and $T_2$ are the initial points of triple collision orbits on the circular boundary of Anosova’s region (Tanikawa and Umehara 1998, Fig. 4). $T_1$, in particular, represents the Lagrange equilateral triple collision. A circle on the x-axis is the initial point of a collinear triple collision orbit (see Tanikawa and Mikkola 2015, Table 2 for a sequence of triple collision points).

In Tanikawa et al. (1995), we introduced the types of collision. The collision point is of type 3 if the point is the initial positions of the orbit for which bodies 1 and 2 collide, the collision point is of type 1 if the point is the initial positions of the orbit for which bodies 2 and 3 collide, and the collision point is of type 2 if the point is the initial positions of the orbit for which bodies 3 and 1 collide. We also introduced the types of collision curves. The collision curve is of type 3 if it comprises collision points of type 3, the collision curve is of type 1 if it comprises collision points of type 1, and the collision is of type 2 if it comprises collision points of type 2. This definition applies in the present paper.

It is to be noted here that there are structures of small scale close to the y-axis with $|x| < 0.01$. We need a special treatment for this region. We neglect this part of Anosova’s region in the present report and will treat it elsewhere.

Fig. 2

The structure of the initial condition plane. a 3-cylinders $_\bullet 132\ldots$ and $_\bullet 131\ldots$, b division by 4-cylinders, $_\bullet 1321\ldots$, $_\bullet 1323\ldots$, $_\bullet 1321\ldots$, $_\bullet 1311\ldots$, and $_\bullet 1313\ldots$. The circle on the x-axis denotes a triple collision point (see Sect. 5)

4 Collision curves

Let us introduce some terminology. A point in the initial condition plane is called a binary collision point (BCP) if it is a starting position of the orbit which experiences a binary collision. BCPs usually form curves in the initial condition plane (Tanikawa et al. 1995; Tanikawa 2000; Tanikawa and Mikkola 2015). We call these the binary collision curves (BCCs), or frequently simply the collision curves. Collision curves are the sections (by the initial condition plane) of the stable and unstable manifolds of the binary collision manifold (Llibre 1982) if the past and future symbol sequences are used. In our case, collision curves are the sections of the stable manifolds since only the future sequences are used. However, in the case of the free-fall problem, the future and the past are identical. So, the collision curves are also the sections of the unstable manifolds.

Property 1

Boundaries of cylinders are formed with collision curves. (Tanikawa et al. 1995; Tanikawa and Mikkola 2008, 2015).

Proof

Suppose that k-cylinders ($k>0$) $A = _\bullet \cdots 1 ***$ and $B = _\bullet \cdots 2 ***$ have a common boundary. In A, body 1 passes through between bodies 2 and 3, while in B, body 2 passes through between bodies 1 and 3 (see the figure below). Then at the boundary, bodies 1 and 2 necessarily collide. The other combinations of the last digits can be treated similarly. $\square$

The boundary collision curve of cylinders $A = _\bullet \cdots 1 ***$ and $B = _\bullet \cdots 2 ***$ is a type-3 curve. Similarly, the boundary curve between $A = _\bullet \cdots 1 ***$ and $C = _\bullet \cdots 3 ***$ a type-2 curve, and $B = _\bullet \cdots 2 ***$ and $C = _\bullet \cdots 3 ***$ a type-1 curve. Thus, different from the case of Tanikawa et al. (1995), types of collision curves are specified by the last digit of symbols of the neighboring two cylinders. As an example, in Fig. 2a, the boundary collision curve of cylinders 132 and 131 is of type 3.

4.1 Orbits which have plural binary collisions along their trajectories

As we have announced in the last paragraph of Introduction, we correct and modify the erroneous statement on triple collision points. Let us introduce new terminology. The boundary collision curves of k-cylinders ($k>0$) will be called the (collision) curves of the kth generation. Let us state a caution. Frequently, a boundary curve of a $(k+1)$-cylinder is a boundary curve of a k-cylinder, that is, some part of the boundaries of cylinders does not change as the number of digits increases. In this case, we call the corresponding boundary the kth generation. If there are given one or more k-cylinders, we sometimes say that these cylinders are of the same (kth) generation.

True triple collision points inside the initial condition plane are shown in Fig. 11 of Tanikawa (2000) and will be treated in the following section.

Assertion. Intersections of collision curves of different generations are the initial points of orbits which have plural collisions along their trajectories.

Let us show the example orbits. One is the orbit starting at $(x,y)=(0.09775, 0.5504)$, and the other is the orbit starting at (0.04273, 0.400). The former point is on the boundary curve of 4-cylinders 1321 and 1323, hence on the curve of the fourth generation, while the latter point is on the boundary curve of 6-cylinders 132311 and 132312, hence on the curve of the sixth generation. We plot the trajectories of both orbits in Fig. 3. The initial conditions are similar. So the forms of the trajectories are close to each other. There are differences. The trajectory in Fig. 3a has a binary collision between body 1 and body 3 at $t=0.6559\ldots$, while the trajectory in Fig. 3b has a binary collision between body 1 and body 2 at $t=1.0051\ldots$. We see two binary collisions are at different places, at different times, and between different pairs of bodies.

Fig. 3

a A collision orbit on the collision curve of type 2 and of the fourth generation. It forms the boundary of cylinders 1321 and 1323. b A collision orbit on the collision curve of type 3 and of the sixth generation. It forms the boundary of cylinders 132311 and 132312

The boundary curves of 4-cylinders 1321 and 1323 and 6-cylinders 132311 and 132312 intersect at point (0.110361, 0.567465). We show the trajectories of the orbit starting at this point in Fig. 4. The trajectories experience collisions at $t=0.67383$ and at $t=1.40746$. We see two (consecutive) collisions along the trajectories. For the moment, we do not have a point where three or more collision curves of different generations cross.

It is to be noted that 4-cylinder 1321 has two components (Fig. 2b). The two components are disconnected also in the shape space as can be seen easily. This phenomenon may complicate in future the study of symbolic dynamics of our three-body problem.

5 Triple collisions inside the initial condition plane

We know that triple collision orbits on the boundary of the initial condition plane have a special property that a lot of (possibly an infinite number of) collision curves pass through their initial points (see, e.g., Fig. 7 of Tanikawa 2000). We have a candidate of triple collision orbits inside the initial condition plane from our previous work. In Fig. 11a and b of Tanikawa (2000), curves of types 1, 2, and 3 meet at a point. We did not confirm that the orbit starting at this point actually ends at triple collision by drawing trajectories. This orbit is included in the present paper.

Fig. 4

An orbit with two collisions as a boundary of cylinders 132131, 132311, 132312, and 132132. The initial point is the intersection of two collision curves

We denote the initial point of a triple collision orbit by a triple collision point (TCP). The corrections for the erroneous statement of the former papers continue. In this section, we try to make clear the conditions of triple collision points in the initial condition plane.

Property 4

Triple collision points are obtained as intersections of different types of collision curves of the same generation.

Proof

Suppose that a collision curve in which bodies i and j collide and a collision curve of the same generation in which bodies i and k collide intersect. Then at intersections, bodies i, j, and k collide at the same instant.

Let us show the division of the initial condition plane by the set of cylinders with increasing digits. We have already shown the divisions by the set of 3- and 4-cylinders in Fig. 2. There, intersections of boundary collision curves are only on the boundaries of the plane. In Fig. 2a, the collision curve of type 3 as the boundary cylinders 132 and 131 crosses the circular boundary of type 2. The intersection is the isosceles triple collision point $T_2$ which we mentioned in the end of “Introduction.” In Fig. 2b, two curves of type 2 cross the circular boundary also of type 2. The intersections are not triple collision points. One of the curves starting at point $T_2$ crosses the x-axis at $x=0.18058\ldots$. This is a collinear TCP (see Tanikawa and Mikkola 2015).

Fig. 5

Divisions of Anosova’s region. a Division by the set of 6-cylinders. There is only one intersection inside Anosova’s region between collision curves. This is the cross point of curves of generations 4 and 6, which means the point is not a triple collision point. b Division by the set of 7-cylinders. There is only one collision curve of generation 7. In this case also, there is not a triple collision point

We see that 3-cylinder 131 is bounded by three curves: the arc of the circular boundary connecting $T_2$ and point B, the arc of the x-axis connecting the cross ($\times$) and B, and a curve connecting $T_2$ and the cross. These are all collision curves. 3-cylinder 132 is bounded by four arcs of collision curves neglecting the structure close to the y-axis. 4-Cylinders in Fig. 2b are also bounded by arcs of collision curves. We do not any more raise the names of collision curves of higher generations. It is a cumbersome work.

The division of the initial condition plane by the set of 6- and 7-cylinders is depicted in Fig. 5. We note that no new regions appear in the division by the set of 5-cylinders. We expect that the shadowed region may contain triple collision points. However, in the present paper, we do not treat the region. This region is divided into an infinite sequence of regions (see, e.g., Fig. 2 of Tanikawa and Umehara 1998). Each of these regions is considered to have a similar phase space structure to our region of the present paper.

In Fig. 5a, a thick curve is the type-3 collision curve of the sixth generation, while thin curves are of younger generations. There are no intersections between curves of the sixth generation. There is an intersection (denoted by $+$) of curves of the fourth and sixth generations in the upper part of the plane. This point is the starting point of the orbit which has two collisions along its trajectories. We describe this orbit in Sect. 4.1 and show its trajectories in Fig. 4.

In Fig. 5b, the division of the initial condition plane by the set of 7-cylinders is shown. There is only one new curve of the seventh generation. As before, we show it by a thick curve, and the curves of younger generations by thin curves. This time, there arise necessarily no triple collision points since there are no intersections between collision curves of the seventh generation.

Finally, we find triple collision points in the division by the set of 8-cylinders. We show the results in Figs. 6 and 7. In Fig. 6, we have four curves of the eighth generation. Two upper thick curves do not intersect each other though they intersect with other curves of younger generations. The lower two curves of the eighth generation intersect each other. The structure in the upper part of Fig. 6 is complicated, so we enlarge in Fig. 7a the region inside the larger box of Fig. 6. In the figure, regions denoted (a), (b), (c), (d), (e), and (f) are 8-cylinders 13231131, 13231123, 13213123, 13231211, 13231121, and 13213213, respectively.

Figure 7b is an enlargement of the small box in Fig. 6. There are four curves. Three thick curves are those of the eighth generation, while one thin curve is of the third generation. Three thick curves intersect at two points (0.19208270, 0.3093601), and (0.22202750, 0.30096440). We find that collision curves of the same generation and of the three types meet at a triple collision point. In other words, three cylinders of the same generation meet at a point. In fact, for the case of the left triple collision point, three 8-cylinders 13213211, 13213212, and 13213213 meet at this point. The same is true for the right triple collision point. We show in Fig. 8a and b the trajectories of the orbits starting at these two points.

Fig. 6

Cylinders in Anosova’s region: 8-cylinders. Boundary curves for digit-8 are illustrated with thick curves. Boundary curves of younger generations are with thin curves. The upper and left cylinders have small areas. So we do not inscribe the symbol sequences

Fig. 7

8-Cylinders in Anosova’s region. a Enlargement of the larger box in the former figure. Cylinders named a–f have the following symbol sequences. a: 13231131; b: 13231123; c: 13213123; d: 13231211; e: 13231121; f: 13213213. b Enlargement of the smaller box in the former figure. Two crosses represent the triple collision points whose orbits are collisionless until triple collision. The coordinates are (0.19208270, 0.30936018), and (0.22202750, 0.30096440)

Fig. 8

Trajectories of triple collision orbits on the boundaries of the 8-cylinders. The initial points are illustrated by two $+$’s in Fig. 7. a The orbit starting at (0.19208270, 0.30936018); b the orbit starting at (0.22202750, 0.30096440)

6 Other triple collision orbits

Now, we are convinced that triple collision points can be found in the regions where three collision curves of the same generation meet. For the moment, our search will be not systematic. We look for the structures at which three cylinders meet. We find eight places. We show in Fig. 9 the places enclosed by boxes. Let us show the structure inside each box one by one.

Fig. 9

Boxes containing triple collision points in the initial condition plane. Some of the collision curves up to and including the eighth generation are inscribed for reference. Represented are the coordinates of the lower left and upper right corners of the boxes. Box 1: (0.145, 0.325), (0.165, 0.345); Box 2: (0.08, 0.365), (0.105, 0.385); Box 3: (0.075, 0.41), (0.085, 0.42); Box 4: (0.08, 0.445), (0.095, 0.465); Box 5: (0.10, 0.515), (0.115, 0.525); Box 6: (0.145, 0.635), (0.165, 0.655); Box 7: (0.18, 0.575), (0.20, 0.595); and Box 8: (0.27, 0.565), (0.29, 0.585)

Fig. 10

The division of the plane in the boxes of Fig. 9. Three curves meet at a triple collision point. Thin curves are boundary curves of younger generations

In Fig. 10a, three 10-cylinders 13213212-11, 12, and 13 meet at (0.15567083,  0.33309483). For conciseness, we denote the cylinder regions by using the last two digits. The same convention will be used in what follows. In Fig. 10b, three 14-cylinders 132312121212-11, 12, and 13 meet at two points (0.09012264, 0.38213664) and (0.10106723, 0.37459122) denoted by $\times$. In Fig. 10c, three 12-cylinders 1323121212-11, 12, and 13 meet at (0.08212247, 0.41682453). In Fig. 10d, three 10-cylinders 13231212-11, 12, and 13 meet at (0.08875296, 0.45639865). In Fig. 10e, three 8-cylinders 132312-11, 12, and 13 meet at (0.10677930, 0.52012268). In Fig. 10f, three 11-cylinders 132132132-11, 12, and 13 meet at (0.15882908, 0.64735217). In Fig. 10g, three 13-cylinders 13231213213-21, 22, and 23 meet at (0.19095011, 0.58286178). Finally, in Fig. 10h, three 13-cylinders 13231213213-21, 22, and 23 meet at (0.27949737, 0.57593177).

We summarize the coordinates of the above triple collision points in Table 1. Here, we provide the coordinates in the precision of eight digits, in contrast to, for example, 25 digits of the figure-8 orbit obtained by Simó (2002) with the aid of, perhaps, multi-precision arithmetic. We use standard double-precision arithmetic and provide the reliable initial eight digits, which are in fact sufficient to reproduce our results.

We added four data. t is the time of approach to triple collision. We cannot obtain the exact collision time. The time in the table is that the integration is available. Our experience says that the integration with the extrapolation method takes much time to return the result if the time exceeds this value. Column “Digits” shows when in the symbol sequence the triple collision takes place. The shortest digits are eight. We do not say that the triple collision points with symbol sequences of length equal to or less than 14 are exhausted because our survey is not complete. Column “Side” shows the side of the triangle formed by three bodies toward triple collision. All orbits start with the front side. Eight of them end with the backside triangle. Finally, column “Figures” indicates the serial numbers of figures in which the positions of the triple collision points and trajectories are shown. Thus, for example, for No. 1 triple collision, the positions are shown in Fig. 7b and trajectories are shown in Fig. 8a.

We find two types of triple collision points as listed in Table 1. One type is shown in Figs. 7b and 10a–e. The other type is shown in Fig. 10f–h. The differences are apparent. One is the difference of angles which cylinders make at the triple collision point. The cylinders with ’11’ at the last two digits have narrow width toward the cross point in the former case. This structure may reflect the dynamics. The other is the difference at which digit the triple collision takes place. In Figs. 7b and 10a–e, triple collision takes place at even digits, whereas in Fig. 10f–h, triple collision takes place at odd digits. Geometrically, the orientation of the triangle is negative in the former case just before the triple collision, whereas the orientation is negative in the latter case. One can confirm this looking at the trajectories in Figs. 8, 11, and 12. For the moment, we do not have a good explanation.

We see a similarity in the structure of divisions of Figs. 7b and 10b. In both cases, two triple collision points are near the top of the tongue-like structure extended from the x-axis. There are a lot of tongue-like structures nested each other or neighboring each other. So, we expect that a lot of (possibly an infinite number of) triple collision points exist in our area.

Table 1 Triple collision points

Fig. 11

The trajectories of triple collision orbits whose initial conditions are shown in Fig. 10

Fig. 12

The trajectories of triple collision orbits whose initial conditions are shown in Fig. 10b and in Table 1

We show the trajectories of the remaining nine triple collision orbits. Seven of them are shown in Fig. 11. Each of the trajectories is named (a) $\sim$ (h) which corresponds the triple collision point in Fig. 10 of the same name. We show in Fig. 12 two trajectories of orbits corresponding to the points of Fig. 10b.

7 Discussions

We expect that the number of triple collision points inside Anosova’s region be infinite. There can be at least two kinds of sequences of these orbits. One sequence comes from the infinite similar structures of Anosova’s region to the lower right point B. The other sequence is inside our region. We already pointed out that the number of tongue-like structures extending from the x-axis may be infinite, and each of these structures may contain triple collision points near the top as in Figs. 7 and 10b.

The next target of research will be the systematic search for the triple collision points. Individual tasks are simple: To find places in the initial condition plane where three cylinders of the same generation meet. How to automatically find this place? This seems not easy. Another direction of study will be to search for triple collision orbits with nonzero initial velocities and yet with zero angular momentum.

The collision curves cross the x-axis perpendicularly because of the symmetry of the problem. So, the structure of the phase plane near the x-axis is expected to be not so much complex. On the other hand, our preliminary study shows that the phase plane near the y-axis has rich structure. This area is worth to be investigated.

Richard Montgomery raised a few questions concerning the characters of symbol sequences for bi-asymptotic solutions to triple collision (Montgomery 2007). One of them is whether any finite symbol sequence is possible or not. The related question is what symbol sequences are possible. The present paper is a first step to answer his questions.

8 Conclusions

In this paper, we give symbols 1, 2, or 3 along an orbit each time when the triangle formed with three bodies $m_1, m_2, m_3$ becomes collinear. Due to the theorem of Montgomery (2007), except for the Lagrange equilateral configuration, all triple systems of any form experience collinear configuration until infinite future or until triple collision, if any. So, the symbol sequence is given to all orbits of the initial points of the free-fall problem except point C of Fig. 1. If we truncate the symbol sequences at the kth digit, k-cylinders ($k>0$) are obtained. For each k, the set of k-cylinders together with their boundaries divide the initial condition plane without gaps.

• 1. We numerically established that a triple collision point (i.e., a point of the initial condition plane whose orbit ends at triple collision) can be found as an intersection of three cylinders of the same generation. We do not obtain triple collision orbits with symbol sequences shorter than eight digits.

• 2. We obtained 11 triple collision points inside Anosova’s region. The orbits starting from these points have finite lengths in the future and in the past since the problem is free fall. These orbits start at triple collision, expand the size until the free-fall states, and go back to triple collision. Thus, these are time symmetric with respect to the time of free fall.

• 3. Two types of triple collision orbits are identified. One type of orbits starts with a positive triangle formed with three bodies and ends at triple collision also with a positive triangle. The other type starts with a positive triangle and ends with a negative triangle.

• 4. The intersections of binary collision curves of different generations are the initial points of orbits with plural binary collisions along their trajectories.