Triple collision orbits in the free-fall three-body system without binary collisions

Abstract

We numerically investigate triple collision orbits of the free-fall three-body system which has no double collisions before three bodies collide. Triple collision is an important property of the three-body system. Tanikawa, Saito, Mikkola (Celest Mech Dyn Astron 131(6):24, 2019) obtained 11 triple collision orbits without double collision for the free-fall three-body problem. In this paper, we present 1658 triple collision orbits including the Lagrange’s homothetic solution, 11 ones found by Tanikawa et al. (2019) and 1646 new triple collision orbits. The symbol sequences of these 1646 new triple collision orbits have digits that range between 1 and 120. With our high-precision results, numerical evidences of the asymptotic property of triple collision orbits are given.

1 Introduction

The three-body problem is an old and challenging problem in celestial mechanics. It has various dynamical behaviors including periodic orbits (Šuvakov and Dmitrašinović 2013; Iasko and Orlov 2014; Dmitrašinović and Šuvakov 2014; Li and Liao 2017; Li et al. 2018; Belbruno et al. 2019; Gao and Llibre 2020; Li et al. 2021), collision orbits (Tanikawa and Mikkola 2015; He and Petrovich 2018; Tanikawa et al. 2019) and chaotic escaping orbits (Urminsky and Heggie 2010; Stone and Leigh 2019). The free-fall three-body problem is to study the triple system without initial velocity. The Pythagorean three-body problem was the first case of the free-fall three-body problem to be numerically investigated by Burrau (1913). The system eventually breaks up into a binary and a single body. Agekyan and Anosova (1968) suggested initial positions in a special region which contains all possible initial configurations of the free-fall three-body problem.

Periodic orbits of the free-fall three-body problem have been well comprehended. Szebehely and Peters (1967) numerically gained the first periodic orbit of the free-fall three-body system with double collision. Standish (1970) found another periodic orbit of the free-fall three-body problem which has no double collision before the three bodies collide. Periodic collisional orbits of the free-fall isosceles three-body system were obtained and their existence was proved in Chen (2013). Twenty-two close-to-periodic orbits of the free-fall three-body system were presented by Yasko and Orlov (2015) . Recently, Li and Liao (2019) employed so-called Clean Numerical Simulation (Liao 2009, 2014) to obtain 313 new periodic orbits of the free-fall three-body system without collision.

Similarly to periodic orbits, collision orbits are also an important property of the three-body system. The triple collision for the collinear three-body problem was investigated by McGehee (1974) and the triple collision for the isosceles three-body system was studied by Devaney (1980). Tanikawa et al. (1995) numerically investigated the double collision orbits and triple collision orbits with double collision for free-fall three-body systems. Triple collision orbits with double collision were obtained for the free-fall collinear three-body system (Tanikawa and Mikkola 2015). All of these triple collision orbits have double collisions before the three bodies collide.

The Lagrange’s homothetic solution was the only one triple collision orbit of the three-body system without double collision before Tanikawa et al. (2019) found 11 new ones. These 11 triple collision orbits were obtained through the intersection of three double collision curves (formed by initial conditions of double collision orbits in the Agekyan and Anosova’s region) with the same number of digits of symbol sequences. The digits of symbol sequences of these triple collision orbits range between eight and fourteen. Tanikawa et al. (2019) expected that there are infinite triple collision orbits inside the Agekyan and Anosova’s region. However, it would be much more complicated to obtain triple collision orbits with longer sequences by the intersection of double collision curves of the same digits. So far, a total of 12 triple collision orbits have been found in the three-body system without double collisions.

In this paper, an exploration for new triple collision orbits of the free-fall three-body system and numerical techniques for locating them are presented. Finally, we numerically study the asymptotic property of triple collision orbits.

2 Numerical search for triple collision orbits of the free-fall problem

2.1 Initial configuration of the free-fall three-body problem

Fig. 1

The initial configuration of the free-fall three-body system. The initial position of body-1 is located at (x, y) in the Agekyan and Anosova’s region D. The initial coordinates of body-2 and body-3 are set at $(-0.5,0)$ and (0.5, 0), respectively

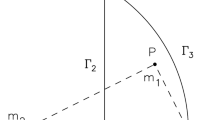
Let us consider the equal-mass free-fall three-body system in the plane. Like other free-falling objects, initial velocities of the free-fall three-body system are equal to zero. Assume that the Newtonian gravitational constant $G=1$ and the masses of the three bodies $m_1=m_2=m_3=1$. In order to study the free-fall three-body problem systematically, we investigate the triple system with initial positions in the Agekyan and Anosova’s region (Agekyan and Anosova 1968) which contains all potential initial positions of the free-fall system. The initial locations of body-2 and body-3 are at $(-0.5, 0)$ and (0.5, 0), respectively. As shown in Fig. 1, the initial position (x, y) of body-1 is set in the Agekyan and Anosova’s region D:

$$\begin{aligned} D = \{(x,y)|x \ge 0; y \ge 0; (x+0.5)^2+y^2 \le 1\}. \end{aligned}$$

(1)

The region D is surrounded by the lines $\overline{OB}$, $\overline{OC}$ and a circular arc $\overset{\smallfrown }{BC}$ of radius 1 centered at $A(-0.5, 0)$. There are triple collision orbits with collinear configurations on the boundary $\overline{OB}$ (McGehee 1974; Tanikawa 2000). Triple collision orbits with binary collision were found on the circular arc $\overset{\smallfrown }{BC}$ (Devaney 1980; Umehara and Tanikawa 2000). In this work, we focus on initial conditions on the boundary $\overline{OC}$ and inside the Agekyan and Anosova’s region D.

2.2 Numerical methods to search for triple collision orbits

Let

$$\begin{aligned} {\varvec{r}}={\varvec{r}}(t;{\varvec{q}}),\;\; t \in {\mathbb {R}}, \;\;\; {\varvec{r}}, {\varvec{q}} \in {\mathbb {R}}^6, \end{aligned}$$

(2)

be the solution of positions of the three-body system with initial position ${\varvec{r}}(0)={\varvec{q}}=(q_1, q_2, q_3, q_4, q_5, q_6)$. We assume the coordinates of the three-body system as ${\varvec{r}}=(r_1, r_2, r_3, r_4, r_5, r_6)$, where $r_{2i-1}$ and $r_{2i}$ are x-axis and y-axis components of the position of the body-i (i=1, 2, 3), respectively.

Since the free-fall three-body system has zero momentum, the center of mass of the triple system is always at a fixed point. If the three bodies collide at one point, then the triple collision point must be located at the center of mass of the triple system. In the Agekyan and Anosova’s initial configuration, the initial position of the body-1 is $(q_1, q_2)$ and $q_3=-q_5=-0.5$ and $q_4=q_6=0$. The center of mass of the triple system is at $(q_1/3, q_2/3)$. Therefore, the triple collision coordinates of the free-fall triple system are ${\varvec{r}}_{c}=(q_1/3, q_2/3, q_1/3, q_2/3,q_1/3, q_2/3)$.

The triple collision orbits satisfy the following equations:

$$\begin{aligned} {\varvec{r}}(T;{\varvec{q}}) - f({\varvec{q}}) = {\varvec{0}}, \end{aligned}$$

(3)

where T is the time of triple collision and $f({\varvec{q}})=(q_1/3, q_2/3, q_1/3, q_2/3,q_1/3, q_2/3)$ denotes the triple collision coordinates of the triple system with initial coordinate ${\varvec{q}}$.

The distance between the coordinates of the three-body system and coordinates of a triple collision can be described as

$$\begin{aligned} d(t,{\varvec{q}}) = |{\varvec{r}}(t;{\varvec{q}})-f({\varvec{q}})|. \end{aligned}$$

(4)

To obtain the roots of the above equations, firstly, we hunt for approximate initial positions of triple collision orbits with grid points in the Agekyan and Anosova’s region D, as shown in Fig. 1. The ODE solver dop853 (Hairer et al. 1993) is applied to numerically integrate the differential equations of the three-body problem till $t=100$. The approximate initial positions ${\varvec{q}}$ and the time T of triple collision are selected when the distance $d(T, {\varvec{q}})<0.1$.

Secondly, we improve these initial positions ($q_1, q_2$) and the time of triple collision T by means of “Clean Numerical Simulation”(CNS) (Liao 2009, 2014; Liao and Wang 2014; Hu and Liao 2020) and the Newton–Raphson method (Farantos 1995; Lara and Pelaez 2002; Abad et al. 2011). Note that we focus on triple collision orbits which have no double collisions before the three bodies collide. So we do not apply binary collision regularization in this study. However, the three-body orbits would be probably close to triple collision. To obtain reliable numerical calculation of three-body orbits, we employ the high-precision numerical strategy called “Clean Numerical Simulation”(CNS) (Liao 2009, 2014; Liao and Wang 2014; Hu and Liao 2020) to integrate the differential equations of the three-body system. The CNS is based on the arbitrary order of the Taylor series method (Barton et al. 1971; Corliss and Chang 1982; Chang and Corhss 1994; Barrio et al. 2005), multiple precision arithmetic (Fousse et al. 2007), and a convergent verification with one more accurate simulation. The adopted numerical precision depends on the individual orbit. The computation is done with the least error tolerance of $10^{-60}$ and the largest significant digits of 90.

We assume that at step n we obtain approximate initial conditions ${\varvec{q}}^{(n)}$ and the time of triple collision $T^{(n)}$. Then we modify these initial positions and the time of triple collision by adding approximate corrections $(\varDelta {\varvec{q}}^{(n)}, \varDelta T^{(n)})$ which satisfy

$$\begin{aligned} {\varvec{r}}(T^{(n)} + \varDelta T^{(n)}; {\varvec{q}}^{(n)} + \varDelta {\varvec{q}}^{(n)}) - f({\varvec{q}}^{(n)} + \varDelta {\varvec{q}}^{(n)}) = 0. \end{aligned}$$

(5)

Using the first-order approximation of Taylor series of the above equations, we obtain

$$\begin{aligned} {\varvec{r}}(T^{(n)};{\varvec{q}}^{(n)}) + \frac{\partial {\varvec{r}}}{\partial {\varvec{q}}} \varDelta {\varvec{q}}^{(n)} + \frac{\partial {\varvec{r}}}{\partial t} \varDelta T^{(n)} - (f({\varvec{q}}^{(n)}) + f(\varDelta {\varvec{q}}^{(n)})) = 0, \end{aligned}$$

(6)

where $\frac{\partial {\varvec{r}}}{\partial {\varvec{q}}}$ is the solution of the variational equations of the three-body system, $\frac{\partial {\varvec{r}}}{\partial t}$ denotes the first derivative of the position with respect to time at $t=T^{(n)}$. Then we can obtain

$$\begin{aligned} \frac{\partial {\varvec{r}}}{\partial {\varvec{q}}} \varDelta {\varvec{q}}^{(n)} - f(\varDelta {\varvec{q}}^{(n)}) + \frac{\partial {\varvec{r}}}{\partial t} \varDelta T^{(n)} = f({\varvec{q}}^{(n)}) - {\varvec{r}}(T^{(n)};{\varvec{q}}^{(n)}) . \end{aligned}$$

(7)

Note that the initial positions of body-2 and body-3 are fixed, so the corrections are $\varDelta q_3=\varDelta q_4=\varDelta q_5=\varDelta q_6=0$. Then the linear equation can be written as

$$\begin{aligned}&\begin{bmatrix} \partial {r_1(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1}-1/3 &{} \partial {r_1(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2} &{} \partial {r_1(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \partial {r_2(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1} &{} \partial {r_2(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2}-1/3 &{} \partial {r_2(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \partial {r_3(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1}-1/3 &{} \partial {r_3(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2} &{} \partial {r_3(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \partial {r_4(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1} &{} \partial {r_4(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2}-1/3 &{} \partial {r_4(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \partial {r_5(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1}-1/3 &{} \partial {r_5(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2} &{} \partial {r_5(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \partial {r_6(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_1} &{} \partial {r_6(T^{(n)};{\varvec{q}}^{(n)})}/{\partial q_2}-1/3 &{} \partial {r_6(T^{(n)};{\varvec{q}}^{(n)})}/{\partial t} \\ \end{bmatrix} \begin{bmatrix} \varDelta q_1^{(n)} \\ \varDelta q_2^{(n)} \\ \varDelta T^{(n)} \\ \end{bmatrix}\nonumber \\&\quad = \begin{bmatrix} q_1^{(n)}/3 - r_1(T^{(n)};{\varvec{q}}^{(n)})\\ q_2^{(n)}/3 - r_2(T^{(n)};{\varvec{q}}^{(n)})\\ q_1^{(n)}/3 - r_3(T^{(n)};{\varvec{q}}^{(n)})\\ q_2^{(n)}/3 - r_4(T^{(n)};{\varvec{q}}^{(n)})\\ q_1^{(n)}/3 - r_5(T^{(n)};{\varvec{q}}^{(n)})\\ q_2^{(n)}/3 - r_6(T^{(n)};{\varvec{q}}^{(n)})\\ \end{bmatrix} \end{aligned}$$

(8)

There are six equations and three unknowns in this linear system. As the unknowns are less than the number of equations, we employ the singular value decomposition (SVD) method (Trefethen and Bau III 1997) to obtain the least-norm solution of the linear system. After solving these equations, we obtain the new initial conditions $q_1^{(n+1)} = q_1^{(n)} + \varDelta q_1^{(n)}$, $q_2^{(n+1)} = q_2^{(n)} + \varDelta q_2^{(n)}$, and the time of triple collision $T^{(n+1)} = T^{(n)} + \varDelta T^{(n)}$. We propose that triple collision orbits are located when the distance between the coordinates of the three bodies and triple collision is $d(T, {\varvec{q}})<10^{-8}$.

After obtaining triple collision orbits, we use the topological method (Montgomery 1998; Tanikawa et al. 2019) to classify these orbits. Montgomery (2007) proved that all three-body orbits without angular momentum have the collinear instant (also called syzygy) except for the Lagrange’s solution. When the three bodies are on the same line, symbols $``1''$, “2” and $``3''$ are identified as body-1, body-2 and body-3 at the center, respectively. Then the topology of triple collision orbits can be described by symbol sequences with $``1''$, $``2''$ and $``3''$ before the three bodies collide (Montgomery 1998; Tanikawa et al. 2019).

3 Numerical results

3.1 Triple collision orbits in the isosceles configuration

Fig. 2

The Lagrange’s solution which has no syzygy. Solid blue line: body-1; dotted red line: body-2; dashed black line: body-3. The solid points denote the initial position

Starting from the equilateral triangular initial configuration, the orbit is the simplest triple collision orbit called Lagrange’s solution, as shown in Fig. 2. Note that the Lagrange’s solution has no syzygies before the three bodies collide. All previously found triple collision orbits with isosceles configuration always have double collisions except for the Lagrange’s solution. We here search for triple collision orbits without double collisions in the isosceles configuration.

We investigate the three-body system with initial positions on the boundary $\overline{OC}$. The x-component of the initial position of body-1 is zero on that boundary. First, we search for the approximate initial positions of the triple collision orbits with grid points on the boundary $\overline{OC}$ with grid size $\delta y =1\times 10^{-6}$. Then we correct the y-axis coordinate of body-1 and the time of triple collision by using the clean numerical simulation and Newton–Raphson method till $d(T, {\varvec{q}})<10^{-8}$. In our numerical search, we obtained the Lagrange’s solution and four new triple collision orbits without double collisions in the isosceles configuration, as shown in Table 1. For the Lagrange’s solution, the exact initial position $y=\sqrt{3}/2$ and the precision of our numerical result is about $10^{-11}$. The symbol sequences of the four new ones are $``1''$, $``11''$, $``111''$ and $``1111''$, respectively.

Table 1 The initial position (x, y) of body-1 and the triple collision time T of triple collision orbits with isosceles triangular (IT) configuration, where $x=0$

Let us study the new triple collision orbit IT-1 with symbol sequence $``1''$. Its trajectory is shown in Fig. 3a. Because of the symmetry of the initial conditions, the orbits of body-2 and body-3 are axial symmetric. Figure 3b displays the y-axis coordinates of the three bodies versus time. We observe from Fig. 3b that the y-axis coordinate of body-1 crosses through the y-axis coordinate of body-2 and body-3 at $t\approx 0.31$, which means they have a syzygy at that moment. Note that body-1 always moves along the y axis. At the beginning, body-1 moves down and has a syzygy with body-2 and body-3. And then body-1 moves up and collide with body-2 and body-3. Thus, its symbol sequence is $``1''$ before the three bodies collide.

Fig. 3

The triple collision orbit IT-1 with symbol sequence $``1''$: a trajectories in the $x-y$ plane, the solid points denote initial positions; b y-axis coordinates of the three bodies versus time

3.2 Triple collision orbits without binary collisions in the general triangular initial configuration

Fig. 4

The initial conditions of triple collision obits in the Agekyan and Anosova’s region

Fig. 5

Some new triple collision orbits with general triangular (GT) initial configuration: a GT-3; b GT-9; c GT-100; d GT-500; e GT-1000; f GT-1653. Their initial conditions and the time of triple collision are listed in Table 2. Solid blue line: body-1; dotted red line: body-2; dashed black line: body-3. The solid points denote the initial positions

For general triangular (GT) initial configurations, we searched for approximate initial positions of triple collision orbits with grid points inside the Agekyan and Anosova’s region with grid size $\delta x = \delta y =0.001$. We obtained 1653 triple collision orbits with $d(T, {\varvec{q}})<10^{-8}$ through our numerical procedures. The minimum of any two bodies’ distance is larger than $10^{-6}$ before the three bodies collide. Thus, we regard these orbits as triple collision orbits without binary collisions. These triple collision orbits include 11 orbits found by Tanikawa et al. (2019) and 1642 newly found orbits. The locations of the initial conditions of these triple collision orbits are shown in Fig. 4. The trajectories of some new triple collision orbits are shown in Fig. 5. The initial conditions and the time of triple collision of the six triple collision orbits are listed in Table 2.

The complete initial conditions and the time of triple collision of all 1653 triple collision orbits are given in the spreadsheets of the supplementary materials. Their symbol sequences are also presented in the supplementary materials. The symbol sequences of these triple collision orbits have digits that range between 3 and 120. Our corresponding labels of No.1-11 of triple collision orbits in Tanikawa et al. (2019) are GT-8, GT-7, GT-6, GT-12, GT-13, GT-17, GT-18, GT-36, GT-33, GT-38, GT-37, respectively.

Table 2 The initial positions (x, y) of body-1 and the time of triple collision T of some new triple collision orbits with general triangular (GT) initial configurations. Their trajectories are shown in Fig. 5

3.3 Asymptotic property of triple collision orbits

Fig. 6

The distance between the trajectory and the triple collision coordinate $|{\varvec{r}}(t;{\varvec{q}})-{\varvec{r}}_c|$ is proportional to $(T-t)^{2/3}$ for the GT-3 case when $(T-t)$ is small, where ${\varvec{q}}$, ${\varvec{r}}_c$, T denote the initial position, the coordinate of the triple collision and the time of triple collision, respectively

There is a singularity for the triple collision orbit which has no double collisions before the three bodies collide. The velocities of triple collision orbits approach to infinity in a finite time. Sundman (1909) proved that a triple collision orbit moves asymptotically to a central configuration for the three-body problem (McGehee 1974). In the theorem of Sundman (1909), the distance between the positions and the triple collision coordinates $|{\varvec{r}}(t;{\varvec{q}})-{\varvec{r}}_c|$ goes asymptotically toward zero like $(T-t)^{2/3}$, where T is the triple collision time and ${\varvec{r}}_c$ denotes the coordinate of the triple collision. Note that $|{\varvec{r}}(t;{\varvec{q}})-{\varvec{r}}_c|^2$ is the moment of inertia of the triple system.

So far there have been no numerical results for this asymptotic property of triple collision orbits of the three-body problem with general triangular initial configuration. Fortunately, we obtain triple collision orbits with high-precision initial conditions and the collision time by means of clean numerical simulation. Thus, we can numerically investigate the asymptotic property of triple collision orbits.

For the newly found triple collision orbit GT-3, the distance between the orbits and the triple collision coordinates $|{\varvec{r}}(t;{\varvec{q}})-{\varvec{r}}_c|$ is proportional to $(T-t)^{2/3}$ when $(T-t)$ is small, as shown in Fig. 6. We also observe that all newly found triple collision orbits have the same asymptotic property. Consequently, we present the numerical evidences for the asymptotic property of triple collision orbits of the three-body problem.

4 Conclusions

In this paper, we searched for triple collision orbits in the Agekyan and Anosova’s region of the free-fall three-body system which has no double collisions before the three bodies collide. Totally, we obtained 1658 triple collision orbits including the Lagrange’s solution, 11 ones found by Tanikawa et al. (2019), and 1646 new triple collision orbits. The symbol sequences of these 1646 new triple collision orbits have digits that range between 1 and 120. With our high-precision results, numerical evidences of the asymptotic property of triple collision orbits were presented.