Triple collision orbits with nonzero initial velocities

Abstract

Triple collision orbits of the three-body problem with nonzero initial velocities have been systematically surveyed. For this purpose, we have formulated the sufficient conditions of the velocities of three bodies so that the total angular momentum of the triple system is zero. The velocity conditions are parameterized by two parameters $\alpha _2$ and $\beta _1$ in the initial condition plane. We introduce the characteristic as the curve in the initial condition plane of the non-free-fall triple collision points (TCPs) parameterized by one parameter, say, $\alpha _2/\beta _1$. The velocity conditions with full parameters suggest that non-free-fall TCPs (nonff-TCPs) occupy two-dimensional areas in the initial condition plane. We plotted five characteristics passing through eight ff-TCPs, one of which forms a closed circuit. Two ff-TCPs on a characteristics are called a twin. This gives us a criterion of classification of TCPs in addition to the one obtained in Tanikawa and Mikkola (Cel Mech Dyn Astron 133:52, 2001) which connects the directions of the initial and final triangles formed by three bodies. We find that the twin ff-TCP TSM-1 and TSM-2 are connected by all the characteristics, which pass through one of them. A neighborhood of ff-TCP TSM-2 has been confirmed to be occupied by nonff-TCPs. We expect that the same is true with a neighborhood of any ff-TCP. Further, we expect that this is true with a neighborhood of any nonff-TCP. We do not continue the characteristics until its end because the continuation seems endless.

1 Introduction

1.1 Preceding works

The three-body problem has been initiated by Isaac Newton in his celebrated book ’Principia’ Newton (1687). Since then many astronomers, physicists, and mathematicians have been involved in this problem including the restricted case and have added their own important contributions. As for the triple collision, there have been also a lot of investigations. Euler (1767) and Lagrange (1772), respectively, found collinear and equilateral periodic solutions with appropriate rotations. It is clear that these symmetrical configurations give triple collision orbits if there are no rotations. So Euler and Lagrange found triple collision orbits. Since then, no analytical solutions of the triple collision orbits are found.

After Poincaré (1890) proved that three-body problem is analytically unsolvable, Siegel (1941) tried to find the true reason of the unsolvability and found that the triple collision is the essential singularity in the complex analysis. Before that, Sundman (1913) proved that zero angular momentum is the necessary condition for a triple collision.

As for the regularization of the problem, the regularization both of Levi-Civita (1920) and Kustaanheimo and Stiefel (1965) cannot be applicable to the triple collision. McGehee (1974) devised a transformation including the time change of $dt \propto r^{3/2} d\tau$ where t and $\tau$ are the original and new time variables and has been successful in regularizing the one-dimensional three-body system. His regularizing variables are now called the McGehee variables and are widely used. Devaney (1980) extended these variables to the isosceles problem. Waldvogel (1982) using the sum of the three edges of the triangle regularized the three-body problem with the same time change $dt \propto r^{3/2} d\tau$. In the McGehee variables, triple collision singularity becomes an invariant manifold, i.e., the triple collision manifold. It takes an infinite time for the solutions to approach or recede from it.

After the introduction of the triple collision manifold, the analyses of the solutions passing close to this manifold and the global behaviors of solutions, which become close to the manifold, have been intensively done by authors such as Moeckel (1983), Moeckel (1989), Waldvogel (1976) and Simó and Martínez (1987). In particular, Moeckel intensively studied the orbits connecting the neighborhoods of different triple collisions.

Numerical investigation have been extensively done by K. Tanikawa and his collaborators. The start was Tanikawa et al. (1995) aiming at the search for collision orbits working on the Anosova region, which is a part of the shape sphere. The numerical results for the collinear or rectilinear triple collisions of the three-body problem are given in Tanikawa and Mikkola (2000a, 2000b), Saito and Tanikawa (2007), those for the isosceles problem are given by Tanikawa and Umehara (1998) and Tanikawa and Mikkola (2015). Finally, in the general planar case, Tanikawa et al. (2019) gave eleven triple collision orbits starting at general initial triangles with zero initial velocities. Tanikawa and Mikkola (2021) confirmed numerically that these orbits are actually triple collision orbits. Li et al. (2021) discovered 1646 new triple collision orbits in response to Tanikawa et al. (2019).

1.2 Motivation of this work

We have obtained eleven free-fall, i.e., with zero initial velocities, triple collision orbits in Tanikawa et al. (2019). Though the number is small, our procedure allows us to find any number of triple collision orbits gradually and systematically by integrating more deeply the initial condition plane. The next target is to obtain triple collision orbits of the three-body problem with nonzero initial velocities. This is a natural continuation of our work. In fact, the cosmic events of high energy should be related to the gravitational interaction of compact bodies, which may be in a close encounter. In a neighborhood of a close triple encounter of three bodies, there should be a triple collision orbit. In this situation, initial velocities of the three bodies are expected to be nonzero.

A search for the triple collision orbits in the three-body problem with nonzero initial velocities but with zero angular momentum is suitable for our method. This is because the procedure consists of forming symbol sequences. The symbol sequences are uniquely determined even in the case with nonzero initial velocities. Starting at free-fall triple collision orbits with a certain symbol sequence, we look for triple collision orbits with initial small velocities of the same symbol sequence in a neighborhood of the free-fall orbits. This is the basic procedure. The precise procedure will be described in Sect. 5.

1.3 Numerical method

The method started developing long ago (Mikkola and Tanikawa 1999) where the principle was explained. Later more were published (Mikkola and Tanikawa 2013a, b). These methods basically use the logarithmic Hamiltonian method, with the simple leapfrog algorithm, to get substeps for a Bulirsch–Stoer integrator. The logarithmic Hamiltonian is

$$\begin{aligned} \varLambda =\log {(T-E)}-\log {U}, \end{aligned}$$

(1)

where T is the kinetic energy, E is the total energy, and U is the absolute value of the potential energy. This leads to a situation in which the leapfrog algorithm gives correct results for two-body orbits (except for time) and so it is regular even in point-mass collisions. The accuracy stay high when the code checks that $\delta E/U\le \epsilon$, in which $\epsilon$ is the required accuracy ($\delta E$ is the energy error). For the $\epsilon$, we usually used the value $10^{-13}$ and that gives normally very high precision.

1.4 Conjectures

Now, we summarize the numerical results as a sequence of conjectures. We cannot formulate either assertions or theorems, since our method is purely numerical. However, the results are instinctively correct based on the mathematically correct procedure. They are simply lack of proofs.

Let us explain terminology. For the shape space or shape sphere, see Moeckel (1988), Kuwabara and Tanikawa (2010) or Montgomery (2015). A TCP is the abbreviation of a triple collision point on the shape space as the initial positions of a triple collision orbit (TCO). A ff-TCP or nonff-TCP is the abbreviation of a free-fall TCP, i.e., a TCP with zero initial velocities, or a non-free-fall TCP, i.e., a TCP with nonzero initial velocities.

Conjecture 1

One parameter family of nonff-TCPs on the shape space forms a smooth curve called a characteristics.

Conjecture 2

Some of the characteristics are the embedded closed curves. The other characteristics are generally the immersed curves.

Conjecture 3

Twin ff-TCPs are connected by all the characteristics, which pass through one of them.

Conjecture 4

In a neighborhood of an ff-TCP, the correspondence of the points and nonff-TCPs are one-to-one. In other words, the neighborhood is occupied by nonff-TCPs of the same symbol length as that of the ff-TCP.

Conjecture 5

Nonff-TCPs of any length of symbols occupy a finite nonzero area of the shape space.

Conjecture 6

Some points of the shape space are nonff-TCPs for infinitely many initial velocities.

1.5 The structure of the paper

In the present paper, we look for nonff-TCPs. In Sect. 2.1, we formulate the sufficient conditions of initial velocities of the three bodies to have zero angular momentum. These conditions have two parameters. In Sect. 2.2, we introduce the geometry of the problem. In Sect. 3, we define the symbol sequences as sequences of syzygy crossings of orbits starting at the shape space. We introduce cylinders, words, and BCCs (binary collision curves) as boundaries of cylinders. In Sect. 4, we review our results in Tanikawa et al. (2019). In Sect. 5, we define the characteristics as a one-parameter curve on the shape space of the nonff-TCPs. In Sect. 5.1, we express the characteristics using parameters $\alpha _2$ and/or $\beta _1$. In Sect. 5.2, we explain the continuation method of characteristics. In Sects. 5.3 and 5.4, we describe the particular characteristics passing through the representative ff-TCPs. In Sect. 5.5, we describe some properties of general characteristics. In Sect. 6, we take up the collection of characteristics. In Sect. 7, we state concluding remarks.

2 Initial velocities

2.1 Formulation

We take the planar three-body problem. Let $m_i$ be the mass of the i-th body. Let t be the time and $\textbf{R}_i$ and $\textbf{V}_i$ be the positions and velocities of body $m_i$ in an inertial barycentric reference system. The equations of motion for the three-body problem are:

$$\begin{aligned} \displaystyle \frac{d \textbf{R}_i}{dt} = \textbf{V}_i,&\ \ \ \displaystyle \frac{d \textbf{V}_i}{dt} = \displaystyle - \sum _{j \ne i} \frac{m_j (\textbf{R}_i - \textbf{R}_j)}{|\textbf{R}_i- \textbf{R}_j|^3}, \ \ \ i=1,2,3 \end{aligned}$$

(2)

We consider the three-body problem with equal masses $m_1=m_2=m_3=1$ and zero angular momentum. Let us formulate the sufficient conditions of initial velocities so that the total angular momentum of the three bodies be zero.

Since the three bodies are in the reference system where the barycenter stands still, we have

$$\begin{aligned} \sum _i \textbf{R}_i= & {} 0 \end{aligned}$$

(3)

$$\begin{aligned} \sum _i \textbf{V}_i= & {} 0 \end{aligned}$$

(4)

The condition of the zero angular momentum is

$$\begin{aligned} \sum _i \textbf{R}_i \times \textbf{V}_i= & {} 0 \end{aligned}$$

(5)

Equations (3) and (4) are rewritten as

$$\begin{aligned} \textbf{R}_3 = - \textbf{R}_1 - \textbf{R}_2 \end{aligned}$$

(6)

and

$$\begin{aligned} \textbf{V}_3 = - \textbf{V}_1 - \textbf{V}_2. \end{aligned}$$

(7)

Substitution of these expressions into Eq. (4) gives us:

$$\begin{aligned} \textbf{R}_1 \times \textbf{V}_1 + \textbf{R}_2 \times \textbf{V}_2 + (\textbf{R}_1 + \textbf{R}_2) \times (\textbf{V}_1 + \textbf{V}_2) = 0 \end{aligned}$$

(8)

We assume that $\textbf{V}_i$ is dependent on the linear combinations of $\textbf{R}_i$ with coefficients $\alpha _1, \alpha _2, \beta _1, \beta _2$. More precisely,

$$\begin{aligned} \textbf{V}_1 = \alpha _1 \textbf{R}_1 + \beta _1 \textbf{R}_2 \end{aligned}$$

(9)

and

$$\begin{aligned} \textbf{V}_2 = \alpha _2 \textbf{R}_1 + \beta _2 \textbf{R}_2 \end{aligned}$$

(10)

Substituting these to zero angular momentum equation (8) we obtain

$$\begin{aligned} (2 \beta _1 - 2\alpha _2 + \beta _2 - \alpha _1) \textbf{R}_1 \times \textbf{R}_2 = 0 \end{aligned}$$

(11)

This is useful as long as the system is not one-dimensional. In this case, the factor in front of $\textbf{R}_1 \times \textbf{R}_2$ must be 0. Solving for $\alpha _1$ we get

$$\begin{aligned} \alpha _1 = 2 \beta _1 + \beta _2 - 2 \alpha _2 \end{aligned}$$

(12)

where $\alpha _2, \beta _1, \beta _2$ are arbitrary and give all possibilities in terms of these three free parameters. In other words, the number of independent parameters reduces to three.

In order to further reduce the number of parameters, we introduce sufficient conditions. Equation (8) is re-arranged to

$$\begin{aligned} \textbf{R}_1 \times (2\textbf{V}_1 + \textbf{V}_2) + \textbf{R}_2 \times (\textbf{V}_1 + 2\textbf{V}_2) = 0. \end{aligned}$$

(13)

The above equality is satisfied if

$$\begin{aligned} (2\textbf{V}_1 + \textbf{V}_2) \propto \textbf{R}_1, \end{aligned}$$

(14)

and

$$\begin{aligned} (\textbf{V}_1 + 2\textbf{V}_2) \propto \textbf{R}_2. \end{aligned}$$

(15)

Let us substitute Eqs. (9) and (10) into the above proportionality. From

$$\begin{aligned} \begin{array}{rl} 2\textbf{V}_1 + \textbf{V}_2 = &{} 2 (\alpha _1 \textbf{R}_1 + \beta _1 \textbf{R}_2) + \alpha _2 \textbf{R}_1 + \beta _2 \textbf{R}_2 \\ = &{} (2 \alpha _1 + \alpha _2)\textbf{R}_1 + (2 \beta _1 + \beta _2) \textbf{R}_2 \\ \textbf{V}_1 + 2\textbf{V}_2 = &{} \alpha _1 \textbf{R}_1 + \beta _1 \textbf{R}_2 + 2 (\alpha _2 \textbf{R}_1 + \beta _2 \textbf{R}_2) \\ = &{} (\alpha _1 + 2 \alpha _2)\textbf{R}_1 + ( \beta _1 + 2 \beta _2) \textbf{R}_2, \end{array} \end{aligned}$$

we get

$$\begin{aligned} 2 \beta _1 + \beta _2= & {} 0, \end{aligned}$$

(16)

$$\begin{aligned} \alpha _1 + 2 \alpha _2= & {} 0, \end{aligned}$$

(17)

and

$$\begin{aligned} 2\textbf{V}_1 + \textbf{V}_2= & {} (2 \alpha _1 + \alpha _2)\textbf{R}_1 = -3 \alpha _2 \textbf{R}_1, \end{aligned}$$

(18)

$$\begin{aligned} \textbf{V}_1 + 2\textbf{V}_2= & {} (\beta _1 + 2 \beta _2)\textbf{R}_2 = -3 \beta _1 \textbf{R}_2. \end{aligned}$$

(19)

The above conditions can be solved for $\textbf{V}_1$ and $\textbf{V}_2$ giving

$$\begin{aligned} \textbf{V}_1= & {} - 2 \alpha _2 \textbf{R}_1 + \beta _1 \textbf{R}_2, \end{aligned}$$

(20)

$$\begin{aligned} \textbf{V}_2= & {} \ \ \ \alpha _2 \textbf{R}_1 - 2 \beta _1 \textbf{R}_2, \end{aligned}$$

(21)

$$\begin{aligned} \textbf{V}_3= & {} \ \ \ - \textbf{V}_1 - \textbf{V}_2, \end{aligned}$$

(22)

with arbitrary $\alpha _2$ and $\beta _1$. Now the number of arbitrary parameters reduces to two. These expressions (20), (21), and (22) give the initial velocities of the three bodies in the present paper.

2.2 Initial settings of positions and velocities

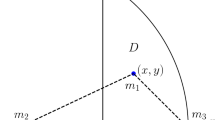
As in the previous works (Agekyan & Anosova 1967; Anosova 1986; Tanikawa et al. 1995, 2019), we adopt the setting of the free-fall three-body problem with equal masses $m_1=m_2=m_3=1$ and zero angular momentum. We put $m_2$ and $m_3$ at $(-0.5,0)$ and (0.5, 0) of the (x, y) plane. We put $m_1$ at $P = (x,y)$ in

$$\begin{aligned} D = \{ (x,y)~|~x \ge 0, y \ge 0, (x+0.5)^2+y^2 \le 1 \} \end{aligned}$$

(21)

(see Fig. 1).

In Fig. 1, $\varGamma _1$ denotes collinear configurations, and $\varGamma _2$ and $\varGamma _3$ denote isosceles configurations. On these segments, the shape of triangles is symmetrical. We already know and easily get free-fall triple collision orbits in these cases (see Sec. 1.1 for some references).

Fig. 1

Geometry of the setting of the free-fall problem. Points other than P are A$(-0.5,0)$, B(0.5, 0), C$(0,\sqrt{3}/2)$, and E(0, 0). $\varGamma _1$ and $\varGamma _2$ are the segments connecting E to B and E to C. $\varGamma _3$ is the circular arc connecting C to B

We give the coordinates (x, y) of $m_1$ and integrate orbits of the three bodies in an inertial barycentric reference system (see Sect. 1 for the integration method and its accuracy). Let $\textbf{X}_k = (x_k, y_k), k=1,2,3$ be the positions of the three bodies in the initial condition space. We have

$$\begin{aligned} \textbf{R}_k = \textbf{X}_k - \textbf{G} \ \ \textrm{with} \ \ \textbf{G} = (\textbf{X}_1 + \textbf{X}_2 + \textbf{X}_3) / 3 \end{aligned}$$

(22)

Substituting

$$\begin{aligned} x_2=-0.5, \ y_2=0.0, \ x_3=0.5, \ y_3=0.0 \end{aligned}$$

we get

$$\begin{aligned} \textbf{R}_1 = \frac{2}{3} (x_1,y_1), \textbf{R}_2 = - \frac{1}{3} (x_1,y_1) - (0.5,0), \textbf{R}_3 = - \frac{1}{3} (x_1,y_1) + (0.5,0). \end{aligned}$$

(23)

3 Symbol sequences

We use symbol sequences to express the solution of the three-body problem (Tanikawa and Mikkola 2008; Tanikawa et al. 2019; Montgomery 1998, 2007). Let us briefly review the construction of symbol sequences. The solution of the three-body problem is a curve in the phase space. We call this a trajectory. The three curves of the motions of the three bodies in the configuration space will be called together an orbit. Sometimes by abuse of terminology, a curve of one body will be called an orbit. Suppose the three bodies experience some event along the trajectory. We assign a symbol each time when the three bodies experience this event. The motion of the three bodies continues indefinitely to the future unless the three bodies collide at some point and the trajectory is not continued any more. Here, binary collisions are analytically continued (Levi-Civita 1920; Kustaanheimo and Stiefel 1965)¹

So the number of symbols along the trajectory is infinite if the event be repeated in a finite interval of time (Montgomery 2007). Then, an infinite number of symbols will be given to a trajectory of the three bodies. We call this sequence of symbols a ‘symbol sequence’.

We adopt the collinear situation (syzygy crossing) as the event. This event is assured to repeat in a finite interval of time except for the Lagrange free-fall orbit (Montgomery 2007). We assign the symbol ‘1’ if $m_1$ is in between $m_2$ and $m_3$, symbol ‘2’ if $m_2$ is in between, and symbol ‘3’ if $m_3$ is in between at the syzygy situation.

Each point (x, y) of the initial condition plane (Fig. 1) is a starting point of the orbit of the three bodies sitting at (x, y), $(-0.5,0)$, and (0.5, 0). We represent this triangle by the point (x, y). We attach the (possibly infinite) symbol sequence of the solution of the equations of motion to this point. Thus, each point (x, y) has its own symbol sequence.

Let us introduce terminology. Take the first k digits of a symbol sequence: $s_1s_2 \ldots s_k$ where $s_i$ ($i=1,2,\ldots ,k$) equals to either 1, 2, or 3. In general, a symbol sequence of finite length is called a word. We denote the word of length k by a k-word. The set of symbol sequences containing a particular k-word $\sigma _k = s_1s_2 \cdots s_k$ in their initial digits with remaining arbitrary infinite digits will be called a k-cylinder ‘$\sigma _k$’. The set of k-cylinders ‘$\sigma _k$’ with all possible ‘$\sigma _k$’ will be called the set of k-cylinders. For convenience of description, we call k-cylinder ‘$\sigma _k$’ the set of points in the initial condition plane, which is the starting points of k-cylinder ‘$\sigma _k$’. Then, the set of k-cylinders for each k divides the initial condition plane into k-cylinders ‘$\sigma _k$’ with all possible ‘$\sigma _k$’. We show the examples of the set of 3-cylinders in Fig. 2. In this figure, two numbers ‘132’ and ‘131’ show that there are two 3-cylinders ‘131’ and ‘132’. The initial condition plane is divided into these two 3-cylinders. The first two digits are both ‘13’, so the initial condition plane is not divided into multiple regions by the set of 2-cylinders. We have only one component in the set of 2-cylinders.

As for the boundary curves between cylinders, we discussed in the preceding works (Tanikawa et al. 2019; Tanikawa and Mikkola 2021). These are binary collision curves (BCCs) which are the set of points whose orbits experience a binary collision at some time. More precisely, the orbit on a BCC experiences a binary collision at the last digit of the symbol sequence when the BCC appears in the initial condition plane. We continue the solution beyond binary collision, so the orbit behaves similarly to the ordinary non-collision orbits after the first binary collision.

Fig. 2

Division of the initial condition plane by 3-cylinders in the free-fall case

Our initial condition plane is a part of the shape plane. The structure of the shape plane divided by the set of 3-cylinders is shown in the figure of Appendix A. This division will be deformed when the velocities are incorporated. We do not show the deformed division.

4 Our previous results

Table 1 Triple collision points (TCPs) with the length of symbols less than or equal to 14. The number codes, initial coordinates (x, y), the time of collision, digits of symbol sequences, and the side of the triangle at triple collision. GT-15 has been obtained in Li et al. (2021)

We have obtained eleven free-fall triple collision points (ff-TCPs) and confirmed numerically the reliability of their existence in the preceding works (Tanikawa et al. 2019; Tanikawa and Mikkola 2021). After our work, Li et al. (2021) found more than 1658 ff-TCPs with symbol lengths from 3 to 120. Their list contains both TCPs which we found and which escaped our search. Among others, their GT-15 attracts our interest. Including this ff-TCP, we listed twelve ff-TCPs in Table 1. The first column of Table 1 shows the name of ff-TCPs which we use in this paper. TSM denotes our ff-TCPs discovered in Tanikawa et al. (2019). The second and third columns represent the positions (x, y) of ff-TCPs in the initial condition plane. The fourth column gives the triple collision time of the orbit, and the fifth column the length of symbol sequences. For later convenience, we plot the positions of these ff-TCPs in Fig. 3.

We here give important remark on the length of symbol sequences of TCOs. In the former work (Tanikawa et al. 2019), the shortest length of symbol sequences until triple collision was seven. We said in Tanikawa et al. (2019) that this number is ‘eight’. This statement is misleading. In fact, a TCP is obtained as a crosspoint of three BCCs (binary collision curves) of symbol sequences with length eight. Each point of the BCCs experiences the eighth syzygy crossing at a binary collision. The TCO starting at the crosspoint of three BCCs does not experience this final syzygy crossing and instead ends up with triple collision. So the corresponding TCP has a symbol sequence of length seven. In other words, if three BCCs of symbol length k meet at a point, this point is a TCP of symbol length $k-1$.

Fig. 3

Free-fall triple collision points (ff-TCPs). Crosses show the ff-TCPs (Tanikawa et al. 2019; Tanikawa and Mikkola 2021). The solid curve, which divides the initial condition plane, indicates the binary collision curve starting at an ff-TCP on the circular boundary

5 Search for triple collision orbits with nonzero initial velocities: characteristics

5.1 Particular sets of initial velocities

We take the positions (x, y) in the initial condition plane. Initial velocities are parametrized by two parameters $\alpha _2$ and $\beta _1$ as in Sect. 2.1. In order to see the distribution of TCPs with nonzero initial velocities (nonff-TCPs) in the initial condition plane, we restrict the initial velocities based on just one parameter, not two. We fix the ratio $\gamma := 2\alpha _2/\beta _1$ when $\beta _1 \ne 0$. Then, Eqs. (21), (21), and (22) become

$$\begin{aligned} \begin{array}{lcl} \textbf{V}_1 &{} = &{} \beta _1 ( - \gamma \textbf{R}_1 + \textbf{R}_2 )\\ \textbf{V}_2 &{} = &{} \frac{\beta _1}{2} (\gamma \textbf{R}_1 - 4 \textbf{R}_2) \\ \textbf{V}_3 &{} = &{} \frac{\beta _1}{2} ( \gamma \textbf{R}_1 + 2 \textbf{R}_2 ) \end{array} \end{aligned}$$

(24)

If $\beta _1=0$, we have

$$\begin{aligned} \begin{array}{lcl} \textbf{V}_1 &{} = &{} - 2 \alpha _2 \textbf{R}_1, \\ \textbf{V}_2 &{} = &{} \ \ \ \alpha _2 \textbf{R}_1, \\ \textbf{V}_3 &{} = &{} \ \ \ \alpha _2 \textbf{R}_1 \end{array} \end{aligned}$$

(25)

The other extreme is the case $\alpha _2=0$. In this case, we have

$$\begin{aligned} \begin{array}{lcl} \textbf{V}_1 &{} = &{} \ \ \ \beta _1 \textbf{R}_2, \\ \textbf{V}_2 &{} = &{} - 2 \beta _1 \textbf{R}_2, \\ \textbf{V}_3 &{} = &{} \ \ \ \beta _1 \textbf{R}_2 \end{array} \end{aligned}$$

(26)

For a fixed ratio $\gamma$, velocities $(\textbf{V}_1, \textbf{V}_2, \textbf{V}_3)$ form a one-parameter family parametrized by $\beta _1$ in Eq. (22). Correspondingly, we expect that nonff-TCPs (non-free-fall TCPs) may form a curve which is parametrized by $\beta _1$ in the case of Eqs. (22) and (24), and by $\alpha _2$ in the case of Eq. (23). This curve passes through an ff-TCP at parameter $\beta _1=0$ or $\alpha _2=0$. Let us call the characteristics a curve of nonff-TCPs parametrized by one parameter.

5.2 Procedure to search for TCOs with nonzero initial velocities

We know the positions in the initial condition plane of twelve ff-TCPs whose orbits satisfy the zero-velocity conditions $\alpha _2=\beta _1=0$ (see Table 1 and Fig. 3). Let us explain the procedure to obtain the characteristics. In the present paper, we mainly use the velocities of the three bodies in Eq. (23). In this case, the velocities are dependent only on parameter $\alpha _2$.

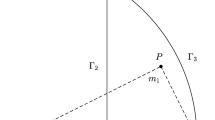
Let us explain the relations of the triangle and velocity vectors of the three bodies for the case of Eq. (23). All the three vectors $\textbf{V}_1, \textbf{V}_2$, and $\textbf{V}_3$ look toward the direction of $\textbf{R}_1$ where $\textbf{R}_1$ is the vector extending from the barycenter to body 1. Therefore, the initial velocity $\textbf{V}_1$ of body 1 looks to the barycenter if $\alpha >0$, while $\textbf{V}_1$ looks away from the barycenter if $\alpha <0$. The velocity vectors $\textbf{V}_2$ and $\textbf{V}_3$ are anti-parallel to $\textbf{V}_1$ and are of half size. The sizes of the velocity vectors are controlled by $|\alpha _2|$. These relations are depicted in Fig. 4.

Fig. 4

Initial velocities. a $\alpha _2>0$ and $\beta _1=0$. b $\alpha _2<0$ and $\beta _1=0$

Now, we describe the details of the numerical calculation. We take TSM-2 at (0.19208270, 0.30936018) as an example of the ff-TCPs and look for nonff-TCPs with the same symbol length as TSM-2. We draw a square $0.191< x< 0.193, 0.308< y < 0.310$ with center nearly at TSM-2 in the initial condition plane. We divide the above square of size $0.02 \times 0.02$ by one hundred in both the x- and y-directions. Then, we obtain a mesh of $0.0002 \times 0.0002$. We put $\alpha _2=0.005$ and $\beta _1=0$. The corresponding velocity vectors are shown in Fig. 4a. The length $|\textbf{V}_1|$ is equal to $|\textbf{R}_1|/100$. We integrate 10000 orbits starting at all the grid point of the mesh. Each point of the mesh has its symbol sequence. We plot three 8-cylinders ’13213212’ ’13213211’ and ’13213212’ in the above square. Then, as we have shown in Tanikawa et al. (2019), TSM-2 is obtained as a cross point of the three cylinders since TSM-2 has symbol sequence of length 7 (Table 1). The numerical results are shown in Fig. 5a. In this figure, $+$ indicates the position of TSM-2 which is for $\alpha _2=0$. The cross point for $\alpha _2=0.005$ is found at the upper-right of TSM-2.

We plot a small square $0.19238< \textit{x} < 0.19248$, $0.30968< \textit{y} < 0.30978$ around the cross point. In order to obtain more accurate coordinates of the cross point, we again divide this square by one hundred in both the x- and y-directions. Then, we obtain a mesh of $10^{-6} \times 10^{-6}$. We integrate 10000 orbits starting at all the grid points of the mesh. The numerical results are shown in Fig. 5b. The cross point is found nearly at the center. At this stage, the coordinates of the cross point have at most six digits. We want to have the coordinates of seven digits. For this, we need one or two repetitions of drawing a small square and integrating orbits with a smaller mesh. Finally, we obtain the coordinates as $(\textit{x},\textit{y})=(0.1924317, 0.3097294)$ for $\alpha _2=0.005, \beta _1=0$.

So far we described the procedure to find a nonff-TCP with $\alpha _2=0.005, \beta _1=0.0$ near TSM-2, the ff-TCP with $\alpha _2=\beta _1=0.0$. We continue to find other nonff-TCPs changing the value of $\alpha _2$ near TSM-2. We expect that a continuous curve may be obtained by continuously changing the value of $\alpha _2$ to positive or negative direction. This curve is the characteristics passing through TSM-2. Actually, we change discretely the value $\alpha _2$ and connect the discrete points. We have done these procedures to obtain characteristics for the eight ff-TCPs.

Fig. 5

An example of the procedure to find a nonff-TCP for $\alpha _2=0.005$, $\beta _1=0$. a Ten thousand orbits are integrated starting at the grid point of the mesh size $0.01 \times 0.01$ in the square $0.191< \textit{x} < 0.193$, $0.308< \textit{y} < 0.310$. The ff-TCP (TSM-2) is denoted by $+$. Our nonff-TCP is obtained as the cross point of the three 8-cylinders ‘13213211’, ‘13213212’, and ‘13213213’. We plotted a small square $0.19238< \textit{x} < 0.19248$, $0.30968< \textit{y} < 0.30978$ around the cross point. b Ten thousand orbits are integrated starting at the grid point of the mesh size $0.0001 \times 0.0001$ in the small square inscribed in Fig. 4a. The cross point is in a small square near the center of the figure. The integration of the orbits is repeated in a smaller square until the necessary accuracy of the cross point is attained

We have thus obtained five characteristics passing through the eight ff-TCPs. This means that three characteristics have two ff-TCPs on them. We do not know if this is an exceptional phenomenon or not. Figure 6 shows the overall features of the characteristics passing through six ff-TCPs TSM-1, TSM-2, TSM-3 and GT-15, TSM-4, TSM-5. One sees only four characteristics in the initial condition plane except the loop characteristics. We note that the characteristics passing through TSM-1 pass through TSM-2. Similarly, the characteristics passing through GT-15 pass through TSM-4. This indicates that TSM-1 and TSM-2 are dynamically related and GT-15 and TSM-4 are also dynamically related though for the moment we do not know what kind of dynamical relations. We denote these two ff-TCPs by a ’twin’.

Another feature of the characteristics is the intersection of different characteristics and the self-intersections. The intersection of different characteristics with different values of $\alpha _2$ means that the orbit starting at this intersection point is a nonff-TCP of one symbol length and a nonff-TCP of another symbol length. The orbit starting at the self-intersection point is a nonff-TCP for one $\alpha _2$ and a nonff-TCP of another $\alpha _2$ of the same symbol sequence. Finally, we have no good interpretation of the loop characteristics.

Fig. 6

All the characteristics obtained in this paper. The curve running from the top to the right boundary is the circular boundary of the initial condition plane. The curve starting at a point on this curve to the bottom boundary is the BCC between 3-cylinders ‘132’ and ‘131’. The remaining curves are all characteristics. Two solid curves are the characteristics passing through TSM-1, TSM-2 and TSM-3. Two dashed curves are the characteristics passing through GT-15, TSM-4 and TSM-5. A dashed elliptical characteristic passes through TSM-10 and TSM-11. The property of the characteristics passing through TSM-1 and TSM-2 will be analyzed in Sect. 5.5

5.3 Characteristics passing through TSM-1, TSM-2 and TSM-3 of symbol length 7

In this and next subsection, we describe more precisely the characteristics with $\alpha _2 \ne 0,\beta _1=0$ shown in Fig. 6. Changing continuously the value of $\alpha _2$ starting at $\alpha _2=0$, we obtain the characteristics passing through TSM-2 at (0.19208270,  0.30936018). The result of the search is given in Fig. 7. The numbers in the figure near the $+$ symbols along the curve are the values of $\alpha _2$. One of the remarkable aspects is that the characteristics pass also TSM-1. TSM-1 and TSM-2 are a twin. We more deeply discuss this relation in Sect. 5.5.

Let us see a more precise behavior of the characteristics as functions of parameter $\alpha _2$. Look at Fig. 7a. If we start at TSM-1 to the lower-left, the values of $\alpha _2$ decrease until $\alpha _2=-6.35$. The curve can be extended to the right. However, we do not know the final destiny of the curve. The integrations are time-consuming. If we tend to the upper-right starting at TSM-1, the value of $\alpha$ increases to 0.46, the curve attains a maximum height, turns down, and to the left and $\alpha _2$ starts to decrease. The value decreases to zero at TSM-2. Then, the value decreases along the curve until $\alpha =-6.225$. The curve can be extended further. It has a self-intersection at around $(x,y)\simeq (0.14, 0.10)$.

Fig. 7

a Characteristics containing TSM-1 and TSM-2 with symbol length 7. b Characteristics containing TSM-3 with symbol length 7

The behavior of the values of $\alpha _2$ along this characteristic is rather simple. The largest value of $\alpha _2$ is around 0.46 along the arc connecting TSM-1 and TSM-2. Below TSM-1 and TSM-2, $\alpha _2$ monotonically decreases. It seems that the two branches of the characteristics tend to the lower-right corner of the initial condition plane.

The characteristics passing through TSM-3 have also a simple behavior. See Fig. 7b. The branch of the positive $\alpha _2$ seems to tend to the lower-right corner of the initial condition plane. The negative branch seems to tend to the y-axis. However, this is not clear because there can be a different structure close to the y-axis. A solid curve running from the upper-right to the middle-right is a part of the circular boundary of the initial condition plane.

We give in Tables 2 and 3 of Appendix B of the electronic supplement the position data of TCPs of Fig. 7.

5.4 Characteristics passing through GT-15, TSM-4 and TSM-5 of symbol length 9

The behavior of the characteristics passing through TSM-4 is complicated. See Fig. 8a. It passes through GT-15, which was discovered by Li et al. (2021) and named GT-15 by them. This characteristic has a self-intersection as in the case of the characteristics passing through TSM-1 and TSM-2 (Fig. 7a). Correspondingly, the behavior of the values of $\alpha _2$ along this characteristic is not simple. In the positive branch, $\alpha _2$ increases up to 2.51, then decreases to zero at GT-15, and further decreases to $-6.37$. We expect that this branch tends to the lower-right corner of the initial condition plane. In the negative branch, $\alpha _2$ decreases to $-2,45$; then, it increases to $-2.185$ and decreases to $-7.0$. This branch seems to tend to $(x,y)=(0.0,0.0)$.

Fig. 8

a Characteristics containing GT-5 and TSM-4 with symbol length 9. b Characteristics containing TSM-5 with symbol length 9

The characteristics passing through TSM-5 have a simple behavior similar to that passing through TSM-3. Correspondingly, the behavior of $\alpha _2$ is simple. The value of $\alpha _2$ increases monotonically from the left to the right (see Fig. 8b).

We give in Tables 4 and 5 of Appendix B of Electronic Supplement the position data of nonff-TCPs of Fig. 8.

5.5 Characteristics for other combinations of $\alpha _2$ and $\beta _1$

Fig. 9

Initial velocities. a $\alpha _2=0$ and $\beta _1>0$. b $\alpha _2=0$ and $\beta _1<0$. c $\alpha _2/\beta _1=3$. d $\alpha _2/\beta _1=-3$

In order to get other kinds of characteristics, let us change both $\alpha _2$ and $\beta _1$. We fix the ratio $\gamma = \alpha _2 / \beta _1$ and change $\beta _1$, which is now the unique parameter and determines the absolute values of the initial velocities of the three bodies (see Eq. (22)). This gives us a family of characteristics for different $\gamma$.

For $\gamma =0$, i.e., $\alpha _2=0, \beta _1 \ne 0$, three initial velocity vectors are shown in Figs. 9a and b. The velocity of body 2 is along the direction connecting body 2 and the center of gravity where the velocity looks toward right for $\beta _1>0$, while toward left for $\beta _1<0$. For $\gamma \ne 0$, we show the three velocity vectors in Figs. 9c and d. One sees that the velocity vectors are not symmetrically directed. We will soon explain the reason why we select the values $\alpha _2/\beta _1=3$ and $-3$.

Fig. 10

Four characteristics with different ratios of $\alpha _2/\beta _1$ connecting TSM-1 and TSM-2. Empty circles stand for TSM-1 (0.2220275, 0.3009644) and TSM-2 (0.1920827, 0.3093602). Curve (1) is the characteristics with $\alpha \ne 0, \beta =0$; Curve (2) is the one with $\alpha =0, \beta \ne 0$; Curve (3) is the one with $\alpha _2 / \beta _1 = 3$; and Curve (4) is the one with $\alpha _2 / \beta _1 = -3$

As we mentioned in Sect. 5.3, TSM-1 and TSM-2 look like a twin because these two are on the same characteristics. In other words, TSM-2 metamorphoses into TSM-1 when we walk along the characteristics by changing the values of $\alpha _2$ with $\beta _1=0$. We are interested in the behavior of other characteristics, which pass through TSM-2. Then, we confirm that the characteristics with $\alpha =0, \beta \ne 0$ also passes through TSM-1. Further, we trace the characteristics with $\alpha /\beta =3$ and $-3$. Then, we find that these two characteristics also pass through both TSM-2 and TSM-1.

We plot the results in Fig. 10. In this figure, the empty circles are TSM-1 and TSM-2. The solid curve (1) represents the characteristics for $\alpha \ne 0, \beta =0$. The dotted curve (2) is the one for $\alpha =0, \beta \ne 0$. The dashed curve (3) is the one for $\alpha _2 / \beta _1 = 3$, and the dotted dash curve (4) is the one for $\alpha _2 / \beta _1 = -3$. We select the values 3 and $-3$ so that the directions of the characteristics starting at TSM-2 are separated reasonably. From this result, we expect that all the characteristics passing through TSM-2 may also pass through TSM-1.

There is a possibility that all the ff-TCPs of the same symbol length might be on an unique characteristics. We can say this is not the case. We show the counter example in Fig. 6. In this figure, there is a loop characteristics which contains TSM-10 and TSM-11 of symbol length 13. Li et al. (2021) found seven ff-TCPs of symbol length 13: GT-37 through GT-43 among which GT-37 and GT-38 correspond to TSM-10 and TSM-11 of ours. So GT-39, GT-40,..., GT-43 belong to other characteristics.

6 Collection of characteristics

6.1 Distribution of nonff-TCPs around a ff-TCP

Until now we consider the characteristics passing through ff-TCPs. Let us consider the characteristics not passing through ff-TCPs. In Eq. (22) of section 5.1, we put $\beta _1 \ne 0$. Then, velocities never become zero. For definiteness, we are going to obtain the characteristics encircling TSM-2. We go back to Eqs. (20), (21), and (22) and write these as:

$$\begin{aligned} \begin{array}{lcl} \textbf{V}_1 &{} = &{} t (- 2 \alpha _2 \textbf{R}_1) \ + \ s \beta _1 \textbf{R}_2 \\ \textbf{V}_2 &{} = &{} \ t (\alpha _2 \textbf{R}_1) \ \ + \ s (- 2 \beta _1) \textbf{R}_2 \\ \textbf{V}_3 &{} = &{} \ \ - \textbf{V}_1 - \textbf{V}_2 \end{array} \end{aligned}$$

We calculate the velocities of the three bodies for fixed $\alpha _2$ and $\beta _1$ changing parameters t and s. $t=s=0$ gives us the initial velocities of TSM-2. We first put $0 \le t \le 1, s=1-t$, which gives us the segment in the first quadrant of the top panel of Fig. 11. Then sequentially, $-1 \le t \le 0, s=-t$, $-1 \le t \le 0, s=-1-t$, and $0 \le t \le 1, s=-t$ give the segments in the second, third, and fourth quadrants, all of which form a closed square circuit in the parameter space (t, s). Corresponding to this circuit, we have a curved square circuit around TSM-2. We choose three sets of parameters $\alpha _2$ and $\beta _1$ in order to have three circuits in the initial condition plane: $(\alpha _2, \beta _1) = (0.05,0.015), (0.10,0.030)$, and (0.15, 0.045).

Now, we have three curved square circuits in the lower panel of Fig. 11. We added radial characteristics emanating from TSM-2. This figure suggests that the correspondence of points of the $(\alpha _2,\beta _1)$ plane and the initial condition plane in the neighborhood of TSM-2 is one-to-one.

Fig. 11

Characteristics in the neighborhood of TSM-2 at (0.1920827, 0.3093602). The solid curves are those emanating from TSM-2. One of them is a part of the characteristics exhibited in Fig. 7a. The three dashed square frames are also the characteristics circulating TSM-2. See Table 8 of Appendix E of the Electronic Supplement for the coordinates data

7 Concluding remarks

• 1. We have formulated sufficient conditions for the velocities of the three bodies so that the total angular momentum of the three-body system is zero.

• 2. The velocity conditions are parametrized by two parameters $\alpha _2$ and $\beta _1$ in the initial condition plane.

• 3. We introduced the characteristic as the curve in the initial condition plane of the non-free-fall TCPs parametrized by one parameter, say, $\alpha _2/\beta _1$. Issue (2) suggests that nonff-TCPs occupy two-dimensional areas in the initial condition plane (see Fig. 11).

• 4. We plot five characteristics passing through the eight ff-TCPs, one of which forms a closed circuit. Two ff-TCPs on a characteristic are called a twin. This gives us a criterion for the classification of TCPs or TCOs in addition to the one obtained in Tanikawa and Mikkola (2021), which connects the directions of the initial and final triangles formed by three bodies.

• 5. We find that the twin TSM-1 and TSM-2 are connected by all the characteristics that pass through them.

• 6. A neighborhood of TSM-2 has been confirmed to be occupied by nonff-TCPs. We expect that the same is true with a neighborhood of any ff-TCP. Further, we expect that this is true with a neighborhood of any nonff-TCP.

• 7. We do not continue the characteristics until its end. The next target of our search should be to find the limiting behavior of these characteristics.

We have obtained numerically interesting properties of the distribution of TCPs as mentioned above. In Sec. 3, we have presented these numerical results in the form of conjectures to be rigorously proven.

Appendix A. Division of the shape space in the free-fall case

Our initial condition space (Fig. 1 of Sect. 2.2) is not enough when the initial velocities are incorporated into the motion of the three bodies. It is only a part of the shape sphere (see, e.g., Fig. 1 of Tanikawa et al. 2019). Here for reference, we show in Fig. 12 the division of the shape space by the 3-cylinders for the free-fall case. The division will be deformed if the initial velocities are incorporated.

Fig. 12

Division by 3-cylinders. $(\alpha _2,\beta _1) = (0,0)$