Periodic motion around libration points in the Elliptic Restricted Three-Body Problem

Abstract

Periodicity of motion around the collinear libration point associated with the Elliptic Restricted Three-Body Problem is studied. A survey of periodic solutions in the Circular Restricted Three-Body Problem is presented considering both Sun–Earth and Earth–Moon systems. Halo, Lyapunov and Vertical families around L1, L2 and L3 points are investigated, and their orbital period ranges through the entire family are reported. Resonant motions within the orbit families in the circular problem are identified and selected as suitable initial guess to find periodic orbits in the elliptic problem, which are targeted using a differential correction algorithm. Periodic solutions found are cataloged depending on the number of revolutions around libration points. Geometry, dynamical behavior and stability properties of single-revolution orbits are shown, as well as double-, triple- and quadruple-revolution solutions.

1 Introduction

The search for periodic solutions in complex non-Keplerian systems represents one of the most promising and challenging problems in modern astrodynamics. Although this problem has been extensively studied in the past decades, still the full comprehension of its dynamics is far to be reached. Simplified models of the motion of a particle under the gravitational attraction of celestial bodies are usually studied. Among them, the Restricted Three-Body Problem (R3BP) gained a lot of popularity in the last few decades and, in some cases, replaces or complements the simpler but less accurate Restricted Two-Body Problem (R2BP) within specific and peculiar applications.

Analytical studies by Farquhar [4] on three-dimensional periodic solutions about libration points in the Earth–Moon three-body system started a new era. Farquhar found three-dimensional periodic orbits in the proximity of libration points and named them ‘Halo’ orbits. Following his work on Halo orbits, Farquhar and Kamel [5] found Lissajous trajectories near the translunar libration point. Later, Howell [9] developed a numerical algorithm to precisely compute them. After them, different families of periodic orbits have been found and computed in the frame of the Circular Restricted Three-Body Problem (CR3BP).

The Elliptic Restricted Three-Body Problem (ER3BP) represents a better approximation, compared to the CR3BP, of the dynamics of a small body in the proximity of two attractors, whose two-body motion is not circular. The nonzero eccentricity of the orbits of primaries is the most notable perturbation leading the orbit not to be periodic [20]. Compared to the widely studied CR3BP, periodic motion in the ER3BP remains still to be explored. Different kinds of orbits have been targeted in the past, with the main focus being either on systematic analysis of the elliptical problem ($e,\mu$) space dependency [2, 12, 13, 18, 25] or on finding multi-revolution orbits about collinear libration points [3, 14, 21, 22]. Relevant studies on periodic motion under ER3BP include also the work by Gurfil and Kasdin [7], Palacian et al. [19] and Nayfeh [16]. The study of periodic motion in the ER3BP is tightly correlated with the study of the resonant motion near libration points. Reference works in this field include studies on the investigation of the dynamics related to the resonance problem [23, 28] and their classification [11, 17].

The present work aims at finding periodic orbits about collinear points in the ER3BP. Section 2 presents the dynamics of the problem and sets the mathematical background in use throughout the paper. Section 3 discusses the numerical method in use and the strategy implemented to find solutions in the elliptic problem. Due to their peculiar nature, such solutions possess natural resonance with the motion of primaries. Section 4 presents a survey of families of periodic orbits in the CR3BP and identifies suitable resonant solutions, which are used as initial guess to compute orbits in the elliptic problem, as shown in Sect. 5. Stability properties of periodic orbits are reported for families of solutions found and their dependency on eccentricity is discussed.

2 Dynamics

The present study is performed under the assumptions related to the Restricted Three-Body Problem (R3BP), which describes the dynamics of a small body (third body) that moves under the gravitational attraction of two massive bodies, called primaries, without influencing their motion. The R3BP is a suitable model of the reality when the mass of the third body is negligible with respect to the mass of the primaries. The motion of the primaries is then influenced only by their mutual attraction: accordingly, their relative trajectory is a conic section, being solution of the Two-Body Problem. The elliptic problem (ER3BP) considers the primaries moving on ellipses around the barycenter of the system, and it represents a generalization (for $e\ne 0$) of the simpler circular problem (CR3BP), where the primaries are constrained to move on circular paths ($e=0$).

2.1 Equations of motion

In analogy to the classical formulation of the circular problem [26], the equations of motion of the ER3BP are commonly expressed in the synodic reference frame [27]. Unlike the CR3BP, the position of the primaries is not fixed in the rotating frame as they move along elliptical orbits: their relative distance $\rho$ is not constant in time

$$\begin{aligned} \rho =\frac{p}{1+e\cos f} \end{aligned}$$

(1)

where p is the semi-latus rectum, f is the true anomaly, and e is the eccentricity of the two-body orbit of the primaries. As a result, when seen from the rotating frame ($\hat{x},\hat{y},\hat{z}$), which rotates with angular velocity equal to that of the primaries (two-body motion), the position of $m_1$ and $m_2$ pulsates along the ${\hat{x}}$ axis.

System 2 shows the equations of motion in nondimensional form

$$\begin{aligned} {\left\{ \begin{array}{ll} x'' - 2y' = U_x\\ y'' + 2x' = U_y\\ z'' = U_z \end{array}\right. } \end{aligned}$$

(2)

where $(\cdot )'$ and $(\cdot )''$ indicate first and second derivative with respect to the true anomaly f, while the notation $U_{(\cdot )}$ indicates the partial derivative of the pseudo-potential with respect to the variable $(\cdot )$. The pseudo-potential function U associated with the problem is defined as

$$\begin{aligned} U= & {} \frac{1}{1+e\cos f} \left[ \frac{1}{2}\left( x^2+y^2-z^2 e\cos f\right) \right. \nonumber \\&\left. + \,\frac{1-\mu }{r_1}+\frac{\mu }{r_2} \right] \end{aligned}$$

(3)

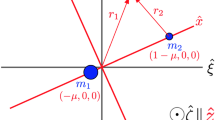
where $r_1$ and $r_2$ represent the distance of the particle from the primaries ($m_1$ and $m_2$), while $\mu$ is the mass ratio of the planetary system

$$\begin{aligned} \mu =\frac{m_2}{m_1+m_2} \end{aligned}$$

(4)

The system 2 is non-autonomous, since the motion of the third body explicitly depends on the position of the primaries, through the true anomaly f.

2.2 State Transition Matrix

The state transition matrix (STM) associated with system 2 is used in the differential correction algorithm to compute periodic orbits. Given the state vector $\varvec{X}=[x,y,z,x',y',z']^\mathrm{T}$, variational equations associated with the problem can be written as

$$\begin{aligned} \varvec{\delta X}'=\mathbf {A}(f) \varvec{\delta X} \end{aligned}$$

(5)

where $\mathbf {A}(f)$ is the Jacobian of system 2

$$\begin{aligned} \mathbf {A}(f)= \begin{bmatrix} \mathbf {0}&\mathbf {I} \\ \mathbf {U}_{{\varvec{X}\varvec{X}}}&2\varvec{\Omega } \end{bmatrix} \end{aligned}$$

(6)

$\mathbf {A}(f)$ is a $6 \times 6$ matrix and its four $3 \times 3$ submatrices are

$$\begin{aligned}&\mathbf {0} =\text {zero matrix}\\&\mathbf {I} =\text {identity matrix}\\&\mathbf {U}_{\varvec{X}\varvec{X}}=\text {matrix of second partial derivatives of U}\\&\varvec{\Omega }= \begin{bmatrix} 0&1&0 \\ -1&0&0 \\ 0&0&0 \end{bmatrix} \end{aligned}$$

Being the STM $\varvec{\Phi }(f,f_0)$ solution of Eq. 5, its components can be computed numerically by solving the system

$$\begin{aligned} {\left\{ \begin{array}{ll} \varvec{\Phi }'(f,f_0)=\mathbf {A}(f) \varvec{\Phi }(f,f_0) \\ \varvec{\Phi }'(f_0,f_0)=\mathbf {I} \end{array}\right. } \end{aligned}$$

(7)

2.3 Periodicity in the elliptic problem

For an orbit to be periodic in the CR3BP, it is sufficient to replicate its six-dimensional state, after a certain time (period of the orbit). The circular problem is known to have an infinite number of periodic solutions which can be collected into families of orbits with continuously varying period. This is not true for the elliptic problem. Due to its explicit time dependency, it is not sufficient for an orbit in the ER3BP to replicate its six-dimensional state: the whole dynamics shall be replicated, including the time-dependent position of primaries. For this reason the ER3BP admits only isolated periodic orbits, with well-determined periods. Since the time dependency of the problem is due to the motion of the primaries, orbits in the ER3BP must be periodic with a period commensurable to that of the primaries. When considering nondimensional Eq. 2, primaries move with normalized period of $2\pi$: accordingly, periodic solutions of the ER3BP must have period of $T=2\pi N$, with $N\in \mathbb {N}^+$. Being the orbit periodic with period equal or multiple to that of the rotating frame, it is periodic both in the rotating and in the inertial frame.

The criterion for an orbit to be periodic in the ER3BP was firstly given by Moulton [15], after merging together the aforementioned period constraint and his considerations on the symmetry of the problem

if the infinitesimal body crosses the x-axis perpendicularly when the finite bodies are at an apse, its motion is symmetric with respect to the x-axis.

The formalization of the periodicity condition is due to Roy and Ovenden [24], who generalized it for the motion of n point-masses in the so-called mirror theorem:

if n point-masses are acted upon by their mutual gravitational forces only, and at a certain epoch each radius vector from the (assumed stationary) center of mass of the system is perpendicular to every velocity vector, then the orbit of each mass after that epoch is a mirror image of its orbit prior to that epoch

According to Moulton [15] and Roy and Ovenden [24], a sufficient condition for the motion in the ER3BP to be periodic is that it has two perpendicular crossings with the ($\hat{x},\hat{z}$) plane, which shall occur when the primaries are at an apse.

2.4 Stability of periodic orbits

The stability of periodic orbits is assessed by studying the properties of the STM over one orbital period (monodromy matrix). The eigenvalues of the monodromy matrix and their evolution as a function of the eccentricity are studied for each family reported in this paper. The monodromy matrix is a $6 \times 6$ matrix and has six eigenvalues which come in complex conjugate or reciprocal pairs [2]. Figure 1 shows possible distribution of eigenvalues. These include cases with (a) three reciprocal real pairs, (b) two real and one complex conjugate pair (on the unit circle), (c) one real and two complex conjugate pairs (on the unit circle), (d) one real and two complex conjugate pairs (not on the unit circle), (e) three complex conjugate pairs (only one on the unit circle), (f) three complex conjugate pairs (on the unit circle). All cases (a–e) are representative of unstable orbits, except for case (f), which indicates a stable orbit. Stability properties of periodic orbits studied are reported in Sect. 5, with reference to types of eigenvalue distributions defined in Fig. 1.

Fig. 1

Distribution of eigenvalues on the complex plane representative of the families of orbits studied in the paper

3 Numerical method

In this work, periodic orbits in the ER3BP have been generated starting from orbits in the CR3BP with same period, through differential corrections and eccentricity continuation techniques.

In agreement with the mirror theorem [24], the differential correction algorithm is implemented to target two perpendicular crossings with the ($\hat{x},\hat{z}$) plane. More in detail, a fixed-time single-shooting algorithm is implemented, based on the algorithm proposed by Howell [9] and adapted for the case of ER3BP.

The initial guess is taken on the ($\hat{x},\hat{z}$) plane; at a time the primaries are at an apse. The correction algorithm targets the second perpendicular crossing that occurs after $\pi$ or multiples of $\pi$, i.e., when the primaries happen to be at an apse again. The time between the two perpendicular crossings is half of the orbital period of the periodic solution. In this case, it is sufficient to find half of the orbit and to propagate it forward for the remaining half period to have the full periodic solution.

With reference to Howell [9], the vector of free variables is written as

$$\begin{aligned} \varvec{\chi }= \begin{bmatrix} x_0 \quad z_0 \quad y'_0 \end{bmatrix}^\mathrm{T} \end{aligned}$$

(8)

where the subscript 0 indicates conditions at initial time, corresponding to initial true anomaly $f_0$ that equals either 0 (periapsis) or $\pi$ (apoapsis). At the end of the trajectory (half orbit), the state must satisfy the following constraint condition, defined such to have perpendicular crossing on the ($\hat{x},\hat{z}$) plane

$$\begin{aligned} \varvec{F}(\varvec{\chi })= \begin{bmatrix} y_h \quad x'_h \quad z'_h \end{bmatrix}^\mathrm{T} = \varvec{0} \end{aligned}$$

(9)

with subscript h indicating the state after half period of the orbit, corresponding to true anomaly $f_h=f_0 + N\pi$. The goal is to compute a solution for the free variable vector $\varvec{\chi }$ that satisfies the constraint condition $\varvec{F}(\varvec{\chi })=\varvec{0}$. The result is found iteratively through a multi-variable Newton’s method:

$$\begin{aligned} \varvec{\chi }_{k+1} = \varvec{\chi }_k - \mathbf {J}(\varvec{\chi }_k)^{-1} \varvec{F}(\varvec{\chi }_k) \end{aligned}$$

(10)

where subscript k indicates the current iteration and $k+1$ the next iteration. The Jacobian matrix $\mathbf {J}(\varvec{\chi })$ of the problem is found by computing the derivatives of the constraint with respect to the free variables

$$\begin{aligned} \mathbf {J}(\varvec{\chi })= & {} \frac{\partial \varvec{F}(\varvec{\chi })}{\partial \varvec{\chi }} = \begin{bmatrix} \frac{\partial y_h}{\partial x_0}&\frac{\partial y_h}{\partial z_0}&\frac{\partial y_h}{\partial y'_0} \\ \frac{\partial x'_h}{\partial x_0}&\frac{\partial x'_h}{\partial z_0}&\frac{\partial x'_h}{\partial y'_0} \\ \frac{\partial z'_h}{\partial x_0}&\frac{\partial z'_h}{\partial z_0}&\frac{\partial z'_h}{\partial y'_0} \end{bmatrix} \nonumber \\= & {} \begin{bmatrix} \varPhi _{21}&\varPhi _{23}&\varPhi _{25} \\ \varPhi _{41}&\varPhi _{43}&\varPhi _{45} \\ \varPhi _{61}&\varPhi _{63}&\varPhi _{65} \end{bmatrix} \end{aligned}$$

(11)

with $\varPhi _{ij}$ being the element (i, j) of the STM $\varvec{\Phi }(f_h,f_0)$.

4 Families in the circular problem

Several studies exist on the characterization of periodic motion near equilibrium points in the CR3BP. Relevant contributions include the work by Breakwell and Brown [1], who computed families of orbits in the Earth–Moon system. Later, their work has been extended to compute families for different systems and study their properties depending on the mass ratio $\mu$ between primaries [9, 10]. More recent works include a comprehensive survey of orbit families in the Earth–Moon system [6, 8] and their classification [29].

This section reports and discusses orbital period ranges within Halo, planar and vertical Lyapunov families around collinear libration points, in the case of Earth–Moon and Sun–Earth three-body systems. Resonant motion in the CR3BP is identified to be used as initial guess to compute periodic orbits in the ER3BP. Table 1 shows periods of common resonant orbits, chosen in the interval between $\pi /5$ and $\pi$, with a maximum of $N=2$, with $M,N\in \mathbb {N^+}$ indicating, respectively, the number of revolution on the orbit and the number of revolution of primaries.

Table 1 Orbital period of common resonant orbits

4.1 Halo family

Table 2 shows orbital period ranges for Halo families around L1, L2 and L3 in both Earth–Moon and Sun–Earth system.

Table 2 Orbital period for Halo families in the CR3BP

Orbital period of L1 and L2 families is shown to be significantly lower than L3 family. Existence of resonant motion in the Halo families can be established by comparing Tables 2 with 1. Resonant 3:1 and 5:2 Halo orbits exist around L1 and L2, in the case of both Earth–Moon and Sun–Earth systems. In the Earth–Moon system, the L2 family has a slightly wider period range with respect to the L1 family and includes 7:2 and 2:1 resonant orbits as well. In the Sun–Earth system, Halo orbits with lower periods exist in the L1 family and 4:1 resonance is found. A significantly larger period is observed for Halo orbits about the L3 point. In this case the period is on the order of $2\pi$ and a 1:1 resonant behavior is observed for orbits of the L3 Halo families in the Sun–Earth system.

4.2 Planar and vertical Lyapunov families

Similar trends are found for planar and vertical Lyapunov families, with the difference that Lyapunov orbits have in general higher period with respect to Halo as they can became very large. For the case of L1 and L2 families, orbital periods ranges between approximately 3 nondimensional units, up to 5–7 nondimensional units. More in detail, 3:2 resonance is found in all planar and vertical Lyapunov families around L1 and L2, in both Earth–Moon and Sun–Earth systems, and 2:1 resonance is found in most of them. Families of Lyapunov about L3 have period of approximately $2\pi$, as in the case of Halo orbit families, leading to 1:1 resonant motion with primaries.

5 Periodic orbits in the elliptic problem

A survey of periodic motion in the ER3BP is presented in this section. The orbits are classified depending on the number of revolutions they perform around collinear points. Stability properties are also reported and classified with reference to Sect. 2.4 and Fig. 1. Examples from both Earth–Moon ($e=0.0554$) and Sun–Earth ($e=0.0167$) systems are shown.

5.1 Single-revolution orbits

Single-revolution orbits in the ER3BP are associated with 1:1 resonance with the motion of the primaries: the spacecraft completes one orbit as the primaries do the same around the barycenter of the system. Suitable initial guess for periodic motion in ER3BP typically refers to 1:1 resonant orbits in the circular problem. In particular, as discussed in Sect. 4, solutions around L3 are of interest, as well as large Lyapunov orbits, with period of $2\pi$. An example, referring to a planar Lyapunov orbit about L2 in the Earth–Moon system, is shown in Fig. 2a. The picture shows the initial guess given to the correction algorithm in red (the 1:1 Lyapunov resonant orbit in the CR3BP) and the periodic solution after correction in the Earth–Moon ER3BP in blue, as seen from the nondimensional rotating-pulsating frame. The eccentricity of the problem is shown to have an effect on the orbit, as it shrinks the amplitude of the orbit along the x axis. However, apart from this small effect, no significant deviation from the circular case is found. This kind of behavior is observed for many 1:1 orbits, including those around L3, which are then not very much affected by the eccentricity of the system. Concerning stability, the planar L2 Lyapunov exhibits a bifurcation at $e=0$ where the two unitary eigenvalues of the CR3BP orbit bifurcate to a complex conjugate pair on the unit circle. There are no further bifurcations observed in the range $e=[0, 0.0554]$ and all orbits in this range are unstable, with two real (one positive and one negative) and one complex conjugate (on the unitary circle) pairs of eigenvalues [type (b)].

Fig. 2

Single-revolution orbits: planar Lyapunov in CR3BP (red) and ER3BP (blue). a L2 orbit in the Earth–Moon system (1:1 in the CR3BP). b L1 orbit in the Sun–Earth system (5:2 in the CR3BP). (Color figure online)

A further example of single-revolution motion is shown in Fig. 2b, with the case of a periodic orbit in the ER3BP generated from a 5:2 planar Lyapunov orbit about L1 in the CR3BP. The corrector converges to a single-revolution orbit, of period $2\pi$ despite the different resonance properties of the same orbit in the CR3BP, which completes 5 revolutions every two revolutions of primaries. With a different period, the geometry of the solution changes and a greater deviation is observed with respect to the previous case. As for the previous case, the orbits are unstable and no bifurcations are observed in the range of eccentricities explored. The distribution of eigenvalues is of type (b) for all orbits, with two negative real and one unitary complex conjugate pair of eigenvalues.

Single-revolution orbits appear to be the only possible periodic motion around L3: no multiple-revolution orbits are observed about L3. The reason is found in typical orbital periods of L3 orbits, which are in the order of $2\pi$. Only 1:1 resonance motion is observed in this particular location. These orbits are stable in the CR3BP and mostly keep their properties in the ER3BP. A bifurcation occurs when $e=0$, with the eigenvalues moving from (1, 0) point to the unitary circle and on the real axis. However, the motion is very small along the range of eccentricities studied and all eigenvalues remains very close to the unitary point.

5.2 Double-revolution orbits

Double-revolution orbits are observed to generate from 2:1 resonance in the circular problem. Since such periodic motion exists in Halo and Lyapunov families around L1 and L2 points, double-revolution orbits are found to be quite common solutions in the ER3BP. Examples related to Halo, vertical and planar Lyapunov are shown here.

Fig. 3

Double-revolution orbits (Earth–Moon system) shown in nondimensional rotating-pulsating frame (left) and Moon-centered inertial frame (right). Solutions generated from 2:1 resonant orbits in CR3BP: a, b planar Lyapunov about L1, c, d Halo about L2, e, f vertical Lyapunov about L1. Projections of 3D ER3BP orbits on $x{-}y$, $x{-}z$ and $y{-}z$ planes are shown in gray

Figure 3 shows examples of double-revolution orbits in the Earth–Moon system. Periodic motion is depicted both in the nondimensional rotating-pulsating frame (figures on the left side) and in the Moon-centered inertial frame (figures on the right side). Figure 3a, b refers to a planar solution that generates from a Lyapunov orbit about L1. As any other orbit shown in this work, the orbit is symmetric with respect to the $x{-}z$ plane. Due to its symmetry, the time between two consecutive perpendicular crossings with the $x{-}z$ plane is $\pi$. This result is in agreement with the aforementioned mirror theorem, since every perpendicular crossing occurs when the primaries are at an apse (every $\pi$). The orbit is made of two loops, and a half (symmetric) orbit includes the two halves of each loop. Each loop has a period of approximately $\pi$, as the initial guess orbit in the CR3BP. In particular, the smaller loop has a period slightly larger than $\pi$, while the bigger loop is flown in a shorter time. Figure 3c, d shows a three-dimensional periodic solution, which generates from a Halo orbit around L2 in the CR3BP. The three-dimensional view is shown together with the projection of the ER3BP orbit on the $x{-}y$, $x{-}z$ and $y{-}z$ planes. The same is shown for the periodic orbit in Fig. 3e, f, which refer to a solution generating from a vertical Lyapunov near the L1 point. For the case of double-revolution orbits shown in this work, all periodic solutions appear to have similar properties in terms of geometry and period with respect to their corresponding CR3BP orbit. Both Halo, planar and vertical Lyapunov orbits in the CR3BP have period of $\pi$ (they replicate their initial state after $2\pi$ as well) and they split into two geometrically similar orbits in the ER3BP. The nonzero eccentricity has the effect of duplicating the single orbit into two semi-orbits, which does not replicate itself after $\pi$ as in the CR3BP, but becomes periodic of period $2\pi$ in the ER3BP. More into detail, the two semi-orbits appear to be symmetric along the x axis, with a contact point shared with their CR3BP reference orbit. The presence of the contact point between ER3BP and CR3BP solutions is enforced by the single-shooting numerical correction algorithm in use, to find a periodic solution in the ER3BP associated with the specific (resonant) solution in the CR3BP. Trajectories as seen from the Moon-centered inertial frame are also of interest. Since the motion is in resonance with primaries, it results to be periodic in the inertial frame as well. Interesting behavior appears both for the planar case (Fig. 3b) and for the three-dimensional cases (Fig. 3d, f), where the orbits are shown to surround the Moon with very peculiar oscillating paths. Double-revolution orbits shown here share similar stability properties and behavior. All orbits are unstable and exhibit a bifurcation at $e=0$, when a pair of eigenvalues departs from point (1, 0). Planar orbits show a type (a) instability (three pairs of positive real eigenvalues), while three-dimensional orbits show a type (b) instability (two positive real and one complex conjugate pair). Results on stability properties and $e=0$ bifurcation are confirmed by results in [3] on double-revolution three-dimensional Halo orbits.

Fig. 4

Triple-revolution orbits (Earth–Moon system) shown in nondimensional rotating-pulsating frame (left) and Moon-centered inertial frame (right). Solution generated from 3:1 resonant Halo about L2 in CR3BP (a, b). Solutions generated from 3:2 resonant orbits in CR3BP: (c, d) vertical Lyapunov about L1, (e, f) vertical Lyapunov about L2. Projections of ER3BP orbits on $x{-}y$, $x{-}z$ and $y{-}z$ planes are shown in gray

5.3 Triple-revolution orbits

As for the case of double-revolution orbits, the existence of 3:1 resonance in all families of Halo and Lyapunov orbits about L1 and L2 makes triple-revolution orbits quite common solutions in the ER3BP. Figure 4 shows some examples of triple-revolution orbits, obtained from corresponding periodic motion in the CR3BP. In this case, periodicity in the state is reached after three orbital loops. With analogy to what observed within the double-revolution cases, a similar orbit to that of CR3BP is replicated three times. In the case of Fig. 4a, b, the periodic motion in the ER3BP is generated starting from a 3:1 resonant Halo orbit about L2 in the CR3BP. Such orbit possesses orbital period of $2/3\pi$. This example is in analogy with the case shown in Fig. 3c, d: both cases refer to a Halo orbit about L2, but with different orbital period. Figure 4c, d shows an ER3BP solution associated with a 3:2 vertical Lyapunov about L1 in the CR3BP. In this case, the CR3BP guess has an orbital period of $4/3\pi$, since it completes three orbital loops as the primaries revolve two times around the barycenter of the system. The orbital period is doubled with respect to the case shown in Fig. 4a, b. Accordingly, the resulting trajectory in the ER3BP is periodic with period $4\pi$. Geometrically, the outcome is similar to those observed so far: the orbit makes three loops and is periodic both in the synodic and in the inertial frame. Same considerations apply for the case of Fig. 4e, f, which refer to a periodic ER3BP solution generated from a 3:2 resonant vertical Lyapunov about L2 in the CR3BP. Periodicity is also observed after two revolutions of primaries ($4\pi$). Very interesting behavior are observed for triple-revolution orbits, as seen from the Moon-centered inertial point of view. As for the case of double-revolution orbits, the trajectory path surrounds the Moon with oscillations associated with the three orbital loops that characterize triple-revolution motion.

A very interesting solution is obtained when providing a 3:1 resonant Halo orbit about L1 in the CR3BP as initial guess. In this case the starting point is a orbit with period $2/3\pi$ and three loops are obtained in the ER3BP, in order to match the period of $2\pi$. The correction algorithm converges into a peculiar solution that connects motion between the neighborhoods of L1 and L2 points. Such solution is in fact a heteroclinic connection between a solution around L1 and a solution around L2 (Fig. 5). This periodic orbit might be of great interest for space applications, since it provides free motion between L1 and L2 and considers the higher fidelity dynamics associated with ER3BP.

Fig. 5

Triple-revolution orbit (Sun–Earth system) shown in a nondimensional rotating-pulsating frame and b Earth-centered inertial frame. Solution generated from 3:1 resonant Halo about L1 in CR3BP. Projections of ER3BP orbit on $x{-}y$, $x{-}z$ and $y{-}z$ planes are shown in gray

Vertical Lyapunov orbits are unstable with eigenvalue distribution of type (a) (L1 orbit) and of type (b) (L2 orbit). In both cases, their real eigenvalues are positive and no bifurcations occur in the range of eccentricities studied. On the contrary, triple-revolution Halo orbits show a more complicated behavior. Figure 6 shows the evolution of the eigenvalue distribution for the case of 3:1 Halo as function of the eccentricity. Several collisions and bifurcations are observed. Figure 6a refers to the Sun–Earth L1 3:1 Halo. In this case, after a bifurcation at $e=0$, the distribution evolves from type (b) (two real and one complex conjugate pair on unitary circle) to type (a) (three real pairs) after a collision in ($-\,1,0$) when $e=0.0085$. A double collision occurs for $e=0.0092$, when two pairs of complex conjugates appears [not on the unitary circle, type (d)]. Figure 6b refers to the triple-revolution Earth–Moon L2 Halo. In this case, the distribution of eigenvalues evolves from type (c) (one negative real and two complex conjugate pairs on the unitary circle) to type (f) (three complex conjugate pairs on the unitary circle) after a collision at ($-1,0$) when $e=0.0454$. It is worth noting that type (f) orbits are stable. A stability region is then identified for this family of orbits in the interval $e=[0.0454,0.0468]$. At $e=0.0468$ a double collision occurs on the unitary circle and two complex pairs are created inside and outside the unitary circle [type (e)].

Fig. 6

Distribution of eigenvalues as function of the eccentricity for the case of triple-revolution families of orbits generated from 3:1 resonant Halo around a Sun–Earth L1 and b Earth–Moon L2

Fig. 7

Quadruple-revolution orbit (Sun–Earth system) shown in a nondimensional rotating-pulsating frame and b Earth-centered inertial frame. Solution generated from 4:1 resonant Halo orbit about L1 in the CR3BP. Projections of ER3BP orbit on $x{-}y$, $x{-}z$ and $y{-}z$ planes are shown in gray

5.4 Quadruple-revolution orbits

The last class of periodic motion reported here is quadruple-revolution motion. The resonance of 4:1 is not very common in the families of vertical and planar Lyapunov. Also, no 4:1 resonance orbit can be found in the Halo families about L1, L2 or L3 in the Earth–Moon system. As for the case under study in this work, such resonance is observed only in the family of Halo orbits around L1, in the Sun–Earth system. Figure 7a, b shows an example of four-revolution solution obtained from the 4:1 Halo about L1 in the Sun–Earth CR3BP. As for the last case of triple-revolution orbits shown, the corrector converges to a heteroclinic connection between L1 and L2 solutions. In this case, the initial guess orbit possesses period of $1/2\pi$ and then, the ER3BP orbit is periodic after looping four times between L1 and L2. The looping behavior is clearly seen when looking at the projection of the motion in the synodic frame on the $y{-}z$ axis. The quadruple-revolution orbit exhibits a type (b) instability, with two positive real and one complex conjugate pair (on the unitary circle) of eigenvalues. No bifurcations are observed in the range of eccentricities observed.

6 Conclusions

The work presents a survey of periodic solutions about collinear libration points in the ER3BP. Results associated with Earth–Moon and Sun–Earth systems are shown. Periodic motion is classified depending on dynamical behavior and geometry, with the focus on the number of revolutions the trajectory does before replicating its initial state. Stability properties are assessed for each orbit found and discussed as function of the eccentricity.

The resonance properties of Halo, planar and vertical Lyapunov families are reported and the existence of corresponding ER3BP solutions in discussed. More in detail, the analysis shows that planar orbits are commonly found as single-revolution orbits in the ER3BP. Also, single-revolution solutions are found to be the only existing solutions in the proximity of the third Lagrangian point, where resonant three-dimensional motion has not been observed. The most common three-dimensional solutions found around L1 and L2 points are double- and triple-revolution orbits. Such solutions are associated with the 2:1, 3:1 or 3:2 resonance motion, which is very common in all families of Halo and vertical Lyapunov orbits. Finally, interesting heteroclinic connections between L1 and L2 solutions have been found associated with 3:1 and 4:1 resonance in the Halo family around L1 point of the Sun–Earth system.