Polynomial equations for science orbits around Europa

Abstract

In this paper, the design of science orbits for the observation of a celestial body has been carried out using polynomial equations. The effects related to the main zonal harmonics of the celestial body and the perturbation deriving from the presence of a third celestial body have been taken into account. The third body describes a circular and equatorial orbit with respect to the primary body and, for its disturbing potential, an expansion in Legendre polynomials up to the second order has been considered. These polynomial equations allow the determination of science orbits around Jupiter’s satellite Europa, where the third body gravitational attraction represents one of the main forces influencing the motion of an orbiting probe. Thus, the retrieved relationships have been applied to this moon and periodic sun-synchronous and multi-sun-synchronous orbits have been determined. Finally, numerical simulations have been carried out to validate the analytical results.

1 Introduction

In the planetary observation field the design of the orbit around a celestial body is a delicate aspect. Therefore, several typologies of orbits should be considered, according to different mission constraints and objectives. Some important examples are the AreoStationary Orbit (ASO) (Alvarellos 2010; Liu et al. 2012; Silva and Pilar 2013), which allows the probe to remain steady with respect to the surface (even if station keeping maneuvers are required), the repeating ground track orbits (Lara 2003), which permit the repeated observation of a given zone, the Sun-Synchronous Orbits (SSOs), which allow the probe to monitor a celestial body in approximately constant solar illumination conditions (same observation local time for a given area), and the Periodic Multi-Sun-Synchronous Orbits (PMSSOs), which permit a given region of a celestial body to be periodically observed in solar illumination conditions that follow a regular cycle and are therefore useful to investigate the evolution of time-varying phenomena and parameters related to the atmosphere and to the surface of the celestial body (Ortore et al. 2013, 2014). For these trajectories, the feasibility to determine the orbit elements of probe by solving analytical equations is a key aspect to both simplify and perform the mission design well. In this regard, in Ortore et al. (2012) and in Circi et al. (2012) mathematical relationships able to provide PMSSOs around Earth and Mars, taking the planetary oblateness into account, were retrieved. In Liu et al. (2010) analytical expressions able to provide several kinds of orbits were presented, taking into account the zonal harmonics of Mars’ gravitational field up to $J_{4}$; repeating ground track orbits, SSOs, frozen orbits (Liu et al. 2011; Coffey et al. 1994), orbits at critical inclination (Coffey et al. 1986) and the ASO around Mars were considered.

About planetary moons, several studies have been carried out on the design of science orbits. Some important examples are here reported: Lara et al. (2005) have investigated the stability of a probe around a moon, highlighting how the gravitational attraction due to the planet around which the moon is orbiting is associated with unstable behaviour in a wide range of inclinations around 90$^{\circ }$. In (Paskowitz and Scheeres 2006) an algorithm, based on a modified form of the Hill three-body problem, has been developed to design long life time trajectories about Europa, including the perturbative effects due to Europa’s gravity field and to the tidal force coming from Jupiter. In (Russell and Lara 2007) repeating ground track orbits with long life times have been retrieved around moons using an unaveraged model in place of the classical doubly averaged techniques. In Lara (2008) an analytical theory, based on the Lie–Deprit perturbation method, which allows the recovery of the short- and long-period terms by means of explicit transformations, has been provided and applied to the computation of science orbits. In this case, the required low eccentricities and high inclinations, have allowed the substitution of the whole sequence of transformations by a single set of simplified equations. Russell and Lara (2009), by considering an unaveraged model, have demonstrated the existence of long-term stable orbits around Enceladus, at about 200 km of altitude, with low eccentricity and inclination close to 65$^{\circ }$.

In the present study, the analytical retrieval of science orbits around Europa has been performed, considering for the primary celestial body (Europa) the zonal harmonics up to $J_{4}$ and for the third body (Jupiter) effect an expansion in Legendre polynomials up to the second order. The planetary Lagrange equations have been used to obtain the variations of the orbit elements due to the above-mentioned orbital perturbations. Then, the retrieved expressions have been introduced into the relationships of periodicity and synchronism with the Sun, allowing the determination of polynomial equations for designing repeating ground track orbits, SSOs and PMSSOs.

The geological and physical characteristics of Europa make this natural satellite one of the major targets in the exploration of the Solar System. On the other hand, the strong magnetic field of Jupiter drastically reduces the probe life time and, consequently, the available time for observation. To extend this life time, the probe should be equipped with an appropriate protection which would significantly increase its weight, making the accomplishment of the mission very expensive. In addition to that, Jupiter’s gravitational perturbations also make the probe orbit design complicated. In this environment, the planning of the trajectory represents a very delicate aspect of the mission, due to the fact that the observation of the entire surface should be carried out in a relatively short time. To this purpose, the possibility of revisiting the same area at regular time intervals and in appropriate solar illumination conditions represents an important mission requirement. The orbits proposed in this paper meet this requirement and therefore represent possible candidates for the exploration of this moon.

The paper is organized as follows: in Sect. 2 the determination of the polynomial equations has been carried out; in Sect. 3 the retrieved equations have been applied to Europa and a comparison with the results deriving from numerical simulations has been performed.

2 Polynomial equations

As mentioned, the repeating ground track orbits (also called periodic orbits) represent one of the principal typologies of trajectories which can be considered in the planetary observation field, as they allow the observation of a certain zone of a celestial body at regular time intervals (ground tracks repeat themselves after a given interval). This condition is satisfied if $mD_n =RT_n$, where $D_n$ is the nodal day of the celestial body (time elapsing between two consecutive nodal line crossings given by a point on the equator of the celestial body), $m$ is the integer number of nodal days after which the ground track is repeated (revisit time), $T_n$ is the nodal period of the probe (time elapsing between two consecutive ascending node passes) and $R$ is the integer number of nodal periods accomplished in $m$ nodal days ($R$ and $m$ are prime one to the other). Since $D_n =2\pi /(\omega _P -\dot{\Omega })$, where $\omega _P$ is the angular rotation of the celestial body around its polar axis and $\dot{\Omega }$ the temporal variation of the RAAN (Right ascension of the Ascending Node) of the probe orbit, and $T_n =2\pi /\dot{\xi }$, where $\dot{\xi }$ is the temporal variation of the argument of latitude of the probe $(\xi )$, given by the sum of the argument of pericentre $(\omega )$ and mean anomaly $(M)$ of the probe, to analytically determine repeating ground track orbits, it is necessary to consider the expressions of $\dot{\Omega }$ and $\dot{\xi }$.

The ASO can be seen as a particular case of repeating ground track orbit, in which $R/m=D_n /T_n =1$ (areosynchronism condition), the probe orbit eccentricity is $e = 0$, the probe orbit inclination is $i = 0$ and the ground track reduces, in the Keplerian case, to a point on the equator of the celestial body.

According to Kozai (1959), the even zonal harmonics of the gravitational field entail secular perturbations of $\Omega$, $\omega$ and $M$. Limiting the analysis up to $J_{4}$, the variations of these parameters due to the primary body (identified by the subscript $J$) can be expressed through the following equations (Merson 1961):

$$\begin{aligned} \dot{\Omega }_J= & {} -\frac{3R_P ^{2}}{2}\frac{n\cos i}{a^{2}(1-e^{2})^{2}}\left\{ {J_2 -\frac{R_P ^{2}J_2 ^{2}}{16}} \right. \frac{12-80\sin ^{2}i-(4+5\sin ^{2}i)e^{2}}{a^{2}(1-e^{2})^{2}} \nonumber \\&\left. {\left. {-\frac{5R_P ^{2}J_4 }{16}\frac{(4-7\sin ^{2}i)(2+3e^{2})}{a^{2}(1-e^{2})^{2}}} \right] } \right\} \end{aligned}$$

(1)

$$\begin{aligned} \dot{\omega }_J= & {} \frac{3R_P ^{2}J_2 }{4}\frac{n(4-5\sin ^{2}i)}{a^{2}(1-e^{2})^{2}}\nonumber \\&+\frac{3R_P ^{4}J_2 ^{2}}{128}\frac{n[10\sin ^{2}i(76-89\sin ^{2}i)+(56-36\sin ^{2}i-45\sin ^{4}i)e^{2}]}{a^{4}(1-e^{2})^{4}} \nonumber \\&-\frac{15R_P ^{4}J_4 }{32}\frac{n\left[ {16-62\sin ^{2}i+49\sin ^{4}i+\left( {18-63\sin ^{2}i+\frac{189}{4}\sin ^{4}i} \right) e^{2}} \right] }{a^{4}(1-e^{2})^{4}} \end{aligned}$$

(2)

$$\begin{aligned} \dot{M}_J= & {} n+\frac{3R_P ^{2}J_2 }{4}\frac{n(2-3\sin ^{2}i)}{a^{2}(1-e^{2})^{3/2}} +\frac{3R_P ^{4}J_2 ^{2}}{32}\nonumber \\&\frac{n\left[ {100\sin ^{2}i\!-\!131\sin ^{4}i \!+\!(20\!-\!98\sin ^{2}i\!+\!67\sin ^{4}i)e^{2}\!-\!\frac{1}{16}(280\!-\!328\sin ^{2}i\!+\!79\sin ^{4}i)e^{4}} \right] }{a^{4}(1\!-\!e^{2})^{9/2}} \nonumber \\&\quad -\frac{45R_P ^{4}J_4 }{128}\frac{ne^{2}(8-40\sin ^{2}i+35\sin ^{4}i)}{a^{4}(1-e^{2})^{7/2}} \end{aligned}$$

(3)

where $R_{P}$ and $\mu _P$ are, respectively, the equatorial mean radius and the planetary constant of the primary body and $n=\sqrt{\frac{\mu _P }{a^{3}}}$ is the mean motion of probe.

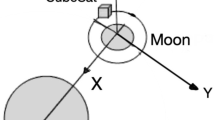
According to Fig. 1, where $(\hat{{C}}_1 ,\hat{{C}}_2 ,\hat{{C}}_3)$ is a generic inertial reference frame, while $m_P$ and $m_T$ are the masses of the primary celestial body and of the third celestial body respectively, the potential $U_{T}$ associated with the presence of the third body, in the motion of the probe with respect to the primary body, is given by:

$$\begin{aligned} U_T =\mu _T \left( {\frac{1}{r_1 }+\frac{1}{d^{3}}\hat{{d}}\cdot \hat{{r}}} \right) \end{aligned}$$

(4)

where $\mu _T$ is the planetary constant of the third body, while $\hat{{d}}$ and $\hat{{r}}$ represent the unit vectors of the distances $\mathbf{d}$ and $\mathbf{r}$, respectively.

Fig. 1

Restricted three body problem

In the case $r\ll d$, the disturbing potential given by Eq. (4) can be approximated with the one associated with the gravity gradient force. This allows a second order approximation of the disturbing potential, expressed by the traditional expansion in Legendre polynomials. Then, by double averaging this approximate form of the potential over the positions of both probe and perturbing body in their motions with respect to the primary body and, subsequently, by replacing this average potential in the Lagrange planetary equations, the so-called long-term temporal variations of the orbit elements and of the mean anomaly of the probe due to the third body perturbation can be retrieved. In this way, the variations of $\Omega$, $\omega$ and $M$ (identified by the subscript $T)$ can be expressed through the following equations (Broucke 2003):

$$\begin{aligned} \dot{\Omega }_T= & {} \frac{3{m}'{n}'^{2}}{8}\frac{\cos i\,[5e^{2}\cos (2\omega )-3e^{2}-2]}{n(1-e^{2})^{1/2}} \end{aligned}$$

(5)

$$\begin{aligned} \dot{\omega }_T= & {} \frac{3{m}'{n}'^{2}}{8}\frac{5\cos ^{2}i-1+e^{2}+5(1-e^{2}-\cos ^{2}i)\cos (2\omega )}{n(1-e^{2})^{1/2}} \end{aligned}$$

(6)

$$\begin{aligned} \dot{M}_T= & {} -\frac{{m}'{n}'^{2}}{8}\frac{(3e^{2}+7)(3\cos ^{2}i-1)+15(1+e^{2})\sin ^{2}i\cos ^{2}\omega }{n} \end{aligned}$$

(7)

where ${m}'=\frac{m_T }{m_P +m_T }$ and ${n}'=\sqrt{\frac{\mu _P +\mu _T }{{a}'^{3}}}$ is the mean motion of the third body in its motion with respect to the primary body, with ${a}'$ semi-major axis of the orbit described by the third body with respect to the primary one. Equations (5)–(7) have been written assuming that the perturbing body describes a circular and equatorial orbit with respect to the primary body. The more general equations which take into account the eccentricity of the third body orbit are retrieved and discussed in Domingos et al. (2008), while the influence of the higher terms of the expansion in Legendre polynomials for the third body disturbing potential is investigated in Prado (2003).

By summing Eqs. (1), (2), (3) to, respectively, (5), (6), (7), the total RAAN and argument of latitude variations can be retrieved:

$$\begin{aligned} \dot{\Omega }= & {} \dot{\Omega }_J +\dot{\Omega }_T =-\frac{3\sqrt{\mu _P }R_P ^{2}}{2}\frac{\cos i}{\left( {1-e^{2}} \right) ^{2}}\,\left[ {\frac{J_2 }{a^{3.5}}+\frac{b_{22} +b_4 }{a^{5.5}}+b_T a^{1.5}} \right] \end{aligned}$$

(8)

$$\begin{aligned} \dot{\xi }= & {} \dot{\xi }_J +\dot{\xi }_T =\dot{\omega }_J +\dot{M}_J +\dot{\omega }_T +\dot{M}_T \nonumber \\= & {} \sqrt{\mu _P }\left[ {\frac{1}{a^{1.5}}+\frac{3R_P ^{2}}{4}\frac{1}{\left( {1-e^{2}} \right) ^{2}}\left( {\frac{c_2 }{a^{3.5}}+\frac{c_{22} +c_4 }{a^{5.5}}+c_T a^{1.5}} \right) } \right] \end{aligned}$$

(9)

where the coefficients have the expressions:

$$\begin{aligned} b_{22}= & {} -\frac{R_P ^{2}J_2 ^{2}}{16}\frac{(12-80\sin ^{2}i)-(4+5\sin ^{2}i)e^{2}}{\left( {1-e^{2}} \right) ^{2}}\\ b_4= & {} -\frac{5R_P ^{2}J_4 }{16}\frac{(4-7\sin ^{2}i)(2+3e^{2})}{\left( {1-e^{2}} \right) ^{2}}\\ b_T= & {} \frac{{m}'{n}'^{2}}{4R_P ^{2}\mu _P }(1-e^{2})^{3/2}[3e^{2}+2-5e^{2}\cos (2\omega )]\\ c_2= & {} J_2 [(1-e^{2})^{1/2}(2-3\sin ^{2}i)+(4-5\sin ^{2}i)]\\ c_{22}= & {} \frac{R_P ^{2}J_2 ^{2}}{32}\frac{1}{(1-e^{2})^{5/2}}\left\{ \left( {1-e^{2}} \right) ^{1/2}\left[ 10\sin ^{2}i(76-89\sin ^{2}i)\right. \right. \nonumber \\&\left. \left. +\,(56-36\sin ^{2}i-45\sin ^{4}i)e^{2} \right] \right. \\&\left. +\,4\left[ {\left( {100\sin ^{2}i-131\sin ^{4}i} \right) +\left( {20-98\sin ^{2}i+67\sin ^{4}i} \right) e^{2}} \right] \right. \nonumber \\&\left. -\,\frac{1}{4}\left( {280-328\sin ^{2}i+791\sin ^{4}i} \right) e^{4} \right\} \\ c_4= & {} \frac{15R_P ^{2}J_4 }{32}\frac{1}{(1-e^{2})^{2}}\left\{ (1-e^{2})^{1/2}\left[ {(40\sin ^{2}i-35\sin ^{4}i-8)e^{2}} \right] \right. \nonumber \\&\left. \left. -\left[ {\frac{4}{3}\left( {16-62\sin ^{2}i+49\sin ^{4}i} \right) } \right. \right. \right. \\&\left. {+(24-84\sin ^{2}i+63\sin ^{4}i)e^{2}} \right] \\ c_T= & {} \frac{{m}'{n}'^{2}}{2R_P ^{2}\mu _P }(1-e^{2})^{3/2}\left\{ {4-5\sin ^{2}i+e^{2}+5(\sin ^{2}i-e^{2})\cos (2\omega )} \right. \\&+\left. {\frac{\left( {1-e^{2}} \right) ^{1/2}}{3}\left[ {(3e^{2}+7)(3\sin ^{2}i-2)-15(1+e^{2})\sin ^{2}i\cos ^{2}\omega } \right] } \right\} \end{aligned}$$

Finally, by replacing Eqs. (8) and (9) in the expressions of nodal day and nodal period respectively ($D_n =2\pi /(\omega _P -\dot{\Omega })$, $T_n =2\pi /\dot{\xi })$ and then going into the condition $mD_n =RT_n$, it is possible to find a polynomial equation which provides repeating ground track orbits taking the zonal harmonics up to $J_{4}$ and the third body effects into account. The result is the following:

$$\begin{aligned} d_T a^{7}+d_1 a^{5.5}+d_K a^{4}+d_2 a^{2}+d_4 =0 \end{aligned}$$

(10)

where:

• $d_T =c_T -b_T \frac{2R}{m}\cos i$    related to the third body effect

• $d_1 =-\frac{4\omega _P }{3\sqrt{\mu _P }R_P ^{2}}\frac{R}{m}(1-e^{2})^{2}$    related to orbit characteristics

• $d_K =\frac{4}{3R_P ^{2}}(1-e^{2})^{2}$    related to the Keplerian motion

• $d_2 =c_2 -J_2 \frac{2R}{m}\cos i$    related to $J_2$ effect

• $d_4 =c_{22} +c_4 -(b_{22} +b_4 )\frac{2R}{m}\cos i$    related to $J_2 ^{2}$ and $J_4$ effects

The coefficients $d_{i}$ are defined as functions of $e,\,i$, $\omega$ and of the ratio $R/m$. By solving Eq. (10), the corresponding value of semi-major axis, identifying an orbit whose ground tracks repeat themselves at regular time intervals of $m$ nodal days, can be determined.

Another category of orbits that can be considered in the planetary observation field is represented by the SSOs, which make it possible to observe a given latitude of a celestial body with quasi-constant solar illumination conditions. To satisfy this objective, it is necessary to design an orbit characterized by a temporal variation of RAAN equal to the mean value of the velocity of the Sun ($\dot{\Omega }_S )$ in its apparent motion with respect to the celestial body: $\dot{\Omega }=\dot{\Omega }_S$. Then, by replacing Eq. (8) in the synchronism condition $(\dot{\Omega }=\dot{\Omega }_S )$ it is possible to retrieve a polynomial equation that provides SSOs taking the zonal harmonics up to $J_{4 }$ and the third body effects into account:

$$\begin{aligned} b_T a^{7}+\frac{2\dot{\Omega }_S }{3\sqrt{\mu _P }R_P ^{2}}\frac{(1-e^{2})^{2}}{\cos i}a^{5.5}+J_2 a^{2}+b_{22} +b_4 =0 \end{aligned}$$

(11)

The requirements of repeating ground track orbit and SSO are often matched so as to gain orbits that are both periodic in terms of ground track and synchronous with the Sun (Periodic Sun-Synchronous Orbits—PSSOs). In this way, a given region of a celestial body is periodically observed by the probe with quasi-constant solar illumination conditions. To this end, it is necessary to solve the system composed of Eqs. (10) and (11). However, considering only the $J_{2}$ and third body effects and retrieving the term $\cos i$ from Eq. (11) to replace it in the coefficients of Eq. (10), a single polynomial equation for the semi-major axis can be found:

$$\begin{aligned} f_1 a^{15}+f_2 a^{13.5}+f_3 a^{12}+f_4 a^{10}\!+\!f_5 a^{8.5}+f_6 a^{7}+f_7 a^{5}+f_8 a^{3.5}+f_9 a^{2}+f_{10} \!=\!0 \end{aligned}$$

(12)

where:

$$\begin{aligned} f_1= & {} \frac{9R_P^2 b_T^2 m^{\prime }n^{\prime 2}}{8\left( {1-e^{2}} \right) ^{3/2}}\left\{ {\left[ {5\cos (2\omega )-1} \right] -\left[ {\frac{5\cos (2\omega )(e^{2}+1)+3e^{2}+1/3}{2\sqrt{1-e^{2}}}} \right] } \right\} \\ f_2= & {} \frac{3R_P^2 b_T^2 \sqrt{\mu _P }}{\left( {1-e^{2}} \right) ^{2}}\frac{R}{m}\left( {\dot{\Omega }_S -\omega _P } \right) \\ f_3= & {} \frac{3R_P^2 b_T^2 \mu _P }{\left( {1-e^{2}} \right) ^{2}}+\frac{\dot{\Omega }_S ^{2}m^{\prime }n^{\prime 2}}{2R_P^2 \mu _P }\left( {1-e^{2}} \right) ^{3/2}\left\{ \,10\sin ^{2}\omega -\sqrt{1-e^{2}}\left[ 5\left( {e^{2}+1} \right) \left( {\sin ^{2}\omega -1} \right) \right. \right. \nonumber \\&\left. +\left. 3e^{2}+7 \right] \right\} \\ f_4= & {} \frac{9J_2 R_P^2 b_T }{4\left( {1-e^{2}} \right) ^{5/2}}\left\{ m^{\prime }n^{\prime 2}\left[ 2(1-e^{2})(5\cos ^{2}\omega -3)+\sqrt{1-e^{2}}\left( e^{2}-5\cos ^{2}\omega \left( {e^{2}+1} \right) \right. \right. \right. \nonumber \\&\left. \left. +\left. 7/3 \right) \right] -\frac{R_P^2 b_T \mu _P }{\left( {1-e^{2}} \right) ^{13/2}}\left[ {1+(1-e^{2})^{5}} \right] \right\} \\ f_5= & {} \frac{6J_2 R_P^2 b_T \sqrt{\mu _P }}{\left( {1-e^{2}} \right) ^{2}}\frac{R}{m}\left( {\dot{\Omega }_S -\omega _P } \right) =\frac{2J_2 }{b_T }f_2\\ f_6= & {} \frac{J_2 }{\left( {1-e^{2}} \right) ^{2}}\left\{ {\dot{\Omega }_S \frac{\left[ {5\left( {1-e^{2}} \right) ^{5}+3} \right] }{\left( {1-e^{2}} \right) ^{3}}+6R_P^2 b_T \mu _P } \right\} \\ f_7= & {} \frac{9J_2^2 R_P^2 }{2\left( {1-e^{2}} \right) ^{5/2}}\left\{ \frac{m^{\prime }n^{\prime 2}}{4}\left[ 2(1-e^{2})(5\cos ^{2}\omega -3)+\sqrt{1-e^{2}}\left( e^{2}-5\cos ^{2}\omega \left( {e^{2}+1} \right) \right. \right. \right. \nonumber \\&\left. \left. \left. +7/3 \right) \right] -\frac{R_P^2 b_T \mu _P }{\left( {1-e^{2}} \right) ^{13/2}}\left[ {1+(1-e^{2})^{5}} \right] \right\} \\ f_8= & {} \frac{3J_2^2 R_P^2 \sqrt{\mu _P }}{\left( {1-e^{2}} \right) ^{2}}\frac{R}{m}\left( {\dot{\Omega }_S -\omega _P } \right) =\frac{J_2^2 }{b_T^2 }f_2\\ f_9= & {} \frac{3J_2^2 R_P^2 \mu _P }{\left( {1-e^{2}} \right) ^{2}}\\ f_{10}= & {} -9J_2^3 R_P^4 \mu _P \left[ {\frac{1+\left( {1-e^{2}} \right) ^{5}}{4\left( {1-e^{2}} \right) ^{9}}} \right] \end{aligned}$$

Thus, for assigned values of $e$, $\omega$ and $R/m$, Eq. (12) provides the semi-major axis of the PSSO. Once retrieved the value of $a$, the corresponding inclination is obtainable by Eq. (11), neglecting $J_2 ^{2}$ and $J_4$ $(b_{22} =0$ and $b_4 =0)$:

$$\begin{aligned} \cos i=-\frac{\dot{\Omega }_S }{\frac{3\sqrt{\mu _P }R_P ^{2}}{2}\frac{J_2 +b_T a^{5}}{\left( {1-e^{2}} \right) ^{2}}}a^{7/2} \end{aligned}$$

(13)

If on one hand the SSOs, minimizing the solar illumination variations, offer the optimal condition to detect the change of the properties of a certain target, on the other hand they do not allow the investigation of parameters characterized by typical diurnal variations (surface temperature, atmospheric density, etc....). These applications can instead be realized by using the PMSSOs. This typology of orbits is identified by a system of equations, constituted by the repeating ground track condition $(mD_n =RT_n )$, by the equation $nD_n =2\pi /\left| {\dot{\Omega }-\dot{\Omega }_S } \right|$, where $n$ is the number of nodal days after which the same observation local time is re-obtained, and by the condition $n=I\,m\,$, with $I$ integer number. In this way, a given region is observed by the probe $I$ times in $n$ nodal days (at regular time intervals of $m$ nodal days) and these $I$ observations ($N$ = 1, 2...$I)$ occur every time at a different local time, being the observation local times phased according to the law: $\hbox {local time }=\hbox {initial local time }+(ND_S )/I$, where $D_S =2\pi /(\omega _P -\dot{\Omega }_S )$ is the solar day of the celestial body.

Similar to the PSSOs, to find the PMSSOs it is necessary to solve a system composed of two equations: Eq. (10) plus the one related to the multi-sun-synchronism condition $(nD_n =2\pi /\left| {\dot{\Omega }-\dot{\Omega }_S } \right| )$, which, once considered Eq. (8), can be written in the following form:

$$\begin{aligned} b_T a^{7}+\frac{2\hat{{\Omega }}}{3\sqrt{\mu _P }R_P ^{2}}\frac{(1-e^{2})^{2}}{\cos i}a^{5.5}+J_2 a^{2}+b_{22} +b_4 =0 \end{aligned}$$

(14)

where ; the sign + refers to the case $\dot{\Omega }>\dot{\Omega }_S$, the sign – to the case $\dot{\Omega }<\dot{\Omega }_S$.

Note that Eq. (14) is formerly identical to the SSO condition [Eq. (11)], with in place of $\dot{\Omega }_S$. In fact, the PSSOs can be seen as a particular case of PMSSOs, in which the probe observes a given latitude always with the same solar illumination. Since the SSOs are identified by the condition $\dot{\Omega }=\dot{\Omega }_S$, from a mathematical point of view they can also be identified, in a more general way, by considering $n\rightarrow \infty$ in the condition $nD_n =2\pi /\left| {\dot{\Omega }-\dot{\Omega }_S } \right|$. Thus, by assuming $n\rightarrow \infty$ in the expression , it results .

Similar to the PSSO case, considering only the $J_{2}$ and third body effects, it is possible to find a unique solving polynomial equation for the semi-major axis. Thus, retrieving the term $\cos i$ from Eq. (14) (written with $b_{22} ,b_4 =0$) and substituting it in the coefficients of Eq. (10) leads to the obtaining of an equation formerly analogous to Eq. (12), where in the coefficients $f_{2},\,f_{3},\,f_{5},\,f_{6},\,f_{8}$, it is enough to replace $\dot{\Omega }_S$ with (the other coefficients remain the same).

For assigned values of $e,\,\omega$ and $R/m$, Eq. (12) (with in place of $\dot{\Omega }_S$) provides the semi-major axis. Once retrieved the value of $a$, the inclination of the corresponding PMSSO is obtainable by Eq. (14).

3 Application to Europa

Important applications of the equations found in Sect. 2 are related to the Jupiter’s satellite Europa and this case is investigated in the present Section. Although such equations are general, science orbits at low altitude with the following values of eccentricity and argument of pericentre have been considered: $e = 0.001,\,\omega = 0$. To such a purpose, it is important to remark that, above a certain value of the probe orbit inclination, nearly circular orbits around Europa are associated with reduced life times (collision probe-moon). In particular, taking into consideration only the third body effect, the conditions $i < 39.23^{\circ }$ and $i > 140.77$ guarantee that the orbit keeps quasi-circular (Scheeres et al. 2001; Broucke 2003), while adding the planetary oblateness effect the inclination limit 39.23$^{\circ }$ increases (and the limit 140.77$^{\circ }$ decreases) for increasing values of $J_{2}$. For Europa, the stability ranges are defined by the following relationships: $i < 45^{\circ }$ and $i >135^{\circ }$ (Lara and San Juan 2005), while orbits with inclination between 70 and 110 deg and altitude of about 100 km provide (under reasonable circumstances) life times of approximately 110 days (Lara and Russell 2007).

To solve the equations provided in Sect. 2, the following values for the planetary parameters have been considered: $\mu _P =3202.72\hbox {km}^{3}/s^{2},R_P =1565 \hbox {km},\omega _P =\hbox {2.0478}\cdot \hbox {10}^{\hbox {-5}}\hbox {rad}/\hbox {s}$. The angular velocity of Europa around the Sun shows only small oscillations with respect to the angular velocity of Jupiter around the Sun (the maximum relative angular shift is 0.0494$^{\circ }$) and it is therefore possible to assume that Europa has the same angular velocity as Jupiter (the mean value is $\dot{\Omega }_S =1.6785 \cdot 10^{-8}\hbox {rad}/\hbox {s})$. The values of $J_{2}$ and $J_{4}$ have been set according to the model proposed by Anderson et al. (1998) $\left( {J_2 =4.355\times 10^{-4}, J_4 =0} \right)$.

Figure 2 shows the relative weight (expressed as percentage of the absolute value) of $J_{2}$ and third body (Jupiter) perturbations on the RAAN variation as a function of the semi-major axis, for $i = 45^{\circ }$.

Fig. 2

Relative effect on the RAAN of $\hbox {J}_{2}$ and third body perturbations on nearly circular orbits around Europa

At low altitude, the two contributions are comparable, presenting the same influence for a semi-major axis of about 1747 km. Approximately the same curves have been obtained as the inclination varies, thus highlighting the very weak dependence on $i$ of the relative weight of $J_{2}$ and third body (for $i = 90^{\circ }$ both $\dot{\Omega }_{J2}$ and $\dot{\Omega }_T$ are null, according to Eqs. (1) and (5) respectively).

Similarly, Fig. 3 shows the relative weight of $J_{2}$ and third body perturbations on the argument of latitude.

Fig. 3

Relative effect on the argument of latitude of $\hbox {J}_{2}$ and third body perturbations on nearly circular orbits around Europa

Note that the sum of the two contributions $\dot{\xi }_{J2} +\dot{\xi }_T$ represents only a minimal part of its total variation, being the most part of the effect related to the mean motion $n$ (Keplerian term).

As for $\dot{\xi }_{J2}$, starting from $i = 0$, the curve goes down as the inclination increases, reaching a null value for $i = 63.43^{\circ }$ (critical inclination). In this critical case the curve coincides with the horizontal axis of Fig. 3. Then, as the inclination increases, the curve goes back up to $i = 90\hbox { deg}$, which coincides with the one at $i = 45^{\circ }$. As for the retrograde inclinations, the curves have symmetrical behaviour with respect to $i = 90^{\circ }$ (the curve with $i = 135\hbox { deg}$ coincides with the one related to $i = 45^{\circ }$, and so on).

As for $\dot{\xi }_T$, starting from $i = 0$, the curve goes down as the inclination increases, reaching a null value for $i = 35.26^{\circ }$ (the curve coincides with the horizontal axis of Fig. 3). Then, as the inclination increases, the curve goes back up to $i = 90^{\circ }$. In particular, the curve at $i = 54.75^{\circ }$ coincides with the one at $i = 0$. As for the retrograde inclinations, the curves have a symmetrical behaviour with respect to $i = 90^{\circ }$.

Figures 4 and 5 show repeating ground track orbits at low altitude ($<$335 km), obtained by solving Eq. (10). In particular, Fig. 4 refers to a revisit time $(m)$ of 1 nodal day, Fig. 5 to $m = 5$ nodal days ($R$ and $m$ have to be prime one to the other and therefore the values of $R$ which are multiple of 5 are not admissible).

Fig. 4

Nearly circular orbits with a revisit time of 1 nodal day

Fig. 5

Nearly circular orbits with a revisit time of 5 nodal days

The number $R$ of nodal periods accomplished by the probe goes from 34 to 44 for $m = 1$ and from 166 to 223 for $m = 5$. All these solutions (pairs of $a-i$ values belonging to a curve) allow a cyclic observation of Europa with a high ground spatial resolution and can be selected according to the mission requirements.

As mentioned, in the planetary observation field, the requirements of repeating ground track and synchronism with the Sun are often considered at the same time. To this purpose, Table 1 shows PSSO solutions, gained by solving Eqs. (12) and (13), while Table 2 reports PMSSO solutions with $i < 45^{\circ }$ (stability range), obtained by solving Eqs. (12) and (13) with in place of $\dot{\Omega }_S$. The same Tables show the modulus of the differences, on semi-major axis, $\left| {\Delta a} \right|$, and inclination, $\left| {\Delta i} \right|$, between analytical and numerical results. The numerical simulations have been executed by the Runge–Kutta–Fehlberg 7(8) integrator and by using the same gravitational model (Anderson et al. 1998) as in the polynomial equations, which includes the effects of $J_{2}$ and assumes $J_3 =0,\,J_4 =0,\,C_{22} =1.31\cdot 10^{-4},\,S_{22} =-1.19\cdot 10^{-5}$. Moreover, the effects related to the gravitational attraction of Jupiter, of the main moons (Io, Ganymede, Callisto) and of the Sun have been considered (although only Jupiter has given relevant effects), taking into account the ephemerides of these celestial bodies (JUP230 for Jupiter and its moons, DE421 for the Sun).

In particular, the numerical values of semi-major axis and inclination have been retrieved as follows:

• 1. the polynomial equations have provided the initial values of semi-major axis and inclination;

• 2. the mean values of nodal day and nodal period have been numerically computed, using the above-mentioned gravitational model, and the periodicity and synchronism conditions have been evaluated;

• 3. the semi-major axis and inclination values which satisfy such conditions have been iteratively found;

• 4. the trajectories corresponding to the obtained values of semi-major axis and inclination have been numerically propagated, over several ground track repeat cycles (while the orbit eccentricity keeps stable), so as to verify the stability of the proposed solutions.

Table 1 Comparison between analytical and numerical PSSO solutions $(e = 0.001,\,\omega = 0)$

Table 2 Comparison between analytical and numerical PMSSO solutions $(e = 0.001,\,\omega = 0)$

Tables 1 and 2 show how the results coming from the polynomial equations found in Sect. 2 are close to the ones gained by means of numerical simulations. In fact, the semi-major axis values present differences ranging from 2.08 to 2.45 km, the inclinations concerning the PMSSOs (Table 2) variations of 0.27–0.31$^{\circ }$ and the inclinations of the PSSOs (Table 1) differences of 1.75–1.78$^{\circ }$.

A numerical investigation into the life times of the solutions of Table 1 has also been carried out, as a function of the angle that the intersection between probe orbital plane and plane of the orbit of Europa around Jupiter forms, at the initial instant, with the line joining Jupiter to Europa (angle $\alpha$ in Fig. 6).

Fig. 6

Initial position of the orbital plane with respect to the line Jupiter–Europa

Table 3 Influence of $J_4$ on the values of semi-major axis and inclination

Table 1 (column 7) reports the minimum and maximum values obtained. The results have highlighted that, for all the solutions, the life time presents the highest values in correspondence to four initial positions of the orbital plane. The related values of $\alpha$ depend on the semi-major axis but they are always in the neighborhood ($\pm$5$^{\circ }$) of respectively 45, 135, 225, 315 deg. Moving by only some degrees from these optimal positions, the life times go down to values less than 100 terrestrial days. The obtained results are in accordance with ones presented in Lara and Russell (2007).

3.1 Effects of $\hbox {J}_{4}$

Although the model Anderson et al. (1998) considers a null value for the zonal harmonic $J_{4}$, in order to investigate its influence, fictitious values for this coefficient have been considered. Table 3 shows, for three solutions of Table 1, the absolute variations on semi-major axis $(\left| {\Delta a} \right| )$ and inclination $(\left| {\Delta i} \right| )$, between the results gained using the complete polynomial Eqs. (10) and (11) and the ones obtained using the polynomial equation with only $J_2$ and third body (Eq. 12). Several plausible values of $J_4$ have been taken into account.

The results show that the maximum differences in semi-major axis and inclination, obtained for $J_4 =5\cdot 10^{-5}$, are respectively of the order of 50–60 m and 0.1$^{\circ }$.

Finally, Table 4 reports, for the same solutions of Table 3, the absolute differences $\left| {\Delta a} \right|$ and $\left| {\Delta i} \right|$ obtained considering the system composed of Eqs. (10) and (11) (polynomial equations taking $J_4$ and $J_2 ^{2}$ into account) with respect to the case of numerical simulations carried out introducing in the model Anderson et al. (1998) the considered values for the coefficient $J_4$.

Table 4 Comparison between analytical and numerical results with different values of $J_4$

In conclusion, the results coming from the analytical expressions are close to the ones gained by means of numerical simulations.

4 Conclusions

Polynomial equations able to provide repeating ground track, sun-synchronous, multi-sun-synchronous orbits have been determined. These equations have been obtained taking into account the perturbative effects given by the zonal harmonics of the planetary gravitational field up to $J_4$ and by the gravity gradient related to the presence of a third celestial body that describes, with respect the primary celestial body, a circular orbit lying on the equatorial plane. The polynomial equations have been applied to probes orbiting around Europa and the trajectories have proved to be close to the ones obtainable by numerical simulations.