1 Introduction

In the last decade, the field of aerial robotics has experienced a fast-growing especially for the case of multi-rotor unmanned aerial vehicles (UAVs). High-performance micro-scale processors and high-efficiency sensors have helped to increase the commercial scope of these flying robots. Possibly the most common multi-rotor aerial platform nowadays is the quadrotor. This simple machine which consists of four individual rotors attached to a rigid cross frame has better 3-D mobility than fixed-wing UAVs. Its ability for vertical take-off and landing, for hovering while changing its heading, and for flying ahead or laterally with the possibility of varying its height have opened a wide spectrum of applications ranging from persistent surveillance (Wallar et al. 2015) to interaction with external objects (Orsag et al. 2014). Amongst such applications, aerial load transportation has attracted the attention of several research groups worldwide. Indeed, the quadrotor has become a standard platform for aerial manipulation research thanks to its payload capacity, flight endurance, and low-cost experimentation. Two approaches have been mainly used for transporting the load. The first one consists on equipping the quadrotor with grippers (Ghadiok et al. 2011; Spica et al. 2012; Thomas et al. 2014; Augugliaro et al. 2014), so the load is carried closer to its center of gravity slowing down the response of the vehicle. The second is to connect the payload to the quadrotor by a cable (Beloti Pizetta et al. 2015; Palunko et al. 2012; Faust et al. 2014; Tang and Kumar 2015; Sreenath et al. 2013; Goodarzi and Lee 2015) which preserves its agility, but the cargo swing can affect the flying characteristics of the aerial robot.

This work falls into the problem of transporting cable-suspended loads. In Beloti Pizetta et al. (2015), the movement of the system (quadrotor plus suspended load) is restricted to the XZ plane and a controller based on feedback linearization guides the quadrotor to follow a series of waypoints or a predefined trajectory. Trajectory generation under the assumption of minimal load swing at the end of a transport motion is addressed for example by Palunko et al. (2012). Dynamic programming and a discrete linearized model of the quadrotor-load system are used to compute an optimal trajectory to be executed by the aerial robot. A similar approach is presented in Faust et al. (2014), but a reinforcement learning technique is adopted to generate a swing-free optimal trajectory in a known obstacle-filled environment. The definition and analysis of the hybrid model for the quadrotor plus suspended-load system are introduced for instance by Sreenath et al. (2013) to deal with the case when the tension on the cable goes to zero. In this work, a geometric controller is designed such that local stability properties are achieved. A similar scenario is considered by Tang and Kumar (2015) where a hybrid model is adopted for the quadrotor carrying a cable-suspended load and the trajectory generation problem is formulated as a mixed integer quadratic program. The general assumption of a massless cable is relaxed in Goodarzi and Lee (2015) where the cable connecting the load with the aerial robot is modeled as serially-connected links. Goodarzi and Lee (2015) use geometric control to stabilize the vehicle such that the links are aligned in their vertical position below the quadrotor.

A common assumption when solving the problem of transporting a cable-suspended load using a quadrotor is that the system is always in the air, so the lift of the load from the ground is not generally considered. However, aerial cargo lifting is a fast and efficient way to move materials to locations beyond the practical reach of perimeter cranes. Furthermore, this maneuver is critical before transporting the payload. For example for cargo lifting using helicopters, the vehicle has to be over the load before the helicopter starts to lift according to safety regulations for this type of operations (Construction Safety Association 2000; UK Civil Aviation Authority 2006). To the best of our knowledge, modeling the problem of lifting a cable-suspended load by a quadrotor UAV as a hybrid system has not been discussed in the literature yet. The quadrotor plus cable-suspended load system experiences switching dynamics during the lifting. This switching behavior arises when for instance the cable goes instantaneously from being slack to being taut, i.e., the cable tension jumps from zero to a non-zero value, while the quadrotor is climbing. In addition, the system experiences another state jump when the load is not in contact with the ground anymore. Indeed, this second switching condition has not been considered in the hybrid model introduced in the literature for the cable-suspended aerial transportation system (Tang and Kumar 2015; Sreenath et al. 2013). Due to these transitions, the lift maneuver can be broken down into a collection of simpler discrete states or modes with different dynamics for each one. This decomposition simplifies the planning and control of the overall system. This approach has been successfully applied to perform backflip maneuvers for quadrotors (Gillula et al. 2011) and motion planning of small-scale helicopters (Frazzoli et al. 2005).

In our previous work (Palunko et al. 2012; Faust et al. 2014), we focused on generating a trajectory that reduced the cable-suspended load oscillation while it was transported by the quadrotor. We move a step further in this paper by addressing the problem of lifting the load from the ground until it arrives at the initial position of the swing-free trajectory. We decompose the lift maneuver into modes that characterize the dynamics of the quadrotor-load system at particular operation regimes. Furthermore, we define a hybrid system based on these modes and show that this hybrid model is differentially-flat according to the definition given by Sreenath et al. (2013). This property facilitates the generation of trajectories since a smooth trajectory with reasonably bounded derivatives can be followed by a differentially-flat system (van Nieuwstadt et al. 1994). Therefore, we generate a minimum jerk trajectory using a series of waypoints associated with the modes of the lift maneuver. Then we design a nonlinear controller that enables the tracking of the generated trajectory.

This paper combines and extends our recent work (Cruz et al. 2015; Cruz and Fierro 2014) where we analyzed the lift maneuver decomposing it into simpler hybrid modes. As compared to these works, this paper presents the experimental evaluation of the proposed approach by using a commercially-available micro-scale quadrotor UAV to lift a cable-suspended load from the ground. We have also modified our proposed nonlinear controller (Cruz et al. 2015; Cruz and Fierro 2014) in order to take into account the attitude control loop already provided on the quadrotor.

The rest of this paper is organized as follows. In Sect. 2, we introduce the dynamic models of a quadrotor and of quadrotor carrying a cable-suspended load. The lifting problem addressed in this work is stated in Sect. 3. In addition, we describe in this section the modes into which we decompose the lift maneuver. Using these simpler modes, we define a hybrid model in Sect. 4 where we also demonstrate that it is a differentially-flat hybrid system. This property facilitates the generation of dynamical feasible trajectories for the full system states. We explain our trajectory generation method in Sect. 5. In Sect. 6, we design a cascade controller for trajectory tracking purposes. The system setup and the experimental results are discussed in Sect. 7. Finally, Sect. 8 gives our concluding remarks.

2 Preliminaries

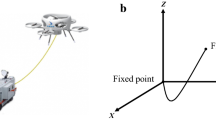
We consider a scenario where a quadrotor has a point-mass load attached by a massless and unstreatchable cable. We assume the cable is attached to the center of mass (CoM) of the quadrotor and the load mass is less than the maximum payload of the quadrotor. Also, we consider that the air drag is negligible.

Figure 1 shows the system together with the inertial coordinate frame \(\lbrace \mathcal {W}\rbrace \), and the body-fixed frame \(\lbrace \mathcal {B}\rbrace \). The origin of \(\lbrace \mathcal {B}\rbrace \) coincides with the CoM of the quadrotor. Based on Fig. 1, we introduce first the following definitions

\(\lbrace \mathbf {x}_\mathcal {W}, \mathbf {y}_\mathcal {W}, \mathbf {z}_\mathcal {W}\rbrace \) :

unit vectors along the axes of \(\lbrace \mathcal {W}\rbrace \),

\(\lbrace \mathbf {x}_\mathcal {B}, \mathbf {y}_\mathcal {B}, \mathbf {z}_\mathcal {B}\rbrace \) :

unit vectors along the axes of \(\lbrace \mathcal {B}\rbrace \) with respect to \(\lbrace \mathcal {W}\rbrace \),

\(m_q \in \mathbb {R}_{> 0}\) :

mass of the quadrotor,

\(\mathbf {J} \in \mathbb {R}^{3\times 3}\) :

inertia matrix of the quadrotor with respect to \(\lbrace \mathcal {W}\rbrace \),

\(\mathbf {r}_q, \mathbf {v}_q \in \mathbb {R}^3\) :

position and velocity of the quadrotor with respect to \(\lbrace \mathcal {W}\rbrace \), \(\mathbf {r}_q = [{x_q y_q z_q}]^T\) and \(\mathbf {v}_q = [{\dot{x}_q \dot{y}_q \dot{z}_q}]^T\),

\(\mathbf {R} \in \text {SO}(3)\) :

rotation matrix from \(\lbrace \mathcal {B}\rbrace \) to \(\lbrace \mathcal {W}\rbrace \),

\({\varvec{\Omega }} \in \mathbb {R}^3\) :

angular velocity of the quadrotor in \(\lbrace \mathcal {B}\rbrace \),

\(F \in \mathbb {R}_{\ge 0}\) :

total thrust produced by the quadrotor,

\(\mathbf {M} \in \mathbb {R}^3\) :

moment produced by the quadrotor,

\(m_l \in \mathbb {R}_{> 0}\) :

mass of the load,

\(\mathbf {r}_l, \mathbf {v}_l \in \mathbb {R}^3\) :

position and velocity of the load with respect to \(\lbrace \mathcal {W}\rbrace \), \(\mathbf {r}_l = [{x_l y_l z_l}]^T\) and \(\mathbf {v}_l = [{\dot{x}_l \dot{y}_l \dot{z}_l}]^T\),

\(\ell \in \mathbb {R}_{>0}\) :

length of the cable,

\(T \in \mathbb {R}_{\ge 0}\) :

tension on the cable.

Fig. 1
figure 1

A quadrotor with an attached cable-suspended load which is lying on the ground. \(\lbrace \mathcal {W}\rbrace \) and \(\lbrace \mathcal {B}\rbrace \) are the inertial and body-fixed coordinate frames, respectively

Full size image

Now, let \(\lbrace \mathbf {u}_1, \mathbf {u}_2, \mathbf {u}_3 \rbrace \) be the three coordinate axis unit vectors without a frame of reference, i.e., \(\mathbf {u}_1=[ 1 0 0]^T\), \(\mathbf {u}_2=[ 0 1 0]^T\) and \(\mathbf {u}_3=[ 0 0 1]^T\), then algebraically \(\mathbf {x}_\mathcal {W} = \mathbf {u}_1, \mathbf {y}_\mathcal {W} = \mathbf {u}_2, \text { and } \mathbf {z}_\mathcal {W} = \mathbf {u}_3\) in \(\lbrace \mathcal {W}\rbrace \). This implies by construction that

$$\begin{aligned} \mathbf {x}_\mathcal {B} = \mathbf {R}\mathbf {x}_\mathcal {W}, \mathbf {y}_\mathcal {B} = \mathbf {R}\mathbf {y}_\mathcal {W}, \text { and } \mathbf {z}_\mathcal {B} = \mathbf {R}\mathbf {z}_\mathcal {W}. \end{aligned}$$
(1)

One of the transitions that the quadrotor-load system experiences during the lift maneuver is the jump of the cable tension T from zero to a nonzero value. This happens when the cable goes instantaneously from being slack to being taut. This transition is known as cable collision (Bisgaard et al. 2009) and because of it, we need to consider the models of the quadrotor without and with a cable-suspended load.

2.1 Quadrotor dynamics

The equations of motion of a quadrotor without carrying any load are the ones defined when just the aerial vehicle is under consideration. Applying the Newton–Euler approach, the dynamics can be written as

$$\begin{aligned} \begin{aligned}&\dot{\mathbf {r}}_q = \mathbf {v}_q,\\&m_q\dot{\mathbf {v}}_q = -m_q g \mathbf {z}_\mathcal {W} + F \mathbf {z}_\mathcal {B},\\&\dot{\mathbf {R}} = \mathbf {R}\hat{{\varvec{\Omega }}},\\&\mathbf {J}\dot{{\varvec{\Omega }}} = -{\varvec{\Omega }} \times \mathbf {J}{\varvec{\Omega }} + \mathbf {M}, \end{aligned} \end{aligned}$$
(2)

where g is the constant gravitational acceleration, and the hat map \(\hat{\cdot }: \mathbb {R}^3 \rightarrow \text {SO}(3)\) denotes the skew-symme- tric matrix defined by the condition that \(\hat{{\varvec{\Omega }}}\mathbf {b} = {\varvec{\Omega }} \times \mathbf {b}\) for the vector cross product of \({\varvec{\Omega }}\) and any vector \(\mathbf {b} \in \mathbb {R}^3\) (Mahony et al. 2012).

2.2 Quadrotor-suspended-load dynamics

When the quadrotor is carrying a cable-suspended load, the cable tension is nonzero. Then, the dynamics of the quadrotor-load system can be easily written down using the tension in the cable

$$\begin{aligned} \begin{aligned}&\dot{\mathbf {r}}_q = \mathbf {v}_q,\\&m_q\dot{\mathbf {v}}_q = -m_q g \mathbf {z}_\mathcal {W} + F \mathbf {z}_\mathcal {B} - T \varvec{\mu },\\&\dot{\mathbf {R}} = \mathbf {R}\hat{{\varvec{\Omega }}},\\&\mathbf {J}\dot{{\varvec{\Omega }}} = -{\varvec{\Omega }} \times \mathbf {J}{\varvec{\Omega }} + \mathbf {M},\\&\dot{\mathbf {r}}_l = \mathbf {v}_l,\\&m_l\dot{\mathbf {v}}_l = -m_l g \mathbf {z}_\mathcal {W} + T \varvec{\mu }. \end{aligned} \end{aligned}$$
(3)

Here, \(\varvec{\mu }\) is the unit vector from the load to the quadrotor. For this system, the quadrotor and load positions are related by

$$\begin{aligned} \mathbf {r}_q = \mathbf {r}_l + \ell \varvec{\mu }. \end{aligned}$$
(4)

3 Lift maneuver

In this section, we first formulate the problem of lifting a cable-suspended load by a quadrotor UAV and then we decompose the lift maneuver into three modes: Setup, Pull and Raise which represent the dynamics of the whole system in specific regimes during the maneuver.

3.1 Problem statement

Starting with the quadrotor hovering at a given altitude not necessarily right on top of the load, see Fig. 1, the goal is to lift the load until it reaches a predefined height denoted as h. Since the quadrotor has attached the cable-suspended load since the beginning, the relative quadrotor-load distance cannot be more than a cable-length apart. Under these conditions, we formulate the lifting problem.

Problem 1

Having a cable-suspended load lying on the ground at the initial position \(\mathbf {r}_{l_0} = \begin{bmatrix} x_{l_0}&y_{l_0}&z_{l_0} \end{bmatrix}^T\) which is attached to a quadrotor UAV hovering at the position \(\mathbf {r}_{q_0} = \begin{bmatrix} x_{q_0}&y_{q_0}&z_{q_0} \end{bmatrix}^T\) such that

$$\begin{aligned} \Vert \mathbf {r}_{q_0} - \mathbf {r}_{l_0}\Vert < \ell , \end{aligned}$$
(5)

the quadrotor has to lift the load until it reaches the final position

$$\begin{aligned} \mathbf {r}_{l_f} = \mathbf {r}_{l_0} + h\mathbf {z}_\mathcal {W}. \end{aligned}$$
(6)

Remark 1

According to (5), the quadrotor does not start right on top of the cable-suspended load with the cable tensioned. However, the aerial robot has to reach and stop at this position before proceeding to lift the load according to safety guidelines for aerial transportation of external payloads (Construction Safety Association 2000; UK Civil Aviation Authority 2006). In fact, the quadrotor can exert the highest lift force when it is right over the load with the cable fully extended. We denote this position as \(\mathbf {r}_{\mathrm{pull}}\) and it is given by

$$\begin{aligned} \mathbf {r}_{\mathrm{pull}} = \mathbf {r}_{l_0} + \ell \mathbf {z}_\mathcal {W}. \end{aligned}$$
(7)

3.2 Lift maneuver modes

The modes of the lift maneuver are sketched in Fig. 2. These modes are Setup, Pull and Raise. We break down the lift maneuver into these simpler modes to characterize the dynamics of the system in specific regimes during the maneuver. This decomposition is due to the jump from zero to nonzero cable tension and because of the load transition from being in contact with the ground to be in the air. The Setup and Pull are modes where the quadrotor gets ready to lift the load, while the Raise mode is where the payload is finally lifted to the final position \(\mathbf {r}_{l_f}\).

Fig. 2
figure 2

The lift maneuver: a Setup, b Pull, and c Raise. The initial state of the system is illustrated in a

Full size image

3.2.1 Setup

From condition (5), the quadrotor starts at an initial position where the cable is not fully extended. Therefore, the cable tension is equal to zero, see Fig. 2a. Due to this condition, the quadrotor and the attached payload can be considered as separate systems. Thus, the dynamics of the aerial vehicle are the ones given in (2), while the load is at rest. Then, the equations of motion for the quadrotor at this mode can be written as

$$\begin{aligned} \begin{bmatrix} \dot{\mathbf {r}}_q \\ \dot{\mathbf {v}}_q \\ \dot{\mathbf {R}} \\ \dot{{\varvec{\Omega }}} \end{bmatrix} = \begin{bmatrix} \mathbf {v}_q \\ -g \mathbf {z}_\mathcal {W} + \frac{F}{m_q} \mathbf {R} \mathbf {z}_\mathcal {W} \\ \mathbf {R}\hat{{\varvec{\Omega }}} \\ \mathbf {J}^{-1} \left( -{\varvec{\Omega }} \times \mathbf {J}{\varvec{\Omega }} + \mathbf {M}\right) \end{bmatrix}. \end{aligned}$$
(8)

Since the load is at rest, \(\mathbf {v}_l = \mathbf {0}\).

The system jumps to the next mode, Pull, when the quadrotor and the load are exactly a cable-length apart, i.e., when the cable is fully extended. We can express this condition as

$$\begin{aligned} \Vert \mathbf {r}_q - \mathbf {r}_l \Vert = \ell . \end{aligned}$$
(9)

For the experimental verification, this condition is assumed as \(\Vert \mathbf {r}_q - \mathbf {r}_l \Vert \ge \ell \) to account errors in the state measurement. When condition (9) holds, the cable jumps from being slack to be taut. This jump, known as cable collision, makes that the positions of the aerial vehicle and the load remain the same, but their change in velocity can be modeled as a perfectly inelastic collision (Bisgaard et al. 2009). For the next derivations, we follow closely the work made by Bisgaard et al. (2009). Any collision, elastic or inelastic, can be modeled using the conservation of momentum. Thus, the relation between translational velocity before and after the impact can be described by

$$\begin{aligned} ^+\mathbf {v}_q= & {} ^-\mathbf {v}_q + \frac{\delta }{m_q} \varvec{\mu } , \text { and} \end{aligned}$$
(10)
$$\begin{aligned} ^+\mathbf {v}_l= & {} ^-\mathbf {v}_l - \frac{\delta }{m_l} \varvec{\mu } , \end{aligned}$$
(11)

where \(\delta \) is the impulse of the collision. Here, the pre-superscript − \((+)\) denotes the situation just before (after) the collision. The relative velocity of the two attachment points on the cable (one in the quadrotor and the other in the load) characterizes an impact by

$$\begin{aligned} -k_e \left( ^-\mathbf {v}_q - {^-\mathbf {v}_l} \right) \cdot \varvec{\mu } = \left( ^+\mathbf {v}_q- {^+\mathbf {v}_l} \right) \cdot \varvec{\mu }, \end{aligned}$$
(12)

where \(k_e \in [0, 1]\) is the elasticity constant such that \(k_e=0\) describes a perfect inelastic collision and \(k_e=1\) describes a perfect elastic collision. The cable collision is modeled as a perfect inelastic collision in order to ensure that \(^+\mathbf {v}_q - ^+\mathbf {v}_l = \mathbf {0}\). Replacing (10) and (11) into (12), the impulse \(\delta \) can be isolated. Since the load is at rest before the perfect inelastic collision, we get

$$\begin{aligned} \delta = -m_q m_l\frac{^-\mathbf {v}_q \cdot \varvec{\mu }}{m_q + m_l}. \end{aligned}$$
(13)

By using (13), one can determine the impulse from the cable collision and then applying (10) and (11), it is possible to compute the states after the transition.

3.2.2 Pull

The cable is fully extended at this mode, so \(T \ne 0\). Even though the cable tension T is not zero anymore, it may not be enough to lift the payload. Therefore, the quadrotor’s equations of motion are given by

$$\begin{aligned} \begin{bmatrix} \dot{\mathbf {r}}_q \\ \dot{\mathbf {v}}_q \\ \dot{\mathbf {R}} \\ \dot{{\varvec{\Omega }}} \end{bmatrix} = \begin{bmatrix} \mathbf {v}_q \\ -g \mathbf {z}_\mathcal {W} + \frac{F}{m_q} \mathbf {R} \mathbf {z}_\mathcal {W} - \frac{T}{m_q} \varvec{\mu }\\ \mathbf {R}\hat{{\varvec{\Omega }}} \\ \mathbf {J}^{-1} \left( -{\varvec{\Omega }} \times \mathbf {J}{\varvec{\Omega }} + \mathbf {M}\right) \end{bmatrix}, \end{aligned}$$
(14)

but its movement is constrained to the sphere with center \(\mathbf {r}_l\) and radius \(\ell \).Footnote 1 This constrain is captured by (9). The load is still at rest, so \(\mathbf {v}_l = \mathbf {0}\) also at this mode.

From the second component in (14), one can find the cable tension during this mode getting

$$\begin{aligned} T = \Vert F \mathbf {R}\mathbf {z}_\mathcal {W} - m_q g \mathbf {z}_\mathcal {W} - m_q \dot{\mathbf {v}}_q\Vert . \end{aligned}$$
(15)

Thus, the total thrust F has to be increased in order to increment the tension on the cable and then lift the load. Once T is slightly over the load weight \(m_l g\), there is enough tension that the cable-suspended load starts being lifted. Therefore, we define the condition

$$\begin{aligned} T > m_lg \end{aligned}$$
(16)

as an indication to jump to the Raise mode. On the other hand, the transition from Pull back to Setup occurs when the cable tension becomes zero, i.e., when the cable returns to be slack. This condition can be expressed as

$$\begin{aligned} T = 0. \end{aligned}$$
(17)

However, we use this condition is modified to \(T < \epsilon \) with \(\epsilon \) small and positive for the experimental implementation.

At this mode, a particular case is to position the quadrotor right on top of the load with the forces acting on the quadrotor-load system perfectly balance. Thus, the whole system is motionless. Because the system is at equilibrium at this particular case, (15) can be reduced to

$$\begin{aligned} T = \Vert F \mathbf {R}\mathbf {z}_\mathcal {W} - m_q g \mathbf {z}_\mathcal {W} \Vert \end{aligned}$$
(18)

3.2.3 Raise

At this stage, the load is in the air with the quadrotor over it with the cable completely taut (Fig. 2c). Thus, the equations of motion are given by the quadrotor-suspended-load dynamics given in (3) from where we get that

$$\begin{aligned} \begin{bmatrix} \dot{\mathbf {r}}_q \\ \dot{\mathbf {v}}_q \\ \dot{\mathbf {R}} \\ \dot{{\varvec{\Omega }}} \\ \dot{\mathbf {r}}_l \\ \dot{\mathbf {v}}_l \end{bmatrix} = \begin{bmatrix} \mathbf {v}_q \\ -g \mathbf {z}_\mathcal {W} + \frac{F}{m_q} \mathbf {R} \mathbf {z}_\mathcal {W} - \frac{T}{m_q} \varvec{\mu } \\ \mathbf {R}\hat{{\varvec{\Omega }}} \\ \mathbf {J}^{-1} \left( -{\varvec{\Omega }} \times \mathbf {J}{\varvec{\Omega }} + \mathbf {M}\right) \\ \mathbf {v}_l \\ -g \mathbf {z}_\mathcal {W} + \frac{T}{m_l} \varvec{\mu } \end{bmatrix}. \end{aligned}$$
(19)

From the last component of (19), it is possible to find the cable tension during this mode obtaining

$$\begin{aligned} T = \Vert m_l \dot{\mathbf {v}}_l + m_l g \mathbf {z}_\mathcal {W}\Vert . \end{aligned}$$
(20)

The cable is fully extended in this mode, so the quadrotor and load positions are related by (4). In addition, the system goes back to the Pull mode when the load is again over the ground with the cable fully taut. We can capture this condition as

$$\begin{aligned} \Vert \mathbf {r}_q - \mathbf {r}_l \Vert = \ell \text { and } \mathbf {v}_{l} = \mathbf {0}. \end{aligned}$$
(21)

Remark 2

Taking into account Remark 1 and Eqs. (18) and (20), the quadrotor has to be positioned on top of the cable-suspended load maintaining a non-zero cable tension greater than the payload weight in order to perform the lifting.

4 Differentially-flat hybrid system

Based on the decomposition of the lift maneuver presented in Sect. 3, we define a hybrid system (see Fig. 3). Following the hybrid automaton representation (Lygeros et al. 2012), we define the hybrid model as the tuple

$$\begin{aligned} \mathcal {H} = (\mathcal {Q}, \mathcal {X}, \mathcal {U}, \mathcal {f}, \mathcal {Dom}, \mathcal {E}, \mathcal {G}, \mathcal {R}, \mathcal {Init}), \end{aligned}$$

where

  • \(\mathcal {Q} = \left\{ \text {Setup, Pull, Raise } \right\} \) is the set of discrete states or modes,

  • \(\mathcal {X} = {\text {SO}}(3) \times \mathbb {R}^{15}\) is the set of continuous states with the state \(\mathbf {x} \in \mathcal {X}\) defined as \(\mathbf {x} = \left\{ \mathbf {r}_q, \mathbf {v}_q, \mathbf {R}, {\varvec{\Omega }}, \mathbf {r}_l, \mathbf {v}_l \right\} \),

  • \(\mathcal {U} = \mathbb {R}^4\) is the set of input variables and we define \(\mathbf {u} = \left[ F \mathbf {M} \right] ^T \in \mathcal {U}\) as the control input of the system,

  • \(\mathcal {f}(\text {Setup }, \mathbf {x}, \mathbf {u})\) given by (8), \(\mathcal {f}(\text {Pull }, \mathbf {x}, \mathbf {u})\) is given by (14), and \(\mathcal {f}(\text {Raise }, \mathbf {x}, \mathbf {u})\) given by (19) are the vector fields,

  • \( \mathcal {Dom}(\text {Setup }) = \left\{ \mathbf {x} \in \mathcal {X} \mid \mathbf {v}_l = \mathbf {0} \text { and } \Vert \mathbf {r}_q - \mathbf {r}_{l} \Vert < \ell \right\} \times \mathcal {U}\), \(\mathcal {Dom}(\text {Pull }) = \left\{ \mathbf {x} \in \mathcal {X} \mid \mathbf {v}_l = \mathbf {0} \text { and } \Vert \mathbf {r}_q - \mathbf {r}_{l} \Vert = \ell \right\} \)

    \(\times \mathcal {U}\), and \( \mathcal {Dom}(\text {Raise }) = \left\{ \mathbf {x} \in \mathcal {X} \mid \Vert \mathbf {r}_q - \mathbf {r}_{l} \Vert = \ell \right\} \times \mathcal {U}\) are the domains,

  • \( \mathcal {E}=\left\{ (\text {Setup, Pull }), (\text {Pull, Setup }), (\text {Pull, Raise }),\right. \)

    \(\left. (\text {Raise },\text {Pull }) \right\} \) is the set of edges,

  • \(\mathcal {G}(\text {Setup, Pull }) = \left\{ \mathbf {x} \in \mathcal {X}, \mathbf {u} \in \mathcal {U} \mid \Vert \mathbf {r}_q - \mathbf {r}_l \Vert = \ell \right\} \),

    \(\mathcal {G}(\text {Pull, Setup }) = \left\{ \mathbf {x} \in \mathcal {X}, \mathbf {u} \in \mathcal {U} \mid T = 0 \right\} \),

    \( \mathcal {G}(\text {Pull, Raise }) = \left\{ \mathbf {x} \in \mathcal {X}, \mathbf {u} \in \mathcal {U} \mid T > m_lg \right\} \), and

    \(\mathcal {G}(\text {Raise, Pull }) = \left\{ \mathbf {x} \in \mathcal {X}, \mathbf {u} \in \mathcal {U} \mid \Vert \mathbf {r}_q - \mathbf {r}_l \Vert = \ell \text { and }\right. \)

    \(\left. \mathbf {v}_l = \mathbf {0}\right\} \) are the guard conditions,

  • the reset map \(\mathcal {R}(\text {Setup, Pull })\) is given by (10) and (11) where \(\delta \) can be found using (13), while we assume that \(\mathcal {R}(\text {Pull, Setup })\), \(\mathcal {R}(\text {Pull, Raise })\), and

    \(\mathcal {R}(\text {Raise, Pull })\) are the identity map, and

  • the set of initial states is \(\mathcal {Init}=\left\{ \text {Setup } \right\} \times \left\{ \mathbf {x} \in \mathcal {X} \mid \right. \)

    \(\left. \mathbf {v}_l = \mathbf {0} \text { and } \Vert \mathbf {r}_{q_0} - \mathbf {r}_{l_0} \Vert < \ell \right\} \).

Fig. 3
figure 3

The lift maneuver represented as a hybrid system. The definitions of its discrete and continuous states, vector fields, domains, edges, guards, and reset maps are given in Sect. 4

Full size image

Notice that the hybrid system \(\mathcal {H}\) has a non-identity reset map only for the transition from Setup to Pull. Also, \(\mathcal {G}(\text {Pull, Setup })\) and \(\mathcal {G}(\text {Pull, Raise })\) are not state-based guard conditions. They depend on the tension value which can be found by (18) for the Pull mode. This hybrid model is an improved version of the one that we introduced in Cruz et al. (2015) for the planar case of the lifting problem. For example, both edges (Pull, Setup) and (Raise, Pull) as well as their guards and reset maps has been added in this paper.Footnote 2

Next, we introduce the definition of differential flatness for the case of a hybrid system. Then, we demonstrate that indeed \(\mathcal {H}\) is a differentially-flat hybrid system.

Definition 1

(Differentially-flat hybrid system) (Sreenath et al. 2013) In general, a system is differen-tially-flat if its state and inputs can be written as functions of the selected outputs and their derivatives. In the case of a hybrid system, each discrete mode has to be differentially-flat with the guards being functions of the flat outputs and their derivatives, and the flat outputs of one mode arise as smooth functions of the flat outputs of the previous mode through the transition or reset map between both modes.

Lemma 1

The hybrid system \(\mathcal {H}\) is a differentially-flat hybrid system.

Proof

First, we show that each discrete mode, Setup, Pull, and Raise, are differentially flat. For the Setup mode, we select \(\mathcal {Y}_\mathrm{setup} = \lbrace \mathbf {r}_q, \psi \rbrace \) as the set of flat outputs where \(\psi \) is the yaw angle of the quadrotor. Notice that the state of the load is always equal to zero in this mode since the load is at rest, so \(\mathbf {v}_l = \mathbf {0}\). Thus, it suffices to show that \(\mathcal {Y}_\mathrm{setup}\) is a set of flat outputs for the quadrotor. Indeed, this has been already proved by Mellinger and Kumar (2011). Therefore, the Setup mode is differentially flat. For the Pull mode, we choose \(\mathcal {Y}_\mathrm{pull} = \lbrace \mathbf {r}_q, \psi \rbrace \) as the set of flat outputs. The load is also motionless at this mode. Thus, based on the same reason as for the previous mode, the Setup mode is also differentially flat. For the Raise mode, we choose \(\mathcal {Y}_\mathrm{raise} = \lbrace \mathbf {r}_l, \psi \rbrace \). The position and velocity of the load can be obtained from \(\mathcal {Y}_\mathrm{raise}\) and \(\dot{\mathcal {Y}}_\mathrm{raise}\). For the quadrotor, we need to show that \(\mathcal {Y}_\mathrm{raise}\) is a set for flat outputs. This has been already proved by Sreenath et al. (2013), so the Raise mode is also differentially flat

We have shown so far that the discrete modes of \(\mathcal {H}\) are differentially-flat. Now, we check the guard conditions. Since \(\mathcal {G}(\text {Setup, Pull })\) and \(\mathcal {G}(\text {Raise, Pull })\) are state-based, both guards are clearly functions of their respectively flat outputs, \(\mathcal {Y}_\mathrm{setup}\) and \(\mathcal {Y}_\mathrm{raise}\), and their corresponding derivatives. The other two guard conditions, \(\mathcal {G}(\text {Pull, Setup })\) and \(\mathcal {G}(\text {Pull, Raise })\), are for the Pull mode and they depend on the cable tension. Indeed, the tension on the cable for this mode can be found applying (18) which depends on \(\mathbf {R}\) and F. As we already showed, these two quantities can be written as functions of the set of flat outputs \(\mathcal {Y}_\mathrm{pull}\) and their derivatives. Hence, the cable tension can be fully determined by knowing \(\mathcal {Y}_\mathrm{pull}\). As a result, the guards \(\mathcal {G}(\text {Pull, Setup })\) and \(\mathcal {G}(\text {Pull, Raise })\) are functions of the set of flat outputs \(\mathcal {Y}_\mathrm{pull}\) and their high-order derivatives.

Finally, the map \(\mathcal {Y}_\mathrm{pull}\) to \(\mathcal {Y}_\mathrm{raise}\) and vice versa are the identity since \(\mathcal {R}(\text {Pull, Raise })\), and \(\mathcal {R}(\text {Raise, Pull })\) are the identity reset map. Similarly, we have for \(\mathcal {Y}_\mathrm{pull}\) to \(\mathcal {Y}_\mathrm{setup}\). For Setup to Pull, the reset map given by (10) and (11) where \(\delta \) can be found using (13) help to do the transition from \(\mathcal {Y}_\mathrm{setup}\) to \(\mathcal {Y}_\mathrm{pull}\).

Consequently, we know for \(\mathcal {H}\) that its discrete modes are differentially-flat, its guards are functions of the selected flat outputs for each mode and their corresponding derivatives, and the selected flat output for every mode arises from the flat output of the previous mode according to the reset maps. Hence by Definition 1, \(\mathcal {H}\) is a differentially-flat hybrid system. \(\square \)

5 Trajectory generation

Building on the results of Sect. 4, we consider a trajectory in the space of flat outputs such as

$$\begin{aligned} \mathcal {Y}(t): [0,t_f] \rightarrow \mathbb {R}^3 \times \mathrm{SO}(2), \end{aligned}$$

where

$$\begin{aligned} \mathcal {Y}(t) = \begin{bmatrix} x_q(t)&y_q(t)&z_q(t)&\psi (t) \end{bmatrix}^T. \end{aligned}$$

Since a change in the yaw angle does not have any effect on the lift maneuver, we assume that \(\psi (t) = 0^\circ \) all the time. Thus, we need to create a trajectory to perform the lift maneuver just for the quadrotor position \(\mathbf {r}_q(t) = [x_q(t) y_q(t) z_q(t)]^T\). Furthermore, minimizing the third or the fourth derivative of the position ensures a smooth trajectory for the quadrotor (Hehn and D’Andrea 2011; Mellinger and Kumar 2011). The third and fourth derivatives of the position are known as jerk and snap, respectively. The minimization of the snap is generally used for tracking fast trajectories employing a geometric controller. Since it is not the case for our application, we employed the jerk as in Hehn and D’Andrea (2011). Next, we present our method to generate an optimal minimum jerk trajectory.

Fig. 4
figure 4

Overview of the trajectory required to execute the lift maneuver

Full size image

Related with each discrete state of the hybrid system, there are reference positions for the quadrotor that can be used to generate a trajectory to execute the lift maneuver. These waypoints are:

  1. 1.

    associated with the Setup mode, the initial position \(\mathbf {r}_{q_0}\) which satisfies condition (5),

  2. 2.

    with the Pull mode, the position \(\mathbf {r}_\mathrm{pull}\) where the quadrotor can exert the highest lift force and it is given by (7), and

  3. 3.

    with the Raise mode, the final position \(\mathbf {r}_{q_f}\) which relates the desired final position of the load with the final position of the quadrotor and it is

    $$\begin{aligned} \mathbf {r}_{q_f} = \mathbf {r}_{l_f} + \ell \mathbf {z}_\mathcal {W}. \end{aligned}$$
    (22)

We consider the second waypoint \(\mathbf {r}_\mathrm{pull}\) as a viapoint between \(\mathbf {r}_{q_0}\) and \(\mathbf {r}_{q_f}\), i.e., a point prior to reach the final quadrotor position. Thus, we generate a trajectory that starts at \(\mathbf {r}_{q_0}\), passes through \(\mathbf {r}_\text {pull}\), and ends at \(\mathbf {r}_{q_f}\) (see Fig. 4). We assume that the aerial vehicle stops at the viapoint \(\mathbf {r}_\text {pull}\) and ends at rest at the final goal point \(\mathbf {r}_{q_f}\). Therefore, we have two segments in our trajectory: from \(\mathbf {r}_{q_0}\) to \(\mathbf {r}_\text {pull}\) and from \(\mathbf {r}_\text {pull}\) to \(\mathbf {r}_{q_f}\), where the quadrotor starts and ends at rest for both cases. Since the generation of the trajectory is identical for both segments and for all the three coordinates, we take as an example the case for \(x_q\), the x-axis component of \(\mathbf {r}_q\). Let \(\mathbf {s}\) be the state defined as

$$\begin{aligned} \mathbf {s} = \begin{bmatrix} s_1&s_2&s_3 \end{bmatrix}^T = \begin{bmatrix} x_q&\dot{x}_q&\ddot{x}_q \end{bmatrix}^T, \end{aligned}$$

then we define the dynamics of \(\mathbf {s}\) as

$$\begin{aligned} \dot{\mathbf {s}} = \begin{bmatrix} s_2&s_3&u \end{bmatrix}, \end{aligned}$$
(23)

with the initial condition \(\mathbf {s}(0) = \left[ x_0 \quad 0 \quad 0\right] ^T\). Notice that \(\dddot{x}_q = \dot{s}_3 = u\) is the jerk. We want to minimize with respect to u the following cost function

$$\begin{aligned} J = \int _0^{t_f} u^2 dt, \end{aligned}$$
(24)

having as final state constraint \(\mathbf {s}(t_f) = \begin{bmatrix} x_f&0&0 \end{bmatrix}^T\). Here, \(t_f\) and \(x_f\) are the desired final time and position, respectively. This constraint has to be satisfied without error, so it is a hard constraint (Stengel 1994; Lewis et al. 2012).

We follow the methodology explained in Lewis et al. (2012) in order to find the solution of our continuous-time optimization problem. The Hamiltonian \(\mathscr {H}\) for our case is

$$\begin{aligned} \mathscr {H} = u^2 + \lambda _1 s_2 + \lambda _2 s_3 + \lambda _3 u, \end{aligned}$$
(25)

where \(\lambda _1, \lambda _2, \lambda _3,\) are the adjoint variables which form the adjoint vector \(\varvec{\lambda } = [\lambda _1 \lambda _2 \lambda _3]^T\). The optimal value of u (denoted as \(u^*\)) can be found by solving

$$\begin{aligned} \begin{aligned} \dot{\mathbf {s}}&= \frac{\partial \mathscr {H}}{\partial \varvec{\lambda }} = \begin{bmatrix} s_2&s_3&u \end{bmatrix}^T,\\ \varvec{\dot{\lambda }}&= -\frac{\partial \mathscr {H}}{\partial \mathbf {s}} = \begin{bmatrix} 0&-\lambda _1&-\lambda _2 \end{bmatrix}^T,\\ 0&= \frac{\partial \mathscr {H}}{\partial u} = 2u + \lambda _3 \end{aligned} \end{aligned}$$
(26)

The last equation in (26) indicates that \(u^* = -\frac{\lambda _3}{2}\), so we need to find \(\lambda _3\) to determine its optimal value. Replacing \(u^*\) into the first equation of (26) yields the state and the adjoint equations

$$\begin{aligned}&\dot{\mathbf {s}} = \begin{bmatrix} s_2&s_3 -\frac{\lambda _3}{2} \end{bmatrix}^T, \text { and}\end{aligned}$$
(27)
$$\begin{aligned}&\varvec{\dot{\lambda }} = \begin{bmatrix} 0&-\lambda _1&-\lambda _2 \end{bmatrix}^T, \end{aligned}$$
(28)

respectively, which have the initial condition \(\mathbf {s}(0) = \left[ x_0 \, 0\, 0\right] ^T\) and the final constraint \(\mathbf {s}(t_f) = \begin{bmatrix} x_f&0&0 \end{bmatrix}^T\). We can solve (28) assuming that we knew the final condition for the adjoint vector \(\varvec{\lambda }(t_f) = [\lambda _{1_f} \lambda _{2_f} \lambda _{3_f}]^T\). Using this solution and replacing it in (27), we can find the state trajectories which yields

$$\begin{aligned} s_1&= x_q = -\frac{\lambda _{1_f}}{240} t^5 + \frac{\lambda _{1_f}t_f + \lambda _{2_f}}{48} t^4 - \frac{k}{24} t^3 + x_0,\nonumber \\ s_2&= \dot{x}_q = -\frac{\lambda _{1_f}}{48} t^4 + \frac{\lambda _{1_f}t_f + \lambda _{2_f}}{12} t^3 - \frac{k}{8} t^2,\nonumber \\ s_3&= \ddot{x}_q = -\frac{\lambda _{1_f}}{12} t^3 + \frac{\lambda _{1_f}t_f + \lambda _{2_f}}{4} t^2 - \frac{k}{4} t, \end{aligned}$$
(29)

where \(k = \lambda _{1_f} t_f^2 + 2 \lambda _{2_f} t_f + 2 \lambda _{3_f}\) and the final conditions for the adjoint variables \(\lambda _{1_f}, \lambda _{2_f}\) and \(\lambda _{3_f}\) are given by

$$\begin{aligned} \begin{bmatrix} \lambda _{1_f} \\ \lambda _{2_f} \\ \lambda _{3_f} \end{bmatrix} = \begin{bmatrix} -\frac{t_f^2}{40}&\quad -\frac{t_f}{16}&\quad -\frac{1}{12}\\ -\frac{t_f^2}{16}&\quad -\frac{t_f}{6}&\quad -\frac{1}{4}\\ -\frac{t_f^2}{12}&\quad -\frac{t_f}{4}&\quad -\frac{1}{2} \end{bmatrix}^{-1} \begin{bmatrix} \frac{x_f - x_0}{t_f^3} \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$
(30)

By applying (29) for each coordinate and for each path segment, we generate the minimum jerk reference trajectory \(\mathbf {r}_q^\mathrm{ref}\) whose first and second derivatives are denoted as \(\mathbf {v}_q^\mathrm{ref}\) and \(\mathbf {a}_q^\mathrm{ref}\), respectively. Tracking this trajectory, we can execute the lift maneuver. In the next section, we design the controller to accomplish this goal.

6 Control design

The quadrotor UAV that we use for experimental validation (Sect. 7) is the “AscTec Hummingbird” (Ascending Technologies 2015). This aerial vehicle is equipped with linear acceleration sensors, gyroscopes measuring the angular velocities, a triple-axial compass module, motor drivers, and a flight control unit (FCU), the “AscTec Autopilot” (Ascending Technologies 2010). This FCU reads sensor data, computes angular velocities and angles in all axes (roll, pitch and yaw), and runs an attitude controller at a rate of 1 kHz sending the desired speed for each motor to the respective driver. Furthermore, the FCU is designed to received attitude (roll and pitch angles), yaw-rate, and thrust commands through a wireless serial link which enables the autonomous control of the quadrotor. In fact, this attitude controller has been extensively tested in a variety of applications (Ascending Technologies 2010; Gurdan et al. 2007; Achtelik et al. 2011).

Fig. 5
figure 5

Block diagram of the cascade control loops: inner attitude control and outer position control

Full size image

We use a cascade control structure that is shown in Fig. 5. As inner loop, the attitude controller provided in the FCU is employed whereas that the outer loop is the position controller. The input commands for the inner loop are desired roll \(\phi \) and pitch \(\theta \) angles, desired yaw rate \(\dot{\psi }\), and desired thrust F. We denote this control input as \(\mathbf {\Upsilon } = [\phi \theta \dot{\psi } F]^T\). The output of the attitude controller are the commanded rotational velocities of the four rotors denoted as \(\varvec{\omega } = [\omega _1 \omega _2 \omega _3 \omega _4]^T\) in Fig. 5. This attitude control loop delivered with the FCU is a black box for the user, so it is not focus of this paper. Please refer to (Ascending Technologies 2010; Gurdan et al. 2007) for a complete discussion about this controller.

For the position control loop, we implement it by applying nonlinear dynamic inversion (Isidori 1995; Wang et al. 2011). Having an adequate knowledge of the plant dynamics, this method transforms the nonlinear system into a linear system without any simplification through suitable control inputs. As a result, standard linear controllers can be then applied. This also aligns well with the differential flatness property shown in Lemma 1. We can perform linear control strategies, like a PD controller, by choosing pseudo control commands in the space of the flat outputs and their derivatives, and finally turning those into desired input commands (Achtelik et al. 2011).

Based on the vector fields defined for each state of the hybrid system \(\mathscr {H}\) (Sect. 4), the translation dynamics of the quadrotor can be expressed as

$$\begin{aligned} \mathbf {a}_q = \frac{1}{m_q}F\mathbf {R}\mathbf {u}_3 - g\mathbf {u}_3 - \frac{1}{m_q}T\varvec{\mu }, \end{aligned}$$
(31)

where \(\mathbf {a}_q\) is the acceleration of the quadrotor, i.e., \(\mathbf {a}_q = \dot{\mathbf {v}}_q = \ddot{\mathbf {r}}_q\), and

$$\begin{aligned} T = \left\{ \begin{array}{cl} 0 &{} \quad \text {for the Setup mode},\\ \Vert F \mathbf {R} \mathbf {z}_\mathcal {W} - m_q g \mathbf {z}_\mathcal {W}\Vert &{}\quad \text {for the Pull mode},\\ \Vert m_l \dot{\mathbf {v}}_l + m_l g \mathbf {z}_\mathcal {W}\Vert &{} \quad \text {for the Raise mode}. \end{array} \right. \end{aligned}$$
(32)

In (31), the attitude angles \(\phi \), \(\theta \), and \(\psi \) are encoded in \(\mathbf {R}\) which is the rotation matrix from the body-fixed frame \(\{\mathcal {B}\}\) and the inertial frame \(\{\mathcal {W}\}\). The rotation sequence \(Z-X-Y\) is generally used to model this rotation (Mahony et al. 2012; Mellinger and Kumar 2011), so the rotation matrix is given by

$$\begin{aligned} \mathbf {R} = \begin{pmatrix} c \psi c \theta - s \phi s \psi s \theta &{}\quad -c \phi s\psi &{}\quad c \psi s \theta + c \theta s \phi s \psi \\ c \theta s \psi + c \psi s \phi s \theta &{}\quad c\phi c\psi &{}\quad s \psi s \theta - c \psi c \theta s \phi \\ -c\phi s\theta &{}\quad s\phi &{}\quad c\phi c\theta \end{pmatrix}, \end{aligned}$$
(33)

where c and s are shorthand forms for cosine and sine, respectively. As we indicated in Sect. 5, a change in the yaw angle \(\psi \) does not have any effect on lifting the load since it is attached at the CoG of the quadrotor. Therefore, we assume that this angle is kept all the time equal to zero, i.e., \(\psi = 0^\circ \) and \(\dot{\psi } = 0 ^\circ /s\). Replacing (33) in (31) and making \(\psi = 0^\circ \), \(\mathbf {a}_q = [\ddot{x}_q \ddot{y}_q \ddot{z}_q]^T\), and \(T\varvec{\mu } = [\tau _z \tau _y \tau _z]^T\) yields that

$$\begin{aligned} m_q \begin{bmatrix} \ddot{x}_q \\ \ddot{y}_q \\ \ddot{z}_q \end{bmatrix} = \begin{bmatrix} F s \theta - \tau _x \\ -F c \theta s \phi - \tau _y \\ F c \theta c \phi - m_q g - \tau _z \end{bmatrix}. \end{aligned}$$
(34)

Solving (34) for the controls of the system \(\theta \), \(\phi \) and F, we get

$$\begin{aligned} \begin{aligned} \theta&= \arcsin \frac{m_q \ddot{x}_q + \tau _x}{F},\\ \phi&= - \arctan \frac{m_q \ddot{y}_q + \tau _y}{m_q \ddot{z}_q + m_q g + \tau _z},\\ F&= \sqrt{f_x^2 + f_y^2 + f_z^2}. \end{aligned} \end{aligned}$$
(35)

Here, \(f_x = m_q \ddot{x}_q + \tau _x\), \(f_y = m_q \ddot{y}_q + \tau _y\), and \(f_z = m_q \ddot{z}_q + m_q g + \tau _z\). From (35), we can find the control input \(\mathbf {\Upsilon } = [\phi \theta 0 F]^T\) for the inner attitude loop based on the desired acceleration for the quadrotor \(\mathbf {a}_q = [\ddot{x}_q \ddot{y}_q \ddot{z}_q]^T\). Consequently, we take \(\mathbf {a}_q\) as our pseudo control input. Since we can only command the second derivative of the quadrotor’s position, a reference trajectory to track has to be sufficiently smooth. We achieve this in Sect. 5 by minimizing the jerk, so we guarantee that the third derivative of the quadrotor’s reference position exists. We compute the pseudo control input by the following linear error controller

$$\begin{aligned} \mathbf {a}_q = \mathbf {a}_q^\mathrm{ref} + \mathbf {K}_\mathrm{v} (\mathbf {v}_q^\mathrm{ref} - \mathbf {v}_q) + \mathbf {K}_\mathrm{p} (\mathbf {r}_q^\mathrm{ref} - \mathbf {r}_q), \end{aligned}$$
(36)

with \(\mathbf {K}_\mathrm{v}\) and \(\mathbf {K}_\mathrm{p}\) being diagonal gain matrices. According to (36), position and speed control are performed by the outer control loop.

Since the load is at rest during two of the three modes of the hybrid model, we have considered mainly the state of the quadrotor for generating the trajectory and for finding the control inputs. Notice the quadrotor and load position during the Raise mode, the only mode where the load is not at rest anymore, are related by (4). A possible modification is to switch to a controller that explicitly accounts for the load state in the Raise mode for instance to reduce residual load swing (Palunko et al. 2012).

Fig. 6
figure 6

a The quadrotor with the cable-suspended payload employed for experimental verification. b The system architecture and its communication links at the Marhes Lab. c General structure of the system architecture components as used for controlling the aerial vehicle

Full size image

7 Experimental verification

7.1 System setup

To validate the proposed method for lifting a cable-suspended load by a quadrotor, we conducted a series of experiments using an AscTec Hummingbird quadrotor (Ascending Technologies 2015) that is part of the robotic testbed of the Marhes Lab at the University of New Mexico (UNM).Footnote 3 The quadrotor with the attached cable-suspended load is shown in Fig. 6a. The Hummingbird quadrotor is 0.54 m in diameter, weighs approximately 500 g including its battery, and has a maximum payload of 200 g. The load is a ball with 0.076 m in diameter and weighs 178 g. This load is suspended from a 1 m long cable.

The system architecture implemented at the Marhes Lab to perform the experimental tests is illustrated in Fig. 6b. This figure also shows the communication links between the system components. The attitude and position of the aerial vehicle and the load are provided by a motion capture system with millimeter accuracy running at 100 Hz. The entire control application is implemented in LabVIEW where we created two programs: user interface and quadrotor interface. The first one runs on a windows-based computer while the second is deployed in a national instrument (NI) CompactRIO (cRIO) real-time controller (National Instruments 2016b). The general structure of these two interfaces is shown in Fig. 6c. The arrows in this figure illustrate the flow of information to implement the cascade control scheme depicted in Fig. 5.

The User Interface program acquires the pose data of the quadrotor and the position data of the suspended load, applies the numeric differentiation algorithm detailed in Al-Alaoui (2008) for velocity and acceleration estimation, and generates the lift trajectory using the methodology explained in Sect. 5. The quadrotor interface program reads the actual position, velocity and attitude data from the User Interface program as well as the generated reference trajectory (position and velocity). It filters high-frequency noise from the actual values by using a low-pass fifth-order finite impulse response (FIR) filter. Subsequently, it computes the input commands for the onboard attitude controller according to the control design detailed in Sect. 6, and then these commands are transmitted to the quadrotor. Since the User Interface program acquires and estimates the state of the quadrotor and the load, we are able to apply (32) as part of the quadrotor interface program for finding the tension in the cable during the experiments. The User Interface and the quadrotor interface are executed at 1 kHz since we employ the LabVIEW real-time (RT) Module to implement them. This module compiles and optimizes the LabVIEW graphical code for executing RT control applications (National Instruments 2016a). More details about the robotic testbed and the control architecture at the Marhes Lab are presented in Bezzo et al. (2014). In particular, the trajectory tracking performance of the controller developed in LabVIEW for performing swing-free maneuvers carryng the cable-suspended load is presented in Palunko et al. (2012).

Fig. 7
figure 7

Z-axis position a and velocity b for the quadrotor during the first experiment. In this experiment, the aerial vehicle is commanded to lift the cable-suspended load to a desired height \(h = 1\) m. Approximately at 4.8 s, the system jumps from Setup to Pull and approximately at 6.8 s from Pull to Raise. These time instants are highlighted by the dashed vertical lines

Full size image

7.2 Results

We report three sets of experiments to demonstrate the validity of the proposed method. A video of these experiments can be found as supplementary material of this paper and it is also available in MARHES LAB (2016).

Fig. 8
figure 8

Performance data results for the first experiment. Trajectory tracking errors for the quadrotor, a position and b velocity errors. c Position error of the cable-suspended load with respect to its desired final position \(\mathbf {r}_{l_f} = [0 \; 0 \; 1]^T\) m

Full size image
Fig. 9
figure 9

Experimental results for a no switching controller. a Desired and actual Z-axis position for the quadrotor. b Desired and actual Z-axis velocity for the quadrotor. c Position error for the load. The dashed vertical lines highlight the time instants when the system switches from Setup to Pull and from Pull to Raise

Full size image
Fig. 10
figure 10

Experimental results for a trajectory generated without considering the via point \(\mathbf {r}_\mathrm{pull}\). a Desired and actual Z-axis position for the quadrotor. b Desired and actual Z-axis velocity for the quadrotor. c Position error for the load. The dashed vertical lines highlight the time instants when the system switches from Setup to Pull and from Pull to Raise

Full size image

In the first experiment, we run the lift maneuver of the load to the desired height of 1 m. Based on the initial positions of the quadrotor and the load, the reference lift trajectory is generated and then we command the aerial vehicle to execute it. The initial positions for the CoM of the load and the aerial robot are \(\mathbf {r}_{l_0} = [0 \; 0 \; 0.038]^T\) m and \(\mathbf {r}_{q_0} = [-0.5 \; 0.5 \; 0.5]^T\) m, respectively. The time allowed for the first trajectory segment (from \(\mathbf {r}_{q_0}\) to \(\mathbf {r}_\mathrm{pull}\)) is 4 s and for the second segment (from \(\mathbf {r}_\mathrm{pull}\) to \(\mathbf {r}_{q_f}\)) is 8 s, with a rest time of 1 s between segments. Figure 7 shows the Z-axis trajectory tracking data for the quadrotor, position \(z_q\) and velocity \(\dot{z_q}\). Approximately at 4.8 s, the guard condition (9) is satisfied making the system jump from Setup to Pull. We draw a dashed vertical line at this time instant in Fig. 7. Subsequently, the system switches between Pull and Setup having as result a series of spikes in \(\dot{z}_q\) before the system stays at the Pull mode, see Fig. 7b. The system then jumps from Pull to Raise since the guard condition \(T > m_l g\) holds. This occurs when the elapsed time is approximately 6.8 s. Similarly as before, this time instant is also pointed up by a dashed vertical line in Fig. 7. In order to verify the performance of executing the lift maneuver, we compute the following errors:

  • the quadrotor position error \(\mathbf {e}_{\mathbf {r}_q} = \mathbf {r}_q^\mathrm{ref} - \mathbf {r}_q\),

  • the quadrotor velocity error \(\mathbf {e}_{\mathbf {v}_q} = \mathbf {v}_q^\mathrm{ref} - \mathbf {v}_q\), and

  • the load position error \(\mathbf {e}_{l} = \mathbf {r}_{l_f} - \mathbf {r}_l\).

The first two errors show the trajectory tracking control performance while the last one is the error of the load position with respect to its desired final height. These errors for the first experiment are shown in Fig. 8. The time instants at when the system jumps from Setup to Pull and from Pull to Raise indicated in Fig. 7 are also underlined in each plot of this figure. The X-axis position error for the quadrotor is less than 0.05 as well as for the Y-axis, but this error is less than 0.03 m for the Z-axis, see Fig. 8a. For the velocity errors, Fig. 8b, they are less than 0.09 m/s for the X and Y axes. This is also the case almost all the time for the Z-axis component except at the instant that the system switches between Setup and Pull. Because the Z-axis velocity experiences a series of spikes during these jumps, see Fig. 7b, the error increases having as maximum 0.18 m/s. From Fig. 8c, the load position errors \(e_{x_l}\) for the X-axis and \(e_{y_l}\) for the Y-axis are both less than 0.1  Meanwhile, \(e_{z_l}\), the load position error for Z-axis, decreases after the system reaches the Raise mode and it is less than 0.05 m at the end of the lift maneuver.

In the second experiment, we study the effect of not considering the hybrid nature of the system for control purposes. Notice that the controller designed in Sect. 6 has a switching behavior since the cable tension T used to find the pseudo control input \(\mathbf {a}_q\) has a different value depending on the mode of the lift maneuver. Indeed, T is given by (32) for the proposed controller. We carry out again the experiment of lifting the load to 1 m, but we set \(T = m_l g\) for computing \(\mathbf {a}_q\) during the entire maneuver. Thus, we do not use (32) for this second experiment. Figure 9 shows the results for \(z_q\), \(\dot{z}_q\), and \(\mathbf {e}_{\mathbf {r}_l}\) . Similarly as for the first experiment, the system jumps from Setup to Pull approximately at 4.8 s. However, the transition from Pull to Raise occurs approximately at 10 s. Indeed, there is a considerable delay on continuing tracking the trajectory (position and velocity) as it can be seen in Fig. 9a, b. This delay causes a transient, especially for \(\dot{z}_q\). For the load position error illustrated in Fig. 9c, it is less than 0.1 m and 0.2 m for the X and Y-component, respectively. Meanwhile, it is less than 0.1 m at the end of the maneuver for the Z-axis. This experiment shows that even though the maneuver can be executed, the performance diminishes when the switching behavior of the quadrotor-suspended-load system is not under consideration for controlling the aerial vehicle.

Fig. 11
figure 11

Comparison of the results for the three experiments reported in Sect. 7.2. These experiments are: load lift applying the full proposed approach (blue solid line), load lift without using a switching controller (red dashed line), and load lift without considering the viapoint during the trajectory generation (yellow dash-dot line). a x-component of the load position error. b y-component of the load position error. c z-component of the load position error. d The total thrust F found by (35) and applied as part of the control signals to the system (Color figure online)

Full size image

For the third experiment, we generate the lift trajectory without using the via point \(\mathbf {r}_\mathrm{pull}\). Therefore, the trajectory just has one segment which goes from \(\mathbf {r}_{q_0}\) to \(\mathbf {r}_{q_f}\) with a total duration time of 12 s. We use the proposed controller without any modification as it was the case for the second experiment. The results for this case are shown in Fig. 10. The system goes from Setup to Pull approximately at 6 s, while it goes from Pull to Raise approximately at 6.8 s. There is a small delay on tracking the Z reference position after the load is starting to be lifted, see Fig. 10a. This delay creates an oscillation in the Z-axis velocity component reaching a maximum of 0.6 m/s, see Fig. 10b. For the position error of the load, Fig. 10c, there is a short swing in the X and Y components right after the quadrotor starts to lift the load. As a result, the error reaches a maximum of 0.5 m and 0.25 m for \(e_{x_l}\) and \(e_{y_l}\), respectively. At the end of the maneuver, \(e_{z_l}\) is less than 0.1 m. Although the load lift starts at a similar time instant that the one for the first experiment, the errors for the load position are higher when the via point \(\mathbf {r}_\mathrm{pull}\) is not considered for generating the trajectory to lift the cable-suspended load.

In the last part of the video provided as supplementary material for this paper and available also in MARHES LAB (2016), we show side by side the three experiments for comparison purposes. Furthermore, Fig. 11 shows side by side \(\mathbf {e}_{l} = \begin{bmatrix} e_{x_l}&e_{y_l}&e_{z_l} \end{bmatrix}^T\), the load position error, for the three experimental cases. Also, the total thrust F for the three experiments are plotted on the same axis in Fig. 11d. F is part of the control inputs of the system and it is found by applying (35). The plots in Fig. 11 help to compare and contrast the results for the three experiments: load lift applying the full proposed approach, load lift without using a switching controller, and load lift without considering the viapoint during the trajectory generation. From the x and y position error plots, Fig. 11a, b, the full proposed strategy performs better than the other two cases. The swing in the cable-suspended payload is less when the proposed approach is applied. Moreover, these oscillations are considerable when the viapoint is not part of the generation of the trajectory. With respect to \(e_{z_l}\) plotted in Fig. 11c, the quadrotors starts lifting the load earlier when the viapoint \(\mathbf {r}_\text {pull}\) is not employed. However, no considering this point causes a higher swing of the load as we indicated before. This effect is mainly because there is not enough time for performing adequately the pull of the load. Therefore, it is important to include and plan the Pull mode into the lift maneuver. About the control input F shown in Fig. 11d, it is clear that a more control effort is required when the full proposed approach is not applied. It takes more time to increase the thrust F to create enough tension to lift the load when no switching controller is employed. Indeed, this delay increases the time that the system stays in the Pull mode, see Fig. 9c. This effect translates on taking more time to start lifting the load as can be seen in Fig. 11c.

8 Conclusions

Lifting a cable-suspended load by an aerial vehicle is an essential step before transporting it. We introduced a novel methodology to perform this maneuver using a quadrotor. We designed a hybrid system that captures specific operating regimes of the quadrotor-suspended-load system during the maneuver. In particular, we proved that this system is a differentially-flat hybrid system. Taking advantage of this property, we generated a dynamically feasible trajectory based on the discrete states of the hybrid system. We designed a non-linear hybrid controller to track this trajectory which in turn carried out the lifting maneuver. We presented experimental results illustrating the effectiveness of our method. Significant improvement in tracking performance and reducing the load position error with respect to the final desired height were achieved when the hybrid modes were considered for generating the trajectory and controlling the aerial vehicle.

The transitions between modes could involve chattering. Indeed, this effect can be observed in Figs. 8b and 9b. However, it is not considerable because the weight and size of the load may not be enough to increase this chattering. Possibly, an adequately planning of the time intervals for the trajectory segments could help to reduce this effect if it is necessary.

Important topics for future work include the implementation of a system mass estimator in order to execute the maneuver even without knowing the payload mass, and the extension of the hybrid model to address the maneuver of placing the cable-suspended load over the ground. This step is also critical in aerial cargo transportation. Another path to take is to study and implement cooperative lifting using multiple quadrotors. Non-uniform and heavier cable-suspended loads can be manipulated since each aerial vehicle can apply a tension force to different attachment points in the load.