Modelling and control of a spatial dynamic cable

Abstract

We study the problem of dynamically controlling the shape of a cable that is fixed at one end and attached to an actuated robot at another end. This problem is relevant to unmanned aerial vehicles (UAVs) tethered to a base. While rotorcrafts, such as quadcopters, are agile and versatile in their applications and have been widely used in scientific, industrial, and military applications, one of the biggest challenges with such UAVs is their limited battery life that make the flight time for a typical UAVs limited to twenty to thirty minutes for most practical purposes. A solution to this problem lies in the use of cables that tether the UAV to a power outlet for constant power supply. However, the cable needs to be controlled effectively in order to avoid obstacles or other UAVs. In this paper, we develop methods for controlling the shape of a cable using actuation at one end. We propose a discrete model for the spatial cable and derive the equations governing the cable dynamics for both force controlled system and position controlled system. We design a controller to control the shape of the cable to attain the desired shape and perform simulations under different conditions. Finally, we propose a quasi-static model for the spatial cable and discuss the stability of this system and the proposed controller.

1 Introduction

1.1 Background and motivation

As the technology of unmanned aerial vehicles (UAVs) develops at a rapid pace, the applications of UAVs are greatly diversifying. Nowadays, the applications of UAV have expanded to commercial, scientific, agricultural, and other areas. It plays an important role in aerial photography, surveillance, agriculture and so on.

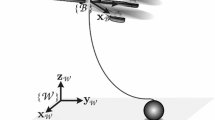
Rotorcrafts, such as quadcopters are agile, can hover in place and can operate in cluttered environments. Such UAVs are usually battery powered, and due to the high power consumption, the flight time of a typical UAV is limited to a less than an hour. Thus, for some applications it is desirable that the UAVs be tethered to a base using a wire or a cable for power supply and high-speed communication (Fig. 1a). The wired UAVs do have longer battery life and can work for longer time, which is a big advantage. However the cable limits the motion of the UAV. When obstacles appear, the cable may be blocked by the obstacles restricting the UAV’s motion. Adjusting the position of UAV manually is a slow and ineffective way to let the cable dodge the obstacles. Instead, it may be desirable to control the shape of the cable using motion of the UAV that would allow it to dodge the obstacles.

Motivated by this application, we develop a method for controlling the shape and position of the cable using the motion of the UAV attached to it. One end of the cable is fixed at a base (e.g. a power outlet or communication base) and the other end is connected to the UAV (Fig. 1b). The cable deforms under the effects of gravity and UAV adjusts the position of cable by applying forces/impulses or by adjusting the position of the end of the cable that it is connected to. At its core this is an under-actuated system with high degrees of freedom (the flexible cable) but only limited controllability (force or position control of its end). Thus our controller is able to achieve the desired shape only approximately (often with a periodicity in the error from the desired shape as demonstrated by our simulation results). However, simulations demonstrate the effectiveness of the controller in attaining a desired shape and we also provide theoretical guarantees on convergence under a quasi-static assumption.

Fig. 1

Tethered UAV. a An UAV tethered to a base, b cable in three dimensions

1.2 Literature review

There has been little to no prior research in tethered UAVs. However, there has been multiple studies on the modeling and simulation of a cable, very few of which however explicitly consider the problem of controlling its shape.

Goriely and McMillen [1] studied the shape of a cracking whip, in which they built a dynamical model for the propagation and acceleration of waves in the motion of whips. Also, the respective contributions of tension, tapering, and boundary conditions in the acceleration of an initial impulse are studied theoretically and numerically.

Koh and Rong [2] presented the dynamic analysis of three-dimensional cable motion, accounting for axial, flexural and torsional deformations as well as geometric non-linearity due to large displacements and rotations. They developed the analytical formulation and numerical strategy. A specific problem of cable motion due to support excitation was used to illustrate the numerical scheme and then validated the accuracy of the numerical results by the shaking table tests. Jimenez et al. [3] studied the motion of a rope falling from a table using Newtonian and canonical methods to analyze the problem.

Breukels and Ockels [4] studied the model of the cable with which the kite is attached to the ground in order to build the fully dynamic simulation of kites. They only considered the slow modes of motion and focused on the damping. The relation between aerodynamic damping and material-based damping was investigated.

Fritzkowski and Kaminski [5] conducted two studies on modeling a rope as a rigid multibody system. They considered the discrete model of a rope as a scleronomic and a rheonomic system. They also performed numerical experiments and discussed the advantages of the applied algorithm on the basis of energy conservation. In their later study, Fritzkowski and Kaminski [6] presented a discrete model of a rope to simulate the planer motion of the rope fixed at one end. They presented two systems, whose members are rigid but non-ideal joints involve elasticity or dissipation. Recently, Williams [7] proposed a lumped-mass discrete model of cable that allows fast and efficient dynamic simulation of quasi-static rope models.

Papacharalampopoulos et al. [8] proposed a method for the estimation of the cables shape for robotic manipulation, which took into account the mechanical behaviour of materials. In the framework of static analyses, a higher-order analytic model of cables is introduced and the need for model calibration is pointed out. Along similar lines, Tonapi et al. [9] developed a continuum model for a cable-like manipulator and studied forward and inverse kinematics of the system.

Most of the above mentioned researches deal with representation and modeling of ropes to understand their physics better with little or no consideration for control of the shape of the rope. There has been some sparse research in controlling shape of a cable. Matsuno and Fukuda [10] described configurations of ropes using a topological models and knot theory. They also proposed a method to reconstruct the structure of a rope from sensor information through charge coupled device (CCD) cameras when a robot manipulates it and used that to perform slow manipulation experiments. In an analogous approach, Takizawa et al. [11] used robotic manipulators for designing manipulation actions for the purpose of tying a knot in a quasi-static cable with the help of support from a table/platform. Nair et al. [12] proposed a learning based approach for rope manipulation. Their robot could manipulate a static rope in two dimensions into target configurations. In a similar work, Wang et al. [13] described a control strategy based on a hybrid intelligent optimization algorithm for planar n-link underactuated manipulator.

In this paper, we however consider highly dynamic rope shape manipulation with potentially high inertial forces, gravity and drag forces. Furthermore we do not have a means of grabbing a rope in the middle (as is possible with a robotic manipulator), and instead have an underactuated system in which the only control inputs possible are the forces exerted by the robot at the free end of the cable. We however do not consider topological complexities such as knots.

Bhattacharya et al. [14] studied the problem of shape control of a planar cable using robots attached to its two ends in context of oil skimming and cleanup operations. They built a discrete model for the rope and simulated in two dimensions, where drag forces were considered. Additionally, they studied a quasi-static model and developed a shape controller based on it. In this paper, we extend the model to three spatial dimensions and thus propose shape controller for a highly dynamic model (as opposed to a quasi-static model). We also use a quasi-static model for theoretical analysis under some special conditions.

While there has been research in the area of controlling under-actuated systems such as steering of a flexible needle [15] and control of a compliant robotic manipulator [16], such systems by design or by environmental influence have higher controllability or stability. A flexible cable, on the other hand, is significantly more dynamic and difficult to control.

1.3 Overview of the paper

In this paper, we first develop a discrete dynamic model of a cable and demonstrate its performance in simulation with force and position control of the free end of the cable. We then develop a shape controller for the cable using the motion of the end as the input and evaluate the proposed controller in simulations. Finally, we also provide theoretical guarantees on the stability of the controller on a quasi-static simplification of the dynamic model.

2 Discrete dynamic model

2.1 Force controlled system

We propose an approximate discrete model. The spatial cable is represented by n rigid cylindrical segments connected to each other by spherical joints. One end of the cable is attached to a fixed base, while the other end is controlled.

In this section, we assume that external input quantities are the forces applied at the free end of the cable, donated by the vector $\begin{bmatrix} f_x\, f_y\, f_z \end{bmatrix}^\mathrm{T}$. This system has 2n degrees of freedom (rotation of an individual segment along its axis, while keeping all the segments in place is ignored and thus do not contribute to any inertial term, nor increase degrees of freedom). As shown in Fig. 2, we choose the polar angles of each of the n segments as the generalized coordinates—$\phi _i$ is the angle made by the i-th segment with the positive Z axis (the latitudinal angle), while $\theta _i$ is the angle made by the projection of the segment on the XY plane with the positive X axis (the longitudinal angle)—all with respect to a global inertial frame of reference (see Fig. 2b).

Fig. 2

Discrete dynamic model. a A discrete dynamic model consisting of n rigid segments, b the i-th segment

Assuming that one end of the cable is fixed at $\begin{bmatrix} 0\, 0\, 0 \end{bmatrix}^\mathrm{T}$ , the position of the center of mass of the i-th segment is given by

$$\begin{aligned} {\varvec{p}}_i=\sum _{j=1}^{i-1} L_j \begin{bmatrix} \cos \theta _j\cdot \sin \phi _j \\ \sin \theta _j\cdot \sin \phi _j \\ \cos \phi _j \end{bmatrix} +\frac{L_i}{2} \begin{bmatrix} \cos \theta _i\cdot \sin \phi _i \\ \sin \theta _i\cdot \sin \phi _i \\ \cos \phi _i \end{bmatrix} \end{aligned},$$

(1)

where $L_i$ is the length of the i-th segment.

Thus the velocity of the center of mass of the i-th segment is given by

$$\begin{aligned} {\varvec{v}}_i=\dot{{\varvec{p}}_i}=\frac{ \mathrm {d}{\varvec{p}}_i}{ \mathrm {d}t} \end{aligned}. $$

(2)

The velocity of a point, ${\varvec{r}}_i(s)$, at a distance s from its center ${\varvec{p}}_i(s)$ (Fig. 2b) is given by

$$\begin{aligned} \varvec{\dot{r}}_i(s)= \frac{ \mathrm {d}}{ \mathrm {d}t} \left( {\varvec{p}}_i + s \begin{bmatrix} \cos {\theta _j} \cdot \sin {\phi _j} \\ \sin {\theta _j}\cdot \sin {\phi _j} \\ \cos {\phi _j} \end{bmatrix} \right) \end{aligned}.$$

(3)

If we consider the drag force, the net external force and torque due to drag on the i-th segment is thus given by

$$\begin{aligned} \begin{aligned} {\varvec{F}}_i&= \begin{bmatrix} F_{i,x} \\ F_{i,y} \\ F_{i,z} \end{bmatrix}=- \int _{-\frac{L_i}{2}}^{\frac{L_i}{2}} C_d \cdot \varvec{\dot{r}}_i(s) \hbox {d}s, \\ \varvec{\tau }_i&=- \int _{-\frac{L_i}{2}}^{\frac{L_i}{2}} {{\varvec{r}}_i(s)} \times [ C_d \cdot \varvec{\dot{r}}_i(s) ] \hbox {d}s, \end{aligned} \end{aligned}$$

(4)

where $C_d$ is the drag coefficient along the transverse direction of the segment, and s is the variable used to integrate the force/torque along the length of the segment.

The angular velocity of the i-th segment is given by

$$\begin{aligned} \varvec{\omega }_i=\dot{\theta _i} \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} +\dot{\phi _i} \begin{bmatrix} -\sin \theta _i \\ \cos \theta _i \\ 0 \end{bmatrix} \end{aligned}.$$

(5)

We can define the free end of the cable in terms of the generalized coordinates as

$$\begin{aligned} \begin{bmatrix} x_f \\ y_f \\ z_f \end{bmatrix} =\sum _{i=1}^n L_i \begin{bmatrix} \cos {\theta _i}\cdot \sin {\phi _i }\\ \sin {\theta _i}\cdot \sin {\phi _i} \\ \cos {\phi _i} \end{bmatrix} \end{aligned}.$$

(6)

Thus, we can define the 2n generalized forces

$$\begin{aligned} \begin{aligned} Q_{\theta _i}&=\begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix} \cdot \frac{\partial {\begin{bmatrix} x_f \\ y_f \\ z_f \end{bmatrix}}}{\partial {\theta _i}}+\sum _{j=1}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\theta _i}}+\sum _{j=1}^{n} \varvec{\tau }_i \cdot \frac{\partial {\varvec{\omega }_j}}{\partial {{{\dot{\theta }}}_i}} \\&=-f_xL_i\sin {\theta _i}\sin {\phi _i}+f_yL_i\cos {\theta _i}\sin {\phi _i}\\&\quad +\sum _{j=1}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\theta _i}}+\sum _{j=1}^{n} \varvec{\tau }_i \cdot \frac{\partial {\varvec{\omega }_j}}{\partial {{{\dot{\theta }}}_i}},\\ Q_{\phi _i}&=\begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix} \cdot \frac{\partial {\begin{bmatrix} x_f \\ y_f \\ z_f \end{bmatrix}}}{\partial {\phi _i}}+\sum _{j=1}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\phi _i}}+\sum _{j=1}^{n} \varvec{\tau _i} \cdot \frac{\partial {\varvec{\omega }_j}}{\partial {{{\dot{\phi }}}_i}}\\&=f_xL_i\cos {\theta _i}\cos {\phi _i}+f_yL_i\sin {\theta _i}\cos {\phi _i}\\&\quad-f_zL_i\sin {\phi _i}+\sum _{j=1}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\phi _i}}+\sum _{j=1}^{n} \varvec{\tau _i} \cdot \frac{\partial {\varvec{\omega }_j}}{\partial {{{\dot{\phi }}}_i}},\\&\quad \forall i=1,2,\ldots ,n,\end{aligned} \end{aligned}$$

(7)

where $m_i$ is the mass of the i-th segment, g is the gravitational acceleration.

Since ${\varvec{p}}_j$ does not depend on $\theta _i$ and $\phi _i$ when $j<i$, and $\varvec{\omega _i}$ only depend on ${{\dot{\theta }}}_i$ and ${{\dot{\phi }}}_i$, we can simplify the expressions above as

$$\begin{aligned} \begin{aligned} Q_{\theta _i}&=-f_xL_i\sin {\theta _i}\sin {\phi _i}+f_yL_i\cos {\theta _i}\sin {\phi _i}\\&\quad +\sum _{j=i}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\theta _i}}+\varvec{\tau _i} \cdot \frac{\partial {\varvec{\omega }_i}}{\partial {{{\dot{\theta }}}_i}},\\ Q_{\phi _i}&=f_xL_i\cos {\theta _i}\cos {\phi _i}+f_yL_i\sin {\theta _i}\cos {\phi _i}\\&\quad -f_zL_i\sin (\phi _i)+\sum _{j=i}^{n} {\varvec{F}}_i \cdot \frac{\partial {{\varvec{p}}_j}}{\partial {\phi _i}}+ \varvec{\tau _i} \cdot \frac{\partial {\varvec{\omega }_i}}{\partial {{{\dot{\phi }}}_i}},\\&\quad \forall i=1,2,\ldots ,n. \end{aligned} \end{aligned}$$

(8)

The kinetic energy of the system is given by

$$\begin{aligned} K=\sum _{i=1}^n \left( \frac{1}{2}m_i{\left| \dot{{\varvec{p}}_i}\right| }^2+\frac{1}{2}\frac{m_i{L_i}^2}{12}{\left| \varvec{\omega }_i\right| }^2\right) \end{aligned}.$$

(9)

The potential energy is given by

$$\begin{aligned} V=\sum _{i=1}^n m_ig\varvec{{\hat{k}}}\cdot {\varvec{p}}_i \end{aligned},$$

(10)

where $\varvec{{\hat{k}}}$ is $\begin{bmatrix} 0\, 0\, 1 \end{bmatrix}^\mathrm{T}$.

Thus, Lagrangian is given by

$$\begin{aligned} {\mathscr {L}}=K-V. \end{aligned}$$

(11)

The Lagrange equations of motion for the system is given by [17]

$$\begin{aligned} \begin{aligned}&\frac{ \mathrm {d}}{\mathrm {d}t}\left( \frac{\partial {{\mathscr {L}}}}{\partial \dot{{\eta }_l}}\right) -\frac{\partial {{\mathscr {L}}}}{\partial {{\eta }_l}}-Q_{{\eta }_l}=0,\\&\qquad \forall ~~{\eta }_l\in \left\{ \theta _1,\theta _2,\ldots ,\theta _n,\phi _1,\phi _2,\ldots ,\phi _n \right\}. \end{aligned} \end{aligned}$$

(12)

The Eq. (12) consist of 2n second order ordinary differential equations in the quantities $\left\{ \theta _1,\theta _2,\ldots ,\theta _n,\phi _1,\phi _2,\ldots ,\phi _n\right\}$. Moreover they are affine in $\left\{ \ddot{\theta _1},\ddot{\theta _2},\ldots ,\ddot{\theta _n},\ddot{\phi _1},\ddot{\phi _2},\ldots ,\ddot{\phi _n}\right\}$. We used Mathematica to perform symbolic computation and simplification of the Eq. (12) to obtain the ordinary diffrential equations (ODEs) which take the form of ${\varvec {M\ddot{\eta }}}+{\varvec {P}} = \mathbf{0}$. We extract the $2n\times 2n$ matrix M (which depend on the generalized coordinates, $\eta _l$), and the $2n\times 1$ vector P (which depends on the generalized coordinates, $\eta _l$, and its time derivatives, ${\dot{\eta }}_l$), which we then export into MATLAB for numerical integration. We use the substitution $\varvec{\zeta} = \varvec{{\dot{\eta }}}$ to convert the second-order ODEs in the generalized coordinates to a set of first-order ODEs in the state variables, $\left[ \begin{array}{c} \varvec{\eta}\, \varvec{\zeta} \end{array} \right]^\mathrm{T}$. Thus, for given initial values of ${\varvec{\eta} } = [\theta _1,\ldots ,\theta _n,\phi _1,\ldots ,\phi _n ]$ and ${\varvec{\zeta}} = [ \dot{\theta _1},\ldots ,\dot{\theta _n},\dot{\phi _1},\ldots ,\dot{\phi _n} ]$ at $t=0$, and given the external force profiles, $\left\{ f_x,f_y,f_z\right\}$ as function of t, we employ ode45 using Runge–Kutta fourth-order algorithm to integrate the ODEs numerically. Figure 3a–d show an example of the force controlled system simulation, where input force function is ${\varvec{F}}=\begin{bmatrix} f_x\, f_y\, f_z \end{bmatrix}^\mathrm{T}=\begin{bmatrix} 0\, 0\, 0 \end{bmatrix}^\mathrm{T}$. The length of each segment of the rope is $L=1~ {\text {m}}$ and the mass of each segment is $m=0.01~ {\text {kg}}$. (All numerical quantities used throughout the paper and displayed on plots are in SI units.)

In general, with nominal external forces, we observe no problem with convergence of the solution using Runge–Kutta type algorithms, and throughout the paper we do not need to use solvers for stiff problems. However, stiff solvers that take the Jacobian as an explicit input can also be employed for the numerical integration if necessary.

Fig. 3

Screenshots from a simulation of a free-falling cable (zero force applied to its end) demonstrates it swing due to gravity (8-segment model with $L=1~\text {m}$ and $m=0.01~\text {kg}$). at = 0 s, bt = 0.7 s, ct = 1.4 s, dt = 2 s

2.1.1 Verification of correctness of simulation model

In Fig. 3 we demonstrate a simulation for a free-fall of the cable under the influence of gravity. To verify the reliability of the simulation of the dynamic model, we check the total mechanical energy of this system ($K+V$). The total mechanical energy over a period of 10 s during the free-fall/swing simulation is shown in Fig. 4. For a free-falling system, the total mechanical energy should be conserved because there are no external non-conservative forces. Indeed Fig. 4 shows that the error in the total mechanical energy was under $0.00004\,\text {J}$, which indicates a good reliability for the dynamic model.

Fig. 4

Total mechanical energy of the free-falling cable (for simulation shown in Fig. 3) plotted over time (blue curve). As can be observed, the error from the initial mechanical energy (red dashed reference, with the origin of height in computing the potential energy (PE) chosen at the point where the cable is attached) is under $0.00004\,\text {J}$ (or about $0.002\%$)

2.2 Position controlled system

For position control of the free end, we need to slightly re-formulate the equations of motion Eq. (12). In position controlled system, $\left\{ f_x,f_y,f_z\right\}$ are unknown and $\left\{ x_f,y_f,z_f\right\}$ are the external inputs.

Thus, we still have 2n generalized coordinates, $\{\theta _1,\theta _2,\ldots ,$$\theta _n,\phi _1,\phi _2,\ldots ,\phi _n\}$. Equations and the expressions for the generalized forces Eq. (8), kinetic energy Eq. (9), and potential energy Eq. (10) still remain the same. We still have 2n Lagrange equations of motion. However now we have $2n+3$ unknowns.

Taking time derivative of the configuration constraint Eq. (6), we obtain the velocity constraint equations

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \dot{x_f} \\ \dot{y_f} \\ \dot{z_f} \end{bmatrix} -\sum _{i=1}^n L_i \left( {{\dot{\theta }}}_i \begin{bmatrix} -\sin {\theta _i} \sin {\phi _i} \\ \cos {\theta _i} \sin {\phi _i} \\ 0 \end{bmatrix}\right. \\ \left. +\,{{\dot{\phi }}}_i \begin{bmatrix} \cos {\theta _i} \cos {\phi _i} \\ \sin {\theta _i} \cos {\phi _i} \\ -\sin {\phi _i} \end{bmatrix} \right) ={\mathbf{0}}. \end{aligned} \end{aligned}$$

(13)

And we differentiating it for a second time we obtain the acceleration constraint equations

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} \ddot{x_f} \\ \ddot{y_f} \\ \ddot{z_f} \end{bmatrix} -\sum _{i=1}^n L_i \left( {{{\dot{\theta }}}_i}^2 \begin{bmatrix} -\cos {\theta _i} \sin {\phi _i} \\ -\sin {\theta _i} \sin {\phi _i} \\ 0 \end{bmatrix}\right. \\&\quad +{{{\dot{\phi }}}_i}^2 \begin{bmatrix} -\cos {\theta _i} \sin {\phi _i} \\ -\sin {\theta _i} \sin {\phi _i} \\ -\cos {\phi _i} \end{bmatrix} +{{\dot{\theta }}}_i{{\dot{\phi }}}_i \begin{bmatrix} -2\sin {\theta _i} \cos {\phi _i} \\ 2\cos {\theta _i} \cos {\phi _i} \\ 0 \end{bmatrix}\\&\left. \quad +\,\ddot{\theta }_i \begin{bmatrix} -\sin {\theta _i}\sin {\phi _i} \\ \cos {\theta _i}\sin {\phi _i} \\ 0 \end{bmatrix} +\ddot{\phi }_i \begin{bmatrix} \cos {\theta _i}\cdot \cos {\phi _i} \\ \sin {\theta _i} \cos {\phi _i} \\ -\sin {\phi _i} \end{bmatrix} \right) ={\mathbf{0}}.\end{aligned} \end{aligned}$$

(14)

Equations (12) and (14) together form $2n+3$ equations, which are corresponding to $2n+3$ unknowns, $\left\{ f_x,f_y,f_z,\ddot{\theta _1},\ddot{\theta _2},\ldots ,\ddot{\theta _n},\ddot{\phi _1},\ddot{\phi _2},\ldots ,\ddot{\phi _n}\right\}$. Thus, for given trajectories of the free end of the cable (i.e. given $\left\{ x_f,y_f,z_f\right\}$ and their derivatives as a function of time), and an initial configuration $\left\{ \theta _1,\theta _2,\ldots ,\theta _n,\phi _1,\phi _2,\ldots ,\phi _n\right\}$ that satisfy the shape constraint equations, and an initial set of angular velocities $\left\{ \dot{\theta _1},\dot{\theta _2},\ldots ,\dot{\theta _n},\dot{\phi _1},\dot{\phi _2},\ldots ,\dot{\phi _n}\right\}$ that satisfy the velocity constraint equations at $t=0$, we can integrate and solve the system of differential-algebraic equations (DAEs) in Eqs. (12) and (14) for $\left\{ f_x,f_y,f_z,\theta _1,\theta _2,\ldots ,\theta _n,\phi _1,\phi _2,\ldots ,\phi _n\right\}$.

As before, for simulating the system, we used Mathematica to simplify the Eqs. (12) and (14) to obtain the ODEs and the coefficients of the second derivatives in the equations. The equations can be numerically integrated by MATLAB. Figure 5a–d show an example of the position controlled system simulation, where input position function is ${\varvec{P}}=\begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix}=\begin{bmatrix} 2{\cos }(\omega t) \\ 2{\sin }(\omega t) \\ 0 \end{bmatrix}$, $\omega = \frac{\uppi }{3}$, t is time.

Fig. 5

Screenshots from a position controlled simulation show traces of complete dynamic simulations of a cable and demonstrate a circular motion of the free end (6-segment system). at = 0 s, bt = 2 s, ct = 4 s, dt = 6 s

3 Shape control of the cable

We next propose a controller for controlling the shape of the cable using the control inputs of $f_x, f_y$, and $f_z$. The second-order dynamics of the cable makes the problem of shape control challenging. Furthermore, in presence of body forces (such as inertial forces or gravity), it is physically not possible to permanently hold a desired shape since gravity would try to bring the shape of the cable back to its equilibrium shape even if the controller instantaneously achieves a good approximation of the desired shape. The system under consideration is also under-actuated—we are trying to control a system with 2n degrees of freedom with only 3 control inputs.

We first develop a general controller for shape control for the full second-order dynamic system. The novelty in our controller lies in the fact that although the system is second-order, the controller does not need desired velocity inputs, and only require a desired shape. Additionally, one feature of our proposed controller is that whenever the body forces try to bring the system back to its equilibrium configuration, the controller tries to recover it to achieve the desired shape, thus achieving a good approximation of the desired shape in a periodic manner. While the full controller for the full dynamic system is not amiable to theoretical analysis, in Sect. 4 we make some simplifying assumptions (quasi-static model and no gravity) and provide theoretical results on the stability of the controller.

3.1 Design of the controller

The governing equations of the system is given by Eq. (12), which constitute of a total of 2n equations (ODEs). These equations involve the $2n+3$ variables, $\{f_x,f_y,f_z,$$\theta _1,\theta _2,\ldots ,\theta _n,$$\phi _1,\phi _2,\ldots ,\phi _n \}$. However, these equations are affine in $f_x,f_y,f_z$ and in the second time derivatives of the generalized coordinates, $\ddot{\theta }_1,\ddot{\theta }_2,\ldots ,\ddot{\theta }_n, \ddot{\phi }_1,\ddot{\phi }_2,\ldots ,\ddot{\phi }_n$. Thus the governing equations can be written as

$$\begin{aligned} {\varvec{M}}_{2n\times 2n} \begin{bmatrix} {\ddot{\varvec{\varTheta}}} \\ {\ddot{\varvec{\varPhi}}} \end{bmatrix} +{\varvec{N}}_{2n\times 1}\left( {\varvec{\varTheta}} ,{\varvec{\varPhi}} ,{{\dot{\varvec{\varTheta} }}},{{\dot{\varvec{\varPhi}}}} \right) +{\mathbf{Q}}_{2n\times 3}\left( {\varvec{\varTheta} }, {\varvec{\varPhi}} \right) \begin{bmatrix} f_x \\ f_y \\ f_z \\ \end{bmatrix}= {\mathbf{0}}, \end{aligned}$$

(15)

where ${\varvec{\varTheta}} =[\theta _1,\theta _2,\ldots ,\theta _n]^\mathrm {T}$, ${\varvec{\varPhi}} =[\phi _1,\phi _2,\ldots ,\phi _n]^\mathrm {T}$, ${{\dot{\varvec{\varTheta}}}}=[{{\dot{\theta }}}_1,{{\dot{\theta }}}_2,\ldots ,{{\dot{\theta }}}_n]^\mathrm {T}$, ${{\dot{\varvec{\varPhi}}}}=[{{\dot{\phi }}}_1,{{\dot{\phi }}}_2,\ldots ,{{\dot{\phi }}}_n]^\mathrm {T}$, $\ddot{\varvec{\varTheta}}=[\ddot{\theta }_1,\ddot{\theta }_2,\ldots ,\ddot{\theta }_n]^\mathrm {T}$, $\ddot{\varvec{\varPhi}}=[\ddot{\phi }_1,\ddot{\phi }_2,\ldots ,\ddot{\phi }_n]^\mathrm {T}$. N is a function of $\varvec{\varTheta}$, $\varvec{\varPhi}$, ${{\dot{\varvec{\varTheta}}}}$, and ${{\dot{\varvec{\varPhi}}}}$. Q is a function of $\varvec{\varTheta}$, and $\varvec{\varPhi}$.

We can substitute p for ${{\dot{\varvec{\varTheta}}}}$, and q for ${{\dot{\varvec{\varPhi}}}}$ such that $\ddot{\varvec{\varTheta}} = \dot{\varvec{p}}$, $\ddot{\varvec{\varPhi}} = \dot{\varvec{q}}$. The complete state of the system can thus be described by ${\varvec{\varTheta}}, {\varvec{\varPhi}}$, p, and q. Thus the governing equations can be written as

$$\begin{aligned} {\varvec{M}} \begin{bmatrix} \dot{\varvec{p}} \\ \dot{\varvec{q}} \end{bmatrix}+{\varvec{N}}+{\varvec{Q}} \begin{bmatrix} f_x \\ f_y \\ f_z \\ \end{bmatrix}={\mathbf{0}}, \end{aligned}$$

(16)

along with the equations ${\varvec{p}} = {{\dot{\varvec{\varTheta}}}}$ and ${\varvec{q}} = {{\dot{\varvec{\varPhi}}}}$. Note that the matrices M, N, and Q depend on the state variables ${\varvec{\varTheta}} , {\varvec{\varPhi}}$ , p, and q only.

Denote the desired shape of the discrete model by ${\varvec{\varTheta}} ^D=[\theta _{1}^D,\theta _{2}^D,\ldots ,\theta _{n}^D]^\mathrm {T}$ and ${\varvec{\varPhi}} ^D=[\phi _{1}^D,\phi _{2}^D,\ldots ,\phi _{n}^D]^\mathrm {T}$. We thus propose that the time derivatives of ${\varvec{\varTheta}}$ and ${\varvec{\varPhi}}$ be proportional to the errors in ${\varvec{\varTheta}}$ and ${\varvec{\varPhi}}$ (from the desired values) in order for them to reach their desired values

$$\begin{aligned} \begin{bmatrix} {\varvec{p}}^D \\ {\varvec{q}}^D \end{bmatrix} = \begin{bmatrix} {{\dot{\varvec{\varTheta }}}}^D \\ {{\dot{\varvec{\varPhi}}}}^D \end{bmatrix} = {\varvec{K}}_1\Bigg ( \begin{bmatrix} {\varvec{\varTheta}} ^D \\ {\varvec{\varPhi}} ^D \end{bmatrix} - \begin{bmatrix} {\varvec{\varTheta}} \\ {\varvec{\varPhi}} \end{bmatrix} \Bigg ), \end{aligned}$$

(17)

where the superscript “D” denotes that it is a desired quantity, and $\varvec{K}_1$ is a $n\times n$ gain matrix. Likewise, given the desired p and q, we have the following desired quantities for $\dot{\varvec{p}}$ and $\dot{\varvec{q}}$

$$\begin{aligned} \begin{bmatrix} {\dot{\varvec{p}}^D} \\ {\dot{\varvec{q}}^D} \end{bmatrix} ={\varvec{K}}_2\Bigg ( \begin{bmatrix} {\varvec{p}}^D \\ {\varvec{q}}^D \end{bmatrix} - \begin{bmatrix} {\varvec{p}} \\ {\varvec{q}} \end{bmatrix} \Bigg ),\end{aligned}$$

(18)

where ${\varvec{K}}_2$ is a $n\times n$ gain matrix.

Equation (18) can now be substituted into Eq. (16) in order to attempt a solution for the required forces for the desired forces, $\{f_x, f_y, f_z\}$. However, with these 3 unknowns, Eq. (16) is an over-constrained system. We thus propose the following control law

$$\begin{aligned} \begin{bmatrix} f_x \\ f_y \\ f_z \\ \end{bmatrix}=-{\varvec{Q}}^{+}\Bigg ( {\varvec{M}} \begin{bmatrix} \dot{\varvec{p}} \\ \dot{\varvec{q}} \end{bmatrix} +{\varvec{N}}\Bigg ), \end{aligned}$$

(19)

where ${(\cdot )}^{+}$ is the Moore–Penrose pseudoinverse [18]. For a given desired $[\dot{\varvec{p}}, \dot{\varvec{q}}]$, due to the property of Moore–Penrose pseudoinverse, the above controller minimizes the quantity  $\Vert {\varvec{M}} \begin{bmatrix} \dot{\varvec{p}} \\ \dot{\varvec{q}} \end{bmatrix}+{\varvec{N}}+{\varvec{Q}} \begin{bmatrix} f_x \\ f_y \\ f_z \\ \end{bmatrix}\Vert _2$.

Substituting the desired quantities $\begin{bmatrix} {\varvec{p}}^D\, {\varvec{q}}^D \end{bmatrix}^\mathrm{T}$ into the control law (19), we can compute the forces which can shape the cable into the desired shape. Using Eqs. (17) and (18), the control law (19) can be written as

$$\begin{aligned} \begin{aligned} \begin{bmatrix} f_x \\ f_y \\ f_z \\ \end{bmatrix}&=-{\varvec{Q}}^{+}\Bigg [ {\varvec{M}} {\varvec{K}}_2\Bigg ( \begin{bmatrix} {\varvec{p}}^D \\ {\varvec{q}}^D \end{bmatrix} - \begin{bmatrix} {\varvec{p}} \\ {\varvec{q}} \end{bmatrix} \Bigg ) +{\varvec{N}}\Bigg ] \\&= -{\varvec{Q}}^{+}\Bigg \{{\varvec{M}} {\varvec{K}}_2\Bigg [ {\varvec{K}}_1\Bigg ( \begin{bmatrix} {\varvec{\varTheta}} ^D \\ {\varvec{\varPhi}} ^D \end{bmatrix} - \begin{bmatrix} {\varvec{\varTheta}} \\ {\varvec{\varPhi}} \end{bmatrix} \Bigg ) - \begin{bmatrix} {\varvec{p}} \\ {\varvec{q}} \end{bmatrix} \Bigg ] +{\varvec{N}}\Bigg \}. \end{aligned} \end{aligned}$$

(20)

Thus for a given desired shape of the discrete model, ${\varvec{\varTheta}} ^D,{\varvec{\varPhi}} ^D$, an initial configuration of the shape and an initial set of angular velocity , we can use Eq. (20) for computing $\{f_x, f_y, f_z\}$ at every time instant, and thus integrate the system. Though we do not have full controllability of the system, with $\{f_x, f_y, f_z\}$ we can use the force controlled system to control the shape of cable and achieve an approximation of the desired shape. As long as the gain matrices are positive definite, due to Eqs. (17) and (18), we can expect the system to take trajectories towards achieving the desired shape reasonably well, although convergence is in general not possible or guaranteed due to the nonlinearities in the system dynamics and the controller Eq. (20).

In the sections that follow, we first provide a few simulation results using the proposed controller. Following that in Sect. 4 we will provide a more rigorous stability analysis for a simplified system with quasi-static assumptions. The control gain matrices are adjusted manually according to the simulation results.

3.2 Simulation results of shape control

3.2.1 Simulations with gravity and without drag force

Fig. 6

Shape control example (with gravity and without drag force): desired shape is a straight line with ${\varvec{\varTheta}} ^D=[0,0, 0,0,0,0,0,0]$ and ${\varvec{\varPhi}} ^D=[\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2}]$. a Initial shape, b final shape attained is approximately a straight line

Fig. 7

Shape control example (with gravity and without drag force): desired shape is a function of time (a straight line with the end of the cable moving in a circle). a Initial shape, b trajectories of the end of the cable is approximately a circle

Figure 6 shows an attempt to control the shape of a 8-segment model. The desired shape is a straight line, where ${\varvec{\varTheta}} ^D=[0,0,$ 0, 0, 0, 0, 0, 0] and ${\varvec{\varPhi}} ^D=[\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2}]$. As shown in Fig. 6b, the controller was able to achieve an approximation of the desired shape, although in absence of any dissipative/drag force, oscillations tend to build up in the system over time. Figure 7 shows an attempt to control the end of a 8-segment cable model doing a circular motion. The desired shape is a function of time, where ${\varvec{\varTheta}} ^D=[\omega t,\omega t,\omega t,\omega t,\omega t,\omega t,\omega t,\omega t]$, ${\varvec{\varPhi}} ^D=[\uppi ,\uppi ,\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},\frac{\uppi }{2},0,0]$, t is the time, and $\omega =\frac{2\uppi }{5}$. As shown in Fig. 7b, the controller was able to do a approximation of the desired motion. The gain matrices used in both the simulations are ${\varvec{K}}_i = 0.5 ~{\varvec{I}}$.

3.2.2 Simulations without gravity or drag force

In some occasions, the control forces applied on the end of the cable are much greater than gravity. Then the control forces are dominant over gravity during the simulation. In order to simplify the simulation, we ignore the gravity during the simulation when control forces dominate over gravity and thus set acceleration due to gravity to $g=0$. For example, if we want to reverse an arch from concaved upwards to concaved downwards, we expect to exert a pair of impulsive forces upward then downward at the end of the cable. In this case, the control force at the end of the cable is much greater than gravity and dominant over gravity. Therefore, simulating this case without gravity is reasonable.

Example with $n = 8$:

Fig. 8

Shape control of an 8-segment model: simulation for “reversing an arch”. a Initial shape, b disired shape, c final shape attained at t = 2.95 s

Fig. 9

Plots of forces and error against time for the simulation of “reversing an arch” (8-segment, model). a Forces, b error

Figure 8a, b shows the initial shape and desired shape for this case (8-segment). The sets of desired angles are ${\varvec{\varTheta}} ^D=[0,0,0,0,0,0,0,0]^\mathrm {T}$ and ${\varvec{\varPhi}} ^D=[0.52,0.79,1.05,$$1.31,1.83,2.10,2.36,2.62]^\mathrm {T}$ and gain matrix used is ${\varvec{K}}_{{i}}=0.7~{\varvec{I}}$. Figure 8c shows the simulation result in MATLAB. We note that when $t = 2.95$ s the shape of the cable approximated the arch which is concaved down. Of course due to inertia, the cable will not stay at the desired shape, but will scillate around it.

We define the error between the attained and desired shape as

$$\begin{aligned} \quad \text {Error} = \frac{\sum _{i=1}^n {\left( \theta _i-\theta _i^D\right) }^2 + \sum _{i=1}^n {\left( \phi _i-\phi _i^D\right) }^2}{2n} \end{aligned},$$

(21)

where n is the number of segments, $\theta _i$ and $\phi _i$ are current angles during the simulation, and $\theta _i^D$ and $\phi _i^D$ are the desired angles. Figure 9 shows the graphs of forces and error of the simulation. From the force graph (Fig. 9a), we note that the control force was impulsive upward at the beginning and then went downward. This result is in line with our expectation. From the error graph (Fig. 9b), we note that the error decreased over time until $t=3$ s and when $t=3$ s the error was nearly zero which means the shape of the cable approximated the desired shape best. When $t>3$ s, the error increases because of inertia. Due to absence of drag force, the energy introduced into the system because of the free end being manipulated, however, starts rapidly building up in the system, causing vigorous oscillations.

Base on the simulation result, the controller was able to achieve a satisfactory approximation of the desired shape in this case. However, the controller in Eq. (20) is based on the Moore–Penrose pseudoinverse and is not guaranteed to achieve the desired shape exactly. Nevertheless, we note that the smaller the number of segments is, lower n will be, and thus Q will be closer to a square matrix, more accurately will Moore–Penrose pseudoinverse approximate a true inverse, and thus the more accurately the cable will be able to attain the desired shape. We can thus have a better simulation result if we use smaller number of segments n.

Example with $n = 3$:

Figure 10a, b shows the initial shape and desired shape for a 3-segment system. The sets of desired angles are ${\varvec{\varTheta}} ^D=[0,0,0]^\mathrm {T}$ and ${\varvec{\varPhi}} ^D=[0.79,1.57,2.36]^\mathrm {T}$ and gain matrix used is ${\varvec{K}}=0.6{\varvec{I}}$. Figure 10c shows the simulation result from MATLAB. We note that when $t = 3.95$ s the shape of the cable was nearly the same as the desired shape.

Figure 11 shows the graphs of forces and error of the simulation of the 3-segment system. The force graph (Fig. 11a) of 3-segment system is consistent with the forces graph of 8-segment system (Fig. 9a). From the error graph (Fig. 11b), we note that the error was minimum when $t = 3.9\; {\text{s}}$. The minimum error of 3-segment system is much smaller than the minimum error of 8-segment system. As evident from the plots, the simulation result of 3-segment system is much better than the result of 8-segment system, thus providing evidence to our earlier observation that it is easier to control a system with smaller n.

Though the shape of the cable can be controlled to attain the desired shape at an instant, it cannot keep the desired shape for a long time due to inertia and gravity. Consequently, the controller should be capable to correct to the desired shape continuously. Figure 12 shows the simulation result of 3-segment system for a longer time. Though the shape of the cable started to deviate the desired shape after $t=3$ s, the controller managed to achieve the desired shape again when $t=20$ s and $t=33.5$ s (Fig. 12a, b). Also from the error graph (Fig. 12c), we can see that the error increased and decreased periodically, which means the shape of cable achieved and deviated the desired shape periodically. The controller kept trying to correct the shape of the cable to the desired shape. Based on these simulations, our proposed controller has the capability to control the shape of the cable continuously, attempting to reduce the error whenever the system diverges from the desired shape.

Fig. 10

Shape control of a 3-segment model: initial shape and desired shape for “reversing an arch” (3-segment). a Initial shape, b disired shape, c final shape attained at t = 3.95 s

Fig. 11

Plots of forces and error with time for the simulation of “reversing an arch” (3-segment model). a Forces, b error

Fig. 12

Best matches with the desired shape a, b from the simulation of “reversing an arch” (3-segment model), shown over a longer period of time. at = 20 s, bt = 33.5 s, c error

3.2.3 Simulations with drag force and without gravity

In some conditions, when the cable moves at a high speed, the air drag plays a significant role on the system, although we can still neglect the effect of gravity because of high inertial forces. Including the drag forces however can actually help dissipate the unwanted build-up of inertial/kinetic energy in the system and thus help attain stability. Figure 13 shows the initial shape and desired shape (resembling a sine curve) for a 5-segment system. The sets of desired angles are ${\varvec{\varTheta}} ^D=[0,0,0,0,0]$ and ${\varvec{\varPhi}} ^D=[\frac{\uppi }{3},\frac{7\uppi }{12},\frac{3\uppi }{4},\frac{7\uppi }{12},\frac{\uppi }{6}]$.

Figure 14 shows the simulation result from MATLAB simulation. We note that when $t > 5$ s the shape of the cable approximated the desired shape and then cable moved with a very low velocity and its shape nearly kept constant, stabilized due to the drag force.

Figure 15 shows the graphs of forces and error of the simulation. From the force graph (Fig. 15a), we note that the control force was very small when $t>5$ s due to the shape was very close to the desired shape. From the error graph (Fig. 15b), we note that the error decreased rapidly until $t=5$ s and then the error decreased in a very low rate, which means cable kept deforming to the desired shape at a low rate.

Fig. 13

Shape control of a 5-segment model in presence of drag force: Initial shape and desired shape (a “sine curve”). a Initial shape, b disired shape

Fig. 14

Simulations with drag force (5-segment model attaining an approximation of a “sine curve”). at = 0 s, bt = 5 s, ct = 10 s, dt = 15 s

Fig. 15

Plots of forces and error for the simulation with drag force (5-segment model attaining an approximation of a “sine curve”). a Forces, b error

3.2.4 Simulations with gravity and drag force

Finally we present a simulation result with a large value of n in presence of small drag ($C_d = 0.001$) and gravity. Figure 16 shows the results from a simulation of a 15-segment model and a plot of error with time. We used ${\varvec{K}}_i=0.6 {\varvec{I}}$ as the gain matrices. As can be observed from the plot of the error, the error oscillates with time, but due to the low drag coefficient and presence of gravity, the system has energy build-up in it, which makes the periodic low error configurations accumulate more error over time.

As discussed earlier we use Mathematica to generate the symbolic equations of motion. With higher values of n the generation of the governing equations take longer. However, the integration of the equations using MATLAB is still quite efficient. In fact, the integration of the governing equations for the period of about 25 s (shown in Fig. 16) in fact took about 17 s of actual processor time to compute, thus making the controller much faster than required in real-time, even for models with large n.

Fig. 16

Simulation of a 15-segment model with gravity and small drag. a Initial shape, b desired shape, c shape attained at t = 3.85 s, d error with time

4 Stability of the shape controller

4.1 Quasi-static model

The controller we designed in the last chapter is a linearized controller for a nonlinear system, and hence complicated for long-term stability analysis. Thus, we need to simplify the discrete segment model in order to obtain the state error function. In some occasions, we can ignore the inertial forces if the drag forces dominate over inertial forces. For examples, a slow-moving light cable in spaceship is justified for the quasi-static model because there is no gravity in space and air resistance exists in the spaceship. In addition, a detector connected to a submarine is also a reasonable example if the buoyancy of the detector and cable equals gravity allowing us to ignore the gravity in water. The water resistance dominates over inertial forces for the detector in a very low speed. Under these slow-moving conditions, the accelerations are extremely small. We assume the accelerations $\ddot{\varvec{\varTheta}}$ and $\ddot{\varvec{\varPhi}}$ and gravity acceleration g are all 0. Thus the potential energy $V=0$ and the Lagrangian ${\mathscr {L}}=K$. Also $\frac{\partial {{\mathscr {L}}}}{\partial {q_l}}=0$ because Lagrangian does not consist of ${\varvec{\varTheta}}$ and ${\varvec{\varPhi}}$, where $\forall q_l\in \left\{ \theta _1,\theta _2,\ldots ,\theta _n,\phi _1,\phi _2,\ldots ,\phi _n \right\}$. Since $\frac{\partial {{\mathscr {L}}}}{\partial \dot{q_l}}$ are linear with ${{\dot{\theta }}}_i$ and ${{\dot{\phi }}}_i$, $\frac{ \mathrm {d}}{\mathrm {d}t}\left( \frac{\partial {{\mathscr {L}}}}{\partial \dot{q_l}}\right)$ are linear with $\ddot{\theta }_i$ and $\ddot{\phi }_i$. According to our assumptions, all the accelerations $\ddot{\theta }_i$ and $\ddot{\phi }_i$ are all 0. Then $\frac{ \mathrm {d}}{\mathrm {d}t}\left( \frac{\partial {{\mathscr {L}}}}{\partial \dot{q_l}}\right) =0$. The Lagrange equations of motion for the system (Eq. (12)) can be simplified to

$$\begin{aligned} \begin{aligned} Q_{\theta _i}&=0,\\ Q_{\phi _i}&=0,\\ \forall i&=1,2,\ldots ,n, \end{aligned} \end{aligned}$$

(22)

where $Q_{\theta _i}$ and $Q_{\phi _i}$ are given by Eq. (8).

We note that the external forces ${\varvec{F}}_i$ and torques $\varvec{\tau _i}$ are linear in the speeds $\left\{ \dot{\theta _1},\dot{\theta _2},\ldots ,\dot{\theta _n},\right.$$\left. \dot{\phi _1},\dot{\phi _2},\ldots ,\dot{\phi _n}\right\}$. Thus the $Q_{\theta _i}$ and $Q_{\phi _i}$ are linear in $\left\{ \dot{\theta _1},\dot{\theta _2},\ldots ,\dot{\theta _n},\dot{\phi _1},\dot{\phi _2},\ldots ,\dot{\phi _n},f_x,f_y,f_z\right\}$.

Consequently, the equations of the quasi-static model can be written as

$$\begin{aligned} {\varvec{A}}_{2n\times 2n}\begin{bmatrix} {{\dot{\varvec{\varTheta}}}} \\ {{\dot{\varvec{\varPhi}}}} \end{bmatrix}+ {\varvec{B}}_{2n\times 3}\begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix}= {\mathbf{0}} \end{aligned},$$

(23)

where ${{\dot{\varvec{\varTheta}}}}=[\dot{\theta _1},\dot{\theta _2},\ldots ,\dot{\theta _n}]^\mathrm {T}$ and ${{\dot{\varvec{\varPhi}}}}=[\dot{\phi _1},\dot{\phi _2},\ldots ,\dot{\phi _n}]^\mathrm {T}$.

By using this quasi-static model, we are able to implement a method to minimize the error. Then we rewrite the controller for the quasi-static model

$$\begin{aligned} \begin{bmatrix} f_x \\ f_y \\ f_z \end{bmatrix}=-{\varvec{B}}^{+}{\varvec{AK}}\left( \begin{bmatrix}{\varvec{\varTheta}} ^D \\ {\varvec{\varPhi}} ^D \end{bmatrix} - \begin{bmatrix} {\varvec{\varTheta}} \\ {\varvec{\varPhi}} \end{bmatrix}\right) \end{aligned},$$

(24)

where $(\cdot )^{+}$ is the Moore–Penrose pseudoinverse and K is an $2n\times 2n$ gain matrix.

Substituting the force controller back into Eq. (23), we have

$$\begin{aligned} {\varvec{A}}\begin{bmatrix} {{\dot{\varvec{\varTheta}}}} \\ {{\dot{\varvec{\varPhi}}}} \end{bmatrix}+{\varvec{B}}\left[ -{\varvec{B}}^{+}{\varvec{AK}}\left( \begin{bmatrix} {\varvec{\varTheta}} ^D \\ {\varvec{\varPhi}} ^D \end{bmatrix} - \begin{bmatrix} {\varvec{\varTheta}} \\ {\varvec{\varPhi}} \end{bmatrix}\right) \right] ={\mathbf{0}} \end{aligned}.$$

(25)

Define the error between the current shape of cable and the desired shape of cable as

$$\begin{aligned} {\varvec{e}}(t)=\begin{bmatrix} {\varvec{\varTheta}} ^D \\ {\varvec{\varPhi}} ^D \end{bmatrix} - \begin{bmatrix} {\varvec{\varTheta}} \\ {\varvec{\varPhi}} \end{bmatrix} \end{aligned}.$$

(26)

Take time derivatives on both sides of Eq. (26)

$$\begin{aligned} \dot{{\varvec{e}}}(t)=- \begin{bmatrix} {{\dot{{\varvec{\varTheta}} }}} \\ {{\dot{{\varvec{\varPhi}}}}} \end{bmatrix} \end{aligned}.$$

(27)

Take Eqs. (26) and (27) back to Eq. (25)

$$\begin{aligned} {\varvec{A}}\left( -\dot{\varvec{e}}(t)\right) +{\varvec{B}}\left[ -{\varvec{B}}^{+}{\varvec{AKe}}(t)\right] ={\mathbf{0}}. \end{aligned}$$

(28)

Then we can write the state error function as

$$\begin{aligned} \dot{\varvec{e}}(t)=-{\varvec{CKe}}(t), \end{aligned}$$

(29)

where matrix ${\varvec{C}}={\varvec{A}}^{+}{\varvec{BB}}^{+}{\varvec{A}}$.

Note that if all ${\text{Re}}\left\{ \lambda _i\left( -{\varvec{CK}}\right) \right\}$ (i.e. the real parts of the eigenvalues of the matrix $-{\varvec{CK}}$) are negative, then e(t) tends to be zero as $t\rightarrow 0$. However, matrix C is not full rank (B being a $2n\times 3$ matrix, the rank of the matrix ${\varvec{C}}={\varvec{A}}^{+}{\varvec{BB}}^{+}{\varvec{A}}$ is in fact 3). Thus some of the eigenvalues of C are zeros. Thus, we can only control the system to be marginally stable by choosing K such that ${\text{Re}}\left\{ \lambda _i\left( -{\varvec{CK}}\right) \right\}$ are non-positive.

If square matrix ${\varvec{C}}_{2n\times 2n}$ is diagonalizable [19], then matrix C can be factorized as

$$\begin{aligned} {\varvec{C}}={\varvec{U}}{\varvec{\varLambda}{\varvec{ U}}}^{-1}, \end{aligned}$$

(30)

where U is the square ($2n\times 2n$) matrix whose i-th column is the eigenvector $q_i$ of C and $\varvec{\varLambda}$ is the diagonal matrix whose diagonal elements are the corresponding eigenvalues.

We can then choose the gain matrix to be ${\varvec{K}}= {\varvec{U}} {\varvec{\varLambda}} ^{+} {\varvec{U}}^{-1}$, where ${\varvec{\varLambda}} ^{+}$ is the pseudoinverse of matrix ${\varvec{\varLambda}}$ (${\varvec{\varLambda}}$ with its non-zero diagonal elements reciprocated). Then

$$\begin{aligned} {\varvec{CK}}= {\varvec{U}} {\varvec{\varLambda}} {\varvec{U}}^{-1}{\varvec{U}}{\varvec{\varLambda}} ^{+} {\varvec{U}}^{-1}= {\varvec{U}}{\varvec{\varLambda}}{\varvec{\varLambda}} ^{+} {\varvec{U}}^{-1} \end{aligned}.$$

(31)

Note that matrix ${\varvec{\varLambda}}{\varvec{ \varLambda}} ^{+}$ is a diagonal matrix whose diagonal elements are only 0 or 1. Thus ${\text{Re}}\left\{ \lambda _i\left( -{\varvec{CK}}\right) \right\}$ becomes all non-positive (only 0 and ${-}1$) and this system is marginally stable. Though the error may not be zero as $t\rightarrow 0$. The cable will eventually reach an approximation of the desired shape after enough long time, though it may not reach the exact desired shape.

4.2 Simulation results

Figure 17a, b shows the initial shape and desired shape. They are the same as the initial shape and desired shape in previous simulation in Sect. 3.2.3. As shown in Fig. 17c, the simulation result shows that the cable was not able to reach the exact desired shape (sine curve) but an approximation after a long time. Compared with Fig. 15b, the error curve shown in Fig. 17d has less oscillations obviously. In addition, the error decreased at a faster rate and reached a smaller value ($< 0.1$), which means the final shape is closer to the desired shape. These results confirmed that we could have a better performance on shape control by controlling the gain matrix.

Fig. 17

Shape control example: simulation result to achieve a sine curve with controlled gain matrix (5-segment). a Initial shape, b desired shape, c final shape attained, d error

5 Conclusion and future direction

In this paper, we have demonstrated a method for controlling the shape of a cable fixed at one end and being manipulated at the other end. This problem is relevant to tethered UAVs that need to avoid obstacles. We have proposed a discrete model and derived the dynamic model of the cable in three dimensions for both force controlled system and position controlled system. We have developed a controller to control the shape of the cable. Also, we have proposed a quasi-static discrete model to simplify the problem and derived the state error function to marginally stabilize this system by adjusting the gain matrix.

In future, we plan to make further refinements to the proposed controller using novel methods, which can control the cable more precisely to attain a better approximation of the desired shape. We will also incorporate material/internal damping in the system which are highly relevant to real cables which do have a certain level of elasticity. As long as such damping results in a set of dynamic equations similar in form as described in Eq. (15), the controller design will be analogous. We also plan to use a continuous dynamic model, which is more realistic but more complex than the discrete model. In addition, practical challenges need to be addressed in the simulation and controller design, such as the friction at the joints, elasticity and the presence of physical obstacles in the environment.