1 Introduction

It is well known that dark matter plays an important role in the formation of large-scale cosmic structures in the universe beginning from the inflationary stage (Binney and Tremaine 1987; Tsiklauri 1998, 2000; Mo et al. 2010; Bertin 2014). This is mainly because of complex coupling dynamics between the neutral gaseous fluid (NGF) clouds and the dark matter fluid (DMF) clouds via mutual gravity. Although dark matter (nonluminous) does not shine, unlike visible bright matter (luminous); but, it still exerts a gravitational force on the matter around it. As a consequence, the gravitational stability analysis in the presence of dark matter is very important, since dark or nonluminous matter together with dark energy constitutes a significant portion (∼90%) of the present expanding universe (Stahler and Palla 2004; Blain 2005). It is pertinent to add that the global cloud collapse leading to bounded structure formation begins whenever the cloud thermal pressure is not sufficient to prevent the gravitational long-range force field (Jeans 1902).

The gravitational interaction of NGF with DMF is well established and substantially well-known towards cosmic structure and cluster formation processes (Tsiklauri 1998, 2000). The DMF presence in the complex clouds induces classically a considerable diminution in the resultant Jeans length, Jeans time and hence, the subsequent Jeans mass (Zhang and Li 1995; Tsiklauri 1998, 2000). In such cosmological environments, many researchers consider cold dark matter, where the constituents have relatively slow motion. This is because the hot dark matter has very large value of kinetic energy (>keV) and randomizes the formation of galactic structural units. Very recently, a close mapping with analogy is demonstrated to exist between interstellar realistic cosmic fluids and purported Maxwell fluids in the form of rich hydrodynamic structures on the lowest-order viscoelastic properties (Brevik 2016). The gravitational fluctuation analyses in such correlative cooperative clouds, amid gravitating dark matter, are, however, yet to be substantially explored and well empathized.

We propose a new theoretical formalism for the gravitational instability in a gravitating composite fluid, composed of NGF and DMF frictionally inter-coupled via mutual gravity, on the cosmological Jeans flat scales of space and time. The model includes the lowest-order viscoelasticity, Coriolis force and inter-layer frictional coupling dynamics in the bi-fluidic charter in spatially-flat geometry. The factors considered afresh are indeed the properties of a true viscoelastic cosmic fluid (Brevik 2016; Borah et al. 2016). The reason for the inclusion of fluid viscoelasticity stems in a rich variety of cosmic structures (Brevik 2016). The cosmic fluids, even with one-component constituents, are well-known to be highly viscoelastic in nature offering a plethora of collective wave excitations (Brevik 2016). The Coriolis force here modifies the dynamics and insures the conservation of angular momentum (Rozelot and Neiner 2009). A multi-scale analysis, which is based on the regular (reductive) perturbation technique (Burgers 1974; Whitham 1999; Ablowitz 2011), is carried out to obtain a conjugate pair of the viscoelastic forced Burgers (VFB) equations. A numerical illustrative platform is elaborately developed to reveal the exact nature of the weakly non-linear natural eigen-modes in both the hydrodynamic and kinetic regimes of the slight perturbations. Finally, new implications and non-trivial applications in the dark matter-dominated astro-cosmic contexts are concisely indicated.

2 Physical model and formulation

We, as a first-step model setup, consider a complex astrocloud composed of interstellar viscoelastic gaseous cloud in the presence of viscoelastic dark matter, inter-coupled frictionally only via mutualistic gravity. The viscoelasticity is considered for the constituent cosmic gravito-coupled fluids. This is because they are widely well known to behave as viscoelastic non-Newtonian fluids (Frenkel 1946; Landau and Lifshitz 1987; Borah et al. 2016; Brevik 2016). Such fluids exhibit a rich spectrum of structures via conjoint action of viscosity (sink for free energy dissipation) and elasticity (source for free energy storage). Therefore, interplay between the two fluid properties in a composite form is expected to support a rich cornucopia variety of hydro-gravitational fluctuation modes. Moreover, our gravitating fluid system is unbounded and infinitely spatially extended on the cosmic Jeansian fluid scales of space and time. And, hence, it is rationally treated in the framework of spatially-flat (sheet-like, planar) geometry approximation. In order to validate this geometric approximation, it is presumed that the radius of curvature of the bi-slab fluidic system (gravitationally confining the complex fluid) is much greater than all the characteristic scale lengths in the system. Such spatially-flat fluid sheet-like (or disk-like, small in thickness) geometry of the expanding universe has already been predicted in the inflationary model descriptions as well (Binney and Tremaine 1987; Mo et al. 2010). We account also for the effect of viscoelasticities, Coriolis forces and frictional coupling forces on the gravitational dynamics in hydrostatic homogenous equilibrium condition. The frictional interaction arises here due to the resistive fluid-layer-coupling between the NGF and the DMF via microscopic particle interactions. The plasma effects (via polarization due to ionic species, sourced by contact interaction with cosmic rays) are ignored due to smallness of the Debye screening length in comparison with the characteristic Jeans lengths (Karmakar and Borah 2016; Borah et al. 2016; Karmakar and Das 2017). The effectuation by interstellar turbulence and gravitational effect of distant astrophysical objects is also not allowed to influence the gravitational dynamics on the defined spatiotemporal scales of current interest.

A quantitative essence of the gravito-thermal coupling of the considered fluids to judge the DMF inclusion may be drawn as follows. We consider the cosmic gaseous cloud as consisting of hydrogen at a temperature of \(T_{g} = 20 \mbox{ K}\) (Stahler and Palla 2004; Gnedin et al. 2016). In such a situation, the gravito-thermal coupling constant of the gaseous fluid on the gas Jeans scale extension (\(\lambda_{Jg}\)), with all the usual notations (Stahler and Palla 2004; Gnedin et al. 2016), is now estimated as \(\varGamma_{g} = ( Gm_{g}^{2} / \lambda_{Jg}k_{B}T ) \sim 4.3 \times 10^{ - 84}\). In parallel, we take the DMF as composed of weakly interacting massive particles (WIMPs) with a typical mass \(m_{d} = 10^{ - 7}\mbox{ kg}\) at temperature \(T_{d} = 10^{11} \mbox{ K}\) (Blain 2005). The gravito-thermal coupling constant for the DMF on the same gas Jeans scale extension is calculated as \(\varGamma_{d} = ( Gm_{d}^{2} / \lambda_{Jd}k_{B}T ) \sim 0.62\). Thus, the ratio of the gas-to-dark matter gravito-thermal coupling on the common gas Jeans scale is \(\varGamma_{g} / \varGamma_{d} \sim 10^{ - 84}\). It clearly indicates why and how the cosmic universe is dominated by the gravitating DMF influences. Hence, the DMF dynamics needs to be included in understanding the real formation mechanism of diverse large-scale structures in galaxies (Blain 2005).

This is well known that a gravitating complex fluid system in the presence of dark matter, as considered in our model configuration here, can be well regarded as a bi-component (bright matter plus dark matter) fluid (Zhang and Li 1995). As a first gradation, herein, our model consists of an infinite complex fluid disk or sheet which may be assumed to be a collection of infinitely populous wires. A constituent wire is supposed to spatially extend from the initial position \(x=0\) at the initial time \(t=0\) to an instantaneous position \(x=x\) at any instant of time \(t=t\). We now implement the modified equations of continuity, momentum transfer, thermodynamic state, gravitational Poisson potential distribution in hydrostatic equilibrium condition in a closed coupled form for both the NGF and DMF; respectively. The subscript “\(g\)” stands for the gas and subscript “\(d\)”, the dark matter. Thus, the neutral gas dynamics of the considered fluid sheet is classically described in the flattened coordination space-time \((x, t)\) in the customary notations with all usual significances (Tsiklauri 1998, 2000; Karmakar and Das 2017) as follows

$$\begin{aligned}& \frac{\partial \rho_{g}}{\partial t} + \frac{\partial}{\partial x} ( \rho_{g}u_{g} ) = 0, \end{aligned}$$
(1)
$$\begin{aligned}& \biggl[ 1 + \tau_{mg} \biggl( \frac{\partial}{\partial t} + u_{g}\frac{\partial}{\partial x} \biggr) \biggr] \\& \qquad{}\times \biggl[ \rho_{g} \biggl( \frac{\partial u_{g}}{\partial t} + u_{g}\frac{\partial u_{g}}{\partial x} \biggr) + \frac{\partial p_{g}}{\partial x} + \rho_{g}\frac{\partial \phi}{ \partial x} \\& \qquad{} - 2\rho_{g}u_{gy}\varOmega_{gz} - \rho_{g}\nu_{dg} ( u_{g} - u_{d} ) \biggr] \\& \quad= \biggl( \frac{4}{3}\eta_{g} + \zeta_{g} \biggr) \frac{\partial^{2}u_{g}}{\partial x^{2}}, \end{aligned}$$
(2)

and

$$ p_{g} = \gamma_{g}n_{g}T_{g} = \gamma_{g} \biggl( \frac{\rho_{g}}{m_{g}} \biggr)T_{g}. $$
(3)

In the above, \(m_{g}\), \(\rho_{g} = m_{g}n_{g}\), \(u_{g}(u_{d})\), \(p_{g}\) and \(T_{g}\) denote the mass, density, velocity (dark matter velocity), pressure and temperature of the NGF; respectively. The viscoelastic relaxation time of the NGF is symbolized as \(\tau_{mg}\). The notations, \(\eta_{g}\) and \(\zeta_{{g}}\), are the shear (or first) viscosity (resistance to flow) and bulk (or second) viscosity (resistance to expansion) of the fluid arising due to microscopic particle motions (Frenkel 1946; Landau and Lifshitz 1987); respectively. For the isothermal NGF, the adiabaticity index is adopted as, \(\gamma_{g} = 1\). Then, \(\varOmega_{gz}\) and \(\nu_{dg}\) are the z-components of the angular frequency of the rotating gas cloud and the binary collisional rate (collisional frequency) of momentum transfer between the DMF to NGF; respectively.

In a standardized way, the dynamics of gravitating DMF is portrayed by a similar set of fluid structuring equations, but in a modified form with all the usual notations (Tsiklauri 1998, 2000; Karmakar and Das 2017), as follows

$$\begin{aligned}& \frac{\partial \rho_{d}}{\partial t} + \frac{\partial}{\partial x} ( \rho_{d}u_{d} ) = 0, \end{aligned}$$
(4)
$$\begin{aligned}& \biggl[ 1 + \tau_{md} \biggl( \frac{\partial}{\partial t} + u_{d}\frac{\partial}{\partial x} \biggr) \biggr] \\& \qquad{}\times \biggl[ \rho_{d} \biggl( \frac{\partial u_{d}}{\partial t} + u_{d}\frac{\partial u_{d}}{\partial x} \biggr) + \frac{\partial p_{d}}{\partial x} + \rho_{d}\frac{\partial \phi}{ \partial x} \\& \qquad{} - 2\rho_{d}u_{dy}\varOmega_{dz} - \rho_{d}\nu_{gd} ( u_{d} - u_{g} ) \biggr] \\& \quad= \biggl( \frac{4}{3}\eta_{d} + \zeta_{d} \biggr) \frac{\partial^{2}u_{d}}{\partial x^{2}}, \end{aligned}$$
(5)

and

$$ p_{d} = \gamma_{d}n_{d}T_{d} = \gamma_{d} \biggl( \frac{\rho_{d}}{m_{d}} \biggr)T_{d}. $$
(6)

Here, analogously, \(m_{d}\), \(\rho_{d} = m_{d}n_{d}\), \(p_{d}\), \(T_{d}\) denote the mass, density, pressure and temperature of the DMF; respectively. The viscoelastic relaxation time of the DMF is symbolized by \(\tau_{md}\). Likewise, \(\eta_{d}\) and \(\zeta_{{d}}\) are the shear viscosity and bulk viscosity (Frenkel 1946; Landau and Lifshitz 1987) of the DMF; respectively. Further, \(\varOmega_{dz}\) and \(\nu_{gd}\) are the z-component of the angular frequency of the rotating DMF and the binary collisional rate (collisional frequency) of momentum transfer from the NGF to DMF. As before, for the isothermal DMF, the adiabaticity index is taken as, \(\gamma_{d} = 1\).

The closure of our model is obtained by the gravitational Poisson equation and the hydrostatic equilibrium condition setup in an inter-coupled fluid form respectively given as

$$ \frac{\partial^{2}\phi}{\partial x^{2}} = 4\pi G \bigl\{ \rho_{g} + \rho_{d} - ( \rho_{g0} + \rho_{d0} ) \bigr\} , $$
(7)

and

$$ \frac{\partial p_{g}}{\partial x} + \frac{\partial p_{d}}{\partial x} = - ( \rho_{g} + \rho_{d} ) \frac{\phi}{x}, $$
(8)

where, \(\phi\) is the unipolar gravitational potential, conjointly contributed by both the coupled NGF and DMF density fields. Further, \(\rho_{g0}\) and \(\rho_{d0}\) are their respective equilibrium (unperturbed) densities. Lastly, \(G=6.673 \times 10^{ - 11}\mbox{ N m}^{2}\mbox{ kg}^{- 2}\) is the universal gravitational (Newtonian) constant via which the cosmic gravitational interaction is perceptible.

It may be pertinent to add here that the momentum conservation laws, as given by Eq. (2) and Eq. (5), are valid only for the most generalized class of compressible fluids with the first-order viscoelasticity. In such a case, none of the viscosity coefficients remarkably change either with the fluid pressure, or with the fluid temperature throughout the fluid transits (Frenkel 1946; Landau and Lifshitz 1987). In other words, both the classes of the viscosity coefficients are spatiotemporally independent (constant) throughout the model setup.

This is a well-established fact that the growth of dark matter fluctuations, gravitationally inter-coupled with neutral gaseous ones, has an organic linkage to the Jeans scale (Papantonopoulos 2007). We, therefore, adopt a standard cosmic normalization scheme relevant on the cosmic Jeans scales of space and time (Jeans 1902; Binney and Tremaine 1987; Papantonopoulos 2007; Mo et al. 2010; Bertin 2014). The normalized set of the basic governing equations (Eqs. (1)–(8)), after using the equations of state (Eq. (3) and Eq. (6)) for both the fluids, is respectively obtained in a closed form as

$$\begin{aligned}& \frac{\partial D_{g}}{\partial \tau} + \frac{\partial}{\partial \xi} ( D_{g}M_{g} ) = 0, \end{aligned}$$
(9)
$$\begin{aligned}& \biggl[ 1 + \tau_{mg}\omega_{Jg} \biggl( \frac{\partial}{\partial \tau} + M_{g}\frac{\partial}{\partial \xi} \biggr) \biggr] \\& \qquad{}\times \biggl[ D_{g} \biggl( \frac{\partial M_{g}}{\partial \tau} + M_{g}\frac{\partial M_{g}}{\partial \xi} \biggr) + \frac{\partial D_{g}}{\partial \xi} + D_{g}\frac{\partial \varPhi}{\partial \xi} \\& \qquad{} - 2D_{g}M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) - D_{g} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g} - M_{d} ) \biggr] \\& \quad = \frac{V_{xg}^{2}}{c_{sg}^{2}}\tau_{mg}\omega_{Jg} \frac{\partial^{2}M_{g}}{\partial \xi^{2}}, \end{aligned}$$
(10)
$$\begin{aligned}& \frac{\partial D_{d}}{\partial \tau} + \frac{\partial}{\partial \xi} ( D_{d}M_{d} ) = 0, \end{aligned}$$
(11)
$$\begin{aligned}& \biggl[ 1 + \tau_{md}\omega_{Jg} \biggl( \frac{\partial}{\partial \tau} + M_{d}\frac{\partial}{\partial \xi} \biggr) \biggr] \\& \quad\quad{}\times \biggl[ D_{d} \biggl( \frac{\partial M_{d}}{\partial \tau} + M_{d}\frac{\partial M_{d}}{\partial \xi} \biggr) + \frac{\partial D_{d}}{\partial \xi} + D_{d}\frac{\partial \varPhi}{\partial \xi} \\& \qquad{} - 2D_{d}M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr) - D_{d} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d} - M_{g} ) \biggr] \\& \quad = \frac{V_{xd}^{2}}{c_{sg}^{2}}\tau_{md}\omega_{Jg} \frac{\partial^{2}M_{d}}{\partial \xi^{2}}, \end{aligned}$$
(12)
$$\begin{aligned}& \frac{\partial^{2}\varPhi}{\partial \xi^{2}} = ( D_{g} + D_{d} ) - ( 1 + D_{d0} ), \end{aligned}$$
(13)

and

$$ \frac{\partial D_{g}}{\partial \xi} + \frac{\partial D_{d}}{\partial \xi} = - ( D_{g} + D_{d} )\frac{\varPhi}{\xi}. $$
(14)

Here, \(V_{xg}^{2} = ( 4 / 3\eta_{g} + \zeta_{g} ) / \rho_{g0}\tau_{mg}\) and \(V_{xd}^{2} = ( 4 / 3\eta_{d} + \zeta_{d} ) / \rho_{g0}\tau_{md}\) are the squares of viscoelastic mode velocities associated with the gas and dark matter, respectively. The independent variables, like position, \(\xi\), and time, \(\tau\), are normalized by the neutral gas Jeans length, \(\lambda_{Jg}\) and Jeans time, \(\tau_{Jg} = \omega_{Jg}^{ - 1} = ( 4\pi \rho_{g0}G )^{ - 1 / 2}\); respectively. The new symbols, \(D_{g}\), \(D_{d}\) and \(D_{d0}\) are the normalized population densities of the NGF, DMF and the DMF equilibrium population density, normalized each by the NGF equilibrium population density, \(\rho_{g0}\); respectively. Also, \(M_{g}\) and \(M_{d}\) are the corresponding normalized velocities (or Mach numbers) of the NGF and DMF; normalized each by the NGF acoustic phase speed, \(c_{sg} = \sqrt{\gamma_{g}p_{g} / \rho_{g}}\). Lastly, the normalized gravitational potential is denoted by \(\varPhi = \phi / c_{sg}^{2}\).

The focal goal of our investigation lies in exploring the excitation processes of weakly nonlinear gravitational fluctuations, where the perturbed density variables are feebler in magnitude than the corresponding equilibrium (average) values. We now apply the standard methodology of reductive perturbation technique (Burgers 1974; Whitham 1999; Wazwaz 2009; Ablowitz 2011) over inter-coupled Eqs. (9)–(15). The relevant dependent physical variables describing the coupled cloud dynamical system are expanded non-linearly as

$$ \left [ \textstyle\begin{array}{l} D_{g} \\ D_{d} \\ M_{g} \\ M_{d} \\ \varPhi \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{l} 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\displaystyle \right ] + \varepsilon \left [ \textstyle\begin{array}{l} D_{g1} \\ D_{d1} \\ M_{g1} \\ M_{d1} \\ \varPhi_{1} \end{array}\displaystyle \right ] + \varepsilon^{2}\left [ \textstyle\begin{array}{l} D_{g2} \\ D_{d2} \\ M_{g2} \\ M_{d2} \\ \varPhi_{2} \end{array}\displaystyle \right ] +\cdots. $$
(15)

In parallel, the normalized space variable, \(\xi\), and the time variable, \(\tau\), are strained into a new space defined by the stretched coordinate transformations as \(X: = \varepsilon^{1 / 2} ( \xi - \tau )\) and \(T: = \varepsilon^{3 / 2}\tau\). Here, \(\varepsilon\) is a small expansion parameter characterizing the normalized relative amplitude of the collective wave excitations. In the new space of slow temporal variation, the linear differential operators transform as, \(\partial / \partial \xi \equiv \varepsilon^{1 / 2}\partial / \partial X\) and \(\partial / \partial \tau \equiv \varepsilon^{3 / 2} \partial / \partial T - \varepsilon^{1 / 2}\partial / \partial X\). We apply the perturbative series expansion (Eq. (15)) in Eqs. (9)–(14) for order-by-order analyses. Thus, equating the like terms in various powers of \(\varepsilon\) from Eq. (9), one gets

$$ O \bigl( \varepsilon^{\frac{3}{2}} \bigr){:}\quad {-} \frac{\partial D_{g1}}{\partial X} + \frac{\partial M_{g1}}{\partial X} = 0, $$
(16)

which implies,

$$\begin{aligned}& D_{g1} = M_{g1}, \end{aligned}$$
(17)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{5}{2}} \bigr){:}\quad {-} \frac{\partial D_{g2}}{\partial X} + \frac{\partial D_{g1}}{\partial T} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\quad} + \frac{\partial}{ \partial X} ( D_{g1}M_{g1} ) + \frac{\partial M_{g2}}{\partial X} = 0, \end{aligned}$$
(18)

and so forth. Similarly, from Eq. (10), one gets

$$\begin{aligned}& O \bigl( \varepsilon^{0} \bigr){:}\quad {-} 2 ( \tau_{mg} \omega_{Jg} ) = 0, \end{aligned}$$
(19)
$$\begin{aligned}& O \bigl( \varepsilon^{1} \bigr){:}\quad {-} 2 ( \tau_{mg}\omega_{Jg} )D_{g1} \\& \phantom{O ( \varepsilon^{1} ){:}\quad\quad} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g1} - M_{d1} ) = 0, \end{aligned}$$
(20)

which implies,

$$\begin{aligned}& 2 ( \tau_{mg}\omega_{Jg} )D_{g1} = - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g1} - M_{d1} ), \end{aligned}$$
(21)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{3}{2}} \bigr){:}\quad {-} \frac{\partial M_{g1}}{\partial X} + \frac{\partial D_{g1}}{\partial X} + \frac{\partial \varPhi_{1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\qquad} + 2 ( \tau_{mg}\omega_{Jg} )M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) \frac{\partial D_{g1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\qquad} + ( \tau_{mg}\omega_{Jg} ) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \frac{\partial}{\partial X} ( M_{g1} - M_{d1} ) \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\quad}= 0, \end{aligned}$$
(22)

with the application of Eq. (17) and Eq. (21) in Eq. (22) yielding

$$\begin{aligned}& \frac{\partial \varPhi_{1}}{\partial X} = 0, \end{aligned}$$
(23)
$$\begin{aligned}& O \bigl( \varepsilon^{2} \bigr){:}\quad {-} 2M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) D_{g2} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g2} - M_{d2} ) \\ & \phantom{O ( \varepsilon^{2} ){:}\quad\quad\quad} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g1} - M_{d1} ) D_{g1} \\ & \phantom{O ( \varepsilon^{2} ){:}\quad\quad\quad} - \tau_{mg}\omega_{Jg}\frac{\partial^{2}D_{g1}}{\partial X^{2}} - \tau_{mg}\omega_{Jg}\frac{\partial^{2}\varPhi_{1}}{\partial X^{2}} \\ & \phantom{O ( \varepsilon^{2} ){:}\quad\quad}= \frac{V_{xg}^{2}}{c_{sg}^{2}} \tau_{mg}\omega_{Jg} \frac{\partial^{2}M_{g1}}{\partial X^{2}}, \end{aligned}$$
(24)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{5}{2}} \bigr){:}\quad \frac{\partial M_{g1}}{\partial T} - D_{g1}\frac{\partial M_{g1}}{\partial X} - \frac{\partial M_{g1}}{\partial X} + M_{g1} \frac{\partial M_{g1}}{\partial X} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} + \frac{\partial D_{g2}}{\partial X} + \frac{\partial \varPhi_{2}}{\partial X} + D_{g1} \frac{\partial \varPhi_{1}}{\partial X} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} - 2\tau_{mg}\omega_{Jg}M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr)\frac{\partial D_{g1}}{\partial T} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} - \tau_{mg}\omega_{Jg} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial T} ( M_{g1} - M_{d1} ) \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} + 2\tau_{mg}\omega_{Jg}M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr)\frac{\partial D_{g2}}{\partial X} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} + \tau_{mg}\omega_{Jg} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} ( M_{g2} - M_{d2} ) \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad}+ \tau_{mg}\omega_{Jg} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} \bigl\{ D_{g1} ( M_{g1} - M_{d1} ) \bigr\} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} + \tau_{mg}\omega_{Jg} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} \bigl\{ D_{g1} ( M_{g2} - M_{d2} ) \bigr\} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad}- 2\tau_{mg}\omega_{Jg}M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr)M_{g1}\frac{\partial D_{g1}}{\partial X} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\qquad\quad} - \tau_{mg}\omega_{Jg} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) M_{g1} \frac{\partial}{\partial X} ( M_{g1} - M_{d1} ) \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\quad} = 0,\quad \end{aligned}$$
(25)

and so on. Likewise, for the DMF, order-by-order analysis of Eq. (11) yields

$$ O \bigl( \varepsilon^{\frac{3}{2}} \bigr){:}\quad {-} \frac{\partial D_{d1}}{\partial X} + \frac{\partial M_{d1}}{\partial X} = 0, $$
(26)

which, in turn, implies,

$$\begin{aligned}& D_{d1} = M_{d1}, \end{aligned}$$
(27)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{5}{2}} \bigr){:}\quad {-} \frac{\partial D_{d2}}{\partial X} + \frac{\partial D_{d1}}{\partial T} \\ & \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\quad}+ \frac{\partial}{ \partial X} ( D_{d1}M_{d1} ) + \frac{\partial M_{d2}}{\partial X} = 0, \end{aligned}$$
(28)

and so on. Similarly, from Eq. (12), one finds

$$\begin{aligned}& O \bigl( \varepsilon^{0} \bigr){:}\quad {-} 2 ( \tau_{md} \omega_{Jg} ) = 0, \end{aligned}$$
(29)
$$\begin{aligned}& O \bigl( \varepsilon^{1} \bigr){:}\quad {-} 2 ( \tau_{md}\omega_{Jg} )D_{d1} \\& \phantom{O ( \varepsilon^{1} ){:}\quad\quad} - \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d1} - M_{g1} ) = 0, \end{aligned}$$
(30)

which yields,

$$\begin{aligned}& 2 ( \tau_{md}\omega_{Jg} ) D_{d1} = - \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d1} - M_{g1} ), \end{aligned}$$
(31)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{3}{2}} \bigr){:}\quad {-} \frac{\partial M_{d1}}{\partial X} + \frac{\partial D_{d1}}{\partial X} + \frac{\partial \varPhi_{1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\qquad} + 2 ( \tau_{md}\omega_{Jg} )M_{wy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr) \frac{\partial D_{d1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\qquad} + ( \tau_{md}\omega_{Jg} ) \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) \frac{\partial}{\partial X} ( M_{d1} - M_{g1} ) \\& \phantom{O ( \varepsilon^{\frac{3}{2}} ){:}\quad\quad} = 0, \end{aligned}$$
(32)

wherein, using Eq. (27) and Eq. (31) in Eq. (32), one gets

$$\begin{aligned}& \frac{\partial \varPhi_{1}}{\partial X} = 0, \end{aligned}$$
(33)
$$\begin{aligned}& O \bigl( \varepsilon^{2} \bigr){:}\quad {-} 2M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr) D_{d2} - \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d2} - M_{g2} ) \\& \phantom{O ( \varepsilon^{2} ){:}\quad\qquad} - \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d1} - M_{g1} ) D_{d1} \\& \phantom{O ( \varepsilon^{2} ){:}\quad\qquad} - \tau_{md}\omega_{Jg}\frac{\partial^{2}D_{d1}}{\partial X^{2}} - \tau_{md}\omega_{Jg}\frac{\partial^{2}\varPhi_{1}}{\partial X^{2}} \\& \phantom{O ( \varepsilon^{2} ){:}\quad\quad} = \frac{V_{xd}^{2}}{c_{sg}^{2}} \tau_{md}\omega_{Jg} \frac{\partial^{2}M_{d1}}{\partial X^{2}}, \end{aligned}$$
(34)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{5}{2}} \bigr){:}\quad \frac{\partial M_{d1}}{\partial T} - D_{d1}\frac{\partial M_{d1}}{\partial X} - \frac{\partial M_{d1}}{\partial X} + M_{d1} \frac{\partial M_{d1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} + \frac{\partial D_{d2}}{\partial X} + \frac{\partial \varPhi_{2}}{\partial X} + D_{d1} \frac{\partial \varPhi_{1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} - 2\tau_{md}\omega_{Jg}M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)\frac{\partial D_{d1}}{\partial T} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} - \tau_{md}\omega_{Jg} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial T} ( M_{d1} - M_{g1} ) \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} + 2\tau_{md}\omega_{Jg}M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)\frac{\partial D_{d2}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} + \tau_{md}\omega_{Jg} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} ( M_{d2} - M_{g2} ) \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad}+ \tau_{md}\omega_{Jg} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} \bigl\{ D_{d1} ( M_{d1} - M_{g1} ) \bigr\} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad} + \tau_{md}\omega_{Jg} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\frac{\partial}{\partial X} \bigl\{ D_{d1} ( M_{d2} - M_{g2} ) \bigr\} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad}- 2\tau_{md}\omega_{Jg}M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)M_{d1}\frac{\partial D_{d1}}{\partial X} \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\qquad}- \tau_{md}\omega_{Jg} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) M_{d1} \frac{\partial}{\partial X} ( M_{d1} - M_{g1} ) \\& \phantom{O ( \varepsilon^{\frac{5}{2}} ){:}\quad\quad} = 0, \end{aligned}$$
(35)

and so on. Now, from Eq. (13), one finds

$$\begin{aligned}& O \bigl( \varepsilon^{0} \bigr){:}\quad 1 - D_{d0} = 0, \end{aligned}$$
(36)
$$\begin{aligned}& O \bigl( \varepsilon^{1} \bigr){:}\quad D_{g1} = - D_{d1}, \end{aligned}$$
(37)
$$\begin{aligned}& O \bigl( \varepsilon^{2} \bigr){:}\quad \frac{\partial^{2}\varPhi_{1}}{\partial X^{2}} = D_{g2} + D_{d2}, \end{aligned}$$
(38)

etc. In a similar way, Eq. (14) gives

$$\begin{aligned}& O \bigl( \varepsilon^{\frac{3}{2}} \bigr){:}\quad \frac{\partial D_{g1}}{\partial X} + \frac{\partial D_{d1}}{\partial X} = 0, \end{aligned}$$
(39)
$$\begin{aligned}& O \bigl( \varepsilon^{\frac{5}{2}} \bigr){:} \quad\frac{\partial D_{g2}}{\partial X} + \frac{\partial D_{d2}}{\partial X} = - ( D_{g1} + D_{d1} ) \frac{\varPhi {}_{1}}{X}, \end{aligned}$$
(40)

and so forth. Using Eq. (37), Eq. (40) becomes

$$ \frac{\partial D_{g2}}{\partial X} + \frac{\partial D_{d2}}{\partial X} = 0. $$
(41)

Also, spatially differentiating Eq. (38), one gets

$$ \frac{\partial^{3}\varPhi_{1}}{\partial X^{3}} = \frac{\partial D_{g2}}{\partial X} + \frac{\partial D_{d2}}{\partial X}. $$
(42)

Moreover, using Eq. (41) in Eq. (42), one obtains

$$ \frac{\partial^{3}\varPhi_{1}}{\partial X^{3}} = 0. $$
(43)

Now, for solving Eq. (42), in the light of Eq. (25) and Eq. (35) after cancelling the higher-order terms due to weakly nonlinear fluctuations, one gets

$$ \begin{aligned}[b] \frac{\partial D_{g2}}{\partial X} ={} &\frac{1}{ \{ 1 + \tau_{mg}\omega_{Jg}M_{gy} ( \frac{\varOmega_{gz}}{\omega_{Jg}} ) \}} \\ &\times\biggl[ - \frac{\partial D_{g1}}{\partial T} + \frac{\partial D_{g1}}{\partial X} - D_{g1} \frac{\partial \varPhi_{1}}{\partial X} \\ & + 4\tau_{mg}\omega_{Jg}M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr)D_{g1}\frac{\partial D_{g1}}{\partial X} \biggr]. \end{aligned} $$
(44)

Similarly, for the DMF dynamics with the derived condition \(D_{d1} = - D_{g1} \) (as in Eq. (37)), we see that Eq. (44) reduces to

$$ \begin{aligned}[b] \frac{\partial D_{d2}}{\partial X} ={} &\frac{1}{ \{ 1 + \tau_{md}\omega_{Jg}M_{dy} ( \frac{\varOmega_{dz}}{\omega_{Jg}} ) \}} \\ &\times\biggl[ \frac{\partial D_{g1}}{\partial T} - \frac{\partial D_{g1}}{\partial X} + D_{g1} \frac{\partial \varPhi_{1}}{\partial X} \\ & + 4\tau_{md}\omega_{Jg}M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)D_{g1}\frac{\partial D_{g1}}{\partial X} \biggr]. \end{aligned} $$
(45)

Now, combining Eqs. (44)–(45) in Eq. (42), one finally gets

$$ \frac{\partial D_{g1}}{\partial T} + \alpha D_{g1}\frac{\partial D_{g1}}{\partial X} = \frac{\partial D_{g1}}{\partial X}, $$
(46)

and

$$ \frac{\partial D_{d1}}{\partial T} - \alpha D_{d1}\frac{\partial D_{d1}}{\partial X} = \frac{\partial D_{d1}}{\partial X}. $$
(47)

Thus, it is seen that the nonlinear perturbation dynamics of the composite cloud is collectively governed by non-static Eqs. (46)–(47) in the framework of nonlinear diffusion as a combined effect of dissipation and dispersion. They form a conjugate pair of the viscoelastic forced Burgers (VFB) equations for the NGF and DMF, viscoelastically inter-coupled via mutualistic gravity alone; respectively. The VFB pair appears in conjugation with the fluid flow convections in opposite phases. It may be noted that there is no damping term in the pair VFB equations, unlike in the conventional Burger equation (Burgers 1974; Whitham 1999; Ablowitz 2011). Instead, a linear self-consistent derivative force-term appears in the derived VFB system. Moreover, it is founded on the fact that the lowest-order density fluctuations of the NGF and DMF propagate in opposite phases. Lastly, it is speculated that the conjugate pair of the VFB equations is well connected via the conjugate bi-fluidic viscoelastic parameter, \(\alpha\), presented as

$$ \begin{aligned}[b] \alpha ={}& 2\left[ \textstyle\begin{array}{l} ( \tau_{mg} \omega_{Jg} )M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) + ( \tau_{md}\omega_{Jg} )M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr) \\ + 4 ( \tau_{mg}\omega_{Jg} )M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) ( \tau_{md}\omega_{Jg} )M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)\end{array}\displaystyle \right] \\ & \Big/{\biggl( ( \tau_{mg}\omega_{Jg} )M_{gy} \biggl( \frac{\varOmega_{gz}}{\omega_{Jg}} \biggr) - ( \tau_{md}\omega_{Jg} )M_{dy} \biggl( \frac{\varOmega_{dz}}{\omega_{Jg}} \biggr)\biggr)}. \end{aligned} $$
(48)

We are interested in the evolutionary fluctuation patterns in both the static (\(\partial / \partial T \sim 0 \)) and dynamic (\(\partial / \partial T \ne 0 \)) forms. As a first step, we look for the steady-state solutions for the fluctuations spatially governed by the conjugate time-stationary derivative VFB pair (Eqs. (51)–(52) in the Appendix). After having it done, as a second step, the spatiotemporal dynamics of the fluctuations is numerically analyzed for the dynamic solutions in the framework of the non-stationary conjugate pair VFB equations (Eqs. (46)–(47)).

3 Results and discussions

The gravity-induced instability analysis of the cosmic viscoelastic clouds, consisting of the gravito-coupled NGF and DMF, is methodically carried out. It applies a non-linear classical perturbation theory in the framework of standard reductive perturbation technique to derive a unique pair of conjugated VFB equations. The lowest-order diffusive eigen-modes stemming in it are numerically explored. The NGF dynamics as in Figs. 1, 2, 3, 4 and the DMF dynamics in Figs. 5, 6, 7, 8 are illustrated. It may be mentioned that the fourth-order Runge–Kutta method (Lindfield and Penny 2012; Gnedin et al. 2016) is implemented to obtain the spatial profiles (Figs. 1, 2, 3 and Figs. 5, 6, 7); and the finite element method (Lindfield and Penny 2012; Gnedin et al. 2016) is utilized to construct the spatiotemporal profiles (Fig. 4 and Fig. 8). The different multi-parametric inputs and initial values employed in the analysis are fed from the diversified sources available in the literature (Binney and Tremaine 1987; Tsiklauri 1998, 2000; Mo et al. 2010; Beringer et al. 2012; Bertin 2014; Karmakar and Das 2017).

Fig. 1
figure 1

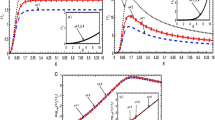
Spatial profiles of the normalized perturbed gas (a) density (\(D_{g1}\)), (b) density gradient (\(\partial D_{g1} / \partial r\)), (c) phase portrait on density (\(D_{g1}\)) and density gradient (\(\partial D_{g1} / \partial r\)), and (d) density gradient scale [\(D_{g1} / ( \partial D_{g1} / \partial r )\)] for different values of the frame-velocity (\(M_{f}\)). Various lines link to (1): \(M_{f} = 0.4\) (Line 1, blue), (2): \(M_{f} = 0.8\) (Line 2, red), and (3): \(M_{f} = 1.2\) (Line 3, black); respectively. The initials and inputs are highlighted in the text

Full size image
Fig. 2
figure 2

Same as Fig. 1, but for different values of the gaseous viscoelastic relaxation time (\(\tau_{mg}\omega_{Jg}\)). Various lines now link to (1): \(\tau_{mg}\omega_{Jg} = 0.1\) (Line 1, blue), (2): \(\tau_{mg}\omega_{Jg} = 0.2\) (Line 2, red) and (3): \(\tau_{mg}\omega_{Jg} = 0.3\) (Line 3, black); respectively

Full size image
Fig. 3
figure 3

Same as Fig. 1, but for different values of the dark-matter viscoelastic relaxation time (\(\tau_{md} \omega_{Jg}\)). Various lines now link to (1): \(\tau_{md} \omega_{Jg} = 1.0 \times 10^{ - 4}\) (Line 1, blue), (2): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 2, red), and (3): \(\tau_{md} \omega_{Jg} = 1.4 \times 10^{ - 4}\) (Line 3, black), respectively

Full size image
Fig. 4
figure 4

Spatiotemporal evolution of the normalized perturbed gaseous matter density (\(D_{g1}\)). The initial conditions and other details are presented in the text

Full size image
Fig. 5
figure 5

Spatial profiles of the normalized perturbed dark-matter (a) density (\(D_{d1}\)), (b) density gradient (\(\partial D_{d1} / \partial r\)), (c) phase portrait on density (\(D_{d1}\)) and density gradient (\(\partial D_{d1} / \partial r\)), and (d) density gradient scale (\(D_{d1} / ( \partial D_{d1} / \partial r )\)) for different values of the frame-velocity (\(M_{f}\)). Various lines link to (1): \(M_{f} = 0.4\) (Line 1, blue), (2): \(M_{f} = 0.8\) (Line 2, red), and (3): \(M_{f} = 1.2\) (Line 3, black); respectively. The initials and inputs are highlighted in the text

Full size image
Fig. 6
figure 6

Same as Fig. 4, but for different values of the gaseous viscoelastic relaxation time (\(\tau_{mg}\omega_{Jg}\)). Various lines now link to (1): \(\tau_{mg}\omega_{Jg} = 0.1\) (Line 1, blue), (2): \(\tau_{mg}\omega_{Jg} = 0.2\) (Line 2, red) and (3): \(\tau_{mg}\omega_{Jg} = 0.3\) (Line 3, black); respectively

Full size image
Fig. 7
figure 7

Same as Fig. 5, but for different values of the dark-matter viscoelastic relaxation time (\(\tau_{md} \omega_{Jg}\)). Various lines link to (1): \(\tau_{md} \omega_{Jg} = 1.0 \times 10^{ - 4}\) (Line 1, blue), (2): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 2, red) and (3): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 3, black); respectively

Full size image
Fig. 8
figure 8

Spatiotemporal evolution of the normalized dark-matter density (\(D_{d1}\)). The initial conditions and other details are presented in the text

Full size image

3.1 Gaseous fluid dynamics

In Fig. 1, we show the spatial profiles of the normalized perturbed gas (a) density (\(D_{g1}\)), (b) density gradient (\(\partial D_{g1} / \partial r\)), (c) phase portrait on density (\(D_{g1}\)) and density gradient (\(\partial D_{g1} / \partial r\)), and (d) density gradient scale [\(D_{g1} / ( \partial D_{g1} / \partial r )\)] for different values of the frame-velocity (\(M_{f}\)). Various lines refer to (1): \(M_{f} = 0.4\) (Line 1, blue), (2): \(M_{f} = 0.8\) (Line 2, red), and (3): \(M_{f} = 1.2\) (Line 3, black); respectively. Various input values used are \(\tau_{mg}\omega_{Jg} = 0.01\), \(\tau_{md}\omega_{Jg} = 1 \times 10^{ - 4}\), \(M_{gy} ( \varOmega_{gz} / \omega_{Jg} ) = 2.8 \times 10^{ - 2}\), \(M_{dy} ( \varOmega_{dz} / \omega_{Jg} ) = 1 \times 10^{ - 4}\). Figure 1(a) shows that, in the subsonic range, the NGF matter perturbed density evolves as extended compressive solitons-like structures. In the supersonic regime, the perturbed gas density propagates as shock-like structures. The inferences are drawn merely from the numerical confirmatory illustrative pedestal. Further, it implicates that \(M_{f} = 1\) must correspond to hybrid phase trajectory structure, intermediate between the two classes, although excluded here in the display for simplicity and consistency. In Fig. 1(b), in the subsonic regime on the defined spatial scale length, an admixture of peakon (compressive) and anti-peakon (rarefactive) structures (Ablowitz 2011) is found to propagate. However, in the supersonic range, only peakon-like structures (Wazwaz 2009) are found to evolve. Figure 1(c) shows the geometrical trajectories of the gas dynamical fluctuations in the defined phase plane. The dynamical evolution of the gaseous eigen-structures is an asymmetric aperiodic one and the phase trajectories are open. Hence, the conjugate VFB system indeed represents a non-conservative dynamics. The phase trajectories are heteroclinic in nature. Figure 1(d) depicts the inhomogeneity scale-behaviour of the fluctuations. Corresponding to the extreme behaviour of the density gradients, irregular resonance poles are found to exist at different distances relative to the centre of the cloud matter distribution. It also shows that the resonance poles exhibit singular behaviours of the fluctuations, which in turn, implicate the possibility of reorganized triggering of mechanical instability on the next higher orders (although weaker). Figure 2 depicts the same as Fig. 1, but for different values of the gaseous viscoelastic relaxation time (\(\tau_{mg}\omega_{Jg}\)). Various lines now correspond to (1): \(\tau_{mg}\omega_{Jg} = 0.1\) (Line 1, blue), (2): \(\tau_{mg}\omega_{Jg} = 0.2\) (Line 2, red) and (3): \(\tau_{mg}\omega_{Jg} = 0.3\) (Line 3, black); respectively. Various input values used are same as Fig. 1, except in the frame velocity, \(M_{f} = 0.5\). Figure 3 is same as Fig. 1, but for different values of the dark-matter viscoelastic relaxation time (\(\tau_{md} \omega_{Jg}\)). Various lines now link to (1): \(\tau_{md} \omega_{Jg} = 1.0 \times 10^{ - 4}\) (Line 1, blue), (2): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 2, red), and (3): \(\tau_{md} \omega_{Jg} = 1.4 \times 10^{ - 4}\) (Line 3, black); respectively. Various input values used here are same as Fig. 1, but for the gaseous viscoelastic relaxation time, \(\tau_{mg}\omega_{Jg} = 0.002\).

Figure 4 depicts the spatiotemporal profile of the gas density fluctuations on the lowest-order. Here too, various input values used here are the same as Fig. 1. The initial condition applied here is \(D_{g1} = \sinh^{ - 1} ( X )\), which is indeed a compressive shock-like pattern, speculatively obtained from the spatial profile description presented before. Unlike in the moving frame, as before, here in this case of lab-frame, the fluctuation dynamics reveals a plethora of eigen-modes of different characteristic features. Initially, it shows a shock-like behaviour over space; but, quite stable in the time frame. Hereafter, the spectral richness of the eigen-modes evolves both in space and time. Thus, the spatiotemporal display reveals a rich spectrum of nonlinear eigen-structures caused by the conjoint mutualistic action of viscoelastic effects of the component gravitating fluids structuring the global composite cloud.

3.2 Dark matter fluid dynamics

In Fig. 5, we depict the spatial profiles of the normalized perturbed dark-matter (a) density (\(D_{d1}\)), (b) density gradient (\(\partial D_{d1} / \partial r\)), (c) phase portrait on density (\(D_{d1}\)) and density gradient (\(\partial D_{d1} / \partial r\)), and (d) density gradient scale (\(D_{d1} / ( \partial D_{d1} / \partial r )\)) for different values of the frame-velocity (\(M_{f}\)). Various lines link to (1): \(M_{f} = 0.4\) (Line 1, blue), (2): \(M_{f} = 0.8\) (Line 2, red), and (3): \(M_{f} = 1.2\) (Line 3, black); respectively. Different input values used are \(\tau_{mg}\omega_{Jg} = 0.01\), \(\tau_{md}\omega_{Jg} = 1 \times 10^{ - 4}\), \(M_{gy} ( \varOmega_{gz} / \omega_{Jg} ) = 2.8 \times 10^{ - 2}\), \(M_{dy} ( \varOmega_{dz} / \omega_{Jg} ) = 1 \times 10^{ - 4}\). In Fig. 5(a), in the subsonic regime, we see hybrid shock-like structures composed of rarefactive extended solitons and compressive monotonic shocks. However, in the supersonic regime, we see only rarefactive extended solitons-like structures over the defined spatial scale length. Figure 5(b) shows that, the dark matter density fluctuations propagate as hybrid structures composed of anti-peakons (rarefactive) accompanied by micro-peakons (compressive). The remaining figures, Fig. 5(c)–(d), convey the same physics, as described previously in Fig. 1(c)–(d). Clearly, \(M_{f} = 1\) must correspond to hybrid trajectory structure, intermediate between the two distinct classes, Fig. 6 is the same as Fig. 5, but for the different gaseous viscoelastic relaxation time (\(\tau_{mg}\omega_{Jg}\)). Various lines now refer to (1): \(\tau_{mg}\omega_{Jg} = 0.1\) (Line 1, blue), (2): \(\tau_{mg}\omega_{Jg} = 0.2\) (Line 2, red) and (3): \(\tau_{mg}\omega_{Jg} = 0.3\) (Line 3, black); respectively. Various input values are same as Fig. 4, but for different value of reference frame velocity \(M_{f} = 0.5\). Likewise, Fig. 7 depicts the same as Fig. 5, but for different values of the dark-matter viscoelastic relaxation time (\(\tau_{md} \omega_{Jg}\)). Various lines link to (1): \(\tau_{md} \omega_{Jg} = 1.0 \times 10^{ - 4}\) (Line 1, blue), (2): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 2, red) and (3): \(\tau_{md} \omega_{Jg} = 1.2 \times 10^{ - 4}\) (Line 3, black); respectively. Different input values are the same as Fig. 5, but except in \(\tau_{mg}\omega_{Jg} = 0.01\) used now.

Finally, in Fig. 8, we show the spatiotemporal fluctuation dynamics of the DMF density perturbations in the lab-frame. It reveals a complex spectrum of diffusive eigen-structures. The initial condition applied here is \(D_{d1} = - \sinh^{ - 1} ( X )\), which is indeed a rarefactive shock-like pattern, judiciously constructed from the earlier steady-state description. Only after a small interval of space and time, the existence of multiple solitons and shocks, together with associated peakon-plethora (Wazwaz 2009), is unveiled. It conforms that the conjugate VFB dynamics internally supports a rich variety of complex modes of both compressive and rarefactive nature in environments like dark matter-dominated dwarf spheroidals in the cosmic universe.

4 Concluding remarks

In conclusion, an semi-analytic formalism is methodologically constructed to see the gravitational non-linear diffusive fluctuation dynamics in a composite cloud fluid on the cosmic Jeans scales of space and time. All the possible realistic factors, sensible for the astro-cosmic fluctuation dynamics, are concurrently considered. The viscoelastic coupling mechanism of the NGF and DMF is included via symbiotic gravity. A new set of basic governing equations is constructed in a standard normalized scale-invariant form. Application of perturbative technique reduces the system into a unique conjugated pair of the coupled VFB equations. The numerical standpoint establishes the eigen-modes to evolve as soliton-shock-like amalgamated hybrid structures. It is important to note that, there is no damping terms in the VFB system, unlike in the conventional Burgers equations. Instead, linear derivative forced terms appear. We demonstrate that the NGF perturbed density evolves as extended compressive solitons-like structures in the supersonic regime. The perturbed density propagates as shock-like structures in the subsonic regime. Also, we obtain an admixture of peakon (rarefactive) and antipeakon (compressive) structures (Wazwaz 2009) in the subsonic regime. However, in the supersonic range, the perturbed density propagates as peakon-like structures. Likewise, in the subsonic regime, the DMF perturbed density propagates as shock-like structures composed of rarefactive extended solitons and compressive monotonic shocks. However, in the supersonic regime, we see only rarefactive extended solitons-like structures over the defined spatial scale length. We further observe that the DMF density fluctuations propagate as hybrid structures composed of anti-peakons (rarefactive) and micro-peakons (compressive) in a commixed form (Wazwaz 2009).

The proposed analysis shows that the viscoelastic properties of the gravitating cosmic fluids give rise to linear derivative sources to the Burgers equations based on nonlinear diffusive sticking mechanisms of cosmo-gravitational origin (Gurbatov et al. 1990). It further fairly confirms the deep-rooted fact that the viscoelasticity of cosmic fluids really reveals a rich structural spectral plethora of eigen-patterns, as already recently reported in the literature (Brevik 2016). It may be noted that the obtained results are valid only on the cosmic Jeans scales of space and time in the presence of dark matter. This is because of the well-established fact that the growth of dark matter fluctuations has an organic linkage to the Jeans scale (Papantonopoulos 2007). Perturbations of smaller size fail to undergo gravitational collapse due to internal pressure support, arising from internal random kinetics, even at low redshift. In contrast, perturbations of larger scale undergo dynamic growth via gravity at the same rate independent of any scale of astrophysical interest (Papantonopoulos 2007; Beringer et al. 2012). The consideration of hydrostatic homogeneous equilibrium in our study can widen the horizon of applicability from the Jeans scales to the ones ranging from galaxies to cluster of galaxies with some facts and faults. It is to be admitted here that a simplistic classical Jeans theory is not self-sufficient in depicting a comprehensive tapestry of star formation processes in the gigantic molecular clouds. The realistic operational mechanisms preventing the gigantic clouds from dynamic collapse are still clearly not understood (Tsiklauri 1998). Despite such complications, the application of the classical Jeans theory reliably determines the accurate mass scale of stellar structures (∼ solar mass) in the interstellar normal molecular clouds (Tsiklauri 1998). We, therefore, finally hope that the results, although obtained here in the classical fluid framework of weak perturbation analysis in the lowest-order, may extensively be useful in understanding the basic formation mechanism of nonlinear organizations in the sub-luminous dark matter-dominated cosmic dwarf spheroidals in the form of panecakes, filamentary edifices or clumps and their merging mechanisms leading to large-scale non-homologous bounded structures from a new cosmic viscoelasticity viewpoint of collective correlative wave-excitation processes in the predictable future.