1 Introduction

The presence of dark matter is an unavoidable entity in the formation processes of large-scale structures through initially small-scale density perturbations of large-scale astrophysical clouds composed of both bright matter and dark matter in the expanding universe (Kates and Kaup 1988; Tsiklauri 1998, 2000; Mo et al. 2010). The structure formation is known to take place in the dense regions of these interstellar and cosmic clouds. The formation mechanism of the galactic structures is yet to be understood due to the presence of the invisible dark matter (cosmic glue). In the formation processes of bounded structures, the fundamental factors, such as non-local gravity, fluid turbulence, cooling and reactive feedback, are of great relevance in the reorganization processes of redistributed collapsing matter. The key mechanism can be mainly understood by the Jeans instability of the self-gravitating matter on a large-scale (Jeans 1902; Binney and Tremaine 1987; Bertin 2014). When the mass of the astro-clouds is greater than the critical fluid mass (Jeans mass), the mechanical long-wavelength wave perturbations grow under the effect of their own self-gravity effects leading to the formation of bounded structures via fragmentation and filamentation processes in astro-cosmic environments.

The interaction of normal gaseous clouds with the dark matter clouds in the modification of the so-called canonical Jeans instability is well known (Kates and Kaup 1988; Zhang and Li 1995; Tsiklauri 1998, 2000). It has been reported in the earlier works that the presence of dark matter reduces the effective Jeans length, Jeans time, and Jeans mass. In most of the studies, the dark matter considered has been constituted of a large-scale fluid made up of the material from brown dwarfs, dwarf satellite spheroidals, axions, etc (Binney and Tremaine 1987; Koch 2009; Mo et al. 2010; Khlopov 2012; Bertin 2014). However, the effects of the lowest-order fluid viscoelasticity, Coriolis force, fluid turbulence effects and inter-layer frictional coupling dynamics on the gravitational instability have been remaining unexplored for decades. As a result, the mechanism of bounded structure formation likely to be modified due to the above factors has long been lying as an open issue of astro-cosmic significance to be well addressed and explored.

The present work is motivated by the previously reported results on dark matter fluid-modified Jeans instability in realistic complex astrofluids to understand the triggering mechanism of bounded structure formation (Zhang and Li 1995; Tsiklauri 1998, 2000). In this work a new theoretical formalism for the gravitational instability in a bi-fluidic mixture composed of the gravitating neutral gas and dark matter fluid is proposed. The model includes the lowest-order viscoelasticity, Coriolis force, turbulence effects, and inter-layer frictional coupling dynamics. Here, in addition to the thermal pressure term, a turbulence pressure is also incorporated by using the modified Larson equation of state (Adams et al. 1994; Gehman et al. 1996). The factors considered afresh are indeed the properties of true astrophysical and cosmic fluids (Brevik 2016; Borah et al. 2016). The reason for the inclusion of fluid viscoelasticity in the present work stems in the fact that a rich variety of dynamic structure formation is supported in viscoelastic fluids via the interplay of elasticity (energy storage) and viscosity (energy dissipation). Moreover, the Coriolis effects are also included, since the Coriolis force modifies the dynamics and insures the conservation of angular momentum (Rozelot and Neiner 2009; Pathania et al. 2012). A linear normal (Fourier) perturbation analysis is methodically carried to reveal and characterize the Jeans instability in a new model form of present astro-cosmic importance.

2 Physical model and formulation

We develop a generalized fluid model of a complex rotating astrocloud composed of gaseous fluid inter-coupled with gyratory dark matter fluid via mutual gravity only. Instead of spherical (3-D) geometry of the complex astrocloud, we consider simplified spatially-flat geometry (1-D) of the sheet-like configuration problem. It is valid provided that the radius of curvature of the fluid-confining boundary is much larger than all the fluid characteristic scale lengths (Binney and Tremaine 1987; Bertin 2014). Such flat sheet-like geometry of the expanding universe is confirmed also by inflationary model descriptions (Mo et al. 2010). The lowest-order viscoelastic properties of both the gaseous and the dark matter fluids are considered due to the fact that cosmic fluids are well known to behave as viscoelastic fluids (Frenkel 1946; Borah et al. 2016; Brevik 2016). Another justification for the adopted generalized fluid model is that viscoelastic fluids exhibit a rich spectrum of structures via conjoint action of viscosity (as a sink for free energy dissipation) and elasticity (as a source for free energy storage). Therefore, interplay between the two fluid properties in a composite form is expected to support a rich variety of hydro-gravitational fluctuation modes previously remaining unexplored in the cosmic context. Moreover, we account for the effect of the Coriolis force, turbulence and the inter-fluid frictional coupling force in the gravitational dynamics (Rozelot and Neiner 2009; Pathania et al. 2012). The frictional interaction arises here due to the inter-layer-coupling (binary collisional interaction) between the gas and dark matter fluids. The turbulence pressures alongside the isothermal pressures are included with the help of the Larson empirical equation of state (Adams et al. 1994; Gehman et al. 1996). It is anticipated that the collision scale lengths among various constituent particles in the complex astrofluids are much smaller than the characteristic scale length of the gravitational fluctuations thereby validating the generalized fluid model consideration. In this direction, it has also been suggested that the dark matter in the outer halo of galaxies could be in the form of cold dense gas clouds with mass, typically on the order of the solar mass; temperature, 10 K; governed by polytropic equations of state with polytropic index, \(5 \le n \le 10\) (Gerhard and Silk 1996; Komatsu and Seljak 2001). Thus, the Jeans spatiotemporal scales for such clouds of mass on the order of the solar mass to undergo the dynamic collapse become a physical reality (Gerhard and Silk 1996; Komatsu and Seljak 2001). Accordingly, our proposed model is framed on a homogeneous hydrostatic equilibrium configuration on the lowest-order perturbations in a standard normalized form (scale-invariant) on the cosmological Jeans scales of space and time. The model formalism, so constructed in a standard scale-invariant normalized form, simultaneously indicates possibility for the existence of a flow regime characterized by chaotic changes in the flow dynamics, which is in principle, relevant in triggering the re-distribution of constituent matter in a reorganized form to undergo realistic kinetic transport processes for various bounded structures to form via dynamic top-down gravitational collapse mechanism in cosmic, space, dwarf spheroidals and various astrophysical environments (Koch 2009).

The equilibrium dynamics of the composite gravitating fluid is governed by the basic equations of viscoelastic fluids (on the lowest-order) in a closed form. It includes the continuity equation for flux density conservation, momentum equation for force density balance, Larson equation of state for the relevant thermodynamic variables and closing gravitational Poisson equation. We introduce the subscript ‘\(g\)’ to denote the neutral gaseous fluid having constant viscosity. The basic governing equations of continuity, momentum and thermodynamic state of the gaseous fluid with all the usual notations and significances in coordination space (\(x, t\)) relative to some reference point, in the customary notations with their usual meanings (Adams et al. 1994; Gehman et al. 1996; Borah et al. 2016), are respectively cast as

$$\begin{aligned}& \frac{\partial \rho_{g}}{\partial t} + \frac{\partial}{\partial x} ( \rho_{g}u_{g} ) = 0, \end{aligned}$$
(1)
$$\begin{aligned}& \biggl[ 1 + \tau_{mg} \biggl( \frac{\partial}{\partial t} + u_{g} \frac{\partial}{\partial x} \biggr) \biggr] \biggl[ \rho_{g} \biggl( \frac{\partial u_{g}}{\partial t} + u_{g}\frac{\partial u_{g}}{\partial x} \biggr) + \frac{\partial p_{g}}{\partial x} \\& \quad\quad{}+ \rho_{g}\frac{\partial \phi}{ \partial x} - 2\rho_{g}u_{gy} \Omega_{gz} - \rho_{g}\nu_{dg} ( u_{g} - u_{d} ) \biggr] \\& \quad = \biggl( \frac{4}{3}\eta_{g} + \zeta_{g} \biggr) \frac{\partial^{2}u_{g}}{\partial x^{2}}, \end{aligned}$$
(2)
$$\begin{aligned}& p_{g} = \biggl( \frac{T_{g}}{m_{g}} \biggr)\rho_{g} + p_{g0}\log \biggl( \frac{\rho_{g}}{\rho_{g0}} \biggr). \end{aligned}$$
(3)

In a similar way, the dark matter fluid dynamics, with all the generic symbols bearing usual significances (Adams et al. 1994; Gehman et al. 1996; Borah et al. 2016), is described as

$$\begin{aligned}& \frac{\partial \rho_{d}}{\partial t} + \frac{\partial}{\partial x} ( \rho_{d}u_{d} ) = 0, \end{aligned}$$
(4)
$$\begin{aligned}& \biggl[ 1 + \tau_{md} \biggl( \frac{\partial}{\partial t} + u_{d} \frac{\partial}{\partial x} \biggr) \biggr] \biggl[ \rho_{d} \biggl( \frac{\partial u_{d}}{\partial t} + u_{d}\frac{\partial u_{d}}{\partial x} \biggr) + \frac{\partial p_{d}}{\partial x} \\& \quad\quad{}+ \rho_{d}\frac{\partial \phi}{ \partial x} - 2\rho_{d}u_{dy} \Omega_{dz} - \rho_{g}\nu_{gd} ( u_{d} - u_{g} ) \biggr] \\& \quad = \biggl( \frac{4}{3}\eta_{d} + \zeta_{d} \biggr) \frac{\partial^{2}u_{d}}{\partial x^{2}}, \end{aligned}$$
(5)
$$\begin{aligned}& p_{d} = \biggl( \frac{T_{d}}{m_{d}} \biggr)\rho_{d} + p_{d0}\log \biggl( \frac{\rho_{d}}{\rho_{g0}} \biggr). \end{aligned}$$
(6)

Finally, the gravitating gaseous fluid and the gravitating dark matter fluid having constant viscosities are inter-coupled via the gravitational Poisson equation for the unipolar gravitational potential distribution by the bi-fluidic density fields as

$$ \frac{\partial^{2}\phi}{\partial x^{2}} = 4\pi G \bigl[ ( \rho_{g} - \rho_{g0} ) + ( \rho_{d} - \rho_{d0} ) \bigr]. $$
(7)

In the above, \(m_{g}\), \(\rho_{g} = m_{g}n_{g}\), \(\rho_{g0} = m_{g}n_{g0}\), \(u_{g}\), \(p_{g}\) and \(T_{g}\) denote the mass, material density, equilibrium value of material density, velocity, net pressure and temperature of the gaseous fluid; respectively. The net pressure of the neutral gaseous and dark matter fluids, \(p_{g}\) and \(p_{d}\), are contributed jointly by the isothermal pressure (first term, RHS) and turbulence pressure (second term, RHS) in the Larson equations of state, Eq. (3) and Eq. (6); respectively. \(p_{g0} (p_{d0})\) is the equilibrium gas (dark matter) pressure. Further, \(\eta_{g}\) and \(\zeta_{{g}}\) are the shear viscosity (indexing resistance against flow) and bulk viscosity (indexing resistance against expansion); respectively. Furthermore, for the isothermal gaseous fluid, the specific heat ratio, \(\gamma_{g} = 1\). Furthermore, \(\Omega_{gz}\) is the considered z-component of the angular frequency of the rotating neutral gas cloud and \(\nu_{dg}\) is the binary collisional rate of momentum transfer from the dark matter fluid to the gaseous one. The symbol \(\tau_{mg} (\tau_{md})\) denotes the viscoelastic relaxation time scale, which signifies how viscoelastic memory effects control wave propagation dynamics through the medium, associated with the gas cloud fluid (dark matter cloud fluid).

Analogously, \(m_{d}\), \(\rho_{d} = m_{d}n_{d}\), \(\rho_{d0} = m_{d}n_{d0}\), \(u_{d}\), \(p_{d}\), \(T_{d}\) denote the mass, material density, equilibrium value of material density, velocity, net pressure and temperature of the dark matter fluid; respectively. \(\Omega_{dz}\) and \(\nu_{gd}\) are the assumed z-components of the angular frequency of the rotating dark matter fluid and the binary collisional rate (collisional frequency) of momentum transfer from the gaseous fluid to the dark matter one. For the isothermal dark matter fluid, the adiabatic index, \(\gamma_{d} = 1\). The symbol \(\phi\) is the gravitational potential conjointly contributed by both the coupled neutral gaseous fluid and dark matter fluid. Lastly, \(G = 6.673 \times 10^{- 11}~\mbox{N}\,\mbox{m}^{2}\,\mbox{kg}^{-2}\) is the universal gravitational (Newtonian) coupling constant via which gravitational interaction is perceptible.

It may be pertinent to note from the excogitated construct of Eq. (7) that, the gravitational potential \(( \phi )\) in a spatially infinitely extended gravitating cloud is developed (as in LHS) by fluid material density perturbations relative to the global average density in the form of \([ ( \rho_{g} - \rho_{g0} ) + ( \rho_{d} - \rho_{d0} ) ] \) (as in RHS). This assumption, the gravitational Poisson equation describing density-potential relationship in a perturbed form, is well known as the Jeans swindle (Jeans 1902; Binney and Tremaine 1987; Bertin 2014). It, although an adhoc local approximation, thereby enables us to simplify the unperturbed multifaceted problem in gravity as an initially homogeneous one with the role of the zeroth-order pressure fields ignored. Such local homogenization assumptions are well validated in the astro-cosmic environments because the wavelength of the mechanical waves of our interest is much smaller than the spatial scales over which the equilibrium fluid densities and pressures considerably change.

To see the scale-invariant features of the gravitational fluctuation dynamics, the basic governing equations for both the gaseous fluid and dark matter fluid are normalized by adopting a standard astrophysical (cosmic) scheme of standardization (Tsiklauri 1998, 2000; Brevik 2016). The normalized set of the gas equations (Eqs. (1)–(2)) and dark matter equations (Eqs. (4)–(5)), after reduction with the proper equations of state (Eqs. (3), (6)), are respectively given as

$$\begin{aligned}& \frac{\partial D_{g}}{\partial \tau} + \frac{\partial}{\partial \xi} ( D_{g}M_{g} ) = 0, \end{aligned}$$
(8)
$$\begin{aligned}& \biggl[ 1 + \tau_{mg}\omega_{Jg} \biggl( \frac{\partial}{\partial \tau} + M_{g}\frac{\partial}{\partial \xi} \biggr) \biggr] \biggl[ D_{g} \biggl( \frac{\partial M_{g}}{\partial \tau} + M_{g}\frac{\partial M_{g}}{\partial \xi} \biggr) \\& \quad\quad{}+ \frac{\partial D_{g}}{\partial \xi} + \frac{1}{D_{g}}\frac{\partial D_{g}}{\partial \xi} + D_{g} \frac{\partial \Phi}{\partial \xi} - 2D_{g}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \\& \quad\quad{}- D_{g} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g} - M_{d} ) \biggr] = M_{xg}^{2}\tau_{mg} \omega_{Jg}\frac{\partial^{2}M_{g}}{\partial \xi^{2}}, \end{aligned}$$
(9)
$$\begin{aligned}& \frac{\partial D_{d}}{\partial \tau} + \frac{\partial}{\partial \xi} ( D_{d}M_{d} ) = 0, \end{aligned}$$
(10)
$$\begin{aligned}& \biggl[ 1 + \tau_{md}\omega_{Jg} \biggl( \frac{\partial}{\partial \tau} + M_{d}\frac{\partial}{\partial \xi} \biggr) \biggr] \biggl[ D_{d} \biggl( \frac{\partial M_{d}}{\partial \tau} + M_{d}\frac{\partial M_{d}}{\partial \xi} \biggr) \\& \quad\quad{}+ \frac{\partial D_{d}}{\partial \xi} + \frac{D_{d0}}{D_{d}}\frac{\partial D_{d}}{\partial \xi} + D_{d} \frac{\partial \Phi}{\partial \xi} - 2D_{d}M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \\& \quad\quad{}- D_{d} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d} - M_{g} ) \biggr] \\& \quad = M_{xd}^{2}\tau_{md} \omega_{Jg}\frac{\partial^{2}M_{d}}{\partial \xi^{2}}, \end{aligned}$$
(11)

Lastly, the closing gravitational Poisson equation (Eq. (7)) in the normalized form is given as

$$ \frac{\partial^{2}\Phi}{\partial \xi^{2}} = \bigl[ ( D_{g} - 1 ) + ( D_{d} - D_{d0} ) \bigr]. $$
(12)

Here, \(V_{xg}^{2} = ( 4 / 3\eta_{g} + \zeta_{g} ) / \rho_{g0}\tau_{mg}\) and \(V_{xd}^{2} = ( 4 / 3\eta_{d} + \zeta_{d} ) / \rho_{g0}\tau_{md}\) are the squares of viscoelastic relaxation mode velocities of the gas and the dark matter; respectively. The independent variables, like position \(\xi\) and time \(\tau\), are normalized by the neutral gas Jeans length, \(\lambda_{Jg}\) and neutral gas Jeans time, \(\tau_{Jg} = \omega_{Jg}^{ - 1} = ( 4\pi \rho_{g0}G )^{ - 1 / 2}\); respectively. The new symbols \(D_{g}\), \(D_{d}\) and \(D_{d0}\) are the normalized population densities of the gaseous fluid, dark matter fluid and the equilibrium population density of the dark matter fluid, each normalized by the equilibrium population density of neutral gas, \(\rho_{g0}\). Also, \(M_{g}\) and \(M_{d}\) are the corresponding normalized velocities of the gaseous and dark matter fluids normalized each by the neutral gas-acoustic phase speed, \(c_{sg} = \sqrt{\gamma_{g}p_{g} / \rho_{g}}\). Lastly, the gravitational potential \(\Phi\) is normalized by the square of the gas-acoustic phase speed, i.e., \(c_{sg}^{2} = \gamma_{g}p_{g} / \rho_{g}\).

3 Linear perturbation analysis

The focal aim of the present study is to study the gravitational fluctuation dynamics of the composite cloud against a slight perturbation relative to the defined hydrostatic homogeneous equilibrium. The relevant physical parameters undergoing such local perturbations are presented as \(D_{g} = 1 + D_{g1}\), \(D_{d} = 1 + D_{d1}\), \(M_{g} = 0 + M_{g1}\), \(M_{d} = 0 + M_{d1}\) and \(\Phi = 0 + \Phi_{1}\).

The linearized form of Eqs. (8)–(12) can now respectively be written as

$$\begin{aligned}& \frac{\partial D_{g1}}{\partial \tau} + \frac{\partial M_{g1}}{\partial \xi} = 0, \end{aligned}$$
(13)
$$\begin{aligned}& \biggl[ 1 + \tau_{mg}\omega_{Jg}\frac{\partial}{\partial \tau} \biggr] \biggl[ \frac{\partial M_{g1}}{\partial \tau} + 2\frac{\partial D_{g1}}{\partial \xi} + \frac{\partial \Phi_{1}}{\partial \xi} \\ & \quad\quad{}- 2M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr)D_{g1} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g1} - M_{d1} ) \biggr] \\ & \quad = M_{xg}^{2}\tau_{mg}\omega_{Jg} \frac{\partial^{2}M_{g1}}{\partial \xi^{2}}, \end{aligned}$$
(14)
$$\begin{aligned}& \frac{\partial D_{d1}}{\partial \tau} + \frac{\partial M_{d1}}{\partial \xi} = 0, \end{aligned}$$
(15)
$$\begin{aligned}& \biggl[ 1 + \tau_{md}\omega_{Jg}\frac{\partial}{\partial \tau} \biggr] \biggl[ \frac{\partial M_{d1}}{\partial \tau} + \frac{\partial D_{d1}}{\partial \xi} + D_{d0} \frac{\partial D_{d1}}{\partial \xi} + \frac{\partial \Phi_{1}}{\partial \xi} \\ & \quad\quad{}- 2M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr)D_{d1} - \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d1} - M_{g1} ) \biggr] \\ & \quad = M_{xd}^{2}\tau_{md}\omega_{Jg} \frac{\partial^{2}M_{d1}}{\partial \xi^{2}}, \end{aligned}$$
(16)
$$\begin{aligned}& \frac{\partial^{2}\Phi_{1}}{\partial \xi^{2}} = ( D_{g1} + D_{d1} ) . \end{aligned}$$
(17)

According to the standard Fourier-based plane-wave analysis (Bertin 2014), the fluctuations in the backdrop of no boundary effects can be assumed as \(\sim \exp [ - i ( \Omega \tau - K\xi ) ]\). Here, \(\Omega\) is the Jeans-normalized frequency and \(K\) is the Jeans-normalized wave number of the fluctuations. It enables us to switch over to the Fourier space \(( \Omega, K )\) with the operator replacement formalism as \(\partial / \partial \xi \to iK\) and \(\partial / \partial t \to - i\Omega\). The Fourier-transformed algebraic forms of Eqs. (13)–(17) are respectively given in simplified construct as

$$\begin{aligned}& D_{g1} = \biggl( \frac{K}{\Omega} \biggr)M_{g1}, \end{aligned}$$
(18)
$$\begin{aligned}& {} [ 1 - i\Omega \tau_{mg}\omega_{Jg} ] \biggl[ - i\Omega M_{g1} + 2iKD_{g1} + iK\Phi_{1} \\ & \quad\quad{} - 2M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr)D_{g1} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) ( M_{g1} - M_{d1} ) \biggr] \\ & \quad = - K^{2}M_{xg}^{2}\tau_{mg} \omega_{Jg}M_{g1}, \end{aligned}$$
(19)
$$\begin{aligned}& D_{d1} = \biggl( \frac{K}{\Omega} \biggr)M_{d1}, \end{aligned}$$
(20)
$$\begin{aligned}& {} [ 1 - i\Omega \tau_{md}\omega_{Jg} ] \biggl[ - i\Omega M_{d1} + iKD_{d1} + D_{d0}iKD_{d1} \\ & \quad\quad{}+ iK \Phi_{1} - 2M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr)D_{d1} \\ & \quad\quad{}- \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) ( M_{d1} - M_{g1} ) \biggr] \\ & \quad = - K^{2}M_{xd}^{2} \tau_{md} \omega_{Jg}M_{d1}, \end{aligned}$$
(21)
$$\begin{aligned}& \Phi_{1} = \frac{1}{K^{2}} ( D_{g1} + D_{d1} ). \end{aligned}$$
(22)

Using Eqs. (18), (22) in Eq. (19), and Eqs. (20), (22) in Eq. (21), we get two decoupling equations in terms of perturbed densities of gaseous matter and dark matter respectively as

$$\begin{aligned}& [ 1 - i\Omega \tau_{mg}\omega_{Jg} ] \biggl[ - \frac{i}{K}\Omega^{2}D_{g1} + 2iKD_{g1} + \frac{i}{K} ( D_{g1} + D_{d1} ) \\ & \quad\quad{}- 2M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr)D_{g1} - \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \biggl( \frac{\Omega}{K}D_{g1} - \frac{\Omega}{K}D_{d1} \biggr) \biggr] \\ & \quad = - \biggl( \frac{\Omega}{K} \biggr)M_{xg}^{2} \tau_{mg}\omega_{Jg}D_{g1}, \end{aligned}$$
(23)
$$\begin{aligned}& {} [ 1 - i\Omega \tau_{md}\omega_{Jg} ] \biggl[ - \frac{i}{K}\Omega^{2}D_{d1} + iKD_{d1} + D_{d0}iKD_{d1} \\ & \quad\quad{}+ \frac{i}{K} ( D_{g1} + D_{d1} ) - 2M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr)D_{d1} \\ & \quad\quad{}- \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) \biggl( \frac{\Omega}{K}D_{d1} - \frac{\Omega}{K}D_{g1} \biggr) \biggr] \\ & \quad = - \biggl( \frac{\Omega}{K} \biggr)M_{xd}^{2} \tau_{md}\omega_{Jg}D_{d1}. \end{aligned}$$
(24)

The above two equations may be written in terms of a set of homogeneous equations as

$$\begin{aligned}& a_{11}D_{g1} + a_{12}D_{d1} = 0, \end{aligned}$$
(25)
$$\begin{aligned}& a_{21}D_{g1} + a_{22}D_{d1} = 0. \end{aligned}$$
(26)

Various coefficients involved here are given as

$$\begin{aligned} a_{11} =& [ 1 - i\Omega \tau_{mg}\omega_{Jg} ] \biggl[ - \frac{i}{K}\Omega^{2} + 2iK + \frac{i}{K} \\ &{}- 2M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) - \biggl( \frac{\Omega}{K} \biggr) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \\ &{}+ \biggl( \frac{\Omega}{ K} \biggr) M_{gx}^{2}\tau_{mg}\omega_{Jg} \biggr], \\ a_{12} =& [ 1 - i\Omega \tau_{mg}\omega_{Jg} ] \biggl[ \frac{i}{K} + \biggl( \frac{\Omega}{K} \biggr) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \biggr], \\ a_{21} =& [ 1 - i\Omega \tau_{md}\omega_{Jg} ] \biggl[ \frac{i}{K} + \biggl( \frac{\Omega}{K} \biggr) \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) \biggr], \\ a_{22} =& [ 1 - i\Omega \tau_{md}\omega_{Jg} ] \biggl[ - \frac{i}{K}\Omega^{2} + iK + iKD_{d0} \\ &{}+ \frac{i}{K} - 2M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) - \biggl( \frac{\Omega}{K} \biggr) \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\\ &{} + \biggl( \frac{\Omega}{ K} \biggr) M_{dx}^{2}\tau_{md} \omega_{Jg} \biggr]. \end{aligned}$$

Solving Eqs. (25) and (26), under the condition of non-zero perturbed postential in the linear order, we obtain a quartic dispersion relation as

$$ \Omega^{4} + A_{1}\Omega^{3} + B_{1} \Omega^{2} + C_{1}\Omega + D_{1} = 0. $$
(27)

Various coefficients involved in Eq. (27) are given as the following

$$\begin{aligned}& A_{1} = - i \biggl[ \biggl( \frac{\nu_{gd}}{\omega_{Jg}} + \frac{\nu_{dg}}{\omega_{Jg}} \biggr) - \bigl( M_{xg}^{2}\tau_{mg} \omega_{Jg} + M_{xd}^{2}\tau_{md} \omega_{Jg} \bigr) \biggr], \\& B_{1} = - K^{2} \biggl[ 3 + D_{d0} + \frac{2}{K^{2}} - \frac{1}{K^{2}} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)M_{xd}^{2}\tau_{md}\omega_{Jg} \\& \phantom{B_{1} =\,\,}{}- \frac{1}{K^{2}} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)M_{xg}^{2} \tau_{mg}\omega_{Jg}\\& \phantom{B_{1} =\,\,}{} + \frac{1}{K ^{2}}M_{xg}^{2} \tau_{mg}\omega_{Jg}M_{xd}^{2} \tau_{md}\omega_{Jg} \\& \phantom{B_{1} =\,\,}{}+ i\frac{2}{K} \biggl[ M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) + M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \biggr] \biggr], \\& C_{1} = - K^{2} \biggl[ \frac{2}{K} \biggl[ M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) + M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \\& \phantom{B_{1} =\,\,}{}- M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr)M_{xd}^{2}\tau_{md}\omega_{Jg} \biggr] + i \biggl[ - 2 \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) \\& \phantom{B_{1} =\,\,}{} + 2M_{xd}^{2}\tau_{md}\omega_{Jg} - \frac{2}{K^{2}} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) - \frac{2}{K^{2}} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \\& \phantom{B_{1} =\,\,}{}+ \frac{1}{K^{2}}M_{xg}^{2} \tau_{mg}\omega_{Jg} + \frac{1}{K^{2}}M_{xd}^{2} \tau_{md}\omega_{Jg} + M_{xg}^{2} \tau_{mg}\omega_{Jg}\\& \phantom{B_{1} =\,\,}{} + D_{d0}M_{xg}^{2} \tau_{mg}\omega_{Jg} - ( 1 + D_{d0} ) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \biggr] \biggr], \\& D_{1} = - K^{2} \biggl[ - 3 - D_{d0} + 2K^{2} ( 1 - D_{d0} ) \\& \phantom{B_{1} =\,\,}{}+ 4M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) - i \biggl[ 4KM_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr)\\& \phantom{B_{1} =\,\,}{} + \frac{2}{K}M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) + 2KM_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr)\\& \phantom{B_{1} =\,\,}{} + 2KD_{d0}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) + \frac{2}{K}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggr] \biggr]. \end{aligned}$$

4 Hydrodynamic regime

The normalized dispersion relation derived after Eq. (27) for the low-frequency wave modes in the hydrodynamic regime (\(\omega_{Jg}\tau_{mg}, \omega_{Jg}\tau_{md} \ll 1\)) can be written as

$$ \Omega^{4} + A_{2}\Omega^{3} + B_{2} \Omega^{2} + C_{2}\Omega + D_{2} = 0, $$
(28)

where, the different involved coefficients are

$$\begin{aligned}& A_{2} = - i \biggl( \frac{\nu_{gd}}{\omega_{Jg}} + \frac{\nu_{dg}}{\omega_{Jg}} \biggr), \\& B_{2} = - K^{2} \biggl[ 3 + D_{d0} + \frac{2}{K^{2}} + \frac{2i}{K} \biggl[ M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \\& \phantom{A_{2} =\,\,}{} + M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \biggr] \biggr], \\& C_{2} = - K^{2} \biggl[ \frac{2}{K} \biggl[ M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)\\& \phantom{A_{2} =\,\,}{} + M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \biggr] - i \biggl[ 2 \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) + \frac{2}{K^{2}} \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr) \\& \phantom{A_{2} =\,\,}{}+ \frac{2}{K^{2}} \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) + ( 1 + D_{d0} ) \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr) \biggr] \biggr], \\& D_{2} = - K^{2} \biggl[ - 3 - D_{d0} + 2K^{2} ( 1 - D_{d0} ) \\& \phantom{A_{2} =\,\,}{}+ 4M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) - i \biggl[ 4KM_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \\& \phantom{A_{2} =\,\,}{}+ \frac{2}{K}M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) + 2KM_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \\& \phantom{A_{2} =\,\,}{}+ 2KD_{d0}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) + \frac{2}{K}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggr] \biggr]. \end{aligned}$$

5 Kinetic regime

In the kinetic regime (\(\omega_{Jg}\tau_{mg}, \omega_{Jg}\tau_{md} \gg 1\)), in which the high-frequency fluctuations get sensible unlike the low-frequency modes in the previous hydrodynamic regime

$$ \Omega^{4} + A_{3}\Omega^{3} + B_{3} \Omega^{2} + C_{3}\Omega + D_{3} = 0. $$
(29)

The different involved coefficients in Eq. (29) are

$$\begin{aligned}& A_{3} = i \bigl( M_{xg}^{2}\tau_{mg} \omega_{Jg} + M_{xd}^{2}\tau_{md} \omega_{Jg} \bigr), \\& B_{3} = \biggl( \frac{\nu_{dg}}{\omega_{Jg}} \biggr)M_{xd}^{2} \tau_{md}\omega_{Jg} + \biggl( \frac{\nu_{gd}}{\omega_{Jg}} \biggr)M_{xg}^{2}\tau_{mg}\omega_{Jg} \\& \phantom{B_{3} =\,\,}{}- M_{xg}^{2}\tau_{mg}\omega_{Jg}M_{xd}^{2} \tau_{md}\omega_{Jg}, \\& C_{3} = - K^{2} \biggl[ \biggl[ - \frac{2}{K}M_{xg}^{2} \tau_{mg}\omega_{Jg}M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \\& \phantom{B_{3} =\,\,}{}- \frac{2}{K}M_{xd}^{2} \tau_{md}\omega_{Jg}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggr] + i \biggl[ 2M_{xd}^{2} \tau_{md}\omega_{Jg} \\& \phantom{B_{3} =\,\,}{}+ M_{xg}^{2} \tau_{mg}\omega_{Jg} + \frac{1}{K^{2}}M_{xd}^{2} \tau_{md}\omega_{Jg} + D_{d0}M_{xg}^{2} \tau_{mg}\omega_{Jg} \\& \phantom{B_{3} =\,\,}{}+ \frac{1}{K^{2}}M_{xg}^{2} \tau_{mg}\omega_{Jg} \biggr] \biggr], \\& D_{3} = - K^{2} \biggl[ - 3 - D_{d0} + 2K^{2} ( 1 - D_{d0} ) \\& \phantom{B_{3} =\,\,}{}+ 4M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) - i \biggl[ 4KM_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) \\& \phantom{B_{3} =\,\,}{}+ \frac{2}{K}M_{dy} \biggl( \frac{\Omega_{dz}}{\omega_{Jg}} \biggr) + 2KM_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \\& \phantom{B_{3} =\,\,}{}+ 2KD_{d0}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) + \frac{2}{K}M_{gy} \biggl( \frac{\Omega_{gz}}{\omega_{Jg}} \biggr) \biggr] \biggr]. \end{aligned}$$

6 Results and discussions

The stability analysis of interstellar (intergalactic) gravitating viscoelastic gaseous clouds in the presence of active dark matter is systematically carried out by applying the Fourier-based linear perturbation technique. It is based on the framework of generalized fluid dynamic model under the non-relativistic approximation of flow regime (cold) because of decoupling of the dark matter fluid from the background radiation and plasma. A quartic dispersion relation is methodically derived and numerically studied. The stability effects of the relevant parameters on the cloud collapse dynamics in both the hydrodynamic and kinetic regimes are discussed.

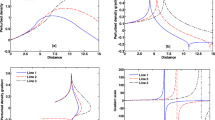
In Fig. 1, we show the profiles of the normalized (a) real frequency \(( \Omega_{r} = \omega_{r} / \omega_{Jg} )\) and (b) damping rate \(( \Omega_{i} )\) with variation in the normalized wave number \(( K = k / k_{Jg} )\) for the different values of normalized rotation frequency of the gaseous matter \(( \Omega_{gz} / \omega_{Jg} )\) in the hydrodynamic regime (low-\(K\) limit) on the gravitating gaseous fluid scales of space and time. As already mentioned, the gravito-acoustic mode gets unstable, characterized by the complex normalized frequency: \(\Omega = \Omega_{r} + i \Omega_{i}\). Various lines link to case (1): \(\Omega_{gz} / \omega_{Jg} = 0.1 \) (blue), case (2): \(\Omega_{gz} / \omega_{Jg} = 0.2 \) (red), and case (3): \(\Omega_{gz} / \omega_{Jg} = 0.3 \) (black); respectively. Various input values used are \(D_{d0} = 1\), \(\Omega_{dz} / \omega_{Jg} = 10^{ - 2}\), \(\nu_{gd} / \omega_{Jg} = \nu_{dg} / \omega_{Jg} = 10^{ - 3}\), \(M_{gy} = 1\), and \(M_{dy} = 1\). The non-linear dispersion behaviour of the fluctuations is ascribable to the pure Jeans mode without any significant electrostatic contribution (Fig. 1(a)). An interesting feature observed here is that the magnitude of the group velocity increases with the gas rotation frequency, and vice-versa. It is clear that, as the rotation frequency of the gaseous matter increases, the decay rate magnitude of the fluctuations increases, and vice-versa (Fig. 1(b)). Hence, the gas rotation frequency introduces a stabilizing effect on the Jeans instability towards the longer wavelength region. This may be as due to a consequence of the centrifugal reduction in the effective gravitational interaction with the Coriolis effects.

Fig. 1
figure 1

Profile of normalized (a) real frequency \(( \Omega_{r} )\) and (b) damping rate \(( \Omega_{i} )\) with variation in the normalized wave number \(( K )\) for different values of the normalized rotation frequency of the gaseous matter \(( \Omega_{gz} / \omega_{Jg} )\) in the hydrodynamic regime (low-\(K\) limit). Various lines link to case (1): \(\Omega_{gz} / \omega_{Jg} = 0.1 \) (blue), case (2): \(\Omega_{gz} / \omega_{Jg} = 0.2 \) (red), and case (3): \(\Omega_{gz} / \omega_{Jg} = 0.3 \) (black); respectively. Various input values used are \(D_{d0} = 1\), \(\Omega_{dz} / \omega_{Jg} = 10^{ - 2}\), \(\nu_{gd} / \omega_{Jg} = \nu_{dg} / \omega_{Jg} = 10^{ - 3}\), \(M_{gy} = 1\), and \(M_{dy} = 1\)

Full size image

As in Fig. 2, we depict the same as Fig. 1, but for \(\Omega_{gz} / \omega_{Jg} = 0.1\) with the different values of normalized rotation frequency of the dark matter \(\Omega_{dz} / \omega_{Jg}\). Various lines link to case (1): \(\Omega_{dz} / \omega_{Jg} = 1 \times 10^{ - 2} \) (blue), case (2): \(\Omega_{dz} / \omega_{Jg} = 5 \times 10^{ - 2} \) (red), and case (3): \(\Omega_{dz} / \omega_{Jg} = 9 \times 10^{ - 2} \) (black); respectively. It is seen that no significant role is played by the dark matter rotation on the propagatory dynamics of the fluctuations (Fig. 2(a)). As we increase the rotation frequency of the dark matter fluid, the magnitude of the decay rate decreases, and vice-versa (Fig. 2(b)). Therefore, we can judiciously say that dark matter rotation frequency acts as a stabilizing agency on the Jeans instability dynamics towards the longer wavelength region in the hydrodynamic regime.

Fig. 2
figure 2

Same as Fig. 1, but with fixed \(\Omega_{gz} / \omega_{Jg} = 0.1\). Various lines link to case (1): \(\Omega_{dz} / \omega_{Jg} = 0.01 \) (blue), case (2): \(\Omega_{dz} / \omega_{Jg} = 0.05 \) (red), and case (3): \(\Omega_{dz} / \omega_{Jg} = 0.09 \) (black); respectively

Full size image

Now, Fig. 3 shows the profiles of the normalized (a) real frequency \(( \Omega_{r} )\) and (b) damping rate \(( \Omega_{i} )\) with variation in the normalized wave number \(( K )\) for the different values of normalized rotation frequency of the gaseous matter \(( \Omega_{gz} / \omega_{Jg} )\) in the kinetic regime (high-\(K\) limit). Various lines link to case (1): \(\Omega_{gz} / \omega_{Jg} = 0.1 \) (blue), and case (2): \(\Omega_{gz} / \omega_{Jg} = 0.2 \) (red), case (3): \(\Omega_{gz} / \omega_{Jg} = 0.3 \) (black); respectively. Various input values used are \(D_{d0} = 1\), \(\Omega_{dz} / \omega_{Jg} = 1 \times 10^{ - 2}\), \(\nu_{gd} / \omega_{Jg} = \nu_{dg} / \omega_{Jg} = 1 \times 10^{ - 2}\), \(M_{gy} = M_{dz} = 1\), \(T_{mg} = 0.01\), \(T_{mg} = 0.001\), \(M_{xg} = 0.01\), and \(M_{xd} = 0.001\). We see that, as the gas rotation frequency becomes higher, propagation of the fluctuation mode becomes faster, and vice-versa (Fig. 3(a)). An interesting speculation to be made here is that there is a quasi-linear coupling between the gravitational fluctuations (high-\(K\)) with non-linear dispersion and mechanical (acoustic) fluctuations (high-\(K\)) with linear dispersion. It is evident that, as the gas rotation frequency increases, the magnitude of decay rate decreases (Fig. 3(b)). Thus, the gas rotation frequency plays a destabilizing effect on the cloud Jeans instability towards the shorter wavelength region in the kinetic regime. It is attributable to a consequence of the centrifugal reduction in the effective gravitational interaction with the Coriolis effects leading thereby to a larger volume of the composite astrofluid arresting the short wavelength fluctuations quasi-linearly transformed from the long wavelength ones (gravitational).

Fig. 3
figure 3

Profile of normalized (a) real frequency \(( \Omega_{r} )\) and (b) damping rate \(( \Omega_{i} )\) with variation in the normalized wave number \(( K )\) for different values of the normalized rotation frequency of the gaseous matter \(( \Omega_{gz} / \omega_{Jg} )\) in the kinetic regime (high-\(K\) limit). Various lines link to case (1): \(\Omega_{gz} / \omega_{Jg} = 0.1 \) (blue), case (2): \(\Omega_{gz} / \omega_{Jg} = 0.2 \) (red), and case (3): \(\Omega_{gz} / \omega_{Jg} = 0.3 \) (black); respectively. Various input values used are \(D_{d0} = 1\), \(\Omega_{dz} / \omega_{Jg} = 1 \times 10^{ - 2}\), \(\nu_{gd} / \omega_{Jg} = \nu_{dg} / \omega_{Jg} = 1 \times 10^{ - 2}\), \(M_{gy} = M_{dz} = 1\), \(T_{mg} = 0.01\), \(T_{mg} = 0.001\), \(M_{xg} = 0.01\), and \(M_{xd} = 0.001\)

Full size image

Lastly, in Fig. 4, we depict the same as Fig. 3, but for \(\Omega_{gz} / \omega_{Jg} = 0.1\) with the different values of normalized rotation frequency of the dark matter (\(\Omega_{dz} / \omega_{Jg}\)). Various lines link to case (1): \(\Omega_{dz} / \omega_{Jg} = 1 \times 10^{ - 2} \) (blue), case (2): \(\Omega_{dz} / \omega_{Jg} = 5 \times 10^{ - 2} \) (red), and case (3): \(\Omega_{dz} / \omega_{Jg} = 9 \times 10^{ - 2} \) (black); respectively. A quasi-linear mode-mode transformation from gravitational to acoustic patterns is speculated (Fig. 4(a)), as before (Fig. 3(a)). Here as well, as the dark matter rotation frequency increases, the instability decay rate decreases, and vice-versa (Fig. 4(b)). So, it can likewise be concluded that the dark matter rotation frequency plays a destabilizing role to the Jeans instability dynamics of the rotating astrocloud towards the shorter wavelength region in the kinetic regime of perturbations.

Fig. 4
figure 4

Same as Fig. 3, but with fixed \(\Omega_{gz} / \omega_{Jg} = 0.1\). Various lines link to case (1): \(\Omega_{dz} / \omega_{Jg} = 0.01 \) (blue), case (2): \(\Omega_{dz} / \omega_{Jg} = 0.05 \) (red), and case (3): \(\Omega_{dz} / \omega_{Jg} = 0.09 \) (black); respectively

Full size image

7 Conclusions

In this work, we theoretically study the gravitational stability behaviour of gravitating flat complex viscoelastic gaseous fluid in the presence of gravitating viscoelastic dark matter fluid against slight perturbation relative to its homogeneous hydrostatic equilibrium. The bright matter and dark matter sectors are inter-coupled only via mutual gravitational interaction. The adopted model considers all the possible realistic effects, such as frictional force, fluid turbulence, Coriolis force, etc. A modified Fourier-based plane-wave analysis is applied over the basic governing equations in a conservative closed form to derive a generalized quartic dispersion relation. The stability features are numerically studied in both the hydrodynamic and kinetic regimes on the cosmological Jeans scales of space and time. A unique type of quasi-linear transformation of the gravitational fluctuations (with non-linear dispersion) into acoustic ones (with linear dispersion) is found to exist in the complex cosmic fluid. In the hydrodynamic regime, the gas as well as dark matter rotation frequencies have stabilizing effects. In contrast, in the kinetic regime, the rotation frequencies play destabilizing roles on the Jeans fluctuation dynamics. It is further seen that the magnitude of the group velocity of the fluctuations increases with both the gas and dark matter rotation frequencies in both the regimes, and vice-versa. The enhancement in the group propagation characteristics with increment in the fluid rotation frequencies implicates that the net volume of the composite astrofluid (composed of bright and dark sectors) increases considerably as a consequence of the centrifugal reduction in the effective gravitational interaction. It thereby puts forward an alternate viewpoint to understand the role of the Coriolis effects on the spectral features of the instability dynamics.

It is pertinent to add that the effects of dark matter in the dynamics of large-scale structure formation are usually realizable on the cosmological (galactic) scales of space and time. The existence of dark matter in dense gas clouds with mass on the solar mass order is well known even on the Jeans spatiotemporal scales (Gerhard and Silk 1996; Komatsu and Seljak 2001). In the proposed study, we consider hydrostatic homogeneous equilibrium and investigate scale-invariant properties of the gravitational fluctuation dynamics, considering both the bright and dark sectors, in a standard normalized form on the cosmic Jeans spatiotemporal scales. Thus, the fluctuation features presented here (on the Jeans spatiotemporal scales) can justifiably be mapped into any spatiotemporal scales of cosmic significance, such as dark matter-dominated stellar objects like dwarfs, dwarf satellite spheroidals, and so forth. We, finally, hope that the obtained instability results could be parallelly helpful in analytically understanding the dynamic physical mechanisms responsible for bounded structure formation via gravitational cloud collapse dynamics in the astrophysical, interstellar (intergalactic) and cosmological contexts.