The cislunar low-thrust trajectories via the libration point

Abstract

The low-thrust propulsion will be one of the most important propulsion in the future due to its large specific impulse. Different from traditional low-thrust trajectories (LTTs) yielded by some optimization algorithms, the gradient-based design methodology is investigated for LTTs in this paper with the help of invariant manifolds of $\mathit{LL}_{1}$ point and Halo orbit near the $\mathit{LL}_{1}$ point. Their deformations under solar gravitational perturbation are also presented to design LTTs in the restricted four-body model. The perturbed manifolds of $\mathit{LL}_{1}$ point and its Halo orbit serve as the free-flight phase to reduce the fuel consumptions as much as possible. An open-loop control law is proposed, which is used to guide the spacecraft escaping from Earth or captured by Moon. By using a two-dimensional search strategy, the ON/OFF time of the low-thrust engine in the Earth-escaping and Moon-captured phases can be obtained. The numerical implementations show that the LTTs achieved in this paper are consistent with the one adopted by the SMART-1 mission.

1 Introduction

Deep Space-1 launched by NASA in 1998 and SMART-1 Lunar probe launched by ESA in 2003 prove that it is feasible to select low-thrust propulsion as the main propulsion in deep-space exploration missions. Another recent famous mission is the DAWN mission, launched by NASA in 2007, in which a gravity-assist method is adopted. The spacecraft explored Ceres and Vesta located in the asteroid belt (Polanskey et al. 2011). Considering that propellant economy is the main factor designed in deep-space exploration missions, low-thrust propulsion will be one of the most important propulsions in the future because of its large specific impulse.

Updates in propulsion are supposed to trigger a revolution in the field of trajectory design. When low-thrust propulsion is used in the designing of trajectories, their adjustment is gradual because of the long-term effects of thrust arcs. A patched conic technique based on a two-body model is normally used in the trans-lunar trajectory; however, when adopting low-thrust propulsion, the large traveling time does not support the working of the patched conic technique. Therefore, another model needs to be proposed based on a three- or four-body problem.

Earth–Moon low-thrust transfer trajectories normally include the Earth-escaping, free-flight, and Moon-captured phases (Racca 2003; Racca et al. 2002; Betts and Erb 2006; Guelman 1995; Herman and Conway 1996). In a conventional LTTs design, the problem is normally transformed into a nonlinear problem (NLP) by using the collocation method, and then trajectories under low thrust can be obtained (Betts and Erb 2006; Guelman 1995; Herman and Conway 1996). This method only uses the optimization algorithm to obtain the target orbit; the search process is blind and requires a considerable amount of calculation. A type of Earth–Moon transfer orbit based on the circular restricted three-body problem (CR3BP) was proposed by Conley (Conley 1968). This type of trajectory passes the collinear libration point $L_{1}$ in the Earth–Moon system to distinguish from the WSB transfer orbit that passes the collinear libration point $L_{2}$, as proposed by Belbruno and Miller (2015), the former is named Earth–Moon $\mathit{LL}_{1}$ transfer orbit, which is being extensively studied by many scholars for further development. These methods can be divided into three classes stated as follows.

First, the direct method of optimization is used by discretizing the trajectories and control variables. Thus, high accuracy is not required for the initial value but a large CPU time is required for trajectory analysis and optimization. More concretely, Howell and Ozimek obtained the solution for a complete time history of the thrust magnitude and direction by solving a calculus of variation problems to locally maximize the final spacecraft mass (Howell and Ozimek 2010). Lee used a direct transcription and collocation method to reformulate the continuous dynamic optimization problem into a discrete optimization problem, which then is solved using nonlinear programming software (Lee et al. 2014).

Second, an indirect method is adopted in the two following studies, in which boundary and first-order necessary conditions for optimality are enforced for a continuous system. Considering that the convergence domain of the method is narrow, a high-precision initial value is required, which is also computationally demanding. Specifically, Graham and Rao used a variable-order Legendre–Gauss–Radau (LGR) quadrature orthogonal collocation method, thus obtaining a high-accuracy minimum-fuel Earth-orbit transfer by using low-thrust propulsion (Graham and Rao 2014). Furthermore, in another paper, they used the same method to obtain a high-accuracy minimum-time Earth-orbit transfer by using low-thrust propulsion (Graham and Rao 2015).

Compared with the aforementioned studies aimed to formulate optimizations for LTTs, some other studies aimed to obtain the initial value of the LTTs by using the libration point. Some representative studies are presented as follows. Petropoulos and Longuski proposed a type of shape-based design (Petropoulos and Longuski 2004). They presented an exponential sinusoid shape function to solve the dynamical equations of a spacecraft. Vellutini and Avanzini improved the method (Vellutini and Avanzini 2015) and proposed a modified exponential sinusoid shape function. The two exponential sinusoid shape functions cannot satisfy the starting and ending velocity boundary conditions; thus, they can only be used to design the trajectories whose launch energy is not zero. Furthermore, Wall and Conway proposed a sixth-order inverse polynomial shape function, which is obtained by fitting the optimal transfer trajectories (Wall and Conway 2009). However, the actual dynamic constraints were not considered; therefore, some feasible trajectories are often omitted when adopting this method.

Unlike conventional LTTs yielded by some optimization algorithms, the present study investigated the gradient-based design methodology for LTTs with the help of invariant manifolds of the $\mathit{LL}_{1}$ point and a Halo orbit near the $\mathit{LL}_{1}$ point. In addition, their deformations under solar gravity perturbation are represented to design LLTs in the restricted four-body model. In this paper, the $\mathit{LL}_{1}$ point and the Halo orbit near it serve as a free-flight phase so that the fuel consumption is as low as possible (when adopting the $\mathit{LL}_{1}$ point as the free-flight, non-thrusting phase, the fuel consumption is decreased). Next, to design the Earth-escaping and Moon-captured phases, an open-loop low-thrust control law used for designing long duration spiral transfers between Earth- and Moon-centered orbits is presented. By using the $\mathit{LL}_{1}$ point and the Halo orbit near it as a starting point, respectively, when backward and forward integrations are completed, the trajectory of Earth-escaping and Moon-captured phases can be respectively obtained.

Compared with the existing shape-based design, there is no need to propose a kind of shape function (exponential sinusoids or inverse polynomial shape functions). In addition, the situation in which feasible trajectories are omitted can be avoided by using this method. Moreover, the Halo orbit near the $\mathit{LL}_{1}$ point is adopted as a free-flight phase, which cuts down the fuel consumption greatly. In this study, the invariant manifolds derived from the transportation tube wall are studied as well.

The obtained cislunar LTTs fundamentally coincide with those of SMART-1, which has similar boundary conditions. Supposing that the obtained trajectories are used as the initial orbit to optimally design low-energy transfer trajectories to Moon, then the search scope can be narrowed and the computation of optimal trajectories can be reduced.

2 Dynamical models

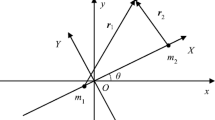
The Moon, Earth, and Sun constitute the general concept of the three-body problem; in this study, the dynamic model is simplified. In a Sun–Earth–Moon System, the accuracy of the Spatial Bi-Circular Model (SBCM) is sufficiently high (Koon et al. 2001). In the model, the inclination of the lunar plane related to the ecliptic plane is considered, as shown in Fig. 1. The Moon and Earth are regarded as a whole system that nearly composes a two-body motion with the Sun, and another two-body motion composed of the Earth and the Moon is not affected by the Sun. The distance between Sun and Earth is considerably larger than that between the Earth and Moon; thus, the torque of the solar gravitation affecting the Earth–Moon system can be ignored and only the force is considered. The coordinate systems used in this model are defined as follows.

Fig. 1

The geometrical view of the SBCM (Xu et al. 2013)

For the geocentric inertial frame, the Earth’s center is defined as the origin, and the intersection of the lunar and ecliptic planes is defined as the $x$-axis. In addition, the normal of the lunar plane is defined as the $z$-axis, whose positive direction is coincident with that of spin angular velocity, and the $y$-axis is determined by the right-hand rule. There is relative acceleration between the defined and inertial frames but the geocentric inertial frame can be approximately regarded as an inertial frame relative to a low-Earth orbit. For the selenocentric inertial frame, the Moon’s center is defined as the origin, and the definitions of coordinate axes are the same as those of the geocentric inertial frame, and the frame can be approximately regarded as an inertial frame relative to a low-Moon orbit. For the inertial frame in the Sun–Earth/Moon systems denoted as $I_{S - E + M}$, the centroid of the Sun–Earth–Moon system is defined as the origin, and the definition of coordinate axes are the same as those of the geocentric inertial frame.

For the syzygy frame in the Sun–Earth/Moon systems denoted as $S_{S - E + M}$, the centroid of the Sun–Earth–Moon system is defined as the origin, and the direction to the centroid of the Earth–Moon system from the Sun is defined as the $x$-axis. Furthermore, the normal of the ecliptic plane is defined as the $z$-axis, whose positive direction is coincident with that of spin angular velocity, and the $y$-axis is determined by the right-hand rule. For the syzygy frame in the Earth–Moon system denoted as $S_{E - M}$, the centroid of the Earth–Moon system is defined as the origin, and the direction toward the Moon from Earth is defined as the $x$-axis. In addition, the normal of the lunar plane is defined as the $z$-axis, whose positive direction is coincident with that of spin angular velocity, and the $y$-axis is determined by the right-hand rule.

In Fig. 1, the inclination of the lunar plane relative to the ecliptic plane is considered, with an average angle of 5°9′; the lunar phasic angle $\beta$ is measured as the angle between the line from the Earth to Moon and the intersecting line of the ecliptic and lunar planes. Moreover, the solar phasic angle $\theta_{s}$ is the angle between the line from the Sun to the barycenter of the Earth–Moon system and the intersecting line of the ecliptic and lunar planes; the ecliptic plane is depicted in yellow, while the lunar plane is depicted in green (Xu et al. 2013).

To improve efficiency and accuracy, a normalized unit based on CR3BP is adopted throughout this investigation (Szebehely 1967). The normalized unit is defined as follows. When the spacecraft is located in the gravitational influence region of two primary bodies ($m_{1}$ and $m_{2}$; Sun and Earth, or Earth and Moon in this paper), the unit of account is normally taken as

$$ \left \{ \textstyle\begin{array}{l} [M] = m_{E} + m_{M} \\ {} [L] = L_{E - M} \\ {} [T] = \bigl[ L_{E - M}^{3}/G ( m_{E} + m_{M} ) \bigr]^{1 / 2} \end{array}\displaystyle \right . $$

(1)

where $L_{E - M}$ is the distance between the two primary bodies, $m_{E}$ is the mass of Earth, and $m_{M}$ is the mass of Moon. According to the new units defined earlier, the gravitational constant is $G = 1$.

For SBCM, the dynamical equation is written as

$$\begin{aligned} \left [ \textstyle\begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array}\displaystyle \right ] =& - 2\left [ \textstyle\begin{array}{c} - \dot{y} \\ \dot{x} \\ 0 \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{c} x \\ y \\ 0 \end{array}\displaystyle \right ] - ( 1 - \mu)\frac{\boldsymbol{r} - \boldsymbol{r}_{E}}{ \Vert \bullet \Vert ^{3}} \\ &{}- \mu\frac {\boldsymbol{r} - \boldsymbol{r}_{M}}{ \Vert \bullet' \Vert ^{3}} + \omega_{s}^{2}R_{z} ( \beta)R_{x} ( i )\boldsymbol{A}_{s} \\ &{}- R_{z} ( \beta)R_{x} ( i )R_{z} ( - \theta_{s} )m_{s}\frac{\boldsymbol{R} - a_{s}\boldsymbol{R}_{s}}{ \Vert \bullet'' \Vert ^{3}} \end{aligned}$$

(2)

where $r_{i}$ $(i = 1,2,3)$ is the distance between the spacecraft and Earth, Moon, and Sun; $\omega_{s}$ is the angular velocity of the Earth relative to the Sun; $i$ is the angle between the lunar plane and the ecliptic plane; $\mu$ is proportion of the mass of Moon in the Earth–Moon system; $\mu_{s}$ is the mass of Sun; $a_{s}$ is the average distance between the Sun and the centroid of the Earth–Moon system; $\theta_{s}$ is the solar phasic angle; and $\beta$ is the lunar phasic angle. In addition, $\boldsymbol{A}_{s} = [ a_{s}\cos\theta_{s},a_{s}\sin\theta_{s},0 ]^{T}$ is the position vector of Sun in $I_{S - E + M}$, and $\boldsymbol{r} = [ x,y,z ]^{T}$ is the position vector of the spacecraft in $S_{E - M},\boldsymbol{r}_{E} = [-\mu\ \ 0\ \ 0]^{T}$ is the position vector of Earth in $S_{E - M}$, $\boldsymbol{r}_{M} = [1 - \mu\ \ 0 \ \ 0]^{T}$ is the position vector of Moon in $S_{E - M}$, $m_{s} = 328900.54$ is the ratio of the mass of Sun to that of the Earth–Moon system, $\boldsymbol{R}$ is the position vector of the spacecraft in the $S_{S - E + M}$, and $\boldsymbol{R}_{s} = [-\mu_{S} \ \ 0 \ \ 0]^{T}$ is the position vector of Sun in $S_{S - E + M}$. The symbol • represents the term $\boldsymbol{r} - \boldsymbol{r}_{E}$, $\bullet'$ represents $\boldsymbol{r} - \boldsymbol{r}_{M}$, and $\bullet''$ represents the term $\boldsymbol {R} - a_{s}\boldsymbol{R}_{s}$.

The initial values $t_{0} = 0$°, $\theta_{s0} = 0$°, and $\beta_{0}$ is undetermined. Therefore, the geometrical relationship between the Sun, Earth, and Moon is only determined by $\beta_{0}$.

3 Cislunar transfers via $\mathit{LL}_{1}$ point and its Halo orbits

3.1 Cislunar transfer via $\mathit{LL}_{1}$ point with lowest energy

In the CR3BP frame, the invariant manifolds of $\mathit{LL}_{1}$ point can be adopted to design the cislunar transfer. In this case, the spacecraft can fly with the stable manifolds from the interior area affected by the gravity of Earth to the $\mathit{LL}_{1}$ point, and then fly from the $\mathit{LL}_{1}$ point to the exterior area affected by the Moon’s gravity with the unstable manifolds. However, considering that the transfer time will approach infinity, this trajectory is unpractical.

For SBCM, under the perturbation of solar gravity, the infinite transfer time is cut down to a finite time; this is quite significant for the Earth–Moon transfers. Considering that a particle at $\mathit{LL}_{1}$ point has the lowest energy that can form a “neck” near the $\mathit{LL}_{1}$ point in the Hill’s open region, the transfer via $\mathit{LL}_{1}$ point will obviously have the lowest energy.

In Fig. 2, only the interval of $\beta$ corresponding to the dotted line can drive the trajectories from Earth to the $\mathit{LL}_{1}$ point. Further, only the interval of $\beta$ corresponding to the solid line can drive the trajectories from the $\mathit{LL}_{1}$ point to Moon. The intersection of these two intervals, that is, [77°, 109°] ∪ [285°, 342°], can be considered as the cislunar transfer opportunity bounded by the vertical dashed lines in Fig. 2. In this paper, it is chosen as $\beta= 286$°.

Fig. 2

Cislunar transfer opportunities measured using the lunar phasic angle $\beta$: in this study, $\beta= 286$°

When considering $\mathit{LL}_{1}$ point as the trajectory in the free-flight phase, the procedure used to search cislunar LTTs is described as follows. In the syzygy frame, for a specific value of $\beta$, substitute it into Eq. (2), and integrate the SBCM dynamics equations. When backward and forward integrations are finished, the trajectories of Earth-escaping and Moon-captured phases can be obtained, respectively. The initial conditions are $\beta= 286$° and $\theta_{s} = 0$°. The integral initial point is $[x_{\mathit{LL}1} \ \ 0 \ \ 0 \ \ 0 \ \ 0 \ \ 0]^{T}$. Figure 3 presents the cislunar low-thrust transfer trajectories in the syzygy frame. Figure 4 presents the history of eccentricity and semi-major axis in free flying without control. The moment when the initial integration is defined is defined as the epoch time $t = 0$.

Fig. 3

Cislunar low-thrust transfer trajectories in the syzygy frame

Fig. 4

History of orbit elements in the free-flying phase without control: (a) the history of eccentricity; (b) the history of semi-major axis

The motion before the Earth-escaping phase and after the Moon-captured phase can be regarded as a two-body problem under perturbation. Commonly, the radius of the Earth’s sphere-of-influence (SOI) is approximately 924647 km, and the radius of the Moon’s SOI is approximately 66190 km. Figure 3 shows that the altitude of the trajectories of the Earth-escaping phase is no more than $4 \times10^{5}$ km, while the maximum distance from the node on the trajectories of the Moon-captured phase to the Moon is approximately $5.5 \times10^{4}$ km. In addition, the trajectories of the Earth-escaping phase are observed to be located entirely in the Earth’s SOI; therefore, when a two-body model is adopted to solve this problem, the accuracy meets the requirement, and the orbit is stable. On the other hand, some parts of the trajectories of the Moon-captured phase are located at the boundary of the Moon’s SOI, and therefore will be unstable; this is proved by the result in Fig. 4. Moreover, in Fig. 4, the eccentricity and semi-major axis are defined with respect to two central bodies depending on time. That is, for $t < 0$, the Earth is the center and for $t < 0$, the Moon is the center.

By considering the instability of the transfer trajectories in Moon captured phase, the trajectory with a lower altitude of periapsis is more appropriate to be adopted in the free-flight phase. If the altitude of periapsis is very high, it will increase the risk of the spacecraft escaping again before being captured.

3.2 Cislunar transfer through the Halo orbit near $\mathit{LL}_{1}$ point with more opportunities

Compared with the cislunar transfers via $\mathit{LL}_{1}$ point, those via the Halo orbit near the $\mathit{LL}_{1}$ point provide more transfer opportunities because another variable is introduced (i.e., the phase of the Halo orbit near the $\mathit{LL}_{1}$ point). This part provides some results about the cislunar transfer via the Halo orbit near the $\mathit{LL}_{1}$ point are obtained, which are similar to those obtained in Sect. 3.1.

The Halo orbit is the periodic solution around the libration point in CR3BP, and results from orbit bifurcations (Barden et al. 1996). It is symmetrical with the $x$–$z$ plane in the syzygy frame. Poincaré mapping $P(z)$ is defined as

$$ P ( z ) = \phi_{T} ( z ),\quad\forall z \in\varGamma( \theta). $$

(3)

Based on the Hamiltonian system’s theory, the derivative of $P(z)$, that is, $\varPhi= D_{z}P ( z )$ is a symplectic matrix. The complex eigenvalues of the matrix are $\vert \lambda_{i} \vert = 1$, $i = 1,2,3,4$, and the real eigenvalues are $\lambda_{5} = \lambda_{6}^{ - 1} > 1$. These eigenvalues of $\varPhi$ are named characteristic exponents of $P(z)$. The real eigenvalues reflect the stability of the Halo orbit.

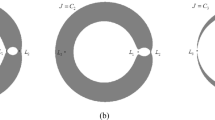
In the symplectic matrix, $\lambda_{5} > 1$ and $\lambda_{6} < 1$; therefore, the Halo orbit has both stable and unstable manifolds. The invariant manifolds of the Halo orbit are globally represented as two-dimensional compact manifolds in the phase space, and their representation in the position space are shown in Fig. 5(a). For the Earth–Moon system, the invariant manifolds of the Halo orbit in CR3BP can be divided into $W_{E}^{s}$, $W_{E}^{u}$, $W_{M}^{s}$, and $W_{M}^{u}$ based on stability and orientation; the subscripts “$E$” and “$M$” represent the Earth and Moon orientations, respectively, and the superscripts “$s$” and “$u$” represent the stable and unstable manifolds, respectively. In Fig. 5(a), the green and red areas represent the stable and unstable manifolds, respectively. Moreover, $W_{E}^{s}$ and $W_{M}^{u}$ consist of the transportation tube wall from Earth to Moon, and $W_{M}^{s}$ and $W_{E}^{u}$ consist of the transportation tube wall from Moon to Earth. The transportation tube wall is still represented as a two-dimensional submanifold in the phase space, while all the transfer orbits between the Earth and Moon with the same energy are comprised only inside the transportation tube (Koon et al. 2000). However, in SBCM, considering that the Halo orbit is affected by the solar gravitational perturbations, the closed orbit is no longer maintained. In addition, the solar gravity can cause the transportation tube to be deformed or broken (Yamato and Spencer 2003, 2004).

Fig. 5

Invariant manifolds of the Halo orbit near the $\mathit{LL}_{1}$ point: (a) the manifolds in the CR3BP frame; and (b) the manifolds in the SBCM frame

In invariant manifolds, the spacecraft travels multiple loops in the elliptical orbit of the Earth or Moon, and can be captured by the Moon or Earth’s gravitational force. It then travels multiple loops in the elliptical orbit of the Moon or Earth after being captured. During the whole process, the spacecraft makes a free flight. $W_{E}^{s}$ and $W_{M}^{u}$ consist of the transportation tube wall from Earth to Moon, represented by the dark area in Fig. 5(b), and $W_{M}^{s}$ and $W_{E}^{u}$ consist of the transportation tube wall from Moon to Earth, represented by the light area in Fig. 5(b). Hill’s forbidden area in SBCM is time-variant but the variation is minute. Therefore, this area can be approximately derived based on CR3BP. Moreover, in Fig. 5(b), the solar and lunar phases in the SBCM are 0° and 60°, respectively.

The spacecraft has enough time to realize the Earth-escaping and Moon-captured phases in the invariant manifolds through the cumulative effects of low thrust. It is not necessary to consider the chaotic behavior that a tiny change in velocity can allow the spacecraft escape from the gravitational field of Earth–Moon system, which exists in the N-body problem.

Although the transportation tube wall based on SBCM is deformed, the invariant manifolds derived from it also differ. The long-term effects of solar gravity limit the transfer time instead of supporting limitlessness; this is significant for the Earth–Moon transfer. Some pairs ($\beta$, $\tau$), ranging over $\beta$ in [$0, 2\pi$] and $\tau$ in [$0,1$], do not represent true transfer opportunities through the $\mathit{LL}_{1}$ Halo orbit as perturbations to the manifolds cause crashes or escapes over short time scales. Only the pairs that enable the transfer from the Earth to the Halo orbit near the $\mathit{LL}_{1}$ point and from the Halo orbit near the $\mathit{LL}_{1}$ point to the Moon can be adopted to design the Earth–Moon transfer; these are depicted in Fig. 6. In this study, the transfer opportunities make up 12.96% of all possible ($\beta, \tau$) combinations, thus satisfying both the contour-maps shown in Fig. 6. In addition, the satisfactory ($\beta, \tau$) pairs are as follows: ([95°, 150°] ∪ [262°, 345°]) × [$0, 1$] and ([100°, 200°] ∪ [270°, 30°]) × ([$0.16, 0.26$] ∪ [$0.47, 0.58$]). In this paper, ($\beta, \tau$) = (150°, 0.5), as marked in Fig. 6.

Fig. 6

Contour map of transfer opportunities: (a) the opportunities for the Earth-escaping phase; the blue areas represent the feasible opportunities. (b) The opportunities for the Moon-captured phase; the blue areas represent the feasible opportunities. In this study, ($\beta, \tau$) = (150°, 0.5)

The procedure used to search for the transfer opportunities is described as follows. (i) The lunar phasic angle $\beta$ changes in the range [0°, 360°], and the phase of serial points on the Halo orbit $\tau$ changes in the range $[0, 360]/360$. By substituting these values in Eq. (3), SBCM dynamics equations can be integrated. After obtaining a backward integration, the trajectory of the Earth-escaping phase can be obtained. When a forward integration is derived, the trajectory of the Moon-captured phase can be obtained. (ii) When reaching the first periapsis in the Earth-escaping or Moon-captured phases, record the altitude of the periapsis and draw the contour map, which can be adopted to find the transfer opportunities. (iii) The position and velocity vectors of serial points on the Halo orbit are at the same initial conditions as those of the two types of integrations (backward and forward). Furthermore, the initial lunar phasic angle $\beta= 0$° and solar phasic angle $\theta_{s}$ change in the range [0°, 360°], the phase of serial points on the Halo orbit $\tau$ changes in the range $[0, 1]$, and the amplitude in the $y$ direction of the Halo orbit is 40142.16 km.

The most important aspect in the designing of LTTs is to determine invariant manifolds to extend the low-thrust arcs. In a time sequence, the spacecraft travels multiple loops in the elliptic orbit of Earth, and then travels in the Halo orbit near the $\mathit{LL}_{1}$ point. It is then captured by the Moon and travels in the elliptic orbit of the Moon. There is no control during the whole process. The initial lunar phasic angle $\beta_{0} = 150$°, and the phase of the Halo orbit is 180°, which has been mentioned earlier.

Similar to the procedure in Sect. 3.1, when considering the Halo orbit near the $\mathit{LL}_{1}$ point as the trajectory in the free-flight phase, the procedure used to search for cislunar LTTs is described as follows. In the syzygy frame, substitute values of a specific pair of ($\beta, \tau$) into Eq. (2), and integrate the SBCM dynamics equations. When backward and forward integrations are completed, the trajectory of the Earth-escaping and Moon-captured phases can be obtained, respectively. The initial lunar phasic angle $\beta_{0} = 150$°, phase of Halo orbit is 180°, as mentioned earlier. Figure 7 presents the cislunar low-thrust transfer trajectories in the syzygy frame. Figure 8 shows the history of eccentricity and semi-major axis in the free-flying phase without control. The moment of initializing integration is defined as the epoch time $t = 0$.

Fig. 7

Cislunar low-thrust transfer trajectories in the syzygy frame

Fig. 8

History of orbit elements in the free-flying phase without control: (a) the history of eccentricity and (b) of semi-major axis

The motion before the Earth-escaping phase and after the Moon-captured phase can be regarded as a two-body problem under perturbation. Commonly, the radius of Earth’s SOI is approximately 924647 km, and the radius Moon’s SOI is approximately 66190 km. Figure 7 shows that the altitude of the trajectories of the Earth-escaping phase is no more than $4 \times 10^{5}$ km, while the maximum distance from the cislunar trajectories to Moon is approximately $5.5 \times10^{4}$ km. The trajectories of the Earth-escaping phase are observed to be located entirely in the Earth’s SOI, indicating that the trajectories are affected mainly by the Earth and will be stable enough around the Earth with a slight change in their eccentricities. Therefore, when a two-body model is adopted to solve this problem, the accuracy meets the requirement, with the orbit being stable in this model. Some parts of the trajectories of the Moon-captured phase are located at the boundary of the Moon’s SOI, and they are therefore unstable. This is proved in the results showed in Fig. 8.

Considering the instability of the transfer trajectories in the Moon-captured phase, the trajectory with a lower altitude of periapsis is more appropriate to be adopted in the free-flight phase. If the altitude of periapsis is very high, it will increase the risk of the spacecraft escaping again before being captured.

4 Low-thrust control strategy for cislunar trajectories

This section shows the low-thrust transfer by transiting the Halo orbit near the $\mathit{LL}_{1}$ point as an instance to design the low-thrust control strategy.

When initial and terminal conditions are limited, a two-point boundary problem must be solved to obtain the ON/OFF time and control law. In this study, the feasibility of the low-thrust transfer based on the transportation tube is the main point of our study. Therefore, the satisfaction of specific phasing requirements of particular missions is not required. In addition, only the semi-major axis ($a_{e}, a_{m}$) and eccentricity ($e_{e}, e_{m}$) are limited in the initial and terminal states, where $a_{e}$ and $e_{e}$ are defined as the semi-major axis and eccentricity of the orbit in the geocentric inertial frame. The parameters $a_{m}$ and $e_{m}$ are defined as the semi-major axis and eccentricity of the orbit in the selenocentric inertial frame.

4.1 Design of subcontrol law for low thrust

Without considering the effects of solar gravity perturbation, when the spacecraft travels from the Earth to Moon, the Jacobi energy integral $J$ changes from small to large and finally to small under the effects of low thrust. In this process, the function of the subcontrol law $I$ is to change the direction of energy along with the maximum gradient direction.

In CR3BP, the maximum energy gradient direction is in the direction of the velocity (Petropoulos 2003). $J = \frac{1}{2} ( x^{2} + y^{2} + z^{2} ) + \bar{U}$ is a constant under the condition of no thrust. When the effects of low thrust are considered, the Hamilton system is no longer conservative. Let the control acceleration $f = [ f_{x},f_{y},f_{z} ]^{T}$, then $\frac{dJ}{dt} = [ \dot{x},\dot{y},\dot{z} ]^{T} \cdot f$. Under the control law $I$, the thrust angle is 0 rad.

For example, consider the Earth-escaping phase. Under the subcontrol law provided in this paper, the change rule of the orbital elements is shown in Fig. 9.

Fig. 9

History of eccentricity in the escaping earth phase under the subcontrol law $I$: (a) the history of the semi-major axis, and (b) of the eccentricity

Under the subcontrol law $I$, the variation of eccentricity will exceed the allowable range ([$0, 0.7927$]). However, the semi-major axis is generally small; therefore, based on the two-body model, another subcontrol law, that is, subcontrol law $\mathit{II}$ is provided to adjust the eccentricity. To avoid the additional change in the semi-major axis, the control law $\mathit{II}$ is made to align with the normal of the inertia velocity, and the thrust angle is $\pi/2$ rad. To demonstrate the foundation of the optimal controls, the governing differential equation for eccentricity is presented as follows:

$$ \dot{e} = \frac{1}{V} \biggl[ 2 ( e + \cos\theta)f_{t} - \frac{1}{a}r\sin\theta f_{n} \biggr] $$

(4)

where $V$ is the inertia velocity, $\theta$ is the true anomaly, $t$ represents the tangential direction of the inertia velocity, and $n$ represents the normal direction of the inertia velocity. In the two-body model, control law $\mathit{II}$ does not result in an additional change of energy.

By applying control law $\mathit{II}$ to Eq. (4),

$$ \dot{e} = \frac{1}{V} \biggl[ - \frac{1}{a}r \vert {\sin\theta} \vert \cdot f_{n} \biggr]. $$

(5)

To obtain more degrees of freedom to develop optimizations, another transitional subcontrol law is used between the two given ones. Instead, a linear subcontrol law is adopted to simplify the problem. The unified control law is presented as follows:

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} 0 \le \vert {\sin\theta} \vert < \kappa_{1} & \alpha= 0 \\ \kappa_{1} \le \vert {\sin\theta} \vert < \kappa_{2} & \alpha= \dfrac{\pi}{2} \biggl( \dfrac{ \vert {\sin\theta} \vert - \kappa_{1}}{\kappa_{2} - \kappa_{1}} \biggr) \\ \kappa_{2} \le \vert {\sin\theta} \vert \le1 & \alpha= \dfrac {\pi}{2}. \end{array}\displaystyle \right . $$

(6)

In the law, two thresholds are adopted so that there are two degrees of freedom to develop optimizations. The optimized object is the thrust angle required to achieve the following target: the eccentricity and semi-major axis can reach the final value simultaneously. The procedure used to describe the control law is as follows.

The termination condition requires both the semi-major axis and eccentricity to reach their target values simultaneously. Thus, the values of $\kappa_{1}$ and $\kappa_{2}$ can be obtained as follows. First, utilize $\kappa_{1}$ in the range of (0, 1) and utilize $\kappa_{2}$ in the range of ($\kappa_{1}, 1$). Second, for each $\kappa_{1}$, a corresponding $\kappa_{2}$ can be obtained according to the termination condition. In this study, the pair $(\kappa_{1}, \kappa_{2}) = (0.2, 0.7)$ is achieved numerically to meet the constraints of both flight time and fuel consumption.

4.2 Design of ON/OFF time

The spacecraft starts up in the low orbit of Earth and accelerates to the OFF time $T_{\mathrm{off}}^{E}$, travels in the free-flight phase, and then travels in the Moon-captured phase. At the time of $T_{\mathrm{on}}^{L}$, the spacecraft starts up again and slows down to the Moon’s low orbit.

In the low-thrust transfer by the transiting of $\mathit{LL}_{1}$ point, the trajectory is stable before the spacecraft escapes from Earth; therefore, the choice of $T_{\mathrm{off}}^{E}$ can be loose. Figure 4 shows that there is an inflection point (near −66.9th day) in the trend curve of both the eccentricity and semi-major axis in the Earth-escaping phase. Furthermore, any time before the inflection point can be adopted as $T_{\mathrm{off}}^{E}$. In this study, it is −66.9th day. After the spacecraft is captured by the Moon’s gravitational force, the trajectory is unstable and the eccentricity increases under the control law; as the eccentricity starts decreasing, the time is chosen as $T_{\mathrm{on}}^{L}$. In this study, it is 9.609th day.

In the low-thrust transfer by the transiting of the Halo orbit near the $\mathit{LL}_{1}$ point, the trajectory is stable before the spacecraft escapes from Earth; therefore, the choice of $T_{\mathrm{off}}^{E}$ is relaxed. Figure 8 shows that there is an inflection point (near −14.4th day) in the trend curve of both the eccentricity and semi-major axis in the Earth-escaping phase. Further, any time before the inflection point can be adopted as $T_{\mathrm{off}}^{E}$. In this study, it is −14.4th day. After the spacecraft is captured by the Moon, the trajectory is unstable and the eccentricity increases under the control law. As the eccentricity starts decreasing, the time is chosen as $T_{\mathrm{on}}^{L}$. In this study, it is 7.075th day.

To satisfy the requirement that $m_{0} = 350$ kg (the mass of SMART-1), an iterative search must be performed. $m_{\mathrm{free}}$ is the parameter of search ($m_{\mathrm{free}}$ is the mass of the spacecraft in the free-flight phase). $\Delta m_{\mathrm{free}}$ is the step size of the search. The diagram is shown in Fig. 10.

Fig. 10

Diagram for iterative search to satisfy the requirement of initial mass

5 Numerical implementations

PPS-1350 Hall ion engine used in SMART-1 is considered in this example. The thrust is 73.19 mN, and the velocity of the fuel gas is 16.434 km/s (Betts and Erb 2006). The initial time is recorded as 0, during which the lunar phase angle is 291.1°, and the mass of the spacecraft is 349.2678 kg. In addition, the semi-major axis of the initial orbit measures 24661.11 km, and the eccentricity is 0.7157.

In the low-thrust transfer by the transiting of the $\mathit{LL}_{1}$ point, the control law functions from the initial time to the 292.2668th day. The free-flight phase must be instantaneous. Then the control law functions from the 292.2668th to the 331.5628th day. At this time, the spacecraft arrives in the terminal orbit and the low-thrust transfer is completed. The semi-major axis of the terminal orbit is 7238.244 km and the eccentricity is 0.5882. The final mass of the spacecraft is 280.7816 kg. Figure 11 depicts the trajectories in geocentric inertial and syzygy frames. The total transfer time is 331.5628 days, and the fuel consumption is 69.2184 kg.

Fig. 11

Trajectory from the Earth to Moon: (a) the trajectory in geocentric inertial frame; (b) the trajectory in syzygy frame

In the low-thrust transfer by the transiting of the Halo orbit near the $\mathit{LL}_{1}$ point, the control law works from the initial time to the 191.5556th day. The free-flight phase ranges from the 191.5556th to the 241.5380th day. Then the control law works from the 241.5380th to the 260.2504th day. At this time, the spacecraft arrives in the terminal orbit and the low-thrust transfer is completed. The semi-major axis of the terminal orbit is 7238.244 km, and the eccentricity is 0.5882. The final mass of the spacecraft is 269.0420 kg. Figure 12 depicts the trajectories in geocentric inertial and syzygy frames. The total transfer time is 260.2504 days, and the fuel consumption is 80.9580 kg, including 18.0242 kg used to control the eccentricity under the subcontrol law $\mathit{II}$.

Fig. 12

Trajectory from the Earth to Moon: (a) the trajectory in geocentric inertial frame; (b) the trajectory in syzygy frame

Betts and Erb (2006) used the direct collocation method to optimize the SMART-1 orbit with similar boundary conditions; however, the total transfer time was 201.7267 days and the fuel consumption was 74.994 kg. The performance comparison of the three trajectories is shown in Table 1.

Table 1 Performance comparison of the three LTTs

The table shows that the fuel consumption of the LTTs when transiting the $\mathit{LL}_{1}$ point is 5.7756 kg less than that of SMART-1; however, the diminution of fuel consumption is at the expense of the transfer time. When making further optimizations to the LLTs when transiting the $\mathit{LL}_{1}$ point, the obtained LLTs may have the lowest fuel consumption. However, compared with the LTTs when transiting the Halo orbit near the $\mathit{LL}_{1}$ point, the window of the passing of LTTs when transiting the $\mathit{LL}_{1}$ point is narrower. In other words, the cislunar transfer opportunities when transiting the $\mathit{LL}_{1}$ point is [77°, 109°] ∪ [285°, 342°], while the ones when transiting the Halo orbit near the $\mathit{LL}_{1}$ point is [0°, 30°] ∪ [96°, 207°] ∪ [269°, 360°].

The fuel consumption of the LTTs when transiting the Halo orbit near the $\mathit{LL}_{1}$ point is 5.964 kg more than that of SMART-1, the main reason of which is described as follows. The following example is based on the deformation in SBCM of invariant manifolds derived from the transportation tube. By considering the dependence on initial values of the solution, the invariant manifolds can still remain a part of the transportation tube. However, LLTs of SMART-1 must be in the transportation tube. Therefore, further optimization is required in the future. This paper provides the boundary of trajectory optimization (i.e., the transportation tube). However, when the trajectory optimization is performed in SMART-1, there is no boundary and a large amount of computation is needed.

6 Conclusions

In this paper, the low-thrust transfer orbit was analyzed by studying the invariant manifolds derived from the transportation tube. The deformation of transportation tube in SBCM was examined thoroughly. Next, a gradient-based design of the LTTs was represented by analyzing the invariant manifolds of the $\mathit{LL}_{1}$ point and the Halo orbit near it. Its deformation under solar gravity perturbation was also presented; this is significant for designing LTTs. In other words, the $\mathit{LL}_{1}$ point and the Halo orbit near it will serve in the free-flight phase such that the fuel consumption can be as low as possible. In addition, the control law that changes energy most rapidly was designed based on CR3BP. Furthermore, a certain ON/OFF time is provided with a two-dimensional search method. The numerical results fundamentally coincide with the SMART-1 orbit, which has similar boundary conditions.

The paper focuses on the feasibility of low-thrust transfer based on the transportation tube. However, the results obtained in this paper have not been optimized. Therefore, the result can be used as an initial low-energy transfer orbit between the Earth and Moon. If further optimization can be conducted, another orbit that can save more energy can be obtained.