Natural and Forced Spacecraft Loitering in a Near Rectilinear Halo Orbit

Abstract

With an increasing number of missions planned to cislunar space, on-orbit servicing, inspection, and docking in a multi-body environment will need to take place in highly perturbed orbits for the first time. Thus, the investigation of these relative motion trajectories between two spacecraft is critical to successfully performing rendezvous and proximity operations in a multi-body environment. In this work, mass- and time-optimal trajectories are generated for a low-thrust chaser spacecraft entering into natural and forced loiter sequences about a target on a near rectilinear halo orbit. Constraints on the allowable region for safe rendezvous and proximity operations are applied to investigate the effects on feasible loitering maneuvers. Fuel costs are compared for transfers to both forced and natural loitering trajectories to determine the propellant reduction from leveraging the relative dynamics of NRHO manifolds.

1 Introduction

Currently, NASA has proposed the Artemis missions to land humans on the Moon by 2025 and eventually establish a long-term presence in cislunar space. International collaboration to construct this lunar orbital platform, Gateway, will help accomplish the latter goal [1]. Although rendezvous and proximity operations have been thoroughly investigated in low-Earth orbit, most notably with the International Space Station (ISS), no rendezvous and proximity operation (RPO) maneuver has been performed in a multi-body orbit [2]. Through the on-orbit construction of Gateway and plans to test RPO maneuvers along a near rectilinear halo orbit (NRHO) with Artemis III, the design of potential types of sequences in cislunar space must be sufficiently explored to extend well-known two-body RPO maneuvers into a three-body environment.

This research focuses on a spacecraft conducting a loiter maneuver, which is a means of maintaining bounded relative motion about a chief in the local-vertical, local-horizontal (LVLH) frame. Loitering in the vicinity of the chief may be required for a variety of reasons such as inspection prior to on-orbit servicing of a spacecraft. It may also be useful to maintain a desired distance and avoid collisions prior to receiving the go ahead to rendezvous. Thus, an important consideration for a spacecraft performing any RPO sequence is that the deputy must take into account potential collisions or conjunctions with the chief or other nearby spacecraft during these maneuvers [3]. Due to the magnitude of relative distance between two spacecraft during an RPO sequence, passive safety is also critical to guarantee mission success which further emphasizes the importance of safe bounded relative trajectories [4].

While previous work has generated forced loitering sequences for a spacecraft utilizing an impulsive engine [5], this research extends previous analysis to encompass RPO in cislunar space using an electric propulsion system. Low-thrust transfers to natural relative trajectories in the circular restricted three-body problem (CR3BP) are also explored. The use of electric propulsion significantly improves the efficiency of a spacecraft, decreasing the required propellant mass and increasing the longevity of a mission [6]. Particularly, for future servicing missions to a cislunar environment, a servicer spacecraft that can operate for a longer lifetime will be advantageous compared to its impulsive counterpart. To make this work applicable to a realistic mission scenario, constraints on acceptable regions for rendezvous and proximity operations are also enforced to generate relative motion in areas of the NRHO where velocities are lower and less sensitive to perturbations [2].

2 Methods

2.1 Problem Dynamics

In this investigation, the problem was formulated using the circular restricted three-body problem (CR3BP) to model the dynamics of both the chief and deputy spacecraft. The first assumption of the CR3BP is that the mass of the third body (the spacecraft) is infinitesimal; therefore, it is much smaller than the two primary bodies and the effects of the third body on the primaries can be ignored. Second, it is assumed that the primary and secondary bodies exhibit circular motion about the system barycenter [7]. Characteristic quantities for mass ($m^{*}$), length ($l^{*}$), and time ($t^{*}$) are introduced to the equations of motion such that the total mass and distance between the primaries equal unity. These quantities are shown in Equation (1), where $\mu$ is the non-dimensional mass ratio, $G^{*}$ is the non-dimensional gravitational constant, $m_{1}$ and $m_{2}$ are the masses of the primary and secondary body, and $r_{1}$ and $r_{2}$ are the distances of the primary and secondary body to the system barycenter. The non-dimensional mean motion of the system is defined to also equal unity, and the system period becomes 2$\pi$ [7]. The characteristic quantities used in this work can be found in Table 1.

$$\begin{aligned} \begin{aligned} m^{*} = m_{1} + m_{2} \\ l^{*} = r_{1} + r_{2} \\ t^{*} = \sqrt{\frac{{{l^{*}}^{3}}}{G^{*}m^{*}}} \\ \mu = \frac{m_{2}}{m^{*}} \end{aligned} \end{aligned}$$

(1)

Table 1 Characteristic quantities

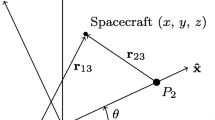
The resulting equations of motion for the deputy and chief spacecraft in the rotating frame, M, with respect to the Moon are defined in Eq. (2). M is centered at the Moon rather than the system barycenter for this analysis in order to derive the local-vertical local-horizontal (LVLH) frame similar to that in low-Earth orbit. $\vec {\omega }_{M/I}$ is the angular velocity of the rotating Moon frame with respect to the inertial frame, I, $\vec {r}_{mi}$ is the chief’s position vector with respect to the Moon, $\vec {r}_{ei}$ is the chief’s position vector with respect to the Earth, and $\vec {r}_{em}$ is the position vector of the Moon relative to the Earth. The relationship between the unit vectors of the Moon frame compared to the standard CR3BP formulation is shown in Eq. (3). Figure 1 shows the LVLH frame, L, centered on the chief, the Moon-centered rotating frame, M, the inertial frame, I, and the standard CR3BP rotating frame defined at the Earth-Moon barycenter, B. In the figure, $\vec {\omega }_{B/I}$ is the angular velocity of the standard CR3BP frame, which in non-dimensional units is unity.

$$\begin{aligned}{} & {} \ddot{\vec {r}}_{mi} = -2\vec {\omega }_{M/I}\times {\dot{\vec {r}}}_{mi} - \vec {\omega }_{M/I}\times {(\vec {\omega }_{M/I}\times {\vec {r}_{mi}})} \nonumber \\{} & {} \quad - \mu \frac{\vec {r}_{mi}}{|\vec {r}_{mi}|^3} - (1-\mu )\left(\frac{\vec {r}_{ei}}{|\vec {r}_{ei}|^3}-\frac{\vec {r}_{em}}{|\vec {r}_{em}|^3}\right) \end{aligned}$$

(2)

$$\begin{aligned}{} & {} \begin{aligned} {\hat{i}}_M = -{\hat{i}}_B,\hspace{0.5cm}{\hat{j}}_M = -{\hat{j}}_B,\hspace{0.5cm}{\hat{k}}_M = {\hat{k}}_B \end{aligned} \end{aligned}$$

(3)

Fig. 1

LVLH and moon-centered CR3BP reference frame

This work utilizes the LVLH frame to define the relative motion of the deputy spacecraft with respect to the chief, synonymous to the definition used in the two-body case. The relative acceleration is found by taking the chief’s position in the Moon centered reference frame, M, and defining the LVLH frame, L, centered on the chief. The LVLH frame is defined in Eq. (4) where $\vec {h}$ is the chief’s angular momentum in the CR3BP, and $\vec {r}_{mi}$ is its position with respect to the Moon [2]. The unit vectors of the LVLH frame are defined by V-bar (${\hat{i}}_L$ direction), H-bar (${\hat{j}}_L$ direction), and R-bar (${\hat{k}}_L$ direction).

$$\begin{aligned} \begin{aligned} {\hat{i}}_L = {\hat{j}}_L\times {{\hat{k}}}_L,\hspace{0.5cm}{\hat{j}}_L = -\frac{\vec {h}}{\mid {\vec {h}}\mid },\hspace{0.5cm}{\hat{k}}_L = -\frac{\vec {r}_{mi}}{\mid {\vec {r}_{mi}}\mid } \end{aligned} \end{aligned}$$

(4)

The relative position between the chief and deputy spacecraft can be found through the relation in Eq. (5) below, where $\vec {p}$ is the position of the deputy relative to the chief, $\vec {r}_{d}$ is the position vector of the deputy, and $\vec {r}_{c}$ is the position vector of the chief in the frame of interest. While this relative position vector can simply be determined in the CR3BP reference frame, it is useful to define the deputy’s position in the LVLH frame. This allows constraints on the position of the deputy relative to the orientation of the chief to be easily evaluated, such as approaching a docking port or inspecting all sides of a chief spacecraft.

$$\begin{aligned} \begin{aligned} \vec {r}_{d} = \vec {r}_{c} + \vec {p} \end{aligned} \end{aligned}$$

(5)

Taking the first derivative with respect to time of Eq. (5) in the inertial frame, I, yields

$$\begin{aligned} \begin{aligned} \dot{\vec {r}}_{ d}^{\hspace{0.1 cm}I} = \dot{\vec {r}}_{c}^{\hspace{0.1 cm}I} + \dot{\vec {p}}^{\hspace{0.1 cm}L} + \vec {\omega }_{L/I}\times {\vec {p}} \end{aligned} \end{aligned}$$

(6)

where $\vec {\omega }_{L/I}$ is the angular velocity of the LVLH frame with respect to the inertial frame. This can be calculated through Eq. (7), where $\vec {\omega }_{L/M}$ is the angular velocity of the LVLH frame with respect to the Moon, and $\vec {\omega }_{M/I}$ is the angular velocity of the Moon frame with respect to the inertial frame (unity in the CR3BP).

$$\begin{aligned} \begin{aligned} \vec {\omega }_{L/I} = \vec {\omega }_{L/M} + \vec {\omega }_{M/I} \end{aligned} \end{aligned}$$

(7)

The calculation of $\vec {\omega }_{L/M}$ requires the evaluation of the time derivatives of the unit vectors of the LVLH frame. Using the results of these derivatives yield an expression of $\vec {\omega }_{L/M}$ in Eq. (8).

$$\begin{aligned} \begin{aligned} \vec {\omega }_{L/M} = -\frac{h}{r^{2}}{\hat{j}}_L - (\frac{r}{h^{2}}\vec {h}\cdot {\ddot{\vec {r}}}_{c}){\hat{k}}_L \end{aligned} \end{aligned}$$

(8)

The second derivative can then be calculated as

$$\begin{aligned} \begin{aligned} \ddot{\vec {r}}_{ d}^{\hspace{0.1 cm}I} = \ddot{\vec {r}}_{c}^{\hspace{0.1 cm}I} + \ddot{\vec {p}}^{\hspace{0.1 cm}L} + 2\vec {\omega }_{L/I}\times {\dot{\vec {p}}^{\hspace{0.1 cm}L}} + {\dot{\vec {\omega }}_{L/I}^{\hspace{0.1 cm}I}}\times {\vec {p}} + \vec {\omega }_{L/I}\times {(\vec {\omega }_{L/I}\times {\vec {p}})} \end{aligned} \end{aligned}$$

(9)

where $\dot{\vec {\omega }}_{L/I}$ is the angular acceleration of the LVLH frame with respect to the inertial frame which is calculated using Eq. (10). In the CR3BP, $\dot{\vec {\omega }}_{M/I}$ is zero, so only the $\dot{\vec {\omega }}_{L/M}$ term contributes to the angular acceleration.

$$\begin{aligned} \begin{aligned} \dot{\vec {\omega }}_{L/I} = \dot{\vec {\omega }}_{L/M} + \dot{\vec {\omega }}_{M/I} \end{aligned} \end{aligned}$$

(10)

The angular acceleration of the LVLH frame, L, relative to the Moon rotating frame, M, can be calculated using

$$\begin{aligned} \begin{aligned} \dot{\vec {\omega }}_{L/M} = \left(-\frac{\dot{h}}{r^{2}}+2\frac{\dot{r}h}{r^{3}}\right) {\hat{j}}_L + \left[(\frac{\dot{r}}{r}-2\frac{\dot{h}}{h})(\vec {\omega }_{L/M}\cdot {{\hat{k}}_L}) - \frac{r}{h^{2}}\cdot {\dddot{\vec {r}}_{c}^{\hspace{0.1 cm}M}}\right] {\hat{k}}_L \end{aligned} \end{aligned}$$

(11)

where $\dddot{\vec {r}}_{c}^{\hspace{0.1 cm}M}$ is the jerk of the chief spacecraft.

$$\begin{aligned} \begin{aligned} \dddot{\vec {r}}_{c}^{\hspace{0.1 cm}M} = -2\vec {\omega }_{M/I}\times {\ddot{\vec {r}}}_{c}^{M} -3\dot{\vec {\omega }}_{M/I}^{\hspace{0.1 cm}M}\times {\dot{\vec {r}}}_{c}^{\hspace{0.1 cm}M} - \ddot{\vec {\omega }}_{M/I}^{\hspace{0.1 cm}M}\times (\vec {\omega }_{M/I}\times {\vec {r}_{c}}) - \\ \vec {\omega }_{M/I}\times {(\dot{\vec {\omega }}}_{M/I}^{\hspace{0.1 cm}M}\times {\vec {r}_c}) - \vec {\omega }_{M/I}\times {(\vec {\omega }}_{M/I}\times {\dot{\vec {r}}_c}^{\hspace{0.1 cm}M}) - \mu \frac{\partial }{\partial \vec {r}}[\frac{\vec {r}_{c}}{r_{c}^{3}}] \dot{\vec {r}}_{c}^{\hspace{0.1 cm}M} - \\ (1-\mu )\left(\frac{\partial }{\partial \vec {r_{c}}}\left[\frac{\vec {r}_{c}+\vec {r}_{em}}{\mid {\vec {r}_{c}+\vec {r}_{em}}\mid ^{3}} \right]({\dot{\vec {r}}}_{c}^{\hspace{0.1 cm}M}+{\dot{\vec {r}}}_{em}^{\hspace{0.1 cm}M}\right)-\frac{\partial }{\partial \vec {r}}\left[\frac{\vec {r}_{em}}{r_{em}^{3}}\right]({\dot{\vec {r}}}_{em}^{\hspace{0.1 cm}M})) \end{aligned} \end{aligned}$$

(12)

Additionally,

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial \vec {q}} \left[\frac{\vec {q}}{q^{3}}\right] = \frac{1}{q^{3}}\left(I - \frac{3\hspace{0.1 cm}\vec {q}\hspace{0.1 cm}\vec {q}^{\hspace{0.1 cm}T}}{q^{2}}\right) \end{aligned} \end{aligned}$$

(13)

where I is an identity matrix with size of 3 × 3 for this problem and $\vec {q}$ is the position vector of interest required to evaluate the equation for jerk given in Eq. (12).

Finally, substituting in the equation for the acceleration of the chief from Eq. (2) and converting to the LVLH frame, L, the deputy’s acceleration can be found in Eq. (14) [2].

$$\begin{aligned} \begin{aligned} \ddot{\vec {p}}&= -2\vec {\omega }_{L/I}\times {\dot{\vec {p}}} - (\dot{\vec {\omega }}_{L/I}\times {\vec {p}}) - \vec {\omega }_{L/I}\times {(\vec {\omega }_{L/I}\times {\vec {p}})}\\ +&\quad \mu \left(\frac{\vec {r}}{{r}^3}-\frac{\vec {r}_{mi}+\vec {p}}{\mid {\vec {r}_{mi}+\vec {p}}\mid ^3}\right) + (1-\mu )\left(\frac{\vec {r}_{mi}+\vec {r}_{em}}{\mid {\vec {r}_{mi}+\vec {r}_{em}}\mid ^3}-\frac{\vec {r}_{mi}+\vec {p}+\vec {r}_{em}}{\mid {\vec {r}_{mi}+\vec {p}+\vec {r}_{em}}\mid ^3}\right) \end{aligned} \end{aligned}$$

(14)

2.2 Safe RPO Region

Due to the dynamics of the NRHO near perilune, it is necessary to perform rendezvous and proximity operations near apolune where spacecraft velocities are lower [2]. For this work, a 9:2 $L_{2}$ resonant NRHO is used which has a period of approximately 6.56 days. Since perilune on the target NRHO passes close to the moon, the velocities are much higher at that point in the orbit. At perilune, the velocities approach 1.7 km/s compared to only 0.1 km/s at apolune. Thus, attempting to perform RPO near perilune becomes particularly challenging due to how quickly velocity errors may accumulate. For this analysis, the region for RPO was bounded between a mean anomaly of 80$^{\circ }$ and 280$^{\circ }$ which puts an upper bound on the maximum time of flight for a given initial state along the NRHO, consistent with previous investigations [2]. Previous work by Bucci et. al. developed this recommended RPO region based on an analysis of the invariant manifolds of the 9:2 NRHO and the resulting unstable behavior near perilune [8]. It is important to note that any long-term loitering in the vicinity of an NRHO will require some natural motion outside of the defined safe RPO bounds. However, limiting a spacecraft’s thrusting arcs to be within the safety region will be critical to ensuring that there is no unnecessary relative error accumulation, and therefore collision risks, due to RPO maneuvers in higher velocity regions The mean anomaly for a spacecraft can be found using Eq. (15), where $t_{p}$ is the time past periapsis, and T is the period of the orbit. This definition is similar to that of two-body Keplerian dynamics. In this case, periapsis is defined as the CR3BP xz plane crossing closest to the Moon [2]. The safe region to perform rendezvous and proximity operations is shown in blue in Fig. 2.

Fig. 2

Safe region for rendezvous and proximity operations on an NRHO

$$\begin{aligned} \begin{aligned} M = 2\pi \frac{t_{p}}{T} \end{aligned} \end{aligned}$$

(15)

2.3 Forced Motion

Forced spacecraft loitering is a well-known RPO maneuver to remain in the vicinity of a chief spacecraft where leveraging the natural motion of the system is infeasible. Specifically, forced circumnavigation refers to a form of loitering where waypoints are placed about the target to ensure the deputy spacecraft passes through one revolution of the chief while maintaining a constant distance at each waypoint [9]. The number of and distance between waypoints can vary depending on specific mission requirements. By remaining a safe distance from the chief through circumnavigation, the RPO sequence can be assumed passively safe to any missed burns once the spacecraft gets onto the circumnavigation trajectory for the purposes of this work. This analysis will focus on mass- and time-optimal forced circumnavigation maneuvers for a spacecraft equipped with a low-thrust propulsion system. Figure 3 shows an example of a forced circumnavigation sequence about the chief, where R is the radius of the circle that contains the waypoints.

Fig. 3

Arbitrary Forced Circumnavigation in the LVLH Frame

The RPO sequence is first transcribed into an optimal control problem to be solved using the Astrodynamics Software and Science Enabling Toolkit (ASSET), developed at the University of Alabama [10]. The problem sequence was transcribed using 5th order Legendre Gauss Lobatto (LGL) direct collocation. ASSET utilizes PSIOPT, a built in non-linear program (NLP) solver which uses interior-point methods, to solve this RPO problem. For this analysis, time-optimal and mass-optimal solutions were explored, where the objective functions can be found in Eqs. (16) and (17), respectively. The sequence is assumed to begin from a hold-point located 100 km from the target. This distance was selected since 100 km is the bound where close proximity operations begin [11]. From this point, the spacecraft burns onto the desired circumnavigation trajectory with a radius of 50 km and six evenly spaced waypoints in terms of distance. The 50 km distance was selected since it is the halfway point between the chaser’s initial position and the target. This distance also ensures passive safety for one period throughout the circumnavigation portion of the trajectory. The initial guess was generated by using simple impulsive targeting with the state transition matrix from the chaser’s dynamics found in Eq. (14). Contrary to the natural motion discussed in the next section, maintaining a constant distance from the target may be necessary for mission requirements. For this example, six waypoints were selected to ensure the resulting trajectory maintained a circular shape; however, some mission requirements may allow for fewer or non-evenly spaced waypoints using various geometries. Finally, the chief spacecraft is assumed to be passive and remains on the NRHO, while the deputy spacecraft is equipped with electric propulsion capable of producing 300 mN of thrust with a specific impulse of 1,800 s. The initial spacecraft mass is assumed to be 1500 kg. Since there are no low-thrust RPO missions currently planned to an NRHO, these parameters were chosen based on a Hall thruster, such as the PPS-5000. The resulting spacecraft acceleration is approximately 20 $\mu$g, and thus, a reasonable thrust level to perform the small maneuvers associated with an RPO sequence, in addition to the larger maneuvers that may be required to initially reach the vicinity of the NRHO [12].

$$\begin{aligned} \begin{aligned} J= & {} -t_f \end{aligned} \end{aligned}$$

(16)

$$\begin{aligned} \begin{aligned} J= & {} \int _{t_0}^{t_f}\mid \vec {u}\mid dt \end{aligned} \end{aligned}$$

(17)

2.4 Natural Motion

In situations where the time of flight and waypoint constraints are not as stringent, leveraging the natural relative motion within a dynamical regime can be useful in reducing fuel costs to maintain bounded trajectories. Within the framework of the CR3BP, manifold structures associated with a periodic orbit exist. These manifold structures can provide propellant-free transfers to and from the associated periodic orbit.

For a given periodic orbit, stability information is obtained from the monodromy matrix, which is defined to be the state transition matrix, $\Phi$, after one period of the orbit, T. In the case of RPO, where the chief spacecraft is on an NRHO with a deputy spacecraft in the vicinity, the CR3BP monodromy matrix of the chief will be used to obtain the manifolds of the NRHO of interest. A 9:2 resonant $L_{2}$ NRHO was selected for this work as it is of particular interest for NASA’s lunar Gateway due to its eclipse avoidance properties. Additionally, NRHOs possess relatively stable behavior which increases its usefulness for future missions [13].

The eigenvalues and eigenvectors associated with the monodromy matrix correspond to six different manifolds: one unstable, one stable, two periodic (unitary), and two center modes [7]. The resulting eigenvalues of the 9:2 NRHO are summarized in Table 2. Additionally, the stability index is another useful way to characterize the stability properties of the orbit based on the eigenvalues [14, 15]. Equation (18) is used to determine the stability index based on each pair of eigenvalues, $\lambda _i$. Since the maximum stability index has a magnitude of 1.323, the NRHO is considered linearly unstable.

$$\begin{aligned} \begin{aligned} \nu = \frac{1}{2} \left(\lambda _i + \frac{1}{\lambda _i}\right) \end{aligned} \end{aligned}$$

(18)

Table 2 9:2 NRHO eigenvalues and stability index

By perturbing the chief’s state vector in the direction of the eigenvector of the monodromy matrix that corresponds to a given eigenvalue, the new state vector can then be integrated in time to generate a trajectory associated with the manifold. Note, since these manifolds are generated by means of a small perturbation, the manifold is no longer a true manifold, but instead an approximation that will still exhibit similar behavior to the true manifold for small perturbations. By converting this perturbed state vector into the LVLH frame, the manifolds can be analyzed from the perspective of a chief spacecraft on the NRHO. This perturbed LVLH state is assumed to be an initial condition for a deputy spacecraft [16]. Thus, this state can be integrated forwards or backwards in time to determine the behavior of a deputy spacecraft along a manifold in the LVLH frame [7, 11].

Figures 4 and 5 show the resulting trajectories associated with the stable and unstable manifolds, respectively, for a deputy spacecraft near an NRHO, where the circular points indicate the initial condition from perturbing an initial state on the NRHO along the manifold’s eigenvector. Additionally, for each manifold, an in-plane view of the LVLH frame (V-bar/R-bar) is shown along with out-of-plane view (V-bar/H-bar). A perturbation step of approximately 5 km was used to generate the initial states as it produced relative motion of similar order of magnitude to the forced motion case. However, the selection of different perturbation step sizes would yield different LVLH trajectories. Initial mean anomalies along the 9:2 NRHO were selected within the bounds of the safe RPO region, defined between 80$^{\circ }$ and 280$^{\circ }$, since it’s assumed that any transfer onto these manifolds would need to take place in that region as previously discussed. The trajectories were propagated for 2 periods of the NRHO (approximately 13 days) starting from the positive and negative direction of the eigenvector, hence the two different clusters of initial conditions. When viewed in the LVLH frame, these manifolds appear to spiral towards the chief (for stable manifolds) and away from chief (for unstable manifolds) in both planar views of the frame since there is an out-of-plane component with respect to the chief’s orbit.

Fig. 4

Stable manifolds in LVLH frame

Fig. 5

Unstable manifolds in LVLH frame

Figures 7 and 6 show the behavior of center and periodic manifolds in the LVLH frame propagated for 2 periods of the NRHO. A perturbation step of approximately 5 km was used to generate initial states for the propagation—the same step size used for the stable and unstable manifold case. These manifolds produce bounded behavior near the chief which can be useful for proximity operation maneuver design. The center manifolds, which are characterized by having imaginary components in their eigenvalues, produce a bounded quasi-periodic motion about the chief. When observing the manifolds in the V-bar/R-bar plane over multiple revolutions of the NRHO, a ‘figure-eight’ shape is apparent. Although, the number of periods required to observe this behavior varies with the initial mean anomaly. Unlike the periodic mode, however, the center manifolds produce an out-of-plane component up to approximately 5 km for the analyzed initial conditions. As shown in Fig. 7, a deputy spacecraft on this manifold would fully circumnavigate the chief at various distances over time. It is also apparent that the initial mean anomalies closer to the upper and lower bounds of the safe RPO region reach a larger maximum distance from the chief as relative velocities increase. For the periodic (unitary) modes, the manifolds maintain an approximately circular shape that stays primarily in the V-bar/R-bar plane of the LVLH frame. This circular, planar behavior will only be valid for small perturbations due to the way that approximate manifolds are generated [7]. Since RPO, by definition, requires small distances from the chief spacecraft, this behavior can be expected for most RPO mission design cases. However, as seen in Fig. 6, these trajectories remain either ‘in front’ of or ‘behind’ the chief and do not fully circumnavigate, which may or may not be desirable depending on the constraints of an RPO mission. Additionally, the periodic manifolds generated near the bounds of the safe RPO region produce larger relative circular motion due to increasing relative velocities.

Fig. 6

Periodic manifolds in LVLH frame

Fig. 7

Center manifolds in LVLH frame after two periods of NRHO

When investigating the behavior of the center manifolds in the LVLH frame over multiple revolutions of the NRHO, the quasi-periodic motion becomes apparent. As an example, the center manifold at apolune is integrated over the course of eight periods of the NRHO; only the initial step in the positive direction of the eigenvector is selected to further simplify the plot. Figure 8 shows the V-bar/R-bar components of the center manifold while Fig. 9 shows the out-of-plane component in the V-bar/H-bar plane. The different line types in the trajectory indicated in the figure show the progression of the manifold over eight periods of the NRHO in the LVLH frame. As shown in the figures, a spacecraft starting on a center manifold at apolune would fully circumnavigate the chief over the first two periods of the NRHO. After approximately four periods, the circumnavigation continues through the other side of the 5 km step in the eigenvector direction and completes the full ‘figure-eight’ motion. Depending on the initial condition along the eigenvector, a spacecraft would initially circumnavigate the chief with more of a positive or negative V-bar component in the LVLH frame.

Fig. 8

Center manifold at apolune in LVLH frame

Fig. 9

Center manifold at apolune in LVLH frame

3 Results

3.1 Forced Motion

After constraints on the allowable rendezvous region are applied, a 50 km forced circumnavigation trajectory is generated to explore the resulting solution. Figure 10 shows an example of a mass- and time-optimal circumnavigation trajectory that commences the RPO sequence at apolune of the NRHO. For the given initial state along the NRHO and circumnavigation constraints, the minimum-time solution is approximately 35.43 h (1.48 days), using 2.27 kg of propellant; whereas, the minimum-fuel solution is about 43.75 h (1.82 days), using 1.53 kg of propellant. Compared with the NRHO’s period of about 6.56 days, these trajectories are much shorter than a full period of the NRHO. The most visible difference between the shapes of the two trajectories occurs during the initial burn from the hold-point to the first waypoint. The mass-optimal solution takes a straighter path along the V-bar direction while the time-optimal solution develops more of an R-bar component due to the continuous thrusting. As shown in the figure, the resulting mass-optimal control exhibits a bang-bang behavior while the time-optimal solution thrusts at full magnitude for the duration of the RPO sequence. Additionally, once the spacecraft enters into the circumnavigation portion of the trajectory, the resulting control direction points away from the chief for both mass- and time-optimal solutions. This ensures that, given any missed burn along the circumnavigation trajectory, the spacecraft will be passively safe and not risk any collisions with the chief for at least one period following the missed burn. Passive safety during the circumnavigation trajectory was verified by propagating ballistic trajectories at various points along the circumnavigation to simulate a missed burn, assuming that a passive safety risk is an approach of less than 10 km from the chief [4]. Note, specific considerations required to ensure passive safety throughout the entire trajectory are beyond the scope of this work.

Fig. 10

Circumnavigation trajectory and control magnitude

Using a range of initial mean anomalies within the allowable limits on rendezvous and proximity operations ([80, 280]$^{\circ }$), the circumnavigation trajectories are optimized for maximizing the spacecraft’s final mass. Figure 11 shows the effects of the initial mean anomaly, $M _{0}$, on the resulting TOF and fuel usage for a 1500 kg deputy spacecraft. For this example, the TOF is defined as the time to complete the initial burn to the circle containing the waypoints and then complete one full revolution around the chief. As shown below, for a circumnavigation trajectory of 50 km, beginning the RPO sequence much later than apolune would not be feasible within the constraints on the safe RPO region. This is due to the limits on the thruster itself which prevents the spacecraft from completing a full revolution about the chief before departing the safe RPO region. Additionally, these constraints cause the mass-optimal TOF to have a linear relationship with the initial mean anomaly; the TOF linearly decreases for trajectories that begin at higher mean anomalies. One important note is that these forced circumnavigation trajectories under the mean anomaly constraints yield TOFs that are much lower than the period required to leverage the natural manifolds to circumnavigate the chief spacecraft due to the relationship of the manifolds to the period of the orbit.

Fig. 11

Effects of initial mean anomaly on TOF and final mass

Finally, extending this analysis to forced motion sequences in other planar orientations has been explored to obtain $\Delta$V costs. Figure 12 shows the resulting $\Delta$V costs for different orientations of the circumnavigation trajectory, assuming the initial hold-point and circumnavigation trajectory from Fig. 10 has been rotated by the same $\varphi$ and $\theta$, respectively. For example, for a fixed $\varphi$ value, varying the $\theta$ parameter will generate forced motion sequences in the same LVLH plane, with different initial conditions about that plane. From the contour plot, the lowest cost solutions occur for inclined solutions into the H-bar directions that generate clockwise motion from the perspective of the chief in the R-bar/V-bar plane. Contrarily, the highest cost solutions occur in similar planes to the minimum cost solution, but with counterclockwise motion. Three point cases were selected from this contour plot to better visualize the orientation of minimum $\Delta$V, maximum $\Delta$V with respect to the original reference case used. Figures 13 and 14 show these three cases. As seen from the contour plot and the corresponding trajectory, the reference case selected produces a relatively average $\Delta$V cost when compared with all possible orientations. However, changing the orientation into the H-bar plane can either improve or worsen costs depending on the resulting relative plane chosen. This change in $\Delta$V cost most likely occurs due to the spacecraft being able to leverage the natural motion exhibited by the CR3BP in certain orientations. However, due to the small magnitude of these RPO sequences, the difference in cost for various orientations of the forced motion is minimal and only varies by approximately 2 m/s over the entirety of the solution space. Thus, this allows for the orientation of the circumnavigation sequence to be selected by the mission designer without needing to consider the $\Delta$V increases that may occur based on the selection.

Fig. 12

Effects of circumnavigation plane on $\Delta$V costs

Fig. 13

Forced motion trajectory comparison

Fig. 14

Forced motion trajectory comparison

3.2 Natural Motion

In addition to forced motion trajectories, low-thrust transfers to both center and periodic manifolds are explored to obtain cheaper options in terms of fuel usage for long-term loitering operations. Starting from the same 100 km hold-point as in the forced motion case, a fixed time of flight burn is performed to match the required position and velocity of the manifold at apolune. For this analysis, a TOF of 18 h was chosen since in the forced motion case, the initial burn phase onto the circumnavigation trajectory is approximately 9 h and travels half the distance of the two natural motion cases that are analyzed. While not exactly the same, this allows for a reasonable fuel comparison between natural motion and forced loitering sequences.

Figure 15 shows an example mass-optimal transfer to a center manifold at apolune. The initial low-thrust burn requires approximately 0.311 kg of propellant; however, once the spacecraft reaches the center manifold, it will maintain the bounded motion behavior unlike the forced motion case which will require continuous thrusting to circumnavigate the chief. Compared to the forced motion mass-optimal trajectory, which used 1.53 kg of propellant, it is immediately evident that leveraging natural motion significantly reduces fuel requirements. For the perturbation size used (5 km) to generate the manifolds, the maximum distance from the chief for the center manifold is approximately 30 km. While this motion is reasonably close in order of magnitude to the fixed 50 km forced motion trajectory, further tuning of the perturbation size along the eigenvector could generate more desirable maximum distances from the chief. From the resulting relative motion sequence, it is apparent that the closest approach distance of this specific center manifold is approximately 2.25 km, at a mean anomaly of 35 degrees, which clearly violates the desired passive safety distance of 10 km. This is one of the significant weaknesses of relying on natural motion to perform RPO maneuvers. Without the use of a low-thrust engine, it becomes difficult to ensure the spacecraft does not enter into keep out zones as there is no authority in waypoint placement.

Fig. 15

Transfer to center manifold at apolune

Figure 16 shows an example mass-optimal transfer to a periodic manifold at apolune. This transfer requires slightly less propellant compared to the center manifold case, using 0.294 kg of fuel. Due to the aforementioned constraint on safe rendezvous and proximity operation regions, a deputy spacecraft entering onto the periodic manifold of the chief would need to get onto the manifold near apolune. This is because relative velocities between the two spacecraft at apolune are the lowest, which corresponds to the part of the manifold closest to the chief in Fig. 16. This also explains the seemingly non-smooth transfer onto the manifold, as relative velocities are so low that it is easy to get onto the manifold once reaching the target location and decreasing the relative velocity. From the resulting relative motion sequence, it is also apparent that the closest approach distance of this specific periodic manifold is approximately 5 km at apolune, which again violates the passive safety sphere. However, this periodic manifold is more easily tunable with enforcing passive safety compared to the center manifold case as increasing the offset distance should bound the minimum approach distance. One important note is that increasing the initial offset distance will cause the resulting RPO trajectory size to increase, which may conflict with mission constraints. Table 3 shows a comparison of fuel used for various bounded relative motion sequences that were analyzed in this work.

Fig. 16

Transfer to periodic manifold at apolune

Table 3 Propellant used for various loitering trajectories

After exploring a single 9 h TOF transfer to periodic and center manifolds, transfers to these manifolds were explored at apolune for various fixed TOFs to determine at what point additional TOF was no longer useful for satisfying fuel and safe RPO requirements. In this example, the TOF is defined as the transfer time to get onto the manifold, since thrusting is no longer required to maintain the motion after the initial burn. While the cheapest solution in terms of propellant would be at higher TOFs due to the constraint on where RPO operations can take place, rendezvousing with a manifold at apolune requires a transfer time of, at most, approximately 1.53 days. Figure 17 shows the required fuel to transfer to a manifold at various fixed TOFs. As apparent in the figure, the propellant required exponentially decays; thus, after around a 30 h transfer, the fuel saved becomes negligible. Thus, a longer transfer is preferable, but constraints of the mission may require non-optimal transfer times. The safe RPO bound also begins to put an upper bound on transfer time– shown in Fig. 17 as a black dashed line. At some point, in this case around 36 h, it would no longer be safe to continue thrusting and performing RPO. Additionally, transferring to a periodic manifold at apolune appears to require slightly less fuel than a transfer to a center manifold.

Fig. 17

Propellant required to transfer to manifold from 100 km hold-point

While both periodic and center manifolds produce bounded behavior, mission requirements may make one manifold type more useful than the other. Since periodic manifolds produce the same behavior with every period of the NRHO, this provides a consistent trajectory for a deputy spacecraft to observe from and perform RPO. However, periodic manifolds do not fully circumnavigate the chief, which may be problematic for missions that require inspection of all sides of the chief spacecraft. In this case, a center manifold may prove more useful since a deputy spacecraft on this manifold would circumnavigate all sides of the chief. However, by leveraging a center manifold, the motion and distance from the chief is continuously changing with every period which may not be desirable for some missions that rely on targeting the same waypoints every revolution.

3.3 Spacecraft loitering DV trade study

To better understand the solution space of forced circumnavigation and transfers to natural motion on a 9:2 NRHO, a trade study was performed to analyze the $\Delta V$ requirements for a mass-optimal, fixed time of flight, loitering trajectory. This allows for a comparison of $\Delta V$ between forced circumnavigation and transfers to manifolds for any given set of initial mean anomalies and TOFs. Mass-optimal trajectories were first generated for the same 100 km hold-point transfer to a 50 km forced circumnavigation trajectory. Times of flight were chosen between the minimum TOF solution and the maximum allowable TOF to stay in the safe RPO region for a given initial mean anomaly. The results of this trade study are shown in Fig. 18. It appears that the initial mean anomaly does not noticeably affect the magnitude of $\Delta V$ required to perform the forced circumnavigation trajectory. However, as TOF increases, the $\Delta V$ begins to non-linearly decrease to a lower bound of approximately 8.4 m/s. These extremely low $\Delta V$ circumnavigation trajectories are only available when the initial mean anomaly is close to the lower bound of the safe RPO region—near 80$^{\circ }$.

Fig. 18

Mass-optimal $\Delta V$ requirements for fixed TOF forced circumnavigation

Similar analysis was performed for fixed TOF transfers to both periodic and center manifolds. As determined in Sect.3.2, transfers to center manifolds at apolune required slightly more propellant than transfers to periodic manifolds. Thus, when investigating the $\Delta V$ costs for these transfers at a range of different initial mean anomalies, transfers to both manifolds appear to require nearly equal $\Delta Vv$ costs. Figures 19 and 20 show the results of the trade study. The two plots appear very similar in order of magnitude of required $\Delta V$ for various fixed TOF transfers. Additionally, as with the forced circumnavigation study, the initial mean anomaly does not appear to have a meaningful effect on a change in $\Delta V$ requirements. However, to achieve the lowest $\Delta V$, it is useful to begin rendezvous and proximity operations closest to the lower bound on the safe RPO region. When compared with the forced circumnavigation contour plot at similar TOFs, the overall $\Delta V$ for the manifold transfers are only a fraction of the cost for a forced circumnavigation trajectory. This behavior is observed due to the manifold transfers only requiring thrust onto the manifold itself which significantly reduces propellant requirements. In general, leveraging the center and periodic manifolds that arise from the CR3BP for rendezvous and proximity operations is a natural extension of similar natural loitering trajectories found in two-body RPO situations, such as natural motion circumnavigation in an LVLH frame [17].

Fig. 19

Mass-Optimal $\Delta V$ requirements for fixed TOF transfer to periodic manifold

Fig. 20

Mass-Optimal $\Delta V$ requirements for fixed TOF transfer to center manifold

4 Conclusion

This analysis explores forced and natural loitering in a cislunar environment that are observed in a chief spacecraft’s LVLH frame under CR3BP dynamics. For situations where leveraging the natural motion of the system is not feasible under mission requirements, generating forced circumnavigation trajectories allows mission designers to produce bounded relative motion subject to constraints on time of flight and desired distance from the target spacecraft. This work investigates the resulting circumnavigation trajectories that arise from maintaining a 50 km distance from the target. Constraints on the safe region for rendezvous and proximity operations were also applied to the problem. For the given low-thrust parameters, circumnavigation trajectories with times of flight between approximately 1.75 and 3.75 days can be generated when starting from a 100 km hold-point in the V-bar direction. Additionally, natural loitering trajectories were analyzed by viewing manifolds of an NRHO in the LVLH frame of the chief spacecraft. By investigating the center and periodic modes from the eigenvalue analysis of the periodic orbit’s monodromy matrix, two bounded types of relative trajectories emerge. Transfers to these manifolds were explored at apolune and compared with the fuel required to maintain one revolution of a forced loitering trajectory from the same initial state. It was found that both center and periodic manifolds are useful for producing bounded trajectories with significantly less fuel than a forced circumnavigation trajectory. However, the lack of chief circumnavigation for a periodic manifold and the quasi-periodic motion of a center manifold necessitates the use of forced circumnavigation in some situations even with the associated higher fuel requirements. It was also determined that the natural motion may sometimes violate passive safety constraints along the trajectory that might not be rectified without selecting a different manifold or offset distance along the NRHO. Future analysis may explore the change in relative motion structure with the selection of different initial offset distances along the NRHO. Additional future work may include transitioning this investigation to higher fidelity dynamic environments. Even though RPO occurs on such a small scale relative to the system dynamics, higher fidelity dynamics will likely cause small changes in $\Delta$V costs for the forced circumnavigation trajectories and possibly introduce required burns for natural motion cases that rely on CR3BP dynamics.