Capture of near-Earth objects with low-thrust propulsion and invariant manifolds

Abstract

In this paper, a mission incorporating low-thrust propulsion and invariant manifolds to capture near-Earth objects (NEOs) is investigated. The initial condition has the spacecraft rendezvousing with the NEO. The mission terminates once it is inserted into a libration point orbit (LPO). The spacecraft takes advantage of stable invariant manifolds for low-energy ballistic capture. Low-thrust propulsion is employed to retrieve the joint spacecraft–asteroid system. Global optimization methods are proposed for the preliminary design. Local direct and indirect methods are applied to optimize the two-impulse transfers. Indirect methods are implemented to optimize the low-thrust trajectory and estimate the largest retrievable mass. To overcome the difficulty that arises from bang-bang control, a homotopic approach is applied to find an approximate solution. By detecting the switching moments of the bang-bang control the efficiency and accuracy of numerical integration are guaranteed. By using the homotopic approach as the initial guess the shooting function is easy to solve. The relationship between the maximum thrust and the retrieval mass is investigated. We find that both numerically and theoretically a larger thrust is preferred.

1 Introduction

Small celestial bodies in the solar system, such as near-Earth asteroids, have gained the attention of several space organizations, such as NASA, ESA, and JAXA. Among all the small bodies, NEOs are the most interesting ones not only in regard to understanding the science of the formation of the solar system but also for the possible exploration of their resources (Sánchez and McInnes 2013).

They are the closest potential threats for Earth impact and the easiest ones to reach from Earth and to capture to the Earth. To classify NEOs by their potential to be gravitationally captured, Yárnoz et al. (2013) proposed a new criterion by which a subset of NEOs is classified into easily retrievable objects (EROs). The cost of a two-impulse transfer to gravitationally capture them is under $500~\mbox{m}/\mbox{s}$. Once captured, their destinations are the LPOs around the collinear libration points $L_{1}$ and $L_{2}$ in the Sun–Earth circular restricted three-body problem (CRTBP). In Yárnoz et al. (2013), 12 EROs are found, of which nine can be placed in the region near $L_{2}$, and three in the region near $L_{1}$. As more small NEOs are to be discovered, it is likely that more EROs will be found in the future.

LPOs and their associated invariant manifolds have gained a lot of interest in recent decades (Gómez et al. 2002; Xu et al. 2012; Xu and Xu 2009). Periodic orbits that show unstable behavior may provide chances for low-energy ballistic transfers (Martin and Jeffrey 2004; Gong et al. 2007). These orbits also represent a class of target orbits for the captured asteroids (Mingotti et al. 2014a). Generally speaking, to reach a target orbit at a low cost, the spacecraft is first guided to the stable invariant manifolds associated with the desired LPO. Once on the stable invariant manifold, the trajectory is purely ballistic. Use of invariant manifolds to find low-energy transfers has been thoroughly investigated. A successful example is the rescue of the Japanese spacecraft Hiten (Belbruno and Miller 1993). Koon et al. (2001) studied ballistic capture mechanics and the combination of the Sun–Earth and Earth–Moon CRTBPs to redesign low-energy transfers from the Earth to the Moon.

There is abundant literature on low-thrust trajectory design that uses $n$-body complex dynamic models. Anderson and Lo (2009) took advantage of invariant manifolds to provide initial guesses for low-thrust trajectories. Interplanetary transfers (Mingotti and Gurfil 2010; Dellnitz et al. 2006) and transfers to LPOs (Mingotti et al. 2007; Ozimek and Howell 2010; Senent et al. 2005) that take advantage of invariant manifolds and low-thrust propulsion have also been investigated. Zhang et al. (2015) optimized low-thrust trajectories from a geostationary transfer orbit to an LPO near $L_{1}$ in the Earth–Moon CRTBP. Many researchers have shown that it is possible to capture asteroids into the near-Earth region (Mingotti et al. 2014a,b; Brophy and Muirhead 2013). NASA has also proposed a near-Earth asteroid retrieval mission (ARM) to capture a noncooperative asteroid in deep space, which requires the development of advanced power and propulsion technology to transport the asteroid back to the Earth–Moon system (Brophy and Muirhead 2013). In this case, the final orbit is a stable orbit around the Moon. Mingotti et al. (2014a) employed invariant manifolds for low-energy capture and estimated the largest retrievable mass. Mingotti et al. (2014b) proposed the idea of coupling together the Sun–Earth and the Earth–Moon CRTBP models following the “patched restricted three-body problems approximation” to capture asteroids into the Earth–Moon distant periodic orbits.

Low-thrust propulsion such as electric propulsion is especially suited for deep-space missions, which usually take a long time. The high specific impulse of low-thrust propulsion helps decrease fuel consumption and thus increase the payload of the spacecraft. Because of the low thrust, the thruster works for a long time to change the velocity of the spacecraft. Because of the long burning time of the engine, optimization of a low-thrust trajectory is difficult. Pontryagin’s minimum principle indicates that bang-bang control is a necessity for fuel-optimal low-thrust trajectories, which require the thrust to be either null or full. The discontinuity of the thrust at isolated moments contributes to the difficulty in optimizing low-thrust trajectories. The methods for optimizing low-thrust trajectories are typically categorized into two groups, direct and indirect methods. Direct methods convert the optimal control problem into a nonlinear programming problem through parameterization. The convergence domain of a direct method is usually larger than that of an indirect method, but direct methods are often less efficient. The results from direct methods are usually less optimal because of parameterization. Indirect methods are based on optimal control theory, and the calculus of variation converts an optimal control problem into a two-point boundary value problem (TPBVP), which is solved through shooting methods. The shooting function is sensitive to the initial guess of the costate variables, which induces a very narrow convergence domain. There are two problems with the convergence of indirect methods: (1) the bang-bang control structure and (2) the unknown bounds of the initial costate variables. Bertrand and Epenoy (2002) proposed a smoothing technique to convert bang-bang controls into continuous controls. The less sensitive shooting function enlarges the convergence domain. Jiang et al. (2012) proposed a method to normalize the initial costate variables so that they are bounded. As a result, they can be initialized on the surface of a high-dimension ball. Thus, indirect methods show advantages both in efficiency and accuracy. Another advantage is that the solution is not prescribed but rather found a posteriori. As a result, there is no need to assign the number of thrusting and coasting segments, and no loss of optimality arises.

In this paper, some techniques are presented to further improve the methods proposed by Jiang et al. (2012), in which the switching detection is rather complex, and a fixed step integrator is chosen that might be less efficient. The perturbation to the performance index is given by a logarithmic function to avoid detecting of switching. As a result, a Runge–Kutta method with adaptive step sizes is used to increase the efficiency of the numerical integration. A more accurate method to detect the switching moments of the thrust is proposed and embedded in the adaptive step integrator. With accurate switching moments, the accuracy of the numerical integration is guaranteed, which benefits the convergence of the shooting method. The analytical Jacobian matrix is introduced to guarantee the convergence in some cases.

The Sun–Earth CRTBP is studied, and the incorporation of invariant manifolds and low-thrust propulsion is investigated to estimate the largest retrievable mass to a desired LPO. In Sect. 2, a brief introduction to the concepts of CRTBP is given. In Sect. 3, a basic simplification to the preliminary design is proposed and particle swarm optimization (PSO) (Kennedy 2010) is selected as the global optimization method. In Sect. 4, both low-energy impulsive and low-thrust transfers are investigated, and both direct and indirect methods are applied to optimize the trajectories. Numerical examples and discussions are given in Sect. 5, and the conclusion is given in Sect. 6.

2 Circular restricted three-body problem

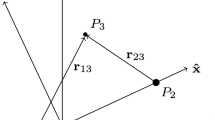
The motion of a spacecraft $P_{3}$ of mass $m_{3}$ is governed by the gravity of the two primaries $P_{1}$ and $P_{2}$ of masses $m_{1}$ and $m_{2}$, respectively, which are assumed to move in circular orbits about their common center of mass. Because the eccentricity of the Earth’s orbit is small, this model is a reasonable approximation to reality. The equations of motion are given in the nondimensional form

$$ \ddot{x} - 2\dot{y} = \frac{{\partial{\varOmega}}}{{\partial x}},\quad\quad\ddot{y} + 2\dot{x} = \frac{{\partial{\varOmega}}}{{\partial y}},\quad\quad\ddot{z} = \frac{{\partial{\varOmega}}}{{\partial z}}, $$

(1)

where $\varOmega$ represents the potential energy of $P_{3}$ in the following form:

$$ {\varOmega} ( {x,y,z,\mu} ) = \frac{1}{2} \bigl( {{x^{2}} + {y^{2}}} \bigr) + \frac{{1 - \mu}}{{{r_{1}}}} + \frac{\mu}{{{r_{2}}}}, $$

(2)

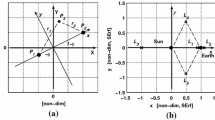
where $\mu = {m_{2}}/ ( {{m_{1}} + {m_{2}}} )$ is the mass parameter for the CRTBP. Equation (1) is written in the barycentric rotating frame (BRF) with nondimensional units: the angular velocity of $P_{1}$ and $P_{2}$ and the distance between them and the sum of their mass are all set to unity. Thus, $P_{1}$ with scaled mass $1-\mu$ is located at $(-\mu, 0)$, and $P_{2}$ with scaled mass $\mu$ is located at $(1-\mu, 0)$. The distance between $P_{3}$ and $P_{1}$ is $r_{1}$, and the distance between $P_{3}$ and $P_{2}$ is $r_{2}$. This model is shown in Fig. 1, where $xOy$ is the inertial reference frame (IRF), and $XOY$ is the BRF.

Fig. 1

IRF and BRF

2.1 Libration point orbits

There are five equilibrium points in CRTBP; three are classified as collinear libration points ($L_{1}$, $L_{2}$, $L_{3}$) and located on the $x$-axis of BRF. The points $L_{1}$ and $L_{2}$ are of greater interest in mission designs because they are in the near-Earth region. There are periodic and quasi-periodic orbits near the equilibrium points. LPOs are of great interest because they can be the final target orbits for retrievable asteroids. Meanwhile, they can also serve as transfer stations to transfer the retrieved asteroids to other periodic orbits in the Earth–Moon CRTBP at low cost.

In this work, the southern and northern halo orbits, which are symmetric about the $xz$-plane, are selected as the target orbits. After calculating an initial guess through analytic approximation (Richardson 1980a) with positive initial amplitude and generating a halo orbit by the differential correction method Richardson (1980b), the northern family of the halo orbits is generated by numerical continuation.

2.2 Structure of invariant manifold

Invariant manifolds associated with LPOs often provide free transport channels. The inherent dynamics makes it possible to design low-cost transfers by taking advantage of stable and unstable invariant manifolds. They are generated by global extension methods (Ozimek and Howell 2010). For a point ${{\boldsymbol{x}}^{q}}$ belonging to an LPO, the monodromy matrix $\boldsymbol{M}_{m}$ is evaluated by integrating the variational equations of the dynamic equations. Denote by ${\boldsymbol{v}}_{s}^{q}$ and ${\boldsymbol{v}}_{u}^{q}$ the stable and unstable normalized eigenvectors of $\boldsymbol{M}_{m}$, respectively. The initial states of stable and unstable invariant manifolds can be generated by adding a small perturbation $\varepsilon$, which is often chosen to be $10^{-6}$ (in normalized units) along the direction of ${\boldsymbol{v}}_{s}^{q}$ and ${\boldsymbol{v}}_{u}^{q}$, respectively (Koon et al. 2000). This is

$$ \left \{ \textstyle\begin{array}{l} {\boldsymbol{x}}_{s}^{q} = {{\boldsymbol{x}}^{q}} \pm\varepsilon{\boldsymbol{v}}_{s}^{q},\\ {\boldsymbol{x}}_{u}^{q} = {{\boldsymbol{x}}^{q}} \pm\varepsilon{\boldsymbol{v}}_{u}^{q}. \end{array}\displaystyle \right . $$

(3)

The symbol ± shows that two branches for each manifold exist. By numerically integrating backward in time starting at ${\boldsymbol {x}}_{s}^{q}$, the stable invariant manifold is generated. By numerically propagating forward with the initial conditions ${\boldsymbol{x}}_{u}^{q}$ an unstable invariant manifold is generated.

3 Preliminary design

The initial condition for this mission is that the spacecraft has already rendezvoused with the asteroid to be retrieved. The asteroid is captured back to a selected halo orbit near $L_{1}$ or $L_{2}$. As found by Yárnoz et al. (2013), it is usually easier to capture asteroids whose semimajor axes are less than 1 AU into regions near $L_{1}$. It costs less to capture those with larger semimajor axes into regions near $L_{2}$. Before the spacecraft starts to retrieve the asteroid, the distance between the target asteroid and the Earth is assumed to be large enough so that the motion of the asteroid follows a two-body dynamic model. Keplerian elements of all the asteroids are obtained through the JPL Small-Body Database Browser.¹ When the capture begins, the joint spacecraft–asteroid system moves in the Sun–Earth CRTBP model, and it relies on either low-thrust propulsion or impulsive burns when it is retrieved to the desired LPO. The joint system is first guided onto the stable invariant manifold and then ballistically captured into the desired LPO.

This problem is investigated to estimate the largest mass that can be captured to the desired LPO with technologies that are currently available or will be in the near future. The main difficulty arises from the size of the thrust for low-thrust propulsion. If the thrust is too low, then the time to get enough velocity increment is too long because of the large mass of the joint spacecraft–asteroid system. In this paper, both low-energy two-impulse and low-energy low-thrust captures are investigated.

3.1 Mission design

For the preliminary design, the model is simplified for efficiency. Instead of low-thrust transfers, a two-impulse transfer is considered to get a quick overview of the problem and determine some parameters for the mission. The design is similar to the one proposed by Yárnoz et al. (2013), and the mission is divided into two segments:

• 1. Employ two impulsive burns to retrieve the asteroid into one of the stable invariant manifolds associated with the target orbit; and

• 2. Coast along the stable invariant manifold for ballistic capture.

Segment 2 uses the Sun–Earth CRTBP model. However, segment 1 falls within the two-body model because it is assumed that the joint spacecraft–asteroid system moves far away from the Earth in this segment. The Lambert solver is used to estimate the transfer costs because of its efficiency.

3.2 Performance index estimate

To insert the joint system into the desired LPO is so small a maneuver that it is neglected in the preliminary design. Denote by $v$ the sum of the magnitudes of the two impulses in segment 1, by $m_{0}$ the initial mass of the spacecraft, of which $m_{\mathrm {d}}$ is the dry mass, by $M$ the sample mass, by $I_{\mathrm{{sp}}}$ the specific impulse of the selected propulsion, and by $g_{0}$ the gravitational acceleration at sea level. If all the fuel is exhausted to retrieve as much mass as possible, it yields

$$ ( {{m_{0}} + M} )\exp \biggl( { - \frac{v}{{{I_{\mathrm {{sp}}}}{g_{0}}}}} \biggr) = M + {m_{\mathrm{d}} }. $$

(4)

The largest sample mass is

$$ M = \frac{{\exp ( { - \frac{v}{{{I_{\mathrm{{sp}}}}{g_{0}}}}} ) - \frac{{{m_{\mathrm{d}} }}}{{{m_{0}}}}}}{{1 - \exp ( { - \frac {v}{{{I_{\mathrm{{sp}}}}{g_{0}}}}} )}}{m_{0}}. $$

(5)

It is convenient to define the parameter $k$ by

$$ k = \frac{M}{m_{0}}=\frac{{\exp ( { - \frac{v}{{{I_{\mathrm {{sp}}}}{g_{0}}}}} ) - {r_{\mathrm{d}} }}}{{1 - \exp ( { - \frac{v}{{{I_{\mathrm{{sp}}}}{g_{0}}}}} )}} $$

(6)

with $r_{\mathrm{d}} = m_{\mathrm{d}}/m_{0}$ as the dry mass ratio for the spacecraft.

For this mission, $v$ is of the order of 100 m/s. Take, for example, $r_{\mathrm{d}} = 0.25$; then the relation between $v$, $I_{\mathrm {{sp}}}$, and $k$ is shown in Fig. 2. A spacecraft with low-thrust propulsion can retrieve much more mass because of its higher specific impulse and should be given priority over others for asteroid retrieval.

Fig. 2

Relation between $v$, $I_{\mathrm{{sp}}}$, and $k$ for $r_{\mathrm{d}} = 0.25$

3.3 Global search with PSO

The parameters to be optimized include the following:

• $A_{z}$: the amplitude to generate the halo orbit

• $\tau$: the point in the target orbit where the insertion takes place

• $t_{m}$: the coasting time on the stable invariant manifold

• $t_{1}$: the starting moment of segment 1

• $t_{2}$: the terminating moment of segment 1

The first three parameters determine the structure of the stable invariant manifold, and the last two determine the moments of impulsive burns. The PSO is an evolutionary search algorithm that simulates the collective behavior of bird flocks to solve complex nonlinear optimization problems. This algorithm has no requirement of any gradient information about the performance index and uses only some basic mathematical operators so that it is conceptually simple. It has been widely used to design optimal space missions (Guo et al. 2011; Zhu et al. 2009; Pontani and Conway 2010; Pontani et al. 2012).

Given a tentative value of the parameters to be optimized, the halo orbit is generated first with the given amplitude $A_{z}$. The state $\boldsymbol{x}^{q}$ when the insertion takes place is derived by integrating Eq. (1) from 0 to $\tau$. By integrating the variational equations over the whole period, the monodromy matrix is obtained, and thus ${\boldsymbol{v}}_{s}^{q}$ is calculated. A perturbation along ${\boldsymbol{v}}_{s}^{q}$ with magnitude of $1\times10^{-6}$ (in normalized units) is added to $\boldsymbol {x}^{q}$, and the terminating state ${\boldsymbol{x}}_{s}^{q}$ is obtained by integrating Eq. (1) from 0 to $-t_{m}$. With the given starting and terminating moments of segment 1, the position and velocity when the retrieval begins can be derived from the ephemeris of the target asteroid. Meanwhile, the position and velocity of the joint system at the moment when it is inserted into the stable invariant manifold can be obtained by transforming ${\boldsymbol {x}}_{s}^{q}$ from the BRF to the IRF. The Lambert solver is used to estimate the magnitudes of the two impulses, and their sum is the performance index to be minimized. The performance index must be calculated many times to find the optimal solution. Since $A_{z}$ and $\tau$ are searched by PSO, numerical integration is necessary to calculate ${\boldsymbol{x}}_{s}^{q}$, which is time-consuming. The large amount of computing effort is one disadvantage of almost every evolutionary algorithm.

4 Low-energy transfer

PSO is a robust method to optimize all design parameters of the mission. Its results serve as initial guesses when the Sun-Earth CRTBP is considered. First a low-energy impulsive transfer is designed first, and then a low-energy low-thrust transfer is optimized.

4.1 Low-energy impulsive transfer

To fix the violations of the constraints and decrease the cost of the two-impulse transfer, both direct and indirect methods are proposed. Only two-impulse transfers are considered here. The first impulse retrieves the asteroid, and the second one inserts the joint system into one of the stable invariant manifolds associated with the target orbit.

4.1.1 Local direct optimization

Direct optimization methods, usually gradient-based, are fast if good initial guesses are provided. The combination of PSO and local optimization methods provides a greater chance of finding the global optimal solution. The equations of motion are built from the Sun-Earth CRTBP to better approximate the real model.

All the parameters to be optimized by PSO are included in the local direct optimization, and the two impulses, denoted as $\Delta v_{1}$ and $\Delta v_{2}$, respectively, are also optimized. The retrieval begins at the moment when the first impulse is imposed. After numerically integrating Eq. (1) from $t_{1}$ to $t_{2}$, the states of the spacecraft, denoted as $\boldsymbol{x}_{s}$, are obtained. The second impulse is imposed to change the velocity of the joint system. The state of the stable invariant manifold, ${\boldsymbol{x}}_{s}^{q}$, when the insertion takes place is obtained using the direct optimization methods. After imposing the constraint

$$ \boldsymbol{x}_{s}^{q} = {{ \boldsymbol{x}}_{s}} $$

(7)

to ensure the continuity of the trajectory, the sum of the magnitudes of the two impulses is minimized, that is

$$ J = \Delta v_{1} + \Delta v_{2} $$

(8)

This is a nonlinear programming problem with the solution provided by the state-of-the-art software SNOPT (Gill et al. 2002) which applies a sequential quadratic programming method. Some derivatives are analytically obtained to improve the efficiency, whereas others have to be provided by a finite difference approximation. They are listed as follows:

• $J$ index with respect to $\Delta v_{1}$ and $\Delta v_{2}$

• Equation (7) with respect to $t_{m}$, $t_{1}$, $t_{2}$, $\Delta v_{1}$, and $\Delta v_{2}$

More precisely, the derivative of $\boldsymbol{x}_{s}^{q}$ with respect to $t_{m}$ and the derivatives of ${{\boldsymbol{x}}_{s}}$ with respect to $t_{2}$ and $\Delta v_{2}$ are obtained directly. However, to obtain the derivatives of ${{\boldsymbol{x}}_{s}}$ with respect to $t_{1}$ and $\Delta v_{1}$, the state transition matrix of the coasting stage from $t_{1}$ to $t_{2}$ has to be derived by integrating the variational equation of (1). The details will be given in a later section.

4.1.2 Local indirect optimization

Indirect methods derived using the calculus of variation convert the problem into a multi-point boundary value problem (MPBVP). Indirect methods are less robust, and the initial costate variables are difficult to guess. However, the convergence is faster when the initial costate variables do successfully converge. Indirect methods are used to optimize the two-impulse transfer trajectory. It is worthwhile to point out that when the two-impulse transfer is used, the MPBVP degenerates into a TPBVP.

The parameters to be optimized include the following

• $\Delta\boldsymbol{v}_{1}$: the first impulse imposed to retrieve the asteroid

• $t_{1}$: the moment when the first impulse is imposed

• $\Delta\boldsymbol{v}_{2}$: the second impulse imposed to insert the joint system into the stable invariant manifold

• $t_{2}$: the moment when the second impulse is imposed

• $t_{m}$: the period the spacecraft coasts along the stable invariant manifold

The parameters $A_{z}$ and $\tau$ are difficult to optimize because the analytical derivatives of ${\boldsymbol{x}}_{s}^{q}$ with respect to them are hard to derive. Instead, they are chosen to be equal to the values obtained by direct methods.

The performance index to be minimized is

$$ \varphi = \bigl\Vert {{\boldsymbol{v}} \bigl( {t_{1}^{+} } \bigr) - {{\boldsymbol{v}}_{a}}} \bigr\Vert + \bigl\Vert {{\boldsymbol{v}} \bigl( {t_{2}^{-} } \bigr) - {{\boldsymbol{v}}_{m}}} \bigr\Vert , $$

(9)

where ${{\boldsymbol{v}}_{a}}$ is the velocity of the asteroid at $t_{1}$, ${{\boldsymbol{v}}_{m}}$ is the velocity of the stable invariant manifold’s state at $t_{2}$, and $t_{1}^{-}$ and $t_{2}^{+}$ represent the moments just before and after the two impulses are imposed, respectively.

Optimal control theory is applied to determine the parameters that minimize $\varphi$. By introducing costate variables ${\boldsymbol {\lambda}} = ( {{{\boldsymbol{\lambda}}_{{r}}};{{\boldsymbol {\lambda}}_{{v}}}} )$, known as Lagrange multipliers, the Hamiltonian is built as

$$ H = {\boldsymbol{\lambda}}_{{r}}^{\mathrm{{T}}}\dot{\boldsymbol{r}} + { \boldsymbol{\lambda}}_{{v}}^{\mathrm{{T}}}\dot{\boldsymbol{v}}, $$

(10)

where $\dot{\boldsymbol{r}} = {\boldsymbol{v}}$ and $\dot{\boldsymbol{ v}}$ is determined by Eq. (1). The Euler–Lagrange equations are given as

$$ \left \{ \textstyle\begin{array}{l} {{\dot{\boldsymbol{\lambda}}}_{r}} = - { ( {\frac{{\partial H}}{{\partial{\boldsymbol{r}}}}} )^{\mathrm{{T}}}} = - {\boldsymbol{\lambda}}_{v}^{\mathrm{{T}}}\frac{\partial}{{\partial {\boldsymbol{r}}}}{ ( {\frac{{\partial{\varOmega}}}{{\partial {\boldsymbol{r}}}}} )^{\mathrm{{T}}}},\\ {{\dot{\boldsymbol{\lambda}}}_{v}} = - { ( {\frac{{\partial H}}{{\partial{\boldsymbol{v}}}}} )^{\mathrm{{T}}}} = - {{\boldsymbol{\lambda}}_{r}} + \left [ { \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0&2&0\\ { - 2}&0&0\\ 0&0&0 \end{array}\displaystyle } \right ]{{ \boldsymbol{\lambda}}_{v}}. \end{array}\displaystyle \right . $$

(11)

The general expressions of the boundary conditions for optimality are as follows (Bryson and Ho 1975):

$$\begin{aligned}& - {\boldsymbol{\lambda}}_{j}^{-} + \frac{{\partial\varphi}}{{\partial {\boldsymbol{x}}_{j}^{-} }} + {{\boldsymbol{\chi}}^{T}} \biggl[ {\frac {{\partial{\boldsymbol{\psi}}}}{{\partial{\boldsymbol{x}}_{j}^{-} }}} \biggr] = \boldsymbol{0}, \end{aligned}$$

(12)

$$\begin{aligned}& {\boldsymbol{\lambda}}_{j}^{+} + \frac{{\partial\varphi}}{{\partial {\boldsymbol{x}}_{j}^{+} }} + {{\boldsymbol{ \chi}}^{T}} \biggl[ {\frac {{\partial{\boldsymbol{\psi}}}}{{\partial{\boldsymbol{x}}_{j}^{+} }}} \biggr] = \boldsymbol{0}, \end{aligned}$$

(13)

$$\begin{aligned}& H_{j}^{-} + \frac{{\partial\varphi}}{{\partial t_{j}^{-} }} + {{\boldsymbol {\chi}}^{T}} \biggl[ {\frac{{\partial{\boldsymbol{\psi}}}}{{\partial t_{j}^{-} }}} \biggr] = 0, \end{aligned}$$

(14)

$$\begin{aligned}& - H_{j}^{+} + \frac{{\partial\varphi}}{{\partial t_{j}^{+} }} + {{\boldsymbol{ \chi}}^{T}} \biggl[ {\frac{{\partial{\boldsymbol{\psi }}}}{{\partial t_{j}^{+} }}} \biggr] = 0, \end{aligned}$$

(15)

where the subscript $j$ indicates the variables when the $j$th impulse is imposed, ${\boldsymbol{\psi}}$ is a vector that collects all equality constraints, and ${\boldsymbol{\chi}}$ is a vector of all numerical multipliers. The equality constraints for this problem include the following:

$$\begin{aligned}& {\boldsymbol{r}} \bigl( {t_{1}^{+} } \bigr) - {{ \boldsymbol{r}}_{a}} = \boldsymbol{0}, \end{aligned}$$

(16)

$$\begin{aligned}& {\boldsymbol{r}} \bigl( {t_{2}^{-} } \bigr) - {{ \boldsymbol{r}}_{m}} = \boldsymbol{0}, \end{aligned}$$

(17)

where ${{\boldsymbol{r}}_{a}}$ is the position of the asteroid at $t_{1}$, and ${{\boldsymbol{r}}_{m}}$ is the position of the stable invariant manifold’s state at $t_{2}$. Denote by ${{\boldsymbol{\chi}}_{i}}\ (i = 1,2)$ the numerical multipliers associated with the constraints in Eqs. (16)–(17). To determine the optimal value of ${t_{m}}$, the partial derivative with respect to ${t_{m}}$ must be 0 to guarantee optimality, that is,

$$ - {{\boldsymbol{\chi}}_{1}} \cdot\frac{{\partial{{\boldsymbol {r}}_{m}}}}{{\partial{t_{m}}}} - {{\boldsymbol{ \chi}}_{2}} \cdot\frac {{\partial{{\boldsymbol{v}}_{m}}}}{{\partial{t_{m}}}} = 0. $$

(18)

Taking into account that ${\boldsymbol{x}}_{s}^{q}$ is numerically propagated from 0 to $- {t_{m}}$, the derivative of ${\boldsymbol {x}}_{s}^{q}$ with respect to ${t_{m}}$ is

$$ \frac{{\partial{{\boldsymbol{r}}_{m}}}}{{\partial{t_{m}}}} = - {{\boldsymbol{v}}_{m}},\quad\quad\frac{{\partial{{\boldsymbol{v}}_{m}}}}{{\partial {t_{m}}}} = - {{\boldsymbol{a}}_{m}}, $$

(19)

where ${{\boldsymbol{a}}_{m}}$ is the acceleration obtained from Eq. (1) with the corresponding $\boldsymbol{r}_{m}$ and $\boldsymbol{v}_{m}$.

By substituting Eqs. (16)–(17) into equations (12)–(15) and eliminating the unknown numerical multipliers, the transversality conditions and the stationary conditions for optimality are derived as follows:

$$\begin{aligned}& {\boldsymbol{\lambda}}_{{v}} \bigl( {t_{1}^{+} } \bigr) + \frac {{\Delta{{\boldsymbol{v}}_{1}}}}{{\Vert {\Delta{{\boldsymbol{v}}_{1}}} \Vert }} = \boldsymbol{0}, \end{aligned}$$

(20)

$$\begin{aligned}& {\boldsymbol{\lambda}}_{{r}} \bigl( {t_{1}^{+} } \bigr) \cdot\Delta {{\boldsymbol{v}}_{1}} = 0, \end{aligned}$$

(21)

$$\begin{aligned}& {\boldsymbol{\lambda}}_{{r}} \bigl( {t_{2}^{-} } \bigr) \cdot\frac {{\partial{{\boldsymbol{r}}_{m}}}}{{\partial{t_{m}}}} + {\boldsymbol {\lambda}}_{{v}} \bigl( {t_{2}^{-} } \bigr) \cdot\frac{{\partial {{\boldsymbol{v}}_{m}}}}{{\partial{t_{m}}}} = 0, \end{aligned}$$

(22)

$$\begin{aligned}& {\boldsymbol{\lambda}}_{{v}} \bigl( {t_{2}^{-} } \bigr) + \frac {{\Delta{{\boldsymbol{v}}_{2}}}}{{\Vert {\Delta{{\boldsymbol{v}}_{2}}} \Vert }} = \boldsymbol{0}, \end{aligned}$$

(23)

$$\begin{aligned}& H \bigl( {t_{2}^{-} } \bigr) = 0. \end{aligned}$$

(24)

Provided with the tentative values of the unknown variables, Eq. (20) is then used to obtain the value of ${\boldsymbol{\lambda}}_{{v}}({t_{1}^{+} })$. To numerically integrate Eqs. (1) and (11) from $t_{1}$ to $t_{2}$, ${\boldsymbol{\lambda}}_{{r}}( {t_{1}^{+} } )$ is guessed, and $\boldsymbol{r}(t_{1}^{+})$ is selected to be equal to the position of the asteroid. The TPBVP is established by satisfying ${\boldsymbol{v}}(t_{2}^{+}) = {{\boldsymbol{v}}_{m}}$ and the boundary conditions given by Eqs. (21)–(24).

To solve this TPBVP, Minpack (Moré et al. 1980) is used. This is a package of FORTRAN subprograms that solve nonlinear equations and nonlinear least-square problems. The Jacobian matrix can be provided by the user or approximated with the forward-difference method, which is used by Minpack. To provide an initial guess for the TPBVP, the approximate results obtained from the PSO search are used, including $t_{1}$, $t_{2}$, and $t_{m}$. The Lambert solver is used to estimate the two impulses, which are first obtained in the IRF and then transformed into the BRF. The initial value of ${\boldsymbol{\lambda}}_{{r}}({t_{1}^{+} })$ is obtained by random guesses with prior satisfaction of Eq. (21).

4.2 Low-energy low-thrust optimization

Indirect methods are applied to optimize the low-energy low-thrust trajectory and estimate the largest retrievable mass. To obtain the fuel-optimal bang-bang control, the homotopic approach is used to find an approximate solution and provide initial guesses. Then the shooting function is built with a switching detection technique embedded into the numerical integrator. With the results from homotopic approach as initial guesses, the shooting method easily converges to the fuel-optimal bang-bang control.

4.2.1 Homotopic approach

The homotopic approach (Bertrand and Epenoy 2002; Jiang et al. 2012) converts bang-bang controls into continuous controls and reduces the sensitivity of the shooting function. The original performance index is included by adding an energy perturbation that decreases gradually so that it tends to settle at the desired bang-bang control. As suggested by Jiang et al. (2012), the performance index is multiplied by another positive numerical factor $\lambda_{0}$, which does not affect the optimality of the solution.

The influence of low thrust is implemented by adding a perturbation to the equations of motion as

$$ \left \{ \textstyle\begin{array}{l} \ddot{\boldsymbol{r}} + 2\left [ { \textstyle\begin{array}{c} { - \dot{y}}\\ {\dot{x}}\\ 0 \end{array}\displaystyle } \right ] = \frac{{\partial{\varOmega}}}{{\partial{\boldsymbol {r}}}} + u\frac{{{T_{\max}}}}{m}{\boldsymbol{\alpha}}, \\ \dot{m} = - u\frac{{{T_{\max}}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}}, \end{array}\displaystyle \right . $$

(25)

where $T_{\max}$ is the maximum thrust, and $m$ is the instantaneous mass of the joint system. The control variables consist of the engine thrust ratio $u\in[0, 1]$ and the thrust direction $\boldsymbol{\alpha }$, which is a unit vector. Length and time are made nondimensional using the aforementioned method. Masses of the joint system are made nondimensional with the spacecraft’s initial mass.

To estimate the largest retrievable mass, the goal is to maximize the initial mass of the joint system. The original performance index of the optimal control problem is

$$ J = - m ( {{t_{0}}} ) + \frac{{{T_{\max}}}}{{{I_{\mathrm {{sp}}}}{g_{0}}}} \int_{{t_{0}}}^{{t_{f}}} {u\mathrm{d} t}, $$

(26)

which requires maximizing the collected mass and minimizing the fuel consumption at the same time.

After adding an energy perturbation and multiplying by $\lambda_{0}$, the new performance index is

$$ J = - {\lambda_{0}}m ( {{t_{0}}} )\mathrm{{ + }} { \lambda_{0}}\frac {{{T_{\max}}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}} \int_{{t_{0}}}^{{t_{f}}} { \bigl\{ {u - \varepsilon\ln \bigl[ {u ( {1 - u} )} \bigr]} \bigr\} {\mathrm{d}} t}. $$

(27)

By introducing Lagrange multipliers ${\boldsymbol{\lambda}} = ( {{{\boldsymbol{\lambda}}_{{r}}};{{\boldsymbol{\lambda }}_{{v}}};{\lambda_{m}}} )$ the Hamiltonian is built as

$$\begin{aligned} H =& {\boldsymbol{\lambda}}_{{r}}^{\mathrm{{T}}}\dot{\boldsymbol{r}} + {\boldsymbol{\lambda}}_{{v}}^{\mathrm{{T}}}\ddot{\boldsymbol{r}} + {\lambda_{m}}\dot{m} \\ &{}+ {\lambda_{0}}{\frac{{{T_{\max}}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}}} \bigl\{ {u - \varepsilon\ln\bigl[ {u ( {1 - u} )} \bigr]} \bigr\} \\ =& {\boldsymbol{\lambda}}_{{v}}^{\mathrm{{T}}} \biggl( {u\frac{{{T_{\max }}}}{m}{\boldsymbol{\alpha}}} \biggr) + {\lambda_{0}}{\frac{{{T_{\max }}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}}}\bigl\{ {u - \varepsilon\ln \bigl[ {u ( {1 - u} )} \bigr]} \bigr\} \\ &{}- {\lambda_{m}}\frac{{u{T_{\max}}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}} + F, \end{aligned}$$

(28)

where $F$ is given by

$$ F = {\boldsymbol{\lambda}}_{{r}}^{\mathrm{{T}}}\dot{\boldsymbol{r}} + { \boldsymbol{\lambda}}_{{v}}^{\mathrm{{T}}}\left ( { \frac{{\partial {\varOmega}}}{{\partial{\boldsymbol{r}}}} - 2\left [ { \textstyle\begin{array}{c} { - \dot{y}}\\ {\dot{x}}\\ 0 \end{array}\displaystyle } \right ]} \right ), $$

(29)

which does not depend on the control variables or affect the minimization of $H$. The optimal control variables are determined by

$$ {\boldsymbol{\alpha}} = - \frac{{{{\boldsymbol{\lambda}}_{v}}}}{{\Vert {{{\boldsymbol{\lambda}}_{v}}} \Vert }} $$

(30)

and

$$ u = \frac{{2\varepsilon}}{{\rho + 2\varepsilon + \sqrt{{\rho^{2}} + 4{\varepsilon^{2}}} }}, $$

(31)

where $\rho$ is the switching function determined by

$$ \rho = 1 - \frac{{{I_{\mathrm{{sp}}}}{g_{0}}\Vert {{{\boldsymbol {\lambda}}_{v}}} \Vert }}{{m{\lambda_{0}}}} - \frac{{{\lambda _{m}}}}{{{\lambda_{0}}}}. $$

(32)

As shown in Fig. 3, the control determined in this way tends to a bang-bang control as $\varepsilon$ tends to 0.

Fig. 3

Relation between $\rho$ and $u$ for Different $\varepsilon$

The adjoint dynamics is readily derived through the Euler–Lagrange equations as

$$ \left \{ \textstyle\begin{array}{l} {{\dot{\boldsymbol{\lambda}}}_{r}} = - { ( {\frac{{\partial H}}{{\partial{\boldsymbol{r}}}}} )^{\mathrm{{T}}}} = - {\boldsymbol{\lambda}}_{v}^{\mathrm{{T}}}\frac{\partial}{{\partial {\boldsymbol{r}}}}{ ( {\frac{{\partial{\varOmega}}}{{\partial {\boldsymbol{r}}}}} )^{\mathrm{{T}}}},\\ {{\dot{\boldsymbol{\lambda}}}_{v}} = - { ( {\frac{{\partial H}}{{\partial{\boldsymbol{v}}}}} )^{\mathrm{{T}}}} = - {{\boldsymbol{\lambda}}_{r}} + \left [ { \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0&2&0\\ { - 2}&0&0\\ 0&0&0 \end{array}\displaystyle } \right ]{{ \boldsymbol{\lambda}}_{v}}, \\ {{\dot{\lambda}}_{m}} = -\frac{{\partial H}}{\partial m} = - \frac {{u{T_{\max}} \Vert {{{\boldsymbol{\lambda}}_{v}}} \Vert }}{{{m^{2}}}}. \end{array}\displaystyle \right . $$

(33)

Another constraint on the mass of the joint system is given by

$$ m ( {{t_{0}}} ) - m ( {{t_{f}}} ) - ( {{m_{0}} - {m_{\mathrm{d}} }} ) = 0, $$

(34)

which means that all the fuel is consumed to maximize the retrievable mass. The starting and terminating boundary conditions constrain the equality about the position and velocity of the joint system. The constraints are written as

$$\begin{aligned} &{\boldsymbol{r}} ( {{t_{0}}} ) - {{\boldsymbol{r}}_{a}} = \boldsymbol{0}, \end{aligned}$$

(35)

$$\begin{aligned} &{\boldsymbol{v}} ( {{t_{0}}} ) - {{\boldsymbol{v}}_{a}} = \boldsymbol{0}, \end{aligned}$$

(36)

$$\begin{aligned} &{\boldsymbol{r}} ( {{t_{f}}} ) - {{\boldsymbol{r}}_{m}} = \boldsymbol{0}, \end{aligned}$$

(37)

$$\begin{aligned} &{\boldsymbol{v}} ( {{t_{f}}} ) - {{ \boldsymbol{v}}_{m}} = \boldsymbol{0}. \end{aligned}$$

(38)

By introducing numerical multipliers ${\chi_{m}}$, ${{\boldsymbol{\chi }}_{{{{r}}_{0}}}}$, ${{\boldsymbol{\chi}}_{{{{v}}_{0}}}}$, ${{\boldsymbol {\chi}}_{{{{r}}_{f}}}}$, and ${{\boldsymbol{\chi}}_{{{{v}}_{f}}}}$ into Eqs. (34)–(38), the transversality conditions at $t_{0}$ and $t_{f}$ are

$$ \left \{ \textstyle\begin{array}{l} {{\boldsymbol{\lambda}}_{{r}}} ( {{t_{0}}} ) + {{\boldsymbol {\chi}}_{{{{r}}_{0}}}} = 0,\\ {{\boldsymbol{\lambda}}_{{v}}} ( {{t_{0}}} ) + {{\boldsymbol {\chi}}_{{{{v}}_{0}}}} = 0,\\ {\lambda_{m}} ( {{t_{0}}} ) + {\chi_{m}} - {\lambda_{0}} = 0 \end{array}\displaystyle \right . $$

(39)

and

$$ \left \{ \textstyle\begin{array}{l} - {{\boldsymbol{\lambda}}_{{r}}} ( {{t_{f}}} ) + {{\boldsymbol {\chi}}_{{{{r}}_{f}}}} = 0,\\ - {{\boldsymbol{\lambda}}_{{v}}} ( {{t_{f}}} ) + {{\boldsymbol {\chi}}_{{{{v}}_{f}}}} = 0,\\ - {\lambda_{m}} ( {{t_{f}}} ) - {\chi_{m}} = 0, \end{array}\displaystyle \right . $$

(40)

respectively. Combining Eqs. (39) and (40) to eliminate $\chi_{m}$ yields

$$ {\lambda_{m}} ( {{t_{0}}} ) - {\lambda_{m}} ( {{t_{f}}} ) - {\lambda_{0}} = 0. $$

(41)

In fact, having free starting and terminating moments increases the number of variables and makes the problem even harder to solve. Their values are chosen to be equal to the results obtained from local direct optimization methods. Therefore, neither of the stationary conditions at $t_{0}$ and $t_{f}$ is introduced. To determine $t_{m}$, it is derived that

$$ - {{\boldsymbol{\chi}}_{{{{r}}_{f}}}} \cdot\frac{{\partial{{\boldsymbol {r}}_{m}}}}{{\partial{t_{m}}}} - {{\boldsymbol{ \chi}}_{{{{v}}_{f}}}} \cdot \frac{{\partial{{\boldsymbol{v}}_{m}}}}{{\partial{t_{m}}}} = 0, $$

(42)

which is combined with Eq. (40) to eliminate the unknown numerical multipliers.

After introducing the boundary conditions at $t_{0}$ and $t_{f}$, the low-thrust trajectory optimization problem is transformed into a TPBVP. When provided with an initial state, with the tentative values for the costate variables and with the mass of the joint system, Eqs. (25) and (33) are numerically integrated from $t_{0}$ to $t_{f}$. The errors on the boundary conditions can be determined. The shooting function is solved numerically using Minpack. The solution usually starts with a relatively large $\varepsilon$, such as 0.01. Then the solution can be used as an initial guess for the next iteration with a smaller $\varepsilon$. However, $\varepsilon$ cannot be adjusted to be 0 because then $u$ is undefined when $\rho\leq0$, as indicated by Eq. (31). Although the bang-bang control cannot be obtained by gradually adjusting $\varepsilon$ to 0, it is still an acceptable approximation. The result is used to provide an initial guess for the next step in the process to obtain perfect bang-bang control.

4.2.2 Switching moments detection method

After rejecting the perturbation, the performance index to be minimized is

$$ J = - {\lambda_{0}}m ( {{t_{0}}} ) + { \lambda_{0}}\frac{{{T_{\max }}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}} \int_{{t_{0}}}^{{t_{f}}} {u{\mathrm{d}} t}. $$

(43)

The Hamiltonian becomes

$$\begin{aligned} H =& {{\boldsymbol{\lambda}}_{r}}\dot{\boldsymbol{r}} + {{\boldsymbol {\lambda}}_{v}}\ddot{\boldsymbol{r}} + {\lambda_{m}}\dot{m} \\ =& {{\boldsymbol{\lambda}}_{v}} \biggl( {u\frac{{{T_{\max }}}}{m}{\boldsymbol{\alpha}}} \biggr) + {\lambda_{0}}\frac{{u{T_{\max }}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}} - {\lambda_{m}}\frac{{u{T_{\max }}}}{{{I_{\mathrm{{sp}}}}{g_{0}}}} + F, \end{aligned}$$

(44)

whose optimal control to minimize $H$ is

$$ {\boldsymbol{\alpha}} = - \frac{{{{\boldsymbol{\lambda}}_{v}}}}{{\Vert {{{\boldsymbol{\lambda}}_{v}}} \Vert }} $$

(45)

and

$$ \left \{ \textstyle\begin{array}{l@{\quad}l} u = 1 & \mbox{if } \rho < 0, \\ u = 0 & \mbox{if } \rho > 0, \\ u\in[0,1] & \mbox{if } \rho=0, \end{array}\displaystyle \right . $$

(46)

where $\rho$ is again given by Eq. (32). To detect the switching moments of $\rho$ during the numerical integration, the derivative of $\rho$ with respect to time is needed. It is calculated as

$$ \dot{\rho}= \frac{{{I_{{\mathrm{sp}} }}{g_{0}}\Vert {{{\boldsymbol {\lambda}}_{v}}} \Vert }}{{{m^{2}}{\lambda_{0}}}}\dot{m} - \frac {1}{{{\lambda_{0}}}}{\dot{\lambda}_{m}} - \frac{{{I_{{\mathrm{sp}} }}{g_{0}}}}{{{\lambda_{0}}m\Vert {{{\boldsymbol{\lambda}}_{v}}} \Vert }}{{\boldsymbol{\lambda}}_{v}} \cdot{\dot{\boldsymbol{\lambda}}_{v}}, $$

(47)

and substituting Eq. (33) into Eq. (47) yields

$$ \dot{\rho}= - \frac{{{I_{{\mathrm{sp}} }}{g_{0}}}}{{{\lambda_{0}}m\Vert {{{\boldsymbol{\lambda}}_{v}}} \Vert }}{{\boldsymbol{\lambda}}_{v}} \cdot{\dot{\boldsymbol{\lambda}}_{v}}. $$

(48)

Because $\boldsymbol{\lambda_{v}}$ and $m$ are always continuous with respect to time, and $\dot{\boldsymbol{\lambda}_{v}}$ does not depend on $u$, the continuity of $\rho$ and $\dot{\rho}$ is guaranteed even if $u$ switches between 0 and 1. It is easy to conclude that $\rho$ is continuous and differentiable.

Integrators with adaptive step sizes are preferable because of their efficiency. Immediately after every integration step, the sign of $\rho$ is checked, and any changes are detected. Because the integration steps are small, the possibility that the sign of $\rho$ changes more than once during a single integration step is neglected. Denote by $[t_{k}, t_{k+1}]$ the domain where the sign of $\rho$ changes and by $t_{m}\in[t_{k}, t_{k+1}]$ the exact moment when $\rho=0$. Because $t_{m}< t_{k+1}$, the integration error from $t_{0}$ to $t_{m}$ is smaller than the required tolerance. The accuracies of $\boldsymbol {x}(t_{m})$ and $\rho(t_{m})$ are guaranteed. Newton’s method is applied to find the accurate $t_{m}$, which is initially chosen to be equal to $t_{f}$ and then corrected according to $\rho(t_{m})$ and $\dot{\rho}(t_{m})$ with

$$ {t_{m}} - \frac{\rho(t_{m})}{{\dot{\rho}(t_{m})}} \to{t_{m}}. $$

(49)

The processes to determine the switching domain and the accurate switching moment are shown in Figs. 4 and 5, respectively.

Fig. 4

Process of numerical integration with switching moments detection

Fig. 5

Process of finding the accurate switching moments

The trajectory is separated into several segments that are categorized into two types according to the sign of $\rho$. Segments with negative $\rho$, called thrusting segments, are subject to full thrust, and $u$ always equals 1 along such segments. The segments with positive $\rho$, called coasting segments, are subject to null thrust, and $u$ always equals 0. The accurate switching moments for the sign of $\rho$ are found using the aforementioned methods. The solution obtained from the homotopic approach with a relatively small $\varepsilon$ is used as the initial guess, which converges easily to perfect bang-bang control.

When the maximum thrust increases, the analytic Jacobian matrix of the shooting function becomes more and more important to ensure convergence. The analytic matrix is more accurate than that computed by finite-difference methods. Sometimes, when the thrust is large, a forward difference approximation has difficult converging, whereas the analytic Jacobian matrix guarantees convergence. In general, denote by ${\boldsymbol{\varphi}} ( {{{\boldsymbol {y}}_{0}},{t_{0}},t} )$ the solution for a system of ordinary differential equations $\dot{\boldsymbol{y}}={\boldsymbol {F}}(t,{\boldsymbol{y}})$. The state transition matrix is defined as ${\boldsymbol{\varPhi}} ( {t,{t_{0}}} ) = \partial{\boldsymbol {\varphi}} ( {{{\boldsymbol{y}}_{0}},{t_{0}},t} )/\partial {{\boldsymbol{y}}_{0}}$, which maps small variations caused by the initial condition difference $\delta{{\boldsymbol{y}}_{0}}$ over ${t_{0}} \to t$, i.e., $\delta{\boldsymbol{y}} ( t ) = {\boldsymbol {\varPhi}} ( {t,{t_{0}}} )\delta{{\boldsymbol{y}}_{0}} ( {{t_{0}}} )$. The matrix ${\boldsymbol{\varPhi}}(t, t_{0})$ is subject to the variational equation

$$ \left \{ \textstyle\begin{array}{l} \dot{\boldsymbol{\varPhi}} ( {t,{t_{0}}} ) = {D_{\boldsymbol {y}}}{\boldsymbol{F\varPhi}} ( {t,{t_{0}}} ),\\ {\boldsymbol{\varPhi}} ( {{t_{0}},{t_{0}}} ) = {{\boldsymbol{I}}_{n \times n}}, \end{array}\displaystyle \right . $$

(50)

where $n$ is the dimension of the ordinary differential equations, and ${D_{\boldsymbol{y}}}{\boldsymbol{F}}$ is the Jacobian of ${\boldsymbol {F}}(t,{\boldsymbol{y}})$. The calculation of ${\boldsymbol{\varPhi}}(t, t_{0})$ often requires a numerical integration of $n(n+1)$ variables for which the accuracy is controllable. Discontinuity of the control makes the calculation of $\boldsymbol{\varPhi} ( {t,{t_{0}}} )$ more difficult because $\boldsymbol{\varPhi} ( {t,{t_{0}}} )$ only maps states along the control that is continuous with respect to time. If $t_{j}$ is a switching moment for the sign of $\rho$, a discontinuity in $\boldsymbol{\varPhi} ( {t,{t_{0}}} )$ occurs and has to be redetermined. Such a discontinuity, denoted as $\boldsymbol{\varPsi} ( {{t_{j}}} )$, is the partial derivative of the state just after $t_{j}$ with respect to the state just before $t_{j}$. The discontinuity $\boldsymbol{\varPsi} ( {{t_{j}}} )$ can be computed by (Zhang et al. 2015; Russell 2007)

$$ \boldsymbol{\varPsi} ( {{t_{j}}} ) = \frac{{\partial{\boldsymbol {y}} ( {t_{j}^{+} } )}}{{\partial{\boldsymbol{y}} ( {t_{j}^{-} } )}} = {{ \boldsymbol{I}}_{n \times n}} + \bigl( {\dot{\boldsymbol{y}}|_{t_{j}^{+} } - \dot{\boldsymbol{y}}|_{t_{j}^{-} } } \bigr) \biggl( {\frac{{\partial\rho}}{{\partial {\boldsymbol{y}}}}\frac{1}{\dot{\rho}}} \biggr), $$

(51)

where $t_{j}^{-}$ and $t_{j}^{+}$ represent the moments immediately before and after $t_{j}$, respectively. If there are $N$ switching points at $t_{1},\dots,t_{N}$, then $\boldsymbol{\varPhi} ( {t_{f},{t_{0}}} )$ is derived as

$$ \boldsymbol{\varPhi} ( {{t_{f}},{t_{0}}} ) = \boldsymbol{ \varPhi} \bigl( {{t_{f}},t_{N}^{+} } \bigr)\boldsymbol{ \varPsi} ( {{t_{N}}} ) \cdots\boldsymbol{\varPsi} ( {{t_{1}}} )\boldsymbol{\varPhi} \bigl( {t_{1}^{-} ,{t_{0}}} \bigr) $$

(52)

When the analytic Jacobian is used, $\lambda_{0}$ is removed to avoid calculating $\partial{\boldsymbol{y}} ( {{t_{f}}} )/\partial {\lambda_{0}}$. The initial guess comes from earlier results and contains $\lambda_{0}$. It is necessary to use ${\boldsymbol{\lambda}} ( {{t_{0}}} )/{\lambda_{0}}$ as the initial guess for the new shooting function.

5 Examples and discussion

One example is presented to demonstrate the validity of the proposed methods. The target asteroid is 2008 UA202, whose classical orbital elements are listed in Table 1, where $a$ is the semimajor axis given in astronomical units, $e$ the eccentricity, $i$ the inclination, $\varOmega$ the longitude of the ascending node, $\omega$ the argument of perigee, and $M_{m}$ the mean anomaly. The PSO search is first applied to find the preliminary parameters of this mission. Then local direct and indirect methods are used to optimize those parameters. Finally, low-energy low-thrust transfers are optimized. The homotopic approach is applied to find an approximation that is used as an initial guess to obtain the fuel-optimal bang-bang control.

Table 1 Classical orbit elements of 2008 UA202

5.1 PSO search

The sum of the magnitudes of the two impulses is the performance index to be minimized. The parameters involved in PSO are set in accordance with Jiang et al. (2012). The maximum number of iterations $n_{\max}$ is set to be 300, and the number of particles is set to be 100.

The epoch when the retrieval starts is between 60400 and 61400 MJD. The duration of the Lambert arc is between 400 and 1000 days. The amplitude of the halo orbit is between $-7\times10^{5}$ and $7\times10^{5}~\mbox{km}$, meaning that both the northern and southern families are taken into consideration. Several results are obtained, which show little difference in the performance index; the best one is chosen and further optimized. The performance index of the optimal result is 402.1 m/s, and the details for the values of the parameters are listed in Table 2.

Table 2 Optimal result for low-energy two-impulse transfer

5.2 Local direct optimization

Local direct optimization continues after the PSO search. All the parameters that were optimized during the PSO search and the two impulse vectors are optimized locally again. Instead of the two-body model, the CRTBP is chosen. The local direct optimization process is quite robust, and the optimal result is also listed in Table 2. Compared with the optimal result from the PSO search, the coasting time along the stable invariant manifold is longer, whereas the transfer time between the two impulses is shorter. The target halo orbit and $\tau$ are also different. The performance index improves a little. A small difference exists between the results from the PSO search and the local direct optimization because Earth’s gravity is taken into consideration. The small difference also demonstrates the rationality of the simplification during the PSO search.

5.3 Local indirect optimization

Local indirect optimization is applied based on the result of the local direct optimization. $A_{z}$ and $\tau$ are chosen to be the same as those obtained from the local direct optimization. As listed in Table 2, the performance index is $393.9~\mbox{m}/\mbox{s}$, which is close to the result from the local direct optimization. The history of $\Vert {{{\boldsymbol{\lambda}}_{{v}}}} \Vert$ is shown in Fig. 6. The magnitude of $\Vert {{{\boldsymbol{\lambda}}_{{v}}}} \Vert$ slightly exceeds unity for a short time during the transfer, which indicates that another impulse can be inserted to lower the cost. Methods to find the optimal three-impulse transfer can be found in Davis et al. (2011), and it is not discussed here because this paper focuses on the difference between direct methods and indirect methods. Compared with the results from local direct optimization, only the coasting time is a little shorter.

Fig. 6

History of $\Vert {{{\boldsymbol{\lambda}}_{{v}}}} \Vert$

In conclusion, assuming that the PSO search provides proper initial guesses, direct methods are better than indirect methods because they are more robust and have clearer physical meaning, so that they are easier to operate. However, indirect methods provide more information to check the optimality of the result.

5.4 Approximation with homotopic approach

To generalize the solutions, the retrievable mass of the asteroid is scaled by the initial mass of the spacecraft. The dry mass is assumed to be 25 % of the spacecraft’s initial mass, and the rest is fuel. Denoting by $m_{0}$ the initial mass of the spacecraft, another variable $a_{0} = T_{\max}/m_{0}$ is introduced to represent the relation between the initial mass of the spacecraft and the maximum thrust of the low-thrust propulsion.

The solution starts with $\varepsilon=0.01$ and $a_{0} = 1\times10^{-3}~\mbox{m}/\mbox{s}^{2}$. The shooting process converges easily even using randomly guessed initial costate variables and a forward-difference Jacobian approximation. The initial costate variables and $\lambda_{0}$ are listed in Table 3. The time to coast along the stable invariant manifold is 1.15 days, which is shorter than it was before. $M$ is the largest retrievable mass and is scaled to the initial mass of the spacecraft. The largest retrievable mass is 46.3, which means that the fuel cost is only 1.62 % of the largest retrievable mass. Evaluated with the same specific impulse, this fuel cost is equivalent to that of the impulsive transfer for a characteristic velocity 480.5 m/s. Figure 7 shows the histories of the magnitude of the thrust and $\rho$. The control is continuous and differentiable, but it is still an acceptable approximation to the bang-bang control. The sensitivity is reduced, and the convergence domain of the shooting function increases. It is obvious that the optimal control for this problem has four thrusting segments, which will be examined in the following section. The magnitude of the thrust changes rapidly when $\rho$ changes sign, which complies with optimal control theory. The last two thrusting segments are very short during which $\rho$ stays negative for a short period and later changes to positive.

Fig. 7

Thrust and $\rho$ for low-energy low-thrust transfer with homotopic form for $a_{0} = 1\times10^{-3}~\mbox{m}/\mbox{s}^{2}$

Table 3 Results for different $\varepsilon$

Figure 8 shows the projection of the optimal trajectory on the $xy$-plane. The joint system is first guided into the stable invariant manifold and then captured ballistically. This solution is used as an initial guess to solve the same problem now with a smaller $\varepsilon$. For example, the results with $\varepsilon=0.001$ are close to the results with $\varepsilon=0.01$, as listed in Table 3. The performance index improves because the control is a better approximation to bang-bang control.

Fig. 8

Projection of optimal trajectory on the $xy$-plane from asteroid to LPO

5.5 Bang-bang control

Starting with the approximate result, the problem is solved again to obtain the fuel-optimal bang-bang control. The result with $\varepsilon= 0.001$ is used as an initial guess, and this guarantees the convergence of the shooting method even with the forward-difference Jacobian approximation. The optimal control is shown in Fig. 9. The performance index corresponding to bang-bang control is close to that with $\varepsilon= 0.001$, which again shows that the homotopic approach provides an acceptable approximation to bang-bang control. The magnitude of the thrust switches between 0 and 1 when $\rho=0$, which demonstrates the validity of the switching detection method. The retrieval of this asteroid has also been studied by Mingotti et al. (2014a), where the optimal control problem is transformed into a nonlinear programming problem and then solved by multiple shooting. The result is not bang-bang, and the optimality decreases. The propellant mass fraction $m_{p}/m_{i}$ (the fraction of the propellant mass out of the initial mass of the joint system) is 3.826 % in Mingotti et al. (2014a). With the methods proposed in this paper, it reduces to 1.584 %. The difference may arise from two factors: (1) different preliminary design results in different boundary conditions; (2) the methods proposed by Mingotti et al. (2014a) converge to a non-bang-bang control that does not strictly satisfy Pontryagin’s minimum principle.

Fig. 9

Thrust and $\rho$ for low-energy low-thrust transfer for $a_{0} = 1\times 10^{-3}~\mbox{m}/\mbox{s}^{2}$

5.6 Influence of the maximum thrust

The problem is further studied using different thrusts to investigate their influence on the final performance index. Three more cases with different thrusts result in different accelerations: $a_{0} = 5\times 10^{-4}~\mbox{m}/\mbox{s}^{2}$, $2\times10^{-3}~\mbox{m}/\mbox{s}^{2}$, and $4\times 10^{-3}~\mbox{m}/\mbox{s}^{2}$. Table 4 lists the results, where $m_{f}=m_{0}-m_{d}$ is the mass of the fuel, and $V$ is the equivalent characteristic velocity.

Table 4 Results for different magnitudes of accelerations

For all these cases, the problem is first solved with the homotopic form. This gives an approximate initial guess to obtain the bang-bang control. A forward-difference approximation is enough to guarantee convergence, except when the acceleration is $4\times10^{-3}~\mbox{m}/\mbox{s}^{2}$. For the exception, the thrust is so large that the shooting function is too sensitive. Its convergence domain is so small that the initial guess must be very close to the solution to overcome the difficulty. The analytic Jacobian matrix is employed to guarantee convergence. A solution with a small $\varepsilon$ (such as 0.0001) is obtained. After that, the initial guesses are generated by adding perturbations with small magnitudes in random directions. Multiple guesses are used until convergence occurs. In this case, the solution to obtain the bang-bang control is quite complex, owing to the narrow convergence domain when the bang-bang control can be solved directly.

The optimal control for all the four cases are shown in Figs. 10, 11, 12. It can be concluded that four thrusting segments are needed for the first two cases with lower thrust, and only three segments are needed for the last two with higher thrust. With larger thrust, the time to coast along the stable invariant manifold is increasing. It can be concluded that the transfer is not feasible if $a_{0}$ is too low, and either more time or larger thrust is needed to get enough velocity increment within a prescribed period.

Fig. 10

Thrust and $\rho$ for low-energy low-thrust transfer for $a_{0} = 5\times 10^{-4}~\mbox{m}/\mbox{s}^{2}$

Fig. 11

Thrust and $\rho$ for low-energy low-thrust transfer for $a_{0} = 2\times 10^{-3}~\mbox{m}/\mbox{s}^{2}$

Fig. 12

Thrust and $\rho$ for low-energy low-thrust transfer for $a_{0} = 4\times 10^{-3}~\mbox{m}/\mbox{s}^{2}$

With the increasing maximum thrust, the largest retrievable mass also increases. Consider two optimal control problems whose only difference is their maximum thrust, denoted as $T_{1}$ and $T_{2}$. Suppose that $T_{1} < T_{2}$ and denote the permission control set for each mission as $\boldsymbol {U}_{1}$ and $\boldsymbol{U}_{2}$. Because the admissible control set with the lower thrust is a proper subset of the admissible control set with higher thrust, i.e., $\boldsymbol{U}_{1}\subset\boldsymbol{U}_{2}$, the optimal control ${\boldsymbol{u}}_{1}^{*} \in{{\boldsymbol{U}}_{2}}$, does not satisfy Pontryagin’s minimum principle. So the optimal result with larger thrust is definitely better than that with lower thrust. When the thrust increases, the duration of thrusting segments decreases. The structure of the optimal control also changes as the number of thrusting segments decreases from 4 to 3.

6 Conclusion

This paper studies a mission to retrieve an NEO on the condition that the spacecraft has already reached the target NEO. By combining low-thrust propulsion and invariant manifolds, the mass that can be captured to the desired LPO is estimated with indirect methods. This can then be used as a criterion to determine the possibility of capturing the whole asteroid. In detail, the joint spacecraft-asteroid system is retrieved into the stable invariant manifold that is extended from the desired LPO, and then the capture is purely ballistic due to the intrinsic dynamics of CRTBP.

PSO search and local optimization methods are used to find the optimal mission parameters. Then both direct and indirect methods are investigated to find the optimal two-impulse transfer in CRTBP, which is an intuitive but suboptimal strategy for low-energy transfer. The results obtained from direct and indirect methods are very close. However, direct methods are preferred for their robustness.

To estimate the largest retrievable mass, an optimal control problem to maximize the initial mass of the spacecraft–asteroid system is proposed. To solve this optimal control problem and overcome the difficulty of solving for bang-bang control, homotopic approaches that can enlarge the convergence domain and ensure the efficiency of numerical computation are used to get an approximation to the bang-bang control. Then the TPBVP is built after rejecting the homotopic. The bang-bang control is implemented to retrieve the joint spacecraft–asteroid system. To guarantee the accuracy of the numerical integration, the accurate switching moments of the thrust are detected. The detection methods are embedded in integrators with variable step sizes to ensure efficiency. The trajectory is divided into several segments, and the analytic Jacobian matrix is generated if necessary. Taking the solution obtained from the homotopic approach as an initial guess, the fuel-optimal bang-bang control is effectively obtained. This approach has been used to optimize the trajectory to place the spacecraft–asteroid system into the stable invariant manifold associated with the desired LPO. In most cases, only a few steps are required to get optimal bang-bang control even with the use of a forward-difference approximation and randomly guessed initial values. This demonstrates the efficiency and robustness of the indirect methods proposed in this paper.

The effect of maximum thrust on the retrieval mass is studied with numerical experiments. It is found that the analytic Jacobian matrix plays a critical role in the convergence of the shooting method when the thrust is large. The results from numerical experiments show that a larger thrust is more likely to capture an asteroid with larger mass. This can be explained by the fact that the optimal control with lower thrust is only a subset of the admissible control set with higher thrust and it does not satisfy Pontryagin’s minimum principle.