1 Introduction

Nowadays, it is strongly believed through different observational schemes such as type Ia Supernovae (Perlmutter et al. 1998; Riess et al. 1998), large scale structure (Tegmark et al. 2004) and cosmic microwave background (Spergel et al. 2003) observations that our universe experiences an accelerated expansion with the passage of time. The combined analysis of cosmological observations favor the spatially flat universe and consists of about 70 % DE, 30 % dust matter and negligible radiations. The WMAP data analysis (Briddle et al. 2003) also provided the confirmation of cosmic acceleration. It is recommended that some mysterious form of energy works behind this accelerated expansion phenomenon which is named as dark energy (DE). This DE possesses strong negative pressure in abundance which causes in pulling apart all the astronomical objects.

Due to ambiguous nature of DE, versatile study have been made in different ways such as cosmological constant, dynamical models, modified and higher dimensional theories (Copeland et al. 2006; Bamba et al. 2012). Moreover, the correspondence phenomenon between some of these DE models has also been adopted for evaluating or solving many DE issues. The cosmological constant (with equation of state (EoS) parameter ω=−1) is the simplest proposal of DE which works as vacuum energy but it has been plagued with severe issues named as cosmic coincidence and fine tuning. As an alternative to this model, many dynamical DE models have been developed in search of more reliable explanation of accelerated expansion phenomenon. These models are phantom, quintessence, k-essence, h-essence, holographic and its different versions and family of Chaplygin gas models (Amendola and Tsujikawa 2010). Different cosmological parameters as well as observational constraints on these models have been established in order to give useful outcomes for DE scenario.

Moreover, Wei (2012) constructed pilgrim DE (PDE) model by realizing the fact that there is a possibility to avoid black hole (BH) formation. He suggested that phantom-like DE can play a crucial role for avoiding the phenomenon of matter collapse. Related to this argument about the fate of BH is also available in the literature. For example, reduction of BH mass though phantom accretion phenomenon (Babichev et al. 2004, 2008; Jamil and Qadir 2011; Bhadra and Debnath 2012; Sharif and Jawad 2013) and the avoidance of event horizon in the presence of phantom-like DE (Lobo 2005a, 2005b; Sharif and Jawad 2014). Also, phantom DE with strong repulsive force can push the universe towards the big-rip singularity where all the physical objects lose the gravitational bounds and finally dispersed. This give motivation to Wei (2012) for suggesting PDE model. He choose with Hubble horizon as an infrared (IR) cutoff and evaluated this model through different possible theoretical and observational ways to make BH free phantom universe through PDE parameter.

The modification of gravitational sector of standard general relativity is another proposal for explaining the DE phenomenon. These modified theories are f(R), f(G), f(R,G) (Nojiri and Odintsov 2007; Bamba et al. 2012), f(T) (Linder 2010), f(R,T) (Harko 2011), Brans-Dicke (Brans and Dicke 1961), \(f(\tilde{R})\) (Chaichian 2010), f(T,T G ) (Kofinas and Saridakis 2014; Kofinas et al. 2014) etc. These modified gravities help in explaining the early inflation as well as late time accelerated expansion scenario (Caramisa and de Mellob 2009). Various classes of modified gravity have been explained in detail in the references (Nojiri and Odintsov 2005, 2011; Olmo 2011). Moreover, \(f(\tilde{R})\) gravity or modified Horava-Lifshitz F(R) (MFRHL) gravity has been introduced by Chaichian (2010) through a general approach which is invariant under foliation-preserving diffeomorphisms. By taking power-law \(F(\tilde{R})\) model, Carloni et al. (2010) evaluated FRW cosmology for finite time singularities and explained reductions of this gravity. Chattopadhyay and Ghosh (2012) have discussed the generalized second law of thermodynamics in this gravity and argued that it remains valid in quintessence phase.

The reconstruction scenario of modified theories of gravity via dynamical DE models is very fascinating and attracted much attention nowadays. Upto now, various works have been done in this direction (Nojiri and Odintsov 2006a, 2006b, 2007). We have also explored different cosmological parameters through reconstruction scenario via different modified theories of gravity as well as dynamical DE models (Jawad et al. 2013a, 2013b, 2013c, 2013d, 2014; Jawad 2014a, 2014b, 2014c; Jawad and Rani 2015). Here, we explore the correspondence phenomenon of (MFRHL) gravity and PDE (GO cutoff) in flat FRW universe. We obtain the \(F(\tilde{R})\) models and discuss the EoS parameter by taking three different scale factors. In the section we give basic formalism of \(F(\tilde{R})\) gravity and PDE. In Sect. 3, we elaborate the \(F(\tilde{R})\) models and EoS parameter. In the last section, we summarize our results.

2 Basic scenario

The action for MFRHL gravity is defined as follows (Chaichian 2010)

$$ \begin{aligned}[b] &S_{F_{HL}}=\int d^4x\sqrt{g^{(3)}}NF(R_{HL}), \\ &\quad \text{with } R_{HL}\equiv K^{ij}K_{ij}- \delta K^2-E^{ij} {\mathcal{G}}_{ijkl}E^{kl}. \end{aligned} $$
(1)

Here δ appear as generalised De Witt metric or super-metric (‘metric of the space of metric’) and also E ij can be defined

$$ \sqrt{g^{(3)}}E^{ij}=\frac{\delta W[g^{(3)}_{kl}]}{\delta g_{ij}} $$
(2)

which is also called detailed balanced condition by using an action \(W[g^{3}_{kl}]\) on the hypersurface Σ t . Moreover, \(\mathcal{G}^{ijkl}\) is defined on three-dimensional hyperspace Σ t as follows

$$ {\mathcal{G}}^{ijkl}=\frac{1}{2} \bigl(g^{(3)ik}g^{(3)jl}+g^{(3)il}g^{(3)jk} \bigr)-\delta g^{(3)ij}g^{(3)kl} $$
(3)

and its inverse can be written as

$$ {\mathcal{G}}_{ijkl}=\frac{1}{2} \bigl(g^{(3)}_{ik}g^{(3)}_{jl}+g^{(3)}_{il}g^{(3)}_{jk} \bigr)-\tilde{\delta} g^{(3)}_{ij}g^{(3)}_{kl}, \quad \tilde{\delta}=\frac{\delta}{3 \delta-1}. $$
(4)

In above stated HL f(R) gravity (Chaichian 2010), the lapse N is considered to be a function of t only, which represents the projectability condition. Further, it was explored a new very general HL-like f(R) gravity, which is a general approach for the construction of modified gravity which is invariant under foliation-preserving diffeomorphism (Chaichian 2010). The new form of generalized gravity is knows as modified f(R) Horava-Lifshitz gravity (MFRHL) whose action is defined as follows (Chaichian 2010)

$$ S_{F(\tilde{R})}=\int d^{4}\sqrt{g^{(3)}}N F( \tilde{R}), $$
(5)

and

$$ \begin{aligned}[b] \tilde{R}&=K^{ij}K_{ij}-\delta K^{2}+2\nu \nabla_{\mu} \bigl(n^{\mu} \nabla_{\nu}n^{\nu}-n^{\nu} \nabla_{\nu}n^{\mu} \bigr) \\ &\quad {}-E^{ij}\mathcal{G}_{ijkl}E^{kl} , \end{aligned} $$
(6)

which takes following form

$$ \begin{aligned}[b] \tilde{R}&=\frac{(3-9\delta)H^2}{N^2}+\frac{6\nu}{a^3 N} \frac{d}{dt} \biggl( \frac{Ha^3}{N} \biggr) \\ &=\frac{ (3-9\delta+18\nu )H^2}{N^2}+ \frac{6\nu}{N}\frac{d}{dt} \biggl( \frac{H}{N} \biggr), \end{aligned} $$
(7)

for flat FRW universe. For δ=ν=1, \(\tilde{R}\Rightarrow R\) and \(F(\tilde{R})\Rightarrow F(R)\) gravity for flat FRW universe. By varying the action (5) over \(g_{ij}^{(3)}\) and setting N=1, we get

$$ \begin{aligned}[b] 0&=F(\tilde{R})-2(1-3\delta+3\nu) \bigl( \dot{H}+3H^2 \bigr)F'(\tilde{R}) \\ &\quad {}-2(1-3\delta)H\frac{dF'(\tilde{R})}{dt}+2\nu \frac{d^2F'(\tilde{R})}{dt^2}+p. \end{aligned} $$
(8)

Here, prime denotes the derivative according to its argument. In the above equation, the matter contribution is involved as pressure p. Taking ρ as the matter density and the conservation equation is

$$ \dot{\rho}+3H(\rho+p)=0. $$
(9)

Using Eq. (8) and Eq. (9), we get

$$ \begin{aligned}[b] 0&=F(\tilde{R})-6 \bigl[(1-3\delta+3 \nu)H^{2}+\nu \dot{H} \bigr]F'(\tilde{R}) \\ &\quad {}+6\mu H\frac{dF'(\tilde{R})}{dt}-\rho-Ca^{-3}, \end{aligned} $$
(10)

where C is an integration constant. Thus, the density corresponding to MFRHL gravity with C=0 turns out to be

$$ \begin{aligned}[b] \rho_{\tilde{R}}&=F(\tilde{R})-6 \bigl[(1-3 \delta+3 \nu)H^{2}+\nu \dot{H} \bigr]F'(\tilde{R}) \\ &\quad {}+6\nu H \frac{dF'(\tilde{R})}{dt}. \end{aligned} $$
(11)

The reconstruction scheme is a very useful technique which is proposed by Nojiri and Odintsov (2006a, 2006b, 2007) and also extended for several cosmological scenarios. Through this technique, one can analyze the role of DE in different modified gravities. Also, our aim in this work is to reconstruct \(F(\tilde{R})\) for new holographic version of PDE by equating their energy densities, i.e. \(\rho_{\tilde{R}}=\rho_{\mathit{DE}}\), which gives

$$\begin{aligned} &6\mu H\dot{\tilde{R}}F''(\tilde{R})-6 \bigl[(1-3\delta+3\nu)H^{2}+\nu \dot{H} \bigr]F'( \tilde{R})+F(\tilde{R}) \\ &\quad {}=3 \bigl(\alpha H^2+\beta\dot{H} \bigr)^{\frac{u}{2}}. \end{aligned}$$
(12)

The PDE model is defined as follows

$$\begin{aligned} \rho_{\mathit{DE}}=3n^2 m_p^{4-u}L^{-u}, \end{aligned}$$
(13)

where n and u are both dimensionless constants. The first property of PDE is

$$\begin{aligned} \rho_{\mathit{DE}}\gtrsim m_p^2 L^{-2}. \end{aligned}$$
(14)

From Eqs. (14) and (13), we have \(L^{2-u}\gtrsim m_{p}^{u-2}=l_{p}^{2-u}\), where l p is the reduced Plank length. Since L>l p , one requires

$$\begin{aligned} u\leq 2. \end{aligned}$$
(15)

The second requirement for PDE is that it gives phantom-like behavior (Wei 2012)

$$\begin{aligned} \omega_{\mathit{DE}}< -1. \end{aligned}$$
(16)

It is stated that (Wei 2012) to obtain the EoS for PDE, we have to choose a particular cut-off L. Taking different IR cutoffs, the accelerated expansion of the universe is discussed by HDE model. For instance, radius of Hubble horizon L=H −1 where H is Hubble parameter, event horizon \(L=R_{E}=a\int_{t}^{\infty}\frac{dt}{a}\) with a is a scale factor, the form \(L=(H^{2}+\dot{H})^{-\frac{1}{2}}\) represented the Ricci length, the Granda-Oliveros (GO) length \((\alpha H^{2}+\beta \dot{H})^{-\frac{1}{2}}\) (Granda and Oliveros 2008), etc. With GO length, the density of HDE model is modified referred as new HDE (NHDE) model.

3 Reconstruction of \(F(\tilde{R})\) models and corresponding cosmological analysis

In this section, we construct \(F(\tilde{R})\) Models corresponding three different scale factors and discuss the EoS parameter.

3.1 Reconstruction scheme for unification of matter dominated and accelerated phases

In this scenario, the Hubble rate is defined as follows (Nojiri and Odintsov 2006a, 2006b)

$$ H(t)=H_2+\frac{H_1}{t}. $$
(17)

The scale factor for this scenario becomes \(a(t)=C_{1} e^{H_{2} t}t^{H_{1}}\). For t≪t 0, in the early universe and \(H(t)\sim \frac{H_{1}}{t}\), the universe was filled with perfect fluid with EOS parameter as \(w=1+\frac{2}{3H_{1}}\). On the other hand, when t≫t 0 the Hubble parameter H(t) is constant H→H 0 and the Universe seems to de-Sitter. So, this form of H(t) provides transition from a matter dominated to the accelerating phase. Using Eq. (17) in Eq. (12), we obtain the following

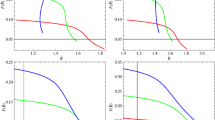
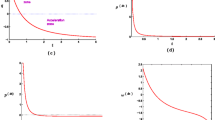
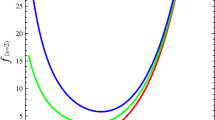
$$\begin{aligned} &{ \bigl(t^2\nu(H_1+t H_2) \bigr) \bigl(H_1 \bigl(-2\nu+\chi H_1} \\ &{\qquad {}+t(1-3\delta+6 \nu)H_2 \bigr) \bigr)^{-1}\frac{d^2F(t)}{dt^2}} \\ &{\qquad {}+ \bigl(H_1(-2\nu+ \chi H_1+H_2 \chi t)^2 \bigr)^{-1}} \\ &{\qquad {}\times t \bigl(\chi(-1 + 3\delta - 3 \nu) H^3_1-H_1 \bigl(-2\nu+t(1-3\delta} \\ &{\qquad {}+3\nu)H_2 \bigr) (-4\nu+3\chi H_2t) +3H^2_1 \bigl(2\nu(1-3\delta+5\nu)} \\ &{\qquad {}-t(1-3\delta+\nu)\chi H_2 \bigr)+3+t H_2 \bigl(-6\nu^2+tH_2 \bigl(4 \chi\nu} \\ &{\qquad {}-t(1-3\delta+3\nu)\chi H_2 \bigr) \bigr) \bigr) \frac{d F(t)}{dt}-F(t)} \\ &{\quad {}=3 \bigl( \bigl(\alpha H^2_1+ t^2 \alpha H_2^2 - H_1(\beta- 2 t \alpha H_2) \bigr)t^{-2} \bigr)^{\frac{u}{2}},} \end{aligned}$$

where χ=1−3δ+6ν. We solve this complicated differential equation numerically for \(f(\tilde{R})\) models and plot it against cosmic time for three different values of PDE parameter u=1,−1,−2 as shown in Figs. 1, 2 and 3. The other constant parameters are δ=0.5, ν=0.1, α=0.91, β=1.21, H 1=0.5. We can analyzed that the reconstructed \(F(\tilde{R})\) model shows increasing behavior initially, then attains a maximum value latter time for the case u=1. After that it shows decreasing behavior and approaches to a fixed value in future time. On the other hand, the reconstructed \(F(\tilde{R})\) model exhibits decreasing behavior initially and then increases with the passage of time for other two cases (u=−1,−2).

Fig. 1
figure 1

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=1. Also, H 0=2.3 (red); H 0=2.4 (green); H 0=2.5 (blue)

Full size image
Fig. 2
figure 2

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−1

Full size image
Fig. 3
figure 3

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−2

Full size image

The EoS parameter, in this scenario becomes

$$\begin{aligned} \omega_{\mathit{DE}} =& \bigl(t^2 H_1 \psi\bigl(-3F(t)+\bigl(t(-1+3 \delta-3\nu) \bigl(3H^2_1+3 t^2 \\ &{}+H^2_2+H_1(-1+6t H_2) \bigr) \dot{F}(t) (H_1 \psi)^{-1} \\ &{}+ \bigl(t(-1+3\delta) (H_1+tH_2) \bigl((-6\nu+3\chi H_1 \\ &{}+ 2 t \chi H_2) \ddot{F}(t)+t\psi \dot{F}(t) \bigr) \bigr) \bigl( H_1\psi^2 \bigr)^{-1} \\ &{} - \bigl( \bigl(H_1\psi^3 \bigr)^{-1} \bigr)t\nu \bigl(-2 \bigl(3(-2\nu+\chi H_1)^2 \\ &{}+3t\chi (-2\nu+\chi H_1)H_2+ t^2 \chi^2H^2_2 \bigr)\dot{F}(t) \\ &{}-t\psi \bigl(2(-6\nu+3\chi H_1+2t\chi H_2) \ddot{F}+t\psi \dddot{F}(t) \bigr) \bigr)\bigr)\bigr) \\ &{}\times \bigl(3 \bigl(t^2 F(t) H_1\psi+ t^5(1-3\delta+3\nu)H^2_2\dot{F}(t) \\ &{}-6\chi\nu H^3_1 \bigl(3 \dot{F}(t)+ t\ddot{F}(t) \bigr)+ tH_1 \bigl( \bigl(-t^2\nu \\ &{}+2H_2 \bigl(-18\nu^2+t^3(1-3\delta+3\nu)+6t\nu\chi H_2 \bigr) \bigr) \dot{F}(t)\\ &{}+6t \nu H_2(-2 \nu+t\chi H_2) \ddot{F}(t) \bigr) \\ &{}+H^2_1 \bigl( \bigl(36\nu^2+ t^3 \bigl((1 - 3\delta+ 3\nu) + 30t \nu\chi H_2 \bigr) \bigr)\dot{F}(t)\\ &{}+12t\nu(-\nu+t \chi H_2) \bigr)\ddot{F}(t) \bigr)\bigr)^{-1}\bigr) \end{aligned}$$

where ψ=−2ν+χH 1+tχH 2. The EoS parameter (Figs. 4, 5 and 6) shows the transition from phantom-like universe towards vacuum era or cosmological constant in all cases of H 0 and for u=1. This evolution parameter remains in the phantom-like universe always for u=−1. However the trajectories of EoS parameter shows quintessence-like DE behavior initial cosmic time while goes to vacuum-like DE in the latter epoch for u=−2.

Fig. 4
figure 4

Plot of ω DE versus t for PDE parameter u=1. Also, H 0=2.3 (red); H 0=2.4 (green); H 0=2.5 (blue)

Full size image
Fig. 5
figure 5

ω DE versus t for PDE parameter u=−1

Full size image
Fig. 6
figure 6

Plot of ω DE versus t for PDE parameter u=−2

Full size image

3.2 On unification of inflation with dark energy

The pioneer framework of unification of inflation with DE in modified gravities has been provided by Nojiri and Odintsov (2003) in f(R) gravity, which was subsequently generalized to more realistic versions (Nojiri and Odintsov 2007; Cognola et al. 2008). The singularity problem possesses importance which describes the early universe and it was investigated by Nojiri and Odintsov (2008). However, it was also pointed that there exists a class of non-singular exponential gravity to unify the early and late time accelerated expansion of the universe (Elizalde et al. 2011; Nojiri and Odintsov 2011). Thus, we also consider the inflationary scenario in this framework as follows

$$ H=\frac{H_1}{t} $$
(18)

which provides the following solution of

$$\begin{aligned} F(t) =&C_1 t^{-((-b_1 - b_2 - \sqrt{-4 b_1 + (b_1 + b_2)^2})(2 b_1)^{-1})} \\ &{}+ C_2 t^{-((-b_1 - b_2 + \sqrt{-4 b_1 + (b_1 + b_2)^2})(2 b_1)^{-1})} \\ &{}+ \bigl( \bigl(b_1 + b_2 - \sqrt{-4 b_1 + (b_1 + b_2)^2} + 2 b_1 u \bigr) \\ &{}\times\bigl(b_1 + b_2+\sqrt{-4 b_1 + (b_1 + b_2)^2} \\ &{}+ 2 b_1 u \bigr) \bigr)^{-1}12 b_1 b_3 t^{-u}, \end{aligned}$$

where C 1 and C 2 are appear as integration constants. This is an inflationary solution and b 1,b 2,b 3 are

$$\begin{aligned} b_1 =&\nu \bigl(2 \nu + (-1 + 3 \delta - 6 \nu) H_1 \bigr)^{-1}, \\ b_2 =& \bigl( \bigl(3\nu \bigl(-2 \nu + (1 - 3 \delta + 6 \nu)H_1 \bigr) \bigr)\\ &{}\times \bigl(2\nu+ (-1 + 3 \delta- 6 \nu) H_1 \bigr)^{-2} \\ &{}+ \bigl(-\nu H_1 + (1 - 3 \delta + 3 \nu) H_2 \bigr) \\ &{}\times \bigl( H_1 \bigl(2\nu + (-1 + 3 \delta - 6 \nu)H_1 \bigr) \bigr)^{-1} \bigr), \\ b_3 =&3 \bigl(-\beta H_1+ \alpha H^2_1 \bigr)^{\frac{u}{2}}. \end{aligned}$$

At inflationary (early) Universe, when t≪t 0, the dominant part of the F(t) becomes

$$ F(t)\sim C_1 t^{-((-b_1 - b_2 - \sqrt{-4 b_1 + (b_1 + b_2)^2})(2 b_1)^{-1})}. $$
(19)

In this limit, the reconstructed \(F(\tilde{R})\) for inflationary era has the form

$$ F(\tilde{R})\sim \tilde{C}_1\tilde{R}^{\frac{-b_1 - b_2 - \sqrt{-4 b_1 + (b_1 + b_2)^2}}{2 b_1}}. $$
(20)

Hence, \(F(\tilde{R})\) produces the inflationary (phantom) solution.

3.3 Reconstruction scheme for intermediate scale factor

This scale factor has the following form (Barrow et al. 2006)

$$ a(t)=\exp \bigl(Bt^l \bigr),\quad 0< m<1. $$
(21)

here B is a constant. The scale factor and Hubble parameter is suitably chosen so that it is consistent with the intermediate expansion:

$$\begin{aligned} H(t)=Blt^{l-1}. \end{aligned}$$
(22)

The scale factor is necessary to perform the analysis and therefore working with a hypothetical scale factor may not be consistent with the inflationary scenario. Hence we picked the intermediate scale factor which is also consistent with astrophysical observations (Barrow et al. 2006). According to this scale factor, we obtain the following form of differential equation

$$\begin{aligned} &{ \bigl(t^2 \nu \bigr) \bigl((-1+l) \bigl(-Bl\chi t^l-(-2 + l)\nu \bigr) \bigr)^{-1}\frac{d^2F(t)}{dt^2}} \\ &{\qquad {} + \bigl(t \bigl(B^2 l^2 t^{2l} - \chi(-1+3\delta-3\nu)+ 2(-2+l)^2 \nu^2}\\ &{\qquad {}+B lt^l \nu \bigl(6(-1+3\nu -5\nu)+ l(4 - 12\delta + 21\nu) \bigr) \bigr) \bigr)} \\ &{\qquad {}\times \bigl((-1+l) \bigl(-Bl \chi t^l- (-2 + l) \nu \bigr)^2 \bigr)^{-1} \frac{d F(t)}{dt}- F(t)} \\ &{\quad {}=-3 \bigl(B^2l^2 t^{-2 + 2 l} \alpha+ B (-1 + l) l t^{-2 + l} \beta \bigr)^{ \frac{u}{2}}.} \end{aligned}$$

We numerically plotted above equation for \(f(\tilde{R})\) models versus cosmic time for three different values of PDE parameter u=1,−1,−2 as shown in Figs. 7, 8 and 9. The other constant parameters are δ=0.5, ν=0.1, α=0.91, β=1.21, B=0.1. We can analyzed that the reconstructed \(F(\tilde{R})\) model shows increasing behavior initially, then attains a maximum value latter time for all the cases u and l which is consistence with the present day observations. The EoS parameter is

$$\begin{aligned} \omega_{\mathit{DE}} =&-3 F(t)+\bigl(t \bigl(-1+l+3B l t^l \bigr) (-1 + 3 \delta - 3 \nu) \dot{F}(t) \\ &{}\times \bigl((-1+l) \bigl(-Bl\chi t^l-(-2+l)\nu \bigr) \bigr)^{-1}\\ &{}+ \bigl(t (-1 + 3 \delta) \bigl((-2 + l) \nu \bigl((-3 + l) \dot{F}(t) - t \ddot{F}(t) \\ &{} + B \chi l t^l \bigl((3 - 2 l) \dot{F}(t) + t \ddot{F}(t) \bigr) \bigr) \bigr) \bigr) \\ &{}\times \bigl((-1 + l) \bigl(B l\chi t^l - (-2 + l)\nu \bigr)^2 \bigr)^{-1}\\ &{}- \bigl(B (-1 + l) l \bigl(B l\chi t^l -(-2 + l)\nu \bigr)^3 \bigr)^{-1}t^{1 - l} \\ &{}\times \nu \bigl((-2 + l)^2 \nu^2 \bigl((-3 + l) \bigl(-(-2 + l) \dot{F}(t) 2 t \ddot{F}(t) \bigr) \\ &{}- t^2\dddot{F}(t) \bigr) -B^2 l^2\chi t^{2 l} \bigr)^2\bigl(2 (-3 + 2 l) \bigl((-1 + l) \dot{F}(t) \\ &{} - t \ddot{F}(t) \bigr) +t^2 \dddot{F}(t) \bigr) - B (-2 + l) l t^ l \\ &{}\times\chi\nu \bigl(3 (-4 + l) (-1 + l) \dot{F}(t)\\ &{}+ 2 t \bigl(-3 (-2 + l) \ddot{F}(t) + t \dddot{F}(t) \bigr) \bigr)\bigr) \\ &{}\times\bigl(3 \bigl(F(t) + \bigl((-1 + l) t^3 \nu \dot{F}(t) + 6 B^2 (-1 + l) l^2 t^{2 l} \\ &{}\times \nu\chi \bigl((-3 + 2 l) \dot{F}(t) - t \ddot{F}(t) \bigr) \\ &{}+ B l t^l \bigl( \bigl(6 (-3 + l) (-2 + l) (-1 + l) \nu^2+t^3 (1 - 3 \delta\\ &{} + 3 \nu) \bigr) \dot{F}(t) - 6 (-2 + l) (-1 + l) t \nu^2 \ddot{F}(t) \bigr) \bigr) \\ &{}\times\bigl((-1 + l) t^2 \bigl(B l\chi t^l-(-2 + l)\nu \bigr) \bigr)^{-1}\bigr)\bigr). \end{aligned}$$

The above EoS parameter is plotted against cosmic time for three specific values of u shown in Figs. 10, 11 and 12. It can be observed from Fig. 10 (for u=1) that the EoS parameter shows quintom-like behavior two times and also shows oscillation about vacuum DE era. It evolutes the universe from phantom to vacuum to quintessence to vacuum to phantom and then approaches to Λ CDM limit in the end for all values of l. Figure 11 (u=−1) shows that EoS parameter evolutes the universe from phantom-like behavior towards quintessence-like behavior by crossing the phantom divide line for all values of l. Figure 12 (u=−2) exhibits the phantom-like behavior initially and then goes towards quintessence-like DE by crossing the phantom divide line for all values of l.

Fig. 7
figure 7

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=1. Also, l=2.2 (red); l=2.4 (green); l=2.6 (blue)

Full size image
Fig. 8
figure 8

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−1

Full size image
Fig. 9
figure 9

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−2

Full size image
Fig. 10
figure 10

Plot of ω DE versus t for PDE parameter u=1. Also, l=2.2 (red); l=2.4 (green); l=2.6 (blue)

Full size image
Fig. 11
figure 11

ω DE versus t for PDE parameter u=−1

Full size image
Fig. 12
figure 12

Plot of ω DE versus t for PDE parameter u=−2

Full size image

3.4 Reconstruction scheme for bouncing scale factor

Inflation is a solution for flatness problem in big-bang cosmology. Bouncing scenario predicts a transitionary inflationary Universe,in which the Universe evolves from a contracting epoch (H<0) to an expanding epoch (H>0). It means the scale factor a(t) reaches a local minima. So the cosmological solution is non-singular. In GB gravity,bouncing solutions widely studied in literature (Bamba et al. 2014a, 2014b; Odintsov et al. 2014).

This scale factor takes the following form (Myrzakulov and Sebastiani 2014)

$$ \begin{aligned}[c] &a(t)=a_0+\alpha(t-t_0)^{2n},\\ &H (t)= \frac{2n\alpha(t-t_0)^{2n-1}}{a_0+\alpha(t-t_0)^{2n}},\quad n=1,2,3\ldots \end{aligned} $$
(23)

where a 0, α are positive (dimensional) constants and n is a positive natural number. The time of the bounce is fixed at t=t 0. When t<t 0, the scale factor decreases and we have a contraction with negative Hubble parameter. At t=t 0, we have the bounce, such that a(t=t 0)=a 0, and when t>t 0 the scale factor increases and the universe expands with positive Hubble parameter. It should be mentioned that for sake of simplicity (without any loss of generality) we have taken n in the power law form as well as in the PDE density (Eq. 13).

The \(f(\tilde{R})\) models versus cosmic time corresponding to this scale factor is shown in Figs. 13, 14 and 15. It can be seen that the reconstructed \(F(\tilde{R})\) model shows increasing behavior for all values of n which is consistence with the present day observations. Also, \(F(\tilde{R})\) models corresponding to u=−1,−2 shows decreasing behavior with the passage of time. The EoS parameter in this scenario has shown in Figs. 16, 17 and 18 for u=1,−1,−2, respectively. This parameter also shows quintom-like behavior (transition from phantom-like to quintessence-like DE by crossing the phantom divide line) in all cases of u and n.

Fig. 13
figure 13

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=1. Also, H 0=2.3 (red); H 0=2.4 (green); H 0=2.5 (blue)

Full size image
Fig. 14
figure 14

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−1

Full size image
Fig. 15
figure 15

Plot of \(F(\tilde{R})\) versus t for PDE parameter u=−2

Full size image
Fig. 16
figure 16

Plot of ω DE versus t for PDE parameter u=1. Also, n=3 (red); n=4 (green); n=5 (blue)

Full size image
Fig. 17
figure 17

ω DE versus t for PDE parameter u=−1

Full size image
Fig. 18
figure 18

Plot of ω DE versus t for PDE parameter u=−2

Full size image

4 Concluding remarks

We have elaborated the reconstruction scenario of MFRHL gravity with new holographic PDE model by assuming three well-known forms of scale factor. We have constructed \(F(\tilde{R})\) models numerically corresponding to three different values of PDE parameter u=1,−1,−2. In first choice of scale factor, we have analyzed that the reconstructed \(F(\tilde{R})\) model shows increasing behavior initially, then attains a maximum value latter time for the case u=1 (Fig. 1). After that it shows decreasing behavior and approaches to a fixed value in future time. On the other hand, the reconstructed \(F(\tilde{R})\) models (Figs. 2–3) exhibits decreasing behavior initially and then increases with the passage of time for other two cases (u=−1,−2). In Intermediate scale factor case, the reconstructed \(F(\tilde{R})\) model shows increasing behavior initially, then attains a maximum value latter time for all the cases u and l which is consistence with the present day observations (Figs. 7–9). In bouncing scale factor case, \(f(\tilde{R})\) models versus cosmic time corresponding to this scale factor is shown in Figs. 13–15. It has been seen that the reconstructed \(F(\tilde{R})\) model shows increasing behavior for all values of n which is consistence with the present day observations. Also, \(F(\tilde{R})\) models corresponding to u=−1,−2 shows decreasing behavior with the passage of time.

Also, we have analyzed the behavior of EoS parameter for above mentioned scenario. For the first scale factor, the EoS parameter is shown in Figs. 4–6. It has shown the transition from phantom-like universe towards vacuum era or cosmological constant in all cases of H 0 and for u=1. This evolution parameter remains in the phantom-like universe always for u=−1. However the trajectories of EoS parameter shows quintessence-like DE behavior initial cosmic time while goes to vacuum-like DE in the latter epoch for u=−2. For Intermediate scale factor, EoS parameter is plotted against cosmic time for three specific values of u shown in Figs. 10–12. It can be observed from Fig. 10 (for u=1) that the EoS parameter shows quintom-like behavior two times and also shows oscillation about vacuum DE era. It evolutes the universe from phantom to vacuum to quintessence to vacuum to phantom and then approaches to Λ CDM limit in the end for all values of l. Figure 11 (u=−1) shows that EoS parameter evolutes the universe from phantom-like behavior towards quintessence-like behavior by crossing the phantom divide line for all values of l. Figure 12 (u=−2) exhibits the phantom-like behavior initially and then goes towards quintessence-like DE by crossing the phantom divide line for all values of l. For bouncing scale factor, EoS parameter has shown in Figs. 16–18 for u=1,−1,−2, respectively. This parameter shows quintom-like behavior (transition from phantom-like to quintessence-like DE by crossing the phantom divide line) in all cases of u and n.

Also, the trajectories of EoS parameter compatible with the constraints as obtained by Ade et al. (2014) (Planck data) which is given as follows:

$$\begin{aligned} \omega_{\mathit{DE}} =&-1.13^{+0.24}_{-0.25}\quad (\mbox{Planck}+\mbox{WP}+\mbox{BAO}), \\ \omega_{\mathit{DE}} =&-1.09\pm0.17\quad (\mbox{Planck}+\mbox{WP}+\mbox{Union 2.1}), \\ \omega_{\mathit{DE}} =&-1.13^{+0.13}_{-0.14}\quad (\mbox{Planck}+\mbox{WP}+\mbox{SNLS}), \\ \omega_{\mathit{DE}} =&-1.24^{+0.18}_{-0.19}\quad (\mbox{Planck}+\mbox{WP}+\mathrm{H}_0). \end{aligned}$$

The trajectories also favor the nine-year WMAP observational data (Hinshaw et al. 2013) which gives the ranges for EoS parameter as

$$\begin{aligned} &{\omega_{\mathit{DE}}=-1.073^{+0.090}_{-0.089}\quad (\mbox{WMAP}+\mbox{eCMB}+\mbox{BAO}+\mathrm{H}_0),} \\ &{\begin{aligned}[c] &\omega_{\mathit{DE}}=-1.084\pm0.063\\ &\quad (\mbox{WMAP}+\mbox{eCMB}+\mbox{BAO}+\mathrm{H}_0+\mbox{SNe}). \end{aligned}} \end{aligned}$$

The above constraints has been obtained by implying different combination of observational schemes at 95 % confidence level.