1 Introduction

The universe is undergoing the accelerated expansion which is one of the perplexing fact in modern cosmology. The cause for this acceleration has been found as some kind of exotic force, named as dark energy (DE) which has a strong negative pressure to pull apart the matter. Different observational data sets such as type Ia Supernovae, large scale structure, WMAP etc reveal these properties of DE as well as proposed some specific values of equation of state (EoS) parameter (Riess et al. 1998; Perlmutter et al. 1998; Miller et al. 1999; Astier et al. 2006; Copeland et al. 2006; Sami 2009; Frieman et al. 2008; Bamba et al. 2012). This parameter relates the energy density with pressure and its negative value corresponds to DE era of the universe. The nature of this force is still under observations. The search for best fit source of DE has become active field of modern cosmology. In this regard, many dynamical DE models, modified theories of gravity, higher dimensional theories, scalar field models have been proposed.

The dynamical DE models and their modified versions have been proposed through energy densities. Holographic DE (HDE) model is one of the extensively used DE model in the literature. The idea of HDE model comes from the holographic principle which is based on a unified scenario (gravity and quantum mechanics). This principle states that “all the information relevant to a physical system inside a spatial region can be observed on its boundary instead of its volume”. The idea of Cohen et al. (1999) (which is used in the development of HDE density) has reconsidered by Wei (2012) with the proposal of pilgrim DE (PDE). According to Wei, the black hole (BH) formation can be avoided through appropriate resistive force which is capable to prevent the matter collapse. In this phenomenon, phantom-like DE can play important role which possesses strong repulsive force as compared to quintessence DE.

The effective role of phantom-like DE onto the mass of BH in the universe has also been observed in many different ways. The accretion phenomenon is one of them which favors the possibility of avoidance of BH formation due to the presence of phantom-like DE in the universe. It has been suggested that accretion of phantom DE (which is attained through family of Chaplygin gas models) reduces the mass of BH (Babichev et al. 2004, 2008; Jamil and Qadir 2011; Bhadra and Debnath 2012; Sharif and Jawad 2014). It has also pointed out that the phantom-like DE also help to get rid of event horizon in the wormhole scenario (Lobo 2005a, 2005b; Sharif and Jawad 2014). It is strongly believed that the presence of phantom DE in the universe will force it towards big-rip singularity. This represents that the phantom-like universe possesses ability to prevent the BH formation. The proposal of PDE model also works on this phenomenon which states that phantom DE contains enough repulsive force which can resist against the BH formation. The energy density of PDE has the following form (Wei 2012)

$$ \rho_{DE}=3\varepsilon^{2}M_{p}^{4-u}L^{-u}, $$
(1)

where both \(\varepsilon\) and \(u\) are dimensionless constants. Wei (2012) developed cosmological parameters for PDE model with Hubble horizon and provided different possibilities for avoiding the BH formation through PDE parameter.

The modified theories of gravity have also widely used in order to illustrate the cosmic acceleration through DE phenomenon. The well-known modified theories of gravity are: \(f(R), f(G), f(R,G)\) (Nojiri and Odintsov 2007a, 2007b, 2007c; Bamba et al. 2012), \(f(T)\) (Linder 2010), \(f(R,T)\) (Harko 2011), Brans-Dicke (Brans and Dicke 1961), \(f(\tilde{R})\) (Chaichian 2010), \(f(T,T_{G})\) (Kofinas and Saridakis 2014; Kofinas et al. 2014) etc. These theories has some interesting features, i.e., the early inflation as well as late time accelerated expansion scenario can be explained through them (Caramisa and de Mellob 2009). Some well-known classes of modified gravity have been given in the literature (Nojiri and Odintsov 2005, 2011; Olmo 2011). Nowadays, \(F(\tilde{R})\) gravity or modified Horava-Lifshitz \(F(R)\) (MFRHL) gravity got much attention for explaining DE phenomenon which was developed by Chaichian et al. (Chaichian 2010) with the help of a general approach which is invariant under foliation-preserving diffeomorphisms.

In this theory, Carloni et al. (2010) explored FRW cosmology for finite time singularities and provided some reductions of this gravity by taking power-law \(F(\tilde{R})\) model. It is analytically shown that they have a quite rich cosmological structure: early/late-time cosmic acceleration of quintessence, as well as of phantom types. Also it is demonstrated that all the four known types of finite-time future singularities may occur in the power-law \(F(\tilde{R})\) gravity. The correspondence scenario between modified theories of gravity and dynamical DE models has also provided some interesting results regarding DE phenomenon. In this direction, many works have been done (Nojiri and Odintsov 2006a, 2006b; Nojiri and Odintsov 2007a, 2007b, 2007c). However, the reconstruction scenario in \(F(\tilde{R})\) has been firstly explored by Carloni et al. (2010). Then, Chattopadhyay and Ghosh (2012) have explored the generalized second law of thermodynamics and pointed out that it holds in quintessence phase in \(F(\tilde{R})\) gravity. We have also made correspondence of different modified theories of gravity with dynamical DE models and calculated different cosmological parameters (Jawad et al. 2013a, 2013b, 2013c, 2013d, 2014; Jawad 2014a, 2014b, 2014c; Jawad and Rani 2015a, 2015b).

Here, we discuss the reconstruction scenario of (MFRHL) gravity and generalized ghost PDE (GGPDE) by the inclusion of some scale factors in flat FRW universe. We obtain the \(F(\tilde{R})\) models numerically and evaluate the corresponding EoS parameter. In Sect. 2, we provide the basic formalism of \(F(\tilde{R})\) gravity and GGPDE. In Sect. 3, we elaborate the \(F(\tilde{R})\) models and EoS parameter. In Sect. 4, we summarized our results.

2 Basic scenario

Here we give some basic equations corresponding to \(F(\tilde{R})\) gravity.

2.1 \(F(\tilde{R})\) gravity

The action of \(F(\tilde{R})\) gravity (the extension of \(F(R)\) Horava-Lifshitz gravity) is defined as follows (Chaichian 2010; Carloni et al. 2010)

$$ S_{f(\tilde{R})}=\int d^{4}x\sqrt{g^{(3)}}N F( \tilde{R}), $$
(2)

with

$$\begin{aligned}& \tilde{R}=K^{ij}K_{ij}-\lambda K^{2}+2\mu \nabla_{\mu} \bigl(n^{\mu}\nabla_{\nu}n^{\nu}-n^{\nu} \nabla_{\nu}n^{\mu} \\& \phantom{\tilde{R}=\,\,}{} -E^{ij} \mathcal{G}_{ijkl}E^{kl} \bigr), \end{aligned}$$
(3)
$$\begin{aligned}& {\mathcal{{G}}}_{ijkl}=\frac{1}{2} \bigl(g^{(3)}_{ik}g^{(3)}_{jl}+g^{(3)}_{il}g^{(3)}_{jk} \bigr)-\tilde{\lambda} g^{(3)}_{ij}g^{(3)}_{kl}, \quad \tilde{\lambda}=\frac{\lambda}{3 \lambda-1}, \end{aligned}$$
(4)

where \(N\) is the lapse function which is assumed to be function of time \(t\) only representing the projectability condition. Moreover, the expression of \(\tilde{R}\) in flat FRW universe turns out to be

$$\begin{aligned} \tilde{R} =&\frac{(3-9\lambda)H^{2}}{N^{2}}+\frac{6\mu}{a^{3} N}\frac{d}{dt} \biggl(\frac{Ha^{3}}{N} \biggr) \\ =&\frac{ (3-9\lambda+18\mu )H^{2}}{N^{2}}+ \frac{6\mu}{N} \frac{d}{dt} \biggl(\frac{H}{N} \biggr). \end{aligned}$$
(5)

We can also recover the usual \(f(R)\) gravity from MFRHL gravity by setting \(\lambda=\mu=1\). Varying the action (2) over \(g_{ij}^{(3)}\) and setting \(N=1\), we obtain

$$\begin{aligned} 0 =&F(\tilde{R})-2(1-3\delta+3\nu) \bigl(\dot{H}+3H^{2} \bigr)F'(\tilde{R}) \\ &{}-2(1-3\delta)H\frac{dF'(\tilde{R})}{dt}+2\nu \frac{d^{2}F'(\tilde{R})}{dt^{2}}+p. \end{aligned}$$
(6)

where \(H=\frac{\dot{a}}{a}\) is the Hubble parameter, \(p\) represents the matter contribution and prime indicates the differentiation with respect to its argument. In the above equation, the matter contribution is involved as pressure \(p\). The conservation equation according to matter density becomes

$$ \dot{\rho_{m}}+3H(\rho_{m}+p_{m})=0 \Rightarrow \rho_{m}=\rho_{m0}a^{-3}. $$
(7)

where \(\rho_{m0}\) is the constant of integration. Using Eq. (6) and Eq. (7) with dust-like matter, we get

$$\begin{aligned} 0 =&F(\tilde{R})-6 \bigl[(1-3\lambda+3\nu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H\frac{dF'(\tilde{R})}{dt}- \rho-Ca^{-3}, \end{aligned}$$
(8)

where \(C\) is an integration constant. Thus, the energy density with respect to MFRHL gravity with \(C=0\) turns out to be

$$\begin{aligned} \rho_{\tilde{R}} =&F(\tilde{R})-6 \bigl[(1-3\lambda+3 \mu)H^{2}+\mu \dot{H} \bigr]F'(\tilde{R}) \\ &{}+6\mu H \frac{dF'(\tilde{R})}{dt}. \end{aligned}$$
(9)

2.2 Cosmic scale factors

Here, we will give brief description of some well-known factors for elaborating our cosmological study.

2.2.1 Bouncing scale factor

Bouncing scenario evolves the universe from a contracting epoch \((H<0)\) to an expanding epoch \((H>0)\). This behavior predicts a transitionary inflationary universe which is a solution for flatness problem in big-bang cosmology. Also, bouncing solutions has been widely discussed in GB gravity (Bamba et al. 2014a, 2014b; Odintsov et al. 2014). The bouncing scale factor can be defined as follows (Myrzakulov and Sebastiani 2014)

$$\begin{aligned}& \begin{aligned} &a(t)=a_{0}+\alpha(t-t_{0})^{2n} ,\\ & H (t)= \frac{2n\alpha(t-t_{0})^{2n-1}}{a_{0}+\alpha(t-t_{0})^{2n}} ,\quad n=1,2,3\ldots \end{aligned} \end{aligned}$$
(10)

where \(a_{0}\), \(\alpha\) appears as positive (dimensional) constants and \(n\) represents the positive natural number. The bouncing time is fixed at \(t=t_{0}\). The scale factor exhibits the decreasing behavior for \(t< t_{0}\) and shows contraction of the universe with negative Hubble parameter. While, it shows increasing behavior for \(t>t_{0}\) which implies the expansion of the universe with positive Hubble parameter.

2.2.2 Intermediate scale factor

We choose this scale factor because it shows consistency with astrophysical observations (Barrow et al. 2006). It also plays a key-role in the cosmological analysis while a hypothetical scale factor may not be consistent with the inflationary scenario. The intermediate form of scale factor can be defined as follows (Barrow et al. 2006)

$$\begin{aligned} a(t)=e^{b_{1}t^{m}},\quad 0< m< 1, \end{aligned}$$
(11)

where \(b_{1}\) is a constant. The corresponding Hubble parameter is

$$\begin{aligned} H(t)=b_{1}mt^{m-1}. \end{aligned}$$
(12)

2.2.3 Unification of matter dominated and accelerated phases

For this framework, the Hubble rate and corresponding scale factor can be defined as follows (Nojiri and Odintsov 2006a, 2006b)

$$ H(t)=H_{2}+\frac{H_{1}}{t}\Rightarrow a(t)=b_{3} e^{H_{2} t}t^{H_{1}}. $$
(13)

This corresponds to early universe (for \(t\ll t_{0}\)) which implies \(H(t)\sim \frac{H_{1}}{t}\) where the universe was filled with perfect fluid with EoS parameter as \(w=1+\frac{2}{3H_{1}}\). For \(t\gg t_{0}\) ⇒ \(H\rightarrow H_{0}\) which seems to be de-Sitter-like universe. Also, the above form of \(H(t)\) shows the transition from a matter dominated to the accelerating phase.

3 Reconstruction of \(F(\tilde{R})\) models and cosmological analysis

Here, we reconstruct and discuss the behavior of different \(F(\tilde{R})\) models along with corresponding EoS parameters and stability through squared speed of sound with the help of three scale factors. The reconstruction scenario is firstly developed by (Nojiri and Odintsov 2006a, 2006b, 2006c; Nojiri and Odintsov 2007a, 2007b, 2007c) as well as extended in several cosmological scenarios. This reconstruction scenario is very fascinating setup for the unification of DE models and modified gravities at one platform. Through this setup, one can investigate the role of DE in different modified gravities. Here, we choose dynamical DE model as follows (Sharif and Jawad 2014)

$$ \rho_{DE}=\bigl(\alpha H+\beta H^{2} \bigr)^{u}. $$
(14)

This model is known as generalized ghost pilgrim DE (GGPDE) model. The conservation equation corresponding to DE model is

$$\begin{aligned} \dot{\rho}_{DE}+3H\rho_{DE}(1+ \omega_{DE}) =&0, \end{aligned}$$
(15)

However, our aim is to reconstruct \(F(\tilde{R})\) models for GGPDE by equating their energy densities, i.e. \(\rho_{\tilde{R}}=\rho_{DE}\), which gives

$$\begin{aligned}& 6\mu H\dot{\tilde{R}}F''(\tilde{R})-6 \bigl[(1-3\lambda+3\mu)H^{2}+\mu \dot{H} \bigr]F'( \tilde{R})+F(\tilde{R}) \\& \quad=3\bigl(\alpha H+\beta H^{2}\bigr)^{\frac{u}{2}}. \end{aligned}$$
(16)

The EoS parameter in this scenario takes the form

$$\begin{aligned} \omega_{DE}=\frac{p_{\tilde{R}}}{\rho_{\tilde{R}}+\rho_{m}}. \end{aligned}$$
(17)

Also, we use squared speed of sound for the stability analysis of \(F(\tilde{R})\) model. This parameter is given by

$$ \upsilon_{s}^{2}=\frac{\dot{p}}{\dot{\rho}}= \frac{p'}{\rho'}. $$
(18)

The sign of \(v_{s}^{2}\) is very important to see the stability of background evolution of the model. A positive value indicates a stable model whereas instability of a given perturbation corresponds to the negative value of \(v^{2}_{s}\).

  • For Bouncing Scale Factor: For this scale factor, we obtain \(F(\tilde{R})\) models versus its argument

    $$\begin{aligned}& \frac{3\mu n}{A}(t-t_{0})^{2} \frac{d^{2}F}{dt^{2}}-B(t-t_{0})\frac{dF}{dt}+F \\ & \quad =3 \biggl[ \frac{2n\alpha}{t-t_{0}}+ \frac{4n^{2}\beta}{(t-t_{0})^{2}} \biggr]^{\frac{u}{2}}, \end{aligned}$$
    (19)

    where

    $$\begin{aligned}& A=n(3-9\lambda+18\mu)-3\mu, \\ & B=\frac{9\mu}{2A}-\frac{3C}{2A}, \\ & C=2n(1-3\lambda+3\mu)-\mu. \end{aligned}$$

    Its solution is

    $$\begin{aligned} F(t) =&C_{1}(t_{0}-t)^{\frac{ 2 A B + 3 n \mu + D}{6 n \mu}} + C_{2}(t_{0}-t)^{\frac{2 A B + 3 n \mu -D}{6 n \mu}}\\ &{}+\frac{1}{ n^{2} (2 + u) \beta D} 32^{\frac{- 2 A B + 3 n \mu - 3 n u \mu - D }{6 n \mu}} A (t - t_{0})^{2} \\ &{}\times \biggl[\frac{(t - t_{0}) \alpha}{n \beta} \biggr]^{\frac{ 2 A B + 3 n \mu + 6 n u \mu -D}{ 6 n \mu}} \\ &{}\times \biggl[\frac{ n (-t_{0} \alpha + t \alpha + 2 n \beta)}{(t - t_{0})^{2}} \biggr]^{\frac{2 + u}{ 2}} \\ &{}\times \biggl[2^{\frac{D}{( 3 n \mu)}}\mathrm{Hypergeometric2F1} \\ &{}\times \biggl[ \frac{2 + u}{2}, \frac{2 A B + 9 n \mu + 6 n u \mu - D}{ 6 n \mu}, \frac{4 + u}{2}, \\ &{}\phantom{{}\times \bigg[} \frac{-t_{0} \alpha + t \alpha + 2 n \beta}{( 2 n \beta)} \biggr] - \biggl[\frac{(t_{0} - t) \alpha}{n \beta} \biggr]^{\frac{D}{3 n \mu}} \\ &{}\times \mathrm{Hypergeometric2F1} \biggl[\frac{2 + u}{2}, \\ &{}\phantom{{}\times \bigg[} \frac{2 A B + 9 n \mu + 6 n u \mu + D}{ 6 n \mu}, \frac{4 + u}{2} , \\ &{}\phantom{{}\times \bigg[} \frac{-t_{0} \alpha + t \alpha + 2 n \beta}{2 n \beta} \biggr] \biggr], \end{aligned}$$
    (20)

    where \(D=\sqrt{[ 4 A^{2} B^{2} + 12 A (-2 + B) n \mu + 9 n^{2} \mu^{2}]}\). Using relation, \(t-t_{0}=2\sqrt{\frac{nA}{\tilde{R}}}\) in the above equation, we can find \(F(\tilde{R})\). Also, we plot it against \(\tilde{R}\) as shown in Fig. 1 for different values of \(u\) and \(n\). We also choose other constant parameters like \(a_{0}=1, b_{2} = 2\).

    1. 1.

      Fig. 1 indicates that \(F(\tilde{R})\) decreases with respect to increasing \(\tilde{R}\) for \(u=1\) and 2 (upper panel plots). As we increase the value of \(n, F(\tilde{R})\) represents steeper behavior. Also, it decreases for \(u=-1\) and −2 (lower panel plots) with less steeper behavior as compared to upper panel plots.

      Fig. 1
      figure 1

      Plots of \(F(\tilde{R})\) versus \(\tilde{R}\) for \(u=2\) (upper left panel), \(u=1\) (upper right panel), \(u=-1\) (lower left panel) and \(u=-2\) (lower right panel) for reconstructed MFRHL GGPDE model. Also, \(n=4\) (red), \(n=5\) (green), \(n=6\) (blue) in each plot of reconstruction scheme for bouncing scale factor

      Full size image
    2. 2.

      However, the EoS parameter shows transition from phantom-like era of the universe towards dust-like matter by evolving the \(\varLambda\mbox{CDM}\) limit and quintessence era for all cases of \(u\) and \(n\) as given in Fig. 2.

      Fig. 2
      figure 2

      Plots of \(\omega_{DE}\) versus \(t\) for bouncing scale factor

      Full size image
    3. 3.

      In this case, the squared speed of sound also positive which implies the stability of the present model in this scale factor as displayed in Fig. 3.

      Fig. 3
      figure 3

      Plots of \(v^{2}_{s}\) versus \(t\) for bouncing scale factor

      Full size image

  • For Intermediate Scale Factor: For this scale factor, \(F(\tilde{R})\) models obtain numerically versus \(\tilde{R}\) corresponding to four values of PDE parameter \(u\) and \(m\) as shown in Fig. 4. The other constant parameters are chosen as follows \(\delta=0.5, \nu = 0.1, \alpha = 1.01, \beta = 2.21, b_{1} = 2.1\).

    1. 1.

      The upper panels of Fig. 4 show that \(F(\tilde{R})\) exhibits the increasing behavior as the value of \(\tilde{R}\) increases for \(u=1, 2\). It represents steeper behavior as \(\tilde{R}\) approaches to zero. On the other hand, in case of \(u=-1,-2\), this function depicts the opposite behavior in contrast to upper panel plots. That is, lower panel plots show decreasing behavior for all values of \(m\).

      Fig. 4
      figure 4

      Plots of \(F(\tilde{R})\) versus \(\tilde{R}\) for \(u=2\) (upper left panel), \(u=1\) (upper right panel), \(u=-1\) (lower left panel) and \(u=-2\) (lower right panel) for reconstructed MFRHL GGPDE model. Also, \(m=0.4\) (red), \(m=0.5\) (green) and \(m=0.6\) (blue) in each plot of reconstruction scheme for intermediate scale factor

      Full size image
    2. 2.

      Using Eqs. (6) and (9) in the Eq. (17) and plot \(\omega_{DE}\) in terms of cosmic time for four different values of \(u\) and \(m\) as shown in Fig. 5. This parameter shows transition from dust-like matter towards phantom-like universe by crossing the quintessence era as well as \(\varLambda\mbox{CDM}\) limit for all cases of \(u\) and \(m\).

      Fig. 5
      figure 5

      Plots of \(\omega_{DE}\) versus \(t\) for intermediate scale factor

      Full size image
    3. 3.

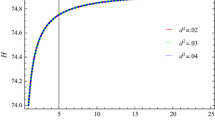
      We also give the graphical representation of squared speed of sound versus \(t\) for the same constant parameters as mentioned above (Fig. 6). We observe that the squared speed of sound remains positive for all values of \(u\) and \(m\) which exhibits the stability of the present models in the scenario of intermediate scale factor.

      Fig. 6
      figure 6

      Plots of \(v^{2}_{s}\) versus \(t\) for intermediate scale factor

      Full size image

  • For Unification of Matter Dominated and Accelerated Phases: In this case, we also attain numerical representation of \(F(\tilde{R})\) models versus cosmic time as displayed in Fig. 7 for different values of \(u\) and \(H_{2}\). We have also chosen other constant parameters like \(b_{3}=1, H_{1} = 0.5\).

    1. 1.

      We can observe that the function \(F(\tilde{R})\) shows decreasing behavior but approaches to a negative minimum value for the case \(u=2\) (left upper panel) while for \(u=1\), it shows increasing behavior (right upper panel). For \(u=-1\) and −2 (lower panel plots), the reconstructed function represents decreasing behavior (Fig. 7).

      Fig. 7
      figure 7

      Plots of \(F(\tilde{R})\) versus \(\tilde{R}\) for \(u=2\) (upper left panel), \(u=1\) (upper right panel), \(u=-1\) (lower left panel) and \(u=-2\) (lower right panel) for reconstructed MFRHL GGPDE model. Also, \(H_{2}=2.2\) (red), \(H_{2}=2.3\) (green), \(H_{2}=2.4\) (blue) in each plot of reconstruction scheme for unification of matter dominated and accelerated phases

      Full size image
    2. 2.

      However, the EoS parameter shows quintessence behavior of the universe for all cases of \(u\) as shown in Fig. 8.

      Fig. 8
      figure 8

      Plots of \(\omega_{DE}\) versus \(t\) for reconstruction scheme for unification of matter dominated and accelerated phases

      Full size image
    3. 3.

      In this case, the squared speed of sound also positive which implies the stability of the present model in this scale factor as displayed in Fig. 9.

      Fig. 9
      figure 9

      Plots of \(v^{2}_{s}\) versus \(t\) for reconstruction scheme for unification of matter dominated and accelerated phases

      Full size image

4 Concluding remarks

The present paper is devoted to study the reconstruction scenario of MFRHL gravity and GGPDE model with the help of some cosmic scale factors. In this scenario, we have developed \(F(\tilde{R})\) models and corresponding EoS parameter for four different values of PDE parameter. For bouncing scale factor, the \(F(\tilde{R})\) models versus cosmic time have been displayed in Fig. 1 for different values of \(u\) and \(n\). Figure 1 indicated that \(F(\tilde{R})\) decreases with respect to \(\tilde{R}\) for \(u=1, 2,-1\) and −2 (upper and lower panels) with steeper and lower steeper behavior respectively. However, the EoS parameter has shown transition from phantom-like era of the universe towards dust-like matter by evolving the \(\varLambda\mbox{CDM}\) limit and quintessence era for all cases of \(u\) and \(n\) as given in Fig. 2. We have also seen that the squared speed of sound remains positive for all values of \(u\) and \(n\) which exhibits the stability of the present models in the scenario of bouncing scale factor (Fig. 3).

For intermediate scale factor, we have observed from Fig. 4 that \(F(\tilde{R})\) shows increasing behavior for \(u=1, 2\) (upper panels), while decreasing behavior in case of \(u=-1,-2\) (lower panels) for all cases of \(m\) with increasing \(\tilde{R}\). In this case, the EoS parameter versus cosmic time has also displayed in Fig. 5. This parameter shows transition from dust-like matter towards phantom-like universe by crossing the quintessence era as well as \(\varLambda\mbox{CDM}\) limit for all cases of \(u\) and \(m\). We have also observed that the squared speed of sound remains positive for all values of \(u\) and \(m\) which exhibits the stability of the present models in the scenario of intermediate scale factor (Fig. 6).

In case of third scale factor, the numerical representation of \(F(\tilde{R})\) models versus \(\tilde{R}\) has been displayed in Fig. 7. We have observed that the function \(F(\tilde{R})\) shows decreasing behavior but approaches to a negative minimum value for the case \(u=2\) while for \(u=1\), it shows increasing behavior. For \(u=-1\) and −2, the reconstructed function represents decreasing behavior. However, the EoS parameter (Fig. 8) have shown the quintessence behavior of the universe for all cases of \(u\). We observe that the squared speed of sound remains positive for all values of \(u\) and \(H_{1}\) which exhibits the stability of the present models (Fig. 9).

4.1 Comparison of results with observational data

Also, we have observed that the trajectories of EoS parameter corresponding to all three scale factors (Figs. 2, 5 and 8) shows consistency with the observational data as obtained by Ade et al. (2014) (Planck data) which is given as follows:

$$\begin{aligned}& \omega_{DE}=-1.13^{+0.24}_{-0.25} \quad (\mbox{Planck}+\mbox{WP}+\mbox{BAO}),\\& \omega_{DE}=-1.09\pm0.17, \quad (\mbox{Planck}+\mbox{WP}+\mbox{Union 2.1})\\& \omega_{DE}=-1.13^{+0.13}_{-0.14}, \quad (\mbox{Planck}+\mbox{WP}+\mbox{SNLS}), \\& \omega_{DE}=-1.24^{+0.18}_{-0.19}, \quad (\mbox{Planck}+\mbox{WP}+H_{0}). \end{aligned}$$

The trajectories also favor the nine-year WMAP observational data (Hinshaw et al. 2012) which gives the ranges for EoS parameter as

$$\begin{aligned}& \omega_{DE}=-1.073^{+0.090}_{-0.089}\quad (\mbox{WMAP}+\mbox{eCMB}+\mbox{BAO}+H_{0}),\\& \omega_{DE}=-1.084\pm0.063, \\& \quad (\mbox{WMAP}+\mbox{eCMB}+\mbox{BAO}+H_{0}+\mbox{SNe}) \end{aligned}$$

The above constraints has been obtained by implying different combination of observational schemes at \(95~\%\) confidence level.

We have also compared our results with Jawad (2014a, 2014b, 2014c) (worked with perfect fluid) and found that the EoS parameter in our case is slightly shows variation with Jawad (2014a, 2014b, 2014c) but consistence with observational data in both cases, i.e., with (our case) and without (Jawad 2014a, 2014b, 2014c) modified gravity. Moreover, the squared speed of sound shows stability of correspondence scenarios with and without modified gravity.