Dust-acoustic solitary and rogue waves in a Thomas-Fermi degenerate dusty plasma

Abstract

The formation and propagation of dust-acoustic (DA) solitary and rogue waves are studied in a non-relativistic degenerate Thomas-Fermi thermal dusty plasma incorporating transverse velocity perturbation effects. The electrons and ions are described by the Thomas-Fermi density distributions, whereas the dust grains are taken as dynamic and classical. By using the reductive perturbation technique, the cylindrical Kadomtsev-Petviashvili (CKP) equation is derived, which is then transformed into a Korteweg-deVries (KdV) equation by using appropriate variable transformations. The latter admits a solitary wave solution. However, when the carrier waves frequency is much smaller than the dust plasma frequency, the DA waves evolve into the nonlinear modulation instability, generating modulated wave packets in the form of Rogue waves. For the study of DA-rogue waves, the KdV equation is transformed into a self-focusing nonlinear Schrödinger equation. The variation of dust temperature and the electron density affects the nonlinearity and dispersion coefficients which suppress the amplitudes of the DA solitary and rogue waves. The present results aim to describe the nonlinear electrostatic excitations in astrophysical degenerate dense plasma.

1 Introduction

Multicomponent dusty plasma has been appeared as a potential subfield of “plasma physics” since the last three decades. It has myriad existence in space and astrophysical bodies, such as cometary tails, asteroid zone, planetary rings, interstellar medium, in lower part of the earth’s ionosphere and in magnetosphere (Horanyi and Mendis 1985; Goertz 1989; Bouchule 1999; Verheest 1996, 2000; Mendis and Rosenberg 1994). In addition, dusty plasma has numerous applications in laboratory, e.g., processing plasmas, Tokamaks, etc.

The study of dusty plasma begins when Rao, Shukla and Yu (Rao et al. 1990) theoretically predicted the existence of dust-acoustic (DA) waves and was experimentally confirmed later (Barkan et al. 1995; Pieper and Goree 1996; Prabhuram and Goree 1996). Since then numerous investigations have been appeared in dusty plasma for different type of waves, for instance, the formation of coherent nonlinear structures, the wave instabilities, etc. (Shukla and Mamun 2002; Fortov and Morfill 2009; Shukla and Eliasson 2009). The experimental investigations have confirmed that the linear and nonlinear properties of plasma depend on the velocity distribution functions of the plasma particles. Moreover, the contamination due to highly charged submicron or micron sized dust-grains alters the properties of normal electron-ion plasma and new eigen modes of oscillations can be studied in plasmas, e.g., dust acoustic mode (Rao et al. 1990), dust ion-acoustic mode (Shukla and Silin 1992), dust lower-hybrid mode (Shukla and Rahman 1998), dust drift-mode (Shukla et al. 1991), Shukla-Varma mode (Shukla and Varma 1993), etc.

In astronomical environments matter exists in extremely dense conditions and the objects, such as, white dwarf, neutron stars, and magnetars, are the few cases of high density degenerate matter. As the thermonuclear burning in these objects are ceased, there must be an opposing pressure to prevent these stars from collapse, therefore this pressure has an origin other than temperature. The only possibility for this pressure which counter-balance the gravitational pull in these objects, is the fermionic degeneracy pressure, arising due to degenerate fermionic kinetic energy and particles interactions (Goldberg and Scadron 1985). The electron number density in these objects could be of the order 10³⁰–10³⁵ cm⁻³ or even more and therefore the de-Broglie wavelength becomes equal to (or greater than) the inter-particle spacing $d_{0} = n_{e0}^{- 1/3}$ (Abdelsalam et al. 2012). Keeping in view the above-mentioned argument, the electron and ion fluids can be assumed as Thomas-Fermi fluids in astrophysical plasmas.

The most puzzling phenomena occurring at the sea in deep waters is the generation of freak waves or rogue waves, arising usually from a relatively calm sea (Müller et al. 2005; Kharif and Pelinovsky 2003; Kharif et al. 2009; Garrett and Gemmrich 2009). Modulational instability can be assumed to be an efficient mechanism for the energy localization associating with the rogue waves in the open sea (Shukla et al. 2006; Grönlund et al. 2009). These waves unexpectedly propagate for short times and then disappear without any trace (Lawton 2001; Kharif et al. 2003). Numerous models have been proposed for investigating their unexpected emergence. Recently, many authors (Akhmediev et al. 2009a, 2009b; Ankiewicz et al. 2009; Eliasson and Shukla 2010; Benchriet et al. 2013) have investigated the properties of rogue waves in different physical environments. The research interests have been shifted from oceanic dynamical problems, towards nonlinear optics (Solli et al. 2007; Kibler et al. 2010, 2012), superfluidity (Ganshin et al. 2008), hydrodynamics (Chabchoub et al. 2011), atmospheric dynamics (Stenflo and Marklund 2010) and even econophysics (Yan 2010; Ivancevic 2010).

The manuscript is organized in the following fashion: Section 2 describes the basic governing equations for nonplanar dusty plasma. By using the reductive perturbation method, a CKP equation is obtained and transformed into a KdV equation admitting a soliton wave solution. Section 3 presents the properties of the DA rogue waves, while expressing the KdV equation in terms of nonlinear Schrodinger equation with a rational solution for rogue waves. In Sect. 4, the numerical results are discussed and summarized in Sect. 5.

2 Governing equations

We study the formation and propagation characteristics of solitary and rogue waves in an unmagnetized collisionless degenerate dusty plasma. Such plasma can be comprised of electrons, ions, and negatively charged dust grains. The electrons and ions are described by the Thomas-Fermi density distributions, whereas the dust grains are taken as classical and dynamic. The charge neutrality condition at equilibrium demands n_e0=n_i0−Z_d0n_d0, where Z_d0 is dust charging state, n_s0 is the equilibrium number density of sth species (s equals e for electrons, i for ions and d for negatively charged dust grains).

For nonlinear analysis of DA solitary/rogue waves, we consider the following set of equations in a two dimensional geometry:

$$\begin{aligned} &{\frac{\partial n_{d}}{\partial t} + \frac{1}{r} \frac{\partial}{\partial r} ( r n_{d} u_{d} ) + \frac{1}{r} \frac{\partial}{\partial\theta} ( n_{d}v_{d} ) =0} \end{aligned}$$

(1)

$$\begin{aligned} &{m_{d} n_{d} \biggl( \frac{\partial u_{d}}{\partial t} + u_{d} \frac{\partial u_{d}}{\partial r} + \frac{v_{d}}{r} \frac{\partial u_{d}}{\partial\theta} - \frac{v_{d}^{2}}{r} \biggr)} \\ &{\quad {}= Z_{d0} n_{d} e \frac{\partial \phi }{\partial r} - \frac{2 k_{B} T_{d} n_{d}}{n_{d0}} \frac{\partial n_{d}}{\partial r},} \end{aligned}$$

(2)

$$\begin{aligned} &{m_{d} n_{d} \biggl( \frac{\partial v_{d}}{\partial t} + u_{d} \frac{\partial v_{d}}{\partial r} + \frac{v_{d}}{r} \frac{\partial v_{d}}{\partial\theta} + \frac{v_{d} u_{d}}{r} \biggr)} \\ &{\quad {}= \frac{Z_{d0}n_{d}}{r} e \frac{\partial \phi }{\partial\theta} - \frac{2 k_{B} T_{d}n_{d}}{n_{d0}} \frac{\partial n_{d}}{r\partial\theta},} \end{aligned}$$

(3)

$$\begin{aligned} &{\frac{1}{r} \frac{\partial}{\partial r} \biggl( r \frac{\partial \phi }{\partial r} \biggr) + \frac{1}{r^{2}} \frac{\partial^{2} \phi }{\partial\theta^{2}} =4 \pi e ( n_{e} - n_{i} + Z_{d0} n_{d} ),} \end{aligned}$$

(4)

$$\begin{aligned} &{n_{e} = n_{e0} \biggl( 1+ \frac{e \phi }{\epsilon_{\mathit{Fe}}} \biggr)^{3/2},} \end{aligned}$$

(5)

and

$$ n_{i} = n_{i0} \biggl( 1- \frac{e \phi }{\epsilon_{\mathit{Fi}}} \biggr)^{3/2}, $$

(6)

where the electron and ion densities are assumed to follow the Thomas-Fermi distributions (Dubinov and Dubinova 2007) and their corresponding expressions (5) and (6) can be derived from the electron and ion momentum equations under the assumption that they are inertialess. In the above expressions, n _s  represents the number density, u _d and v _d are the radial and angular velocity components of the dust fluid, ϕ is the electrostatic potential, m _d is the dust mass, e is the electronic charge, and ϵ _Fj (=2k _B T _Fj ) is the Fermi energy, k _B  is the Boltzmann constant and T _Fj is the Fermi temperature of the species (j equals e for electrons and i for ions).

Normalizing Eqs. (1)–(6), we obtain

$$\begin{aligned} &{\frac{\partial \overline{n}_{d}}{\partial \overline{t}} + \frac{1}{\overline{r}} \frac{\partial}{\partial \overline{r}} ( \overline{r}\overline{n}_{d} \overline{u}_{d} ) + \frac{1}{\overline{r}} \frac{\partial}{\partial\theta} ( \overline{n}_{d} \overline{v}_{d} ) =0,} \end{aligned}$$

(7)

$$\begin{aligned} &{\frac{\partial \overline{u}_{d}}{\partial\overline{t}} + \overline{u}_{d} \frac{\partial \overline{u}_{d}}{\partial \overline{r}} + \frac{\overline{v}_{d}}{\overline{r}} \frac{\partial \overline{u}_{d}}{\partial\theta} - \frac{\overline{v}_{d}^{2}}{\overline{r}} = \frac{\partial \overline{\phi }}{\partial \overline{r}} - \sigma_{d} \frac{\partial \overline{n}_{d}}{ \partial \overline{r}},} \end{aligned}$$

(8)

$$\begin{aligned} &{\frac{\partial \overline{v}_{d}}{\partial \overline{t}} + \overline{u}_{d} \frac{\partial \overline{v}_{d}}{\partial \overline{r}} + \frac{\overline{v}_{d}}{\overline{r}} \frac{\partial \overline{v}_{d}}{\partial\theta} + \frac{\overline{v}_{d} \overline{u}_{d}}{\overline{r}} = \frac{1}{ \overline{r}} \frac{\partial \overline{\phi }}{\partial\theta} - \frac{\sigma_{d}}{\overline{r}} \frac{\partial \overline{n}_{d}}{\partial\theta},} \end{aligned}$$

(9)

$$\begin{aligned} &{\frac{1}{\overline{r}} \frac{\partial}{\partial \overline{r}} \biggl( \overline{r} \frac{\partial \overline{\phi }}{\partial \overline{r}} \biggr) + \frac{1}{ \overline{r}^{2}} \frac{\partial^{2} \overline{\phi }}{ \partial \theta^{2}} = \overline{n}_{e} \mu_{e} - \overline{n}_{i} \mu_{i} + \overline{n}_{d},} \end{aligned}$$

(10)

$$\begin{aligned} &{\overline{n}_{e} = ( 1+ \sigma_{i} \overline{ \phi } )^{3/2},} \end{aligned}$$

(11)

and

$$ \overline{n}_{i} = ( 1 - \overline{\phi } )^{3/2} $$

(12)

The bars over the dependent and independent variables in the above equations imply that they are in a dimensionless form. The variables are normalized as $\overline{n}_{d} = n_{d} / n_{d0}$, $\overline{u}_{d} = u_{d} / c_{d}$, $\overline{\phi }=e \phi / 2 k_{B} T_{\mathit{Fi}}$, $\overline{t} =t\omega_{pd}$ and $\overline{r} = r/ \lambda_{0}$, where C _d =(2Z_d0k _B T _Fi /m _d )^1/2, $\omega_{pd} = ( 4 \pi e^{2} Z_{d 0}^{2} n_{d0} / m_{d} )^{1/2}$ and λ₀=(2k _B T _Fi /4πZ_d0e² n_d0)^1/2, are the characteristic dust acoustic speed, the dust plasma frequency and the characteristic length, respectively. We have also defined the density and temperature ratios as μ _e =n_e0/n_d0Z_d0, μ _i =n_i0/n_d0Z_d0 and σ _i =T _Fi /T _Fe , σ _d =T _d /Z_d0T _Fi , respectively, and T _d is the dust temperature.

One can relate the density ratios through the quasi-neutrality condition of dusty plasma at equilibrium as

$$\mu_{i} = \mu_{e} +1, $$

where μ _e describes the electron concentration in a dusty plasma so that μ _e >0, when μ _i >1. The inverse of μ _e is called the Havness Parameter $(h = \frac{n_{d0} Z_{d0}}{ n_{e0}})$ which characterizes the dust concentration. To study small amplitude DA waves in Thomas-Fermi dusty plasma, we use the reductive perturbation method to obtain a CKP equation. For this purpose, the independent variables are stretched (Xue 2003; Mushtaq 2007) in the following manner:

$$R= \epsilon^{1/2} (r - \lambda t),\qquad \varTheta = \epsilon^{- 1/2} \theta\quad \mbox{and}\quad T= \epsilon^{3/2} t, $$

where λ is the phase speed of the DA waves and will be determined later. The dependent variables can be expended as

$$\begin{aligned} &{n_{e} = 1+ \epsilon n_{e1} + \epsilon^{2} n_{e2} +\cdots,} \\ &{n_{i} = 1+ \epsilon n_{i1} + \epsilon^{2} n_{i2} +\cdots,} \\ &{\begin{aligned}[c] &n_{d} = 1+\epsilon n_{d1} + \epsilon^{2} n_{d2} +\cdots, \\ &u_{d} = 0+ \epsilon u_{d1} + \epsilon^{2} u_{d2} +\cdots, \end{aligned}} \\ &{v_{d} = 0+ \epsilon^{3/2} v_{d1} + \epsilon^{5/2} v_{d2} +\cdots,} \\ &{\phi = 0+\epsilon \phi _{1} + \epsilon^{2} \phi _{2} +\cdots,} \end{aligned}$$

(13)

where ϵ is a small parameter (ϵ≪1) involving the amplitude of the wave, and the bar on the variables is dropped for simplicity. Substituting the stretched co-ordinates and Eqs. (13) into Eqs. (7)–(12) and collecting the lowest orders of ϵ, we obtain:

$$\begin{aligned} &{n_{d1} = \frac{\phi _{1}}{\sigma_{d} - \lambda^{2}},\qquad u_{d1} = \frac{\lambda \phi _{1}}{\sigma_{d} - \lambda^{2}},} \\ &{\frac{\partial v_{d1}}{\partial R} = \frac{1}{T ( \sigma_{d} - \lambda^{2} )} \frac{\partial \phi _{1}}{\partial \varTheta}} \end{aligned}$$

and

$$ \lambda = \biggl( \sigma_{d} + \frac{1}{d} \biggr)^{1/2} $$

(14)

where $d = \frac{3}{2} (\mu_{e} ( \sigma_{i} + 1 )+ 1 )$, and in terms of Havness parameter h it can be expressed as $d = \frac{3}{2} ( \frac{\sigma_{i} + 1}{h} + 1 )$. Physically $d = \frac{3}{ 2} ( \mu_{e} ( \sigma_{i} + 1 )+ 1 )/\lambda_{0}^{2}$ is the quantum analogue of the Debye charge screening radius (square). Equation (14) represents the phase speed of DA solitary waves in a Thomas-Fermi dusty plasma.

In the limiting case, when T _d =0 which implies that σ _d =0 and the phase speed becomes as $\lambda = ( d )^{- 1/2} = ( \frac{3}{2} ( \mu _{e} ( \sigma_{i} + 1 )+ 1 ) )^{- 1/2}$, which is in agreement with Abdelsalam et al. (2012). The next order equations in ϵ can be expressed as

$$\begin{aligned} &{\lambda \frac{\partial n_{d1}}{\partial T} - \lambda^{2} \frac{\partial n_{d2}}{\partial R} + \lambda \frac{\partial u_{d2}}{\partial R} + \lambda \frac{\partial ( n_{d1} u_{d1} )}{\partial R}} \\ &{ \quad {} + \frac{u_{d1}}{ T} + \frac{1}{T} \frac{\partial v_{d1}}{\partial \varTheta} = 0} \end{aligned}$$

(15)

$$\begin{aligned} &{\frac{\partial u_{d1}}{\partial T} - \lambda \frac{\partial u_{d2}}{\partial R} + u_{d1} \frac{\partial u_{d1}}{\partial R} + \sigma_{d} \frac{\partial n_{d2}}{\partial R} - \frac{\partial \phi _{2}}{\partial R} = 0} \end{aligned}$$

(16)

and

$$ \frac{ \partial^{2}\phi _{1}}{\partial R^{2}} = \frac{3}{8} \bigl(\mu _{e} \bigl(\sigma_{i}^{2} - 1 \bigr) - 1 \bigr) \phi _{1}^{2} + \phi _{2} d + n_{d2} $$

(17)

Simplifying Eqs. (15)–(17) and using Eq. (14) the CKP equation turns out to be

$$ \begin{aligned}[b] &\frac{\partial}{\partial R} \biggl(\frac{\partial \phi _{1}}{\partial T} + \frac{\phi _{1}}{2T} + A \phi _{1} \frac{\partial \phi _{1}}{\partial R} + B\frac{\partial ^{3}\phi _{1}}{\partial R^{3}} \biggr)\\ &\quad {} + \frac{1}{2 \lambda T^{2}} \frac{\partial ^{2}\phi _{1}}{\partial \varTheta^{2}} = 0 \end{aligned} $$

(18)

where

$$ \begin{aligned}[c] &A = - \biggl( \frac{\frac{3}{2} \lambda ^{2}}{\lambda (\lambda ^{2} - \sigma_{d} )} + \frac{\frac{3}{8} ( \mu _{e} (\sigma_{i}^{2} - 1 ) - 1 ) ( \lambda ^{2} - \sigma_{d} )^{2}}{\lambda } \biggr)\\ &\mbox{and}\quad B = \frac{(\lambda ^{2} - \sigma_{d} )^{2}}{2\lambda} \end{aligned} $$

(19)

are the nonlinearity and dispersion coefficients, respectively. For assuming the limit T _d =0, which implies that σ _d =0. As a consequence, the nonlinearity and dispersion coefficients reduce to $A = - \frac{1}{\lambda } ( \frac{3}{2} + \frac{3}{8} \lambda^{4} ( \mu_{e} ( \sigma_{i}^{2} -1 ) - 1 ) )$ and $B = \frac{\lambda ^{3}}{2}$. It is important to note that if the temporal stretching coordinate of the form T=ϵ^3/2 v _s t is used, instead of T=ϵ^3/2 t, then our Eq. (19) exactly coincides with the result of Abdelsalam et al. (2012). Thus, the difference of 1/λ can be removed by taking into account the dimensional temporal coordinate as given in Abdelsalam et al. (2012). See that for neglecting the angular dependence, the cylindrical KP equation (18) also reduces to a usual cylindrical KdV equation. The latter is usually solved numerically as it is difficult to solve analytically. However, the exact solution of the cylindrical KP equation can be obtained by using a suitable variables transformation (Xue 2003; Mushtaq 2007; Ali et al. 2008). In Eq. (18), the terms (1/2T)ϕ₁ and (1/2λT²)∂² ϕ₁/∂Θ² can be canceled out by assuming the potential perturbations (Xue 2003; Mushtaq 2007; Ali et al. 2008) as:

$$ \phi _{1} = \phi _{1} ( \chi, \overline{T} ),\quad \mbox{with } \chi = R - \frac{\lambda}{2} \varTheta^{2} T, \mbox{ and } \overline{T} = T. $$

(20)

The above transformations implies that

$$ \begin{aligned}[c] &\frac{\partial}{\partial R} \rightarrow \frac{\partial}{ \partial\chi},\qquad \frac{\partial}{\partial\varTheta} \rightarrow {-}\lambda\varTheta T \frac{\partial}{\partial\chi}\quad \mbox{and}\\ &\frac{\partial}{\partial T} \rightarrow \frac{\partial}{\partial \overline{T}} - \frac{\lambda}{2} \varTheta^{2} \frac{\partial}{ \partial\chi} \end{aligned} $$

(21)

Substituting Eqs. (19) and (20) into Eq. (18), we obtain a standard KdV equation,

$$ \frac{\partial \phi _{1}}{\partial T} +A \varphi _{1} \frac{\partial \phi _{1}}{ \partial\chi} +B \frac{\partial^{3} \phi _{1}}{\partial \chi^{3}} =0. $$

(22)

Here the bar has been dropped out for simplicity. Introducing a single moving variable η=χ−u₀T, where u₀ is the soliton speed. A steady state soliton solution of the above KdV equation (21) is obtained under the boundary conditions, ϕ₁→0 and $\frac{\partial \phi _{1}}{\partial\chi} \rightarrow 0$, at χ=±∞.

The soliton solution of KdV equation is as:

$$ \phi _{1} = \phi _{0} \operatorname{Sech}^{2} \biggl( \frac{\eta}{ w} \biggr) $$

(23)

where

$$ \phi _{0} = \frac{3u_{0}}{A}\quad \mbox{and}\quad w = \biggl(\frac{4B}{u_{0}} \biggr)^{1/2} $$

(24)

are the maximum amplitude and width of the DA soliton. The moving co-ordinate can be expressed as:

$$\begin{aligned} \eta =& R - \biggl( u_{0} + \frac{\lambda}{2} \varTheta^{2} \biggr) T \\ \equiv& \epsilon^{1/2} \biggl[r - \biggl( \lambda + \epsilon u_{0} + \frac{\lambda}{2} \theta^{2} \biggr) t \biggr]. \end{aligned}$$

(25)

3 Generation of lowest order rogue wave

When the frequency of the carrier waves is much smaller than the dust plasma frequency, a modulation instability gives rise to rogue waves. To investigate modulated packets of rogue waves by self-focusing NLS equation, we use the following expansions (Shimizu and Ichikawa 1972; El-Labany 1995; El-Labany et al. 2012) for dependent variable into Eq. (21)

$$ \phi ( \chi,T ) = \sum_{n =1}^{\infty} \epsilon^{n} \sum_{l = -\infty}^{\infty} \varphi _{l}^{ ( n )} ( \xi, \tau ) \exp \bigl[i l ( k \chi-\omega T )\bigr] $$

(26)

where k is the carrier wave number and ω is the angular frequency. We also employ the following variables transformations:

$$ \xi = \epsilon ( \chi-\varLambda T )\quad \mbox{and}\quad \tau = \epsilon^{2}T, $$

(27)

where Λ is the group velocity, which will be determined later. $\varphi _{l}^{ ( n )}$ signifies the lth harmonic of nth order approximation. It is a real and therefore equals to its complex conjugate i.e. $\varphi _{- l}^{ ( n )}= \varphi _{l}^{( n )^{*}}$.

The above variables transformations thus implies that

$$ \begin{aligned}[c] &\frac{\partial}{\partial\chi} \rightarrow {-}\frac{\partial}{\partial\chi} + \epsilon \frac{\partial}{\partial\xi}\quad \mbox{and}\\ &\frac{\partial}{\partial T} \rightarrow \frac{\partial}{\partial T} - \epsilon \varLambda \frac{\partial}{\partial\xi} + \epsilon^{2} \frac{\partial}{\partial\tau} \end{aligned} $$

(28)

Using Eqs. (26)–(28) into Eq. (22), we obtain

$$\begin{aligned} &{-il\omega \varphi _{l}^{ ( n )} - \varLambda \frac{\partial \varphi _{l}^{ ( n - 1 )}}{\partial\xi} + \frac{\partial \varphi _{l}^{ ( n - 2 )}}{\partial\tau}} \\ &{\quad {} + A\sum_{n' = 1}^{\infty} \sum _{i' = -n}^{n} \biggl[ -i ( l - l' ) k \varphi _{l - l'}^{ ( n - n' )} \varphi _{l'}^{( n' )}} \\ &{\quad {} + \varphi _{l'}^{(n')} \frac{\partial \varphi _{l - l'}^{( n - n'' - 1 )}}{\partial\xi} \biggr]} \\ &{\quad {} + B \biggl( i l^{3} k^{3} \varphi _{l}^{ ( n )} - 3 l^{2} k^{2} \frac{\partial \varphi _{l}^{ ( n - 1 )}}{\partial\xi}} \\ &{\quad {} + 3 ilk \frac{\partial ^{2} \varphi _{l}^{ ( n - 2 )}}{\partial \xi^{2}} + \frac{\partial ^{3} \varphi _{l}^{ ( n - 3 )}}{\partial \xi^{3}} \biggr) = 0} \end{aligned}$$

(29)

For taking l=1 in the first-order approximation (n=1), the dispersion relation gives

$$ \omega = Bk^{3}. $$

(30)

For second-order approximation (n=2) and taking the first harmonic l=1, we obtain

$$ \varLambda = - 3Bk^{2}, $$

(31)

which is the group velocity. For second harmonic l=2, in the second order approximation, Eq. (24) implies that

$$ \varphi _{2}^{( 2 )} = \frac{A}{6B k^{2}} \varphi _{1}^{( 1 )2}, $$

(32)

whereas for the zeroth harmonic (l=0), we get

$$ \varphi _{0}^{( 2 )} = \biggl(\frac{A}{\varLambda} \biggr) \bigl\vert \varphi _{1}^{( 1 )}\bigr\vert ^{2} $$

(33)

Proceeding to the third-order approximation (n=3) and solving for the first harmonic equations (l=1), an explicit compatibility condition will be found, from which one can easily obtain the NLS equation

$$ i \frac{\partial\varPsi}{\partial\tau} + \frac{P}{2} \frac{\partial^{2} \varPsi}{\partial \zeta^{2}}+Q\vert \varPsi \vert ^{2} \varPsi = 0 $$

(34)

where we have replaced $\varphi _{1}^{(1)}$ by Ψ. The dispersion and nonlinearity coefficients P and Q can be defined as

$$ P = 6Bk $$

(35)

and

$$ Q =A^{2} /6 Bk $$

(36)

respectively. The lowest order rational solution of NLS equation for DA rogue waves can be obtained (Akhmediev et al. 2009c; El-Labany et al. 2011), as

$$ \varPsi = \frac{1}{\sqrt{Q}} \biggl( \frac{4(1+2i\tau)}{1+4 \tau^{2} + \frac{4}{P} \xi^{2}} -1 \biggr) \exp [i \tau] $$

(37)

The above solution for rogue waves is derived under the assumption that frequency of carrier waves is much smaller than the dust plasma frequency. The solution lies on a nonzero background of plasma and is localized in τ and ξ coordinates. The solution for rogue waves concentrates a substantial amount of energy into a small region of space. It represent a modulated envelop of DA waves, which has a wavelength smaller than the central region of envelope.

4 Results & discussions

In this section, we numerically study the DA solitary and rogue waves in a 2D cylindrical, degenerate dense dusty plasma. Such plasma may have its relevance in white dwarfs, magnetars, neutron stars, etc. For numerical illustration, we have chosen some typical numerical values (Abdelsalam et al. 2012; Ren et al. 2009, and Hippel et al. 2012) for the degenerate dense plasma, as n_e0∼2×10²⁷ cm⁻³, n_d0∼1.9×10²¹ cm⁻³, Z_d0∼10³, T _Fe ∼6.71×10⁷ K, T _Fi ∼2946 K and T _d =900 K. To determine the electron-ion Fermi Temperatures, we use the formulas, T _Fe =(ħ²/2m _e k _B )(3π² n_e0)^2/3, and T _Fi =(ħ²/2m _i k _B )(3π² n_i0)^2/3, respectively. For a degenerate dense plasma, one can express the ion-to-electron Fermi temperature ratio in terms of Havness parameter, as: σ _i =(m _e /m _i )(n_i0/n_e0)^2/3≡(m _e /m _i )(1+h)^2/3. This expression reduces to σ _i ≅(m _e /m _i )(1+2h/3), when h is small. However, for large value of h, it approaches to σ≅(m _e /m _i )h^2/3. The charge-neutrality condition at equilibrium can be expressed in terms of Havness parameter h, as μ _i =1+1/h. We are interested to examine the effects of the equilibrium number density (n_e0) and dust grain temperature (T _d ) on the profiles of DA solitary and rogue waves.

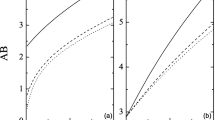
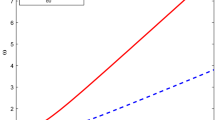
The variation of electron density affects the Debye radius and as a result the strength of the space charge electric field is also affected. Therefore, the phase speed of the DA waves decreases with increasing the electron number density as depicted in Fig. 1 by the dashed curve at T _d =0 K. However, the change in dust grain temperature (T _d =900 K) leads to enhance the magnitude of the phase speed for the given range of electron density [see solid curve in Fig. 1]. Since the nonlinearity and dispersion coefficients A and B involve the dependence of phase speed (λ) via Eq. (19), therefore, the DA wave propagation is strongly influenced by the electron density and the phase speed, resulting in the modification of DA wave profiles. The enhancement of n_e0 and T _d leads to increase (decrease) the coefficient A (B), showing the existence of negative soliton pulses for A<0 and B>0 [see Fig. 2]. We have also noticed from Fig. 3 that the soliton amplitude (ϕ₀) and width (w) decreases as the number density increases. Figure 4 represents the effects of the dust temperature on the excitations of DA wave. It is examined that a reduction in amplitude and width occurs for varying the dust temperature T _d (=0,900) K.

Fig. 1

The phase speed of DA waves λ is plotted against the equilibrium number density n_e0 at T _d =0 K (dashed curve) and T _d =900 K (solid curve)

Fig. 2

The nonlinearity and dispersion coefficients A and B are plotted against the equilibrium number density n_e0 for T _d =0 K (dashed curve) and T _d =900 K (solid curve)

Fig. 3

The amplitude ϕ₀ and width w of DA solitary waves are depicted versus the equilibrium number density n_e0 at u₀=0.01 and T _d =900 K

Fig. 4

The electrostatic potential ϕ₁ is plotted versus η at n_e0=2×10²⁷ cm⁻³, T _d =900 K (solid curve) and T _d =0 K (dashed curve). The effect of dust temperature is to reduce both the amplitude and width of DA solitary wave

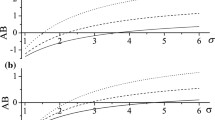
The electrostatic potential (ϕ₁) [as given in Eq. (23)] is plotted against η for different values of Havness parameter [viz., h=0.00047 (Top curve), h=0.00063 (Middle curve), and h=0.00095 (Bottom curve)] with fixed soliton speed u₀=0.01 and dust temperature T _d =900 K, as shown in Fig. 5. It is observed that for large dust concentration (h), we have taller and wider solitons corresponding to low electron concentration. Thus, in such plasmas the balance between the dispersion and nonlinearity gives rise to solitary waves with enhanced amplitude and width. Figure 6 displays the potential excitation associated with DA solitary waves as a function of radial distance (r) and azimuthal angle (θ) for t=1, u₀=0.01, ϵ=0.06 and T _d =900 K. It is found that the transverse perturbation θ makes the solitary pulse to deviate in the radial direction. The radial deviation of solitary pulse increases as the value of transverse perturbation increases [see Fig. 7]. This behavior of the solitary wave arises due to cylindrical geometry and cannot be noticed in the one-dimensional Cartesian geometry. In Fig. 8, the absolute rational solution (Ψ) [as given in Eq. (37)] of NLS equation for DA rogue waves is plotted against ξ and τ with fixed electron density n_e0=2×10²⁷ cm⁻³ and dust temperature T _d =900 K. See that the amplitude of DA rogue wave reaches to its maximum value at ξ=0 and then it decays on both sides for ξ<0 and ξ>0. Figure 9 depicts the dispersion and nonlinearity co-efficients P and Q of self-focusing NLS equation against the number density n_e0. Since these co-efficients contain A and B [as given in Eqs. (35)–(36)], therefore, the variation of n_e0 affects significantly P and Q. The increase in n_e0 leads to decrease P and increase Q. As a consequence, the amplitude of DA rogue wave drops for increasing the electron density as can be seen from Fig. 10. Furthermore, for finite value of dust temperature T _d =900 K, the coefficients P decreases and Q increases for the given range of number densities (as is described by solid curve in Fig. 9). So, the temperature ratio (σ _d ) modifies the amplitude of the DA rogue waves as in Fig. 10. Physically, the coefficients P and Q result in piling up the wave energy locally in plasmas and therefore the amplitude of rogue wave grows (Chen 1983). The absolute of rogue wave solution is plotted against ξ in Fig. 11 for different times (τ>0). We have shown that as the time goes on, the amplitudes decay, and the width increases.

Fig. 5

The profiles of DA solitary waves ϕ₁ are plotted versus η for different values of h at T _d =900 K

Fig. 6

The electrostatic potential perturbation ϕ₁ is plotted versus the co-ordinates r and θ, for n_e0=2×10²⁷ cm⁻³, t=1, u₀=0.01, ϵ=0.06 and T _d =900 K

Fig. 7

The electrostatic potential perturbation ϕ₁ is plotted versus r for n_e0=2×10²⁷ cm⁻³, t=1, u₀=0.01, ϵ=0.06 and T _d =900 K for different values of θ

Fig. 8

The absolute of rogue wave profile Ψ versus ξ and τ is depicted for the electron number density n_e0=2×10²⁷ cm⁻³, dust temperature T _d =900 K and wave vector k=0.9

Fig. 9

The nonlinearity and dispersion coefficients, Q and P (at T _d =0 K, dashed curve and T _d =900 K, solid curve) of NLSE are plotted against the number density n_e0

Fig. 10

The variation in absolute amplitude of rogue wave Ψ with respect to σ _d and n_e0

Fig. 11

The absolute of rogue wave are plotted versus ξ(−0.01,0.01) at n_e0=2×10²⁷ cm⁻³, T _d =900 K and k=0.9 for different times

5 Summary

To summarize, we have considered dense degenerate dusty plasma, whose constituents are the electrons, ions and negatively charged dust grains. By using the fluid model analysis, the nonlinear wave evolutions and propagation characteristics of DA solitary and rogue waves are studied. The electrons and ions are assumed to follow the Thomas-Fermi density distributions, whereas dust-grains are taken as classical and dynamic. With the aid of reductive perturbation technique, a CKP equation is derived, which is then reduced to a KdV equation by using suitable variable transformations. For DA rogue waves, a self-focused NLS equation is deduced admitting a rational solution. Various effects are examined on the wave characteristics by variation of different plasma parameters. It is shown that the higher values of electron number density lead to reduce the amplitude of the DA solitary and rogue waves. The inclusion of dust temperature in the fluid model affects significantly the amplitudes of the DA solitary and rogue waves. The present results might be helpful to understand the DA solitary and rogue waves in astrophysical environments, where dust grains are present.