Multi-dimensional instability of dust acoustic waves in magnetized quantum plasmas by two-fluid quantum hydrodynamics model

Abstract

Study on dust acoustic waves (DAWs) described by two-fluid quantum hydrodynamics model (QHM) in a magnetized dusty plasmas composed of negatively and positively charged mobile dust, intertialess quantum electrons as well as ions is presented. The Zakharov-Kuznetsov (ZK) equation is derived via reductive perturbation technique. The solitary wave solution of ZK equation is given and the numerical analysis of the solution with parameters in dust crystals is performed to study the properties of the DAWs with positive and negative dust. The multi-dimensional instability of these solitary waves is investigated via small-k perturbation method. The instability criterion and growth rate relying on obliqueness, the density ratio between ions and dust, the dust cyclotron frequency, the Fermi temperatures ratio between electrons to ions, quantum diffraction parameter and the ratio between charge-to-mass ratio of positive dust and that of negative dust are discussed for compressive solitary waves (CSWs) and rarefactive solitary waves (RSWs). The implications of these results to the interior of white dwarf stars and magnetars have been briefly discussed.

1 Introduction

In recent years, quantum plasma has attracted a lot of attention because of its important applications [1] for scientific and technological areas, e.g., dense astrophysical environments [2], solid-state physics, laser-produced plasmas [3], micro- and nano-electronic systems, as well as ultracold plasmas [4]. In quantum plasmas there are many topics attracting considerable attention [5], such as, the modified quantum Zakharov equations [6], the quantum ion-acoustic waves [7], the quantum multi-stream instabilities [8], the quantum corrected electron holes [9], the quantum dust modes [10], and so on. There are three noted mathematical methods, such as Wigner-Poison, Schrodinger-Poison and quantum hydrodynamics, diffusely applied in quantum plasmas. Without challenging the complexities of the first two methods, the quantum hydrodynamics model (QHD) is a reduced model directly researching the collective dynamics. Taking advantage of the standard definition for averaging macroscopic quantities, the first two methods can result in the same equations known as QHD [11].

The effects of quantum diffraction and statistic on the amplitude and width of the dust acoustic waves (DAWs) were investigated both analytically and numerically by QHM for a three-species quantum plasma [12]. The study of DAWs with weakly transverse perturbations in cylindrical geometry was carried out by the QHM in an ultracold quantum dusty plasma consisting of inertialess ions and electrons, and inertial negatively charged dust [13]. For the dust lower hybrid waves, the dispersion relation was derived by using the QHM in a quantum dusty plasma with a uniform external magnetic field [14]. The quantum DAWs with transverse perturbations in nonplanar geometry and the influence of quantum effects on the nonlinear structures were studied by the two-dimensional QHM [15]. In a four component quantum dusty plasma consisting of both positive and negative ions, electrons, and immobile charged dust particles, Misra et al. studied the structure of ion-acoustic shocks, considering the dispersion due to the charge separation, the dissipation caused by kinematic viscosity and the quantum tunneling related with the Bohm potential [16]. By using a two-fluid QHM, ion-acoustic soliton was investigated in an electron-dust-ion plasma, where electrons and ions are assumed to obey quantum mechanical behaviours in dust background, considering the higher-order corrections [17]. The head-on collision of the two ion acoustic solitons was presented, and the trajectories and the phase shifts were analyzed in quantum pair-ion dusty plasma [18]. Based on the QHM, the feature of nonplanar quantum ion-acoustic solitary waves was studied by the modified Gardner equation in an unmagnetized quantum plasma composed of Fermi electrons with quantum effects, inertial ions and negatively charged immobile dust grains [19]. Due to the external magnetic field and oblique collision, the trajectory and the phase shift of DAWs structures were modified in a three-dimensional magnetized qutuman dusty plasma [20]. The influences of quantum effect on the excitation of two instabilities as the results of the free streaming of ion/dust particles were investigated by employing a QHM in uniformly magnetized dusty plasmas [21]. It is found that as the streaming velocity of ion and the electrons concentration increase, the instability raises because of more energetic species having a high speed in the dense plasma particle system.

Recently, the multi-dimensional instability (MDI) of solitary waves by small-k perturbation method in plasmas has been paid more attention. The MDI of electrostatic solitary waves obliquely propagating was investigated theoretically in magnetized, hot and non-thermal dusty plasmas containing Boltzmann electrons, non-thermal ions and negatively charged hot dust fluid [22]. The MDI of dust ion-acoustic solitary waves (DIASWs) was presented in magnetized hot adiabatic dusty plasmas composed of adiabatic inertial ions, adiabatic inertialess electrons and negatively charged static dust [23]. Shalaby et al. showed the MDI of DIASWs obliquely propagating in a magnetized hot adiabatic dusty plasma composed of hot adiabatic inertialess electrons and inertial ions, and charged static dust particles (positive or negative), and it is obvious that the instability criterion and growth rate rely on obliqueness, external magnetic field, the number density of charged dust particles, ion-dust and ion-neutral collisions [24]. The MDI of DIASWs described by modified ZK equation was presented in a magnetized dusty plasma whose composition is hot adiabatic inertial ions fluid, two different kinds of nonisothermal electrons and immobile negatively charged dust grains [25]. The MDI of DIASWs described by ZK equation was analyzed in a magnetized dusty plasma consisting of heavy negative ions and variable-charge stationary dust grains [26]. The MDI of DAWs described by modified ZK equation, and effect of nonthermal ions and dust charge fluctuation on the growth rate and critical point were presented in magnetized dusty plasma, and it is noted that the magnitude and direction of external magnetic field where the instability occurs were extremely influenced by the rate of dust charge variation and nonthermality of ions [27].

However, the multi-dimensional instability (MDI) of DAWs described by the two-fluid QHM has not been investigated by small-k perturbation method in a magnetized dusty plasma composed of inertial negatively and positively dust, inertialess quantum electrons as well as ions. In this paper, we aim at solving this question. First of all, we get a ZK equation for such dusty plasma by making use of the two-fluid QHM and the reductive perturbation technique (RPT). The multi-dimensional instability of DAWs is researched by the small-k perturbation method. The instability criterion and growth rate which have some connection with obliqueness, the density ratio of ions to dust, the dust cyclotron frequency, the ratio of charge-to-mass ratio of positive dust to that of negative dust, the Fermi temperatures ratio between electrons and ions as well as quantum diffraction parameter are discussed. The paper is organized as follows. In Sects. 2 and 3, the basic equations and solitary wave of ZK equation are given. The instablitily for ZK equation by small-k perturbation method is discussed in Sect. 4. Finally, the main conclusions are presented in Sect. 5.

2 Basic equations and derivation of the ZK equation

We consider a four species magnetized quantum dusty plasma consisting of negatively and positively charged mobile dust, and intertialess electrons as well as ions. The external magnetic field is in the direction of the z-axis: $\mathbf {B}=B_{0}\hat{\mathbf {z}}$ ($\hat{\mathbf {z}}$ is unit vector along the z-direction). At equilibrium, $Z_{n}n_{n0}-Z_{p}n_{p0}-n_{i0}+n_{e0}=0$, which can also be expressed as $1-\mu _{p}-\mu _{i}+\mu _{e}=0$, where $\mu _{p}=\frac{Z_{p}n_{p0}}{Z_{n}n_{n0}}$, $\mu _{i}=\frac{n_{i0}}{Z_{n}n_{n0}}$, and $\mu _{e}=\frac{n_{e0}}{Z_{n}n_{n0}}$. $n_{i0}$, $n_{e0}$, $n_{n0}$ and $n_{p0}$ are the unperturbed ion, electron, negative and positive dust number densities, respectively. $Z_{n}(Z_{p})$ represents the charge state of negative (positive) dust. The wave dynamics is governed by the following set of normalized fluid equations [28, 29]:

$$\begin{aligned}&\frac{\partial n_{n}}{\partial t}+\nabla .(n_{n}\mathbf {u}_{n})=0, \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial n_{p}}{\partial t}+\nabla .(n_{p}\mathbf {u}_{p})=0, \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial \mathbf {u}_{n}}{\partial t} + (\mathbf {u}_{n}.\nabla )\mathbf {u}_{n}=\nabla \varphi - \omega _{cd}(\mathbf {u}_{n} \times \hat{\mathbf {z}}), \end{aligned}$$

(3)

$$\begin{aligned}&\frac{\partial \mathbf {u}_{p}}{\partial t} + (\mathbf {u}_{p}.\nabla )\mathbf {u}_{p}=-\mu \nabla \varphi +\mu \omega _{cd}(\mathbf {u}_{p} \times \hat{\mathbf {z}}), \end{aligned}$$

(4)

$$\begin{aligned}&\nabla \varphi +\frac{1}{3}n_{i}^{-1/3}\nabla n_{i}-\frac{H^{2}_{i}}{2}\nabla [\frac{\nabla ^{2}\sqrt{n_{i}}}{\sqrt{n_{i}}}]=0, \end{aligned}$$

(5)

$$\begin{aligned}&\nabla \varphi -\frac{\sigma }{3}n_{e}^{-1/3}\nabla n_{e}+\frac{H^{2}_{e}}{2}\nabla [\frac{\nabla ^{2}\sqrt{n_{e}}}{\sqrt{n_{e}}}]=0, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{\partial ^{2} \varphi }{\partial x^{2}}+\frac{\partial ^{2} \varphi }{\partial y^{2}} +\frac{\partial ^{2} \varphi }{\partial z^{2}}=n_{n}+\mu _{e}n_{e}-\mu _{i}n_{i}-\mu _{p}n_{p}.\nonumber \\ \end{aligned}$$

(7)

At thermal equilibrium and zero temperature, the three-dimensional pressure for quantum Fermi gas can be written as $P_{j}=\frac{V_{Fj}^{2}m_{j}}{5n_{j0}^{2/3}}n_{j}^{5/3}$, where $j = i(e)$ for ions (electrons), Fermi thermal speed for jth particle is $V_{Fj}=\sqrt{\frac{2k_{B}T_{Fj}}{m_{j}}}$, $k_{B}T_{Fj}=\frac{\hbar ^{2}(3\pi ^{2})^{2/3}n_{j0}^{2/3}}{2m_{j}}$, where $T_{Fj}$ is the Fermi temperature of the particle, $k_{B}$ is the Boltzmann constant. The dust fluid velocity $u_{s}=u_{s}/C_{n}(s=n,p)$, the space $\nabla =\nabla /\lambda _{dn}$, time $t=t\omega _{dn}$ and potential $\varphi =e\varphi /2K_{B}T_{Fj}$, where the dust acoustic speed is $C_{n}=(Z_{n}k_{B}T_{Fi}/m_{n})^{1/2}$, the dust plasma Debye length $\lambda _{dn}=(Z_{n}k_{B}T_{Fi}/4\pi e^{2} n_{n0}Z_{n})^{1/2}$ and the period $\omega ^{-1}_{pn}=(m_{n}/4\pi e^{2}Z_{n}^{2}n_{n0})^{1/2}$. The dust cyclotron frequency $\omega _{cd}=(\frac{Z_{n}}{m_{n}}eB_{0})/\omega _{pn}$ is normalized to $\omega _{pn}$. $\sigma =\frac{T_{Fe}}{T_{Fi}}$ is the ratio of Fermi temperatures between electrons and ions and quantum diffraction parameters for ions and electrons are $H_{i(e)}=\sqrt{\frac{\hbar ^{2}\omega _{pn}^{2}Z_{n}}{m_{n}m_{i(e)}C_{n}^{4}}}$. $\mu =\frac{Z_{p}m_{n}}{Z_{n}m_{p}}$.

Integrating Equations Eqs. (5) and (6) with the boundary conditions $\varphi =0$ and $n_{i}=n_{e}=1$ at infinity, we obtain $n_{i}=(1-2\varphi +H_{i}^{2}\nabla ^{2}\frac{\sqrt{n_{i}}}{n_{i}})$ and $n_{e}=(1+\frac{2\varphi }{\sigma }+\frac{H_{e}^{2}}{\sigma }\nabla ^{2}\frac{\sqrt{n_{e}}}{n_{e}})$, which reflects the relationship between electrostatic potential and charged particles (ions and electrons) density. What needs to be noted here is that quantum diffraction parameters ($H_{i}$, $H_{e}$) reflect the quantum diffraction effects.

For the purpose of investigating the features of nonlinear quantum DAWs, we make use of the standard reductive perturbation technique in space and time coordinates as $X=\varepsilon ^{1/2}x$, $Y=\varepsilon ^{1/2}y$, $Z=\varepsilon ^{1/2}(z-V_{0}t)$ and $\tau =\varepsilon ^{3/2}t$. $V_{0}$ is the dust-acoustic phase velocity. The dependent variables are expanded as follows $n_{s}=1+\varepsilon n_{s1}+\varepsilon ^{2} n_{s2}+...$, $\varphi =\varepsilon \varphi _{1}+\varepsilon ^{2} \varphi _{2}+...$, $u_{sz}=\varepsilon u_{sz1}+\varepsilon ^{2} u_{sz2}+...$, $u_{sx}=\varepsilon ^{3/2} u_{sx1}+\varepsilon ^{2} u_{sx2}+...$, $u_{sy}=\varepsilon ^{3/2} u_{sy1}+\varepsilon ^{2} u_{sy2}+...$, where $s=n, p$. Substituting these expanded physical quantities into the normalized dynamics equations, and equating the coefficient powers of $\varepsilon$ in the lowest order, we get $n_{n1}=-\frac{1}{V_{0}^{2}}\varphi _{1}$, $n_{p1}=\frac{\mu }{V_{0}^{2}}\varphi _{1}$, $u_{nx1}=u_{px1}=-\frac{1}{\omega _{cn}}\frac{\partial \varphi _{1}}{\partial Y}$, $u_{ny1}=u_{py1}=\frac{1}{\omega _{cd}}\frac{\partial \varphi _{1}}{\partial X}$, $u_{nz1}=-\frac{1}{V_{0}}\varphi _{1}$, $u_{pz1}=\frac{\mu }{V_{0}}\varphi _{1}$ and $V_{0}=\sqrt{\frac{\sigma (1+\mu \mu _{p})}{3(\sigma \mu _{i}+\mu _{e})}}$. Taking the next higher order, we get $u_{nx2}=-\frac{V_{0}}{\omega _{cd}^{2}}\frac{\partial ^{2}\varphi _{1}}{\partial X \partial Z}$, $u_{ny2}=-\frac{V_{0}}{\omega _{cd}^{2}}\frac{\partial ^{2}\varphi _{1}}{\partial Y \partial Z}$, $u_{px2}=\frac{V_{0}}{\mu \omega _{cd}^{2}}\frac{\partial ^{2}\varphi _{1}}{\partial X \partial Z}$, $u_{py2}=\frac{V_{0}}{\mu \omega _{cd}^{2}}\frac{\partial ^{2}\varphi _{1}}{\partial Y \partial Z}$, and finally obtain the ZK equation:

$$\begin{aligned} \frac{\partial \varphi _{1}}{\partial \tau }+AB \varphi _{1} \frac{\partial \varphi _{1}}{\partial Z}+\frac{A}{2}\frac{\partial ^{3} \varphi _{1}}{\partial Z^{3}} +\frac{AD}{2}(\frac{\partial ^{3} \varphi _{1}}{\partial Z \partial X^{2}}+\frac{\partial ^{3} \varphi _{1}}{\partial Z \partial Y^{2}})=0, \end{aligned}$$

(8)

where $\,A{=}V_{0}^{3}\frac{9\mu _{i}\sigma ^{2}H_{i}^{2}\!+\!9\mu _{e}H_{e}^{2}{-}4\sigma ^{2}}{4\sigma ^{2}(\mu \mu _{p}{-}1)}$, $B{=}\frac{6\sigma V_{0}^{4}(\mu {-}\sigma \mu _{i}){+}6\sigma ^{2}(1{-}\mu ^{2}\mu _{p})}{V_{0}^{3}(9\mu _{i}\sigma ^{2}H_{i}^{2}{+}9\mu _{e}H_{e}^{2}{-}4\sigma ^{2})}$ and $D=\frac{\mu \omega _{cd}^{2}(9\mu _{i}\sigma ^{2}H_{i}^{2}+9\mu _{e}H_{e}^{2}-4\sigma ^{2})-4\sigma ^{2}}{\mu \omega _{cd}^{2}(9\mu _{i}\sigma ^{2}H_{i}^{2}+9\mu _{e}H_{e}^{2}-4\sigma ^{2})}.$

3 Solitary wave analysis

In order to investigate the feature of solitary waves, we assume that the solitary waves propagate in an angle $\theta$ direction with the Z-axis and the external magnetic field lies in the $Z-X$ plane. Firstly, through an angle $\theta$ we rotate the coordinate axes (X, Z), keeping the y-axis fixed. Then, we perform the following transformations: $\zeta =X\text {cos}\theta -Z\text {sin}\theta$, $\xi =X\text {sin}\theta +Z\text {cos}\theta$, $\eta =Y$ and $t=\tau$. The ZK equation can be written in the form

$$\begin{aligned}&\frac{\partial \varphi _{1}}{\partial t}+\theta _{1}\varphi _{1}\frac{\partial \varphi _{1}}{\partial \xi }+\theta _{2}\frac{\partial ^{3} \varphi _{1}}{\partial \xi ^{3}}+\theta _{3}\varphi _{1}\frac{\partial \varphi _{1}}{\partial \zeta }+\theta _{4}\frac{\partial ^{3} \varphi _{1}}{\partial \zeta ^{3}}\nonumber \\&+\theta _{5}\frac{\partial ^{3} \varphi _{1}}{\partial \xi ^{2} \partial \zeta }+\theta _{6} \frac{\partial ^{3} \varphi _{1}}{\partial \xi \partial \zeta ^{2}}+\theta _{7} \frac{\partial ^{3} \varphi _{1}}{\partial \xi \partial \eta ^{2}}+\theta _{8} \frac{\partial ^{3} \varphi _{1}}{\partial \zeta \partial \eta ^{2}}=0,\nonumber \\ \end{aligned}$$

(9)

where $\theta _{1}=AB\text {cos}\theta$, $\theta _{2}=\frac{1}{2}A(\text {cos}^{3}\theta +D\text {sin}^{2}\theta \text {cos}\theta )$, $\theta _{3}=-AB\text {sin}\theta$, $\theta _{4}=-\frac{1}{2}A(\text {sin}^{3}\theta +D\text {sin}\theta \text {cos}^{2}\theta )$, $\theta _{5}=A[D(\text {sin}\theta \text {cos}^{2}\theta -\frac{1}{2}\text {sin}^{3}\theta )-\frac{3}{2}\text {sin}\theta \text {cos}^{2}\theta ]$, $\theta _{6}=-A[D(\text {sin}^{2}\theta \text {cos}\theta -\frac{1}{2}\text {cos}^{3}\theta )-\frac{3}{2}\text {sin}^{2}\theta \text {cos}\theta ]$, $\theta _{7}=\frac{1}{2}AD\text {cos}\theta$ and $\theta _{8}=-\frac{1}{2}AD\text {sin}\theta$.

A steady state solution of ZK equation Eq. (9) is $\varphi _{1}=\varphi _{0}(Z)$, where $Z=\xi -u_{0}t$ and $u_{0}$ is a constant speed. By using these transformations, this ZK equation in the steady state form can be rewritten as

$$\begin{aligned} -u_{0}\frac{d\varphi _{0}}{dZ}+\theta _{1}\varphi _{0}\frac{d\varphi _{0}}{dZ} +\theta _{2}\frac{d^{3}\varphi _{0}}{dZ^{3}}=0. \end{aligned}$$

(10)

The solitary wave solution of this equation is given by

$$\begin{aligned} \varphi _{0}(Z)=\varphi _{m}\text {sech}^{2}\left( \frac{Z}{W}\right) \end{aligned}$$

(11)

where $\varphi _{m}=3u_{0}^{2}/\theta _{1}$ and $W=\sqrt{4\theta _{2}/u_{0}^{2}}$ are the amplitude and the width of the solitary waves, respectively. The appropriate boundary conditions, viz., $\varphi _{1}\longrightarrow 0$, $d\varphi _{1}/dZ\longrightarrow 0$, and $d^{3}\varphi _{1}/dZ^{3}\longrightarrow 0$ as $Z\longrightarrow \pm \infty$, are used.

Fig. 1

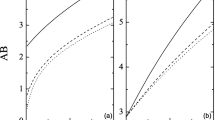
a Variation of AB with $\sigma$ for $\mu =0.5$ (solid curve), $\mu =0.6$ (dashed curve) and $\mu =0.7$ (dotted curve), $\mu _{e}=0.1$, $\mu _{p}=0.9$; b Variation of AB with $\sigma$ for $\mu _{p}=0.82$ (solid curve), $\mu _{p}=0.86$ (dashed curve) and $\mu _{p}=0.9$ (dotted curve), $\mu _{e}=0.1$, $\mu =0.6$

Fig. 2

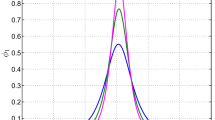
a Showing how the amplitude of CSWs depends on $\sigma$ for different $H_{i}$, $\mu _{e}=0.2$, $\mu _{p}=0.9$, $\mu =0.7$, $\theta =30^{\circ }$. b Showing how the amplitude of CSWs depends on $\mu$ for different $\mu _{p}$, $H_{i}=0.01$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$. c Showing how the width of CSWs depends on $\sigma$ for different $H_{i}$, $\mu _{e}=0.2$, $\mu _{p}=0.9$, $\mu =0.7$, $\theta =30^{\circ }$. d Showing how the width of CSWs depends on $\mu$ for different $\mu _{p}$, $H_{i}=0.01$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$

Applying the QHM, the feature of DAWs in magnetized quantum dusty plasmas is researched. According to the theoretical prediction and experimental datas [30, 31] about dust crystal, we select the typical parameters in the astrophysical region, in which dusts existing in the form of carbon crystals with quantum ions and electrons are considered, $n_{i0}=1.001\times 10^{25}\text {cm}^{-3}-1.001\times 10^{27}\text {cm}^{-3}$, $n_{e0}=1.0\times 10^{25}\text {cm}^{-3}-1.0\times 10^{27}\text {cm}^{-3}$, $n_{d0}=10^{7}n_{e0}$, $B_{0}=1.0\times 10^{8}\text {cm}^{-3}-1.5\times 10^{8}\text {cm}^{-3}G$, $T_{i}\simeq T_{e}=10^{5}K$ and $T_{Fe}=10^{6}-10^{7}K$. It is noted from Eq. (8) that solitary wave is either compressive or rarefactive, depending on AB is positive or negative. It is found that AB is related to the concentration of electrons $\mu _{e}$, ions $\mu _{i}$ and positively charged dust grains $\mu _{p}$, the Fermi temperatures ratio between electrons and ions, and the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust, as shown in Fig. 1. It is obvious that there exists compressive or rarefactive solitary wave, depending on the values of $\sigma$, $\mu _{p}$ and $\mu$. Under our chosen parameters $\mu _{e}=0.1$ and $\mu _{p}=0.9$, when $\mu =0.5$ the critical Fermi temperatures ratio between electrons and ions is 3.6, when $\mu _{p}=0.82$ the critical Fermi temperatures ratio between electrons and ions is 4.7, and the critical values decrease with the increasing $\mu$ and $\mu _{p}$, as shown in Fig. 1a and b, respectively.

Fig. 3

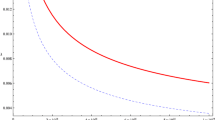
a Showing how amplitude of RSWs depends on $\sigma$ for different $H_{i}$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\mu =0.5$, $\theta =30^{\circ }$. b Showing how the amplitude of RSWs depends on $\mu$ for different $\mu _{p}$, $H_{i}=0.03$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$. c Showing how the width of RSWs depends on $\sigma$ for different $H_{i}$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\mu =0.5$, $\theta =30^{\circ }$. d Showing how the width of RSWs depends on $\mu$ for different $\mu _{p}$, $H_{i}=0.03$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$

The amplitudes of RSWs and CSWs are relevant to the Fermi temperatures ratio $\sigma$ between electrons and ions, the quantum diffraction parameter $H_{i}$, the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust, the concentration $\mu _{p}$ of positively charged dust grains and obliqueness $\theta$, which also affects the width of RSWs and CSWs, as shown in Figs. 2 and 3.

Figure 2a shows how the amplitude of CSWs decreases with the increasing ratio $\sigma$ of Fermi temperatures of electrons to ions, and it is noted that when the Fermi temperature of electrons is close to that of ions, the amplitude decreases rapidly. Figure 2a also shows that the quantum diffraction parameter $H_{i}$ has no effect on the amplitude of CSWs for our chosen parameters. Figure 2b reveals that the amplitude of CSWs decreases as the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust and the concentration of positively charged dust grains $\mu _{p}$ increase. The effects of $\sigma$ and $H_{i}$ on the width of CSWs are shown in Fig. 2c, and the results show that when the Fermi temperature of electrons is close to that of ions, the quantum diffraction parameter $H_{i}$ has a little impact on the width of CSWs. According to Fig. 2d, the width of CSWs increases with the increasing $\mu$ and $\mu _{p}$, and it is found that the smaller $\mu$ is, the smaller the effect of $\mu _{p}$ on the width is.

Figure 3a shows how the amplitude of RSWs increases with the increasing ratio $\sigma$ of Fermi temperatures of electrons to ions, and it is noted that when the Fermi temperature electrons is close to that of ions, the amplitude increases slowly. Figure 3a also shows that the quantum diffraction parameter $H_{i}$ has no effect on the amplitude of RSWs for our chosen parameters. Figure 3b reveals that the amplitude of RSWs increases as the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust increases and the concentration of positively charged dust grains $\mu _{p}$ decreases. It is obvious that when $\mu$ is less than 1, $\mu _{p}$ almost has no effect on the width. The effects of $\sigma$ and $H_{i}$ on the width of RSWs are shown in Fig. 3c, and the results show that when the Fermi temperature of electrons is close to that of ions, the quantum diffraction parameter $H_{i}$ has a little impact on the width of RSWs, which is similar to the case of CSWs. According to Fig. 3d, the width of RSWs decreases with the increasing $\mu$ and $\mu _{p}$, and it is found that the smaller $\mu$ is, the smaller the effect of $\mu _{p}$ on the width is.

We also find that external magnetic field has no effect on the amplitudes for both RSWs and CSWs.

4 Instablitily for ZK equation

By way of the small-k perturbation expansion, the instability of the obliquely propagating solitary waves is investigated as follows [24]. Firstly, assume that

$$\begin{aligned} \varphi _{1}=\varphi _{0}(Z)+\psi (Z,\zeta ,\eta ,t), \end{aligned}$$

(12)

where $\varphi _{0}$ is defined by Eq. (11) and $\psi (Z,\zeta ,\eta ,t)$ is given by

$$\begin{aligned} \psi (Z,\zeta ,\eta ,t)=\phi (Z)e^{i[k(l_{\eta }\eta +l_{\zeta }\zeta +l_{\xi }Z)-\omega \tau ]}, \end{aligned}$$

(13)

for a long-wavelength plane wave perturbation with direction cosines $(l_{\zeta },l_{\xi },l_{\eta })$, where $l_{\zeta }^{2}+l_{\xi }^{2}+l_{\eta }^{2}=1$. For small k, $\phi (Z)$ and $\omega$ can be extended as

$$\begin{aligned} \phi (Z)= & {} \phi _{0}(Z)+k\phi _{1}(Z)+k^{2}\phi _{2}(Z)+\cdots , \end{aligned}$$

(14)

$$\begin{aligned} \omega= & {} k\omega _{1}(Z)+k^{2}\omega _{2}(Z)+\cdots . \end{aligned}$$

(15)

By substituting Eq. (12) into Eq. (9) and linearizing with respect to $\varphi$, the linearized ZK equation can be obtained

$$\begin{aligned}&\frac{\partial \psi }{\partial t}-u_{0}\frac{\partial \psi }{\partial Z} +\theta _{1}\varphi _{0}\frac{\partial \psi }{\partial Z}+\theta _{1}\psi \frac{\partial \varphi _{0}}{\partial Z}+ \theta _{2}\frac{\partial ^{3} \psi }{\partial Z^{3}}\nonumber \\&\quad +\theta _{3}\varphi _{0}\frac{\partial \psi }{\partial \zeta }+\theta _{4}\frac{\partial ^{3} \psi }{\partial \zeta ^{3}}+\theta _{5}\frac{\partial ^{3} \psi }{\partial Z^{2} \partial \zeta }+\theta _{6} \frac{\partial ^{3} \psi }{\partial Z \partial \zeta ^{2}}\nonumber \\&\quad +\theta _{7} \frac{\partial ^{3} \psi }{\partial Z \partial \eta ^{2}}+\theta _{8} \frac{\partial ^{3} \psi }{\partial \zeta \partial \eta ^{2}}=0. \end{aligned}$$

(16)

By solving the zeroth, first and second-order equations [from Eq. (14) to Eq. (16)], $\omega _{1}$ is found. After integration, the zeroth-order equations can be written as

$$\begin{aligned} (-u_{0}+\theta _{1}\varphi _{0})\phi _{0}+\theta _{2}\frac{d^{2}\phi _{0}}{dZ^{2}}=C, \end{aligned}$$

(17)

where C is an integration constant. It is obvious from Eq. (17) that this equation has two linearly independent solutions in the homogeneous part, namely, $f=\frac{d\varphi _{0}}{dZ}$ and $g=f\int ^{Z}\frac{dZ}{f^{2}}$. Therefore, the common solution of this zeroth-order equation can be

$$\begin{aligned} \phi _{0}\!=\!C_{1}f+C_{2}g-Cf\int ^{Z}\frac{g}{\theta _{2}}dZ\!+\!Cg\int ^{Z}\frac{f}{\theta _{2}}dZ, \end{aligned}$$

(18)

where $C_{1}$ and $C_{2}$ are integration constants. Now, evaluating all integrals, the common solution of this zeroth-order equation can finally be simplified to

$$\begin{aligned} \phi _{0}=C_{1}f, \end{aligned}$$

(19)

for $\phi _{0}$ not tending to $\pm \infty$ as $Z\longrightarrow \pm \infty$.

After integration, the first-order equation obtained from Eqs. (14) to (16) and Eq. (19), can be expressed as

$$\begin{aligned} (-u_{0}+\theta _{1}\varphi _{0})\phi _{1}+\theta _{2}\frac{d^{2}\phi _{1}}{dZ^{2}}=iC_{1}(\alpha _{1}+\beta _{1}tanh^{2}\frac{Z}{W})\varphi _{0}+K, \end{aligned}$$

(20)

where K is another integration constant, and $\alpha _{1}$ and $\beta _{1}$ are given by

$$\begin{aligned} \begin{aligned} \alpha _{1}&=(\omega _{1}+l_{\xi }u_{0})-\frac{1}{2}\varphi _{m}\mu _{1}+2\frac{\mu _{2}}{W^{2}},\\ \beta _{1}&=\frac{1}{2}\varphi _{m}\mu _{1}-6\frac{\mu _{2}}{W^{2}}\\ \mu _{1}&=\theta _{1}l_{\xi }+\theta _{3}l_{\zeta }\\ \mu _{2}&=3\theta _{2}l_{\xi }+\theta _{5}l_{\zeta }. \end{aligned} \end{aligned}$$

(21)

The general solution of this first-order equation can be written as

$$\begin{aligned} \phi _{1}=K_{1}f+\frac{iC_{1}W^{2}}{8\theta _{2}}[(\alpha _{1}+\beta _{1})Zf+\frac{2}{3}(3\alpha _{1}+\beta _{1})\varphi _{0}], \end{aligned}$$

(22)

for $\phi _{1}$ not tending to $\pm \infty$ as $Z\longrightarrow \pm \infty$.

The second-order equation can be written as

$$\begin{aligned}&\left[ -u_{0}\frac{d}{dZ}+\theta _{1}\frac{d\varphi _{0}}{dZ} +\theta _{2}\frac{d^{3}}{dZ^{3}}\right] \phi _{2}\nonumber \\&\quad =i\omega _{2}\phi _{0}+i(\omega _{1}+l_{\xi }u_{0})\phi _{1}\nonumber \\&\quad -i\mu _{1}\varphi _{0}\phi _{1}+\mu _{3}\frac{d\phi _{0}}{dZ}-i\mu _{2}\frac{d^{2}\phi _{1}}{dZ^{2}}, \end{aligned}$$

(23)

where $\mu _{3}=3\theta _{2}l_{\xi }^{2}+2\theta _{5}l_{\xi }l_{\zeta }+\theta _{6}l_{\zeta }^{2}+\theta _{7}l_{\eta }^{2}$.

The solution of this second-order equation exists if the righthand side is orthogonal to a kernel of the operator adjoint to the operator $-u_{0}\frac{d}{dZ}+\theta _{1}\frac{d\varphi _{0}}{dZ} +\theta _{2}\frac{d^{3}}{dZ^{3}}$. This kernel must tend to zero when $Z\longrightarrow \pm \infty$ is $\varphi _{0}/\varphi _{m}=sech^{2}(Z/W)$. Then we can obtain the following equation about $\omega _{1}$:

$$\begin{aligned}&\int _{-\infty }^{+\infty }\varphi _{0}\left[ i\omega _{2}\phi _{0}+i(\omega _{1}+l_{\xi }u_{0})\phi _{1} -i\mu _{1}\varphi _{0}\phi _{1}\right. \nonumber \\&\quad \left. +\mu _{3}\frac{d\phi _{0}}{dZ}-i\mu _{2}\frac{d^{2}\phi _{1}}{dZ^{2}}\right] dZ=0. \end{aligned}$$

(24)

Now, substituting the expressions $\phi _{1}$ and $\phi _{2}$ given by Eqs. (19) and (22), respectively, and performing the integration, we derive the following dispersion relation:

$$\begin{aligned} \omega _{1}=\Omega -l_{\xi }u_{0}+(\Omega ^{2}-\Upsilon )^{1/2}, \end{aligned}$$

(25)

where $\Omega =\frac{2}{3}\varphi _{m}\mu _{1}-2\frac{\mu _{2}}{W^{2}}$ and $\Upsilon =\frac{16}{45}(\varphi _{m}^{2}\mu _{1}^{2}-3\varphi _{m}\mu _{1}\mu _{2}/W^{2}-3\mu _{2}^{2}/W^{4}+12\theta _{2}\mu _{3}/W^{4})$. It is noted from the dispersion relation Eq. (25) that if $(\Upsilon -\Omega ^{2})>0$ there is always instability, then the instability criterion can be expressed as $S_{i}>0$, where

$$\begin{aligned} S_{i}=[Y-4\sigma sin^{2}\theta ]l_{\eta }^{2}+[Y-\frac{5}{3}(Y-4\sigma )tan^{2}\theta ]l_{\zeta }^{2}, \end{aligned}$$

(26)

where $Y=\mu \omega _{cd}^{2}(9\mu _{i}\sigma ^{2}H_{i}^{2}+9\mu _{e}H_{e}^{2}-4\sigma ^{2})$.

If the instability criterion $S_{i}>0$ is satisfied, the growth rate

$$\begin{aligned} \Gamma =\frac{2u_{0}}{\sqrt{15Y}}\frac{\sqrt{DS_{i}}}{(D-1)sin^{2}\theta +1}. \end{aligned}$$

(27)

Fig. 4

CSWs: a Variation of the growth rate $\Gamma$ with $\sigma$ for different values of $H_{i}$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\mu =0.7$, $l_{\zeta }/l_{\eta }=0.2$, $\omega _{cd}=0.2$, $\theta =30^{\circ }$. b Variation of the growth rate $\Gamma$ with $\mu$ for different values of $\mu _{p}$, $H_{i}=0.01$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$, $l_{\zeta }/l_{\eta }=0.2$, $\omega _{cd}=0.2$. c Variation of the growth rate $\Gamma$ with $\omega _{cd}$ for different values of $l_{\eta }$, $H_{i}=0.01$, $\sigma =3.0$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\theta =30^{\circ }$, $l_{\zeta }/l_{\eta }=0.2$, $\mu =0.6$. d Variation of the growth rate $\Gamma$ with $\theta$ for different values of $l_{\zeta }/l_{\eta }$, $H_{i}=0.01$, $\mu _{p}=0.9$, $\mu _{e}=0.1$, $\sigma =3.0$, $\mu =0.6$, $\omega _{cd}=0.2$. $H_{e}=\sqrt{1836}H_{i}$

Fig. 5

RSWs: a Variation of the growth rate $\Gamma$ with $\sigma$ for different values of $H_{i}$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\mu =0.5$, $l_{\zeta }/l_{\eta }=0.6$, $\omega _{cd}=0.2$, $\theta =30^{\circ }$. b Variation of the growth rate $\Gamma$ with $\mu$ for different values of $\mu _{p}$, $H_{i}=0.03$, $\mu _{e}=0.1$, $\theta =30^{\circ }$, $\sigma =3.0$, $l_{\zeta }/l_{\eta }=0.6$, $\omega _{cd}=0.2$. c Variation of the growth rate $\Gamma$ with $\omega _{cd}$ for different values of $l_{\eta }$, $H_{i}=0.03$, $\sigma =2.0$, $\mu _{e}=0.1$, $\mu _{p}=0.9$, $\theta =30^{\circ }$, $l_{\zeta }/l_{\eta }=0.6$, $\mu =0.2$. d Variation of the growth rate $\Gamma$ with $\theta$ for different values of $l_{\zeta }/l_{\eta }$, $H_{i}=0.01$, $\mu _{p}=0.9$, $\mu _{e}=0.1$, $\sigma =2.0$, $\mu =0.5$, $\omega _{cd}=0.2$. $H_{e}=\sqrt{1836}H_{i}$

It is apparent from Eq. (27) that the growth rate $\Gamma$ of instability for RSWs and CSWs depends on the Fermi temperatures ratio $\sigma$ between electrons and ions, the quantum diffraction parameter $H_{i}$, the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust, the concentration $\mu _{p}$ of positively charged dust grains and obliqueness $\theta$, dust cyclotron frequency $\omega _{cd}$, direction cosines $l_{\zeta }$ and $l_{\eta }$.

As can be seen from Fig. 4a, the growth rate $\Gamma$ of CSWs increases with the increasing quantum diffraction parameter $H_{i}$ and decreases with the ratio $\sigma$ of Fermi temperatures of electrons to ions, and it is clear that when the Fermi temperature of electrons is far greater than that of ions, the growth rate decreases moderately. Figure 4b reveals that the growth rate of CSWs decreases with the rising ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust and the concentration of positively charged dust grains $\mu _{p}$ has no effect on the growth rate. As can be seen from the Fig. 4c, the three curves show the fluctuation of growth rate with dust cyclotron frequency $\omega _{cd}$ for different values of $l_{\eta }$, and the growth rate grows down as $\omega _{cd}$ raises and $l_{\eta }$ drops. Figure 4d leads us to the conclusion that the growth rate drops with the rising obliqueness $\theta$ for different values of $l_{\zeta }$, and the statistics show that obliqueness $\theta$ is less than about $8^{\circ }$, the growth rate increases with the rising $l_{\zeta }$, otherwise, the growth rate decreases. Figure 4d also illustrates that the maximum value of $\theta$ for which the wave becomes unstable is dependent of the direction cosine $l_{\zeta }$.

As can be seen from Fig. 5a, the growth rate $\Gamma$ of RSWs decreases with the increasing quantum diffraction parameter $H_{i}$ and increases with the ratio $\sigma$ of Fermi temperatures of electrons to ions, and it is clear that when the Fermi temperature of electrons is far greater than that of ions, the growth rate increases moderately. Figure 5b reveals that the growth rate of CSWs increases as the increasing ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust and the concentration of positively charged dust grains $\mu _{p}$ has no effect on the growth rate. As can be seen from the Fig. 5c, the three curves show the fluctuation of growth rate with dust cyclotron frequency $\omega _{cd}$ for different values of $l_{\eta }$, and the growth rate raises as $\omega _{cd}$ and $l_{\eta }$ raises. Figure 5d leads us to the conclusion that the growth rate drops with the rising obliqueness $\theta$ for different values of $l_{\zeta }$, and the statistics show that obliqueness $\theta$ is less than about $8^{\circ }$, the growth rate decreases with the rising $l_{\zeta }$, otherwise, the growth rate increases. Figure 5d also illustrates that the maximum value of $\theta$ for which the wave becomes unstable is dependent of the direction cosine $l_{\zeta }$.

5 Conclusions

In this paper, we consider a four species quantum dusty plasma with external magnetic field. The dusty plasma involves charged mobile dusts (both positive and negative), quantum electrons and ions. The features of DAWs described by two-fluid QHM and the multi-dimensional instability have been researched. By way of the reductive perturbation method, the three-dimensional ZK equation is derived and then the instability of these solitary waves is discussed by making use of small-k expansion method. The results found in this paper may be pointed out as follows.

• 1. The nature of solitary waves is modified by the quantum electrons as well as ions in a dusty plasmas. Whether solitary waves are compressive or rarefactive relies on the concentration of electrons $\mu _{e}$, ions $\mu _{i}$ and positively charged dust grains $\mu _{p}$, the Fermi temperatures ratio $\sigma$ between electrons and ions, and the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust. It is worth mentioning that there exist RSWs and CSWs for different parameters in this system (Fig. 1).

• 2. The amplitude and width of RSWs and CSWs are relevant to the Fermi temperatures ratio $\sigma$ between electrons and ions, the quantum diffraction parameter $H_{i}$, the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust, the concentration $\mu _{p}$ of positively charged dust grains and obliqueness $\theta$. It is apparent that the amplitude of DAWs is not influenced by quantum diffraction parameter $H_{i}$ which has a little impact on the width when the Fermi temperature of electrons is close to that of ions. (Figs. 2 and 3).

• 3. The solitary wave amplitude is not influenced by the magnitude of external magnetic field which does have a straightforward impact on solitary wave width in the quantum dusty plasma.

• 4. For RSWs and CSWs, the growth rate $\Gamma$ of instability depends on the ratio $\sigma$ of Fermi temperatures of electrons to ions, the quantum diffraction parameter $H_{i}$, the ratio $\mu$ of charge-to-mass ratio of positive dust to that of negative dust, the concentration $\mu _{p}$ of positively charged dust grains and obliqueness $\theta$, dust cyclotron frequency $\omega _{cd}$, direction cosines $l_{\zeta }$ and $l_{\eta }$. The results reflect that when the Fermi temperature of electrons is far greater than that of ions the growth rate decreases moderately, and the maximum value of $\theta$ for which the wave becomes unstable is dependent of the direction cosine $l_{\zeta }$ (Figs. 4, 5).

The theoretical research related to wave phenomena we present should be beneficial to understand different nonlinear characteristics of unstable electrostatic disturbances in many astrophysical dusty plasmas, such as the interior of white dwarf stars, in magnetars, and so on, in which the main plasma species comprises of charged dust grains, quantum electrons as well as ions.