1 Introduction

Contemporary observational results form supernova type Ia (Perlmutter et al. 1999; Riess et al. 2007), anisotropy measurement in current cosmic microwave background from WMAP (Spergel et al. 2007), large scale structure (Hawkins et al. 2003; Tegmark et al. 2004), baryon acoustic oscillations (Eisentein et al. 2005) and weak lensing (Jain and Taylor 2003) indicate that the universe is accelerating in the current epoch. The unknown form of energy component usually named as dark energy (DE) is considered as the prime source to make this striking change in the cosmic history. Dark energy is recognized by its distinctive nature from ordinary matter sources having negative pressure which may lead to cosmic expansion counter striking the gravitational pull. This is appeared as enigmatic cosmic ingredient and interpretation of its gravitational effects is a dynamic research field. There are two representative directions to address the issue of cosmic acceleration. One is to introduce the “exotic energy component” in the context of general relativity. A number of alternative models have been proposed in this perspective to explain the role of DE in the present cosmic acceleration.

In particular, the holographic DE (HDE) turns out to be one of the most prominent candidates which has extensively been studied in literature (Huang and Gong 2004; Zhang and Wu 2005). Gao et al. (2009) introduced another proposal for DE resulting in new form of HDE termed as Ricci DE. Granda and Oliveros (2008, 2009) suggested a new infra red (IR) cut-off for HDE in terms of H and its derivative which generalizes the Ricci DE known as new HDE. We have discussed the reconstruction and stability of f(R,T) models for both Ricci and modified Ricci DE models (Sharif and Zubair 2014a). Wei (2012) proposed a new model of DE named as pilgrim DE (PDE) based on the idea that phantom DE is strong enough to avoid the formation of BH. He considered Hubble horizon as an IR cut-off and developed constraints on PDE using the latest cosmic observations. Recently, we have discussed the cosmological evolution of PDE for particle, event and conformal age of the universe cut-offs (Sharif and Zubair 2014b). The phantom cosmic acceleration is established in these scenarios which is well supported by other cosmological parameters such as deceleration parameter.

The issue of cosmic acceleration can also be counted on the basis of modified theories of gravity. In the process of modification of Einstein-Hilbert action, various candidates have been proposed to unravel the mysterious nature of DE namely, f(R) (Sotiriou and Faraoni 2010) \(f(\mathcal{T})\) (Ferraro and Fiorini 2007), where \(\mathcal{T}\) is the torsion scalar, Gauss-Bonnet gravity (Cognola et al. 2006), f(R,T) gravity (Harko et al. 2011; Sharif and Zubair 2012, 2013a, 2013b, 2013c, 2013d) and f(R,T,R μν Tμν) (Haghani et al. 2013; Sharif and Zubair 2013e, 2013f) gravities, T is the trace of the energy-momentum tensor. The f(R) theory is defined by the Lagrangian

$$ \mathcal{I}=\int{ \biggl[\frac{M_p^2}{2}f(R)+ \mathcal{L}_{(M)} \biggr] \sqrt{-g}dx^4}, $$
(1)

where variation implies the field equations

$$ R_{\alpha\beta}-\frac{1}{2}Rg_{\alpha\beta}=M^{-2}_pT^{(M)}_{\alpha\beta}+ T^{(\mathit{curv})}_{\alpha\beta}, $$
(2)

and

$$ T_{\alpha\beta}^{(\mathit{curv})}=\frac{1}{F} \biggl[ \frac{1}{2}g_{\alpha\beta}(f-RF) +F^{;{\mu\nu}}(g_{\alpha\mu}g_{\beta\nu}-g_{\alpha\beta}g_{\mu\nu}) \biggr], $$

appears due to the share from the curvature part, \(T_{{\mu}{\nu}}^{(M)}=\hat{T}_{{\mu}{\nu}}^{(M)}/f(R)\), \(\hat{T}_{{\mu}{\nu}}^{(M)}\) is matter energy-momentum tensor and F=df/dR. Recently, some explicit models of f(R,T) gravity are reconstructed for anisotropic universe which can produce phantom era of DE (Sharif and Zubair 2013b, 2013c, 2013d). We have also reconstructed f(R,T) functions corresponding to the evolution background in FRW universe (Sharif and Zubair 2014a, 2014c). It is shown that any cosmological evolution including ΛCDM, phantom or non-phantom eras and possible phase transition from accelerating to decelerating can be reproduced in this theory. We have proposed some specific forms of Lagrangian in the perspective of de Sitter and power law expansion history.

In this work, we consider PDE as promising candidate of phantom energy and reconstruct f(R) function as an effective description to such behavior. We analyze the evolution of f(R) for the essential parameter μ<0 according to the recent Planck and WMAP9 results. The paper is arranged in the following format. In the next section, we provide numerical reconstruction of f(R) gravity according to PDE. The evolution of f(R) is presented for three different cut-offs that can be differentiated according to the cosmic evolution. In Sect. 3, we conclude our results.

2 Reconstructing f(R) gravity from PDE

Cosmological reconstruction in modified theories is one of the promising aspects in cosmology. In this perspective, different schemes have been proposed for known cosmic evolutions to find the corresponding particular Lagrangian (Elizalde et al. 2010; Goheer et al. 2009a, 2009b; Nojiri et al. 2010; Sharif and Zubair 2013b). Karami and Khaledian (2011) reconstructed different f(R) models in the spatially flat FRW universe according to ordinary and entropy-corrected versions of holographic and new agegraphic DE models. Capozziello et al. (2005) proposed an effective method to reconstruct f(R) from a given Hubble parameter H(z) in metric formalism. In this scheme, one needs to know the relation of H(z) for a given DE model so that f(R) Lagrangian can be reconstructed implying the same dynamics. Following (Capozziello et al. 2005), Wu and Zhu (2008) reconstructed f(R) theory according to HDE and interpreted the distinctive behavior of reconstructed theory depending on parameter c. This approach is also applied to construct f(R) theory corresponding to Ricci DE (Feng 2009). We have reconstructed f(R) function corresponding to new agegraphic as well as new HDE models (Sharif and Zubair 2013g) and shown the cosmological evolution of the reconstructed function under the role of essential parameters.

We follow this scheme to determine Lagrangian f(R) which gives rise to same dynamics as in PDE with particle and event horizons as well as cosmological time scale. The field equations in f(R) gravity can be represented as

$$\begin{aligned} \begin{array}{@{}l} 3M^{2}_pH^2= \rho_\mathit{curv}+\rho_M, \\ -M^{2}_p \bigl(2\dot{H}+3H^2\bigr)=p_\mathit{curv}+p_M, \end{array} \end{aligned}$$
(3)

where

$$\begin{aligned} & {\rho_\mathit{curv}=\frac{1}{F} \biggl[\frac{1}{2}(f-RF)-3H \dot{R}F_R \biggr], }\\ & {p_\mathit{curv}=\frac{1}{F} \biggl[-\frac{1}{2}(f-RF)+2H \dot{R}F_R+\ddot{R}F_R+ {\dot{R}}^2F_{RR} \biggr]. } \end{aligned}$$

The total energy density, ρ tot =ρ curv +ρ M , satisfies the standard conservation equation \(\dot{\rho}_{\mathit{tot}}+3H(\rho_{\mathit{tot}}+p_{\mathit{tot}})=0\). We combine Eq. (3) and continuity equation to a single equation

$$ \dot{H}=\frac{-1}{2f} \bigl[3H_0^2 \varOmega_{M0}e^{-3x}+(\ddot{R}-H\dot{R})F + \dot{R}^2F_{R} \bigr]. $$
(4)

We replace cosmic time by x employing the relation d/dt=Hd/dx so that Eq. (4) can be translated into third order differential equation in f(x) as

$$\begin{aligned} \mathcal{C}_3(x)\frac{d^3f}{dx^3}+\mathcal{C}_2(x) \frac{d^2f}{dx^2}+\mathcal{C}_1(x)\frac{df}{dx} =-3H^2_0\varOmega_{M0}e^{-3x}, \end{aligned}$$
(5)

where \(\mathcal{C}_{i}\) (i=1,2,3) are given in terms of H(x) and its derivatives as shown in Appendix. If one knows the function H(x) and its derivatives then C i ’s can be evaluated which help to find f(R) according to known DE model. To solve Eq. (5) for f(R[x]), we set the boundary conditions (Capozziello et al. 2005)

$$\begin{aligned} \begin{array}{@{}l} \biggl(\frac{df}{dx} \biggr)_{x=0}= \biggl( \frac{dR}{dx} \biggr)_{x=0}, \\ \biggl(\frac{d^2f}{dx^2} \biggr)_{x=0}= \biggl(\frac{d^2R}{dx^2} \biggr)_{x=0}, \\ f(x=0)=f(R_0)=6H_0^2(1- \varOmega_{M0})+R_0. \end{array} \end{aligned}$$
(6)

Initially, Cohen et al. (1999) set up a relation between ultraviolet (UV) and infrared (IR) cut-offs due to the limit made by the formation of a BH. If ρ ϑ is the quantum zero-point energy density associated with UV cut-off then entire energy in a system of size L should not exceed BH mass of the same size so that \(L^{3}\rho_{\vartheta}\leqslant{L}M_{p}^{2}\), \(M_{p}=1/\sqrt{8\pi{G}}\) is the reduced Planck mass. The largest IR cut-off saturates the inequality and one gets the HDE density

$$ \rho_{\vartheta}=\frac{3c^2M^{2}_p}{L^{2}}, $$

where 3c2 is a numerical constant. Feng (2008) made an early attempt to generalize the Cohen relation and postulated a relation of UV and IR cutoff as \((L\varLambda)^{n}\leqslant{L}^{2}M_{p}^{2}\), where n is a dimensionless parameter. This relation helps to define the vacuum energy density of the form \(\rho_{\varLambda}=3c^{2}L^{\frac{8}{n}-4}M_{p}^{\frac{8}{n}}\). It is shown that the fine tuning problem can be resolved for this choice of energy density. However, in pilgrim DE, Wei (2012) introduced the concept that phantom DE is strong enough to prevent the formation of black hole. In this perspective the energy bound set by Cohen et al. (1999) could be violated. The PDE is defined by the relation (Wei 2012)

$$ \rho_{\vartheta}=3n^2M_p^{4-\mu}L^{-\mu}, $$
(7)

where μ and n are dimensionless constants. The parameter μ is adjusted according to the idea of phantom like behavior of DE and most acceptable choice is μ⩽0 (Wei 2012; Sharif and Zubair 2014b). In Sharif and Zubair (2014b) the PDE model is studied by taking IR cut-offs as particle and event horizons as well as conformal age of the universe.

For flat FRW, the corresponding Friedmann equation is

$$ 3M_p^2H^2=\rho_M+ \rho_{\vartheta}. $$
(8)

By setting the fractional energy densities \(\varOmega_{M}=\frac{\rho_{M}}{\rho_{cri}}, \varOmega_{\vartheta}=\frac{\rho_{\vartheta}}{\rho_{cri}}, \rho_{cri}=3M^{2}_{p}H^{2}\), Eq. (8) can be interpreted as

$$ H(x)=H_0 \biggl(\frac{\varOmega_{M0}e^{-3x}}{ 1-\varOmega_{\vartheta}} \biggr)^{1/2}. $$
(9)

In the following, we reconstruct f(R) gravity corresponding to PDE for particle and event horizons as well as cosmological time scale.

2.1 Particle horizon

The particle horizon is given as (Li 2004)

$$ L=R_{p}=a(t)\int^{t}_{0}{ \frac{d\hat{t}}{a(\hat{t})}} =a(t)\int^{a}_{0}{ \frac{da'}{Ha'^{2}}}. $$
(10)

The corresponding dynamical equation of fractional energy density is

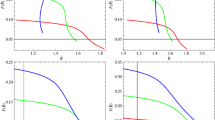
$$\begin{aligned} \varOmega'_{\vartheta} =& \varOmega_{\vartheta}(1- \varOmega_{\vartheta}) \biggl(3-\mu - \frac{\mu}{C}(1\,{-}\,\varOmega_{\vartheta})^{1/2-1/\mu} \\ &{}\times (\varOmega_{\vartheta})^{1/\mu} e^{(3/2-3/\mu)x} \biggr), \end{aligned}$$
(11)

where \(C= (\frac{n^{2}M_{p}^{2-\mu}}{H_{0}^{2-\mu}\varOmega_{m0}^{1-\mu/2}} )^{1/\mu}\) and prime denotes derivative with respect to x=lna. For PDE with particle horizon as an IR cut-off, analytic expression of H(x) is not on cards but depends upon the evolution of Ω ϑ . We represent H(x), its derivatives and hence the coefficients C i ’s in terms of Ω ϑ and \(\varOmega'_{\vartheta}\). The system of Eqs. (5) and (11) is solved numerically using the conditions (6) as well as Ωϑ0=1−Ωm0 and results are shown in Figs. 1 and 2. We set the recent values of Ω m and H as Ωm0=0.27 and H0=74 (Ade et al. 2014). In this study, we set μ=−1,−2,−3 and n=2 which favor the phantom regime of the universe. For these parameters, the plot of f(R) against R is shown in Fig. 1(a). It is obvious that evolution trajectories appear distinct if |R| is large and coincides for small values of |R|. These trajectories are also shown on lf−lR plane in Fig. 1(b), where lf=ln(−f) and lR=ln(−R). To show the distinctive behavior of μ, we consider the future evolution scenario. Figure 2(a) clearly shows the characteristic evolution of R for future cosmic evolution. We also show the future growth of f versus z, for μ=−1, the curve is smooth whereas for other two choices there is sudden variation as z→−1 (see Fig. 2(b)).

Fig. 1
figure 1

Evolution trajectories of reconstructed f(R) for PDE with particle horizon in (a) f−R and (b) lf−lR planes with 0⩽z⩽10

Full size image
Fig. 2
figure 2

(a) Evolution trajectories of Ricci scalar and (b) reconstructed f(R) versus redshift with −1⩽z⩽1

Full size image

2.2 Event horizon

Li (2004) proposed the event horizon as

$$ L=R_{\hat{E}}=a(t)\int^{\infty}_{t}{ \frac{d\hat{t}}{a(\hat{t})}} =a(t)\int^{\infty}_{a}{ \frac{da'}{Ha'^{2}}} . $$
(12)

Using the relation of PDE (10) and event horizon, we obtain

$$\begin{aligned} \varOmega'_{\vartheta} =&\varOmega_{\vartheta}(1- \varOmega_{\vartheta}) \biggl(3-\mu+ \frac{\mu}{C}(1-\varOmega_{\vartheta})^{1/2-1/\mu} \\ &{}\times (\varOmega_{\vartheta})^{1/\mu} e^{(3/2-3/\mu)x} \biggr). \end{aligned}$$
(13)

For PDE with event horizon, the situation is similar to the one discussed in Wu and Zhu (2008), cosmic history of H(z) depends on the evolution of Ω ϑ and one needs to solve the system of dynamical equations (5) and (13). Though Ω ϑ can be solved independently but here we consider it as part of the system. Thus we can reconstruct f(R) corresponding to the evolution of PDE with event horizon. We choose μ<0 which produces the phantom regime of the universe as shown in Sharif and Zubair (2014b). The reconstructed function f(R) is presented in Fig. 3. The difference in evolution trajectories of f is quite evident depending on the values of parameter μ for large |R| and the distinctive property vanishes for very small values of |R|. We also show these curves on lf−lR plane in Fig. 3(b). Figure 3 shows the role of parameter μ in remote past.

Fig. 3
figure 3

Evolution of reconstructed function f(R) in f−R and lf−lR planes corresponding to PDE with event horizon and 0⩽z⩽10

Full size image

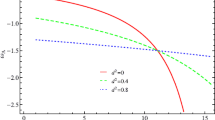
To explain how the reconstructed theory reflects the distinctive nature of parameter μ, we present the cosmic evolution for later times. Figure 4(a) shows the future evolution of |R| which is alike for different values of μ. As expected for μ⩽−1, the curve shows that |R|→∞ in the future, which is the distinctive phantom DE evolution. This behavior is due to dominance of DE (with ω ϑ <−1) over matter components and in such case phantom increases with time which would split the structures and hence the big rip is unavoidable. We plot the future evolution of the reconstructed function f(R) which more effectively reflects the difference in choice of parameter μ. The most common property in these plots is the point of reversion where decreasing |R| starts increasing which reveals that phantom DE dominates the matter components.

Fig. 4
figure 4

Future evolution trajectories of Ricci scalar versus redshift with −1⩽z⩽2. Future evolution of reconstructed f(R) is also shown for μ=−1 with −1⩽z⩽3, μ=−2 with −1⩽z⩽4, μ=−3 with −1⩽z⩽5, respectively. Different choices of redshift are used to have more clear behavior of evolution trajectories for the reconstructed f. The dots denote the present day values at x=0 and stars indicate the point of reversion where DE begins to dominate the matter part and hence total energy components

Full size image

For μ=−1, the point of reversion is in the future as the universe evolves, |R| keeps on growing whereas f initially decreases approaching the turn around point and then becomes positive leading to infinity as shown in Fig. 4(b). The parameters μ=−2 and μ=−3 show almost identical behavior where rapid decrease in f is observed for increasing |R| (see Figs. 4(c) and 4(d)). It can be checked that the point of reversion approaches near future for small values of μ, i.e., the dominance of phantom DE starts earlier for small μ. We remark that point of reversion is a universal property of all reconstructed functions f(R) representing the phantom like DE models as a result of context between DE and matter components.

2.3 Conformal age of the universe

In Sharif and Zubair (2014b), it is shown that only μ=−1 supports the cosmological constant regime where as μ⩽−55 favors the quintessence era in later times of the universe. Here, we are interested to represent the evolution trajectories of reconstructed function f(R) for μ=−1. Following the same procedure as in the previous cases, we numerically solve the system of dynamical equations shown in Fig. 5. The reconstructed function f(R) for PDE with cosmological time scale is represented in f−R and lf−lR planes as shown in Figs. 5(a) and 5(b). The future evolution of R can also be seen in Fig. 5(c). For the future evolution, Fig. 5(d) shows linear dependence of f on R upto a constant which is consistent with de Sitter phase resulting in f=R+Λ. This result is consistent with that in HDE for c=1 (Wu and Zhu 2008), Ricci DE for α=0.5 (Feng 2009) and NHDE for (μ,ν)=(1,0.63) (Sharif and Zubair 2013g).

Fig. 5
figure 5

Evolution trajectories of reconstructed function f(R) in f−R and lf−lR planes with 0⩽z⩽10. Future evolution of Ricci scalar versus redshift and f versus R with −1⩽z⩽1 are also shown in plots (c) and (d), respectively

Full size image

3 Conclusions

The f(R) theory stands among the fascinating models in modified gravitational theories where the generic nonlinear function f succeeds the Ricci scalar R. Over the past few years, this theory has received great deal of attention to count the late time acceleration and provided number of interesting results on cosmological scales. We have developed the correspondence of PDE with f(R) theory and reconstructed the functions yielding the same dynamics as in PDE. We have used the numerical reconstruction scheme (Capozziello et al. 2005; Feng 2009; Sharif and Zubair 2014b; Wu and Zhu 2008) and shown the evolution paradigm of reconstructed functions. For the reconstructed f(R) functions, we set the parameters according to their behavior in Sharif and Zubair (2014b) and studied the evolution functions f of PDE with three cut-offs namely particle horizon, event horizon and conformal age of the universe in FRW spacetime. The results are summarized as follows.

For particle horizon, the evolution trajectories of f and R are shown in f−R, lf−lR, R−z and f−z planes which indicate the evolution of PDE. We employ the parameter μ=−1,−2,−3, n=2 and future evolution is shown in Fig. 2. The evolution trajectories of f correspond to the plots (1)–(3) in Sharif and Zubair (2014b). In case of PDE with event horizon, the difference in evolution trajectories of f is quite evident as shown in Fig. 3. The behavior of R clearly shows the dominance of DE in future evolution. We set the evolution parameters according to Sharif and Zubair (2014b) and distinctive nature of f is shown in Fig. 4 which does favor the phantom evolution. The evolution trajectories in case of conformal time scale favors the ΛCDM regime which is obvious from Fig. 5. Thus the reconstructed f(R) functions corresponding to PDE are consistent with that of cosmological parameters in Sharif and Zubair (2014b). It is to be noted that PDE model is developed in the context of general relativity rather than in any modified theory. The PDE parameter is constrained from latest observational data to speculate the phantom behavior of DE. In fact f(R) theory is modified Einstein gravity where scalar curvature R is replaced by an arbitrary function and it is formulated to understand various cosmic issues. In this work, we have developed the correspondence of f(R) theory with PDE and reconstructed f(R) by considering curvature part as an effective description for PDE.