1 Introduction

Ever since the formulation of Einstein–Maxwell field equations, a search of new exact solution with certain geometrical and physical conditions is the interest of venture of relativist. Because this facilitates the modeling and distribution of matter in the interior of stellar objects such as quasar, neutron star, pulsar, quark star, black-hole or other super-dense objects, Bonnor (1965) pointed out that the presence of some charge may avert the gravitational collapse by counter balancing the gravitational attraction by electric repulsion in addition to the pressure gradient. Ivanov (2002) proposed a model for charged perfect fluid and concluded that the inclusion of charge inhibits the growth of space time curvature which has a great role to avoid singularities. Thus it is pleasing to study the implications of Einstein–Maxwell field equations with reference to the general relativistic prediction of gravitational collapse. For this purpose charged fluid ball models are required and the external field of such a ball is to be matched with the Reissner–Nordström solution.

Due to the strong nonlinearity of Einstein’s field equations and the lack of a comprehensive algorithm to generate all solutions, it becomes difficult to obtain new exact solutions. A well number of exact solutions of field equations are known to date but not all of them are physically relevant in the description of relativistic structure of compact stellar objects. Now there exist a number of comprehensive collections of static, spherically symmetric solutions (Delgaty & Lake 1998; Stephani & et al. 2003) which provide a useful guide to the literature.

A class of fluid spheres for whose surface density equals to typical nuclear density where the pressure vanishes may be a good approximation for normal matter neutron stars (this class includes Tolman VII solution (1939) and Buchdahl solutions (1967)). Other classes of solutions for which surface density is finite, about 2–3 times the normal nuclear matter saturation density, at the surface where pressure vanishes may be taken as an analytical model of self-bound strange quark star. Such models include Tolman’s IV solution (1939) and the solutions discussed by Wyman (1949), Buchdahl (1964), Mehra (1966), Leibovitz (1969), Heintzmann (1969), Adler (1974), Adams & Cohen (1975), Kuchowicz (1975), Vaidya & Tikekar (1982), Durgapal (1982), Durgapal & Bannerji (1983), Durgapal & Fuloria (1985), Tikekar (1990), Pant & Pant (1993), Pant (1994), Pant (1996), Gupta & Jasim (2003), Tikekar & Jotania (2005), Tikekar & Thomas (1998), Sharma & et al. (2006), Jotania & Tikekar (2006), Takisa & Maharaj (2013) and Maurya et al. (2014a, 2014b).

All the solutions mentioned above are in curvature coordinates. Out of 127 static spherically symmetric solutions very few solutions in isotropic coordinates such as Nariai (1950) and Goldman (1978) are known to pass the elementary tests of physical relevance and hence relevant in modeling compact stellar objects in astrophysics (Delgaty & Lake 1998). Kuchowicz presented some practical methods to solve Einstein’s equations in isotropic coordinates. The method outlined in his series of papers (Kuchowicz 1971a, b, 1972a, b, 1973) was able to yield all possible exact solutions for spheres of perfect fluid in isotropic coordinates. Such exact solutions provide simplified models of static relativistic objects. The generation technique used by Hajj-Boutros (1986) leads directly to several new solutions in isotropic coordinates. Rahman & Visser (2002) and Lake (2003) also discussed a simplified algorithm for constructing all possible spherically symmetric perfect fluid solutions of Einstein’s equations in isotropic coordinates. By means of a matrix transformation, Mak & Harko (2005) have reduced Einstein’s equations to two independent Riccati differential equations for which three classes of solutions are obtained. John & Maharaj (2006) reduced the condition for pressure isotropy to a recurrence equation with variable, rational coefficients of order three. They found an exact solution to the field equations corresponding to a static spherically symmetric gravitational potential in terms of elementary functions. The metric functions, the energy density and the pressure are found continuous and well behaved which implies that this solution could be used to model the interior of a relativistic star. The discussion of compact astrophysical objects within the frame work of classical general relativity is relatively simple. Our principal motivation of this work is to present a simple particular class of exact relativistic compact stellar astrophysical objects by solving Einstein–Maxwell gravitational field equations in isotropic coordinates. In recent past, one successful attempt in isotropic coordinates has been made by Pant et al. (2010, 2014). These solutions are not only well behaved but also simple in terms of expressions of field and physical variables. We present here a new class of solutions of Einstein–Maxwell field equations with well behaved neutral counterpart in isotropic coordinates with the motivation by Das & et al. (2011), Ivanov (2012) and Murad & Pant (2014). Such solutions are expected to provide simplified but easy to mathematically analyzed compact stellar model of bare strange quark star.

2 Field equations in isotropic coordinates

The interior metric of a static spherically symmetric matter distribution in isotropic coordinates may be taken as

$$ \mathrm{d}s^{2}=-\mathrm{e}^{\omega}[\mathrm{d}r^{2}+r^{2}(\mathrm{d}\theta^{2}+\sin^{2}\theta \mathrm{d}\varphi^{2})]+c^{2}\mathrm{e}^{\nu}\mathrm{d}t^{2}, $$
(1)

where α and β are functions of r only.

Einstein–Maxwell field equations of gravitation for a non empty space-time are

$$\begin{array}{@{}rcl@{}} R_{j}^{i}-\frac{1}{2}R\delta^{i}_{j}&=&-\frac{8\pi G}{c^{4}}T^{i}_{j}\\ &=&\frac{8\pi G}{c^{4}}\left[(p+\rho c^{2})\nu^{i}\nu_{j}-p\delta^{i}_{j}+\frac{1}{4\pi}\left( -F^{im}F_{jm}+\frac{1}{4}\delta^{i}_{j}F_{mn}F^{mn}\right)\right], \end{array} $$
(2)

where R i j is a Ricci tensor, T i j is the energy-momentum tensor, R is the scalar curvature, F i j is the electromagnetic field tensor, p denotes the pressure distribution, ρ the density distribution and ν i the velocity vector, satisfying the relation

$$ g_{ij}\nu^{i}\nu^{j}=1. $$
(3)

Since the field is static, therefore

$$ \nu^{i}=\nu^{i}=\nu^{i}=0\qquad\text{and}\qquad\nu^{4}=\frac{1}{\sqrt{g_{44}}}. $$
(4)

For the metric equation (1) the Einstein–Maxwell field equations (2) of gravitation for a nonempty space-time reduce to the following set of relevant equations (Pradhan & Pant 2014)

$$ \frac{8\pi G}{c^{4}}p=\mathrm{e}^{-\omega}\left( \frac{\omega^{\prime2}}{4}+\frac{\omega^{\prime}}{r}+\frac{\omega^{\prime}\nu^{\prime}}{2}+\frac{\nu^{\prime}}{r}\right)+\frac{q^{2}}{r^{4}}, $$
(5)
$$ \frac{8\pi G}{c^{4}}p=\mathrm{e}^{-\omega}\left( \frac{\omega^{\prime\prime}}{2}+\frac{\nu^{\prime\prime}}{2}+\frac{\nu^{\prime2}}{4}+\frac{\omega^{\prime}}{2r}+\frac{\nu^{\prime}}{2r}\right)-\frac{q^{2}}{r^{4}}, $$
(6)
$$ \frac{8\pi G}{c^{2}}\rho=-\mathrm{e}^{-\omega}\left( \omega^{\prime\prime}+\frac{\omega^{\prime2}}{4}+\frac{2\omega^{\prime}}{r}\right)-\frac{q^{2}}{r^{4}}, $$
(7)

where prime (\(^{\prime }\)) denotes the differentiation with respect to r. Eliminating the pressure p from equations (5) and (6), we obtain following differential equation known as the ‘pressure isotropy’ equation,

$$ \mathrm{e}^{-\omega}\left( \omega^{\prime\prime}+\nu^{\prime\prime}+\frac{\nu^{\prime2}}{2}-\frac{\omega^{\prime2}}{2}-\omega^{\prime}\nu^{\prime}-\frac{\omega^{\prime}}{r}-\frac{\nu}{r}\right)-\frac{4q^{2}}{r^{4}}=0. $$
(8)

Our task is to explore the solutions of equation (8) and to obtain a physically meaningful matter distribution described by the fluid parameters p and ρ from equations (5) and (7). To solve the above equation, we consider a seed solution (Pant & et al. 2010), and the electric intensity E of the following form:

$$ \frac{E^{2}}{b}=\frac{q^{2}}{br^{4}}=\frac{Kbr^{2}}{\text{cosec}^{2}(a+br^{2})} $$
(9)

where Kis a positive constant. The electric intensity is so assumed that the model is physically significant and well behaved, i.e. E remains regular and positive throughout the sphere. In addition, E vanishes at the center of the star and increases towards the boundary.

3 Conditions for a well behaved solution

For well behaved nature of the solution in isotropic coordinates, the following conditions should be satisfied:

  1. (i)

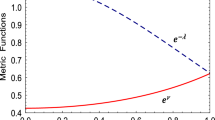
    The solution should be free from physical and geometrical singularities i.e. finite and positive values of central pressure, central density and non zero positive values of eω and eν.

  2. (ii)

    The solution should have positive and monotonically decreasing expressions for pressure and density (p and ρ) with the increase of r. The solution should have positive value of ratio of pressure–density and less than 1 (weak energy condition) and less than 1/3 (strong energy condition) throughout within the star, monotonically decreasing as well.

  3. (iii)

    The causality condition should be obeyed i.e. velocity of sound should be less than that of light throughout the model. In addition to the above, the velocity of sound should be decreasing towards the surface i.e. (d/dr)(dp/dρ)>0 for 0≤r≤r b , i.e. the velocity of sound increases with the increase in density. In this context, it is worth mentioning that the equation of state at ultra-high distribution has the property that the speed of sound decreases outwards (Canuto & Lodenquai 1975).

  4. (iv)

    p/ρ ≤ dp/dρ everywhere within the ball. \(\gamma =\mathrm {d}\ln p/\mathrm {d}\ln \rho =(\rho /p)\mathrm {d}p/\mathrm {d}\rho \Rightarrow \mathrm {d}p/\mathrm {d}\rho =\gamma p/\rho \) for realistic matter γ≥1.

  5. (v)

    The redshift Z should be positive, finite and monotonically decreasing in nature with the increase of r.

  6. (vi)

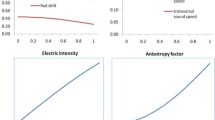
    Electric intensity E, such that E r=0=0, is taken to be monotonically increasing.

Under these conditions, we have to assume one of the gravitational potential components in such a way that the field equation (8) can be integrated and solution should be well behaved. Further, the mass of such a modeled super dense object can be maximized by assuming surface density for neutron star ρ b =2×1014 g cm −3 (Brecher & Caporaso 1976) and for SQM star ρ b =4.6888×1014 g cm −3 (Zdunik 2000; Fatema & Murad 2013).

4 Boundary conditions in isotropic coordinates

For exploring the boundary conditions, we use the principle that the metric coefficients g i j and their first derivatives g i j,k in interior solution (I) as well as in exterior solution (E) are continuous on the boundary B (Bonnor & Vickers 1981). The continuity of metric coefficients g i j of I and E on the boundary is known as the first fundamental form. The continuity of derivatives of metric coefficients g i j of I and E on the boundary is known as the second fundamental form.

The exterior field of a spherically symmetric static charged fluid distribution is described by Reissner–Nordström metric given by

$$ \mathrm{d}s^{2}{\kern-2.5pt}={\kern-2.5pt}\left( {\kern-1.5pt}1{\kern-1.5pt}-{\kern-1.5pt}\frac{2GM}{c^{2}R}{\kern-1.5pt}+{\kern-1.5pt}\frac{q^{2}}{R^{2}}{\kern-1.5pt}\right)c^{2}\mathrm{d}t-\left( {\kern-1.5pt}1{\kern-1.5pt}-{\kern-1.5pt}\frac{2GM}{c^{2}R}{\kern-1.5pt}+{\kern-1.5pt}\frac{q^{2}}{R^{2}}{\kern-1.5pt}\right)^{-1} \mathrm{d}R^{2}{\kern-1.5pt}-{\kern-1.5pt}R^{2}\mathrm{d}\theta^{2}{\kern-1.5pt}-{\kern-1.5pt}R^{2}\sin^{2}\theta\mathrm{d}\varphi^{2}, $$
(10)

where M is the mass of the fluid ball as determined by the external observer and R is the radial coordinate of the exterior region. Since equation (10) is considered as the exterior solution, we shall arrive at the following conclusions by matching the first and second fundamental forms:

$$ \mathrm{e}^{\nu_{b}}=\left( 1-\frac{2GM}{c^{2}R_{b}}+\frac{q_{b}^{2}}{R_{b}^{2}}\right), $$
(11)
$$ R_{b}=r_{b}\cdot \mathrm{e}^{\frac{\omega_{b}}{2}} q_{(\text{at}\;r=r_{b})}=q_{b} $$
(12)
$$ \frac{1}{2}\left( \omega^{\prime}+\frac{2}{r}\right)_{b}r_{b}=\left( 1-\frac{2GM}{c^{2}R_{b}}+\frac{q_{b}^{2}}{R_{b}^{2}}\right)^{\frac{1}{2}}, $$
(13)
$$ \frac{1}{2}(\nu^{\prime})_{b}r_{b}=\left( \frac{GM}{c^{2}R_{b}}-\frac{q_{b}^{2}}{R_{b}^{2}}\right)\left( 1-\frac{2GM}{c^{2}R_{b}}+\frac{q_{b}^{2}}{R_{b}^{2}}\right)^{-\frac{1}{2}}. $$
(14)

Equations (11) to (14) are four conditions, known as the boundary conditions in isotropic coordinates. Moreover, (12) and (14) are equivalent to zero pressure of the interior solution on the boundary.

5 A new class of solution

Equation (8) is solved by assuming the seed solution as in Pant & et al. (2010) and the electric intensity E in such a manner that the solution can be obtained and physically viable. Thus we have

$$\begin{array}{@{}rcl@{}} \mathrm{e}^{\frac{\omega}{2}}=\text{cosec}(a+x),\quad x=br^{2},~~~~~~~~~~~~~\\ y=\frac{\mathrm{d}\nu}{\mathrm{d}x}\; \quad\text{and}\quad q^{2}=\frac{K}{b}x^{3}\cdot \text{cosec}^{-2}(a+x). \end{array} $$
(15)

On substituting the above in equation (8), we get the following Riccati differential equation in y,

$$ \frac{\mathrm{d}y}{\mathrm{d}x}=(k-2)-2\cot(a+x)y-\frac{1}{2}y^{2} $$
(16)

which yields the following solution:

$$ \mathrm{e}^{\frac{\nu}{2}}=[c_{1}\mathrm{e}^{-sx}+c_{2}\mathrm{e}^{sx}]\text{cosec}(a+x), $$
(17)

where a, b, c 1, c 2 and K are arbitrary constants and

$$ s=\sqrt{\frac{K}{2}-2}\quad \text{is real for}\; K>4. $$
(18)

The expressions for density and pressure are given by

$$ \frac{8\pi G}{c^{2}}\rho=\frac{1}{\text{cosec}^{2}(a+x)}(12b\cot(a+x)-12bx\cot^{2}(a+x)-8bx+kbx), $$
(19)
$$ \frac{8\pi G}{c^{4}}p=\frac{1}{\text{cosec}^{2}(a+x)}\left[\begin{array}{c}12bx\cot^{2}(a+x)-8bx\cot(a+x)\frac{L^{\prime}}{L}\\-8b\cot(a+x)+4b\frac{L^{\prime}}{L}+Kbx\end{array}\right], $$
(20)

where

$$ L=c_{1}\mathrm{e}^{-sx}+c_{2}\mathrm{e}^{sx},\;s=\sqrt{\frac{K}{2}-2}\quad\text{and}\quad K>4. $$
(21)

6 Properties of the new solution

The central values of pressure and density are given by

$$ \left( \frac{8\pi G}{c^{4}}p\right)_{r=0}=\frac{1}{\text{cosec}^{2}a}\left[-8b\cot a+\frac{4b(-c_{1}+c_{2})}{c_{1}+c_{2}}\right], $$
(22)
$$ \left( \frac{8\pi G}{c^{2}}\rho\right)_{r=0}=\frac{1}{\text{cosec}^{2}a}[12b\cot a]=6b\sin 2a. $$
(23)

The central values of pressure and density will be non zero positive definite, if the following conditions will be satisfied

$$ \frac{c_{1}}{c_{2}}<\frac{s-2\cot a}{s+2\cot a}\quad\text{and}\quad\sin2a>0. $$
(24)

In view of equations (19) and (20), the ratio of pressure-density is given by

$$ \frac{p}{c^{2}\rho}=\frac{\left[\begin{array}{c}12bx\cot^{2}(a+x)-8bx\cot(a+x)L^{\prime}/L\\-8b\cot(a+x)+4b{L^{\prime}}/{L}+Kbx\end{array}\right]}{12b\cot(a+x)-12bx\cot^{2}(a+x)-8bx+kbx}. $$
(25)

Subjecting the condition that positive value of ratio of pressure-density and less than 1 at the centre, i.e. p 0/c 2 ρ 0≤1, leads to the following inequality:

$$ \left( \frac{p}{c^{2}\rho}\right)_{r=0}=\frac{-2\cot a+\frac{c_{2}-c_{1}}{(c_{1}+c_{2})}}{3\cot a}. $$
(26)

All the values of a which satisfy equation (24) will also lead to the condition p 0/c 2 ρ 0≤1. Differentiating equation (20) with respect to x, we get

$$\begin{array}{@{}rcl@{}} \frac{8\pi G}{c^{4}}\frac{\mathrm{d}p}{\mathrm{d}x}&=&12b\cos^{2}(a+x)-12bx\sin 2(a+x)-4b\frac{L^{\prime}}{L}\sin 2(a+x)\\ &&-8b\frac{L^{\prime}}{L}x\cos2(a+x)-4bx\sin2(a+x)\frac{LL^{\prime\prime-(L^{\prime})^{2}}}{L^{2}}\\ &&-8b\cos2(a+x)+4b\frac{L^{\prime}}{L}\sin2(a+x)+4\sin^{2}(a+x)\frac{LL^{\prime\prime}-(L^{\prime})}{L^{2}}\\ &&+Kbx\sin2(a+x)+Kb\sin(a+x), \end{array} $$
(27)
$$\begin{array}{@{}rcl@{}} &&{\kern-9.6pc}\left( \frac{8\pi G}{c^{4}}\frac{\mathrm{d}p}{\mathrm{d}x}\right)_{x=0}=12b\cos^{2}a+4b{\frac{f}{g}}-\sin2a-8b\cos2a\\ &&{\kern-2.6pc}+4s^{2}\left( 1-\frac{f}{g}\right)b\sin^{2}a+Kb\sin^{2}a, \end{array} $$
(28)

where f=−c 1 s + c 2 s, g = c 1 + c 2. Thus it is found that extrema of p occur at the centre i.e.,

$$ p^{\prime}=0\Rightarrow r=0\quad\text{and}\quad\frac{8\pi G}{c^{4}}(p^{\prime\prime})_{r=0}<0 $$
(29)

Thus the pressure is maximum at the centre and decreases monotonically. Now differentiating equation (19) with respect to x, we get

$$\begin{array}{@{}rcl@{}} \frac{8\pi G}{c^{2}}\frac{\mathrm{d}\rho}{\mathrm{d}x}&=&[-8b+12b\cos2(a+x)-4b\cos^{2}(a+x)+4bx\sin2(a+x)\\ &&-kb\sin^{2}(a+x)-kbx\sin2(a+x)]. \end{array} $$
(30)

Extrema of ρ occur at the centre if

$$ \rho^{\prime}=0\Rightarrow r=0\qquad\text{and}\qquad\frac{8\pi G}{c^{2}}(\rho^{\prime\prime})_{r=0}<0. $$
(31)

Thus, the density ρ is maximum at the centre and decreases monotonically. The square of adiabatic sound speed at the centre, (dp/c 2dρ) r=0, is given by

$$ \frac{1}{c^{2}}\left( \frac{\mathrm{d}p}{\mathrm{d}\rho}\right)_{r=0}=\frac{\left[-4\cos^{2}a+8+4\frac{f}{g}\sin2a+4s^{2}\left( 1-\frac{f}{g}\right)\sin^{2}a+K\sin^{2}a\right]}{20\cos^{2}a-20+K \sin^{2}a} $$
(32)

and

$$0<\frac{1}{c^{2}}\left( \frac{\mathrm{d}p}{\mathrm{d}\rho}\right)_{r=0}<1. $$

The causality condition is obeyed at the centre for all values of constants satisfying condition (24). Due to cumbersome expressions of equations (25) and (32), the trend of pressure–density ratio and adiabatic sound speed is studied analytically after applying the boundary conditions. Applying the boundary conditions from equations (11) to (14), we get the values of the arbitrary constants in terms of Schwarzschild parameters u = G M/c 2 R b and radius of the star R b :

$$ c_{1}=\left[2s-\frac{1-d}{x}-\frac{u-e^{2}}{\mathrm{d}X}\right]d\sin(a+x)\frac{\mathrm{e}^{sX}}{4s}, $$
(33)
$$ c_{1}=\left[2s+\frac{1-d}{x}+\frac{u-e^{2}}{\mathrm{d}X}\right]d\sin(a+x)\frac{\mathrm{e}^{-sX}}{4s}, $$
(34)
$$ X=br^{2}_{b}=\frac{1-d}{2\cot(a+x)}, $$
(35)

where we define a new parameter called the Reissner–Nordström parameter d by

$$ d=\left( 1-2u+\frac{q_{b}^{2}}{R_{b}^{2}}\right)^{\frac{1}{2}} $$
(36)

whose value is less than 1,

$$0<d<1\qquad\text{for}\;br^{2}_{b}>0. $$

The central and surface redshifts are given by

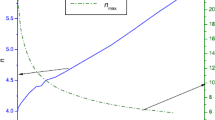
$$ Z_{0}=\frac{\sin a}{c_{1}+c_{2}}-1,\quad Z_{b}=\mathrm{e}^{-\frac{\nu_{b}}{2}}-1. $$
(37)

Mass M can be calculated as

$$ M=\frac{c^{2}R_{b}}{2G}[1-d^{2}+kX^{2}\sin^{4}(a+x)]. $$
(38)

Radius R b can be determined from surface density ρ b in equation (19) as

$$ R_{b}^{2}=\frac{Xc^{2}\text{cosec}^{2}(a+x)}{8\pi G\rho_{b}}[6\sin2(a+X)-8X-4X\cos^{2}(a+X)-kX\sin^{2}(a+x)]. $$
(39)

Now theexpression for gravitational red-shift z and adiabatic index γ are given as

$$ z=\mathrm{e}^{-\frac{\nu}{2}}-1\quad\text{and}\quad\gamma=\frac{\mathrm{d}p}{\mathrm{d}\rho}\left/\frac{p}{\rho}\right.\!. $$
(40)

7 Discussions and conclusions

It has been observed from Table 1 and Figure 1 that the physical parameters (p,ρ,p/c 2 ρ,z) are positive at the centre and within the limit of realistic state equation and monotonically decreasing while the electric intensity and stiffness parameter increases from the center to the surface.

Table 1 The march of pressure, density, pressure–density ratio, square of adiabatic speed of sound, γ, red shift and electric field intensity within the ball corresponding to K=6.13 and X=0.077.
Full size table
Figure 1
figure 1

The variation of p, \(\rho , \frac {p}{\rho c^{2}}\), Z, \(\frac {1}{c^{2}}\left ({\frac {\mathrm {d}p}{\mathrm {d}\rho }} \right )\), γ, E, etc. from the centre to the surface for K=6.13 and X = 0.077 are shown in the following graphs.

Full size image

Our solution is well behaved in all respects for all values of X lying in the range 0<X≤0.11, K lying in the range 4<K≤6.2 and Schwarzschild compactness parameter u lying in the range 0<u≤0.247. Since our solution is well behaved for wide ranges of the parameters, we can model many different types of ultra-cold compact stars like quark stars and neutron stars.

From Table 2, we observe that corresponding to X=0.077 and K=6.13 for which u=0.2051 and by assuming surface density ρ b =4.6888×1014 g cm −3, the mass and radius are found to be 1.509M ⊙, 10.906 km, respectively which match with the observed values of mass 1.51M ⊙ and radius 10.90 km of the quark star XTE J1739-217.

Table 2 Comparison of experimental values of mass and radius for well known quark star XTE J1739-217 with our calculated values.
Full size table