1 Introduction

Nowadays the research works on the nonlinear propagation of solitary waves (SWs) in electron-positron-ion (e-p-i) plasmas have been received a considerable attention because of significant importance to understand the behavior of space plasmas viz. supernovas, pulsar environments, cluster explosions, and active galactic nuclei (Begelman et al. 1984; Miller and Witta 1987; Tribeche et al. 2009). Some theoretical investigations (Popel et al. 1995; Shukla et al. 2004; Mahmood and Ur-Rehman 2009) have been made on the nonlinear propagation of ion-acoustic (IA) SWs in e-p-i plasmas based on Maxwellian assumption.

Recently, the nonlinear phenomena (viz. solitons, shocks, double layers, etc.) associated with positron-acoustic (PA) waves have been attracted to a number of authors (Tribeche et al. 2009; Nejoh 1996; Tribeche 2010; Sahu 2010; El-Shamy et al. 2012). PA waves are basically acoustic-type of waves, in which the inertia is provided by the cold positron mass, and the restoring force is provided by the thermal pressure of hot positrons. Nejoh (1996) studied the nonlinear wave structures of large-amplitude PA waves in an electron-positron plasma with an electron beam. Tribeche et al. (2009) investigated the PA SWs in a four-component plasma system consisting of mobile cold positrons, immobile positive ions, and Boltzmann distributed electrons and positrons. One year later, Tribeche (2010) analyzed the small amplitude PA double layers (DLs) in e-p-i plasmas considering the same plasma species. Sahu (2010) investigated the planar and nonplanar PA shock waves in an unmagnetized plasma consisting of mobile cold positrons, stationary positive ions and Boltzmann-distributed electrons and hot positrons. Using the Poincaré-Lighthill-Kuo method El-Shamy et al. (2012) theoretically investigated the characteristics of the head-on collision between two PA SWs considering the same plasma model as like as the considered model of Tribeche et al. (2009), Tribeche (2010) and Sahu (2010). However, all of these works (Tribeche et al. 2009; Tribeche 2010; Sahu 2010; El-Shamy et al. 2012) are concerned with Maxwellian distributed electrons and positrons.

A wide range of investigations of space plasmas are characterized by a particle distribution function with high energy tail and they may deviate from the Maxwellian (Alam et al. 2013a; Alam 2013). In the heliospheric environments, the plasma contains the nonthermally distributed ions (Tasnim et al. 2013a; Shuchy et al. 2013) or electrons (Mamun et al. 1996; Shukla and Mamun 2002; Verheest and Pillay 2008). Thus population of energetic or nonthermal particles and their distribution have received a great deal of attention in understanding the nonlinear electrostatic perturbations in space plasmas, particularly in the upper Martian ionosphere (Lundin et al. 1989), in the lower part of magnetosphere (Boström 1992), in/around the Earth’s bow shock (Matsumoto et al. 1994), etc. Cairns et al. (1995) used nonthermal distributed electrons to study the IA SWs which were observed by the Freja and Viking satellites (Boström 1992; Dovner et al. 1994; Mamun 2000). Baluku and Hellberg (2011) studied the arbitrary amplitude IA SWs and DLs by using the Sagdeev potential approach in an e-p-i plasma consisting of nonthermal (Cairns-distributed) electrons, Boltzmann positrons and cold ions. Jilani et al. (2012) analyzed the IA solitons in e-p-i plasma with nonthermal electrons. Verheest et al. (2013) studied the dust-ion-acoustic (DIA) super solitons in a dusty plasma with immobile negative dust, cold fluid protons, and nonthermal electrons through a Sagdeev pseudopotential approach. Recently, Chatterjee et al. (2012) investigated the nonlinear propagation of IA shock waves in an unmagnetized plasma consisting of nonthermal electrons, nonthermal positrons, and singly charged adiabatically hot positive ions. Alinejad (2010) rigorously studied the DIA SWs and shock structures in a dusty plasma with nonthermal electrons.

However, all of these works (Popel et al. 1995; Shukla et al. 2004; Mahmood and Ur-Rehman 2009; Nejoh 1996; Tribeche 2010; Sahu 2010; El-Shamy et al. 2012; Baluku and Hellberg 2011; Jilani et al. 2012; Chatterjee et al. 2012; Alinejad 2010) are limited to one dimensional (1D) planar geometry associated with either IA SWs or PA SWs in e-p-i plasmas which may not be a realistic situation in space and laboratory devices. Since in many cases, the wave structures observed in space or laboratory devices are certainly not infinite (unbounded) in one dimension (Shukla and Rosenberg 1999). The nonplanar geometries of practical interest are capsule implosion (spherical geometry), shock tube (cylindrical geometry), star formation, supernova explosions, etc.

Some of the investigations (Sahu and Roychoudhury 2005; Jehan et al. 2007; Sabry et al. 2009) have been reported on the study of nonplanar IA SWs in e-p-i plasmas. Moslem et al. (2007) used cylindrical geometry to study the propagation of nonlinear excitations in an e-p-i plasma in the inner region of the accretion disc. They inferred that the solitary potential excitations suffer a velocity modification because of the deviation from the radial direction. Li (2010) investigated the interaction of IA SWs in a nonplanar quantum plasma and found that the variations of phase shifts with quantum Bohm potential for compressive and rarefactive IA SWs are quite different. These works (Sahu and Roychoudhury 2005; Jehan et al. 2007; Sabry et al. 2009; Moslem et al. 2007; Li 2010) are concerned with nonplanar IA SWs in e-p-i plasmas.

Recently, a number of authors have been investigated the nonlinear propagation of planar GSs (Deeba et al. 2012; Masud et al. 2012; Tasnim et al. 2013b; Alam et al. 2014; Lee 2009) and nonplanar GSs (Mannan and Mamun 2011; Akhter et al. 2013; Ghosh et al. 2013; Alam et al. 2013b) in their considered plasma system. But up to now, no theoretical investigation has been performed on the cylindrical and spherical PA GSs in e-p-i plasmas with nonthermal (Cairns distributed) electrons and hot positrons. Therefore, we consider a four-component plasma system consisting of nonthermal distributed electrons and hot positrons, mobile cold positrons, and immobile positive ions. In this paper, we see that cylindrical and spherical geometries associated with PA GSs differ qualitatively from those in 1D planar geometries and we also observe that how nonthermal electrons and hot positrons significantly affect them.

It is noted here that reductive perturbation method is used for small amplitude SWs (Verheest and Cattaert 2004; Gogoi et al. 2012). Small-amplitude SWs observed in the auroral plasma between altitudes of 6000 and 8000 km (Temerin et al. 1982). Higher order approximations can not be neglected in case of large amplitude SWs (specially DLs) and perturbation method is not adequate to study such waves (Gogoi et al. 2012). Sagdeev was the first to use non-perturbative approach to study SWs in plasmas. Sagdeev’s pseudopotential method is suitable to study large amplitude SWs and DLs (Gogoi et al. 2012). However, our intention here is to study small amplitude SWs by using reductive perturbation method.

The manuscript is organized as follows. The governing equations are provided in Sect. 2. The MG equation is derived by using the reductive perturbation method in Sect. 3. The analytical and numerical solutions are presented in Sect. 4. A brief discussion is finally given in Sect. 5.

2 Governing equations

We consider a nonplanar (cylindrical or spherical) geometry, and nonlinear propagation of the PA waves in a four-component plasma system consisting of nonthermal distributed electrons and hot positrons, mobile cold positrons, and immobile positive ions. Hence, at equilibrium, n e0=n pc0+n ph0+n i0, where n i0, n e0 are the unperturbed ion number density and electron number density respectively. n pc0 (n ph0) is the number density of unperturbed cold (hot) positron.

The electrons and hot positrons are assumed to obey nonthermal distribution on the PA wave time scale and are given by the following expressions (Cairns et al. 1995):

$$\begin{aligned} &{n_e=n_{e0}\bigl(1-\beta\phi+\beta \phi^2\bigr)\exp{\biggl(\frac{e\phi}{T_e}\biggr)},} \\ &{n_{ph}=n_{ph0}\bigl(1+\beta\phi+\beta \phi^2\bigr)\exp{\biggl(\frac{-e\phi}{T_{ph}}\biggr)},} \end{aligned}$$

where β is the nonthermal parameter, n e and n ph are the number densities of perturbed electron and hot positron, while T e and T ph are the temperatures of electron and hot positron (in the energy units), respectively. The range of the nonthermal parameter β is 0≤β≤4/3 (El-Taibany et al. 2010; El-Labany et al. 2012; Gogoi et al. 2012). When β→0, the above two equations give the Boltzmann distribution of electrons and hot positrons, respectively.

The normalized basic equations governing the dynamics of the PA waves in a nonplanar geometry are given in dimensionless variables as follows:

$$\begin{aligned} &{\frac{\partial n_{pc}}{\partial t} +\frac{1}{r^\nu} \frac{\partial}{\partial r} \bigl(r^\nu n_{pc} u_{pc}\bigr)=0,} \end{aligned}$$
(1)
$$\begin{aligned} &{\frac{\partial u_{pc}}{\partial t} + u_{pc} \frac{\partial u_{pc}}{\partial r}=- \frac{\partial \phi}{\partial r},} \end{aligned}$$
(2)
$$\begin{aligned} &{\frac{1}{r^\nu}\frac{\partial}{\partial r} \biggl(r^\nu \frac{\partial\phi}{\partial r} \biggr)=-\rho,} \end{aligned}$$
(3)
$$\begin{aligned} &{-\rho=-n_{pc}-\mu_{1}\bigl(1+\beta \sigma_1\phi+\beta\sigma_1^{2} \phi^{2}\bigr)\exp{(-\sigma_1\phi)}} \\ &{\phantom{-\rho=} {}+\mu_{2}\bigl(1-\beta\sigma_2 \phi+\beta\sigma_2^{2}\phi^{2}\bigr)\exp{( \sigma_2\phi)}-\mu_{3}.} \end{aligned}$$
(4)

It is to be noted that ν=0 for 1D planar geometry, and ν=1 (2) for a nonplanar cylindrical (spherical) geometry. Here n pc is the cold positron number density normalized by its equilibrium value n pc0, u pc is the cold positron fluid speed normalized by C pc =(k B T ef /m p )1/2, ϕ is the electrostatic wave potential normalized by k B T ef /e, the time variable t is normalized by \(\omega_{pc}^{-1}=(m_{p}/4\pi n_{pc0}e^{2})^{1/2}\) and the space variable x is normalized by the Debye length λ Dm =(k B T ef /4πn pc0 e 2)1/2, k B is the Boltzmann constant, m p is the positron mass, ρ is the surface charge density, and e is the magnitude of the electron charge, σ 1=T ef /T ph , σ 2=T ef /T e , μ 1=n ph0/n pc0, μ 2=n e0/n pc0, μ 3=n i0/n pc0, and T ef =T e T ph /(μ 1 T e +μ 2 T ph ) is the effective temperature. It should be noted here that for any plasma species having two different temperatures, many authors use effective temperature for normalization (Jones et al. 1975; Masood et al. 2009). However, instead of effective temperature one can use other species temperature for normalization. It is, in fact, not important which temperature we use for normalization. Since the physics of the work does not depend on normalization at all.

3 Derivation of the MG equation

To study the finite amplitude PA GSs by analyzing the ingoing solutions of Eqs. (1)–(4), we first introduce the stretched coordinates:

$$\begin{aligned} &{\zeta={\epsilon}(r - V_pt),} \end{aligned}$$
(5)
$$\begin{aligned} &{\tau={\epsilon}^3t,} \end{aligned}$$
(6)

where V p is the phase speed (ω/k) of the perturbation mode and ϵ is a smallness parameter measuring the weakness of the dispersion (0<ϵ<1). To obtain a dynamical equation, we also expand the perturbed quantities n pc , u pc , ϕ, and ρ in power series of ϵ. Let M be any of the system variables n pc , u pc , ϕ, and ρ describing the systems’s state at a given position and instant. We consider small deviations from the equilibrium state M (0)—which explicitly is \(n_{pc}^{(0)}=1\), \(u_{pc}^{(0)}=0\), ϕ (0)=0, and ρ (0)=0 by taking

$$\begin{aligned} M= M^{(0)}+\sum_{n=1}^\infty { \epsilon^n M^{(n)}}. \end{aligned}$$
(7)

To the lowest order in ϵ, Eqs. (1)–(7) give

$$\begin{aligned} &{u_{pc}^{(1)}=\frac{1}{V_p}\psi,} \end{aligned}$$
(8)
$$\begin{aligned} &{n_{pc}^{(1)}=\frac{1}{V_p^2}\psi,} \end{aligned}$$
(9)
$$\begin{aligned} &{\rho^{(1)}=0,} \end{aligned}$$
(10)
$$\begin{aligned} &{V_p=\frac{1}{\sqrt{(1-\beta)(\mu_1\sigma_1+\mu_2\sigma_2)}},} \end{aligned}$$
(11)

where ψ=ϕ (1). Equation (11) represents the phase speed of the PA waves propagating in a plasma system under consideration. To the next higher order of ϵ, we obtain a set of equations, which, after using Eqs. (8)–(11), can be simplified as

$$\begin{aligned} &{u_{pc}^{(2)}=\frac{1}{2V_p^3}\psi^2+ \frac{1}{V_p}\phi^{(2)},} \end{aligned}$$
(12)
$$\begin{aligned} &{n_{pc}^{(2)}=\frac{3}{2V_p^4}\psi^2+ \frac{1}{V_p^2}\phi^{(2)},} \end{aligned}$$
(13)
$$\begin{aligned} &{\rho^{(2)}=-\frac{1}{2}A\psi^2=0,} \end{aligned}$$
(14)
$$\begin{aligned} &{A=\frac{V_p^3}{2} \biggl[\frac{3}{V_p^4}+\mu_1 \sigma_1^2-\mu_2\sigma_2^2 \biggr].} \end{aligned}$$
(15)

It is obvious from Eqs. (14) that A=0 since ψ≠0. Therefore, the solution of A(μ 1=μ c )=0 for μ 1 is given by

$$\begin{aligned} \mu_{1} =&\mu_{c}=-\frac{1}{6 P^2}+\frac{\sqrt{\sigma_1^2+12\mu_2\sigma_2P^2(\sigma_1+\sigma_2)}}{6\sigma_1 P^2} \\ &{}-\frac{\mu_2\sigma_2}{\sigma_1}, \end{aligned}$$
(16)

where P=(−1+β). Equation (16) represents the critical value of μ 1 above (below) which the SWs with a positive (negative) potential exists. We can find A=0 for a certain (critical) value of μ 1, i.e. A=0 for μ 1=μ c ≃0.116 [obtained from A(μ 1=μ c )=0 for a set of plasma parameters viz. μ 2=0.7, σ 1=3, σ 2=1.5, and β=0.7]. We let A=A 0 when μ 1≠μ c , but μ 1∼μ c . So, for μ 1 around its critical value (μ c ), A=A 0 can be expressed as

$$\begin{aligned} A_0\simeq s \biggl(\frac{\partial A}{\partial \mu_{1}} \biggr)_{\mu_{1}=\mu_{c}}| \mu_{1}-\mu_{c}|=c_1s\epsilon, \end{aligned}$$
(17)

where \(c_{1}=\sigma_{1}^{2}\), |μ 1−μ c | is a small and dimensionless parameter, and can be taken as the expansion parameter ϵ, i.e. |μ 1−μ c |≃ϵ, and s=1 for μ 1>μ c and s=−1 for μ 1<μ c . So, ρ (2) can be expressed as

$$\begin{aligned} \epsilon^2\rho^{(2)}\simeq -\epsilon^3 \frac{1}{2}c_1s\psi^2, \end{aligned}$$
(18)

which, therefore, must be included in the third order Poisson’s equation. To the next higher order in ϵ, we obtain a set of equations:

$$\begin{aligned} &{\frac{\partial n_{pc}^{(1)}}{\partial \tau} -V_p\frac{\partial n_{pc}^{(3)}}{\partial \zeta} + \frac{\partial u_{pc}^{(3)}}{\partial \zeta} +\frac{\partial }{\partial \zeta} \bigl[n_{pc}^{(1)}u_{pc}^{(2)} \bigr]} \\ &{\quad{}+\frac{\partial }{\partial \zeta} \bigl[n_{pc}^{(2)}u_{pc}^{(1)} \bigr] +\frac{\nu u_{pc}^{(1)}}{V_p\tau}=0,} \end{aligned}$$
(19)
$$\begin{aligned} &{\frac{\partial u_{pc}^{(1)}}{\partial \tau}-V_p\frac{\partial u_{pc}^{(3)}}{\partial \zeta}+u_{pc}^{(1)} \frac{\partial u_{pc}^{(2)}}{\partial \zeta}+u_{pc}^{(2)}\frac{\partial u_{pc}^{(1)}}{\partial \zeta}} \\ &{\quad{}+\frac{\partial \phi^{(3)}}{\partial \zeta}=0,} \end{aligned}$$
(20)
$$\begin{aligned} &{\frac{\partial n_{pc}^{(3)}}{\partial \zeta}-\frac{2}{V_p^3}\frac{\partial\psi}{\partial\tau}- \frac{15}{2V_p^6}\psi^2\frac{\partial\psi}{\partial\zeta}-\frac{3}{V_p^4} \frac{\partial}{\partial\zeta} \bigl[\psi\phi^{(2)} \bigr]} \\ &{\quad{}-\frac{\nu}{V_p^3\tau}\psi -\frac{1}{V_p^2}\frac{\partial\phi^{(3)}}{\partial\zeta}=0,} \end{aligned}$$
(21)
$$\begin{aligned} &{\frac{\partial^2 \psi}{\partial \zeta^2}+\frac{1}{2}c_1s \psi^2+n_{pc}^{(3)}-(1-\beta) (\mu_1 \sigma_1+\mu_2\sigma_2)\phi^{(3)}} \\ &{\quad{}+\bigl(\mu_1\sigma_1^2- \mu_2\sigma_2^2\bigr)\psi\phi^{(2)}} \\ &{\quad{}-\frac{1}{2}\bigl(\mu_1\sigma_1^3+ \mu_2\sigma_2^3\bigr) \biggl( \frac{1}{3}+\beta\biggr)\psi^3=0.} \end{aligned}$$
(22)

Now, using Eqs. (11)–(14) and Eqs. (19)–(22), we obtain a equation of the form:

$$\begin{aligned} \frac{\partial\psi}{\partial \tau}+\frac{\nu}{2\tau}\psi+c_1sB\psi \frac{\partial \psi}{\partial \zeta} +\alpha B\psi^2\frac{\partial \psi}{\partial \zeta} + B \frac{\partial^3 \psi}{\partial \zeta^3}=0, \end{aligned}$$
(23)

where

$$\begin{aligned} &{\alpha=\frac{15}{2V_p^6}-\frac{1}{2}(1+3\beta) \bigl( \mu_1\sigma_1^3+\mu_2 \sigma_2^3\bigr),} \end{aligned}$$
(24)
$$\begin{aligned} &{B=\frac{V_p^3}{2}. } \end{aligned}$$
(25)

Equation (23) is known as MG equation. The modification is due to the extra term (viz. \(\frac{\nu}{2\tau}\psi\)), which arises due to the effects of the nonplanar geometry. Equation (23) contains the geometrical term \(\frac{\nu}{2\tau}\psi\) which is singular at τ→0 (Javidan 2013). Therefore, we can analyze the behaviour of SWs near the singularity. It is clear that Eq. (23) is symmetrical respect to time and therefore we can (numerically) solve Eq. (23) in the left limit (τ<0) or right limit (τ>0) of the singularity (Javidan 2013). The evolution of a SW which moves toward the singularity (τ<0) is the same as its evolution when it goes far away from the singularity (τ>0). It should be mentioned that for larger values of τ, the term \(\frac{\nu}{2\tau}\psi\) is negligible. However, as the value of τ decreases, the term \(\frac{\nu}{2\tau}\psi\) becomes dominant. The nonplanar geometrical effect is significant when τ→0 and weaker for larger value of τ.

It would be mentioned here that if we neglect ψ 3 term, and set

$$\begin{aligned} c_1sB=A=\frac{V_p^3}{2} \biggl[\frac{3}{V_p^4}+ \mu_1\sigma_1^2-\mu_2 \sigma_2^2 \biggr], \end{aligned}$$

the MG equation reduces to a modified K-dV equation, which can be derived by using a lower-order stretching, viz.

$$\begin{aligned} \zeta={\epsilon^{1/2}}(r - V_pt),\qquad \tau={ \epsilon}^{3/2}t. \end{aligned}$$

However, in this modified K-dV equation, the nonlinear term vanishes at μ 1=μ c and is not valid near μ 1=μ c , which makes soliton amplitude large enough to break down the validity of the reductive perturbation method. However, the MG equation derived here is valid for nonplanar geometry as well as for μ 1≃μ c .

4 SW solution of MG equation

We have already mentioned that ν=0 corresponds to a 1D planar geometry which reduces Eq. (23) to a standard Gardner equation. Before going to numerical solutions of MG equation, we will first analyze stationary GSs solution of Gardner equation (23) [with ν=0]. To do so, we first introduce a transformation ξ=ζ−U 0 τ which allows us to write Eq. (23), under the steady state condition, as

$$\begin{aligned} \frac{1}{2} \biggl(\frac{d\psi}{d\xi} \biggr)^2+V(\psi)=0, \end{aligned}$$
(26)

where the pseudo-potential V(ψ) is

$$\begin{aligned} V(\psi)=-\frac{U_0}{2B}\psi^2+\frac{c_1s}{6} \psi^3+\frac{\alpha}{12}\psi^4. \end{aligned}$$
(27)

It would be mentioned here that U 0 and B are always positive. It is obvious from Eq. (27) that

$$\begin{aligned} &{V(\psi)\big\vert _{\psi=0}=\frac{dV(\psi)}{d\psi}\bigg|_{\psi=0}=0,} \end{aligned}$$
(28)
$$\begin{aligned} &{\frac{d^2V(\psi)}{d\psi^2}\bigg|_{\psi=0}<0.} \end{aligned}$$
(29)

The conditions Eqs. (28) and (29) imply that SW solutions of Eq. (26) exist if

$$\begin{aligned} V(\psi)|_{\psi=\psi_m}=0. \end{aligned}$$
(30)

The latter can be solved as

$$\begin{aligned} &{U_{0}=\frac{c_1sB}{3}\psi_{m1,2}+ \frac{\alpha B}{6}\psi_{m1,2}^2,} \end{aligned}$$
(31)
$$\begin{aligned} &{\psi_{m1,2}=\psi_m \biggl[1\mp\sqrt{1+ \frac{U_0}{V_0}} \biggr],} \end{aligned}$$
(32)

where ψ m =−c 1 s/α, and \(V_{0}=c_{1}^{2}s^{2}B/6\alpha\). Now, using Eqs. (27) and (32) in Eq. (26) we have

$$\begin{aligned} \biggl(\frac{d\psi}{d\zeta} \biggr)^2+\gamma\psi^2(\psi- \psi_{m1}) (\psi-\psi_{m2})=0, \end{aligned}$$
(33)

where γ=α/6. The SW solution of Eq. (26) or Eq. (33) is, therefore, directly given by

$$\begin{aligned} \psi= \biggl[\frac{1}{\psi_{m2}}- \biggl(\frac{1}{\psi_{m2}} -\frac{1}{\psi_{m1}} \biggr)\cosh^2 \biggl(\frac{\xi}{\delta} \biggr) \biggr]^{-1}, \end{aligned}$$
(34)

where ψ m1,2 are given in Eq. (32), and SWs width δ is

$$\begin{aligned} \delta=\frac{2}{\sqrt{-\gamma\psi_{m1}\psi_{m2}}}. \end{aligned}$$
(35)

We note that Eq. (34) represents a SW solution of Eq. (23). It is clear from Eqs. (14) and (17) that the solitary potential profile is negative (positive) if A<0 (A>0). Therefore, A(μ 1=μ c )=0, where μ c is the critical value of μ 1 above (below) which the SWs with a positive (negative) potential exists. To find the parametric regimes for which the positive and negative solitary potential profiles exist, we have numerically analyzed A, and obtain A(μ 1=μ c )=0 surface plots. The A(μ 1=μ c )=0 surface plots are shown in Figs. 1 and 2. From Fig. 1, it is observed that the critical value μ c increases with the increase of nonthermal parameter β, but gradually decreases with the increase of relative temperature ratio σ 2. From Fig. 2, it is seen that μ c gradually increases with the increase of relative temperature ratio σ 1. Therefore, for typical plasma parameters μ 2=0.7, σ 1=3, σ 2=1.5, and β=0.7, we found the existence of the small amplitude SWs with a positive potential for μ 1>μ c , and with a negative potential for μ 1<μ c .

Fig. 1
figure 1

Variation of μ c [obtained from A(μ 1=μ c )=0] with σ 2 and β

Full size image
Fig. 2
figure 2

Variation of μ c [obtained from A(μ 1=μ c )=0] with σ 1 and β

Full size image

We now turn to Eq. (23) with the term \(\frac{\nu}{2\tau}\psi\), which is due to the effects of the nonplanar (cylindrical or spherical) geometry. An exact analytical solution of Eq. (23) is not possible. Therefore, we have numerically solved Eq. (23), and studied the effects of cylindrical and spherical geometries on time-dependent PA GSs, as well as nonthermal distributed electrons and nonthermal distributed hot positrons on PA GSs. The results are depicted in Figs. 3–8. The initial condition, that we have used in our numerical analysis, is in the form of the stationary solution of Eq. (23) without the term \(\frac{\nu}{2\tau}\psi\).

Fig. 3
figure 3

Effects of cylindrical (ν=1) geometry on PA positive GSs for μ 1=0.12, μ 2=0.7, σ 1=3, σ 2=1.5, β=0.7, s=1, and U 0=0.06

Full size image

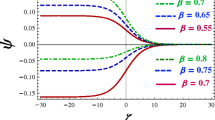
Figures 3 and 4 show the effects of cylindrical geometry on the PA positive and negative GSs and Figs. 5 and 6 show the effects of spherical geometry on the PA positive and negative GSs. We have also observed (in Figs. 7 and 8) that the amplitude of the positive GSs decreases with the increase of nonthermal parameter β and the amplitude of the negative GSs increases with the increase of relative number density ratio μ 2.

Fig. 4
figure 4

Effects of cylindrical (ν=1) geometry on PA negative GSs for μ 1=0.1, μ 2=0.7, σ 1=3, σ 2=1.5, β=0.7, s=−1, and U 0=0.06

Full size image
Fig. 5
figure 5

Effects of spherical (ν=2) geometry on PA positive GSs for μ 1=0.12, μ 2=0.7, σ 1=3, σ 2=1.5, β=0.7, s=1, and U 0=0.06

Full size image
Fig. 6
figure 6

Effects of spherical (ν=2) geometry on PA negative GSs for μ 1=0.1, μ 2=0.7, σ 1=3, σ 2=1.5, β=0.7, s=−1, and U 0=0.06

Full size image
Fig. 7
figure 7

Variation of amplitude of the positive GSs with β for μ 1=0.12, μ 2=0.7, σ 1=3, σ 2=1.5, and s=1. The upper (red) curve is for β=0.1, the middle (blue) one is for β=0.2, and the lower (pink) one is for β=0.3

Full size image
Fig. 8
figure 8

Variation of amplitude of the negative GSs with μ 2 for μ 1=0.1, β=0.7, σ 1=3, σ 2=1.5, and s=−1. The upper (red) curve is for μ 2=0.5, the middle (blue) one is for μ 2=0.6, and the lower (pink) one is for μ 2=0.7

Full size image

5 Discussions

We have considered an unmagnetized four-component plasma system [consisting of nonthermal electrons, nonthermal hot positrons, mobile cold positrons, and immobile positive ions] and studied the nonplanar (cylindrical and spherical) geometry effects on the nonlinear propagation of PA GSs. We have derived the MG equation by using the reductive perturbation method, and numerically analyzed that MG equation. The results that have been found from our investigation can be summarized as follows:

  1. 1.

    The plasma system under consideration supports finite amplitude GSs, whose basic features (viz. amplitude, polarity, speed, and thickness) strongly depend on different plasma parameters, particularly, μ 1, μ 2, σ 1, σ 2, and β.

  2. 2.

    The GSs are shown to exist around μ 1=μ c , and are found to be different from the K-dV solitons, which do not exist around μ 1=μ c .

  3. 3.

    The positive GSs exist when μ 1>μ c and negative GSs exist when μ 1<μ c .

  4. 4.

    The amplitude of the positive GSs decreases with the increase of nonthermal parameter β as depicted in Fig. 7 and the amplitude of the negative GSs increases steeply with the increase of relative number density ratio μ 2 as displayed in Fig. 8.

  5. 5.

    Equation (23) shows that \(\frac{\nu}{2\tau}\psi\) goes to infinity when τ→0. Therefore, this term is singular at τ=0. For large values of τ, this term vanishes, and we have usual Gardner equation. In the direction of time, we can start from a sufficient large τ (like τ=−20) where the term \(\frac{\nu}{2\tau}\psi\) is negligible. It is obvious from Eq. (23) that the nonplanar geometrical effect is important when τ→0 and weaker for larger value of τ.

  6. 6.

    The numerical solutions of Eq. (23) reveal that for a large value of τ (e.g. τ=−20), the planar and nonplanar PA GSs are identical, but the amplitude of both cylindrical and spherical PA GSs increases with the decrease of the value of τ. However, as the value of τ decreases, the term \(\frac{\nu}{2\tau}\psi\) becomes dominant, and cylindrical and spherical GSs differ from 1D planar ones. It is found that the amplitude of cylindrical PA GSs is larger than those of 1D planar ones, but smaller than that of the spherical ones. The amplitudes of both cylindrical and spherical PA GSs increase with the decrease of τ (displayed in Figs. 3–6).

In our considered plasma system, cylindrical and spherical geometries as well as electron and positron nonthermality effects play a significant role in the basic properties (viz. amplitude, width, polarity, etc.) of PA GSs. The amplitude of the positive GSs decreases with the increase of nonthermal parameter β, whereas the amplitude of the negative GSs increases steeply with the increase of relative number density ratio μ 2. In case of positive GSs, amplitude decreases gradually with the increase of nonthermal parameter β. The nonplanar geometry effect for PA GSs is very strong for a small value of τ and there are differences between the cylindrical and spherical PA GSs. The amplitude decreases with increase in τ. In conclusion, we note that our present theory is valid only for small but finite amplitude solitary structures, but not arbitrary amplitude solitary structures. It may be stressed that the results of our present investigation should be useful for understanding the basic nonlinear features of PA perturbations in various interstellar space plasmas [viz. ionosphere (Bremer et al. 1996), auroral acceleration regions (Ergun et al. 1998; Franz et al. 1998), supernovas, pulsar environments, cluster explosions, active galactic nuclei, etc.] as well as laboratory plasmas [viz. semiconductor plasmas (Shukla et al. 1986), intense laser fields (Berezhiani et al. 1992)] in which nonthermal electrons, nonthermal hot positrons, mobile cold positrons, and immobile positive ions are the major plasma species.