Attitude stability of a spacecraft with two flexible solar arrays on a stationary orbit around an asteroid subjected to gravity gradient torque

Abstract

In the gravity field of an asteroid with the second order and degree harmonics C ₂₀ and C ₂₂, the attitude stability of a spacecraft with two flexible solar arrays on a stationary orbit subjected to the fourth-order gravity gradient torque is investigated in this paper. The sufficient conditions of attitude stability of the spacecraft are obtained, the effect of the direction of the flexible solar arrays and some special cases are discussed. Taking the asteroids 4769 Castalia, 25143 Itokawa and the imaginary asteroids as examples, the attitude stability domains, determined by the sufficient conditions, of the spacecrafts moving on stationary orbits around them are presented. It is found that the attitude stability domains of the spacecraft with two flexible solar arrays are evidently different when the solar arrays are installed in different directions; the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids has the significant influence on the attitude stability domains of the spacecrafts with flexible appendages moving on stationary orbits; in the certain case, the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids has no influence on the attitude stability domains of the rigid spacecrafts moving on stationary orbits, but in the other cases, the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids has also the significant influence on the attitude stability domains of the rigid spacecrafts moving on stationary orbits; whether the harmonics C ₂₀ and C ₂₂ of the asteroids are considered or not, the effect of flexible appendages decreases the attitude stability domains.

1 Introduction

The modern spacecrafts often have flexible appendages. The attitude dynamics of the spacecrafts has received extensive attention in the space technology, and many achievements have been obtained (Hughes 1973; Modi 1974; Ibrahim and Misra 1982; Liu 1994; Ge and Liu 1999; Riverin and Misra 2002; Misra and Panchenko 2006; Kumar 2008; Wang and Xu 2012). Liu and Ge discussed the attitude stability of an unsymmetrical spacecraft with a flexible plate and a spacecraft with two flexible solar arrays in the Earth’s central gravity field (Liu 1994; Ge and Liu 1999). At present, the spacecraft mission to asteroids is one of hot spots in the deep space exploration. The attitude dynamics of the spacecraft around the asteroids is a fundament problem in the mission, and it can be studied by means of the previous methods in the Earth’s spacecraft. But the results of the Earth’s spacecraft cannot be applied to the spacecraft around the asteroids directly for the fast rotational state and distinctive non-spherical mass distribution of the asteroids. Wang and Xu presented a full fourth-order gravity gradient torque model of spacecraft around asteroids (Wang and Xu 2013a), and used this model to analyze the equilibrium attitude and stability of a spacecraft on a stationary orbit around an asteroid in the second order and degree gravity field (Wang and Xu 2013b, 2013c). Wang and Xu also investigated the nonlinear attitude stability of the spacecraft in a modified energy-Casimir method (Wang and Xu 2013d). However, they considered a rigid spacecraft merely in their works.

Based on the methodology stated in Liu (1994) and Ge and Liu (1999), we further investigate the attitude stability of a spacecraft with two flexible solar arrays on a stationary orbit subjected to the fourth-order gravity gradient torque in the gravity field of an asteroid with the second order and degree harmonics C ₂₀ and C ₂₂ in this paper. The sufficient conditions of attitude stability of the spacecraft are derived, the effect of the direction of the flexible solar arrays and some special cases are discussed. Taking the specific examples, the attitude stability domains determined by the sufficient conditions are analyzed.

2 Attitude dynamic equations of the spacecraft

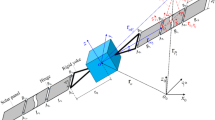
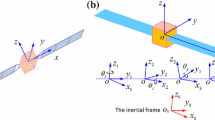
Similar to Wang and Xu (2013b) and Ge and Liu (1999), we present the sketch map of a spacecraft B with two flexible solar arrays moving on a stationary orbit around the asteroid P in Fig. 1 and the structural representation of the spacecraft B in Fig. 2. Three configurations of the spacecraft B are considered, in which the flexible solar arrays are installed in different directions. We first investigate the attitude stability of the spacecraft B with the configuration (I) in the text, and then discuss that with the configurations (II) and (III).

Fig. 1

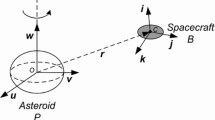
A spacecraft B with two flexible solar arrays moving on a stationary orbit around the asteroid P (similar to Wang and Xu 2013b)

Fig. 2

The spacecraft with two flexible solar arrays (similar to Ge and Liu 1999), in which three configurations are considered

The reference frames O–XYZ and o–xyz are the body-fixed ones of the asteroid P and the spacecraft B respectively, with their origins O and o are fixed at the mass centers and their coordinate axes are aligned along the principal axes of inertia. Meantime, the mass center of the asteroid is supposed to be stationary in the inertial space. The reference frame o–x ₀ y ₀ z ₀ is the orbital one fixed at the mass center of the spacecraft. The y ₀-axis is along the positive normal to the orbital plane (i.e. in the direction of the orbital angular momentum) and parallel to the Z-axis, the z ₀-axis is in the direction of the Y-axis, and the x ₀-axis is determined by the right hand rule and builds the orthogonal triad. We can easily obtain the coordinate transformation matrix from O–XYZ to o–x ₀ y ₀ z ₀ is R _z (π)R _x (−π/2). Introduce yaw, pitch and roll angles (ϕ _yaw,θ _pitch,ψ _roll) to describe the attitude motion of the spacecraft with respect to o–x ₀ y ₀ z ₀, and the coordinate transformation matrix from o–x ₀ y ₀ z ₀ to o–xyz is R _x (ψ _roll)R _y (θ _pitch)R _z (ϕ _yaw). Here R _x , R _y and R _z refer to the axis rotation matrixes. The asteroid P with their principal moments of inertia I _p,zz >I _p,yy >I _p,xx rotates about Z-axis uniformly, and the rotation angular rate is ω _c . The spacecraft B is composed of a primary rigid body and two same rectangular flexible solar arrays and moves on a stable stationary orbit of the asteroid P lying on Y-axis with the radius R _S . The mass of the primary rigid body is far more than the solar arrays, and hence the mass center displacement arising from the elastic deformation of the solar arrays can be neglected. These two flexible solar arrays are thin cantilever plates and fixed at the primary rigid body symmetrically. For the spacecraft B with the configuration (I), the direction of elastic displacement of the solar arrays is along the x-axis of o–xyz, the fixed edges of the solar arrays are parallel to the y-axis, and the middle plane of the solar arrays without deformation is just the yz-coordinate plane (see Fig. 2). The coordinate of an arbitrary point in this middle plane can be expressed as y j+z k, and the elastic displacement of this point is u ₁ i or u ₂ i (u ₁ corresponds to the point in the left solar array, while u ₂ corresponds to the point in the right solar array) (Ge and Liu 1999). Here i, j and k are unit vectors of o–xyz. In addition, the distance of the middle point of the solar arrays’ fixed end from the mass center o of the spacecraft is a, and the length, width, thickness and density of the arrays are b, c, h and ρ respectively.

The attitude motion of the spacecraft B is assumed to be subjected to gravity gradient torque of the asteroid P only. But the second order and degree gravity field of the asteroid with the harmonic coefficients C ₂₀ and C ₂₂ is considered in the text. Using the full fourth-order gravity gradient torque (Wang and Xu 2013a) and noting that the spacecraft without deformation has three symmetrical planes, the third- and fourth-order inertia integrals of the spacecraft are then all zero except these fourth-order inertia integrals J _xxxx , J _yyyy , J _zzzz , J _xxyy , J _xxzz and J _yyzz (Wang and Xu 2013b). Neglect the tiny effect of elastic deformation of the solar arrays on the principal moments of inertia I _xx , I _yy and I _zz of the spacecraft, but its effect on the products of inertia I _xy , I _xz , I _yx and I _zx of the spacecraft with the configuration (I) must be considered in the attitude motion (Liu 1994). Moreover, the third- and fourth-order inertia integrals associated with the terms $u_{i}^{2}, u_{i}^{3}, \ldots (i = 1,2)$ arising from the elastic deformation of the solar arrays are also neglected for the elastic displacement is small. Here the inertia integrals arising from the elastic deformation of the solar arrays of the spacecraft with the configuration (I) are defined by

$$\begin{aligned} J'_{\underbrace{x \cdots x}_{p \mbox{-} times}\underbrace{y \cdots y}_{q \mbox{-} times}\underbrace{z \cdots z}_{r \mbox{-} times}} =& h\rho \biggl[\iint_{S_{1}} (u_{1})^{p}(y)^{q}(z)^{r}dydz \\ &{} + \iint_{S_{2}} (u_{2})^{p}(y)^{q}(z)^{r}dydz \biggr]. \end{aligned}$$

(1)

The fields of integration S ₁ is a≤z≤a+b and −c/2≤y≤c/2; while S ₂ is −a−b≤z≤−a and −c/2≤y≤c/2. Namely, the S ₁ and S ₂ are middle planes of those two solar arrays without deformation.

Under the assumptions that the attitude motion is small and the orbital motion is unaffected by changes in the attitude, using the similar deductions stated in Liu (1994), Ge and Liu (1999), Curtis (2005) and Wang and Xu (2013b), we obtain the linearized equations of attitude motion of the spacecraft B with the configuration (I):

$$ \begin{cases} I_{xx}\ddot{\psi}_{\mathrm{roll}} + (I_{xx} + I_{zz} - I_{yy})\omega_{c}\dot{\phi}_{\mathrm{yaw}} \\ \quad{}+ [(\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})(I_{yy} - I_{zz})\\ \quad{} - \frac{\mu}{2R_{S}^{5}}(I_{yy} - I_{zz})(21\tau_{0} + 102\tau_{2}) \\ \quad{} + \frac{5\mu}{2R_{S}^{5}}(3J_{xxyy} - 3J_{xxzz} + 3J_{yyyy}\\ \quad{} - 21J_{yyzz} + 4J_{zzzz})]\psi_{\mathrm{roll}} \\ \quad{}- 2\omega_{c}h\rho (\iint_{S_{1}} \frac{\partial u_{1}}{\partial t}ydydz\\ \quad{} + \iint_{S_{2}} \frac{\partial u_{2}}{\partial t}ydydz) = 0, \\ I_{yy}\ddot{\theta}_{\mathrm{pitch}} + [\frac{3\mu}{R_{S}^{3}}(I_{xx} - I_{zz}) - \frac{5\mu}{2R_{S}^{5}}(I_{xx} - I_{zz})(3\tau_{0} \\ \quad{}+ \frac{114}{5}\tau_{2})\\ \quad{} + \frac{5\mu}{2R_{S}^{5}}(3J_{xxxx} + 3J_{xxyy} - 21J_{xxzz} - 3J_{yyzz}\\ \quad{} + 4J_{zzzz})]\theta_{\mathrm{pitch}} + h\rho (\iint_{S_{1}} \frac{\partial^{2}u_{1}}{\partial t^{2}}zdydz\\ \quad{} + \iint_{S_{2}} \frac{\partial^{2}u_{2}}{\partial t^{2}}zdydz) + \frac{3\mu}{R_{S}^{3}}h\rho (\iint_{S_{1}} u_{1}zdydz\\ \quad{} + \iint_{S_{2}} u_{2}zdydz)\\ \quad{} + \frac{3\mu}{2R_{S}^{4}}h\rho [\iint_{S_{1}} u_{1}(y^{2} - 4z^{2})dydz\\ \quad{} + \iint_{S_{2}} u_{2}(y^{2} - 4z^{2})dydz] \\ \quad{}+ \frac{5\mu}{2R_{S}^{5}}h\rho [\iint_{S_{1}} u_{1}(4z^{3} - 3y^{2}z)dydz\\ \quad{} + \iint_{S_{2}} u_{2}(4z^{3} - 3y^{2}z)dydz] = 0, \\ I_{zz}\ddot{\phi}_{\mathrm{yaw}} + (I_{yy} - I_{zz} - I_{xx})\omega_{c}\dot{\psi}_{\mathrm{roll}}\\ \quad{} + [\omega_{c}^{2}(I_{yy} - I_{xx}) - \frac{3\mu}{R_{S}^{5}}\\ \quad{}\times(I_{yy} - I_{xx})(\tau_{0} - 2\tau_{2})]\phi_{\mathrm{yaw}} \\ \quad{} - h\rho (\iint_{S_{1}} \frac{\partial^{2}u_{1}}{\partial t^{2}}ydydz + \iint_{S_{2}} \frac{\partial^{2}u_{2}}{\partial t^{2}}ydydz)\\ \quad{} + \omega_{c}^{2}h\rho (\iint_{S_{1}} u_{1}ydydz + \iint_{S_{2}} u_{2}ydydz) = 0. \end{cases} $$

(2)

In Eq. (2), μ is the product of the gravitational constant by the mass of the asteroid P, $\tau_{0} = a_{e}^{2}C_{20}$, $\tau_{2} = a_{e}^{2}\sqrt{C_{22}^{2} + S_{22}^{2}}$, a _e is mean equatorial radius of the asteroid P, C ₂₀, C ₂₂ and S ₂₂ are the spherical harmonic coefficients of the asteroid’s gravitational field. Due to the reference frame O–XYZ is fixed at the mass center and their coordinate axis are aligned along the principal axes of inertia of the asteroid, S ₂₂=0 and $\tau_{2} = a_{e}^{2}C_{22}$ virtually. Similar to Liu (1994) and Ge and Liu (1999), we derive the elastic deformation of flexible solar arrays of the spacecraft B with the configuration (I) meets the forced vibration equations:

$$\begin{aligned} &{D\nabla^{4}u_{i} + h\rho \frac{\partial^{2}u_{i}}{\partial t^{2}} + h\rho \biggl[\biggl(\ddot{\theta}_{\mathrm{pitch}} + \frac{3\mu}{ R_{S}^{3}} \theta_{\mathrm{pitch}}\biggr)z} \\ &{\quad{} - \bigl(\ddot{\phi}_{\mathrm{yaw}} - 2\omega_{c} \dot{\psi}_{\mathrm{roll}} - \omega_{c}^{2}\phi_{\mathrm{yaw}} \bigr)y\biggr] = 0,} \\ &{\quad (i = 1,2),} \end{aligned}$$

(3)

where D is flexural stiffness of the solar arrays. It is pointed out that the coordinate references chose in the text are different from the ones in Liu (1994), Ge and Liu (1999) and Wang and Xu (2013b), but consistent with Curtis (2005).

3 Sufficient conditions of attitude stability

Similar to Liu (1994) and Ge and Liu (1999), adopting Galerkin’s method (Barton 1951; Meirovitch 1967) and using the free vibration modes Φ _j (y,z) and the mode coordinates q _ij (t) (i=1,2;j=1,2,…,n) of thin cantilever plates fixed at the primary rigid body, from Eqs. (2) and (3) we derive the discrete attitude dynamic equations of the spacecraft B with the configuration (I):

$$ \begin{cases} I_{xx}\ddot{\psi}_{\mathrm{roll}} + (I_{xx} + I_{zz} - I_{yy})\omega_{c}\dot{\phi}_{\mathrm{yaw}} + [(\omega_{c}^{2}\\ \quad{} + \frac{3\mu}{R_{S}^{3}})(I_{yy} - I_{zz})\\ \quad{} - \frac{\mu}{2R_{S}^{5}}(I_{yy} - I_{zz})(21\tau_{0} + 102\tau_{2}) \\ \quad{} + \frac{5\mu}{2R_{S}^{5}}(3J_{xxyy} - 3J_{xxzz} + 3J_{yyyy} - 21J_{yyzz}\\ \quad{} + 4J_{zzzz})]\psi_{\mathrm{roll}} - 2\omega_{c}\sum_{j = 1}^{n} \alpha_{j}(\dot{q}_{1j} + \dot{q}_{2j}) = 0, \\ I_{yy}\ddot{\theta}_{\mathrm{pitch}} + [\frac{3\mu}{R_{S}^{3}}(I_{xx} - I_{zz}) - \frac{5\mu}{2R_{S}^{5}}(I_{xx} - I_{zz})(3\tau_{0}\\ \quad{} + \frac{114}{5}\tau_{2}) + \frac{5\mu}{2R_{S}^{5}}(3J_{xxxx} + 3J_{xxyy} - 21J_{xxzz} \\ \quad{}- 3J_{yyzz} + 4J_{zzzz})]\theta_{\mathrm{pitch}} \\ \quad{} + \sum_{j = 1}^{n} \beta_{j} (\ddot{q}_{1j} + \ddot{q}_{2j})\\ \quad{} + \frac{3\mu}{R_{S}^{3}}\sum_{j = 1}^{n} \beta_{j} (q_{1j} + q_{2j})\\ \quad{} + \frac{3\mu}{2R_{S}^{4}}\sum_{j = 1}^{n} \xi_{j} (q_{1j} + q_{2j})\\ \quad{} + \frac{5\mu}{2R_{S}^{5}}\sum_{j = 1}^{n} \eta_{j} (q_{1j} + q_{2j}) = 0, \\ I_{zz}\ddot{\phi}_{\mathrm{yaw}} + (I_{yy} - I_{zz} - I_{xx})\omega_{c}\dot{\psi}_{\mathrm{roll}}\\ \quad{} + [\omega_{c}^{2}(I_{yy} - I_{xx})\\ \quad{} - \frac{3\mu}{R_{S}^{5}}(I_{yy} - I_{xx})(\tau_{0} - 2\tau_{2})]\phi_{\mathrm{yaw}} \\ \quad{} - \sum_{j = 1}^{n} \alpha_{j} (\ddot{q}_{1j} + \ddot{q}_{2j})\\ \quad{} + \omega_{c}^{2}\sum_{j = 1}^{n} \alpha_{j} (q_{1j} + q_{2j}) = 0, \\ \delta_{jk}(\ddot{q}_{1j} + \sigma_{j}^{2}q_{1j}) + \beta_{j}(\ddot{\theta}_{\mathrm{pitch}} + \frac{3\mu}{R_{S}^{3}}\theta_{\mathrm{pitch}})\\ \quad{} - \alpha_{j}(\ddot{\phi}_{\mathrm{yaw}} - 2\omega_{c}\dot{\psi}_{\mathrm{roll}} - \omega_{c}^{2}\phi_{\mathrm{yaw}}) = 0, \\ \delta_{jk}(\ddot{q}_{2j} + \sigma_{j}^{2}q_{2j}) + \beta_{j}(\ddot{\theta}_{\mathrm{pitch}} + \frac{3\mu}{R_{S}^{3}}\theta_{\mathrm{pitch}})\\ \quad{} - \alpha_{j}(\ddot{\phi}_{\mathrm{yaw}} - 2\omega_{c}\dot{\psi}_{\mathrm{roll}} - \omega_{c}^{2}\phi_{\mathrm{yaw}}) = 0, \end{cases} $$

(4)

where

$$ \begin{cases} \alpha_{j} = h\rho \iint_{S_{1}} \varPhi_{j}(y,z)ydydz \\ \phantom{\alpha_{j}}= h\rho \iint_{S_{2}} \varPhi_{j}(y,z)ydydz, \\ \beta_{j} = h\rho \iint_{S_{1}} \varPhi_{j}(y,z)zdydz \\ \phantom{\alpha_{j}}= h\rho \iint_{S_{2}} \varPhi_{j}(y,z)zdydz, \\ \xi_{j} = h\rho [\iint_{S_{1}} \varPhi_{j}(y,z)(y^{2} - 4z^{2})dydz\\ \phantom{\xi_{j}}= h\rho [\iint_{S_{2}} \varPhi_{j}(y,z)(y^{2} - 4z^{2})dydz, \\ \eta_{j} = h\rho [\iint_{S_{1}} \varPhi_{j}(y,z)(4z^{3} - 3y^{2}z)dydz\\ \phantom{\eta_{j}} = h\rho [\iint_{S_{2}} \varPhi_{j}(y,z)(4z^{3} - 3y^{2}z)dydz, \\ \delta_{jk} = \iint_{S_{1}} \varPhi_{j}(y,z)\varPhi_{k}(y,z)dydz \\ \phantom{\delta_{jk}}= \iint_{S_{2}} \varPhi_{j}(y,z)\varPhi_{k}(y,z)dydz,\\ \quad(j,k = 1,2, \ldots n), \\ \sigma_{j}^{2}\delta_{jk} = D\iint_{S_{1}} [\nabla^{4}\varPhi_{j}(y,z)]\varPhi_{k}(y,z)dydz\\ \phantom{\sigma_{j}^{2}\delta_{jk}} = D\iint_{S_{2}} [\nabla^{4}\varPhi_{j}(y,z)]\varPhi_{k}(y,z)dydz. \end{cases} $$

(5)

Equations (5) are based on the corresponding formula in Ge and Liu (1999), and the last two equations in Eqs. (5) are the orthogonality conditions of vibration mode virtually. σ _j is the j-th natural frequency of free vibration of the solar arrays. Note that the assumption that these two flexible solar arrays of the spacecraft have the same mode functions is used in Eqs. (4) and (5). The above discrete attitude dynamic equations can be further expressed as $\boldsymbol{M}\ddot{\boldsymbol{q}} + \boldsymbol{G}\dot{\boldsymbol{q}} + \boldsymbol{K} = 0$, which is similar to the linear model of the gyrosystem without damping forces. Here q=[ψ _roll,θ _pitch,ϕ _yaw,q _1j ,…,q _1n ,q _2j ,…,q _2n ]^T, and M, G and K are 2n+3 order matrixes. The matrix M is symmetrical and just the so-called mass matrix. Moreover, it is easy to derive that the matrix M must be positive definite (Ge and Liu 1999). With the aid of the analysis of stability of the gyrosystem, if the matrix K is also symmetrical, i.e. corresponds to the so-called stiffness matrix, the attitude stability of the spacecraft is determined by the positive definiteness of the symmetrical stiffness matrix based on the Kelvin-Tait-Chetayev theorem (Zajac 1964; Liu 1994; Ge and Liu 1999). However, the specific expression of K is

$$ \boldsymbol{K} = \left [ \begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} Q_{1} & 0 & 0 & 0 & \cdots & 0 & 0 & \cdots & 0 \\ 0 & Q_{2} & 0 & \gamma_{1} & \cdots & \gamma_{n} & \gamma_{1} & \cdots & \gamma_{n} \\ 0 & 0 & Q_{3} & \omega_{c}^{2}\alpha_{1} & \cdots & \omega_{c}^{2}\alpha_{n} & \omega_{c}^{2}\alpha_{1} & \cdots & \omega_{c}^{2}\alpha_{n} \\ 0 & \frac{3\mu}{R_{S}^{3}}\beta_{1} & \omega_{c}^{2}\alpha_{1} & \sigma_{1}^{2} & 0 & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & 0 & \ddots & 0 & 0 & 0 & 0 \\ 0 & \frac{3\mu}{R_{S}^{3}}\beta_{n} & \omega_{c}^{2}\alpha_{n} & 0 & 0 & \sigma_{n}^{2} & 0 & 0 & 0 \\ 0 & \frac{3\mu}{R_{S}^{3}}\beta_{1} & \omega_{c}^{2}\alpha_{1} & 0 & 0 & 0 & \sigma_{1}^{2} & 0 & 0 \\ \vdots & \vdots & \vdots & 0 & 0 & 0 & 0 & \ddots & 0 \\ 0 & \frac{3\mu}{R_{S}^{3}}\beta_{n} & \omega_{c}^{2}\alpha_{n} & 0 & 0 & 0 & 0 & 0 & \sigma_{n}^{2} \end{array} \right ], $$

(6)

where

$$ \left \{ \begin{array}{l} Q_{1} = (\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})(I_{yy} - I_{zz}) - \frac{\mu}{2R_{S}^{5}}(I_{yy} - I_{zz})(21\tau_{0} \\ \quad{}+ 102\tau_{2}) + \frac{5\mu}{2R_{S}^{5}}(3J_{xxyy} - 3J_{xxzz} + 3J_{yyyy} - 21J_{yyzz}\\ \quad{} + 4J_{zzzz}), \\ Q_{2} = \frac{3\mu}{R_{S}^{3}}(I_{xx} - I_{zz}) - \frac{5\mu}{2R_{S}^{5}}(I_{xx} - I_{zz})(3\tau_{0} + \frac{114}{5}\tau_{2})\\ \quad{} + \frac{5\mu}{2R_{S}^{5}}(3J_{xxxx} + 3J_{xxyy} - 21J_{xxzz} - 3J_{yyzz} + 4J_{zzzz}), \\ Q_{3} = \omega_{c}^{2}(I_{yy} - I_{xx}) - \frac{3\mu}{R_{S}^{5}}(I_{yy} - I_{xx})(\tau_{0} - 2\tau_{2}), \end{array} \right . $$

(7)

and

$$ \gamma_{j} = \frac{3\mu}{R_{S}^{3}}\beta_{j} + \frac{3\mu}{ 2R_{S}^{4}}\xi_{j} + \frac{5\mu}{2R_{S}^{5}}\eta_{j},\quad(j = 1,2, \ldots,n). $$

(8)

It is seen that the matrix K is not symmetrical formally. However, because the inertia integrals of the flexible solar arrays are small and R _S is a big number, $\frac{3\mu}{R_{S}^{3}}\beta_{j}$ is often larger than $\frac{3\mu}{2R_{S}^{4}}\xi_{j}$ and $\frac{5\mu}{ 2R_{S}^{5}}\eta_{j}$ virtually. We can approximatively regard as $\gamma_{j} \approx \frac{3\mu}{R_{S}^{3}}\beta_{j}$, i.e. further neglect the third- and fourth-order inertia integrals arising from the elastic deformation of the flexible solar arrays. Then the matrix K becomes symmetrical, and now the attitude stability of the spacecraft is determined by the positive definiteness of the symmetrical stiffness matrix K (Zajac 1964; Liu 1994; Ge and Liu 1999). After a serious of elementary transformations of matrix K, we derive the sufficient conditions of attitude stability of a spacecraft B with the configuration (I) moving on a stationary orbit around the asteroid P:

$$ \left \{ \begin{array}{l} Q_{1} > 0, \\ Q_{2} > 18(\frac{\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}, \\ Q_{3} > 2\omega_{c}^{4}\sum_{j = 1}^{n} (\frac{\alpha_{j}}{\sigma_{j}})^{2} + 36\omega_{c}^{4}(\frac{\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha_{j}\beta_{j}}{\sigma_{j}^{2}})^{2} /[Q_{2}\\ \quad{} - 18(\frac{\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2} ]. \end{array} \right . $$

(9)

4 Discussion

4.1 The effect of the direction of the flexible solar arrays

In the above analysis, the direction of elastic displacement of the solar arrays is along the x-axis of o–xyz, the fixed edges of the solar arrays is parallel to the y-axis, and the middle plane of the solar arrays without deformation is just the yz-coordinate plane (i.e. the configuration (I) in Fig. 2). In this section, we further investigate the attitude stability of the spacecraft B with the configurations (II) and (III) (see Fig. 2), in which the solar arrays are installed in other directions of o–xyz. Note that the reference frames O–XYZ and o–x ₀ y ₀ z ₀ are unchanged in the analysis, and the direction of the flexible solar arrays does not change the j-th natural frequency σ _j of free vibration of the solar arrays.

For the spacecraft B with the configuration (II), the direction of elastic displacement of the solar arrays is along the y-axis of o–xyz, the fixed edges of the solar arrays is parallel to the x-axis, and the middle plane of the solar arrays without deformation is just the xz-coordinate plane. The coordinate of an arbitrary point in this middle plane can be expressed as x i+z k, and the elastic displacement of this point is $u'_{1}\boldsymbol{j}$ or $u'_{2}\boldsymbol{j}$ ($u'_{1}$ corresponds to the point in the left solar array, while $u'_{2}$ corresponds to the point in the right solar array). The corresponding linearized equations of attitude motion of the spacecraft B with the configuration (II) are

$$ \left \{ \begin{array}{l} I_{xx}\ddot{\psi}_{\mathrm{roll}} + (I_{xx} + I_{zz} - I_{yy})\omega_{c}\dot{\phi}_{\mathrm{yaw}} + Q_{1}\psi_{\mathrm{roll}} \\ \quad{}- (\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})h\rho (\iint_{S'_{1}} u'_{1}zdxdz + \iint_{S'_{2}} u'_{2}zdxdz) \\ \quad{} - h\rho (\iint_{S'_{1}} \frac{\partial^{2}u'_{1}}{\partial t^{2}}zdxdz + \iint_{S'_{2}} \frac{\partial^{2}u'_{2}}{\partial t^{2}}zdxdz) \\ \quad{}- \frac{3\mu}{2R_{S}^{4}}h\rho [\iint_{S'_{1}} u'_{1}(x^{2} - 4z^{2})dxdz + \iint_{S'_{2}} u'_{2}(x^{2} \\ \quad{}- 4z^{2})dxdz] - \frac{5\mu}{2R_{S}^{5}}h\rho [\iint_{S'_{1}} u'_{1}(4z^{3} - 3x^{2}z)dxdz\\ \quad{} + \iint_{S'_{2}} u'_{2}(4z^{3} - 3x^{2}z)dxdz] = 0, \\ I_{yy}\ddot{\theta}_{\mathrm{pitch}} + Q_{2}\theta_{\mathrm{pitch}} = 0, \\ I_{zz}\ddot{\phi}_{\mathrm{yaw}} + (I_{yy} - I_{zz} - I_{xx})\omega_{c}\dot{\psi}_{\mathrm{roll}} + Q_{3}\phi_{\mathrm{yaw}} \\ \quad{} + h\rho (\iint_{S'_{1}} \frac{\partial^{2}u'_{1}}{\partial t^{2}}xdxdz + \iint_{S'_{2}} \frac{\partial^{2}u'_{2}}{\partial t^{2}}xdxdz)\\ \quad{} + \omega_{c}^{2}h\rho (\iint_{S'_{1}} u'_{1}xdxdz + \iint_{S'_{2}} u'_{2}xdxdz) = 0, \\ D\nabla^{4}u'_{i} + h\rho \frac{\partial^{2}u'_{i}}{\partial t^{2}} + h\rho [(\ddot{\phi}_{\mathrm{yaw}} + \omega_{c}^{2}\phi_{\mathrm{yaw}})x - (\ddot{\psi}_{\mathrm{roll}}\\ \quad{} + \omega_{c}^{2}\psi_{\mathrm{roll}} + \frac{3\mu}{R_{S}^{3}}\psi_{\mathrm{roll}})z] = 0,\quad(i = 1,2), \end{array} \right . $$

(10)

where the fields of integration $S'_{1}$ is −a−b≤z≤−a and −c/2≤x≤c/2; while $S'_{2}$ is a≤z≤a+b and −c/2≤x≤c/2. Using the same deduction as stated above, we then derive the following sufficient conditions of attitude stability of a spacecraft B with the configuration (II) moving on a stationary orbit around the asteroid P:

$$ \left \{ \begin{array}{l} Q_{1} > 2(\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}, \\ Q_{2} > 0, \\ Q_{3} > 2\omega_{c}^{4}\sum_{j = 1}^{n} (\frac{\alpha '_{j}}{\sigma_{j}})^{2} + 4\omega_{c}^{4}(\omega_{c}^{2}\\ \quad{} + \frac{3\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha '_{j}\beta '_{j}}{\sigma_{j}^{2}})^{2} /[Q_{1} - 2(\omega_{c}^{2}\\ \quad{} + \frac{3\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2} ], \end{array} \right . $$

(11)

where

$$ \left \{ \begin{array}{l} \alpha '_{j} = h\rho \iint_{S'_{1}} \varPhi_{j}(x,z)xdxdz = h\rho \iint_{S'_{2}} \varPhi_{j}(x,z)xdxdz, \\ \beta '_{j} = h\rho \iint_{S'_{1}} \varPhi_{j}(x,z)zdxdz = h\rho \iint_{S'_{2}} \varPhi_{j}(x,z)zdxdz. \end{array} \right . $$

(12)

For the spacecraft B with the configuration (III), the direction of elastic displacement of the solar arrays is along the z-axis of o–xyz, the fixed edges of the solar arrays is parallel to the y-axis, and the middle plane of the solar arrays without deformation is just the xy-coordinate plane. The coordinate of an arbitrary point in this middle plane can be expressed as x i+y j, and the elastic displacement of this point is $u''_{1}\boldsymbol{k}$ or $u''_{2}\boldsymbol{k}$ ($u''_{1}$ corresponds to the point in the left solar array, while $u''_{2}$ corresponds to the point in the right solar array). The corresponding linearized equations of attitude motion of the spacecraft B with the configuration (III) are

$$ \left \{ \begin{array}{l} I_{xx}\ddot{\psi}_{\mathrm{roll}} + (I_{xx} + I_{zz} - I_{yy})\omega_{c}\dot{\phi}_{\mathrm{yaw}} + Q_{1}\psi_{\mathrm{roll}}\\ \quad{} - (\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})h\rho (\iint_{S''_{1}} u''_{1}ydxdy\\ \quad{}+ \iint_{S''_{2}} u''_{2}ydxdy) \\ \quad{} + h\rho (\iint_{S''_{1}} \frac{\partial^{2}u''_{1}}{\partial t^{2}}ydxdy \\ \quad{}+ \iint_{S''_{2}} \frac{\partial^{2}u''_{2}}{\partial t^{2}}ydxdy)\\ \quad{} + \frac{15\mu}{2R_{S}^{5}}h\rho [\iint_{S''_{1}} u''_{1}(y^{3} + x^{2}y)dxdy\\ \quad{} + \iint_{S''_{2}} u''_{2}(y^{3} + x^{2}y)dxdy] = 0, \\ I_{yy}\ddot{\theta}_{\mathrm{pitch}} + Q_{2}\theta_{\mathrm{pitch}} - h\rho (\iint_{S''_{1}} \frac{\partial^{2}u''_{1}}{\partial t^{2}}xdxdy\\ \quad{} + \iint_{S''_{2}} \frac{\partial^{2}u''_{2}}{\partial t^{2}}xdxdy) + \frac{3\mu}{R_{S}^{3}}h\rho (\iint_{S''_{1}} u''_{1}xdxdy\\ \quad{} + \iint_{S''_{2}} u''_{2}xdxdy) - \frac{15\mu}{2R_{S}^{5}}h\rho [\iint_{S''_{1}} u''_{1}(x^{3}\\ \quad{} + xy^{2})dxdy + \iint_{S''_{2}} u''_{2}(x^{3} + xy^{2})dxdy] = 0, \\ I_{zz}\ddot{\phi}_{\mathrm{yaw}} + (I_{yy} - I_{zz} - I_{xx})\omega_{c}\dot{\psi}_{\mathrm{roll}} + Q_{3}\phi_{\mathrm{yaw}}\\ \quad{} - 2\omega_{c}h\rho (\iint_{S''_{1}} \frac{\partial u''_{1}}{\partial t}ydxdy\\ \quad{}+ \iint_{S''_{2}} \frac{\partial u''_{2}}{\partial t}ydxdy) = 0, \\ D\nabla^{4}u''_{i} + h\rho \frac{\partial^{2}u''_{i}}{\partial t^{2}} + h\rho [(\ddot{\psi}_{\mathrm{roll}}\\ \quad{} + 2\omega_{c}\dot{\phi}_{\mathrm{yaw}} - \omega_{c}^{2}\psi_{\mathrm{roll}}\\ \quad{} - \frac{3\mu}{R_{S}^{3}}\psi_{\mathrm{roll}})y - (\ddot{\theta}_{\mathrm{pitch}} - \frac{3\mu}{R_{S}^{3}}\theta_{\mathrm{pitch}})x] = 0,\\ \quad{}\quad(i = 1,2), \end{array} \right . $$

(13)

where the fields of integration $S''_{1}$ is −a−b≤x≤−a and −c/2≤y≤c/2; while $S''_{2}$ is a≤x≤a+b and −c/2≤y≤c/2. Using the same deduction as stated above, we then derive the following sufficient conditions of attitude stability of a spacecraft B with the configuration (III) moving on a stationary orbit around the asteroid P:

$$ \left \{ \begin{array}{l} Q_{1} > 2(\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2}, \\ Q_{2} > 18(\frac{\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\beta ''_{j}}{\sigma_{j}})^{2} + 36(\omega_{c}^{2}\\ \phantom{Q_{2} >}{} + \frac{3\mu}{R_{S}^{3}})^{2}(\frac{\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha ''_{j}\beta ''_{j}}{\sigma_{j}^{2}})^{2} \\ \phantom{Q_{2} >}{}/[Q_{1} - 2(\omega_{c}^{2} + \frac{3\mu}{R_{S}^{3}})^{2}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2} ], \\ Q_{3} > 0, \end{array} \right . $$

(14)

where

$$ \left \{ \begin{array}{l} \alpha ''_{j} = h\rho \iint_{S''_{1}} \varPhi_{j}(x,y)ydxdy = h\rho \iint_{S''_{2}} \varPhi_{j}(x,y)ydxdy, \\ \beta ''_{j} = h\rho \iint_{S''_{1}} \varPhi_{j}(x,y)xdxdy = h\rho \iint_{S''_{2}} \varPhi_{j}(x,y)xdxdy. \end{array} \right . $$

(15)

From Eqs. (9), (11) and (14), it is seen that the sufficient conditions of attitude stability of a spacecraft B with two flexible solar arrays moving on a stationary orbit around the asteroid P are evidently different when the solar arrays are installed in different directions.

4.2 Some special cases

According to the above analysis, we present some special cases as follows:

(1) Let all those fourth-order inertia integrals in Eqs. (7) be zero, Eqs. (9), (11) and (14) are respectively reduced to:

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}})\\ \quad{} > 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}})\\ \quad{} > 2\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\alpha_{j}}{\sigma_{j}})^{2} \\ \quad{} + \frac{12(\frac{\mu}{R_{S}^{3}})^{2}[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}(\sum_{j = 1}^{n} \frac{\alpha_{j}\beta_{j}}{\sigma_{j}^{2}})^{2}}{[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}}) - 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}}, \end{array} \right . $$

(16)

$$\begin{aligned} \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 8\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 2\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\alpha '_{j}}{\sigma_{j}})^{2} \\ \quad{} + \frac{16(\frac{\mu}{R_{S}^{3}})^{2}[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}(\sum_{j = 1}^{n} \frac{\alpha '_{j}\beta '_{j}}{\sigma_{j}^{2}})^{2}}{[1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) - 8\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}}, \end{array} \right . \end{aligned}$$

(17)

and

$$\begin{aligned} \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 8\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}}) > 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta ''_{j}}{\sigma_{j}})^{2} \\ \quad{} + \frac{48(\frac{\mu}{R_{S}^{3}})^{2}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}(\sum_{j = 1}^{n} \frac{\alpha ''_{j}\beta ''_{j}}{\sigma_{j}^{2}})^{2}}{[1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) - 8\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2}}, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 0. \end{array} \right . \end{aligned}$$

(18)

In Eqs. (16)–(18), the equation on the radius of stationary orbit $R_{S}^{5} - \frac{\mu}{\omega_{c}^{2}}(R_{S}^{2} - \frac{3}{2}\tau_{0} - 9\tau_{2}) = 0$ (Hu 2002; Wang and Xu 2013b) is used, and I _xx =I _roll, I _yy =I _pitch and I _zz =I _yaw.

Actually, through magnitude comparison, we can neglect the effect of the third- and fourth-order inertia integrals of the spacecraft based on the conclusion of Wang and Xu (2013b) in the analysis, even though they appear in the full fourth-order gravity gradient torque. Equations (16)–(18) are the more immediate sufficient conditions of attitude stability of a spacecraft B with two flexible solar arrays moving on a stationary orbit around the asteroid P. In addition, the elastic displacement of the flexible solar arrays is small, and the third- and fourth-order inertia integrals arising from the elastic deformation of the solar arrays are smaller than the corresponding third- and fourth-order inertia integrals of the spacecraft. Hence the above approximate treatment on the third- and fourth-order inertia integrals arising from the elastic deformation of the solar arrays is reasonable, and the sufficient conditions of attitude stability are valid.

It is worth noting that why we do not neglect these third- and fourth-order inertia integrals in the model from the start: on the one hand, the model with these third- and fourth-order inertia integrals is more precise evidently in theory; on the other hand, we aim to reveal this approximate treatment, and explain its rationality clearly.

(2) Let all those fourth-order inertia integrals in Eqs. (7) be zero, and C ₂₀=C ₂₂=0 (i.e. the spacecraft B is subjected to the central gravity gradient torque merely), Eqs. (9), (11) and (14) or Eqs. (16)–(18) respectively reduce to the sufficient conditions of attitude stability of a spacecraft B with two flexible solar arrays moving on a stationary orbit around the asteroid P in the central gravity field:

$$ \left \{ \begin{array}{l} I_{\mathrm{pitch}} > I_{\mathrm{yaw}}, \\ I_{\mathrm{roll}} > I_{\mathrm{yaw}} + 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}, \\ I_{\mathrm{pitch}} > I_{\mathrm{roll}} + 2\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha_{j}}{\sigma_{j}})^{2} \\ \quad{}+ 12(\frac{\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha_{j}\beta_{j}}{\sigma_{j}^{2}})^{2} /[I_{\mathrm{roll}}\\ \quad{} - I_{\mathrm{yaw}} - 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2} ], \end{array} \right . $$

(19)

$$ \left \{ \begin{array}{l} I_{\mathrm{pitch}} > I_{\mathrm{yaw}} + 8\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}, \\ I_{\mathrm{roll}} > I_{\mathrm{yaw}}, \\ I_{\mathrm{pitch}} > I_{\mathrm{roll}} + 2\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha '_{j}}{\sigma_{j}})^{2}\\ \quad{} + 16(\frac{\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha '_{j}\beta '_{j}}{\sigma_{j}^{2}})^{2} /[I_{\mathrm{pitch}} - I_{\mathrm{yaw}}\\ \quad{} - 8\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2} ], \end{array} \right . $$

(20)

and

$$ \left \{ \begin{array}{l} I_{\mathrm{pitch}} > I_{\mathrm{yaw}} + 8\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2}, \\ I_{\mathrm{roll}} > I_{\mathrm{yaw}} + 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta ''_{j}}{\sigma_{j}})^{2}\\ \quad{} + 48(\frac{\mu}{R_{S}^{3}})^{2}(\sum_{j = 1}^{n} \frac{\alpha ''_{j}\beta ''_{j}}{\sigma_{j}^{2}})^{2} /[I_{\mathrm{pitch}} - I_{\mathrm{yaw}}\\ \quad{} - 8\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2} ], \\ I_{\mathrm{pitch}} > I_{\mathrm{roll}}. \end{array} \right . $$

(21)

And then the stability conditions can be applied to the spacecraft with two flexible solar arrays moving on a circular orbit in the Earth’s central gravity field. Equation (21) is just consistent with the result in Ge and Liu (1999) essentially.

(3) Let all those fourth-order inertia integrals in Eqs. (7) be zero, and $\alpha_{j} = \alpha '_{j} = \alpha ''_{j} = 0$ (j=1,2,…,n) (i.e. those two flexible solar arrays reduce to flexible levers), Eqs. (9), (11) and (14) or Eqs. (16)–(18) respectively reduce to the sufficient conditions of attitude stability of a spacecraft B with two flexible levers moving on a stationary orbit around the asteroid P in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂:

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}})\\ \quad{} > 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 0, \end{array} \right . $$

(22)

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}})\\ \quad{} > 8\frac{\mu}{R_{S}^{3}}[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 0, \end{array} \right . $$

(23)

and

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}})\\ \quad{} > 6\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta ''_{j}}{\sigma_{j}})^{2}, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 0. \end{array} \right . $$

(24)

(4) Let all those fourth-order inertia integrals in Eqs. (7) be zero, C ₂₀=C ₂₂=0 and $\alpha_{j} = \alpha '_{j} = \alpha ''_{j} = 0$ (j=1,2,…,n), Eqs. (9), (11) and (14) or Eqs. (16)–(18) respectively reduce to the sufficient conditions of attitude stability of a spacecraft B with two flexible levers moving on a stationary orbit around the asteroid P in the central gravity field:

$$ I_{\mathrm{pitch}} > I_{\mathrm{roll}} > I_{\mathrm{yaw}} + 6\frac{\mu}{ R_{S}^{3}}\sum _{j = 1}^{n} \biggl(\frac{\beta_{j}}{\sigma_{j}} \biggr)^{2}, $$

(25)

$$ \left \{ \begin{array}{l} I_{\mathrm{pitch}} > I_{\mathrm{yaw}} + 8\frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}, \\ I_{\mathrm{pitch}} > I_{\mathrm{roll}} > I_{\mathrm{yaw}}, \end{array} \right . $$

(26)

and

$$ I_{\mathrm{pitch}} > I_{\mathrm{roll}} > I_{\mathrm{yaw}} + 6\frac{\mu}{ R_{S}^{3}}\sum _{j = 1}^{n} \biggl(\frac{\beta ''_{j}}{\sigma_{j}} \biggr)^{2}. $$

(27)

And then the stability conditions can be applied to the spacecraft with two flexible levers moving on a circular orbit in the Earth’s central gravity field. Equation (27) is just consistent with the result in Liu (1995) and Ge and Liu (1999) essentially.

(5) Let all those fourth-order inertia integrals in Eqs. (7) be zero, $\alpha_{j} = \alpha '_{j} = \alpha ''_{j} = 0$ and $\beta_{j} = \beta '_{j} = \beta ''_{j} = 0$ (j=1,2,…,n) (i.e. the spacecraft B reduces to a rigid one), Eqs. (9), (11) and (14) or Eqs. (16)–(18) reduce to the same sufficient conditions of attitude stability of a rigid spacecraft B moving on a stationary orbit around the asteroid P in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂:

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{roll}} - I_{\mathrm{yaw}}) > 0, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}](I_{\mathrm{pitch}} - I_{\mathrm{roll}}) > 0. \end{array} \right . $$

(28)

And then the stability conditions can be applied to the spacecraft stated in Wang and Xu (2013b) evidently, and they are consistent with the nonlinear stability conditions derived in Wang and Xu (2013d).

(6) Let all those fourth-order inertia integrals in Eqs. (7) be zero, C ₂₀=C ₂₂=0, $\alpha_{j} = \alpha '_{j} = \alpha ''_{j} = 0$ and $\beta_{j} = \beta '_{j} = \beta ''_{j} = 0$ (j=1,2,…,n), Eqs. (9), (11) and (14) or Eqs. (16)–(18) reduce to the same sufficient condition of attitude stability of a rigid spacecraft B moving on a stationary orbit around the asteroid P in the central gravity field of an asteroid P:

$$ I_{\mathrm{pitch}} > I_{\mathrm{roll}} > I_{\mathrm{yaw}}. $$

(29)

And then the result is just the well-known condition of attitude stability of a rigid spacecraft subjected to the central gravity gradient torque (Curtis 2005).

5 Attitude stability domains and illustrated examples

Just as Curtis (2005), Liu (1994) and Ge and Liu (1999), introducing the following dimensionless parameters

$$ \left \{ \begin{array}{l} k_{Y} = \frac{I_{\mathrm{pitch}} - I_{\mathrm{roll}}}{I_{\mathrm{yaw}}},\qquad k_{R} = \frac{I_{\mathrm{pitch}} - I_{\mathrm{yaw}}}{I_{\mathrm{roll}}},\\ \quad(\vert k_{Y} \vert < 1,\vert k_{R} \vert < 1), \\ \delta = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}},\\ \varepsilon = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}}, \\ \delta ' = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha '_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}},\\ \varepsilon ' = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta '_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}}, \\ \delta '' = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\alpha ''_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}},\\ \varepsilon '' = \frac{\mu}{R_{S}^{3}}\sum_{j = 1}^{n} (\frac{\beta ''_{j}}{\sigma_{j}})^{2}/I_{\mathrm{pitch}}, \end{array} \right . $$

(30)

and neglecting the quadratic terms of small parameters δ and ε (δ′ and ε′, δ″ and ε″) for the inertia integrals arising from the elastic deformation of the solar arrays are small, the sufficient conditions of attitude stability Eqs. (16)–(18) can be further respectively expressed as:

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}k_{R}}{1 - k_{Y}k_{R}} > 0, \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}}{1 - k_{Y}k_{R}} > 6\varepsilon, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{Y} - k_{Y}k_{R}}{1 - k_{Y}k_{R}}\\ \quad > 2[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\delta. \end{array} \right . $$

(31)

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}k_{R}}{1 - k_{Y}k_{R}} \\ \quad> 8[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\varepsilon ', \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}}{1 - k_{Y}k_{R}} > 0, \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{Y} - k_{Y}k_{R}}{1 - k_{Y}k_{R}} \\ \quad{}> 2[1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\delta ', \end{array} \right . $$

(32)

and

$$ \left \{ \begin{array}{l} [1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}k_{R}}{1 - k_{Y}k_{R}} \\ \quad{}> 8[1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}\delta '', \\ {}[1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{R} - k_{Y}}{1 - k_{Y}k_{R}} > 6\varepsilon '', \\ {}[1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2}]\frac{k_{Y} - k_{Y}k_{R}}{1 - k_{Y}k_{R}} > 0. \end{array} \right . $$

(33)

With the aid of the parameters k _Y and k _R , we can present the attitude stability domains determined by Eqs. (31)–(33). Taking the asteroids 4769 Castalia and 25143 Itokawa as examples first, we present the attitude stability domains of the spacecrafts moving on stationary orbits around them. The main parameters of the asteroids 4769 Castalia (Scheeres et al. 1996) and 25143 Itokawa (Scheeres et al. 2006) are listed in Table 1.

Table 1 The main parameters of the asteroids 4769 Castalia (Scheeres et al. 1996) and 25143 Itokawa (Scheeres et al. 2006)^a

Let δ=δ′=δ″=0.005 and ε=ε′=ε″=0.0075, the attitude stability domains of the spacecraft with three different configurations moving on the stationary orbits around the asteroids 4769 Castalia and 25143 Itokawa are presented in Fig. 3 respectively. It is seen that the attitude stability domains of the spacecraft are evidently different when the solar arrays are installed in different directions.

Fig. 3

The attitude stability domains (shadow areas) of the spacecraft with three different configurations moving on stationary orbits around the asteroids 4769 Castalia and 25143 Itokawa

Corresponding to six cases discussed in Sect. 4.2, from Eqs. (31) the attitude stability domains of the spacecraft with the configuration (I) moving on a stationary orbit around the asteroid 4769 Castalia are presented in Fig. 4, in which we let δ=0.01 and ε=0.015 for the corresponding cases. It is seen that:

• (i) Refer to the case (1) vs (2), and the case (3) vs (4) in Fig. 4, for the spacecrafts with flexible appendages moving on a stationary orbit, the harmonics C ₂₀ and C ₂₂ of the asteroid 4769 Castalia have the significant influence on the attitude stability domain.

  Fig. 4

  

  Corresponding to six cases discussed in Sect. 4.2, the attitude stability domains (shadow areas) of the spacecraft with the configuration (I) moving on a stationary orbit around the asteroid 4769 Castalia

• (ii) Refer to the case (5) vs (6) in Fig. 4, for the spacecrafts without flexible appendages (rigid spacecraft) moving on a stationary orbit, the harmonics C ₂₀ and C ₂₂ of the asteroid 4769 Castalia have no influence on the attitude stability domain, i.e. the attitude stability domains of the cases (5) and (6) are the same. Moreover, the attitude stability domains of the cases (5) and (6) are the classical Lagrange regions and consistent with the corresponding nonlinear stability domain in the case of a _e /R _S =0.8 presented in Wang and Xu (2013d).

• (iii) Whether the effect of the harmonics C ₂₀ and C ₂₂ of the asteroid 4769 Castalia is considered (refer to the cases (1), (3) and (5) in Fig. 4) or not (refer to the cases (2), (4) and (6) in Fig. 4), the effect of flexible appendages decreases the attitude stability domains.

Corresponding to six cases discussed in Sect. 4.2, the attitude stability domains of the spacecraft with the configuration (I) moving on a stationary orbit around the asteroid 25143 Itokawa are presented in Fig. 5, in which we let δ=0.02 and ε=0.03 for the corresponding cases. The similar phenomena to the asteroid 4769 Castalia can be observed from Fig. 5, except that the effect of the harmonics C ₂₀ and C ₂₂ of the asteroid 25143 Itokawa has not so significant influence on the attitude stability domain as the 4769 Castalia. In addition, the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids is neglected in the cases (2), (4) and (6) in Figs. 4 and 5, the corresponding attitude stability domains of the spacecraft with the configuration (I) around the asteroids 4769 Castalia and 25143 Itokawa are determined by the same conditions with different parameters δ and ε associated with flexibility actually from Eqs. (31), which can be regarded as the analysis of attitude stability domains is disconnected from the specific asteroid. Then comparing the cases (2) and (4) in Fig. 4 with that in Fig. 5, it is further seen that the attitude stability domains decrease with the increase of δ and ε as stated in Liu (1994) and Ge and Liu (1999). Meantime, for the spacecraft with the configuration (I) around the asteroids 4769 Castalia and 25143 Itokawa, even the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids is considered, the attitude stability domains of the spacecraft with flexible appendages moving on a stationary orbit around an asteroid also decrease with the increase of δ and ε, which is verified by the results of the corresponding spacecraft with two flexible solar arrays and that with two flexible levers around the asteroids 4769 Castalia and 25143 Itokawa in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂ (Figs. 6 and 7). In Figs. 6 and 7, we setup different values of δ and ε.

Fig. 5

Corresponding to six cases discussed in Sect. 4.2, the attitude stability domains (shadow areas) of the spacecraft with the configuration (I) moving on a stationary orbit around the asteroid 25143 Itokawa

Fig. 6

The attitude stability domains (shadow areas) of the corresponding spacecraft with two flexible solar arrays (left) and that with two flexible levers (right) moving on a stationary orbit around the asteroid 4769 Castalia in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂, in which different values of δ and ε are adopted: (a) δ=0.02 and ε=0.03; (b) δ=0.012 and ε=0.015; (c) δ=0.01 and ε=0.015; (d) δ=0 and ε=0.03; (e) δ=0 and ε=0.015

Fig. 7

The attitude stability domains (shadow areas) of the corresponding spacecraft with two flexible solar arrays (left) and that with two flexible levers (right) moving on a stationary orbit around the asteroid 25143 Itokawa in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂, in which different values of δ and ε are adopted: (a) δ=0.02 and ε=0.03; (b) δ=0.012 and ε=0.015; (c) δ=0.01 and ε=0.015; (d) δ=0 and ε=0.03; (e) δ=0 and ε=0.015

Comparing Eqs. (28) with Eq. (29), the phenomenon that the harmonics C ₂₀ and C ₂₂ of the asteroids 4769 Castalia and 25143 Itokawa have no influence on the attitude stability domains of the rigid spacecraft moving on a stationary orbit (refer to the case (5) vs (6) in Figs. 4 and 5) originates from that the C ₂₀, C ₂₂ and a _e /R _S meet the following conditions

$$ \left \{ \begin{array}{l} A_{ast} = 1 - 3C_{20}(\frac{a_{e}}{R_{S}})^{2} - 15C_{22}(\frac{a_{e}}{R_{S}})^{2} > 0, \\ B_{ast} = 1 - \frac{5}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 19C_{22}(\frac{a_{e}}{R_{S}})^{2} > 0, \\ C_{ast} = 1 - \frac{9}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 3C_{22}(\frac{a_{e}}{R_{S}})^{2} > 0. \end{array} \right . $$

(34)

Actually, we can further generalize a conclusion: for the rigid spacecraft moving on a stationary orbit around an asteroid, if the conditions Eqs. (34) hold, the harmonics C ₂₀ and C ₂₂ of the asteroid have no influence on the attitude stability domain, i.e. the attitude stability domains determined with and without C ₂₀ and C ₂₂ are the same, and are the classical Lagrange regions. Based on the result of Wang and Xu (2013c), the conditions Eqs. (34) always hold in the case of $0.2 < a_{e}/R_{S} < 2/\sqrt{19}$, −0.5<C ₂₀<0 and −0.25<C ₂₂<0.25, and hence the harmonics C ₂₀ and C ₂₂ of this kind of asteroid have no influence on the attitude stability domain of its rigid spacecraft moving on the stationary orbit. It is exactly because the conditions Eqs. (34) hold in the attitude stability domains of the cases (5) and (6) in Figs. 4 and 5 and in the corresponding nonlinear stability domain in the case of a _e /R _S =0.8 presented in Wang and Xu (2013d), they seem to be consistent, and are all the classical Lagrange regions. Here the attitude stability domains of the cases (5) in Figs. 4 and 5 and the corresponding nonlinear stability domains in the case of a _e /R _S =0.8 presented in Wang and Xu (2013d) determined by the same formula Eqs. (28) for the rigid spacecraft actually as stated in Sect. 4.2.

Note that the attitude stability domains of the spacecraft around the asteroids 4769 Castalia and 25143 Itokawa presented in Figs. 4–7 are determined by Eqs. (31), i.e. corresponding to the spacecraft with the configuration (I). For the spacecraft with the configurations (II) and (III), the attitude stability domains are determined by Eqs. (32) and (33) respectively, and the similar phenomena to the configuration (I) can be observed, except that the attitude stability domains of the spacecraft with flexible appendages moving on a stationary orbit around an asteroid always decrease with the increase of δ″. Under certain cases, the phenomenon that the variation of δ″ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, and that the attitude stability domain of the spacecraft with two flexible solar arrays is the same as that with two flexible levers may occur. For example, the case (1) in Sect. 4.2 with δ″=0.012, ε″=0.015 and δ″=0.01, ε″=0.015, and the cases (2) and (4) in Sect. 4.2 with δ″=0.01, ε″=0.015 and δ″=0, ε″=0.015 respectively for the spacecraft with the configuration (III) around the asteroid 4769 Castalia; the case (1) in Sect. 4.2 when δ″=0.012, ε″=0.015 and δ″=0.01, ε″=0.015, and the cases (2) and (4) in Sect. 4.2 with δ″=0.02, ε″=0.03 and δ″=0, ε″=0.03 respectively for the spacecraft with the configuration (III) around the asteroid 25143 Itokawa (see Fig. 8). These phenomena can be explained in theory as described below.

Fig. 8

The attitude stability domains (shadow areas) of the spacecraft with the configuration (III) moving on stationary orbits around the asteroids 4769 Castalia and 25143 Itokawa

Moreover, according to the results of Wang and Xu (2013d), in terms of the class conditions:

• (a) A _ast , B _ast and C _ast are all positive, i.e. Eqs. (34),

• (b) A _ast and C _ast are positive, and B _ast is negative,

• (c) C _ast is positive and A _ast and B _ast are negative,

there are three possible types of attitude stability domains of the spacecraft moving on the stationary orbit, for most asteroids in our Solar System with the parameters C ₂₀, C ₂₂ and a _e /R _S in the ranges of −0.5<C ₂₀<0, −0.25<C ₂₂<0.25 and 0.2<a _e /R _S <0.8. In fact, we can also reach this conclusion from another standpoint. We preliminarily infer that there are eight possible types of attitude stability domains determined by the sufficient conditions in theory, when the C ₂₀, C ₂₂ and a _e /R _S meet the different conditions: arbitrary combination of the plus-minus of A _ast , B _ast and C _ast . But for most asteroids in our Solar System with the parameters in the restrictive ranges stated above, C _ast is always positive (Wang and Xu 2013c). Meantime, the case of A _ast <0 and B _ast >0 in the above restrictive ranges is nonexistent by calculation. Then we finally infer that there are only three possible types of attitude stability domains determined by the sufficient conditions in theory.

Taking the imaginary asteroid with C ₂₀=−0.2790, C ₂₂=0.1850 and a _e /R _S =0.7048 satisfying the class condition (b), and the imaginary asteroid with C ₂₀=−0.2500, C ₂₂=0.1990 and a _e /R _S =0.7004 satisfying the class condition (c) as examples, the attitude stability domains of the spacecraft with three different configurations moving on the stationary orbits around them are presented in Fig. 9 respectively, in which we let δ=δ′=δ″=0.001 and ε=ε′=ε″=0.0015. The similar phenomenon to the asteroids 4769 Castalia and 25143 Itokawa that the attitude stability domains of the spacecraft are evidently different when the solar arrays are installed in different directions can be observed from Fig. 9. But the attitude stability domains of the imaginary asteroids are obviously different from the ones of the asteroids 4769 Castalia and 25143 Itokawa satisfying the class condition (a), the attitude stability domains of the imaginary asteroid satisfying the class condition (b) are in the isosceles right triangle region above the straight line k _Y =k _R in the first quadrant of k _Y –k _R plane; while the attitude stability domains of the imaginary asteroid satisfying the class condition (c) are in the second quadrant of k _Y –k _R plane.

Fig. 9

The attitude stability domains (shadow areas) of the spacecraft with three different configurations moving on stationary orbits around the imaginary asteroids, in which (1)–(3) correspond to the imaginary asteroid satisfying the class condition (b) and (4)–(6) correspond to the imaginary asteroid satisfying the class condition (c)

Corresponding to six cases discussed in Sect. 4.2, from Eqs. (31) the attitude stability domains of the spacecraft with the configuration (I) moving on stationary orbits around the imaginary asteroids with the parameters stated above are respectively presented in Figs. 10 and 11. In Fig. 10, we let δ=0.01 and ε=0.015 for the corresponding cases, and in Fig. 11, we let δ=0.02 and ε=0.03 for the corresponding cases. The attitude stability domains of the cases (2), (4) and (6) in Figs. 10 and 11 are the same as the corresponding ones in Figs. 4 and 5 for they are determined by the same attitude stability conditions without C ₂₀ and C ₂₂ essentially. The attitude stability domains of the case (5) in Figs. 10 and 11 are just the isosceles right triangle region above the straight line k _Y =k _R in the first quadrant and the second quadrant of k _Y –k _R plane respectively, and they are consistent with the corresponding ones of nonlinear stability domain in the case of a _e /R _S =0.8 presented in Wang and Xu (2013d) for they meet the same class conditions and determined by the same attitude stability conditions Eqs. (28). From Figs. 10 and 11, it is also seen that the harmonics C ₂₀ and C ₂₂ of the imaginary asteroids have the significant influence on the attitude stability domain; whether the effect of the harmonics C ₂₀ and C ₂₂ of the imaginary asteroids is considered or not, the effect of flexible appendages decreases the attitude stability domains. These phenomena are similar to the asteroids 4769 Castalia and 25143 Itokawa. But the effect of the harmonics C ₂₀ and C ₂₂ of the imaginary asteroids makes the attitude stability domains be completely changed. The attitude stability domains determined without C ₂₀ and C ₂₂ are in the classical Lagrange region (in the isosceles left triangle region below the straight line k _Y =k _R in the first quadrant of k _Y –k _R plane); while the attitude stability domains determined with C ₂₀ and C ₂₂ are in the isosceles right triangle region above the straight line k _Y =k _R in the first quadrant or the second quadrant of k _Y –k _R plane. Moreover, the harmonics C ₂₀ and C ₂₂ of the imaginary asteroids satisfying the class conditions (b) and (c) have also significant influence on the attitude stability domain of the spacecrafts without flexible appendages (rigid spacecraft) moving on a stationary orbit, i.e. the attitude stability domains of the cases (5) and (6) in Figs. 10 and 11 are evidently different, for the conditions Eqs. (34) do not hold now. The similar phenomena stated above can be also observed for the spacecraft with the configurations (II) and (III) moving on the stationary orbits around these imaginary asteroids. In addition, the attitude stability domains of the cases (1) and (2) in Fig. 10 are the same, i.e. the variation of δ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, which can be explained in theory as described below.

Fig. 10

Corresponding to six cases discussed in Sect. 4.2, the attitude stability domains (shadow areas) of the spacecraft with the configuration (I) moving on a stationary orbit around the imaginary asteroid satisfying the class condition (b)

Fig. 11

Corresponding to six cases discussed in Sect. 4.2, the attitude stability domains (shadow areas) of the spacecraft with the configuration (I) moving on a stationary orbit around the imaginary asteroid satisfying the class condition (c)

According to the internal relations of three inequalities in the attitude stability conditions Eqs. (31)–(33), we can further analyze the effect of δ, δ′ and δ″ on the attitude stability domains in theory. It is found that:

For the spacecraft with the configuration (I), if

$$ \left \{ \begin{array}{l} - \frac{3\varepsilon}{B_{ast}} > \frac{D_{ast}\delta}{C_{ast}},\quad(A_{ast} > 0,C_{ast} > 0,B_{ast} < 0), \\ D_{ast} = [1 - \frac{3}{2}C_{20}(\frac{a_{e}}{R_{S}})^{2} - 9C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}, \end{array} \right . $$

(35)

the variation of δ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, and the attitude stability domain of the spacecraft with two flexible solar arrays is the same as that with two flexible levers. The cases (1) and (2) in Fig. 10 just satisfy Eqs. (35), so the corresponding phenomenon can be observed.

For the spacecraft with the configuration (II), if

$$ \left \{ \begin{array}{l} \frac{4E_{ast}\varepsilon '}{A_{ast}} > \frac{D_{ast}\delta '}{C_{ast}},\quad(A_{ast} > 0,C_{ast} > 0,B_{ast} < 0), \\ E_{ast} = [1 - \frac{3}{8}C_{20}(\frac{a_{e}}{R_{S}})^{2} - \frac{9}{4}C_{22}(\frac{a_{e}}{R_{S}})^{2}]^{2}, \end{array} \right . $$

(36)

the variation of δ′ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, and the attitude stability domain of the spacecraft with two flexible solar arrays is the same as that with two flexible levers.

For the spacecraft with the configuration (III), if

$$ \frac{3\varepsilon ''}{B_{ast}} > \frac{4E_{ast}\delta''}{A_{ast}},\quad (A_{ast} > 0,B_{ast} > 0,C_{ast} > 0), $$

(37)

the variation of δ″ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, and the attitude stability domain of the spacecraft with two flexible solar arrays is the same as that with two flexible levers. The cases presented in Fig. 8 just satisfy Eq. (37), so the corresponding phenomena can be observed.

6 Conclusions

In this paper, the attitude stability of a spacecraft with two flexible solar arrays on a stationary orbit subjected to the fourth-order gravity gradient torque is investigated in the gravity field of an asteroid with the second order and degree harmonics C ₂₀ and C ₂₂. The sufficient conditions of attitude stability of the spacecraft are derived. The results obtained are generalized and encompass some special cases. The attitude stability domains determined by the sufficient conditions are analyzed, and some conclusions can be obtained:

• (1) The attitude stability domains of the spacecraft with two flexible solar arrays are evidently different when the solar arrays are installed in different directions.

• (2) For the spacecrafts with flexible appendages moving on a stationary orbit, the harmonics C ₂₀ and C ₂₂ of the asteroids have the significant influence on the attitude stability domains. Especially, for the asteroids satisfying the class conditions (b) and (c), the effect of the harmonics C ₂₀ and C ₂₂ of the asteroids makes the attitude stability domains be completely changed from the ones without C ₂₀ and C ₂₂ in the classical Lagrange region to the ones in the isosceles right triangle region above the straight line k _Y =k _R in the first quadrant or the second quadrant of k _Y –k _R plane.

• (3) For the rigid spacecraft moving on a stationary orbit around an asteroid satisfying the class condition (a), i.e. Eqs. (34) holding, the harmonics C ₂₀ and C ₂₂ of the asteroid have no influence on the attitude stability domain, i.e. the attitude stability domains determined with and without C ₂₀ and C ₂₂ are the same and both the classical Lagrange regions. The asteroids 4769 Castalia and 25143 Itokawa just belong to this kind of asteroid. However, the harmonics C ₂₀ and C ₂₂ have also significant influence on the attitude stability domains of the rigid spacecrafts moving on stationary orbits for the asteroids satisfying the class conditions (b) and (c).

• (4) Whether the harmonics C ₂₀ and C ₂₂ of the asteroids are considered or not, the effect of flexible appendages decreases the attitude stability domains. Moreover, the attitude stability domains often decrease with the increase of δ and ε (δ′ and ε′, δ″ and ε″) associated with flexibility. The large values of δ and ε (δ′ and ε′, δ″ and ε″) can even make the stability domain vanish. But note that under certain conditions, the variation of δ, δ′ and δ″ does not change the attitude stability domain of the spacecraft with two flexible solar arrays, and the attitude stability domain of the spacecraft with two flexible solar arrays is the same as that with two flexible levers.

This paper expands the work of Ge and Liu (1999) and Wang and Xu (2013b; 2013c; 2013d). In comparison to Ge and Liu (1999), the attitude stability of the spacecraft with two flexible solar arrays moving on a circular orbit in the Earth’s gravitational field is generalized to the spacecraft with two flexible solar arrays moving on a stationary orbit around an asteroid subjected to the fourth-order gravity gradient torque in the gravity field with the second order and degree harmonics C ₂₀ and C ₂₂. Due to the significant effect of C ₂₀ and C ₂₂ of the asteroid, the sufficient conditions of attitude stability and attitude stability domains determined by the conditions are different from that of the Earth’s spacecraft evidently. In addition, the effect of the direction of the flexible solar arrays is analyzed in this paper. In comparison to Wang and Xu (2013b; 2013c; 2013d), the effect of the flexible appendages of the spacecraft is considered in the analysis of attitude stability in this paper, and the sufficient conditions of attitude stability are derived through the different approach. In sum, the effects of C ₂₀ and C ₂₂ of the asteroid and the flexible appendages of the spacecraft should be considered in the analysis of attitude motion of the modern spacecraft mission to asteroids.