Studies on global analytical mode for a three-axis attitude stabilized spacecraft by using the Rayleigh–Ritz method

Abstract

With extending the Rayleigh–Ritz procedure to study the hub-plate system, the characteristics of global analytical modes are addressed for a typical rigid–flexible coupling dynamic system, i.e., a three-axis attitude stabilized spacecraft installed with a pair of solar arrays. The displacement field of the solar arrays is expressed as a series of admissible functions which is a set of characteristic orthogonal polynomials generated directly by employing Gram–Schmidt process. The rigid body motion of spacecraft is represented by the product of constant and generalized coordinate. Then, through Rayleigh–Ritz procedure, the eigenvalue equation of the three-axis attitude stabilized spacecraft installed with a pair of solar arrays is derived. Solving this eigenvalue equation, the frequencies and analytical expressions of global modes for the flexible spacecraft are obtained. To validate the present analysis, comparisons between the results of the present method and ANSYS software are performed and very good agreement is achieved. The convergence studies demonstrate the high accuracy, excellent convergence and high efficiency of the present approach. Finally, the method is applied to study the characteristics of global modes of the flexible spacecraft.

1 Introduction

Large-span solar arrays are used to provide sufficient power to achieve various functions of modern spacecraft employed for communications, remote sensing or other applications [1, 2]. As a result, those spacecraft are extremely flexible and have low-frequency vibration modes which interact with the spacecraft attitude motion and might be excited by orbital operations such as attitude maneuver or quick tracking [3]. Hence, obtaining the global rigid–flexible coupling modes of the spacecraft installed with solar arrays and investigating its dynamic behaviors are of practical importance to design efficient controllers to suppress the induced vibrations effectively during orbital operations.

The flexible spacecraft studied in this research consists of a central rigid hub and a pair of solar arrays (see Fig. 1). The flexible solar panels are distributed parameter system; however, numerous controllers for attitude motion of spacecraft and vibration of solar arrays are designed by using discretized dynamic model of the system. Thus, deformations of solar panels should be discretized with finite element method (FEM) [4] or modal approach using mode shapes [5–8]. The FEM model is not convenient for designing control system, because its degree of freedom is usually too large [9]. On the contrary, the modal approach can reduce the number of degrees of freedom for the system and thus increases computational efficiency [10]. The quality of results obtained with this approach depends on the quality of the mode shapes used in the simulations that is on how accurate the mode shapes can represent the real deformations. The research conducted by Pan and Liu [11] demonstrated that the mode functions with statically determinate boundary conditions, such as free–free, cantilevered-free and simply supported boundaries, are suitable for modeling flexible multibody system; however, the use of modes with statically indeterminate boundary conditions may lead to significant error. In Ref. [12], the authors pointed out that the use of suitable quasi-comparison functions obtained by combining eigenfunctions and static deformation modes of flexible body can improve the convergence of the simulation. It should be pointed out that the modes used in Refs. [5–8, 11, 12] are modes for a particular flexible body, such as beam functions [8] or other admissible basis functions satisfying the geometric boundary conditions of flexible structures [5, 7], not for the whole system. In other words, those modes of particular appendages are used to assume the global modes of the system and thus called ‘assumed modes.’ In fact, the elastic modes of flexible solar arrays are inevitably influenced by the rigid hub [13]. However, either modes of free–free, cantilevered-free or simply supported beam cannot represent the modes of the whole system, i.e., the global modes.

Using the continuum modal analysis approach, the characteristics of global modes of flexible spacecraft are investigated in great detail by Hughes [14–16] and Hablani [17–20]. In their researches, the global and assumed modes are denoted as unconstrained and constrained modes. For a general flexible spacecraft, they derived the orthogonality conditions of the global modes, studied the momentum interaction between different parts of the spacecraft (the flexible appendages and rigid hub, for instance), proposed modal identities methods such as frequencies, modal momentum coefficients and the modal angular-momentum coefficients, and developed modal truncation criterion for constructing a discrete model using global modes obtained from finite element model. A general conclusion is made from their studies that: though the assumed and global modal expansions are mathematically equivalent if an infinite number of terms are taken in each of the two expansions, the global modal expansions will be more accurate than the assumed ones because only a finite number of terms are included in the sum in practical applications. It should be noted that the studies in Ref. [14–20] are only focused on the modal analysis for the general flexible spacecraft by using the continuum approach and no specific analytical expressions of global mode shapes are given for a certain type of flexible spacecraft, such as spacecraft installed with a pair of solar arrays considered in this paper.

There are quite a few researches focused on obtaining the global modes and studying modal characteristics of spacecraft installed with solar arrays (a typical rigid–flexible coupling dynamic system). Hablani [18] and Zhang and Wang [21] used the finite element method to obtain the global mode shapes of flexible spacecraft and got low-order modal expansions by employing some particular truncation criterions such as completeness index [18]. This approach is too tedious and inconvenient to model the spacecraft because those modal expansions are numerical rather than analytical expressions. Also, the global modes of the spacecraft can be obtained by using component mode synthesis [22] and the Craig–Bampton method is the most representative one [23]. However, the global modes of the spacecraft given by this method are approximate and their expressions may be complex. Johnston and Thornton [13] investigated the effects of varying rigid-hub mass moment of inertia on the frequencies of a flexible spacecraft which are simplified as a hub-beam system. By applying numerical studies and experimental tests, Yang et al. [24] studied the modal characteristics of a rigid–flexible coupling system consisting of a rigid hub and a flexible beam with tip mass. They concluded that the frequencies of the beam in this system are quite different from those of the single beam, and the frequencies of the flexible beam increase as the ratio of the beam inertia to the rigid-hub inertia increases.

In the authors’ previous work [25], a preliminary global modal analysis was conducted for a flexible spacecraft similar to that considered in this paper (see Fig. 1). The solar array with small width-to-length ratio is modeled by flexible beam, and the spacecraft is simplified as a hub-beam system. The analytical expressions of global modes of this system can be directly solved from the dynamic equations (a set of integrodifferential equations) and corresponding boundary conditions which are derived by using Hamiltonian principle [25–28]. If the width-to-length ratio of solar panel is not small, i.e., the solar panel is relatively short, one has to model it as plate and simplify the spacecraft as hub-plate system to reveal the coupling effect between the three-dimensional vibration of solar panel and the rigid body motion (three-axis attitude motion and translation) of the spacecraft. In this case, the method in Refs. [25–28] is not proper to be used to obtain the system’s global mode shapes, because it is a difficult work to solve the partial differential equation describing the vibration of rectangular plate (solar panel) if the boundary of this plate is not simply supported at four edges. Hence, the modal characteristic studies of flexible spacecraft based on the planar rotating hub-beam system [13, 24–26] may be not proper for a spacecraft installed with a pair of solar arrays. Also, the analytical expressions of global modes of hub-beam system cannot be employed in the discretization procedure to obtain a high-precision discretized dynamic model with low degree of freedom and in the design of efficient controller of attitude maneuver and vibration suppression.

In this paper, a novel method is proposed to obtain the global analytical modes and analyze the modal characteristics of a three-axis attitude stabilized spacecraft installed with a pair of solar arrays by extending the Rayleigh–Ritz procedure to study the hub-plate system. Rayleigh–Ritz method, known as one kind of energy methods, is widely used to study the modal characteristics of elastic structures, such as plates and shells, with a variety of boundary conditions [29–31], due to its simplicity in implementation and capability to provide satisfactory results. In the present study, Rayleigh–Ritz method is extended to investigate the modal characteristics of a rigid–flexible coupling system. Each solar array whose main structure is a honeycomb sandwich panel is modeled by an equivalent isotropic plate. Its displacement formulations are assumed by characteristic orthogonal polynomial series, which are generated directly by using a Gram–Schmidt process [29]. The rigid body motion of spacecraft is represented by the product of constant and generalized coordinate. By using the Rayleigh–Ritz method, the eigenvalue equation of the three-axis attitude stabilized flexible spacecraft can be derived. Also, a finite element model is established using ANSYS software to verify the present research. Furthermore, the influences of flexible spacecraft parameters, such as the moment of inertia of rigid hub and the length of solar arrays, on the modal characteristics of the system are studied.

After this introduction, there are other three sections in this paper. Section 2 presents the procedure of extended Rayleigh–Ritz method to derive the eigenvalue equation of the flexible spacecraft. Section 3 presents numerical results and discussions to validate the method proposed in Sect. 2 and conduct parameter studies on modal characteristics of the rigid–flexible coupling dynamic system. Finally, the paper is concluded in Sect. 4.

2 Theoretical formulation

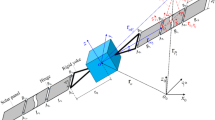
Figure 1a shows a typical model of three-axis attitude stabilized spacecraft installed with a pair of solar arrays. The tripods connecting the solar panels and the rigid body of spacecraft are assumed to be rigid. There are several ways to enlarge the rigidity of tripods, such as using composite material with relatively higher elastic modular, reinforcing the tripod structure, or embedding tension elements in the tripods. Therefore, the flexible spacecraft is modeled as a cubic rigid hub fixed with a pair of plates (hub-plate system, see Fig. 1b). Point o is the center of rigid hub. Coordinate system $o_{0}-x_{0} y_{0} z_{0}$ is defined as the inertial frame. $o-x_1 y_1 z_1$ is parallel with $o_{0}-x_{0}y_{0}z_{0}$. $o-xyz$ is defined as the body frame fixed on the central rigid hub, and it is obtained by rotating $o-x_{1} y_{1} z_{1}$ around axis $z_{1}$ with ${\theta }_{z}$, then around axis $x_{2}$ with ${\theta }_{x}$, and finally around axis ${y}_{3}$ with ${\theta }_{y}$, as shown in Fig. 1. The transformation matrix from $o-xyz$ to $o_{0}-x_{0}y_{0}z_{0}$ is expressed as follows

$$\begin{aligned} \mathbf{A}=\left[ {{\begin{array}{lll} {\cos {\theta }_z}&{}\quad {-\sin {\theta }_{z}}&{}\quad 0 \\ {\sin {\theta }_z}&{}\quad {\cos {\theta }_z}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{lll} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad {\cos {\theta }_x}&{}\quad {-\sin {\theta }_x}\\ 0&{}\quad {\sin {\theta }_x}&{}\quad {\cos {\theta }_x}\\ \end{array}}}\right] \left[ {{\begin{array}{lll} {\cos {\theta }_y}&{}\quad 0&{}\quad {\sin {\theta }_y}\\ 0&{}\quad 1&{}\quad 0 \\ {-\sin {\theta }_y}&{}\quad 0&{}\quad {\cos {\theta }_y}\\ \end{array}}}\right] . \end{aligned}$$

(1)

$o_{P_{1}}-x_{P_{1}}y_{P_{1}} z_{P_{1}}$ and $o_{P_{2}}-x_{P_{2}}y_{P_{2}}z_{P_{2}}$ illustrated in Fig. 2 are coordinate frames attached on the two solar panels. The transformation matrices from those two frames to $o-xyz$ are given by

$$\begin{aligned} \mathbf{A}_{P_{1}}=\left[ {{\begin{array}{lll} 1&{}\quad 0&{}\quad 0 \\ 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] ,\quad \mathbf{A}_{P_{2}}=\left[ {{\begin{array}{lll} {-1}&{}\quad 0&{}\quad 0 \\ 0&{}\quad {-1}&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] . \end{aligned}$$

(2)

Fig. 1

Model of the three-axis attitude stabilized spacecraft installed with a pair of solar arrays: a sketch of spacecraft, b coordinate systems

Fig. 2

Coordinate frames attached on solar panels (top view)

Fig. 3

Solar array model: a section view of solar array, b the cell of honeycomb core

Fig. 4

Equivalent isotropic model for the honeycomb sandwich panel

As illustrated in Fig. 3, the solar array consists of a back board made from honeycomb sandwich panel, on which solar cells are installed and covered by glass fiber sheets. In this research, only honeycomb panel is considered since it is the main structure of solar array. The honeycomb core and face sheet are both made of aluminum. $E_{0}$, $G_{0}$ and ${\rho }_{0}$ are the elastic and shear modulus and mass density of aluminum, respectively. The heights of the honeycomb core, face sheet and the whole honeycomb panel are denoted by ${2h}_{c}$, $h_{f}$ and 2h. $l_{c}$ and ${\delta }_{c}$ are cell size and thickness of the cell of honeycomb core. The subscripts c and f represent the honeycomb core and face sheet, respectively. The average mass density of honeycomb core can be expressed as [32]

$$\begin{aligned} {\rho }_{c}=\frac{8}{3}\frac{{\delta }_{c}}{l_{c}}{\rho }_{0}. \end{aligned}$$

(3)

The honeycomb sandwich panel is replaced by an equivalent isotropic plate in the following formulation, as shown in Fig. 4. The thickness $t_\mathrm{eq}$ and material properties of the equivalent plate are given by [32]

$$\begin{aligned} t_\mathrm{eq}= & {} \sqrt{12h_c^2 +12h_c h_f +4h_{f}^{2}}, \quad E=2h_f E_f /t_\mathrm{eq},\nonumber \\ G= & {} 2h_f G_f /t_\mathrm{eq},\quad \rho =({2h_f \rho _f +2h_c \rho _c})/t_\mathrm{eq}, \end{aligned}$$

(4)

where $E_f({=}E_{0})$, $G_f({=}G_{0})$ and ${\rho }_{f}({=}{\rho }_{0})$ are the elastic and shear modulus and the mass density of face sheet, respectively. The other geometric constants of the flexible spacecraft studied in this research are $r_{0}$ (the half of side length of the cubic rigid hub), L and 2b (the length and width of each equivalent plate), as shown in Figs. 2 and 4. In the following formulations, $t_\mathrm{eq}$ is replaced by another symbol ‘2H’ for convenience.

2.1 Expressions of the flexible spacecraft’s energy

Fig. 5

Deformation of the right solar panel

As illustrated in Fig. 5, the position vector of the hub mass center o in inertial frame $o_{0}-x_{0}y_{0}z_{0}$ is expressed as

$$\begin{aligned} \mathbf{r}_{o}=x_{o}{} \mathbf{i}_{0}+y_{o}{} \mathbf{j}_{0}+z_{o}{} \mathbf{z}_{0}, \end{aligned}$$

(5)

where $x_{o}$, $y_{o}$ and $z_{o}$ are the coordinates of hub mass center o in $o_{0}-x_{0}y_{0}z_{0}$. $\mathbf{i}_{0}$, $\mathbf{j}_{0}$ and $\mathbf{z}_{0}$ are unit vectors of $o_{0}-x_{0}y_{0}z_{0}$ in $x_{0}$, $y_{0}$ and $z_{0}$ directions. Point $P_{0}$, whose coordinates in $o_{P_{1}}-x_{P_{1}} y_{P_{1}}z_{P_{1}}$ are (x, y, z), is the initial position of an arbitrary point P on the right solar panel. $\mathbf{r}_{P_0}^{(1)}$ and $\mathbf{r}_1^0$ are initial and deformed position vectors of point P in the body frame $o-xyz$, respectively. And $\mathbf{r}_P^{(1)}$ is the relative position vector of point P in $o_{P_{1}} -x_{P_{1}}y_{P_{1}}z_{P_{1}}$. Then $\mathbf{r}_1^0$ can be written as

$$\begin{aligned} \mathbf{r}_{1}^{0}=\mathbf{r}_{P_0}^{(1)}+\mathbf{A}_{P_{1}}{} \mathbf{r}_P^{(1)}, \end{aligned}$$

(6)

where $\mathbf{r}_{P_0}^{(1)}$ and $\mathbf{r}_P^{(1)}$ are expressed in corresponding coordinate systems as

$$\begin{aligned} \mathbf{r}_{P_0}^{(1)}=\left[ {{\begin{array}{l} {r_0 +x} \\ y \\ z \\ \end{array} }} \right] ,\quad \mathbf{r}_P^{(1)} =\left[ {{\begin{array}{l} {u_1 } \\ {v_1 } \\ {w_1 } \\ \end{array} }} \right] , \end{aligned}$$

(7)

where $u_1$, $v_1$ and $w_1$ represent the displacements of point P(x, y, z) on the right solar panel in $x_{P_{1}}$, $y_{P_{1}}$ and $z_{P_{1}}$ directions, respectively.

The rotation velocity of flexible spacecraft, i.e., the attitude angular velocity, is very small, even for those so-called agile spacecraft. For instance, the largest angular velocity of the first satellite of the Pléiades system [33], an agile satellite launched by France, reaches values up to 3.4$^{\circ }$/s (0.06 rad/s) during the maneuvers, which is far less than the angular velocity at which the dynamic stiffening effect [34] should be taken into account. Hence, it is not necessary to consider the effect of dynamic stiffening during the modeling process of flexible spacecraft, and the ZOAC models [5–7] are sufficiently precise to reveal the system’s dynamic characteristics. So, $u_1$, $v_1$ and $w_1$ may be written as

$$\begin{aligned} u_1=-z\frac{\partial w_{1}({x,y,t})}{\partial x},\quad v_1=-z\frac{\partial w_1({x,y,t})}{\partial y},\quad w_1 =w_1({x,y,t}). \end{aligned}$$

(8)

Then, the position and velocity vectors of point P on the right solar panel in inertial frame $o_{0}-x_{0}y_{0} z_{0}$, denoted by $\mathbf{r}_{1}$ and $\mathbf{v}_{1}$, respectively, can be expressed as

$$\begin{aligned} \mathbf{r}_{1} =\mathbf{r}_o+\mathbf{Ar}_1^0,\quad \mathbf{v}_{1} =\dot{\mathbf{r}}_1 = \dot{ \mathbf{r}}_o +\dot{\mathbf{A}}{} \mathbf{r}_1^0 + \mathbf{A}\dot{\mathbf{r}}_1^0, \end{aligned}$$

(9)

where $(\dot{\square })$ denotes the time derivative. Similarly, the position and velocity vectors of any point on the left solar panel in $o_0 -x_0 y_0 z_0$ are given by

$$\begin{aligned} \mathbf{r}_2=\mathbf{r}_o+\mathbf{Ar}_2^0,\quad \mathbf{v}_2 = \dot{\mathbf{r}}_2 =\dot{\mathbf{r}}_o +\dot{ \mathbf{A}}{} \mathbf{r}_2^0 +\mathbf{A}\dot{\mathbf{r}}_2^0, \end{aligned}$$

(10)

where $\mathbf{r}_{2}^{0}$ can be defined by the following expressions

$$\begin{aligned} \mathbf{r}_2^0=\mathbf{r}_{P_0}^{(2)}+\mathbf{A}_{P_{2}}{} \mathbf{r}_P^{(2)} ,\quad \mathbf{r}_{P_0}^{(2)}=\left[ {{\begin{array}{l} {-r_0 -x} \\ y \\ z \\ \end{array} }} \right] , \quad \mathbf{r}_P^{(2)} =\left[ {{\begin{array}{l} {u_2 } \\ {v_2 } \\ {w_2 } \\ \end{array} }} \right] . \end{aligned}$$

(11)

The symbols in expression (11) are similar to those associated with the right solar panel.

The three axes of $o-xyz$ are the central principal axes of inertia of the cubic rigid hub, and its central principle moment matrix of inertia is $\mathbf{J}=\hbox {diag}(J_z, J_x, J_y)$. The angular velocity vector of spacecraft with respect to the inertial frame $o_0 -x_0 y_0 z_0$ is

$$\begin{aligned} \varvec{\upomega }=\left[ {{\begin{array}{l} {\omega _z } \\ {\omega _x } \\ {\omega _y } \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} {\cos \theta _x \cos \theta _y }&{}\quad {\sin \theta _y }&{}\quad 0 \\ {-\cos \theta _x \sin \theta _y }&{}\quad {\cos \theta _y }&{}\quad 0 \\ {\sin \theta _x }&{}\quad 0&{}\quad 1 \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\dot{\theta }_z } \\ {\dot{\theta }_x } \\ {\dot{\theta }_y } \\ \end{array} }} \right] . \end{aligned}$$

(12)

For modal analysis, the attitude angles ${\theta }_x$, ${\theta }_y$ and ${\theta }_z$ are assumed to be small. Then, the following first-order approximate expressions can be obtained by using Taylor formula

$$\begin{aligned} \sin {\theta }_q={\theta }_q,\quad \cos {\theta }_q =1,\quad q=x,y,z. \end{aligned}$$

(13)

The kinetic energy of the flexible spacecraft can be expressed as

$$\begin{aligned} T=\frac{1}{2}\rho {\int }_{V_R } {\mathbf{v}_1 \cdot \mathbf{v}_1 \hbox {d}V} +\frac{1}{2}\rho \int _{V_L } {\mathbf{v}_2 \cdot \mathbf{v}_2 \hbox {d}V} +\frac{1}{2}m_R ({\dot{x}_o^2 +\dot{y}_o^2 +\dot{z}_o^2})+\frac{1}{2}{{\varvec{\upomega }} }^{\mathrm{T}}\mathbf{J{\varvec{\upomega }}}, \end{aligned}$$

(14)

where $V_R$ and $V_L$ are the volumes of the right and left solar panels, and $m_R$ is the mass of rigid hub.

The expression of strain energy for the flexible spacecraft is given as follows

$$\begin{aligned} U=\frac{1}{2} \int _{V_R+V_L}{({{\sigma }_x {\varepsilon }_x+{\sigma }_y {\varepsilon }_y+{\tau }_{xy}{\gamma }_{xy}} )\hbox {d}V}, \end{aligned}$$

(15)

where ${\sigma }_x$, ${\sigma }_y$, ${\tau }_{xy}$, ${\varepsilon }_x$, ${\varepsilon }_y$ and ${\gamma }_{xy}$ are stresses and strains at point P(x, y, z). The strains are defined as following

$$\begin{aligned} {\varepsilon }_x=\frac{\partial u}{\partial x},\quad \varepsilon _y =\frac{\partial v}{\partial y},\quad \gamma _{xy} =\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}. \end{aligned}$$

(16)

The stress–strain relationship of an isotropic plate is given by

$$\begin{aligned} \left[ {{\begin{array}{l} {\sigma _x } \\ {\sigma _y } \\ {\tau _{xy} } \\ \end{array}}}\right] =\left[ {{\begin{array}{lll} {Q_{11} }&{}\quad {Q_{12} }&{}\quad 0 \\ {Q_{12} }&{}\quad {Q_{22} }&{}\quad 0 \\ 0&{}\quad 0&{}\quad {Q_{66} } \\ \end{array}}}\right] \left[ {{\begin{array}{l} {\varepsilon _x } \\ {\varepsilon _y } \\ {\gamma _{xy} } \\ \end{array} }} \right] , Q_{11} =Q_{22} =\frac{E}{1-{\mu }^{2}},\quad Q_{12}=\frac{\mu E}{1-\mu ^{2}},\quad Q_{66}=G, \end{aligned}$$

(17)

where $\mu$ is Poisson’s ratio.

Substituting relative terms in Eqs. (14) and (15), the expanded expressions of kinetic and strain energy of the spacecraft installed with a pair of solar arrays can be written as

$$\begin{aligned} T= & {} \frac{1}{2}\rho \int _{V_R } {\left\{ {z^{2}\left( {\frac{\partial \dot{w}_1 }{\partial x}} \right) ^{2}} \right. } +z^{2}\left( {\frac{\partial \dot{w}_1 }{\partial y}} \right) ^{2}+\dot{w}_1 ^{2}+\left( {x+r_0 } \right) ^{2}\left( {\dot{\theta }_z ^{2}+\dot{\theta }_y ^{2}} \right) +y^{2}\left( {\dot{\theta }_x ^{2}+\dot{\theta }_z ^{2}} \right) +z^{2}\nonumber \\&\times \left( {\dot{\theta }_y ^{2}+\dot{\theta }_x ^{2}} \right) +\dot{x}_o^2 +\dot{y}_o^2 +\dot{z}_o^2 +2\dot{z}_o \left[ {\dot{w}_1 -\left( {x+r_0 } \right) \dot{\theta }_y +y\dot{\theta }_x } \right] +2\left( {x+r_0 } \right) \dot{\theta }_z \dot{y}_o -2y\dot{\theta }_z \dot{x}_o \nonumber \\&\left. {-2\left[ {\left( {x+r_0 } \right) \dot{w}_1 +z^{2}\frac{\partial \dot{w}_1 }{\partial x}} \right] \dot{\theta }_y +2\left( {y\dot{w}_1 +z^{2}\frac{\partial \dot{w}_1 }{\partial y}} \right) \dot{\theta }_x -2\left( {x+r_0 } \right) y\dot{\theta }_x \dot{\theta }_y } \right\} \hbox {d}V \nonumber \\&+\frac{1}{2}\rho \int _{V_L } {\mathfrak {R}_T \hbox {d}V} +\frac{1}{2}m_R \left( {\dot{x}_o^2 +\dot{y}_o^2 +\dot{z}_o^2 } \right) +\frac{1}{2}\left( {J_z \dot{\theta }_z ^{2}+J_x \dot{\theta }_x ^{2}+J_y \dot{\theta }_y ^{2}} \right) , \end{aligned}$$

(18)

$$\begin{aligned} U= & {} \frac{1}{2}\int _{V_R } {z^{2}\left[ {Q_{11} \left( {\frac{\partial ^{2}w_1 }{\partial x^{2}}} \right) ^{2}+2Q_{12} \frac{\partial ^{2}w_1 }{\partial x^{2}}\frac{\partial ^{2}w_1 }{\partial y^{2}}} \right. } \left. +\,{Q_{22}\left( {\frac{\partial ^{2}w_1 }{\partial y^{2}}} \right) ^{2}+4Q_{66} \left( {\frac{\partial ^{2}w_1 }{\partial x\partial y}} \right) ^{2}} \right] \hbox {d}V\nonumber \\&+\,\frac{1}{2}\int _{V_L}{\mathfrak {R}_U \hbox {d}V}. \end{aligned}$$

(19)

In Eq. (18), the expression of ${\mathfrak {R}}_T$ can be obtained from the first integral expression by replacing $r_0$ and $w_1$ with $-r_0$ and $w_2$. Also, in Eq. (19), $\mathfrak {R}_U$ can be obtained from the first integral expression by replacing $w_1$ with $w_2$. It should be pointed out that the third- and higher-order coupling terms involving products of $w_1$, $w_2$, ${\theta }_x$, ${\theta }_y$, ${\theta }_z$, $x_o$, $y_o$ and $z_o$ and/or the partial derivatives respect to time t, x and/or y are neglected in the expression of the kinetic energy.

2.2 Approximation of the displacement field for solar panels

The transverse displacement functions for the two solar panels, $w_1$ and $w_2$, undergoing free vibration can be written as

$$\begin{aligned} w_i (x,y,t)=W_i (x,y)\sin \omega t,\quad i=1,2, \end{aligned}$$

(20)

where $\omega$ represents the circular frequency of the flexible spacecraft. $W_i(x,y)$ is modal shape and can be expressed in terms of basis functions which should be determined according to specific boundary conditions. So and Leissa [35] employed simple algebraic polynomials as basis functions to describe the axial displacement of a hollow circular cylinder and conducted modal analysis for the system. Simple algebraic polynomials can be constructed easily, but large number of terms should be included to predict more frequencies and modes with satisfactory accuracy. Zhou et al. [36] also studied the same problem by taking the Chebyshev polynomial series multiplied by a boundary function to satisfy the geometric boundary conditions as the admissible functions. Compared with simple algebraic polynomials, this kind of admissible functions can derive higher accuracy with less number of terms. However, these functions which satisfy geometric boundary conditions cannot be constructed directly. The beam functions can also be used as basis functions [37]. Those beam functions are hyperbolic and/or trigonometric forms. The integral and differential operations for the products of those functions are difficult to be calculated. As a result, the computation process of Rayleigh–Ritz method may be time-consuming. In our paper, characteristic orthogonal polynomials firstly employed by Bhat [29] to obtain natural frequencies of rectangular plates are used as basis functions to describe the displacements of solar panels. This set of characteristic orthogonal polynomials is generated by using a Gram–Schimidt process and can be constructed directly to satisfy given boundary conditions. Good convergence and high accuracy of using characteristic orthogonal polynomials in Rayleigh–Ritz method are shown in the studies of Sun et al. [30] and Liu et al. [31].

$W_i(x,y)$ can be expressed in terms of characteristic orthogonal polynomials in the x and y directions as

$$\begin{aligned} W_i (x,y)=\sum \limits _{m=1}^{m_t}{\sum \limits _{n=1}^{n_t}{A_{mn}^{(i)}{\varphi }_{m}^{(i)} (x){\varphi }_n^{(i)}(y)}},\quad i=1,2, \end{aligned}$$

(21)

where ${\varphi }_m^{(i)}(x)$ and ${\varphi }_n^{(i)}(y)$ are characteristic orthogonal polynomials in x and y directions for the right ($i=1$) and left ($i=2$) solar panels, respectively. $m_t$ and $n_t$ are the numbers of terms truncated in practical calculation. $A_{mn}^{(i)}$ is unknown coefficient.

Given a polynomial ${\psi }_1^{(i)}(\xi )(i=1,2)$, an orthogonal set of polynomials in the interval $a_{1}\le \xi \le a_{2}$ can be constructed according to the following Gram–Schmidt recursive formulas [29]

$$\begin{aligned} {\psi }_2^{(i)}(\xi )= & {} ({\xi -B_1^{(i)}})\psi _1^{(i)} (\xi ),\nonumber \\ {\psi }_{k+1}^{(i)}(\xi )= & {} ({\xi -B_k^{(i)}}){\psi } _k^{(i)}(\xi )-C_k^{(i)}{\psi }_{k-1}^{(i)} (\xi ),\quad k\ge 2, \end{aligned}$$

(22)

where

$$\begin{aligned} B_k^{(i)} =\frac{\int _{a_1 }^{a_2 } {\xi [{\psi _k^{(i)} (\xi )} ]} ^{2}\hbox {d}\xi }{\int _{a_1 }^{a_2 } {[{\psi _k^{(i)} (\xi )} ]^{2}\hbox {d}\xi }},\quad C_k^{(i)} =\frac{\int _{a_1 }^{a_2 } {\xi \psi _{k-1}^{(i)}(\xi )} \;\psi _k^{(i)} (\xi )\hbox {d}\xi }{\int _{a_1 }^{a_2}{[{\psi _{k-1}^{(i)} (\xi )}]^{2}\hbox {d}\xi }}. \end{aligned}$$

(23)

Then, the characteristic orthogonal polynomials are normalized according to the following formula

$$\begin{aligned} {\varphi }_k^{(i)}(\xi )=\frac{\psi _k^{(i)} (\xi )}{\sqrt{\int _{a_1 }^{a_2 } {[{\psi _k^{(i)} (\xi )}]^{2}\hbox {d}\xi } }},\quad i=1,\;2;\quad k=1, 2,\ldots \end{aligned}$$

(24)

If the first member of polynomials ${\varphi }_k^{(i)}(\xi )(i=1,2;k=1,2,\ldots )$ satisfies the geometric boundary conditions, it can be easily checked that other polynomials also satisfy the geometric boundary conditions. The relationship between any two members of the set of orthogonal polynomials is given by

$$\begin{aligned} \int _{a_1}^{a_2}{\left[ {{\varphi }_{k_1}^{(i)}(\xi ){\varphi }_{k_2}^{(i)}(\xi )}\right] \;\hbox {d}\xi }=\left\{ {\begin{array}{ll} 0&{}\quad k_1 \ne k_2 \\ 1&{}\quad k_1 =k_2 \\ \end{array}} \right. ,\quad i=1,2;\quad k_1,k_2=1,2,\ldots \end{aligned}$$

(25)

In this paper, the integral intervals and boundary conditions for ${\varphi }_m^{(i)}(x)$ and ${\varphi }_n^{(i)}(y)$ are listed in Table 1. The procedure for constructing the corresponding first member ${\psi }_1^{(i)}(\xi )(i=1,2)$ is displayed in Ref. [29].

Table 1 Integral intervals and boundary conditions for characteristic orthogonal polynomials

2.3 Rayleigh–Ritz procedure

The vibrations of solar panel are coupled with the rigid body motion of the spacecraft. That means the translations and attitude angles of spacecraft can also be written as products of a constant and a term varying with time. Then, the following expressions can be obtained

$$\begin{aligned} q_o =S_o \sin \omega t,\quad {\theta }_q={\theta }_0^{(q)} \sin \omega t,\quad q=x,y,z,\quad S=X,Y,Z, \end{aligned}$$

(26)

where $S_o$ and ${\theta }_0^{(q)}$ are unknown coefficients.

Substituting displacement field (20) and Eq. (26) in the kinetic and strain energy expressions, Eqs. (18) and (19), and minimizing the Rayleigh quotient with respect to the coefficients $X_o$, $Y_o$, $Z_o$, ${\theta }_0^{(x)}$, ${\theta }_0^{(y)}$, ${\theta }_0^{(z)}$, $A_{mn}^{(1)}$ and $A_{mn}^{(2)}$, yield the eigenvalue equation of spacecraft installed with a pair of solar arrays

$$\begin{aligned} ({\mathbf{K}-{\omega }^{2}{} \mathbf{M}})\mathbf{X}=\mathbf{0}, \end{aligned}$$

(27)

in which $\mathbf{X}$ is a column vector which is composed of the unknown coefficients as follows

$$\begin{aligned} \mathbf{X}=[{X_o,Y_o,Z_o,{\theta }_0^{(x)},{\theta }_0^{(y)},{\theta }_0^{(z)}, A_{11}^{(1)}, A_{12}^{(1)},\ldots ,A_{m_t n_t}^{(1)},A_{11}^{(2)} ,A_{12}^{(2)},\ldots ,A_{m_t n_t}^{(2)}} ]^{\mathrm{T}}. \end{aligned}$$

(28)

$\mathbf{K}$ is a $({6+2m_t n_t})\times ({6+2m_t n_t})$ matrix given by

$$\begin{aligned} \mathbf{K}=\left[ {{\begin{array}{lll} {\mathbf{0}_{6\times 6} }&{}\quad {\mathbf{0}_{6\times m_t n_t } }&{}\quad {\mathbf{0}_{6\times m_t n_t } } \\ {\mathbf{0}_{m_t n_t \times 6} }&{}\quad {\mathbf{K}_{77} }&{}\quad {\mathbf{0}_{m_t n_t \times m_t n_t } } \\ {\mathbf{0}_{m_t n_t \times 6} }&{}\quad {\mathbf{0}_{m_t n_t \times m_t n_t } }&{}\quad {\mathbf{K}_{88} } \\ \end{array}}} \right] , \end{aligned}$$

(29)

where $\mathbf{K}_{77}$ and $\mathbf{K}_{88}$ are block matrices of $\mathbf{K}$, and their size is $m_t n_t \times m_t n_t$. The elements of $\mathbf{K}_{77}$ and $\mathbf{K}_{88}$ are given as

$$\begin{aligned} ({\mathbf{K}_{77}})_{ij}= & {} \frac{2}{3}H^{3}\int _0^L \int _{-b}^{\;b}\left\{ {2Q_{11}\frac{{\partial }^{2}{\varphi }_{m_i}^{(1)} }{\partial x^{2}}{\varphi }_{n_i}^{(1)}\frac{{\partial }^{2}{\varphi }_{m_j }^{(1)}}{\partial x^{2}}{\varphi }_{n_j}^{(1)}+2Q_{12}}\right. \left[ {{\varphi }_{m_i}^{(1)}\frac{{\partial }^{2}{\varphi }_{n_i}^{(1)}}{\partial y^{2}}\frac{{\partial }^{2}{\varphi }_{m_j}^{(1)}}{\partial x^{2}}{\varphi } _{n_j}^{(1)}}\right. +\frac{{\partial }^{2}{\varphi }_{m_i}^{(1)} }{\partial x^{2}}{\varphi }_{n_i}^{(1)}\nonumber \\&\left. {\times \,{\varphi }_{m_j}^{(1)} \frac{{\partial }^{2}{\varphi }_{n_j}^{(1)}}{\partial y^{2}}} \right] +2Q_{22}{\varphi }_{m_i}^{(1)} \frac{{\partial }^{2}{\varphi }_{n_i }^{(1)}}{\partial y^{2}}{\varphi }_{m_j}^{(1)} \frac{{\partial }^{2}{\varphi } _{n_j}^{(1)}}{\partial y^{2}}+\left. {8Q_{66}\frac{\partial {\varphi } _{m_i}^{(1)}}{\partial x}\frac{\partial {\varphi }_{n_i}^{(1)} }{\partial y}\frac{\partial {\varphi }_{m_j}^{(1)}}{\partial x}\frac{\partial {\varphi }_{n_j}^{(1)}}{\partial y}} \right\} \hbox {d}y\hbox {d}x, \end{aligned}$$

(30)

$$\begin{aligned} ({\mathbf{K}_{88}})_{ij}= & {} \frac{2}{3}H^{3}\int _{-L}^{0}\int _{-b}^{\;b}\left\{ {2Q_{11} \frac{{\partial }^{2}{\varphi }_{m_i}^{(2)}}{\partial x^{2}}{\varphi }_{n_i }^{(2)}\frac{{\partial }^{2}{\varphi }_{m_j}^{(2)}}{\partial x^{2}}{\varphi } _{n_j}^{(2)}+2Q_{12}}\right. \left[ {{\varphi }_{m_i}^{(2)} \frac{{\partial }^{2}{\varphi }_{n_i}^{(2)}}{\partial y^{2}}\frac{{\partial }^{2}{\varphi }_{m_j}^{(2)}}{\partial x^{2}}{\varphi } _{n_j}^{(2)}}\right. +\frac{{\partial }^{2}{\varphi }_{m_i}^{(2)} }{\partial x^{2}}{\varphi }_{n_i}^{(2)}\nonumber \\&\left. {\times \,{\varphi }_{m_j}^{(2)} \frac{{\partial }^{2}{\varphi }_{n_j}^{(2)}}{\partial y^{2}}} \right] +2Q_{22} {\varphi }_{m_i}^{(2)} \frac{\partial ^{2}{\varphi }_{n_i }^{(2)}}{\partial y^{2}}{\varphi }_{m_j}^{(2)}\frac{\partial ^{2}{\varphi } _{n_j}^{(2)}}{\partial y^{2}}+\left. {8Q_{66} \frac{\partial {\varphi } _{m_i}^{(2)}}{\partial x}\frac{\partial {\varphi }_{n_i}^{(2)} }{\partial y}\frac{\partial {\varphi }_{m_j}^{(2)}}{\partial x}\frac{\partial {\varphi }_{n_j}^{(2)}}{\partial y}} \right\} \hbox {d}y\hbox {d}x, \end{aligned}$$

(31)

where $m_i,m_j=1,2,\ldots ,m_t$ and $n_i,n_j =1,2,\ldots ,n_t$. $\mathbf{M}$ is a $({6+2m_t n_t})\times ({6+2m_t n_t})$ matrix given by

$$\begin{aligned} \mathbf{M}=\left[ {{\begin{array}{llllllll} {M_{11} }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {M_{16} }&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ 0&{}\quad {M_{22} }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {M_{26} }&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ 0&{}\quad 0&{}\quad {M_{33} }&{}\quad {M_{34} }&{}\quad {M_{35} }&{}\quad 0&{}\quad {\mathbf{M}_{37} }&{}\quad {\mathbf{M}_{38} } \\ 0&{}\quad 0&{}\quad {M_{43} }&{}\quad {M_{44} }&{}\quad 0&{}\quad 0&{}\quad {\mathbf{M}_{47} }&{}\quad {\mathbf{M}_{48} } \\ 0&{}\quad 0&{}\quad {M_{53} }&{}\quad 0&{}\quad {M_{55} }&{}\quad 0&{}\quad {\mathbf{M}_{57} }&{}\quad {\mathbf{M}_{58} } \\ {M_{61} }&{}\quad {M_{62} }&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {M_{66} }&{}\quad \mathbf{0}&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad {\mathbf{M}_{73} }&{}\quad {\mathbf{M}_{74} }&{}\quad {\mathbf{M}_{75} }&{}\quad \mathbf{0}&{}\quad {\mathbf{M}_{77} }&{}\quad \mathbf{0} \\ \mathbf{0}&{}\quad \mathbf{0}&{}\quad {\mathbf{M}_{83} }&{}\quad {\mathbf{M}_{84} }&{}\quad {\mathbf{M}_{85} }&{}\quad \mathbf{0}&{}\quad \mathbf{0}&{}\quad {\mathbf{M}_{88} } \\ \end{array} }} \right] , \end{aligned}$$

(32)

where

$$\begin{aligned} M_{11}= & {} 16\rho LbH+2m_R,\quad M_{22} =M_{11},\quad M_{33}=M_{11},\nonumber \\ M_{16}= & {} -\rho \int _0^L {\int _{-b}^{\;b} {4Hy\hbox {d}y\hbox {d}x}}-\rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {4Hy\hbox {d}y\hbox {d}x}},\quad M_{61} =M_{16},\nonumber \\ M_{26}= & {} \rho \int _0^L {\int _{-b}^{\;b} {4H\left( {x+r_0 } \right) \hbox {d}y\hbox {d}x} } +\rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {4H\left( {x-r_0 } \right) \hbox {d}y\hbox {d}x}}, \quad M_{62}=M_{26},\nonumber \\ M_{34}= & {} -M_{16}, \quad M_{35} =-M_{26}, \quad M_{43} =M_{34},\quad M_{53} =M_{35}.\nonumber \\ M_{44}= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left( {4Hy^{2}+\frac{4}{3}H^{3}} \right) \hbox {d}y\hbox {d}x} } +\rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left( {4Hy^{2}+\frac{4}{3}H^{3}} \right) \hbox {d}y\hbox {d}x} } +2J_x, \nonumber \\ M_{55}= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left[ {4H(x+r_0 )^{2}+\frac{4}{3}H^{3}} \right] \hbox {d}y\hbox {d}x} } +\rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left[ {4H(x-r_0 )^{2}+\frac{4}{3}H^{3}} \right] \hbox {d}y\hbox {d}x} } +2J_y, \nonumber \\ M_{66}= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left[ {4H(x+r_0 )^{2}+4Hy^{2}} \right] \hbox {d}y\hbox {d}x} } +\rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left[ {4H(x-r_0 )^{2}+4Hy^{2}} \right] \hbox {d}y\hbox {d}x} } +2J_z.\nonumber \\ \end{aligned}$$

(33)

$\mathbf{M}_{37}, \quad \mathbf{M}_{38}, \quad \mathbf{M}_{47}, \quad \mathbf{M}_{48}, \quad \mathbf{M}_{57}$    and    $\mathbf{M}_{58}$ are $1\times m_t n_t$ row vectors. Their elements are given as follows

$$\begin{aligned} ({\mathbf{M}_{37}})_i= & {} \rho \int _0^L {\int _{-b}^{\;b} {4H\varphi _{m_i }^{(1)} \varphi _{n_i }^{(1)} \hbox {d}y\hbox {d}x}},\nonumber \\ ({\mathbf{M}_{38}})_i= & {} \rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {4H\varphi _{m_i }^{(2)} \varphi _{n_i }^{(2)} \hbox {d}y\hbox {d}x}}, \nonumber \\ ({\mathbf{M}_{47}})_i= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left[ {4Hy\varphi _{m_i }^{(1)} \varphi _{n_i }^{(1)} +\frac{4}{3}H^{3}\varphi _{m_i }^{(1)} \frac{\partial \varphi _{n_i }^{(1)} }{\partial y}} \right] \hbox {d}y\hbox {d}x}},\nonumber \\ ({\mathbf{M}_{48}})_i= & {} \rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left[ {4Hy\varphi _{m_i }^{(2)} \varphi _{n_i }^{(2)} +\frac{4}{3}H^{3}\varphi _{m_i }^{(2)} \frac{\partial \varphi _{n_i }^{(2)} }{\partial y}} \right] \hbox {d}y\hbox {d}x}},\nonumber \\ ({\mathbf{M}_{57}})_i= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left[ {-4H(x+r_0 )\varphi _{m_i }^{(1)} \varphi _{n_i }^{(1)} -\frac{4}{3}H^{3}\frac{\partial \varphi _{m_i }^{(1)} }{\partial x}\varphi _{n_i }^{(1)} } \right] \hbox {d}y\hbox {d}x}},\nonumber \\ ({\mathbf{M}_{58}})_i= & {} \rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left[ {-4H(x-r_0 )\varphi _{m_i }^{(2)} \varphi _{n_i }^{(2)} -\frac{4}{3}H^{3}\frac{\partial \varphi _{m_i }^{(2)} }{\partial x}\varphi _{n_i }^{(2)} } \right] \hbox {d}y\hbox {d}x}}. \end{aligned}$$

(34)

$\mathbf{M}_{73}, \quad \mathbf{M}_{83}, \quad \mathbf{M}_{74}, \quad \mathbf{M}_{84}, \quad \mathbf{M}_{75}$ and $\mathbf{M}_{85}$ are $m_t n_t \times 1$ column vectors and given by

$$\begin{aligned} \mathbf{M}_{73} =\mathbf{M}_{37}^{\mathrm{T}},\;\;\;\mathbf{M}_{83} =\mathbf{M}_{38}^{\mathrm{T}}, \quad \mathbf{M}_{74}=\mathbf{M}_{47}^{\mathrm{T}} ,\quad \mathbf{M}_{84}=\mathbf{M}_{48}^{\mathrm{T}},\quad \mathbf{M}_{75}=\mathbf{M}_{57}^{\mathrm{T}},\quad \mathbf{M}_{85}=\mathbf{M}_{58}^{\mathrm{T}}. \end{aligned}$$

(35)

$\mathbf{M}_{77}$ and $\mathbf{M}_{88}$ are $m_t n_t \times m_t n_t$ matrices, and their elements are given as

$$\begin{aligned} ({\mathbf{M}_{77}})_{ij}= & {} \rho \int _0^L {\int _{-b}^{\;b} {\left[ {\frac{4}{3}H^{3}\frac{\partial \varphi _{m_i }^{(1)} }{\partial x}\varphi _{n_i }^{(1)} \frac{\partial \varphi _{m_j }^{(1)} }{\partial x}\varphi _{n_j }^{(1)} +\frac{4}{3}H^{3}\varphi _{m_i }^{(1)} \frac{\partial \varphi _{n_i }^{(1)} }{\partial y}} \right. } } \left. {\varphi _{m_j }^{(1)} \frac{\partial \varphi _{n_j }^{(1)} }{\partial y}+4H\varphi _{m_i }^{(1)} \varphi _{n_i }^{(1)} \varphi _{m_j }^{(1)} \varphi _{n_j }^{(1)} } \right] \hbox {dyd}x,\nonumber \\ \end{aligned}$$

(36)

$$\begin{aligned} ({\mathbf{M}_{88}})_{ij}= & {} \rho \int _{-L}^{\;0} {\int _{-b}^{\;b} {\left[ {\frac{4}{3}H^{3}\frac{\partial \varphi _{m_i }^{(2)} }{\partial x}\varphi _{n_i }^{(2)} \frac{\partial \varphi _{m_j }^{(2)} }{\partial x}\varphi _{n_j }^{(2)} +\frac{4}{3}H^{3}\varphi _{m_i }^{(2)} \frac{\partial \varphi _{n_i }^{(2)} }{\partial y}} \right. } } \left. {\varphi _{m_j }^{(2)} \frac{\partial \varphi _{n_j }^{(2)} }{\partial y}+4H\varphi _{m_i }^{(2)} \varphi _{n_i }^{(2)} \varphi _{m_j }^{(2)} \varphi _{n_j }^{(2)} } \right] \hbox {dyd}x.\nonumber \\ \end{aligned}$$

(37)

The frequencies and the analytical expressions of mode shapes for the flexible spacecraft can be yielded by solving the eigenvalue equation (27). It should be pointed out that the first six frequencies are zero and relative to rigid body translations ($x_o$, $y_o$ and $z_o$) and rotations (${\theta }_x$, ${\theta }_y$ and ${\theta }_z$) of the whole flexible spacecraft. In this situation, the solar panels are undeformed. Hence, those zero frequencies are neglected in the following analyses.

3 Numerical results and discussions

3.1 Validation and convergence studies

The geometric and material properties of the spacecraft installed with a pair of solar arrays studied in this paper are listed in Table 2. To check the accuracy of present method, comparisons are made with results obtained from the commercial finite element software ANSYS. Figure 6 is the finite element model of the spacecraft installed with a pair of solar arrays in ANSYS. The rigid hub is modeled using solid elements, and the solar panels are discretized by employing shell elements. The multi-point constrains (MPCs) are used to model the constraints of solar panels imposed by the rigid hub. The rigid body motion of the spacecraft has three translational and three rotational degrees of freedom.

Table 2 Geometric and material parameters of the flexible spacecraft

Fig. 6

Finite element model of the flexible spacecraft in ANSYS

Table 3 Comparison of the first eight frequencies for a flexible spacecraft $f(\hbox {Hz}) (L=8\,\hbox {m})$

Table 4 First eight frequencies for spacecraft with different solar panel length $f\,(\hbox {Hz})$

Table 3 shows the first eight frequencies for the flexible spacecraft ($L=8\;\hbox {m}$) calculated by using ANSYS and the present approach. It can be seen that, at $m_t =11$ and $n_t=7$, the absolute values of relative tolerances between the present results and frequencies obtained from ANSYS are <0.21 %. That means very excellent agreement can be achieved provided that enough number of terms for characteristic orthogonal polynomials is truncated in practical calculation. Further investigations are conducted in Table 4. The comparison carried out in this table also shows good agreement for a wide variety of modes of flexible spacecraft with other solar panel length.

Figures 7 and 8 show the further convergence investigations. Without loss of generality, frequencies corresponding to the second and eighth modes are studied. In order to investigate the convergence of the present method conveniently, the relative tolerance is defined as follows

$$\begin{aligned} Rt=\frac{f_{m_t n_t } -f_\mathrm{exact} }{f_\mathrm{exact} }\times 100\,\%, \end{aligned}$$

(38)

where $f_{m_t n_t}$ represents the frequency with respect to polynomial terms of $m_t$ and $n_t$, and $f_\mathrm{exact}$ denotes the exact value of the frequency which is derived by using relatively larger number of terms of modal function $W_i (x,y) (i=1,\;2)$. As observed from Table 3, using polynomial terms of $m_t =11$ and $n_t =7$ for $W_i (x,y)(i=1,2)$ is adequate for convergent results. Therefore, the results yielded by using 13 terms of characteristic orthogonal polynomials ($m_t =13$ and $n_t =13$) can be used as exact values. From Figs. 7 and 8, it can be seen that the trends of the variation of relative tolerance surfaces of the system frequencies with respect to $m_t$ and $n_t$ for flexible spacecraft with different solar panel length are similar. All the relative tolerances of the system frequencies decrease gradually as the number of terms for characteristic orthogonal polynomials truncated in practical calculations increases, and maintain at a steady level close to zero. That means the obtained system frequencies converge at exact values. For lower-order frequency, as shown in Figs. 7a and 8a, both the relative tolerances for spacecraft with short ($L=2\;\hbox {m}$) and long ($L=8\;\hbox {m}$) solar panels are below 1 % with 3 terms of orthogonal polynomials, i.e., $m_t =n_t =3$. For higher-order frequency illustrated in Figs. 7b and 8b, although the relative tolerances are very high when $m_t =n_t =3$, they decrease sharply to a level <1 % as $m_t$ and $n_t$ grow. In a word, terms of polynomials $m_t =11$ and $n_t =7$ are enough to obtain favorable results for spacecraft installed with a pair of solar panels. It may indicate that the present method has excellent convergence and high efficiency.

Fig. 7

Variation of relative tolerances of the frequencies with respect to the number of terms for orthogonal polynomials truncated in practical calculation ($L=2\;\hbox {m}$): a the 2nd frequency, b the 8th frequency

Fig. 8

Variation of relative tolerances of the frequencies with respect to the number of terms for orthogonal polynomials truncated in practical calculation ($L=8\;\hbox {m}$): a the 2nd frequency, b the 8th frequency

3.2 Global analytical modes

In this section, an analysis is presented for the characteristics of global analytical modes of spacecraft installed with a pair of solar panels.

There are two approaches to obtain the global modes of the spacecraft in this paper. One is using ANSYS, and the other is using the extended Rayleigh–Ritz method proposed in this research. The modes from ANSYS are numerical and not convenient to be used in the discretization of the deformation of solar panels and in the design of controllers for both the attitude maneuver and vibration suppression. However, the analytical expressions of modes given by the method presented in this paper can be easily used to do so. Solving the eigenvalue equation (27), the frequencies and corresponding eigenvectors can be obtained. The first six frequencies and eigenvectors are relative to the six rigid body motions ($x_o$, $y_o$, $z_o$, $\theta _x$, $\theta _y$ and $\theta _z )$, and those six frequencies are zero and neglected in the following analyses. The first six elements of each eigenvector corresponding to nonzero frequencies represent the amplitudes of $x_o$, $y_o$, $z_o$, $\theta _x$, $\theta _y$ and $\theta _z$, respectively, and can be used to determine whether the deformation of solar panel is coupled with rigid body motion of the spacecraft as shown in Table 5 and Fig. 10. The other elements are values of those unknown coefficients $A_{mn}^{(i)} \;(i=1,2)$ of the modal shape $W_i (x,y)$ shown in expression (21), then the analytical expression of each order global mode can be obtained and the mode shapes are plotted as illustrated in Fig. 10. In order to vividly display the coupling between the solar deformation and the spacecraft rigid body motion, the first eight mode shapes obtained from ANSYS are given in Fig. 9 for a flexible spacecraft with solar panel length $L=8\;\hbox {m}$.

Fig. 9

First eight global mode shapes of the flexible spacecraft ($L=8\;\hbox {m}$): a the 1st mode, S(1, 1); b the 2nd mode, AS(1, 1); c the 3rd mode, S(2, 1); d the 4th mode, AS(2, 1); e the 5th mode, AS(1, 2); f the 6th mode, S(1, 2); g the 7th mode, S(3, 1); h the 8th mode, AS(3, 1). The rigid body motion of spacecraft is exaggerated

Table 5 Model numbers (m, n) and corresponding rigid body motion ($x_o$, $y_o$, $z_o$, ${\theta }_x$, ${\theta }_y$ and ${\theta }_z)$ for different solar array length of flexible spacecraft

As shown in Fig. 9, there are two kinds of global modes for the same mode number (m, n) of solar panel. Here, m and n are corresponding to x and y directions, respectively. For example, when $(m,n)=(2,1)$, the mode shapes illustrated by Fig. 9c is associated with the third system frequency, while that shown in Fig. 9d is the fourth mode shape. The former one is denoted as S(2, 1) because the two solar panels vibrate symmetrically. In this case, there is no rotation of the whole spacecraft but translation $z_o$. That means the elastic vibration of solar panels is coupled with spacecraft translation. The latter one is represented by AS(2, 1) because the deformation of the two solar panels is antisymmetric. For this mode, the spacecraft rotates with attitude ${\theta }_y$, which implies that the mode of solar panel is coupled with spacecraft attitude motion. On the other hand, the global modes with mode number $(m,n)=(1,2)$, i.e., AS(1, 2) and S(1, 2), shown in Fig. 9e, f have different characteristics. The solar panels’ deformation of AS(1, 2) is not coupled with any rigid body motion of the spacecraft, however, that of S(1, 2) coupled with spacecraft attitude motion ${\theta }_x$. Table 5 shows the model numbers and corresponding rigid body motion of the first eight global modes of spacecraft with other solar panel length. The mode shapes for those global modes are displayed in Figs. 9 and 10. Combining Table 5 and Figs. 9 and 10, a useful conclusion can be made: If the mode number n is an odd number, the S(m, n) global modes are coupled with translation $z_o$ of the whole spacecraft, and AS(m, n) global modes with spacecraft attitude motion ${\theta }_y$; if the mode number n is an even number, the S(m, n) global modes are coupled with spacecraft attitude motion ${\theta }_x$, and AS(m, n) global modes are not coupled with any rigid body motion.

Fig. 10

Mode shapes of flexible spacecraft for different solar panel length: a–d $L=1\;\hbox {m}$; e and f $L=4\;\hbox {m}$; g $L=32\;\hbox {m}$

Table 6 displays the comparison between frequencies of spacecraft global modes and the first four frequencies of a cantilever solar panel ($L=8\;\hbox {m}$). The frequency of AS(1, 2) mode underlined in Table 6 is the same as that of the (1, 2) mode of cantilever solar panel since AS(1, 2) mode is not coupled with any rigid body motion of the spacecraft. The frequencies of other global modes coupled with rigid body motion of spacecraft are higher than those of corresponding modes of cantilever solar panel. Another conclusion can be drawn that when mode number n is an odd number, the frequency increase rate of modes coupled with spacecraft attitude motion ${\theta }_y$, such as AS(1, 1), AS(2, 1) and AS(3, 1), is much higher than that of modes coupled with spacecraft translation $z_o$, i.e., S(1, 1), S(2, 1) and S(3, 1). Moreover, the assumed modes used in many researches are the modes of cantilever solar panel, i.e., the rigid body motion of the spacecraft hub is fully limited, which results in failure in reflecting the effects of spacecraft rigid body motion and rigid hub on the elastic modes of solar panels. So, one can conclude that the discretized models derived by using assumed modes may be not accurate for a flexible spacecraft, and the global analytical modes [expression (21)] obtained by using the present method should be adopted in the discretization of dynamic equations of the system.

Table 6 Comparison between frequencies of spacecraft global modes and those of the first four modes of cantilever solar panel ($L=8\;\hbox {m}$)

3.3 Parameter studies

Using the method presented in this paper, some parameter studies are conducted to investigate the influence of varying rigid-hub mass moment of inertia $J_R(J_x =J_y =J_z =J_R )$ and solar array length L on the global modes of the flexible spacecraft.

Fig. 11

Variation of the 1st, 2nd, 7th and 8th frequencies with respect to the moment of inertia of the hub $J_R$ for spacecraft installed with solar panels ($L=8\;\hbox {m}$)

Fig. 12

Variation of the 3rd through 6th frequencies with respect to the moment of inertia of the hub $J_R$ for spacecraft installed with solar panels ($L=8\;\hbox {m}$): a the full view, b enlarged views at No. 1 to No. 4 areas

Fig. 13

Variation of the first eight frequencies with respect to the solar array length L of a flexible spacecraft ($J_R =100\;\hbox {kg}\;\hbox {m}^{2}$): a full view for $4\;\hbox {m}\le L\le 14\;\hbox {m}$, b enlarged views at area $\hbox {I}$ and area $\hbox {II}$ in a, c full view for $14\;\hbox {m}\le L\le 32\;\hbox {m}$

Figures 11 and 12 depict the variation of the first eight frequencies with respect to the moment of inertia of the hub for the spacecraft installed with a pair of solar arrays ($L=8\;\hbox {m}$). As illustrated in the figures, the frequency of each global mode coupled with spacecraft translation, such as S(1, 1), S(2, 1) or S(3, 1), decreases rapidly with $J_R$ and then converges to a certain value. Meanwhile, the frequencies of modes coupled with attitude motion ${\theta }_y$, i.e., AS(1, 1), AS(2, 1) and AS(3, 1), reduce gradually when $J_R$ is growing, and converge to the frequencies of corresponding symmetric modes, S(1, 1), S(2, 1) and S(3, 1). Because AS(1, 2) is not coupled with the rigid body motion of spacecraft, the frequency of this mode is unchanged as $J_R$ increases. However, its corresponding symmetric mode S(1, 2) is coupled with spacecraft attitude motion ${\theta }_x$, and thus, the frequency of S(1, 2) decreases with $J_R$ and tends to that of AS(1, 2). What is more, there are big differences between the frequencies of S(m, n) mode and AS(m, n) mode for lower-order global modes or small $J_R$ (i.e., the spacecraft is very flexible).

As $J_R$ increases, the frequency veering phenomena among the 3rd to the 6th modes are also observed in Fig. 12 when the adjacent natural frequencies are close to each other. The interesting mode shift phenomenon occurs with the frequency veering phenomenon. Take the frequency variation between AS(2, 1) and S(1, 2) as an example. When $0<J_R \le 10\;\hbox {kg}\;\hbox {m}^{2}$, the 5th and 6th modes in Fig. 12 are dominated by AS(2, 1) and S(1, 2), respectively; when $J_R$ is in the range 10–53 kg m$^{2}$, the 5th and 6th modes are dominated by S(1, 2) and AS(2, 1), respectively. Similar frequency veering phenomenon between S(1, 2) and AS(2, 1) occurs again when $J_R \approx 54\;\hbox {kg}\;\hbox {m}^{2}$. Another two frequency veering phenomena happen between AS(1, 2) and S(2, 1) at NO.1 area, AS(1, 2) and AS(2, 1) at NO.4 area, as shown in Fig. 12.

The simulation results for different solar panel length are shown in Table 5, Figs. 10 and 13. It can be observed from Table 5 that the mode shapes of solar panel are dominated by deformation in the direction of width (y direction in this paper) for small L. Meanwhile, some lower-order coupled modes, such as S(1, 2), are coupled with attitude motion ${\theta }_x$, and other modes with attitude motion ${\theta }_y$. Therefore, the spacecraft is three-axis attitude stabilized. In this case, the solar array should be modeled by plate to describe this feature of the system. As the length of solar array increases, the deformation in the direction of length (x direction in this paper) gradually becomes the main part of mode shapes, and the order of coupled modes coupled with ${\theta } _x$ raises progressively. The low-order modes of solar panel are coupled with ${\theta }_y$. Then, it is appropriate to model long solar panel with flexible beam which can only describe planar deformation in the direction of length which is coupled with ${\theta }_y$.

Figure 13 illustrates the variation of the first eight frequencies with respect to the length of solar panel L for a flexible spacecraft. It can be seen that the frequencies gradually decrease as L increases. Also, frequency veering phenomena occur between different global modes as shown in Fig. 13b, c. In addition, the high-order global modes dominated by deformation in the direction of width (y direction in this paper) disappear among the first eight modes of flexible spacecraft and are replaced by high-order modes dominated by deformation in the direction of length (x direction in this paper). AS(2, 2) and S(2, 2) illustrated in area I of Fig. 13b, for example, are the 7th and 8th modes of the system when $L<5.5\;\hbox {m}$ and then are displaced by S(3, 1) and AS(3, 1) when L exceeds $5.5\;\hbox {m}$. Similar mode replacement happens again near $L=30.8\;\hbox {m}$, as shown in Fig. 13c.

4 Conclusions

The Rayleigh–Ritz method has been successfully extended to obtain the global analytical modes and analyze the modal characteristics of a typical rigid–flexible coupling dynamic system (hub-plate system), i.e., a three-axis attitude stabilized spacecraft installed with a pair of solar arrays. Also the method in this paper can be used to study modal features of other rigid–flexible coupling systems such as hub-beam system. Validation of this method has been checked by comparisons with results obtained from ANSYS software. The method presented can efficiently calculate high-precision frequencies of the flexible spacecraft and makes it possible to obtain the analytical expressions of the global modes, which can be conveniently used in the discretization of the dynamic equations of flexible spacecraft and in the design of controllers for both the attitude maneuver and vibration suppression. However, the FEM such as ANSYS can only obtain numerical modes which are not easy to be used to do so. What is more, different from FEM, the frequencies and mode shapes derived in this paper are based on analytical formulations, so effect of given system parameters on modal characteristics of the flexible spacecraft can be studied easily and more insight into the modal characteristics can be provided. To sum up, the method presented in this paper is a relative convenient, efficient and exact method dealing with global mode analysis of flexible spacecraft in engineering applications.

Moreover, using the method presented in this paper, the characteristics of global modes of the spacecraft installed with a pair of solar arrays have been investigated. Some main conclusions are summarized as follows:

• (1) For the same mode number (m, n) of solar panel: (1) if the mode number n is an odd number, the symmetric (m, n) global modes are coupled with spacecraft translation $z_o$, and antisymmetric (m, n) global modes with spacecraft attitude motion $\theta _y$; (2) if the mode number n is an even number, the antisymmetric (m, n) global modes are not coupled with any rigid body motion, and symmetric (m, n) global modes are coupled with spacecraft attitude motion $\theta _x$. In both two cases, frequencies of latter modes are higher than those of former ones, and converge to the former frequencies as the hub inertial moment increases.

• (2) The frequencies of global modes coupled with rigid body motion of spacecraft are higher than those of corresponding modes of cantilever solar panel which are used as assumed modes in many researches. That means the assumed modes fail to reflect the effects of spacecraft rigid body motion and rigid hub on the elastic modes of solar panels. So, the global analytical modes rather than assumed ones should be adopted in the discretization of dynamic equations of the system.

• (3) For small solar array length, the solar panel should be modeled by plate to describe the three-axis attitude stability of the spacecraft. However, it is appropriate to model long solar array with flexible beam which can only describe planar deformations in the direction of solar length. In addition, the interesting frequency veering and mode shift phenomena have also been observed during the parameter studies on rigid-hub mass moment of inertia and solar panel length.