1 Introduction

The linear and nonlinear propagation of electrostatic waves in dusty plasmas which occur in both space and laboratory environments have received a considerable attention for the last many years (Shukla and Mamun 2002; Merlino and Goree 2004; Ishihara 2007). Researchers have been showing great interest in nonlinear structures because they offer deep physical insight underlying the nonlinear phenomena. The nonlinearity in plasma contributes to localization of waves, leading to different types of interesting coherent nonlinear wave structures such as solitons, shock waves, vortices and double layers. Most of the space and astrophysical environments show the presence of dust particles. Dust particles are often of micron to submicron size, with masses in the range of 106 to 1012 proton masses. Dust particles are usually found to have negative charge (possibly as large as ∼104 electron charges), depending on the environment where they occur. On the other hand, smaller dust grains may be found to be positively charged. Because of high charge and large mass of the grain particulates compared to those of ions, new time and space scales come into play, giving rise to either new or modified waves in dusty plasmas (Rao et al. 1990; Shukla and Silin 1992; Kaw and Sen 1998; Rao 1999; Tribeche et al. 2000). Dust acoustic wave (DAW) is one of the low frequency mode that occurs in dusty plasmas, where the dust particle mass provides the inertia and the pressures of the inertialess electrons and ions provide the restoring force. In recent years, a great deal of attention has been paid to study properties of collective waves in dusty plasmas in astrophysical and space plasma environments e.g., in planetary rings, comets, the Earth’s ionosphere, interstellar molecular clouds, circumstellar disks, etc. (Horanyi and Mendis 1985, 1986; Verheest 1996; Goertz 1992). At earlier stage, studies in dusty plasma were based on the theoretical prediction of the existence of dust-acoustic waves (DAWs) by Rao et al. (1990), which were later confirmed by several experimental groups (Barkan et al. 1995; Pieper and Goree 1996; Prabhuram and Goree 1996). Mamun et al. (1996) showed that a dusty plasmas with ions following Boltzmann distribution possess only negative solitons associated with DAWs. The coexistence of both dust acoustic DA solitons and double layers has been studied in unmagnetized four component dusty plasma using Sagdeev’s pseudopotential method (Sakanaka and Shukla 2000).

A double-layer (DL) is a narrow isolated region of abrupt potential jump or trough in the amplitude due to localised dipole sheet of space charge surrounded by large regions of effectively uniform potential. Since a localized dipole-sheet nature is required for the space charge distribution (Quon and Wong 1976; Hasegawa and Sato 1982), such states are called monotonic double layers (DLs). DLs occur naturally in a number of space plasma environments (e.g., solar winds, extragalactic jets, etc.). DLs have ability to accelerate, decelerate or reflect the plasma particles. A double layer forms in plasma when electric charge flows through it. DLs are formed in the plasma environments of earth, as well as around the stars, creating phenomena like auroral and electromagnetic radiations from pulsar. Laboratory experiments, space plasma observations, and theoretical studies (Quon and Wong 1976; Sato and Okuda 1980; Temerin et al. 1982; Hasegawa and Sato 1982) have shown that plasmas can develop states which have narrow, isolated regions of abrupt potential jumps surrounded by large regions with effectively uniform plasma potential. In the past decades, the double-layers have also attracted a great deal of attention because of their relevance to cosmic applications and in plasma thrusts for space properties (Alfven and Carlqvist 1967; Temerin et al. 1982; Borovsky 1984; Bharuthram and Shukla 1992; Mishra et al. 2002; Amour and Tribeche 2009; Chatterjee et al. 2010). Furthermore, since space plasmas are of multispecies type they offer a rich source for studying double-layers. Their relevance further stems from the fact that these are considered as the source of Earth’s aurora. It was also discovered that acoustic double-layers are responsible for auroral electron precipitation. Moreover, electrostatic double-layers provide a mechanism for the acceleration of the particles. Characteristics of dust acoustic solitary waves and double layers in a dusty plasma with two temperature isothermal ions have been studied by Tagare (1997). It was reported that both compressive and rarefactive solitons and DLs exist. Gill et al. (2004) examined the effect of non-thermal electrons on double layers in a plasma consisting of positive and negative ions. It was noticed that the amplitude of double layers is sensitive to variation in nonthermality of electrons. The dependance of DLs structure on various parameters such as non-thermal parameter, dust temperature and electron concentration has been studied by Maharaja et al. (2006), in three-component unmagnetized dusty plasma comprising negative dust, stationary non-thermal ions and Boltzmann electrons.

The plasma systems with two temperature ions and other species have been studied extensively for the last many years. Large amplitude dust-acoustic DLs were reported in an unmagnetized dusty plasma comprising Boltzmann electrons, two temperature ions and a negatively charged cold dust fluid (Bharuthram and Shukla 1992). Roychoudhury and Chatterjee (1999) considered a three-component plasma, a dust fluid and two ion populations of different temperatures. They examined the effect of dust temperature and ion concentration on the characteristics of dust-acoustic solitons and double layers. Xie et al. (1999) employed a four-component plasma comprising Boltzmann electrons, two populations of Boltzmann distributed ions with different temperatures and a negatively charged dust fluid. They found that both compressive and rarefactive solitons exist. The combined effects of the nonthermal parameters, the electron temperature and temperature of lower and higher temperature nonthermal ions on DAWs in dusty plasma have been examined by Zhou et al. (2012). It has been noticed that for this system only compressive solitons exist. Roy et al. (2012) have addressed the problem of DA double layers in four component dusty plasma with Boltzmann distributed ions and superthermal electrons. It is seen that superthermality of electrons has a significant effect on the existence of large amplitude double-layers.

The nonextensive statistical mechanisms based on the deviation from Boltzmann-Gibbs-Shannon (BGS) entropy measures has been given a keen attention for the last many years to study the dynamics of solitary waves in various nonlinear media. For the first time, nonextensive generalization of BGS entropy for statistical equilibrium was recognized (Renyi 1955) and later the standard additives of entropies were extended to the nonlinear nonextensive case (Tsallis 1988), where entropy index q characterizes the degree of nonextensivity of a system. The non-additive entropy of Tsallis and the ensuing generalized statistics have been employed with success in a wide range of phenomena characterized by nonextensivity (Lima et al. 2000; Kaniadakis 2001; Leubner 2008; Liyan and Du 2008; Livadiotis 2009). From various observations, it is confirmed that Maxwellian distribution is inadequate to model the systems with the long range interactions, such as plasma and gravitational systems, where the nonequilibrium stationary states exist. Over the past many years, various investigations confirmed that systems with long-time memory, long-range interactions, and fractality of the corresponding space-time/phase-space are not tractable within the conventional Boltzmann-Gibbs (BG) statistics (Tsallis 1994). To deal with the statistical properties of systems with long-range correlations, Tsallis (1988) extended BG thermodynamics (by generalizing the concept of entropy) to the nonextensive regimes. A large number of investigations found a connection among Tsallis entropy and various systems e.g., plasma physics (Lima et al. 2000), gravitational systems, long-range Hamiltonian systems (Latora et al. 2001) and other applications (Abe and Okamoto 2001). The existence of non-Maxwellian velocity distribution was confirmed experimentally by Lima et al. (2000) and explained that the q-nonextensive formalism is very important for systems having long-range interactions those occurred in astrophysical environments. From various observations, it has been shown that distributions very close to kappa-distributions are a consequence of the generalized entropy favored by nonextensive statistics. The transformation linking q-distribution and κ-distribution is \(\kappa=\frac{1}{q-1}\). The κ-distributions turned out as a consequence of the entropy generalization, thus providing the missing link between power-law models of suprathermal tails and fundamental physics (Leubner 2004). It is believed that q nonextensive distribution is more generalized distribution as compared to other Maxwellian/non-Maxwellian distributions. When q→1 the results lead to the same as thermally equilibrium system, i.e. Maxwellian limit.

To model the effects of nonextensivity, we refer to the one dimensional q-equilibrium distribution function (Silva et al. 1998)

$$ f_\alpha(v_x) = C_{q\alpha} \biggl \{1-(q_\alpha-1) \biggl[\frac {m_\alpha v_x^2}{2T_\alpha}\pm\frac{e\phi}{T_\alpha} \biggr] \biggr\} ^{1/(q_\alpha-1)} $$
(1)

where α=i,e and ± sign stands for ions and electrons respectively. C qα is the constant of normalization:

$$ C_{qe}= n_{e0}\frac{\varGamma (\frac{1}{1-q_e} )}{\varGamma (\frac{1}{1-q_e}-\frac{1}{2} )}\sqrt{\frac{m_e(1-q_e)}{2\pi T_e}} $$
(2)

for −1<q e <1 and for q e >1:

$$\begin{aligned} &C_{qe}= n_{e0} \biggl(\frac{1+q_e}{2} \biggr) \frac{\varGamma (\frac {1}{q_e-1}+\frac{1}{2} )}{\varGamma (\frac{1}{q_e-1} )}\sqrt {\frac{m_e(q_e-1)}{2\pi T_e}} \end{aligned}$$
(3)
$$\begin{aligned} &C_{qi}= n_{i0}\frac{\varGamma (\frac{1}{1-q_i} )}{\varGamma (\frac{1}{1-q_i}-\frac{3}{2} )} \biggl[\frac{m_i(1-q_i)}{2\pi T_i} \biggr]^{3/2} \end{aligned}$$
(4)

for −1<q i <1 and for q i >1:

$$ C_{qi}= n_{i0} \biggl(\frac{3q_i-1}{2} \biggr) \frac{\varGamma (\frac {1}{q_i-1}+\frac{3}{2} )}{\varGamma (\frac{1}{q_i-1} )} \biggl[\frac{m_i(q_i-1)}{2\pi T_i} \biggr]^{3/2} $$
(5)

The quantity Γ stands for the standard gamma function and q α stands for the strength of the electrons/ions nonextensivity. For q α <−1, the q α -distribution (1) is unnormalizable. For the extensive limiting case i.e., q α →1 distribution (1) reduces to well known Maxwell-Boltzmann distribution function.

The integration of the distribution function in Eq. (1) yields the number density for electrons and ions given as (Gougam and Tribeche 2011)

$$ n_j= n_j \biggl[1\mp ( q_j-1 ) \frac{e\phi}{T_j} \biggr]^{\frac {(q_j+1)}{2(q_j-1)}} $$
(6)

where j=i,e and ∓ sign stands for ions and electrons respectively. The q-entropy may provide a convenient frame for the analysis of many astrophysical and cosmological scenarios, such as stellar polytropes (Plastino and Plastino 1993), solar neutrino problem (Kaniadakis et al. 1996), and peculiar velocity distribution of galaxy clusters (Lavangno et al. 1998). Plasmas with particles obeying non-Maxwellian velocity distribution are crucial to the understanding of space and astrophysical plasma dynamics. The nonextensive distribution is the most generalized distribution to study the linear and nonlinear properties of solitary waves in various plasma systems.

In the frame work of Tsallis q-distribution (nonextensive), a large number of investigations related to study of nonlinear structures, viz., solitons, double-layers, shocks, vortices etc. have been reported (Caruso and Tsallis 2008; Tribeche and Djebarni 2010; Nobre et al. 2011; Gougam and Tribeche 2011; Bains et al. 2011; Tribeche and Merriche 2011; Pakzad 2011; Mayout and Tribeche 2011; Sahu and Tribeche 2012; Tribeche and Sabry 2012; El-Taibany and Tribeche 2012; Rabia et al. 2012; Shahmansouri and Tribeche 2012, 2013). The effect of q-parameter for electrons on the formation of double layers has been studied by Pakzad (2011) in an unmagnetized collisionless plasma comprising of cold electron fluid, stationary ions and nonextensive hot electrons. It has been observed that both compressive and rarefactive double layers exist over different parameter regimes. Dust-acoustic solitons with nonextensive distribution have been addressed by Tribeche and Merriche (2011). The problem of dust acoustic solitary (DAS) waves for electron depleted plasma with two temperature superthermal ions has been addressed by Mayout and Tribeche (2011). They observed that only negative potential DAS waves structures are formed. The influence of different parameters was also studied on the Mach number. Bora et al. (2012) have studied the dust acoustic solitons with multispecies ions and kappa distributed electrons in the dusty plasmas. Sahu and Tribeche (2012) have focussed their study on properties of DA double-layers in an unmagnetized dusty plasma without electrons in which ions follow q-nonextensive distribution. It has been shown that the onset of double-layers sensitively depends upon the nonextensive parameter. Both compressive and rarefactive double-layers exist.

Recently, Shahmansouri and Tribeche (2012) have studied the characteristics of DAS waves and DA double-layers (DLs) using pseudo-potential approach in electron depleted plasma with two temperature superthermal ions. It is observed that suprathermalilty of ions drastically effects the amplitude and width of DA solitons and also the formation of DLs. Very recently Shahmansouri and Tribeche (2013) by using the pseudo-potential approach has studied the formation of DAWs in plasma comprising of negative dust, nonextensive electrons and nonextensive ions. It has been observed that both compressive and rarefactive solitons exists and soliton profile is highly sensitive to ions and electrons nonextensivity.

The aim of a study in the present investigation is to elucidate the combined effects of nonextensivity of electrons as well as two temperature ions, dust density and ion concentration on the propagation of small amplitude DASWs and double-layers in a dusty plasma having dust-fluid, nonextensive electrons and low/high temperature ions obeying nonextensive distribution. By employing reductive perturbation method, we have derived the Korteweg-de Vries (KdV) equation. It is observed that dust concentration and nonextensivity of ions as well as electrons significantly influence the amplitude and width of dust-acoustic solitary waves. We also observe that at certain critical values of nonextensive parameter, the nonlinear coefficient of KdV equation vanishes and hence we consider higher order nonlinearities and derive modified-KdV equation. For critical values of physical parameters (nonextensivity of electrons and ions, concentration of ions etc.), where nonlinear coefficient of KdV equation vanishes, modified KdV has been derived. Later on the parametric regimes for existence of mKdV solitons and double-layers have also been examined.

Paper is organised as follows: In Sect. 2, fluid model is discussed. In Sect. 3, KdV equation is derived and effect of different parameters is studied on characteristics of solitons. In Sect. 4, mKdV equation is derived for critical values of different physical parameters and its solution is discussed in detail. Double-layers solution and existence conditions for solitary structures have been discussed in Sect. 5 and Sect. 6 is left for overall conclusions.

2 Fluid model equations

We have considered an unmagnetized four component dusty plasma system consisting of extremely massive, highly negatively charged inertial dust grains, inertialess nonextensively distributed electrons and two temperature ions. Charge neutrality at equilibrium requires:

$$ \sum_{j=l,h}n_{ij0}=Z_{d0}N_{d0}+n_{e0} $$
(7)

where n ij0 and n e0 are the unperturbed densities of ions (low or high temperature) and electrons respectively. N d0 is the unperturbed dust number density and Z d0 is the unperturbed number of charges residing on the dust grain. The number densities of nonextensive ions and electrons are given as:

$$\begin{aligned} &n_{ij} = n_{ij0} \bigl[1- ( q_{ij}-1 )e \phi/T_{eff} \bigr]^{(q_{ij}+1)/(2(q_{ij}-1))} \quad j=l,h \\ &n_e = n_{e0} \bigl[1+ ( q_i-1 )e \phi/T_{eff} \bigr]^{(q_e+1)/(2(q_e-1))}. \end{aligned}$$

The dynamics of one dimensional dust-acoustic waves whose phase speed is much smaller (larger) than the electron (ion) thermal speed, can be described by the following normalized equations in a nonextensive negative dusty plasma:

$$\begin{aligned} &\frac{\partial N_d}{\partial t}+\frac{\partial (N_dU_d )}{\partial x}=0 \end{aligned}$$
(8)
$$\begin{aligned} &\frac{\partial U_d}{\partial t}+U_d \frac{\partial U_d}{\partial x}=\frac{\partial\phi}{\partial x} \end{aligned}$$
(9)
$$\begin{aligned} &\frac{\partial^2\phi}{\partial x^2}=N_d+\nu n_e- \sum _{j=l,h}\mu_j n_{ij} \end{aligned}$$
(10)

where U d , N d and ϕ are the normalized dust fluid velocity, the number density of dust and the electrostatic potential, respectively. N d and ϕ are normalized by N d0 and T eff /e respectively. U d is normalized by the dust-acoustic speed C d =(Z d0 T eff /m d )1/2. The space variable x and time variable t are normalized by the Debye Length λ Dd =(T eff /4πZ d0 n d0 e 2)1/2 and inverse dust plasma frequency \(\omega^{-1}_{pd}=(m_{d}/4\pi Z_{d0}n_{d0}e^{2})^{1/2}\) respectively, where m d is the dust mass grain and T eff is the effective temperature given by T eff =Z d0 n d0/(n e0 T e +n il0 T il +n ih0 T ih ), T e is the temperature of electrons; T il and T ih are low and high temperatures of nonextensive ions. Obviously, the charge neutrality at equilibrium leads to

$$ \sum_{j=l,h}\mu_j-\nu=1 $$
(11)

where ν=n e0/Z d0 N d0,μ j =n ij0/Z d0 N d0. The normalized number density of electrons and ions may be written in the expanded form as

$$\begin{aligned} &n_{e} = \nu\bigl(1+c_{1e}\phi+c_{2e} \phi^2+c_{3e}\phi^3\bigr) \end{aligned}$$
(12)
$$\begin{aligned} &n_{ij} = \mu_l\bigl(1+c_{1j} \phi+c_{2j}\phi^2+c_{3j}\phi^3\bigr) \quad j=l,h \end{aligned}$$
(13)

and the different coefficients are

$$\begin{aligned} \begin{aligned} &c_{1e}=\frac{(q_e+1)}{2} \\ &c_{2e}=-\frac{(q_e+1)(q_e-3)}{8} \\ &c_{3e}=\frac{(q_e+1)(q_e-3)(3q_e-5)}{48} \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} &c_{1j}=-\frac{(q_{ij}+1)}{2} \\ &c_{2j}=-\frac{(q_{ij}+1)(q_{ij}-3)}{8} \\ &c_{3j}=-\frac{(q_{ij}+1)(q_{ij}-3)(3q_{ij}-5)}{48} \end{aligned} \end{aligned}$$
(15)

3 Derivation of Korteweg-de Vries (KdV) equation

To study finite small amplitude dust-acoustic solitary waves in multispecies plasma model, we construct a weakly nonlinear theory which lead to scaling of independent variables, hence we introduce the stretched coordinates as

$$\begin{aligned} &\xi=\epsilon^{1/2}(x-v_0t) \\ &\tau=\epsilon^{3/2}t \end{aligned}$$

where ϵ is a small parameter characterizing the strength of nonlinearity and v 0 is the solitary wave velocity normalized by C d . The variables N d , U d and ϕ are expanded about the unperturbed states in power series of ϵ as:

$$\begin{aligned} \begin{aligned} & N_d = 1+n_{1}+ n_{2}+\cdots \\ & U_d = u_{1}+\epsilon^2 u_{2}+\cdots \\ & \phi = \epsilon\phi_1+\epsilon^2 \phi_2+ \cdots \end{aligned} \end{aligned}$$
(16)

Substituting the above expansions (16) and Eqs. (12)–(13) into Eqs. (8)–(10) and collecting the terms of different powers of ϵ; for the lowest order of ϵ, we get the following equations:

$$\begin{aligned} \begin{aligned} &-v_0\frac{\partial n_1}{\partial\xi}+ \frac{\partial u_1}{\partial\xi } = 0 \\ &v_0\frac{\partial u_1}{\partial\xi}+ \frac{\partial\phi_1}{\partial\xi } = 0 \\ &n_1 +C_1 \phi_1 = 0 \end{aligned} \end{aligned}$$
(17)

and for next higher order of ϵ, we get:

$$\begin{aligned} \begin{aligned} &\frac{\partial n_1}{\partial\tau}-v_0\frac{\partial n_2}{\partial\xi }+ \frac{\partial u_2}{\partial\xi}+ \frac{\partial n_1u_1}{\partial \xi} = 0 \\ &\frac{\partial u_1}{\partial\tau}-v_0\frac{\partial u_2}{\partial\xi }+ u_1 \frac{\partial u_1}{\partial\xi} = 0 \\ &\frac{\partial^2 \phi_1}{\partial\xi^2}-n_2-C_1\phi_2-C_2 \phi_1^2 = 0 \end{aligned} \end{aligned}$$
(18)

where the coefficients are defined as

$$\begin{aligned} \begin{aligned} &C_1 = c_{1e}\nu-\sum _{j=l,h}c_{1j}\mu_j \\ &C_2 = c_{2e}\nu-\sum_{j=l,h}c_{2j} \mu_j \end{aligned} \end{aligned}$$
(19)

Using Eq. (17) and eliminating the second order variables from Eq. (18), and after the various algebraic calculations, we obtain the following KdV equation

$$ \frac{\partial\phi_1}{\partial\tau}+A\phi_1\frac{\partial\phi _1}{\partial\xi}+B\frac{\partial^3\phi_1}{\partial\xi^3}=0 $$
(20)

where

$$ A=- \biggl\{\frac{C_2}{C_1^{3/2}}+\frac{3}{2}C_1^{1/2} \biggr\} $$
(21)

is nonlinear coefficient and

$$ B=\frac{1}{2(C_1)^{3/2}} $$
(22)

is dispersion coefficient.

The nature of solitons mainly depend upon the nonlinear coefficient A. For A>0, positive polarity (compressive) solitons are formed and for A<0, negative polarity (rarefactive) solitons are formed. Neglecting the nonextensive distribution for electrons and also considering ions at one temperature, the KdV equation (20) is in good agreement with the findings of Tribeche and Merriche (2011). Since C 1 is always positive for the formation of solitons, we note from the expression of A, Eq. (21) that the negative and positive polarity solitons are formed for \(\frac{C_{2}}{C_{1}^{2}}+\frac{3}{2}>0\) and \(\frac{C_{2}}{C_{1}^{2}}+\frac{3}{2}<0\) respectively. In other words, we can say that we get negative and positive polarity solitons for \(C_{2}>-\frac {3}{2}C_{1}^{2}\) and \(C_{2}<-\frac{3}{2}C_{1}^{2}\) respectively. So it can be said that the formation of solitons depends purely upon the value of coefficient C 2.

Using transformation, η=ξ−U 0 τ, the stationary state solution of KdV equation (20) is given as

$$ \phi=\phi_1=\phi_m \operatorname{sech}^2 \biggl(\frac{\xi-U_0\tau}{\Delta} \biggr) $$
(23)

where ϕ m =3U 0/A is the maximum amplitude and \(\Delta=\sqrt{4B/U_{0}}\) is the width of the soltions.

Keeping in mind the charge neutrality condition at equilibrium, we plot nonlinear coefficient A versus q e (See Figs. 1, 2, 3 and 4) for different values of μ l and keeping others parameters fixed. We observe that A is always negative for either of the positive values of nonextensive parameter for ions (q il and q ih ), and hence negative polarity solitons are observed. The result is in contrast with Zhou et al. (2012) where compressive solitons are formed for nonthermal distributed ions. Positive as well as negative polarity solitons are observed, when either q il or q ih or both are negative. For these cases we find the critical value of q e for which positive and negative polarity solitons exist. Further, we observe that with increase in density parameter μ l , the non-extensive parameter of electrons (q e ) changes its values (increases or decreases) significantly depending mainly upon the values of q il ,q ih and μ h .

Fig. 1
figure 1

A vs. qe for q il =0.3,q ih =−0.3,μ h =0.5 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image
Fig. 2
figure 2

A vs. qe for q il =q ih =−0.3,μ h =0.5 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image
Fig. 3
figure 3

A vs. qe for q il =q ih =0.3,μ h =0.7 for different values of μ l . Solid line for μ l =0.4, dashed for μ l =0.5 and dotted for μ l =0.6

Full size image
Fig. 4
figure 4

A vs. qe for q il =0.3,q ih =−0.3,μ h =0.7 for different values of μ l . Solid line for μ l =0.4, dashed for μ l =0.5 and dotted for μ l =0.6

Full size image

On plotting the nonlinear coefficient A versus μ h for different values of μ l , both positive and negative polarity solitons are observed if both q il and q ih are negative, irrespective of the value of q e (see Fig. 5). On the other hand, it is seen that only negative polarity solitons exist for positive values of either q il or q ih (figures not shown), irrespective of the value of q e whether positive or negative. It is also seen numerically that μ h decreases with increase in μ l or q e for fixed values of other parameters. Similar type of behaviour is seen if we plot A versus μ h for different positive and negative values of q e with fixed values of μ l . It is also seen that effect of density parameter μ l is more pronounced as compared to the effect of nonextensive parameter q e on the value of nonlinear coefficient A.

Fig. 5
figure 5

A vs. μ h for q e =0.1,q il =q ih =−0.3 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image

By setting non-linear coefficient, A=0, we have contour plot (see Fig. 6) for the variation of density parameter μ h (ratio of density of hot ions to dust) with nonextensive parameter of electrons q e for different values of density parameter for low temperature ions μ l . Further, from this figure, we can determine the parametric domain for the existence of negative/positive potential solitary structures. It is noticed that nonlinear coefficient A is negative on left of the curve and is the region of anomalous propagation of DAWs. A is positive on right of the curve, leading to normal propagation. This implies that in (μ h , q e ) region bounded by the curve, the negative potential solitons may exist (since A<0), and otherwise (i.e., for A>0), positive potential solitons exist. Further, it is observed numerically that nonextensive parameter for electrons q e , above which A does not change sign, decreases significantly with increase in density parameter for low temperature ions (via μ l ). Similarly, μ h decreases with increase in μ l . This shows that dust density parameter plays a significant role to modify the solitary structures (figures not shown).

Fig. 6
figure 6

Variation of density parameter μ h with nonextensive parameter q e for μ l =0.4 (solid), 0.5 (dashed), 0.6 (dotted) along the curve, A=0, on left of the curve A<0 while on right of the curve A>0

Full size image

Figures 7 and 8 depict the positive potential (compressive) and negative potential (rarefactive) KdV profile solitons for the fixed values of nonextensivity for electrons (q e ) and ions (q il,h ) but different values of density parameter μ l . We notice that with increase in the value of μ l , amplitude and width are increased. The parameter μ h is very crucial to get opposite polarity solitons. As we increase the value of μ h and checking the corresponding value of q e , the negative polarity solitons start appearing in the given plasma system. This parametric range for the existence of opposite polarity solitons, one can find from the Fig. 6.

Fig. 7
figure 7

KdV soliton (compressive) profile for q e =−0.1, q il =q ih =−0.3, μ h =0.5 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image
Fig. 8
figure 8

KdV soliton (rarefactive) profile for q e =−0.1, q il =q ih =−0.3, μ h =0.7 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image

For ν=0 i.e., electron depleted plasma and q il =q ih =1, the values of nonlinear coefficient A and dispersion coefficient B are in good agreement with as derived by Mayout and Tribeche (2011) for κ→∞.

4 The modified KdV (mKdV) equation

Singularity exists when the nonlinear coefficient A becomes zero (Figs. 1–5) and it leads to failure of the KdV theory. The value of a nonlinear coefficient A of KdV equation is zero on the curve for critical values of q e , μ l and μ h (see Fig. 6). To find the existence of solitary structures for critical values of physical parameters (q e ,μ l ,μ h ), we have derived the modified KdV (mKdV) equation with higher order coefficients. To describe the evolution of these critical situations, one has to seek another equation suitable that describes the evolution of the system. This implies that stretching coordinates mentioned previously are not valid and so for this purpose, we include higher order effects, and hence new stretching coordinates are introduced, namely,

$$\begin{aligned} &\xi=\epsilon(x-v_0t) \\ &\tau=\epsilon^3t \end{aligned}$$

and also use the dependent variables given in Eq. (15). Substituting in Eqs. (8)–(10) and collecting the terms of different powers of ϵ, we obtain the following results for the higher order of ϵ:

$$\begin{aligned} &n_2=\frac{3}{2}C_1^2 \phi_1^2-C_1\phi_2 \end{aligned}$$
(24)
$$\begin{aligned} &u_2=\frac{C_1^{3/2}}{2}\phi_1^2-C_1^{1/2} \phi_2 \end{aligned}$$
(25)
$$\begin{aligned} &\frac{\partial n_1}{\partial\tau}-v_0\frac{\partial n_3}{\partial\xi }+\frac{\partial u_3}{\partial\xi}+ \frac{ (\partial n_1u_2 )}{\partial\xi}+\frac{ (\partial n_2u_1 )}{\partial\xi}=0 \end{aligned}$$
(26)
$$\begin{aligned} &\frac{\partial u_1}{\partial\tau}-v_0\frac{\partial u_3}{\partial\xi }+u_1 \frac{\partial u_2}{\partial\xi}+u_2\frac{\partial u_1}{\partial\xi }-\frac{\partial\phi_3}{\partial\xi}=0 \end{aligned}$$
(27)
$$\begin{aligned} &\frac{\partial^2\phi_1}{\partial\xi^2}-n_3-C_1\phi_3-2C_2 \phi_1\phi _2-C_3\phi_1^3=0 \end{aligned}$$
(28)

where

$$ C_3 = c_{3e}\nu-\sum _{j=l,h}c_{3j}\mu_j $$
(29)

Eliminating the third orders quantities from the above set of equations, we obtain the following mKdV equation:

$$ \frac{\partial\phi_1}{\partial\tau}+A\frac{\partial (\phi_1 \phi _2 )}{\partial\xi}+B\frac{\partial^3 \phi_1}{\partial\xi^3}+S \phi _1^2\frac{\partial\phi_1}{\partial\xi}=0 $$
(30)

where

$$ S=\frac{-3}{2}\frac{C_3}{C_1^{3/2}}+\frac{15}{4}C_1^{3/2} $$
(31)

and is known as coefficient of cubic nonlinearity. A and B are the same coefficients as in KdV equation. At A=0, using single variable transformation, η=ξ−U 0 τ the stationary solution of Eq. (30) can be written as

$$ \varPhi=\phi_1=\pm\phi_m \operatorname{sech} \biggl[ \frac{\eta}{W} \biggr] $$
(32)

where U 0 is the solitary speed, \(\phi_{m}= \sqrt{\frac{6U_{0}}{S}}\) and \(W=\sqrt{\frac{B}{U_{0}}}\) are the peak amplitude and width of the solitons, respectively. Thus, mKdV solitons exist for the positive values of S, i.e. S>0.

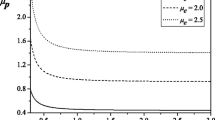
From numerical analysis of solution of mKdV equation, we have seen the influence of various physical parameters on the amplitude and width of solitons which is depicted in different figures. Figure 9 depicts the variation of coefficient S with μ h for fixed values of q il , q ih and negative value of q e , but for different values of μ l ; whereas Fig. 10 shows the variation of S with μ h for fixed values of q il , q ih and μ l , but for different positive values of q e . It is noticed that S attains both positive as well as negative values for either q il or q ih and both are negative. For the positive values of q il and q ih , S remains positive always (figures not shown). Figures 11 and 12 describe the variation in amplitude and width of mKdV solitons for the critical values of physical parameters that leads to the failure of KdV theory (i.e., where A=0 as observed from the Fig. 6). In Fig. 11, amplitude and width of the solitons shrink with increase in the values of μ l and μ h (i.e., increase concentrations of low and high temperature ions). Both amplitude and width decrease with increase in μ l and negative value of q e (see Fig. 12). It is realized that the ion concentrations are very effective for modifying mKdV solitons. Both compressive and rarefactive solitons coexist according to the solution (32).

Fig. 9
figure 9

S vs. μ h for q e =−0.1,q il =q ih =−0.3 for different values of μ l . Solid line for μ l =0.51, dashed for μ l =0.52 and dotted for μ l =0.53

Full size image
Fig. 10
figure 10

S vs. μ h for q il =qih=−0.3,μ l =0.51 for different +ve values of q e . Solid line for q e =0.4, dashed for q e =0.5 and dotted for q e =0.6

Full size image
Fig. 11
figure 11

mKdV solitons (at A=0) for q il =q ih =−0.3, q e =−0.07163. and different values of μ l and μ h . Solid line for μ l =0.4, μ h =0.5026, dashed for μ l =0.5, μ h =0.6028 and dotted for μ l =0.6,μ h =0.7021

Full size image
Fig. 12
figure 12

mKdV solitons (at A=0) for q il =q ih =−0.3,μ h =0.7179 and different values of q e and μ l . Solid line for q e =−0.2289, μ l =0.4, dashed for q e =−0.6746, μ l =0.5 and dotted for q e =−0.8385, μ l =0.6

Full size image

5 Double-layer solution

In this section, we present the double-layer solution associated with mKdV equation (30). We investigate the conditions under which the double layers can be formed. When A→0, but A≠0 then (30) reduces to

$$ \frac{\partial\phi_1}{\partial\tau}+D\phi_1\frac{\partial \phi _1}{\partial\xi}+B\frac{\partial^3 \phi_1}{\partial\xi^3}+S \phi _1^2\frac{\partial\phi_1}{\partial\xi}=0 $$
(33)

where we have used Aϕ 2→Dϕ 1/2 (Watanabe 1984; Xie et al. 1999). Equation (33) is modified KdV (mKdV). Further we use the transformation: η=ξ−U 0 τ in (33) (where η is the transformed coordinates with respect to a frame moving with velocity U 0, for the steady-state solution of the mKdV equation), and using the boundary conditions: ϕ 1→0, dϕ 1/dη→0 and d 2 ϕ 1/dη 2→0, as |η|→∞ and integrating we get

$$ \frac{1}{2} \biggl(\frac{d\phi_1}{d\eta} \biggr)^2+V ( \phi_1 )=0 $$
(34)

where V(ϕ 1), the Sagdeev potential is given by:

$$ V (\phi_1 )= \frac{\phi_1^2}{2B} \biggl(\frac{S}{6} \phi_1^2+\frac {D}{3}\phi_1-U_0 \biggr) $$
(35)

where,

$$ U_0=-\frac{S}{6}\psi_d^2 $$
(36)

\(\psi_{d}=-\frac{D}{S}\) is the one of the extreme points of Sagdeev potential. The double-layer solution of (33) is given by

$$ \psi=\phi_1=\frac{\psi_d}{2} \biggl[1-\operatorname{tanh} \biggl( \frac{2\eta}{\Delta _d} \biggr) \biggr] $$
(37)

where

$$ \Delta_d=\frac{4\sqrt{\frac{6B}{-S}}}{|\psi_d|} $$
(38)

is thickness of the double layer.

It should be noted from Eqs. (37) and (38) that for the existence of double layers the following condition must be satisfied

$$ -\frac{B}{S}>0 \quad \mbox{or} \quad S<0 \quad\mbox{as } B \biggl(= \frac {1}{2C_1^{3/2}} \biggr)>0 $$
(39)

It is observed from the expression for the coefficient of cubic nonlinearity (31) that condition (39) is satisfied if and only if

$$ S<0 \quad \mbox{thus} \ \frac{C_3}{C_1^3}-\frac{5}{2}>0 $$
(40)

The nature of the double layers, i.e., whether the system will support a compressive or rarefactive double layers, depends upon the sign of coefficient of quadratic nonlinear term (D). The system support compressive double layers for D>0 and rarefactive double layers for D<0. Figure 13 depicts the variation of amplitude of double layers for different values of μ l and keeping other parameters fixed. In this case we have considered the negative values of q parameter for electrons and ions. Only positive polarity (compressive) double layers are formed. Both amplitude and steepness of DLs are increased with increase in concentration low temperature ions (i.e., decrease in dust concentration). The result is in contrast with Shahmansouri and Tribeche (2012) where both positive polarity (compressive) and negative polarity (rarefactive) DLs are formed. Further, we have examined the variation of both amplitude and steepness of DLs with change in the nonextensitivity of electrons (via q e ) (see Fig. 14). Both Amplitude and steepness of DLs are enhanced with increase in nonextensitivity of electrons. Ion concentration and nonextensitivity of electrons have a significant effect on the variation of amplitude of DLs. Similar kind of changes are observed in amplitude of DLs for positive values of nonextenstivity of both temperatures ions (figures not shown).

Fig. 13
figure 13

Double-layers (S<0) for q e =−0.1, q il =q ih =−0.3, μ h =0.7 and different values of μ l . Solid line for μ l =0.4, dashed for μ l =0.5 and dotted for μ l =0.6

Full size image
Fig. 14
figure 14

Double-layers (S<0) for q il =q ih =−0.3, μ l =0.51, μ h =0.6 and different values of q e . Solid line for q e =0.4, dashed for q e =0.5 and dotted for q e =0.6

Full size image

In this investigation, Fig. 15 presents a very significant information about the critical limit for the values of various parameters for the existence of KdV solitons, mKdV solitons and double layers. Figure 15 shows the contour plot for S between μ h and q e . The mKdV solitons exist for the parametric values those lies in the region where S is positive (i.e., S>0) and double layers exists for negative values of S (i.e., S<0). For along the curve S=0, Eq. (33) again reduce to already derived KdV equation (20) (i.e, KdV solitons exist for the parametric values where S=0).

Fig. 15
figure 15

Variation of density parameter μ h with nonextensive parameter q e for μ l =0.4 (solid), 0.5 (dashed), 0.6 (dotted), along the curve S=0, inside the curve S<0 while outside the curve S>0, i.e. we get mKdV solitons

Full size image

6 Conclusions

We have addressed the problem of dust acoustic solitary waves in a dusty plasma having negative dust with two temperature ions and electrons following nonextensive q-distribution. The KdV and mKdV equations have been derived using reductive perturbation technique. The formation of double layers is studied. Further, we have determined the existence domain of parameters of dust acoustic solitary waves in a plasma. The effect of different ranges of the parameter μ h and q e with different values of density parameter μ l on soliton formation has been studied. We have noticed the following findings of the present problem:

  • Solitons of both polarity (compressive and rarefactive) exist.

  • The nonextensivity of ions (q il and q ih ) for fixed values of μ h is very crucial to modify the solitary structures. Positive and negative polarity solitons exists only if both q il and q ih are positive.

  • Characteristics of DASWs are affected by physical parameters, viz., nonextensivity of electrons and ions (via q e , q il and q ih ) and density parameters (via μ l and μ h ).

  • We have also observed that effect of concentration of ions μ l is more visible as compared to the effect of q e on the formation of solitons.

  • From Fig. 6, we have determined the domain for parametric values for the existence of opposite polarity solitons. The values on left of the curve, show the existence of negative polarity solitons but on right of the curve, parametric values provide the existence of positive polarity solitons.

  • A very small change in the nonextensive parameter for electrons, has a significant effect on change in polarity of the solitary structures.

  • μ h is very sensitive to show the change in polarity of solitons. μ h <0.7 provides the existence of negative polarity solitons but for μ h >0.7, positive polarity solitons appear.

  • On the curve, A is equal to zero and singularity exists for the critical values of physical parameters (q e , μ l and μ h ). The modified KdV (mKdV) equation (30) is derived to see the existence for solitons for critical values (or above these values) of physical parameters.

  • The combined effects of various physical parameters are observed on the solitonic solutions of mKdV equation. These parameters significantly influence the characteristics of DA solitons.

  • The condition for the formation of double-layers is studied and observed the existence of compressive DLs.

  • We have also determined the parametric domain for the critical values of physical parameters to see the existence of KdV solitons, mKdV solitons and double layers (see Fig. 15).

Findings of the present investigation may be important for understanding the nonlinear electrostatic excitations in space and laboratory dusty plasmas. This investigation may also be useful to study nonlinear structures in quark-gluon plasma (Gervino et al. 2012) in interstellar, circumstellar plasmas, dark-matter halos (Feron and Hjerth 2008).