1 Introduction

A dusty plasma system is typically characterised as an assortment of particles that includes ions, electrons, and solid micro or nanoparticles (dust grains) immersed in plasma [1, 2]. In recent years, dusty plasma have garnered a great deal of attention, mainly due to the large mass and higher charge characteristics of the associated micrometre-sized plasma particles. Dust particles are frequently negatively charged, but they might also be positively or negatively charged depending on the rivalry between several processes, including secondary emission and electron and ion currents. A variety of wave modes can be produced by the inclusion of dust particles in electron–ion plasmas [3, 4]. The dust ion-acoustic wave (DIAW) is one of such significant wave modes. The subject of the current work is to investigate the dynamics of small-amplitude DIA nonlinear structures under the combined effects of different physical parameters. The inertia of the dust mass generates the dust acoustic waves (DAWs), while the thermal pressure of electrons and ions provides the restoring force [5]. Since dust in the plasma has numerous applications in industry and microelectronics [6] as well as in the laboratory (i.e., cancer therapy with the cold atmosphere plasma) and in astrophysical environments, such as interstellar molecular clouds, cometary tails, Phobos dust rings, planetary rings, and the Earth’s inner magnetosphere [4, 7], it is essential to study the features of nonlinear wave structures in such type of plasma. Numerous studies are done to investigate the various DIA nonlinear structures in magnetised and unmagnetised dusty plasmas within the context of Maxwellian and non-Maxwellian distributions [8,9,10]. Chatterjee et al. [11] derived the Burgers’ equation and its solutions to study the characteristics of DIAWs by employing Darboux transformation in an unmagnetised dusty plasma containing fluid ions and κ-distributed electrons. They observed a combination of rarefactive soliton with a shock structure.

Nonlinear wave structures in plasma are astounding manifestations of nature that arise from variations in properties such as nonlinearity, dispersion, and dissipation. Various techniques, such as RPM [12] and the Sagdeev pseudopotential method [13], are commonly used to examine and analyse nonlinear waves in plasma. The RPM, also known as the multiple scales method, is useful when dealing with weakly nonlinear phenomena where the amplitude of the wave is small compared to other characteristic scales in the system. However, this method does not allow for the study of large-amplitude excitations. To overcome the limitation of small-amplitude approximations, the Sagdeev pseudopotential method is considered an option, which is a powerful tool that provides an exact approach for analysing arbitrary-amplitude nonlinear waves. The Korteweg-de Vries (K-dV) equation is a useful mathematical tool for modelling and comprehending the behaviour of certain types of nonlinear phenomena in a variety of scientific contexts, such as neutral fluids, plasma physics, and nonlinear optics, as well as in mathematics and other disciplines [14]. One of the most famous features of the K-dV equation is its ability to support a variety of wave solutions, such as soliton solutions, periodic wave solutions, and dispersive shock solutions, that have been used to study nonlinear wave phenomena in both experimental and space observations. A large number of investigations confirm the existence of various solitons and other nonlinear structures in the solutions of the K-dV and its modified form, within the framework of the RPM in multicomponent plasmas [2, 15, 16]. The investigation of both small and arbitrary-amplitude solitary waves was carried out by El-Awady et al. [17] by employing both K-dV and energy integral equations. Saini et al. [18] derived the K-dV equation to analyse the oblique propagation of DIAWs in a strongly magnetised and rotating plasma comprising superthermal electrons and positrons. In the plasma system considered by the authors, both positive and negative potential solitary waves were observed. Singhadiya et al. [19] have studied the properties of the IASWs in a plasma consisting of ions, positrons, and two-temperature superthermal electrons by deriving the K-dV and modified K-dV equations. The shock wave is one of the nonlinear wave phenomena that has already been observed experimentally as well as theoretically. This type of wave is characterised by a modified form of the K-dV equation known as the K-dV-Burgers' (K-dVB) equation. In addition to the nonlinear and dispersion terms, the usual form of the K-dV equation is modified by adding a dissipative term. The dissipative component in the K-dVB equation originates from implementing the collision between charged and neutral particles, the Landau damping, and the kinematic viscosity of the plasma components [20]. In this regard, a number of investigations have been carried out in the context of nonlinear ion-acoustic shock waves (IASHWs) in different plasma media [20,21,22]. El-Hanbaly et al. [23] examined the influence of dust kinematic viscosity on linear and nonlinear dust acoustic waves in an unmagnetised dusty plasma system by deriving the K-dVB equation. Michael et al. [24] studied the IASHWs in a cometary plasma model consisting of oppositely charged oxygen ions, lighter hydrogen ions, and hot and cold electrons. Using the K-dVB equation, they found that the intensity of the shock profile decreased with increasing the temperature of positively charged oxygen ions and the densities of negatively charged oxygen ions. In a dissipatively magnetised dusty plasma system, El-Helbawy [25] studied the nonlinear solitary and shock wave behaviour using the K-dVB equation. They demonstrated the presence of solitary and periodic travelling waves in a bifurcation diagram by employing a planar dynamical theory.

Electron-positron-ion (e-p-i) plasma is a type of ambiplasma that consists of electrons, positrons, and ions in a quasineutral space plasma. The study of the propagation of localised structures in an e-p-i plasma is significant for researchers because such plasma exists in the inner areas of the accretion discs surrounding black holes [26], in the early universe [27], in pulsar magnetospheres [28], in active galactic nuclei [29], in the polar regions of neutron stars [30], in the core of our galaxy [31], and in plasmas under high laser fields [32]. This type of e-p-i plasma may also be discovered in laboratories; in particular, during the propagation of a short, intense relativistic laser pulse in matter, the photoproduction of pairs owing to photon scattering by nuclei can result in the generation of e-p-i plasmas. Because of the aforementioned cases, there has been a lot of interest in the last several decades in the characteristics of IA structures in e-p-i plasma [18, 33,34,35,36,37,38,39]. The dynamical properties of IAWs in e-p-i plasmas vary significantly from those of electron-ion plasmas due to differences in species concentration ratios and temperatures. The nonlinear dynamical structures of IASWs in an e-p-i plasma have been studied by Popel et al. [40]. They demonstrated that the existence of the positron components reduces the amplitude of the soliton structure. In an e-p-i plasma, Tiwari et al. [16] observed the effects of temperature and density of the positron on an IA-dressed soliton. These findings can help us better comprehend the localised structures of Maxwellian e-p-i plasmas.

However, in different spaces and astrophysical plasmas, where the plasma particles are energetic, they usually follow a non-Maxwellian distribution, which can be successfully represented by the generalised Lorentzian or κ-type distribution function [41]. The study of such non-Maxwellian plasma is more important in comprehending astrophysical plasmas, such as the solar wind, ionospheres, and the magnetosphere of the Earth [42]. Vasyliunas first introduced the superthermal κ-distribution to explain the high-energy tails seen in non-Maxwellian plasma systems [43]. The parameter κ in the κ-distribution determines the robustness of the superthermality or nonthermality of the plasma medium. Smaller κ values indicate stronger nonthermality, whereas higher κ values indicate weaker nonthermality, and when κ approaches infinity, the velocity distribution behaves like the Maxwellian. A number of research works have explored the consequences of electron superthermality on electrostatic excitations [44,45,46,47,48,49]. Shahmansouri et al. [50] investigated the fundamental features of nonlinear IAWs in a superthermal e-p-i plasma using weak transverse perturbations. The propagation of IASHWs in a superthermal e-p-i magnetoplasma has been studied by Heera et al. [51]. They revealed that the considered model accommodates both positive and negative shock patterns. Recently, Shahein et al. [52] has shown the nonlinear characteristics of IAWs in an unmagnetised collisionless superthermal e-p-i plasma. They have shown a new form of blow-up solitary wave by using the \(\left(\frac{{G^{\prime}}}{G}\right)\) expansion method, and the diffusion structure is visually depicted.

Bifurcation is a phenomenon that shows qualitative alterations in the behaviour of a nonlinear system as physical parameters are changed. In dynamical systems, bifurcation plays an essential role because it allows for transitions and instabilities when the system’s parameters are varied. The bifurcations of various nonlinear travelling wave properties in different plasma models have been studied using the principles of dynamical systems [53,54,55]. Moreover, in the past few decades, the study of periodic waves has grown in importance due to its relevance in a wide range of fields of physics. This type of wave signal is commonly seen in auroral, magnetospheric, and tokamak plasmas as IA soliton and double-layer structures [56]. Kaladze and Mahmood [57] explored electrostatic IA solitary and periodic waves in unmagnetised e-p-i plasmas, where electrons and positrons follow κ-distribution. They demonstrate that the amplitude of periodic waves and solitons reduces for κ-distributed electron and positron plasmas compared to Maxwellian-distributed electron and positron plasmas. Chapagai et al. [58] studied the bifurcation analysis of nonlinear and supernonlinear periodic IAWs in a three-constituent superthermal plasma, considering the variations of different physical parameters. Moreover, Zhang et al. [59] studied peakons and a series of new exact travelling wave solutions, including bell-shaped, kink-type solitary waves, shock waves, periodic waves, and Jacobi elliptic solutions, using the auxiliary equation method. Saha et al. [60] carried out the bifurcation analysis of IA shocks and periodic waves in a dense quantum plasma model. For the first time, they observed the periodic waves of the Burgers’ equation in plasmas using the Jacobi elliptic method. An investigation on the properties of the IA solitary, kink, and periodic waves has been carried out by Abdikian et al. [61] in a confined plasma system that experiences rotating motions. They have observed that only the positive potential IA periodic waves are emerging. El-Taibany et al. [62] performed solitary and periodic DAWs investigations in a self-gravitating dusty plasma in the presence of moving ions and electrons. But as far as we know, no attempt has been made to study the DIA periodic wave solution in magnetised κ-distributed electron and positron dusty plasma systems. Moreover, the phase plan analysis of DIAWs in superthermal electron-positron dissipative media has not been studied previously. Although Roy et al. [63] recently demonstrated the occurrence of solitary and shock waves in a dissipative medium using phase portrait analysis, they established their work only in the context of a non-extensive dusty plasma system. Therefore, in the present work, we have plotted the phase portrait profile to predict the existence of the IA solitary, shock, and periodic wave solutions in a superthermal dissipative plasma. Based on our numerical results, their corresponding wave structures are analysed graphically.

2 Basic Equations

In our present investigation, we have considered a dissipative plasma model containing negatively charged dust grains, inertial ions, non-Maxwellian electrons, and positrons following the \(\kappa\)- distribution. In the presence of an external magnetic field \({B}_{0}\) along the z-axis, the dynamics of dust IAWs can be characterised by the following set of normalised equations:

Continuity equation

$$\frac{\partial {n}_{i}}{\partial t}+\frac{\partial({n}_{i}{u}_{x})}{\partial x}+\frac{\partial({n}_{i}{u}_{y})}{\partial y}+\frac{\partial({n}_{i}{u}_{z})}{\partial z}=0,$$
(1)

Momentum equation

$$\frac{\partial {u}_{x}}{\partial t}+{u}_{x}\frac{\partial {u}_{x}}{\partial x}+{u}_{y}\frac{\partial {u}_{x}}{\partial y}+{u}_{z}\frac{\partial {u}_{x}}{\partial z}+\frac{\partial \phi }{\partial x}=\eta \frac{{\partial }^{2}{u}_{x}}{\partial {x}^{2}}+{\omega }_{ci}{u}_{y},$$
(2)
$$\frac{\partial {u}_{y}}{\partial t}+{u}_{x}\frac{\partial {u}_{y}}{\partial x}+{u}_{y}\frac{\partial {u}_{y}}{\partial y}+{u}_{z}\frac{\partial {u}_{y}}{\partial z}+\frac{\partial \phi }{\partial y}=\eta \frac{{\partial }^{2}{u}_{y}}{\partial {y}^{2}}-{\omega }_{ci}{u}_{x},$$
(3)
$$\frac{\partial {u}_{z}}{\partial t}+{u}_{x}\frac{\partial {u}_{z}}{\partial x}+{u}_{y}\frac{\partial {u}_{z}}{\partial y}+{u}_{z}\frac{\partial {u}_{z}}{\partial z}+\frac{\partial \phi }{\partial z}=\eta \frac{{\partial }^{2}{u}_{z}}{\partial {z}^{2}},$$
(4)

Poisson’s equation [64]

$$\frac{{\partial }^{2}\phi }{\partial {x}^{2}}+\frac{{\partial }^{2}\phi }{\partial {y}^{2}}+\frac{{\partial }^{2}\phi }{\partial {z}^{2}}={\mu }_{e}{n}_{e}-{\mu }_{p}{n}_{p}-{n}_{i}+{\mu }_{d}.$$
(5)

The superthermal electron and positron distributions [51, 65] are

$$n_e=\left(1-\frac\phi{\kappa_e-3/2}\right)^{-\kappa_e+1/2},$$
$$\cong \left(1+{c}_{1}\phi +{c}_{2}{\phi }^{2}+{c}_{3}{\phi }^{3}+...\right),$$
(6)

and

$${n}_{p}={\left(1+\frac{{\sigma }_{p}\phi }{{\kappa }_{p}-3/2}\right)}^{-{\kappa }_{p}+1/2},$$
$$\cong \left(1-{b}_{1}{\sigma }_{p}\phi +{b}_{2}{\sigma }_{p}^{2}{\phi }^{2}-{b}_{3}{\sigma }_{p}^{3}{\phi }^{3}+...\right),$$
(7)

where

$$c_1=\frac{2\kappa_e-1}{2\kappa_e-3},\;c_2=\frac{\left(2\kappa_e-1\right)\left(2\kappa_e+1\right)}{2\left(2\kappa_e-3\right)^2},\;c_3=\frac{\left(2\kappa_e-1\right)\left(2\kappa_e+1\right)\left(2\kappa_e+3\right)}{6\left(2\kappa_e-3\right)^3},$$
$${b}_{1}=\frac{2{\kappa }_{p}-1}{2{\kappa }_{p}-3}, {b}_{2}=\frac{\left(2{\kappa }_{p}-1\right)\left(2{\kappa }_{p}+1\right)}{2{\left(2{\kappa }_{p}-3\right)}^{2}}, {b}_{3}=\frac{\left(2{\kappa }_{p}-1\right)\left(2{\kappa }_{p}+1\right)\left(2{\kappa }_{p}+3\right)}{6{\left(2{\kappa }_{p}-3\right)}^{3}}.$$

In Eqs. (1)-(5), the ion number density ni is normalised by ni0; the velocity of the ions is normalised by the ion-acoustic speed \({C}_{p}={\left(\nicefrac{{k}_{B}{T}_{E}}{{m}_{p}}\right)}^{1/2}\). The electrostatic potential ϕ and time t are normalised by \(\left(\nicefrac{{k}_{B}{T}_{e}}{e}\right)\) and the inverse of the plasma frequency \({\omega }_{p}^{-1}\), respectively. The space variables (x, y, z) are normalised by Debye length \({\lambda }_{D}={\left(\nicefrac{{k}_{B}{T}_{e}}{4\pi {e}^{2}{n}_{i0}}\right)}^{1/2}\). η is the kinematic viscosity of ions normalised by \({m}_{i}{n}_{i0}{\omega }_{p}{\lambda }_{D}^{2}\); the ion cyclotron frequency \({\omega }_{ci}\) is normalised by the period of ion plasma. The parameters \({\mu }_{e}=\frac{1}{1-p+d}\), \({\mu }_{p}=\frac{p}{1-p+d}\), \({\mu }_{d}=\frac{d}{1-p+d}\), and \({\sigma }_{p}=\frac{{T}_{e}}{{T}_{p}}\) are obtained due to the non-dimensional process, where \(p=\frac{{n}_{p0}}{{n}_{e0}}\), \(d=\frac{{z}_{d0}{n}_{d0}}{{n}_{e0}}\), and Te and Tp are the temperature of electrons and positrons.

3 Derivation of the Nonlinear K-dV-Burgers’ Equation

To procure the K-dV-Burgers’ equation, we have utilised the RPM. According to RPM, we stretch the independent variables as [66,67,68]

$$\xi ={\varepsilon }^{1/2}\left({l}_{x}x+{l}_{y}y+{l}_{z}z-{V}_{0}t\right), \tau ={\varepsilon }^{3/2}t, \eta ={\varepsilon }^{1/2}{\eta }_{0};$$
(8)

here, V0 is the phase velocity of DIAWs, and ɛ measures the strength of nonlinearity. The use of stretching enables us to see in detail what happens on different scales of distance and time in the system. The dependent physical quantities ni, ux, uy, uz, and ϕ are expressed as a power series expansion of ɛ in the following ways:

$${n}_{i}=1+\varepsilon {n}^{1}+{\varepsilon }^{2}{n}^{2}+{\varepsilon }^{3}{n}^{3}...,$$
$${u}_{x,y}={\varepsilon }^{3/2}{u}_{x,y}^{1}+{\varepsilon }^{2}{u}_{x,y}^{2}+{\varepsilon }^{5/2}{u}_{x,y}^{3}...,$$
(9)
$${u}_{z}=\varepsilon {u}_{z}^{1}+{\varepsilon }^{2}{u}_{z}^{2}+{\varepsilon }^{3}{u}_{z}^{3}...,$$
$$\phi =\varepsilon {\phi }^{1}+{\varepsilon }^{2}{\phi }^{2}+{\varepsilon }^{3}{\phi }^{3}...$$

Now, using stretched variables from Eq. (8) into Eqs. (1)-(5) and after substituting the above expansions, the lowest order of ɛ gives.

$${n}^{1}=\frac{{l}_{z}^{2}}{{V}_{0}^{2}}{\phi }^{1}, {u}_{z}^{1}=\frac{{l}_{z}}{{V}_{0}}{\phi }^{1},$$
$${u}_{x}^{1}=-\frac{{l}_{y}}{{\omega }_{ci}}\frac{\partial {\phi }^{1}}{\partial \xi }, {\mu }_{e}{c}_{1}{\phi }^{1}+{\mu }_{p}{b}_{1}{\sigma }_{p}{\phi }^{1}-{n}^{1}=0,$$
(10)
$${u}_{y}^{1}=\frac{{l}_{x}}{{\omega }_{ci}}\frac{\partial {\phi }^{1}}{\partial \xi }.$$

Now, the phase velocity expression is obtained as

$${V}_{0}=\frac{{l}_{z}}{\sqrt{{\mu }_{e}{c}_{1}+{\mu }_{p}{b}_{1}{\sigma }_{p}}}.$$
(11)

Considering the higher-order coefficients of ɛ, we have

$$\frac{\partial {n}^{1}}{\partial \tau }-{V}_{0}\frac{\partial {n}^{2}}{\partial \xi }+{l}_{x}\frac{\partial {u}_{x}^{2}}{\partial \xi }+{l}_{y}\frac{\partial {u}_{y}^{2}}{\partial \xi }+{l}_{z}\frac{\partial {u}_{z}^{2}}{\partial \xi }+{l}_{z}\frac{\partial }{\partial \xi }\left({n}^{1}{u}_{z}^{1}\right)=0,$$
(12)
$${u}_{x}^{2}=\frac{{l}_{x}{V}_{0}}{{\omega }_{ci}^{2}}\frac{{\partial }^{2}{\phi }^{1}}{\partial {\xi }^{2}},$$
(13)
$${u}_{y}^{2}=\frac{{l}_{y}{V}_{0}}{{\omega }_{ci}^{2}}\frac{{\partial }^{2}\phi }{\partial {\xi }^{2}},$$
(14)
$$\frac{\partial {u}_{z}^{1}}{\partial \tau }-{V}_{0}\frac{\partial {u}_{z}^{2}}{\partial \xi }+{u}_{z}^{1}{l}_{z}\frac{\partial {u}_{z}^{1}}{\partial \xi }+{l}_{z}\frac{\partial {\phi }^{2}}{\partial \xi }={\eta }_{0}\frac{{\partial }^{2}{u}_{z}^{1}}{\partial {\xi }^{2}},$$
(15)
$$\frac{{\partial }^{2}{\phi }^{1}}{\partial {\xi }^{2}}=({\mu }_{e}{c}_{1}+{\mu }_{p}{b}_{1}{\sigma }_{p}){\phi }^{2}+({\mu }_{e}{c}_{2}-{\mu }_{p}{b}_{2}{\sigma }_{p}^{2})({\phi }^{1})^{2}-{n}^{2}.$$
(16)

Eliminating all the second-order quantities \({u}_{x}^{2}, {u}_{y}^{2},{u}_{z}^{2},{n}^{2}\) and \({\phi }^{2}\) from the above equations with the aid of Eq. (10), we finally get the following K-dV-Burgers’ equation as

$$\frac{\partial {\phi }^{1}}{\partial \tau }+A{\phi }^{1}\frac{\partial {\phi }^{1}}{\partial \xi }+B\frac{{\partial }^{3}{\phi }^{1}}{\partial {\xi }^{3}}-C\frac{{\partial }^{2}{\phi }^{1}}{\partial {\xi }^{2}}=0,$$
(17)

with the coefficients

$$A=\frac{{V}_{0}^{3}}{2{l}_{z}^{2}}\left(\frac{4{l}_{z}^{4}}{{V}_{0}^{4}}+2{\mu }_{p}{b}_{2}{\sigma }_{p}^{2}-2{\mu }_{e}{c}_{2}\right),$$
$$B=\frac{{V}_{0}^{3}}{2{l}_{z}^{2}}\left(1+\frac{1-{l}_{z}^{2}}{{\omega }_{ci}^{2}}\right),$$

and

$$C=\frac{{\eta }_{0}}{2}.$$

A, B, and C are the nonlinear, dispersion, and dissipative coefficients, respectively. The coefficient C, also known as Burger’s term, suggests the potential of getting a shock-type solution.

4 Bifurcation Analysis of K-dV- Burgers’ Equation

To perform phase plan analysis of the K-dV-Burgers’ equation, we have used another variable transformation, \(\chi =\xi -{u}_{0}\tau\), where u0 is a constant speed. After replacing the independent variables ξ and τ with the new variable χ and then integrating, Eq. (17) is written as follows

$$\frac{{d}^{2}{\phi }^{1}}{d{\chi }^{2}}-\frac{C}{B}\frac{d{\phi }^{1}}{d\chi }+\frac{A}{2B}{({\phi }^{1})}^{2}-\frac{{u}_{0}}{B}{\phi }^{1}=0.$$
(18)

Equation (18) can be transformed into the following system of planar dynamical equations

$$\left\{\begin{array}{l}\frac{d{\phi}^{1}}{d\chi}=z\\ \frac{dz}{d\chi }=\frac{{u}_{0}}{B}{\phi }^{1}-\frac{A}{2B}{({\phi }^{1})}^{2}+\frac{C}{B}z\end{array}\right..$$
(19)

For C = 0, let \({g}_{1}\left({\phi }^{1},z\right)=z\) and \({g}_{2}\left({\phi }^{1},z\right)=\frac{{u}_{0}}{B}{\phi }^{1}-\frac{A}{2B}\) is Hamiltonian system if \(\frac{\partial {g}_{1}}{\partial {\phi }^{1}}+\frac{\partial {g}_{2}}{\partial z}=0\). The system (19) has a Hamiltonian function defined as

$$H=\frac{1}{2}{\left(\frac{d{\phi }^{1}}{d\chi }\right)}^{2}-\frac{{u}_{0}}{2B}{\left({\phi }^{1}\right)}^{2}+\frac{A}{6B}{\left({\phi }^{1}\right)}^{3},$$
(20)

with the potential function

$$V\left({\phi }^{1}\right)=-\frac{{u}_{0}}{2B}{\left({\phi }^{1}\right)}^{2}+\frac{A}{6B}{\left({\phi }^{1}\right)}^{3}.$$
(21)

The system of Eq. (19) has two equilibrium points \({E}_{1}\left(\mathrm{0,0}\right)\) and \({E}_{2}\left(\frac{2{u}_{0}}{A},0\right)\).

Now to calculate the eigenvalues at E1 and E2, the Jacobian matrix for the system (19) is given as

$$J=\left(\begin{array}{cc}0& 1\\ \frac{{u}_{0}}{B}-\frac{A}{B}{\phi }^{1}& \frac{C}{B}\end{array}\right).$$

The Jacobian matrices at \({E}_{1}\left(\mathrm{0,0}\right)\) and \({E}_{2}\left(\frac{2{u}_{0}}{A},0\right)\) are

$${J}_{{E}_{1}}=\left(\begin{array}{cc}0& 1\\ \frac{{u}_{0}}{B}& \frac{C}{B}\end{array}\right),$$
(22)
$${J}_{{E}_{2}}=\left(\begin{array}{cc}0& 1\\ -\frac{{u}_{0}}{B}& \frac{C}{B}\end{array}\right).$$
(23)

When the dissipative coefficient is dominant over the dispersive term (i.e. B = 0), then, Eq. (17) becomes

$$\frac{\partial {\phi }^{1}}{\partial \tau }+A{\phi }^{1}\frac{\partial {\phi }^{1}}{\partial \xi }-C\frac{{\partial }^{2}{\phi }^{1}}{\partial {\xi }^{2}}=0.$$
(24)

We transform the above equation using the same transformation \(\chi =\xi -{u}_{0}\tau\) as

$$-{u}_{0}\frac{d{\phi }^{1}}{d\chi }+A{\phi }^{1}\frac{d{\phi }^{1}}{d\chi }-C\frac{{d}^{2}{\phi }^{1}}{d{\chi }^{2}}=0.$$
(25)

After integrating, we get

$$-{u}_{0}{\phi }^{1}+\frac{A}{2}{\left({\phi }^{1}\right)}^{2}-C\frac{d{\phi }^{1}}{d\chi }=0.$$
(26)

Then combining Eqs. (25) and (26), we can deduce the following system of equations as

$$\left\{\begin{array}{l}\frac{d{\phi }^{1}}{d\chi }={z}^{\prime}\\ \frac{d{z}^{\prime}}{d\chi }=\frac{A}{2{C}^{2}}{\phi }^{1}\left({\phi }^{1}-\frac{{u}_{0}}{A}\right)\left({\phi }^{1}-\frac{2{u}_{0}}{A}\right)\end{array}\right..$$
(27)

Now let us discuss three different cases.

Case I

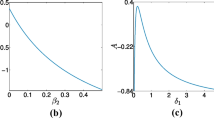
When \(C=0\) and \(B\ne 0\), the potential function defined in Eq. (21) and the phase plot of the system of Eqs. (19) are shown graphically in Fig. 1a–f. The potential function is plotted as a function of \({\phi }^{1}\) for distinct values of the nonthermal parameter \({\kappa }_{e}\) in Fig. 1a. The potential curve has one hump and a pit, and it gets shallower as \({\kappa }_{e}\) rises. This makes it clear that by increasing \({\kappa }_{e}\), the width of the solitons is increased. The figure also shows that when \({\kappa }_{e}\) is raised, the pseudopotential curve broadens in the positive direction of the \({\phi }^{1}\) axis. This is caused by the existence of compressive solitary waves. From the Jacobian matrix (22), the eigenvalues at the equilibrium point E1 are \(\lambda =\pm \sqrt{\frac{{u}_{0}}{B}}\), which are real and distinct, so we classify E1 as an unstable saddle point, see Fig. 1b. Also from the Jacobian matrix (23), the eigenvalues corresponding to the equilibrium point E2 are \(\lambda =\pm i\sqrt{\frac{{u}_{0}}{B}}\), which are purely imaginary, so we classify E2 as a stable centre point (see Fig. 1c). In the phase portrait, the hump of the potential curve corresponds to the saddle point at E1 and the pit corresponds to the centre point at E2. There is a homoclinic orbit in the phase plot profile encompassing the saddle points E1 and centre point E2 and periodic orbits around the centre point E2, as shown in the Fig. 1d–f. Each trajectory in the phase plot refers to a travelling wave solution for that plasma configuration. The existence of homoclinic and periodic orbits indicates the presence of solitary and periodic travelling wave solutions of the K-dV-Burgers’ equation, which will be discussed broadly in the next section. Significantly, the impact of rising \({\kappa }_{e}\) is crucial in lengthening the distance between two equilibrium positions (see Fig. 1d–f). This means that increasing the value of \({\kappa }_{e}\) raises the amplitude of the waves.

Fig. 1
figure 1

a Variation of \(V\left({\phi }^{1}\right)\) vs \({\phi }^{1}\) for distinct \({\kappa }_{e}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\). b Saddle point \({E}_{1}\left(\mathrm{0,0}\right)\), with \({\kappa }_{e}=2.1\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\). c Centre point \({E}_{2}\left(\frac{2{u}_{0}}{A},0\right)\), with \({\kappa }_{e}=2.1\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\). d Phase plot of the system (19), with \({\kappa }_{e}=2.1\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\). e Phase plot of the system (19), with \({\kappa }_{e}=2.3\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\). f Phase plot of the system (19), with \({\kappa }_{e}=2.5\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\).

Full size image

Case II

When \(C\ne 0\) and \(B\ne 0\), shock wave phenomena are predicted. Here, the equilibrium point \({E}_{1}\left(\mathrm{0,0}\right)\) is an unstable saddle, and at the equilibrium point \({E}_{2}\left(\frac{2{u}_{0}}{A},0\right)\), we have trajectories that spiral and go out, so the equilibrium point \({E}_{2}\left(\frac{2{u}_{0}}{A},0\right)\) is unstable. These trajectories are seen in Fig. 2a–c.

Fig. 2
figure 2

a Phase plot of the system (19), with \({\kappa }_{e}=2.1\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{p}=2.8\). b Phase plot of the system (19), with \({\kappa }_{e}=2.3\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{p}=2.8\). c Phase plot of the system (19), with \({\kappa }_{e}=2.5\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{p}=2.8\)

Full size image

Case III

When \(C\ne 0\) and \(B=0\), the phase plot diagram of system (27) is depicted in Fig. 3. There are three fixed points F1, F2, and F3 in the system. Among these fixed points, F2 is surrounded by a family of periodic orbits, while fixed points F1 and F3 are connected by a pair of heteroclinic orbits. In general, a heteroclinic orbit in the phase plot diagram signifies the emergence of both kink and anti-kink shock wave solutions in the considered system.

Fig. 3
figure 3

Phase plot of the system (27) with \({\kappa }_{e}=2.1\), \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{p}=2.8\)

Full size image

5 Results and Discussion of Soliton and Shock Wave Solutions

To investigate the features of DIA soliton structures, we have considered a situation in which the impact of dispersion dominates that of dissipation. In this case, Eq. (17) becomes the original K-dV equation as

$$\frac{\partial {\phi }^{1}}{\partial \tau }+A{\phi }^{1}\frac{\partial {\phi }^{1}}{\partial \xi }+B\frac{{\partial }^{3}{\phi }^{1}}{\partial {\xi }^{3}}=0,$$
(28)

and the analogous solitary wave solution is [19]

$${\phi }^{1}={\phi }_{m}{\mathrm{sech}}^{2}\left(\frac{\chi }{\Delta }\right),$$
(29)

where \({\phi }_{m}=\frac{3{u}_{0}}{A}\) is the amplitude and \(\Delta =\sqrt{\frac{4B}{{u}_{0}}}\) is the width of the solitary waves in the absence of the dissipative coefficient.

Since nonlinear and dispersion coefficients depend on a number of physical parameters, the impact of these parameters on the properties of DIASWs may be traced through changes in these coefficients with regard to the pertinent parameters. So, in this part, we inspect the contribution of the plasma components, namely, the dust-to-electron density ratio (d), the positron-to-electron density ratio (p), the electron-to-positron temperature ratio \(\left({\sigma }_{p}\right)\), and the parameters of the superthermal electron \(\left({\kappa }_{e}\right)\) and positron \(\left({\kappa }_{p}\right)\), on the configuration of the IASWs with the help of graphical representations. In order to attain this, we have selected some specific plasma parameters prevalent in the astrophysical dusty plasma atmospheres [51, 63, 64]. Figure 4a illustrates the soliton profile \({\phi }^{1}\) against χ for increasing values of dust-to-electron density ratio \(\left(d={z}_{d0}{n}_{d0}/{n}_{e0}\right)\). This figure clarifies that the solitary waves get wider and have a larger amplitude as d increases. In general, increasing the density ratio (d) indicates the enhancement of dust density to that of electrons. Enhancing dust density plays a substantial role in increasing the potential energy of the plasma system. Thus, there is an upward tendency in the amplitude of solitary waves. On the contrary, the opposite behaviour of the solitary waves can be seen in Fig. 4b, where \({\phi }^{1}\) is changed with different values of positron-to-electron density ratio \(\left(p={n}_{p0}/{n}_{e0}\right)\), i.e., the amplitude of the soliton structures diminishes with increasing p. The decrease in amplitude implies an increase in the nonlinearity of the system when it alters with p. Enhancement of the density ratio (p) indicates the enhancement of positron density compared to that of electrons. Increasing the positron density in this system has a detrimental influence on the overall potential energy of the system. As a result, the soliton constantly degrades and loses potential energy. The influence of the electron-to-positron temperature ratio \({\sigma }_{p}\) on the feature of the soliton profile is displayed in Fig. 4c. It is evident that as \({\sigma }_{p}\) increases, the amplitude and breadth of the solitary wave diminish. The effect of \({\kappa }_{e}\) and \({\kappa }_{p}\) on \({\phi }^{1}\) is shown in Fig. 4d and e. Figures suggest that raising \({\kappa }_{e}\) and \({\kappa }_{p}\) increases the amplitude and width of the soliton, and it is very sensitive to low ranges of \({\kappa }_{e}\) and \({\kappa }_{p}\). This means that when there is an abundance of superthermal elements, the nonlinear factor of the K-dV equation becomes smaller, and hence, the amplitude of the soliton wave increases. Contrarily, we can assert that the amplitude and width of solitons are observed to decrease as the plasma nonthermality increases. It follows that taller and broader solitary waves are expected to occur in a Maxwellian plasma with higher values of \({\kappa }_{e}\) and \({\kappa }_{p}\) than those produced in a nonthermal plasma with lower values of \({\kappa }_{e}\) and \({\kappa }_{p}\). This indicates that an increase in the nonthermality of electrons and positrons in the plasma medium has a favourable effect on the gain of total potential energy in the system. As a result, the soliton is constantly growing and acquiring positive energy. Similar kinds of variation of IAS structures with superthermality of electrons and positrons are observed in the research work by Shahein et al. [52]. The magnetic field strength (cyclotron frequency, \({\omega }_{ci}\)) has an influence on the soliton profile, which is illustrated in Fig. 4f. It has been shown that changing the magnetic field effect has no impact on the amplitude of solitary waves. The single-pulse soliton solution \({\phi }^{1}\) is illustrated against ξ at different time scales τ in Fig. 4g.

Fig. 4
figure 4

Variation of \({\phi }^{1}\) vs χ a for distinct d with \(p=0.2\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\), b for distinct p with \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\), c for distinct \({\sigma }_{p}\) with \(p=0.2\), \(d=0.1\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\), d for distinct \({\kappa }_{e}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), and \({\kappa }_{p}=2.8\), e for distinct \({\kappa }_{p}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\) and \({\kappa }_{e}=2.1\), f for distinct \({\omega }_{ci}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\), g for distinct τ with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\)

Full size image

In order to examine the attributes of DIASH formation, we investigate a scenario in which the dissipative component prevails over the dispersive term. In that particular case, Eq. (17) is reduced to the Burgers’ equation of the form

$$\frac{\partial {\phi }^{1}}{\partial \tau }+A{\phi }^{1}\frac{\partial {\phi }^{1}}{\partial \xi }=C\frac{{\partial }^{2}{\phi }^{1}}{\partial {\xi }^{2}},$$
(30)

which bears kink and anti-kink shaped monotonic shock profile solutions.

To acquire DIA kink and anti-kink wave solutions, we employ the conventional tanh method. We follow the same procedure as in Ref. [60] to find the kink and anti-kink wave solutions of the obtained Burgers’ Eq. (30). As a consequence, the anti-kink wave solution caused by the heteroclinic orbit connecting fixed point F1 to fixed point F3 can be expressed as

$${\phi }^{1}={\phi }_{m}\left[1-\mathrm{tanh}\left(\frac{\chi }{\Delta }\right)\right],$$
(31)

and the kink wave solution of Burgers’ Eq. (30) caused by the heteroclinic orbit connecting fixed point F3 to fixed point F1 can be expressed as

$${\phi }^{1}=-{\phi }_{m}\left[1-\mathrm{tanh}\left(\frac{\chi }{\Delta }\right)\right].$$
(32)

Here, \({\phi }_{m}\) is the amplitude and \(\Delta\) represents the width of the shock waves, respectively, and are expressed as,

$${\phi }_{m}=\frac{{u}_{0}}{A}\;and\;\Delta =\frac{2C}{{u}_{0}}.$$

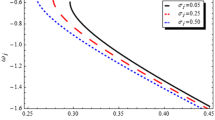
Since the nonlinear and dissipation coefficients depend on the ratios of dust-to-electron density (d), positron-to-electron density (p), electron-to-positron temperature \(\left({\sigma }_{p}\right)\), effect of the viscosity \(\left({\eta }_{0}\right)\), and superthermal parameters of electrons \(\left({\kappa }_{e}\right)\) and positrons \(\left({\kappa }_{p}\right)\), the solution of shock formation is an explicit function of these parameters. Therefore, numerical findings that show how these physical parameters affect the dust acoustic shock profile controlled by Burgers’ Eq. (30) are shown in Figs. 5a–n.

Fig. 5
figure 5figure 5

Variation of a anti-kink and b kink wave for distinct d with \(p=0.2\), σp = 1.4, \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\); c anti-kink and d kink wave for distinct p with \(d=0.1\), σp = 1.4, \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\); e anti-kink and f kink wave for distinct σp with \(p=0.2\), \(d=0.1\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\); g anti-kink and h kink wave for distinct κe with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{p}=2.8\); i anti-kink and j kink wave for distinct κp with \(p=0.2\), \(d=0.1\), σp = 1.4, \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), and \({\kappa }_{e}=2.1\); k anti-kink and l kink wave for distinct \({\eta }_{0}\) with \(p=0.2\), \(d=0.1\), σp = 1.4, \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\); m anti-kink and n kink wave for distinct \(\theta\) with \(p=0.2\), \(d=0.1\), σp = 1.4, \({u}_{0}=0.2\), \({\eta }_{0}=0.5\), \({\kappa }_{e}=2.1\), and \({\kappa }_{p}=2.8\)

Full size image

The influence of the dust-to-electron density ratio (d) on the anti-kink and kink shock structures is displayed in Fig. 5a and b. The results confirm that an increase in the dust-to-electron density ratio (d) leads to a greater amplitude of shock waves; however, the anti-kink and kink wave profiles’ smoothness remains constant. In Fig. 5c and d, the DIA anti-kink and kink waves are shown at distinct values of the positron-to-electron number density ratio (p) at equilibrium conditions. It can be shown that increasing the positron density reduces the amplitudes of both wave profiles. Figure 5e and f present the structures of the shock wave profile for different values of the electron-to-positron temperature ratio via σp. We can infer from the graphs that smaller amplitude shock structures are supported by higher values of σp. Figure 5g and h show the DIA anti-kink and kink shock solutions for distinct values of the nonthermal parameters of electron \(\left({\kappa }_{e}\right)\) with specific values of other parameters. We can see that the amplitudes of the anti-kink and kink wave profiles considerably increase as \({\kappa }_{e}\) is increased. The effects of superthermal positron parameter κp on the anti-kink and kink waves can be observed from Fig. 5i and j, and it is clear that the amplitude of the anti-kink and kink profiles grows with an increase in the value of κp. It has also been apparent to Heera et al. [51] in their study of IASHWs that the amplitude of the positive shock profile grows as the value of κe increases. But an opposite result has been shown for the variation of κp. This happened due to the different values of the electron-to-positron temperature ratio \(\left({\sigma }_{4}={T}_{e}/{T}_{p}\right)\). Figure 5k and l represent the DIA anti-kink and kink wave formation for different values of the coefficient of viscosity η0 with suitable physical parameters. We have noticed that the amplitude of shock formation is independent of the rate of dissipation; i.e., it remains invariant regardless of whether η0 is increased or decreased, while the breadth of the shock waves rises with an increase in the coefficient of viscosity η0 in both anti-kink and kink DA shock waves. Furthermore, it can also be stated that as dissipation increases, the shock structures become more smooth and feeble. These results are in agreement with those reported in Ref. [69]. We have observed that the external magnetic field has the ability to drastically alter the configuration of the IASHWs in the plasma. Figure 5m and n show the anti-kink and kink waves as they are affected by the oblique angle \(\theta\), which is the angle between the direction of the external magnetic field and the direction of the wave propagation. It has been observed from Fig. 5m and n that the magnitude of the amplitude of the anti-kink and kink shock profiles rises as the value of the oblique angle \(\theta\) increases.

6 Nonlinear Periodic Wave Solution

In order to derive the periodic wave solution of the K-dV Eq. (28), we assumed the solution to be \({\phi }^{1}\left(\chi \right)\). Introducing the same variable transformation \(\chi =\xi -{u}_{0}\tau\), Eq. (28) can be expressed as

$$B\frac{{d}^{3}\Phi }{d{\chi }^{3}}+\frac{d}{d\chi }\left(\frac{A}{2}{\Phi }^{2}-{u}_{0}\Phi \right)=0,$$
(33)

where \(\Phi ={\phi }^{1}\left(\chi \right)\). After integrating Eq. (33), we obtain a conservative nonlinear equation, which has the form

$$\frac{{d}^{2}\Phi }{d{\chi }^{2}}=-\frac{dW}{d\Phi },$$
(34)

where \(W=W\left(\Phi \right)\) is the Sagdeev’s potential, defined as

$$W\left(\Phi \right)=\frac{A}{6B}{\Phi }^{3}-\frac{{u}_{0}}{2B}{\Phi }^{2}+{\rho }_{0}\Phi.$$
(35)

There are two points of extremum of the potential function \(W\left(\Phi \right)\), which are defined at \(\frac{\partial W}{\partial \Phi }=0\), namely

$${\Phi }_{\mathrm{1,2}}=\frac{{u}_{0}}{A}\pm \sqrt{\frac{{u}_{0}^{2}}{{A}^{2}}-\frac{2}{A}{\rho }_{0}B}.$$
(36)

Furthermore, for the existence of real values, \(\frac{{u}_{0}^{2}}{{A}^{2}}>\frac{2{\rho }_{0}B}{A}\) must hold. The zeros \((\Phi ={z}_{1},{z}_{2},{z}_{3})\) of the potential function (35) are given as.

$${z}_{1}=0,{z}_{\mathrm{2,3}}=\frac{3}{A}\left(\frac{{u}_{0}}{2}\pm \sqrt{\frac{{u}_{0}^{2}}{4}-\frac{2A}{3}{\rho }_{0}B}\right).$$
(37)

Now, \(\frac{{u}_{0}^{2}}{4}-\frac{2A{\rho }_{0}B}{3}>0\) must persist in order to properly mould the potential. Equation (34) is associated with the first integral of the energy that can be inspired by

$$\frac{1}{2}{\left(\frac{d\Phi }{d\chi }\right)}^{2}+W\left(\Phi \right)=\frac{{E}_{0}^{2}}{2},$$
(38)

with the integration constant \({E}_{0}^{2}\). Substituting Eq. (35) in (38), we get

$${\left(\frac{d\Phi }{d\chi }\right)}^{2}={E}_{0}^{2}-\frac{A}{3B}{\Phi }^{3}+\frac{{u}_{0}}{B}{\Phi }^{2}-2{\rho }_{0}\Phi.$$
(39)

Let us consider the initial conditions \(\Phi \left(0\right)={\phi }_{0}\) and \(\frac{d{\phi }_{0}}{d\chi }=0\). We can find

$${E}_{0}^{2}=\frac{{A}_{1}}{3{B}_{1}}{\phi }_{0}^{3}-\frac{{u}_{0}}{{B}_{1}}{\phi }_{0}^{2}+2{\rho }_{0}{\phi }_{0}.$$
(40)

Using Eq. (40) in Eq. (39) and after factorization, we get

$${\left(\frac{d\Phi }{d\chi }\right)}^{2}=\frac{A}{3B}\left({\phi }_{0}-\Phi \right)\left(\Phi -{\phi }_{1}\right)\left(\Phi -{\phi }_{2}\right),$$
(41)

where

$${\phi }_{1}=\frac{3}{2}\left[\frac{{u}_{0}}{A}-\frac{{\phi }_{0}}{3}+\sqrt{\frac{1}{3}\left({\psi }_{1}-{\phi }_{0}\right)\left({\phi }_{0}-{\psi }_{2}\right)}\right].$$
$${\phi }_{2}=\frac{3}{2}\left[\frac{{u}_{0}}{A}-\frac{{\phi }_{0}}{3}-\sqrt{\frac{1}{3}\left({\psi }_{1}-{\phi }_{0}\right)\left({\phi }_{0}-{\psi }_{2}\right)}\right].$$

and

$${\psi }_{\mathrm{1,2}}=\frac{{u}_{0}}{A}\pm 2\sqrt{\frac{{u}_{0}^{2}}{{A}^{2}}-2{\rho }_{0}\frac{B}{A}}.$$

The inequality \({\psi }_{2}\le {\phi }_{0}\le {\psi }_{1}\) or \({\psi }_{1}\le {\phi }_{0}\le {\psi }_{2}\) in the last relationships should be held. Furthermore, we may derive the following relationship from Eqs. (38) and (41).

$${u}_{0}=\frac{A}{3}\left({\phi }_{0}+{\phi }_{1}+{\phi }_{2}\right)$$
(42)

The periodic wave solution of Eq. (41) in terms of the three roots \({\phi }_{0}\), \({\phi }_{1}\) and \({\phi }_{2}\) can be written as follows

$$\Phi \left(\chi \right)={\phi }_{1}+\left({\phi }_{0}-{\phi }_{1}\right)c{n}^{2}\left(D\chi ,m\right),$$
(43)

where cn denotes the Jacobian elliptic function. The modulus m and D are defined as

$$m=\sqrt{\frac{{\phi }_{0}-{\phi }_{1}}{{\phi }_{0}-{\phi }_{2}}},$$

and

$$D=\sqrt{\frac{A}{12B}\left({\phi }_{0}-{\phi }_{2}\right)}.$$

The parameter m serves as a nonlinearity indicator in this case. The prerequisites \({\phi }_{1}\le \Phi \le {\phi }_{0}\) and \({\phi }_{0}>{\phi }_{1}\ge {\phi }_{2}\) are necessary for the periodic solution. Furthermore, the periodic wave frequency \(\upsilon\) and wavelength \(\lambda\) are defined as

$$\upsilon =\frac{V}{\lambda },$$
$$\lambda =4\sqrt{\frac{3B}{A\left({\phi }_{0}-{\phi }_{2}\right)}}K\left(m\right),$$

where \(K\left(m\right)\) represents the first kind of complete elliptic integral.

The influence of the electron-to-positron temperature ratio \(\left({\sigma }_{p}\right)\) and the superthermality parameters of electrons and positrons on the fundamental properties of IA periodic waves is demonstrated in Fig. 6. In Fig. 6a, the effect of the electron-to-positron temperature ratio \(\left({\sigma }_{p}\right)\) has been displayed on the profile of the periodic waves against χ. It is apparent that the amplitude of the periodic wave is decreasing, whereas the width is increasing as a result of the increase in \(\left({\sigma }_{p}\right)\). The shape of the periodic wave profiles against the super-thermal electron and positron components is depicted in Fig. 6b and c. As seen in these figures, the superthermality of electrons and positrons alters the periodic wave profiles’ breadth in addition to their amplitude. The magnitude of the amplitude and width grow in proportion to the values of \({\kappa }_{e}\) and \({\kappa }_{p}\).

Fig. 6
figure 6

Variation of periodic wave \(\Phi \left(\chi \right)\) vs χ a for distinct \({\sigma }_{p}\) with \(p=0.2\), \(d=0.1\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\kappa }_{e}=2.5\), \({\kappa }_{p}=2.8\), and \({\rho }_{0}=0.002\); b for distinct \({\kappa }_{e}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\kappa }_{p}=2.8\), and \({\rho }_{0}=0.002\), c for distinct \({\kappa }_{p}\) with \(p=0.2\), \(d=0.1\), \({\sigma }_{p}=1.4\), \({l}_{z}=0.4\), \({\omega }_{ci}=0.5\), \({u}_{0}=0.2\), \({\kappa }_{e}=2.1\), and \({\rho }_{0}=0.002\)

Full size image

7 Conclusions

We have addressed the bifurcations of the IA solitons, shock, and periodic wave features represented by the K-dV-Burgers’ equation in a magnetised superthermal plasma consisting of electrons and positrons obeying \(\kappa\)- distribution. The RPM has been applied to demonstrate small-amplitude DIAWs. Consideration of the kinematic viscosity of ions in the plasma constituents leads to the survival of the dissipative coefficient in the nonlinear K-dVB equation. The phase plane analysis of planar dynamical systems is applied, whose advantage is the ability to predict different types of existing travelling wave solutions in the system corresponding to different phase orbits.

When there is no influence from the dissipation \(\left(C=0\right)\), the bifurcation associated with the K-dVB equation is analysed graphically. The topology of the potential and phase portrait diagrams refers to the numerical behaviour of different kinds of nonlinear travelling wave solutions. One of these solutions, known as the soliton solution, is attained when the dissipative coefficient is insignificant in contrast to the nonlinearity and dispersion coefficients. The behaviour of such a solution is illustrated graphically against different physical parameters. It is evident that the basic features of solitary waves are significantly influenced by plasma nonthermality (via \({\kappa }_{e}\) and \({\kappa }_{p}\)). Solitary waves in a Maxwellian plasma \(\left(\kappa \to \infty \right)\) are projected to be taller and wider than those in a nonthermal plasma.

In that case, when there is the existence of dissipation (\(C\ne 0\)) and the absence of dispersion \(\left(B=0\right)\), the K-dVB equation recovers the Burgers’ equation, which admits a kink and anti-kink monotonic shock profile due to the heteroclinic orbit found in the corresponding phase portrait diagram. The shape of the amplitude of both kink and anti-kink shock structures is unaffected by variations in the kinematic viscosity of the ions \(\left({\eta }_{0}\right)\), while the width of the shock profile rises with the variation of the same parameter.

The variations of the periodic wave profile are displayed graphically with the change of the superthermal parameters of electrons (κe) and positrons (κp) and the electron-to-positron temperature ratio (σp). It can be concluded that changes in the amplitude and width of IA periodic waves are the same as those of IA solitary and shock wave formation.