1 Introduction

The nature and characteristics of dusty plasma which are observed initially not only in astrophysical (Goertz 1989) environment but also in space and laboratory environment, are the subject of intense research during the last few years. Peculiar characteristics of charged dust make a system complex and are therefore expected to be substantially different from the ordinary two component plasmas (Lonngren 1983). Because of dust charge and mass are not fixed, a new time and space scales come into play. Therefore new types of low frequency waves or different wave modes are established. Among them one of the most important, well established low frequency wave is dust ion- acoustic (DIA) waves where the dust grains do not participate in the wave motion. Recently, considerable attention has been paid to study the DIA waves (Shukla and Silin 1992; Nakamura et al. 1999; D’Angelo 1995) due to its wide applications in laboratory and space plasma. Experimental observations (Nakamura et al. 1999; Barkan et al. 1996) in several low-temperature dusty plasma devices make more enthusiastic about its re-exploration.

Most of the authors have studied DIA SWs (Rahman and Mamun 2011; Mamun 2007; Mamun et al. 2009; Alinejad 2010, 2011a; Rahman et al. 2011; El-Labany et al. 2012; Kundu et al. 2012) by using the dusty plasma model consisting of ions, electrons, and negatively charged stationary dust. The consideration of negatively charged dust is due to the fact that in low-temperature laboratory plasmas, collection of plasma particles (viz. electrons and ions) is the only important charging process, and the thermal speeds of electrons far exceeds that of ions. The authors have studied different phenomena of plasma limiting themselves to a simple model consisting of one pieces of ions and electrons, and ignored completely the interactions of multiple ions or electrons. For example, Rahman and Mamun (2011) have studied the DIA SWs consisting of cold mobile ions, electrons following vortex-like distribution, and arbitrarily charged static dust by employing the reductive perturbation technique. Using pseudo-potential approach Mamun (2007) investigated arbitrary amplitude SWs, and inferred that negative SWs [which are found to exist in a dusty plasma for Z d n d0/n i0>2/3, where Z d is the number of electrons residing on the dust grain surface, n i0 (n d0) is the density of unperturbed ion (dust)] can not be formed due to the effects of adiabaticity of electrons. The combined effects of adiabatic electrons and negatively charged stationary dust were explicitly examined by Mamun. Moreover, a large number of authors have also studied the SWs (Das and Tagare 1975; Xie et al. 1999; Tagare 1997) in plasmas including the multiple ion species of different kinds. Tagare (1997) studied the basic features of SWs with cold dust particles and isothermal two-temperature ions by taking into account the sufficient depletion of electron number density but limited himself to the investigation performing with multiple ions and completely ignored the soliton behaviour of two-temperature electron plasma. To some extent all the above mentioned plasma models are simplified since the interaction of multiple electrons (i.e. two-temperature electron) which describes more generalized plasma, were not considered by them. The interaction of such multiple electrons, i.e. two types of electron populations, namely, cold and hot (Lakhina et al. 2008), and hot ions are present in many space (Geiss et al. 1978) observations, such as in the cusp and the auroral field lines. The Viking satellite frequently observed cold and hot electrons at the times of bursts of electrostatic SWs in the auroral region (Lakhina et al. 2008; Dubouloz et al. 1993). Electrons at two different temperatures have also been encountered in double-plasma machines (Spileman et al. 1976), hot turbulent strong plasmas of thermonuclear (Morals and Lee 1974; Estabrook and Krueer 1978), noctilucent cloud region in Earth’s atmosphere, where the energetic particle precipitation affects the mesosphere charge balance (Shah et al. 2009), hot cathode discharges (Oleson and Found 1946), etc. Jones et al. (1975) were the first to investigate the effects of double temperature electrons in linear approximation for the ion-acoustic waves. They investigated the wave dynamics in a three component plasma consisting of cold ions, and two types of electrons including different thermal effects. Motivated by the observation of Jones et al. (1975), Nishida and Nagasawa (1986) produced two temperature electron species using rf heating and investigated for the first time the rarefactive soliton in such plasma. It was observed that the interactions between the hot and the cold electron components in the presence of a finite ion temperature produced rarefaction of the localized density.

All of this previous studies (Jones et al. 1975; Lakhina et al. 2008; Geiss et al. 1978; Dubouloz et al. 1993; Spileman et al. 1976; Morals and Lee 1974; Estabrook and Krueer 1978; Shah et al. 2009; Oleson and Found 1946; Asaduzzaman and Mamun 2012a; Alinejad 2011b; Masud et al. 2012) regarding double temperature plasma, are limited to a planar (one-dimensional) geometry which may not be a realistic situation in space and laboratory devices, since the waves observed in space (laboratory devices) are certainly not infinite (unbounded) in one dimension. Therefore further investigation would necessary to delimit the study in such a planar geometry. We focus on cylindrical and spherical DIA SWs in an unmagnetized two-electron temperature dusty plasma, and show how the DIA SWs in cylindrical and spherical geometries differ qualitatively from that in one-dimensional planar geometry. It is important to mention that we have taken higher order nonlinear equation which is quite valid around critical value of dust density ratio of typical dusty plasma parameters, since at critical value the K-dV soliton can not be formed due to infinite large amplitude solitary structures. To overcome this we have followed a higher order nonlinear equation (known as modified Gardner (mG) equation (Asaduzzaman and Mamun 2012b; Mannan and Mamun 2011; Hossain et al. 2011)) which describes the nonlinear features of the finite amplitude cylindrical and spherical DIA SWs in a two-electron temperature dusty plasma.

The manuscript is organized as follows. The governing equations are provided in Sect. 2. The mG equation is derived by using the reductive perturbation method in Sect. 3. The analytical and numerical solutions are presented in Sect. 4. A brief discussion is finally given in Sect. 5.

2 Governing equations

We consider a nonplanar geometry, and nonlinear propagation of the DIA waves in an unmagnetized dusty plasma system consisting of negatively charged stationary dust, inertial ions and Boltzmann distributed two populations of electrons having different thermal effects. Thus, at equilibrium we have n io =n e10+n e20+Z d n d0, where n e10 (n e20) is the density of unperturbed lower (higher) temperature electron. The nonlinear dynamics of the DIA (Rahman and Mamun 2011; Mamun 2007; Mamun et al. 2009; Alinejad 2011a) waves, whose phase speed is much smaller than electron thermal speed but larger than ion thermal speed in a nonplanar geometry, is governed by

(1)
(2)
(3)
(4)

where ν=0 for 1D planar geometry, and ν=1 (2) for a nonplanar cylindrical (spherical) geometry, n i is the ion particle number density normalized by its equilibrium value n i0, u i is the ion fluid speed normalized by C i =(k B T e1/m i )1/2, ϕ is the electrostatic wave potential normalized by k B T e1/e, ρ is the normalized surface charge density, σ=T e1/T e2, μ e1=n e10/n i0, μ e2=n e20/n i0, μ = Z d n d0/n i0=1−μ e1−μ e2. It should be noted that T e1(T e2) is the lower (higher) electron temperature, T i is the ion temperature, k B is the Boltzmann constant, and e is the magnitude of the electron charge. The time variable t is normalized by \(\omega_{pi}^{-1}=(m_{i}/4\pi n_{i0}e^{2})^{1/2}\) and the space variable is normalized by λ Dm =(k B T e1/4πn i0 e 2)1/2.

3 Derivation of mG equation

To study the finite amplitude DIA Gardner solitons (GSs) by analyzing the ingoing solutions of Eqs. (1)–(4), we first introduce the stretched coordinates:

(5)
(6)

where 0<ϵ<1 (ϵ measures the weakness of the dispersion), and V p is the phase speed (ω/k) of the perturbation mode. The variables n i , u i , ϕ, and ρ can be expanded in power series of ϵ, viz.

(7)
(8)
(9)
(10)

Now, expressing Eqs. (1)–(4) in terms of ζ and τ, and substituting Eqs. (7)–(10) into the resulting equations [Eqs. (1)–(4) expressed in terms of ζ and τ], one can easily develop different sets of equations in various powers of ϵ. To the lowest order in ϵ one obtains

(11)
(12)
(13)

where ψ=ϕ (1). Equation (13) represents the dispersion properties of the DIA waves propagating in a dusty plasma under consideration where two populations of electrons significantly modify the basic features of the phase speed of the DIA wave. To the next higher order in ϵ, we obtain a set of equations, which, after using Eqs. (11)–(13), can be simplified as

(14)
(15)
(16)
(17)

We note that Eqs. (16) and (17) are obtained from Eqs. (3) and (4) by taking the co-efficients of ϵ 2. Here ρ (2)=0 does not mean that the usual net surface charge density is zero. It is obvious from Eqs. (16) and (17) that A=0 since ψ≠0. We can find A=0 for a certain (critical) value of μ e1, i.e. A=0 for μ e1=μ c ≃0.319 (which is a solution of A=0) since 0<μ e1<1 is always valid. We let A=A 0 when μ e1≠μ c , but μ e1∼μ c . So, for μ e1 around its critical value (μ c ), A=A 0 can be expressed as

$$ A_0\simeq s \biggl(\frac{\partial A}{\partial \mu_{e1}} \biggr)_{\mu_{e1} =\mu_c}| \mu_{e1}-\mu_c|=c_1s\epsilon, $$
(18)

where c 1≃0.962, |μ e1−μ c | is a small and dimensionless parameter, and can be taken as the expansion parameter ϵ, i.e. |μ e1−μ c |≃ϵ, and s=1 for μ e1>μ c and s=−1 for μ e1<μ c . So, ρ (2) can be expressed as

$$ \epsilon^2\rho^{(2)}\simeq -\epsilon^3 \frac{1}{2}c_1s\psi^2, $$
(19)

which, therefore, must be included in the third order Poisson’s equation. To the next higher order in ϵ, we obtain a set of equations:

(20)
(21)
(22)
(23)

Now, using Eqs. (13)–(17) and Eqs. (20)–(23), we obtain a equation of the form:

$$ \frac{\partial\psi}{\partial \tau}+\frac{\nu}{2\tau}\psi+c_1s\beta\psi \frac{\partial \psi}{\partial \zeta} +\alpha\beta\psi^2\frac{\partial \psi}{\partial \zeta} + \beta \frac{\partial^3 \psi}{\partial \zeta^3} = 0, $$
(24)

where

(25)
(26)

Equation (24) is known as modified Gardner (mG) equation. The modification is due the extra term (viz. \(\frac{\nu}{2\tau}\psi\)), which arises due to the effects of the nonplanar geometry. It is important to note that if we neglect ψ 3 term, and put \(c_{1}s=A=3/V_{p}^{4}-\mu_{e1}-\mu_{e2}\sigma^{2}\), the mG equation reduces to a lower order modified K-dV (mK-dV)equation which can be derived by using a lower order stretching viz. ζ=ϵ 1/2(r−V p t),τ=ϵ 3/2 t. However, in this mK-dV equation, the nonlinear term vanishes at μ e1=μ c , and is not valid near μ e1=μ c which makes soliton amplitude large enough to break down the validity of the reductive perturbation method. But the mG equation derived here is valid for nonplanar geometry as well as for μ e1 near its critical value (μ c ).

4 SW solution of MG equation

We have already mentioned that ν=0 corresponds to a 1D planar geometry which reduces Eq. (24) to a standard Gardner equation. Before going to numerical solutions of mG equation, we will first analyze stationary GSs solution of Gardner equation (24) [with ν=0]. To do so, we first introduce a transformation ξ=ζ−U 0 τ which allows us to write Eq. (24), under the steady state condition, as

$$ \frac{1}{2} \biggl(\frac{d\psi}{d\xi} \biggr)^2+V(\psi)=0, $$
(27)

where the pseudo-potential V(ψ) is

$$ V(\psi)=-\frac{U_0}{2\beta}\psi^2+\frac{c_1s}{6} \psi^3+\frac{\alpha}{12}\psi^4+\cdots. $$
(28)

It would be mentioned here that U 0 and β are always positive. Further numerical simulation gives opportunity to anyone to express the shock speed (in the reference frame) in terms of β, α, and the wave amplitude, as

$$ U_{0}=\frac{c_1s\beta}{3}\psi_{m1,2}+\frac{\alpha\beta}{6} \psi_{m1,2}^2, $$
(29)

where ψ m1,2 is the amplitude of the SWs, and the value of ψ m1,2 can be found in some other contexts (Asaduzzaman and Mamun 2012b; Mannan and Mamun 2011; Hossain et al. 2011). The solitary wave solution or solitary profile of the quadrature Eq. (27), often called as an “energy integral” of an oscillating particle of unit mass, with pseudo-position ψ, pseudo-time ξ, and pseudo-speed dψ/dξ, and pseudo-potential V(ψ), and the width (δ) of such DIA SWs can be represented as

(30)
(31)

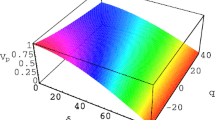
We note that Eq. (30) represents a SW solution of Eq. (27). It is clear from Eqs. (17) and (18) that the solitary potential profile is negative (positive) if A<0 (A>0). Therefore, A(μ e1=μ c )=0, where μ c is the critical value of μ e1 above (below) which the solitary waves with a positive (negative) potential exists, gives the value of μ c . To find the parametric regimes for which the positive and negative solitary potential profiles exist, we have numerically analyzed A, and obtain A(μ e1=μ c )=0 surface plots. The A(μ e1=μ c )=0 surface plots are shown in Fig. 1. From Fig. 1 it is obvious that if we increase (decrease) the relative concentration of electron (at higher temperature)-to-ion number density then the critical value of other parameters (viz. μ e1=μ c ) decreases (increases). Therefore, for typical dusty plasma parameters (Ghosh et al. 2008; Shalaby et al. 2009; Moslem et al. 2005; Moslem and El-Taibany 2005; Chatterjee and Roychoudhury 1997), σ=0.01–0.9 and μ e2=0.01–0.3, we have the existence of the small amplitude solitary waves with a positive potential for μ e1>μ c , and with a negative potential for μ e1<μ c . Moreover, a small percentage of cold electron concentration may predominate the DIA speed, especially if the difference between the two electron temperatures increases, then the critical value of such a parameter μ c is also increased. It is clear from the amplitude of the K-dV SWs (Rahman and Mamun 2011; Mamun et al. 2009; Alinejad 2010, 2011b) (ψ m =3U 0/A) that ψ m =∞ at μ e1=μ c . This means that the small amplitude solitary waves with a negative (positive) potential exist for a set of dusty plasma parameters corresponding to any point which is much below (above) the A(μ e1=μ c )=0 surfaces shown in the surface plots in Fig. 1.

Fig. 1
figure 1

Showing how μ c [obtained from A(μ e1=μ c )=0] varies with σ

Full size image

We now turn to Eq. (24) with the term (ν/2τ)ψ, which is due to the effects of the non-planar (cylindrical or spherical) geometry. An exact analytic solution of Eq. (24) is not possible. Therefore, we have numerically solved Eq. (24), and have studied the effects of cylindrical and spherical geometries on time-dependent DIA GSs, as well as to consider the effects of two-electron temperature. The results are depicted in Figs. 2–6. The initial condition, that we have used in our numerical analysis, is in the form of the stationary solution of Eq. (24) without the term (ν/2τ)ψ. The effect of two populations of electrons having different thermal temperatures is shown in Fig. 6, retaining the initial condition of the stationary solution ν=0. It has been observed that the increase of the number density of lower temperature electron can play a significant role on the amplitude of the propagating DIA SWs. This means that amplitude of such SWs is increased due to the increase of the relative number density of lower-to-higher temperature electron. Figures 2 and 3 show how the effects of a cylindrical geometry modify the DIA negative and positive GSs and Figs. 4 and 5 show how the effects of a spherical geometry modify the DIA negative and positive GSs. We have also observed (not shown in figure) that the amplitude (i.e. magnitude of the amplitude) of both the positive and negative GSs increases with the increase of μ e1 but the width of both the positive and negative GSs decreases by taking into account the effects of nonplanar cylindrical (ν=1) and spherical (ν=2) geometries.

Fig. 2
figure 2

Showing the effects of cylindrical (ν=1) geometry on DIA negative GSs for μ e1=0.318, μ e2=0.04, σ=0.2, and U 0=0.03

Full size image
Fig. 3
figure 3

Showing the effects of cylindrical (ν=1) geometry on DIA positive GSs for μ e1=0.32, μ e2=0.04, σ=0.2, and U 0=0.03

Full size image
Fig. 4
figure 4

Showing the effects of spherical (ν=2) geometry on DIA negative GSs for μ e1=0.318, μ e2=0.04, σ=0.2, and U 0=0.03

Full size image
Fig. 5
figure 5

Showing the effects of spherical (ν=2) geometry on DIA positive GSs for μ e1=0.32, μ e2=0.04, σ=0.2, and U 0=0.03

Full size image
Fig. 6
figure 6

Showing the effects of electron temperature on DIA negative GSs for σ=0.2 (upper plot), σ=0.6 (middle plot), and σ=0.9 (lower plot)

Full size image

5 Discussions

We have considered a nonplanar geometry, and have studied the nonlinear propagation of the DIA waves in an unmagnetized dusty plasma containing negatively charged stationary dust, inertial ions, and Boltzmann distributed electrons of two distinctive temperatures. We have derived the mG equation by using the reductive perturbation method, and numerically analyzed that mG equation. The results which have been found from this investigation can be pinpointed as follows:

  1. 1.

    The dusty plasma system under consideration supports finite amplitude GSs, whose basic features (polarity, amplitude, width, etc.) strongly depend on different plasma parameters, particularly, T e1, T e2, and n e1, n e2.

  2. 2.

    The positive (negative) GSs exist when μ e1>(<)0.319, μ e2=0.04, σ=0.2.

  3. 3.

    The amplitude of the positive and negative GSs increases with the increase of μ e1 as well as with σ. The latter is more essential since one can get the higher amplitude of DIA SWs dominated by the increase of two-electron temperatures effect.

  4. 4.

    The width of positive and negative GSs decreases with the increase of μ e1.

  5. 5.

    The numerical solutions of (24) [displayed in Figs. 2–5] reveal that for a large value of τ (e.g. τ=−30), the spherical and cylindrical solitary waves are similar to 1D structures. This is because of a large value of τ the term (ν/2τ)ψ, which is due to the effects of the cylindrical or spherical geometry, is no longer dominant. However, as the value of τ decreases, the term (ν/2τ)ψ becomes dominant, and spherical and cylindrical solitary wave structures differ from 1D ones. It is to be pointed out that the amplitude observed in cylindrical (ν=1) geometry is half of the amplitude that is observed in spherical geometry (ν=2). It is found that as the value of τ decreases, the amplitude of these localized pulses increases. It is also found that the amplitude of cylindrical DIA SWs is larger than those of 1D ones, but smaller than that of the spherical ones.

It is important to note here that the mG equation is valid for μ e1∼0.319, and are found to be different from K-dV solitons, which are not valid for μ e1=0.319 and μ e1∼0.319 i.e. it vanishes the nonlinear coefficients (A) of that (K-dV) equation.

The ranges (σ=0.01–0.9 and μ e2=0.01–0.3) of the dusty plasma parameters used in our numerical analysis are very wide. It may be stressed here that the results of this investigation could be useful for understanding the nonlinear features of electrostatic disturbances in laboratory (Oleson and Found 1946) and space plasmas (Geiss et al. 1978; Dubouloz et al. 1993), particularly in noctilucent cloud region in Earth’s atmosphere (Shah et al. 2009), at the edges of the AKR (Auroral Kilometric Radiation) source region (Ergun et al. 1998), Saturn’s E-ring, double-plasma machines (Spileman et al. 1976), hot turbulent thermonuclear (Estabrook and Krueer 1978) plasma, rf discharge plasma (Nishida and Nagasawa 1986), etc. where electrons of different kinds involving thermal effects are the major plasma species. Our present investigation comprising with DIA GSs in nonplanar dusty plasma system is limited to small but finite amplitude SWs. It may also be stressed here that the analysis of small or large amplitude double layers, vortices, shocks, etc. would be essential to describe the localized nonlinear perturbations of such laboratory (Oleson and Found 1946; Spileman et al. 1976; Nishida and Nagasawa 1986) and space plasma (Geiss et al. 1978; Dubouloz et al. 1993; Shah et al. 2009; Alinejad 2011b; Ergun et al. 1998) but beyond the scope of our present investigation. To conclude, we propose to perform a new experiment to test the theory that we have presented in this work.