1 Introduction

The concept of intuitionistic fuzzy sets(IFSs), a generalization of the concept of fuzzy sets, was first introduced by [1]. In IFSs, the relationship between an element and a set is described by two numbers, i.e., the membership degree and the non-membership degree of the element to the set, respectively. Thereafter, [2] proposed the notion of interval-valued intuitionistic fuzzy sets (IVIFSs) as an extension of IFSs. In IVIFSs, the membership degree and the non-membership degree of an element to a set are given as interval numbers.

For more than twenty years, the IVIFSs have been studied from multiple perspectives, such as entropy theory, distance theory, score functions, and accuracy functions. For more details on this issue please see [6, 14, 15, 18], etc. Multiple criteria decision making (MCDM) is one of the processes for selecting the optimal alternative from all the feasible alternatives according to some criteria or attributes. When the theories of IFSs or IVIFSs are applied to MCDM, the most important topic worthy of attention is how to compare and rank the IFSs or IVIFSs. Many scholars have paid great attention to this issue. [4] suggested a score function of vague values. Later, [8] defined an accuracy function of vague values. Similar to the aforementioned studies, [19] introduced a score function and an accuracy function on IFSs. Furthermore, by using both of them, they recommended a well-known order relation to rank intuitionistic fuzzy numbers (IFNs), and offered a series of measures to indicate the similarity degree between IFNs. Besides, the properties of IFNs are also studied broadly from geometric perspective. For example, [22] proposed a hybrid arithmetic to rank IFNs. It is noteworthy that this order relation is very prospective and outstanding. However, the importance of the score values of IFNs is much more prominent than the accuracy values in this order relation, which leads to relatively strict conditions of application. In the past ten years, some new score functions and accuracy functions have been propounded to rank the IFNs or the interval-valued intuitionistic fuzzy numbers (IVIFNs), where the proposed score functions and accuracy functions are not combined any more, they work alone. For more details on this issue please see [12, 16, 17, 20, 26]. Later, [24] and [23] indicated that there are some difficulties in the proposed score functions or accuracy functions for ranking the IFNs or IVIFNs. Much more recently, [9] provided some optimum techniques to balance between group consensus and individual independence. [7] first developed an intuitionistic fuzzy Bayesian network to obtain the practical attribute weights under uncertain environment in information fusion and dynamic decision making process. The aforementioned studies have enriched the research system on IFSs, which laid a solid foundation for this study.

In general, the essence of generalized score value on an IFS is the “quality” of the membership degree of an element to the given set. From the viewpoint of utility, two factors need to be considered on the comparison between the “qualities” of different membership degrees on IFNs or IVIFNs. One factor is the classical score values, and the other one is the classical accuracy values. The bigger the classical score value of an IVIFN (IFN) is, the greater its utility; the bigger the classical accuracy value of an IVIFN (IFN) is, the greater its utility. Therefore, the coordination of the two factors is worthy of consideration. From the standpoint of probability theory, there are infinite possibilities to combine the classical score value and accuracy value of an IVIFN (IFN). All the existing score functions or accuracy functions are the moment estimation functions of the relationship between the two factors. Therefore, they can only be used in certain environments.

Hong and Choi [8] once indicated that “the relation between the classical score and accuracy functions on IFSs (the original text is ‘vague sets’, which is interlinked with IFSs in essence) is similar to the relation between mean and variance in statistics”. However, the functions, proposed to rank the IVIFSs respectively, are called accuracy function or score function optionally. For uniformity in this study, the functions used to rank IVIFSs solely are termed as “generalized score function”. Meanwhile, [3] proposed a model which demonstrates the influence driven evolution of experts’ opinions and its convergence properties. Referring to the decision making thoughts proposed by [8] and [3], the comparison between IVIFNs is conducted based on the attitudinal characters of decision-makers in this study. Furthermore, to reduce the risk of errors in the comparing process on IVIFNs (IFNs), this study uses the integral theory to aggregate the infinite possibilities combining the classical score and accuracy values of an IVIFN (IFN).

The rest of this paper is organized as follows. In Section 2, the definitions of IFSs and IVIFSs, as well as the concepts of the classical score function and accuracy function of IFSs and IVIFSs are introduced. In Section 3, two kinds of principles are suggested to guide the ranking of IVIFNs; then, according to the newly proposed principles, two novel generalized score functions on IVIFSs are proposed; subsequently, two kinds of generalized score functions on IVIFSs are proposed based on preference information of decision-makers; thereafter, two kinds of generalized score functions on IVIFSs are proposed based on integral. In Section 4, three kinds of MCDM methods in intuitionistic fuzzy setting are offered. Section 5 provides an example to demonstrate the effectiveness of the proposed methods. Section 6 ends this study with some important conclusions.

2 Preliminaries

In this section, the concepts of IFSs and IVIFSs, the classical score and accuracy functions are reviewed. Primarily, the concepts of IFSs and IVIFSs are introduced as follows.

Definition 1

[1]. Let X be a non-empty set. An IFS A in X is denoted as \(A=\{\langle x, \mu _{A}(x),\nu _{A}(x) \rangle \mid x \in X \}\), where \( \mu _{A}(x): X\rightarrow [0,1], \nu _{A}(x): X\rightarrow [0,1]\) with the condition \(0\leq \mu _{A}(x) + \nu _{A}(x) \leq 1\) for any \(x \in X\). Here, \( \mu _{A}(x)\) and \( \nu _{A}(x)\) denote the membership degree and the non-membership degree of x to A, respectively. For any \(x\in X\), the hesitancy degree of x to A is denoted as πA(x) = 1 − μA(x) − νA(x); the complementary set of A is defined as \( A^{c}=\{ \langle x, \mu _{A}(x),\nu _{A}(x) \rangle \mid x \in X \}\).

For convenience, [16] denoted the intuitionistic fuzzy numbers (IFNs) as \(A = \langle \mu ,\nu \rangle \).

Definition 2

[2]. Let \(D[0,1] \) be the set of all closed sub-intervals of the interval \([ 0,1 ]\) and \(X(\neq {\Phi })\) be a given set. An IVIFS A in the universe of discourse X is defined as \( A=\left \lbrace \left \langle x,\mu _{A}(x),\nu _{A}(x) \right \rangle \mid x \in X \right \rbrace \), where \( \mu _{A}(x): X\rightarrow D[0,1], \nu _{A}(x): X\rightarrow D[0,1]\) with the condition \(0\leq sup(\mu _{A}(x)) + sup(\nu _{A}(x)) \leq 1\) for any \(x \in X\). The intervals \(\mu _{A}(x)\) and νA(x) represent the membership degree and non-membership degree of the element x to the set A, respectively. Denote the lower and upper end points as \(\mu _{AL}(x), \mu _{AU}(x), \nu _{AL}(x)\), and \(\nu _{AU}(x)\), respectively, i.e.,

$$ A=\left\lbrace \left\langle x,[\mu_{AL}(x),\mu_{AU}(x)],[\nu_{AL}(x),\nu_{AU}(x)]\right\rangle \mid x \in X\right\rbrace, $$
(1)

where \(0\leq \mu _{AU}(x) + \nu _{AU}(x) \leq 1, 0\leq \mu _{AL}(x) \) and \( 0\leq \nu _{AL}(x) \).

For any \(x\in X\), the interval intuitionistic index of x to A is denoted as

$$\begin{array}{@{}rcl@{}} \pi_{A}(x) &=& [\pi_{AL}(x),\pi_{AU}(x)]= [1-\mu_{AU}(x)\\ &&-\nu_{AU}(x),1-\mu_{AL}(x)-\nu_{AL}(x)]. \end{array} $$
(2)

The complementary set \(A^{c}\) of an IVIFS A is defined as

$$ A^{c}=\left\lbrace \left\langle x,[\nu_{AL}(x),\nu_{AU}(x)],[\mu_{AL}(x),\mu_{AU}(x)]\right\rangle \mid x \in X \right\rbrace. $$
(3)

Xu and Yager [19] called the pair \((\mu _{A}(x), \nu _{A}(x))\) as an IVIFN, and simplified it as \(\widetilde \alpha =([a,b],[c,d]), \)where \([a,b]\subset [0,1],[c,d]\subset [0,1],b+d\leq 1\). Thereafter, [19] proposed the classical score and accuracy functions on IFNs as follows.

Definition 3

[19] Let \(\alpha =(\mu ,\nu )\) be an IFN, then the classical score function on \(\alpha \) is defined as \(S(\alpha )=\mu -\nu \).

Definition 4

[19] Let \(\alpha =(\mu ,\nu )\) be an IFN, then the classical accuracy function on \(\alpha \) is defined as \(H(\alpha )=\mu +\nu \).

By using the classical score and accuracy functions, [16] proposed a well-known approach to rank IFNs as follows.

Definition 5

[16] Let \(\alpha _{i}=(\mu _{i},\nu _{i})(i = 1,2)\) be two IFNs, and let \(S(\alpha _{i})\) and \(H(\alpha _{i})\) be the score values and the accuracy values of \(\alpha _{i}(i = 1,2)\), respectively. Then the following conditions hold:

  1. (i)

    \(if S(\alpha _{1})>S(\alpha _{2}), then \alpha _{1}\succ \alpha _{2}\);

  2. (ii)

    \(if S(\alpha _{1})=S(\alpha _{2}), then\),

    1. (1)

      \(if H(\alpha _{1})>H(\alpha _{2}), then \alpha _{1}\succ \alpha _{2}\);

    2. (2)

      \(if H(\alpha _{1})=H(\alpha _{2}), then \alpha _{1} = \alpha _{2}\);

    3. (3)

      \(if H(\alpha _{1})<H(\alpha _{2}), then \alpha _{1}\prec \alpha _{2}\).

The most significant contributions of Definition 5 is that it gives a procedure to compare different IFNs. Furthermore, the following conclusions are obtained under interval-valued intuitionistic fuzzy environments.

Definition 6

[17] Let \( \widetilde \alpha =([a,b],[c,d]) \) be an IVIFN, then the score function of \(\widetilde \alpha \) is defined as \( S_{xu}(\widetilde \alpha )= \frac {1}{2}(a+b-c-d)\), and the accuracy function of \(\widetilde \alpha \) is defined as \(H_{xu}(\widetilde \alpha )= \frac {1}{2}(a+b+c+d)\).

3 Main results

3.1 Problem analysis

In this subsection, the IVIFNs are studied through data analysis. Take an IVIFN \( \widetilde \alpha =([a,b],[c,d]) \) for example, at present, there are many kinds of generalized score functions or accuracy functions on \( \widetilde \alpha \). For example, [12, 16, 17, 20] and [26] proposed some kinds of them. Since the differences between different IVIFNs mainly depend on two parameters. One parameter is \(S_{xu}(\widetilde \alpha )\), which represents the closeness between the IVIFN \( \widetilde \alpha \) and the fuzzy concept “excellence”; the other parameter is \(H_{xu}(\widetilde \alpha )\), which represents the credibility of the IVIFN \( \widetilde \alpha \). It is difficult to find a sole function to rank all the IVIFNs without self-contradictory in some cases. For example, when comparing two IVIFNs \( \widetilde \alpha _{1} =([a_{1},b_{1}],[c_{1},d_{1}]) \) and \(\alpha _{2} =([a_{2},b_{2}],[c_{2},d_{2}])\), we should compare not only the difference between \(S_{xu}(\widetilde \alpha _{1})\) and \(S_{xu}(\widetilde \alpha _{2})\), but also the difference between \(H_{xu}(\widetilde \alpha _{1})\) and \(H_{xu}(\widetilde \alpha _{2})\). In the comparing process, how important is \(S_{xu}(\cdot )\), and how important is Hx u(⋅)? Is \(S_{xu}(\cdot )\) more or less important than \(H_{xu}(\cdot )\)? Practically, the importance degrees of \(S_{xu}(\cdot )\) and \(H_{xu}(\cdot )\) are relative rather than absolute. Different decision-makers have different viewpoints on them, and any certain viewpoint on them is only suitable for comparing the IVIFNs in certain decision making circumstances. Therefore, when a novel generalized score or accuracy function on IVIFSs is proposed, its application scope should also be pointed out.

Frequently, fuzziness problems lack the illustrating information that leads us to suitable generalized score functions or accuracy functions. Therefore, it is of great interest to propose the fundamental principles to evaluate the effectiveness of these generalized score or accuracy functions. In the following subsection, some principles are introduced on the basis of practice. Furthermore, under the guidance of these fundamental principles, two kinds of illustrative generalized score functions on IVIFSs are proposed.

3.2 Applicable conditions of generalized score functions on IVIFSs

In this subsection, the applicable conditions of generalized score functions on IVIFSs are proposed through two theorems. Thereafter, two specific generalized score functions on IVIFS which satisfy the aforementioned two theorems are introduced.

Theorem 1

Let \(\widetilde \alpha _{i}=([a_{i},b_{i}],[c_{i},d_{i}])(i = 1,2)\) be two IVIFNs, and let \(\widetilde S (\cdot )\) be the generalized score function which is proposed to rank IVIFNs by itself. Then \(\widetilde S (\cdot )\) should satisfy the following properties:

  1. (i)

    \(if (a_{1}-d_{1})-(b_{2}-c_{2})>0, (a_{1}+c_{1})-(b_{2}+d_{2}) > 0\) , then, \(\widetilde S(\widetilde \alpha _{1})>\widetilde S(\widetilde \alpha _{2})\) ;

  2. (ii)

    \(if (b_{1}-c_{1})-(a_{2}-d_{2})<0, (b_{1}+d_{1})-(a_{2}+c_{2}) < 0\) , then, \(\widetilde S(\widetilde \alpha _{1})<\widetilde S(\widetilde \alpha _{2})\) ;

  3. (iii)

    \(if \widetilde S(\widetilde \alpha _{1})>\widetilde S(\widetilde \alpha _{2})\) , then, \(\widetilde S(\widetilde {\alpha _{1}^{c}})<\widetilde S(\widetilde {\alpha _{2}^{c}})\) ;

  4. (iv)

    \(\widetilde S(\widetilde \alpha _{i})\in [0,1]\) , for any \(i = 1,2\) ;

  5. (v)

    \(\widetilde S\left (([0,0],[1,1])\right ) = 0, \widetilde S\left (([1,1],[0,0])\right ) = 1\) .

Analogously, for \(i = 1,2\) , when \(a_{i}=b_{i}\) , and \(c_{i}=d_{i}\) , we have the following theorem.

Theorem 2

Let \( \alpha _{i}=(\mu _{i},\nu _{i})(i = 1,2)\) be two IFNs, and let \(S (\cdot )\) be the generalized score function which is proposed to rank IFNs by itself. Then S(⋅) should satisfy the following properties:

  1. (i)

    \(if (\mu _{1}-\nu _{1})-(\mu _{2}-\nu _{2})>0, (\mu _{1}+\nu _{1})-(\mu _{2}+\nu _{2}) > 0\) , then, \(S(\alpha _{1})>S(\alpha _{2})\) ;

  2. (ii)

    if \((\mu _{1}-\nu _{1})-(\mu _{2}-\nu _{2})<0, (\mu _{1}+\nu _{1})-(\mu _{2}+\nu _{2}) < 0\) , then, \(S(\alpha _{1})<S(\alpha _{2})\) ;

  3. (iii)

    if \(S(\alpha _{1})>S(\alpha _{2})\) , then, \(S({\alpha _{1}^{c}})<S({\alpha _{2}^{c}})\) .

  4. (iv)

    \(S(\alpha _{i})\in [0,1]\) , for any \(i = 1,2\) ;

  5. (v)

    \(S\left ((0,1)\right ) = 0, S\left ((1,0)\right )= 1\) .

It is noteworthy that Theorem 1 and 2 are consistent with Definition 5. However, Definition 5 is a kind of method to compare IVIFSs. Different from Definition 5, Theorem 1 and 2 are mainly used to evaluate the generalized score functions which rely on one parameter. Meanwhile, Theorem 1 and 2 can not be used to compare IVIFSs directly in many cases, since they only work under very specific conditions. For example, when comparing two IVIFNs \(\widetilde \alpha _{1}\) and \(\widetilde \alpha _{2}\) by any generalized score function, the condition (i) in Thm. 1 means that if the classical score value of \(\widetilde \alpha _{1}\) is larger than that of \(\widetilde \alpha _{2}\), and the classical accuracy value of \(\widetilde \alpha _{1}\) is larger than that of \(\widetilde \alpha _{2}\) hold at the same time, \(\widetilde S(\widetilde \alpha _{1})\) should be prior to \(\widetilde S(\widetilde \alpha _{2})\).

To illustrate Theorem 1 and 2 more clearly, two kinds of illustrative novel generalized score functions are introduced as follows.

Definition 7

Let \(\tilde \alpha =([a,b],[c,d])\) be an IVIFN. Then, two generalized score functions \(F_{1}(\cdot )\) and \(F_{2}(\cdot )\) on IVIFNs are proposed as

$$\begin{array}{@{}rcl@{}} F_{1}(\tilde\alpha)\!&=&\!\frac{1}{2}\left[ s(\tilde\alpha)\cdot\sqrt{abs\left( \frac{(a\,-\,c)\,+\,(b\,-\,d)}{2}\right)\cdot \frac{(a\,+\,c)\,+\,(b\,+\,d)}{2}}\,+\,1\right],\\ \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} F_{2}(\tilde\alpha)\!&=&\!\frac{1}{2}\left\lbrace \frac{s(\tilde\alpha)}{2} \cdot\left[ abs\left( \frac{(a\,-\,c)\,+\,(b\,-\,d)}{2}\right) \,+\, \frac{(a\,+\,c)\,+\,(b\,+\,d)}{2}\right] \,+\,1\right\rbrace,\\ \end{array} $$
(5)

where \(s(\tilde \alpha )=sgn \left [\frac {(a-c)+(b-d)}{2}\right ]\); \(sgn(\cdot )\) represents the sign function; \(abs(\cdot )\) represents the absolute value function. Obviously, 0 ≤ F1(⋅),F2(⋅) ≤ 1.

Obviously, \(F_{1} (\cdot )\) and \(F_{2} (\cdot )\) satisfy the five properties of Theorem 1 or Theorem 2. Besides, though \(F_{1} (\cdot )\) and \(F_{2} (\cdot )\) consider the classical score and accuracy values of IVIFSs without distinction, the score values of \(F_{1} (\cdot )\) and \(F_{2} (\cdot )\) on the same given IVIFN are usually different. To illustrate the effectiveness of the score functions \(F_{1} (\cdot )\) and \(F_{2} (\cdot )\), an example is introduced.

Case 1

Assume that there are two IVIFNs, where

$$\begin{array}{@{}rcl@{}} \widetilde \alpha_{1}=([a_{1},b_{1}],[c_{1},d_{1}])=([0.65,0.75],[0.15,0.20]),\\ \widetilde \alpha_{2}=([a_{2},b_{2}],[c_{2},d_{2}])=([0.45,0.50],[0.10,0.15]), \end{array} $$

please compare them.

On one hand, by calculation, it is obtained that

$$\begin{array}{@{}rcl@{}} (a_{1}-d_{1})-(b_{2}-c_{2})= 0.45-0.40 = 0.05>0,\\ (a_{1}+c_{1})-(b_{2}+d_{2})= 0.80-0.60 = 0.20>0. \end{array} $$

Therefore, according to the property \(({\romannumeral 1})\) in Theorem 1, their ranking is as \(\widetilde \alpha _{1}\succ \widetilde \alpha _{1}\).

On the other hand, by using (4), it is obtained that \(F_{1}(\tilde \alpha _{1})= 0.839, F_{1}(\tilde \alpha _{2})= 0.729\). Similarly, by using (5), it is obtained that \(F_{2}(\tilde \alpha _{1})= 0.850, F_{2} (\tilde \alpha _{2})= 0.738\). Therefore, it holds that \(F_{1}(\alpha _{1})>F_{1}(\alpha _{2}), F_{2}(\alpha _{1})>F_{2}(\alpha _{2})\). As a result, it is concluded that \(\widetilde \alpha _{1}\succ \widetilde \alpha _{2}\), which satisfies the property \((\lowercase \expandafter {\romannumeral 1})\) of Theorem 1. Meanwhile, by using (4), it is obtained that \(F_{1}({\tilde \alpha _{1}^{c}})= 0.161, F_{1}({\tilde \alpha _{2}^{c}})= 0.271\). Similarly, by using (5), it is obtained that \(F_{2}({\tilde \alpha _{1}^{c}})= 0.150, F_{2}({\tilde \alpha _{2}^{c}})= 0.263\). Therefore, it holds that \(F_{1}({\alpha _{2}^{c}})>F_{1}({\alpha _{1}^{c}})\). As a result, it is concluded that \(\widetilde {\alpha _{2}^{c}}\succ \widetilde {\alpha _{1}^{c}}\), which satisfies the property \((\lowercase \expandafter {\romannumeral 3})\) of Theorem 1.

3.3 Two kinds of generalized score functions on IVIFSs based on preference information of decision-makers

Similar to \(F_{1}(\cdot )\) and \(F_{2}(\cdot )\), there are many generalized score functions which were proposed to compare IVIFSs. Since the differences between different IVIFNs mainly depend on two parameters, the classical score value, and the classical accuracy value, it is considered that any given generalized score function on IVIFSs reflects a certain relationship between the classical score function and the classical accuracy function. Therefore, in order to serve different types of decision makers targetedly, two kinds of generalized score functions on IVIFSs are suggested based on preference information of decision-makers. The first kind of generalized score function on IVIFSs is based on geometric weighted operators; while the second one is based on arithmetic weighted operator. Besides, these two kinds of generalized score functions are of two parameters. More details are as follows.

Definition 8

Let \(\tilde \alpha =([a,b],[c,d])\) be an IVIFN. A novel generalized weighted geometric average score function \(F_{3}(\cdot )\) on IVIFNs is defined as

$$\begin{array}{@{}rcl@{}} F_{3}(\tilde\alpha)=\frac{1}{2}\left\lbrace s(\tilde\alpha)\cdot\left[ abs\left( \frac{(a-c)+(b-d)}{2}\right)\right]^{t}\right.\\ \cdot \left. \left[ \frac{(a+c)+(b+d)}{2}\right]^{1-t} + 1\right\rbrace, \end{array} $$
(6)

where \(s(\tilde \alpha )=sgn \left [\frac {(a-c)+(b-d)}{2}\right ], t\in [0,1]\).

Meanwhile, a novel generalized weighted arithmetic average score function with parameters is proposed as follows.

Definition 9

Let \(\tilde \alpha =([a,b],[c,d])\) be an IVIFN, a novel generalized weighted arithmetic average score function \(F_{4}(\cdot )\) on IVIFNs is defined as

$$\begin{array}{@{}rcl@{}} F_{4}(\tilde\alpha)&=&\frac{1}{2}\left\lbrace s(\tilde\alpha)\cdot\left[ t* abs\left( \frac{(a-c)+(b-d)}{2}\right)\right.\right.\\ && \qquad + \left.\left. (1-t)* \frac{(a+c)+(b+d)}{2}\right] + 1\right\rbrace, \end{array} $$
(7)

where \(s(\tilde \alpha )=sgn \left [\frac {(a-c)+(b-d)}{2}\right ], t\in [0,1]\).

To illustrate the effectiveness of the generalized score functions \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\), an example is introduced.

Case 2

Assume that there are two IVIFNs, where

$$\begin{array}{@{}rcl@{}} \widetilde \alpha_{3}=([a_{3},b_{3}],[c_{3},d_{3}])=([0.15,0.20],[0.05,0.15]),\\ \widetilde \alpha_{4}=([a_{4},b_{4}],[c_{4},d_{4}])=([0.40,0.45],[0.35,0.40]), \end{array} $$

please compare them.

By (6), they get that \(F_{3}(\tilde \alpha _{3})= 0.5*(0.075^{t}*0.275^{1-t}+ 1), F_{3}(\tilde \alpha _{4})= 0.5*(0.050^{t}*0.800^{1-t}+ 1)\). It is proved that when \(0\leq t < 0.724\), they hold that \(F_{2}(\alpha _{3})<F_{2}(\alpha _{4})\), while when \(0.724 < t \leq 1\), they hold that \(F_{2}(\alpha _{3})>F_{2}(\alpha _{4})\).

By (7), they get that \(F_{4}(\tilde \alpha _{3})= 0.5*(1.275-0.2t), F_{4}(\tilde \alpha _{4})= 0.5*(1.8-0.75t)\). It is proved that when \(0\leq t < 0.954\), they hold that \(F_{4}(\alpha _{3})<F_{4}(\alpha _{4})\), while when \(0.954 < t \leq 1\), they hold that \(F_{4}(\alpha _{3})>F_{4}(\alpha _{4})\).

This case shows that the generalized score functions \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\) have their own characteristics. Besides, there are some common properties between these two functions: \((i)~t\) represents the decision makers’ attitudinal character on the classical score values of IVIFNs, where the bigger the parameter t, the larger the influence of the classical score values of IVIFNs on them; \((ii)~1-t\) represents the decision makers’ attitudinal character on the classical accuracy values of IVIFNs, where the bigger the parameter \(1-t\), the larger the influence of the classical accuracy values of IVIFNs on them.

3.4 Two kinds of generalized score functions on IVIFSs based on integral

In the following, two kinds of generalized score functions on IVIFSs are proposed based on integral. When there is no information about the relationship between the classical score function and the classical accuracy function, these generalized score functions are available.

Definition 10

Let \( \widetilde A= ([a,b],[c,d])\) be an IVIFN. Then, two kinds of generalized score functions on IVIFNs are proposed as

$$\begin{array}{@{}rcl@{}} F_{5}(\widetilde A)&=&\frac{1}{2}\left( 1\,+\, \displaystyle{\int}_{0}^{1} s(\tilde\alpha)\cdot\left[ abs\left( \frac{(a\,-\,c)\,+\,(b\,-\,d)}{2}\right)\right]^{t}\right.\\ &&\qquad\qquad \cdot \left. \left[ \frac{(a+c)+(b+d)}{2}\right]^{1-t}dt \right) , \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} F_{6}(\widetilde A)&=&\frac{1}{2}\left( 1\,+\,\displaystyle{\int}_{0}^{1} s(\tilde\alpha)\cdot\left[ t\cdot abs\left( \frac{(a\,-\,c)\,+\,(b\,-\,d)}{2}\right)\right.\right.\\ && \qquad\qquad + \left.\left. (1\,-\,t)\cdot \frac{(a\,+\,c)\,+\,(b\,+\,d)}{2}\right] dt\right), \end{array} $$
(9)

where \(s(\tilde \alpha )=sgn \left [\frac {(a-c)+(b-d)}{2}\right ]\).

3.5 Supplement explanations

(1) The relationships between \(F_{1}(\cdot )\) and \(F_{3}(\cdot )\), and between \(F_{2}(\cdot )\) and \(F_{4}(\cdot )\) are summarized as follows.

Proposition 1

Let \(\tilde \alpha =([a,b],[c,d])\) be an IVIFN. When \(t = 0.5\) , the generalized score function \(F_{3}(\cdot )\) on \(\tilde \alpha \) is reduced to the generalized score function \(F_{1}(\cdot )\) , i.e., \(F_{3}(\tilde \alpha )\mid _{t = 0.5}=F_{1}(\tilde \alpha )\) ; the generalized score function \(F_{4}(\cdot )\) on \(\tilde \alpha \) is reduced to the generalized score function \(F_{2}(\cdot )\) , i.e., \(F_{4}(\tilde \alpha )\mid _{t = 0.5}=F_{2}(\tilde \alpha )\) .

(2) The relationships between \(F_{3}(\cdot )\) and \(S_{xu}(\cdot )\), and between \(F_{4}(\cdot )\) and \(S_{xu}(\cdot )\) are summarized as follows.

Proposition 2

Let \(\tilde \alpha _{1}=([a_{1},b_{1}],[c_{1},d_{1}])\) and \(\tilde \alpha _{2}=([a_{2},b_{2}],[c_{2},d_{2}])\) be two IVIFNs. When \(t = 1\) and Sx u(α1)≠Sx u(α2), it is obtained that

$$\begin{array}{@{}rcl@{}} & [S_{xu}(\tilde\alpha_{1})-S_{xu}(\tilde\alpha_{2})]\cdot[F_{3}(\tilde\alpha_{1})-F_{3}(\tilde\alpha_{2})]>0, \end{array} $$
(10)
$$\begin{array}{@{}rcl@{}} & [S_{xu}(\tilde\alpha_{1})-S_{xu}(\tilde\alpha_{2})]\cdot[F_{4}(\tilde\alpha_{1})-F_{4}(\tilde\alpha_{2})]>0; \end{array} $$
(11)

when \(t = 1\) and \(S_{xu}(\tilde \alpha _{1})= S_{xu}(\tilde \alpha _{2})\), it is obtained that \(F_{3}(\tilde \alpha _{1})=F_{3}(\tilde \alpha _{2})\), and \(F_{4}(\tilde \alpha _{1})=F_{4}(\tilde \alpha _{2})\); when \(t = 1, a_{1}=b_{1}= 1, c_{1}=d_{1}= 0\), it is obtained that \(F_{3}(\tilde \alpha _{1})= F_{4}(\tilde \alpha _{1})= 1\); when \(t = 1, a_{1}=b_{1}= 0, c_{1}=d_{1}= 1\), it is obtained that \(F_{3}(\tilde \alpha _{1})= F_{4}(\tilde \alpha _{1})= 0\);.

(3) The relationships between \(F_{3}(\cdot )\) and \(H_{xu}(\cdot )\), and between \(F_{4}(\cdot )\) and \(H_{xu}(\cdot )\) are summarized as follows.

Proposition 3

Let \(\tilde \alpha _{1}=([a_{1},b_{1}],[c_{1},d_{1}])\) and \(\tilde \alpha _{2}=([a_{2},b_{2}],[c_{2},d_{2}])\) be two IVIFNs. When \(t = 0\) and \(H_{xu}(\tilde \alpha _{1})\neq H_{xu}(\tilde \alpha _{2})\) , it is obtained that

$$\begin{array}{@{}rcl@{}} & [H_{xu}(\tilde\alpha_{1})-H_{xu}(\tilde\alpha_{2})]\cdot[F_{3}(\tilde\alpha_{1})-F_{3}(\tilde\alpha_{2})]>0, \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} & [H_{xu}(\tilde\alpha_{1})-H_{xu}(\tilde\alpha_{2})]\cdot[F_{4}(\tilde\alpha_{1})-F_{4}(\tilde\alpha_{2})]>0; \end{array} $$
(13)

when \(t = 0, s(\tilde \alpha _{1})= s(\tilde \alpha _{2})\) , and \(H_{xu}(\tilde \alpha _{1})= H_{xu}(\tilde \alpha _{2})\) , it is obtained that \(F_{3}(\tilde \alpha _{1})=F_{3}(\tilde \alpha _{2}), F_{4}(\tilde \alpha _{1})=F_{4}(\tilde \alpha _{2})\) ; when \(t = 0, s(\tilde \alpha _{1})= s(\tilde \alpha _{2})= 1, a_{1}+c_{1}= 1, b_{1}+d_{1}= 1\) , it is obtained that \(F_{3}(\tilde \alpha _{1})= F_{4}(\tilde \alpha _{1})= 1\) ; when \(t = 0, s(\tilde \alpha _{1})= s(\tilde \alpha _{2})=-1, a_{1}+c_{1}= 1, b_{1}+d_{1}= 1\) , it is obtained that \(F_{3}(\tilde \alpha _{1})= F_{4}(\tilde \alpha _{1})= 0\) .

(4) The relationships between \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\) are summarized as follows.

Proposition 4

Let \(\tilde \alpha _{1}=([a_{1},b_{1}],[c_{1},d_{1}])\) and \(\tilde \alpha _{2}=([a_{2},b_{2}],[c_{2},d_{2}])\) be two IVIFNs. For any given \(t\in [0,1]\) , it doesn’t always hold that

$$ [F_{3}(\alpha_{1})-F_{3}(\alpha_{2})]\cdot[F_{4} (\alpha_{1})-F_{4}(\alpha_{2})]>0. $$
(14)

(5) There are some important special cases on \(F_{5}(\cdot )\) and \(F_{6}(\cdot )\) as follows.

Proposition 5

Let \( \widetilde \alpha = ([a,b],[c,d])\) be an IVIFN. When \(a=b = 1, c=d = 0\), it is obtained that \(F_{5}(\widetilde \alpha )= F_{6}(\widetilde \alpha )= 1\); when a = b = 0,c = d = 1, it is obtained that \(F_{5}(\widetilde \alpha )= F_{6}(\widetilde \alpha )= 0\).

Studying the aforementioned propositions, it shows that \(F_{1}(\cdot ), F_{2}(\cdot ), F_{3}(\cdot ), F_{4}(\cdot ), F_{5}(\cdot )\) and \(F_{6}(\cdot )\) are all suitable to be used as generalized score functions.

(6) The relationships between the newly proposed generalized score functions are shown in Fig. 1.

Fig. 1
figure 1

The relationships between the newly proposed generalized score functions

Full size image

4 Three kinds of MCDM methods on IVIFSs

At present, the intuitionistic fuzzy sets are widely used to solve MCDM problems (more details please see [11, 21, 25], etc). In this paper, the studied MCDM problem in interval-valued intuitionistic fuzzy setting is introduced as follows.

Let \(A=\lbrace A_{1},A_{2}, \cdots ,A_{m}\rbrace \) be a discrete set of alternatives, \(C=\lbrace C_{1},C_{2}, \cdots ,C_{n}\rbrace \) be a set of decision making criteria. Let W = {w1, w2,⋯ ,wn} be the weight vector of the criteria, where \(w_{j} \in [0,1], \sum \limits _{j = 1}^{n}w_{j}= 1, j = 1,2,\cdots ,n\). Let \(\tilde Y =(\tilde \alpha _{ij})_{m\times n}=([a_{ij},b_{ij}],[c_{ij},d_{ij}])_{m\times n}\) be an interval-valued intuitionistic fuzzy decision matrix, where \( [a_{ij},b_{ij}]\) indicates the degree that the alternative \(A_{i}\) satisfies the criterion \(C_{j}\), whereas \( [c_{ij},d_{ij}]\) indicates the degree that the alternative \(A_{i}\) does not satisfy the criterion Cj. Besides, \([a_{ij},b_{ij}]\subset [0,1], [c_{ij},d_{ij}]\subset [0,1], b_{ij}+d_{ij} \leq 1, i = 1,2,\cdots , m, j = 1,2,\cdots , n\). And then, for any \(i = 1,2,\cdots ,m\), the characteristic of the alternative \(A_{i}\) is expressed by an IVIFS: \(\widetilde A_{i}=\{\langle C_{j},[a_{ij},b_{ij}],[c_{ij},d_{ij}]\rangle \mid C_{j} \in C \}\). Under the above conditions, how to rank the alternatives, and how to select the optimal alternative? To solve this problem, three kinds of MCDM methods are proposed.

  1. (1)

    By using the generalized score function \(F_{1}(\cdot )\) or \(F_{2}(\cdot )\), a series of novel MCDM methods are proposed as follows.

    • Step 1 Calculate the generalized score values of all the elements of the matrix \(\tilde Y =(\tilde \alpha _{ij})_{m\times n}\) by (4) (or (5)), and denote the results as \(\tilde Y_{1}=(F_{1}(\tilde \alpha _{ij}))_{m\times n}\) (or \(\tilde Y_{2} =(F_{2}(\tilde \alpha _{ij}))_{m\times n}\)).

    • Step 2 For any \(j = 1,2,\cdots ,n\), by using the thoughts of Shannon entropy method [25], the weight value for the attribute \(C_{j}\) is calculated, and the weight vector for C is denoted as \(W=(w_{1},w_{2},\cdots ,w_{n})\), where

      $$ w_{j}\,=\,\frac{\sum\limits_{i = 1}^{m}\sqrt{\frac{1}{2}[(1\,-\,\pi_{\tilde\alpha_{ij}L})^{2}\,+\,(1\,-\,\pi_{\tilde\alpha_{ij}U})^{2}]}}{\sum\limits_{j = 1}^{n}\sum\limits_{i = 1}^{m}\sqrt{\frac{1}{2}[(1\,-\,\pi_{\tilde\alpha_{ij}L})^{2}\,+\,(1\,-\,\pi_{\tilde\alpha_{ij}U})^{2}]}}, j\!\in\! \{1,2,\cdots,n\}. $$
      (15)

    • Step 3 Calculate the comprehensive attribute value of each alternative. For any \(i = 1,2,\cdots ,m\), denote the comprehensive attribute value of \(A_{i}\) as \(Z_{i}\), where \(Z_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{1}(\tilde \alpha _{ij})\) (or \(Z_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{2} (\tilde \alpha _{ij}))\)).

    • Step 4 Rank all the alternatives and select the optimal alternative \(A^{*}\) by comparing the comprehensive attribute values \(Z_{1},Z_{2},\cdots , Z_{m}\).

  2. (2)

    By using the generalized score functions \(F_{3}(\cdot )\) or \(F_{4} (\cdot )\), a series of novel MCDM methods are proposed as follows.

    • Step 1 Determine the parameter t by decision makers according to the given decision making environments.

    • Step 2 Calculate the generalized score values of all the elements of the matrix \(\tilde Y =(\tilde \alpha _{ij})_{m\times n}\) by (6) (or (7)), and denote the results as \(\tilde Y_{3}=(F_{3}(\tilde \alpha _{ij}))_{m\times n}\) (or \(\tilde Y_{4} =(F_{4} (\tilde \alpha _{ij}))_{m\times n}\)).

    • Step 3 For any \(j = 1,2,\cdots ,n\), by (15), the weight values for all the attributes \(C_{j}(j = 1,2,\cdots ,n)\) are calculated, and the weight vector for C is denoted as \(W=(w_{1},w_{2},\cdots ,w_{n})\).

    • Step 4 Calculate the comprehensive attribute value of each alternative. For any \(i = 1,2,\cdots ,m\), denote the comprehensive attribute value of \(A_{i}\) as \(Z^{\prime }_{i}\), where \(Z^{\prime }_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{3}(\tilde \alpha _{ij})\) (or \(Z^{\prime }_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{4}(\tilde \alpha _{ij})\)).

    • Step 5 By comparing the values \(Z^{\prime }_{1},Z^{\prime }_{2},\cdots ,Z^{\prime }_{m}\), the optimal alternative \(A^{*\prime }\) is obtained.

  3. (3)

    By using the generalized score functions \(F_{5}(\cdot )\) or \(F_{6}(\cdot )\), a series of novel MCDM methods are proposed as follows.

    • Step 1 Calculate the generalized score values of all the elements of the matrix \(\tilde Y =(\tilde \alpha _{ij})_{m\times n}\) by (8) (or (9)), and denote the results as \(\tilde Y_{5}=(F_{5}(\tilde \alpha _{ij}))_{m\times n}\) (or \(\tilde Y_{6}=(F_{6}(\tilde \alpha _{ij}))_{m\times n}\)).

    • Step 2 For any \(j = 1,2,\cdots ,n\), by (15), the weight values for all the attribute \(C_{j}(j = 1,2,\cdots ,n)\) are calculated, and the weight vector for C is denoted as W = (w1, w2,⋯ ,wn).

    • Step 3 Calculate the comprehensive attribute value of each alternative. For any \(i = 1,2,\cdots ,m\), denote the comprehensive attribute value of \(A_{i}\) as \(Z^{\prime \prime }_{i}\), where \(Z^{\prime \prime }_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{5}(\tilde \alpha _{ij})\) (or \(Z^{\prime \prime }_{i}={\sum }_{j = 1}^{n}w_{j}\cdot F_{6}(\tilde \alpha _{ij})\)).

    • Step 4 By comparing the values \(Z^{\prime \prime }_{1},Z^{\prime \prime }_{2},\cdots ,Z^{\prime \prime }_{m}\), the optimal alternative \(A^{*\prime \prime }\) is obtained.

In the next section, an example is introduced to illustrate the effectiveness of the proposed generalized score functions and the proposed MCDM methods.

5 Supplier selection example

Since supply chains depend on the time compression, flexible response and unit cost reduction, suppliers play an important role in the whole supply chain. Suppliers are also critical in providing essential components and resources for goods in today’s globalization supply chain networks. The number of components comprising a finished product may be small or immense as in aircraft manufacturing and other complex products. Even in the case of simpler products, such as bread, all the ingredients of it may travel across the globe as inputs into production processes. Suppliers are also decision-makers and they compete with one another to provide components to downstream manufacturing firms. Thus, the optimized performance will be elusive without building a good relationship with a reliable supplier, establishing a system to evaluate performance and offer improvements on cost reduction, which will have a significant impact on the whole supply chain.

Up to now, many researchers have paid attentions to supplier selection problem. Among the studies, some aim to enhance the competitiveness or to decrease the costs in supply chain from suppliers. For example, [13] studied the model for decreasing the costs in supply chain. This model reveals the importance of suppliers in the supply chain management, particularly the role of alternative suppliers, and tries to compensate the weakness of the supply chain. Considering supplier selection is an important issue in supply chain management, [5] proposed a series of AHP methods based on a novel effective and feasible representation of uncertain informations, which extend the classical AHP method. Meanwhile, [10] proposed an integrated approach of fuzzy multi attribute utility theory and multi-objective programming for rating and selecting the best green suppliers. However, the aforementioned studies did not consider the supplier selection problem in a framework which is composed of positive and negative factors. With that in consideration, this study applies IFSs to solve supplier selection problem.

Assuming that a manufacturing company is searching for the best global supplier for one of its most critical parts used in assembling process, the attributes which are considered in the selection process are: \(f_{1}\), overall cost of the product; \(f_{2}\), quality of the product; \(f_{3}\), service performance of supplier; \(f_{4}\), supplier’s profile; and \(f_{5}\), risk factor. Here, \(f_{1}\) and \(f_{5}\) are cost type attributes, whereas \(f_{2}, f_{3}\),and \(f_{4}\) are benefit type attributes. The alternative set is A = {A1, A2, A3, A4}. A decision maker group is formed to evaluate the characteristics of each potential global supplier with respect to each attribute on the fuzzy concept “excellence”. By aggregating the decision making results of each decision maker, a matrix \(\tilde Y=(\tilde y_{ij})_{4\times 5}\) is obtained as

$$\begin{array}{@{}rcl@{}} &&\begin{array}{lll} f_{1} & f_{2} & f_{3} \end{array}\\ Y=\begin{array}{c} A_{1}\\ A_{2}\\ A_{3}\\ A_{4} \end{array}\left( \begin{array}{ccc} \langle[0.482,0.627],[0.177,0.301]\rangle & \langle[0.300,0.451],[0.354,0.481]\rangle & \langle[0.626,0.726],[0.126,0.226]\rangle \\ \langle[0.349,0.475],[0.355,0.503]\rangle & \langle[0.131,0.314],[0.292,0.506]\rangle & \langle[0.324,0.424],[0.403,0.503]\rangle \\ \langle[0.358,0.506],[0.300,0.427]\rangle & \langle[0.626,0.775],[0.100,0.225]\rangle & \langle[0.554,0.776],[0.100,0.224]\rangle \\ \langle[0.300,0.427],[0.358,0.506]\rangle & \langle[0.100,0.225],[0.626,0.775]\rangle & \langle[0.100,0.224],[0.554,0.776]\rangle \end{array} \right. \\ &&\begin{array}{ccc}f_{4} & f_{5} \end{array} \\ &&\left. \begin{array}{ll} \langle[0.500,0.625],[0.100,0.275]\rangle & \langle[0.158,0.356],[0.381,0.552]\rangle \\ \langle[0.174,0.299],[0.557,0.679]\rangle & \langle[0.626,0.751],[0.126,0.226]\rangle \\ \langle[0.427,0.605],[0.227,0.327]\rangle & \langle[0.525,0.650],[0.201,0.326]\rangle \\ \langle[0.227,0.327],[0.427,0.605]\rangle & \langle[0.201,0.326],[0.525,0.650]\rangle \end{array} \right)_{.}\\ \end{array} $$

By using the generalized score function \(F_{3}(\cdot ),F_{4}(\cdot ), F_{5}(\cdot )\), or \(F_{6}(\cdot )\), the given problem is solved, specific details are as follows.

  • Step 1 Since there is no information about the attitudinal characters of the decision-makers on the classical score functions and the accuracy functions on IVIFSs, the parameter t is dealt with as a variable, and \(t\in [0,1]\).

  • Step 2 By using (6), (7), (8), and (10), the matrix \(\tilde Y=(\tilde y_{ij})_{4\times 5}\) is calculated, respectively. The calculation results are as follows.

    $$\begin{array}{@{}rcl@{}} &&Y_{3,t}=\\ &&\begin{array}{llll} \qquad\qquad\qquad\qquad\quad f_{1} & \qquad\qquad\qquad\qquad\qquad\qquad\quad f_{2} & \qquad\qquad\qquad\qquad\qquad\qquad\qquad f_{3} \end{array}\\ && \left( \begin{array}{ccc} F_{3,t}(\langle[0.482,0.627],[0.177,0.301]\rangle) & F_{3,t}(\langle[0.300,0.451],[0.354,0.481]\rangle) & F_{3,t}(\langle[0.626,0.726],[0.126,0.226]\rangle) \\ F_{3,t}(\langle[0.349,0.475],[0.355,0.503]\rangle) & F_{3,t}(\langle[0.131,0.314],[0.292,0.506]\rangle) & F_{3,t}(\langle[0.324,0.424],[0.403,0.503]\rangle) \\ F_{3,t}(\langle[0.358,0.506],[0.300,0.427]\rangle) & F_{3,t}(\langle[0.626,0.775],[0.100,0.225]\rangle) & F_{3,t}(\langle[0.554,0.776],[0.100,0.224]\rangle) \\ F_{3,t}(\langle[0.300,0.427],[0.358,0.506]\rangle) & F_{3,t}(\langle[0.100,0.225],[0.626,0.775]\rangle) & F_{3,t}(\langle[0.100,0.224],[0.554,0.776]\rangle) \end{array}\right.\\ & & \begin{array}{lll} \qquad\qquad\qquad\qquad\qquad f_{4} & \qquad\qquad\qquad\qquad\qquad\qquad\qquad f_{5} \end{array}\\ && \qquad \left. \begin{array}{ccc} F_{3,t}(\langle[0.500,0.625],[0.100,0.275]\rangle) & F_{3,t}(\langle[0.158,0.356],[0.381,0.552]\rangle) \\ F_{3,t}(\langle[0.174,0.299],[0.557,0.679]\rangle)& F_{3,t}(\langle[0.626,0.751],[0.126,0.226]\rangle) \\ F_{3,t}(\langle[0.427,0.605],[0.227,0.327]\rangle) & F_{3,t}(\langle[0.525,0.650],[0.201,0.326]\rangle) \\ F_{3,t}(\langle[0.227,0.327],[0.427,0.605]\rangle) & F_{3,t}(\langle[0.201,0.326],[0.525,0.650]\rangle) \end{array}\right)_{,} \end{array} $$
    $$\begin{array}{@{}rcl@{}} &&Y_{4,t}=\\ &&\begin{array}{llll} \qquad\qquad\qquad\qquad\quad f_{1} & \qquad\qquad\qquad\qquad\qquad\qquad\quad f_{2} & \qquad\qquad\qquad\qquad\qquad\qquad\qquad f_{3} \end{array}\\ &&\left( \begin{array}{ccc} F_{4,t}(\langle[0.482,0.627],[0.177,0.301]\rangle) & F_{4,t}(\langle[0.300,0.451],[0.354,0.481]\rangle) & F_{4,t}(\langle[0.626,0.726],[0.126,0.226]\rangle) \\ F_{4,t}(\langle[0.349,0.475],[0.355,0.503]\rangle) & F_{4,t}(\langle[0.131,0.314],[0.292,0.506]\rangle) & F_{4,t}(\langle[0.324,0.424],[0.403,0.503]\rangle) \\ F_{4,t}(\langle[0.358,0.506],[0.300,0.427]\rangle) & F_{4,t}(\langle[0.626,0.775],[0.100,0.225]\rangle) & F_{4,t}(\langle[0.554,0.776],[0.100,0.224]\rangle) \\ F_{4,t}(\langle[0.300,0.427],[0.358,0.506]\rangle) & F_{4,t}(\langle[0.100,0.225],[0.626,0.775]\rangle) & F_{4,t}(\langle[0.100,0.224],[0.554,0.776]\rangle) \end{array}\right.\\ &&\begin{array}{ll} \qquad\qquad\qquad\qquad\qquad f_{4} & \qquad\qquad\qquad\qquad\qquad\qquad\qquad f_{5} \end{array}\\ && \qquad \left.\begin{array}{ll} F_{4,t}(\langle[0.500,0.625],[0.100,0.275]\rangle) & F_{4,t}(\langle[0.158,0.356],[0.381,0.552]\rangle) \\ F_{4,t}(\langle[0.174,0.299],[0.557,0.679]\rangle)& F_{4,t}(\langle[0.626,0.751],[0.126,0.226]\rangle) \\ F_{4,t}(\langle[0.427,0.605],[0.227,0.327]\rangle) & F_{4,t}(\langle[0.525,0.650],[0.201,0.326]\rangle) \\ F_{4,t}(\langle[0.227,0.327],[0.427,0.605]\rangle) & F_{4,t}(\langle[0.201,0.326],[0.525,0.650]\rangle) \end{array} \right)_{,} \end{array} $$
    $$\begin{array}{@{}rcl@{}} Y_{5} &=& \left( \begin{array}{ccccc} 0.7594 & 0.3722 & 0.8302 & 0.7705 & 0.7077 \\ 0.3944 & 0.3230 & 0.3408 & 0.2065 & 0.8369 \\ 0.6487 & 0.8439 & 0.8258 & 0.7310 & 0.7729 \\ 0.3514 & 0.1562 & 0.1742 & 0.2691 & 0.2272 \end{array} \right)_{,}\\ Y_{6} &=& \left( \begin{array}{ccccc} 0.7753 & 0.2913 & 0.8380 & 0.7813 & 0.7335 \\ 0.2855 & 0.3003 & 0.2735 & 0.1908 & 0.8445 \\ 0.7163 & 0.8503 & 0.8325 & 0.7580 & 0.7938 \\ 0.2838 & 0.1498 & 0.2123 & 0.2420 & 0.2063 \end{array} \right)_{.} \end{array} $$

  • Step 3 By using (15), the attribute weight vector corresponding to each attribute is obtained as

    $$W=(0.199,0.195,0.206,0.197,0.203). $$

  • Step 4 The comprehensive attribute values of the four alternatives are calculated, and the results are obtained as

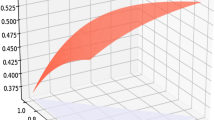
    $$\begin{array}{@{}rcl@{}} Z_{F_{3}}(A_{1},t)&=& \frac{1}{2}\langle 0.199\times(1 + 0.32^{t}\times 0.79^{1-t})+ 0.195\times (1-0.04^{t}\times 0.79^{1-t})+ 0.206\times (1 + 0.50^{t}\times 0.85^{1-t})\\ &&+ 0.197\times (1 + 0.38^{t}\times 0.75^{1-t})+ 0.203\times (1 + 0.21^{t}\times 0.72^{1-t})\rangle, \\ Z_{F_{3}}(A_{2},t)&=& \frac{1}{2}\langle 0.199\times(1-0.02^{t}\times 0.84^{1-t})+ 0.195\times (1-0.18^{t}\times 0.62^{1-t})+ 0.206\times (1-0.08^{t}\times 0.83^{1-t})\\ &&+ 0.197\times (1-0.38^{t}\times 0.86^{1-t})+ 0.203\times (1 + 0.51^{t}\times 0.87^{1-t})\rangle, \\ Z_{F_{3}}(A_{3},t)&=& \frac{1}{2}\langle 0.199\times(1 + 0.07^{t}\times 0.80^{1-t})+ 0.195\times (1 + 0.54^{t}\times 0.86^{1-t})+ 0.206\times (1 + 0.50^{t}\times 0.83^{1-t})\\ &&+ 0.197\times (1 + 0.24^{t}\times 0.79^{1-t})+ 0.203\times (1 + 0.32^{t}\times 0.85^{1-t})\rangle, \\ Z_{F_{3}}(A_{4},t)&=& \frac{1}{2}\langle 0.199\times(1-0.07^{t}\times 0.80^{1-t})+ 0.195\times (1-0.54^{t}\times 0.86^{1-t})+ 0.206\times (1-0.50^{t}\times 0.83^{1-t})\\ &&+ 0.197\times (1-0.24^{t}\times 0.79^{1-t})+ 0.203\times (1-0.32^{t}\times 0.85^{1-t})\rangle.\\ Z_{F_{4}}(A_{1},t)&=&0.7361-0.0999\times{t}, \\ Z_{F_{4}}(A_{2},t)&=&0.2751 + 0.2135\times{t}, \\ Z_{F_{4}}(A_{3},t)&=&0.9130-0.2457\times{t}, \\ Z_{F_{4}}(A_{4},t)&=&0.0870 + 0.1005\times{t}, \end{array} $$

    where \(t\in [0,1]\). For convenience, the sketch maps of them are shown in Fig. 2.

    Fig. 2
    figure 2

    The comprehensive attribute values calculated by F3(⋅) and F4(⋅)

    Full size image

As shown in Fig. 2, the results are consistent on the whole that the optimal alternative is \(A_{3}\), and the ranking is \(Z(A_{3})\succ Z(A_{1}) \succ Z(A_{2}) \succ Z(A_{4})\). Meanwhile, by using the generalized score function \(F_{5}(\cdot )\) and \(F_{6}(\cdot )\), the given problem can be solved as \(Z_{F_{5}}(A_{1})= 0.6901, Z_{F_{5}}(A_{2})= 0.4223, Z_{F_{5}}(A_{3})= 0.7646, Z_{F_{5}}(A_{4})= 0.2354\), and \(Z_{F_{6}}(A_{1})= 0.6865, Z_{F_{6}}(A_{2})= 0.3808, Z_{F_{6}}(A_{3})= 0.7903, Z_{F_{6}}(A_{4})= 0.2189\), respectively. Then, it gets \(Z(A_{3})\succ Z(A_{1}) \succ Z(A_{2}) \succ Z(A_{4})\), and the optimal alternative is also \(A_{3}\).

It is interesting that the aforementioned comparing results are consistent on the whole that \(A_{3}\) is the optimal alternative. This phenomenon has a certain component and an accidental component. Specifically, the ranking result obtained by \(F_{5}(\cdot )\) is determined by that obtained by \(F_{3}(\cdot )\) while the ranking result obtained by \(F_{6}(\cdot )\) is determined by that obtained by \(F_{4}(\cdot )\). Meanwhile, it is a coincidence that the ranking results obtained by \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\) are the same in this example. Though there are some common properties on \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\), they have their own characteristics. In essence, \(F_{3}(\cdot )\) is a kind of exponential function, while F4(⋅) is a kind of linear function. Therefore, \(F_{3}(\cdot )\) is more sensitive to extreme large or small classical score or accuracy values than \(F_{4}(\cdot )\), which could lead to inconsistent comparing results obtained by \(F_{3}(\cdot )\) and \(F_{4}(\cdot )\) in some cases.

Besides, this study has studied the problem using the method proposed by [4], and the calculation results are obtained as \(Z(A_{1})= 0.139, Z(A_{2})= 0.533, Z(A_{3})= 0.298\), and \(Z(A_{4})= 0.355\). Obviously, it gets \(Z(A_{2})\succ Z(A_{4}) \succ Z(A_{3}) \succ Z(A_{1})\), and the optimal alternative as \(A_{2}\).

By comparing the novel score functions and score functions proposed by [4], it is found that the internal mechanism of them is different. In particular, by using operations of fetching maximum or minimum, and operations of union and intersection, the techniques proposed in [4] put emphasis on extreme large or small decision making values. On the whole, [4] is more suitable to deal with acute problems. In contrast, the novel generalized score functions proposed in this study emphasize the subjective attitude of the decision-makers. Usually, different decision viewpoints bring different decision results. Therefore, decision makers should choose suitable decision making methods according to their different decision making problem.

6 Conclusion

Since any given generalized score function is only suitable for comparing the IVIFNs in certain circumstances, the IVIFS is studied from the viewpoint of the types of decision-makers in this study. According to the illustrative examples, some conclusions are shown as follows.

  1. (i)

    Two series of principles are proposed to evaluate generalized score functions on IVIFNs. Furthermore, according to the newly proposed principles, two novel generalized score functions on IVIFSs are suggested. However, Theorem 1 and 2 are only periodical results. As the internal mechanism of IVIFSs is exposed further, more theorems would be proposed in the future.

  2. (ii)

    Two kinds of generalized score functions on IVIFSs are proposed based on preference information of decision-makers. Both of the two kinds of generalized score functions are of two parameters, which represent the decision makers’ attitudinal characters on the classical score function and the classical accuracy function on IVIFNs, respectively. Thereafter, two kinds of generalized score functions, which are suitable for ranking the IVIFNs when there is no information about the relationship between the classical score values and the classical accuracy values on IVIFNs, are suggested based on integral. For the next step, the parameters in \(F_{3}(\cdot ) F_{4}(\cdot )\) would be studied in details. Moreover, the comparing methods on generalized score functions would be studied as well.

  3. (iii)

    Three kinds of MCDM methods in intuitionistic fuzzy setting are proposed, and the effectiveness of these methods is illustrated by an example. The example shows that any given generalized score function is only suitable for comparing the IVIFNs in certain circumstances, and when there is little comparing information on IVIFNs, the integral-based generalized score functions can be used to reduce the risk of errors. For the next step, more applications of the novel generalized score functions would be carried on in the port management and shipping optimization fields.