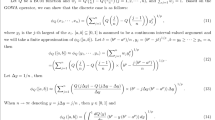1 Introduction

To describe the fuzzy nature of the real world more comprehensively, Atanassov [1] introduced an intuitionistic fuzzy set (IFS), which is an extension of the traditional fuzzy set [2]. Then, IFSs have been wildly applied in fuzzy multiple attribute decision-making (MADM) problems. Numerous methods have been developed to solve the complex MADM problems with intuitionistic fuzzy information [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18]. However, how to aggregate intuitionistic fuzzy information is an important research topic in MADM problems. So, Xu and Yager [4] proposed some geometric aggregation operators for intuitionistic fuzzy values (IFVs) (basic elements in IFSs), including the intuitionistic fuzzy weighted geometric averaging (IFWGA) operator, the intuitionistic fuzzy ordered weighted geometric averaging (IFOWGA) operator, and the intuitionistic fuzzy hybrid geometric averaging (IFHGA) operator, and applied the IFHGA operator to MADM problems with IFV information. Then, Xu [7] presented some arithmetic aggregation operators, including the intuitionistic fuzzy weighted arithmetic averaging (IFWAA) operator, the intuitionistic fuzzy ordered weighted arithmetic averaging (IFOWAA) operator, and the intuitionistic fuzzy hybrid aggregation (IFHA) operator. Xu and Wang [19] further introduced the induced generalized intuitionistic fuzzy ordered weighted averaging (I-GIFOWA) operator, which contains all the characteristics of both the generalized IFOWAA operator and the induced IFOWAA operator, for decision making. Yu and Xu [20] developed a prioritized intuitionistic fuzzy aggregation operator for MADM problems. Zhao and Wei [21] proposed the intuitionistic fuzzy Einstein hybrid arithmetic averaging (IFEHAA) operator and the intuitionistic fuzzy Einstein hybrid geometric averaging (IFEHGA) operator for MADM problems with IFV information.

In the aforementioned aggregation operators of IFVs, the IFWAA, IFOWAA, IFWGA, and IFOWGA operators are four common aggregation operators in the fields of information fusion and decision making. They have been wildly applied to various decision-making problems in engineering, economics, and management. However, the IFWAA, IFOWAA, IFWGA, and IFOWGA operators imply some shortcomings in some cases. For example, the aggregated results of the IFWAA and IFOWAA operators tend to the maximum value, while the aggregated results of the IFWGA and IFOWGA operators tend to the maximum weight value. Furthermore, the IFWAA and IFOWAA operators emphasize group’s major points [4, 7] and the IFWGA and IFOWGA operators focus on personal major points [4, 7]. To overcome the shortcomings of the IFWAA, IFWGA, IFOWAA, and IFOWGA operators for aggregating IFVs, this paper proposes an intuitionistic fuzzy hybrid weighted arithmetic and geometric aggregation (IFHWAGA) operator and an intuitionistic fuzzy hybrid ordered weighted arithmetic and geometric aggregation (IFHOWAGA) operator for obtaining more suitable results in aggregating IFVs and investigates the desired properties of the IFHWAGA and IFHOWAGA operators. Further, a MADM method for the selection problem of mechanical design schemes is established based on the proposed IFHWAGA or IFHOWAGA operator and applied to the decision making problem regarding design schemes of press machine under an intuitionistic fuzzy environment.

The rest of this paper is organized as follows. Section 2 reviews some basic concepts of IFSs, the IFWAA, IFOWAA, IFWGA, and IFOWGA operators for IFVs and presents some shortcomings of these aggregation operators. Section 3 proposes the IFHWAGA and IFHOWAGA operators and discusses their suitability by numerical examples. A MADM method of mechanical design schemes is developed based on the IFHWAGA or IFHOWAGA operator in Section 4. In Section 5, the decision-making problem regarding mechanical design schemes of press machine is provided as a case to demonstrate the application of the presented method. In Section 6, the proposed MADM method is compared with the related methods to show the effectiveness of the presented method. Section 7 contains some conclusions and further research.

2 Preliminaries of IFSs

2.1 Some basic concepts of IFSs

To describe the fuzzy nature of the real world more comprehensively, Atanassov [1] introduced IFS, which is an extension of the traditional fuzzy set [2], and gave its definition.

Definition 1

[1]. Let U be a universal of discourse. An IFS S in U is described by a membership function t S (x), a non-membership function f S (x), where the values of the two functions t S (x) and f S (x) are real numbers in the interval [0, 1], such that t S (x) ∈ [0, 1], f S (x) ∈ [0, 1], and 0 ≤ t S (x) + f S (x) ≤ 1 for x ∈ U. Thus, the IFS S is denoted by the following mathematical form:

$$S=\left\{ {\left\langle {x,t_{S} (x),f_{S} (x)} \right\rangle \vert x\in U} \right\}. $$

Then, h S (x) = 1 − t S (x) − f S (x) for h S (x) ∈ [0, 1] and x ∈ U is called the intuitionistic index (hesitancy).

For convenience, a basic element <x, t S (x), f S (x)>in an IFS S is denoted by s = <t, f> for short, which is called an IFV [4, 7].

Let s 1 = < t 1, f 1> and s 2 = < t 2, f 2>be two IFVs, then there are the following relations [1, 4, 7]:

  1. (1)

    (s 1)c = < f 1, t 1> (complement of s 1);

  2. (2)

    s 1 ≥ s 2 if and only if t 1 ≥ t 2 and f 1 ≤ f 2;

  3. (3)

    s 1 = s 2 if and only if t 1 = t 2 and f 1 = f 2;

  4. (4)

    s 1 + s 2 = 〈t 1 + t 2 − t 1 t 2,f 1 f 2〉;

  5. (5)

    s 1 × s 2 = 〈t 1 t 2,f 1 + f 2 − f 1 f 2〉;

  6. (6)

    \(\rho s_{1} =\left \langle {1-(1-s_{1} )^{\rho },f_{1}^{\rho } } \right \rangle \) for ρ>0;

  7. (7)

    \(s_{1}^{\rho } =\left \langle {s_{1}^{\rho } ,1-(1-f_{1} )^{\rho }} \right \rangle \) for ρ>0.

For any IFV s = <t, f>, its score and accuracy functions [22, 23] are introduced, respectively, as follows:

$$ E(s)=t-f,\quad E(s)\in [-1,1], $$
(1)
$$ N(s)=t+f,\quad N(s)\in [0, 1]. $$
(2)

Definition 2

[4, 7]. Let s 1 = < t 1, f 1 > and s 2 = < t 2, f 2 > be two IFVs, then based on their score and accuracy values, their comparative relations are given as follows:

  1. (1)

    If E(s 1)< E(s 2), then s 1 < s 2;

  2. (2)

    If E(s 1) = E(s 2) and N(s 1)< N(s 2), then s 1 < s 2;

  3. (3)

    If E(s 1) = E(s 2) and N(s 1) = N(s 2), then s 1 = s 2.

Assume that s j = < t j , f j >(j = 1, 2, …, n) is a collection of IFVs. Then the following IFWAA and IFWGA operators [4, 7] are introduced as follows:

$$\begin{array}{@{}rcl@{}} IFWAA(s_{1} ,s_{2} ,...,s_{n} )&=&\sum\limits_{j=1}^{n} w_{j} s_{j}\\ &=&\! \left\langle\! 1\,-\,\prod\limits_{j=1}^{n} {(1\,-\,t_{j} )^{w_{_{j} } }}, \prod\limits_{j=1}^{n} {(f_{j} )^{w_{_{j} } }} \!\right\rangle\!,\\ \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} IFWGA(s_{1} ,s_{2} ,...,s_{n} )\!&=&\!\prod\limits_{j=1}^{n} {s_{j}^{w_{j} } }\\ &=&\!\left\langle\! \prod\limits_{j=1}^{n}\! {(t_{j} )^{w_{_{j} } }}, 1\,-\,\prod\limits_{j=1}^{n} {(1\,-\,f_{j} )^{w_{_{j} } }}\right\rangle,\\ \end{array} $$
(4)

where w j (j = 1, 2, …, n) is the weight of s j (j = 1, 2, …, n) with w j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {w_{j} } =1\).

Furthermore, if the orders of all the given arguments are considered in aggregating IFVs, the IFOWAA and IFOWGA operators [4, 7] are introduced as follows:

$$\begin{array}{@{}rcl@{}} IFOWAA(s_{1} ,s_{2} ,...,s_{n} )\!&=&\!\sum\limits_{j=1}^{n} \omega_{j} s_{\delta (j)}\\ &=&\! \left\langle\! 1\,-\,\prod\limits_{j=1}^{n} \!{(1\,-\,t_{\delta (j)} )^{\omega_{_{j} } }},\prod\limits_{j=1}^{n}\!{(f_{\delta (j)})^{\omega_{_{j}}}}\right\rangle\!,\\ \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} IFOWGA(s_{1} ,s_{2} ,...,s_{n} )\!&=&\!\prod\limits_{j=1}^{n} s_{\delta (j)}^{\omega_{j} }\\ &=&\! \left\langle\prod\limits_{j=1}^{n}\!{(t_{\delta (j)} )^{\omega_{_{j}}}}, 1\,-\,\prod\limits_{j=1}^{n}\!{(1\,-\,f_{\delta (j)} )^{\omega_{_{j} }}}\!\right\rangle\!,\\ \end{array} $$
(6)

where (δ(1), δ(2), . . . , δ(n)) is a permutation of (1, 2, . . . , n), such that δ(j −1) ≥ δ(j) for j = 2, 3, . . . , n; (ω 1, ω 2, …, ω n ) is an associated weight vector with ω j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {\omega _{j} } =1\). The IFOWAA and IFOWGA operators can reflect the important degrees of the ordered positions of arguments.

2.2 Some shortcomings of the IFWAA, IFOWAA, IFWGA, and IFOWGA operators

As we know, the IFWAA, IFOWAA, IFWGA, and IFOWGA operators are usually used for MADM problems. However, their aggregated values may imply some unreasonable results when some values tend toward the maximum arguments or the maximum weight values. Let us consider the following two cases.

Case 1

Take two IFVs s 1 = <0.001, 0> and s 2 = <1, 0> with their weights w 1 = ω 1 = 0.9 and w 2 = ω 2 = 0.1, respectively. By (3)–(6), there are IFWAA(s 1, s 2) = <1, 0>, IFWGA(s 1, s 2) = <0.002, 0>, IFOWAA(s 1, s 2) = <1, 0>, and IFOWGA(s 1, s 2) = <0.5012, 0>.

Case 2

Again take two IFVs s 1 = <0.001, 0> and s 2 = <1, 0> with their weights w 1 = ω 1 = 0.1 and w 2 = ω 2 = 0.9, respectively. By (3)–(6), there are IFWAA(s 1, s 2) = <1, 0>, IFWGA(s 1, s 2) = <0.5012, 0>, IFOWAA(s 1, s 2) = <1, 0>, and IFOWGA(s 1, s 2) = <0.002, 0>.

From the above results, we observe that the aggregated values of the IFWAA and IFOWAA operators tend to the maximum argument, while the aggregated values of the IFWGA and IFOWGA operators tend to the maximum weight value. In the two cases, the IFWAA, IFOWAA, IFWGA, and IFOWGA operators may not give the reasonable results. Therefore, it is necessary that we improve these aggregation operators to overcome these shortcomings.

3 Hybrid aggregation operators of IFVs

To overcome the aforementioned shortcomings of the IFWAA, IFWGA, IFOWAA, IFOWGA operators, we propose hybrid aggregation operators so as to give the moderate values.

3.1 Hybrid weighted arithmetic and geometric aggregation operator of IFVs

Definition 3

Let s j = < t j , f j >(j = 1, 2, …, n) be a collection of IFVs. Then the IFHWAGA operator is defined as follows:

$$ IFHWAGA(s_{1} ,s_{2} ,...,s_{n} )\,=\,\left( {\sum\limits_{j=1}^{n} {w_{j} s_{j} } }\!\right)^{\lambda }\!\left( {\prod\limits_{j=1}^{n} {s_{j}^{w_{j} } } } \!\right)^{(1-\lambda )} $$
(7)

where w j (j = 1, 2, …, n) is the weight of s j (j = 1, 2, …, n) with w j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {w_{j} } =1\); λ is any real number in the interval [0, 1].

Theorem 1

Let s j = < t j , f j > ( j = 1, 2, …, n)be a collection of IFVs and λ be any real number in the interval [0, 1]. Then, the aggregated value of the IFHWAGA operator is also an IFV, and

$$\begin{array}{@{}rcl@{}} IFHWAGA(s_{1} ,s_{2} ,...,s_{n} )\!&=&\!\left( {\sum\limits_{j=1}^{n} {w_{j} s_{j} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{j}^{w_{j} } } } \right)^{(1-\lambda )}\\ \!&=&\!\left\langle {\left( {1\,-\,\prod\limits_{j=\!1}^{n} {(1\,-\,t_{j} )^{w_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=\!1}^{n} {t_{j}^{w_{j} } } } \right)^{(1\!-\lambda )},1\,-\,\left( {1\,-\,\prod\limits_{j=\!1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=\!1}^{n} {(1\,-\,f_{j} )^{w_{j} }} } \right)^{(1\!-\lambda )}} \right\rangle, \end{array} $$
(8)

where w j ( j = 1, 2, …, n)is the weight of s j ( j = 1, 2, …, n)with w j ∈[0, 1] and \(\sum \nolimits _{j=1}^{n} {w_{j} } =1\)

Proof

Based on the IFWAA and IFWGA operators and the operational laws of IFVs, we have

$$\begin{array}{l} IFHWAGA(s_{1} ,s_{2} ,...,s_{n} )=\left( {\sum\limits_{j=1}^{n} {w_{j} s_{j} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{j}^{w_{j} } } } \right)^{(1-\lambda )} \\ =\left\langle {1-\prod\limits_{j=1}^{n} {(1-t_{j} )^{w_{j} }} ,\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right\rangle^{\lambda }\left\langle {\prod\limits_{j=1}^{n} {t_{j}^{w_{j} } } ,1-\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right\rangle^{(1-\lambda )} \\ =\left\langle {\left( {1-\prod\limits_{j=1}^{n} {(1-t_{j} )^{w_{j} }} } \right)^{\lambda },1-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }} \right\rangle \left\langle {\left( {\prod\limits_{j=1}^{n} {t_{j}^{w_{j} } } } \right)^{(1-\lambda )},1-\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right\rangle \\ =\left\langle {\begin{array}{l} \left( {1-\prod\limits_{j=1}^{n} {(1-t_{j} )^{w_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{j}^{w_{j} } } } \right)^{(1-\lambda )},\left[ {1-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }+1-\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right] \\ -\left[ {1-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }} \right]\left[ {1-\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right] \\ \end{array}} \right\rangle \\ =\left\langle {\begin{array}{l} \left( {1-\prod\limits_{j=1}^{n} {(1-t_{j} )^{w_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{j}^{w_{j} } } } \right)^{(1-\lambda )},\left[ {1-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }+1-\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right] \\ -\left[ {1-\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }+\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right] \\ \end{array}} \right\rangle \\ =\left\langle {\left( {1-\prod\limits_{j=1}^{n} {(1-t_{j} )^{w_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{j}^{w_{j} } } } \right)^{(1-\lambda )},1-\left( {1-\prod\limits_{j=1}^{n} {f_{j}^{w_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {(1-f_{j} )^{w_{j} }} } \right)^{(1-\lambda )}} \right\rangle . \\ \end{array} $$

Therefore, this completes the proof of (8). □

For different values of λ ∈ [0, 1], it is possible to investigate the families of the IFHWAGA operator individually. Especially, if λ = 1, the IFHWAGA operator is reduced to the IFWAA operator; if λ = 0, the IFHWAGA operator is reduced to the IFWGA operator; if λ = 0.5, the IFHWAGA operator is the mean of the IFWGA and IFWGA operators.

According to the properties of the IFWAA and IFWGA operators [4, 7], it is clear that the IFHWAGA operator also satisfies the properties of idempotency, boundedness and monotonicity:

  1. (1)

    Idempotency

    If s j = s for j = 1, 2, . . . , n, then

    $$IFHWAGA(s_{1} ,s_{2} ,{\ldots} ,s_{n} )=\left( {\sum\limits_{j=1}^{n} {w_{j} s_{j} } }\! \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{j}^{w_{j} } } } \!\right)^{(1-\lambda )}=s. $$
  2. (2)

    Boundedness

    If s min = min(s 1,s 2,...,s n ) and s max = max(s 1,s 2,...,s n )for j = 1, 2, . . . , n, then

    $$s_{\min } \le IFHWAGA(s_{1} ,s_{2} ,{\ldots} ,s_{n} )\le s_{\max. } $$
  3. (3)

    Monotonicity

    If \(s_{j} \le \quad s_{j}^{\ast }\) for j = 1, 2, . . . , n then

    $$IFHWAGA(s_{1} ,s_{2} ,\ldots,s_{n} )\le IFHWAGA(s_{1}^{\ast } ,s_{2}^{\ast } ,{\ldots} ,s_{n}^{\ast } ). $$

3.2 Hybrid ordered weighted arithmetic and geometric aggregation operator of IFVs

Definition 4

Let s j = < t j , f j >(j = 1, 2, …, n) be a collection of IFVs. Then the IFHOWAGA operator is defined as follows:

$$ IFHOWAGA(s_{1} ,s_{2} ,...,s_{n} )=\left( {\sum\limits_{j=1}^{n} {\omega_{j} s_{\delta (j)} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )}, $$
(9)

where (δ(1), δ(2), . . . , δ(n)) is a permutation of (1, 2, . . . , n), such that δ(j −1) ≥ δ(j) for j = 2, 3, . . . , n; (ω 1, ω 2, …, ω n ) is an associated weight vector with ω j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {\omega _{j} } =1\); λ is any real number in the interval [0, 1]. The IFHOWAGA operator can reflect the important degrees of the ordered positions of arguments.

Theorem 2

Let s j = < t j , f j > ( j = 1, 2, …, n)be a collection of IFVs and λ be any real number in the interval [0, 1]. Then, the aggregated value of the IFHOWAGA operator is also an IFV, and

$$ \begin{array}{l} IFHOWAGA(s_{1} ,s_{2} ,...,s_{n} )=\left( {\sum\limits_{j=1}^{n} {\omega_{j} s_{\delta (j)} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )} \\ =\left\langle {\left( {1-\prod\limits_{j=1}^{n} {(1-t_{\delta (j)} )^{\omega_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )},1-\left( {1-\prod\limits_{j=1}^{n} {f_{\delta (j)}^{\omega_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {(1-f_{\delta (j)} )^{\omega_{j} }} }\right)^{(1-\lambda )}} \right\rangle \\ \end{array} $$
(10)

where (δ(1), δ(2), . . . , δ(n))is a permutationof (1, 2, . . . , n),such that δ(j − 1) ≥ δ(j)for j = 2, 3, .. . , n; (ω 1, ω 2, …, ω n )is an associatedweight vector with ω j ∈[0, 1] and \(\sum \nolimits _{j=1}^{n} {\omega _{j} } =1\).

By the similar proof of (8) in Theorem 1, (10) can be obtained (the proof is omitted).

According to the properties of the IFOWAA and IFOWGA operators [4, 7], it is clear that the IFHOWAGA operatoralso satisfies the properties of idempotency, boundedness monotonicity and commutativity:

  1. (1)

    Idempotency

    If s j = s for j = 1, 2, . .. , n, then

    $$IFHOWAGA(s_{1} ,s_{2} ,...,s_{n} )=\left( {\sum\limits_{j=1}^{n} {\omega_{j} s_{\delta (j)} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )}=s. $$
  2. (2)

    Boundedness

    If s min = min(s 1,s 2,...,s n )and s max = max(s 1,s 2,...,s n )for j = 1,2, . . . , n, then

    $$s_{\min } \le IFHOWAGA(s_{1} ,s_{2} ,{\ldots} ,s_{n} )\le s_{\max. } $$
  3. (3)

    Monotonicity

    If \(s_{j} \le \quad s_{j}^{\ast }\)for j = 1,2, . . . , n then

    $$IFHOWAGA(s_{1} ,s_{2} ,{\ldots} ,s_{n} )\le IFHOWAGA(s_{1}^{\ast } ,s_{2}^{\ast } ,{\ldots} ,s_{n}^{\ast } ) $$
  4. (4)

    Commutativity

    If \((s_{1}^{\prime } ,s_{2}^{\prime } ,{\ldots } ,s_{n}^{\prime } )\)is anypermutation of (s 1,s 2,…,s n ),then

    $$IFHOWAGA(s_{1} ,s_{2} ,{\ldots} ,s_{n} )=IFHOWAGA(s_{1}^{\prime} ,s_{2}^{\prime} ,\ldots ,s_{n}^{\prime} ) $$

3.3 Numerical examples

To show the suitability of the aggregated values of the IFHWAGA and IFHOWAGA operators, again let us consider the above two cases in the Section 2.2. Generally taking λ = 0.5, we use the IFHWAGA and IFHOWAGA operators for the two cases.

For Case 1, by (8), there is IFHWAGA(s 1, s 2) = <0.0447, 0>, which is between IFWAA(s 1, s 2) = <1, 0>and IFWGA(s 1, s 2) = <0.002, 0>; by (10), there is IFHOWAGA(s 1, s 2) = <0.7079, 0>, which is between IFOWAA(s 1, s 2) = <1, 0> and IFOWGA(s 1, s 2) = <0.5012, 0>.

For Case 2, by (8), there is IFHWAGA(s 1, s 2) = <0.7079, 0>, which is between IFWAA(s 1, s 2) = <1, 0> and IFWGA(s 1, s 2) = <0.5012, 0>; by (10), there is IFHOWAGA(s 1, s 2) = <0.0447, 0>, which is between IFO WAA(s 1, s 2) = <1, 0> and IFOWGA(s 1, s 2) = <0.002, 0>.

In the above two cases, the IFHWAGA and IFHOWAGA operators indicate the moderate values. It is obvious that they can overcome the shortcomings of tending to the maximum argument shown by the existing IFWAA and IFOWAA operators and the maximum weight value shown by the existing IFWGA and IFOWGA operators. Therefore, the IFHWAGA and IFHOWAGA operators are effective and reasonable in the information aggregations.

4 MADM method of mechanical design schemes using the IFHWAGA or IFHOWAGA operator

In the conceptual design stage, mechanical design schemes and their evaluation are two main tasks. Designers usually present various primary design schemes (alternatives) based on the designers’ knowledge and experience. Then, the decision makers/designers evaluate these design schemes based on some decision-making method and select the best one.

In the decision-making process, mechanical design schemes (alternatives) must satisfy the requirement of design indexes (attributes). Then, the design indexes may contain uncertain and incomplete information in the conceptual design stage. Therefore, the selection problem of design schemes is a MADM problem with uncertain and incomplete information. For this case, we present a MADM method for solving MADM problems of mechanical design schemes based on the IFHWAGA or IFHOWAGA operator under an intuitionistic fuzzy environment.

In a MADM problem of mechanical design schemes, assume that P = { p 1, p 2, …, p m } is a set of alternatives (mechanical design schemes) and Q = { q 1, q 2, …, q n } is a set of attributes (design indexes). Then, the characteristic value of each attribute q j on each alternative p i is given by decision-makers’ suitability evaluation, which is expressed by an IFV s i j = < t i j , f i j > for t i j ≥ 0, f i j ≥ 0, and 0 ≤ t i j + f i j ≤ 1 (j = 1, 2, …, n; i = 1, 2, …, m). In the IFV s i j = < t i j , f i j >, t i j indicates the degree that the alternative p i is suitable for the attribute q j and f i j indicates the degree that the alternative p i is unsuitable for the attribute q j . For all the evaluation values, thus, we can establish an IFV decision matrix M = (s i j ) m×n .

Therefore, a MADM method for mechanical design schemes is given and its decision steps are described as follows:

  1. Step 1

    If the weight of each attribute q j is given as w j (j = 1, 2, …, n) with w j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {w_{j} } =1\), then the aggregated value of s i (i = 1, 2, …, m) for each alternative p i (i = 1, 2, …, m) is calculated by the following IFHWAGA operator:

    $$ \begin{array}{l} s_{i} =IFHWAGA(s_{i1} ,s_{i2} ,...,s_{in} )=\left( {\sum\limits_{j=1}^{n} {w_{j} s_{ij} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{ij}^{w_{j} } } } \right)^{(1-\lambda )} \\ =\left\langle {\left( {1-\prod\limits_{j=1}^{n} {(1-t_{ij} )^{w_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{ij}^{w_{j} } } } \right)^{(1-\lambda )},1-\left( {1-\prod\limits_{j=1}^{n} {f_{ij}^{w_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {(1-f_{ij} )^{w_{j} }} } \right)^{(1-\lambda )}} \right\rangle \\ \end{array} $$
    (11)

    If the ordered important positions of all the given arguments are considered by the associated weight vector (ω 1, ω 2, …, ω n ) satisfying ω j ∈ [0, 1] and \(\sum \nolimits _{j=1}^{n} {\omega _{j} } =1\), then the aggregated value of s i (i = 1, 2, …, m) for each alternative p i (i = 1, 2, …, m) is calculated by the following IFHOWAGA operator:

    $$ \begin{array}{l} s_{i} =IFHOWAGA(s_{i1} ,s_{i2} ,...,s_{in} )=\left( {\sum\limits_{j=1}^{n} {\omega_{j} s_{i\delta (j)} } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {s_{i\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )} \\ =\left\langle {\left( {1-\prod\limits_{j=1}^{n} {(1-t_{i\delta (j)} )^{\omega_{j} }} } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {t_{i\delta (j)}^{\omega_{j} } } } \right)^{(1-\lambda )},1-\left( {1-\prod\limits_{j=1}^{n} {f_{i\delta (j)}^{\omega_{j} } } } \right)^{\lambda }\left( {\prod\limits_{j=1}^{n} {(1-f_{i\delta (j)} )^{\omega_{j} }} } \right)^{(1-\lambda )}} \right\rangle \\ \end{array}. $$
    (12)
  2. Step 2

    The score values of E(s i ) (accuracy degrees of N(s i ) if necessary) (i = 1, 2, …, m) are calculated by (1) ((2) if necessary).

  3. Step 3

    All the alternatives are ranked according to the score values (accuracy degrees) in a descending order and the best choice is determined corresponding to the alternative with the largest value.

  4. Step 4

    End.

5 Decision-making of mechanical design schemes for press machine

In this section, a decision-making problem regarding mechanical design schemes of press machine is presented as a case to show the application and effectiveness of the proposed method.

Let us consider the conceptual design of press machine adapted from [24] as a case, a mechanical designer generally considers the design of movement schemes, such as the reducing mechanism and the working mechanism, with respect to press machine. According to the functional requirements of press machine, a set of four design schemes (alternatives) P = { p 1, p 2, p 3, p 4} is proposed primarily by specialists’ analyses and designers’ experiences, which are shown in Table 1. To evaluate these design schemes (alternatives), they must satisfy the requirements of four attributes: (1) q 1 is the manufacturing cost; (2) q 2 is the mechanical structure; (3) q 3 is the transmission effectiveness; (4) q 4 is the reliability. The four possible alternatives of p i (i = 1, 2, 3, 4) are to be evaluated by the chief designer (decision maker) under the above four attributes according to suitability evaluation (fit evaluation), and then the evaluation values are represented by IFV s i j = < t i j , f i j > for t i j ≥ 0, f i j ≥ 0, and 0 ≤ t i j + f i j ≤ 1 (j = 1, 2, …, n; i = 1, 2, …, m), which can be constructed as the following intuitionistic fuzzy decision matrix:

$$M=(s_{ij} )_{4\times 4} ={\begin{array}{ll} & { \; q_{1} \; \;\; q_{2} \;\;\; q_{3} \;\;\; q_{4}}\\ {{\begin{array}{l} {p_{1} }\\ {p_{2} }\\ {p_{3} }\\ {p_{4} }\\ \end{array} }}& {\left[ {{\begin{array}{llll} {\left\langle {0.9,0.1} \right\rangle }& {\left\langle {0.92,0.05} \right\rangle }& {\left\langle {0.9,0.1} \right\rangle }& {\left\langle {0.7,0.2} \right\rangle }\\ {\left\langle {0.9,0.1} \right\rangle }& {\left\langle {0.97,0.0} \right\rangle }& {\left\langle {0.85,0.1} \right\rangle }& {\left\langle {0.8,0.1} \right\rangle }\\ {\left\langle {0.8,0.1} \right\rangle }& {\left\langle {0.65,0.3} \right\rangle }& {\left\langle {0.8,0.1} \right\rangle }& {\left\langle {0.7,0.2} \right\rangle }\\ {\left\langle {0.7,0.2} \right\rangle }& {\left\langle {0.8,0.15} \right\rangle }& {\left\langle {0.75,0.2} \right\rangle }& {\left\langle {0.9,0.1} \right\rangle }\\ \end{array}}} \right]}\\ \end{array}}. $$
Table 1 Four design schemes (alternatives) for press machine
Full size table

Thus, the proposed method can be applied to the MADM problem regarding design schemes of press machine.

When the weight vector of the four attributes is considered as w = (0.3, 0.25, 0.25, 0.2) in the decision-making problem, the decision procedures are described as follows:

  1. Step 1

    The aggregated values of s i (i = 1, 2, …, m) for each alternative p i (i = 1, 2, …, m) are calculated by (11) (generally taking λ = 0.5) as follows:

    s 1 = <0.8713 0.1028>, s 2 = <0.8944 0.0387>, s 3 = <0.7450 0.1629>, and s 4 = <0.7831, 0.1652>.

  2. Step 2

    The score values of E(s i ) for each alternative p i (i = 1, 2, 3, 4) are calculated by (1) as follows:

    E(s 1) = 0.7685 E(s 2) = 0.8556, E(s 3) = 0.5821 and E(s 4) = 0.6179

  3. Step 3

    According to the ranking order of the score values E(s 2) > E(s 1) > E(s 4) > E(s 3) the four design schemes are ranked as p 2 > p 1 > p 4 > p 3. Hence, the best design scheme is p 2.

When the ordered important positions of all the given arguments are considered as the associated weight vector ω = (0.1, 0.7, 0.1, 0.1) in the decision-making problem, the decision procedures are described as follows:

  1. Step 1’

    The aggregated values of s i (i = 1, 2, …, m) for each alternative p i (i = 1, 2, …, m) are calculated by (12) for λ = 0.5 as follows:

    s 1 = <0.8852 0.129>, s 2 = <0.8960, 0.0463>, s 3 = <0.7764 0.1261>, and s 4 = <0.7974, 0.1540>.

  2. Step 2’

    The score values of E(s i ) for each alternative p i (i = 1, 2, 3, 4) are calculated by (1) as follows:

    E(s 1) = 0.7823, E(s 2) = 0.8497, E(s 3) = 0.6503, and E(s 4) = 0.6434.

  3. Step 3’

    According to the ranking order of the score values E(s 2) > E(s 1) > E(s 3) > E(s 4) the four design schemes are ranked as p 2 > p 1 > p 3 > p 4. Hence, the best design scheme is p 2.

6 Comparison with related methods

Firstly, compared with the decision-making method based on cosine similarity measures of IFSs introduced in [24], the ranking order of the developed method based on the IFHWAGA operator is in accordance with [24] although decision-making methods are different under an intuitionistic fuzzy environment. Then, a few differences between the method based on the IFHOWAGA operator and the method based on cosine similarity measures in [24] are shown in the ranking orders because the IFHOWAGA operator considers the ordered position weight values of the given arguments. However, the best design scheme given in all the decision-making methods shows the same results. Clearly, the ordered position weight values of the given arguments may influence the ranking order of the design schemes, but the effect is small in this decision-making case.

Then, by comparing the proposed approach with existing related methods based on the IFWAA IFWGA, IFOWAA, and IFOWGA operators [4, 7], all the results have been given in Table 2.

Table 2 Decision results based on various aggregation operators
Full size table

The results given in Table 2 show that all the aggregated values of the IFHWAGA and IFHOWAGA operators are more or less closed to moderate values between the aggregated values of the IFWAA and IFWGA operators and between the aggregated values of the IFOWAA and IFOWGA operators. Then, all the ranking orders based on the IFWAA IFWGA, and IFHWAGA operators are identical; while the ranking orders based on the IFOWAA IFOWGA, and IFHOWAGA operators are identical. However, the ranking orders based on the IFWAA IFWGA, and IFHWAGA operators are different from the ones based on the IFOWAA IFOWGA, and IFHOWAGA operators, where the ordered position weight values of the given arguments show bigger differences. Since decision makers in the developed MADM method can select some desired value of λ according to their preference or practical demands, the developed MADM method is more flexible than the existing MADM methods using the IFWAA, IFOWAA, IFWGA and IFOWGA operators [4, 7].

Although the same ranking orders are shown in Table 2 based on the previous operators (IFWAA and IFWGA or IFOWAA and IFOWGA) and the new operator (IFHWAGA or IFHOWAGA), the results discussed in the aforementioned numerical examples (Cases 1 and 2) have indicated that the new operators can avoid the shortcomings of the previous operators. In the extreme cases, however, the previous operators may result in unsuitable results, while the new operators can demonstrate the moderate values in the information aggregations (as mentioned in the Section 3.3). Then, the previous operators indicate different focal points because the IFWAA and IFOWAA operators emphasize group’s major points [4, 7] and the IFWGA and IFOWGA operators emphasize personal major points [4, 7]. It is obvious that the new operators can overcome the shortcomings of the previous operators and show their rationality in the information aggregations. Furthermore, because the new operators improve the previous operators and the previous operators are the special cases of the new operators, the new operators are superior to the previous operators in the intuitionistic fuzzy information aggregations. Therefore, the presented decision-making method using the IFHWAGA or IFHOWAGA operators is more suitable and more effective than the existing decision-making methods based on the IFWAA, IFOWAA, IFWGA, and IFOWGA operators and shows better applied perspective under an intuitionistic fuzzy decision-making environment.

7 Conclusion

To overcome some shortcomings implied by the IFWAA, IFOWAA, IFWGA, and IFOWGA operators for aggregating intuitionistic fuzzy information in some cases, this paper presented the IFHWAGA and IFHOWAGA operators for IFVs and investigated their suitability by the numerical examples. Then, we developed the MADM method of mechanical design schemes based on the IFHWAGA or IFHOWAGA operator. Finally, the decision-making problem regarding mechanical design schemes of press machine was provided as a case to demonstrate the application of the proposed method. However, the proposed method is more suitable and more flexible than existing related methods based on the IFWAA, IFOWAA, IFWGA, and IFOWGA operators under an intuitionistic fuzzy environment. In the future work, the developed method will be further extended to interval-valued IFVs, neutrosophic sets, and other applications, such as pattern recognition and medical diagnosis.