An enhanced KNN-based twin support vector machine with stable learning rules

Abstract

Among the extensions of twin support vector machine (TSVM), some scholars have utilized K-nearest neighbor (KNN) graph to enhance TSVM’s classification accuracy. However, these KNN-based TSVM classifiers have two major issues such as high computational cost and overfitting. In order to address these issues, this paper presents an enhanced regularized K-nearest neighbor-based twin support vector machine (RKNN-TSVM). It has three additional advantages: (1) Weight is given to each sample by considering the distance from its nearest neighbors. This further reduces the effect of noise and outliers on the output model. (2) An extra stabilizer term was added to each objective function. As a result, the learning rules of the proposed method are stable. (3) To reduce the computational cost of finding KNNs for all the samples, location difference of multiple distances-based K-nearest neighbors algorithm (LDMDBA) was embedded into the learning process of the proposed method. The extensive experimental results on several synthetic and benchmark datasets show the effectiveness of our proposed RKNN-TSVM in both classification accuracy and computational time. Moreover, the largest speedup in the proposed method reaches to 14 times.

1 Introduction

Support vector machine (SVM) proposed by Vapnik et al. [3] is a state-of-the-art binary classifier. It is on the basis of statistical learning theory and structural risk minimization (SRM) [36]. Due to the SVM’s great generalization ability, it has been applied successfully in a wide variety of applications, such as arrhythmia detection [22, 31], medical diagnosis [14], network intrusion [1], and spam detection [25]. Its main idea is to find an optimal separating hyperplane between two classes of samples by solving a complex Quadratic Programming Problem (QPP) in the dual space.

Researchers have proposed many classifiers on the basis of SVM [24]. For example, Fung and Mangasrian [18] proposed proximal support vector machine (PSVM) which generates two parallel hyperplanes for classifying samples instead of a single hyperplane. In 2002, Lin and Wang proposed [16] fuzzy support vector machine (FSVM) which introduces fuzzy membership of samples to each of the classes. As a result, the output model of FSVM is less sensitive to noise and outliers. Later Mangasrian and Wild [19] proposed generalized eigenvalue proximal SVM (GEPSVM) on the basis of PSVM. It generates two non-parallel hyperplanes such that each plane is closest to one of the two classes and as far as possible from the other class.

In 2007, Jayadeva et al. [15] proposed twin support vector machine (TSVM) to reduce the computational complexity of standard SVM. TSVM does classification by generating two non-parallel hyperplanes. Each of which is as close as possible to one of the two classes and as far as possible from samples of the other class. To obtain two non-parallel hyperplanes, TSVM solves two smaller-sized QPPs. This makes the learning speed of TSVM classifier four times faster than that of SVM in theory.

Over the past decade, many extensions of TSVM have been proposed [5, 6, 13]. In 2012, Yi et al. [42] proposed weighted twin support vector machines with local information (WLTSVM). By finding k-nearest neighbors for all the samples, WLTSVM gives different weights to samples of each class based on the number of its nearest neighbors. This approach is better than TSVM in terms of accuracy and computational complexity. It also considers only one penalty parameter as opposed to two parameters in TSVM. In 2014, Nasiri et al. [23] proposed an energy-based least squares twin support vector machine (ELS-TSVM) by introducing an energy parameter for each hyperplane. In ELS-TSVM, different energy parameters are selected according to prior knowledge to reduce the effect of noise and outliers.

In 2015, Pan et al. [26] proposed K-nearest neighbor-based structural twin support vector machine (KNN-STSVM). Similar to S-TSVM [30], this method incorporates the data distribution information by using Ward’s linkage clustering algorithm. However, the KNN method applied in S-TSVM to give different weight to each sample and remove redundant constraints. As a result, the classification accuracy and computational complexity of S-TSVM were improved.

In 2016, Xu [40] proposed K-nearest neighbor-based weighted multi-class twin support vector machine (KWM-TSVM). It embodies inter-class and intra-class information into the objective function of Twin-KSVC [41]. As a result, the computational cost and prediction accuracy of the classifier were improved. Recently, Xu [27] proposed a safe instance reduction to reduce the computational complexity of KWM-TSVM. This method is safe and deletes a large portion of samples of two classes. Therefore, the computational cost will be decreased significantly.

It should be noted that many weighted TSVM methods were proposed over the past few years. However, this paper is concerned with KNN-based TSVM methods [26, 40, 42]. Therefore, it addresses the drawbacks of these methods which are explained as follows:

• 1. These methods give weight to samples of each class solely by counting the number of k-nearest neighbors of each sample. However, they do not consider the distance between pairs of nearest neighbors. To further improve the identification of highly dense samples, weight can be given to a sample with respect to the distance from its nearest neighbors. In other words, a sample with closer neighbors is given higher weight than the one with farther neighbors.

• 2. Similar to TSVM, these classifiers minimize the empirical risk in their objective functions, which may lead to the overfitting problem and reduce the prediction accuracy [33]. To address this issue, the trade-off between overfitting and generalization can be determined by adding a stabilizer term to each objective function.

• 3. These KNN-based classifiers utilize full search algorithm (FSA) to find k-nearest neighbors of each sample. The FSA method has a time complexity of ${\mathcal {O}}(n^2)$ which is time-consuming for large-scale datasets. However, scholars have proposed new KNN methods which have lower computational cost than that of the FSA algorithm. For instance, Xia et al. [39] proposed location difference of multiple distances-based k-nearest neighbors algorithm (LDMDBA). This method can be used to reduce the overall computational complexity of KNN-based TSVM classifiers.

Motivated by the above discussion and studies, we propose an enhanced regularized K-nearest neighbor-based twin support vector machine (RKNN-TSVM). Different from other KNN-based TSVM methods [26, 40, 42], the proposed method gives weight to each sample with respect to the distance from its nearest neighbors. This further enhances the identification of highly dense samples, outliers and, noisy samples. Moreover, due to the minimization of the SRM principle, the optimization problems of the proposed method are positive definite and stable.

The high computational cost is the main challenge of our proposed method, especially for large-scale datasets. So far, many fast KNN algorithms were proposed to accelerate finding K-nearest neighbors of samples, including k-dimensional tree (k-d tree) [8], a lower bound tree (LB tree) [2], LDMDBA algorithm [39] and so on. The recently proposed LDMDBA method has a time complexity of ${\mathcal {O}}(\log {d}n\log {n})$ which is less than the FSA algorithm and most of other KNN methods. In addition, this method does not rely on any tree structure so that it is efficient for datasets of high dimensionality. In this paper, the LDMDBA algorithm is introduced into our proposed method to speed up KNN finding.

The main advantages of our proposed method can be summarized as follows:

• In comparison with other KNN-based TSVM classifiers [26, 40, 42], the proposed method gives weight to samples differently. The weight of each sample was calculated based on the distance between its nearest neighbors. This further improves fitting hyperplanes with highly dense samples. In the proposed method, samples with closer neighbors are weighted more heavily than the one with farther neighbors.

• The proposed method has two additional parameters for determining the trade-off between overfitting and generalization. As a result, the learning rules of our RKNN-TSVM are stable and do not overfit the output model to all the training samples.

• As previously stated, the KNN finding reduces significantly the learning speed of our classifier. The LDMDBA algorithm [39] was employed to further reduce the overall computational complexity of the proposed method. This KNN algorithm has lower time complexity than the FSA algorithm. Moreover, the LDMDBA algorithm is effective for nonlinear case where samples are mapped from input space to higher dimensional feature space.

• Due to the giving weight to samples w.r.t the distance from their nearest neighbors, the proposed method gives much less weight to noisy samples and outliers. Consequently, the output model is less sensitive and potentially more robust to the outliers and noise.

The rest of this paper is organized as follows. Section 2 presents the notation used in the rest of the paper, briefly reviews TSVM, WLTSVM, and LDMDBA algorithm. Section 3 gives the detail of the proposed method, including linear and nonlinear cases. Algorithm analysis of RKNN-TSVM is given in Sect. 4. Section 5 discusses the experimental results on synthetic and benchmark datasets to investigate the validity and effectiveness of our proposed method. Finally, the concluding remarks are given in Sect. 6.

2 Backgrounds

This section defines the notation that will be used in the rest of the paper and includes the brief description of conventional TSVM, WLTSVM, and LDMDBA algorithm.

2.1 Notation

Let $T=\{(x_1, y_1), \ldots , (x_n, y_n)\}$ be the full training set of nd-dimensional samples. where $x_{i} \in {\mathbb {R}}^{d}$ is a feature vector and $y_{i} \in \{-1, 1\}$ are corresponding labels. Let $X^{(i)} = [x_{1}^{(i)},x_{2}^{(i)},\ldots ,x_{n_{i}}^{(i)}],i=1,2$ be a matrix consisting of $n_{i}$ samples that are d dimensional in class i, $X^{(i)} \in T$, $X^{(i)} \in {\mathbb {R}}^{n_{i} \times d}$. For convenience, matrix A in ${\mathbb {R}}^{n_1 \times d}$ represents the samples of class 1 and matrix B in ${\mathbb {R}}^{n_2 \times d}$ represents the samples of class $-1$, where $n_1 + n_2 = n$. Table 1 provides a summary of the notation used in this paper.

Table 1 Summary of notation used throughout the paper

2.2 Twin support vector machine

TSVM [15] is binary classifier whose idea is to find two non-parallel hyperplanes. To explain this classifier, consider a binary classification problem of $n_{1}$ samples belonging to class $+1$ and $n_{2}$ samples belonging to class $-1$ in the d-dimensional real space ${\mathbb {R}}^{d}$. The linear TSVM [15] seeks a pair of non-parallel hyperplanes as follows:

$$\begin{aligned} {{x}^T}{{w}_{1}}+{{b}_{1}}=0 \quad {\text {and}} \quad {{x}^T}{{w}_{2}}+{{b}_{2}}=0 \end{aligned}$$

(1)

such that each hyperplane is closest to the samples of one class and far from the samples of other class, where $w_{1} \in {\mathbb {R}}^{d}$, $w_{2} \in {\mathbb {R}}^{d}$, $b_{1} \in {\mathbb {R}}$ and $b_{2} \in {\mathbb {R}}$.

To obtain the above hyperplanes (1), TSVM solves two primal QPPs with objective function corresponding to one class and constrains corresponding to other class.

$$\begin{aligned} {\mathop {{ \text {min}}}\limits _{w_{1} ,b_{1}}}&\qquad \frac{1}{2}{{\left\| A{{w}_{1}}+{{e}_{1}}{{b}_{1}} \right\| }^{2}}+{{c}_{1}}e_{2}^{T}\xi \nonumber \\ {\text {s.t. }}&\qquad -(B{{w}_{1}}+{{e}_{2}}{{b}_{1}})+\xi \ge {{e}_{2}},\xi \ge 0\end{aligned}$$

(2)

$$\begin{aligned} \,{\mathop {{\text {min}}}\limits _{w_{2} ,b_{2}}}&\qquad \frac{1}{2}{{\left\| B{{w}_{2}}+{{e}_{2}}{{b}_{2}} \right\| }^{2}}+{{c}_{2}}e_{1}^{T}\eta \nonumber \\ {\text {s.t.} }&\qquad (A{{w}_{2}}+{{e}_{1}}{{b}_{2}})+\eta \ge {{e}_{1}},\eta \ge 0 \end{aligned}$$

(3)

where $c_1$ and $c_2$ are positive penalty parameters, $\xi _{1}$ and $\xi _{2}$ are slack vectors, $e_1$ is the column vectors of ones of $n_{1}$ dimensions and $e_{2}$ is the column vectors of ones of $n_{2}$ dimensions.

By introducing Lagrangian multipliers $\alpha \in {\mathbb {R}}^{n_{2}}$ and $\beta \in {\mathbb {R}}^{n_{1}}$, the Wolfe dual of QPPs (2) and (3) are given by:

$$\begin{aligned} {\mathop {{ \text {min}}}\limits _{\alpha }}&\qquad \frac{1}{2}{{\alpha }^{T}}G{{({{H}^{T}}H)}^{-1}}{{G}^{T}}\alpha -e_{2}^{T}\alpha \nonumber \\ {\text {s.t. }}&\qquad 0{{e}_{2}}\le \alpha \le {{c}_{1}}{{e}_{2}}\end{aligned}$$

(4)

$$\begin{aligned} {\mathop {{ \text {min}}}\limits _{\beta }}&\qquad \frac{1}{2}{{\beta }^{T}}H{{({{G}^{T}}G)}^{-1}}{{H}^{T}}\beta -e_{1}^{T}\beta \nonumber \\ {\text {s.t. }}&\qquad 0{{e}_{1}}\le \beta \le {{c}_{2}}{{e}_{1}} \end{aligned}$$

(5)

where $H=[A \,e]$ and $G=[B\,e]$. From the dual problems of (4) and (5), one can notice that QPPs (4) and (5) have $n_1$ and $n_2$ parameters, respectively, as opposed to $n=n_{1}+n_{2}$ parameters in standard SVM.

After solving the dual QPPs (4) and (5), the two non-parallel hyperplanes are given by:

$$\begin{aligned} \left[ \begin{aligned}&{{w}_{1}} \\&{{b}_{1}} \\ \end{aligned}\right] = -{{({{H}^{T}}H)}^{-1}}{{G}^{T}}\alpha \end{aligned}$$

(6)

and

$$\begin{aligned} \left[ \begin{aligned}&{{w}_{2}} \\&{{b}_{2}} \\ \end{aligned}\right] = {{({{G}^{T}}G)}^{-1}}{{H}^{T}}\beta \end{aligned}$$

(7)

In addition to solving dual QPPs (4) and (5), TSVM also requires inversion of matrices ${{H}^{T}}H$ and ${{G}^{T}}G$ which are of size $(d+1)\times (d+1)$ where $d \ll n$.

A new testing sample $x \in {\mathbb {R}}^{d}$ is assigned to class $i(i=-1,+1)$ by

$$\begin{aligned} \underset{{}}{\mathop {{\text{Class}}\,i=\underset{j=1,2}{\mathop {arg\min }}\,}}\,\frac{\left| {{x}^{T}}{{w}_{j}}+{{b}_{j}} \right| }{\left\| w_j\right\| } \end{aligned}$$

(8)

where |.| denotes the perpendicular distance of sample x from the hyperplane. TSVM was also extended to handle nonlinear kernels by using two non-parallel kernel generated-surfaces [15].

In TSVM, if the number of samples in two classes is approximately equal to n/2, then its computational complexity is ${\mathcal {O}}(1/4n^{3})$. This implies that TSVM is approximately four times faster than standard SVM in theory [15].

2.3 Weighted twin support vector machine with local information

One of the issues of TSVM is that it fails to determine the contribution of each training sample to the output model. Therefore, its output model becomes sensitive to noise and outliers. WLTSVM [42] addressed this issue by finding the KNNs of all training samples. This method constructs intra-class graph $W_{s}$ and inter-class graph $W_{d}$ to embed weight of each samples into optimization problems of TSVM. As a result, it fits samples with high-density as opposed to TSVM whose hyperplane fits all the samples of its own class. Figure 1 indicates a geometrical comparison between linear TSVM and linear WLTSVM classifier in two-dimensional real space ${\mathbb {R}}^{2}$. As shown in Fig. 1, WLTSVM is less sensitive to outliers and noisy samples than TSVM.

Fig. 1

The geometric comparison of standard TSVM with WLTSVM classifier

WLTSVM solves a pair of smaller sized QPPs as follows:

$$\begin{aligned} {\mathop {{ \min }}\limits _{w_{1} ,b_{1}}} \qquad&\frac{1}{2}\sum \limits _{i=1}^{n_{1}}{\sum \limits _{j=1}^{n_{1}}{W^{(1)}_{s,ij}(w^{T}_{1}x^{(1)}_{j}+b_{1})^{2}}}+c\sum \limits _{j=1}^{n_{2}}\xi _j \nonumber \\ {\text {s.t.} } \qquad&-f^{(2)}_{j}(w^{T}_{1}x^{(2)}_{j}+b_{1})+\xi _{j} \ge f^{(2)}_{j} \nonumber \\&\xi _{j} \ge 0,\quad j=1,\ldots ,n_{2} \end{aligned}$$

(9)

and

$$\begin{aligned} {\mathop {{ \min }}\limits _{w_{2} ,b_{2}}}&\qquad \frac{1}{2}\sum \limits _{i=1}^{n_{2}}{\sum \limits _{j=1}^{n_{2}}{W^{(2)}_{s,ij}(w^{T}_{2}x^{(2)}_{j}+b_{2})^{2}}}+c\sum \limits _{j=1}^{n_{1}}\eta _j \nonumber \\ {\text {s.t. }}&\qquad f^{(1)}_{j}(w^{T}_{2}x^{(1)}_{j}+b_{2})+\eta _{j} \ge f^{(1)}_{j} \nonumber \\&\quad \eta _{j} \ge 0,\quad j=1,\ldots ,n_{2} \end{aligned}$$

(10)

In the optimization problems of WLTSVM (9) and (10), different weights are given to the samples of each class according to their KNNs. Unlike TSVM, the optimal hyperplane should be far from the margin points instead of all the samples of other class. This further reduces the time complexity by keeping only margin points in the constraints. Moreover, WLTSVM has only one penalty parameter as opposed to two in TSVM.

To obtain the solution, the dual problems for (9) and (10) are solved, respectively:

$$\begin{aligned} {\mathop {{ \min }}\limits _{\alpha }}&\qquad \frac{1}{2}{{\alpha }^{T}}(F^{T}G){{({{H}^{T}}DH)}^{-1}}{({G}^{T}F)}\alpha -e_{2}^{T}F\alpha \nonumber \\ {\text {s.t.} }&\qquad 0{{e}_{2}}\le \alpha \le {{c}}{{e}_{2}}\end{aligned}$$

(11)

$$\begin{aligned} {\mathop {{ \min }}\limits _{\beta }}&\qquad \frac{1}{2}{{\beta }^{T}}(P^{T}H){{({{G}^{T}}QG)}^{-1}}{({H}^{T}P)}\beta -e_{1}^{T}P\beta \nonumber \\ {\text {s.t.} }&\qquad 0{{e}_{1}}\le \beta \le {{c}}{{e}_{1}} \end{aligned}$$

(12)

where $D={\mathrm{diag}}(d^{(1)}_{1},d^{(1)}_{2},\dots ,d^{(1)}_{n_{1}})$, $Q={\mathrm{diag}}(d^{(2)}_{1},d^{(2)}_{2}, \dots ,d^{(2)}_{n_{2}})$, $F={\mathrm{diag}}(f^{(2)}_{1},f^{(2)}_{2},\ldots ,f^{(2)}_{n_{2}})$ and $P={\mathrm{diag}}(f^{(1)}_{1}, f^{(1)}_{2},\dots ,f^{(1)}_{n_{1}})$ are diagonal matrices, respectively ($f_{j}$ is either 0 or 1.). Both $e_1$ and $e_2$ are vectors of all ones of $n_1$ and $n_2$ dimensions, respectively.

Similar to TSVM, a new sample is classified as class $+1$ or class $-1$ depends on which of the two hyperplanes it lies nearest to. Although WLTSVM has clear advantages over TSVM such as better classification ability and less computational cost, it has the following drawbacks:

• 1. WLTSVM gives different treatments and weight to each sample by only counting the number of its nearest neighbors. For instance, the weight of each sample in class $+1$ can be computed as follows:

  $$\begin{aligned} {{d}_{j}^{(1)}}=~\underset{i=1}{\overset{{{n}_{1}}}{\mathop \sum }}\,{{W}_{s,ij}}~,~j=1,2,\ldots ,{{n}_{1}} \end{aligned}$$

  (13)

  where $d_{j}^{(1)}$ denotes the weight of sample $x_{j}$. It should be noted that $W_{s,ij}$ is either 0 or 1. This implies that WLTSVM treats the nearest neighbors of each sample similarly. Therefore, the weight matrix $W_{s,ij}$ contains only binary values.

• 2. In order to deal with matrix singularity, the inverse matrices $({H}^{T}DH)^{-1}$ and $({G}^{T}QG)^{-1}$ are approximately replaced by $({H}^{T}DH + \varepsilon I)^{-1}$ and $({G}^{T}QG + \varepsilon I)^{-1}$, respectively, where $\varepsilon$ is a positive scalar. Hence only approximate solutions to (11) and (12) are obtained.

• 3. Although WLTSVM reduces the time complexity by keeping only margin points in the constraints, it has to find k-nearest neighbors for all the samples. Consequently, the overall computational complexity of WLTSVM is about ${\mathcal {O}}(2n_{1}^{3}+n^{2}logn)$ under the assumption that $n_{1}=n_{2}$, where $n_{1},n_{2} \ll n$. This makes WLTSVM impractical for large-scale datasets. To mitigate this problem, fast KNN methods can be utilized.

The proposed method addresses these aforementioned issues.

2.4 Location difference of multiple distances-based nearest neighbors searching algorithm (LDMDBA)

The LDMDBA algorithm [39] introduced the concept of location difference among different samples. The central idea of this method is that the nearest neighbors of each sample can be found when their distance from some reference points is known. Due to this idea, the LDMDBA algorithm avoids computing distance between each pair of samples.

Consider the KNN finding problem with training set T (defined in Table 1), a sample $x_{j} \in T$ and the distance from reference point $O_{1}$ to $x_j$ is denoted as $Dis_{1}(x_{j})=\left\| x_{j}-O_{1}\right\|$. According to [39], the number of reference points is taken as $\log _{2}{d}$. The values of the first i dimensions of the ith reference point $O_{i}$ can be set to $-1$ and other values are set to 1 (i.e., $O_{i}=(-1,-1,\dots ,-1,1,\dots ,1)$, where the number of value $-1$ is equal to i). The neighbors of the sample $x_j$ found using the ith reference point are denoted by $Nea_{i}(x_{j})$.

To compute $Nea_{i}(x_{j})$, the distance from all the reference points to the sample $x_{i}$ are first computed. After sorting the distance values, a sorted sequence is obtained. The k-nearest neighbors of sample $x_{j}$ are mostly located in a subsequence with the center sample $x_{j}$ in the sequence. The length of the subsequence can be denoted as $2k*\varepsilon$ where $\varepsilon$ is set to $\log _{2}{\log _{2}{n}}$ (more information on how the value $\varepsilon$ was determined can be found in [39]). Finally, all the exact Euclidean distance between samples in the subsequence are computed. Those samples corresponding to the k-smallest distances in the subsequence can be considered as the k-nearest neighbor of the sample $x_{j}$. For clarity, the LDMDBA algorithm is explicitly stated.

Algorithm 1 LDMDBA (location difference of multiple distances-based algorithm) Given a training set T, let k be the number of nearest neighbors in the algorithm. Starting with $i=1$, the k-nearest neighbors of each sample $x_{j} \in T$ can be obtained using the following steps:

• 1. The ith reference point $O_{i}$ is set as a vector whose values of the first i dimensions are equal to $-1$, and the other values are set to 1.

• 2. Compute the distance from ith reference point $O_{i}$ to all the samples using $Dis_{i}(x_{j})=\left\| x_{j}-O_{i}\right\| , \forall i \in \{1,\dots ,\log _{2}{d}\}$.

• 3. Sort the samples by the values of $Dis_{i}$ and generate a sorted sequence.

• 4. For a subsequence of the samples with the fixed range $2k*\log _{2}{\log _{2}{n}}$ and center sample $x_{j}$, compute all the exact Euclidean distances from the sample $x_{j}$ to the samples in the subsequence.

• 5. Sort the distance values obtained in the step 4.

• 6. The k-smallest Euclidean distances in the sorted subsequence are k-nearest neighbors of the sample $x_j$.

• 7. If the neighbors of all the samples using all the reference points have been computed, terminate; otherwise, set $i=i+1$, and go to the step 1.

In the Algorithm 1, the time complexity of the step 3 and the step 5 is determined by the used sorting algorithm which is ${\mathcal {O}}(n\log _{2}{n})$. Therefore, the overall computational complexity of the LDMDBA algorithm is ${\mathcal {O}}(\log {d}n\log {n})$. However, the FSA algorithm has a time complexity of ${\mathcal {O}}(n^{2}\log _{2}n)$ as described in the Algorithm 2.

Moreover, LDMDBA algorithm does not rely on any dimensionality dependent tree structure. As a result, it can be effectively applied to various high dimensional datasets. The experimental results of [39] indicate the effectiveness of LDMDBA algorithm over the FSA algorithm and other existing KNN algorithms.

3 Regularized k-nearest neighbor based twin support vector machine (RKNN-TSVM)

In this section, we present our classifier called regularized k-nearest neighbor-based twin support vector machine (RKNN-TSVM). It gives weight to each sample with respect to the distance from its nearest neighbors. Also, the proposed method avoids overfitting by considering the SRM principle in each objective function.

3.1 The definition of weight matrices

As discussed in Sect. 1, the existing KNN-based TSVM classifiers [26, 40, 42] constructs a k-nearest neighbor graph G to exploit similarity among samples. In these methods, the weight of G is defined as:

$$\begin{aligned} W_{ij} = {\left\{ \begin{array}{ll} 1, &{} {\text{ if }} x_i \in Nea\left( x_j\right) {\text{ or }} x_j \in Nea\left( x_i\right) ,\\ 0, &{} {\text{ otherwise}}. \end{array}\right. } \end{aligned}$$

(14)

where $Nea(x_{j})$ stands for the set of k-nearest neighbors of the sample $x_{j}$ which is defined as:

$$\begin{aligned} Nea(x_j) = \{x^{i}_{j} \mid {\text {if }} x^{i}_{j} {\text { is\, a\, knn\, of }} x_{j} ,1 \le i \le k \} \end{aligned}$$

(15)

the set $Nea(x_{j})$ is arranged in an increasing order in terms of Euclidean distance $d(x_{j},x^{i}_{j})$ between $x_{j}$ and $x^{i}_{j}$.

$$\begin{aligned} d(x_{j},x^{i}_{j})= \sqrt{(x_{j} - x^{i}_{j})^{T}(x_{j} - x^{i}_{j})} \end{aligned}$$

(16)

However, the value of $W_{ij}$ is either 0 or 1. This implies that weight of the sample $x_{j}$ is obtained by solely counting the number of its nearest neighbors. To address this issue, weight can be given to a sample based on the distance between its nearest neighbors. Motivated by [7, 10], the matrix of G is redefined as follows:

$$\begin{aligned} W_{ij} = {\left\{ \begin{array}{ll} \acute{w_{ij}}, & {\text {if }} x_{i} \in Nea\left( x_{j}\right) {\text { or} } x_j \in Nea\left( x_i\right) , \\ 0, & {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(17)

where $\acute{w_{ij}}$ is the weight of i-th nearest neighbor of the sample $x_{j}$ which is given by:

$$\begin{aligned} \acute{w_{ij}} = {\left\{ \begin{array}{ll} \frac{d(x_{i},x^{k}_{j}) - d(x_{i},x_{j})}{d(x_{i},x^{k}_{j}) - d(x_{i},x^{1}_{j})}, & {\text {if }} d\left( x_{i},x^{k}_{j} \right) \ne d\left( x_{i},x^{1}_{j} \right) , \\ 1, & {\text {if }} d\left( x_{i},x^{k}_{j} \right) = d\left( x_{i},x^{1}_{j} \right) . \end{array}\right. } \end{aligned}$$

(18)

According to Eq. (18), It can be noted that a neighbor $x_{i}$ with smaller distance is weighted more heavily than the one with the greater distance. Therefore, the values of $\acute{w_{ij}}$ are scaled linearly to the interval $\left[ 0,1\right]$.

Similar to (17), the weight matrices for class $+1$ and $-1$ are defined in (19) and (20), respectively.

$$\begin{aligned} W_{s,ij} = {\left\{ \begin{array}{ll} \acute{w_{ij}}, &{} {\text {if }} x_{i} \in Nea_{s}\left( x_{j}\right) {\text { or }} x_j \in Nea_{s}\left( x_i\right) , \\ 0, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(19)

and

$$\begin{aligned} W_{d,ij} = {\left\{ \begin{array}{ll} \acute{w_{ij}}, &{} {\text {if }} x_{i} \in Nea_{d}\left( x_{j}\right) , \\ 0, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(20)

where $Nea_{s}(x_{j})$ stands for the k-nearest neighbors of the sample $x_{j}$ in the class $+1$ and $Nea_{d}(x_{j})$ denotes the k-nearest neighbors of the sample $x_{j}$ in the class $-1$. Specifically,

$$\begin{aligned} Nea_{s}\left( x_j\right) = \{x^{i}_{j} \mid l(x^{i}_{j}) = l(x_{j}), 1 \le i \le k \} \end{aligned}$$

(21)

and

$$\begin{aligned} Nea_{d}\left( x_j\right) = \{x^{i}_{j} \mid l(x^{i}_{j}) \ne l(x_{j}), 1 \le i \le k \} \end{aligned}$$

(22)

where $l(x_{j})$ denotes the class label of the sample $x_{j}$. Clearly, $Nea_{s}(x_j)\,\cap \, Nea_{d}(x_j)= \varnothing$ and $Nea_{s}(x_j)\, \cup \, Nea_{d}(x_j) = Nea(x_j)$. When $W_{s,ij} \ne 0$ or $W_{d,ij} \ne 0$, an undirected edge between node $x_{i}$ and $x_{j}$ is added the corresponding graph.

Unlike TSVM, only the support vectors (SVs) instead of all the samples of the other class are important for optimal production of the hyperplane of the corresponding class. To directly extract possible SVs (margin points) from the samples in class $-1$, we redefine the weight matrix $W_{d}$ as follows:

$$\begin{aligned} f_{j} = {\left\{ \begin{array}{ll} 1, &{} \exists j, W_{d,ij} \ne 0, \\ 0, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(23)

The procedure of computing weight of samples and extracting margin points is outlined in the Algorithm 3.

3.2 Linear case

As stated in Sect. 3.1, the distance of a sample from its nearest neighbors plays an important role in finding highly dense samples. Following this, the yielded hyperplane is closer to highly dense samples of its own class. Figure 2 shows the basic thought of our RKNN-TSVM on a toy dataset. In this toy example, the hyperplanes of the proposed method are closer to the highly dense samples than WLTSVM. It can be observed that our RKNN-TSVM is potentially more robust to the outliers and noisy samples.

After finding the KNNs of all the samples, the weight matrix of class $+1$ (i.e., $W^{(1)}_{s_ij}$) and the margin points of class $-1$ (i.e., $f^{(2)}_{j}$) are obtained. The regularized primal problems of the proposed method are expressed as follows:

$$\begin{aligned} {\mathop {{ \min }}\limits _{w_{1} ,b_{1}}}&\quad \frac{1}{2}\sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}(w^{T}_{1}x^{(1)}_{i}+b_{1})^{2}}+c_{1}e_{2}^{T}\xi +\frac{c_{2}}{2}(\left\| w_{1}\right\| ^{2}+b^{2}_{1}) \nonumber \\ {\text {s.t. }}&\quad -f^{(2)}_{j}(w^{T}_{1}x^{(2)}_{j}+b_{1})+\xi _{j} \ge f^{(2)}_{j} \nonumber \\&\xi _{j} \ge 0,\quad j=1,\ldots ,n_{2} \end{aligned}$$

(24)

and

$$\begin{aligned} {\mathop {{ \min }}\limits _{w_{2} ,b_{2}}}&\quad \frac{1}{2}\sum \limits _{i=1}^{n_{2}}{d^{(2)}_{i}(w^{T}_{2}x^{(2)}_{i}+b_{2})^{2}}+c_{1}e_{1}^{T}\eta +\frac{c_{3}}{2}(\left\| w_{2}\right\| ^{2}+b^{2}_{2}) \nonumber \\ {\text {s.t. }}&\quad f^{(1)}_{j}(w^{T}_{2}x^{(1)}_{j}+b_{2})+\eta _{j} \ge f^{(1)}_{j} \nonumber \\ \quad\eta _{j} \ge 0,&\ j=1,\ldots ,n_{1} \end{aligned}$$

(25)

where $d^{(1)}_{j}$ denotes the weight of the sample $x^{(1)}_{j}$ which is given by

$$\begin{aligned} d^{(1)}_{j}=\sum ^{n_1}_{i=1} W^{(1)}_{s,ij},\quad j=1,2,\dots ,n_1 \end{aligned}$$

(26)

$c_{1},c_{2},c_{3} \ge 0$ are positive parameters. $\xi$ and $\eta$ are nonnegative slack variables, both $e_{1}$ and $e_{2}$ are column vectors of ones of $n_{1}$ and $n_{2}$ dimensions, respectively.

The difference between the primal problems of the proposed method and the existing KNN-based TSVM classifiers [26, 40, 42] is as follows:

• 1. Unlike WLTSVM, the value of $d^{(1)}_{j}$ depends on the distance of sample $x^{(1)}_{j}$ from its k-nearest neighbors. Therefore, the bigger the value of $d^{(1)}_{j}$, the higher dense is the sample $x^{(1)}_{j}$.

• 2. Different from these classifiers, a stabilizer $\frac{c_{2}}{2}(\left\| w_{1}\right\| ^{2}+b^{2}_{1})$ is added to the primal problems of (24) and (25). This makes the learning rules of our proposed method stable. In addition, the trade-off between overfitting and generalization is dependent upon the parameters $c_{2}$ and $c_{3}$.

Fig. 2

The basic thought of our RKNN-TSVM classifier. The high-density samples are denoted by green circles

Moreover, the proposed method also inherits the advantages of the existing KNN-based TSVM classifiers which are as follows:

• 1. The optimization problems (24) and (25) are convex QPPs which have globally optimal solution.

• 2. Similar to these classifiers, the computational complexity of the proposed method was reduced by only keeping the possible SVs (margin points) in the constraints.

To solve the optimization problem (24), the Lagrangian function is given by:

$$\begin{aligned}&L_{1}(w_{1},b_{1},\xi , \alpha , \gamma ) \nonumber \\&\quad = \frac{1}{2}\sum \limits _{i=1}^{n_{1}}{d^{(1)}_{j}(w^{T}_{1}x^{(1)}_{j}+b_{1})^{2}}+c_{1}e_{2}^{T}\xi +\frac{c_{2}}{2}(\left\| w_{1}\right\| ^{2}+b^{2}_{1}) \nonumber \\&\qquad -\,\sum \limits _{j=1}^{n_{2}}{\alpha _{j}(-f^{(2)}_{j}(w^{T}_{1}x^{(2)}_{j}+b_{1})+\xi _{j} - f^{(2)}_{j})} - \gamma ^{T}\xi \end{aligned}$$

(27)

where $\alpha =(\alpha _{1}, \alpha _{2}, \dots ,\alpha _{n_{2}})^{T}$ and $\gamma =(\gamma _{1}, \gamma _{2}, \dots , \gamma _{n_{2}})^{T}$ are the vectors of Lagrangian multipliers. By differentiating the Lagrangian function $L_{1}$ (27) with to respect to $w_{1}$, $b_{1}$, $\xi$, we can obtain the following the Karush-Kuhn-Tucker (KKT) conditions:

$$\begin{aligned} \frac{\partial L_{1}}{\partial w_{1}}&= {} \sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}x^{(1)}_{i}(w^{T}_{1}x^{(1)}_{i} + b_{1})} + c_{2}w_{1}\nonumber \\&\quad + \sum \limits _{j=1}^{n_{2}}{\alpha _{j}f_{j}^{(2)}x_{j}^{(2)}}=0, \end{aligned}$$

(28)

$$\begin{aligned} \frac{\partial L_{1}}{\partial b_{1}}&= \sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}(w^{T}_{1}x^{(1)}_{i} + b_{1})} + c_{2}b_{1} +\sum \limits _{j=1}^{n_{2}}{\alpha _{j}f_{j}^{(2)}}=0, \end{aligned}$$

(29)

$$\begin{aligned} \frac{\partial L_{1}}{\partial \xi }&= c_{1}e_{2} - \alpha - \gamma =0, \end{aligned}$$

(30)

$$\begin{aligned} \alpha \ge 0,\, \gamma \ge 0. \end{aligned}$$

(31)

Arranging Eqs. (28) and (29) in their matrix forms, we get the following equations:

$$\begin{aligned} A^{T}D(Aw_{1}+e_{1}b_{1})+c_{2}w_{1}+B^{T}F\alpha =0, \end{aligned}$$

(32)

$$\begin{aligned} e^{T}_{1}D(Aw_{1}+e_{1}b_{1}) + c_{2}b_{1}+e^{T}_{2}F\alpha =0, \end{aligned}$$

(33)

where $D={\mathrm{diag}}(d^{(1)}_{1},d^{(1)}_{2},\dots ,d^{(1)}_{n_{1}})$ (here, $d^{(1)}_{j} \ge 0$, $j=1,2,\dots ,n_{1}$) and $F={\mathrm{diag}}(f^{(2)}_{1},f^{(2)}_{2},\dots ,f^{(2)}_{n_{2}})$ are diagonal matrices. Obviously, $f^{(2)}_{j}$($j=1,2,\dots ,n_{2}$) is either 0 or 1. Since $\gamma \ge 0$, from (30) we have

$$\begin{aligned} 0e_{2} \le \alpha \le c_{1}e_{2} \end{aligned}$$

(34)

Next, combining (32) and (33) leads to the following equation

$$\begin{aligned} ([A^{T}\ e^{T}_{1}]D[A\ e_{1}] + c_{2}I)[w_{1}\ b_{1}]^{T} + [B^{T}\ e^{T}_{2}]F\alpha = 0. \end{aligned}$$

(35)

where I is an identity matrix of appropriate dimensions. Defining $H=[A\,e_{1}]$ and $G=[B\,e_{2}]$, Eq.(35) can be rewritten as

$$\begin{aligned} \begin{aligned}&(H^{T}DH+c_{2}I)\left[ \begin{matrix} {{w}_{1}} \\ {{b}_{1}} \\ \end{matrix} \right] + G^{T}F\alpha =0. \\&i.e., \left[ \begin{matrix} {{w}_{1}} \\ {{b}_{1}} \\ \end{matrix} \right] = -(H^{T}DH+c_{2}I)^{-1}G^{T}F\alpha \end{aligned} \end{aligned}$$

(36)

Using (27) and the above KKT conditions, the Wolfe dual of (24) is derived as follows:

$$\begin{aligned} {\mathop {{max}}\limits _{\alpha }}&\quad e_{2}^{T}F\alpha -\frac{1}{2}{{\alpha }^{T}}(F^{T}G){(H^{T}DH+c_{2}I)^{-1}}{({G}^{T}F)}\alpha \nonumber \\ {\text {s.t.} }&\quad 0{{e}_{2}}\le \alpha \le {c_{1}}{{e}_{2}} \end{aligned}$$

(37)

One can notice that the parameter $c_{2}$ in the dual problem (37) can be replaced by $\varepsilon$, $\varepsilon > 0$. However, the parameter $\varepsilon$ is a very small positive scalar ($\varepsilon =1e-8$) for avoiding matrix singularity, whereas $c_2$ is a hyper-parameter which determines the trade-off between overfitting and generalization [34].

Similarly, the Lagrangian function of the primal problem (25) is defined as follows:

$$\begin{aligned}&L_{2}(w_{2},b_{2},\eta , \beta , \nu ) \nonumber \\&\quad = \frac{1}{2}\sum \limits _{i=1}^{n_{2}}{d^{(2)}_{j}(w^{T}_{2}x^{(2)}_{j}+b_{2})^{2}}+c_{1}e_{1}^{T}\eta +\frac{c_{3}}{2}(\left\| w_{2}\right\| ^{2}+b^{2}_{2}) \nonumber \\&\qquad -\,\sum \limits _{i=1}^{n_{1}}{\beta _{j}(f^{(1)}_{j}(w^{T}_{2}x^{(2)}_{j}+b_{2})+\eta _{j} - f^{(1)}_{j})} - \nu ^{T}\eta \end{aligned}$$

(38)

where $\beta =(\beta _{1}, \beta _{2}, \dots ,\beta _{n_{1}})^{T}$ and $\nu =(\nu _{1}, \nu _{2}, \dots ,\nu _{n_{1}})^{T}$ are the vectors of Lagrangian multipliers. After differentiating the Lagrangian function (38) with respect to $w_{2}$,$b_{2}$ and $\eta$, the Wolfe dual of (25) is obtained as follows:

$$\begin{aligned} {\mathop {{max}}\limits _{\beta }}&\quad e_{1}^{T}P\beta -\frac{1}{2}{{\beta }^{T}}(P^{T}H){(G^{T}QG+c_{3}I)^{-1}}{({H}^{T}P)}\beta \nonumber \\ {\text {s.t.} }&\quad 0{{e}_{1}}\le \beta \le {c_{1}}{{e}_{1}} \end{aligned}$$

(39)

where $Q={\mathrm{diag}}(d^{(2)}_{1},d^{(2)}_{2},\dots ,d^{(2)}_{n_{2}})$ (i.e., the weight matrix of class $-1$) and $P={\mathrm{diag}}(f^{(1)}_{1},f^{(1)}_{2},\dots ,f^{(1)}_{n_{1}})$ (i.e., the weight matrix of class $+1$) are diagonal matrices. $f^{(1)}_{j}$ is either 0 or 1. Furthermore, it can be observed from the dual QPPs (37) and (39) that the computational complexity in the learning phase of the proposed method is affected by the number of margin points.

Once the dual QPP (39) is solved, we can obtain the following augmented vector.

$$\begin{aligned} \left[ \begin{matrix} {{w}_{2}} \\ {{b}_{2}} \\ \end{matrix} \right] = (G^{T}QG+c_{3}I)^{-1}H^{T}P\beta \end{aligned}$$

(40)

Once the augmented vectors of (36) and (40) are obtained from the solutions of (37) and (39), a new testing sample $x \in {\mathbb {R}}^{d}$ is assigned to class $i(i=-1,+1)$ depending on which of the two hyperplanes it lies closest to. The decision function of the proposed method is given by

$$\begin{aligned} d(x) = {\left\{ \begin{array}{ll} +1, &{} {\text {if }} \frac{\left| {{x}^{T}}{{w}_{1}}+{{b}_{1}} \right| }{\left\| w_1\right\| } < \frac{\left| {{x}^{T}}{{w}_{2}}+{{b}_{2}} \right| }{\left\| w_2\right\| } \\ -1, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(41)

where $\left| \ .\ \right|$ denotes the absolute value. For the sake of clearness, we explicitly state our linear RKNN-TSVM algorithm.

Algorithm 4 Linear RKNN-TSVM classifier Given a training set T and the number of nearest neighbors k. The linear RKNN-TSVM can be obtained using the following steps:

• 1. To obtain the set $Nea(x_{j})$, find the k-nearest neighbor of each sample $x_{j} \in T$ using either the FSA or LDMDBA algorithm.

• 2. Define the weight matrices $W_s$ and $W_d$ for classes $+1$ and $-1$ using (19) and (20).

• 3. Construct the diagonal matrices D, Q, F and P using (26) and (23).

• 4. Construct the input matrices $A \in {\mathbb {R}}^{n_1 \times d}$ and $B \in {\mathbb {R}}^{n_2 \times d}$. Also define $H=[A\,e_{1}]$ and $G=[B\,e_{2}]$.

• 5. Select parameters $c_1$, $c_2$ and $c_3$. These parameters are usually selected based on validation.

• 6. Obtain the optimal solutions $\alpha$ and $\beta$ by solving the convex QPPs (37) and (39), respectively.

• 7. Determine the parameters of two non-parallel hyperplanes using (36) and (40).

• 8. Calculate the perpendicular distance of a new testing sample $x \in {\mathbb {R}}^{d}$ from the two hyperplanes. Then assign the test sample x to $i(i=+1,-1)$ using (41).

Remark 1

In order to obtain the augmented vectors of (36) and (40), two matrix inversion $(H^{T}DH+c_{2}I)^{-1}$ and $(G^{T}QG+c_{3}I)^{-1}$ of size $(d+1)\times (d+1)$ are required, where d is much smaller than the total number of samples in the training set (i.e., $d \ll n$).

Remark 2

It should be noted that the matrices $(H^{T}DH+c_{2}I)$ and $(G^{T}QG+c_{3}I)$ are positive definite matrices due to stabilizer term. Therefore, the proposed method is stable and avoids the possible ill-conditioning of $H^{T}DH$ and $G^{T}QG$.

3.3 Nonlinear case

In the real world, a linear kernel cannot always separate most of the classification tasks. To make nonlinear types of problems separable, the samples are mapped to a higher dimensional feature space. Thus, we extend our RKNN-TSVM to nonlinear case by considering the following kernel-generated surfaces:

$$\begin{aligned} K(x){{\mu }_{1}}+{{b}_{1}}=0, \quad {\text {and}} \quad K(x){{\mu }_{2}}+{{b}_{2}}=0 \end{aligned}$$

(42)

where

$$\begin{aligned} K(x) = [K(x_{1},x),K(x_{2},x),\ldots ,K(x_{n},x)]^{T} \end{aligned}$$

(43)

and K(.) stands for an arbitrary kernel function. The primal optimization problems of nonlinear RKNN-TSVM can be reformulated as follows:

$$\begin{aligned} {\mathop {{ \min }}\limits _{\mu _{1} ,b_{1}}}&\quad \frac{1}{2}\sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}(\mu ^{T}_{1}K(x^{(1)}_{i})+b_{1})^{2}}+c_{1}e_{2}^{T}\xi \nonumber \\&\quad +\,\frac{c_{2}}{2}(\left\| \mu _{1}\right\| ^{2}+b^{2}_{1})\nonumber \\ {\text {s.t. }}&\quad -f^{(2)}_{j}(\mu ^{T}_{1}K(x^{(2)}_{j}) + b_{1})+\xi _{j} \ge f^{(2)}_{j}\nonumber \\&\quad \xi _{j} \ge 0,\quad j=1,\ldots ,n_{2} \end{aligned}$$

(44)

and

$$\begin{aligned} {\mathop {{ \min }}\limits _{\mu _{2} ,b_{2}}}&\quad \frac{1}{2}\sum \limits _{i=1}^{n_{2}}{d^{(2)}_{i}(\mu ^{T}_{2}K(x^{(2)}_{i})+b_{2})^{2}}+c_{1}e_{1}^{T}\eta \nonumber \\&\quad +\,\frac{c_{3}}{2}(\left\| \mu _{2}\right\| ^{2}+b^{2}_{2})\nonumber \\ {\text {s.t. }}&\quad f^{(1)}_{j}(\mu ^{T}_{2}K(x^{(1)}_{j})+b_{2})+\eta _{j} \ge f^{(1)}_{j}\nonumber \\&\quad \eta _{j} \ge 0,\quad j=1,\ldots ,n_{1} \end{aligned}$$

(45)

where $c_{1},c_{2},c_{3}$ are parameters, $\xi$ and $\eta$ are the slack vectors, $d_{j}$ and $f_{j}$ are defined as in the linear case. However, the standard Euclidean metric and the distance are computed as the higher dimensional feature space instead of input space in the linear case.

Similar to the linear case, the Lagrangian function of the primal optimization problem (44) is defined as follows:

$$\begin{aligned}&L_{1}(\mu _{1},b_{1},\xi , \alpha , \gamma ) \nonumber \\&\quad =\frac{1}{2}\sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}(\mu ^{T}_{1}K(x^{(1)}_{i})+b_{1})^{2}}+c_{1}e_{2}^{T}\xi +\frac{c_{2}}{2}(\left\| \mu _{1}\right\| ^{2}+b^{2}_{1}) \nonumber \\&\qquad -\,\sum \limits _{j=1}^{n_{2}}{\alpha _{j}(-f^{(2)}_{j}(\mu ^{T}_{1}K(x^{(2)}_{j})+b_{1})+\xi _{j} - f^{(2)}_{j})} - \gamma ^{T}\xi \end{aligned}$$

(46)

where $\alpha =(\alpha _{1}, \alpha _{2}, \dots ,\alpha _{n_{2}})^{T}$ and $\gamma =(\gamma _{1}, \gamma _{2}, \dots , \gamma _{n_{2}})^{T}$ are the vectors of Lagrangian multipliers. The KKT conditions for $\mu _{1}$, $b_{1}$, $\xi$ and $\alpha$, $\gamma$ are given by

$$\begin{aligned} \frac{\partial L_{1}}{\partial \mu _{1}}&= \sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}K(x^{(1)}_{i})(\mu ^{T}_{1}K(x^{(1)}_{i}) + b_{1})} + c_{2}\mu _{1} \nonumber \\&\quad+\, \sum \limits _{j=1}^{n_{2}}{\alpha _{j}f_{j}^{(2)}K(x_{j}^{(2)})}=0, \end{aligned}$$

(47)

$$\begin{aligned} \frac{\partial L_{1}}{\partial b_{1}}&= \sum \limits _{i=1}^{n_{1}}{d^{(1)}_{i}(\mu ^{T}_{1}K(x^{(1)}_{i}) + b_{1})} + c_{2}b_{1} \nonumber \\&\quad +\,\sum \limits _{j=1}^{n_{2}}{\alpha _{j}f_{j}^{(2)}}=0, \end{aligned}$$

(48)

$$\begin{aligned} \frac{\partial L_{1}}{\partial \xi }&= c_{1}e_{2} - \alpha - \gamma =0, \end{aligned}$$

(49)

$$\begin{aligned}&\alpha \ge 0,\, \gamma \ge 0. \end{aligned}$$

(50)

Arranging Eqs. (47) and (48) in their matrix forms, we obtain

$$\begin{aligned}&K(A)^{T}D(K(A)\mu _{1}+e_{1}b_{1})+c_{2}\mu _{1}+K(B)^{T}F\alpha =0, \end{aligned}$$

(51)

$$\begin{aligned}&e^{T}_{1}D(K(A)\mu _{1}+e_{1}b_{1}) + c_{2}b_{1}+e^{T}_{2}F\alpha =0, \end{aligned}$$

(52)

where K(A) and K(B) are the kernel matrices of sizes $n_{1} \times n$ and $n_{2} \times n$, respectively ($n=n_{1}+n_{2}$). Since $\gamma \ge 0$, from (50) we have

$$\begin{aligned} 0e_{2} \le \alpha \le c_{1}e_{2} \end{aligned}$$

(53)

Similarly, combining (51) and (52) leads to

$$\begin{aligned} ([K(A)^{T}\ e^{T}_{1}]D[K(A)\ e_{1}] + c_{2}I)[\mu _{1}\ b_{1}]^{T} + [K(B)^{T}\ e^{T}_{2}]F\alpha = 0. \end{aligned}$$

(54)

Let $R=[K(A)\,e_{1}]$ and $S=[K(B)\,e_{2}]$, Eq.(54) can be rewritten as

$$\begin{aligned} \left[ \begin{matrix} {{\mu }_{1}} \\ {{b}_{1}} \\ \end{matrix} \right] = -(R^{T}DR+c_{2}I)^{-1}S^{T}F\alpha \end{aligned}$$

(55)

Then we obtain the Wolfe dual of (44)

$$\begin{aligned} {\mathop {{max}}\limits _{\alpha }}&\quad e_{2}^{T}F\alpha -\frac{1}{2}{{\alpha }^{T}}(F^{T}S){(R^{T}DR+c_{2}I)^{-1}}{({S}^{T}F)}\alpha \nonumber \\ {\text {s.t.} }&\quad 0{{e}_{2}}\le \alpha \le {c_{1}}{{e}_{2}} \end{aligned}$$

(56)

In a similar manner, we can obtain the Wolfe dual of the primal optimization problem (45) by reversing the roles of K(A) and K(B) in (56):

$$\begin{aligned} {\mathop {{\max}}\limits _{\beta }}&\quad e_{1}^{T}P\beta -\frac{1}{2}{{\beta }^{T}}(P^{T}R){(S^{T}QS+c_{3}I)^{-1}}{({R}^{T}P)}\beta \nonumber \\ {\text {s.t.} }&\quad 0{{e}_{1}}\le \beta \le {c_{1}}{{e}_{1}} \end{aligned}$$

(57)

Once the dual QPP (57) is solved, we will obtain

$$\begin{aligned} \left[ \begin{matrix} {{\mu }_{2}} \\ {{b}_{2}} \\ \end{matrix} \right] = (S^{T}QS+c_{3}I)^{-1}R^{T}P\beta \end{aligned}$$

(58)

Here, the specifications of the matrices D, F, P and Q are analogous to the linear case. In the nonlinear case, a new testing sample x is assigned to class $i(i=-1,+1)$ depending on which of the two hypersurfaces it lies closest to. The decision function of nonlinear RKNN-TSVM is as follows

$$\begin{aligned} d(x) = {\left\{ \begin{array}{ll} +1, &{} {\text {if }}\quad \frac{\left| {K({x})}{{\mu }_{1}}+{{b}_{1}} \right| }{\left\| \mu _1\right\| } < \frac{\left| {K({x})}{{\mu }_{2}}+{{b}_{2}} \right| }{\left\| \mu _2\right\| } \\ -1, &{} {\text {otherwise}}. \end{array}\right. } \end{aligned}$$

(59)

We now state explicitly our nonlinear RKNN-TSVM algorithm.

Algorithm 5 Nonlinear RKNN-TSVM classifier

Given a training set T and the number of nearest neighbors k. The nonlinear RKNN-TSVM can be obtained using the following steps:

• 1. Choose a kernel function K.

• 2. In the high dimensional feature space, find the k-nearest neighbor of each sample $x_{j} \in T$ using either the FSA or LDMDBA algorithm.

• 3. Define the weight matrices $W_s$ and $W_d$ for classes $+1$ and $-1$ using (19) and (20).

• 4. Construct the diagonal matrices D, Q, F and P using (26) and (23).

• 5. Construct the input matrices $A \in {\mathbb {R}}^{n_1 \times d}$ and $B \in {\mathbb {R}}^{n_2 \times d}$. Also define $R=[K(A)\,e_{1}]$ and $S=[K(B)\,e_{2}]$.

• 6. Select parameters $c_1$, $c_2$ and $c_3$. These parameters are usually selected based on validation.

• 7. Obtain the optimal solutions $\alpha$ and $\beta$ by solving the convex QPPs (56) and (57), respectively.

• 8. Determine the parameters of two hypersurfaces using (55) and (58).

• 9. Calculate the perpendicular distance of a new testing sample $x \in {\mathbb {R}}^{d}$ from the two hypersurfaces. Then assign the test sample x to $i(i=+1,-1)$ using (59).

Remark 3

It can be noted that our nonlinear RKNN-TSVM requires inversion of matrix of size $(n \times 1) \times (n \times 1)$ twice. In order to reduce the computational cost, two approaches can be applied to our nonlinear RKNN-TSVM:

• 1. The rectangular kernel technique [18] can be used to reduce the dimensionality.

• 2. The Sherman–Morisson–Woodbury (SMW) formula [9] can be utilized to compute the matrix inverses of smaller dimension than $(n \times 1) \times (n \times 1)$.

4 Analysis of algorithm and a fast iterative algorithm clipDCD

4.1 The framework of RKNN-TSVM

Similar to other KNN-based TSVM classifiers, the output model of the proposed method is created by performing 3 steps. However, each step in the framework of our RKNN-TSVM was improved. These steps are explained as follows:

• 1. In the first step, the KNNs of all the training samples are computed. Nonetheless, the LDMDBA algorithm was employed to accelerate the process of KNN finding.

• 2. After KNN computation, the intra-class matrix $W_{s,ij}$ and inter-class matrix $W_{d,ij}$ are obtained. Using $W_{s}$ matrix, weight is given to each sample with respect to the distance from its nearest neighbors. Finally, margin points are determined using inter-class $W_{d}$ matrix.

• 3. In order to obtain the output model, two dual optimization problems and two systems of linear equations are solved. The third step was improved by considering the SRM principle in the optimization problems of the proposed method.

Figure 3 shows the overview of steps performed by the proposed method.

Fig. 3

Overview of steps performed by the proposed method

4.2 Comparison with other related algorithms

In this subsection, we compare our RKNN-TSVM with other related algorithms.

4.2.1 Comparison with TSVM

Compared with TSVM [15], our RKNN-TSVM gives weight to the samples of each class by using the KNN graph. As a result, the hyperplanes of the proposed method are closer to the samples with greater weight and far from the margin points of the other class instead of all the samples. Moreover, the proposed method improves the computational cost of solving QPPs by only keeping the margin points in the constraints.

TSVM only considers the empirical risk which may lead to overfitting problem. However, our RKNN-TSVM implements the SRM principle by adding a stabilizer term to objective function. As a result, the proposed method achieves better classification accuracy and generalization.

4.2.2 Comparison with WLTSVM

Unlike WLTSVM [42], our RKNN-TSVM gives weight to each sample with respect to the distance from its nearest neighbors. As a result, the neighbors with smaller distance were weighted more heavily than the one with greater distance. Moreover, the proposed method finds KNNs of all the samples by utilizing fast KNN method such as LDMDBA [39] algorithm. This makes the learning speed of our RKNN-TSVM faster than that of WL-TSVM.

Different from WLTSVM, the optimization problems of the proposed method are regularized and stable. Hence two parameters $c_2$ and $c_3$ can be adjusted to determine trade-off between overfitting and generalization. This makes our RKNN-TSVM better in terms of classification accuracy.

4.2.3 Comparison with KNN-STSVM

Similar to WLTSVM, KNN-STSVM [26] gives weight to each sample by only counting the number of its nearest neighbors. Also, it does not consider the SRM principle which makes the classifier stable. Moreover, KNN-STSVM extracts the data distribution information in the objective functions by using the Ward’s linkage clustering method.

In summary, KNN-STSVM consists of three steps: (1) Getting proper clusters. (2) KNN finding. (3) Solving two smaller-sized QPPs. The overall computational complexity of this classifier is around ${\mathcal {O}}(1/4n^{3} + d(n^{2}_{1} + n^{2}_{2}) + n^{2}\log {n})$. Therefore, it cannot handle large-scale datasets.

4.3 The computational complexity of RKNN-TSVM

The major computation in our RKNN-TSVM involves two steps:

• 1. To obtain the output model, the proposed method needs to solve two smaller-sized dual QPPs. However, the size of dual problems is affected by the number of extracted margin points. After all, the optimization problems of RKNN-TSVM costs around ${\mathcal {O}}(n^{3})$.

• 2. To compute the weight matrices, RKNN-TSVM has to find k-nearest neighbors for all n training samples. By using the FSA algorithm, the KNN step costs about ${\mathcal {O}}(n^{2}\log {n})$. To reduce the computational cost of the KNN step, the proposed method employs a fast KNN method, the LDMDBA algorithm which has computational complexity of ${\mathcal {O}}(\log {d}n\log {n})$.

Thus, the overall computational complexity of RKNN-TSVM is about ${\mathcal {O}}(1/4n^{3}+\log {d}n\log {n})$. For the sake of comparison, the computational complexity of the proposed method and other similar methods are shown in Table 2.

Table 2 The comparison of computational complexity between the proposed method and other similar methods

From Table 2, it can be observed that the computational complexity of RKNN-TSVM with LDMDBA algorithm is better than that of WLTSVM and KNN-STSVM. Because WLTSVM method employs the FSA algorithm, which is significantly slower than the LDMDBA algorithm. As described in Sect. 4.2.3, KNN-STSVM method consists of three major computational steps. However, the proposed method has two major computational steps. Finally, TSVM is the fastest method among other methods in Table 2. It only solves two smaller-sized QPPs and does not compute the KNN graph.

4.4 The limitation of our RKNN-TSVM

We should acknowledge that our RKNN-TSVM has the following limitations:

• 1. Because of solving two systems of linear equations, the matrix inverse operation is unavoidable in our RKNN-TSVM. The computational complexity of the matrix inverse is ${\mathcal {O}}(n^{3})$. This implies that the computational cost rapidly increases with the increase of matrix order.

• 2. For large-scale datasets, the memory consumption of the proposed method is very high. Because two nearest neighbor graphs need to be stored.

• 3. Even though the SRM principle boosts the classification accuracy of our RKNN-TSVM, it comes at the cost of tuning two additional parameters. In total, there are four parameters $c_{1}$, $c_{2}$, $c_{3}$, k in our RKNN-TSVM which need to be adjusted. Therefore, the parameter selection of the proposed method is computationally expensive. In the experiments, we set $c_{2} = c_{3}$ to reduce the computational cost of parameter selection.

4.5 The scalability of RKNN-TSVM

Similar to WLTSVM, our RKNN-TSVM introduces the selection vector $f_{j}$ to the constraint of the optimization problems. As a result, it considers only the margin points instead of all the samples for obtaining the output model. This further reduces the time complexity of solving dual problems. However, the proposed method has a better scalability in comparison with WLTSVM. It utilizes LDMDBA algorithm to find KNNs of all the samples. This algorithm decreases the computational cost of KNN finding and makes our RKNN-TSVM more suitable for large-scale datasets.

4.6 The clipDCD algorithm

In our RKNN-TSVM, there are four strictly convex dual QPPs to be solved: (37), (39), (56) and (57). These optimization problems can be rewritten in the following unified form:

$$\begin{aligned} {\mathop {{ \min }}\limits _{\alpha }}&\qquad f(\alpha )=\frac{1}{2} \alpha ^{T}Q\alpha - e^{T}\alpha , \nonumber \\ {\text {s.t. }}&\qquad 0 \le \alpha \le c. \end{aligned}$$

(60)

where $Q \in {\mathbb {R}}^{n \times n}$ is positive definite. For example, the matrix Q in (60) can be substituted by

$$\begin{aligned} (F^{T}S){(R^{T}DR+ c_{2}I)^{-1}}{({S}^{T}F)}. \end{aligned}$$

To solve the dual QPP problem (60), a solver algorithm is required. So far, many fast training algorithms were proposed which may include but not limited to, interior-points methods [35], successive overrelaxation (SOR) technique [17] and dual coordinate descent (DCD) algorithm [12]. On the basis of DCD algorithm, Peng et al. proposed the clipping dual coordinate descent (clipDCD) algorithm [29].

In this paper, we employed the clipDCD algorithm [29] to speed up the learning process of our RKNN-TSVM. The main characteristics of this algorithm are fast learning speed and easy implementation. The clipDCD is a kind of the gradient descent method. Its main idea is to orderly select and update a variable which is based on the maximal possibility-decrease strategy [29].

Unlike the DCD algorithm, this method does not consider any outer and inner iteration. That is, only one component of $\alpha$ is updated at each iteration, denoted $\alpha _{L} \rightarrow \alpha _{L} + \lambda$, $L \in \{1,\dots ,n\}$ is the index. Then the objective function is defined as follows:

$$\begin{aligned} f(\lambda )=f(0) + \frac{1}{2}\lambda ^{2}Q_{LL} - \lambda (e_{L} - \alpha ^{T}Q_{.,L}). \end{aligned}$$

(61)

where $Q_{.,L}$ is the Lth column of the Q matrix. Setting the derivation of $\lambda$

$$\begin{aligned} \frac{df(\lambda )}{d\lambda }=0 \Rightarrow \lambda = \frac{(e_{L} - \alpha ^{T}Q_{.,L})}{Q_{LL}} \end{aligned}$$

(62)

The largest decrease on the objective value can be derived by choosing the L index as:

$$\begin{aligned} L = {\mathop {{\text{arg}}\,\max}\limits _{i \in S}}\Big \{\frac{(e_{i} - \alpha ^{T}Q_{.,i})^{2}}{Q_{ii}}{} \Big \}, \end{aligned}$$

(63)

where the index set S is

$$\begin{aligned} \small S&= \Big \{i:\alpha _{i}> 0 {\text { if }} \frac{e_{i} - \alpha ^{T}Q_{.,i}}{Q_{ii}}< 0 \nonumber \\&{\text { or }}\alpha _{i} < c {\text { if} } \frac{e_{i} - \alpha ^{T}Q_{.,i}}{Q_{ii}} > 0 \Big \}. \end{aligned}$$

(64)

The stopping criteria of the clipDCD algorithm is defined as follows:

$$\begin{aligned} \frac{(e_{L} - \alpha ^{T}Q_{.,L})^{2}}{Q_{LL}} < \epsilon , \quad \epsilon > 0 \end{aligned}$$

(65)

where the tolerance parameter $\epsilon$ is a positive small number. We set $\epsilon =10^{-5}$ in our experiments. The whole process of solving convex dual QPPs using clipDCD solver is summarized in the Algorithm 6. More information on the convergence of this algorithm and other theoretical proofs can be found in [29].

5 Numerical experiments

In this section, we conduct extensive experiments on several synthetic and benchmark datasets to investigate the classification accuracy and the computational cost of our RKNN-TSVM. In each subsection, the experimental results and the corresponding analysis are given.

5.1 Experimental setup and implementation details

For experiments with TSVM, we used LightTwinSVM¹ program [20] which is an open source and fast implementation of standard TSVM classifier. All other classifiers were implemented in Python² 3.5 programming language. NumPy [38] package was used for linear algebra operations such as matrix multiplication and inverse. Moreover, SciPy [37] package was used for distance calculation and statistical functions. For model selection and cross-validation, Scikit-learn [28] package was employed. To solve dual QPPs, the C++ implementation of clipDCD optimizer within LightTwinSVM’s code was used. The LDMDBA algorithm was implemented in C++ with GNU Compiler Collection³ 5.4 (GCC). Pybind 11⁴ was employed to create Python binding of C++ code. All the experiments were carried out on Ubuntu 16.04 LTS with an Intel Core i7 6700K CPU (4.2 GHz) and 32.0 GB of RAM.

Fig. 4

The performance and graphical representation of WLTSVM and RKNN-TSVM on Ripley’s dataset with linear kernel

Fig. 5

The performance and graphical representation of WLTSVM and RKNN-TSVM on checkerboard dataset with Gaussian kernel

5.2 Parameters selection

The classification performance of TSVM-based classifiers depends heavily on the choice of parameters. In our experiments, the grid search method is employed to find the optimal parameters. In the case of nonlinear kernel, the Gaussian kernel function $K(x_{i},x_{j})={\mathrm {exp}}(-\frac{\left\| x_{i}-x_{j}\right\| }{2\sigma ^{2}})$ is used as it is often employed and yields great generalization performance. The optimal value of the Gaussian kernel parameter $\sigma$ was selected over the range $\{2^{i} \mid i=-10,-9,\dots ,2 \}$. The optimal value of the parameters $c_{1}$, $c_{2}$, $c_{3}$ was selected from the set $\{2^{i} \mid i=-8,-7,\dots ,2 \}$. To reduce the computational cost of the parameter selection, we set $c_{1}=c_{2},c_{3}=c_{4}$ in TBSVM and $c_{2} = c_{3}$ for RKNN-TSVM. In addition, the optimal value for k in RKNN-TSVM and WLTSVM was chosen from the set $\{2,3,\dots ,15\}$.

5.3 Experimental results and discussion

In this subsection, we analyze the results of the proposed method on several synthetic and benchmark datasets from the perspective of the prediction accuracy and computational efficiency.

5.3.1 Synthetic datasets

To demonstrate graphically the effectiveness of our RKNN-TSVM over WLTSVM, we conducted experiments on two artificially generated synthetic datasets. For experiments with these datasets, 70% of samples are randomly chosen as the training samples.

In the first example, we consider the two dimensional Ripley’s synthetic dataset [32] which includes 250 samples. Figure 4 shows the performance and graphical representation of WLTSVM and RKNN-TSVM on Ripley’s dataset with linear kernel. By inspecting Fig. 4, one can observe that our linear RKNN-TSVM obtains better classification performance and its hyperplanes are proximal to the highly dense samples. This is because the proposed method gives weight to each sample with respect to the distance from its nearest neighbors.

The second example is a two-dimensional checkerboard dataset [11] which includes 1000 samples. Figure 5 visually displays the performance of WLTSVM and RKNN-TSVM on checkerboard dataset with Gaussian kernel. As shown in Fig. 5, the accuracy of our nonlinear is better than that of nonlinear WLTSVM. Because our RKNN-TSVM considers the SRM principle which improves the generalization ability. Moreover, as mentioned earlier, the proposed method gives weight based on the distance between a sample and its nearest neighbors.

5.3.2 Benchmark datasets

To further validate the efficiency of the proposed method, we compare the performance of our RKNN-TSVM with TSVM, TBSVM and WLTSVM on benchmark datasets from the UCI machine learning repository⁵. It should be noted that all the datasets were normalized such that the feature values locate in the range $\left[ 0,1\right]$. The characteristics of these datasets are shown in Table 3.

Experiments were performed using 5-fold cross-validation in order to evaluate the performance of these algorithms and tune parameters. More specifically, the dataset is split randomly into 5 subsets, and one of those sets is reserved as a test set. This procedure is repeated 5 times, and the average of 5 testing results is used as the performance measure.

The classification accuracy and running time of TSVM, TBSVM, WLTSVM and RKNN-TSVM are summarized in Table 4. Here, “Accuracy” denotes the mean value of the testing results (in %) and the corresponding standard deviation. “Time” denotes the mean value of training time.

Table 3 The characteristics of benchmark datasets

Table 4 Performance comparison of TSVM, TBSVM, WLTSVM and, RKNN-TSVM on benchmark datasets with Gaussian kernel

Table 5 Average rank on classification accuracy of five algorithms

From the perspective of classification accuracy, our proposed RKNN-TSVM outperforms other classifiers, i.e., TSVM and WLTSVM on most datasets. This is due to the characteristics of our RKNN-TSVM which are explained as follows:

• 1. The proposed method gives weight to each sample with respect to the distance from its nearest neighbors. As a result, noisy samples and outliers are ignored in the production of the output model. This improved the prediction accuracy of our RKNN-TSVM. On the other hand, WLTSVM gives weight to each sample by only counting the numbers of its nearest neighbors. This approach still ignores noise and outliers. However, it is not as effective as the proposed method.

• 2. Similar to TBSVM [34], an extra stabilizer term was added to the optimization problems of our RKNN-TSVM. Therefore, two additional parameters $c_{2}$ and $c_{3}$ in RKNN-TSVM can be adjusted which improves the classification accuracy significantly. However, these parameters are small fixed positive scalar in TSVM and WLTSVM.

From Table 4, it can be seen that not only our RKNN-TSVM with the LDMDBA algorithm outperforms TSVM, TBSVM, and WLTSVM but also it has better prediction accuracy than the RKNN-TSVM with FSA algorithm. This further validates that using a different KNN method such as the LDMDBA algorithm may improve the classification performance of our RKNN-TSVM.

From the training time comparison of the classifiers, TSVM is faster than WLTSVM and RKNN-TSVM. Because the major computation in TSVM involves solving two smaller-sized QPPs. However, the proposed method and WLTSVM have to find KNNs for all the training samples as well as solving two smaller-sized QPPs. In order to reduce the overall computational cost, the LDMDBA algorithm was employed. Section 5.3.2 investigates the effectiveness of RKNN-TSVM with LDMDBA algorithm for large-scale datasets.

Figure 6 shows the influence of k on training time of RKNN-TSVM with the FSA and LDMDBA algorithm on Pima-Indian dataset. As shown in Fig. 6, the training time of RKNN-TSVM increases with the growth of k. However, RKNN-TSVM with LDMDBA algorithm is significantly faster than RKNN-TSVM with the FSA algorithm for each value of k. This also confirms our claim that the LDMDBA algorithm reduces the computational cost of the proposed method significantly.

Fig. 6

The influence of k on training time of RKNN-TSVM with FSA and LDMDBA algorithm on Pima-Indian dataset

Fig. 7

The performance of linear RKNN-TSVM on parameters $c_{1}$ and $c_{2}$ for two benchmark datasets

5.3.3 Statistical tests

Since differences in accuracy between classifiers are not very large, nonparametric statistical tests can be used to investigate whether significant differences exist among classifiers. Hence we use Friedman test with corresponding post hoc tests as it was suggested in Demsar [4]. This test is proved to be simple, nonparametric and safe. To run the test, average ranks of five algorithms on accuracy for all datasets were calculated and listed in Table 5. Under the null-hypothesis that all the classifiers are equivalent, the Friedman test is computed according to (66):

$$\begin{aligned} \chi ^2_F = \frac{12N}{k(k + 1)}\bigg [\sum _{j} R^2_j - \frac{k(k + 1)^2}{4} \bigg ], \end{aligned}$$

(66)

where $R_j=\frac{1}{N}\sum _{i}r^j_i$, and $R^j_i$ denotes rank of the j-th of k algorithms on the i-th of N datasets. Friedman’s $\chi ^2_F$ is undesirably conservative and derives a better statistic

$$\begin{aligned} F_F = \frac{(N - 1)\chi ^2_F}{N(k - 1) - \chi ^2_F} \end{aligned}$$

(67)

which is distributed according to the F-distribution with $k-1$ and $(k-1)(N-1)$ degrees of freedom.

We can obtain $\chi ^2_F = 24.636$ and $F_F = 12.723$ according to (66) and (67). With five classifiers and eleven datasets, $F_F$ is distributed according to F-distribution with $k-1$ and $(k-1)(N-1) = (4, 40)$ degrees of freedom. The critical value of F(4, 40) is 1.40 for the level of significance $\alpha =0.25$; similarly, it is 2.09 for $\alpha =0.1$ and 2.61 for $\alpha =0.05$. Since the value of $F_F$ is much larger than the critical value, the null hypothesis is rejected. It means that there is a significant difference among five classifiers. From Table 5, it can be seen that the average rank of RKNN-TSVM with the LDMDBA algorithm is far lower than the other classifiers.

To further analyze the performance of five classifiers statistically, we used another statistical analysis which is Win/Draw/Loss (WDL) record. The number of datasets was counted for which the proposed method with the LDMDBA algorithm performs better, equally well or worse than other four classifiers. The results are shown at the end of Table 4. It can be found that our RKNN-TSVM with LDMDBA algorithm is significantly better than other four classifiers.

Fig. 8

The performance of linear RKNN-TSVM on parameters $c_{1}$ and k for two benchmark datasets

5.3.4 Parameter sensitivity

In order to achieve a better classification accuracy, it is essential to appropriately choose parameters of our RKNN-TSVM. Hence we conducted experiments on Australian and Hepatitis datasets to analyze the sensitivity of the proposed method to parameters $c_{1}$, $c_{2}$ and k.

For each dataset, $c_{1}$, $c_{2}$ and k can take 17 different values, resulting in 289 combinations of $(c_{1},c_{2})$ and $(c_{1}, k)$. Figure 7 shows the performance of linear RKNN-TSVM on parameters $c_{1}$ and $c_{2}$ for two benchmark datasets. As can be seen from Fig. 7, the values of parameter $c_{2}$ can improve the classification accuracy of the proposed method. Note that the parameter $c_{2}$ was introduced by adding a stabilizer term to objective function. This further shows that the SRM principle improves the prediction accuracy of our RKNN-TSVM.

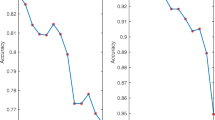
Figure 8 shows the performance of linear RKNN-TSVM on parameters $c_{1}$ and k for two benchmark datasets. From Fig. 8, it can be observed that the classification accuracy of our RKNN-TSVM also depends on the value of k. As shown in Fig. 8b, the classification accuracy improves for Hepatitis dataset as the value of k increases. This is because a large value of k in the KNN graph reduces the effect of noisy samples and outliers on classification accuracy.

From these figures, it is clear that the prediction accuracy of RKNN-TSVM is affected by the choices of the mentioned parameters. Therefore, an appropriate selection of the mentioned parameters is crucial.

5.3.5 Experiments on NDC datasets

In order to analyze the computational efficiency of our RKNN-TSVM on large-scale datasets, we conducted experiments on NDC datasets which were generated using David Musicant’s NDC Data Generator [21]. The detailed description of NDC datasets is given in Table 6. For experiments with NDC datasets, the penalty parameters of all classifiers were fixed to be one (i.e., $c_{1}=1$, $c_{2}=1$, $c_{3}=1$). The Gaussian kernel with $\sigma =2^{-15}$ was used for all experiments with nonlinear kernel. The neighborhood size k is also 5 for all datasets.

Table 6 The description of NDC datasets

Table 7 Comparison on NDC datasets with linear kernel

Table 8 Comparison on NDC datasets with RBF kernel

Table 7 shows the comparison of training time for TSVM, WLTSVM and our RKNN-TSVM with linear kernel. Similar to TSVM, TBSVM solves two smaller-sized QPPs. Therefore, training time of TBSVM is not included. The last column shows the speedup of LDMDBA algorithm which is defined as:

$$\begin{aligned} \small {\text {Speedup}} = \frac{\text {The\, training\, time\, of\, RKNN-TSVM(FSA)}}{\text {The\, training\, time\, of \,RKNN-TSVM(LDMDBA)}} \end{aligned}$$

From Table 7, it can be seen that the LDMDBA algorithm makes our RKNN-TSVM obtain much faster learning speed. It can be found that when the size of training set increases, RKNN-TSVM with the LDMDBA algorithm becomes much faster than WLTSVM and RKNN-TSVM with the FSA algorithm. For instance, the proposed method with the LDMDBA algorithm is 3.25 times faster than the proposed method with the FSA algorithm on NDC-25K dataset. Moreover, our linear RKNN-TSVM with the LDMDBA algorithm is almost as fast as linear TSVM which is evident from Table 7.

Table 8 shows the comparison of training time for TSVM, WLTSVM and our RKNN-TSVM with RBF kernel. The results indicate that our RKNN-TSVM with the LDMDBA algorithm performed several orders of magnitude faster than WLTSVM and RKNN-TSVM with the FSA algorithm. As shown in Table 8, the largest speedup is almost 14 times. However, TSVM is almost 2 times faster than RKNN-TSVM (LDMDBA) with reduced kernel. This is because even with the reduced kernel of dimension $(n \times \bar{n})$, RKNN-TSVM with the LDMDBA algorithm still requires solving two dual QPPs as well as finding KNNs for all the samples.

The experimental results of NDC datasets with RBF kernel confirmed our claim that the LDMDBA algorithm is efficient for high dimensional feature space. In summary, our RKNN-TSVM with the LDMDBA algorithm is much better than WLTSVM in terms of computational time.

6 Conclusion

In this paper, we proposed a new classifier, i.e., an enhanced regularized K-nearest neighbor-based twin support vector machine (RKNN-TSVM). The proposed method has three clear advantages over KNN-based TSVM classifier such as WLTSVM: (1) It gives weight to each sample with respect to the distance from its nearest neighbors. This improves fitting hyperplanes with highly dense samples and makes our classifier potentially more robust to outliers. (2) Our RKNN-TSVM avoids overfitting problem by adding a stabilizer term to each primal optimization problem. Hence two parameters $c_{2}$ and $c_{3}$ were introduced which are the trade-off between overfitting and generalization. This further improved the classification ability of our proposed method. (3) The proposed method utilizes a fast KNN method, the LDMDBA algorithm. Not only this algorithm makes the learning speed of our RKNN-TSVM faster than that of WLTSVM but also improves the prediction accuracy of our proposed method.

The comprehensive experimental results on several synthetic and benchmark datasets indicate the validity and effectiveness of our proposed method. Moreover, the results on NDC datasets reveal that our RKNN-TSVM is much better than WLTSVM for handling large-scale datasets. For example, the largest speed up in our RKNN-TSVM with the LDMDBA algorithm reaches to 14 times. There are 4 parameters in our RKNN-TSVM which increases the computational cost of parameter selection. This limitation can be addressed in the future. The high memory consumption of the proposed method is also main topic of future research.