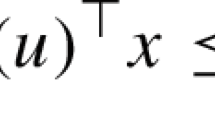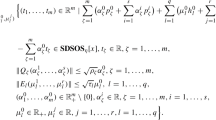Robust Pareto solutions for convex quadratic multiobjective optimization problems under data uncertainty

Abstract

In this paper, we consider a convex quadratic multiobjective optimization problem, where both the objective and constraint functions involve data uncertainty. We employ a deterministic approach to examine robust optimality conditions and find robust (weak) Pareto solutions of the underlying uncertain multiobjective problem. We first present new necessary and sufficient conditions in terms of linear matrix inequalities for robust (weak) Pareto optimality of the multiobjective optimization problem. We then show that the obtained optimality conditions can be alternatively checked via other verifiable criteria including a robust Karush–Kuhn–Tucker condition. Moreover, we establish that a (scalar) relaxation problem of a robust weighted-sum optimization program of the multiobjective problem can be solved by using a semidefinite programming (SDP) problem. This provides us with a way to numerically calculate a robust (weak) Pareto solution of the uncertain multiobjective problem as an SDP problem that can be implemented using, e.g., MATLAB.

1 Introduction

Multiobjective (or multiple objective/multicriteria/vector) optimization problems refer to mathematical optimization models that can handle the multiple decision making problems and have been found in applications in various areas of real life and work such as defence, engineering, economics and logistics (Nguyen and Cao, 2019; Ehrgott, 2005; Jahn, 2004; Miettinen, 1999; Steuer, 1986; Luc, 1989). Multiobjective optimization problems are often involved in the presence of trade-offs between two or more conflicting objectives from a set of feasible choices. Consequently, identifying Pareto fronts or Pareto solutions that are trade-offs among the conflicting objectives of a nontrivial multiobjective optimization program is generally hard by its natural structure (Wiecek, 2007; Boţ et al. 2009,; Chinchuluun and Pardalos, 2007; Zhou et al., 2011; Niebling and Eichfelder, 2019).

A decision making problem that arises in defence, for example, may contain parameters that are unknown at the time when decision must be made, e.g., future technology, threats, costs and environments and these parameters are often obtained by prediction or estimation. Unknown environment factors of a defence force problem such as land surface, air and sea surroundings or weather would be shown up when a defence system is operating in a new terrain. The land combat vehicle (LCV) system (Nguyen and Cao, 2017, 2019) is formulated as a multiobjective optimization problem that contains uncertainty data caused by incomplete and noisy information or by unknown environment factors, and also by the interdependencies between LCV system configurations. Force Design (FD) is ultimately about selecting a portfolio of thousands of strategic investment projects in future Australian Defence Force (ADF) capabilities (Peacock et al., 2019). The challenge is to optimise the combination of invested projects that give government the overall capability it requires to achieve multiple effects (objectives) across a range of scenarios, whilst achieving the budget constraints.

This paper is the first step in extending some earlier approaches successfully used for evaluating and optimising defence problems such as the LCV system specifications and configurations for Australian Army, to more complex problems with higher dimensions that are relevant to force design (Nguyen and Cao, 2019; Nguyen et al., 2016; Nguyen and Cao, 2017) by considering a class of uncertain multiobjective optimization problems where the objectives and constraints are continuous functions and uncertain parameters also influence its search space. Robust approaches (or, robust optimization) (see e.g., Ben-Tal et al., 2009; Bertsimas et al., 2011; Ehrgott et al., 2014; Kuroiwa and Lee, 2012) have emerged as promising and efficient framework for solving mathematical programming problems under data uncertainty, and so a robust optimisation approach will be used instead of the heuristic methods from the previous work to handle this class of uncertain multiobjective optimization problems. It is worth mentioning that the robust approach of (scalar) uncertain programs was first considered in Soyster (1973). This is based on the principle that the robust counterpart of an uncertain program that enforced for all possible parameter realizations within the underlying uncertainty sets admits feasible solutions that are immunized against uncertainty data.

Nowadays, the robust approach has been deployed in real-world multiobjective optimization problems involving uncertain data (Ehrgott et al., 2014; Kuroiwa and Lee, 2012) as the robust multiobjective models better satisfy future performance demands in practical scenarios, see e.g., Zhou-Kangas and Miettinen (2019), Ide and Schobel (2016), Doolittle et al. (2018). The concept of minmax robustness from Ben-Tal et al. (2009) was extended to the setting of multiobjective optimization in Ehrgott et al. (2014), Kuroiwa and Lee (2012). Moreover, one can see in Ehrgott et al. (2014) how robust solutions of an uncertain multiobjective optimization problem are calculated, and in Kuroiwa and Lee (2012) how optimality conditions of robust multiobjective optimization problems are established. Over the years, different and various research aspects of robust multiobjective optimization have been intensively studied and developed by many researchers. For example, Goberna et al. (2014) provided dual characterizations of robust weak Pareto solutions of a multiobjective linear semi-infinite programs under constraint data uncertainty (i.e, the problem involves uncertain parameters only in its constraints). Georgiev et al. (2013) established a necessary and sufficient condition and provided formulas to compute the radius of robustness of a linear multiobjective programming problem. In a nonsmooth and nonlinear setting, Zamani et al. (2015) provided formulas for calculating such radius of robustness. These results were further developed for semi-infinite multiobjective programs in Rahimi and Soleimani-damaneh (2018a) and for general robust vector optimization problems in Rahimi and Soleimani-damaneh (2018b).

By considering the objectives of an uncertain multiobjective optimization problem as set-valued functions, Eichfelder et al. (2020) proposed a numerical algorithm to calculate the optimal solutions of an unconstrained multiobjective optimization problem in which the objective functions are twice continuously differentiable. Engau and Sigler (2020) established a complete characterization of an alternative efficient set hierarchy based on different ordering relations with respect to the multiple objectives and scenarios. Lee and Lee (2018) examined optimality conditions and duality relations for weak efficient solutions of robust semi-infinite multiobjective optimization problems, where the related functions are continuously differentiable. Employing advanced techniques of variational analysis, Chuong (2020) obtained robust optimality conditions and robust duality for an uncertain nonsmooth multiobjective optimization problem under arbitrary uncertainty nonempty sets.

One of the recent research trends in robust multiobjective optimization has focused on exploiting special structures of the objective and constraint functions or the uncertainty sets to provide verifiable optimality conditions and calculate robust (weak) Pareto solutions by using semidefinite programming (SDP) (see e.g., Blekherman et al., 2012) problems. Chuong (2017) provided a characterization for weak Pareto solution of a robust linear multiobjective optimization problem based on a robust alternative theorem. In the setting of sum of squares (SOS)-convex polynomials (Helton and Nie, 2010), Chuong (2018) examined optimality conditions and duality by means of linear matrix inequalities for robust multiobjective SOS-convex polynomial programs, while Lee and Jiao (2021) employed an approximate scalarization technique to find robust Pareto solutions for a multiobjective optimization problem under the constraint data uncertainty. The interested reader is referred to a very recent work (Chuong and Jeyakumar, 2021) for calculating robust (weak) Pareto solutions for uncertain linear multiobjective optimization problems in terms of two-stage adjustable variables.

To the best of our knowledge, there are no results establishing verifiable optimality conditions and finding numerically robust (weak) Pareto solutions of an uncertain convex quadratic multiobjective optimization problem, where uncertain parameters involve in both the objective and constraint functions and reside in structured uncertainty sets such as spectrahedra (see e.g., Ramana and Goldman, 1995). The examination of such an uncertain multiobjective optimization problem is often complicated due to the challenges posed in dealing with the data uncertainty of both the objective and constraint functions. In this work, we consider a convex quadratic multiobjective optimization problem, where both the objective and constraint functions involve data uncertainty. In our model, the uncertain parameters in the objective and constraint functions are allowed to vary affinely in the corresponding uncertainty sets, which are spectrahedra (cf. Ramana and Goldman, 1995).

To handle the proposed uncertain multiobjective optimization problem, we employ the robust deterministic approach (see e.g., Ben-Tal et al., 2009; Bertsimas et al., 2011; Ehrgott et al., 2014; Kuroiwa and Lee, 2012) to examine robust optimality conditions and find robust (weak) Pareto solutions of the underlying uncertain multiobjective problem. More precisely, we first present necessary and sufficient conditions in terms of linear matrix inequalities for robust (weak) Pareto optimality of the multiobjective optimization problem. We then show that the obtained optimality conditions can be alternatively checked via other verifiable criteria including a robust Karush-Kuhn-Tucker condition. To achieve these goals, we employ a special variable transformation combined with a classical minimax theorem (see e.g., Sion, 1958) and a commonly used alternative theorem in convex analysis (cf. Rockafellar, 1970). Moreover, we establish that a (scalar) relaxation problem of a robust weighted-sum optimization program of the multiobjective problem can be solved by using a semidefinite programming (SDP) problem. This provides us with a way to numerically calculate a robust (weak) Pareto solution of the uncertain multiobjective problem as an SDP problem that can be implemented using, e.g., MATLAB.

It is worth mentioning here that Chuong (2018) examined a robust multiobjective optimization problem with a general class of SOS-convex polynomials but it contained uncertain parameters only on the constraints (i.e., the objective functions of the problem do not have uncertain parameters). Our problem deals with convex quadratic functions, where both the objective functions and constrained functions involve uncertain parameters. Due to the uncertainty data of both the objective and constraint functions, optimality conditions for robust (weak) Pareto solutions obtained in this paper would not be derived from the corresponding conditions in Chuong (2018). Even in a special framework, where there is no uncertain parameters in the objective functions of the underlying problem, we would not obtain such necessary optimality conditions by applying the results in Chuong (2018). This is because Theorem 2.3(i) of Chuong (2018) is formulated under the (classical) Slater condition, while the necessary optimality condition of the current paper (see Theorem 3.1 below) is established under a more general qualification of closedness of characteristic cone which can be regarded as the weakest regularity conditions guaranteeing strong duality in robust convex programming (Jeyakumar and Li, 2010). To make use of the closedness of characteristic cone condition in establishing necessary optimality conditions, we employ novel dual techniques based on the epigraphical convex optimization approach. Moreover, our paper proposes a scheme (see Theorem 4.1 below) to calculate a robust (weak) Pareto solution of the uncertain multiobjective problem by solving an SDP reformulation. A scheme to identify robust (weak) Pareto solutions of an uncertain multiobjective optimization problem was not available in Chuong (2018), where one only found weighted-sum efficient values for the underlying multiobjective problem.

The organization of the paper is as follows. Section 2 presents some notation and the definitions of uncertain and robust multiobjective optimization problems as well as their solution concepts that will be studied. Section 3 establishes necessary and sufficient optimality conditions along with other equivalent verifiable conditions for the underlying multiobjective optimization problem. In Sect. 4, we show that a (scalar) relaxation problem of a robust weighted-sum optimization program of the multiobjective problem can be solved by using an SDP problem. Section 5 summarizes the obtained results and provides some potential perspectives for a further study. Appendix presents numerical examples that show how we can employ the obtained SDP reformulation scheme to find robust (weak) Pareto solutions of uncertain convex quadratic multiobjective optimization problems.

2 Preliminaries and robust multiobjective programs

Let us start with some notation and definitions. The notation $\mathbb {R}^m$ signifies the Euclidean space whose norm is denoted by $\Vert \cdot \Vert$ for each $m\in \mathbb {N}:=\{1,2,\ldots \}$. The inner product in $\mathbb {R}^m$ is defined by $\langle y,z\rangle :=y^T z$ for all $y, z\in \mathbb {R}^m.$ The origin of any space is denoted by 0 but we may use $0_m$ to denote the origin of $\mathbb {R}^m$ for the sake of clarification. The nonnegative orthant of $\mathbb {R}^m$ is denoted by $\mathbb {R}^m_+:=\{(x_1,\ldots ,x_m)\in \mathbb {R}^m\mid x_i\ge 0, i=1,\ldots ,m\}.$ For a nonempty set $\Gamma \subset \mathbb {R}^m,$ $\mathrm{conv\,}\Gamma$ denotes the convex hull of $\Gamma$ and $\mathrm{cl\,}\Gamma$ (resp., $\mathrm{int\,}\Gamma$) stands for the closure (resp., interior) of $\Gamma$, while $\mathrm{coneco\,}\Gamma :=\mathbb {R}_+\mathrm{conv\,}\Gamma$ stands for the convex conical hull of $\Gamma \cup \{0_m\}$, where $\mathbb {R}_+:=[0,+\infty )\subset \mathbb {R}.$ As usual, the symbol $I_m\in \mathbb {R}^{m\times m}$ stands for the identity $(m\times m)$ matrix. Let $S^m$ be the space of all symmetric $(m\times m)$ matrices. A matrix $A\in S^m$ is said to be positive semidefinite, denoted by $A\succeq 0$, whenever $x^TAx\ge 0$ for all $x\in \mathbb {R}^m.$ If $x^TAx> 0$ for all $x\in \mathbb {R}^m\setminus \{0_m\}$, then A is called positive definite, denoted by $A\succ 0$. The trace of a square $(m\times m)$ matrix A is defined by $\mathrm{Tr}(A)=\sum \nolimits _{i=1}^ma_{ii}$, where $a_{ii}$ is the entry in the ith row and ith column of A for $i=1,\ldots ,m$.

For a closed convex subset $\Gamma \subset \mathbb {R}^m$, its indicator function $\delta _\Gamma :\mathbb {R}^m \rightarrow \overline{\mathbb {R}}:=\mathbb {R}\cup \{+\infty \}$ is defined as $\delta _\Gamma (x):=0$ if $x\in \Gamma$ and $\delta _\Gamma (x):=+\infty$ if $x\notin \Gamma$. Given an extended real-valued function $\varphi :\mathbb {R}^m\rightarrow \overline{\mathbb {R}}$, the domain and epigraph of $\varphi$ are defined respectively by

$$\begin{aligned} \text{ dom }\,\varphi :=\{x\in \mathbb {R}^m\mid \varphi (x)<+\infty \},\quad \text{ epi }\,\varphi :=\{(x,\mu )\in \mathbb {R}^m\times \mathbb {R}\; |\; \mu \ge \varphi (x)\}. \end{aligned}$$

The conjugate function of $\varphi$, denoted by $\varphi ^*:\mathbb {R}^m\rightarrow \overline{\mathbb {R}},$ is defined by

$$\begin{aligned} \varphi ^*(v)=\sup {\{ v^Tx -\varphi (x)\mid x\in \mathrm{dom\,}\varphi \}},\; v\in \mathbb {R}^m. \end{aligned}$$

Letting $\varphi _1$ and $\varphi _2$ be proper lower semicontinuous convex functions, it is well known (see e.g., Zalinescu, 2002; Burachik and Jeyakumar, 2005; Rockafellar, 1970) that $\mathrm{epi}(\lambda \varphi _1)^*=\lambda \mathrm{epi}\varphi _1^*$ for any $\lambda >0$ and

$$\begin{aligned} \mathrm{epi}(\varphi _1+\varphi _2)^*=\mathrm{cl}(\mathrm{epi}\varphi _1^*+\mathrm{epi}\varphi _2^*),\end{aligned}$$

(2.1)

where the closure operation is superfluous if one of $\varphi _1,\varphi _2$ is continuous at some point $x_0\in \mathrm{dom}\varphi _1\cap \mathrm{dom}\varphi _2$.

In this paper, we consider a convex quadratic multiobjective optimization problem under data uncertainty that can be captured as the following model:

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}}{\big \{ \big (f_1(x,u^1),\ldots ,f_p(x,u^p)\big ) \mid g_l(x, v^l) \le 0, l=1,\ldots ,k\big \}}, \end{aligned}$$

(UP)

where $u^r, r=1,\ldots ,p\in \mathbb {N}$ and $v^l, l=1,\dots ,k\in \mathbb {N}$ are uncertain parameters and they reside, respectively, in the uncertainty sets $\Omega _r\subset \mathbb {R}^m$ and $\Theta _l\subset \mathbb {R}^s$, and $f_r:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}, g_l:\mathbb {R}^n\times \mathbb {R}^{s}\rightarrow \mathbb {R}$ are bi-functions.

Throughout this paper, the uncertainty sets $\Omega _r, r=1,\ldots , p$ and $\Theta _l, l=1,\ldots ,k$ are assumed to be spectrahedra (see e.g., Ramana and Goldman, 1995) given by

$$\begin{aligned} \Omega _r&:=\{u^r:=(u^r_1,\ldots ,u^r_m)\in \mathbb {R}^{m}\mid A^r+\sum _{i=1}^mu^r_iA^r_i\succeq 0\}, \nonumber \\ \Theta _l&:=\{v^l:=(v_1^l,\ldots ,v_s^l)\in \mathbb {R}^{s}\mid B^l+\sum _{j=1}^sv^l_jB^l_j\succeq 0\} \end{aligned}$$

(2.2)

with given symmetric matrices $A^r, A^r_i, i=1,\ldots , m\in \mathbb {N}$ and $B^l, B^l_j, j=1,\ldots ,s\in \mathbb {N}$, while the bi-functions $f_r, r=1,\ldots , p$ and $g_l, l=1,\ldots ,k$ are convex quadratic functions given by

$$\begin{aligned} f_r(x,u^r):=&x^TQ^rx+(\xi ^r)^Tx+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^Tx+ \beta ^r_i\big ), x\in \mathbb {R}^n, \nonumber \\ u^r:=&(u^r_1,\ldots ,u^r_{m})\in \Omega _r, \nonumber \\ g_l(x,v^l):=&x^TM^lx+(\theta ^{l})^Tx+ \gamma ^l+\sum \limits _{j=1}^{s} v_j^l\big ((\theta ^{l}_j)^Tx+ \gamma ^l_j\big ), x\in \mathbb {R}^n,\nonumber \\ v^l :=&(v^l_1,\ldots ,v^l_{s})\in \Theta _l \end{aligned}$$

(2.3)

with $Q^r\succeq 0, \xi ^r\in \mathbb {R}^n, \xi ^r_i\in \mathbb {R}^n, \beta ^r\in \mathbb {R}, \beta _i^r\in \mathbb {R}, i=1,\ldots ,m$ and $M^l\succeq 0, \theta ^l\in \mathbb {R}^n, \theta ^l_j\in \mathbb {R}^n, \gamma ^l\in \mathbb {R}, \gamma ^l_j\in \mathbb {R}, j=1,\ldots ,s$ fixed.

The spectrahedral data uncertainty sets in (2.2) encompass all important popular data uncertainty sets used in practical robust models such as box uncertainty set, ball uncertainty set or ellipsoidal uncertainty set (see e.g., Vinzant, 2014). Moreover, spectrahedra admit the special structures of linear matrix inequalities that empower us to employ variable transformations and express optimality conditions in terms of linear matrix inequalities. We assume that the uncertainty sets in (2.2) are nonempty and compact.

To treat the uncertain multiobjective problem (UP), we associate with it a robust counterpart that can be formulated as

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}}{\big \{\big (\max _{u^1\in \Omega _1} f_1(x,u^1),\ldots ,\max _{u^p\in \Omega _p}f_p(x,u^p)\big ) \mid g_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}}. \end{aligned}$$

(RP)

In this model, the uncertain parameters of the objective and constraint functions are enforced for all possible realizations within the corresponding uncertainty sets, and so the robust counterpart problem (RP) aims at locating a (weak) Pareto solution which is immunized against the data uncertainty. It is worth mentioning that by taking the maximum on each uncertainty set to all possible realizations of the corresponding objective, the underlying problem becomes a multiobjective problem with nonsmooth objective functions. The transformed problem is a nonsmooth multiobjective problem involving an infinite number of constraints, and so solving this problem is in general computationally intractable for general compact convex uncertainty sets by using the duality approach as in Chuong (2020).

The following solution concepts are in the sense of minmax robustness (see e.g., Ehrgott et al., 2014; Kuroiwa and Lee, 2012) for multiobjective optimization.

Definition 2.1

(Robust Pareto and weak Pareto solutions) Let $\bar{x} \in C:=\{x\in \mathbb {R}^n \mid g_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}.$

(i) We say that $\bar{x}$ is a robust Pareto solution of problem (UP) if it is a Pareto solution of problem (RP), i.e., there is no other point $x\in C$ such that

$$\begin{aligned} \max _{u^r\in \Omega _r} f_r(x,u^r)&\le \max _{u^r\in \Omega _r}f_r(\bar{x},u^r),\; r=1,\ldots , p\; \text{ and } \; \\ \max _{u^r\in \Omega _r} f_r(x,u^r)&<\max _{u^r\in \Omega _r}f_r(\bar{x},u^r) \; \text{ for } \text{ some } r\in \{1,\ldots , p\}. \end{aligned}$$

(ii) We say that $\bar{x}$ is a robust weak Pareto solution of problem (UP) if it is a weak Pareto solution of problem (RP), i.e., there is no other point $x\in C$ such that

$$\begin{aligned} \max _{u^r\in \Omega _r} f_r(x,u^r) < \max _{u^r\in \Omega _r}f_r(\bar{x},u^r),\; r=1,\ldots , p. \end{aligned}$$

3 Robust optimality conditions

In this section, we present necessary as well as sufficient conditions for robust (weak) Pareto optimality of the uncertain multiobjective problem (UP).

Theorem 3.1

Let $\bar{x}\in \mathbb {R}^n$ be a robust feasible point of problem (UP), i.e., $\bar{x}\in C:=\{x\in \mathbb {R}^n \mid g_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}.$

(i) (Necessary optimality) Assume that the characteristic cone $K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v^l), v^l\in \Theta _l, l=1,\ldots ,k\}$ is closed. If $\bar{x}$ is a robust weak Pareto solution of problem (UP), then there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that

$$\begin{aligned}&\left( \begin{array}{cc} \sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l &{} \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1} \alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1} \alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1} \lambda ^j_l\theta ^l_j)\big )^T&{} \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l \gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\\ \end{array}\right) \succeq 0, \end{aligned}$$

(3.1)

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^m\alpha ^i_rA^r_i\succeq 0, r=1,\ldots ,p, \; \lambda _lB^l+\sum _{j=1}^s\lambda _l^jB^l_j\succeq 0, l=1,\ldots ,k, \end{aligned}$$

(3.2)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r} f_r(\bar{x},u^r)$ for $r=1,\dots ,p.$

(ii) (Sufficiency for robust weak Pareto solutions) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.1) and (3.2) hold, then $\bar{x}$ is a robust weak Pareto solution of problem (UP).

(iii) (Sufficiency for robust Pareto solutions) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.1) and (3.2) hold, then $\bar{x}$ is a robust Pareto solution of problem (UP).

Proof

Denote $F_r(x):= \max \limits _{u^r\in \Omega _r} f_r(x,u^r), r=1,\dots ,p$ and $G_l(x):= \max \limits _{v^l\in \Theta _l} g_l(x,v^l), l=1,\dots ,k$ for $x\in \mathbb {R}^n.$ It is easy to see that $F_r, r=1,\dots ,p$ and $G_l, l=1,\ldots ,k$ are convex functions finite on $\mathbb {R}^n$.

(i) Let the cone K be closed, and let $\bar{x}$ be a robust weak Pareto solution of problem (UP). We see that

$$\{x\in C\mid F_r(x)-F_r(\bar{x})<0, r=1,\ldots ,p\}=\emptyset ,$$

where $C:=\{x\in \mathbb {R}^n \mid g_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}$ is the robust feasible set of problem (UP). Invoking a classical alternative theorem in convex analysis (cf. Rockafellar, 1970, Theorem 21.1), we find $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}$ such that

$$\begin{aligned} \sum _{r=1}^p \alpha _r F_r(x)\ge \sum _{r=1}^p \alpha _rF_r(\bar{x})\; \text{ for } \text{ all } \; x\in C. \end{aligned}$$

This shows that

$$\begin{aligned} \inf _{x\in C}\Big \{\sum _{r=1}^p\alpha _r\max \limits _{u^r\in \Omega _r}\big \{x^TQ^rx+(\xi ^r)^Tx+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^Tx+ \beta ^r_i\big )\big \}\Big \}\ge \sum _{r=1}^p \alpha _rF_r(\bar{x}), \end{aligned}$$

(3.3)

where $u^r:=(u_1^r,\ldots ,u^r_m), r=1,\ldots ,p.$ Let $\Omega :=\Pi _{r=1}^p\Omega _r\subset \mathbb {R}^{pm}.$ We see that $\Omega$ is a convex compact set and (3.3) becomes the following inequality

$$\begin{aligned} \inf _{x\in C}\max \limits _{(u^1,\ldots ,u^p)\in \Omega }\Big \{\sum _{r=1}^p\alpha _r\Big (x^TQ^rx+(\xi ^r)^Tx+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^Tx+ \beta ^r_i\big )\Big )\Big \}\ge \sum _{r=1}^p \alpha _rF_r(\bar{x}). \end{aligned}$$

(3.4)

Let $H:\mathbb {R}^{n}\times \mathbb {R}^{pm}\rightarrow \mathbb {R}$ be defined by $H(x,u):=\sum \limits _{r=1}^p\alpha _r\big (x^TQ^rx+(\xi ^r)^Tx+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^Tx+ \beta ^r_i\big )\big )$ for $x\in \mathbb {R}^n$ and $u:=(u^1,\ldots ,u^p)\in \mathbb {R}^{pm}.$ Then, H is an affine function in variable u and a convex function in variable x and so, we invoke a classical minimax theorem (see e.g., Sion, 1958, Theorem 4.2) and (3.4) to claim that

$$\begin{aligned} \max _{u\in \Omega }{\inf \limits _{x\in C}{H(x,u)}}=\inf _{x\in C}{\max \limits _{u\in \Omega }{H(x,u)}}\ge \sum _{r=1}^p \alpha _rF_r(\bar{x}). \end{aligned}$$

Therefore, we can find $\bar{u}:=(\bar{u}^1,\ldots ,\bar{u}^p)$, where $\bar{u}^r:=(\bar{u}^r_1,\ldots ,\bar{u}^r_m) \in \Omega _r, r=1,\ldots ,p$, such that $\inf \limits _{x\in C}{H(x,\bar{u})} \ge \sum \limits _{r=1}^p \alpha _rF_r(\bar{x}).$ This shows that

$$\begin{aligned} \big (0_n,-\sum _{r=1}^p \alpha _rF_r(\bar{x})\big )\in \mathrm{epi}\,\big (H(\cdot ,\bar{u})+\delta _C\big )^*. \end{aligned}$$

Due to the continuity of $H(\cdot ,\bar{u})$ on $\mathbb {R}^n$, by taking (2.1) into account, we arrive at

$$\begin{aligned} \big (0_n,-\sum _{r=1}^p \alpha _rF_r(\bar{x})\big )\in \mathrm{epi}\,H^*(\cdot ,\bar{u}) + \mathrm{epi}\,\delta _C^*. \end{aligned}$$

Moreover, we have (cf. Jeyakumar and Li, 2010, Page 3390 or Jeyakumar, 2003, p. 951) that $\mathrm{epi}\,\delta _C^*={\text {cl}}K=K$, where the last equality holds as the cone $K:={\text {coneco}}\{(0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot , v^l), v^l\in \Theta _l, l=1,\ldots ,k\big \}$ is assumed to be closed. Consequently,

$$\begin{aligned} \big (0_n,-\sum _{r=1}^p \alpha _rF_r(\bar{x})\big )\in \mathrm{epi}\,H^*(\cdot ,\bar{u}) + K, \end{aligned}$$

which means that there exist $(w,\lambda )\in \mathrm{epi}\,H^*(\cdot ,\bar{u})$ and $\bar{v}^{lt} := (\bar{v}^{lt}_1,\ldots ,\bar{v}^{lt}_{s}) \in \Theta _l$, $(\bar{w}^{lt},\bar{\lambda }^{lt}) \in \mathrm{epi}\,g_l^*(\cdot ,\bar{v}^{lt})$, $\bar{\alpha }\ge 0, \bar{\alpha }^{lt} \ge 0, l=1,\ldots ,k, t=1,\ldots ,s_l$ such that

$$\begin{aligned} 0_n = w+\sum \limits _{l=1}^{k}\sum \limits _{t=1}^{s_l} \bar{\alpha }^{lt}\bar{w}^{lt},\quad -\sum _{r=1}^p \alpha _rF_r(\bar{x})=\lambda +\bar{\alpha }+\sum \limits _{l=1}^{k}\sum \limits _{t=1}^{s_l} \bar{\alpha }^{lt}\bar{\lambda }^{lt}. \end{aligned}$$

(3.5)

Observe by $(\bar{w}^{lt},\bar{\lambda }^{lt})\in \mathrm{epi}\,g_l^*(\cdot ,\bar{v}^{lt})$, $l=1,\ldots ,k$, $t=1,\ldots , s_l$ that, for each $x\in \mathbb {R}^n$, one has $\bar{\lambda }^{lt} \ge (\bar{w}^{lt})^T x- g_l(x,\bar{v}^{lt})$. This together with (3.5) and the relation $(w,\lambda )\in \mathrm{epi}\,H^*(\cdot ,\bar{u})$ implies that, for each $x\in \mathbb {R}^n$,

$$\begin{aligned} H(x,\bar{u}) \ge w^\top x-\lambda \ge -\sum \limits _{l=1}^{k}\sum _{t=1}^{s_l} \bar{\alpha }^{lt}g_l(x,\bar{v}^{lt}) + \sum _{r=1}^p \alpha _rF_r(\bar{x}). \end{aligned}$$

(3.6)

Letting $\alpha ^i_r:= \alpha _r\bar{u}^r_i, r=1,\ldots ,p, i=1,\ldots ,m$, we assert that

$$\begin{aligned} \alpha _rA^r+\sum _{i=1}^m\alpha ^i_rA^r_i=\alpha _r\Big (A^r+\sum _{i=1}^m\bar{u}^r_iA^r_i\Big )\succeq 0, r=1,\ldots ,p.\end{aligned}$$

(3.7)

To see this, recall that $\alpha _r\ge 0$ and $\bar{u}^r\in \Omega _r$ (and so $A^r+\sum \limits _{i=1}^m\bar{u}^r_iA^r_i\succeq 0$) for $r=1,\ldots ,p.$ Similarly, by letting $\lambda _l:= \sum \limits _{t=1}^{s_l}\bar{\alpha }^{lt} \ge 0, \lambda ^j_l:= \sum \limits _{t=1}^{s_l}\bar{\alpha }^{lt} \bar{v}^{lt}_j, l=1,\ldots ,k, j=1,\ldots , s,$ we see that

$$\begin{aligned} \lambda _lB^l+\sum \limits _{j=1}^s\lambda _l^jB^l_j=\sum \limits _{t=1}^{s_l} \big [\bar{\alpha }^{lt}\big (B^l+\sum \limits _{j=1}^s\bar{v}^{lt}_jB^l_j\big )\big ]\succeq 0, l=1,\ldots ,k \end{aligned}$$

due to $\bar{\alpha }^{lt}\big (B^l+\sum \limits _{j=1}^s\bar{v}^{lt}_jB^l_j\big )\succeq 0, l=1,\ldots ,k, t=1,\ldots ,s_l$. Consequently, (3.2) holds.

Now, we deduce from (3.6) that

$$\begin{aligned}&x^T \Big (\sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l\Big )x +\Big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r) +\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\Big )^Tx\\&\quad + \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l \gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0\, \text{ for } \text{ all } \, x\in \mathbb {R}^n.\end{aligned}$$

This is equivalent to (cf. Ben-Tal and Nemirovski, 2001, Simple lemma, p. 163) the following matrix inequality

$$\begin{aligned}{\left( \begin{array}{cc} \sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l &{} \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big )^T&{} \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l\gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\\ \end{array} \right) \succeq 0}, \end{aligned}$$

showing that (3.1) is also established and so the assertion in (i) has been justified.

(ii) Let $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ be such that (3.1) and (3.2) hold.

Consider any $r\in \{1,\ldots ,p\}$. By the compactness of $\Omega _r$, we assert by (3.2) that if $\alpha _r=0$, then $\alpha _r^i=0$ for all $i=1,\ldots ,m.$ Suppose, on the contrary, that $\alpha _r=0$ but there exists $\tilde{i} \in \{1,\ldots ,m\}$ with $\alpha _r^{\tilde{i}}\ne 0.$ In this case, we get by (3.2) that $\sum \limits ^{m}_{i=1}\alpha _r^iA^r_i\succeq 0$. Let $\bar{u}^r:= (\bar{u}^r_1,\ldots ,\bar{u}^r_m)\in \Omega _r.$ It follows by definition that $A^r+\sum \limits _{i=1}^m\bar{u}^r_iA^r_i\succeq 0$ and

$$\begin{aligned} A^r+\sum _{i=1}^m(\bar{u}^r_i+\lambda \alpha _r^i)A^r_i =\left( A^r+\sum _{i=1}^m\bar{u}^r_iA^r_i\right) +\lambda \sum _{i=1}^m\alpha _r^iA^r_i\succeq 0 \text{ for } \text{ all } \lambda >0. \end{aligned}$$

This guarantees that $\bar{u}^r+\lambda (\alpha _r^1,\ldots ,\alpha _r^m)\in \Omega _r$ for all $\lambda >0$, which contradicts the fact that $(\alpha _r^1,\ldots ,\alpha _r^m)\ne 0_m$ and $\Omega _r$ is a bounded set. Thus, our claim must be true.

Now, take $\hat{u}^r:=(\hat{u}^r_1,\ldots ,\hat{u}^r_m)\in \Omega _r$ and define $\tilde{u}^r:=(\tilde{u}^r_1,\ldots ,\tilde{u}^r_m)$ with

$$\tilde{u}_i^r:={\left\{ \begin{array}{ll} \hat{u}^r_i &{} \text{ if } \alpha _r=0,\\ \frac{\alpha _r^i}{\alpha _r} &{} \text{ if } \alpha _r\ne 0,\end{array}\right. }\; i=1,\ldots , m.$$

This shows that $\tilde{u}^r\in \Omega _r.$ Then, for any $x\in \mathbb {R}^n,$ we have

$$\begin{aligned}&\alpha _rx^TQ^rx+ (\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)^Tx +\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r\nonumber \\&\quad =\alpha _r\Big (x^TQ^rx+ (\xi ^r)^Tx+ \beta ^r+\sum \limits ^{m}_{i=1}\tilde{u}^r_i\big ((\xi _i^r)^Tx + \beta _i^r\big )\Big )=\alpha _rf_r(x,\tilde{u}^r), \end{aligned}$$

(3.8)

where we remind that if $\alpha _r=0$, then $\alpha _r^i=0$ for all $i=1,\ldots ,m$ as said above. Similarly, by (3.2), we can find $\tilde{v}^l:=(\tilde{v}^l_1,\ldots ,\tilde{v}^l_s)\in \Theta _l,\; l=1,\ldots ,k$ such that

$$\begin{aligned}&\lambda _lx^TM^lx+ (\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta _j^l)^Tx +\lambda _l \gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma _j^l\nonumber \\&\quad =\lambda _l\Big (x^TM^lx+ (\theta ^l)^Tx+ \gamma ^l+\sum \limits ^{s}_{j=1}\tilde{v}^l_j\big ((\theta _j^l)^Tx + \gamma _j^l\big )\Big )=\lambda _lg_l(x,\tilde{v}^l),\; l=1,\ldots ,k \end{aligned}$$

(3.9)

for each $x\in \mathbb {R}^n.$

Arguing as in the proof of (i), (3.1) can be equivalently rewritten as

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _r \big (x^TQ^rx+(\xi ^r)^Tx+\beta ^r\big )+\sum \limits _{r=1}^p\sum \limits ^{m}_{i=1} \alpha ^i_r\big ((\xi _i^r)^Tx+\beta _i^r\big )\\&\quad +\sum \limits ^{k}_{l=1}\lambda _l\big (x^TM^lx+(\theta ^l)^Tx+\gamma ^l\big )+\sum \limits _{l=1}^k\sum \limits ^{s}_{j=1}\lambda ^j_l\big ((\theta ^l_j)^Tx+\gamma ^l_j\big )\\&\quad -\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0\, \text{ for } \text{ all } \, x\in \mathbb {R}^n, \end{aligned}$$

and so, by (3.8) and (3.9), we arrive at

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _rf_r(x,\tilde{u}_r) +\sum \limits ^{k}_{l=1}\lambda _lg_l(x,\tilde{v}^l)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0\, \text{ for } \text{ all } \, x\in \mathbb {R}^n. \end{aligned}$$

(3.10)

Next, let $\hat{x}\in \mathbb {R}^{n}$ be a robust feasible point of problem (UP). Then, it shows that $g_l(\hat{x},\tilde{v}^l)\le 0$ for $\tilde{v}^l\in \Theta _l, l=1,\ldots ,k.$ Estimating (3.10) at $\hat{x}$, we obtain that $\sum \limits _{r=1}^p\alpha _rf_r(\hat{x},\tilde{u}_r) \ge \sum \limits _{r=1}^p\alpha _rF_r(\bar{x})$ and so,

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _rF_r(\hat{x})\ge \sum _{r=1}^p\alpha _rF_r(\bar{x}) \end{aligned}$$

(3.11)

due to the fact that $\alpha _r\ge 0$ and $F_r(\hat{x})\ge f_r(\hat{x}, \tilde{u}^r)$ for $r=1,\ldots ,p.$

By $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}$, (3.11) guarantees that there is no other robust feasible point $\hat{x}\in \mathbb {R}^{n}$ such that

$$\begin{aligned}F_r(\hat{x})< F_r(\bar{x}),\; r=1,\ldots , p,\end{aligned}$$

and so $\bar{x}$ is a robust a weak Pareto solution of problem (UP).

(iii) Let $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ be such that (3.1) and (3.2) are valid. Proceeding similarly as in the proof of (ii), we arrive at the conclusion in (3.11). This, together with $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+$, ensures that $\bar{x}$ is a robust a Pareto solution of problem (UP). The proof of the theorem is complete. $\square$

Remark 3.2

Note that the closedness of the characteristic cone K in Theorem 3.1 is fulfilled if at least one of the following conditions is valid: a) (see e.g., Chuong and Jeyakumar, 2017) $g_l(\cdot ,v^l), v^l\in \Theta _l, l=1,\ldots ,k$ are linear functions and $\Theta _l, l=1,\ldots ,k$ are polytopes; b) (see e.g., Jeyakumar and Li, 2010, Proposition 3.2) the Slater constraint qualification holds, i.e., there exists $\tilde{x} \in \mathbb {R}^{n}$ such that

$$\begin{aligned} g_l(\tilde{x}, v^l)< 0, \forall v^l\in \Theta _l, l=1,\ldots ,k.\end{aligned}$$

(3.12)

The following example illustrates that the optimality conditions in (3.1) and (3.2) may go awry if the closedness of the characteristic cone K imposed in Theorem 3.1 is violated.

Example 3.3

(The importance of the closedness regularity) Consider a robust convex quadratic multiobjective optimization problem of the form:

$$\begin{aligned}&\min _{x:=(x_1,x_2)\in \mathbb {R}^2}\big \{(\max \limits _{u:=(u_1,u_2)\in \Omega }\{x^2_2+x_1+u_1\},\max \limits _{u:=(u_1,u_2)\in \Omega }\{x^2_2+3x_1-u_2\})\mid v_1x_1 \\&\quad +(v_2+1)x_2 \le 0, \forall v:=(v_1,v_2)\in \Theta \big \}, \end{aligned}$$

(EP1)

where $\Omega :=\{u:=(u_1,u_2)\in \mathbb {R}^2\mid \frac{u_1^2}{2} +\frac{u_2^2}{3}\le 1\}$ and $\Theta :=\{v:=(v_1,v_2)\in \mathbb {R}^2\mid v^{2}_1+v^2_2 \le 1\}.$ The problem (EP1) can be expressed in terms of problem (RP), where $\Omega _1:=\Omega _2:=\Omega$ and $\Theta _1:=\Theta$ are described respectively by

$$\begin{aligned} A^r&:= \left( \begin{array}{ccc} 2 &{} 0 &{}0 \\ 0&{}3&{}0\\ 0&{}0&{}1\\ \end{array} \right) , A^r_1:=B^1_1= \left( \begin{array}{ccc} 0 &{} 0 &{}1 \\ 0&{}0&{}0\\ 1&{}0&{}0\\ \end{array} \right) , A^r_2:=B^1_2= \left( \begin{array}{ccc} 0 &{} 0 &{}0 \\ 0&{}0&{}1\\ 0&{}1&{}0\\ \end{array}\right) , \\ B^1&:=I_3, r=1,2, \end{aligned}$$

and $f_r, r=1,2, g_1,$ are given respectively by $Q^r:=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{}1\\ \end{array} \right) ,$ $\xi ^1:=(1,0), \xi ^2:=(3,0), \xi ^r_1:=\xi ^r_2:=0_2, \beta ^r:=\beta ^1_2:=\beta ^2_1:=0,\beta ^1_1:=1, \beta ^2_2:=-1, r=1,2$ and $M^1:=0_{2\times 2}, \theta ^1:=(0,1), \theta ^1_1:=(1,0), \theta ^1_2:=(0,1), \gamma ^1:= \gamma ^1_1:=\gamma ^1_2:=0.$

By direct computation, we see that the feasible set of problem (EP1) is given by

$$\begin{aligned}C:=\{x\in \mathbb {R}^2\mid g_1(x,v)\le 0,\forall v\in \Theta \}=\{0\}\times (-\infty ,0].\end{aligned}$$

Moreover, it can be checked that $\bar{x}:=(0,0)$ is a Pareto solution of the robust problem (EP1). However, we assert that the conditions in (3.1) and (3.2) are not valid at $\bar{x}$ for this setting. To see the conclusion, assume on the contrary that there exist $(\alpha _1,\alpha _2)\in \mathbb {R}^2_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,2, i=1,2,$ $\lambda _1 \in \mathbb {R}_+, \lambda _1^j\in \mathbb {R}, j=1,2$ such that

$$\begin{aligned}&\left( \begin{array}{cc} \sum \limits _{r=1}^2\alpha _rQ^r+\lambda _1M^1 &{} \frac{1}{2}\big (\sum \limits _{r=1}^2(\alpha _r\xi ^r+\sum \limits ^{2}_{i=1}\alpha ^i_r\xi _i^r)+\lambda _1\theta ^1+\sum \limits ^{2}_{j=1}\lambda ^j_1\theta ^1_j \big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^2(\alpha _r\xi ^r+\sum \limits ^{2}_{i=1}\alpha ^i_r\xi _i^r)+ \lambda _1\theta ^1+\sum \limits ^{2}_{j=1}\lambda ^j_1\theta ^1_j \big )^T&{} \sum \limits _{r=1}^2(\alpha _r \beta ^r+\sum \limits ^{2}_{i=1}\alpha ^i_r\beta _i^r)+ \lambda _1\gamma ^1+\sum \limits ^{2}_{j=1}\lambda ^j_1\gamma ^1_j -\sum \limits _{r=1}^2\alpha _rF_r(\bar{x})\\ \end{array} \right) \succeq 0, \end{aligned}$$

(3.13)

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^2\alpha ^i_rA^r_i\succeq 0, r=1,2,\; \lambda _1B^1+\sum _{j=1}^2\lambda ^j_1B^1_j\succeq 0, \end{aligned}$$

(3.14)

where $F_1(\bar{x}):=\max \limits _{u \in \Omega } f_1(\bar{x},u)=\sqrt{2}$ and $F_2(\bar{x}):=\max \limits _{u \in \Omega } f_2(\bar{x},u)=\sqrt{3}$. Note that (3.14) amounts to the following inequalities

$$\begin{aligned}&\frac{(\alpha ^1_r)^2}{2} +\frac{(\alpha ^2_r)^2}{3}\le (\alpha _r)^2, r=1,2, \end{aligned}$$

(3.15)

$$\begin{aligned}&(\lambda ^1_1)^2 +(\lambda ^2_1)^2 \le (\lambda _1)^2. \end{aligned}$$

(3.16)

We deduce from (3.13) that

$$\begin{aligned} (\alpha _1+ \alpha _2)x^2_2+(\alpha _1+3\alpha _2+\lambda ^1_1)x_1+(\lambda _1+\lambda _1^2)x_2+\alpha ^1_1-\alpha ^2_2-\sqrt{2}\alpha _1-\sqrt{3}\alpha _2\ge 0 \end{aligned}$$

for all $x_1\in \mathbb {R}$ and all $x_2\in \mathbb {R}.$ This entails that

$$\begin{aligned}&(\alpha _1+3\alpha _2+\lambda ^1_1)x_1+\alpha ^1_1-\alpha ^2_2-\sqrt{2}\alpha _1-\sqrt{3}\alpha _2\ge 0 \; \text{ for } \text{ all } \; x_1\in \mathbb {R}, \end{aligned}$$

(3.17)

$$\begin{aligned}&(\alpha _1+ \alpha _2)x^2_2+(\lambda _1+\lambda _1^2)x_2+\alpha ^1_1-\alpha ^2_2-\sqrt{2}\alpha _1-\sqrt{3}\alpha _2\ge 0 \; \text{ for } \text{ all } \; x_2\in \mathbb {R}, \end{aligned}$$

(3.18)

On the one hand, we get by (3.17) that $\alpha _1+3\alpha _2+\lambda ^1_1=0$ and

$$\begin{aligned} \alpha ^1_1-\alpha ^2_2-\sqrt{2}\alpha _1-\sqrt{3}\alpha _2\ge 0. \end{aligned}$$

On the other hand, it holds that $\alpha ^1_1-\sqrt{2}\alpha _1\le |\alpha _1^1|-\sqrt{2}\alpha _1\le 0,$ where the last inequality holds by virtue of (3.15). Similarly, we have $-\alpha ^2_2-\sqrt{3}\alpha _2\le |\alpha _2^2|-\sqrt{3}\alpha _2\le 0,$ and so

$$\begin{aligned} \alpha ^1_1-\sqrt{2}\alpha _1-\alpha ^2_2-\sqrt{3}\alpha _2\le 0. \end{aligned}$$

Therefore, $\alpha ^1_1-\alpha ^2_2-\sqrt{2}\alpha _1-\sqrt{3}\alpha _2= 0.$ This and (3.18) guarantee that $\lambda _1+\lambda ^2_1=0.$

Substituting now $\lambda ^1_1=-\alpha _1-3\alpha _2$ and $\lambda ^2_1=-\lambda _1$ into (3.16), we arrive at $(\alpha _1+3\alpha _2)^2\le 0$, which is absurd due to the fact that $(\alpha _1,\alpha _2)\in \mathbb {R}^2_+\setminus \{0\}.$ Consequently, the conclusion of (i) in Theorem 3.1 does not hold for this setting. The reason is that the characteristic cone

$$\begin{aligned} K&:={\text {coneco}} \{ (0_2,1)\cup \mathrm{epi}\,g^*_1(\cdot ,v), v \in \Theta \}\\&\quad ={\text {coneco}}\big \{(0,0,1),(v_1,v_2+1,0)\mid v_1^2+v_2^2\le 1\big \}\end{aligned}$$

is not closed for this problem. To see this, we select a sequence $c_m:=(1,\frac{1}{m},0)=m(\frac{1}{m},\frac{1}{m^2},0)\in K$ for all $m\in \mathbb {N}$. Clearly, it holds that $c_m\rightarrow c_0:=(1,0,0)$ as $m\rightarrow \infty$ but $c_0\notin K.$

In the next proposition, we show how the optimality conditions obtained in (3.1) and (3.2) can be alternatively checked via verifiable criteria including a robust Karush-Kuhn-Tucker (KKT) condition. To this end, let $\bar{x}\in \mathbb {R}^n$ be a robust feasible point of problem (UP). One says (see e.g., Chuong, 2020 for a more general nonsmooth setting) that the robust (KKT) condition of problem (UP) holds at $\bar{x}$ if there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \bar{u}^r\in \Omega _r, r=1,\ldots ,p$ and $(\lambda _1,\ldots ,\lambda _k)\in \mathbb {R}^k_+, \bar{v}^l\in \Theta _l, l=1,\ldots ,k$ such that

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _r\nabla _1 f_r(\bar{x},\bar{u}^r)+\sum \limits _{l=1}^k\lambda _l\nabla _1g_l(\bar{x},\bar{v}^l)=0,\;\lambda _l g_l(\bar{x},\bar{v}^l)=0,\; l=1,\ldots ,k, \end{aligned}$$

(3.19)

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\bar{u}^r) = \sum \limits _{r=1}^p\alpha _rF_r(\bar{x}), \end{aligned}$$

(3.20)

where $\nabla _1f$ denotes the derivative of $f(\cdot ,\cdot )$ with respect to the first variable. Note that in the particular case, where there are no uncertain parameters in the objective functions of problem (UP), the condition (3.20) is redundant and in this case, its corresponding robust (KKT) condition was examined in Chuong (2018) for an SOS-convex polynomial setting. It is worth noticing further that the robust (KKT) condition of problem (UP) holds at $\bar{x}$ is equivalent to saying that the (classical) (KKT) condition of robust problem (RP) holds at $\bar{x}$.

Proposition 3.4

(Optimality characterizations via verifiable criteria) Let $\bar{x}\in \mathbb {R}^n$ be a robust feasible point of problem (UP). The following statements are equivalent:

(i) The optimality conditions in (3.1) and (3.2) are valid.

(ii) The robust (KKT) condition of problem (UP) holds at $\bar{x}$.

(iii) There exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ $\mu ^0_j\in \mathbb {R}_+, \mu ^i_j\in \mathbb {R}, j=1,\ldots ,q, i=1,\ldots ,s$ such that

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _r\big (2Q^r\bar{x}+ \xi ^r\big )+\sum \limits _{r=1}^p\sum \limits ^{m}_{i=1}\alpha ^i_r \xi _i^r+\sum \limits _{l=1}^k\lambda _l\big (2M^l\bar{x}+ \theta ^l\big )+\sum \limits _{l=1}^k\sum \limits ^{s}_{j=1}\lambda ^j_l \theta _j^l=0, \end{aligned}$$

(3.21)

$$\begin{aligned}&\lambda _l\big (\bar{x}^TM^l\bar{x}+(\theta ^l)^T\bar{x}+\gamma ^l\big ) +\sum \limits _{j=1}^s\lambda ^j_l\big ((\theta _j^l)^T\bar{x}+\gamma ^l_j\big )=0,\; l=1,\ldots ,k,\end{aligned}$$

(3.22)

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _r\big (\bar{x}^TQ^r\bar{x}+ (\xi ^r)^T\bar{x}+\beta ^r\big )+\sum \limits _{r=1}^p\sum \limits ^{m}_{i=1}\alpha ^i_r\big ( (\xi _i^r)^T\bar{x}+\beta ^r_i\big )=\sum \limits _{r=1}^p\alpha _rF_r(\bar{x}), \end{aligned}$$

(3.23)

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^m\alpha ^i_rA^r_i\succeq 0, r=1,\ldots ,p, \; \lambda _lB^l+\sum _{j=1}^s\lambda _l^jB^l_j\succeq 0, l=1,\ldots ,k, \end{aligned}$$

(3.24)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega ^r} f_r(\bar{x},u^r)$ for $r=1,\dots ,p.$

Proof

[(i) $\Longrightarrow$ (ii)] Assume that there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.1) and (3.2) hold. Following the proof of Theorem 3.1(ii), we first assert that there exist $\tilde{u}^r\in \Omega _r, r=1,\ldots , p$ and $\tilde{v}^l\in \Theta _l, l=1,\ldots ,k$ such that

$$\begin{aligned}&h(x):=\sum \limits _{r=1}^p\alpha _rf_r(x,\tilde{u}^r) +\sum \limits ^{k}_{l=1}\lambda _lg_l(x,\tilde{v}^l)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0\, \text{ for } \text{ all } \, x\in \mathbb {R}^n, \end{aligned}$$

(3.25)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r} f_r(\bar{x},u^r)$ for $r=1,\dots ,p.$ Substituting $x:=\bar{x}$ into (3.25), we obtain that

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r) +\sum \limits ^{k}_{l=1}\lambda _lg_l(\bar{x},\tilde{v}^l)\ge \sum \limits _{r=1}^p\alpha _rF_r(\bar{x}). \end{aligned}$$

(3.26)

As $\bar{x}$ is a robust feasible point of problem (UP), it holds that $\lambda _lg_l(\bar{x},\tilde{v}^l)\le 0, l=1,\ldots ,k$ and so,

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r) +\sum \limits ^{k}_{l=1}\lambda _lg_l(\bar{x},\tilde{v}^l) \le \sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r)\le \sum \limits _{r=1}^p\alpha _rF_r(\bar{x}),\end{aligned}$$

(3.27)

where the last inequality holds due to the fact that $\alpha _r\ge 0$ and $F_r(\bar{x})\ge f_r(\bar{x}, \tilde{u}^r)$ for $r=1,\ldots ,p.$ Combining (3.26) and (3.27) gives us

$$\begin{aligned} \sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r) = \sum \limits _{r=1}^p\alpha _rF_r(\bar{x}),\quad \sum \limits ^{k}_{l=1}\lambda _lg_l(\bar{x},\tilde{v}^l)=0. \end{aligned}$$

(3.28)

Note that the last equality in (3.28) means that $\lambda _lg_l(\bar{x},\tilde{v}^l)=0$ for $l=1,\ldots ,k$.

Observe now by (3.28) and (3.25) that $h(x)\ge 0=h(\bar{x})$ for all $x\in \mathbb {R}^n;$ i.e., $\bar{x}$ is a minimizer of h on $\mathbb {R}^n.$ This entails that $\nabla h(\bar{x})=0$, and so we arrive at

$$\begin{aligned}&\sum \limits _{r=1}^p\alpha _r\nabla _1 f_r(\bar{x},\tilde{u}^r)+\sum \limits _{l=1}^k\lambda _l\nabla _1g_l(\bar{x},\tilde{v}^l)=0,\; \lambda _l g_l(\bar{x},\tilde{v}^l)=0,\; l=1,\ldots ,k,\\ {}&\sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r) = \sum \limits _{r=1}^p\alpha _rF_r(\bar{x}),\end{aligned}$$

which shows that the robust (KKT) condition of problem (UP) holds at $\bar{x}.$

[(ii) $\Longrightarrow$ (iii)] Assume that the robust (KKT) condition of problem (UP) holds at $\bar{x}$. This means that there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \bar{u}^r:=(\bar{u}^r_1,\ldots ,\bar{u}^r_m)\in \Omega _r, r=1,\ldots ,p$ and $(\lambda _1,\ldots ,\lambda _k)\in \mathbb {R}^k_+, \bar{v}^l:=(\bar{v}^l_1,\ldots ,\bar{v}^l_s)\in \Theta _l, l=1,\ldots ,k$ such that (3.19) and (3.20) are valid. The relation $\bar{u}^r:=(\bar{u}^r_1,\ldots ,\bar{u}^r_m)\in \Omega _r$ means that $A^r+\sum \limits _{i=1}^m\bar{u}^r_iA^r_i\succeq 0$ for $r=1,\ldots ,p.$ By letting $\alpha ^i_r:= \alpha _r\bar{u}^r_i, r=1,\ldots ,p, i=1,\ldots ,m$, we obtain that $\alpha _rA^r+\sum \limits _{i=1}^m\alpha ^i_rA^r_i=\alpha _r\Big (A^r+\sum \limits _{i=1}^m\bar{u}^r_iA^r_i\Big )\succeq 0, r=1,\ldots ,p$ and that

$$\begin{aligned} \alpha _rf_r(x,\bar{u}^r)=\alpha _r\big (x^TQ^rx+ (\xi ^r)^Tx+ \beta ^r\big )+\sum \limits ^{m}_{i=1} \alpha ^i_r\big ((\xi _i^r)^Tx + \beta _i^r\big ),\; r=1,\ldots ,p. \end{aligned}$$

(3.29)

Similarly, by letting $\lambda ^j_l:= \lambda _l\bar{v}^l_j, l=1,\ldots ,k, j=1,\ldots ,s$, we get by $\bar{v}^l:=(\bar{v}^l_1,\ldots ,\bar{v}^l_s)\in \Theta _l, l=1,\ldots ,k$ that $\lambda _lB^l+\sum \limits _{j=1}^s\lambda ^j_lB^l_j\succeq 0, l=1,\ldots ,k$ and that

$$\begin{aligned} \lambda _lg_l(x,\bar{v}^l)=\lambda _l\big (x^TM^lx+ (\theta ^l)^Tx+ \gamma ^l\big )+\sum \limits ^{s}_{j=1} \lambda ^j_l\big ((\theta _j^l)^Tx + \gamma _j^l\big ),\; l=1,\ldots ,k. \end{aligned}$$

(3.30)

Substituting now (3.29) and (3.30) into (3.19) and (3.20), we arrive at the conclusion of (iii).

[(iii) $\Longrightarrow$ (i)] Assume that there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.21), (3.22), (3.23) and (3.24) hold. Proceeding similarly as in the proof of Theorem 3.1(ii), we assert from (3.24) that there exist $\tilde{u}^r\in \Omega _r, r=1,\ldots , p$ and $\tilde{v}^l\in \Theta _l, l=1,\ldots ,k$ such that

$$\begin{aligned} \alpha _rf_r(x,\tilde{u}^r)&=\alpha _r\big (x^TQ^rx+ (\xi ^r)^Tx+ \beta ^r\big )+\sum \limits ^{m}_{i=1} \alpha ^i_r\big ((\xi _i^r)^Tx + \beta _i^r\big ),\; r=1,\ldots ,p,\; \forall x\in \mathbb {R}^n, \end{aligned}$$

(3.31)

$$\begin{aligned} \lambda _lg_l(x,\tilde{v}^l)&=\lambda _l\big (x^TM^lx+ (\theta ^l)^Tx+ \gamma ^l\big )+\sum \limits ^{s}_{j=1} \lambda ^j_l\big ((\theta _j^l)^Tx + \gamma _j^l\big ),\; l=1,\ldots ,k,\; \forall x\in \mathbb {R}^n. \end{aligned}$$

(3.32)

Consider the function $h:\mathbb {R}^n\rightarrow \mathbb {R}$ given as above, i.e., $h(x):=\sum \limits _{r=1}^p\alpha _rf_r(x,\tilde{u}^r) +\sum \limits ^{k}_{l=1}\lambda _lg_l(x,\tilde{v}^l)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x}), x\in \mathbb {R}^n$. We conclude by (3.21), (3.22) and (3.32) that $\nabla h(\bar{x})=0$ and that $\lambda _lg_l(\bar{x},\tilde{v}^l)=0, l=1,\ldots , k$. This, together with the convexity of h, implies that

$$\begin{aligned} h(x)\ge h(\bar{x})=\sum \limits _{r=1}^p\alpha _rf_r(\bar{x},\tilde{u}^r) -\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})=0,\;\forall x\in \mathbb {R}^n, \end{aligned}$$

where the last equality holds by virtue of (3.23) and (3.31). Therefore, taking (3.31) and (3.32) into account, we deduce from $h(x)\ge 0$ for all $x\in \mathbb {R}^n$ that

$$\begin{aligned}&x^T \Big (\sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l\Big )x+\Big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\Big )^Tx\\ {}&+ \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l\gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0\, \text{ for } \text{ all } \, x\in \mathbb {R}^n. \end{aligned}$$

This amounts to the matrix inequality in (3.1) (cf. Ben-Tal and Nemirovski, 2001, Simple lemma, p. 163). Consequently, the assertion of (i) is valid, which completes the proof. $\square$

Robust linear multiobjective optimization. Let us now consider a robust linear multiobjective optimization problem as

$$\begin{aligned} \min _{x\in \mathbb {R}^{n}}{\big \{\big (\max _{u^1\in \Omega _1} L_1(x,u^1),\ldots ,\max _{u^p\in \Omega _p}L_p(x,u^p)\big ) \mid h_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}}, \end{aligned}$$

(RL)

where $L_r, r=1,\ldots , p$ and $h_l, l=1,\ldots ,k$ are affine functions given by

$$\begin{aligned} L_r(x,u^r):=&(\xi ^r)^Tx+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^Tx+ \beta ^r_i\big ), x\in \mathbb {R}^n, u^r:=(u^r_1,\ldots ,u^r_{m})\in \Omega _r, \\ h_l(x,v^l):=&(\theta ^{l})^Tx+ \gamma ^l+\sum \limits _{j=1}^{s} v_j^l\big ((\theta ^{l}_j)^Tx+ \gamma ^l_j\big ), x\in \mathbb {R}^n, v^l:=(v^l_1,\ldots ,v^l_{s})\in \Theta _l \end{aligned}$$

with $\xi ^r\in \mathbb {R}^n, \xi ^r_i\in \mathbb {R}^n, \beta ^r\in \mathbb {R}, \beta _i^r\in \mathbb {R}, i=1,\ldots ,m$ and $\theta ^l\in \mathbb {R}^n, \theta ^l_j\in \mathbb {R}^n, \gamma ^l\in \mathbb {R}, \gamma ^l_j\in \mathbb {R}, j=1,\ldots ,s$ fixed. Here, the uncertainty sets $\Omega _r, r=1,\ldots , p$ and $\Theta _l, l=1,\ldots ,k$ are given as in (2.2).

The following corollary presents necessary/sufficient optimality conditions for (weak) Pareto solutions of problem (RL).

Corollary 3.5

(Optimality for robust linear optimization) Let $\bar{x}\in \mathbb {R}^n$ be a feasible point of problem (RL), i.e., $\bar{x}\in \{x\in \mathbb {R}^n \mid h_l(x, v^l)\le 0, \forall v^l\in \Theta _l, l=1,\ldots ,k\big \}.$

(i) Assume that the characteristic cone $K:=\mathrm{coneco}\big \{\big (0_n,1\big ), \big (\theta ^l+\sum \limits _{j=1}^{s} v_j^l \theta ^{l}_j,-\gamma ^l-\sum \limits _{j=1}^{s} v_j^l\gamma ^{l}_j\big ), v^l:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k\big \}$ is closed. If $\bar{x}$ is a weak Pareto solution of problem (RL), then there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that

$$\begin{aligned}&\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r) +\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)=0, \end{aligned}$$

(3.33)

$$\begin{aligned}&\sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k (\lambda _l\gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\ge 0, \end{aligned}$$

(3.34)

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^m\alpha ^i_rA^r_i\succeq 0, r=1,\ldots ,p, \; \lambda _lB^l+\sum _{j=1}^s\lambda _l^jB^l_j\succeq 0, l=1,\ldots ,k, \end{aligned}$$

(3.35)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r} f_r(\bar{x},u^r)$ for $r=1,\dots ,p.$

(ii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.33), (3.34) and (3.35) hold, then $\bar{x}$ is a weak Pareto solution of problem (RL).

(iii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.33), (3.34) and (3.35) hold, then $\bar{x}$ is a Pareto solution of problem (RL).

Proof

Observe first that the problem (RL) is a particular case of problem (RP) with $Q^r:=M^l:=0_{n\times n}, r=1,\ldots , p, l=1,\ldots , k.$ In this setting, we see that $\mathrm{epi}\,h_l^*(\cdot ,v^l)=\big (\theta ^l+\sum \limits _{j=1}^{s} v_j^l \theta ^{l}_j,-\gamma ^l-\sum \limits _{j=1}^{s} v_j^l\gamma ^{l}_j\big )+\{0_n\}\times \mathbb {R}_+$ for $v^l:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k$ and so,

$$\begin{aligned} K:&=\mathrm{coneco}\big \{\big (0_n,1\big ), \big (\theta ^l+\sum \limits _{j=1}^{s} v_j^l \theta ^{l}_j,-\gamma ^l-\sum \limits _{j=1}^{s} v_j^l\gamma ^{l}_j\big ),\\ v^l&:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k\big \}\\&={\text {coneco}} \{ \mathrm{epi}\,h^*_l(\cdot ,v^l)\mid v^l\in \Theta _l, l=1,\ldots ,k\}.\end{aligned}$$

Now, our desired conclusions are followed by invoking Theorem 3.1. $\square$

Remark that the assertions (i) and (ii) in Corollary 3.5 develop optimality characterizations for robust weak Pareto solutions given in Chuong (2017, Theorem 3.1) by using a robust alternative approach and in Chuong (2018, Corollary 2.4) by using an SOS-convex polynomial approach, where there were no uncertain parameters on the objective functions $L_r, r=1,\ldots ,p$. The interested reader is referred to Chuong and Jeyakumar (2021) for related optimality conditions in terms of two-stage linear multiobjective approach.

We now consider the uncertain multiobjective optimization problem (UP), where $\Omega _r, r=1,\ldots ,p$ and $\Theta _l, l=1,\ldots ,k$ in (2.2) are replaced by the following ball uncertainty sets:

$$\begin{aligned} \Omega _r:=\{u^r \in \mathbb {R}^{m}\mid ||u^r||\le 1\}, \;\; \Theta _l:=\{v^l \in \mathbb {R}^{s}\mid ||v^l||\le 1\}.\end{aligned}$$

(3.36)

In this case, we obtain necessary/sufficient optimality conditions for robust (weak) Pareto solutions of problem (UP) under ball uncertainty.

Corollary 3.6

(Robust optimality with ball uncertainty) Consider the problem (UP) with $\Omega _r$ and $\Theta _l$ given by (3.36), and let $\bar{x}\in \mathbb {R}^n$ be a robust feasible point of problem (UP).

(i) Assume that the characteristic cone $K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v^l), v^l\in \Theta _l, l=1,\ldots ,k\}$ is closed. If $\bar{x}$ is a robust weak Pareto solution of problem (UP), then there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that

$$\begin{aligned}&{\left( \begin{array}{cc} \sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l &{} \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big )^T&{} \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l\gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\\ \end{array} \right) \succeq 0},\end{aligned}$$

(3.37)

$$\begin{aligned}&\left( \begin{array}{cc} \alpha _rI_m &{} \alpha ^r \\ (\alpha ^r)^T&{} \alpha _r \\ \end{array} \right) \succeq 0, r=1,\ldots ,p, \; \left( \begin{array}{cc} \lambda _lI_s &{} \lambda ^l \\ (\lambda ^l)^T&{} \lambda _l \\ \end{array} \right) \succeq 0, l=1,\ldots ,k, \end{aligned}$$

(3.38)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r} f_r(\bar{x},u^r)$, $\alpha ^r:=(\alpha ^1_r,\ldots ,\alpha ^m_r)$ and $\lambda ^l:=(\lambda ^1_l,\ldots ,\lambda ^s_l).$

(ii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.37) and (3.38) hold, then $\bar{x}$ is a robust weak Pareto solution of problem (UP).

(iii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.37) and (3.38) hold, then $\bar{x}$ is a robust Pareto solution of problem (UP).

Proof

Let $A^r$ and $A^r_i, r=1,\ldots ,p, i= 1,\ldots ,m$ be $(m+1)\times (m+1)$ matrices given by

$$\begin{aligned} A^r:= I_{m+1},\quad A^r_i:= \left( \begin{array}{cc} 0 &{} e_i \\ e^T_i&{} 0 \\ \end{array} \right) ,\end{aligned}$$

where $e_i\in \mathbb {R}^{m}$ is a vector whose ith component is one and all others are zero. For each $r\in \{1,\ldots ,p\}$, we have

$$\begin{aligned}&\big \{u^r:=(u^r_1,\ldots , u^r_m)\in \mathbb {R}^{m}\mid A^r+\sum _{i=1}^{m}u^r_iA^r_i\succeq 0\big \}\\ {}&=\big \{u^r:=(u^r_1,\ldots , u^r_m)\in \mathbb {R}^{m}\mid \left( \begin{array}{cc} I_m &{} u^r \\ (u^r)^T&{} 1 \\ \end{array} \right) \succeq 0\big \}\\ {}&=\big \{u^r:=(u^r_1,\ldots , u^r_m)\in \mathbb {R}^{m}\mid 1-(u^r)^T I_mu^r\ge 0\big \}=\Omega _r,\end{aligned}$$

which means that $\Omega _r$ in (3.36) lands in the form of the spectrahedral sets in (2.2). In this way, we can verify that, for each $r\in \{1,\ldots ,p\},$

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^{m}\alpha ^i_rA^r_i\succeq 0 \Leftrightarrow \left( \begin{array}{cc} \alpha _rI_m &{} \alpha ^r \\ (\alpha ^r)^T&{} \alpha _r \\ \end{array} \right) \succeq 0,\; \end{aligned}$$

where $\alpha _r\ge 0$ and $\alpha ^r:=(\alpha ^1_r,\ldots ,\alpha ^m_r)$ with $\alpha ^i_r\in \mathbb {R}, i=1,\ldots ,m$. Similarly, let $B^l$ and $B^l_j, l=1,\ldots ,k, j= 1,\ldots ,s$ be $(s+1)\times (s+1)$ matrices given by

$$\begin{aligned} B^l:=I_{s+1},\quad B^l_j:= \left( \begin{array}{cc} 0 &{} e_j \\ e^T_j&{} 0 \\ \end{array} \right) , \end{aligned}$$

where $e_j\in \mathbb {R}^{s}$ is a vector whose jth component is one and all others are zero. We can show that $\Theta _l$ in (3.36) lands in the form of the spectrahedral sets in (2.2) and that

$$\begin{aligned}&\lambda _lB^l+\sum _{j=1}^{s}\lambda ^j_lB^l_j\succeq 0 \Leftrightarrow \left( \begin{array}{cc} \lambda _lI_s &{} \lambda ^l \\ (\lambda ^l)^T&{} \lambda _l \\ \end{array} \right) \succeq 0, \end{aligned}$$

where $\lambda _l\ge 0, l=1,\ldots ,k$ and $\lambda ^l:=(\lambda ^1_l,\ldots ,\lambda ^s_l)$ with $\lambda _l^j\in \mathbb {R}, j=1,\ldots ,s.$ Now, invoking Theorem 3.1, we arrive at the desired result. $\square$

Let us now consider the uncertain multiobjective optimization problem (UP), where $\Omega _r, r=1,\ldots ,p$ and $\Theta _l, l=1,\ldots ,k$ in (2.2) are replaced by the following box uncertainty sets:

$$\begin{aligned}&\Omega _r:=\big \{u^r:=(u^r_1,\ldots ,u^r_m)\in \mathbb {R}^{m}\mid |u^r_i|\le 1, i=1,\ldots ,m\big \},\nonumber \\&\quad \Theta _l:=\big \{v^l:=(v^l_1,\ldots ,v^l_s)\in \mathbb {R}^{s}\mid |v^l_j|\le 1, j=1,\ldots ,s\big \}. \end{aligned}$$

(3.39)

In this case, we obtain necessary/sufficient optimality conditions for robust (weak) Pareto solutions of problem (UP) under box uncertainty.

Corollary 3.7

(Robust optimality with box uncertainty) Consider the problem (UP) with $\Omega _r$ and $\Theta _l$ given by (3.39), and let $\bar{x}\in \mathbb {R}^n$ be a robust feasible point of problem (UP).

(i) Assume that the characteristic cone $K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v^l), v^l\in \Theta _l, l=1,\ldots ,k\}$ is closed. If $\bar{x}$ is a robust weak Pareto solution of problem (UP), then there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that

$$\begin{aligned}&{\left( \begin{array}{cc} \sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l &{} \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\theta ^l_j)\big )^T&{} \sum \limits _{r=1}^p(\alpha _r \beta ^r+\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l\gamma ^l+\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\\ \end{array} \right) \succeq 0}, \end{aligned}$$

(3.40)

$$\begin{aligned}&\alpha _r\ge |\alpha ^i_r|, i=1,\ldots ,m, r=1,\ldots ,p, \; \lambda _l\ge |\lambda ^j_l|, j=1,\ldots ,s, l=1,\ldots ,k, \end{aligned}$$

(3.41)

where $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r} f_r(\bar{x},u^r)$.

(ii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.40) and (3.41) hold, then $\bar{x}$ is a robust weak Pareto solution of problem (UP).

(iii) If there exist $(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that (3.40) and (3.41) hold, then $\bar{x}$ is a robust Pareto solution of problem (UP).

Proof

Let $A^r$ and $A^r_i, r=1,\ldots ,p, i=1,\ldots ,m$ be $(2m\times 2m)$ matrices given by

$$\begin{aligned} A^r:=I_{2m},\quad A^r_i:= \left( \begin{array}{cc} E_i &{} 0 \\ 0&{} -E_i \\ \end{array} \right) ,\end{aligned}$$

where $E_i$ is an $(m\times m)$ diagonal matrix with one in the (i, i)th entry and zeros elsewhere. Then, we have

$$\begin{aligned}&\big \{u^r:=(u^r_1,\ldots , u^r_m)\in \mathbb {R}^{m}\mid A^r+\sum _{i=1}^{m}u^r_iA^r_i\succeq 0\big \}\\ {}&=\big \{u^r:=(u^r_1,\ldots , u^r_m)\in \mathbb {R}^{m}\mid 1+u^r_i\ge 0, 1-u^r_i\ge 0, i=1,\ldots ,m\big \}=\Omega _r,\end{aligned}$$

which means that $\Omega$ in (3.39) lands in the form of the spectrahedral sets in (2.2). In this way, we can verify that, for each $r\in \{1,\ldots ,p\},$

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^{m}\alpha ^i_rA^r_i\succeq 0 \Leftrightarrow \alpha _r\ge |\alpha ^i_r|, \; i=1,\ldots ,m, \end{aligned}$$

where $\alpha _r\ge 0$ and $\alpha ^i_r\in \mathbb {R}, i=1,\ldots ,m$. Similarly, let $B^l$ and $B^l_j, l=1,\ldots ,k, j= 1,\ldots ,s$ be $(2s\times 2s)$ matrices given by

$$\begin{aligned} B^l:= I_{2s},\quad B^l_j:= \left( \begin{array}{cc} E_j &{} 0 \\ 0&{} -E_j \\ \end{array} \right) ,\end{aligned}$$

where $E_j$ is an $(s\times s)$ diagonal matrix with one in the (j, j)th entry and zeros elsewhere. We can show that $\Theta _l$ in (3.36) lands in the form of the spectrahedral sets in (2.2) and that

$$\begin{aligned}&\lambda _lB^l+\sum _{j=1}^{s}\lambda ^j_lB^l_j\succeq 0 \Leftrightarrow \lambda _l\ge |\lambda ^j_l|, j=1,\ldots ,s, \end{aligned}$$

where $\lambda _l\ge 0, l=1,\ldots ,k$ and $\lambda _l^j\in \mathbb {R}, j=1,\ldots ,s.$ Now, invoking Theorem 3.1, we arrive at the desired result. $\square$

4 Finding robust Pareto solutions via semidefinite programming

In this section, we provide a way to find robust (weak) Pareto solutions for the uncertain multiobjective optimization problem (UP) by solving a related semidefinite programming (SDP) problem. Since the underlying problems are convex, our approach is based on commonly used weighted-sum scalarizarion methods that allow one to find both robust weakly Pareto solutions and robust Pareto solutions. This is done by defining robust weighted-sum scalarizarion optimization problems of (RP) as follows.

For each $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\},$ we consider a robust weighted-sum optimization problem of the form:

where $f_r, r=1,\ldots , p$ and $g_l, l=1,\ldots ,k$ are bi-functions given as in (2.3), and $\Omega _r, r=1,\ldots , p$ and $\Theta _l, l=1,\ldots ,k$ are uncertainty sets given as in (2.2).

We propose a semidefinite programming (SDP) reformulation problem for the problem ($\hbox {RP}_{\alpha }$) as follows:

We are now ready to establish solution relationships between the robust multiobjective optimization problem (RP) and the (scalar) semidefinite programming (SDP) reformulation problem $(\hbox {RP}^*_{\alpha })$, which is a relaxation problem of the corresponding robust weighted-sum optimization problem ($\hbox {RP}_{\alpha }$). This result provides us a way to find robust (weak) Pareto solutions of the uncertain multiobjective optimization problem (UP) by solving the (scalar) SDP reformulation problem $(\hbox {RP}^*_{\alpha })$.

Theorem 4.1

(Robust (weak) Pareto solutions via SDP) Let the characteristic cone $K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v^l), v^l\in \Theta _l, l=1,\ldots ,k\}$ be closed, and assume that there exist $\tilde{u}^r:= (\tilde{u}^r_1,\ldots ,\tilde{u}^r_m)\in \mathbb {R}^m, r=1,\ldots ,p$ and $\tilde{v}^l:= (\tilde{v}^l_1,\ldots ,\tilde{v}^l_s)\in \mathbb {R}^s, l=1,\ldots ,k$ such that

$$\begin{aligned} A^r+\sum _{i=1}^m\tilde{u}^r_iA^r_i\succ 0,\; B^l+\sum _{j=1}^s\tilde{v}^l_jB^l_j\succ 0.\end{aligned}$$

(4.1)

Then, the following assertions hold:

(i) If $\bar{x}$ is a robust weak Pareto solution of problem (UP), then there exist $\alpha \in \mathbb {R}^p_+\setminus \{0\}$ and $\tilde{Z}^r_0\succeq 0, Z^l_0\succeq 0, r=1,\ldots ,p, l=1,\ldots ,k$ such that $(\bar{x}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$, where $\bar{W}:=\bar{x}\bar{x}^T,$ $\bar{\lambda }^r:=\bar{x}^TQ^r\bar{x}+(\xi ^r)^T\bar{x}+\beta ^r$ and $\bar{t}^l:=\bar{x}^TM^l\bar{x}+(\theta ^l)^T\bar{x}+\gamma ^l.$

(ii) (Finding robust weak Pareto solutions) Let $\alpha \in \mathbb {R}^p_+\setminus \{0\}$ be such that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution. If $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$, then $\bar{w}$ is a robust weak Pareto solution of problem (UP).

(iii) (Finding robust Pareto solutions) Let $\alpha \in \mathrm{int}\mathbb {R}^p_+$ be such that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution. If $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$, then $\bar{w}$ is a robust Pareto solution of problem (UP).

Proof

(SDP reformulation with optimal solutions for $(\hbox {RP}^*_{\alpha })$) Let $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}$ be such that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution and assume that $\bar{x}$ is an optimal solution of problem ($\hbox {RP}_{\alpha }$). Denote by $\mathrm{val}(\hbox {RP}_{\alpha })$ and $\mathrm{val} (\hbox {RP}^*_{\alpha })$ the optimal values of problems ($\hbox {RP}_{\alpha }$) and $(\hbox {RP}^*_{\alpha })$), respectively.

We first show that there exist $\tilde{Z}^r_0\succeq 0, Z^l_0\succeq 0, r=1,\ldots ,p, l=1,\ldots ,k$ such that $(\bar{x}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$, where $\bar{\lambda }^r:=\bar{x}^TQ^r\bar{x}+(\xi ^r)^T\bar{x}+\beta ^r, \bar{t}^l:=\bar{x}^TM^l\bar{x}+(\theta ^l)^T\bar{x}+\gamma ^l$ and $\bar{W}:=\bar{x}\bar{x}^T$, is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$) and

$$\begin{aligned} \mathrm{val}(\hbox {RP}_{\alpha })= \mathrm{val} (\hbox {RP}^*_{\alpha })=\sum _{r=1}^p\alpha _r\big (\bar{\lambda }^r+\mathrm{Tr}(\tilde{Z}^r_0A^r)\big ).\end{aligned}$$

(4.2)

Let $F_r(\bar{x}):= \max \limits _{u^r\in \Omega _r}f_r(\bar{x},u^r)$ for $r=1,\dots ,p.$ As $\bar{x}$ is an optimal solution of problem ($\hbox {RP}_{\alpha }$), we obtain that

$$\begin{aligned} \mathrm{val}(\hbox {RP}_{\alpha })=\sum _{r=1}^p\alpha _rF_r(\bar{x}),\end{aligned}$$

(4.3)

and that

$$\begin{aligned}&\max \limits _{v^l:=(v^l_1,\ldots ,v^l_{s})\in \Theta _l}{\{\bar{x}^TM^l\bar{x}+(\theta ^{l})^T\bar{x}+ \gamma ^l+\sum \limits _{j=1}^{s} v_j^l\big ((\theta ^{l}_j)^T\bar{x}+ \gamma ^l_j\big ) \}}\le 0, \; l=1,\ldots , k,\end{aligned}$$

which can be equivalently expressed as

$$\begin{aligned}{}[v^l:=(v^l_1,\ldots ,v^l_{s})\in \mathbb {R}^s, B^l+\sum _{j=1}^sv^l_jB^l_j\succeq 0] \Rightarrow \bar{t}^l+\sum \limits _{j=1}^{s} v_j^l \bar{t}^{l}_j \le 0,\; l=1,\ldots ,k,\end{aligned}$$

(4.4)

where $\bar{t}^l:=\bar{x}^TM^l\bar{x}+(\theta ^l)^T\bar{x}+\gamma ^l$ and $\bar{t}^l_j:= (\theta ^l_j)^T\bar{x}+\gamma ^l_j$. The condition (4.1) shows that the strict feasibility condition holds for (4.4). Hence, invoking a strong duality in semidefinite programming (cf. Blekherman et al., 2012, Theorem 2.15), we find $Z^l_0\succeq 0, l=1,\ldots ,k$ such that

$$\begin{aligned}&\bar{t}^l+\mathrm{Tr}(Z^l_0B^l)\le 0, l=1,\ldots ,k,\\&\bar{t}^l_j+\mathrm{Tr}(Z^l_0B^l_j)= 0, j=1,\ldots ,s, l=1,\ldots ,k. \end{aligned}$$

Similarly, by $\max \limits _{u^r:=(u^r_1,\ldots ,u^r_{m})\in \Omega _r}\{\bar{x}^TQ^r\bar{x}+(\xi ^r)^T\bar{x}+ \beta ^r+\sum \limits _{i=1}^{m} u^r_i\big ((\xi _i^r)^T\bar{x}+ \beta ^r_i\big )\}=F_r(\bar{x}), r=1,\dots ,p$, we have

$$\begin{aligned}{}[u^r:=(u^r_1,\ldots ,u^r_{m})\in \mathbb {R}^m, A^r+\sum _{i=1}^mu^r_iA^r_i\succeq 0] \Rightarrow \bar{\lambda }^r+\sum \limits _{i=1}^{m} u_i^r \bar{\lambda }^{r}_i \le F_r(\bar{x}),\; r=1,\ldots ,p,\end{aligned}$$

where $\bar{\lambda }^r:=\bar{x}^TQ^r\bar{x}+(\xi ^r)^T\bar{x}+\beta ^r$ and $\bar{\lambda }^r_i:=(\xi ^r_i)^T\bar{x}+\beta ^r_i.$ Therefore, we can find $\tilde{Z}^r_0\succeq 0, r=1,\ldots ,p$ such that

$$\begin{aligned}&\bar{\lambda }^r +\mathrm{Tr}(\tilde{Z}^r_0A^r) \le F_r(\bar{x}), r=1,\ldots ,p,\nonumber \\&\bar{\lambda }^r_i+\mathrm{Tr}(\tilde{Z}^r_0A^r_i)= 0, i=1,\ldots ,m, r=1,\ldots ,p. \end{aligned}$$

(4.5)

Now, letting $\bar{W}:=\bar{x}\bar{x}^T$, we see that $(\bar{x}, \bar{W},\bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is a feasible point of problem $(\hbox {RP}^*_{\alpha })$), and it also entails that

$$\begin{aligned} \mathrm{val}(\hbox {RP}^*_{\alpha })\le \sum _{r=1}^p\alpha _r\big (\bar{\lambda }^r+\mathrm{Tr}(\tilde{Z}^r_0A^r)\big )\le \sum _{r=1}^p\alpha _rF_r(\bar{x}) = \mathrm{val}(\hbox {RP}_{\alpha }), \end{aligned}$$

(4.6)

where the second inequality holds by noting (4.5) and the fact that $\alpha _r\ge 0, r=1,\ldots ,p$, while the equality holds by (4.3).

Next, we show that $\mathrm{val}(\hbox {RP}_{\alpha })\le \mathrm{val}(\hbox {RP}^*_{\alpha })$. To do this, let $(w, W,\lambda ^r, t^l, \tilde{Z}^r, Z^l, r=1,\ldots ,p, l=1,\dots ,k)$ be a feasible point of problem ($\hbox {RP}^*_{\alpha }$). Then, $w\in \mathbb {R}^n, W\in S^n, \lambda ^r\in \mathbb {R}, t^l\in \mathbb {R}, \tilde{Z}^r\succeq 0, Z^l\succeq 0, r=1,\ldots ,p, l=1,\ldots ,k$ and

$$\begin{aligned}&\left( \begin{array}{cc} 1 &{} w^T \\ w&{} W\end{array}\right) \succeq 0, \end{aligned}$$

(4.7)

$$\begin{aligned}&\beta ^r +(\xi ^r)^Tw+ \mathrm{Tr}(WQ^r)-\lambda ^r= 0, r=1,\ldots ,p,\nonumber \\&\quad \beta ^r_i+(\xi ^r_i)^Tw+\mathrm{Tr}(\tilde{Z}^r A^r_i)=0,i=1,\ldots ,m, r=1,\ldots ,p,\nonumber \\&\quad t^l+\mathrm{Tr}(Z^l B^l)\le 0, l=1,\ldots ,k, \end{aligned}$$

(4.8)

$$\begin{aligned}&\gamma ^l+(\theta ^l)^Tw+\mathrm{Tr}(WM^l)-t^l= 0, l=1,\ldots ,k, \end{aligned}$$

(4.9)

$$\begin{aligned}&\gamma ^l_j+ (\theta ^l_j)^Tw+\mathrm{Tr}(Z^l B^l_j)=0, j=1,\ldots ,s, l=1,\ldots ,k. \end{aligned}$$

(4.10)

Note, for any $v^l:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k,$ that $\mathrm{Tr}\big [Z^l(B^l+\sum \limits _{j=1}^sv^l_jB^l_j)\big ]\ge 0, l=1,\ldots ,k$ due to $Z^l \succeq 0$ and $B^l+\sum \limits _{j=1}^sv^l_jB^l_j\succeq 0$. Then, we deduce from (4.8) and (4.9) that, for given $v^l:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k,$

$$\begin{aligned}&\gamma ^l+(\theta ^l)^Tw+\mathrm{Tr}(ww^TM^l)-\sum _{j=1}^sv^l_j\mathrm{Tr}(Z^l B^l_j)\le \gamma ^l+(\theta ^l)^Tw+\mathrm{Tr}(ww^TM^l)+\mathrm{Tr}(Z^l B^l)\\ {}&=t^l+\mathrm{Tr}(Z^l B^l)-\mathrm{Tr}\big ((W-ww^T)M^l\big )\le 0, l=1,\ldots ,k, \end{aligned}$$

where we should note that $\mathrm{Tr}\big ((W-ww^T)M^l\big )\ge 0$ due to $M^l\succeq 0$ and, by (4.7), $W-ww^T \succeq 0$. Therefore, by (4.10), for given $v^l:=(v^l_1,\ldots ,v^l_s)\in \Theta _l, l=1,\ldots ,k,$

$$\begin{aligned}g_l(w,v^l)= \gamma ^l+(\theta ^l)^Tw+\mathrm{Tr}(ww^TM^l)-\sum _{j=1}^sv^l_j\mathrm{Tr}(Z^l B^l_j)\le 0,\;l=1,\ldots ,k.\end{aligned}$$

This shows that w is a feasible point of problem ($\hbox {RP}_{\alpha }$), and so

$$\begin{aligned} \mathrm{val}(\hbox {RP}_{\alpha })\le \sum \limits _{r=1}^p\alpha _rF_r(w),\end{aligned}$$

(4.11)

where $F_r(w):= \max \limits _{u^r\in \Omega _r} f_r(w,u^r) , r=1,\dots ,p$.

Similarly, for given $u^r:=(u^r_1,\ldots ,u^r_m)\in \Omega _r, r=1,\ldots ,p,$ we have

$$\begin{aligned} \beta ^r+(\xi ^r)^Tw+\mathrm{Tr}(ww^TQ^r)-\sum _{i=1}^mu^r_i\mathrm{Tr}(\tilde{Z}^r A^r_i)\le \lambda ^r+\mathrm{Tr}(\tilde{Z}^r A^r), r=1,\ldots ,p, \end{aligned}$$

which entails that

$$\begin{aligned}F_r(w)&=\max _{u^r:=(u^r_1,\ldots ,u^r_m)\in \Omega _r}\big \{\beta ^r+(\xi ^r)^Tw+\mathrm{Tr}(ww^TQ^r)-\sum _{i=1}^mu^r_i\mathrm{Tr}(\tilde{Z}^r A^r_i)\big \}\\ {}&\le \lambda ^r+\mathrm{Tr}(\tilde{Z}^r A^r),\; r=1,\ldots ,p. \end{aligned}$$

This together with (4.11) shows that $\mathrm{val}(\hbox {RP}_{\alpha })\le \sum \limits _{r=1}^p\alpha _r\big ( \lambda ^r+\mathrm{Tr}(\tilde{Z}^r A^r)\big ),$ and so $\mathrm{val}(\hbox {RP}_{\alpha })\le \mathrm{val}(\hbox {RP}^*_{\alpha })$ inasmuch as $(w, W,\lambda ^r, t^l, \tilde{Z}^r, Z^l, r=1,\ldots ,p, l=1,\dots ,k)$ was arbitrarily taken.

Now, taking (4.6) into account, we arrive at the conclusion that

$$\begin{aligned} \mathrm{val}(\hbox {RP}_{\alpha })= \mathrm{val}(\hbox {RP}^*_{\alpha })=\sum _{r=1}^p\alpha _r\big (\bar{\lambda }^r+\mathrm{Tr}(\tilde{Z}^r_0 A^r)\big ), \end{aligned}$$

which further ensures that $(\bar{x}, \bar{W},\bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$). In other words, (4.2) has been established.

(i) Let $\bar{x}$ be a robust weak Pareto solution of problem (UP). Under the closedness of the cone K, we invoke Theorem 3.1(i) to assert that there exist $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}, \alpha ^i_r\in \mathbb {R}, r=1,\ldots ,p, i=1,\ldots ,m$ and $\lambda _l\ge 0, \lambda _l^j\in \mathbb {R}, j=1,\ldots ,s, l=1,\ldots ,k$ such that

$$\begin{aligned}&{\left( \begin{array}{cc} \sum \limits _{r=1}^p\alpha _rQ^r+\sum \limits ^{k}_{l=1}\lambda _lM^l &{} \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1} \alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1} \lambda ^j_l\theta ^l_j)\big ) \\ \frac{1}{2}\big (\sum \limits _{r=1}^p(\alpha _r\xi ^r+\sum \limits ^{m}_{i=1} \alpha ^i_r\xi _i^r)+\sum \limits _{l=1}^k(\lambda _l\theta ^l+\sum \limits ^{s}_{j=1} \lambda ^j_l\theta ^l_j)\big )^T&{} \sum \limits _{r=1}^p(\alpha _r \beta ^r +\sum \limits ^{m}_{i=1}\alpha ^i_r\beta _i^r)+\sum \limits _{l=1}^k(\lambda _l\gamma ^l +\sum \limits ^{s}_{j=1}\lambda ^j_l\gamma ^l_j)-\sum \limits _{r=1}^p\alpha _rF_r(\bar{x})\\ \end{array}\right) \succeq 0} \end{aligned}$$

(4.12)

$$\begin{aligned}&\alpha _rA^r+\sum _{i=1}^m\alpha ^i_rA^r_i\succeq 0, r=1,\ldots ,p, \; \lambda _lB^l+\sum _{j=1}^s\lambda _l^jB^l_j\succeq 0, l=1,\ldots ,k. \end{aligned}$$

(4.13)

Denoting by C the robust feasible set of problem (UP), it holds that C is also the feasible set of the corresponding robust weighted-sum optimization problem ($\hbox {RP}_{\alpha }$). Proceeding similarly as in the proof of Theorem 3.1(ii), we conclude by (4.12) and (4.13) that

$$\begin{aligned} \sum _{r=1}^p \alpha _rF_r(x)\ge \sum _{r=1}^p \alpha _rF_r(\bar{x})\; \text{ for } \text{ all } \; x\in C, \end{aligned}$$

which shows that $\bar{x}$ is an optimal solution of problem ($\hbox {RP}_{\alpha }$). Then, as shown above, there exist $\tilde{Z}^r_0\succeq 0, Z^l_0\succeq 0, r=1,\ldots ,p, l=1,\ldots ,k$ such that $(\bar{x}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$), where $\bar{\lambda }^r:=\bar{x}^TQ^r\bar{x}+(\xi ^r)^T\bar{x}+\beta ^r, \bar{t}^l:=\bar{x}^TM^l\bar{x}+(\theta ^l)^T\bar{x}+\gamma ^l$ and $\bar{W}:=\bar{x}\bar{x}^T$.

(ii)

(Finding a robust weak Pareto solution of (UP) via $(\hbox {RP}^*_{\alpha })$) Let $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}$ be such that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution. Then, as shown by (4.2), it holds that

$$\begin{aligned} \mathrm{val}(\hbox {RP}_{\alpha })= \mathrm{val} (\hbox {RP}^*_{\alpha }).\end{aligned}$$

(4.14)

Now, let $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ be an optimal solution of problem $(\hbox {RP}^*_{\alpha })$). Then, $\bar{w}\in \mathbb {R}^n, \bar{W}\in S^n, \bar{\lambda }^r\in \mathbb {R}, \bar{t}^l\in \mathbb {R}, \tilde{Z}^r_0\succeq 0, Z^l_0\succeq 0, r=1,\ldots ,p, l=1,\ldots ,k$ and

$$\begin{aligned}&\mathrm{val} (\hbox {RP}^*_{\alpha })=\sum _{r=1}^p\alpha _r\big (\bar{\lambda }^r +\mathrm{Tr}(\tilde{Z}^r_0A^r)\big ), \end{aligned}$$

(4.15)

$$\begin{aligned}&\left( \begin{array}{cc} 1 &{} \bar{w}^T \\ \bar{w}&{} \bar{W}\end{array}\right) \succeq 0, \end{aligned}$$

(4.16)

$$\begin{aligned}&\beta ^r +(\xi ^r)^T\bar{w}+ \mathrm{Tr}(\bar{W}Q^r)-\bar{\lambda }^r= 0, r=1,\ldots ,p, \end{aligned}$$

(4.17)

$$\begin{aligned}&\beta ^r_i+(\xi ^r_i)^T\bar{w}+\mathrm{Tr}(\tilde{Z}^r_0 A^r_i)=0,i=1,\ldots ,m, r=1,\ldots ,p,\end{aligned}$$

(4.18)

$$\begin{aligned}&\bar{t}^l+\mathrm{Tr}(Z^l_0 B^l)\le 0, l=1,\ldots ,k,\end{aligned}$$

(4.19)

$$\begin{aligned}&\gamma ^l+(\theta ^l)^T\bar{w}+\mathrm{Tr}(\bar{W}M^l)-\bar{t}^l= 0, l=1,\ldots ,k,\end{aligned}$$

(4.20)

$$\begin{aligned}&\gamma ^l_j+(\theta ^l_j)^T\bar{w}+\mathrm{Tr}(Z^l_0 B^l_j)=0, j=1,\ldots ,s, l=1,\ldots ,k. \end{aligned}$$

(4.21)

Arguing as above, we can conclude from (4.16), (4.19), (4.20) and (4.21) that $\bar{w}$ is a feasible point of problem ($\hbox {RP}_{\alpha }$), and so $\bar{w}$ is also a robust feasible point of problem (UP). Similarly, we get by (4.16), (4.17) and(4.18) that

$$\begin{aligned} F_r(\bar{w}) \le \bar{\lambda }^r+\mathrm{Tr}(\tilde{Z}^r_0A^r), \; r=1,\ldots ,p. \end{aligned}$$

(4.22)

We claim that $\bar{w}$ is a robust weak Pareto solution of problem (UP). Assume on the contrary that there exists another robust feasible point $\hat{x}$ of problem (UP) such that

$$\begin{aligned}F_r(\hat{x})< F_r(\bar{w}),\; r=1,\ldots , p,\end{aligned}$$

where $F_r(w):= \max \limits _{u^r\in \Omega _r} f_r(w,u^r) , r=1,\dots ,p$. Note here that $\hat{x}$ is also a feasible point of problem ($\hbox {RP}_{\alpha }$). Then, by (4.22) and (4.15), we have

$$ \mathrm{val}(\hbox {RP}_{\alpha })\le \sum _{r=1}^p \alpha _rF_r(\hat{x})< \sum _{r=1}^p \alpha _rF_r(\bar{w})\le \mathrm{val}(\hbox {RP}^*_{\alpha }), $$

which contradicts (4.14). Consequently, $\bar{w}$ is a robust weak Pareto solution of problem (UP).

(iii)

(Finding a robust Pareto solution of (UP) via $(\hbox {RP}^*_{\alpha })$) Let $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathrm{int}\mathbb {R}^p_+$ be such that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution and assume that $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,\ldots ,p, l=1,\dots ,k)$ is an optimal solution of problem $(\hbox {RP}^*_{\alpha })$. Clearly, the assertions in (4.14)–(4.22) are valid for this case. Arguing similarly as in the proof of (ii), we can show that there is no other robust feasible point $\hat{x}$ of problem (UP) such that

$$\begin{aligned}F_r(\hat{x})\le F_r(\bar{w}),\; r=1,\ldots , p\; \text{ and } F_r(\hat{x})< F_r(\bar{w}) \text{ for } \text{ some } r\in \{1,\ldots ,p\},\end{aligned}$$

where $F_r(w):= \max \limits _{u^r\in \Omega _r} f_r(w,u^r) , r=1,\dots ,p$. Therefore, $\bar{w}$ is a robust Pareto solution of problem (UP). $\square$

Remark 4.2

If the uncertainty sets $\Omega _r, r=1,\ldots ,p$ and $\Theta _l, l=1,\ldots ,k$ in (2.2) have nonempty interiors, we can find $\tilde{u}^r:= (\tilde{u}^r_1,\ldots ,\tilde{u}^r_m)\in \mathbb {R}^m, r=1,\ldots ,p$ and $\tilde{v}^l:= (\tilde{v}^l_1,\ldots ,\tilde{v}^l_s)\in \mathbb {R}^s, l=1,\ldots ,k$ such that (4.1) holds.

Under the closedness of the cone K and the validation of (4.1), assume that the problem ($\hbox {RP}_{\alpha }$) admits an optimal solution for each $\alpha :=(\alpha _1,\ldots ,\alpha _p)\in \mathbb {R}^p_+\setminus \{0\}$. Then, Procedure 1 below presents the above SDP scheme for finding robust (weak) Pareto solutions of problem (UP).

5 Conclusion and perspectives

In this paper, we have considered a convex quadratic multiobjective optimization problem, where both the objective and constraint functions involve data uncertainty. To handle the proposed uncertain multiobjective program, we have employed the robust deterministic approach to examine robust optimality conditions and find robust (weak) Pareto solutions of the underlying uncertain multiobjective problem. More specifically, necessary conditions and sufficient conditions in terms of linear matrix inequalities for robust (weak) Pareto optimality of the multiobjective optimization problem have been established. It has been shown that the obtained optimality conditions can be verified by way of checking alternatively other criteria including a robust Karush-Kuhn-Tucker condition. In addition, we have proved that a (scalar) relaxation problem of a robust weighted-sum optimization program of the multiobjective optimization problem can be solved by using a semidefinite programming (SDP) problem. This result has demonstrated that the obtained SDP scheme can be employed to numerically calculate a robust (weak) Pareto solution of the uncertain multiobjective problem that is implemented in MATLAB.

It would be interesting to know how we can employ another approach such as the primal reformulation/relaxation as in Ben-Tal et al. (2015) to find (weak) Pareto solutions of a robust convex quadratic multiobjective optimization problem and perform a comparison with the results obtained in this paper. Besides, a land combat vehicle system or other defence systems (cf. Nguyen et al., 2016; Nguyen and Cao, 2017, 2019) can be expressed in terms of multiobjective optimization problems that contain uncertainty data due to the incomplete, error estimation or noisy information. For example, unknown environment factors such as land surface, air and sea surroundings or weather would be shown up when a defence system is operating in a new terrain. The different types of operation scenarios and physical links between defence system components pose a challenge to the decision maker in providing the “best" combination (solution) of defence system configuration. For a force design problem, this would have to be scaled up to what is the “best" combination of defence systems to achieve multiple objectives under various threats and scenarios assumptions. It would be of great interest to see how we can employ our obtained SDP scheme to develop a suit of efficient algorithms, which allow end-users to easily elicit the decision maker’s preferences and perform a good visualization in large scale defence scenarios for uncertain force design problems.

Appendix: Numerical examples

The following examples show how we can employ the SDP reformulation scheme obtained in Theorem 4.1 (Procedure 1) to find robust (weak) Pareto solutions of uncertain convex quadratic multiobjective optimization problems.

The first example is dealt with a family of uncertain convex quadratic multiobjective problems of ($\hbox {EU}_c$) by specifying the value c of the objectives, while the second example is concerned with a family of uncertain convex quadratic multiobjective problems of (EU$_n$) by specifying the dimension n of the decision variables.

Example 6.1

(Calculating Pareto solutions via SDP) Let us consider a family of uncertain convex quadratic multiobjective problems:

where $c\in [0,+\infty )$ is a given parameter, $u:=(u_1,u_2)\in \Omega$ and $v:=(v_1,v_2)\in \Theta$ are uncertain parameters and $f_r, r=1,2,3,4$ and $g_l, l=1,2,3,4,5,6$ are bi-functions given by

$$\begin{aligned} f_1(x,u)&:=x_1^2+x_2^2-cx_1+1+u_1+u_2,\; f_2(x,u):=x^2_2+1-u_1+u_2,\\ f_3(x,u)&:=x_2^2+2x_2+u_1,\;f_4(x,u):=x_1^2+4x_2^2-cx_1+x_2-u_2,\\ g_1(x,v)&:=x_2^2-x_1+v_1x_2+v_2x_1-2c-4,\; g_2(x,v):=-x_1+v_1-3,\\ g_3(x,v)&:=-x_2-v_2-3,\;g_4(x,v):=x^2_1+x_2^2-v_1x_1-v_2x_2-c^2-2c-5,\\ g_5(x,v)&:=x_2-4,\;g_6(x,v):=x_1-c-4,\;x:=(x_1,x_2)\in \mathbb {R}^2. \end{aligned}$$

Here, the uncertainty sets $\Omega$ and $\Theta$ are given by

$$\begin{aligned} \Omega :=\{u:=(u_1,u_2)\in \mathbb {R}^2\mid u_1^2+ u_2^2\le 1\},\; \Theta :=\{v:=(v_1,v_2)\in \mathbb {R}^2\mid \frac{v_1^2}{4}+\frac{v^2_2}{9}\le 1\}. \end{aligned}$$

(6.1)

Now, we consider the robust convex quadratic multiobjective problem of ($\hbox {EU}_c$) as follows:

Note that the problem ($\hbox {ER}_c$) can be expressed in terms of problem (RP), where $\Omega _r:=\Omega , r=1,2,3,4,$ $\Theta _l:=\Theta , l=1,2,3,4,5,6$ are described respectively by

$$\begin{aligned} A^r&:=I_3, B^l:= \left( \begin{array}{ccc} 4 &{} 0 &{}0 \\ 0&{}9&{}0\\ 0&{}0&{}1\\ \end{array} \right) , A^r_1:=B^l_1= \left( \begin{array}{ccc} 0 &{} 0 &{}1 \\ 0&{}0&{}0\\ 1&{}0&{}0\\ \end{array} \right) , A^r_2:=B^l_2= \left( \begin{array}{ccc} 0 &{} 0 &{}0 \\ 0&{}0&{}1\\ 0&{}1&{}0\\ \end{array} \right) \end{aligned}$$

and $f_r, r=1,2,3,4, g_l, l=1,2,3,4,5,6$ are given respectively by $Q^1:=I_2, Q^2:=Q^3:=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{}1\\ \end{array} \right) , Q^4:=\left( \begin{array}{cc} 1 &{} 0 \\ 0&{}4\\ \end{array} \right) ,$ $\xi ^1:=(-c,0), \xi ^2:=0_2, \xi ^3:=(0,2), \xi ^4:=(-c,1), \xi ^r_i:=0_2, r=1,2,3,4, i=1,2, \beta ^1:=\beta ^2:=1, \beta ^3:=\beta ^4:=0, \beta ^1_1:=\beta ^1_2:=\beta ^2_2:=\beta ^3_1:=1, \beta ^2_1:=\beta ^4_2:=-1, \beta ^3_2:=\beta ^4_1:=0$ and $M^1:=\left( \begin{array}{cc} 0 &{} 0 \\ 0&{}1\\ \end{array} \right) ,$ $M^2:=M^3:=M^5:=M^6:=0_{2\times 2}$, $M^4:=I_2, \theta ^1:=\theta ^2:=(-1,0)$, $\theta ^3:=(0,-1), \theta ^4:=0_2, \theta ^5:=(0,1)$, $\theta ^6:=(1,0)$, $\theta ^1_1:=(0,1), \theta ^1_2:=(1,0)$, $\theta ^2_1:=\theta ^2_2$ $:=\theta ^3_1:=\theta ^3_2:=\theta ^5_1:=\theta ^5_2$ $:=\theta ^6_1:=\theta ^6_2:=0_2, \theta ^4_1:=(-1,0)$, $\theta ^4_2=(0,-1), \gamma ^1:=-2c-4$, $\gamma ^2:=\gamma ^3:=-3, \gamma ^4:=-c^2-2c-5$, $\gamma ^5:=-4, \gamma ^6:=-c-4, \gamma ^1_1:=\gamma ^1_2$ $:=\gamma ^2_2:=\gamma ^3_1$ $:=\gamma ^4_1:=\gamma ^4_2:=\gamma ^5_1$ $:=\gamma ^5_2:=\gamma ^6_1:=\gamma ^6_2:=0$, $\gamma ^2_1:=1,\gamma ^3_2:=-1.$

We now use the SDP reformulation, obtained in Theorem 4.1, to find a robust (weak) Pareto solution of problem ($\hbox {EU}_c$). Taking $\tilde{x}:=(c,1),$ we see that $g_l(\tilde{x},v) <0$ for all $v\in \Theta$ and $l=1,2,3,4,5,6.$ Thus, the characteristic cone $K:={\text {coneco}} \{ (0_2,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v), v\in \Theta , l=1,2,3,4,5,6\}$ is closed by virtue of Remark 3.2. Moreover, by taking $\tilde{u}:=\tilde{v}:=(0,0)\in \mathbb {R}^2,$ it holds that $A^r+\sum \limits _{i=1}^2\tilde{u}_iA^r_i\succ 0, r=1,2,3,4$ and $B^l+\sum \limits _{j=1}^2\tilde{v}_jB^l_j\succ 0, l=1,2,3,4,5,6$. Namely, all the assumptions of Theorem 4.1 are fulfilled in this setting.

Let $\alpha :=(1,1,1,1)\in \mathrm{int}\mathbb {R}^4_+,$ and consider a corresponding robust weighted-sum optimization problem of ($\hbox {ER}_c$) as follows:

Note that the (scalar) weighted-sum problem (E$_c$) has optimal solutions as its objective function is a continuous function and its feasible set is a compact set.

The SDP reformulation problem of (E$_c$) is given by

Using the Matlab toolbox CVX (see e.g., Grant and Boyd, 2014), we solve the problem (E$^{*}_c$) with (for instance) $c:=4$ and the solver returns the weighted-sum optimal value as $-1.17157$ and an optimal solution of problem (E$^{*}_c$) with $c:=4$ as $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,2,3,4, l=1,2,3,4,5,6)$, where $\bar{w}=(2.0000, -2.9400\text {e-}08)\approx (2,0)$. By Theorem 4.1(iii), we conclude that $\bar{w}=(2, 0)$ is a robust (weak) Pareto solution of problem ($\hbox {EU}_c$) with $c:=4$. (In this setting, we can re-check directly that $\bar{w}$ is a (weak) Pareto solution of problem ($\hbox {ER}_c$) with $c:=4$.)

Similarly, we test with some other values of c (see Table 1). These the numerical tests are conducted on a computer with a 1.90GHz Intel(R) Core(TM) i7-8650U and 16.0GB RAM, equipped with MATLAB R2018b. In Table 1, “Robust Pareto Solutions” are optimal decision variables $x:=(x_1,x_2)$ of ($\hbox {EU}_c$) and “Weighted-sum Values” are optimal values of (E$^{*}_c$) with the corresponding values of c.

Table 1 Robust Pareto solutions for ($\hbox {EU}_c$) with other values of c

Example 6.2

(Calculating Pareto solutions with higher dimensional decision variables) Let us consider a family of uncertain convex quadratic multiobjective problems:

where $n\in \mathbb {N}, n\ge 3,$ is a given parameter, $u:=(u_1,u_2)\in \Omega$ and $v:=(v_1,v_2,v_3)\in \Theta$ are uncertain parameters and $f_r, r=1,2,3,4,5$ and $g_l, l=1,2,3$ are bi-functions given by

$$\begin{aligned} f_1(x,u)&:=x_1^2+x_2^2-nx_n+1+u_1-u_2,\; f_2(x,u):=x^2_2-x_1-\ldots -x_n+1-u_1+u_2,\\ f_3(x,u)&:=x_2^2+2x_2-x_n+u_1+u_2,\;f_4(x,u):=x_1^2+4x_2^2-x_1+nx_n-u_2,\\ f_5(x,u)&:=x_1+x_2+\ldots +x_n-u_1+u_2,\\ g_1(x,v)&:=x_2^2-x_1+v_1x_2+v_2x_1-2n,\; g_2(x,v):=x_1^2+x_2^2+\ldots +x^2_n-n+v_1-v_3,\\ g_3(x,v)&:=x^2_1+x_2^2-v_1x_1-v_2x_2-x_n-n+v_3,\;x\in \mathbb {R}^n. \end{aligned}$$

Here, the uncertainty sets $\Omega$ and $\Theta$ are given by

$$\begin{aligned}&\Omega :=\{u:=(u_1,u_2)\in \mathbb {R}^2\mid u_1^2+\frac{1}{2} u_2^2\le 1, u_1\ge 0\},\\&\quad \Theta :=\{v:=(v_1,v_2,v_3)\in \mathbb {R}^3\mid v_1^2+v^2_2+v^2_3\le 1\}. \end{aligned}$$

Now, we consider the robust convex quadratic multiobjective problem of (EU$_n$) as follows:

Note that the problem (ER$_n$) can be expressed in terms of problem (RP), where $\Omega _r:=\Omega , r=1,2,3,4,5,$ $\Theta _l:=\Theta , l=1,2,3$ are described respectively by

$$\begin{aligned}&A^r:= \left( \begin{array}{cccc} 1 &{} 0 &{}0&{}0 \\ 0&{}2&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0\\ \end{array} \right) , A^r_1:= \left( \begin{array}{cccc} 0 &{} 0 &{}1&{}0 \\ 0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\\ \end{array} \right) , A^r_2:= \left( \begin{array}{cccc} 0 &{} 0 &{}0&{}0 \\ 0&{}0&{}1&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}0&{}0\\ \end{array} \right) ,\\ {}&B^l:=I_4, B^l_1:= \left( \begin{array}{cccc} 0 &{} 0 &{}0&{}1 \\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 1&{}0&{}0&{}0\\ \end{array} \right) , B^l_2:= \left( \begin{array}{cccc} 0 &{} 0 &{}0&{}0 \\ 0&{}0&{}0&{}1\\ 0&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ \end{array} \right) , B^l_3:= \left( \begin{array}{cccc} 0 &{} 0 &{}0&{}0 \\ 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}1&{}0\\ \end{array} \right) \end{aligned}$$

and $f_r, r=1,2,3,4,5, g_l, l=1,2,3$ are given respectively by

$$\begin{aligned}&Q^1:= \left( \begin{array}{ccccc} 1 &{} 0 &{}0&{}\cdots &{}0 \\ 0&{}1&{}0&{}\cdots &{}0\\ 0&{}0&{}0&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}0&{}0\\ \end{array} \right) , Q^2:= Q^3:= \left( \begin{array}{ccccc} 0 &{} 0 &{}0&{}\cdots &{}0 \\ 0&{}1&{}0&{}\cdots &{}0\\ 0&{}0&{}0&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}0&{}0\\ \end{array} \right) , Q^4:= \left( \begin{array}{ccccc} 1 &{} 0 &{}0&{}\cdots &{}0 \\ 0&{}4&{}0&{}\cdots &{}0\\ 0&{}0&{}0&{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\ddots &{}\vdots \\ 0&{}0&{}0&{}0&{}0\\ \end{array} \right) , \end{aligned}$$

$Q^5:=0_{n\times n}, \xi ^1:=(0,0,\ldots ,0,-n), \xi ^2:=(-1,-1,\ldots ,-1), \xi ^3:=(0,2,0,\ldots ,0,-1), \xi ^4:=(-1,0,\ldots ,0,n), \xi ^5:=(1,1,\ldots ,1), \xi ^r_i:=0_n, r=1,2,3,4,5, i=1,2, \beta ^1:=\beta ^2:=1, \beta ^3:=\beta ^4:=\beta ^5:=0, \beta ^1_1:=\beta ^2_2:=\beta ^3_1:=\beta ^3_2:=\beta ^5_2:=1, \beta ^1_2:=\beta ^2_1:=\beta ^4_2:=\beta ^5_1:=-1, \beta ^4_1:=0$ and $M^1:= Q_3, M^2:=I_{n}, M^3:=Q_1,$ $\theta ^1:=(-1,0,\ldots ,0), \theta ^2:=0_n, \theta ^3:=(0,\ldots ,0,-1), \theta ^1_1:=(0,1,0,\ldots ,0), \theta ^1_2:=(1,0,\ldots ,0), \theta ^1_3:=0_n, \theta ^2_1:=\theta ^2_2:=\theta ^2_3:=0_n,$ $\theta ^3_1:=(-1,0,\ldots ,0), \theta ^3_2=(0,-1,0,\ldots ,0), \theta ^3_3:=0_n, \gamma ^1:=-2n, \gamma ^2:=\gamma ^3:=-n, \gamma ^1_1:=\gamma ^1_2:=\gamma ^1_3:=\gamma ^2_2:=\gamma ^3_1:=\gamma ^3_2:=0,$ $\gamma ^2_1:=\gamma ^3_3:=1,\gamma ^2_3:=-1.$

We now use the SDP reformulation, obtained in Theorem 4.1, to find a robust (weak) Pareto solution of problem (EU$_n$). Taking $\tilde{x}:=0_n,$ we see that $g_l(\tilde{x},v) <0$ for all $v\in \Theta$ and $l=1,2,3.$ Thus, the characteristic cone $K:={\text {coneco}} \{ (0_n,1)\cup \mathrm{epi}\,g^*_l(\cdot ,v), v\in \Theta , l=1,2,3\}$ is closed by virtue of Remark 3.2. Moreover, by taking $\tilde{u}:=(\frac{1}{2},0)\in \mathbb {R}^2, \tilde{v}:=0_3\in \mathbb {R}^3,$ it holds that $A^r+\sum \limits _{i=1}^2\tilde{u}_iA^r_i\succ 0, r=1,2,3,4,5$ and $B^l+\sum \limits _{j=1}^3\tilde{v}_jB^l_j\succ 0, l=1,2,3$. Namely, all the assumptions of Theorem 4.1 are fulfilled in this setting.

Let $\alpha :=(1,1,1,1,1)\in \mathrm{int}\mathbb {R}^5_+,$ and consider a corresponding robust weighted-sum optimization problem of (ER$_n$) as follows:

Note that the (scalar) weighted-sum problem (E$_n$) has optimal solutions as its objective function is a continuous function and its feasible set is a compact set.

The SDP reformulation problem of (E$_n$) is given by

Using the Matlab toolbox CVX (see e.g., Grant and Boyd, 2014), we solve the problem (E$^{*}_n$) with (for instance) $n:=5$ and the solver returns the weighted-sum optimal value as $+7.56512$ and an optimal solution of problem (E$^{*}_n$) with $n:=5$ as $(\bar{w}, \bar{W}, \bar{\lambda }^r, \bar{t}^l, \tilde{Z}^r_0, Z^l_0, r=1,2,3,4,5, l=1,2,3)$, where $\bar{w}=(0.2206, -0.1376, 0, 0, 1.8757)$. By Theorem 4.1(iii), we conclude that $\bar{w}=(0.2206, -0.1376, 0, 0, 1.8757)$ is a robust (weak) Pareto solution of problem (EU$_n$) with $n:=5$. (In this setting, we can re-check directly that $\bar{w}$ is a (weak) Pareto solution of problem (ER$_n$) with $n:=5$.)

Similarly, we test with some other values of n (see Table 2). These the numerical tests are conducted on a computer with a 1.90GHz Intel(R) Core(TM) i7-8650U and 16.0GB RAM, equipped with MATLAB R2018b. In Table 2, “Robust Pareto Solutions” are optimal decision variables $x:=(x_1,\ldots , x_n)$ of (EU$_n$) and “Weighted-sum Values” are optimal values of (E$^{*}_n$) with the corresponding values of n.

Table 2 Robust Pareto solutions for (EU$_n$) with other values of n