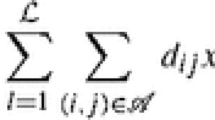Abstract
Robust optimization addressing decision making under uncertainty has been very well developed for problems with a single objective function and applied to areas of human activity such as portfolio selection, investment decisions, signal processing, and telecommunication-network planning. As these decision problems typically have several decisions or goals, we extend robust single objective optimization to the multiobjective case. The column-wise uncertainty model can be carried over to the multiobjective case without any additional assumptions. For the row-wise uncertainty model, we show under additional assumptions that robust efficient solutions are efficient to specific instance problems and can be found as the efficient solutions of another deterministic problem. Being motivated by the fact that Internet traffic must be maintained in a reliable yet affordable manner in situations of complex and dynamic usage, we apply the row-wise model to an intradomain multiobjective routing problem with polyhedral traffic uncertainty. We consider traditional objective functions corresponding to link utilizations and implement the biobjective case using the parametric simplex algorithm to compute robust efficient routings. We also present computational results for the Abilene network and analyze their meaning in the context of the application.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Robust optimization has developed as an alternative to stochastic programming to model decision making problems under conditions of uncertainty and to find decisions that remain feasible over all scenarios by relying on worst-case scenario bounds.
Robust single objective optimization has been well studied. Soyster (1973) studies linear programs with continuous uncertainty sets having specific characteristics. Kouvelis and Yu (1997) present the case of a discrete uncertainty set consisting of realizable scenarios and develop complexity results for many types of uncertain optimization problems. El-Ghaoui and Lebret (1997) examine least squares problems with bounded but uncertain coefficient matrices. Ben-Tal and Nemirovski (1998), Ben-Tal et al. (2009), and Bertsimas et al. (2011) present results for general and convex continuous uncertainty sets. Their approach makes use of a semi-infinite program, which has a finite number of variables but an infinite number of constraints, to model the uncertainty. Bertsimas and Sim (2004, 2006) introduce an approach whose level of conservatism can be adjusted by problem parameters, but provide only a probabilistic guarantee that the solution will remain feasible for every scenario.
Robust multiobjective optimization is a growing area of study. Initially, the concepts and methods of multiobjective optimization were applied to solve uncertain single objective problems (Iancu and Trichakis 2013; Klamroth et al. 2013; Köbis and Tammer 2012; Ogryczak 2014). In some of these studies, multiple scenarios are modeled with vector-valued functions. However, the interest in robust multiobjective optimization increases both theoretically and in applications, which is reflected in a variety of recent studies.
Concepts of robust solutions for multiobjective optimization problems without uncertainty being explicitly present in the models were proposed by Deb and Gupta (2005, 2006) in engineering design. Because uncertainty can be introduced to multiobjective optimization problems in different ways and each of these cases can be differently approached, two aspects are important when discussing the state of the art in robust multiobjective optimization: (i) the components of the multiobjective optimization problem that are assumed to be uncertain and (ii) the approach to solving the problem.
Uncertainty can be carried in the objective or constraints functions, or in the parameters used to scalarize the vector-valued objective. When uncertainty is present in the objective functions, by adding auxiliary variables the multiobjective problem may be reformulated to a problem that is deterministic in the objectives and uncertain in the constraint functions. However, Bokrantz and Fredriksson (2014), Dellnitz and Witting (2009), Ehrgott et al. (2014), Kuhn et al. (2016), and Witting et al. (2013), who address the case of uncertain objectives, and Fliege and Werner (2014), Goberna et al. (2015), and Kuroiwa and Lee (2012), who assume that both objective and constraint functions are uncertain, do not make use of this reformulation and develop new results specific to the multiobjective setting. In effect, the case where uncertainty is present solely in the constraint functions of the multiobjective problem has not been addressed. Additionally, Palma and Nelson (2010) and Hu and Mehrotra (2012) consider uncertain weights in the scalarized objective function.
The worst-case scenario approach is carried over from single-objective optimization by Bokrantz and Fredriksson (2014), Ehrgott et al. (2014), Fliege and Werner (2014), and Kuroiwa and Lee (2012). They follow the classical multiobjective optimization scheme of scalarization and perform robust (single-objective) optimization on the scalarized problem. Interestingly, the presence of uncertainty in the objective functions allows the authors to propose new concepts of robust solutions and to formulate auxiliary optimization problems leading to their computation (Ehrgott et al. 2014; Ide and Schöbel 2015; Kuhn et al. 2016). We refer to Goberna et al. (2015) for a recent literature review on robust multiobjective optimization.
Still another approach to modeling and resolving uncertainty is based on parametric optimization where parameters model the unknown data. Dellnitz and Witting (2009) combine techniques of multiobjective optimization with path-following algorithms while Witting et al. (2013) consider calculus of variation to solve parameter-dependent multiobjective optimization problems. Kuroiwa and Lee (2012) combine parametric optimization with the worst-case scenario approach.
Applications of robust multiobjective optimization include forestry management (Palma and Nelson 2010), airline scheduling (Kuhn et al. 2016), portfolio management (Fliege and Werner 2014), and radiation therapy (Bokrantz and Fredriksson 2014).
Robust Internet routing is a critical direction of research because the Internet today plays a crucial role in everyone’s life. Improving its global performance (e.g., faster, more reliable, higher quality) is one of the main challenges for network operators and principally depends on the management of the underlying routing protocols. Until the twenty-first century, most of the routing optimization problems in the Internet required some estimate of the traffic demands (e.g., worst-case or average traffic) expected to be carried throughout. Predicting patterns of Internet traffic is a difficult task due to the size and diversity of the Internet (Ben-Ameur 2007; Ben-Ameur et al. 2012). Traffic engineering (TE) involves assigning the number and type of circuits and switching equipment that are necessary to meet these expected traffic demands on a network (TIA 2012). Quality of service (QoS), being a qualitative measure of how well a routing is performing, is a main goal of network operators. Robust routing optimization emerges as a means to achieve trade-offs between the conflicting objectives of TE and QoS. Ben-Ameur et al. (2012) present an overview of robust routing with a focus on the most common uncertainty sets and routing strategies considered in communication networks. Casas (2010) shows that decreases in QoS can be due to overloaded links (utilizations larger than one) allowing the QoS routing problem to be considered a subproblem of the robust routing problem. Hijazi et al. (2013), in particular, focus on one facet of QoS, network response time, and present both theoretical results and numeric experiments regarding the delay constrained routing problem.
Ben-Ameur and Kerivin (2005) introduce the concept of stable robust routing within the context of Virtual Private Network provisioning, which appears to be an application of uncertain linear programs (Ben-Tal and Nemirovski 1999). They represent the traffic uncertainty as a polytope and compute a stable (i.e., fixed) routing scheme which is valid for all the traffic configurations within the polytope. Their model, called the polyhedral traffic model, allows the network operator to exploit, for instance, temporal and geographical correlations and link-traffic measurements.
Many approaches to solving uncertain single objective Internet routing optimization problems differ in the way the semi-infinite program, created by the approach of Ben-Tal and Nemirovski (1999), is managed. Ben-Tal and Nemirovski (1999), Ben-Ameur and Kerivin (2005), and Casas (2010) deal with the semi-infinite programs by reducing the uncertainty set to its convex hull, which is then known as the uncertainty polytope. This technique only considers uncertain constraints for the extreme points of the uncertainty polytope, and manage the potentially huge, but finite, number of such constraints through a cutting-plane method. Altin et al. (2010), Belotti and Pinar (2008), and Tabatabaee et al. (2007) deal with the semi-infinite programs by taking the dual of these programs. Kodialam et al. (2006) create a separation oracle linear program related to the semi-infinite program, and apply a two-phase routing technique to take the dual of the separation oracle linear program. Gunnar and Johansson (2011) eliminate the use of the semi-infinite program by adopting techniques combining column and constraint generation to find a robust routing.
Another distinguishing characteristic of many applications is the network representation. Altin et al. (2010), Belotti and Pinar (2008), Ben-Ameur and Kerivin (2005), Casas (2010), Gunnar and Johansson (2011), Minoux (2009), and Tabatabaee et al. (2007) deal with the path decomposition formulation of the robust routing problem. One the other hand, Kodialam et al. (2006) describe a problem that has both arc and path aspects due to the two-phase nature of the routing.
A drawback to considering a single objective is that too much focus is set on a specific TE or QoS criterion while other criteria are ignored. However, a very few telecommunications studies deal with a multiobjective problem, none with more than two objectives. Because optimization under uncertainty is often seen as more complex than deterministic optimization, researchers who have attempted to consider two objectives in those problems tend to use linear combinations of both objective functions with a priori chosen scalars as in Casas (2010). Robust routing under traffic uncertainty with multiple objectives has not been studied in a multiobjective context. However, robust routing under conditions of equipment failure with multiple objectives has been previously considered. In particular, the works of Nucci et al. (2003) and Yuan (2003) consider the latter.
Of interest to this work is which components of the multiobjective optimization problem are considered to be uncertain. We consider solely the case where uncertainty is carried in the coefficients of constraint functions. Despite the growing interest in robust multiobjective optimization, the prominent approaches of column-wise and row-wise uncertainty developed by Soyster (1973) and Ben-Tal and Nemirovski (1999) in a single-objective setting specifically for this case have not been extended to a multiobjective setting. As indicated earlier in this section, other studies on robust multiobjective optimization do not explicitly cover this type of uncertainty in multiobjective optimization. Hence, the first contribution of the current paper is an examination of the validity of these two models in the presence of a vector-valued objective and without scalarization. We show that the column-wise uncertainty model can be carried over to the multiobjective case without any additional assumptions. For the row-wise uncertainty model, we make additional assumptions such that robust efficient solutions are efficient to specific instance problems and can be found as the efficient solutions of another deterministic problem.
We then apply the results we obtain for the row-wise uncertainty case to some Internet routing problems under traffic uncertainty. We compute nondominated routing schemes when different performance criteria are simultaneously considered. Our work is in contrast to the very few studies on robust routing in which criteria are combined into one by applying the weighted sum scalarization. For any of those studies, this approach only provides a nondominated routing scheme associated with a priori fixed weight associated with each criterion. Our second contribution thus is a method to generate nondominated routing schemes in order to let a decision maker a posteriori choose the most suitable scheme.
The paper is organized in five sections. In Sect. 2, we present theoretical results on the extension of robust optimization to the multiobjective case, while a robust biobjective routing problem with the necessary notation is motivated and developed in Sect. 3. The computational results are reported and discussed in Sect. 4. We conclude with Sect. 5.
2 Robust multiobjective optimization
We consider an optimization problem of the form
with uncertainty vector \(\mathbf {u}\) that belongs to a given compact uncertainty set \(\mathcal{U} \subseteq \mathbb {R}^r\). Here \(\mathbf {x} \in \mathbb {R}^n\) represents the vector of decision variables, \(\mathbf {g}: \mathbb {R}^n \times \mathbb {R}^r \rightarrow \mathbb {R}^m\), \(\mathcal{K} \subseteq \mathbb {R}^m\), and \(\mathcal{X} \subseteq \mathbb {R}^n\) are the structural elements of the constraints, and \(\mathbf {f}: \mathbb {R}^n \rightarrow \mathbb {R}^p\) is the vector-valued objective function with component functions \(f_k: \mathbb {R}^n \rightarrow \mathbb {R}\) for all \(k \in \{1,\ldots ,p\}\). Hereafter, problem (1) is referred to as an uncertain multiobjective optimization problem.
With every uncertain vector \(\mathbf {u} \in \mathcal{U}\), one associates a deterministic multiobjective optimization problem
called an instance of the uncertain multiobjective optimization problem. Let \(\mathcal{X}_{\mathbf {u}}\) denote the set of feasible solutions to deterministic multiobjective optimization problem (2) associated with \(\mathbf {u} \in \mathcal{U}\), that is,
For any \(\mathbf {u} \in \mathcal U,\) the feasible set \(\mathcal{X}_{u}\) is a subset of the decision space \(\mathbb {R}^n\), whereas its image set \(\mathcal{Y}_{u} = \mathbf {f}(\mathcal{X}_{u})\) is a subset of the objective space \(\mathbb {R}^p\).
In a real-life context, one uncertainty realization \(\mathbf {u} \in \mathcal{U}\) is attained at a time. Therefore problem (1) models a decision situation in which instance problems (2) are never solved simultaneously but rather one at time, each for the associated uncertainty \(\mathbf {u} \in \mathcal{U}\). Obviously, the decision maker expects to make the best decision possible for every uncertainty realization.
2.1 Terminology and reformulation
In multiobjective optimization, the existence of feasible solutions simultaneously minimizing all the objective functions [i.e., the so-called ideal point (Ehrgott 2005)] is extremely rare due to conflict among objectives (e.g., cost versus quality of service for Internet routing problems). To cope with the necessity of trade-offs between objectives, decision makers generally consider some preferences between the outcomes and then seek preferred solutions and outcomes. One of the most common concepts to model these preferences is the well-known concept of nondominated optimality (Pareto 1896) which is associated with the classical partial orderings on \(\mathbb {R}^p\)
A vector \(\mathbf {y} \in \mathbb {R}^p\) is said to (strictly) dominate a vector \(\mathbf {y'} \in \mathbb {R}^p\) if and only if \(\mathbf {y} (<) \le \mathbf {y'}\). Let \(\mathbb {R}^p_{\geqq } = \{\mathbf {y} \in \mathbb {R}^p : \mathbf {y} \geqq \mathbf {0}\}\) and \(\mathbb {R}^p_{\ge }\) be defined accordingly.
Definition 1
Let \(\mathbf {u} \in \mathcal U\). Outcome \(\mathbf {y} \in \mathcal{Y}_{u} \subset \mathbb {R}^p\) is called (weakly) nondominated (or (weakly) nondominated optimal) to multiobjective optimization problem (2) if there does not exist \(\mathbf {y'} \in \mathcal{Y}_{u}\) that (strictly) dominates \(\mathbf {y}\).
The set of all (weakly) nondominated outcomes of multiobjective optimization problem (2), associated with \(\mathbf {u} \in \mathcal U\), is denoted by (\({{\mathrm{\textit{w-N}}}}(\mathcal{Y}_{u})\)) \(N(\mathcal{Y}_{u})\). Weakly nondominated outcomes form a larger set than \(N(\mathcal{Y}_{u})\), and despite being less useful in practice, tend to be easier to generate than nondominated outcomes. The elements composing the pre-images of the nondominated outcomes in \(N(\mathcal{Y}_{u})\) are called efficient to problem (2) and they form the efficient set to multiobjective optimization problem (2)
where \(\mathcal{X}_{u} = f^{-1}(\mathcal{Y}_{u}) \subseteq \mathbb {R}^n\) is the pre-image of \(\mathcal{Y}_{u}\). The set of weakly efficient solutions associated with \(\mathbf {u} \in \mathcal U\) is defined analogously, that is,
If the pre-image \(f^{-1}(\mathbf {y}) =\{\mathbf {x} \in \mathcal{X}_u: \mathbf {f(x)} = \mathbf {y}\}\) of nondominated outcome \(\mathbf {y}\) in \(N(\mathcal{Y}_{u})\) is a singleton, the unique element of \(E(\mathcal{X}_{u})\) belonging to \(f^{-1}(\mathbf {y})\) then is called a strictly efficient solution to problem (2). Let \({{\mathrm{\textit{s-E}}}}(\mathcal{X}_{u})\) denote the set composed of all the strictly efficient solutions to multiobjective optimization problem (2) associated with \(\mathbf {u}\in \mathcal U\).
The concept of epsilon-nondominated outcome was introduced by Kutateladze (1979) and Loridan (1984) to approximate the nondominated outcomes. Let \({\varvec{\epsilon }} \in \mathbb {R}^p_{\geqq }\). A vector \(\mathbf {y} \in \mathbb {R}^p\) is said to \({\varvec{\epsilon }}\)-dominate a vector \(\mathbf {y'} \in \mathbb {R}^p\) if and only if \(\mathbf {y} \le \mathbf {y'} - {\varvec{\epsilon }}\).
Definition 2
Let \(\mathbf {u} \in \mathcal U\) and \({\varvec{\epsilon }}^{\mathbf {u}} \in \mathbb {R}^p_{\ge }\). Outcome \(\mathbf {y} \in \mathcal{Y}_{u}\) is called \({\varvec{\epsilon }}^{\mathbf {u}}\)-nondominated to multiobjective optimization problem (2) if there does not exist \(\mathbf {y'} \in \mathcal{Y}_{u}\) which \({\varvec{\epsilon }}^{\mathbf {u}}\)-dominates \(\mathbf {y}\).
The set of all \({\varvec{\epsilon }}^{\mathbf {u}}\)-nondominated outcomes of multiobjective optimization problem (2) associated with \({\varvec{\epsilon }}^{\mathbf {u}}\) for \(\mathbf {u} \in \mathcal U\) is denoted by \(\varvec{\epsilon }^{\mathbf {u}}\)-\(N(\mathcal{Y}_{u})\). The union of all the pre-images of the \({\varvec{\epsilon }}^{\mathbf {u}}\)-nondominated outcomes of problem (2) form the \({\varvec{\epsilon }}^{\mathbf {u}}\)-efficient set to problem (2), that is,
An essential attribute of problem (1) lies in the uncertain constraints
which must be satisfied no matter what the actual realization of uncertainty vector \(\mathbf {u}\) is, provided the latter belongs to \(\mathcal{U}\). Because uncertain vector \(\mathbf {u}\) is unknown at the time of solving problem (1), but uncertainty set \(\mathcal{U}\) is given, the solution vector(s) to problem (1) can be obtained by solving the following problem, called the robust counterpart of uncertain multiobjective optimization problem (1),
Robust counterpart (4) deals with solutions which remain feasible to uncertain multiobjective optimization problem (1) regardless of the future realization of vector \(\mathbf {u}\) in \(\mathcal{U}\). In a real-life setting, robust counterpart (4) models a decision situation in which all uncertainty realizations are attained simultaneously and therefore (4) is not a true problem. However, the robust counterpart turns out to be instrumental for developing a methodology oriented toward a worst-case approach. This methodology was initially developed by Soyster (1973) and later by Ben-Tal and Nemirovski (1998, 1999) and El-Ghaoui and Lebret (1997).
Let \(\mathcal{X}_{RC}\) denote the set of feasible solutions to robust counterpart (4), that is,
A vector in \(\mathcal{X}_{RC}\) (in \(\mathcal{Y}_{RC} = f(\mathcal{X}_{RC})\), respectively) then is said to be a robust feasible solution to (a robust outcome of, respectively) uncertain multiobjective optimization problem (1). A direct consequence of definition (5) is the following proposition.
Proposition 1
If the robust counterpart (4) is feasible, then so are all the instances (2). \(\square \)
The converse of Proposition 1 is not necessarily true, even in the case that constraint (3) involves linear inequalities with uncertain coefficients, the set \(\mathcal{X} = \mathbb {R}^n_+\), and the uncertainty set \(\mathcal{U}\) is a polytope (Ben-Tal and Nemirovski 1999).
When a scalar-valued objective function (i.e., \(p=1\)) is considered, an optimal solution \(\mathbf {x^*}\) to robust counterpart (4) is called robust optimal to uncertain optimization problem (1) and the objective-function value at \(\mathbf {x^*}\) is the robust optimal value of problem (1) (Ben-Tal et al. 2009). In the multiobjective case (i.e., \(p \ge \) 2), the concepts of (strictly/weakly/epsilon) efficient solutions to or nondominated outcomes of robust counterpart (4) can be defined similarly as previously done for the instances (2).
Robust multiobjective optimization thus consists of finding the (strictly/weakly/epsilon) efficient set of robust counterpart (4). A (strictly/weakly/epsilon) efficient solution to robust counterpart (4) is called a robust (strictly/weakly/epsilon) efficient solution to uncertain multiobjective optimization problem (1). Let (s/w)-\(E(\mathcal{X}_{RC})\) denote the set of robust (stricly/weakly) efficient solutions to (4) and \(\varvec{\epsilon }\)-\(E(\mathcal{X}_{RC})\), \(\varvec{\epsilon }\in \mathbb {R}^p_{\geqq }\), the robust epsilon-efficient solutions to (4). Similarly one talks about robust (weakly/epsilon) nondominated outcomes of uncertain multiobjective optimization problem (1) and consider the sets w-\(N(\mathcal{Y}_{RC})\), \(N(\mathcal{Y}_{RC})\), and \(\varvec{\epsilon }\)-\(N(\mathcal{Y}_{RC})\).
As a single-objective optimization problem may have no optimal solutions, the efficient set of a multiobjective optimization problem does not necessarily exist. A function \(f:\mathbb {R}^n\rightarrow \mathbb {R}\) is called lower (upper) semicontinuous throughout \(\mathbb {R}^n\) if for every \(\alpha \in \mathbb {R}\), the lower (upper) level set (also called (superlevel) sublevel set) \(S_\alpha = \{\mathbf {x}: f(\mathbf {x}) \le (\ge ) \alpha \}\) is closed (Rockafellar 1997). Combining the lower semicontinuity property on the component functions \(f_1,\ldots ,f_p\) of the vector-valued objective function \(\mathbf {f}\) with additional properties on the feasible set X, sufficient conditions for the existence of the efficient set have been obtained as stated in the following theorem [see, e.g., Theorem 2.19 in Ehrgott (2005)].
Theorem 1
The efficient set to a multiobjective optimization problem \(\min \{(f_1(\mathbf {x}),\ldots ,f_p(\mathbf {x})): \mathbf {x} \in \mathcal{X} \subseteq \mathbb {R}^n\}\) is nonempty, if the feasible set \(\mathcal{X}\) is nonempty and compact, and the scalar-valued functions \(f_k\), for all \(k \in \{1,\ldots ,p\}\), are lower semicontinuous. \(\square \)
To ensure the existence of robust efficient solutions to uncertain multiobjective optimization problem (1), we introduce the following assumptions on the structural elements of its constraints, that is, \(\mathbf {g}\), \(\mathcal{X}\), and \(\mathcal{K}\) and on the component functions \(f_k\) of the vector-valued objective function \(\mathbf {f}\). Due to the developments presented later in this section, we require the objective component functions to be continuous rather than lower semicontinuous.
Assumption 1
From now on, we assume that
-
(i)
\(\mathcal{X} \subseteq \mathbb {R}^n\) is a nonempty compact set;
-
(ii)
functions \(\mathbf {g}(\cdot ,\mathbf {u})\) are continuous on \(\mathcal{X}\) for all \(\mathbf {u} \in \mathcal{U}\);
-
(iii)
\(\mathcal{K} \subseteq \mathbb {R}^m\) is closed;
-
(iv)
functions \(f_k\) are continuous on \( \mathbb {R}^n\) for all \(k \in \{1,\ldots ,p\}\).
The assumptions on the structural elements of the constraints ensure that the feasible set to robust counterpart (4) is a compact set in \(\mathbb {R}^n\), as stated in the next proposition.
Proposition 2
Set \(\mathcal{X}_{RC}\) is compact.
Proof
The case \(\mathcal{X}_{RC} = \emptyset \) is trivial, so assume that \(\mathcal{X}_{RC}\) is nonempty. Let \(\mathbf {u} \in \mathcal{U}\). Because compactness is preserved by continuous functions, by Assumption 1(i), (ii), the set \(\mathbf {g}(\mathcal{X},\mathbf {u})\), that is, the set consisting of the images of all \(\mathbf {x}\in \mathcal{X}\) under \(\mathbf {g(\cdot , u)}\), is a compact set in \(\mathbb {R}^m\). Assumption 1(iii) implies that the set \(\mathbf {g}(\mathcal{X},\mathbf {u}) \cap \mathcal{K}\) is also compact. By the continuity of \(\mathbf {g}(\cdot ,\mathbf {u})\), the set \(\mathcal{X}_{\mathbf {u}} = \mathcal{X} \cap \big ( \bigcup _{\varvec{\vartheta } \in \mathbf {g}(\mathcal{X},\mathbf {u}) \cap \mathcal{K}} \mathbf {g}^{-1}(\varvec{\vartheta },\mathbf {u})\big )\) is also compact. Consequently, the set \(\mathcal{X}_{RC} = \bigcap _{\mathbf {u} \in \mathcal{U}} \mathcal{X}_{\mathbf {u}}\) is compact. \(\square \)
Proposition 2, combined with Assumption 1(iv) on the component functions of the objective function to robust counterpart (4), immediately implies the following corollary of Theorem 1, showing that a robust efficient solution to uncertain multiobjective optimization problem (1) exists as long as a robust feasible solution exists to robust counterpart (4).
Corollary 1
If feasible set \(\mathcal{X}_{RC}\) is nonempty, then so is the efficient set \(E(\mathcal{X}_{RC})\). \(\square \)
Because an efficient solution also is a weakly efficient one, Assumption 1 ensures the existence of the weakly efficient set \({{\mathrm{\textit{w-E}}}}(\mathcal{X}_{RC})\) as well.
We now wish to establish connections between the efficient solutions to the robust counterpart (4) and those to the instances (2). As pointed out by Ben-Tal and Nemirovski (1998) in the single-objective case, there might exist a gap between the optimal value of the robust counterpart and the optimal values to all the instances; the former being greater than the latter. We investigate this issue in the multiobjective setting. The concept of epsilon-nondominated outcomes allows one to develop a connection between the efficient solutions to robust counterpart (4) and the \({\varvec{\epsilon }}^{\mathbf {u}}\)-efficient set to multiobjective optimization problem (2). To accomplish this, given a feasible solution to robust counterpart (4), \({\bar{\mathbf {x}}} \in \mathcal{X}_{RC}\), we formulate a parametric optimization problem denoted \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\},\)
where \(\mathcal{U}\) is a parameter space in \(\mathbb {R}^r.\) Let \(\mathcal{X}_{\bar{x}}\) denote the point-to-set mapping from \(\mathcal{U}\) to \(\mathbb {R}^n\) defined as
Note that \(\mathcal{X}_{\bar{x}}(\mathbf {u}) \ne \emptyset \) for each \(\mathbf {u} \in \mathcal{U}\) since \({\bar{\mathbf {x}}}\) is an element of \(\mathcal{X}_{\bar{x}}(\mathbf {u})\) for every \(\mathbf {u} \in \mathcal{U}\). Hence the parametric problem \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\}\) is feasible. We apply the theory of parametric optimization to problem (6) as given in Fiacco (1983). A solution to (6) is constructed by making use of the Implicit Function Theorem to write the variables \(\mathbf {x}\) as functions of the parameter \(\mathbf {u}\). To make sure that problem (6) is suitable for our work, we make Assumption 2.
Assumption 2
Let the following holds for problem (6):
-
(i)
mapping \(\mathcal{X}_{\bar{x}}\) is continuous on \(\mathcal{U}\);
-
(ii)
functions \(\mathbf {x} = \mathbf {x(\mathbf {u})}\) are uniformly bounded on \(\mathcal{U}\);
-
(iii)
function \(f_s\) is continuous on \(\mathbb {R}^n\);
-
(iv)
function \(f_s\) is bounded on \( \mathcal{X}_{\bar{x}}(\mathbf {u})\) for all \(\mathbf {u} \in \mathcal{U}\).
Note that Assumption 2(iii) holds due to Assumption 1(iv), and Assumption 2(iv) holds because each function \( f_i, i = 1, \ldots , p,\) is bounded. A bound from above is given by the inequality constraint in (6) and a bound from below results from the existence of the efficient set for each instance problem (2). Assumptions 2(i) and (ii) must be additionally made.
Each element \(\mathbf {u}\) of \(\mathcal{U}\) is mapped to an optimal solution \(\mathbf {x^*}\) and the optimal objective value \(f_s^*\). The result of this mapping is an optimal solution function \(\mathbf {x^*(\mathbf {u})}\) and the optimal value function \(f_s^*(\mathbf {u}) = f_s(\mathbf {x^*(\mathbf {u})})\). Under Assumption 2, the existence of an optimal solution to (6) is addressed in Leverenz (2015). An important property of the optimal value function to (6) is provided by Fiacco (1983).
Proposition 3
Let Assumptions 2(i) and (iii) hold. Then the optimal value function \(f_s^*(\mathbf {u})\) to problem (6) is continuous on \(\mathcal{U}\).
Consider again problem (6) but with the parameter \(\mathbf {u}\) being fixed, i.e., \(\mathbf {u}\) is equal to a specific vector \(\mathbf {u^{\prime }} \in \mathcal{U}\). Let \(P(\mathbf {u^{\prime }}, {\bar{\mathbf {x}}})\) denote the resulting optimization problem given as
where \({\bar{\mathbf {x}}} \in E(\mathcal{X}_{RC})\), and let \(\mathbf {x^{\mathbf {u^{\prime }}}}\) denote its optimal solution. By Assumption 1, an optimal solution to \(P(\mathbf {u^{\prime }}, {\bar{\mathbf {x}}})\) exists. More importantly, based on a result in Wendell and Lee (1977), an optimal solution to \(P(\mathbf {u^{\prime }}, {\bar{\mathbf {x}}})\) is an efficient solution to instance (2) for \(\mathbf {u} = \mathbf {u^{\prime }}\). Let \(\left\| {\mathbf {y}}\right\| _1\) denote the \(\ell _1\)-norm of a vector \(\mathbf {y} \in \mathbb {R}^p\).
Proposition 4
Every efficient solution \({\bar{\mathbf {x}}}\) to robust counterpart (4) is \({\varvec{\epsilon }}^{\mathbf {u}}\)-efficient to each instance (2) for some \({\varvec{\epsilon }}^{\mathbf {u}} \in \mathbb {R}^p_{\geqq }\) such that
where \(\mathbf {x^*(\mathbf {u})}\) is an optimal solution function to problem (6).
Proof
Let problem \(P(\mathbf {u^{\prime }}, {\bar{\mathbf {x}}})\) admit an optimal solution \(\mathbf {x^{\mathbf {u^{\prime }}}}\). At optimality of \(P(\mathbf {u^{\prime }}, {\bar{\mathbf {x}}})\), the inequality constraint may be active or not. If \(\mathbf {f(\mathbf {x^{\mathbf {u^{\prime }}}})} = \mathbf {f}(\bar{\mathbf {x}})\) then
and the point \({\bar{\mathbf {x}}}\) is efficient to instance (2). If \(\mathbf {f(\mathbf {x^{\mathbf {u^{\prime }}}})} \le \mathbf {f}(\bar{\mathbf {x}})\) then
and there does not exist \(\mathbf {x'} \in \mathcal{X_{\mathbf {u^{\prime }}}}\) such that \(\mathbf {f(x')} \le \mathbf {f}(\bar{\mathbf {x}}) - \varvec{\epsilon }^{\mathbf {u^\prime }}\), where \(\varvec{\epsilon }^{\mathbf {u^\prime }} = \mathbf {f}({\bar{\mathbf {x}}}) - \mathbf {f}(\mathbf {x^{\mathbf {u^{\prime }}}}) \in \mathbb {R}^p_{\ge }\) and
From both cases we conclude that \({\bar{\mathbf {x}}}\) is \(\varvec{\epsilon }^{\mathbf {u^\prime }}\)-efficient to instance (2) for \(\varvec{\epsilon }^{\mathbf {u^\prime }} \in \mathbb {R}^p_{\geqq }\) and such that
Since \(\mathbf {u^{\prime }} \in \mathcal{U}\) is arbitrary, \({\bar{\mathbf {x}}}\) is \(\varvec{\epsilon }^{\mathbf {u^\prime }}\)-efficient to each instance (2) for some \(\varvec{\epsilon }^{\mathbf {u^\prime }} \in \mathbb {R}^p_{\geqq }\) satisfying
We have \(\sup \{ {f_s(\mathbf {x^{\mathbf {u^{\prime }}}})}, \mathbf {u^{\prime }} \in \mathcal{U}\} = \sup _{\mathbf {u} \in \mathcal{U}} {f_s(\mathbf {x^*(\mathbf {u})})}\), where \(\mathbf {x^*(\mathbf {u})}\) is an optimal solution function to problem (6). Since the set \(\mathcal{U}\) is compact, and by Proposition 3 the function \(f_s(\mathbf {x^*(\mathbf {u})})\) is continuous on \(\mathcal{U}\), we obtain the desired result. \(\square \)
In robust optimization, uncertainty can be represented by the triplet \((\mathbf {g},\mathcal{K},\mathcal{U})\), that is, by the two structural elements of the uncertain constraints, \(\mathbf {g}\) and \(\mathcal{K}\), of problem (1) and the uncertainty set \(\mathcal{U}\). In the case of uncertain convex single-objective optimization problems, (Ben-Tal and Nemirovski 1998) considered some additional properties on the uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\), that we will mention in Sect. 2.2, that make this gap vanish. To obtain a similar result in the multiobjective case, we introduce the following type of uncertainty that encompasses the one introduced by Ben-Tal and Nemirovski (1998).
Definition 3
Uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) is called robust-counterpart suitable if for every compact set \(\mathcal{X} \subseteq \mathbb {R}^n\), robust counterpart (4) is feasible whenever all the instances (2) are feasible.
Proving that uncertainty is robust-counterpart suitable may be difficult in practice, so we also consider a more restrictive definition where convexity is enforced on the deterministic part of the constraints (i.e., set \(\mathcal X\)). This new definition of robust-counterpart suitability will appear useful later in the paper.
Definition 4
Uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) is called convex robust-counterpart suitable if for every convex compact set \(\mathcal{X} \subseteq \mathbb {R}^n\), robust counterpart (4) is feasible whenever all the instances (2) are feasible.
Under robust-counterpart-suitable uncertainty, Proposition 1 implies that robust counterpart (4) is feasible if and only if all the instances (2) are feasible. This feasibility equivalence allows us to prove the following proposition connecting the efficient solutions to robust counterpart (4) with those to all the instances (2).
Proposition 5
If the uncertainty is robust-counterpart suitable, then every efficient solution \({\bar{\mathbf {x}}}\) to robust counterpart (4) satisfies
where \(\mathbf {x^*(\mathbf {u})}\) is an optimal solution function to problem (6).
Proof
Let \({\bar{\mathbf {x}}} \in E(\mathcal{X}_{RC})\) and let \(s^*\) denote the right-hand-side of (9). By (7) we have
Assume \(s^* < f_s({\bar{\mathbf {x}}})\) and consider the set
By Assumption 1(iv), the sum \(\sum \limits _{k = 1}^p f_k\) is a continuous function. Thus the sublevel sets defining \(\mathcal{P}({\bar{\mathbf {x}}})\) are closed. From \(\mathcal X\) being compact, we then deduce that \(\mathcal{X} \cap \mathcal{P}({\bar{\mathbf {x}}})\) is compact.
Consider now the uncertain multiobjective optimization problem
that has the same uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) as UMOP problem (1). Let \(\mathcal{X}_{\mathbf {u}}(\bar{\mathbf {x}})\) denote the feasible set to the instance of problem (10) associated with \(\mathbf {u} \in \mathcal U\), that is,
To show that every instance of problem (10) is feasible, we observe that for every \(\mathbf {u^{\prime }} \in \mathcal{U}\), an optimal solution \(\mathbf {x}(\mathbf {u}^{\prime })\) to problem \(P(\mathbf {u}^{\prime },{\bar{\mathbf {x}}})\) belongs to \(\mathcal{X}_{\mathbf {u}}(\bar{\mathbf {x}})\). All the instances of (10) induced by the vectors in \(\mathcal{U}\) are therefore feasible. Since the uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) is robust-counterpart suitable, the robust counterpart of (10) is also feasible, that is, there exists \(\mathbf {x}' \in \mathcal{X} \cap \mathcal{P}({\bar{\mathbf {x}}}) \subseteq \mathcal{X}_{RC}\) such that
We therefore obtain \(\mathbf {f}(\mathbf {x}') \le \mathbf {f}({\bar{\mathbf {x}}})\), a contradiction to \(\bar{\mathbf {x}}\) being efficient to robust counterpart (4). \(\square \)
Based on the developments above we obtain a stronger result on the relationship between the efficient solutions to robust counterpart (4) and the efficient solutions to multiobjective optimization problem (2).
Theorem 2
Let the uncertainty be robust-counterpart suitable, and \(\mathbf {x^*(\mathbf {u})}\) and \(f_s(\mathbf {x^*(\mathbf {u})})\) be optimal solution and value functions, respectively, to problem \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\}\). If \({\bar{\mathbf {x}}}\) is an efficient solution to robust counterpart (4) then \({\bar{\mathbf {x}}}\) is efficient to the instance (2) associated with \(\mathbf {u^*} \in \mathcal U\), where \(\mathbf {u^*}\) is an optimal solution to \( \max _{\mathbf {u} \in \mathcal{U}} f_s(\mathbf {x^*(\mathbf {u})})\).
Proof
If the uncertainty is robust-counterpart suitable and \({\bar{\mathbf {x}}}\) is an efficient solution to robust counterpart (4) then (9) holds. Equivalently, \(f_s({\bar{\mathbf {x}}}) = f_s(\mathbf {x^*(\mathbf {u^{*}})})\), where \( \mathbf {u^{*}} \in \mathrm{argmax}_{\mathbf {u} \in \mathcal{U}} f_s(\mathbf {x^*(\mathbf {u})})\). This implies that there exists an instance \(\mathbf {u^*} \in \mathcal U\) for which, based on Proposition 4, \(\varvec{\epsilon }^{\mathbf {u^{*}}} = \mathbf 0 \) and for which \({\bar{\mathbf {x}}}\) is efficient. \(\square \)
Note that under under the assumptions of Theorem 2, \({\bar{\mathbf {x}}}\) may not be strictly efficient to the instance (2) associated with \(\mathbf {u^*} \in \mathcal U\). Equality (9) holding for \(\mathbf {u^*} \in \mathcal U\) implies \(f_s(\mathbf {x^*(\mathbf {u^*})}) = f_s({\bar{\mathbf {x}}})\). Since \(\mathbf {f}(\mathbf {x^*(\mathbf {u^*})})\leqq \mathbf {f}({\bar{\mathbf {x}}})\), because \(\mathbf {x^*(\mathbf {u^*})}\) is feasible to problem \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\}\), it must be \(\mathbf {f}(\mathbf {x^*(\mathbf {u^*})}) = \mathbf {f}({\bar{\mathbf {x}}}).\) Since, by Theorem 2, \({\bar{\mathbf {x}}}\) is efficient to the instance (2) associated with \(\mathbf {u^*}\), so is \(\mathbf {x^*(\mathbf {u^*})}\). If \(\mathbf {x^*(\mathbf {u^*})} \ne {\bar{\mathbf {x}}}\) then none of the two solutions is strictly efficient.
For convex robust-counterpart suitable uncertainty, obtaining a similar relationship between the efficient solutions to the robust counterpart and those to the related instances follows by considering some additional convexity-preserving property on the objective component functions. A function \(f: \mathbb {R}^n \rightarrow \mathbb {R}\) is said to be quasiconvex if for all \(\alpha \in \mathbb {R}\), the sublevel sets \(S_{\alpha } = \{\mathbf {x} \in \mathbb {R}^n: f(\mathbf {x}) \le \alpha \}\) are convex. Adding the quasiconvex property on the component functions of the vector-valued objective function of robust counterpart (4) enables us to prove a similar result of Proposition 5.
Proposition 6
If \(\mathcal{X}\) is convex and the uncertainty is convex robust-counterpart suitable, the functions \(f_k\) are quasiconvex for \(k \in \{1, \ldots , p\}\), and their sum is also quasiconvex, then every efficient solution \({\bar{\mathbf {x}}}\) to robust counterpart (4) satisfies
where \(\mathbf {x^*(\mathbf {u})}\) is an optimal solution function to problem (6).
Proof
As in the proof of Proposition 5, let \(\bar{\mathbf {x}} \in E(\mathcal{X}_{RC})\) and let \(s^* = \max \limits _{\mathbf {u} \in \mathcal U} f_s(\mathbf {x^*}(\mathbf {u}))\) with
Proceeding as in the proof of Proposition 5, we define set \(\mathcal{P}({\bar{\mathbf {x}}})\) that is closed by the continuity of functions \(f_k\) for all \(k \in \{1,\ldots ,k\}\). Since these functions and their sum are quasiconvex, the sets \(\{\mathbf {x} \in \mathbb {R}^n: f_k(\mathbf {x}) \le f_k(\bar{\mathbf {x}})\}\) for \(k \in \{1,\ldots ,p\}\) and \(\{\mathbf {x} \in \mathbb {R}^n: f_s(\mathbf {x}) \le s^*\}\) are convex. Therefore \(\mathcal{P}({\bar{\mathbf {x}}})\) is the intersection of convex sets and is convex. Hence \(\mathcal{X} \cap \mathcal{P}({\bar{\mathbf {x}}})\) is a convex compact set.
Consider now problem (10), introduced in the proof of Proposition 5, that has the same uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) that is convex robust-counterpart suitable. Using a similar argument as in the end of the proof of Proposition 5, a contradiction to \(\bar{\mathbf {x}}\) being efficient can be reached. \(\square \)
Propositions 4 and 6 yield a similar result for convex robust-counterpart suitable uncertainty to Theorem 2. We omit the proof of the next theorem since it is identical to the one of Theorem 2.
Theorem 3
Let \(\mathcal{X}\) be convex, the uncertainty be convex robust-counterpart suitable, the functions \(f_k\) be quasiconvex for \(k \in \{1, \ldots , p\}\) and their sum be also quasiconvex, and \(\mathbf {x^*(\mathbf {u})}\) and \(f_s(\mathbf {x^*(\mathbf {u})})\) be optimal solution and value functions, respectively, to problem \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\}\). If \({\bar{\mathbf {x}}}\) is an efficient solution to robust counterpart (4) then \({\bar{\mathbf {x}}}\) is efficient to the instance (2) associated with \(\mathbf {u^*} \in \mathcal U\), where \(\mathbf {u^*}\) is an optimal solution to \( \max _{\mathbf {u} \in \mathcal{U}} f_s(\mathbf {x^*(\mathbf {u})})\). \(\square \)
Similar to Theorem 2, under the assumptions of Theorem 3, \({\bar{\mathbf {x}}}\) may not be strictly efficient to the instance (2) associated with \(\mathbf {u^*} \in \mathcal U\). Additionally, if the functions \(f_k\) for \(k \in \{1, \ldots , p\}\) are convex rather than quasiconvex, no assumption about their sum is needed in Proposition 6 and Theorem 3.
So far, uncertainty has only been considered in constraints (3), and each component function of the objective function \(\mathbf {f}\) of uncertain multiobjective optimization problem (1) is assumed to be deterministic. If, however, some component functions of \(\mathbf {f}\) are subject to uncertainty and the uncertain multiobjective optimization problem is formulated as
then the worst-case-oriented approach, commonly used in robust optimization, leads us to consider as the objective function in the robust counterpart
where, for \(\mathbf {x} \in \mathbb {R}^n\), \(\mathbf {F(x)}\) is the p-dimensional vector whose components are
Similarly to what was done for problem (1), we define the concepts of robust (strictly/weakly) efficient solutions and (weakly) nondominated outcomes of problem (12) through the (strictly/weakly) efficient solutions and (weakly) nondominated outcomes of its robust counterpart
Using p additional variables \(\beta _1,\ldots ,\beta _p\) and p additional constraints
the next proposition introduces an uncertain multiobjective optimization problem equivalent to problem (12), which has a deterministic objective function and uncertainty only in the constraints as in problem (1).
Proposition 7
Let \(\varvec{\beta } \in \mathbb {R}^p\) and associate with problem (12) the following uncertain multiobjective optimization problem
The following statements hold.
-
(i)
If \((\bar{\mathbf {x}},\bar{\varvec{\beta }})\) is robust (strictly/weakly) efficient to problem (14), then \(\bar{\mathbf {x}}\) is robust (strictly/weakly) efficient to problem (12).
-
(ii)
If \(\bar{\mathbf {x}}\) is robust (strictly/weakly) efficient to problem (12), then \((\bar{\mathbf {x}},\mathbf {F}(\bar{\mathbf {x}}))\) is robust (strictly/weakly) efficient to problem (14).
Proof
We first notice that if \(\mathbf {x}\) is feasible to robust counterpart (13), then \((\mathbf {x},\mathbf {F(x)})\) is feasible to the robust counterpart of uncertain multiobjective optimization problem (14)
Conversely, any feasible solution \((\mathbf {x},\varvec{\beta })\) to robust counterpart (15) has its \(\mathbf {x}\)-component feasible to robust counterpart (13). We prove the result with respect to efficiency to both robust counterparts, a similar argument works for strict efficiency and weak efficiency.
Let \((\bar{\mathbf {x}},\bar{\varvec{\beta }})\) be an efficient solution to robust counterpart (15), that is, \(\bar{\mathbf {x}}\) is feasible to robust counterpart (13) and \(\mathbf {F}(\bar{\mathbf {x}}) \leqq \bar{\varvec{\beta }}\). Suppose that \(\bar{\mathbf {x}}\) is not efficient to robust counterpart (13). There then exists \(\mathbf {x^*}\), feasible to robust counterpart (13), such that
Because \((\mathbf {x^*},\mathbf {F(x^*)})\) is feasible to robust counterpart (15) and outcome \(\mathbf {F(x^*)}\) dominates outcome \(\bar{\varvec{\beta }}\), the solution \((\bar{\mathbf {x}},\bar{\varvec{\beta }})\) then is not efficient to robust counterpart (15).
Consider now an efficient solution \(\tilde{\mathbf {x}}\) to robust counterpart (13). Suppose that \((\tilde{\mathbf {x}},\mathbf {F}(\tilde{\mathbf {x}}))\) is not efficient to robust counterpart (15). There then exists \((\mathbf {x'},\varvec{\beta }')\) such that \(\mathbf {x'}\) is feasible to robust counterpart (13) and \(\varvec{\beta }' \le \mathbf {F}(\tilde{\mathbf {x}})\). Because \(\mathbf {F(x')} \leqq \varvec{\beta }'\) by the feasibility of \((\tilde{\mathbf {x}},\mathbf {F}(\tilde{\mathbf {x}})\)) for problem (15), we deduce that outcome \(\mathbf {F(x')}\) dominates outcome \(\mathbf {F}(\tilde{\mathbf {{x}}})\), a contradiction. \(\square \)
It is worth noticing that if \((\bar{\mathbf {x}}, \bar{\varvec{\beta }})\) is robust (strictly) efficient to uncertain multiobjective optimization problem (14), then \(\bar{\varvec{\beta }} = \mathbf {F}(\bar{\mathbf {x}})\), because otherwise, by the constraints \(\mathbf {f}(\mathbf {x}, \mathbf {u}) - \bar{\varvec{\beta }} \in \mathbb {R}^p_{\leqq }\) for all \(\mathbf {u}\) in \(\mathcal{U}\), outcome \(\mathbf {F}(\bar{\mathbf {x}})\) would dominate outcome \(\bar{\varvec{\beta }}\). On the other hand, if \((\bar{\mathbf {x}},\bar{\varvec{\beta }})\) is robust weakly efficient to uncertain multiobjective optimization problem (14), the concept of a strictly nondominated outcome, together with the aforementioned constraints, then imply that \(\mathbf {F}(\bar{\mathbf {x}}) \leqq \bar{\varvec{\beta }}\) with at most \((p-1)\) strict inequalities. In Proposition 7, we imply that, without loss of generality, one may assume that the vector-valued objective function in problem (1) is not subject to any uncertainty. From now on, this assumption is always made when referring to an uncertain multiobjective optimization problem. We note here that Proposition 7 does not eliminate the need to study multiobjective problems with uncertainty in the objective functions. Not making use of Proposition 7 or even defining other robust counterpart problems may offer new insight into robust multiobjective optimization (Goberna et al. 2015; Witting et al. 2013, and others).
2.2 Methodology
Soyster (1973) was among the first to consider a robust-counterpart methodology to handle uncertainty in single-objective optimization problems, in what he called set-inclusive constraints.
Definition 5
If uncertainty set \(\mathcal{U}\) is the Cartesian product of n convex sets of \(\mathbb {R}^m\), that is, \(\mathcal{U} = \mathcal{U}_1 \times \cdots \times \mathcal{U}_n\) where \(\mathcal{U}_j \subseteq \mathbb {R}^m\) is convex for \(j \in \{1,\ldots ,n\}\), \(\mathbf {g(x,u)} = \sum _{j=1}^n x_j\mathbf {u_j}\) where \(\mathbf {u_j} \in \mathcal{U}_j\) for \(j \in \{1,\ldots ,n\}\), and \(\mathcal{K}\) is a convex set, then the uncertainty is called set-inclusive, now known as column-wise.
The feasible region of the optimization problem Soyster considered is
where the symbol \(+\) represents the Minkowski sum of sets. Soyster showed that \(\mathcal{X^S}\) is a convex set, and that if \(\mathcal{K}\) is a polyhedral set having the form \(\mathcal{K}(\mathbf {b}) = \{\mathbf {z} \in \mathbb {R}^m: \mathbf {z} \le \mathbf {b}\}\), for some \(\mathbf {b} \in \mathbb {R}^m\), then
where \(\bar{G} = \begin{bmatrix} \bar{g}_{ij} \end{bmatrix}\) is the \(m \times n\) matrix whose components are \(\bar{g}_{ij} = \sup \{u_{ij}: \mathbf {u_j} \in \mathcal{U}_j\}\) for all \(i \in \{1,\ldots ,m\}\) and \(j \in \{1,\ldots ,n\}\). Note that if some components of \(\mathbf {x}\) are nonnegative, one then needs to consider the infimum instead of the supremum in the corresponding components of \(\bar{G}\). Soyster also pointed out that if, in the definition of \(\mathcal{K}(\mathbf {b})\), one has \(z_i = b_i\) for some \(i \in \{1,\ldots ,m\}\), then the set \(\mathcal{U}_j\) can be omitted from the definition of \(\mathcal{X}^S\) whenever the ith component of \(\mathbf {u}_j\) takes more than one value. Solving a single-objective optimization problem with column-wise uncertainty and the set \(\mathcal{K}\) polyhedral therefore reduces to optimizing the objective function over polyhedron (16). This reduction clearly is independent of the objective function. Consequently, we obtain the following generalization of Soyster’s result to uncertain multiobjective optimization problem (1).
Theorem 4
Consider uncertain multiobjective optimization problem (1) with column-wise uncertainty, set \(\mathcal{K}(\mathbf {b})\) polyhedral, and \(\mathcal{X} \subseteq \mathbb {R}^p_{\geqq }\). Its robust (strictly/weakly) efficient set is identical to the robust (strictly/weakly) efficient set of the multiobjective optimization problem
\(\square \)
Soyster’s model is very conservative because it simultaneously combines the worst-case values for all the uncertain parameters. Later, Ben-Tal and Nemirovski (1998, 1999) followed a robust-counterpart-based approach for uncertain single-objective inequality-constrained problems with the so-called row-wise uncertainty in order to provide a less conservative model.
Definition 6
If \(\mathbf {g(x,u)}\) is an m-dimensional vector whose components are \(g_i(\mathbf {x},\mathbf {u^i})\) with \(g_i: \mathbb {R}^n \times \mathbb {R}^{r_i} \rightarrow \mathbb {R}\) and \(r_i \in \mathbb {Z}_+\) for all \(i \in \{1,\ldots ,m\}\), \(\mathcal{U}\) is the Cartesian product of m closed and convex sets of the spaces of \(\mathbf {u^i}\) (i.e., \(\mathcal{U} = \mathcal{U}_1 \times \ldots \times \mathcal{U}_m\) with \(\mathcal{U}_i \in \mathbb {R}^{r_i}\) for all \(i \in \{1,\ldots ,m\}\)), and \(\mathcal{K} = \mathbb {R}^m_\leqq \), then the uncertainty set \(\mathcal{U}\) is called row-wise.
With row-wise uncertainty, the robust counterpart of uncertain multiobjective optimization problem (1) then assumes the form
We wish to develop a connection between uncertain multiobjective optimization problem (1) with row-wise uncertainty and its robust counterpart (17). As mentioned earlier, the converse of Proposition 1 is not always true, that is, there might exist some uncertain multiobjective optimization problem with all its instances being feasible but whose robust counterpart is infeasible. Ben-Tal and Nemirovski (1998) provided some conditions for the converse of Proposition 1 to be true in the multiobjective setting as described in the following proposition [see, e.g., Theorem 2.1 in Ben-Tal and Nemirovski (1998)].
Proposition 8
Assume that \(g_i\) is convex and continuous in \(\mathbf {x}\) and affine in \(\mathbf {u^i}\) for all \(i \in \{1,\ldots ,m\}\) and \(\mathcal{X}\) is convex and compact. There exists an infeasible instance of uncertain multiobjective optimization problem (1) with row-wise uncertainty if and only if its robust counterpart (17) is infeasible. \(\square \)
Under the conditions of Proposition 8, row-wise uncertainty is convex robust-counterpart suitable. Moreover, provided the component functions of the objective function \(\mathbf {f}\) satisfy the quasiconvexity properties stated in Proposition 6, we obtain the following row-wise version of Theorem 3.
Corollary 2
Assume that \(g_i\) is convex and continuous in \(\mathbf {x}\) and affine in \(\mathbf {u^i}\) for all \(i \in \{1,\ldots ,m\}\), \(\mathcal{X}\) is convex and compact, and the functions \(f_k\) for all \(k \in \{1,\ldots ,p\}\) and their sum are quasiconvex. Let \(\mathbf {x^*(\mathbf {u})}\) and \(f_s(\mathbf {x^*(\mathbf {u})})\) be optimal solution and value functions, respectively, to problem \(\{P(\mathbf {u}, {\bar{\mathbf {x}}}), \mathbf {u} \in \mathcal{U}\}\). If \({\bar{\mathbf {x}}}\) is an efficient solution to robust counterpart (17) then \({\bar{\mathbf {x}}}\) is efficient to the instance (2) associated with \(\mathbf {u^*} \in \mathcal U\), where \(\mathbf {u^*}\) is an optimal solution to \( \max _{\mathbf {u} \in \mathcal{U}} f_s(\mathbf {x^*(\mathbf {u})})\). \(\square \)
Robust counterpart (17) of uncertain multiobjective optimization problem (1) with row-wise uncertainty is a semi-infinite problem and therefore is challenging to solve, in particular, it may be computationally prohibitive. In the remainder of this section, we show how robust counterpart (17) can be transformed into a more tractable problem while preserving the (strictly/weakly) efficient set.
For any \(i \in \{1,\ldots ,m\}\) and any \(\mathbf {x} \in \mathbb {R}^n\), let
be the worst-case value of the left-hand-side of ith constraint of robust counterpart (17) associated with \(\mathbf {x}\). Notice that since \(\mathcal{U}_i\) is a nonempty subset of a compact set for any \(i \in \{1,\ldots ,m\}\), \(V_i(\mathbf {x})\) is finite for any \(\mathbf {x} \in \mathcal{X}\). Consider the following bilevel optimization problem
and let \(\mathcal{X}_B \subseteq \mathbb {R}^n\) be its set of feasible solutions. From the definition of \(V_1(\mathbf {x}),\ldots ,V_m(\mathbf {x})\), we straightforwardly obtain the following result.
Proposition 9
\(\mathcal{X}_{RC} = \mathcal{X}_B\) \(\square \)
Bilevel optimization problem (19) has a finite number of lower-level constraints \(V_i(\mathbf {x}) \le 0\), namely m of them. Recall that the lower-level variables \(\mathbf {u}^i\) correspond to the uncertain parameters of uncertain multiobjective optimization problem (1), and the robust (strictly/weakly) efficient solutions to the latter, that is, the upper-level variables \(\mathbf {x}\), need to be independent of any specific \(\mathbf {u}^i\)-variable values. Therefore we make use of Lagrangian duality theory to reformulate problem (19) into another bilevel multiobjective problem whose lower-level constraints do not explicitly incorporate the variables \(\mathbf {u}^i\). According to this duality theory, under certain conditions, convex nonlinear programs are equivalent to their dual counterparts in the sense that their optimal objective functions values are equal (Bazaraa et al. 2013). Let \(i \in \{1,\ldots ,m\}\) and let
be the optimal objective value of a dual problem to the left-hand side of each lower-level constraints [i.e., to optimization problem (18)] associated with i, where \(\mathbf {v}^i \in \mathcal{D}_i(\mathbf {x}) \subseteq \mathbb {R}^{s_i}\) are the dual variables and \(\mathcal{D}_i(\mathbf {x})\) is their feasible set. By weak duality, we have \(V_i(\mathbf {x}) \le w(\mathbf {v}^i)\) for all \(\mathbf {v}^i \in \mathcal{D}_i(\mathbf {x})\). Moreover, if the dual gap is zero (i.e., \(V_i(\mathbf {x}) = W_i(\mathbf {x})\)), problems (18) and (20) form a strong-dual pair. Consider then the following bilevel optimization problem
and let \(\mathcal{X}_D \subseteq \mathbb {R}^n\) be its set of feasible solutions. A direct consequence of strong duality holding for all the lower-level constraints of bilevel optimization problem (19) clearly is the following.
Proposition 10
Assume problems (18) and (20) form a strong-dual pair for all \(i \in \{1\ldots ,m\}\). We have \(\mathcal{X}_{RC} = \mathcal{X}_D\). \(\square \)
The final step of our reformulation process for robust counterpart (17) is to eliminate the optimization problem in the lower-level constraints of bilevel optimization problem (21). This leads us to consider the following optimization problem
where \(\mathbf {v} = (\mathbf {v}^1,\ldots ,\mathbf {v}^m) \in \mathbb {R}^{s_1}\times \ldots \times \mathbb {R}^{s_m}\). Let \(\mathcal{X}_E \subseteq \mathbb {R}^n \times (\mathbb {R}^{s_1}\times \ldots \times \mathbb {R}^{s_m})\) denote the set of feasible solutions to optimization problem (22). We now show that the projection of \(\mathcal{X}_E\) onto \(\mathbf {x}\), hereafter denoted \({{\mathrm{proj}}}_{\mathbf {x}} \mathcal{X}_E\), corresponds exactly to \(\mathcal{X}_{RC}\). In other words, any feasible solution to robust counterpart (4) relates to a feasible solution to problem (22) having the same \(\mathbf {x}\)-variables and vice versa.
Proposition 11
Assume problems (18) and (20) form a strong-dual pair for all \(i \in \{1\ldots ,m\}\). We have \(\mathcal{X}_{RC} = {{\mathrm{proj}}}_{\mathbf {x}} \mathcal{X}_E\).
Proof
By Propositions 9 and 10, we only have to prove that \(\mathcal{X}_D = {{\mathrm{proj}}}_{\mathbf {x}} \mathcal{X}_E\). Let \(\bar{\mathbf {x}} \in \mathcal{X}_D\). For all \(i \in \{1,\ldots ,m\}\), let \(\bar{\mathbf {v}}^i\) denote any optimal solution to problem (20), that is, \(w_i(\bar{\mathbf {v}}^i) = W_i(\bar{\mathbf {x}}) \le 0\), the inequality coming from problem (21). Therefore \((\bar{\mathbf {x}},\bar{\mathbf {v}}^1,\ldots ,\bar{\mathbf {v}}^m)\) belongs to \(\mathcal{X}_E\). Consequently \(\mathcal{X}_D \subseteq {{\mathrm{proj}}}_{\mathbf {x}} \mathcal{X}_E\).
Conversely, let \((\tilde{\mathbf {x}},\tilde{\mathbf {{v}}}^1,\ldots ,\tilde{\mathbf {{v}}}^m) \in \mathcal{X}_E\). From the definition of problem (20) and the constraints of problem (22), we have \(W_i(\tilde{\mathbf {x}}) \le w_i(\tilde{\mathbf {v}}^i) \le 0\) for all \(i \in \{1,\ldots ,m\}\). Because \(\tilde{\mathbf {x}} \in \mathcal{X}\), we obtain \(\tilde{\mathbf {x}} \in \mathcal{D}\) and therefore \({{\mathrm{proj}}}_{\mathbf {x}} \mathcal{X}_E \subseteq \mathcal{X}_D\). \(\square \)
Considering problem (22) instead of robust counterpart (4) therefore guarantees the robust feasibility of the restriction to the decision space of any feasible solution to problem (22). In the next theorem, we examine the relationship between the (strictly/weakly) efficient sets to both robust counterpart (4) and problem (22). We prove that \(\bar{\mathbf {x}}\) is (strictly/weakly) efficient to robust counterpart (4) if and only if \((\bar{\mathbf {x}},\bar{\mathbf {v}})\) is (strictly/weakly) efficient to robust counterpart (22).
Theorem 5
Assume problems (18) and (20) form a strong-dual pair for all \(i \in \{1\ldots ,m\}\). We have
-
(i)
\(E(\mathcal{X}_{RC}) = {{\mathrm{proj}}}_{\mathbf {x}} E(\mathcal{X}_E)\),
-
(ii)
\({{\mathrm{\textit{s-E}}}}(\mathcal{X}_{RC}) = {{\mathrm{proj}}}_{\mathbf {x}} {{\mathrm{\textit{s-E}}}}(\mathcal{X}_E)\),
-
(iii)
\({{\mathrm{\textit{w-E}}}}(\mathcal{X}_{RC}) = {{\mathrm{proj}}}_{\mathbf {x}} {{\mathrm{\textit{w-E}}}}(\mathcal{X}_E)\),
where \(E(\mathcal{X}_{E})\), \({{\mathrm{\textit{s-E}}}}(\mathcal{X}_{E})\), and \({{\mathrm{\textit{w-E}}}}(\mathcal{X}_{E})\) are the efficient, strictly efficient, and weakly sets to problem (22), respectively.
Proof
By Propositions 9 and 10, we only have to prove that \(E(\mathcal{X}_{RC}) = {{\mathrm{proj}}}_{\mathbf {x}} E(\mathcal{X}_D)\). Notice that both problems (21) and (22) have the same objective function which is independent of the \(\mathbf {v}\)-variables. Therefore, the result follows directly from Proposition 11. \(\square \)
In Sect. 3 we make use of the results developed in this section to find robust efficient solutions to an uncertain multiobjective linear optimization problem arising in Internet traffic engineering.
3 An application to Internet traffic engineering
The Internet now appears as one of the main actors in everyone’s life. The omnipresence of network services and Internet applications has generated a massive increase in the Internet traffic which has also become more and more complex and dynamic. To cope with the challenges of Internet traffic growth and nature, network managers have focused on Internet traffic engineering which encompasses on one hand the measurement, modeling, characterization, and control of Internet traffic, and, on the other hand, the simultaneous optimization of network resource utilization and traffic performance (Awduche et al. 1999; Awduche 1999).
The architecture of the Internet corresponds to the interconnection of Autonomous Systems (ASes). Each AS is a collection of routers (i.e., nodes) and links owned and controlled by a single administrative entity (e.g., university, company, Internet Service Provider); by contrast, the Internet operates without a central administrative entity. The routing of Internet traffic specifies how the packets of information are routed to reach their destinations, and it is monitored by routing protocols. Many ASes may be involved in the routing paths, so a routing configuration determines how the traffic flow is managed within and between the ASes. The routing through the Internet is then performed hierarchically with each AS implementing its autonomous routing policies, the intradomain routing, and with the routing between ASes using mainly the Border Gateway Protocol (BGP), the interdomain routing. In this section, we only focus on the intradomain routing, because the AS’ administrative entity can determine how to configure its traffic routing with respect to the chosen routing protocol. To learn more about Internet routing optimization, we refer to Rexford (2006).
3.1 Intradomain robust routing
Over the last 15 years, intradomain traffic engineering has received much attention because it contributes to better management and performance of the Internet (Feldmann and Rexford 2001; Applegate and Cohen 2003; Casas 2010). Intradomain traffic engineering is mainly composed of two closely related aspects, the estimation of the traffic that needs to be routed and the design of the routing configurations.
The traffic that needs to be routed across an AS is usually aggregated into Origin-Destination (OD) pairs, where each pair consists of all the traffic having the same origin node and the same destination node (Casas 2010). The volume representation of traffic is described by a traffic matrix, wherein each entry is associated with an OD-pair and represents the cumulative volume of traffic transmitted from the origin to the destination. The traffic matrix has become extremely difficult to accurately estimate, mainly because of the significant cost of collecting traffic data and of the high complexity of analyzing these data. To bypass this difficulty, AS operators commonly assume that the traffic matrix belongs to a set \(\mathcal{U}\) which contains a wide range of possible traffic configurations, as initially proposed by Ben-Ameur and Kerivin (2005). The set \(\mathcal U\) can be designed based on traffic measurements and geographical and behavioral information, among others. Network operators favor implementing stable routing plans, that is, routing paths which remain the same despite traffic variations, because they are easier to manage and any routing modification may cause service disruptions and thus QoS deterioration. Intradomain robust routing therefore consists of determining, for each OD-pair, the routing paths that would permit to carry any traffic matrix in \(\mathcal U\) with respect to the network resources.
Several routing protocols, called Interior Gateway Protocols (IGP), can be considered within an AS. Open Shortest Path First (OSPF) and Intermediate System-Intermediate System (IS-IS) route evenly the traffic of each OD-pair on shortest paths based on link weights (Rexford 2006; Ben-Ameur and Gourdin 2003; Fortz and Thorup 2000). These IGP are highly distributed and scalable, but one of their main drawbacks is that they do not consider the characteristics of offered traffic and network capacity constraints when making routing decisions (Awduche 1999). This may result in unbalanced utilization of the network resources (e.g., congested versus underutilized links or routers). The Multi-Protocol Label Switch (MPLS) protocol, which appeared in 1999 (Awduche et al. 1999), allows to better control the routing through explicit paths and the specification of the proportions of the traffic of each OD-pair being routed along these paths. This more flexible routing protocol is very suitable when performing traffic engineering because it enables a better link capacity management and tends to prevent congestion. Because it has become unrealistic to keep upgrading the link capacities to cope with the faster growing Internet traffic, we consequently focus, in this section, on the intradomain robust routing based on MPLS or on similar routing protocols.
A single robust routing that would be optimal or efficient for all the traffic matrices in \(\mathcal U\) may not generally exist. An alternative, which is most often preferred by network operators, is to seek an oblivious robust routing, that is, a robust routing which has the minimum worst-case performance over the traffic matrix set \(\mathcal U\). The performance metric most commonly used to evaluate the performance of a routing consists of minimizing the Maximum Link Utilization (MaxLU), that is, the maximum, over all the links, of the ratio of the load present on the link to the capacity of the link. One of the benefits of this metric is that the lower the link utilization is, the better the network may support sudden traffic variations. This metric may lead to bad distributions of traffic loads, especially with heterogeneous link capacities, and therefore, may deteriorate some important QoS indicators such as the end-to-end delay and packet loss (Casas et al. 2009). From a QoS point of view, a more pertinent metric would be related to the path end-to-end delay which is defined as the sum of the delays on the links composing the path. The link delay is divided into the queuing delay and the propagation delay, the former being dependent on the link load and the latter being constant. Because of the queuing-delay component, dealing with end-to-end delay metrics leads to computationally difficult traffic engineering problems. As proposed and empirically verified by Casas et al. (2009) [see also Casas (2010)], an interesting alternative with respect to QoS performance is to consider the Mean Link Utilization (MeanLU), that is, the average link utilization. The MeanLU metric provides a more global performance and, when combined with a local-performance indicator such as MaxLU, leads to efficient robust routing configurations with respect to end-to-end delay. In their simulations (Casas et al. 2009) considered a single-objective robust optimization problem where both MaxLU and MeanLU were aggregated through a weighted sum. In the remainder of this paper, we study the intradomain robust routing problem from a multiobjective point of view by considering simultaneously the MaxLU and MeanLU metrics.
3.2 Robust multiobjective multicommodity flow problem
In this subsection we focus on the intradomain robust routing, yet it is worth mentioning that the upcoming mathematical models remain applicable, or can be easily adapted, to any type of network (or layer in a network), any type of link (i.e., unidirectional versus bidirectional), or any type of traffic (asymmetric versus symmetric), as long as the traffic is distributed throughout the network using an explicit routing protocol such as MPLS.
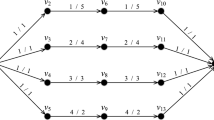
The AS is represented by a directed graph \(D = (V,A)\) where each vertex in V corresponds to a router and each arc in A corresponds to a link. Each arc a of A is associated with a positive value \(c_a\) which represents the installed (or available) capacity on the corresponding AS’ link. Each OD-pair is represented by a triplet (o, d, t), later called commodity, where \(o \in V\) is the origin vertex, \(d \in V \setminus \{o\}\) is the destination vertex, and \(t \in \mathbb {R}_{>}\) is the amount of traffic having to be routed from o to d across D. Let K be the set composed of all the commodities. The uncertain traffic matrix then is the specification of all the commodity volumes \(t_k\), for \(k \in K\), and the traffic matrix can be represented by a vector \(\mathbf {t}\) of \(\mathbb {R}_{>}^{|K|}\). The traffic matrix set \(\mathcal{U}\) therefore is a subset of \(\mathbb {R}^{|K|}\). For practical reasons, we assume that the uncertainty set \(\mathcal U\) is compact. Recalling that the desired routing configuration must be stable, that is, the selected routing paths must be independent of any traffic matrix in \(\mathcal U\), the intradomain robust routing problem then consists of selecting one or more paths in D for each commodity of K along which to carry the associated commodity traffic. These paths are chosen such that, whichever traffic matrix of \(\mathcal U\) is considered, (i) the flow (i.e., traffic) is always distributed in the same proportions on the commodity‘s paths for each commodity of K, and (ii) the total amount of flow carried on an arc never exceeds the arc capacity for each arc of A. In other words, we consider a multicommodity flow problem in D (Ahuja et al. 1993).
For each commodity k of K and each arc a of A, let \(x^k_a \in [0,1]\) represent the proportion of flow associated with commodity k and carried on arc a. For the sake of convenience, let
be the |K|-dimensional row vector composed of the flow variables associated with arc a of A, and let
be the |A|-dimensional column vector composed of the flow variables associated with commodity k of K. The flow-proportion variables \(x^k_a\) can be represented by a |K|-tuple \(\mathbf {x} = (\mathbf {x^{k_1}},\mathbf {x^{k_2}},\ldots ,\mathbf {x^{k_{|K|}}})\) of the |K|-ary Cartesian power of \(\mathbb {R}^{|A|}\) (i.e., \((\mathbb {R}^{|A|})^{|K|}\)). For each commodity k of K, we define the |V|-dimensional column vector \(\mathbf {b^k}\), called the supply/demand vector, as
As we deal with flow variables representing traffic proportions instead of traffic volumes, the origin (destination, respectively) vertex of a commodity supplies (demands, respectively) one unit, that is, the entire commodity traffic. For each commodity k of K, a vector \(\mathbf {x^k}\) is an \(o_kd_k\)-flow proportion if it satisfies the flow-conservation constraints
where \(\delta ^+(v)\) and \(\delta ^-(v)\) denote the set of arcs of A leaving and entering node v, respectively, and the flow-proportion constraints
Constraints (23) may be compactly written in vector and matrix notation as
where M is the \(|V| \times |A|\) incidence matrix of D. For each arc a of A, to comply with the capacity requirement (ii) given above, a vector \(\mathbf {x}_{\varvec{a}}\) needs to satisfy the capacity constraint
where \(\mathbf {t} = \begin{bmatrix} t_1&t_2&\ldots&t_{|K|} \end{bmatrix}^T\) denotes whichever traffic matrix of \(\mathcal U\) that might be considered.
To model both MaxLU and MeanLU criteria as linear functions, with each arc a of A we associate a variable \(p_a \in [0,1]\) which corresponds to the proportion of the arc capacity \(c_a\) being used to carry some flow, often called utilization, that is,
for any given traffic matrix \(\mathbf {t}\) of \(\mathcal U\). Let \(\mathbf {p}\) be the |A|-dimensional vector whose components are the \(p_a\)-variables. For the MaxLU that needs to be minimized, we define the function \(f_1: \mathbb {R}^{|A|} \rightarrow \mathbb {R}\) as
whereas for the MeanLU which also needs to be minimized, we define the function \(f_2: \mathbb {R}^{|A|} \rightarrow \mathbb {R}\) as
We can now formulate the intradomain robust routing problem as the following uncertain biobjective optimization problem

where \(\mathbf {t} \in \mathbb {R}^{|K|}\) and \(\mathbf {0}\) and \(\mathbf {1}\) are the all-zero and all-one vectors, respectively; we do not specify their dimensions because they are always clear from the context. In uncertain multiobjective optimization problem (25), the only uncertain constraints are the proportion equations (24). Because we aim to use the robust-counterpart approach developed in Sect. 2 to solve problem (25), being equality constraints, these proportion equations may appear to be an obstacle. In fact, they would require us to find robust feasible vectors \(\bar{\mathbf {x}}\) and \(\bar{\mathbf {p}}\) satisfying the restrictive condition that the uncertainty set \(\mathcal U\) is contained in the hyperplanes \(\{\mathbf {t} \in \mathbb {R}^{|K|}: \bar{\mathbf {x}}_{\varvec{a}} \mathbf {t} = \bar{p}_ac_a\}\) associated with all the arcs a of A. To avoid this, we substitute the capacity constraints
for proportion equations (24) in problem (25). As stated in the next proposition, any instance of the resulting uncertain biobjective optimization problem

has the same (strictly/weakly) efficient set as the corresponding instance of problem (25).
Proposition 12
Let \(\mathbf {t}\) be any traffic matrix in \(\mathcal U\). The (strictly/weakly) efficient set to the instance of problem (26) associated with \(\mathbf {t}\) equals the (strictly/weakly) efficient set to the instance of problem (25) associated with \(\mathbf {t}\).
Proof
Let \((25)_{\mathbf {t}}\) and \((26)_{\mathbf {t}}\) denote the instance of problems (25) and (26), respectively, associated with \(\mathbf {t}\) in \(\mathcal{U}\). We only prove for the efficient set, the cases of strictly or weakly efficient set are similar and left to the reader.
Consider any efficient point \((\mathbf {x^*},\mathbf {p^*})\) to \((26)_{\mathbf {t}}\), and suppose that there exists an arc, say \(\alpha \), of A such that \(\mathbf {x}_{\varvec{\alpha }}^*\mathbf {t} < p^*_\alpha c_\alpha \). Let \(\epsilon = p^*_\alpha c_\alpha - \mathbf {x}_{\varvec{\alpha }}^*\mathbf {t}\). The point \((\mathbf {x^*},\mathbf {p^*} - \epsilon \mathbf {e}_{\varvec{\alpha }})\) clearly is feasible to \((26)_{\mathbf {t}}\) and dominates \((\mathbf {x^*},\mathbf {p^*})\), where \(\mathbf {e}_{\varvec{\alpha }}\) is the vector whose \(\alpha \)-th component equals 1 and all its other components are zero. This contradicts the efficiency of \((\mathbf {x^*},\mathbf {p^*})\). All of the capacity constraints of \((26)_{\mathbf {t}}\) are binding at \((\mathbf {x^*},\mathbf {p^*})\), which therefore is feasible to \((25)_{\mathbf {t}}\).
Let \((\bar{\mathbf {x}},\bar{\mathbf {p}})\) be an efficient point to \((25)_{\mathbf {t}}\). This point also is feasible to \((26)_{\mathbf {t}}\). If \((\bar{\mathbf {x}},\bar{\mathbf {p}})\) was not efficient to \((26)_{\mathbf {t}}\), it would be dominated by a point \((\mathbf {x^*},\mathbf {p^*})\), which is efficient to \((26)_{\mathbf {t}}\). From what we proved above, \((\mathbf {x^*},\mathbf {p^*})\) would also be feasible to \((25)_{\mathbf {t}}\), a contradiction with the efficiency of \((\bar{\mathbf {x}},\bar{\mathbf {p}})\).
Consequently, any efficient point to \((25)_{\mathbf {t}}\) remains efficient to \((26)_{\mathbf {t}}\) and vice versa. \(\square \)
Problem (26) does not have row-wise uncertainty and therefore Proposition 8 is not applicable. To bypass this difficulty and fit into the robust-optimization framework, we consider a more conservative setting with row-wise uncertainty. So from now on, we deal with the following uncertain biobjective optimization problem

where \(\mathcal{U}_{rw}\) is the |A|-ary Cartesian power of \(\mathcal U\). Note that the traffic matrix \(\mathbf {t}_a\) considered in the capacity constraint of problem (27) associated with a specific arc a of A is independent of the traffic matrices considered in the capacity constraints associated with the other arcs of A, but all those traffic matrices belong to the same set \(\mathcal U\). This new row-wise-uncertainty model actually has its origin in the telecommunication industry before any connection with robust optimization was made. The robust counterpart of problem (27) was first considered by Ben-Ameur and Kerivin (2003, 2005, 2007) within the context of Virtual Private Network (VPN) services provided by telecommunication operators to reduce planning and management costs without any quality of service deterioration. Row-wise uncertainty has become a classical way to represent traffic uncertainty in telecommunication-network optimization problems ever since this VPN work in the early twentyfirst century.
Problem (27) corresponds to problem (1) where
the vector-valued function \(\mathbf {g}: (\mathbb {R}^{|A|})^{|K|} \times \mathbb {R}^{|A|}\times (\mathbb {R}^{|K|})^{|A|} \rightarrow \mathbb {R}^{|A|}\) is defined as
and set \(\mathcal K\) is the non-positive orthant \(\mathbb {R}^{|A|}_\le \). The structural elements of problem (27), that is, the deterministic constraints defined by \(\mathcal X\), the uncertain constraints defined by \(\mathbf {g}\) and \(\mathcal K\), and both objective functions \(f_1\) and \(f_2\) clearly satisfy Assumption 1. Consequently the robust counterpart of problem (27)
has a feasible set, denoted \(\mathcal{X}_{RC}^{IRR}\), that is compact by Proposition 2 and convex by the linearity of the capacity constraints for fixed \(\mathbf {t}_a\). As pointed out by Ben-Tal et al. (2009) [see, e.g., Section 1.2.1, observation C of Ben-Tal et al. (2009)], the set of robust feasible solutions to problem (27) remains intact when the uncertainty set \(\mathcal U\) is extended to either its convex hull or its closure. From now on, we may therefore assume that the uncertainty set \(\mathcal U\) is closed and convex.
Because the components \(g_i\) of the uncertain vector-valued function \(\mathbf {g}\) are linear for all \(i \in \{1,\ldots ,|A|\}\) and the deterministic set \(\mathcal{X}\) is defined by linear constraints, the convexity assumptions of Proposition 8 are met, and therefore, uncertainty \((\mathbf {g},\mathcal{K},\mathcal{U})\) is convex robust-counterpart suitable. In other words, robust counterpart (28) is feasible (i.e., \(\mathcal{X}_{RC}^{IRR} \not = \emptyset \)) if and only if all the instances of problem (27) associated with the traffic matrices in \(\mathcal{U}_{rw}\) are feasible. This computational tractability of UMOP (27) feasibility through Proposition 8 is in contrast with that of UMOP (26) which, based on Theorem 2.3 in Chekuri et al. (2007), is coNP-complete. Moreover, objective functions MaxLU and MeanLU are convex, and thus so is their sum. Because every convex function also is quasiconvex, from Corollary 2 we obtain the following.
Proposition 13
Any efficient solution to problem (28) is an efficient solution to the instance of problem (27) associated with a specific traffic matrix vector of \(\mathcal{U}_{rw}\). \(\square \)
Several types of uncertainty sets lead to computationally tractable representations of robust counterpart (28) which, by Theorem 5, enables the generation of the robust (strictly/weakly) efficient solutions to uncertain biobjective optimization problem (27). Ben-Tal et al. (2009) showed that when the uncertainty set \(\mathcal U\) is represented by a polyhedron, an ellipsoid, or more generally through some conic representation of a perturbation set, then the capacity constraints
would reduce to explicit systems of linear inequalities, conic quadratic inequalities, or linear matrix inequalities. The type of uncertainty set that appears the most pertinent for the intradomain robust routing problem is the polyhedral uncertainty set, that is,
where R is an \(s \times |K|\) matrix and \(\mathbf {d}\) is an s-dimensional vector, although the upcoming developments could be derived for ellipsoidal uncertainty as well. In fact, the polyhedral uncertainty set for the design, operation, and management of virtual private networks was first introduced by Ben-Ameur and Kerivin (2003) [see also Ben-Ameur and Kerivin (2005)]. Their model has replaced the long-time considered deterministic traffic matrix \(\bar{\mathbf {t}} = \begin{bmatrix} \bar{t}_1&\ldots&\bar{t}_{|K|} \end{bmatrix}^T\), where for each k in K, \(\bar{t}_k = \max \{t_k : \mathbf {t} \in \mathcal{U}\}\). Each component of the traffic matrix \(\bar{\mathbf {t}}\) represents the worst-case scenario in terms of volume of traffic for each corresponding OD-pair, and considering \(\bar{\mathbf {t}}\) in a robust routing problem would fit within Soyster’s approach described in Sect. 2. (It is important to note that \(\bar{\mathbf {t}}\) does not generally belong to the uncertainty set \(\mathcal U\).)
Let \((\bar{\mathbf {x}},\bar{\mathbf {p}})\) be in \((\mathbb {R}^{|A|})^{|K|} \times \mathbb {R}^{|A|}\). For each arc a of A, the worst-case value of the left-hand-side of capacity constraints (29) is the optimal value of the following linear-optimization problem
whose dual problem is
where \(\mathbf {z}_{\varvec{a}}\) is the s-dimensional row vector of dual variables associated with arc a. Both \(V_a(\bar{\mathbf {x}},\bar{\mathbf {p}})\) and \(W_a(\bar{\mathbf {x}},\bar{\mathbf {p}})\) are the optimal objective values of the linear-optimization problems that form a strong-dual pair. By Propositions 9, 10, and 11, the feasible set \(\mathcal{X}_{RC}^{IRR}\) to robust counterpart (28) is the projection onto the original variables \((\mathbf {x},\mathbf {p})\) of the feasible set, denoted \(\mathcal{X}_E^{IRR}\), to biobjective linear-optimization problem

Notice that all the constraints of problem (31) are deterministic, that is, they do not explicitly address the uncertain traffic matrix \(\mathbf {t}\). The size of reformulation (31) now is polynomial in |A|, |K|, and the number of rows in R. Applying Theorem 5 enables us to obtain the robust (strictly/weakly) efficient sets to uncertain intradomain robust routing problem (27).
It is well-known that a flow represented by arc values can be decomposed into a flow represented by path values (and possibly some cycle values). This flow decomposition permits us to obtain the robust (strictly/weakly) efficient routing paths for each OD-pair, but it does not allow us to handle routing constraints (e.g., hop constraints) which may be relevant in practice. To model the multicommodity flow problem, an alternative formulation based on path-flow variables, known as the arc-path formulation, could be considered (Ahuja et al. 1993). For each commodity k of K, let \(\mathcal{P}(k)\) be the set of all the elementary paths from \(o_k\) to \(d_k\) in D. Besides the \(x_a^k\)-variables previously introduced, for each path p of \(\mathcal{P}(k)\), let \(x_p \in [0,1]\) represent the proportion of flow associated with commodity k and carried on path p. Flow-conservation constraints (23) could be replaced by the constraints
together with
Note that the flow variables \(x_a^k\) are not necessary in the arc-path formulation, yet we keep them for the sake of clarity and simplicity when dealing with capacity constraints (29). Despite the significantly increased number of variables, capacity constraints (29) remain the only ones with uncertainty. Therefore, as long as some column-generation technique can be applied to efficiently manage the large number of \(x_p\)-variables, an arc-path formulation for the intradomain robust routing problem can be handled similarly to problem(27).
Obviously, problem (27) and its transformation to problem (31) is not limited to the objective functions MaxLU and MeanLU, and we could have considered any other objective functions, even nonlinear or nonconvex ones. For instance, we could have minimized the routing cost as in Ben-Ameur and Kerivin (2005) or the end-to-end path queuing delay as in Casas (2010). The strength of our approach lies in the fact that the reformulation of robust counterpart (28) into deterministic problem (31) does not depend on the type or number of objective functions.
3.3 Solution method
Many methods have been proposed for solving multiobjective optimization problems (Ehrgott 2005). For biobjective problems with linear constraints and objectives, one of the most effective and simplest methods consists of applying the parametric simplex algorithm (Ehrgott 2005). To linearize the MaxLU objective in problem (31), we introduce the variable \(p_{max} \in [0,1]\), the constraints
and substitute \(f_1^\prime (p_{max}) = p_{max}\) for the first objective \(f_1(\mathbf {p}) = \max \{p_a: a \in A\}\). We therefore obtain the following biobjective linear optimization problem
It is straightforward that the projection of the feasible-solution set to problem (33) onto \((\mathbf {x},\mathbf {p},\mathbf {z})\) is nothing but the feasible-solution set to problem (31). This immediately implies that the (strictly/weakly) efficient solutions to the latter problem can be obtained through solving the former one.
In multiobjective linear optimization problems, all efficient solutions have the same property of being properly efficient. Different definitions of proper efficiency were introduced by Benson, Borwein, Geoffrion, and Kuhn and Tucker [see Ehrgott (2005)], and all these definitions appear to be equivalent when dealing with multiobjective linear optimization problems. We only define proper efficiency in Geoffrion’s sense (Geoffrion 1968) because it carries the essence of avoiding having to deal with “unfair” efficient solutions for which a marginal gain of some objective could be made arbitrarily large with respect to each of the other objective losses.
Definition 7
A feasible solution \((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) to problem (33) is called properly efficient in Geoffrion’s sense if
-
(i)
it is efficient
-
(ii)
there exists a real number \({\varOmega }> 0\) such that for every feasible solution \((\mathbf {x},\mathbf {p},\mathbf {z},p_{max})\)
-
(a)
satisfying \(p_{max} < \hat{p}_{max}\), one has \(f_2(\hat{\mathbf {p}}) < f_2(\mathbf {p})\) with
$$\begin{aligned} \frac{\hat{p}_{max} - p_{max}}{f_2(\mathbf {p}) - f_2(\hat{\mathbf {p}})} \le {\varOmega }, \end{aligned}$$ -
(b)
or satisfying \(f_2(\mathbf {p}) < f_2(\hat{\mathbf {p}})\), one has \(\hat{p}_{max} < p_{max}\) with
$$\begin{aligned} \frac{f_2(\hat{\mathbf {p}}) - f_2(\mathbf {p})}{p_{max}-\hat{p}_{max}} \le {\varOmega }. \end{aligned}$$
-
(a)
Proper efficiency for the intradomain robust routing problem therefore means that the trade-off between the local performance indicator (i.e., \(p_{max}\)) and the global QoS performance indicator (i.e., \(\frac{1}{|A|}\sum \nolimits _{a \in A}p_a\)) is bounded from above. From a computational point of view, all the properly efficient solutions of a multiobjective convex optimization problem can be obtained by minimizing a weighted sum of the objectives, provided the weights are positive (Geoffrion 1968). Moreover, for multiobjective linear optimization problems, Isermann (1974) proved that all efficient solutions are properly efficient in Geoffrion’s sense. Consequently, to find all the (properly) efficient solutions to problem (33) we can convert it into the following parametric linear optimization problem
where \(\mathcal {\lambda }\) is a scalar parameter in [0, 1]. The following theorem summarizes the equivalence relationships between the optimal solutions to parametric linear optimization problem (34) and the (strictly/weakly/properly) efficient solutions to biobjective linear optimization problem (33) (Ehrgott 2005).
Theorem 6
Let \((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) be a feasible solution to problem (34).
-
(i)
\((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is (properly) efficient to problem (33) if and only if there exists \(\lambda > 0\) such that \((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is an optimal solution to problem (34).
-
(ii)
\((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is strictly efficient to problem (33) if and only if there exists \(\lambda \ge 0\) such that \((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is the unique optimal solution to problem (34).
-
(iii)
\((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is weakly efficient to problem (33) if and only if there exists \(\lambda \ge 0\) such that \((\hat{\mathbf {x}},\hat{\mathbf {p}},\hat{\mathbf {z}},\hat{p}_{max})\) is an optimal solution to problem (34). \(\square \)
The parametric simplex algorithm for biobjective linear optimization problems (Ehrgott 2005) can be used to solve problem (34). This algorithm proceeds, for a fixed value of \(\lambda \), as the classical simplex algorithm (Dantzig 1963) and scans the interval [0, 1] to find the critical values of \(\lambda \) (i.e., those which would make a current optimal basis no longer optimal) as follows:
-
(i)
look for an optimal basis for problem (34) with \(\lambda = 1\);
-
(ii)
find the largest value of \(\lambda \), lower than the current one, that would lead to a new basis becoming optimal.
This second step is repeated until no new value of \(\lambda \) is found. The algorithm then outputs a sequence of \(\lambda \)-values \(1=\lambda _1> \lambda _2> \ldots > \lambda _\ell \ge 0\), \(\ell \ge 2\), such that the optimal basis found for \(\lambda = \lambda _k\) remains optimal for \(\lambda \in (\lambda _{k+1},\lambda _k]\), for all \(k \in \{1,\ldots ,\ell -1\}\). The (weakly) nondominated outcomes of problem (34) can be easily found by computing the images of the (weakly) efficient points in the objective space.
Given an optimal basis \(\mathcal{B}_k\) for problem (34) with respect to some given critical value \(\lambda ^k\), \(k \in \{1,\ldots ,\ell -1\}\), let \(\bar{\mathbf {c}^1}\) and \(\bar{\mathbf {c}^2}\) be the reduced-cost vectors associated with objective functions \(f_1\) and \(f_2\), respectively. If \(\mathcal{N}_k\) denotes the set of nonbasic variables associated with \(\mathcal{B}_k\), the next critical value \(\lambda _{k+1}\) is obtained by solving
where \(\mathcal{I}^k = \{j \in \mathcal{I}^k: \bar{c}^2_j < 0, \bar{c}^1_j \ge 0\}\).
In the next section, we present the numerical work on solving intradomain uncertain biobjective routing problem (27) where associated robust counterpart (28) is reformulated into (34) and then solved using the preceding parametric simplex algorithm. In particular, we discuss the data, the numerical issues encountered, and the results obtained. We also show how the results can support a decision making process in the telecommunication industry.
4 Computational experience
4.1 Network data
In our experiments we use the Abilene Network (Fig. 1) with its topology and capacities as of April 2003 (Abilene Backbone Network 2003). The Abilene Network is composed of 12 Points of Presence (PoPs) across the USA connected by 15 high-speed optical links (i.e., 14 OC-192Footnote 1 lines and 1 OC-48.Footnote 2 line) (Note that Atlanta has two PoPs with the OC-48 line connecting it to Indianapolis.) The Abilene Network then corresponds to a directed graph \(D=(V, A)\), having 12 vertices and 30 arcs.
All the possible OD-pairs among the 12 PoPs are considered, which gives a set K composed of 132 commodities to route through the Abilene Network. The volumes for the commodities are not precisely known, yet 24 real observational data sets were compiled by Zhang and are available online (Zhang 2004). In the data set, Zhang (2004) provides a routing matrix for the Abilene Network which corresponds to the coefficient matrix R in the linear system defining the uncertainty set \(\mathcal {U}\) as in definition (30). The routing matrix has \(|A|=30\) rows and \(|K|=132\) columns. The right-hand-side vector \(\mathbf{d}\) defining \(\mathcal {U}\) is an |A|-dimensional vector whose components represent the largest observed volume of traffic carried on each arc as reported by Zhang (2004).
4.2 Numerical difficulties
Several difficulties appeared during the computational work. First, parametric linear optimization problem (34) is a highly degenerate linear program having 3960 \(\mathbf{x}\)-variables, 30 t-variables, and 900 \(\mathbf{z}\)-variables for a total of 4890 variables. For some test cases, there were at least 200 bases representing the same basic feasible solution. A high level of numerical precision was required to insure that the degeneracy did not lead to cycling.
Second, note that the decision space of problem (31) has dimension of almost 5000, but the objective space has dimension of 2. When solving problem (34), multiple efficient basic feasible solutions to problem (31) are mapped to the same nondominated outcomes in the objective space. This phenomenon is known as collapsing between the decision space and the objective space (Dauer 1987; Sebo 1981). Computationally, as the algorithm visits adjacent efficient extreme points in the decision space, it may be stationary in the objective space.
Third, different weights \(\lambda \) in problem (34) yield the same nondominated outcomes to problem (31), which we discuss below.
4.3 Results and analysis
The routing matrix R associated with the network and the vectors \(\mathbf{d}\) associated with each of the 24 data sets (Zhang 2004) were applied to parametric linear optimization problem (34) and solutions were computed using the CPLEX 12.0 solver (IBM 2012). The obtained solutions are (strictly/weakly) efficient to problem (31), and also to robust counterpart (28), and therefore they are robust (strictly/weakly) efficient solutions to uncertain problem (27). Based on Proposition 13, these solutions are also efficient to some instances of problem (27). The images of these solutions being nondominated outcomes to problem (31) (and also robust nondominated outcomes to problem (27) and to some of its instances), are depicted in several figures for various representative data sets from among the 24 sets and under different assumptions.
In each figure, the nondominated sets associated with particular data sets can be compared against each other or the nondominated outcomes within each set can be analyzed. In the former case, the information about the dependence of network utilization on traffic conditions can be explored. In the latter case, given specific traffic conditions, trade-offs between nondominated outcomes can be quantified.
Figure 2 presents the nondominated outcomes of problem (31) obtained for seven data sets. For each data set, the robustness of each nondominated outcome is reflected in the fact that this outcome remains feasible for any realizable traffic matrix. Additionally, decison maker’s confidence can increase knowing that this outcome is also nondominated for some traffic matrix. As mentioned above, the utilization of the network is highly dependent on the traffic matrix of a given data set. For example, comparing data sets 1 and 4, we see that the largest maximum utilization for the robust nondominated outcomes vary from around 0.45 to 1. This observation demonstrates that the network is more heavily utilized under the traffic conditions of data set 4 than it is under the conditions of data set 1, thus in the former traffic conditions, the network will be less adaptable in the case of a link failure or other QoS degradation.
Table 1 displays the results obtained for selected data sets. The first column of Table 1 presents the distinct nondominated outcomes to problem (31). The values of the objective functions at the nondominated outcomes reveal by how much one objective can be improved, while the other must deteriorate when moving from one outcome to an adjacent one. The ratio between these values is referred to as a the trade-off associated with two adjacent nondominated outcomes (Eskelinen and Miettinen 2012) which may help the decision maker to choose between the two outcomes. The second and third columns present the \(\lambda \)-interval over which the nondominated outcome resulted as the image of the optimal solutions of parametric linear optimization problem (34).
The meaning of the weights \(\lambda \) and \(1-\lambda \) when generating the nondominated set with the weighted-sum method has been examined in the literature very well. Among others, the reader is referred to Choo et al. (1999) for many interpretations of the weights which could also be applied in the context of Internet routing. Below we continue to analyze the results, focusing on specific features characteristic only to the presented model of Internet routing. Note that some of the \(\lambda \)-intervals are much larger than others. Consider, for example, the intervals \(\dagger \) and \(\ddagger \) associated with data set 4. The large interval [0.934185, 0.285714] and the small interval [0.276217, 0.25] are associated with two adjacent nondominated outcomes. Here, we explore what changes in the network caused the algorithm to move from a solution that is preferred for the largest \(\lambda \)-interval, \(\dagger \), to a solution preferred for the smallest \(\lambda \)-interval, \(\ddagger \). This change in efficient solutions is characterized in the network by both gains and losses of utilization, not necessarily in equal amounts. Table 2 reports these two nondominated outcomes and the related changes of arc utilization \(\mathbf {p}\) associated with each arc in the network carrying some traffic. Note that the arcs presented in Table 2 are those whose utilization changes due to moving from one nondominated outcome to the other. Utilization is lost on the Seattle to Denver cycle (arcs 10 and 27), the Atlanta-1 to Washington D.C. link (arc 5), the Denver to Kansas City link (arc 8), and the Houston to Atlanta-1 link (arc 11). Utilization is gained on the Sunnyvale to Denver cycle (arcs 9 and 24), the Chicago to Indianapolis link (arc 6), and the New York to Washington D.C link (arc 23). The changes show a shift away from Atlanta-1 and significant differences in the network usage around Denver. This could be explained by the decreased preference on minimizing the maximum utilization and simultaneous increased preference on minimizing the average utilization.
Comparing the arc utilizations for the two nondominated outcomes, we observe that for the nondominated outcome associated with the largest \(\lambda \)-interval, \(\dagger \), all utilizations are in the interval (0.58, 0.86). Comparatively, the utilizations of the nondominated outcome associated with the smallest \(\lambda \)-interval, \(\ddagger \), are in the interval (0, 0.96). Due to the robustness, these utilizations guarantee that the network will be operational for every realizable traffic demand. However, the first network utilization plan is more balanced and may be preferred over the other.
Consider the nondominated outcome \((f_1^\prime (p_{max}), f_2(\mathbf{p})) = (1, 0.379885)\) obtained from data set 4 from \(\lambda \)-interval [0.249606, 0]. Table 3 reports the arc utilization \(\mathbf {p}\) associated with each arc in the network for this outcome. Based on the arc utilization here, the Atlanta-2 to Atlanta-1 link (arc 2), the Atlanta-1 to Washington D.C. link (arc 5), the Denver to Sunnyvale link (arc 9) and the New York to Washington D.C. link (arc 23) emerge as the most important because they are either at their full capacity or totally unused. These arcs are shown in Fig. 3. The arcs at full capacity would be critical arcs to maintain because the loss of one due to failure would have a great effect on network quality. On the other hand, arcs not being used can fail with no penalty.
As our stated goal is to solve the intradomain robust routing problem and to select one or more paths in D for each commodity to travel, we recall that every point \((f_1^\prime (p_{max}), f_2(\mathbf{p}))\) in the objective space has a pre-image \((\mathbf {x},\mathbf {p},\mathbf {z}, p_{max})\) in the decision space that represents the efficient path(s) in the network for each OD-pair. While Table 3 and Fig. 3 only report the values of \(\mathbf {p}\) for the nondominated outcome (1, 0.379885), the vector \(\mathbf {x}\) from the pre-image can be used to construct the exact efficient path(s) on which a given OD-pair will travel.
We have assumed, to this point, that all of the arcs may be using the full capacity. Now we explore the solutions in which only a fixed proportion of the capacity, but the same proportion across all arcs in the network, is available for all arcs. Figures 4, 5, and 6 show the nondominated outcomes when the network capacity has been reduced to 90, 70, and 50%, respectively. Note that as the available capacity decreases, the overall utilization of the network increases because the nondominated outcomes move in the upper-right direction. Data sets 4 and 10 are not shown in Fig. 5 due to infeasibility. Similarly, data sets 4, 7, 8, and 10 are not shown in Fig. 6 due to infeasibility.
As was the case with the full capacity network, the traffic matrices making up the data sets in the upper right-hand region of Figs. 4, 5, and 6 utilize more of the network and are thus going to represent realizations that are less adaptable in the case of changes in the network architecture.
Finally, we explore the solutions in which only a fixed proportion of the capacity, but possibly a different proportion for each arc in the network, is available for each arc. These capacities are generated as uniform random variables in the interval (0.5, 0.9). The same vector of random proportions is used for all data sets to allow for accurate comparisons. Figure 7 shows the nondominated outcomes when the network capacity has been reduced by a random amount between 50 and 90%. Data sets 4 and 10 are not shown in Fig. 7 due to infeasibility. This case is important to consider as it can be interpreted as mimicking the effects of degradation on different parts of the network.
Comparing Figs. 5 and 7, we note that for most data sets randomly decreasing the network capacity by 50 to 90% is approximately the same as reducing the capacity by 70%. Note that nondominated outcomes of data set 14 in the case of random decreases in the network capacity, Fig. 7, are dominated by the nondominated outcomes generated in the case of a 70% reduction is capacity, Fig. 5. Because this dominance appears clearly in only this data set, it is likely due to the nature of the random capacity selection.
Numerical results for data set 1 with varying proportions of available capacity are presented in Table 4. Figure 8 depicts the robust nondominated outcomes reported in Table 4.
Data sets 4 and 10, which are included in Table 1, are not evaluated here because neither data set is feasible if the available capacity is reduced below 90%. As expected, the efficient link utilizations increase as the arc capacity decreases. It is interesting to note that the \(\lambda \)-intervals are fairly consistent regardless of the available capacity. Further, as expected, the nondominated outcomes for the capacity reduced to 70% are approximately equal to the nondominated outcomes for the randomly reduced capacity.
It is of note that when considering the cases where the capacity across the network is uniformly restricted (e.g., 90, 70%, and 50% capacity) there is a similar number of \(\lambda \)-intervals associated with the nondominated outcomes. Furthermore, these intervals are fairly consistent, regardless of the percentage (i.e., within 3/100 in all cases except one). In the case of random capacity, a larger number of \(\lambda \)-intervals were generated. This may be due to the more drastic fluctuations in the arc capacities.
5 Conclusion
This paper provides a theoretical study of robust multiobjective optimization by verifying that the techniques of robust single objective optimization remain valid in the case of a vector-valued objective function. For the column-wise uncertainty of Soyster (1973), we obtained an immediate generalization to the multiobjective case. For the the row-wise uncertainty model of Ben-Tal and Nemirovski (1999) and under some conditions, we showed that robust efficient solutions to the original uncertain problem are also efficient to specific instances of this problem. We presented a methodology to compute the robust efficient solutions by computing the efficient solutions to the robust counterpart associated with the original uncertain problem. While the relationship between the uncertain problem and its instances pertains only to the efficient solutions, the methodology for computing the solutions to the robust counterpart is also valid for its strictly/weakly efficient solutions.
The developed approach was then applied to Internet routing, in particular, to robust intradomain routing in the presence of an explicit routing protocol. It was necessary to apply robust multiobjective optimization here because of the inaccuracy of estimating Internet traffic, which is caused by the cost of data collection and the complexity of data analysis. The uncertain intradomain routing problem was formulated as a biobjective multicommodity flow problem by minimizing the maximum utilization of any link and the mean utilization of all links while the uncertainty originated from the amount of traffic in the network. The associated biobjective counterpart problem was then solved for its efficient solutions using the parametric simplex algorithm. These solutions are the robust efficient solutions to the original uncertain problem and, based on our theoretical results, are also efficient solutions to the instances associated with specific realizations of the amount of traffic in the network. Finally, we presented the results on an existing network, the Abilene Network, and discussed their relevance to decision making.
There are many opportunities to continue this work. These opportunities fall into five categories: the current model, the uncertainty set, the multiobjective optimization problem, the solution methodology, and the application. For the current uncertain multiobjective model with the row-wise uncertainty of Ben-Tal and Nemirovski (1999), results for strictly/weakly efficient sets are needed. A key assumption of our work is that all of the uncertainty occurs in the constraints. However, it may be of interest to maintain the uncertainty at the level of the objective function. Other types of uncertainty sets may be considered to offer other theoretical results. These types of sets include conic quadratic sets or sets of linear matrix inequalities, as both types of sets have been associated with the necessary concept of duality used in this paper. Additionally, we may endeavor to study different sets of objective functions, including the previously mentioned path end-to-end delay. A natural research extension is to study uncertain multiobjective optimization problems with three or more objective functions. Computationally, the work of Dauer (1987) and others could be incorporated into our approach to identify the extreme points and edges of the efficient set (in the decision space) that are necessary to define the nondominated set (in the objective space), potentially decreasing the complexity of the solution technique in terms of reducing the amount of degeneracy (as the dimension of the decision space may still be quite large). We could also engage in applications in other areas of robust Internet routing such as interdomain routing or routing with an implicit protocol, or, more generally, other domains of human activity.
Notes
Optical Carrier with a data rate of 9953.28 Mbit/s, that is, 10 Gbit/s.
Optical Carrier with a data rate of 2488.32 Mbit/s, that is, 2.5 Gbit/s.
References
Abilene Backbone Network. (2003). Internet2. http://www.internet2.edu/
Ahuja, R. K., Magnanti, T. L., & Orlin, J. B. (1993). Network flows: Theory, algorithms, and applications. Englewood Cliffs, NJ: Prentice Hall.
Applegate, D., & Cohen, E. (2003). Making intra-domain routing robust to changing and uncertain traffic demands: Understanding fundamentals tradeoffs. In SIGCOMM’03 (pp. 313–324).
Altin, A., Belotti, P., & Pinar, M. Ç. (2010). OSPF routing with optimal oblivious performance ratio under polyhedral demand uncertainty. Optimization and Engineering, 11(3), 395–422.
Awduche, D. (1999). MPLS and traffic engineering in IP networks. In IEEE communications magazine (pp. 42–47).
Awduche, D., Malcolm, J., Agogbua, J., O’Dell, M., & McManus, J. (1999). Requirements for traffic engineering over MPLS. Internet Engineering Task Force, Request for Comments 2702. http://www.ietf.org/rfc/rfc2702.
Bazaraa, M. S., Sherali, H. D., & Shetty, C. M. (2013). Nonlinear programming: Theory and algorithms. New York: Wiley.
Belotti, P., & Pinar, M. Ç. (2008). Optimal oblivious routing under linear and ellipsoidal uncertainty. Optimization and Engineering, 9, 257–271.
Ben-Ameur, W. (2007). Between fully dynamic routing and robust stable routing. In Proceedings of DRCN.
Ben-Ameur, W., & Gourdin, E. (2003). Internet routing and related topology issues. SIAM Journal on Discrete Mathematics, 17, 18–49.
Ben-Ameur, W., & Kerivin, H. (2003). New economical virtual private networks. Communications of the ACM, 46, 69–73.
Ben-Ameur, W., & Kerivin, H. (2005). Routing of uncertain traffic demands. Optimization and Engineering, 6, 283–313.
Ben-Ameur, W., & Kerivin, H. (2007). Method and system for determining the parameters of a data transmission network for creating, in that network, a virtual private network. European Patent EP1355449 (issued on February 28, 2007).
Ben-Ameur, W., Ouorou, A., & Zotkiewicz, M. (2012). Robust routing in communication networks. In R. Mahjoub (Ed.), Progress in Combinatorial Optimization (pp. 353–389). New York: Iste & Wiley.
Ben-Tal, A., El Ghaoui, L., & Nemirovski, A. (2009). Robust optimization. Princeton, NJ: Princeton Academic Press.
Ben-Tal, A., & Nemirovski, A. (1998). Robust convex optimization. Mathematics of Operations Research, 23, 769–805.
Ben-Tal, A., & Nemirovski, A. (1999). Robust solutions of uncertain linear programs. Operations Research Letters, 25, 1–13.
Bertsimas, D., Brown, D., & Caramanis, C. (2011). Theory and applications of robust optimization. SIAM Review, 53(3), 464–501.
Bertsimas, D., & Sim, M. (2004). The price of robustness. Operations Research, 52(1), 35–53.
Bertsimas, D., & Sim, M. (2006). Tractable approximations to robust conic optimization problems. Mathematical Programming, 107, 5–36.
Bokrantz, R., & Fredriksson, A. (2014). Necessary and sufficient conditions for Pareto efficiency in robust multiobjective optimization. Preprint, arXiv:1308.4616.
Casas, P. (2010). Statistical analysis of network traffic for anomaly detection and quality of service provisioning. Ph.D. Thesis, École Nationale Supérieure des Télécommunications de Bretagne, Brest, France.
Casas, P., Larroca, F., & Vaton, S. (2009). Robust routing mechanism for intradomain traffic engineering in dynamic networks. In Proceedings of Latin American network operations and management symposium (LANOMS) (pp. 23–32).
Chekuri, C., Oriolo, G., Scutellá, M. G., & Shepherd, F. B. (2007). Hardness of robust network design. Networks, 50(1), 50–54.
Choo, E. U., Schoner, B., & Wedley, W. C. (1999). Interpretation of criteria weights in multicriteria decision making. Computers and Industrial Engineering, 37(3), 527–541.
Dantzig, G. (1963). Linear programming and extensions. Princeton, NJ: Princeton University Press.
Dauer, J. (1987). Analysis of the objective space in multiple objective linear programming. Journal of Mathematical Analysis and Applications, 125(2), 579–593.
Deb, K., & Gupta, H. (2005). Searching for robust Pareto-optimal solutions in multi-objective optimization. In C. A. Coello, A. Hernández Aguirre, & E. Zitzler (Eds.), Evolutionary multi-criterion optimization (pp. 150–164). Berlin: Springer.
Deb, K., & Gupta, H. (2006). Introducing robustness in multi-objective optimization. Evolutionary Computation, 14(4), 463–494.
Dellnitz, M., & Witting, K. (2009). Computation of robust Pareto points. International Journal of Computing Science and Mathematics, 2(3), 243–266.
Ehrgott, M. (2005). Multicriteria optimization. Berlin: Springer.
Ehrgott, M., Ide, J., & Schöbel, A. (2014). Minmax robustness for multiobjective optimization problems. European Journal of Operations Research, 239, 17–31.
El-Ghaoui, L., & Lebret, H. (1997). Robust solutions to least-square problems to uncertain data matrices. SIAM Journal on Matrix Analysis and Applications, 18, 1035–1064.
Eskelinen, P., & Miettinen, K. (2012). Trade-off analysis approach for interactive nonlinear multiobjective optimization. OR Spectrum, 34, 803–816.
Feldmann, A., & Rexford, J. (2001). IP network configuration for intradomain traffic engineering. IEEE Network, 15, 46–57.
Fiacco, A. (1983). Introduction to sensitivity and stability analysis in nonlinear programming. volume 165 of Mathematics in Science and Engineering, Cambridge: Academic Press.
Fliege, J., & Werner, R. (2014). Robust multiobjective optimization and applications in portfolio optimization. European Journal of Operations Research, 234, 422–433.
Fortz, B., & Thorup, M. (2000). Internet traffic engineering by optimizing OSPF weights. Proceedings of IEEE INFOCOM, 2000, 519–528.
Geoffrion, A. M. (1968). Proper efficiency and the theory of vector maximization. Journal of Mathematical Analysis and Applications, 22(3), 618–630.
Goberna, M. A., Jeyakumar, V., Li, G., & Vicente-Pérez, J. (2015). Robust solutions to multi-objective linear programs with uncertain data. European Journal of Operational Research, 242(3), 730–743.
Gunnar, A., & Johansson, M. (2011). Robust load balancing under traffic uncertainty–tractable models and efficient algorithms. Telecommunication Systems, 48(1–2), 93–107.
Hijazi, H., Bonami, P., & Ouorou, A. (2013). Robust delay-constrained routing in telecommunications. Annals of Operations Research, 206(1), 163–181.
Hu, J., & Mehrotra, S. (2012). Robust and stochastically weighted multiobjective optimization models and reformulations. Operations Research, 60(4), 936–953.
Iancu, D. A., & Trichakis, N. (2013). nondominated efficiency in robust optimization. Management Science, 60(1), 130–147.
IBM ILOG CPLEX Optimizer. (2012). http://www-01.ibm.com/software/integration/optimization/cplex-optimizer/.
Ide, J., & Schöbel, A. (2015). Robustness for uncertain multi-objective optimization: A survey and analysis of different concepts. OR Spectrum, 38(1), 235–271.
Isermann, H. (1974). Proper efficiency and the linear vector maximum problem. Operations Research, 22(1), 189–191.
Klamroth, K., Köbis, E., Schöbel, A., & Tammer, C. (2013). A unified approach for different concepts of robustness and stochastic programming via non-linear scalarizing functionals. Optimization, 62(5), 649–671.
Köbis, E., & Tammer, C. (2012). Relations between strictly robust optimization problems and a nonlinear scalarization method. AIP Conference Proceedings, 1479, 2371–2374.
Kodialam, M., Lakshman, T. V., & Sengupta, S. (2006). Maximum throughput routing of traffic in the hose model. In Proceedings of INFOCOM, 25th IEEE international conference on computer communications (pp. 1–11).
Kouvelis, P., & Yu, G. (1997). Robust discrete optimization and its application. Boston, MA: Kluwer Academic.
Kuhn, K., Raith, A., Schmidt, M., & Schöbel, A. (2016). Bi-criteria robust optimisation. European Journal of Operational Research, 252(2), 418–431.
Kuroiwa, D., & Lee, G. M. (2012). On robust multiobjective optimization. Vietnam Journal of Mathematics, 40, 305–317.
Kutateladze, S. S. (1979). Convex \(\epsilon \)-programming. Soviet Mathematics, Doklady, 20(2), 391393.
Leverenz, J. (2015). Network target coordination for multiparametric programming. Ph. D. Thesis, Department of Mathematical Sciences, Clemson University, Clemson, SC.
Loridan, P. (1984). \(\epsilon \)-solutions in vector minimization problems. Journal of Optimization Theory and Applications, 43, 265–276.
Minoux, M. (2009). On robust maximum flow with polyhedral uncertainty sets. Optimization Letters, 3, 367–376.
Nucci, A., Schroeder, B., Bhattacharyya, S., Taft, N., & Diot, C. (2003). IGP link weight assignment for transient link failures. In Proceedings of international teletraffic congress.
Ogryczak, W. (2014). Tail mean and related robust solution concepts. International Journal of Systems Science, 45(1), 29–38.
Palma, C. D., & Nelson, J. D. (2010). Bi-objective multi-period planning with uncertain weights: A robust optimization approach. European Journal of Forest Research, 129(6), 1081–1091.
Pareto, V. (1896). Cours d’Économie politique. Lausanne: Rouge.
Rexford, J. (2006). Route optimization in IP networks. In M. C. Resende, & P. M. Pardalos (Eds.), Handbook of optimization in telecommunications (pp. 679–700).
Rockafellar, R. T. (1997). Convex analysis. Princeton, NJ: Princeton University Press.
Sebo, D. E. (1981). Multiple objective linear programming in objective space. Ph.D. Thesis, The University of Nebraska, Lincoln.
Soyster, A. L. (1973). Convex programming with set-inclusive constraints and applications to inexact linear programming. Operations Research, 21(5), 1154–1157.
Tabatabaee, V., Kashyap, A., Bhattacharjee, B., La, R. J., Shayman, M. A. (2007). Robust routing with unknown traffic matrices. In Proceedings of INFOCOM, 26th IEEE international conference on computer communications (pp. 2436–2440).
Telecommunications Industry Association (TIA). (2012). TIA’s glossary of telecommunication terms. http://www.tiaonline.org/resources/telecom-glossary?goto=Iy.
Witting, K., Ober-Blöbaum, S., & Dellnitz, M. (2013). A variational approach to define robustness for parametric multiobjective optimization problems. Journal of Global Optimization, 57(2), 331–345.
Wendell, R. E., & Lee, D. N. (1977). Efficiency in multiple objective optimization problems. Mathematical Programming, 12, 406–414.
Yuan, D. (2003). A bicriteria optimization approach for robust OSPF routing. In 3rd IEEE workshop on IP operations and management (pp. 91–98).
Zhang, Y. (2004). Personal website. http://www.cs.utexas.edu/~yzhang/research/AbileneTM/.
Acknowledgements
The authors would like to express their sincere gratitude to the anonymous reviewers for their thorough and helpful reviews which significantly improved the quality of the paper. The second author recognizes partial support from Clemson University through Grant URGC 2009/2010. The third author recognizes partial support from the Office of Naval Research through Grant Number N00014-16-1-2725.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Doolittle, E.K., Kerivin, H.L.M. & Wiecek, M.M. Robust multiobjective optimization with application to Internet routing. Ann Oper Res 271, 487–525 (2018). https://doi.org/10.1007/s10479-017-2751-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-017-2751-5