Managing a sustainable integrated inventory model for imperfect production process with type one and type two errors

Abstract

Unlike previous research, this study develops an integrated inventory model for controllable lead time with defective items, errors in inspection, and variable lead time considering sustainability. The research investigates the effect of controlling lead time and capital investment in the setup cost. We assume that the buyer receives a lot size that may contain some defective items with a known defective probability. The buyer’s inspector conducts a 100% quality inspection and may incorrectly classify a non-defective item as a defective item (type one (I) error) or incorrectly classify a defective item as a non-defective item (type two (II) error). The mathematical inventory model considering carbon emission cost is developed, and the solution procedure is designed using the heuristic algorithm to derive the optimal or near optimal solution. Finally, numerical examples and sensitivity analysis are given to illustrate the results. The results show that the defective rate, and type I type II inspection errors, have a significant impact on the shipment lot. This leads to the changes in the total cost, lead time, and the carbon emissions. Our study provides cost savings of 4.39% and carbon emission savings of 28.44%.

Graphic abstract

Introduction

During the last decades, joint inventory problem research has received much attention (Heydari et al. 2017; Tiwari et al. 2018b). In the era of modern business management and globalization, many companies try to efficiently manage their supply chains with the integrated joint inventory policy. The focus in inventory integration in the supply chain system is one of the ways to gain a competitive business advantage.

In recent years, the issues of economics and sustainability in the supply chain have attracted considerable attention from governments, universities, and other non-profit organizations. Over the decades, many researchers have focused on extending the traditional inventory model to consider coordination mechanisms of the channel members, i.e., coordination between the vendor and buyer (Jauhari 2018; Tiwari et al. 2018b). Most of the traditional inventory models assume perfect production processes and error-free inspection. However, in the most production processes, some defective items will be produced. To ensure good quality, the buyer conducts a 100% quality check for all products received from the vendor. In general, vendors make assumption that the product is a perfect quality (zero defect). In reality, it is rare to find 100% zero defect products from the vendor's production process. Therefore, to identify possible defective items and ensure good quality, the buyer screen all products by 100% inspection (Khan et al. 2011; Jauhari 2016). During the inspection, some of the non-defective items may be rejected as defective items (type I error) while other defective items may be accepted as non-defective items (type II error) (Khan et al. 2011; Hsu and Hsu 2012). The earliest research of the EOQ model with defective items was made by Salameh and Jaber (2000). They assumed a perfect inspection to screen out and dispose of the defective items. During the last two decades, other researchers have studied defective items under various conditions. Goyal and Cárdenas-Barrón (2002) developed optimized the total profit of a simple lot size model considering defective products. The optimal integrated vendor–buyer inventory policy for defective quality items with a certain probability of occurrence was investigated by Goyal et al. (2003). By minimizing the expected total cost per item, Wang (2005) optimized the production time frame and product inspection policy. Furthermore, Papachristos and Konstantaras (2006) maximized the total profit considering the timing of imperfect quality goods withdrawal from stock. An optimal inventory model for goods with imperfect quality and insufficient initial orders was studied by Wee et al. (2007). An EOQ model with no backorders and several damaged items lots was developed by Eroglu and Ozdemir (2007). Konstantaras et al. (2007) considered a production-inventory model with a random proportion of defective units and imperfect quality items. Maddah and Jaber (2008) investigated the effect of filtering speed and variability of the supply process. Khan et al. (2011) determined the optimal economic order quantity (EOQ) for items with imperfect quality and inspection errors. Hsu and Hsu (2012) extended Khan et al. (2011)’s model by assuming the defective items in the inspection process are sold to a secondary market at a discounted price. Jauhari (2016) modified Khan et al. (2011)’s model by considering probabilistic demand. Jauhari et al. (2017) developed an unequal-sized shipment policy for a single-vendor and a single-buyer integrated inventory model with deterministic demand, defective items, and errors in the inspection. Khan et al. (2017) proposed a mathematical inventory model for a supply chain system with stochastic lead time. Jauhari (2018) developed a two-echelon inventory model with stochastic demand, defective items, and carbon emissions cost. Tiwari et al. (2018a) proposed a vendor–buyer inventory model considering carbon emissions, deteriorating, and imperfect quality items. Tiwari et al. (2018b) investigated the impact of the investment of ordering and setup cost reduction and controllable lead time on the cost of the supply chain system. Wangsa and Wee (2019) developed an integrated inventory model considering freight cost and stochastic lead time. Recently, Tiwari et al. (2020) investigated the impact of human errors, variable lead time, and capital investment.

Our contribution

In this paper, we consider a joint optimization model with inspection errors, defective items, stochastic demand, controllable lead time, carbon emissions, setup cost reduction, and freight cost. The lead time demand follows a normal distribution, and the setup cost is a logarithmic function of the capital investment. The purpose of this study is to minimize the joint total cost (JTC) by optimizing the order quantity, lead time, safety factor, number of deliveries, and setup cost. This paper presents carbon emissions as a function of the transportation and defective items. By considering carbon emissions from these sources, we investigate how the defective items and mode of transportation affect the optimal solution. This paper combined the elements of stochastic demand, defective items, inspection errors, controllable lead time, and setup cost reduction from Tiwari et al. (2020)’s work, as well as the elements of carbon emission and freight cost from Wangsa (2017)’s work and Wangsa and Wee (2019)’s work. Our study is different from the model by Fallahi et al. (2021), Öztürk (2021) and Zhu (2021) who considered sustainable production-inventory model with defective items, inspection errors, preventive maintenance and inspection errors under demand probabilistic, as well as investigating the impact of a price-sensitive demand and temporary price reduction on the total profit. The research gaps are illustrated in Table 1 where the uniqueness of our study with an integrated inventory model considering the stochastic demand, defective items, inspection errors, controllable lead time, carbon emission, setup cost reduction, and freight cost is highlighted. This study can provide managerial insights for logistic managers in their decision making and system improvement.

Table 1 Research gap: comparison between the proposed model and previous models

The rest of the paper is organized as follows. “Notations and assumptions” section provides the notation and assumptions. “Model development” section develops the proposed mathematical model and algorithm to derive the optimal solution. “Numerical example and sensitivity analysis” section presents the numerical example and sensitivity analysis. Finally, the conclusions and future research directions are given in “Conclusions and future research directions” section.

Notations and assumptions

Notations

The notations used to develop the model are listed below:

Decision variables:

$Q$ :

the size of shipments from the vendor to the buyer (units).

$m$ :

the number of deliveries (times).

$k$ :

safety factor, the factor to determine safety stock due to fluctuating demand (times).

$S$ :

setup cost per setup ($/setup).

$L$ :

lead time (unit time).

Parameters:

$D$ :

average demand (units/unit time).

$P$ :

production rate of the vendor, $P>D$ (units/unit time).

$\sigma$ :

standard deviation of demand (units/unit time).

$A$ :

ordering cost per order ($/order).

${S}_{0}$ :

initial setup cost per setup ($/setup).

${h}_{b}$ :

buyer’s holding cost ($/unit/unit time).

${h}_{v}$ :

vendor’s holding cost ($/unit/unit time).

${C}_{s}$ :

inspection cost ($/unit).

$x$ :

inspection rate (units/unit time).

${C}_{w}$ :

cost of producing defective item ($/unit).

${e}_{1}$ :

probability of Type I inspection error.

${e}_{2}$ :

probability of Type II inspection error.

$\gamma$ :

probability of defective items (defect rate).

${B}_{1}$ :

defective items in each shipment size of $Q$ (units).

${B}_{2}$ :

returned items from market in each shipment size of $Q$ (units).

${C}_{pb}$ :

buyer’s post-sales for each defective item ($/unit).

${C}_{pv}$ :

vendor’s post-sales for each defective item ($/unit).

${C}_{r}$ :

cost of rejecting a non-defective item ($/unit).

$\theta$ :

additional cost for pick-up policy ($/trip).

${d}_{v}$ :

the vendor’s distance to the freight (miles).

${d}_{b}$ :

the freight’s distance to the buyer (miles).

$u$ :

fuel consumption of a truck (L/mile).

$w$ :

weight of product (lbs/unit).

$\alpha$ :

discount factor for LTL shipments, $0\le \alpha \le 1$ (%).

${F}_{x}$ :

cost of freight based on full truckload (FTL) ($/lb/mile).

${F}_{y}$ :

cost of freight based on less-than-truckload ($/lb/mile).

${W}_{x}$ :

full truckload (FTL) shipping weight (lbs).

${W}_{y}$ :

actual weight of shipping $\left({W}_{y}\le {W}_{x}\right)$ (lbs).

$\pi$ :

buyer’s backorder cost ($/unit).

${C}_{ghg}$ :

carbon emission cost ($/ton-CO₂).

${\Delta T}_{1}$ :

buyer’s indirect emission factor (ton-CO₂/L).

${\Delta T}_{2}$ :

buyer’s direct emission factor (ton-CO₂/lb).

${e}_{co}$ :

electricity energy consumption (kWh).

${s}_{co}$ :

steam energy consumption (kWh).

${h}_{co}$ :

heating energy consumption (kWh).

${c}_{co}$ :

cooling energy consumption (kWh)

${L}_{r}$ :

energy loss rate (%).

${\Delta V}_{1}$ :

vendor’s indirect emission factor (ton-CO₂/kWh).

${\Delta V}_{2}$ :

vendor’s direct emission factor (ton-CO₂/unit).

$Y$ :

annual fractional cost of capital investment ($/unit time).

$I\left(S\right)$ :

capital investment in setup cost reduction ($).

$\xi$ :

the percentage decrease in $S$ per dollar increase in $I\left(S\right)$

${c}_{i}$ :

minimum duration of ith lead time component (unit time).

${d}_{i}$ :

normal duration of ith lead time component (unit time).

${e}_{i}$ :

crashing cost per days of ith lead time component ($/unit time).

$JTC$ :

joint total cost ($/unit time).

Assumptions

The following assumptions are used to develop the model:

• 1. This research considers a single item with a single-vendor and a single-buyer.

• 2. The demand follows a normal distribution with mean $D$ and standard deviation $\sigma$.

• 3. The vendor manufactures a batch of $mQ$ units and ships $Q$ (units) to the buyer in each of the $m$ times. The setup cost $S$ is paid by the vendor for each production run, and the ordering cost $A$ is paid by the buyer for each order of quantity $Q$.

• 4. The vendor produces the items with a finite production rate $P$ is higher than the demand rate $D$.

• 5. The lead time $L$ consists of $n$ mutually independent components. For each ith lead time component, ${d}_{i}$ is the normal duration, ${c}_{i}$ is the minimum duration, and ${e}_{i}$ is the crashing cost per unit time. We rearrange ${e}_{i}$ such that ${e}_{1}\le {e}_{2}\le \dots {e}_{j}$. The lead time reduction should first occur on component 1 (i.e., ordering time) where lead time 1 is the initial total lead time minus the crashing of component 1. Lead time 2 is lead time 1 minus the crashing of component 2 (i.e., process time) and so on.

• 6. The crashing cost is paid by the buyer if a shorter lead time is requested.

• 7. The capital investment $I\left(S\right)$ in reducing the vendor’s setup cost is a logarithmic function of the setup cost, $S$. That is, $I\left(S\right)=B \mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$ for $0<S\le {S}_{0}$ where $B=\frac{1}{\xi }$. (Tiwari et al. 2018b, 2020).

• 8. The vendor’s production processes may produce defective items with the defective percentage $\gamma$ and probability density function of $f\left(\gamma \right)$. The lot received by the buyer receives a 100% quality check for all items by the inspector with a screening rate $x$. The screening rate is assumed to be greater than the demand rate, $x>D$.

• 9. The buyer’s inspector will inspect all incoming items from the vendor. There are two type of classification errors. The inspector may incorrectly classify non-defective items as defective $\left({e}_{1}\right)$ with a probability density function of $f\left({e}_{1}\right)$ and may incorrectly accept defective items as non-defective $\left({e}_{2}\right)$ with a probability density function of $f\left({e}_{2}\right)$.

• 10. The cost of producing defective item $\left({C}_{w}\right)$ and the cost of rejecting a non-defective item $\left({C}_{r}\right)$ are paid by the vendor.

• 11. Shortages are allowed and fully backordered.

• 12. The items will be scheduled to be picked up by the freight and delivered to the buyer’s site. This cost (surcharge cost per shipment, $\theta$) is paid by the buyer for the pick-up.

• 13. The freight cost is paid by the buyer.

• 14. Defective items will be returned to the vendor at the end of the inspection process.

Model development

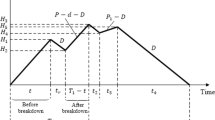
In this paper, we develop a sustainable integrated inventory under a vendor–buyer system taking into account the crashing lead time, defective items, inspection errors, freight cost, and investment for setup cost reduction. Liao and Shyu (1991) developed an inventory model where lead time can be decomposed into several components; and the lead time for each component may be reduced with a crashing cost. An equal-sized shipment policy is adopted by the system to deliver the items. The vendor produces a batch of items $\left(mQ\right)$ with a percentage of defective items. The vendor delivers the lot to the buyer over $m$ shipments.

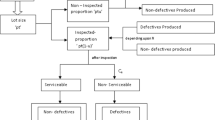
The buyer’s inspector screens out the defective items from the shipment lot with two types of mistakes: classifying non-defective items as defective items $\left({e}_{1}\right)$ and classifying defective items as non-defective items $\left({e}_{2}\right)$. The four possible cases may be found during an inspection process. They are:

• Case 1:

  Number of items which are non-defective but are rejected as defective items = $\left(1-\gamma \right)Q{e}_{1}$

• Case 2:

  Number of items which are non-defective are accepted = $\left(1-\gamma \right)Q\left(1-{e}_{1}\right)$

• Case 3:

  Number of items which are defective but are accepted as non-defective items = $\gamma Q\left(1-{e}_{2}\right)$

• Case 4:

  Number of items which are defective are rejected = $\gamma Q{e}_{2}$

Further, the development of the expected total cost for the buyer, expected total cost for the vendor, and the joint total expected cost are formulated in the following subsections.

Expected total cost for the buyer

In this section, we modify Wangsa and Wee (2019)’s model by considering emission cost. The ordering cost, surcharge cost, lead time crashing cost, shortage cost, inspection cost, type II error cost, and the holding cost are given by the following equations:

$$\text{Ordering cost}=\frac{DA}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(1)

$$\text{Surcharge cost}=\frac{D\theta }{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(2)

$$\text{Lead time crashing cost}=\frac{DR\left(L\right)}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(3)

$$\text{Shortage cost}=\frac{D\pi \sigma \sqrt{L}\psi \left(k\right)}{Q\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(4)

$$\text{Inspection cost}=\frac{D{C}_{s}}{\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(5)

As described in the previous section, this study considers two types of inspection errors. Let ${e}_{1}$ and ${e}_{2}$ denote the probabilities of classifying a non-defective item as defective, and a defective item as non-defective, respectively. To formulate the cost of type II error and the buyer’s holding, we refer to the formulations developed by Wangsa and Wee (2019).

$$\text{Type II error cost}=\frac{D{C}_{pb}\gamma {e}_{2}}{\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(6)

$$\text{Buye{r}'s holding cost}={h}_{b}\left\{\frac{DQ\left[\left(1-\gamma \right){e}_{1}+\gamma \left(1-{e}_{2}\right)\right]}{x\left(1-\gamma \right)\left(1-{e}_{1}\right)}+\frac{Q\left[1-\left({e}_{1}+\gamma \right)+\gamma \left({e}_{1}+2{e}_{2}\right)\right].\left(1-\gamma \right)\left(1-{e}_{1}\right)}{2\left(1-\gamma \right)\left(1-{e}_{1}\right)}+k\sigma \sqrt{L}\right\}$$

(7)

By considering the above-mentioned costs (Eqs. 1–7), the buyer’s expected initial total cost $\left({TEC}_{b0}\right)$ is given by:

$$\text{TEC}_{b0}\left(Q,k,L,m\right)=\frac{D\left[A+\theta +R\left(L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)+mQ\left({C}_{s}+{C}_{pb}\gamma {e}_{2}\right)\right]}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+{h}_{b}\left\{\frac{DQ\left[\left(1-\gamma \right){e}_{1}+\gamma \left(1-{e}_{2}\right)\right]}{x\left(1-\gamma \right)\left(1-{e}_{1}\right)}+\frac{Q\left[1-\left({e}_{1}+\gamma \right)+\gamma \left({e}_{1}+2{e}_{2}\right)\right].\left(1-\gamma \right)\left(1-{e}_{1}\right)}{2\left(1-\gamma \right)\left(1-{e}_{1}\right)}+k\sigma \sqrt{L}\right\}$$

(8)

The logistic provider offers pick-up services at a freight cost rate $\left({F}_{x}\right)$. Wangsa and Wee (2019) developed freight cost based on the actual shipping weight, ${W}_{y}=Qw\left(1-\gamma \right)\left(1-{e}_{1}\right)$. Therefore, the buyers expected freight cost can be expressed by:

$$\text{FC}_{b}=\frac{Dm\alpha {F}_{x}{W}_{x}\left(2{d}_{V+}{d}_{b}\right)}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+D\left(1-\alpha \right){F}_{x}w\left(2{d}_{V+}{d}_{b}\right)$$

(9)

Furthermore, this study also considers the carbon emission cost. The cost is divided into 2 categories, namely direct and indirect emissions. To derive the carbon emission cost equation, we refer to Wangsa (2017)’s equation. The expression of carbon emission cost is given by:

$$\text{CE}_{b}=D{C}_{ghg}\left[\frac{\Delta {T}_{1}u\left(2{d}_{V+}{d}_{b}\right)}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+\Delta {T}_{2}w\right]$$

(10)

By considering and combining the buyer’s expected initial total cost in Eq. (8), the freight cost in Eq. (9), and the carbon emission cost in Eq. (10), the buyer’s expected final total cost can be rewritten as follows:

$$\text{TEC}_{b}\left(Q,k,L,m\right)=\frac{D\left[\begin{array}{l}A+\theta +R\left(L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)+mQ\left({C}_{s}+{C}_{pb}\gamma {e}_{2}\right)\\ +\left(m\alpha {F}_{x}{W}_{x}+{C}_{ghg}\Delta {T}_{1}u\right)\left(2{d}_{V+}{d}_{b}\right)\end{array}\right]}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+{h}_{b}\left\{\frac{DQ\left[\left(1-\gamma \right){e}_{1}+\gamma \left(1-{e}_{2}\right)\right]}{x\left(1-\gamma \right)\left(1-{e}_{1}\right)}+\frac{Q\left[1-\left({e}_{1}+\gamma \right)+\gamma \left({e}_{1}+2{e}_{2}\right)\right].\left(1-\gamma \right)\left(1-{e}_{1}\right)}{2\left(1-\gamma \right)\left(1-{e}_{1}\right)}+k\sigma \sqrt{L}\right\}+D\left[\left(1-\alpha \right){F}_{x}w\left(2{d}_{V+}{d}_{b}\right)+{C}_{ghg}\Delta {T}_{2}w\right]$$

(11)

Expected total cost for the vendor

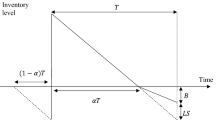
The expected initial total cost for the vendor consists of holding cost, setup cost, rework cost for defective items, type I error cost, and type II error cost. The average inventory of vendor per cycle equal to [bold area] minus [shaded area] and can be formulated by:

$${I}_{v}=\frac{\left[nQ\left(\frac{Q}{P}+\left(n-1\right)T\right)-\frac{{n}^{2}{Q}^{2}}{2P}\right]-T\left[Q+2Q+\dots +\left(n-1\right)Q\right]}{nT}$$

(12)

By substituting $T=\frac{Q\left(1-\gamma \right)\left(1-{e}_{1}\right)}{D}$ into Eq. (6) and then simplifying the equation, one has:

$${I}_{v}=\frac{\left\{nQ\left[\frac{Q}{P}+\left(n-1\right)\frac{Q\left(1-\gamma \right)\left(1-{e}_{1}\right)}{D}\right]-\frac{{n}^{2}{Q}^{2}}{2P}\right\}-T\left[Q+2Q+\dots +\left(n-1\right)Q\right]}{\frac{nQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}{D}}$$

$${I}_{v}=\left\{\frac{Q}{2}+\frac{\left(n-2\right)Q}{2}\left[1-\frac{D}{\left(1-\gamma \right)\left(1-{e}_{1}\right)P}\right]\right\}$$

(13)

The vendor’s holding cost per unit time is given by the following expression:

$$\text{Vendo{r}'s holding cost}={h}_{v}\left\{\frac{Q}{2}+\frac{\left(m-2\right)Q}{2}\left[1-\frac{D}{\left(1-\gamma \right)\left(1-{e}_{1}\right)P}\right]\right\}$$

(14)

Next, the vendor’s setup cost, rework cost for defective items, type I error cost, and type II error cost are given in the following equations:

$$\text{Setup cost}=\frac{DS}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(15)

$$\text{Rework cost}=\frac{D{C}_{w}\gamma }{\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(16)

$$\text{Type I error cost}=\frac{D{C}_{r}\left(1-\gamma \right){e}_{1}}{\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(17)

$$\text{Type II error cost}=\frac{D{C}_{pv}\gamma {e}_{2}}{\left(1-\gamma \right)\left(1-{e}_{1}\right)}$$

(18)

Thus, the vendor’s initial expected total cost per unit time is given by:

$$\text{TEC}_{v}\left(Q,m\right)=\frac{D\left\{S+mQ\left[{C}_{w}\gamma +{C}_{r}\left(1-\gamma \right){e}_{1}+{C}_{pv}\gamma {e}_{2}\right]\right\}}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+{h}_{v}\left\{\frac{Q}{2}+\frac{\left(m-2\right)Q}{2}\left[1-\frac{D}{\left(1-\gamma \right)\left(1-{e}_{1}\right)P}\right]\right\}$$

(19)

Capital investment to reduce setup cost is regarded as the most effective means of minimizing the vendor’s total cost. In this paper, we optimize the initial setup cost $\left(S\right),$ and assume the capital investment $I\left(S\right)$ in reducing the vendor’s setup cost is a logarithmic function of the vendor’s setup cost (Tiwari et al. 2018b, 2020).

$$I\left(\mathrm{S}\right)=B \mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$$

(20)

Subject to: $0<S\le {S}_{0}$; where $B=\frac{1}{\xi }$; $\xi$ is the percentage decrease in $\mathrm{S}$ per dollar increase in $I\left(\mathrm{S}\right)$. If $Y$ is the vendor’s fractional setup cost technology investment, then the formulation is:

$$\text{ISC}_{v}=YI\left(\mathrm{S}\right)=YB\mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$$

(21)

Similarly, the buyer’s emission cost and the vendor’s carbon emission cost are divided into 2 categories, namely direct and indirect emissions. The vendor’s carbon emission cost equation is given by:

$$\text{CE}_{v}=D{C}_{ghg}\left[\frac{\Delta {V}_{1}\left({e}_{co}+{s}_{co}+{h}_{co}+{c}_{co}\right){L}_{r}{C}_{ghg}}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+D\Delta {V}_{2}{C}_{ghg}\right]$$

(22)

Thus, the vendor’s expected final total cost per unit time can be formulated by combining the vendor’s initial expected total cost in Eq. (19), the investment for reducing setup cost in Eq. (21), and the vendor’s carbon emission cost in Eq. (22). One has:

$$\text{TEC}_{v}\left(Q,m,S\right)=\frac{D\left\{\begin{array}{l}S+mQ\left[{C}_{w}\gamma +{C}_{r}\left(1-\gamma \right){e}_{1}+{C}_{pv}\gamma {e}_{2}\right]\\ +\Delta {V}_{1}\left({e}_{co}+{s}_{co}+{h}_{co}+{c}_{co}\right){L}_{r}{C}_{ghg}\end{array}\right\}}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+{h}_{v}\left\{\frac{Q}{2}+\frac{\left(m-2\right)Q}{2}\left[1-\frac{D}{\left(1-\gamma \right)\left(1-{e}_{1}\right)P}\right]\right\}+D\Delta {V}_{2}{C}_{ghg}+YB\mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$$

(23)

Joint total cost

The joint total cost for the vendor–buyer system is the summation of the buyer’s expected final total cost given by Eq. (11), and the vendor’s expected final total cost given by Eq. (23). One has:

$$\text{JTC}\left(Q,k,L, m,S\right)=\frac{D\left\{\begin{array}{l}A+S+\theta +R\left(L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)\\ +mQ\left\{{C}_{s}+\gamma \left[{e}_{2}\left({C}_{pb}+{C}_{pv}\right)+{C}_{w}\right]+{C}_{r}\left(1-\gamma \right){e}_{1}\right\}\\ +\left(m\alpha {F}_{x}{W}_{x}+{C}_{ghg}\Delta {T}_{1}u\right)\left(2{d}_{V+}{d}_{b}\right)\\ +\Delta {V}_{1}\left({e}_{co}+{s}_{co}+{h}_{co}+{c}_{co}\right){L}_{r}{C}_{ghg}\end{array}\right\}}{mQ\left(1-\gamma \right)\left(1-{e}_{1}\right)}+{h}_{b}\left\{\frac{DQ\left[\left(1-\gamma \right){e}_{1}+\gamma \left(1-{e}_{2}\right)\right]}{x\left(1-\gamma \right)\left(1-{e}_{1}\right)}+\frac{Q\left[1-\left({e}_{1}+\gamma \right)+\gamma \left({e}_{1}+2{e}_{2}\right)\right].\left(1-\gamma \right)\left(1-{e}_{1}\right)}{2\left(1-\gamma \right)\left(1-{e}_{1}\right)}+k\sigma \sqrt{L}\right\}+{h}_{v}\left\{\frac{Q}{2}+\frac{\left(m-2\right)Q}{2}\left[1-\frac{D}{\left(1-\gamma \right)\left(1-{e}_{1}\right)P}\right]\right\}+D\left[\left(1-\alpha \right){F}_{x}w\left(2{d}_{V+}{d}_{b}\right)+{C}_{ghg}\left(\Delta {T}_{2}w+\Delta {V}_{2}\right)\right]+YB\mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$$

(24)

To simplify the notation, we let:

$${\overline{X} }_{1}=\left(1-\gamma \right)\left(1-{e}_{1}\right)$$

(25)

$${\overline{X} }_{2}=\left(1-\gamma \right){e}_{1}+\gamma \left(1-{e}_{2}\right)$$

(26)

$${\overline{X} }_{3}=1-\left({e}_{1}+\gamma \right)+\gamma \left({e}_{1}+2{e}_{2}\right)$$

(27)

$$\overline{{Y }_{1}}\left(m,S, L\right)=A+S+\theta +R\left(L\right)+\left(m\alpha {F}_{x}{W}_{x}+{C}_{ghg}\Delta {T}_{1}u\right)\left(2{d}_{V+}{d}_{b}\right)+\Delta {V}_{1}\left({e}_{co}+{s}_{co}+{h}_{co}+{c}_{co}\right){L}_{r}{C}_{ghg}$$

(28)

$$\overline{{Y }_{2}}={C}_{s}+\gamma \left[{e}_{2}\left({C}_{pb}+{C}_{pv}\right)+{C}_{w}\right]+{C}_{r}\left(1-\gamma \right){e}_{1}$$

(29)

$$\overline{{Y }_{3}}\left(m\right)=\left\{1+\left(m-2\right)\left[1-\frac{D}{{\overline{X} }_{1}P}\right]\right\}$$

(30)

$$\overline{{Y }_{4}}\left(S\right)=D\left[\left(1-\alpha \right){F}_{x}w\left(2{d}_{V+}{d}_{b}\right)+{C}_{ghg}\left(\Delta {T}_{2}w+\Delta {V}_{2}\right)\right]+YB\mathrm{ln}\left(\frac{{S}_{0}}{S}\right)$$

(31)

Then, Eq. (24) can be reduced to:

$$\text{JTC}\left(Q,k,L, m,S\right)=\frac{D\left[\overline{{Y }_{1}}\left(m,S, L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)+mQ\overline{{Y }_{2}}\right]}{mQ{\overline{X} }_{1}}+{h}_{b}\left[\frac{DQ{\overline{X} }_{2}}{x{\overline{X} }_{1}}+\frac{Q{\overline{X} }_{3}}{2}+k\sigma \sqrt{L}\right]+\frac{Q{h}_{v}\overline{{Y }_{3}}\left(m\right)}{2}+\overline{{Y }_{4}}\left(S\right)$$

(32)

Solution methodology

The joint total cost in Eq. (32) is formulated as a function of $\left(Q,k,L,m, S\right)$. Here, a methodology is suggested to find the solutions of the proposed model. First, for a fixed value of $\left(L,m\right)$, by finding the first partial derivative of the joint total cost with respect to $\left(Q,k,S\right)$ and by setting these equations equal to zero, we have:

$$\frac{\partial \text{JTC}\left(Q,k,L,m, S\right)}{\partial Q}=0$$

(33)

$$\frac{-D\left[\overline{{Y }_{1}}\left(m,s,L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)\right]}{m{Q}^{2}{\overline{X} }_{1}}+{h}_{b}\left(\frac{D{\overline{X} }_{2}}{x{\overline{X} }_{1}}+\frac{{\overline{X} }_{3}}{2}\right)+\frac{{h}_{v}\overline{{Y }_{3}}\left(m\right)}{2}=0$$

$${2h}_{b}\left(\frac{D{\overline{X} }_{2}}{x{\overline{X} }_{1}}+\frac{{\overline{X} }_{3}}{2}\right)+{h}_{v}\overline{{Y }_{3}}\left(m\right)=\frac{2D\left[\overline{{Y }_{1}}\left(m,s,L\right)+m\pi \sigma \sqrt{L}\psi \left(k\right)\right]}{m{Q}^{2}{\overline{X} }_{1}}$$

$${Q}^{*}=\sqrt{\frac{\frac{2D}{{\overline{X} }_{1}}\left[\frac{\overline{{Y }_{1}}\left(m,s,L\right)}{m}+\pi \sigma \sqrt{L}\psi \left(k\right)\right]}{{2h}_{b}\left(\frac{D{\overline{X} }_{2}}{x{\overline{X} }_{1}}+\frac{{\overline{X} }_{3}}{2}\right)+{h}_{v}\overline{{Y }_{3}}\left(m\right)}}$$

(34)

$$\frac{\partial \text{JTC}\left(Q,k,L,m, S\right)}{\partial k}=0$$

(35)

$$\frac{Dm\pi \sigma \sqrt{L}}{mQ{\overline{X} }_{1}}\left[-1+\Phi \left({k}^{*}\right)\right]+{h}_{b}\sigma \sqrt{L}=0$$

$$\left[-1+\Phi \left({k}^{*}\right)\right]=\frac{-{h}_{b}mQ{\overline{X} }_{1}\sigma \sqrt{L}}{Dm\pi \sigma \sqrt{L}}$$

$$\Phi \left({k}^{*}\right)=1-\frac{{h}_{b}Q{\overline{X} }_{1}}{D\pi }$$

(36)

$$\frac{\partial JTC\left(Q,k,L,m, S\right)}{\partial S}=0$$

(37)

$$\frac{D}{mQ{\overline{X} }_{1}}-\frac{YB}{S}=0$$

$${S}^{*}=\frac{mQYB{\overline{X} }_{1}}{D}$$

(38)

Solution procedure

The following solution procedure to derive the optimal order quantity, safety factor, lead time, setup cost, and the number of shipments in one production cycle is developed. We propose a solution procedure which is developed based on the ideas from Wangsa and Wee (2019) and Tiwari et al. (2020). A solution procedure is provided as follows:

• Step 1 Set $m$ = 1.

• Step 2 For each ${L}_{i}$ perform (2.1)–(2.7), i = 0, 1, 2, …, j

  • (2.1) Start with ${S}_{i1}= {S}_{0}$ and ${k}_{i1}=0$ [implies $\psi \left({k}_{i1}\right)=0.39894$, which can be obtained by checking the standard normal table $\varphi \left({k}_{i1}\right)=0.39894$ and $\Phi \left({k}_{i1}\right)=0.5$].

  • (2.2) Substitute $\psi \left({k}_{i1}\right), {S}_{i1}$ into ${Q}_{i1}=\sqrt{\frac{\frac{2D}{{\overline{X} }_{1}}\left[\frac{\overline{{Y }_{1}}\left(m,s,L\right)}{m}+\pi \sigma \sqrt{L}\psi \left(k\right)\right]}{{2h}_{b}\left(\frac{D{\overline{X} }_{2}}{x{\overline{X} }_{1}}+\frac{{\overline{X} }_{3}}{2}\right)+{h}_{v}\overline{{Y }_{3}}\left(m\right)}}$ to evaluate ${Q}_{i1}$.

  • (2.3) Check the actual shipping weight, $\left({W}_{y}=Qw\right)$; if $\left({W}_{y}>{W}_{x}\right)$ is not satisfied then revise the lot quantity $\left({Q}_{i1}=\frac{{W}_{x}}{w}\right)$ and go to the next step. Otherwise, $\left({W}_{y}\le {W}_{x}\right)$, we go on to the next step.

  • (2.4) Utilize ${Q}_{i1}$, and then determine the value of $\Phi \left({k}_{i2}\right)=1-\frac{{h}_{b}{Q}_{i}{\overline{X} }_{1}}{D\pi }$ and ${S}_{i2}=\frac{mQYB{\overline{X} }_{1}}{D}.$

  • (2.5) Repeat (2.2)–(2.4) until no change in the value of $\left({Q}_{i}, {k}_{i},{S}_{i} \right).$

  • (2.6) Compare the decision variables of ${S}_{i}$ and ${S}_{0}$.

    • (i). If ${S}_{i}<{S}_{0}$ then the optimal solution for the given${L}_{i}$. We denote the optimal solution by $\left({{Q}_{i}}^{*}, {{k}_{i}}^{*},{{S}_{i}}^{*} \right).$

    • (ii). If ${S}_{i}\ge {S}_{0}$ then we set ${{S}_{i}}^{*}={S}_{0}$ and utilize Eqs. (34) and (36) to determine the new $\left({{Q}_{i}}^{*}, {{k}_{i}}^{*}\right)$ by the same procedure (2.2)–(2.4) then the result is denoted $\left({{Q}_{i}}^{*}, {{k}_{i}}^{*},{{S}_{i}}^{*} \right).$

  • (2.7) Calculate $JTC$ using Eq. (32).

• Step 3 Find ${min}_{i=\mathrm{0,1},2,\dots .,j} JTC$ for each model. Let $JTC$ optimal is ${min}_{i=\mathrm{0,1},2,\dots .,j} JTC$ then the decision variables are the optimal solution for fixed $m$.

• Step 4 Set $m=m+1$, repeat steps 2 and 3 to get $JTC$ with fixed $m$.

• Step 5 If $JTC\left({Q}_{\left(m\right)}^{*},{k}_{\left(m\right)}^{*},{L}_{\left(m\right)}^{*},m, {S}_{\left(m\right)}^{*}\right)\le JTC\left({Q}_{\left(m-1\right)}^{*},{k}_{\left(m-1\right)}^{*},{L}_{\left(m-1\right)}^{*},m-1, {S}_{\left(m-1\right)}^{*}\right)$, then go to Step 4, otherwise go to step 6.

• Step 6 The optimal decision variables,$\left({Q}^{*},{k}^{*},{L}^{*},{m}^{*},{S}^{*}\right)=\left({Q}_{\left(m-1\right)}^{*},{k}_{\left(m-1\right)}^{*},{L}_{\left(m-1\right)}^{*},m-1, {S}_{\left(m-1\right)}^{*}\right)$, then $\left({Q}^{*},{k}^{*},{L}^{*},{m}^{*},{S}^{*}\right)$ is the optimal solution.

Numerical example and sensitivity analysis

To illustrate the above-proposed solution procedure, we consider an integrated inventory system with the data (Table 2) adopted from Saga et al. (2019), Wangsa and Wee (2019), Tiwari et al. (2020). The lead time data are shown in Table 3.

Table 2 Input data

Table 3 Lead time data

Similar to Khan et al. (2011, 2017), Wangsa and Wee (2019), and Saga et al. (2019), we assume that the probability of defective items and inspection errors follows a uniform distribution, so one has:

$$f\left(\gamma \right)=\left\{\begin{array}{l}\frac{1}{\beta }, 0\le \gamma \le \beta \\ \\ 0,\mathrm{otherwise}\end{array}f\left({e}_{1}\right)=\left\{\begin{array}{l}\frac{1}{\delta }, 0\le {e}_{1}\le \delta \\ \\ 0,\mathrm{otherwise}\end{array}\right. f\left({e}_{2}\right)=\left\{\begin{array}{l}\frac{1}{\rho }, 0\le {e}_{2}\le \rho \\ \\ 0,\mathrm{otherwise}\end{array}\right.\right.$$

then, we have

$$E\left[\gamma \right]=\int\limits_{0}^{\beta }\gamma f\left(\gamma \right)d\gamma =\frac{\beta }{2}E\left[{e}_{1}\right]=\int\limits_{0}^{\delta }{e}_{1}f\left({e}_{1}\right)d{e}_{1}=\frac{\delta }{2} E\left[{e}_{2}\right]=\int\limits_{0}^{\rho }{e}_{2}f\left({e}_{2}\right)d{e}_{2}=\frac{\rho }{2}$$

Apply the solution procedure with defective items shape parameter, type I error, and type II error as $\beta =\delta =\rho$ = 0.04, respectively, the optimal solutions can be derived. We obtain the $JTC$ as $75,513.64/year, ${Q}^{*}$ = 1603.53 units, ${k}^{*}$ = 1.97, ${m}^{*}$ = 4, ${{W}_{y}}^{*}$ = 35,277.64 pounds, lead time $\left({L}^{*}\right)$ = 21 days, defective items based on screening process $\left({{B}_{1}}^{*}\right)$ = 62.86 units, defective items returned from the market $\left({{B}_{2}}^{*}\right)$ = 0.64 units, and the total emissions $\left({TE}^{*}\right)$ = 0.0798 ton-CO₂.

Next, we compare the results of the integrated optimal policy with those of the independent policies. In the independent model, the players optimize their total cost policy separately. The result shows that the optimal order quantity is ${Q}^{*}$ = 2070.95 units, safety factor ${k}^{*}$ = 1.85, ${{W}_{y}}^{*}$ = 45,560.94 lbs., ${L}^{*}$ = 21 days, ${{B}_{1}}^{*}$ = 81.18 units, ${{B}_{2}}^{*}$ = 0.83 units, ${TE}^{*}$ = 0.1115 ton-CO_2, and the buyer’s total expected cost is $33,973.26/year. The vendor’s total expected cost is $45,005.78/year. Thus, the total expected cost for the independent policy is $78,979.04/year. The comparison analysis between independent and integrated decisions is shown in Table 4. The integrated decision provides a cost saving by $3465.40/year or 4.39% and emission saving by 0.04 ton-CO₂ or 28.44%.

Table 4 The optimal results of the independent and integrated models

Figure 1 depicts the impact of type I error, type II error, and defects probabilities on $JTC$. The analysis is examined by changing each of the parameters from − 75 to + 250%. The results show that $JTC$ has increased the sensitivity to the variation in the defects as well as the type I error probabilities. This is due to the higher number of rejected items and the rework cost. It is also observed that the type I error has a greater impact on the $JTC$ than that of type II error.

Fig. 1

Sensitivity analysis for defects, type I error, and type II error on the $JTC$ ($/year)

Next, we analyse the effect of these parameters on the defective items after screening $\left({B}_{1}\right)$ and on after-sales from the market $\left({B}_{2}\right)$, for which the results are shown in Figs. 2 and 3. The analysis is examined by changing each of the parameters from − 75 to + 250%. The results from Fig. 2 show that ${B}_{1}$ significantly increases as the defects and type I error probabilities increase. In contrast to the type I error change for ${B}_{1}$, the effect of the changes in type II error on ${B}_{1}$ seems to be insignificant. Yet in Fig. 3, ${B}_{1}$ increases significantly as the type II error and defects probabilities increase and remain almost unchanged when the type I error probability increases. We also observe from Figs. 2 and 3 that the values of ${B}_{1}$ and ${B}_{2}$ increase due to the increase in the defective probability. Figure 4 shows the impact of type I error, type II error, and defective item probabilities on total emissions released from the supply chain. The result shows that if the defects and type I error probabilities increase gradually; the total emissions drastically increase. The total emissions seem to remain unchanged due to the increase in the type II error probability.

Fig. 2

Sensitivity analysis for defects, type I error, and type II error probabilities on the ${B}_{1}$ (units)

Fig. 3

Sensitivity analysis for defects, type I error, and type II error probabilities on the ${B}_{2}$ (units)

Fig. 4

Sensitivity analysis for defects, type I error, and type II error probabilities on the $TE$ (ton-CO₂)

Table 5 and Figs. 5, 6 and 7 show that the total expected cost, lot size, safety factor, the number of deliveries, lead time, and setup cost are sensitive to changes in parameters: $D$, $P$, $\beta$, $\delta$, $\rho$, ${h}_{b}$, ${h}_{v}$, $x$, ${S}_{0}$, $Y$, and ${C}_{ghg}$. In the sensitivity analysis, the parameter values are varied from − 50 to + 50%, and the comparison between independent and integrated decisions is provided to show which policy has a better performance in minimizing the total cost of the supply chain. Figures 5, 6, and 7 show the cost saving between the $JTC$ and the independent total cost. The results shows the cost saving increases as the buyer’s holding cost (${h}_{b}$), demand ($D$), setup cost reduction investment ($Y$), and carbon emission cost (${C}_{ghg}$) increase (3.74–6.63%; 4.3–5.6%; 4.24–4.54%; and 1.63–6.87%, respectively). The cost savings are insignificant for increasing defective rate probability, type I inspection error probability, type II inspection error probability, and initial setup cost ($\gamma$, ${e}_{1}$, ${e}_{2}$, and ${S}_{0}$). However, the cost saving decreases from 6.61 to 3.75%, 6.90 to 2.75% and 4.46 to 4.36%, respectively, as the parameters $P$, ${h}_{v}$ and $x$ increase from − 50 to + 50%.

Table 5 The sensitivity analysis

Fig. 5

Sensitivity analysis of $D$, $P$, ${h}_{b}$, ${h}_{v}$, and ${C}_{ghg}$ on cost savings for the independent and the integrated optimal policies

Fig. 6

Sensitivity analysis of $x$ and $Y$ on cost savings for the independent and the integrated optimal policies

Fig. 7

Sensitivity analysis of $\gamma$, ${e}_{1}$, ${e}_{2}$, and ${S}_{0}$ on cost savings for the independent and the integrated optimal policies

Conclusions and future research directions

This paper investigates an integrated inventory model for a single-vendor and single-buyer system with defective items, inspection errors, setup cost reduction, controllable lead time, and carbon emissions. We consider two types of inspection errors; namely, type I error (if the inspector incorrectly classifies non-defective items as defective items) and type II error (if the inspector incorrectly classifies defective items as non-defective items). In addition, the freight cost and emission cost are also incorporated and analyzed in the proposed model. The freight cost is derived as a function of the weight of shipping and the vendor’s distance to the buyer. The emission cost is formulated as a function of direct and indirect emissions that are generated from vendor and buyer activities. The objective is to minimize the joint total cost incurred by the supply chain. The analysis is performed to study the effect of changes in demand, production rate, probability of defective items, probability of type I error, probability of type II error, screening rate, holding cost, initial setup cost, investment, and carbon emission cost on the optimal solutions.

The results obtained from the numerical example show that the defective rate and inspection errors have a pronounced impact on costs, lead time, and total carbon emissions. The changes in type I error and type II error probabilities have a significant impact on the shipment lot size, which affects the total cost and the total emissions. Thus, in view of the changing inspection errors, management needs to carefully control the system to ensure that the total cost and the total emissions be maintained at the appropriate level. Furthermore, the results show that the integrated policy more cost effective when compared with the independent policy. For future research, this study can be extended to consider the effect of learning to decrease the Type I and Type II errors probability. Further study may consider the impact of returned products, as well as considering multiple vendors and buyers.