1 Introduction

The food quality, especially the quality of perishable foods, has always played a focal point since it permeates every level of the management of food supply chains. As pointed out in Trienekens and Zuurbier (2008), food quality will dominate the process of production and distribution in the future. In a sense, the importance of food quality may be more prominent in the retail process since it affects directly a consumer’s purchase decision. Generally speaking, when the foods are good value for money, they will be on the list of consumers’ purchasing.

In recent decades, marketing researchers have taken the product quality as an important influential factor of demand. Teng and Thompson (1996) develop general price-quality decision models of new products with learning production costs, in which dynamic demand is a function of price and quality level, as well as cumulative sales. Considering cumulative productivity and quality knowledge as state variables, Vörös (2006) provides an optimization formulation and characterizes the dynamics of optimal price, quality and investment decisions. Chenavaz (2012) assumes that the demand depends on price and quality, and analyzes the dynamic relationships between the price and quality under an additive and a separable multiplicative demand function, respectively. Especially, there has been a considerable body of literature which mainly focuses on food quality. Owing to the range of quality attributes, dynamics of food characteristics and storage conditions, the study regarding food quality has been viewed as a challenge. Péneau et al. (2007) take freshness as a quality criterion of consumers’ acceptance of fruit and vegetables and uncover sensory attributes influencing consumer perception of the freshness of strawberries and carrots that varies in cultivar, as well as with time and storage conditions. Integrating food quality in production and distribution planning, Rong et al. (2011) present a mixed-integer linear programming model, where food quality is strongly related to temperature control. Wang and Li (2012) further develop a food quality degradation model by introducing a temperature dependent quality deterioration rate. Based on dynamically identified food shelf life, they adopt discount policies to maximize the food retailer’s profit. Other researchers such as Broekmeulen (1998), Lukasse and Polderdijk (2003) and Ferguson and Ketzenberg (2006) also study the management problem of food quality.

In practice, the deterioration rate of perishable foods can be controlled and reduced through various efforts, e.g., procedural changes and specialized equipment acquisition. Therefore, producers or retailers, according to the realistic situations, can make decisions on whether some preservation technologies could be adopted by means of effective investment strategy to reduce the deterioration rate of foods. Lee (2008) constructs investment models to measure the impact of quality programs and predict the return of an investment in a multi-level assembly system, which can be applied by decision makers to decide whether and how much to invest in quality improvement projects. Hsu et al. (2010) investigate the optimal replenishment cycle, shortage period, order quantity and preservation technology cost when the retailer invests in preservation technology to reduce the deterioration rate of products. Based on the sensitivity analysis in numerical examples, Geetha and Uthayakumar (2010) and Maihami and Kamalabadi (2012) find that effectively reducing the deterioration rate leads to more profits. However, Dye and Hsieh (2012) propose that when the deterioration rate is small enough, the investment will reach zero, which implies that the inventory system doesn’t need to invest. As shown in Hsieh and Dye (2013), the effective investment strategy can not only reduce unnecessary waste and economic losses, but also enhance the service level to customers and business competitiveness. Due to these competitive advantages, the firm will have the initiative in pricing and other aspects. Other papers related to investment constraint issue refer to Hong and Hayya (1995), Gurnani et al. (2007), Mathur and Shah (2008) and others.

Another active area is pricing and inventory control for perishable products, as reported in review articles by Nahmias (1982) and Goyal and Giri (2001). Chatwin (2000) develops a continuous-time inventory model for perishable products under some assumptions, in which the retailer can only choose from a finite number of allowable prices. On the basis of the construction of optimal pricing policies directly characterized by a family of continuous pricing functions, Anjos et al. (2005) present a general methodology to react to any changes in the predicted purchase patterns for perishable products. To obtain the optimal prices and inventory allocations for a perishable product with a predetermined lifetime, Chew et al. (2009) construct a discrete time dynamic programming model, where the price is assumed to increase over time when it perishes approaches as in the airline industry and the demand is price sensitive. Wang and Lin (2012) develop an optimal replenishment strategy with pricing manipulation for a deteriorating product whose demand continuously decreases over time and is sensitive to price. The proposed model can be used to determine the optimal product life cycle. Based on the situation that some perishable assets’ value becomes zero after a fixed expiry date, Banerjee and Turner (2012) develop a flexible and versatile model to assign optimal prices to these perishable assets. In addition, several researchers investigate the dynamic pricing and inventory control problem for other products, e.g., Adida and Perakis (2010) and Akan et al. (2013).

In the existing literature, while the dynamic pricing or investment policy in preservation technology for perishable foods has been extensively studied, simultaneously considering both strategies as decision variables receives little attention. Accordingly, our paper complements these previous works by determining the joint dynamic pricing and investment strategy for perishable foods to maximize the total profit in a monopoly setting. Moreover, since the quality of perishable foods can be perceived more accurately with the technological development and application of food traceability systems, it has become a direct influential factor of a consumer’s purchase decision. As for a retailer, the effective investment strategy in reducing the deterioration rate of the quality plays an important role in the retail process. Therefore, we also wish to answer the following twofold question: under what circumstances does a retailer invest in preservation technology for perishable foods, and how do key system parameters affect the investment time horizon when the investment activity occurs?

To that end, we develop an inventory system for perishable foods controlled by a monopolistic retailer, in which both inventory level and food quality are treated as state variables of the dynamic system. The former evolves from a given initial inventory level to zero due to demand, while the latter decays continuously owing to the nature of perishable foods. There are also two control variables in this system: price and preservation technology investment. The retailer affects the demand directly through pricing and indirectly through food quality by investing in preservation technology to reduce its deterioration rate, and thus maximizes the net profit over a time horizon, taking inventory holding and investment costs into consideration.

Our contributions are as follows: First, for appropriate initial inventory level, we prove the existence and uniqueness of solution for the proposed dynamic pricing and inventory control problem by means of Filippov–Cesari theorem and Pontryagin’s maximum principle. Second, our results suggest that investing in preservation technology in the whole time horizon for the retailer may be inadvisable. In particular, numerical analysis shows that for relatively high natural deterioration coefficient and low unit investment cost, there exists a time threshold, before which, the retailer will implement investment activity and after which, the retailer will not invest. Whereas, when the natural deterioration coefficient is relatively low and unit investment cost is relatively high, the optimal strategy for the retailer is not to invest. Third, we carry out the sensitivity analysis of main parameters and obtain some interesting results.

The preceding sections are organized as follows. Section 2 outlines the model notations and assumptions used throughout this paper. Section 3 characterizes the joint dynamic pricing and investment model in detail. In Sect. 4, we prove the existence of an optimal solution based on Filippov–Cesari theorem, obtain all the candidates and conditions that make a certain candidate be an optimal solution according to Pontryagin’s maximum principle, and present an effective algorithm to find the optimal strategy. In Sect. 5, two numerical examples are used to elucidate the proposed solution procedure, followed by sensitivity analysis and managerial insights. Conclusions are drawn in Sect. 6.

2 Model notations and assumptions

The model in this paper is developed on the basis of the following notations and assumptions.

2.1 Notations

\({[}0, T{]}\) :

The time horizon, in which the terminal time \(T\) is finite and unspecified

\(I(t)\) :

The inventory level (state variable)

\(q(t)\) :

The food quality (state variable)

\(p(t)\) :

The retail price per unit (control variable)

\(u(t)\) :

The investment rate (control variable)

\(\theta (u)\) :

The deterioration coefficient under investment

\(D(p,q)\) :

The demand rate

\(I_{0}\) :

The initial inventory level

\(q_{0}\) :

The initial quality

\(\theta _{0}\) :

The natural deterioration coefficient

\(h\) :

The holding cost per unit

\(c\) :

The investment cost per unit

\(U\) :

The maximum investment rate

\(k\) :

The reduced value of deterioration coefficient under per unit investment

\(\alpha ,\beta ,\gamma \) :

The coefficients of relationships among price, quality and demand rate

2.2 Assumptions

A1.:

The inventory system involves a single kind of perishable food.

A2.:

The demand rate \(D(p,q)\) is a function of the retail price and quality of perishable foods, taking the form of \(D(p,q)=\gamma q(\alpha -\beta p)\).

A3.:

The sales cycle ends once the foods are exhausted.

A4.:

There are no production and replenishment occurring in the whole process.

A5.:

The intertemporal profit is not discounted.

The system parameters \(I_{0}, q_{0}, \theta _{0}, h, c, U, k, \alpha ,\beta ,\gamma \) are all positive. In addition, the demand function in assumption A2 follows the separable multiplicative form between control variable and state variable, which is common in the existing literature (e.g., Jørgensen and Zaccour 1999; El Ouardighi and Kogan 2013). The consideration of price-quality dependent demand is useful for perishable foods such as fruits, meats and so on (e.g., Wang and Li 2012).

3 Joint dynamic pricing and investment model

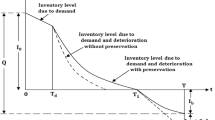
In this section, we consider a retailer having \(I_{0}\) units of perishable food at the beginning of the sales cycle in a local place. According to assumptions A3 and A4, the evolution of the inventory level can be described as

$$\begin{aligned} \dot{I}(t)=-D(p(t),q(t)),\quad I(0)=I_0,\ I(T)=0, \end{aligned}$$
(1)

where \(T\) is the unspecified terminal time.

In daily life, consumers tend to pay more attention to the price and quality of perishable foods. Hence, these two important influential factors are taken into consideration when constructing the demand function. Based on assumption A2, the demand function is defined as

$$\begin{aligned} D(p(t),q(t))=\gamma q(t)(\alpha -\beta p(t)). \end{aligned}$$
(2)

Due to the fact that the price and demand should remain non-negative, i.e., \(p(t)\ge 0\) and \(D(p(t),q(t))\ge 0\), we assume that

$$\begin{aligned} 0\le p(t)\le \displaystyle \frac{\alpha }{\beta }. \end{aligned}$$
(3)

In view of the nature of perishable food, its quality can also be treated as a dynamic state that decays continuously. Here, we suppose that the quality decays from the initial quality \(q_{0}\) according to first-order reactions

$$\begin{aligned} \dot{q}(t)=-\theta (u(t)) q(t),\quad q(0)=q_0. \end{aligned}$$
(4)

In practice, most perishable foods are affected by the storage environment, so the retailer makes decisions on whether some investments in preservation technologies are adopted to reduce the deterioration rate. In general, the investment rate \(u(t)\) is finite due to resource limitations. Assuming that the maximum investment rate is \(U\), the investment rate is bounded as

$$\begin{aligned} 0\le u(t)\le U. \end{aligned}$$
(5)

The linear function regarding the deterioration coefficient \(\theta (u(t))\) and investment rate \(u(t)\), for simplicity, is formulated as

$$\begin{aligned} \theta (u(t))=\theta _{0}-ku(t). \end{aligned}$$
(6)

Note that for perishable foods, the quality will still decay continuously despite that the retailer invests maximum capital. Thus it is natural to set \(k<\frac{\theta _{0}}{U}\).

The inventory holding and investment costs are constructed as \(hI(t)\) and \(cu(t)\), respectively. The total profit, therefore, can be described as follows

$$\begin{aligned} J=\displaystyle \int \nolimits _{0}^{T} \Big (p(t)D(p(t),q(t))-hI(t)-cu(t)\Big )\mathrm {d}t. \end{aligned}$$
(7)

The objective is to find a joint dynamic pricing and investment strategy that maximizes the total profit (7), which is formulated as the following optimization problem

$$\begin{aligned} \begin{array}{ll} \max \limits _{p(\cdot ), u(\cdot )}&{}J=\displaystyle \int \nolimits _{0}^{T}\Big (\gamma q(t)p(t) (\alpha -\beta p(t))-hI(t)-cu(t)\Big )\mathrm {d}t\\ \quad \mathrm {s}.\mathrm {t}.&{} \dot{I}(t)=-\gamma q(t)(\alpha -\beta p(t)),\quad I(0)=I_0,\ I(T)=0,\\ &{}\dot{q}(t)=-(\theta _{0}-ku(t))q(t), \quad q(0)=q_0,\\ &{}0\le p(t)\le \displaystyle \frac{\alpha }{\beta }, \ 0\le u(t)\le U. \end{array} \end{aligned}$$
(8)

4 Optimal strategy of the dynamic system

In this section, we first use Filippov–Cesari theorem (see, e.g., Seierstad and Sydsæer 1987, p. 145; Hartl et al. 1995; Adida and Perakis 2007) to prove the existence of an optimal solution. Then, we obtain all the candidates and provide the conditions that make a certain candidate be an optimal solution based on Pontryagin’s maximum principle. Finally, an effective algorithm is presented to search for the joint optimal strategy.

4.1 Existence of an optimal solution

To address the existence of an optimal solution for (8) by using Filippov–Cesari theorem, we define the feasible control set

$$\begin{aligned} \Omega =\displaystyle \left\{ (p, u)\mid 0\le p\le \frac{\alpha }{\beta }, 0\le u\le U \right\} , \end{aligned}$$

and the set

$$\begin{aligned} Q(I, q, t)&= \left\{ \big (\gamma qp(\alpha -\beta p)-hI-cu+b,-\gamma q(\alpha -\beta p),-(\theta _0-ku)q\big )\mid b\le 0,\right. \\&\left. (p, u)\in \Omega \right\} . \end{aligned}$$

In the following proposition, we verify that the four conditions listed in Filippov–Cesari theorem are satisfied.

Proposition 1

For the optimization problem (8), there exists an optimal, measurable control \((p^*,u^*)\).

Proof

  1. (i)

    Consider the strategy

    $$\begin{aligned} p=0,\quad u=U. \end{aligned}$$

From both state equations in (8), the following equation

$$\begin{aligned} I_0+\frac{\alpha \gamma q_0}{\theta _0-kU} \left( e^{(kU-\theta _0)T}-1\right) =0 \end{aligned}$$

can be obtained immediately.

For notational simplicity, let

$$\begin{aligned} F(t)=I_0+\frac{\alpha \gamma q_0}{\theta _0-kU}\left( e^{(kU-\theta _0)t}-1\right) . \end{aligned}$$

Obviously, function \(F(t)\) is continuous. Since \(F(0)=I_0>0\) and \(\lim \limits _{t\rightarrow +\infty }F(t)<0\) when \(I_0<\frac{\alpha \gamma q_0}{\theta _0-kU}\), we obtain that \(F(t)=0\) has a solution \(T^*\) for the appropriate initial inventory level.

Hence, this strategy satisfying all the constraints is an admissible pair.

  1. (ii)

    Let \((x_1, y_1, z_1), (x_2, y_2, z_2)\in Q(I, q, t)\) with

    $$\begin{aligned} \begin{array}{lll} \qquad x_1&{}=&{}\gamma qp_1(\alpha -\beta p_1)-hI-cu_1+b_1,\\ \qquad x_2&{}=&{}\gamma qp_2(\alpha -\beta p_2)-hI-cu_2+b_2,\\ \qquad y_1&{}=&{}-\gamma q(\alpha -\beta p_1),\\ \qquad y_2&{}=&{}-\gamma q(\alpha -\beta p_2), \\ \end{array} \end{aligned}$$
    $$\begin{aligned} \begin{array}{lll} \qquad z_1&{}=&{}-(\theta _0-ku_1)q,\\ \qquad z_2&{}=&{}-(\theta _0-ku_2)q,\\ \qquad b_1&{}\le &{} 0, \\ \qquad b_2&{}\le &{} 0, \\ (p_1, u_1)&{}\in &{}\Omega , \\ (p_2, u_2)&{}\in &{}\Omega .\\ \end{array} \end{aligned}$$

We will show that \((\hat{x}, \hat{y}, \hat{z})= \mu (x_1, y_1, z_1)+(1-\mu )(x_2, y_{2}, z_2)\in Q(I, q, t)\) for any \(\mu \in [0, 1]\).

Let \((\hat{p},\hat{u})=\mu (p_1, u_1)+(1-\mu )(p_2, u_2).\) It is easy to verify that \((\hat{p},\hat{u})\in \Omega \). Clearly, \(\hat{y}=-\gamma q(\alpha -\beta \hat{p})\) and \(\hat{z}=-(\theta _0-k\hat{u})q\).

Since the function \(J(p,u)=\gamma qp(\alpha -\beta p)-hI-cu\) is concave in \((p,u)\), which implies

$$\begin{aligned} \begin{array}{ll} &{}\gamma q\hat{p}(\alpha -\beta \hat{p})-hI-c\hat{u}\\ &{}\quad \ge \mu (\gamma qp_1(\alpha -\beta p_1)-hI-cu_1)+(1-\mu )(\gamma qp_2(\alpha -\beta p_2)-hI-cu_2)\\ &{}\quad =\mu (x_1-b_1)+(1-\mu )(x_2-b_2),\\ \end{array} \end{aligned}$$

there exists \(b_3\le 0\) such that

$$\begin{aligned} \gamma q\hat{p}(\alpha -\beta \hat{p})-hI-c\hat{u}+b_3=\hat{x}-\mu b_1-(1-\mu )b_2. \end{aligned}$$

Let \(\hat{b}=\mu b_1+(1-\mu )b_2+b_3\le 0\). It follows that

$$\begin{aligned} \hat{x}=\gamma q\hat{p}(\alpha -\beta \hat{p})-hI-c\hat{u}+\hat{b}. \end{aligned}$$

Then \((\hat{x},\hat{y}, \hat{z})\in Q(I, q, t)\) and thus \(Q(I, q, t)\) is convex for each \((I, q, t)\).

  1. (iii)

    Obviously, the feasible control set \(\Omega \) is closed and bounded.

  2. (iv)

    There exist numbers \(I_0\) and \(q_0\) such that \(|I|\le I_0\) and \(|q|\le q_0\) for any \(t\in [0,T]\) and all admissible pairs \((I,q,p,u)\).

As a result, according to Filippov–Cesari theorem, there exists an optimal solution \((p^*,u^*)\) to the optimization problem (8). \(\square \)

4.2 Candidates for an optimal solution

In the following, we apply Pontryagin’s maximum principle with control variables constrains (see Sethi and Thompson 2000, pp. 57–80) to solve the optimal control problem (8).

Introduce the adjoint variables \(\lambda _{1}\) and \(\lambda _{2}\) to form the Hamiltonian function

$$\begin{aligned} H(I, q, p, u, \lambda _1, \lambda _2, t )\!=\!\gamma qp(\alpha -\beta p)\!-\!hI-cu\!-\!\lambda _{1}\gamma q (\alpha \!-\!\beta p)\!-\!\lambda _{2}(\theta _{0}-ku)q. \end{aligned}$$
(9)

The adjoint variables \(\lambda _{1}\) and \(\lambda _{2}\) satisfy the adjoint equations \(\dot{\lambda }_{1}=-\frac{\partial H}{\partial I}\) and \(\dot{\lambda }_{2}=-\frac{\partial H}{\partial q}\), respectively, that is

$$\begin{aligned} \dot{\lambda }_{1}=h, \quad \lambda _{1}(T)=c_1, \end{aligned}$$
(10)

where \(c_{1}\) is a constant to be determined, and

$$\begin{aligned} \dot{\lambda }_{2}=\gamma (\lambda _{1}-p)(\alpha -\beta p)+\lambda _{2}(\theta _{0}-ku),\quad \lambda _{2}(T)=0. \end{aligned}$$
(11)

It follows from (10) that

$$\begin{aligned} \lambda _{1}=h(t-T)+c_{1}, \end{aligned}$$
(12)

which is strictly increasing in \(t\).

Since the terminal time \(T\) is unspecified, it can be determined by the following equation

$$\begin{aligned} H(I, q, p, u, \lambda _1, \lambda _2, t )\mid _{t=T}=0. \end{aligned}$$
(13)

Note that the Hamiltonian in (9) is separable in control variables \(p\) and \(u\). Furthermore, it is strictly concave in the control variable \(p\) and linear in the control variable \(u\). Hence, maximizing the Hamiltonian and considering the control variables constrains \(0\le p\le \frac{\alpha }{\beta }\) and \(0\le u\le U\) shown in (3) and (5), respectively, the optimal control \(p^*\) lies within or on a boundary of the set of the feasible controls, and the optimal control \(u^*\) is singular (corner solution).

The foregoing discussion yields the optimal solution \((p^*, u^*)\) as follows

$$\begin{aligned}&p^{*}= \left\{ \! \begin{array}{ll} 0 ,&{}\quad \mathrm if \;\lambda _{1}\le -\displaystyle \frac{\alpha }{\beta }\\ \displaystyle \frac{1}{2}\left( \displaystyle \frac{\alpha }{\beta }+\lambda _{1}\right) , &{}\quad \mathrm if \;-\displaystyle \frac{\alpha }{\beta }<\lambda _{1} \le \displaystyle \frac{\alpha }{\beta }\\ \displaystyle \frac{\alpha }{\beta }, &{}\quad \mathrm if \; \lambda _{1}>\displaystyle \frac{\alpha }{\beta }, \end{array} \right. \end{aligned}$$
(14)
$$\begin{aligned}&u^{*}= \left\{ \! \begin{array}{ll} 0, &{}\quad \ \ \mathrm if \; \lambda _{2}q<\displaystyle \frac{c}{k}\\ undefined, &{}\quad \ \ \mathrm if \; \lambda _{2}q=\displaystyle \frac{c}{k}\\ U, &{}\quad \ \ \mathrm if \; \lambda _{2}q>\displaystyle \frac{c}{k}.\\ \end{array} \right. \end{aligned}$$
(15)

Since \(\lambda _2(T)=0\), from (15) we have

$$\begin{aligned} u^*(T)=0. \end{aligned}$$
(16)

Proposition 2

Assume that \((\tau , T]\) with \(0\le \tau <T\) is the last time interval in which the price \(p^{*}\) can’t switch. The optimal price

$$\begin{aligned} p^{*}=\displaystyle \frac{1}{2}\left( \displaystyle \frac{\alpha }{\beta }+\lambda _{1}\right) ,\ \forall t\in (\tau ,T]. \end{aligned}$$
(17)

Proof

Suppose that \(p=0\) for any \(t\in (\tau , T]\), which follows from (14) that \(\lambda _{1}\le -\frac{\alpha }{\beta }\). However, substituting (9) and the boundary conditions with respect to \(T\) in (1), (11) and (16) into (13) yields \(q(T)\lambda _1(T)=0\), so \(\lambda _1(T)=0\), which is a contradiction.

Suppose that \(p=\frac{\alpha }{\beta }\) for any \(t\in (\tau , T]\). It follows from the first state equation in (8) that \(\dot{I}=0\). Since \(I(T)=0\), we obtain \(I=0\) for any \(t\in (\tau , T]\). This is a contradiction with assumption A3.

As a result, the optimal price is shown in (17).\(\square \)

Then, using (10) and (17), we obtain \(p^{*}(T)=\frac{1}{2}\left( \frac{\alpha }{\beta }+c_1\right) .\) Inserting (9) and the boundary conditions with respect to \(T\) in (1), (11) and (16) into (13), we further obtain

$$\begin{aligned} c_1=\frac{\alpha }{\beta }, \end{aligned}$$
(18)

which implies from (12) that

$$\begin{aligned} \lambda _1=h(t-T)+\frac{\alpha }{\beta }. \end{aligned}$$
(19)

Based on Proposition 2 and the monotonicity of \(\lambda _1\), the following proposition can be obtained immediately.

Proposition 3

If \(\lambda _{1}(0)<-\frac{\alpha }{\beta }\), i.e., \(T>\frac{2\alpha }{\beta h},\) the optimal price

$$\begin{aligned} p^{*} = \left\{ \! \begin{array}{ll} 0 ,&{}\quad 0\le t\le t_1\\ \displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2}\left( t-T\right) , &{}\quad t_1<t \le T,\\ \end{array} \right. \end{aligned}$$
(20)

where \(t_1=T-\frac{2\alpha }{\beta h}.\) Otherwise, the optimal price

$$\begin{aligned} p^{*} =\displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2}\left( t-T\right) \end{aligned}$$
(21)

over the time horizon \([0, T].\)

Proof

The proof can be easily done by virtue of (14), (19), Proposition 2 and the monotonicity of \(\lambda _1\). \(\square \)

Note from (20) and (21) that the optimal price \(p^*\) is increasing over time and its terminal value \(p^*(T)=\frac{\alpha }{\beta }\), which can be interpreted by the following two reasons from an economic viewpoint. First, the retailer will adopt a lower initial price at the beginning to promote the demand and reduce inventory level more quickly in order to avoid incurring more holding costs, then the retailer gradually raises the retail price until the maximum value. Second, as the quality decays continuously, the price sensitivities decrease with time, which means the foods become more attractive to some customers as long as the foods are fit for sale and consumption.

Define

$$\begin{aligned} G(t)=\lambda _{2}(t)q(t),\quad t\in [0, T]. \end{aligned}$$
(22)

Then \(G(T)=0\) since \(\lambda _2(T)=0\).

Lemma 1

The function \(G\) is strictly decreasing over the time horizon.

Proof

It follows from the second state equation in (8) and the adjoint Eq. (11) that

$$\begin{aligned} \dot{\lambda }_{2}=\gamma (\lambda _{1}-p)(\alpha -\beta p)-\displaystyle \frac{\lambda _{2}\dot{q}}{q}. \end{aligned}$$
(23)

Therefore, from (22) and (23) we obtain

$$\begin{aligned} \dot{G}=\gamma q(\lambda _{1}-p)(\alpha -\beta p). \end{aligned}$$
(24)

Notice from (19), (20) and (21) that \(\lambda _{1}<p^*\) and \(\alpha >\beta p^*\) for any \(t\in [0,T)\). Hence \(\dot{G}<0,\) i.e., the function \(G\) is strictly decreasing over the time horizon. \(\square \)

Proposition 4

If \(G(0)>\frac{c}{k}\), the optimal investment rate

$$\begin{aligned} u^{*} =\left\{ \! \begin{array}{ll} U, &{}\quad 0\le t<t_2\\ 0, &{}\quad t_2\le t\le T,\\ \end{array} \right. \end{aligned}$$
(25)

where \(t_2=G^{-1}\left( \frac{c}{k}\right) \). Otherwise, the optimal investment rate

$$\begin{aligned} u^{*}=0 \end{aligned}$$
(26)

over the time horizon \([0, T].\)

Proof

Owing to the continuity and monotonicity of \(G(t)\) and \(G(T)=0\), if \(G(0)>\frac{c}{k}\), there exists a unique time point \(t_2=G^{-1}\left( \frac{c}{k}\right) \) satisfying \(0< t_2<T\) and \(G(t)<\frac{c}{k}\) for any \(t\in (t_2, T]\). Combining (15) with (22), we get Eq. (25). If \(G(0)\le \frac{c}{k}\), from Lemma 1, we have \(G(t)\le \frac{c}{k}\) for any \(t\in [0, T]\). By virtue of (15) and (22), we get Eq. (26). \(\square \)

This result reflects two intuitive situations for the management of perishable foods. On one hand, if the investment cost per unit is relatively high and the deterioration rate of food quality is relatively low, the retailer will choose not to invest. On the other hand, if the investment cost per unit is relatively low while the deterioration rate of food quality is relatively high, the retailer will invest for a period of time and the investment activity will come to an end when the inventory level becomes low.

Based on Propositions 3 and 4, the following four cases may arise:

Case 1 :

\( p=\displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2} \left( t-T\right) , \quad u=0\).

Case 2 :

\(p= \left\{ \! \begin{array}{ll} 0 ,&{}\quad 0\le t\le t_{1}\\ \displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2} \left( t-T\right) , &{}\quad t_{1}<t\le T, \\ \end{array} \right. \quad u=0.\)

Case 3 :

\( p=\displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2} \left( t-T\right) , \quad u= \left\{ \! \begin{array}{ll} U, &{}\quad 0\le t<t_{2}\\ 0, &{}\quad t_{2}\le t\le T.\\ \end{array} \right. \)

Case 4 :

\(p=\left\{ \! \begin{array}{ll} 0 ,&{}\quad 0\le t\le t_{1} \\ \displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2} \left( t-T\right) , &{}\quad t_{1}<t\le T, \end{array} \right. \quad u=\left\{ \! \begin{array}{ll} U, &{}\quad 0\le t<t_{2}\\ 0, &{}\quad t_{2}\le t\le T.\\ \end{array} \right. \)

We, one by one, provide the conditions that make a certain candidate be an optimal strategy in the following.

As for Case 1, the strategy is

$$\begin{aligned} p=\displaystyle \frac{\alpha }{\beta }+\displaystyle \frac{h}{2} \left( t-T\right) , \quad u=0, \end{aligned}$$
(27)

so from (24) and the first state equation in (8) we respectively get

$$\begin{aligned} \dot{G}=-\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{-\theta _{0}t}, \end{aligned}$$
(28)

and

$$\begin{aligned} \dot{I}=-\frac{1}{2}\gamma q_{0}\beta h(T-t)e^{-\theta _{0}t}. \end{aligned}$$
(29)

Using the conditions \(G(T)=0,\,I(0)=I_0\) and \(I(T)=0\), we further obtain from (28) and (29) that

$$\begin{aligned} G(0)=\displaystyle \frac{\gamma q_0\beta h^{2} }{4\theta _{0}^{3}}\left( \theta _0^{2}T^{2}-2\theta _0T+2 -2e^{-\theta _0T}\right) , \end{aligned}$$
(30)

and

$$\begin{aligned} I_{0}-\displaystyle \frac{\gamma q_{0}\beta h }{2\theta _{0}^{2}} \left( e^{-\theta _{0}T}+\theta _{0}T-1\right) =0. \end{aligned}$$
(31)

To determine \(T\), we solve Eq. (31). If it has a solution such that \(0<T\le \frac{2\alpha }{\beta h}\) and \(G(0)\le \frac{c}{k}\), from Propositions 3 and 4, we obtain that the strategy given in (27) is optimal.

As for Case 2, the strategy is

$$\begin{aligned} p= \left\{ \! \begin{array}{ll} 0 ,&{}\quad 0\le t\le t_{1}\\ \displaystyle \frac{\alpha }{\beta } +\displaystyle \frac{h}{2}\left( t-T\right) , &{}\quad t_{1}<t\le T,\\ \end{array} \right. \quad u=0. \end{aligned}$$
(32)

Hence, from (24) and the first state equation in (8) we have

$$\begin{aligned} \dot{G}= \left\{ \! \begin{array}{ll} \alpha \gamma q_{0}\left( h(t-T)+\displaystyle \frac{\alpha }{\beta }\right) e^{-\theta _{0}t} ,&{}\quad 0\le t\le t_{1}\\ -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{-\theta _{0}t}, &{}\quad t_{1}<t\le T,\\ \end{array} \right. \end{aligned}$$
(33)

and

$$\begin{aligned} \dot{I}= \left\{ \! \begin{array}{ll} -\alpha \gamma q_{0}e^{-\theta _{0}t} ,&{}\quad 0\le t\le t_{1}\\ -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{-\theta _{0}t}, &{}\quad t_{1}<t\le T.\\ \end{array} \right. \end{aligned}$$
(34)

By virtue of \(G(T)=0,\,I(0)=I_0,\,I(T)=0\) and the continuity of functions \(G(t)\) and \(I(t)\), we further obtain from (33) and (34) that

$$\begin{aligned} G(0)&=\displaystyle \frac{\alpha \gamma q_0}{\theta _0}\left( -\displaystyle \frac{\alpha }{\beta }e^{-\theta _0t_1} -\frac{\alpha }{\beta }+hT+\frac{h}{\theta _0}\left( e^{-\theta _0t_1}-1\right) \right) \nonumber \\&\quad +\displaystyle \frac{\gamma q_0\beta h^{2}}{4\theta _{0}^{3}}\left( \theta _0^{2}(t_1-T)^{2}e^{-\theta _0t_1} +2\theta _0(t_1-T)e^{-\theta _0t_1} +2e^{-\theta _0t_1}-2e^{-\theta _0T}\right) , \end{aligned}$$
(35)

and

$$\begin{aligned} \begin{array}{l} h(t_{1}\!-\!T)+\displaystyle \frac{2\alpha }{\beta }=0,\\ I_{0}\!+\!\displaystyle \frac{\alpha \gamma q_{0}}{\theta _{0}}\left( e^{-\theta _{0}t_{1}}-1\right) \!-\!\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}}(T-t_{1})e^{-\theta _{0}t_{1}}\! -\!\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}^{2}}(e^{-\theta _{0}T}\!-\!e^{-\theta _{0}t_{1}})\!=\!0.\\ \end{array} \end{aligned}$$
(36)

Solve Eq. (36) for \(t_1\) and \(T\). If there are solutions satisfying \(0<t_1<T\) and \(G(0)\le \frac{c}{k}\), Propositions 3 and 4 show that the strategy in (32) is optimal.

As for Case 3, the corresponding strategy is

$$\begin{aligned} p=\displaystyle \frac{\alpha }{\beta } +\displaystyle \frac{h}{2}\left( t-T\right) ,\quad u=\left\{ \! \begin{array}{ll} U, &{}\quad 0\le t<t_{2}\\ 0, &{}\quad t_{2}\le t\le T.\\ \end{array} \right. \end{aligned}$$
(37)

It follows from (24) and the first state equation in (8) that

$$\begin{aligned} \dot{G}= \left\{ \! \begin{array}{ll} -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{(kU-\theta _{0})t}, &{}\quad 0\le t<t_{2}\\ -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{kUt_2-\theta _{0}t}, &{}\quad t_{2}\le t\le T,\\ \end{array} \right. \end{aligned}$$
(38)

and

$$\begin{aligned} \dot{I}= \left\{ \! \begin{array}{ll} -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{(kU-\theta _{0})t}, &{}\quad 0\le t<t_{2}\\ -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{kUt_2-\theta _{0}t}, &{}\quad t_{2}\le t\le T.\\ \end{array} \right. \end{aligned}$$
(39)

Owing to the conditions that \(G(t_2)=\frac{c}{k},\,G(T)=0,\,I(0)=I_0,\,I(T)=0\) and the functions \(G(t)\) and \(I(t)\) are continuous, we further get from (38) and (39) that

$$\begin{aligned} \begin{array}{l} \left( \displaystyle \frac{(t_2-T)^{2}}{\theta _{0}} \!+\!\displaystyle \frac{2(t_2-T)}{\theta _{0}^{2}}\right) e^{\left( kU-\theta _{0}\right) t_{2}}\!-\!\displaystyle \frac{2e^{kUt_2}}{\theta _{0}^{3}} \left( e^{-\theta _{0}T}\!-\!e^{-\theta _{0}t_{2}}\right) \!=\!\displaystyle \frac{4c}{k\beta h^{2}\gamma q_{0}},\\ I_{0}\!+\!\displaystyle \frac{\gamma q_{0}\beta h }{2(\theta _{0}-kU)}\left( T\!-\!\frac{1}{\theta _{0}-kU}\right) \left( e^{(kU-\theta _{0})t_{2}}\!-\!1\right) \!-\! \displaystyle \frac{\gamma q_{0}\beta h}{2(\theta _{0}-kU)}t_{2}e^{(kU-\theta _{0})t_{2}}\\ \quad -\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}}(T-t_{2})e^{(kU-\theta _{0})t_{2}} -\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}^{2}}\left( e^{kUt_{2}-\theta _{0}T} -e^{(kU-\theta _{0})t_{2}}\right) =0.\\ \end{array} \end{aligned}$$
(40)

If there are solutions \(t_2\) and \(T\) for (40) such that \(0<t_2<T\le \frac{2\alpha }{\beta h}\), from Propositions 3 and 4, the optimal strategy is shown in (37).

As for Case 4, the corresponding strategy is

$$\begin{aligned} p=\left\{ \! \begin{array}{ll} 0 ,&{}\quad 0\le t\le t_{1}\\ \displaystyle \frac{\alpha }{\beta } +\displaystyle \frac{h}{2}\left( t-T\right) , &{}\quad t_{1}<t\le T, \end{array} \right. \quad u=\left\{ \! \begin{array}{ll} U, &{}\quad 0\le t<t_{2}\\ 0, &{}\quad t_{2}\le t\le T.\\ \end{array} \right. \end{aligned}$$
(41)

Subcase 4.1: \(t_1\ge t_2\).

It follows from (24) and the first state equation in (8) that

$$\begin{aligned} \dot{G}= \left\{ \! \begin{array}{ll} \alpha \gamma q_{0}\left( h(t-T)+\displaystyle \frac{\alpha }{\beta }\right) e^{(kU-\theta _{0})t}, &{}\quad 0\le t<t_{2}\\ \alpha \gamma q_{0}\left( h(t-T)+\displaystyle \frac{\alpha }{\beta }\right) e^{kUt_2-\theta _{0}t}, &{}\quad t_2\le t<t_{1}\\ -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{kUt_2-\theta _{0}t}, &{}\quad t_{1}\le t\le T. \end{array} \right. \end{aligned}$$
(42)

and

$$\begin{aligned} \dot{I}= \left\{ \! \begin{array}{ll} -\alpha \gamma q_{0}e^{(kU-\theta _{0})t}, &{}\quad 0\le t<t_{2}\\ -\alpha \gamma q_{0}e^{kUt_2-\theta _{0}t}, &{}\quad t_2\le t<t_{1}\\ -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{kUt_2-\theta _{0}t}, &{}\quad t_{1}\le t\le T. \end{array} \right. \end{aligned}$$
(43)

By virtue of the conditions \(G(t_2)=\frac{c}{k},\,G(T)=0,\,I(0)=I_0,\,I(T)=0\), the continuity of \(G(t)\) and \(I(t)\), and Eqs. (42) and (43), we obtain the following equations

$$\begin{aligned} \begin{array}{l} h(t_{1}-T)+\displaystyle \frac{2\alpha }{\beta }=0,\\ \displaystyle \frac{\alpha \gamma q_{0}}{\theta _{0}}\left( \left( ht_2\!+\!\displaystyle \frac{\alpha }{\beta } \!+\!\displaystyle \frac{h}{\theta _{0}}\!-\!hT\right) e^{(kU-\theta _{0})t_2}\!-\!\left( ht_1+\displaystyle \frac{\alpha }{\beta } +\displaystyle \frac{h}{\theta _{0}} -hT\right) e^{kUt_2-\theta _{0}t_1}\right) \\ -\displaystyle \frac{\gamma q_{0}\beta h^{2}}{4}\left( \displaystyle \frac{(t_1-T)^{2}}{\theta _{0}} +\displaystyle \frac{2(t_1-T)}{\theta _{0}^{2}}\right) e^{kUt_{2}-\theta _{0}t_{1}} \\ +\displaystyle \frac{\gamma q_{0}\beta h^{2}}{2\theta _{0}^{3}}\left( e^{kUt_{2}-\theta _{0}t_{1}} -e^{kUt_{2}-\theta _{0}T}\right) =-\displaystyle \frac{c}{k},\\ I_{0}+\displaystyle \frac{\alpha \gamma q_{0}}{\theta _{0}-kU}\left( e^{(kU-\theta _{0})t_{2}}-1\right) +\displaystyle \frac{\alpha \gamma q_{0}}{\theta _{0}}\left( e^{kUt_{2}-\theta _{0}t_{1}} -e^{(kU-\theta _{0})t_{2}}\right) \\ -\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}}(T-t_{1}) e^{kUt_{2}-\theta _{0}t_{1}} -\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}^{2}}\left( e^{kUt_{2}-\theta _{0}T} -e^{kUt_{2}-\theta _{0}t_{1}}\right) =0.\\ \end{array} \end{aligned}$$
(44)

If there exist solutions \(t_1,\,t_2\) and \(T\) satisfying \(0<t_2\le t_1<T\), from Propositions 3 and 4, we obtain that the strategy given in (41) is optimal.

Subcase 4.2: \(t_1<t_2\).

From (24) and the first state equation in (8), we respectively get

$$\begin{aligned} \dot{G}= \left\{ \! \begin{array}{ll} \alpha \gamma q_{0}\left( h(t-T)+\displaystyle \frac{\alpha }{\beta }\right) e^{(kU-\theta _{0})t}, &{} 0\le t<t_{1}\\ -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{(kU-\theta _{0})t}, &{} t_1\le t<t_{2}\\ -\displaystyle \frac{1}{4}\gamma q_{0}\beta h^2(T-t)^{2}e^{kUt_2-\theta _{0}t}, &{} t_{2}\le t\le T,\\ \end{array} \right. \end{aligned}$$
(45)

and

$$\begin{aligned} \dot{I}= \left\{ \! \begin{array}{ll} -\alpha \gamma q_{0}e^{(kU-\theta _{0})t}, &{} 0\le t<t_{1}\\ -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{(kU-\theta _{0})t}, &{} t_1\le t<t_{2}\\ -\displaystyle \frac{1}{2}\gamma q_{0}\beta h(T-t)e^{kUt_2-\theta _{0}t}, &{}\ t_{2}\le t\le T.\\ \end{array} \right. \end{aligned}$$
(46)

Using the conditions \(G(t_2)=\frac{c}{k},\,G(T)=0,\,I(0)=I_0,\,I(T)=0\), the continuity of \(G(t)\) and \(I(t)\), and Eqs. (45) and (46), we have the following equations

$$\begin{aligned}&h(t_{1}-T)+\displaystyle \frac{2\alpha }{\beta }=0,\nonumber \\&\left( \displaystyle \frac{(t_2-T)^{2}}{\theta _{0}} \!+\!\displaystyle \frac{2(t_2-T)}{\theta _{0}^{2}}\right) e^{(kU-\theta _{0})t_{2}}\!-\!\displaystyle \frac{2e^{kUt_{2}}}{\theta _{0}^{3}} \left( e^{-\theta _{0}T}\!-\!e^{-\theta _{0}t_{2}}\right) \!=\!\displaystyle \frac{4c}{k\beta h^{2}\gamma q_{0}},\nonumber \\&I_{0}+\displaystyle \frac{\alpha \gamma q_{0}}{\theta _{0}-kU} \left( e^{(kU-\theta _{0})t_{1}}-1\right) +\frac{\gamma q_{0}\beta hT}{2(\theta _{0}-kU)} \left( e^{(kU-\theta _{0})t_{2}}-e^{(kU\!-\!\theta _{0})t_{1}}\right) \nonumber \\&-\displaystyle \frac{\gamma q_{0}\beta h}{2(\theta _{0}-kU)^2} \left( e^{(kU-\theta _{0})t_{2}}-e^{(kU-\theta _{0})t_{1}}\right) -\displaystyle \frac{\gamma q_{0}\beta h}{2\theta _{0}}(T-t_{2})e^{(kU-\theta _{0})t_{2}} \nonumber \\&-\displaystyle \frac{\gamma q_{0}\beta h }{2(\theta _{0}\!-\!kU)}\!\left( t_{2}e^{(kU\!-\!\theta _{0})t_{2}}\! -\!t_{1} e^{(kU\!-\!\theta _{0})t_{1}}\!\right) \!-\!\displaystyle \frac{\gamma q_{0}\beta he^{kUt_{2}}}{2\theta _{0}^{2}}\!\left( e^{\!-\!\theta _{0}T} \!-\! e^{-\theta _{0}t_{2}}\!\right) \!=\!0. \end{aligned}$$
(47)

If there exist solutions \(t_1,\,t_2\) and \(T\) which satisfy \(0<t_1< t_2<T\), from Propositions 3 and 4, we obtain the optimal strategy specified in (41).

4.3 Algorithm

We have proven the existence of an optimal solution based on Filippov–Cesari theorem and obtained all the candidates by maximum principle. To gain the optimal pricing and investment strategies, an important problem is to seek for the critical time points \(t_1,\,t_2\) and \(T\) by solving Eqs. (31), (36), (40), (44) and (47), and verify whether the solutions satisfy the corresponding conditions. Hence, a simple and effective algorithm is designed to obtain the optimal solution \((p^*,u^*)\) of the optimization problem (8).

Algorithm:

Step 1 :

Solve Eq. (31). If the solution \(T\) satisfies \(0<T\le \frac{2\alpha }{\beta h}\) and \(G(0)\le \frac{c}{k},\) then the optimal strategy is shown in (27) and stop. Otherwise, go to step 2.

Step 2 :

Solve Eq. (36). If the solutions \(t_1\) and \(T\) satisfy \(0<t_1<T\) and \(G(0)\le \frac{c}{k},\) then the optimal strategy is shown in (32) and stop. Otherwise, go to step 3.

Step 3 :

Solve Eq. (40). If the solutions \(t_2\) and \(T\) satisfy \(0<t_2<T\le \frac{2\alpha }{\beta h}\), then the optimal strategy is shown in (37) and stop. Otherwise, the optimal strategy is shown in (41) and stop.

Through this algorithm, we can get the optimal strategy \((p^*,u^*)\) and then obtain the corresponding optimal total profit \(J^*\).

5 Illustrative examples

In this section, two numerical examples are employed to illustrate the solution procedure and the results.

Example 1

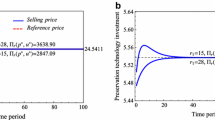
Let \(\alpha =10, \beta =1, \gamma =5, h=0.2, \theta _0=0.035, k=0.01, U=3, q_0=1, I_0=300, c=10.\) These parameters are chosen according to previous studies with respect to the pricing and inventory models (e.g., Wang and Li 2012), which allows for a comprehensive illustration. Executing the algorithm procedure proposed in Sect. 4.3, the computational results are shown in Table 1 where C (S) denotes that the algorithm procedure continues (stops). Under Case 1 corresponding to Step 1, we solve Eq. (31) and obtain \(T=43.2927\le \frac{2\alpha }{\beta h}=100\) and \(G(0)=963.2280\le \frac{c}{k}=1000\). Hence, the optimal strategy is (27), namely

$$\begin{aligned} p^*=0.1t+5.6707, \quad u^*=0, \quad \forall t\in [0, 43.2927], \end{aligned}$$

which implies the retail price is positive and the retailer will not invest to improve the store conditions at the sales cycle. The corresponding total profit is \(J^*=~1365.6617\).

Table 1 Computational results of example 1
Full size table

Varying natural deterioration coefficient and keeping others unchanged, we identify a threshold value \(\hat{\theta }_0=0.0387\), before and after which the retailer will adopt different investment strategies. When \(\theta _0<\hat{\theta }_0\), i.e., for a relatively low deterioration rate of the food quality, the optimal strategy for the retailer is not to invest, while for a relatively high natural deterioration rate of the food quality (\(\theta _0>\hat{\theta }_0\)), the retailer implements investment activity for a certain time and then doesn’t invest any more. In the same way, we can obtain the corresponding strategies by changing another parameter, such as \(\gamma ,\,h\) or \(c\). These observations are practical and well validate the results acquired by theoretical analysis.

In the following example, we investigate the case that the natural deterioration rate of the food quality is relatively high and the unit investment cost is relatively low, and provide the optimal strategies.

Example 2

Let \(\alpha =10, \beta =1, \gamma =5, h=0.2, \theta _0=0.06, k=0.01, U=3, q_0=1, I_0=300, c=2.\) Executing the algorithm procedure proposed in Sect. 4.3, the computational results are shown in Table 2. Under Case 3 corresponding to Step 3, we solve Eq. (40) and obtain \(t_2=13.8254\) and \(T=43.8142\), which satisfy \(0<t_2<T\le \frac{2\alpha }{\beta h}\). Therefore, the optimal strategy is (37), i.e.,

$$\begin{aligned} p^*=0.1t+5.6186,\quad u^*= \left\{ \! \begin{array}{ll} 3, &{}\quad 0\le t<13.8254\\ 0, &{}\quad 13.8254\le t\le 43.8142, \end{array} \right. \end{aligned}$$

which shows that the retailer will invest from the beginning to the time point \(t^*_2=13.8254\) and will not invest after \(t^*_2\). The corresponding total profit is \(J^*=1287.6712\).

Table 2 Computational results of example 2
Full size table

To obtain more managerial insights, we conduct sensitivity analysis on key model parameters based on example 2. Specifically, we study the effects of changes in the values of parameters \(\theta _0,\,\gamma ,\,h\) and \(c\) on the optimal demand rate \(D^*\), investment time \(t_2^{*}\), sales cycle \(T^{*}\), price \(p^*\) elucidated by the initial price \(p_0^*\), and total profit \(J^{*}\). Varying one parameter at a time and keeping the remaining parameters unchanged, the results are concluded in Figs. 1–4 and Table 3.

Fig. 1
figure 1

The demand rate with different \(\theta _0\)

Full size image
Fig. 2
figure 2

The demand rate with different \(\gamma \)

Full size image
Fig. 3
figure 3

The demand rate with different \(h\)

Full size image
Fig. 4
figure 4

The demand rate with different \(c\)

Full size image
Table 3 Sensitivity analysis with respect to the system parameters
Full size table

Based on the computational results, the following observations can be made:

  1. (1)

    When the natural deteriorating coefficient \(\theta _0\) increases and other parameters are fixed, as shown in Fig. 1, the optimal demand rate \(D^*\) increases at the beginning, then decreases and finally increases again. Table 3 reveals that the optimal investment time \(t_2^*\) and sales cycle \(T^*\) increase while the optimal initial price \(p_0^*\) and total profit \(J^*\) decrease. From an economic viewpoint, this implies that when a retailer faces a higher deteriorating rate, he may adopt a lower initial price to promote demand. Hence, the demand rate increases with respect to \(\theta _0\) at the beginning. As the quality decays continuously, the food with a higher deteriorating rate has a greater negative effect on the demand rate, which drops the demand rate more quickly. Then, the demand rate begins decreasing from some time point. What’s more, the retailer will manage the inventory system with a higher deteriorating rate by prolonging the investment time, so the demand rate begins increasing from a certain time point again. Obviously, a higher deterioration rate will overall drop the demand rate, and increase the corresponding sales cycle for a given initial inventory level, thus leading to a lower total profit.

  2. (2)

    The optimal demand rate \(D^*\) first increases and then decreases, and the optimal investment time \(t_2^*\) and sales cycle \(T^*\) decrease whereas the optimal initial price \(p_0^*\) and total profit \(J^*\) increase with an increase in \(\gamma \). This feature is reflected in Fig. 2 and Table 3. This result means that with an increase in the value of \(\gamma \), the demand rate increases at the beginning, then the retailer will raise the corresponding initial price. Since the price is increasing gradually, a higher price will drop the demand rate more quickly. Hence, the demand rate begins decreasing from some time point. Moreover, a higher \(\gamma \) meaning a greater demand rate leads to a shorter investment time. The demand rate on the whole is increasing as \(\gamma \) increases, which leads to a shorter sales cycle. Note that the average price also increases, so the total profit increases.

  3. (3)

    For fixed values of \(\theta _0,\,\gamma \) and \(c\), it can be observed from Fig. 3 and Table 3 that as the holding cost per unit \(h\) increases, the optimal demand rate \(D^*\) first increases and then decreases from a certain time point, and the optimal investment time \(t_2^*\), sales cycle \(T^*\), initial price \(p_0^*\) and total profit \(J^*\) decrease. It is reasonable that when facing a higher holding cost per unit, the retailer will adopt a lower initial price to promote the demand and reduce inventory level more quickly in order to avoid incurring more holding costs. However, higher holding cost per unit will make the retailer increase the retail price more quickly, so the demand rate decreases from a certain time point. Overall, the demand rate is increasing, which leads to a shorter sales cycle. The higher the holding cost per unit is, the lower total profit is.

  4. (4)

    Table 3 shows that with an increase in the value of \(c\), the optimal sales cycle \(T^*\) increases while the optimal investment time \(t_2^*\), initial price \(p_0^*\) and total profit \(J^*\) decrease. The corresponding managerial insight is that as the investment cost per unit increases, the retailer tends to moderately shorten the investment time and reduce the initial price. Moreover, a higher investment cost leads to a longer sales cycle and a lower total profit. Figure 4 indicates that the impact of the unit investment cost \(c\) on the optimal demand \(D^*\) is similar to that of the initial deteriorating coefficient.

6 Conclusions

In most of inventory models in the literature, the inventory deterioration of perishable foods has been extensively studied, while the quality degradation has received less attention. In this paper, taking the joint dynamic pricing and investment strategy into consideration, we formulate an inventory model for perishable foods, in which the demand depends on the price and quality that decays continuously. The analytic results show that whether the retailer should invest and how long the investment time should be adopted have a significant influence on the total profit. At the same time, we also find that the quality degradation leads apparent changes to the demand.

The major feature of this research is simultaneously determining the dynamic pricing strategy and investment strategy in reducing the deterioration rate of the quality for perishable foods, and considering the quality as a state variable and an important influential factor on the demand. A potential extension of this paper is to consider different function forms regarding the investment rate and deterioration coefficient. Future research can also consider competitions among several retailers.