Introduction

Deterioration refers to a product’s quality change over time [10]. In traditional inventory management, we assume the shelf life of deteriorating items like fruit, vegetables, and medicines is constant while stored. Contrarily, in reality deteriorating items’ shelf life changes over time [1]. The shelf life of deteriorating items depends on the products’ packing, holding, atmosphere, and nature [26]. After a specific period, these products become outdated and unsuitable for final consumption. The recent study highlights that the U.S.A. accounts 10% of food wastage at the retail level [24]. Moreover, approximately 30% of fresh agricultural items were lost due to deterioration [52]. Similarly, due to deterioration, China suffered a tremendous economic loss of 43 billion U.S$ [57]. The wastage of food items at a large scale has a twofold implication, as it involves direct economic loss and, at the same time, overburdens natural resources.

Therefore, the inventory loss due to the deterioration needs to be addressed, and it has gained wide scientific attention recently [15]. Therefore, to overcome this challenge [14] introduced the preservative technology concept to control the deterioration effects of deteriorating items. Retailers invest in preservative technology like refrigerators, packing, etc. Consequently, the deteriorating items’ shelf life enhances food’s final consumption time period [40]. As a result, retailers obtain extra revenue from Preservative Technology Investment (PTI). In the traditional industry, retailers have to pay immediately after the purchase. However, it does not seem to be a pragmatic approach if we look at today’s competitive business environment’s present scenario. Therefore, we need to alter this classical business assumption. The primary drawback of this approach is the increasing inventory cost at the retailer’s end; concomitantly, future demand is unexpected (He et al., 2020). Consequently, retailers order minimum items to avoid their future sale risk. Concurrently, the supplier also bears a massive loss due to the retailers’ minimum order of sale items. Therefore, The Permissible Delay in Payment (PDP) concept was introduced by [9]. However, extensive research has been carried out by several researchers like [17], [2, 37], [56] & [18] to concise the riddle task of existing research gap.

Literature Review

We are introducing PDP and PTI approaches coherent with meticulous analysis of deterioration in different cases. Keeping in view of readers’ perspective the, literature review is subdivided into three segments.

  1. (1)

    Literature review on permissible delay in payment (PDP).

  2. (2)

    Preservative technology investment (PTI).

  3. (3)

    PDP and PTI coherent approach.

Permissible Delay in Payment (PDP)

The suppliers offer retailers a specific period to settle their dues without an extra charge. Thus, the permissible delay in payment plays a vital role for retailers because they accumulate more revenue in the form of interest from the bank. Besides, suppliers also get additional revenue through additional orders processed by retailers. Hence, PDP eventually allows suppliers to enhance their sale orders, which is of utmost important task in supply chain management.

Several researchers [6]; [8], [33] worked on deteriorating items for linear demand function of Price and time. A study reported by Jaggi et al. [16] Introduced a fuzzy approach for the permissible delay in payment for the price-dependent linear demand function. Their study focused on optimal decision policies for retailers for maximum profit. Hence, they discussed the possibility of a higher interest earned than the interest charged rate (\(I_{e} > I_{c}\)). A study reported by [44] Worked on the generalized reduced gradient (GRG) method to minimize inventory costs for deteriorating items. [42] presented a price and stock-dependent inventory model without shortage. They allowed two levels of trade credit in their research. The optimal replenishment policy for retailers through the advance cash credit approach is reported by [51]. The study focuses on, a special discount provided to retailers if they pay some advance cash to suppliers. Recently, [32] presented a modified model of [5, 31] with more realistic approaches. Concurrently [41], (Shaikh, A. A., Cárdenas-Barrón, L. E., & Tiwari, 2018), [43, 45] and [50] extended,the PDP approach with several price-depended demand functions. Afterward, different types of demand emerged in the market for decaying items. When demand changes into two phases, it is known as ‘ramp-type demand.’ This type of demand pattern follows in the seasonal demand of deteriorating items or new electronic items arriving. Its demand adolescent in phase I, then become constant in other phases. [48] introduced a new strategy to reduce the overall inventory cost through their model. A time-dependent ramp-type demand was adopted for PDP with a partial backlog. [4] proposed an inventory model for ramp-type demand for the PDP approach. Their study was vernalizing the exponential rate of deterioration. After that, A pragmatic approach was shared by [52] through their comparison study, with and without permissible payment delay for time-dependent, ramp-type demand. Later, [47] proposed a new approach of permissible delay in payment for ramp-type demand function of price and time. Their study explains how retailers get extra revenue through the effect of permissible delays in payment.

Preservative Technology Investment (PTI)

Several researchers considered deterioration as an uncontrollable exogenous variable. Several organizations manage inventory at a fixed rate of deterioration. Therefore, they envisage huge losses periodically. Furthermore, there was a need to control deterioration to enhance the revenue and avoid unnecessary waste of deteriorating items. Then, several techniques were implemented as ‘process improvement’ and enhancing ‘storage techniques’, even though storage industries still suffered from leviathan loss due to deterioration effect over the storage period. Therefore, industries required a salient investment to control the deterioration effect over time. Moreover, the term preservative technology was introduced by [14]. Their study proposed a solution procedure for deterministic demand and controllable deterioration rate. The retailer may invest some amount in preservative technology and revert more profit due to deterioration control. Then, [12] extended the work of [39] and [58] with a preservative approach to seasonal demand for deteriorating items. After that, [21, 22, 34] proposed an inventory model for deteriorating items to trapezoidal demand. Their study briefs us on the impact of preservative technology investment on inventory through their comparison study. Further, [35] introduced an inventory model for the seasonal demand of deteriorating items. They considered price and stock-dependent demand function and extended the model of [12] as a particular case in their study. [30] represented the effect of preservative technology over cycle length and deterioration rate consistently for price-dependent demand and time-dependent deterioration rate. Concurrently, [3] Introduced the concept of price discounts with the PDP approach under the 20–40% price discounts concept after selling inventory 50–90%, respectively. Recently (S. [23, 29], [38], and [20] briefly introduced an inventory model for ramp-type demand with partial shortage.

Permissible Delay in Payment and Preservative Approach (PDP and PTI)

PDP and PTI approaches are significant from retailers’ profit point of view, even though few researchers coherent work on nascent approaches towards igniting profit. [49] Investigated an inventory model for deteriorating items under the assumption of PDP and PTI together. The retailer’s optimum order policy for supply chain management was discussed in their study for deteriorating items. Then, [54] discussed an integrated production–distribution model under the assumption of SCM. They discussed adequate decision of optimal supply chain for deteriorating items under the PDP, and PTI approaches separately. Similarly, [53] introduced an inventory policy to reduce the existing deterioration rate due to an additional investment in preservative technology. In their study, remaining stock of deteriorating items shifted to another market as a trade credit approach. Later, [36] developed an inventory model to control the deterioration rate through the PTI under the PDP policy. Their study emphasized joint effect over optimal ordering policy. (M. [28] introduced the inventory model for PDP and PTI approaches together. Here, suppliers provide a specific time limit to retailers without an interest charge. After that, retailers either pay interest amounts or order more quantities to avoid envisaging interest charges. Recently, [46] Developed an inventory model for deteriorating items with the concept of PTI, and a single level of trade credit allowed for ramp-type demand with partial backlog. Then, [7] discussed an inventory model under PTI and the trade credit approach. A Price-dependent demand is illustrated through the ‘swarn optimizing’ method in their study.

Research Gap and Contribution

Many researchers worked on PDP and PTI approaches. However, very limited studies combine the capabilities of both concepts. Recently, [25] depicted that Bangladesh procure $7.05 Million additional income during fiscal year 2020–21 with only mango sale.

There are enormous studies available in the field of permissible delay in payment and the preservative approach separately. Even though prescience research gap stimulate to develop a coherent PDP and PTI approaches. Therefore, suggested study introduces the concept of permissible delay in payment with a preservation technology approach (freezing) to enhance the profit of suppliers and retailers. This study does not apply only to suppliers’ and retailers’ points of view. Moreover, it will provide significant input to the overall economic growth of any region. As extra demands result in extra sales, job opportunities may be generated in a community that is imperative for the sustenance of any society and economy. Symmetrically, preservative technology enhances the shelf life of deteriorating items; as a result, society overcomes food security issues through the preservative technology approach, and retailers may earn extra revenue due to additional inventory saved by PTI. We are adopting both approaches in the current study, which shall be overwhelmed effects on managerial decisions of extra revenue as well as on society in the form of food security. Here the suggested model focused on combine effect of both approaches uniquely. Moreover, a fix deterioration rate is considered for inventory models. Yet, the suggested model controls deterioration as a derivative rate of deterioration itself due to PTI investment. Apart from them, the suggested model considered a price and time dependent demand function which exhibits a comprehensive result for retailers rather than a price or time dependent only. The optimal price and replenishment policy due to both approaches attract retailers marvelously. Therefore, novel results in Table 10, Investigates a fabulous contribution into the existing literature to find the answers to the following questions. (1) Where do retailers get maximum profit (2) Should retailers invest continuously in preservative technology after a specific time (3) Should retailers get maximum profit when adopting our study approaches (4) Can we find the effect of permissible delay and preservative technology separately (5) Up to what point can we store the maximum inventory of deteriorating items.

The rest of the study is described as follows: Sect. “Literature Review” covers the literature review as in Table 1. We define all notations and assumptions in Sect. “Notations and Assumptions”, then analyze them in Sect. “Analysis” with optimality conditions and Hessian Matrix analysis. Further, we cross-verify the optimality through numerical examples and graphs in Sect. “Solution Procedure”. Then, the Advances of the proposed model, sensitivity analysis, and their results are described in Sect.  6, and managerial insight is available in Sect. “Managerial Insights”. Finally, we concluded the study with future remarks in Sect. “Conclusion”.

Table 1 Summary of Literature Review
Full size table

Notations and Assumptions

We developed the proposed model through the stated assumptions and notations.

Notations

T1: Time up to which demand increases \(\left( {{\text{in weeks}},{\text{ i}}.{\text{e}}.,\frac{70}{{10}} = 7weeks} \right)\)

T2: Time up to which demand remains constant.

\(T_{L} :\) Shortage started point from Phase I Phase II.

I: Inventory levels at the start.

Ib: Backlogged shortage.

c0: Ordering cost.

c1: Holding cost per unit time.

c: The purchase price per unit of an item.

θ: Deterioration rate without PTI.

\(\left( {\theta - \tfrac{1}{\theta }} \right)\): Diminishing deterioration rate per unit after preservation technology Investment derivate w.r.t. θ itself.

P: Per unit selling price of the item.

λP: Backlogged Price; \((0 < \lambda < 1)\).

\(\gamma (\eta )\): Waiting time for replenishment of inventory.

H: Holding cost for each Phase.

R: Revenue earned for each Phase.

Net: Profit for each Phase.

Demand Function

This paper considered fruit and vegetables as deteriorating items for seasonal demand. We worked on the ‘EOQ’ model, assuming that PDP and PTI concepts affect them together. Here, the proposed study considered a ramp-type demand, which is price and time-dependent with \(\left( {\theta - \tfrac{1}{\theta }} \right)\) deterioration rate with respect to time due to investment in preservative technology rather than the traditional constant rate of deterioration. The second motive of the study is how to enhance the sale of suppliers. We apply a one-time permissible delay in the payment concept. Hence, suppliers and retailers get additional revenue through the proposed model. The assumption of inventory level decreased with respect to time and deterioration, then reached zero at the level considered.

For Phase I:\(f_{1} \left( {P,t} \right) = \frac{a + bt}{{P^{j} }}\); 0 ≤ t ≤ T1

For Phase II:\(f_{2} \left( {P,t} \right) = \frac{{a + bT_{1} }}{{P^{j} }}\); T1 ≤ t ≤ T2

Our study is based on price and time then ‘a’, ‘b,’ and ‘j’ are other considered demand parameters.

Assumptions

  1. (1)

    Special discount to loyal customers waiting during the shortage period. \(\gamma (\eta ) = 1 - (\eta /T) \, ; \, 0 \, \le \, \eta \, \le \, T\).

  2. (2)

    The backorder price is \(\lambda P \,\) such that \(c < \lambda P{\text{ < P}}\) for this \(\tfrac{c}{P} < \lambda < 1\).

  3. (3)

    Consider a positive demand function of price and time; \(f_{F} (P,t) > 0\).

  4. (4)

    Consider that the SP of items is higher than the purchase price per unit.

  5. (5)

    Consider that the backlog amount shall be precise in the next replenishment.

  6. (6)

    Considering a seasonal demand for the deteriorating items in our study.

  7. (7)

    The replenishment period is a finite horizon.

Analysis

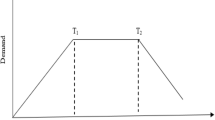
We considered a ramp-type demand for seasonal items like fruit and vegetables where demand increases in phase I due to customers’ preference for fresh items; then, after a specific time period, it becomes constant demand. The inventory vanishes at \(T_{1} \& T_{2}\) as in Fig. 1.

Fig. 1
figure 1

Ramp-type Demand

Full size image

Figure 1 represents ramp-type demand with grace period ‘M’; Fig. 2 compares profit against cases I and II.

Fig. 2
figure 2

Comparison of Profits for Cases I & II

Full size image

Phase 1: Inventory depletes in the growth phase \(\left( {0 \le T_{{L_{1} }} \le T_{1} } \right)\)

$$H_{1} = c_{1} \left[ {\int\limits_{0}^{{T_{{L_{1} }} }} {\left\{ {\left( {T_{{L_{1} }} - 0} \right)f_{1} \left( {P,t} \right) + \left( {\theta - \tfrac{1}{\theta }} \right)} \right\}} dt} \right]$$
$$R_{1} = \int\limits_{0}^{{T_{{L_{1} }} }} {Pf_{1} \left( {P,t} \right)dt + \lambda PI_{{{\mathbf{b}}_{1} }} }$$
$$I_{{b_{1} }} = \int\limits_{{T_{{L_{1} }} }}^{{T_{1} }} {f_{1} \left( {P,t} \right)*\gamma \left( {T_{1} - t} \right)dt} { + }\int\limits_{{T_{1} }}^{{T_{2} }} {f_{2} \left( {P,t} \right)*\gamma \left( {T_{2} - t} \right)dt}$$
$$I_{1} = \int\limits_{0}^{{T_{{L_{1} }} }} {\left\{ {f_{1} \left( {p,t} \right) \, + \, \left( {\theta - \tfrac{1}{\theta }} \right)} \right\} \, dt}$$
$${\text{I}}_{{e_{1} }} {\text{ = P*Ie*}}\int\limits_{0}^{{T_{{L_{1} }} }} {\left( {{\text{T}}_{{{\text{L}}_{1} }} {\text{ - t}}} \right){*}\left( {\frac{{\text{a + bt}}}{{{\text{P}}^{{\text{j}}} }}} \right){\text{dt}}}$$
$$I_{c} = c * I_{c} \left[ {\int\limits_{M}^{{T_{{L_{1} }} }} {\left( {t - M} \right) * \left( {\left( {\frac{a + bt}{{P^{j} }}} \right) + \left( {\theta - \tfrac{1}{\theta }} \right)} \right)dt} } \right]$$
$$Net_{1} = \left( {R_{1} - H_{1} - c_{0} - c\left( {I_{1} + I_{{b_{1} }} } \right) + \left( {I_{{e_{1} }} - I_{{c_{1} }} } \right)/T_{2} } \right)$$
(1)

Phase II: Inventory depletes in a constant phase \((T_{1} \le T_{{L_{2} }} \le T_{2} )\)

$$H_{2} = c_{1} \left[ {\int\limits_{0}^{{T_{1} }} {\left\{ {\left( {T_{1} - 0} \right)f_{1} \left( {P,t} \right) + \left( {\theta - \tfrac{1}{\theta }} \right)} \right\}} dt{ + }\int\limits_{{T_{1} }}^{{T_{{L_{2} }} }} {\left\{ {\left( {T_{{L_{2} }} - 0} \right)f_{2} \left( {P,t} \right) + \left( {\theta - \tfrac{1}{\theta }} \right)} \right\}} dt} \right]$$
$$R_{2} = \int\limits_{0}^{{T_{1} }} {Pf_{1} \left( {P,t} \right)} dt + \int\limits_{{T_{1} }}^{{T_{{L_{2} }} }} {Pf_{2} \left( {P,t} \right)} dt + \lambda PI_{{b_{2} }}$$
$$I_{{b_{2} }} = \int\limits_{{T_{{L_{2} }} }}^{{T_{2} }} {f_{2} \left( {P,t} \right)*\gamma \left( {T_{2} - t} \right)dt} \,$$
$$I_{2} = \int\limits_{0}^{{T_{1} }} {\left\{ {f_{1} \left( {p,t} \right) \, + \, \left( {\theta - \tfrac{1}{\theta }} \right) \, } \right\}dt} + \int\limits_{{T_{1} }}^{{T_{{L_{2} }} }} {\left\{ {f_{2} \left( {p,t} \right) \, + \, \left( {\theta - \tfrac{1}{\theta }} \right) \, } \right\}dt}$$
$$I_{{e_{2} }} = P*I_{e} \left[ {\int\limits_{0}^{{T_{1} }} {\left( {T_{1} - t} \right) * \left( {\frac{a + bt}{{P^{j} }}} \right)} dt + \int\limits_{{T_{1} }}^{{T_{{L_{2} }} }} {\left( {T_{{L_{2} }} - t} \right) * \left( {\frac{a + bt}{{P^{j} }}} \right)} dt} \right]$$
$$Net_{2} = \left( {R_{2} - H_{2} - c_{0} - c\left( {I_{2} + I_{{b_{2} }} } \right) + \left( {I_{e} - I_{c} } \right)} \right)/T_{2}$$
(2)

Theorem 1

(a) \(Net_{1}\) is a concave function in \(T_{{L_{1} }}^{{}}\) iff.

$$\begin{gathered} 2a\left[ {T_{1} (P^{1 - j} + \theta c\left( { - 1 + I_{c} \left( {M - T_{{L_{1} }} } \right)} \right) + \theta T_{{L_{1} }} \left( {c - P\lambda } \right)} \right] + 2b\theta T_{{L_{1} }}^{2} \left( { - c + I_{e} + c - P\lambda } \right) \hfill \\ + T_{{L_{1} }} T_{1} [I_{e} P^{1 - j} - c_{1} P^{ - j} - 2\theta \left\{ {bc\left( {1 + MI_{c} } \right) - T_{{L_{1} }} I_{c} } \right\} \le P^{j} - \theta^{2} \hfill \\ \end{gathered}$$
(3)

(b) \(Net_{2}\) is a concave function in \(T_{{L_{2} }}^{{}}\) iff.

$$\begin{gathered} T_{1}^{2} b\theta \left( {c_{1} - I_{e} P + cI_{c} } \right) + T_{1} \left[ \begin{gathered} a\theta \left( {c_{1} - bT_{{L_{2} }} + cI_{{c_{2} }} } \right) + b\theta ( - c + T_{{L_{2} }} \left( {c\left( {I_{c} - 1} \right) - P\lambda } \right) \hfill \\ + \theta P^{j} (c_{1} \left( {\theta - \tfrac{1}{\theta }} \right) + cI_{c} \theta + \tfrac{{bT_{{L_{2} }} }}{{P^{j} }}\left( {c - P\lambda } \right) \hfill \\ \end{gathered} \right] \hfill \\ + a\theta T_{{L_{2} }} \left[ {c\left( {1 + I_{c} } \right) + P\left( {1 + I_{e} } \right)} \right] \hfill \\ + P^{j} \left[ {c_{1} T_{{L_{2} }} \left( {T_{1} - \theta^{2} } \right) + c(1 - \theta^{2} \left( {1 - T_{{L_{2} }} I_{c} } \right)} \right] + a\theta \left( {T_{2} P - } \right)c \le \tfrac{ - 1}{{p^{ - j} }} \hfill \\ \end{gathered}$$
(4)

Case II

(2a).\(Net_{1}\) Is a concave function in \(T_{{L_{1} }}^{{}}\) iff.

$$\begin{gathered} 2McI_{c} \left[ {T_{1} P^{j} \theta + aT_{1} + bT_{1} T_{{L_{1} }} } \right] + T_{{L_{1} }}^{2} bT_{1} \left[ { - 2c_{1} + I_{e} P - 2c^{2} I_{c} } \right] \hfill \\ + 2T_{1} T_{{L_{1} }} \left[ { - P^{2} \theta \left( {c_{1} + cI_{c} } \right) + a\left( { - c_{1} + I_{e} P - cI_{c} } \right) + b\left( {P - c} \right)} \right] \hfill \\ + 2T_{1} \left[ {a\left( {P - c} \right) - cP^{j} \theta } \right] + 3T_{{L_{1} }} \left( {c - P\lambda } \right) \le \tfrac{1}{{P^{ - j} }} \hfill \\ \end{gathered}$$
(5)

(2b) \(Net_{2}\) is a concave function in \(T_{{L_{2} }}^{{}}\) iff.

$$\begin{gathered} T_{1} T_{2} \left[ {c_{1} \left( {1 + a - bT_{{L_{2} }} } \right) + P\left( {b - aI_{c} P} \right) + bT_{{L_{2} }} \left( {I_{e} P - c_{1} } \right)} \right] + bT_{1}^{2} T_{2} \left( {c_{1} - I_{e} P} \right) \hfill \\ \quad + T_{2} \left[ {a(P - T_{{L_{2} }} \left( {c_{1} + I_{e} P} \right) - c_{1} T_{{L_{2} }} - c\theta \left( {i - I_{c} T_{{L_{2} }} } \right)} \right] + cI_{c} \left[ { - c + 2\left( {T_{1} - T_{{L_{2} }} } \right) - \tfrac{1}{{I_{c} }}} \right] \hfill \\ \quad + 2T_{{L_{2} }} \left( {c - P\lambda } \right) \le 0 \hfill \\ \end{gathered}$$
(6)

Proof

(a) On partially differentiating \(Net_{1}\) with concerning \(T_{{L_{1} }}\).

Now on solving for \(T_{{L_{1} }}\) we get

$$\begin{array}{l} T_{{L_{1} }} = (- bP^{1 - j} - aI_{e} PP^{1 - j} + bcP^{ - j} - \frac{{acP^{ - j} }}{{T_{1} }} + ac_{1} P^{ - j} - bcI_{c} MP^{ - j} - \frac{{cI_{c} }}{\theta } + cI_{c} \theta + \frac{{aP^{1 - j} \lambda }}{{T_{1} }} \hfill \\ - \frac{{acP^{ - j} }}{{T_{1} }} + ac_{1} P^{ - j} + acI_{c} P^{ - j} - bcI_{c} MP^{ - j} - \frac{{cI_{c} }}{\theta } + cI_{c} \theta + \frac{{aP^{1 - j} \lambda }}{{T_{1} }} \hfill \\ - \sqrt {\Big( \left( {bP^{1 - j} + aI_{e} P^{1 - j} - bcP^{ - j} + \frac{{acP^{ - j} }}{{T_{1} }} - ac_{1} P^{ - j} - acI_{c} P^{ - j} + bcI_{c} MP^{ - j} + \frac{{cI_{c} }}{\theta } - cI_{c} \theta - \frac{{aP^{1 - j} \lambda }}{{T_{1} }}} \right)^{2} } \hfill \\ - 4\left( {aP^{1 - j} - acP^{ - j} + acI_{c} MP^{ - j} + \frac{c}{\theta } - \frac{{cI_{c} M}}{\theta } - c\theta + cI_{c} M\theta } \right) \hfill\\ \quad \left( {\frac{1}{2}bI_{e} P^{1 - j} + \frac{{bcP^{ - j} }}{{T_{1} }} - bc_{1} P^{ - j} - bcI_{c} P^{ - j} - \frac{{bP^{1 - j} \lambda }}{{T_{1} }}} \right)\Big)\Big) \Big/ \hfill \\ \left( {2\left( {\frac{1}{2}bI_{e} P^{1 - j} + \frac{{bcP^{ - j} }}{{T_{1} }} - bc_{1} P^{ - j} - bcI_{c} P^{ - j} - \frac{{bP^{1 - j} \lambda }}{{T_{1} }}} \right)} \right) \end{array}$$
(7)
$$\begin{gathered} \frac{{\partial Net_{1} }}{{\partial T_{{L_{1} }} }} = \tfrac{1}{{2T_{1} T_{2} \theta }}P^{ - j} \left( {T_{1} \left( {2a\left( {P - c_{1} + I_{e} PT_{{L_{1} }} } \right)} \right) + bT_{{L_{1} }} \left( { - 2c_{1} T_{{L_{1} }} + P\left( {2 + I_{e} T_{{L_{1} }} } \right)} \right)} \right)\theta + 2T_{1} c \hfill \\ \left( { - 1 + I_{c} \left( {\left( {M - T_{{L_{1} }} } \right)} \right)\left( {\left( {a + bT_{{L_{1} }} } \right)\theta + p^{J} \left( { - 1 + \theta^{2} } \right)} \right) + 2T_{{L_{1} }} \left( {a + bT_{{L_{1} }} } \right)\theta \left( {c - p\lambda } \right)} \right) \hfill \\ \end{gathered}$$
(8)
$$\frac{{\partial^{2} Net_{1} }}{{\partial T_{{L_{1} }}^{2} }} = \tfrac{1}{{T_{1} T_{2} \theta }}P^{ - j} \left( \begin{gathered} T_{1} \left( {a\left( { - c_{1} + I_{e} P} \right) + b\left( {P - 2c_{1} T_{{L_{1} }} + I_{e} PT_{{L_{1} }} } \right)} \right)\theta \hfill \\ - T_{1} c\left( {b\theta + I_{c} \left( {a - bM + 2bT_{{L_{1} }} } \right)\theta + I_{c} P^{j} \left( { - 1 + \theta^{2} } \right)} \right) + \left( {a + 2bT_{{L_{1} }} } \right)\theta \left( {c - P\lambda } \right) \hfill \\ \end{gathered} \right)$$
(9)

The right-hand side of the expression mentioned above (3)

$$\begin{gathered} 2aT_{1} P^{1 - j} - 2acT_{1} \theta + 2a\theta T_{1} cMI_{c} - 2a\theta T_{1} cT_{{L_{1} }} I_{c} + 2a(\theta T_{{L_{1} }} - 2aPT_{{L_{1} }} \lambda \theta - 2bc_{1} T_{{L_{1} }}^{2} \theta \hfill \\ \quad + 2bI_{e} T_{{L_{1} }}^{2} \theta + 2bc\theta T_{{L_{1} }}^{2} - 2bP\lambda \theta T_{{L_{1} }}^{2} + T_{1} I_{e} P^{1 - j} T_{{L_{1} }} - T_{1} c_{1} T_{{L_{1} }} P^{ - j} - 2bT_{{L_{1} }} \theta T_{1} c \hfill \\ \quad + 2bT_{{L_{1} }} \theta T_{1} cMI_{c} - 2bT_{{L_{1} }} \theta T_{1} T_{{L_{1} }} I_{c} - P^{j} + \theta^{2} \hfill \\ \end{gathered}$$
$$\begin{gathered} = 2a\left[ {T_{1} \left( {P^{1 - j} + \theta c\left( { - 1 + MI_{c} - T_{{L_{1} }} I_{c} } \right)} \right) + \theta T_{{L_{1} }} \left( {c - P\lambda } \right)} \right] \hfill \\ \quad + 2b\theta T_{{L_{1} }}^{2} \left( { - c_{1} + I_{e} + c - P\lambda } \right) \hfill \\ \quad + T_{{L_{1} }} T_{1} \left[ {I_{e} P^{1 - j} - c_{1} P^{ - j} - 2\theta \left( {bc + bcMI_{c} - T_{{L_{1} }} I_{c} } \right)} \right] - P^{j} + \theta^{2} \hfill \\ \end{gathered}$$

After simplifying, we get,

$$\begin{gathered} 2a\left[ {T_{1} \left( {P^{1 - j} + \theta c\left( { - 1 + I_{c} \left( {M - T_{{L_{1} }} } \right)} \right) + \theta T_{{L_{1} }} \left( {c - P\lambda } \right)} \right)} \right] + 2b\theta T_{{L_{1} }}^{2} \left( { - c + I_{e} + c - P\lambda } \right) \hfill \\ + T_{{L_{1} }} T_{1} \left[ {I_{e} P^{1 - j} - c_{1} P^{ - j} - 2\theta \left\{ {bc\left( {1 + MI_{c} } \right) - T_{{L_{1} }} I_{c} } \right\}} \right] \le P^{j} - \theta^{2} \hfill \\ \end{gathered}$$

If the above condition is met, we can conclude that it is a concave function with respect to \(T_{{L_{1} }}^{{}}\).

(b) On partially differentiating \(Net_{2}\) with respect to \(T_{{L_{2} }}\),

$$T_{{L_{2} }} = \left( {T_{2} \left( \begin{gathered} cP^{j} - T_{1} c_{1} P^{j} - ac\theta - bT_{1} c\theta + aT_{1} c_{1} \theta + bT_{1}^{2} c_{1} \theta + aT_{1} cI_{c} \theta + bT_{1}^{2} cI_{c} \theta \hfill \\ + aP\theta + bT_{1} P\theta - aT_{1} I_{e} P\theta - bT_{1}^{2} I_{e} P\theta - cP^{j} \theta^{2} + T_{1} c_{1} P^{j} \theta + T_{1} cI_{c} P^{j} \theta^{2} \hfill \\ \end{gathered} \right)} \right)$$
(10)
$$\frac{{\partial Net_{2} }}{{\partial T_{{L_{2} }} }} = \tfrac{1}{{T_{2}^{2} \theta }}P^{ - j} \left( \begin{gathered} - T_{2} \left( {\left( {a + bT_{1} } \right)c_{1} \theta + \theta \left( {acI_{c} + bT_{1} cI_{c} - aI_{e} P - bT_{1} I_{e} P + cI_{c} P^{j} \theta } \right) + c_{1} P^{j} \left( { - 1 + \theta^{2} } \right)} \right) \hfill \\ + \left( {a + bT_{1} } \right)\theta \left( {c - P\lambda } \right) \hfill \\ \end{gathered} \right)$$
(11)

The RHS of the above expression is

$$\begin{gathered} c_{1} T_{2} P^{j} T_{{L_{2} }} + aT_{2} P\theta + bc_{1} T_{1}^{2} \theta - bT_{1}^{2} I_{e} P\theta - ac_{1} T_{{L_{2} }} \theta + aI_{e} PT_{{L_{2} }} \theta + aT_{1} c_{1} \theta - abT_{1} T_{{L_{2} }} \theta \hfill \\ - ac\theta + aT_{1} cI_{c} \theta - I_{c} T_{{L_{2} }} ac\theta - bT_{1} c\theta + bcT_{1}^{2} I_{c} \theta - bT_{1} T_{{L_{2} }} c\theta I_{c} - c_{1} P^{j} T_{{L_{2} }} \theta^{2} \hfill \\ - T_{1} c_{1} P^{j} + T_{1} c_{1} P^{j} \theta^{2} + cP^{j} - cP^{j} \theta^{2} + cP^{j} T_{1} I_{c} \theta^{2} + bT_{1} \theta cT_{{L_{2} }} - bT_{1} \theta P\lambda T_{{L_{2} }} \hfill \\ \end{gathered}$$

After the simplification of the stated above, we find

$$\begin{gathered} T_{1}^{2} b\theta \left( {c_{1} - I_{e} P + cI_{c} } \right) + T_{1} \bigg[a\theta \left( {c_{1} - bT_{{L_{2} }} + cI_{c} } \right) + b\theta ( - c + T_{{L_{2} }} \left( {c\left( {I_{c} - 1} \right) - P\lambda } \right) \hfill \\ \quad + \theta P^{j} (c_{1} \left( {\theta - \tfrac{1}{\theta }} \right) + cI_{c} \theta + \tfrac{{bT_{{L_{2} }} }}{{P^{j} }}\left( {c - P\lambda } \right) \bigg] + a\theta T_{{L_{2} }} \left[ {c\left( {1 + I_{c} } \right) + P\left( {1 + I_{e} } \right)} \right] \hfill \\ \quad + P^{j} \left[ {c_{1} T_{{L_{2} }} \left( {T_{1} - \theta^{2} } \right) + c(1 - \theta^{2} \left( {1 - T_{{L_{2} }} I_{c} } \right)} \right] + a\theta \left( {T_{2} P - c} \right) \le \tfrac{ - 1}{{P^{ - j} }} \hfill \\ \end{gathered}$$
(12)

If the above condition is met, we can conclude that it is a concave function with respect to \(T_{{L_{2} }}\)

Further, we check the concavity with respect to P.

$$\begin{aligned} \frac{{\partial Net_{1} }}{\partial P} & = \frac{1}{{6T_{1} T_{2}^{2} }}P^{ - 1 - j} \left( b\left( {T_{1} T_{2} \left( {c_{j} \left( {3T_{{L_{1} }}^{2} + I_{c} \left( {M - T_{{L_{1} }} } \right)^{2} \left( {M - 2T_{{L_{1} }} } \right)} \right) + T_{{L_{1} }}^{2} (2c_{1} jT_{{L_{1} }} - \left( { - 1 + j} \right)P\left( {3 + I_{e} T_{{L_{1} }} } \right)} \right)} \right) \hfill \right. \\ & \left. \quad 3T_{1}^{4} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) + 2T_{1}^{3} T_{2} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) + 3T_{1}^{2} T_{2}^{2} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) - 2T_{2} T_{{L_{1} }}^{3} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right)) \right. \\ & \left. \quad - 3a\left( T_{1}^{3} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) - T_{1}^{2} T_{2} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) + T_{2} T_{{L_{1} }}^{2} \left( {c_{j} - \left( { - 1 + j} \right)P\lambda } \right) \hfill \right.\right. \\ &\quad \left. \left. - T_{1} T_{2} \left( {T_{2} cj + c_{1} jT_{{L_{1} }}^{2} + cj\left( {I_{c} \left( {M - T_{{L_{1} }} } \right)^{2} + 2T_{{L_{1} }} } \right) - \left( { - 1 + j} \right)PT_{{L_{1} }} \left( {2 + I_{e} T_{{L_{1} }} } \right) - T_{2} \left( { - 1 + j} \right)P\lambda } \right) \right) \right)\end{aligned} $$
(13)
$$\begin{aligned} \frac{{\partial^{2} Net_{1} }}{{\partial P^{2} }} & = \frac{1}{{6T_{1} T_{2}^{2} }}jP^{ - 2 - j} (b( - T_{1} T_{2} (c\left( {1 + j} \right)\left( {3T_{{L_{1} }}^{2} - I_{c} \left( {M - T_{{L_{1} }} } \right)^{2} \left( {M - 2TT_{{L_{1} }} } \right)} \right) + T_{{T_{{L_{1} }} }}^{2} (cc_{1} \left( {1 + j} \right)T_{{L_{1} }} \hfill \\ &\quad - \left( { - 1 + j} \right)P\left( {3 + I_{e} T_{{L_{1} }} } \right))) + 3T_{1}^{4} \left( {c + cj + P\lambda - jP\lambda } \right) - 2T_{1}^{3} T_{2} \left( {c + cj + P\lambda - jP\lambda } \right) \hfill \\ &\quad - 3T_{1}^{3} T_{2}^{2} \left( {c + cj + P\lambda - jP\lambda } \right) + 2T_{2} T_{{T_{{L_{1} }} }}^{2} \left( {c + cj + P\lambda - jP\lambda } \right)) + 3a(T_{1}^{3} \left( {c + cj + P\lambda - jP\lambda } \right) \hfill \\ &\quad - T_{1}^{2} T_{2} \left( {c + cj + P\lambda - jP\lambda } \right) + T_{2} T_{{T_{{L_{1} }} }}^{2} \left( {c + cj + P\lambda - jP\lambda } \right) - T_{1} T_{2} (c\left( {1 + j} \right)\left( {I_{c} \left( {M - T} \right)_{{L_{1} }}^{2} + 2T_{{L_{1} }} } \right) \hfill \\ &\quad + T_{{L_{1} }} \left( {c_{1} \left( {1 + j} \right)T_{{L_{1} }} - \left( { - 1 + j} \right)P\left( {2 + I_{e} T_{{L_{1} }} } \right)} \right) + T_{2} \left( {c + cj + P\lambda - jP\lambda } \right)))) \hfill \\ \end{aligned}$$
(14)

The abovementioned calculation is exceptionally lengthy, so we only check their concavity through the graphical method illustrated in Fig. 2.

Hessian Analysis

$$\left| {H_{M} } \right| = \left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} Net_{2} }}{{\partial T^{2} }}} & {\frac{{\partial^{2} Net_{2} }}{\partial T\partial P}} \\ {\frac{{\partial^{2} Net_{2} }}{\partial P\partial T}} & {\frac{{\partial^{2} Net_{2} }}{{\partial P^{2} }}} \\ \end{array} } \right]_{2 \times 2}$$
$$= \left[ {\begin{array}{*{20}c} { - .06027} & {.04683} \\ { - 2.43023} & {618.294} \\ \end{array} } \right]_{2 \times 2}$$
$$= - 37.2616 + .1138$$
$$\Rightarrow - 37.1478 < 0$$

The Hessian matrix analysis culminates that the proposed study ignites the profound profit to retailers. Moreover, It reconciles mathematically to prove the concavity of the suggested model.

Solution Procedure

For F = 1.

Step 1: Solve \(\frac{{\partial Net_{1} }}{\partial T} = 0\) and \(\frac{{\partial Net_{1} }}{\partial P} = 0\) from the expressions 8 and 13 to obtain the value of \(T_{{L_{1} }}^{*}\) and \(P^{*}\).

Step 2: \(Check(0 < T_{{L_{1} }} < T_{1} )\& P^{*} > \Pr ice\) Floor. If the result is positive, then move to the next step; otherwise, find the primary value.

Step 3. For this set was obtained from expressions 11 and 14. If we get a negative value, then move to the next step.

Step 4. For this set of \((T_{{L_{1} }}^{*} ,P^{*} )\) find the value of Net1 from expression (1).

Step 5: Repeat steps 1 to 4 for F = 2. Towards then, we choose the highest value.

Numerical Example

Case I

Preservative technology and permissible delay in payment allowed:

Example 1

We consider the stated values and parameters to the solution procedure of the model.

$$M = 35,I_{c} = .008,I_{e} = .003,T_{1} = 45,T_{2} = 75,a = 20,b = 7.6,j = 2.5,c_{0} = 100,\lambda = 0.99,c_{1} = 0.001,c = 0.5$$

Results Case I Tables 2 and 3 of case I shows the computational results. We discussed the practical results of different parameters of demand functions. The profit commences from Phase I and attains maximum profit = 130.925$ in Phase II, when both both PDP and PTI, both approaches are applied together. We restrict the optimum replenishment point of Phase II, as a consequence, the price and backlog amount on inventory become constant in Phase II. Hence, we attain less backlog amount as compared to Phase I. The concavity is seen in the stated Figs. 3 and 4 swhich supports the proposed study.

Table 2 Result of Phase I \((0 < T_{{L_{1} }} < T_{1} )\) When PD and PT Allowed
Full size table
Table 3 Result of Phase II, \((T_{1} < T_{{L_{2} }} < T_{2} )\) When PD and PT Allowed
Full size table
Fig. 3
figure 3

Illustrates the joint concavity of the profit function of Case I and Phase I

Full size image
Fig. 4
figure 4

Illustrates the joint concavity of the profit function of Case I and Phase II

Full size image

Case II

When Preservation technology and Permissible delay in payment are not allowed:

Example 2

We consider the stated values and parameters of the solution procedure of the model \(T_{1} = 40,T_{2} = 75,T_{3} = 100,r = 1,a = 20,b = 5.5,j = 1.7,c_{0} = 100,\lambda = 0.99,c_{1} = 0.001,c = 0.5\)

Results Case II The computational results are shown in Tables 4 and 5 of Case II. We discussed the practical results of different parameters of demand functions. The profit commences from Phase I and attains attained \(I_{2}^{*} = 27831.18\)27831.18 in phase II, without both approaches. We restrict the optimum replenishment points of Phase II; consequently, the price and backlog amount on inventory become constant in Phase II. Hence, attain less backlog amount as compared to Phase I.

Table 4 Result of Phase I, \((0 < T_{{L_{1} }} < T_{1} )\) When PD and PT not allowed
Full size table
Table 5 Result of Phase II, When PD and PT not allowed \((T_{1} < T_{{L_{2} }} < T)\)
Full size table

A crepuscular change was observed due to PTI. The invested amount attracts additional revenue w.r.t. time and vice versa. The invested amount controls the decimate deterioration rate \(\left( {\theta - \tfrac{1}{\theta }} \right)\) impulsively. Therefore, retailers yield a surplus inventory replenishment period. The P = 0.00186$ excess price per unit received due to PTI. Consequently, 3.97$ per unit additional profit and 698 units of inventory space profound through PTI. Moreover, Retailers shall invest \(5.105 \times 10^{10}\) per unit investment to ignite their profit.

Case III

When Permissible, delay in payment is allowed only:

Example 3

We consider the stated values and parameters to the solution procedure of the model.

$$M = 35,I_{c} = .008,I_{e} = .003,T_{1} = 45,T_{2} = 75,a = 20,b = 7.6,j = 2.5,c_{0} = 100,\lambda = 0.99,c_{1} = 0.001,c = 0.5$$

Results Case III The computational results are shown in Tables 6 and 7 of case III. We discussed the practical results of different parameters of demand functions. The profit commences from phase I and attains a maximum \(Net_{2}^{*} = 129.724\$\) and \(I_{2}^{*} = 27475.8\) in phase II, when PDP is applied only. We restrict \(T_{{L_{2} }}^{*} = 66.0022\) as optimum replenishment points of Phase II; as a consequence, the price and backlog amount on inventory become constant in Phase II. Hence, we attain less backlog amount as compared to phase I.

Table 6 Result of Phase I When PD Allowed \((0 < T_{{L_{1} }} < T_{1} )\)
Full size table
Table 7 Result of Phase II, \((T_{1} < T_{{L_{2} }} < T_{2} )\) When PD and PT Allowed
Full size table

Case IV

When Preservation Technology Allowed only:

Example 4

We consider the stated values and parameters to the solution procedure of the model.

$$M = 35,I_{c} = .008,I_{e} = .003,T_{1} = 45,T_{2} = 75,a = 20,b = 7.6,j = 2.5,c_{0} = 100,\lambda = 0.99,c_{1} = 0.001,c = 0.5$$

Results Case IV The computational results are shown in the Tables 8 and 9 of case III. We discussed the effective results of different parameters of demand functions. The profit commences from phase I and attain \(Net_{2}^{*} = 128.869\$\) and \(I_{2}^{*} = 27840.2\) in phase II, when PTI approach envisage. We restrict the optimum replenishment point of Phase II consequently, the price and backlog amount on inventory become constant in Phase II. Hence, we attain less backlog amount as compared to phase I. Therefore, it is suggested to retailers, more inventory items to be stored to fulfill future backlog orders.

Table 8 Result of Phase I \((0 < T_{{L_{1} }} < T_{1} )\) When PT Allowed only.
Full size table
Table 9 Result of Phase II, \((T_{1} < T_{{L_{2} }} < T_{2} )\) When PT Allowed only.
Full size table

Advances of the proposed model and sensitivity analysis

Advances of the proposed model

The advances of the study is considered an integral part of every study. Therefore, Table 10 consists of a compendious case study after comparison with the proposed model.

Table 10 Advances Results with Proposed Model
Full size table

The retailers may obtain additional revenue if the proposed study applied to their previous parameters. The optimal replenishment time and price suitably enhance an incredible profit. Each study exhibits novel profit, especially [22], instigating an eminent profit from additional demand due to the optimal replenishment period of inventory. Therefore, the above table depicts the novel results of the study after interspersing several demand parameters of distinguishing studies into the proposed model.

Sensitivity Analysis

As per our study, the retailer may attain maximum profit \(Net_{2}^{*} = 130.925\$\) in phase II of case I, although many uncertainties are possible in decision-making. So, we need to check all possibilities of indebting solutions for profit maximization. Hence, a change in the values of all variables and parameters is required due to uncertainties in the future. Sensitivity analysis is applied to find the effect of optimality due to changes in demand parameters. We obtain various outcomes, juxtaposed into the stated Table.

The Loss percentage is calculated as

$$\frac{{\left( {Net_{2}^{*} - Net_{2} } \right)}}{{Net_{2}^{*} }} \times 100$$

We applied sensitivity analysis with respect to loss percentage from − 25% to 100% in their initial value. From Table 11. We find different sensitive variables and parameters of the price and time-dependent demand function. As per our observation,

  1. 1.

    P is the most sensitive variable, so if we change the − 75% initial value of parameter P, we attain a maximum profit of − 2543.3%. The retailer may attain maximum profit if they increase the selling price of items. Hence, we find ‘P’ as the most sensitive parameter of the proposed study.

  2. 2.

    In the competitive world, it is complicated to hike the price so much that’s why we can opt to control the price of the items. Therefore, the retailer may attain maximum profit =  − 147.18% when we change + 100% in the initial value of the ‘j’ parameter.

  3. 3.

    We attain maximum profit in ‘a’ and ‘b’ when we + 100% change their parameter’s initial value.

Table 11 Sensitivity Analysis Results
Full size table

We are calculating loss percentage, so; most minus results show the most profit to retailers regarding changes in demand parameters and variables. Further, we choose every sensitive variable from each parameter and apply it to obtain max profit, max inventory, and backlog inventory requirement as per change in the sensitive variable on different loss percentage parameters in Table 12.

Table 12 Results of change of effects as a change in their parameter
Full size table

The attempt to envisage the relationship of sensitivity analysis results with respect to different variables and their effects on profit is made through the graphs below.

Further, Table 12 identified the impact of several patterns on inventory decisions. The managers can develop a contingency plan due to parameter fluctuations.

  1. 1.

    The retailer may attain maximum profit \(Net_{a} = 121.289\$\) and maximum inventory \(I_{a} = 25011\) as a 100% change in the initial value of parameter ‘a’.

  2. 2.

    Backlog Inventory plays a significant role in inventory management because pending orders shall be treated as expected future sales. We attain maximum backlog \(I_{b} = 19343.2\) when we change + 100% in the initial parameter of ‘T.’ Here, we attain maximum profit as \(Net_{T} = 21.6248\$\) of the ‘T’ parameter. As per our study, if the replenishment period is short, the retailer will receive more profit because the deterioration impact is much less on fresh items if the length is small. So, retailers are suggested to opt for a maximum replenishment policy to attain maximum profit.

  3. 3.

    The demand function becomes price-dependent only when we apply a + 100% change in the initial value of ‘b’. Here we receive \(Net_{b} = 11.5811\$\). Otherwise, we procured only loss due to a change in initial value. So, it is suggested that when retailers suffer a loss; they may purchase very few amounts of deteriorating items and not store them for a long time. Yet they shall not receive max profit as the model becomes price dependent only, but at least they earn some profit during the recession period. The retailer may attain the intended maximum loss when we change -100% in the initial value of parameter ‘b’.

  4. 4.

    ‘j’ is the price-dependent parameter; hence, when we put j = 1, then the demand function will be free from the effect of ‘j’. We attain maximum profit \(Net_{j} = 92.901\$\) when we change + 100% in the initial value of parameter ‘j’.

  5. 5.

    The comparison study of sensitivity analysis and their effects on different variables and parameters is available in Table 12. Our study insights fluctuation in price, concurrently, observed most consistency in variable ‘a’. Extreme price fluctuation is not appreciated in the real world, so it is suggested that retailers analyze our study before investing during extreme fluctuations in price.

  6. 6.

    In Fig. 5a, we compare the change of effect between profits vs. sensitivity analysis. We find more profit due to the sensitive variable ‘a’ and less profit or even loss due to variable ‘b’.

  7. 7.

    In Fig. 5b and c, we compare the change of effect in backlog orders vs. sensitivity analysis. Then, find a significant consistency of inventory due to the sensitive variable ‘a’

Fig. 5
figure 5

a Change of effect on profit due to most sensitive variables, b Change of effect on inventory due to most sensitive variables, c Change of effect on backlog due to most sensitive variables, and d Comparison of profit and deterioration between all cases

Full size image

Managerial Insights

The study already encapsulates risk analysis through Tables 11 and 12 description. Moreover, perfunctory managerial insights construe to overcome business risk as stated below.

  1. 1.

    Figure 5d depicts the relationship between profit and deterioration in different cases. When it increases, the retailer’s profit is reduced as per the natural law of deterioration. Here, a threshold point (PTI) exists to control the rate of deterioration due to investment in preservative technology. It is suggested that investing in preservative technology is very useful in enhancing retailers’ profit.

  2. 2.

    In this paper, we have another remedy to overcome the effect of deterioration. Permissible delay in payment (PDP) can control the impact of deterioration because retailers receive some extra amount from the bank due to a specific time to settle their dues. Hence, it is suggested that the coherence of both techniques was significant to retailers.

  3. 3.

    In case I, retailers may attain maximum profit \(Net_{I} = 130.925\$\) when PDP and PTI are applied coherently. They earn 3.128% extra revenue as compared to case II. Concurrently, When both PDP and PTI are not allowed, we observe case II; we attain a minimum profit \(Net_{{II}} = 126.954\$\).

  4. 4.

    We observe in case III, when PDP is allowed only. Then, retailers attain 2.18% extra revenue as compared to case II. While, observe in the case of IV, when PTI is allowed only. Then, we procured 1.508% extra revenue as compared to case II.

  5. 5.

    More time for permissible delay offers more revenue to retailers as they can control the inventory cost and inflation effects. Suppliers also get more revenue due to additional orders by retailers. Hence, a longer time period for PDP is suggested as suitable for an extra sale.

  6. 6.

    It is observed that retailers attain invincible inventory when preservation techniques are allowed only. This extra inventory exists due to the investment by retailers in preservative technology. Later, this additional inventory shall convert into additional profit for retailers.

  7. 7.

    When the replenishment period is short due to high sales, then it is suggested that retailers refill as often deteriorating items as possible. In this way, the holding cost and deterioration effect shall be less, which converts into the retailer’s profit. Besides, customers get fresh items for final consumption. Further, Industries incorporate findings for long-term planning to ensure eminent inventory management as below.

  8. 8.

    Optimal Inventory Management: The suggested model stimulates a dynamic inventory replenishment policy where industries can easily adjust re-order quantities as per existing demand patterns. Further, excess stock may be reduced by implementing the suggested model.

  9. 9.

    Financial Impact: The suggested model overwhelmingly impacts cash flow and working capital requirements. The industries can develop a permissible delay payment policy that balances customer financial risk.

  10. 10.

    Efficient preservative Technology Investment: The industries can assess a cross-functional effective preservative investment to implement in supply chain management with respect to deterioration rates. Moreover, the suggested model enhances industries’ profit by performing cost–benefit analysis.

  11. 11.

    Overcome supply chain risk: The industries can identify critical points to mitigate future risks. The industries shall develop contingency plans against disruption of inventory management in terms of additional buffer uncertainties.

  12. 12.

    Competitive strategies: The optimal selling price and commitment to the product available can differentiate businesses from competitors. The industries may develop potential plans to ensure flexibility in competitive strategies.

Conclusion

Several researchers worked separately on an inventory model on Permissible delay in payment and Preservative technology investment. There was still some gap in finding maximum profit for retailers. Hence, the proposed model combine the capabilities of both models to find maximum profit for retailers. We opted for four different cases to characterize our results. In case I, retailers attained maximum profit when PDP and PTI were both techniques adopted\(Net_{I} = 130.925\$\). Then, we worked on PDP-allowed case. Then procure\(Net_{{III}} = 129.724\$\). Further, working over PTI allowed the only case to receive for the extensive study, we compare the proposed model when both of the techniques are not allowed; we attain less profit\(Net_{{II}} = 126.954\$\). Therefore, attains impetuous enough profit to retailers with appropriate insights. The sensitivity analysis broadcasts future insights when different demand parameters and variables change simultaneously. All expected results are juxtaposed through several tables and graphs. Therefore, retailers may make future decisions to overcome their unexpected risks.

The present study proves several theoretical connectivity results through theorems, numerical examples and graphs. Our study justifies the role of deterioration, PDP, and PTI coherently. The retailers may attain impetuous enough profit by controlling the deterioration rate through the PTI approach. Parallels, the supplier gives a specific credit period to retailers to settle their dues; then, the retailer may obtain more profit from both sides. Besides, suppliers also obtain extra revenue due to additional orders by retailers. The proposed study is not useful only from the retailer’s point of view, even though additional demands always create additional jobs in the market, which is the most required in the current scenario after the world pandemic. Secondly, PTI enhances the shelf life of deteriorating items. Consequently, the proposed model plays a significant role for retailers and society. Finally, the young researcher may develop further models based on our study. The future is unexpected, so they will find different demand patterns in the future; at that time, they can apply the proposed model to overcome future risks towards expected demands like stochastic and quadratic as future insights.