1 Introduction

Biological conservation is tightly coupled to ecology. Ecology is about the understanding how the ecosystem works, while biological conservation involves applying this knowledge to develop scientific basis for conserving and managing the ecosystem. The aim of biological conservation is to protect the species from extinction and maintain the ecological balance. Population dynamics is the dominant branch of mathematical biology that deals with forces affecting changes in population densities or affecting the form of population growth. It is clear that predator population depends on their prey species for survival and they lower the survival and fecundity rate of prey species. Therefore, predator population is affected by changes in prey population. Refuge used by prey has a stabilizing effect on predator–prey system. The characteristics of refuges influence the density of prey species. Predation, inter-specific competition, and prey refuge space affects local prey diversity (Kar 2005, 2006; Chen et al. 2010; Chakraborty et al. 2011; Cressmana and Garay 2009; Mchich et al. 2005).

The proportion of refuge space in the habitats determines the responses of prey diversity to predation and competition (Hixon 1991). Effects of competitive refuges as well as refuges from predators on prey-diversity responses were also discussed. Equilibrium density of prey population increases as prey refuge increase while decrease that of predators and the stability of interior equilibrium is determined by refuge used by prey species. Prey population reaches its maximum carrying capacity when refuge used by prey is high enough (Ma et al. 2009). Prey dispersal and refuges play a vital role on predator–prey dynamics. The system experienced transitions from predator extinction to predator–prey oscillatory coexistence, to predator–prey non-oscillatory coexistence, when dispersal between the prey-refuge and predator–prey habitats increased. The availability of refuges and dispersal of prey population increased the impact of population (Berezovskaya et al. 2010). Yu and Sun (2013) described a predator–prey model incorporating a constant prey refuge with Hassell–Varley type functional response.

The quality and quantity of alternative food supplied to the predators is known to play a vital role in the prey–predator dynamics. Additional food altered the interaction of co-occurring predators sharing same primary prey. In presence of primary prey, two predator species survived but they were failed to reproduce. When primary prey and alternative food was provided, both predator species survived and reproduced. There is an important role of predator–predator interaction on suppression of prey population densities (Onzo et al. 2005). To study the effects of additional food on the system dynamics, a predator–prey model with type II functional response with additional food to predator was considered (Srinivasu et al. 2007). It was observed that prey population can be controlled by varying the quality and quantity of additional food. The quality and supply level of additional food to predators was discussed in this paper for the benefit of biological control. A long run dynamics of a prey–predator model with an alternative prey was discussed (Kar and Chattopadhyay 2010). They have shown that individual harvesting efforts and digesting factors relative to alternative determine the positive value of the population in the long run. A two species prey–predator model with alternative prey was considered to study the effect of alternative food to predator and harvesting effort (Kar and Ghosh 2012).

The dynamics of prey–predator system has long been considered to be one of the dominant themes under mathematical biology (Ghordaf et al. 2004; Chakraborty et al. 2012; Das et al. 2012; Arditi and Ginzburg 1989; Chakraborty et al. 2013a, b). It has often been suggested that refuges are a crucial factor allowing prey to persist with predators, relatively few qualititative studies have directly addressed the patterns or implications of refuge use. Again, the use of additional food has been widely recognized by experimental scientists as one of the important tools for biological conservation. The quality and quantity of additional food supplied to the predators is known to play a vital role in the controllability of the system. According to our best knowledge, it is relevant to point out from the existing literature that no attempt has been made to study the dynamics of a prey predator system which incorporates constant prey refuge through provision of alternative food to predators.

The paper is organized in the following manner. Mathematical model is formulated in Sect. 2. The boundedness of the system is discussed in Sect. 3. Existence of equilibriums points have been examined in Sect. 4. Local stability of the system is analyzed in Sect. 5. Global stability of the system at the interior equilibrium point has been studied in Sect. 6. Bionomic equilibrium of the proposed system is analyzed in Sect. 7. Optimal harvesting policy is discussed in Sect. 8. We have performed numerical simulation in Sect. 9. A brief conclusion is also provided in the final section.

2 Model Formulation

We consider a prey–predator system with harvesting. It is assumed that prey species follows logistic law of growth. Let us assume x and y are respectively the size of prey and predator population at time t. Predator population consumes prey according to Holling type II functional response. There is a conflict for common resource (prey) between predators and harvesting agencies. Again, predator mortality is assumed to be a rate proportional to y 2 rather than y. This non-linear dependency reflects the combined effects of increased predation by super predator (not considered in the model directly) and the interface or competition among the predators. So the growth of the predator species in the second equation is limited due to the presence of the term γy 2 and even if the density of the prey is very high. It is assumed that the prey population incorporates constant prey refuge towards its protection from predators. The dynamical system of the problem is represented by following differential equation:

$$ \begin{gathered} \frac{dx}{dt} = rx\left( {1 - \frac{x}{K}} \right) - \frac{\alpha (x - m)y}{1 + a(x - m)} - h_{1} (t), \hfill \\ \frac{dy}{dt} = sy + \frac{\alpha \beta (x - m)y}{1 + a(x - m)} - \gamma y^{2} - h_{2} (t), \hfill \\ \end{gathered} $$
(2.1)

where r is the intrinsic growth rate of prey, s is the intrinsic growth rate of the predator, K is the environmental carrying capacity of the prey, m is the constant prey refuge, a is the Half saturation constant, α is the maximal relative increase of predation, β is the conversion factor, γ is the arte of intra-specific competition, h 1 (t) and h 2 (t) be the amount of resource harvested respectively from prey and predator population at time t. All the parameters are assumed to be positive.

The term sy in the model represents a growth rate of the predator due to the availability of alternative food sources. It is quite natural that when focal prey is low, the predators increase their feeding on alternative prey. But when the focal prey increases, the predator uses less alternative prey and as focal prey approaches to its saturation value K, the amount of alternative prey consumed by the predator tends to zero and then only predation of the focal prey occurs. For this reason, we modify the term sy, reported in literature, by the factor sy(1 – x/K).

Harvesting has a strong impact on the dynamic evaluation of a population subjected to it. First of all, depending on the nature of the applied harvesting strategy, the long-run stationary density of a population may be significantly smaller than the long-run stationary density of a population in the absence of harvesting. Therefore, while a population can, in the absence of harvesting, be free of extinction risk, harvesting can lead to the incorporation of a positive extinction probability and therefore, to potential extinction in finite time. Secondly, if a population is subjected to a positive extinction rate then harvesting can drive the population density to a dangerously low level at which extinction becomes sure no matter how the harvest affects the population afterwards.

The functional form of the harvest is generally considered using the phrase Catch-Per-Unit-Effort (CPUE) hypothesis (Clark 1990) to describe on assumption that CPUE is proportional to the stock level. We now take the harvested rate in the following form

$$ \begin{gathered} h_{1} (t) = q_{1} Ex, \hfill \\ h_{2} (t) = q_{2} Ey, \hfill \\ \end{gathered} $$

where, q 1 and q 2 are catchability coefficients of the prey and predator population, E is the combined harvesting effort.

Introducing h 1 (t) and h 2 (t) in (2.1), the system finally becomes

$$ \begin{gathered} \frac{dx}{dt} = rx\left( {1 - \frac{x}{k}} \right) - \frac{\alpha (x - m)y}{1 + a(x - m)} - q_{1} Ex \hfill \\ \frac{dy}{dt} = sy\left( {1 - \frac{x}{k}} \right) + \frac{\alpha \beta (x - m)y}{1 + a(x - m)} - \gamma y^{2} - q_{2} Ey \hfill \\ \end{gathered} $$
(2.2)

with initial conditions x(0) > 0, y(0) > 0.

3 Boundedness of the System

Lemma 1

All the solutions of (2.2) which start in \( R_{ + }^{2} \) are uniformly bounded.

Proof

We define the function

$$ \omega = x + \frac{1}{\beta }y $$
(3.1)

The time derivative of Eq. (3.1) is

$$ \frac{d\omega }{dt} = rx\left( {1 - \frac{x}{k}} \right) - \frac{sy}{\beta }\left( {1 - \frac{x}{k}} \right) - \frac{\gamma }{\beta }y^{2} - q_{1} Ex - \frac{{q_{2} Ey}}{\beta } $$

For each \( \upsilon > 0 \), upon computing the square separately in x and y the following inequality holds

$$ \frac{d\omega }{dt} + \upsilon \omega \le \frac{k}{4r}(\upsilon + r - q_{1} E)^{2} + \frac{1}{4\beta \gamma }(\upsilon + s - q_{2} E)^{2} $$
(3.2)

It is clear that the right hand side of inequality (3.2) is bounded for all \( (x,y) \in R_{ + }^{2} \), provided E is bounded. Thus we choose μ > 0 such that

$$ \frac{d\omega }{dt} + \upsilon \omega < \mu . $$

Applying the theory of differential inequality, we obtain

$$ 0 < \omega \left( {x,y} \right) < \frac{\mu }{\upsilon }\left( {1 - e^{ - \upsilon t} } \right) + \omega \left( {x(0),y(0)} \right)e^{ - \upsilon t} $$
(3.3)

which, upon letting \( t \to \infty \), yields \( 0 < \omega < \frac{\mu }{\upsilon } \).

So, we have, that all the solution of Eq. (2.2) that start in \( R_{ + }^{2} \) are confined to the region B, where \( B = \left\{ {(x,y) \in R_{ + }^{2} :\omega = \frac{\mu }{\upsilon } + \varepsilon ,\,\,{\text{for any}}\,\,\varepsilon > 0} \right\} \), Birkoff and Rota (1982).

4 Existence of Equilibria

The possible steady states of system (2.2) are as follows:

$$ E_{0} :(0,0), $$
$$ E_{1} :(\bar{x},0),\,\bar{x} = (r - q_{1} E)\frac{K}{r}, $$
$$ E_{2} :(0,\bar{y}),\,\,\bar{y} = \frac{1}{\gamma }\left( {s + \frac{\alpha \beta m}{1 - am} - q_{2} E} \right), $$
$$ E_{3} :(x^{*} ,y^{*} ), $$

where,

$$ y^{*} = \frac{s}{\gamma }\left( {1 - \frac{{x^{*} }}{K}} \right) + \frac{{\alpha \beta \left( {x^{*} - m} \right)}}{{\gamma \left[ {1 + a\left( {x^{*} - m} \right)} \right]}} - \frac{{q_{2} E}}{\gamma }. $$
(4.1)

and \( x^{*} \) satisfying the following equation:

$$ p_{1} x^{*4} + p_{2} x^{*3} + p_{3} x^{*2} + p_{4} x^{*} + p_{5} = 0 $$
(4.2)

where, \( p_{1} = \frac{{a^{2} r}}{K}, \)

$$ p_{2} = a^{2} r - \frac{{2a^{2} mr}}{K} + \frac{2ar}{K} + \frac{a\alpha s}{K\gamma } - q_{2} Ea^{2} , $$
$$ \begin{gathered} p_{3} = 2ar - 2a^{2} mr - \frac{r}{K} + \frac{{a^{2} m^{2} r}}{K} - \frac{2amr}{K} + \frac{\alpha s}{K\gamma } - \frac{a\alpha ms}{K\gamma } + \frac{{\alpha^{2} \beta }}{\gamma } + \frac{{aq_{2} E\alpha }}{\gamma } \hfill \\ + 2a^{2} q_{2} Em - 2aq_{2} E, \hfill \\ \end{gathered} $$
$$ p_{4} = r + a^{2} m^{2} r - 2amr + \frac{{2\alpha^{2} \beta m}}{\gamma } + q_{2} E\left( {\frac{\alpha }{\gamma } - \frac{m\alpha }{\gamma } - \frac{a\alpha m}{\gamma } - 1 - a^{2} m^{2} + 2am} \right), $$
$$ p_{5} = \frac{{\alpha q_{2} Em^{2} }}{\gamma } - \frac{{\alpha^{2} \beta^{2} m}}{\gamma } - \frac{{\alpha mq_{2} E}}{\gamma }. $$

The ratio \( \frac{r}{q} \) of the biotic potential (r) to the catchability coefficient (q) is known as the biotechnical productivity (BTP) of the species. It is easy to see that the equilibrium point E 1 exists if \( E < \frac{r}{{q_{1} }} \) or E < BTP x .

Similarly, E 2 exists if \( E < \frac{1}{{q_{2} }}\left( {\frac{s + \alpha \beta m}{1 - am}} \right) \) and \( m < \frac{1}{a} \).

It is to be noted that \( y^{*} > 0 \) if \( E < \frac{1}{{q_{2} }}\left[ {s\left( {1 - \frac{{x^{*} }}{K}} \right) + \frac{{\alpha \beta \left( {x^{*} - m} \right)}}{{\left[ {1 + a\left( {x^{*} - m} \right)} \right]}}} \right] \) and \( m < x^{*} < K \).

It may also be noted from equation (4.2) that p 1 > 0,

Again, p 5 > 0 if \( m > \left( {1 + \frac{{\alpha \beta^{2} }}{{Eq_{2} }}} \right) \).

Consequently, it is possible to get at least one positive solution of \( x^{*} \) depending on the sign of p 2, p 3 and p 4.

However, we shall consider such a positive root of \( x^{*} \) which satisfies the conditions for the existence of \( y^{*} . \)

Therefore, the interior equilibrium point E 3 exists.

5 Local Stability Analysis

We shall now investigate the local behaviour of the model system (2.2) around the steady states. The variational matrix of the system of Eq. (2.2) is

$$ V(x,y) = \left[ {\begin{array}{*{20}l} {r - \frac{2rx}{K} - \frac{\alpha y}{{(1 + ax - am)^{2} }} - q_{1} E} \hfill & { - \frac{\alpha (x - m)}{1 + a(x - m)}} \hfill \\ { - \frac{sy}{K} + \frac{\alpha \beta y}{{(1 + ax - am)^{2} }}} \hfill & {s - \frac{sx}{K} + \frac{\alpha \beta (x - m)}{1 + a(x - m)} - 2\gamma y - q_{2} E} \hfill \\ \end{array} } \right] $$
(5.1)

We now prove the following theorems.

Theorem 5.1

A necessary and sufficient condition that the origin is a stable node is

$$ E > \hbox{max} \left( {\frac{r}{{q_{1} }},\frac{1}{{q_{2} }}\left[ {s - \frac{\alpha \beta m}{1 - am}} \right]} \right),s > \frac{\alpha \beta m}{1 - am}\,{\text{and}}\,m < \frac{1}{a}. $$

Proof

Let us assume that the origin is a stable node then two eigenvalues must be both negative. The two eigenvalues of variational matrix are

$$ \begin{gathered} \lambda_{1} = r - q_{1} E, \hfill \\ \lambda_{2} = s - \frac{\alpha \beta m}{1 - am} - q_{2} E. \hfill \\ \end{gathered} $$

Eigenvalue \( \lambda_{1} \) will be negative if \( E > \frac{r}{{q_{1} }} \) and eigenvalue \( \lambda_{2} \) will be negative if \( E > \frac{1}{{q_{2} }}\left[ {s - \frac{\alpha \beta m}{1 - am}} \right] \) where, \( s > \frac{\alpha \beta m}{1 - am} \) and \( m < \frac{1}{a} \).

Necessary and sufficient condition that origin is a stable node is

$$ E > \hbox{max} \left( {\frac{r}{{q_{1} }},\frac{1}{{q_{2} }}\left[ {s - \frac{\alpha \beta m}{1 - am}} \right]} \right),\,\,s > \frac{\alpha \beta m}{1 - am}\,{\text{and}}\,m < \frac{1}{a}. $$

Theorem 5.2

A necessary and sufficient condition that the steady state \( \left( {\bar{x},0} \right) \) is a stable node is

$$ E > \frac{1}{{q_{2} }}\left[ {s - \frac{{s\bar{x}}}{K} + \frac{{\alpha \beta \left( {\bar{x} - m} \right)}}{{1 + a(\bar{x} - m)}}} \right]\,\,{\text{and}}\,\,\bar{x} > m. $$

Proof

The two eigenvalues of variational matrix \( V\left( {\bar{x},0} \right) \) are

$$ \lambda_{1} = - \frac{r}{k}\bar{x}\,\,{\text{and}}\,\,\lambda_{2} = s - \frac{{s\bar{x}}}{K} + \frac{{\alpha \beta (\bar{x} - m)}}{{1 + (\bar{x} - m)}} - q_{2} E. $$

Obviously λ 1 < 0 and if \( \left( {\bar{x},0} \right) \) is a stable node, the other eigenvalue λ 2 must also be negative. This requires that

$$ E > \frac{1}{{q_{2} }}\left[ {s - \frac{{s\bar{x}}}{K} + \frac{{\alpha \beta \left( {\bar{x} - m} \right)}}{{1 + a(\bar{x} - m)}}} \right]\,\,{\text{and}}\,\,\bar{x} > m. $$

Theorem 5.3

A necessary and sufficient condition that the steady state (0, \( \bar{y} \)) is a stable node is \( \frac{1}{{q_{1} }}\left[ {r - \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }}} \right] < E < \frac{\gamma }{{q_{2} }}\left[ {s + \frac{3\alpha \beta m}{1 - am}} \right] \) and \( r > \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }} \).

Proof

The eigenvalues of variational matrix \( (0,\bar{y}) \) are

$$ \lambda_{1} = r - \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }} - q_{1} E\,\,{\text{and}}\,\,\lambda_{2} = - s - \frac{3\alpha \beta m}{1 - am} + q_{2} \frac{E}{\gamma }. $$

The eigenvalue λ 1 will be negative if

$$ E > \frac{1}{{q_{1} }}\left[ {r - \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }}} \right]. $$

The eigenvalue λ 2 will be negative if

$$ E < \frac{\gamma }{{q_{2} }}\left[ {s + \frac{3\alpha \beta m}{1 - am}} \right]. $$

Therefore necessary and sufficient conditions are

$$ \frac{1}{{q_{1} }}\left[ {r - \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }}} \right] < E < \frac{\gamma }{{q_{2} }}\left[ {s + \frac{3\alpha \beta m}{1 - am}} \right]\,\,{\text{and}}\,\,r > \frac{{\alpha \bar{y}}}{{\left( {1 - am} \right)^{2} }}. $$

Theorem 6

A necessary and sufficient condition that the steady state (\( x^{*} ,y^{*} \)) is a stable node is \( \frac{r}{K}x^{*} + \frac{{\alpha y^{*} }}{{(1 + ax - am)^{2} }} > \frac{{\alpha y^{*} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}} \) and \( x^{*} > m \).

Proof

The eigenvalues of the variational matrix V (\( x^{*} ,y^{*} \)) are

$$ \lambda_{1} = - \frac{r}{K}x^{*} - \frac{{\alpha y^{*} }}{{(1 + ax^{*} - am)^{2} }} + \frac{{\alpha y^{*} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}}\,\,{\text{and}}\,\,\lambda_{2} = - \gamma y^{*} . $$

The eigenvalues of the variotional matrix V (\( x^{*} ,y^{*} \)) are the roots \( \lambda_{i} \) \( (i = 1,2) \) of the quadratic equation

$$ \begin{gathered} \lambda^{2} - \lambda \left[ {\frac{{\alpha y^{*} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}} - \frac{r}{K}x^{*} - \frac{{\alpha y^{*} }}{{(1 + ax^{*} - am)^{2} }} - \gamma y^{*} } \right] \hfill \\ + \frac{{\alpha \gamma y^{{*^{2} }} }}{{(1 + ax^{*} - am)^{2} }} + \frac{r\gamma }{K}x^{*} y^{*} - \frac{{\alpha \gamma y^{{*^{2} }} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}} = 0 \hfill \\ \end{gathered} $$
(5.2)

In Eq. (5.2)

$$ \lambda_{1} + \lambda_{2} = - \frac{r}{K}x^{*} - \frac{{\alpha y^{*} }}{{(1 + ax^{*} - am)^{2} }} + \frac{{\alpha y^{*} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}} - \gamma y^{*} $$
$$ {\text{and}}\,\,\,\lambda_{1} \lambda_{2} = - \frac{{\alpha \gamma y^{{*^{2} }} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}} + \frac{r\gamma }{K}x^{*} y^{*} + \frac{{\alpha \gamma y^{{*^{2} }} }}{{(1 + ax^{*} - am)^{2} }}. $$

Assuming that (\( x^{*} ,y^{*} \)) is a stable node, we must have \( \lambda_{1} + \lambda_{2} < 0 \) and \( \lambda_{1} \lambda_{2} > 0 \).

This requires the following conditions,

$$ \frac{r}{K}x^{*} + \frac{{\alpha y^{*} }}{{(1 + ax^{*} - am)^{2} }} > \frac{{\alpha y^{*} (x^{*} - m)}}{{x^{*} (1 + ax^{*} - am)}}\,\,{\text{and}}\,\,x^{*} > m. $$
(5.3)

Hence the conditions (5.3) are necessary for \( (x^{*} ,y^{*} ) \) to be stable.

Hence, the theorem is proved.

6 Global Stability

In this section, we consider the global stability of system (2.2) by constructing a suitable Lyapunov function. We define a Lyapunov function

$$ V(x,y) = \left[ {\left( {x - x^{*} } \right) - x^{*} \log \left( {\frac{x}{{x^{*} }}} \right)} \right] + d\left[ {\left( {y - y^{*} } \right) - y^{*} \log \left( {\frac{y}{{y^{*} }}} \right)} \right] $$

where d is a suitable constant to be determined in the subsequent steps. It can be easily verified that the function V is zero at the equilibrium (\( x^{*} ,y^{*} \)) and is positive for all other positive values of x, y.

The time derivatives of V along the trajectories of (2.2) is

$$ \frac{dV}{dt} = \left( {\frac{{x - x^{*} }}{x}} \right)\frac{dx}{dt} + d\left( {\frac{{y - y^{*} }}{y}} \right)\frac{dy}{dt} $$
$$ \begin{aligned} = \left( {x - x^{*} } \right)\left[ {\left( {r\left( {1 - \frac{x}{K}} \right) - \frac{\alpha (x - m)y}{{x\left( {1 + a(x - m)} \right)}} - q_{1} E} \right) - \left( {r\left( {1 - \frac{{x^{*} }}{K}} \right) - \frac{{\alpha (x^{*} - m)y^{*} }}{{x^{*} \left( {1 + a(x^{*} - m)} \right)}} - q_{1} E} \right)} \right] \hfill \\ + d\left( {y - y^{*} } \right)\left[ {\left( {s\left( {1 - \frac{x}{K}} \right) + \frac{\alpha \beta (x - m)}{1 + a(x - m)} - q_{2} E - \gamma y} \right) - \left( {s\left( {1 - \frac{{x^{*} }}{K}} \right) + \frac{{\alpha \beta (x^{*} - m)}}{{1 + a(x^{*} - m)}} - q_{2} E - \gamma y^{*} } \right)} \right] \hfill \\ \end{aligned} $$
$$ = - \left[ {\left( {x - x^{*} } \right)^{2} \left[ {\frac{r}{K} + \frac{{\alpha \left( {axx^{*} y - my^{*} \left( {ma + 1} \right)} \right)}}{{xx^{*} \left( {1 + a\left( {x - m} \right)} \right)\left( {1 + a\left( {x^{*} - m} \right)} \right)}}} \right]} \right. $$
$$ + \left( {x - x^{*} } \right)\left( {y - y^{*} } \right)\left[ {\frac{s}{\beta K} - \frac{{\alpha \left( {m\left( {ma + 1} \right) - 2ma - ax^{*} } \right)}}{{x\left( {1 + a\left( {x - m} \right)} \right)\left( {1 + a\left( {x^{*} - m} \right)} \right)}}} \right] + \left. {\frac{\gamma }{\beta }\left( {y - y^{*} } \right)^{2} } \right] $$

where,

$$ d = \frac{1}{\beta } $$
(6.1)

The above equation can be written as \( - X^{T} AX \) where \( X^{T} = \left[ {\left( {x - x^{*} } \right),\left( {y - y^{*} } \right)} \right] \) and

$$ A = \left[ {\begin{array}{*{20}l} {\frac{r}{K} + \frac{{S\left( {axx^{*} y - my^{*} \left( {ma + 1} \right)} \right)}}{{xx^{*} }}} & {\frac{1}{2}\left[ {\frac{s}{\beta K} - \frac{{S\left( {m\left( {ma + 1} \right) - 2ma\,x - axx^{*} } \right)}}{x}} \right]} \\ {\frac{1}{2}\left[ {\frac{s}{\beta K} - \frac{{S\left( {m\left( {ma + 1} \right) - 2ma\,x - axx^{*} } \right)}}{x}} \right]} & {\frac{\gamma }{\beta }} \\ \end{array} } \right] $$

where, \( S = \frac{\alpha }{{\left( {1 + a\left( {x - m} \right)} \right)\left( {1 + a\left( {x^{*} - m} \right)} \right)}} \) \( \frac{dV}{dt} < 0 \), if the matrix A is positive definite.

The matrix A is positive definite if \( axx^{*} y > my^{*} \left( {ma + 1} \right) \) and \( x^{*} \left[ {sx - S\beta K\left( {m\left( {ma + 1} \right) - 2ma\,x - axx^{*} } \right)} \right]^{2} > 4\gamma \left[ {rxx^{*} + SK\left( {axx^{*} y - my^{*} \left( {ma + 1} \right)} \right)} \right] \)

The above result can be stated as follows:

Theorem 6.1

The interior equilibrium point \( E^{*} (x^{*} ,y^{*} ) \) is globally asymptotically stable if the interior equilibrium is locally stable and \( axx^{*} y > my^{*} \left( {ma + 1} \right) \), \( x^{*} \left[ {sx - S\beta K\left( {m\left( {ma + 1} \right) - 2ma\,x - axx^{*} } \right)} \right]^{2} > 4\gamma \left[ {rxx^{*} + SK\left( {axx^{*} y - my^{*} \left( {ma + 1} \right)} \right)} \right] \) both the conditions simultaneously hold.

7 Bionomic Equilibrium

The term bionomic equilibrium is an amalgamation of the concepts of biological equilibrium and economic equilibrium. A bionomic equilibrium is given by \( \dot{x} = 0 = \dot{y} \). the economic equilibrium is said to be achieved when TR (the total revenue obtained by selling the harvested biomass) equals TC (the total cost for the effort devoted to harvesting).

Let p 1 = constant price per unit biomass of the first species; q 1 = constant price per unit biomass of the s second species; C = constant fishing cost per unit effort

The economic rent (revenue at any time) is given by

$$ \pi \left( {x,y,E} \right) = p_{1} q_{1} xE + p_{2} q_{2} yE - CE $$
(7.1)

Although the harvesting cost per unit effort (C) is not a constant, we take it to be a constant for sake of simplicity. Now

$$ \dot{x} = 0 \Rightarrow x = 0\,\,\,or,E = \frac{r}{{q_{1} }} - \frac{rx}{{kq_{1} }} - \frac{\alpha y}{{q_{1} (1 + a(x - m))}} + \frac{\alpha my}{{q_{1} x\left[ {1 + a(x - m)} \right]}}\,\,{\text{and}} $$
$$ \dot{y} = 0 \Rightarrow y = 0\,\,\,or,E = \frac{\alpha \beta (x - m)}{{q_{2} \left( {1 + a(x - m)} \right)}} + \frac{s}{{q_{2} }}\left( {1 - \frac{x}{k}} \right) - \frac{\gamma y}{{q_{2} }} $$

Hence the nontrivial equilibrium solution \( (\dot{x} = \dot{y} = 0) \) occurs at a point on the curve

$$ \begin{gathered} x^{3} \left( {\frac{as}{{q_{2} }} - \frac{ar}{{q_{1} }}} \right) + x^{2} \left( {\frac{akr}{{q_{1} }} - \frac{r}{{q_{1} }} + \frac{amr}{{q_{1} }} - \frac{\alpha \beta k}{{q_{2} }} - \frac{aks}{{q_{2} }} + \frac{s}{{q_{2} }} - \frac{ams}{{q_{2} }} + \frac{ak\gamma y}{{q_{2} }}} \right) \hfill \\ \hfill \\ \quad+ x\left( {\frac{kr}{{q_{1} }} - \frac{amrk}{{q_{1} }} - \frac{\alpha ky}{{q_{1} }} + \frac{\alpha \beta km}{{q_{2} }} - \frac{ks}{{q_{2} }} + \frac{amks}{{q_{2} }} + \frac{k\gamma y}{{q_{2} }} + \frac{ak\gamma my}{{q_{2} }}} \right) + \frac{\alpha kmy}{{q_{1} }} = 0 \hfill \\ \end{gathered} $$
(7.2)

The bionomic equilibrium \( (x_{\infty } ,y_{\infty } ) \) of the open-access fishery is determined by (7.2), together with the condition

$$ \pi = TR - TC = (p_{1} q_{1} x - p_{2} q_{2} y - C)E = 0 \Rightarrow p_{1} q_{1} x + p_{2} q_{2} y - C = 0 $$
(7.3)

Eliminating y from Eqs. (7.2) and (7.3),we get

$$ A_{1} x^{3} + B_{1} x^{2} + C_{1} x + D_{1} = 0 $$
(7.4)

where \( A_{1} = \left( {\frac{as}{{q_{2} }} - \frac{ar}{{q_{1} }} - \frac{{ak\gamma p_{1} q_{1} }}{{p_{2} q_{2}^{2} }}} \right) \),

$$ B_{1} = \left( {\frac{akr}{{q_{1} }} - \frac{r}{{q_{1} }} + \frac{amr}{{q_{1} }} - \frac{\alpha \beta k}{{q_{2} }} - \frac{aks}{{q_{2} }} + \frac{s}{{q_{2} }} - \frac{ams}{{q_{2} }} - \frac{{k\gamma p_{1} q_{1} }}{{p_{2} q_{2}^{2} }} + \frac{Cak\gamma }{{p_{2} q_{2}^{2} }} + \frac{{ak\gamma mp_{1} q_{1} }}{{p_{2} q_{2}^{2} }}} \right), $$
$$ C_{1} = \left( {\frac{kr}{{q_{1} }} - \frac{amrk}{q} - \frac{\alpha kC}{{p_{2} q_{1} q_{2} }} + \frac{{p_{1} }}{{p_{2} q_{2} }} - \frac{{\alpha kmp_{1} }}{{p_{2} q_{2} }} + \frac{\alpha \beta km}{{q_{2} }} - \frac{ks}{{q_{2} }} + \frac{amks}{{q_{2} }} + \frac{Ck\gamma }{{p_{2} q_{2}^{2} }} - \frac{ak\gamma mC}{{p_{2} q_{2}^{2} }}} \right), $$
$$ D_{1} = \frac{\alpha kmC}{{p_{2} q_{1} q_{2} }}. $$

It is to be noted from Eq. (7.4) that \( A_{1} > 0 \) if \( \frac{s}{{q_{2} }} > \frac{r}{{q_{1} }} + \frac{{K\gamma p_{1} q_{1} }}{{p_{2} q_{2}^{2} }} \) and \( D_{1} > 0. \)

It is possible to get at least one positive solution of x from equation (7.4) depending on the sign of B 1 and C 1.

Therefore, we may have either at least one bionomic equilibria or no bionomic equilibria at all.

8 Optimal Harvesting Policy

The emphasis of this section is on the profit-making aspect of fisheries. It is a through study of the optimal harvesting policy and the profit earned by harvesting, focusing on quadratic costs and conservation of fish population by constraining the latter to always stay above a critical threshold. It is assumed that price is a function which decreases with increasing biomass. To maximize the total discounted net revenues from the fishery, the optimal problem can be formulated as:

$$ J = \int\limits_{{t_{0} }}^{{t_{f} }} {e^{ - \delta t} \left[ {(p_{1} - v_{1} q{}_{1}Ex)q_{1} Ex + (p_{2} - v_{2} q_{2} Ey)q_{2} Ey - cE} \right]dt} $$
(8.1)

where \( v_{1} \) and \( v_{2} \) are the economic constants and \( \delta \) denotes the instantaneous annual rate of discount. Our problem (8.1), subject to the state Eq. (2.2) and control constraints \( 0 \le E \le E_{\hbox{max} } \), can be solved by applying Pontryagin’s Maximum Principle. The convexity of the objective function with respect to E, the linearity of the differential equations in the control and compactness of the range values of the state variables can be combined to give the existence of the optimal control.

Suppose \( E_{\delta } \) is an optimal control with corresponding states \( x_{\delta } \) and \( y_{\delta } \).

We take \( A_{\infty } \left( {x_{\infty } ,y_{\infty } } \right) \) as optimal equilibrium point.

Here we intend to derive optimal control \( E_{\delta } \) such that

$$ J\left( {E_{\delta } } \right) = \hbox{max} \left\{ {J\left( E \right):E \in U} \right\}, $$

where U is the control set defined by\( U = \left\{ {E:\left[ {t_{0} ,t_{f} } \right] \to \left[ {0,E_{\hbox{max} } } \right]\left| E \right.} \right. \) is Lebesgue measurable}.

The Hamiltonian of this control problem is given by

$$ \begin{aligned} H & = \left[ {(p_{1} - v_{1} q_{1} Ex)q_{1} Ex + (p_{2} - v_{2} q_{2} Ey)q_{2} Ey - cE} \right] + \lambda_{1} \left[ {rx(1 - \frac{x}{K}) - \frac{\alpha (x - m)y}{1 + a(x - m)} - q_{1} Ex} \right] \\ \quad + \lambda_{2} \left[ {sy(1 - \frac{x}{K}) + \frac{\alpha \beta (x - m)y}{1 + a(x - m)} - \gamma y^{2} - q_{2} Ey} \right] \\ \end{aligned} $$

where \( \lambda_{1} (t) \)and \( \lambda_{2} (t) \) are adjoint variables.

The transversality conditions give \( \lambda_{1} (t_{f} ) = 0,i = 1,2. \)

Now, it is possible to find the characterization of the optimal control \( E_{\delta } \).

On the set \( \left\{ {t\left| {0 < E_{\delta } (t) < E_{\hbox{max} } } \right.} \right\} \), we have

$$ \frac{\partial H}{\partial E} = (p_{1} - \lambda_{1} )q_{1} x + (p_{2} - \lambda_{2} )q_{2} y - c - 2E(v_{1} q_{1}^{2} x^{2} + v_{2} q_{2}^{2} y^{2} ) = 0\,\,{\text{at}}\,\,E_{\delta } (t). $$

This implies that,

$$ E_{\delta } (t) = \frac{{(p_{1} - \lambda_{1} )q_{1} x + (p_{2} - \lambda_{2} )q_{2} y - c}}{{2(v_{1} q_{1}^{2} x^{2} + v_{2} q_{2}^{2} y^{2} )}}. $$

Now adjoint equations at the point \( (x_{\infty } ,y_{\infty } ) \) are

$$ \begin{gathered} \frac{{d\lambda_{1} }}{dt} = \delta \lambda_{1} - \frac{\partial H}{\partial x}\left| {_{{A_{\infty } }} } \right. = \delta \lambda_{1} - \left[ {p_{1} q_{1} E - \lambda_{1} q_{1} E - 2v_{1} q_{1}^{2} E^{2} x} \right. + \lambda_{1} \left\{ {r - \frac{2xr}{K} - \frac{\alpha y}{{\left( {1 + ax - am} \right)^{2} }}} \right\} \hfill \\ + \lambda_{2} \left. {\left\{ {\frac{sy}{K} + \frac{\alpha \beta y}{{\left( {1 + ax - am} \right)^{2} }}} \right\}} \right] \hfill \\ \end{gathered} $$
(8.2)
$$ \begin{aligned} \frac{{d\lambda_{2} }}{dt} & = \delta \lambda_{2} - \frac{\partial H}{\partial y}\left| {_{{A_{\infty } }} } \right. = \delta \lambda_{2} - \left[ {p_{2} q_{2} E - \lambda_{2} q_{2} E - 2v_{2} q_{2}^{2} E^{2} - 2y\gamma \lambda_{2} + \lambda_{1} \left\{ { - \frac{\alpha (x - m)}{1 + a(x - m)}} \right\}} \right. \\ \quad + \lambda_{2} \left. {\left\{ {s - \frac{sx}{K} + \frac{{\alpha \beta \left( {x - m} \right)}}{1 + a(x - m)}} \right\}} \right] \\ \end{aligned} $$
(8.3)

Equations (8.2) and (8.3) are first order system of simultaneous differential equations and it is easy to get the analytical solution of the equations with the help of initial conditions \( \lambda_{1} \left( {t_{f} } \right) = 0,i = 1,2 \).

Theorem 8.1

There exists an optimal control \( E_{\delta } \) and corresponding solutions \( x_{\delta } \) and \( y_{\delta } \) that maximized J over U. Furthermore, there exists adjoint functions \( \lambda_{1} \) and \( \lambda_{2} \) satisfying the Eqs. (8.2) and (8.3) with transversality conditions give \( \lambda_{i} (t_{f} ) = 0,i = 1,2 \). Moreover, the optimal control is given by

$$ E_{\delta } (t) = \frac{{(p_{1} - \lambda_{1} )q_{1} x + (p_{2} - \lambda_{2} )q_{2} y - c}}{{2(v_{1} q_{1}^{2} x^{2} + v_{2} q_{2}^{2} y^{2} )}}. $$

8.1 Numerical Simulation to Study the Stability of the System

It may be noted that it is quite difficult to have numerical value of the parameters of the system based on real world observations. On the other hand, it is necessary to have some idea regarding the sensitivity of the parameters in connection to the observed real system. Therefore, the major results described by the simulations presented should be considered from a qualitative, rather than a quantitative point of view. However, numerous scenarios covering the breath of the biological feasible parameter space were conducted and the results shown above display the breadth of dynamical results collected from all the scenarios tested. MATLAB and Mathematica are the main software used for the purpose of simulation experiments. We, therefore, take here some hypothetical data with the sole purpose of solving the system numerically to obtain the results after numerical simulations.

In order to ensure the existence of stable solution of the system, we consider the following parameter set:

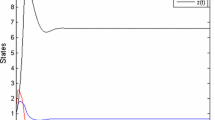
$$ \begin{gathered} r = 1.5,K = 100,\alpha = 0.8,m = 1.28,a = 0.2,s = 1.2,\beta = 0.5,\gamma = 0.3,\delta = 0.01,p_{1} = 0.6, \hfill \\ p_{2} = 0.4,q_{1} = 0.23,q_{2} = 0.397,v_{1} = 0.02,v_{2} = 0.04,c = 0.5,x_{0} = 0.4,y_{0} = 0.8,t = 100 \hfill \\ \end{gathered} $$

It is clearly observed from Figs. 1 and 2 that \( E_{3} \left( {x^{*} ,y^{*} } \right) \) is locally asymptotically stable.

Fig. 1
figure 1

Solution curves of prey and predator population with increasing time

Full size image
Fig. 2
figure 2

Phase plane trajectories of prey and predator population beginning with different initial levels

Full size image

8.2 Numerical Simulation of Optimal Control Problem

By using the fourth-order Runge–Kutta forward–backward sweep method, the numerical simulation of optimal control (Workman and Lenhart 2007) under various parameter sets can be done. The Eq. (2.2) and their corresponding adjoint Eqs. (8.2) and (8.3) are simultaneously solved. First we make a guess for optimal control and then solved the system of the state Eq. (2.2) forward in the time using the Runge–Kutta method with initial condition x 0 and y 0. The adjoint Eqs. (8.2) and (8.3) are solved backward in time using the Runge–Kutta method with transversality conditions. Using the values for the state and adjoint variables, the optimal control is updated. The updated control replaces the initial control and the process are repeated until the successive iterative of control values are sufficiently close. The convergence of such an iterative method is based on the work of Hackbush (1978).

At first, we discretize the interval \( \left[ {t_{0} ,t_{n} } \right] \) at the point \( t_{i} = t_{0} + ih,i = 0,1,2, \ldots n \), where h is the time step such that\( t_{n} = t_{f} \). Now a combination of forward and backward difference approximation is considered to solve the system. The time derivative of the state variables can be expressed by their first-order forward difference as follows:

$$ \begin{gathered} \frac{{x_{i + 1} - x_{i} }}{h} = rx_{i + 1} \left( {1 - \frac{{x_{i + 1} }}{K}} \right) - \frac{{\alpha (x_{i + 1} - m)y_{i} }}{{1 + a(x_{i + 1} - m)}} - q_{1} E_{i} x_{i + 1} \hfill \\ \frac{{y_{i + 1} - y_{i} }}{h} = sy_{i} \left( {1 - \frac{{x_{i + 1} }}{K}} \right) + \frac{{\alpha \beta (x_{i + 1} - m)y_{i} }}{{1 + a(x_{i + 1} - m)}} - \gamma y_{i}^{2} - q_{2} E_{i} y_{i} \hfill \\ \end{gathered} $$

By using a similar technique, we approximate the time derivative of the adjoint variables by their first order backward difference and we use the appropriate scheme as follows:

$$ \begin{aligned} \frac{{\lambda _{1}^{{n - i}} - \lambda _{1}^{{n - i - 1}} }}{h} & = \delta \lambda _{1}^{{n - i - 1}} - \left[ {p_{1} q_{1} E_{i} - \lambda _{1}^{{n - i - 1}} q_{1} E_{i} - 2v_{1} q_{1}^{2} E_{i} ^{2} x_{{i + 1}} } \right. \\ & \quad + \lambda _{1}^{{n - i - 1}} \left\{ {r - \frac{{2x_{{i + 1}} r}}{K} - \frac{{\alpha y_{{i + 1}} }}{{\left( {1 + ax_{{i + 1}} - am} \right)^{2} }}} \right\} + \lambda _{2}^{{n - i}} \left. {\left\{ {\frac{{sy_{{i + 1}} }}{K} + \frac{{\alpha \beta y_{{i + 1}} }}{{\left( {1 + ax_{{i + 1}} - am} \right)^{2} }}} \right\}} \right] \\ \end{aligned} $$
$$ \begin{aligned} \frac{{\lambda_{2}^{n - i} - \lambda_{2}^{n - i - 1} }}{h} & = \delta \lambda_{2}^{n - i - 1} - \left[ {p_{2} q_{2} E_{i} - \lambda_{2}^{n - i - 1} q_{2} E_{i} - 2v_{2} q_{2}^{2} E_{i}^{2} - 2y_{i + 1} \gamma \lambda_{2}^{n - i - 1} + \lambda_{1}^{n - i - 1} \left\{ { - \frac{{\alpha (x_{i + 1} - m)}}{{1 + a(x_{i + 1} - m)}}} \right\}} \right. \\ \quad + \lambda_{2}^{n - i - 1} \left. {\left\{ {s - \frac{{sx_{i + 1} }}{K} + \frac{{\alpha \beta \left( {x_{i + 1} - m} \right)}}{{1 + a(x_{i + 1} - m)}}} \right\}} \right]. \\ \end{aligned} $$

Figure 3 describes the variation of prey population, predator population, harvesting effort and total harvest with increasing time. Prey refuge plays an important role on the dynamic of the system. It is clearly observed from Fig. 1 that that prey population has an initial increasing trend in presence of prey refuge. It is to be noted that prey population is decreasing when m = 0. It is further noted that predator population is increased with time when m = 0. Figure 1 also depicts that harvesting effort is getting increased. This is due to fact that combined harvesting effort is used to harvest both the species and at initial stage availability of resource is ensured in both the situation with and without refuge. As a consequence, total harvest is also getting increased.

Fig. 3
figure 3

Variation of prey population, predator population, harvesting effort and total harvest with and without refuge (m). The black line corresponds with refuge and red line corresponds without refuge. (Color figure online)

Full size image

It is noted from Fig. 4 that predator population is increased with time when alternative food is provided. It is also observed that predator population is decreased when s = 0. It is interesting to observe that prey population density is increased with time in absence of alternative food. This is due to the effect of prey refuge in the system. So the prey population may have got protection up to some extent. It is further noted that both harvesting effort and total harvest increased with time in both the condition with and without alternative food which is quite natural.

Fig. 4
figure 4

Variation of prey population, predator population, harvesting effort and total harvest with and without alternative food (s). The black line corresponds with alternative food and red line corresponds without alternative food. (Color figure online)

Full size image

It is easy to understand that when there is no predation i.e., α = 0, prey population increased with time. It is clearly observed that predator population is increased with time in presence of predation. It is also noted that both harvesting effort and total harvest increased with time when α = 0. This result is clearly observed in Fig. 5.

Fig. 5
figure 5

Variation of prey population, predator population, harvesting effort and total harvest with and without predation (α). The black line corresponds with predation and red line corresponds without predation. (Color figure online)

Full size image

The intrinsic growth rate of the population plays an important role on the dynamics of the system. It clearly observed from Fig. 6 that density of prey population increased with its intrinsic growth rate. Again, in general density of predator population is inversely proportional to prey population therefore it is obvious that the density of predator population is getting decreased. It may be noted that harvesting effort is getting increased. Subsequently, total harvest is also getting increased.

Fig. 6
figure 6

Variation of prey population, predator population, total harvest and total present value with increasing harvesting effort. The black line corresponds to r = 1.5, the blue line to r = 1.0 and red line to r = 2.0. (Color figure online)

Full size image

The impacts of prey refuge are illustrated in Fig. 7. It is observed that prey population density increased with the increasing value of m whereas density of predator population is getting decreased. It is to be noted from Fig. 7 that due to the presence of prey and predator population in the system total harvesting effort is getting increased. Therefore total present value is increased with increasing harvesting effort.

Fig. 7
figure 7

Variation of prey population, predator population, total harvest and total present value with increasing harvesting effort. The black line corresponds to m = 1.5, the blue line to m = 1.0 and red line to m = 2.0. (Color figure online)

Full size image

Alternative prey has great impact on the dynamic of the system. It is obvious that with the increasing alternative food density of predator population is getting increased so predation pressure is also increased. Therefore, prey population density is decreasing with the increasing alternative food to the predator. However, the effect of combined harvesting effort is also present in the system so it is natural that the species can be sustainably managed through controlling alternative food. The results are clearly observed in Fig. 8.

Fig. 8
figure 8

Variation of prey population, predator population, total harvest and total present value with increasing harvesting effort. The black line corresponds to s = 1.2, the blue line to s = 0.4 and red line to s = 2.0. (Color figure online)

Full size image

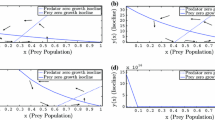
It is clear from Fig. 9 that the size of prey population available to the predator is dependent on the intrinsic growth of the prey population. Subsequently, it is to be noted from Fig. 10 that if prey is refusing predator population then functional response is decreasing with time though at the initial stage it is increasing.

Fig. 9
figure 9

Variation of functional response (prey consumed by the predator) with increasing time. The black line corresponds to r = 1.5, the blue line to r = 1.0 and red line to r = 2.0. (Color figure online)

Full size image
Fig. 10
figure 10

Variation of functional response (prey consumed by the predator) with increasing time. The black line corresponds to m = 1.5, the blue line to m = 1.0 and red line to m = 0.5. (Color figure online)

Full size image

The availability of alternative food to the predator population has a great influence to the stability of the system. It is to be noted from Fig. 11 that due to availability of alternative food the consumption of prey by predator is getting decreased with increasing time for a constant rate of prey refuge. In order to have a stable system, the availability of alternative food should be increased with less prey refuge as depicted in Fig. 12. With the increasing rate of prey consumption by predator, it is obvious that the availability of alternative food to the predator should be increased which is clearly observed in Fig. 13. It is to be further noted that if the rate of intra-specific competition of predators is increased then the size of predator population is getting decreased subsequently the availability of alternative food in terms of prey should be increased as shown in Fig. 14.

Fig. 11
figure 11

Variation of functional response (prey consumed by the predator) with increasing time. The black line corresponds to s = 1.2, the blue line to s = 0.4 and red line to s = 2.0. (Color figure online)

Full size image
Fig. 12
figure 12

Variation of alternative food (available to the predator) with increasing time. The black line corresponds to m = 1.5, the blue line to m = 1.0 and red line to m = 0.5. (Color figure online)

Full size image
Fig. 13
figure 13

Variation of alternative food (available to the predator) with increasing time. The black line corresponds to α = 0.8, the blue line to α = 0.6 and red line to α = 0.4. (Color figure online)

Full size image
Fig. 14
figure 14

Variation of alternative food (available to the predator) with increasing time. The black line corresponds to γ = 0.3, the blue line to γ = 0.2 and red line to γ = 0.4. (Color figure online)

Full size image

9 Concluding Remarks

This paper deals with a problem of non-selective harvesting of a prey–predator system in which both prey the prey and predator species obey logistic law of growth. We consider a prey–predator model incorporating constant prey refuge through provision of alternative food to predators. In this study, it is pointed out that prey refuge as well as quality and quantity of additional food play a vital role in the controllability of the system. Our interest is to maximize the monetary social benefit through protect the predator species from extinction, keeping the ecological balance. We have determined the steady states of the system and analyzed the dynamical behavior of the system. Global stability is examined by taking a suitable Lyapunov function. We are then examined the possibilities of existence of bionomic (biological as well as economic) equilibria of the system. Next, the optimal harvesting policy is solved with the help of Pontryagin’s maximal principle.

Also, we analyze the dynamical behavior of the system. It is clear from the obtained results that existence of refuge has important effects on the predator and prey population. It is observed that prey population density is increased in presence of prey refuge. We also noted that predator population is increased in absence of refuge due to the presence of alternative food. Our analysis also shows that the impact of intrinsic growth rate on dynamic of the system. We explore the dynamics of prey–predator system when alternative food is provided to the predators. Our objective is to examine the consequences of exploitation in this model. It is noted that predator population is increased with time when alternative food is provided. Our result also shows that total harvest increases as both the population increase. Success depends on the quality and quantity of additional food supplied to the predators as well as appropriate amount of harvesting efforts to both the species. This study enables us to develop management strategies that determine the supply amount of alternative food for the biological control of the system.