Dynamics of a predator–prey model with harvesting and reserve area for prey in the presence of competition and toxicity

Abstract

The aim of this paper is to present and study a three-dimensional continuous time dynamical system modeling a predator–prey with harvesting and reserve zone for the prey in the presence of competition and toxicity. We first prove that our model is ecologically and mathematically well-posed. In addition, the stability analysis is investigated by direct and indirect Lyapunov methods. By using the Pontryagin’s maximum principle, an optimal harvesting policy is established. Furthermore, numerical simulations are given in order to illustrate our theoretical results.

1 Introduction

In recent years, various species are extinct due to several ecological and economic factors such as the over predation and harvesting, the pollution, and the mismanagement of commercial exploitation of the biological resource like fisheries and forestry. For these reasons, many mathematical models have been proposed and developed to better describe the relationship between predator and prey populations by taking into account the harvesting [6, 8], the optimal harvesting policy [9, 11, 13], the toxicity [2, 3] and the harvesting and reserve area for the prey in the presence of toxicity [12].

In reality, there is always a competition between species that is an important topic in ecology. This phenomenon is very common in a habitat with finite common resources and it is considered by many authors (see, for example [5, 10]). The purpose of this paper is to investigate the effects of competition and toxicity on dynamics of the following predator–prey model:

$$\begin{aligned} \frac{dx}{dt}= & {} r_1x\left( 1-\displaystyle \frac{x}{K}\right) -\sigma _1x+\sigma _2y-ux^2-\frac{axz}{b+x}-q_1Ex-n_1xy,\nonumber \\ \frac{dy}{dt}= & {} r_2y+\sigma _1x-\sigma _2y-vy^2-n_2xy,\nonumber \\ \frac{dz}{dt}= & {} \frac{\beta axz}{b+x}-dz-wz-q_2Ez, \end{aligned}$$

(1)

where x(t), y(t) and z(t) denote the biomass densities of the prey species inside the unreserved area, reserved area, and the predator species at time t, respectively. The intrinsic growth rates of prey species inside the unreserved and reserved areas are $r_{1}$ and $r_{2}$, respectively. The carrying capacity of fish species in the unreserved area is K. The catchability coefficients for the predator species in the unreserved area are $q_{1}$ and $q_{2}$, respectively. The effort applied for harvesting the fish population in the unreserved area and the predator populations in the unreserved area is E. Migration rate from unreserved area to reserved area and reserved area to unreserved are $\sigma _{1}$ and $\sigma _{2}$, respectively. The terms $ux^{2}$ and $vy^{2}$ represent the infection of the prey species by an external toxic substance and the term wz for the predator species. The term $\frac{axz}{b+x}$ denotes the Holling type II functional response. The parameter d is the death rate of predator species. Finally, $n_1$ and $n_2$ are the competition coefficients. It very important to note that when $n_1=n_2=0$, we get the model presented by Yang and Jia in [12].

From [4], we know that if there is no migration of fish population from reserve area to free fishing zone (i.e. $\sigma _2=0$) and $r_1 \sigma _1-q_1E < 0$, then $\frac{dx(t)}{dt} < 0$. Similarly, if there is no migration of fish population from free fishing zone to reserve area (i.e. $\sigma _1=0$) and $r_2-\sigma _2 < 0$, then $\frac{dy(t)}{dt} < 0$. The first three terms of the third equation of (1) is always negative if $\beta a-d-w<0$. Hence throughout our analysis, we assume that

$$\begin{aligned} r_1-\sigma _1-q_1E>0,\quad r_2-\sigma _2>0, \quad \beta a-d-w >0. \end{aligned}$$

(2)

The rest of the paper is organized as follows. The next section deals with basic results and equilibria. The stability analysis is investigated in Sect. 3. The optimal harvesting policy is discussed in Sect. 4. Some numerical simulations are presented in Sect. 5 in order to illustrate the theoretical results. The paper ends with discussion and conclusion in Sect. 6.

2 Basic results and equilibria

In this section, we first prove the uniform boundedness of the solutions of system (1).

Lemma 2.1

All solutions of system (1) with positive initial value $(x_0,y_0,z_0)$ are positively invariant within $\Omega$, where

$$\begin{aligned} \Omega = \left\{ \left( x,y,z\right) \in \mathbf {R}^{3}: x+y+\frac{1}{\beta } z\le \frac{\mu }{d+w+q_2E} \right\} , \end{aligned}$$

with

$$\begin{aligned} \mu =\frac{(r_1-q_1E+d+w+q_2E)^2}{4\left( \frac{r_1}{K}+u\right) }+\frac{(r_2+d+w+q_2E)^2}{4v}. \end{aligned}$$

Proof

Let $X(t)=x(t)+y(t)+\frac{1}{\beta }z(t)$. Then

$$\begin{aligned} \quad \frac{dX(t)}{dt}+(d+w+q_2E)X(t)= & {} (r_1-q_1E+d+w+q_2E)x(t)-\left( \frac{r_1}{K}+u\right) x^2(t)\\&-\,(n_1+n_2)x(t)y(t) +(r_2+d+w+q_2E)y(t)\\&-\,vy^2(t)\\\le & {} \frac{(r_1-q_1E+d+w+q_2E)^2}{4\left( \frac{r_1}{K}+u\right) }+\frac{(r_2+d+w+q_2E)^2}{4v}\\= & {} \mu . \end{aligned}$$

Applying the theory of differential inequality [1, 7], we get

$$\begin{aligned} X(t)\le & {} \frac{\mu }{d+w+q_2E}\\&-\,\left( \frac{\mu }{d+w+q_2E}-(x(0)+y(0)+\frac{1}{\beta }z(0))\right) e^{-(d+w+q_2E)t} \end{aligned}$$

and for $t\rightarrow +\infty$, we have $X(t)\le \frac{\mu }{d+w+q_2E}$. This completes the proof. $\square$

In the following, we discuss the existence of equilibria of the system (1).

Clearly, the vanishing equilibrium point $P_0(0,0,0)$ always exists.

The predator free-equilibrium point $\bar{P}(\bar{x}, \bar{y}, 0)$, where $(\bar{x},\bar{y})$ is the positive solution of the following equations:

$$\begin{aligned} r_1x\left( 1-\displaystyle \frac{x}{K}\right) -\sigma _1x+\sigma _2y-ux^2-q_1Ex-n_1xy= & {} 0,\nonumber \\ r_2y+\sigma _1x-\sigma _2y-vy^2-n_2xy= & {} 0. \end{aligned}$$

(3)

Consequently, x is satisfied by the following cubic equation

$$\begin{aligned} A_3x^3+A_2x^2+A_1x+A_0=0, \end{aligned}$$

where

$$\begin{aligned} A_3= & {} \left( u+\frac{r_1}{K}\right) \left[ -v\left( u+\frac{r_1}{K}\right) +n_1n_2\right] ,\\ A_2= & {} 2v\left( u+\frac{r_1}{K}\right) (r_1-\sigma _1-q_1E)-n_2\sigma _2\left( u+\frac{r_1}{K}\right) \\&-\,n_1(r_2-\sigma _2)\left( u+\frac{r_1}{K}\right) -n_1n_2(r_1-\sigma _1-q_1E)+n_1^2\sigma _1,\\ A_1= & {} -v(r_1-\sigma _1-q_1E)^2+(n_2\sigma _2+n_1(r_2-\sigma _2))(r_1-\sigma _1-q_1E)\\&+\,\left( u+\frac{r_1}{K}\right) (r_2-\sigma _2)\sigma _2-2\sigma _1\sigma _2n_1,\\ A_0= & {} -\sigma _2(r_2-\sigma _2)(r_1-\sigma _1-q_1E)+\sigma _1\sigma _2^2. \end{aligned}$$

$A_1>0$ if $E>\frac{1}{q_1}\left( r_1-\sigma _1-\frac{\sqrt{\Delta _1+n_2\sigma _2+n_1(r_2-\sigma _2)}}{2v}\right)$,

where $\Delta _1=\left( n_2\sigma _2+n_1(r_2-\sigma _2)\right) ^2+4v(u+\frac{r_1}{K})(r_2-\sigma _2)\sigma _2$,

$A_0>0$ if $E>\frac{1}{q_1}\left( r_1-\sigma _1-\frac{\sigma _1\sigma _2}{r_2-\sigma _2}\right)$. Then,

$$\begin{aligned}&\displaystyle E>\max \left( \frac{1}{q_1}\left( r_1-\sigma _1-\frac{\sigma _1\sigma _2}{r_2-\sigma _2}\right) , \frac{1}{q_1}\left( r_1-\sigma _1-\frac{\sqrt{\Delta _1+n_2\sigma _2+n_1(r_2-\sigma _2)}}{2v}\right) \right) \end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle A_3<0 \text{ if } n_1n_2<v\left( u+\frac{r_1}{K}\right) \end{aligned}$$

(5)

$$\begin{aligned}&\displaystyle A_2>0 \text{ if } v(r_1-\sigma _1-q_1E)> n_2\sigma _2+n_1(r_2-\sigma _2). \end{aligned}$$

(6)

The first equation of (3), we have

$$\begin{aligned} \bar{y}=\left( \frac{\left( u+\frac{r_1}{K}\right) \bar{x}-(r_1-\sigma _1-q_1E)}{\sigma _2-n_1\bar{x}}\right) \bar{x}>0, \end{aligned}$$

(7)

where

$$\begin{aligned} \frac{r_1-\sigma _1-q_1E}{u+\frac{r_1}{K}}<\bar{x}<\frac{\sigma _2}{n_1}\quad \text{ or } \quad \frac{\sigma _2}{n_1}<\bar{x}<\frac{r_1-\sigma _1-q_1E}{u+\frac{r_1}{K}}. \end{aligned}$$

(8)

For the equilibrium point $P^*(x^*,y^*,z^*)$, $(x^*,y^*,z^*)$ is the positive solution of the equations:

$$\begin{aligned} r_1x\left( 1-\frac{x}{K}\right) -\sigma _1x+\sigma _2y-ux^2-\frac{axz}{b+x}-q_1Ex-n_1xy= & {} 0,\nonumber \\ r_2y+\sigma _1x-\sigma _2y-vy^2-n_2xy= & {} 0,\nonumber \\ \frac{\beta axz}{b+x}-dz-wz-q_2Ez= & {} 0. \end{aligned}$$

(9)

Then, the third equation

$$\begin{aligned} x^*=\frac{b(d+w+q_2E)}{\beta a-d-w-q_2E}>0. \end{aligned}$$

(10)

if

$$\begin{aligned} E <\frac{1}{q_2}(\beta a -d-w). \end{aligned}$$

(11)

Substituting $x^*$ to the second equation of (9), this equation has unique positive equation

$$\begin{aligned} y^*=\frac{r_2-\sigma _2-n_2x^*+\sqrt{(r_2-\sigma _2-n_2x^*)^2+4v\sigma _1x^*}}{2v}. \end{aligned}$$

(12)

Substituting $x^*$, $y^*$ to the first equation of (9)

$$\begin{aligned} z^*=\frac{(b+x^*)\left[ -\left( u+\frac{r_1}{K}\right) x^{*2}+(r_1-\sigma _1-q_1E-n_1y^*)x^*+\sigma _2y^*\right] }{ax^*}. \end{aligned}$$

(13)

Then, $z^*>0$ if

$$\begin{aligned} x^*<\frac{(r_1-\sigma _1-q_1E-n_1y^*)+\sqrt{(r_1-\sigma _1-q_1E-n_1y^*)^2+4\left( u+\frac{r_1}{K}\right) \sigma _2y^*}}{2\left( u+\frac{r_1}{K}\right) }. \end{aligned}$$

(14)

Taking (14) into account, we can get the following theorem.

Theorem 2.2

The trivial equilibrium point $P_0(0,0,0)$ exists. If (4)–(8) hold, the predator equilibrium $\bar{P}(\bar{x}, \bar{y}, 0)$ exists. If (11)–(14) holds, the interior equilibrium $P^*(x^*,y^*,z^*)$ exists.

3 Stability analysis

In this section, we establish the local stability of equilibria.

Theorem 3.1

Suppose that (2) holds. The trivial equilibrium $P_0(0,0,0)$ is always unstable.

Proof

The Jacobian matrix

$$\begin{aligned} V(0,0,0)=\left( \begin{array}{ccc} r_1-\sigma _1-q_1E &{} \sigma _2 &{} 0 \\ \sigma _1 &{} r_2-\sigma _2 &{} 0\\ 0 &{} 0 &{} -(d+w+q_2E) \end{array} \right) . \end{aligned}$$

Then the characteristic equation of system at $P_0$ is

$$\begin{aligned} (\lambda +d+w+q_2E)\left( (\lambda -(r_1-\sigma _1-q_1E))(\lambda -(r_2-\sigma _2))-\sigma _1\sigma _2\right) =0 \end{aligned}$$

Firstly, It is clear that $\lambda _1=-(d+w+q_2E)<0$. If $\lambda _2$ and $\lambda _3$ are the two other roots, then $\lambda _2+\lambda _3>0$ with (2) holds. Therefore $\lambda _2$ and $\lambda _3$ have one positive value. Hence, $P_0$ is unstable. $\square$

Theorem 3.2

Suppose that (2) holds, if $\bar{x}<\frac{b(d+w+q_2E)}{\beta a-d-w-q_2E}=x^*$, the predator equilibrium point $\bar{P}(\bar{x},\bar{y},0)$ is locally asymptotically stable.

Proof

The Jacobian matrix of the point $(\bar{x},\bar{y},0)$ is

$$\begin{aligned} V(\bar{x},\bar{y},0)=\left( \begin{array}{ccc} V_1 &{} \sigma _2-n_1\bar{x} &{} \frac{-a\bar{x}}{b+\bar{x}} \\ \sigma _1-n_2\bar{y} &{} V_2 &{} 0\\ 0 &{} 0 &{} V_3 \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} V_1= & {} -2\left( u+\frac{r_1}{K}\right) \bar{x}+(r_1-\sigma _1-q_1E)-n_1\bar{y},\\ V_2= & {} r_2-\sigma _2-2v\bar{y}-n_2\bar{x}, \\ V_3= & {} \frac{\beta a\bar{x}}{b+\bar{x}}-(d+w+q_2E). \end{aligned}$$

Then, the characteristic equation of system at $\bar{P}$ is

$$\begin{aligned}&\left( \lambda -\frac{\beta a\bar{x}}{b+\bar{x}}+(d+w+q_2E)\right) \left( \phantom {\frac{\beta a\bar{x}}{b+\bar{x}}}\left( \phantom {\frac{\beta a\bar{x}}{b+\bar{x}}}\lambda +2\left( u+\frac{r_1}{K}\right) \bar{x}\right. \right. \\&\quad \left. \left. -(r_1-\sigma _1-q_1E)+n_1\bar{y}\phantom {\frac{r_1}{K}}\phantom {\frac{\beta a\bar{x}}{b+\bar{x}}}\right) (\lambda -r_2+\sigma _2+2v\bar{y}+n_2\bar{x})\right. \\&\quad \left. -(\sigma _2-n_1\bar{x})(\sigma _1-n_2\bar{y})\phantom {\frac{\beta a\bar{x}}{b+\bar{x}}}\right) =0. \end{aligned}$$

Obviously, $\lambda _1=\frac{\beta a\bar{x}}{b+\bar{x}}-(d+w+q_2E)$. This root is $\lambda _1<0$ if $\bar{x}<\frac{b(d+w+q_2E)}{\beta a-d-w-q_2E}=x^*$. Let $\lambda _2$ and $\lambda _3$ be the two other eigenvalues. These are the roots of the equation:

$$\begin{aligned} \lambda ^2+s_1\lambda +s_2=0, \end{aligned}$$

where,

$$\begin{aligned} s_1= & {} 2\left( u+\frac{r_1}{K}\right) \bar{x}-(r_1-\sigma _1-q_1E)+n_1\bar{y}-r_2+\sigma _2+2v\bar{y}+n_2\bar{x},\\ s_2= & {} \left( 2\left( u+\frac{r_1}{K}\right) \bar{x}-(r_1-\sigma _1-q_1E)+n_1\bar{y}\right) (-r_2+\sigma _2+2v\bar{y}+n_2\bar{x})\\&-\,(\sigma _2-n_1\bar{x})(\sigma _1-n_2\bar{y}). \end{aligned}$$

Using to $\bar{y}=\frac{(u+\frac{r_1}{K})\bar{x}-(r_1-\sigma _1-q_1E)}{\sigma _2-n_1\bar{x}}\bar{x}$ and $\bar{x}=\frac{v\bar{y}^2+(-r_2+\sigma _2)\bar{y}}{\sigma _1-n_2\bar{y}}$, we get

$$\begin{aligned} s_1= & {} \frac{\bar{y}(\sigma _2-n_1\bar{x})}{\bar{x}}+\left( u+\frac{r_1}{K}\right) \bar{x}+\frac{\bar{x}(\sigma _1-n_2\bar{y})}{\bar{y}}+v\bar{y}+n_2\bar{x}+n_1\bar{y}>0,\\ s_2= & {} \frac{\bar{y}(\sigma _2-n_1\bar{x})}{\bar{x}}\left( v\bar{y}+n_2\bar{x}\right) \\&+\left( \left( u+\frac{r_1}{K}\right) \bar{x}+n_1\bar{y}\right) \left( \frac{\bar{x}(\sigma _1-n_2\bar{y})}{\bar{y}}+v\bar{y}+n_2\bar{x}\right) >0. \end{aligned}$$

Then, it is to verify that $\lambda _2+\lambda _3=-s_1<0$ and $\lambda _2\lambda _3=s_2>0$.

So $\lambda _1,\;\lambda _2,\;\lambda _3<0$. Thus the predator equilibrium point $\bar{P}(\bar{x},\bar{y},0)$ of the system (1) is locally asymptotically stable. $\square$

Theorem 3.3

Under assumptions (11)–(14), the predator equilibrium $\bar{P}(\bar{x},\bar{y},0)$ exists. Then it is globally asymptoticlly stable if $n_1+\frac{\sigma _2\bar{y}n_2}{\sigma _1\bar{x}}<2\min \left( \left( \frac{r_1}{K}+u\right) ,\frac{\sigma _2\bar{y}v}{\sigma _1 \bar{x}}\right)$.

Proof

The Lyapunov function is given by

$$\begin{aligned} V(x,y,0)=\left( x-\bar{x}-\bar{x}\ln \left( \frac{x}{\bar{x}}\right) \right) +l\left( y-\bar{y}-\bar{y}\ln \left( \frac{y}{\bar{y}}\right) \right) , \end{aligned}$$

where l for is positive constant to be determined in the subsequent steps.

$$\begin{aligned} \frac{dV}{dt}= & {} (x-\bar{x})\left( -\left( \frac{r_1}{K}+u\right) (x-\bar{x})+\sigma _2\left( \frac{y}{x}-\frac{\bar{y}}{\bar{x}}\right) -n_1(y-\bar{y})\right) \\&+\,l(y-\bar{y})\left( -v(y-\bar{y})+\sigma _1\left( \frac{x}{y}-\frac{\bar{x}}{\bar{y}}\right) -n_2(x-\bar{x})\right) \\ \end{aligned}$$

Let us choose $l=\frac{\sigma _2 \bar{y}}{\sigma _1 \bar{x}}$, we have,

$$\begin{aligned} \frac{dV}{dt}= & {} -\left( \frac{r_1}{K}+u\right) (x-\bar{x})^2-\frac{\sigma _2\bar{y}v}{\sigma _1 \bar{x}}(y-\bar{y})^2-\frac{\sigma _2}{x\bar{x}y}(y\bar{x}-x\bar{y})^2\\&-\, \left( n_1+\frac{\sigma _2\bar{y}n_2}{\sigma _1\bar{x}}\right) (x-\bar{x})(y-\bar{y}),\\\le & {} \left( -\left( \frac{r_1}{K}+u\right) +\frac{1}{2}\left( n_1+\frac{\sigma _2\bar{y}n_2}{\sigma _1\bar{x}}\right) \right) (x-\bar{x})^2\\&+\,\left( \frac{1}{2}\left( n_1+\frac{\sigma _2\bar{y}n_2}{\sigma _1\bar{x}}\right) -\frac{\sigma _2\bar{y}v}{\sigma _1 \bar{x}}\right) (y-\bar{y})^2-\frac{\sigma _2}{x\bar{x}y}(y\bar{x}-x\bar{y})^2. \end{aligned}$$

Then, $\frac{dV}{dt}\le 0$ if $n_1+\frac{\sigma _2\bar{y}n_2}{\sigma _1\bar{x}}<2\min \left( \left( \frac{r_1}{K}+u\right) ,\frac{\sigma _2\bar{y}v}{\sigma _1 \bar{x}}\right)$. $\square$

Theorem 3.4

Under assumptions (11)–(14), the interior equilibrium point $P^*(x^*,y^*,z^*)$ exists. Then $P^*$ is locally asymptotically stable if $m_0>0$, $m_2>0$ and $m_1m_2-m_0>0$, where $m_0$, $m_1$ and $m_2$ are given in the proof.

Proof

The Jacobian matrix of the point $(x^*,y^*,z^*)$ is

$$\begin{aligned} V(x^*,y^*,z^*)=\left( \begin{array}{ccc} V_4 &{} \sigma _2-n_1x^* &{} \frac{-ax^*}{b+x^*} \\ \sigma _1-n_2y^* &{} V_5 &{} 0\\ \frac{\beta abz^*}{(b+x^*)^2} &{} 0 &{} V_6 \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} V_4= & {} -2\left( u+\frac{r_1}{K}\right) x^*+(r_1-\sigma _1-q_1E)-n_1y^*-\frac{abz^*}{(b+x^*)^2},\\ V_5= & {} r_2-\sigma _2-2vy^*-n_2x^*, \\ V_6= & {} \frac{\beta ax^*}{b+x^*}-(d+w+q_2E). \end{aligned}$$

The characteristic equation of system at $P^*$ is

$$\begin{aligned}\lambda ^3+m_2\lambda ^2+m_1\lambda +m_0=0, \end{aligned}$$

where

$$\begin{aligned} m_2= & {} -Tr(V(x^*,y^*,z^*))=-(V_4+V_5+V_6),\\ m_1= & {} V_4V_5+V_5V_6+V_6V_4-(\sigma _2-n_1\bar{x})(\sigma _1-n_2\bar{y})+\frac{\beta a^2bx^*z^*}{(b+x^*)^3},\\ m_0= & {} -V_4V_5V_6-V_5\frac{\beta a^2bx^*z^*}{(b+x^*)^3}+V_6(\sigma _2-n_1\bar{x})(\sigma _1-n_2\bar{y}). \end{aligned}$$

Then, the interior equilibrium point $P^*$ of the system is locally asymptotically stable if $m_2>0$ and $m_1m_2-m_0>0$. $\square$

Theorem 3.5

Suppose the equilibrium point $P^*(x^*, y^*, z^*)$ exists, if $n_1+\frac{\sigma _2y^*n_2}{\sigma _1x^*}<2\min \left( \left( \frac{r_1}{K}+u\right) -\frac{az^*}{b(b+x^*)},\frac{\sigma _2y^*v}{\sigma _1 x^*}\right)$, then $P^*$ is globally asymptotically stable.

Proof

The Lyapunov function is given by

$$\begin{aligned} V(x,y,z)= & {} \left( x-x^*-x^*\ln \left( \frac{x}{x^*}\right) \right) +l_1\left( y-y^*-y^*\ln \left( \frac{y}{y^*}\right) \right) \\&+\,l_2\left( z-z^*-z^*\ln \left( \frac{z}{z^*}\right) \right) . \end{aligned}$$

where $l_i$ for $i=1,2$ are positive constants to be determined in the subsequent steps.

$$\begin{aligned} \frac{dV}{dt}= & {} (x-x^*)\left( -\left( \frac{r_1}{K}+u\right) (x-x^*)-a\left( \frac{z}{b+x}-\frac{z^*}{b+x^*}\right) \right. \\&\left. +\,\sigma _2\left( \frac{y}{x}-\frac{y^*}{x^*}\right) -n_1(y-y^*)\right) \\&+\,l_1(y-y^*)\left( -v(y-y^*)+\sigma _1\left( \frac{x}{y}-\frac{x^*}{y^*}\right) -n_2(x-x^*)\right) \\&+\,l_2(z-z^*)\beta a \left( \frac{x}{b+x}-\frac{x^*}{b+x^*}\right) . \end{aligned}$$

Let us choose $l_1=\frac{\sigma _2 y^*}{\sigma _1 x^*}$ and $l_2=\frac{b+x^*}{b \beta }$, then we have,

$$\begin{aligned} \frac{dV}{dt}= & {} -\left( \frac{r_1}{K}+u\right) (x-x^*)^2-\frac{\sigma _2y^*v}{\sigma _1 x^*}(y-y^*)^2-\frac{\sigma _2}{xx^*y}(yx^*-xy^*)^2\\&+\,\frac{az^*}{(b+x)(b+x^*)}(x-x^*)^2- \left( n_1+\frac{\sigma _2y^*n_2}{\sigma _1x^*}\right) (x-x^*)(y-y^*),\\\le & {} \left( \frac{az^*}{b(b+x^*)}-\left( \frac{r_1}{K}+u\right) +\frac{1}{2}\left( n_1+\frac{\sigma _2y^*n_2}{\sigma _1x^*}\right) \right) (x-x^*)^2\\&-\,\left( \frac{\sigma _2y^*v}{\sigma _1 x^*}-\frac{1}{2}\left( n_1+\frac{\sigma _2y^*n_2}{\sigma _1x^*}\right) \right) (y-y^*)^2-\frac{\sigma _2}{xx^*y}(yx^*-xy^*)^2. \end{aligned}$$

Then, $\frac{dV}{dt}\le 0$ if $n_1+\frac{\sigma _2y^*n_2}{\sigma _1x^*}<2\min \left( \left( \frac{r_1}{K}+u\right) -\frac{az^*}{b(b+x^*)},\frac{\sigma _2y^*v}{\sigma _1 x^*}\right)$. $\square$

4 Optimal harvesting policy

In this section, the Pontryagins Principle is used to obtain a path of optimal harvesting policy. Let D be the constant harvesting cost per unit effort, $p_1$ is the constant price per unit biomass of the prey in the unreserved zone, $p_2$ is the constant price per unit biomass of the predator.

The net economic revenue at any time t is given by

$$\begin{aligned} \pi (x,y,z,E) = p_1 q_1 E(t) x(t) + p_2 q_2 E(t) z(t) - D E(t). \end{aligned}$$

In what follows, our goal is to solve the problem of maximization

$$\begin{aligned} I= & {} \int _{0}^{T} \pi (x,y,z,E) \; e^{-\delta \, t} dt, \\= & {} \int _{0}^{T} \big ( \; p_1 q_1 x(t) \; + \; p_2 q_2 z(t) \;-\; D \; \big ) \;E(t)\; e^{-\delta \, t} dt, \\ \end{aligned}$$

where $\delta$ is the instantaneous discount rate, subject to the state equations (9) and the control contraints $0\le E\le E_{\max }$.

Thus, to solve the problem of maximization, we use the Pontryagin’s maximum principle. The Hamiltonian function H is given by

$$\begin{aligned} H= & {} e^{-\delta \, t}\big ( \; p_1 q_1 x(t) \; + \; p_2 q_2 z(t) \;-\; D \; \big ) \;E(t)\;+ \lambda _1(t)\, \bigg (r_1x(t)\left( 1-\displaystyle \frac{x(t)}{K}\right) \\&-\sigma _1x(t)+\sigma _2y(t)-ux(t)^2-\frac{ax(t)z(t)}{b+x(t)}-q_1Ex(t)-n_1x(t)y(t)\bigg )\\&+ \lambda _2(t)\,\bigg (r_2y(t)+\sigma _1x(t)-\sigma _2y(t)-vy(t)^2-n_2x(t)y(t)\bigg )\\&+ \lambda _3(t)\,\bigg (\frac{\beta ax(t)z(t)}{b+x(t)}-dz(t)-wz(t)-q_2E(t)z(t)\bigg ), \end{aligned}$$

where $\lambda _i$ for $i=1,2,3$ are the adjoint variables.

H will be maximized under the control set $0\le E\le E_{\max }$ if the switching function given by

$$\begin{aligned} \psi (t):= & {} \frac{\partial H}{\partial E} = \big (p_1 q_1 x(t) \; + \; p_2 q_2 z(t) \;-\; D\big ) e^{-\delta \, t} \\&-\; q_1 \lambda _1(t) x(t) \;-\; q_2 \lambda _3(t) z(t)=0. \end{aligned}$$

This is a necessary condition for singular control to be optimal. Using the Maximum Principle, we get the adjoint equations

$$\begin{aligned} \frac{d \lambda _1}{d t}= & {} -\frac{\partial H}{\partial x}\\= & {} - p_1 q_1 e^{-\delta \, t} E(t) - \lambda _1(t) \bigg (r_1-2\frac{r_1}{K} x(t) -\sigma _{1} -2ux(t) -\frac{abz(t)}{(b+x(t))^2}\\&-q_1E(t)-n_1y(t)\bigg ) - \lambda _2(t) \bigg (\sigma _{1}-n_2 y(t)\bigg ) - \lambda _3(t) \frac{\beta a b z(t)}{(b+x(t))^2},\\ \frac{d \lambda _2}{d t}= & {} -\frac{\partial H}{\partial y}\\= & {} - \lambda _1(t) \bigg (\sigma _{2}-n_1 x(t)\bigg ) - \lambda _2(t) \bigg (r_2-\sigma _2-2vy(t)-n_2x(t)\bigg ),\\ \frac{d \lambda _3}{d t}= & {} -\frac{\partial H}{\partial z}\\= & {} - p_2 q_2 e^{-\delta \, t} E(t) - \lambda _1(t) \frac{a x(t)}{b+x(t)} - \lambda _3(t) \bigg (\frac{\beta a x(t)}{b+x(t)} -(d+w+q_2 E(t))\bigg ). \end{aligned}$$

Let denote that the optimal harvesting policy is

$$\begin{aligned} \left\{ \begin{array}{ll} E=E_{max} &{}\quad \text{ when } \psi (t)>0,\\ E=E^* &{}\quad \text{ when } \psi (t)=0,\\ E=0 &{}\quad \text{ when } \psi (t)<0, \end{array} \right. \end{aligned}$$

(15)

where $E^*$ the optimal control.

If $\psi (t)=0$, then

$$\begin{aligned} q_1 \lambda _1(t) e^{\delta \, t} x \;+\; q_2 \lambda _3(t) e^{\delta \, t} z \;=\; p_1 q_1 x \; + \; p_2 q_2 z \;-\; D\;=\;\frac{\partial \pi }{\partial E}. \end{aligned}$$

To find the optimal equilibrium solution for this system, we consider x, y, z and E as constants.

For the interior equilibrium $P^*$ and under (10), (12), (13), we have

$$\begin{aligned} \frac{d \lambda _3}{d t}= M_1 \lambda _3 - M_2 e^{-\delta t}, \end{aligned}$$

where $M_1=\frac{-aq_2z^*}{q_1(b+x^*)}$, and    $M_2=p_2 q_2 E-\frac{\big (p_1q_1x^*+p_2q_2z^*-D\big )a}{q_1(b+x^*)}$. Then,

$$\begin{aligned} \lambda _3(t) \;=\; \frac{M_2}{M_1+\delta } \; e^{-\delta t}. \end{aligned}$$

In the same way, we have

$$\begin{aligned} \frac{d \lambda _2}{d t}= N_1 \lambda _2 - N_2 e^{-\delta t}, \end{aligned}$$

where $N_1=-r_2+\sigma _2+2vy^*+n_2x^*$ and $N_2=\frac{\big (p_1q_1x^*+p_2q_2z^*-D\big )\big (\sigma _2-n_1x^*\big )}{q_1x^*}\;+\; \frac{M_2q_2z^*\big (\sigma _2-n_1x^*\big )}{\big (M_1+\delta \big )q_1 x^*}$.

Hence

$$\begin{aligned} \lambda _2(t) \;=\; \frac{N_2}{N_1+\delta } \; e^{-\delta t}. \end{aligned}$$

The expression of $\frac{d \lambda _1}{d t}$ can be written as

$$\begin{aligned} \frac{d \lambda _1(t)}{d t}= B_1 \lambda _1(t) - B_2 e^{-\delta t}, \end{aligned}$$

where $B_1=-\big (r_1-\sigma _1-q_1E\big ) \;+\; \bigg (\frac{2r_1}{K}+2u\bigg )x^* \;+\; \frac{abz^*}{(b+x^*)^2}+n_2y^*$ and

$B_2=p_1 q_1 E-\frac{N_2 \big (\sigma _1-n_2 y^*\big )}{N_1+\delta } \;+\; \frac{\beta M_2 a b z^*}{\big (M_1+\delta \big )\big (b+x^*\big )^2}$.

By calculation, we get

$$\begin{aligned} \lambda _1(t) \;=\; \frac{B_2}{B_1+\delta } \; e^{-\delta t}. \end{aligned}$$

Thus, the previous calculation, leads to

$$\begin{aligned} \frac{B_2}{B_1+\delta }q_1x^*+\frac{M_2}{M_1+\delta }q_2z^*=p_1 q_1 x^* + p_2 q_2 z^* - D. \end{aligned}$$

(16)

So, in case of infinite discount rate, the net economic revenue to the society becomes zero and the fishery would remain closed.

We consider the function

$$\begin{aligned} F(x)= & {} \frac{K\bigg (\sigma _{1}-n_2 y\bigg )\bigg (\sigma _{2}-n_1 x\bigg )\bigg (p_1q_1x+p_2q_2 z -D\bigg )\bigg (b+x\bigg )^2}{ \Delta _2\bigg (\delta -r_2 +\sigma _{2}-n_1x+2 v y \bigg )}\\&+ \,\frac{K p_1 q_1^2 E \bigg (b+x\bigg )^2}{\Delta _2} - \frac{K \beta a^2 b q_1 x z \bigg (p_1q_1x+p_2q_2 z -D\bigg )}{\Delta _2 \bigg (\delta -r_2 +\sigma _{2}-n_1x+2 v y \bigg )}\\&+\, \frac{K q_1 p_2 q_2^2 E z \bigg (\sigma _{1}-n_2 y\bigg )\bigg (\sigma _{2}-n_1 x\bigg ) \bigg (b+x\bigg )^3}{\Delta _2 \bigg (\delta -r_2 +\sigma _{2}-n_1x+2 v y \bigg )\bigg (\delta q_1(b+x)-a q_2 z\bigg )}\\&-\, \frac{K a q_2 z \bigg (\sigma _{1}-n_2 y\bigg )\bigg (\sigma _{2}-n_1 x\bigg ) \bigg (p_1q_1x+p_2q_2 z -D\bigg )\bigg (b+x\bigg )^2 }{\Delta _2\bigg (\delta -r_2 +\sigma _{2}-n_1x+2 v y \bigg )\bigg (\delta q_1(b+x)-a q_2 z\bigg )}\\&+\, \frac{K \beta a b q_1^2 p_2 q_2 E x z \bigg (b+x\bigg ) \bigg (\delta -r_2 + \sigma _{2}-n_1 x + 2 v y\bigg )}{\Delta _2\bigg (\delta -r_2 +\sigma _{2}-n_1x+2 v y \bigg )\bigg (\delta q_1(b+x)-a q_2 z\bigg )}\\&+\, \frac{q_1 p_2 q_2^2 E z \bigg (b+x\bigg ) - a q_2 z \bigg (p_1q_1x+p_2q_2 z -D\bigg ) }{\delta q_1\bigg (b+x\bigg )-a q_2 z} \\&-\, \bigg (p_1q_1x+p_2q_2 z -D\bigg ), \end{aligned}$$

where

$$\begin{aligned} \Delta _2= & {} K\bigg (b+x\bigg )^2 \bigg (\delta - r_1+\sigma _{1}+q_1 E\bigg ) + 2\bigg (r_1+uK\bigg )\bigg (b+x\bigg )^2 \\&+ n_2 y \bigg (b+x\bigg )^2 + a b K x. \end{aligned}$$

Thus, the (16) can be written as $F (x^*) = 0$. On the one hand, the calculation gives $F (0)> 0$, and the other, $F'(x)<0$ for $0<x<K$. Then, there exists a unique positive solution $x^*=x_{\delta }$ of the equation $F(x)=0$.

So, according to the above analysis, we propose the following theorem.

Theorem 4.1

If $\frac{\beta a x_{\delta }}{b+x_{\delta }}-d-w>0$, then the optimal harvesting control $E_{\delta }=\frac{1}{q_2}\left( \frac{\beta a x_{\delta }}{b+x_{\delta }}-d-w\right)$ and the corresponding solutions

$$\begin{aligned} x_{\delta }= & {} x^*,\\ y_{\delta }= & {} \frac{r_2-\sigma _2-n_2x_{\delta }+\sqrt{(r_2- \sigma _2-n_2x_{\delta })^2+4v\sigma _1x_{\delta }}}{2v},\\ z_{\delta }= & {} \frac{(b+x_{\delta })\left[ -\left( u+\frac{r_1}{K}\right) x_{\delta }^2+(r_1-\sigma _1-q_1E-n_1y_{\delta })x_{\delta }+\sigma _2y_{\delta }\right] }{ax_{\delta }} \end{aligned}$$

exist that maximize I over $\left[ \ 0, E_{\max }\right]$.

5 Numerical simulations

For our simulation works, we take system parameters as:

$$\begin{aligned} r_1= & {} 5\;,r_2 =1,\;K =4,\sigma _1 =1,\;\sigma _2 =1,\; a=0.94,\; b=0.7,\;q_1 =0.1,\;\nonumber \\ q_2= & {} 0.2, E=0.8,\beta =0.998,\;u=0.0001,\; v=0.333,\;w=0.00003,\;\nonumber \\ d= & {} 0.03,\; n_1=0.5,\; n_2=0.3. \end{aligned}$$

(17)

For the set of value parameters mentioned above, we note that the positive equilibrium $P^*( x^*, y^*, z^*)$ exists and is given by

$$\begin{aligned} x^* = 0.1778, \quad y^* = 0.6550, \quad z^* = 6.5873. \end{aligned}$$

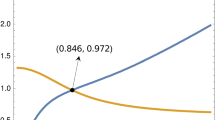
We plot the dynamics of the system (1) for the set of values parameters (17). The behavior of x, y and z with respect to time t is plotted in Fig. 1. From this figure, we note that x, y and z increase for a short time and then they decrease and finally attain their equilibrium level.

Fig. 1

Solution curves corresponding to the set values parameters (17), beginning with $x=1,\; y=1, z=1$

As in Fig. 2, the Fig. 3 shows the behavior of x, y and z with different initial values. From this figure, we see that all trajectories starting with different initial points converge to $P^*( 0.1778, 0.6550, 6.5873)$. Thus $P^*$ is globally asymptotically stable.

Fig. 2

The equilibrium point $P^*$ of is globally asymptotically stable. x, y, z states for different initial points

Fig. 3

The phase trajectory of the system for the set values parameters (17)

We observe that $n_1$ and $n_2$ are also an important parameters which governs the dynamics of system (1). The behavior of x, y and z with respect to time t for different values of $n_1$ and $n_2$ are shown in Figs. 4 and 5. From Fig. 4, we note that x and y decrease in a short time and increase after as $n_1$ increases, but z decreases as $n_1$ increases. From Fig. 5, we note that x decreases in a short time and increases after as $n_2$ increases, but y and z decrease as $n_2$ increases.

Fig. 4

Plot of x, y, z with respect to time t for different values of $n_1$, others values of parameters are same as given in (17)

Fig. 5

Plot of x, y, z with respect to time t for different values of $n_2$ and $n_1=0.3$, others values of parameters are same as given in (17)

The results found are compatible with the analysis and the study presented in the Sect. 3. From Figs. 4 and 5, $x^*$ is invariant with respect to $n_1$ and $n_2$, $z^*$ is variable with respect to $n_1$ and $n_2$ and $y^*$ is invariant with respect to $n_1$ and is variable with respect to $n_2$. These results justify the formulas (10), (12) and (13) of which $x^*$ does not depend on $n_1$ nor on $n_2$, $y^*$ depends on $n_2$ but not on $n_1$. Finally $z^*$ depends on $n_1$ and $n_2$.

6 Conclusion

We proposed and analyzed a model of predator-predator Holling II functional response with harvest for reserve fishery resources and incorporate toxic substances released by external agents into natural systems taking into account competition and consider an ecosystem where a species Predator depends on simple prey species with harvest. And the habitat consists of an unrestricted zone, where the predator attacks its only food prey, and the reserved area, where the prey lived safely. Our model represents a development from other preliminary studies. We analyze the positivity and the limit of these solutions. We also study the criteria for the existence of all the possible equilibria of this system, as well as discuss the local stability of different equilibria of the system. We are also discussing the optimal harvest policy by the maximal Pontryagins principle. By simulation, we show the rich dynamic properties of the proposed system. First, from the conditions of Theorem, we see that the locally asymptotically stable free point of equilibrium of the predator $\bar{P}$ of the system (1). Secondly, the internal equilibrium point $P^*$ of the system (1) is globally asymptotically stable, which is consistent with the theoretical analysis.