A comparative study of bioeconomic ratio-dependent predator–prey model with and without additional food to predators

Abstract

We present two models which incorporate prey harvesting to the classical and a modified ratio-dependent predator–prey model with additional food supply to the predators. We analyze the existence and stability of the equilibrium points of both the models and determine the maximum sustainable harvesting effort. The optimal harvesting policy is determined by using Pontryagin’s maximum principle. The results obtained are numerically illustrated. We examine the consequences of providing additional food (as a part of the total harvest effort) to predators in prey harvesting. Our study shows that the system can sustain a much improved optimal prey harvesting rate with additional food supply.

1 Introduction

In the ecological world, one observes varied and complex interactions of species with the most common being intraspecies (for instance competition for food) and interspecies (like predator–prey relation). Ecological modeling of such interactions has seen significant development since the pioneering work of Lotka and Volterra [1], which was further improved upon by the introduction of various functional responses by Holling [1–4]. These functional responses, namely Holling type I, II and III are based on extensive analysis of field data, which has driven the area of modeling of predator–prey interaction. An alternative to the formulation of the functional response as being only prey-dependent was proposed through a ratio-dependent functional response by Arditi and Ginzburg [5]. They argued that the functional response should be dependent on the ratio of densities of population, since the natural predation process happens at a much faster rate as compared to the growth of the population densities. Several articles on the analysis of the ratio-dependent model have appeared in the literature [6–8]. Kuang and Beretta [6] did a global analysis of the ratio-dependent predator–prey system. Xiao and Ruan [7] also analyzed the global dynamics of the model and observed that the origin is a critical point of higher order in the model. A stochastic model for a ratio-dependent model by incorporating white noise in a ratio-dependent model was analyzed by Ji et al. [9]. A diffusive ratio-dependent model with Turing instabilities were studied in [10]. An extensive bifurcation analysis for a diffusive ratio-dependent predator–prey model was carried out in a recent work by Song and Zou [11].

The balance between harvesting and conservation is a key problem in bioeconomic management of species in an ecological environment. There has been significant amount of work in bioeconomic modeling and management of renewable resources. The book by Clark [12] is a classical and excellent introduction in this area and is devoted to the theoretical study on management of renewable resources under bioeconomic conservation. The application and usefulness of optimal control theory in bioeconomic management of population of species in an ecological environment are discussed in detail by Goh [13]. Bioeconomics of a renewable resource, namely the prey population, in presence of a predator is discussed in [14]. A part of the effort during the harvesting process is dedicated toward prey harvesting, while the remaining effort is directed at decreasing the levels of predator population. The determination of optimal strategy for prey harvesting while ensuring conservation of the predator population is discussed in [15] under several considerations. The dynamical properties under a nonzero constant rate of harvesting of prey population for classical ratio-dependent model are studied in [16]. The implications of incorporating two different non-constant harvesting functions for predator harvesting and the resulting dynamics for a ratio-dependent model are presented in [17]. More recently, Kar and Ghosh [18] studied the consequences of additional food being supplied to the predators and the effect of harvesting of both the prey and predator population modeled through a Holling type II functional response. Taking the adverse impact of over exploitation of populations, a harvesting model with a two-patch environment was proposed in [19]. The predator–prey model with a Holling type II functional response was considered in an area with two patches, one in which free fishing was allowed and the other patch which was a reserve area with a prohibition on fishing effort. Jana and Kar [20] investigate the role of pesticide control and derive the optimal pest control strategy in an ecological system comprising of pest and its natural enemy, the predator. In a recent paper by Sharma and Samanta [21], the optimized harvest policy is derived for a two species competition model with imprecise biological parameters.

We consider a predator–prey system in which the prey population is subject to harvesting, while the predator population is excluded from the harvesting process. The latter exclusion can be alluded to various reasons such as lack of economic viability of such harvesting, predator conservation, etc. In effect, both the predator and the harvester are competing for the same resource, namely the prey population. While the harvesting effort does not have an explicit effect on the predator population levels, the indirect effect (as a consequence of harvesting induced reduced availability of prey) does exist. On the other hand, the predator population also has an implicit effect on the harvesting, resulting in reduced economic gains for the harvesters. The provision of additional food (non-prey) for the predators reduces the pressure of natural predation of prey population by the predators. Also, this could lead to the growth of the predator population independent of the preys (as observed in a communicated paper of the authors). One would expect that in both the cases, the harvesters will achieve greater economic benefit as compared to the system where no additional food is available to the predators. The idea of introducing the predators to this additional food (as a part of total harvest effort) can be helpful in conservation of both the species and better economic returns.

We consider a predator–prey system whose dynamics is modeled via a ratio-dependent functional response. The classical ratio-dependent model is modified to incorporate supply of additional food, the rationale for which has been discussed earlier in this section. This supply of additional food for consumption by predators is assumed to be at a constant level [22, 23]. The analysis of this model has been carried out in (in a communicated paper of the authors). In this paper, we study these two models with the incorporation of the harvesting term. For the purpose of better understanding, we study the dynamics of each individual bioeconomic model under three cases for the classical ratio-dependent model (1) When interior equilibrium point does not exist, (2) When interior equilibrium point exists with unstable nature and (3) When interior equilibrium point exists with stable nature. Though our model is quite general, one instance where this can be applied in an ecological setting is that of birds (predators) and humans (fish harvesters) competing for shellfish (prey) [15].

The organization of the paper is as follows. In Sect. 2, we show the boundedness of the solution of a class of predator–prey system which includes all the three specific models discussed in this paper. In Sect. 3, the stability analysis of the classical ratio-dependent model is outlined and parametric conditions for all the three cases mentioned above are presented. The conditions on harvesting effort for the classical and the modified ratio-dependent model by way of stability analysis are derived in Sects. 4 and 5, respectively. The optimal harvesting policy derived by using Pontryagin’s maximum principle for both these models are discussed and numerically illustrated in Sects. 6 and 7, respectively.

2 Boundedness of the solution for a class of predator–prey systems

We consider a class of predator–prey system, which is given by

$$\begin{aligned}&\frac{\mathrm{d}x}{\mathrm{d}t}= x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi }-qEx,\nonumber \\&\frac{\mathrm{d}y}{\mathrm{d}t}= m\left( \frac{b(x+\xi )}{x+y+\alpha \xi }-1\right) y,\\&x(0)>0, y(0)>0, ~c,\alpha ,q,m,b>0, ~\xi ,E\ge 0.\nonumber \end{aligned}$$

(1)

Here, $x(t)$ and $y(t)$ represent the densities of prey and predator population, respectively. The parameter $c$ is the rate of predator attack on prey. Parameters $\alpha$ and $\xi$ represent the quality and quantity of the additional food, which is provided to predators. $q$ and $E$ represent the prey catchability coefficient and harvesting effort, respectively. Finally, the parameter $m$ represents the per capita mortality rate of the predators, while $bm$ represents the per capita conversion efficiency of the predators.

The system (1) includes all the three predator–prey systems to be discussed in this paper, namely system (3) i.e., the classical ratio-dependent system (when $\xi ,E=0$), system (4) i.e., the ratio-dependent system with prey harvesting (when $\xi =0, E>0$) and system (6) i.e., the modified (by way of supply of additional food to the predators) ratio-dependent system with prey harvesting (when $\xi ,E>0$).

We will show that the solution for this class of predator–prey system (1) [(i.e., solution for systems (3), (4), (6)] is bounded in the first quadrant of $\mathbb {R}^{2}$.

Theorem 2.1

If $(x(t),y(t))$ are the solution of system (1), then $x(t)$ will be bounded for any initial condition $x(0)\ge 0,~y(0)\ge 0$.

Proof

It can be shown, by vector field analysis, that the solutions of the general class of system (1) are nonnegative. It can be seen from the first equation of (1) that,

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}\le x(1-x)~\Rightarrow ~\lim _{t \rightarrow +\infty } \sup x(t)\le 1. \end{aligned}$$

Thus, we conclude that $x(t)$ will be bounded for any nonnegative initial condition.

Theorem 2.2

If $(x(t),y(t))$ are the solution of system (1) and $x(t)$ is bounded above, then $y(t)$ will also be bounded above for any initial condition $x(0)\ge 0$, $y(0)\ge 0$.

Proof

We have already proved that $\lim \nolimits _{t\rightarrow +\infty }\sup x(t)$ $\le 1$. Therefore, for any $\epsilon >0$ there exist a $T>0$, s.t. $x(t)\le 1+\epsilon /b$  $\forall ~t\ge T$. Thus, from the second equation of (1)

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}&= m\left( \frac{b(x+\xi )}{x+y+\alpha \xi }-1\right) y\\&\le m\left( b\left( 1+\frac{\epsilon }{b}+\xi \right) -y\right) , \quad t \ge T\\&\Rightarrow \lim _{t \rightarrow +\infty } \sup y(t)\le b(1+\xi )+\epsilon \end{aligned}$$

Since $\epsilon >0$ is arbitrary, therefore we get, $\lim \nolimits _{t \rightarrow +\infty } \sup$ $y(t)\le b(1+\xi )$. Hence, $y(t)$ is bounded for any nonnegative initial condition. $\square$

3 Stability of the classical ratio-dependent prey–predator system

The first model that we consider is the classical ratio-dependent predator–prey model due to Arditi and Ginzburg [5],

$$\begin{aligned}&\frac{\mathrm{d}N}{\mathrm{d}T}= rN\left( 1-\frac{N}{K}\right) -\frac{e_{1}\left( \frac{N}{P}\right) }{1+ e_{1}h_{1}\left( \frac{N}{P}\right) }P,\nonumber \\&\frac{dP}{\mathrm{d}T}=\frac{n_{1}e_{1}\left( \frac{N}{P}\right) }{1+e_{1}h_{1}\left( \frac{N}{P}\right) }P- m'P. \end{aligned}$$

(2)

Here, the prey and predator densities are represented by $N(T)$ and $P(T)$, respectively. The prey population is assumed to have logistic growth (when there is no predation) with an intrinsic growth rate of $r$ and a carrying capacity of $K$. The per capita natural death rate of the predator is $m'$. The parameter $e_{1}$ represents the rate of predator attack on prey per unit search time, $h_{1}$ is the handling time of the predator per unit ratio $N/P$ of prey biomass and $n_{1}$ stands for the nutritional value of the prey. The transformation, $x=N/K$, $y=P/Ke_{1}h_{1}$ and $t=rT$ result in the following non-dimensionalized system,

$$\begin{aligned}&\frac{\mathrm{d}x}{\mathrm{d}t} = x\left( 1-x\right) -\frac{cxy}{x+y},\nonumber \\&\frac{\mathrm{d}y}{\mathrm{d}t} = m\left( \frac{bx}{x+y}-1\right) y, \end{aligned}$$

(3)

where $c=e_{1}/r$, $m=m'/r$ and $b=n_{1}/m'h_{1}$.

3.1 Existence of equilibrium points

This system (3) admits three equilibrium points, namely $(0,0)$ (see [8]), $(1,0)$ and the interior equilibrium point $(\check{x},\check{y})$, obtained by solving the prey and predator isoclines given by $\left( 1-x\right) -\frac{cy}{x+y}=0$ and $\frac{bx}{x+y}-1=0$, respectively. While $(0,0)$ represents the extinction of both the species, $(1,0)$ represents the extinction of the predator population with the prey population being at its carrying capacity. The coexistence of both the species is represented by the interior equilibrium point $(\check{x},\check{y})$, where $\check{x}=(1-c)+\frac{c}{b}$ and $\check{y}=(b-1)\check{x}$. The conditions for the existence of the three equilibrium points are summarized in Table 1.

Table 1 Conditions on parameters for existence of equilibrium points of the classical ratio-dependent system

3.2 Local asymptotic stability analysis

We present a summary of the local asymptotic stability analysis. The Jacobian matrix for the system (3) is given by

$$\begin{aligned} J=\begin{bmatrix} \left( 1-x\right) -\frac{cy}{x+y}+x\left[ -1+\frac{cy}{(x+y)^{2}}\right]&\quad -\frac{cx^{2}}{(x+y)^{2}}\\ \frac{bmy^{2}}{(x+y)^{2}}&\quad m\left( \frac{bx}{x+y}-1\right) -\frac{bmxy}{(x+y)^{2}} \end{bmatrix}. \end{aligned}$$

We observe that $(1,0)$ is stable whenever $b<1$. The interior equilibrium point $(\check{x},\check{y})$ will not exist whenever this happens. Consequently, when the interior equilibrium point exists, then $(1,0)$ will be a saddle. The condition for the interior equilibrium point (provided it exists) to be stable is

$$\begin{aligned} c<\frac{b\left( m(b-1)+b\right) }{b^{2}-1}. \end{aligned}$$

Observe that the Jacobian cannot be evaluated at $(0,0)$ since it renders some of the entries in the matrix to be undefined. We analyze this case by making use of a transformed system proposed by Jost et al. [8]. The transformations used are $u=\frac{x}{y},y=y$ and $x=x, v=\frac{y}{x}$ and referred to as the $u-y$ system and the $x-v$ system, respectively. This results in the following $u-y$ system,

$$\begin{aligned}&\frac{\mathrm{d}u}{\mathrm{d}t} = u\left( 1+m-uy\right) -\frac{u(c+bmu)}{u+1},\\&\frac{\mathrm{d}y}{\mathrm{d}t} = m\left( \frac{bu}{u+1}-1\right) y. \end{aligned}$$

The nature of stability of $(0,0)$ will depend on the sign of $1+m-c$. It can be easily seen that $(0,0)$ is a saddle when $c<m+1$ and an attractor when $c>m+1$. We can similarly obtain the $x-v$ system as,

$$\begin{aligned}&\frac{\mathrm{d}x}{\mathrm{d}t} = x\left[ \left( 1-x\right) -\frac{cv}{v+1}\right] ,\\&\frac{dv}{\mathrm{d}t} = v(x-1-m)+\frac{v(bm+cv)}{v+1}. \end{aligned}$$

In this case, the nature of stability of $(0,0)$ will depend on the sign of $-1-m+bm$. Thus, $(0,0)$ is a saddle when $b<(m+1)/m$. On the other hand when $b>(m+1)/m$, then $(0,0)$ is a repeller. Thus, in this case, $(0,0)$ cannot be stable.

Reasoning on the lines of Jost et al. [8], we see that in the $u-y$ system, $(0,0)$ is an attractor when $c>m+1$ and saddle when $c<m+1$. The ramification of this for $(0,0)$ in the original $x-y$ system is that a trajectory will approach to $(0,0)$ only when the approach rate of $x$ toward $0$ is more rapid than the approach rate of $y$.

3.3 Global stability analysis

Theorem 3.1

Suppose that the interior equilibrium point $(\check{x},\check{y})$ is locally asymptotically stable and the condition $m(b-1)\ge 1$ holds, then $(\check{x},\check{y})$ is also globally stable.

Proof

We first define the following function,

$$\begin{aligned} L_{1}(x,y)&= \frac{\partial }{\partial x}\left( B_{1}(x,y)f_{1}(x,y)\right) \\&\quad +\,\frac{\partial }{\partial y}\left( B_{1}(x,y)g_{1}(x,y)\right) , \end{aligned}$$

where $f_{1}(x,y)=x\left( 1-x\right) -\frac{cxy}{x+y},~g_{1}(x,y)= m\left( \frac{bx}{x+y}-1\right) y$ and $B_{1}(x,y)=\frac{x+y}{xy^{2}}$.

After simplification, we obtain,

$$\begin{aligned} L_{1}(x,y)&= \frac{1-(b-1)m-2x-y}{y^{2}}. \end{aligned}$$

Now, $L_{1}(x,y)<0$ whenever $x>0$ and $y>0$, since $m(b-1)\ge 1$. Thus, by using the Dulac’s criterion [24], the system (3) will not have any non-trivial periodic orbit in $\mathbb {R}_{+}^{2}$. Note that both the trivial and the axial equilibrium points are saddle and have $y-$axis and $x-$axis as their respective stable manifolds. Using this in conjunction with the Poincare–Bendixson theorem [24] gives us that the interior equilibrium point $(\check{x},\check{y})$ will be globally stable. $\square$

We finally summarize the various parametric conditions in Table 2, for all the three cases

Table 2 Conditions on parameters for the classical ratio-dependent system under all the three cases

Note that  $\frac{b}{b-1}\le \frac{b}{b^{2}-1}(b+m(b-1)) \Longleftrightarrow m(b-1)\ge 1$.

4 Stability of the classical ratio-dependent model with prey harvesting

We now formulate a model to incorporate prey harvesting to the classical ratio-dependent model as follows,

$$\begin{aligned}&\frac{\mathrm{d}x}{\mathrm{d}t}= x\left( 1-x\right) -\frac{cxy}{x+y}-qEx\nonumber ,\\&\frac{\mathrm{d}y}{\mathrm{d}t} = m\left( \frac{bx}{x+y}-1\right) y. \end{aligned}$$

(4)

where $q$ and $E$ represent the prey catchability coefficient and harvesting effort respectively. The above system admits the equilibria $(0,0)$, $(1-qE,0)$ and the interior equilibrium point given by,

$$\begin{aligned} (\bar{x},\bar{y})=\left( 1-c+\frac{c}{b}-qE,(b-1)\bar{x}\right) . \end{aligned}$$

One can easily observe from interior equilibria of the system (3) and (4), that prey harvesting results in the reduction in the equilibrium level of both prey and predator, due to the increase in the mortality rate of the prey population and the consequent decrease in the availability of prey to predators. In order for the interior equilibrium point to exist, we need $1-c+\frac{c}{b}-qE>0$ which implies $E<\frac{1}{q}\left( 1-c+\frac{c}{b}\right)$. Also, note that in this case $E<\frac{1}{q}\left( 1-c+\frac{c}{b}\right) <\frac{1}{q}$. So, whenever the interior equilibrium point of the system (4) exists, then axial equilibrium point $(1-qE,0)$ will also exist.

In order to determine a suitable harvesting effort ensuring the conservation of both the prey and predator populations, we need the equilibria $(0,0)$ and $(1-qE,0)$ to be saddle and the interior equilibrium $(\bar{x},\bar{y})$ to be stable in nature.

The Jacobian matrix for (4) is given by,

$$\begin{aligned} J=\begin{bmatrix} \left( 1-x\right) -\frac{cy}{x+y}-qE+x\left[ -1+\frac{cy}{(x+y)^{2}}\right]&\quad -\frac{cx^{2}}{(x+y)^{2}}\\ \frac{bmy^{2}}{(x+y)^{2}}&\quad m\left( \frac{bx}{x+y}-1\right) -\frac{bmxy}{(x+y)^{2}} \end{bmatrix}. \end{aligned}$$

One can show (on similar lines as in the preceding section) that the trivial equilibrium point $(0,0)$ will be a saddle if $E<\frac{1}{q}(1-c+m)$. It can be seen that the axial equilibrium point $(1-qE,0)$ is a saddle if $b>1$, and the interior equilibrium $(\bar{x},\bar{y})$ will be asymptotically stable when $E<\frac{1}{q}\left( 1-c+m+\frac{c-bm}{b^{2}}\right)$. Also, $\frac{1}{q}\left( 1-c+\frac{c}{b}\right) <\frac{1}{q}\left( 1-c+m+\frac{c-bm}{b^{2}}\right) <\frac{1}{q}\left( 1-c+m\right) \iff c<bm$. So, as long as the condition $c<bm$ holds, the non-trivial equilibrium point for the system (4) is locally stable whenever it exists. It can be proven that $c<bm \iff c<1+m$, whenever $m(b-1)\ge 1$. Thus, under Case 3, $(\bar{x},\bar{y})$ is locally stable (if it exists).

Finally, considering the same Lyapunov function $B_{1}(x,y)$ as for system (3) and proceeding on similar lines, we find that the following inequality holds true for global stability of the interior equilibrium point $(\bar{x},\bar{y})$.

$$\begin{aligned} E\ge \frac{1}{q}\left( 1-m(b-1)\right) . \end{aligned}$$

This inequality always holds as a result of the condition for global stability of the interior equilibrium point of the system (3).

Finally, we summarize all the conditions on effort $E$ in order to achieve ecologically sustainable harvesting for the classical ratio-dependent system in Table 3.

Table 3 Conditions on harvesting effort for the ratio-dependent system

This table indicates that prey harvesting should not be initiated with a random effort level $E$. Stability analysis gives us the way of determining an appropriate effort level since a randomly chosen effort level may lead to population extinction. For example, we choose the parameter values $c=1.1,m=1$ and $b=3$ for which the interior equilibrium point of the system (3) is globally stable (as seen in Fig. 1 for the classical ratio-dependent model). With this same set of parameters and choosing $q=1$ (for example), the interior equilibrium points $(\bar{x},\bar{y})$ of the system (4) will not be globally stable for any choice of $E>0.2667$. Thus, in this case, ecological conservation requires that the effort level $E$ be kept below $0.2667$. This is illustrated by the phase-portraits in Figs. 2 and 3. In Fig. 2, $E=0.2<0.2667$ resulting in conservation of both the species, whereas in Fig. 3, we take $E=0.5>0.2667$ and observe the extinction of both the species.

Fig. 1

Phase-portrait for the system (3) with parameter values $c=1.1,m=1$ and $b=3$

Fig. 2

Phase-portrait for the system (4) with parameter values $c=1.1,m=1,b=3,q=1$ and $E=0.2$

Fig. 3

Phase-portrait for the system (4) with parameter values $c=1.1,m=1,b=3,q=1$ and $E=0.5$

5 Stability of the modified ratio-dependent model with prey harvesting

We now consider a modified ratio-dependent model that incorporates the supply of additional food to the predators. The biomass $A$ of this additional food supply is assumed to be available uniformly within the ecological domain [22]. Accordingly, the modified model (introduced in a communicated paper of the authors) is given by,

$$\begin{aligned} \frac{\mathrm{d}N}{\mathrm{d}T}&= rN\left( 1-\frac{N}{K}\right) -\frac{e_{1}\left( \frac{N}{P}\right) }{1+e_{1}h_{1}\left( \frac{N}{P}\right) +e_{2}h_{2}\left( \frac{A}{P}\right) }P,\\ \frac{dP}{\mathrm{d}T}&= \frac{n_{1}e_{1}\left( \frac{N}{P}\right) +n_{2}e_{2}\left( \frac{A}{P}\right) }{1+e_{1}h_{1}\left( \frac{N}{P}\right) +e_{2}h_{2}\left( \frac{A}{P}\right) }P- m'P. \end{aligned}$$

Here, $e_{2}$ is the rate of predator attack on additional food per unit search time, $h_{2}$ is the handling time of the predator per unit of the ratio $A/P$ additional food biomass and $n_{2}$ is the nutritional value of the additional food. The other parameters have already been described in Sect. 3. Using the transformations $x = N/K, y = P/Ke_{1}h_{1}, t=rT$ (as before) and defining $c=e_{1}/r$, $\alpha =n_{1}h_{2}/n_{2}h_{1}$, $\xi =\eta A/K$, $m=m'/r$, $b=n_{1}/m' h_{1}$ and $\eta =n_{2}e_{2}/n_{1}e_{1}$, we obtain the following non-dimensionalized system,

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&= x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi },\nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}&= m\left( \frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1\right) y. \end{aligned}$$

(5)

Here, the ecological parameters $c$, $m$ and $b$ are the same as in the original model, while $\alpha$ and $\xi$ are the parameters representative of the biological control, where $\alpha$ characterizes the quality (in terms of nutritional value) of the additional food compared that of the prey. On the other hand, $\xi$ is representative of the quantity of additional food supplied to the predators.

One can observe that system (5) reduces to the original ratio-dependent system (3) when $\xi =0$. From the functional response of (3) and (5), it can be seen that the predation pressure on the prey is reduced due to introduction of additional food to the predators. Also, we note that when $x=0$, then the predator equation will be

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}t}=m\left( \frac{b\xi }{y+\alpha \xi }-1\right) y, \end{aligned}$$

from which we can infer that the possibility of predator survival (without their natural prey) exists only if additional food of quality $\alpha <b$ is supplied to the predators.

The model incorporating prey harvesting to the modified ratio-dependent model is given as,

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&= x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi }-qEx,\nonumber \\ \frac{\mathrm{d}y}{\mathrm{d}t}&= m\left( \frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1\right) y. \end{aligned}$$

(6)

The model (6) comprises of two economic components, namely the harvesting effort $E$ and the supply of additional food $A$.

5.1 Existence of equilibrium points

The system (6) admits the trivial equilibrium point $(0,0)$, two axial equilibria, $(1-qE,0)$ and $(0,(b-\alpha )\xi )$ and two interior equilibria $(x_{i},y_{i}),~i=1,2$ given by the solution of following equations,

$$\begin{aligned}&1-x-\frac{cy}{x+y+\alpha \xi }-qE=0\nonumber \\&\frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1=0. \end{aligned}$$

(7)

Solving (7), we obtain $(x_{i},y_{i}),~i=1,2$ as,

$$\begin{aligned}&x_{i}=\frac{1-qE-c+\frac{c}{b}-\xi }{2}\\&\quad +\frac{(-1)^{i}}{2}\sqrt{\left( qE+c-1-\frac{c}{b}+\xi \right) ^{2} -4\xi \left( qE+c-1-\frac{\alpha c}{b}\right) }\\&y_{i}=(b-1)x_{i}+(b-\alpha )\xi . \end{aligned}$$

The following relation can be derived from (7),

$$\begin{aligned} x_{i}=1-c+\frac{c}{b}-qE+\frac{c(\alpha -1)\xi }{b(x_{i}+\xi )}. \end{aligned}$$

This relation is satisfied by the interior equilibria $(x_{i},y_{i})$ when they exist. From this relation, we can conclude that whenever $\alpha >1$, the supply of additional food to predators reduces the pressure of predation (on prey) as well as the pressure (on both prey and predator) resulting from harvesting. Defining $\varDelta$ as the expression under the square root term of $x_{i}$, we obtain the conditions (see Table 4) on the model parameters, required for the existence of the above equilibrium points.

Table 4 Conditions on parameters for existence of equilibrium points of the modified ratio-dependent system with prey harvesting

Under the condition $0<x_{i}<1-qE$, we have $y_{i}>0$. To see this, consider $y_{i}=\frac{(1-qE-x_{i})(x_{i}+\alpha \xi )}{x_{i}+c-1+qE}$. Observe that if $c\ge 1- qE$, then $y_{i}>0$. For the case when $c<1-qE$ and noting that $x_{i}=1-c-qE$ is an asymptote to the prey isocline $y_{i}=\frac{(1-qE-x_{i})(x_{i}+\alpha \xi )}{x_{i}+c-1+qE}$, we obtain $x_{i}>1-c-qE$. Thus $y_{i}>0$ for $c<1-qE$ also.

5.2 Stability analysis

The Jacobian matrix for (6) is given by

$$\begin{aligned} J=\begin{bmatrix} \left( 1-x\right) -\frac{cy}{x+y+\alpha \xi }-qE+x\left[ -1+\frac{cy}{(x+y+\alpha \xi )^2}\right]&\quad -\frac{cx(x+\alpha \xi )}{(x+y+\alpha \xi )^2}\\ \frac{bmy(y+\alpha \xi -\xi )}{(x+y+\alpha \xi )^2}&\quad m\left( \frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1\right) -\frac{bm(x+\xi )y}{(x+y+\alpha \xi )^2} \end{bmatrix}. \end{aligned}$$

Hence, the Jacobian matrix at the equilibria of the system (6) is of the following form,

$$\begin{aligned}&J_{(0,0)}= \begin{bmatrix} 1-qE&0\\ 0&\frac{m}{\alpha }(b-\alpha ) \end{bmatrix},\\&J_{(1-qE,0)}= \begin{bmatrix} -(1-qE)&-\frac{c(1-qE)}{1-qE+\alpha \xi }\\ 0&\frac{m\left( (b-1)(1-qE)+(b-\alpha )\xi \right) }{1-qE+\alpha \xi } \end{bmatrix},\\&J_{(0,(b-\alpha )\xi )}= \begin{bmatrix} 1-qE-c+\frac{c\alpha }{b}&0\\ \frac{m(b-\alpha )(b-1)}{b}&-\frac{m(b-\alpha )}{b} \end{bmatrix},\\&J_{(x_{i},y_{i})}= \begin{bmatrix} x_{i}\left[ -1+\frac{cy_{i}}{(x_{i}+y_{i}+\alpha \xi )^2}\right]&-\frac{cx_{i}(x_{i}+\alpha \xi )}{(x_{i}+y_{i}+\alpha \xi )^2}\\ \frac{bmy_{i}(y_{i}+\alpha \xi -\xi )}{(x_{i}+y_{i}+\alpha \xi )^2}&-\frac{bm(x_{i}+\xi )y_{i}}{(x_{i}+y_{i}+\alpha \xi )^2} \end{bmatrix}. \end{aligned}$$

For population conservation (while harvesting) to be ensured, we need the equilibria $(0,0),(1-qE,0)$ and $(0,(b-\alpha )\xi )$ to be unstable in nature. The equilibrium $(0,0)$ is always unstable in nature provided the axial equilibrium point $(1-qE,0)$ exists. However, $(1-qE,0)$ always exists in order to ensure the existence of the interior equilibrium point. Thus, $(0,0)$ is always unstable. The conditions $(b-1)(1-qE)+(b-\alpha )\xi >0$ and $1-qE-c+\frac{c\alpha }{b}>0$ ensure the saddle nature of $(1-qE,0)$ and $(0,(b-\alpha )\xi )$, respectively. Note that, the condition for the saddle nature of $(1-qE,0)$ is satisfied whenever any one of the interior equilibrium point exists. This is because $0<y_{i}=(b-1)x_{i}+(b-\alpha )\xi <(b-1)(1-qE)+(b-\alpha )\xi$.

The stability of interior equilibria $(x_{i},y_{i})$ can be analyzed by using the determinant and trace of the Jacobian matrix $J_{(x_{i},y_{i})}$ given by

$$\begin{aligned}&\det {J_{(x_{i},y_{i})}}=\frac{bcmx_{i}y_{i}}{(x_{i}+y_{i}+\alpha \xi )^{3}}\left[ \xi (\alpha -1)+\frac{b}{c}(x_{i}+\xi )^{2}\right] ,\\&tr~J_{(x_{i},y_{i})} \\&\quad = \frac{-(b+1)x_{i}^{2}-\left[ (b\xi -1)+m(b-1)\right] x_{i}-m(b-\alpha )\xi }{b(x_{i}+\xi )}. \end{aligned}$$

We study the stability of interior equilibrium points (for all the three cases) when $(0,(b-\alpha )\xi )$ either exists with saddle nature or does not exist at all. Here, only interior equilibrium point $(x_{2},y_{2})$ can exist, if $x_{2}<1-qE$ holds. We summarizes the conditions as follows,

Cases	Interior equilibrium point exists	Stable
Case 1	$(x_{2},y_{2})$	if  $tr~J_{(x_{2},y_{2})}<0$
Case 2	$(x_{2},y_{2})$	if  $tr~J_{(x_{2},y_{2})}<0$
Case 3	$(x_{2},y_{2})$	always

5.3 Global stability analysis

Theorem 5.1

Suppose that the interior equilibrium point $(x_{2},y_{2})$ is locally asymptotically stable and the conditions $\alpha \xi \ge 1-qE$ and $\alpha >\left( 1-\frac{1-qE}{c}\right) b$ hold, then $(x_{2},y_{2})$ is also globally stable.

Proof

We first define the following function,

$$\begin{aligned} L_{2}(x,y)&= \frac{\partial }{\partial x}\left( B_{2}(x,y)f_{2}(x,y)\right) \\&\quad +\frac{\partial }{\partial y}\left( B_{2}(x,y)g_{2}(x,y)\right) , \end{aligned}$$

where $f_{2}(x,y)=x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi }-qEx~,~g_{2}(x,y)$ $=m\left( \frac{b(x+\xi )}{x+y+\alpha \xi }-1\right) y~\text {and}~B_{2}(x,y)=\frac{x+y+\alpha \xi }{xy}$.

After simplification, we obtain

$$\begin{aligned} L_{2}(x,y)=\frac{(1-qE-\alpha \xi )}{y}-\frac{(2x+y)}{y}-\frac{m}{x}. \end{aligned}$$

Now, $L_{2}(x,y)<0$ whenever $x>0$ and $y>0$, since $\alpha \xi \ge 1-qE$. Thus, by the Dulac’s criterion [24], the system (6) will not have any non-trivial periodic orbit in $\mathbb {R}_{+}^{2}$. Note that, when $\left( 1-\frac{1-qE}{c}\right) b<\alpha <b$, then the trivial equilibrium point is a repeller and the two axial equilibria, $(1-qE,0)$ and $(0,(b-\alpha )\xi )$, are both saddle and have $x-$axis and $y-$axis as their respective stable manifolds. On the other hand, when $\alpha >b$, then both $(0,0)$ and $(1-qE,0)$ are saddle and have $y-$axis and $x-$axis as their respective manifolds. Using these, in conjunction with the Poincare–Bendixson theorem [24] gives us that the interior equilibrium point $(x_{2},y_{2})$ will be globally stable. $\square$

Finally, we summarize (in Table 5) the parametric conditions required to ensure stability of various equilibria so as to achieve ecologically sustainable harvesting by way of population conservation.

Table 5 Conditions on harvesting effort for the modified ratio-dependent system

Clearly, here, one can see that ecologically sustainable harvesting is possible under all three cases, whereas without additional food, it is possible only under Case 3. Also, one can observe that bounds on harvesting effort $E$ depend on the additional food parameters, namely $\alpha$ and $\xi$. A choice of $\alpha >1$ results in an increase in the upper bound for ecologically sustainable harvesting effort (corresponding to the global stability of interior equilibrium point) as compared to the case without additional food. On the other hand, a choice of $\xi >1/b$ ensures that the condition $~tr~J_{(x_{2},y_{2})}<0$ (required for global stability of $(x_{2},y_{2})$ under Case 1 and Case 2) is satisfied. This illustrates the advantage of providing additional food to the predators over the scenario of no additional food being provided. A consequence of this is that a higher effort level can be achieved with the choice of an appropriate level of additional food supply. For example, we choose the same parameter values, $c=1.1,m=1,b=3$ and $q=1$ as in Sect. 4. Recall that in this example, the ecological conservation required that the effort level $E$ be kept below $0.2667$. As an illustration, we choose $E=0.5$, which results in the extinction of both the populations, when no additional food is provided. However, an appropriate level of additional food (for example, $\alpha =2$ and $\xi =0.5$ for which coexistence is achieved for $0<E<0.633$) ensures the stability of the interior equilibrium point and hence conservation of both the species. The phase-portrait for this example is given in Fig. 4.

Fig. 4

Phase-portrait for the system (6) with parameter values $c=1.1,m=1,b=3,q=1,E=0.5,\alpha =2$ and $\xi =0.5$

6 Optimal harvesting policy for the ratio-dependent model

We now formulate the problem of optimal harvesting policy in case of the classical ratio-dependent model as follows:

$$\begin{aligned} \max _{0\le E\le E_{\max }}\int \limits _{0}^{\infty } \mathrm{e}^{-\delta t}\left[ pqx-c_{1}\right] E \mathrm{d}t \end{aligned}$$

(8)

subject to the system (4)

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&= x\left( 1-x\right) -\frac{cxy}{x+y}-qEx,\\ \frac{\mathrm{d}y}{\mathrm{d}t}&= m\left( \frac{bx}{x+y}-1\right) y. \end{aligned}$$

and the effort constraint

$$\begin{aligned} E \in [0, E_{\max }]. \end{aligned}$$

with the initial and terminal conditions being $(x(0),$ $y(0))=(x_{0},y_{0})$ and $(x(\infty ),y(\infty ))=(\bar{x},\bar{y})$, respectively. Here, $p$ is the price per unit stock of the prey biomass, $c_{1}$ is the cost per unit effort for harvesting and $E_{\max }$ is the maximum effort capacity of the harvesting industry. Also, $\delta$ denotes the continuously compounded annual rate of discount. The objective of the problem is to find the optimal harvesting effort, i.e., $E(t)\in [0, E_{\max }]$ for $t\ge 0$ so as to achieve the bioeconomic objective of maximizing the profits from harvesting while ensuring population conservation.

In order to use the Pontryagin’s maximum principle [25], we define the Hamiltonian for this control problem as,

$$\begin{aligned} \mathcal {H}&= \mathrm{e}^{-\delta t}\left[ pqx-c_{1}\right] E\\&+\,\lambda _{1}\left[ x\left( 1-x\right) -\frac{cxy}{x+y}-qEx\right] \\&+\,\lambda _{2}\left[ m\left( \frac{bx}{x+y}-1\right) y\right] . \end{aligned}$$

Using the maximum principle results in the state equation being given by (4) while the co-state equations are given by

$$\begin{aligned} \frac{\mathrm{d}\lambda _{1}}{\mathrm{d}t}&= -\frac{\partial \mathcal {H}}{\partial x}= -\mathrm{e}^{-\delta t}pqE\nonumber \\&\quad {}-\lambda _{1}\left( 1-2x-\frac{cy^{2}}{(x+y)^{2}}-qE\right) - \lambda _{2}\frac{bmy^{2}}{(x+y)^2},\nonumber \\ \frac{\mathrm{d}\lambda _{2}}{\mathrm{d}t}&= -\frac{\partial \mathcal {H}}{\partial y}=\lambda _{1}\frac{cx^{2}}{(x+y)^{2}}-m\lambda _{2}\left( \frac{bx^{2}}{(x+y)^{2}}-1\right) . \end{aligned}$$

(9)

Since $\mathcal {H}$ is linear in control $E$, so the optimal control is combination of bang-bang and singular control [13]. The condition for the optimal control can be obtained from the relation

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial E}=\mathrm{e}^{-\delta t}(pqx-c_{1})-\lambda _{1}qx=0. \end{aligned}$$

Chaudhuri [26] (citing Goh [13]) points out that the harvesting policy for a zero-discount rate (i.e., $\delta =0$) is more robust than the nonzero rate of discount. In order to obtain the singular optimal equilibrium solution $(\widetilde{x},\widetilde{y})$, the interior equilibrium points of system (4) and (9) are substituted into $\frac{\partial H}{\partial E}=0$ to get,

$$\begin{aligned} x=\frac{1}{2}\left[ \frac{c_{1}}{pq}+\left( 1-c+\frac{c}{b}\right) \right] . \end{aligned}$$

(10)

The necessary conditions for the singular control to be optimal are that the generalized Legendre condition [13]

$$\begin{aligned}&(\lambda _{1}-2p)x+(\lambda _{1}-p)\left( -1+\frac{c}{b^{2}}(b-1)^{2}+qE\right) \\&\quad +\,\frac{(\lambda _{1}c-\lambda _{2}bm)}{b^{3}}(b-1)^{2}\ge 0 \end{aligned}$$

is satisfied along singular solution. Hence, optimal harvesting policy will be

$$\begin{aligned} E^{~\text {RD}}(t)= {\left\{ \begin{array}{ll} E_{\max } &{}\quad \text {if }~ x>\widetilde{x} \\ \widetilde{E} &{}\quad \text {if }~ x=\widetilde{x}\\ 0 &{}\quad \text {if }~ x<\widetilde{x}, \end{array}\right. } \end{aligned}$$

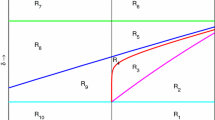
where $\widetilde{x}$ is the value of $x$ in (10) (called the singular optimal equilibrium prey population size). Also, $\widetilde{E}$ is called the singular control of the system (4) corresponding to the singular solution $(\widetilde{x},\widetilde{y})$. The optimal control policy for the harvested ratio-dependent system (4) is shown in Fig. 5.

Fig. 5

Figure illustrates how effort $E$ must be chosen (for the harvested system without additional food) once we know the singular optimal equilibrium level $\widetilde{x}$ for the prey population. If the prey size is above this threshold value (i.e., $x>\widetilde{x}$), then one can choose the maximum harvest effort, while at the threshold value (i.e., $x=\widetilde{x}$), harvest effort will be the singular optimal harvest effort. When the prey size falls below this threshold value (i.e., $x<\widetilde{x}$), then there will be no harvesting effort

We illustrate this with a numerical example. For this purpose, we choose the parameter values to be $c=1.1, m=1, b=3, q=1, p=1$ and $c_{1}=0.005$. For this set of parameter values, $\widetilde{x}=0.1358$ [from Eq. (10)]. Recall that the interior equilibrium point of system (4) is globally asymptotically stable if $E\in [0,0.2667)$. So, we can take $E_{\max }$ to be $0.2667$. Thus, according to the optimal harvest policy, if at time $t$ the prey population size is greater than the optimal equilibrium prey population size $\widetilde{x}=0.1358$, i.e., $x(t)>0.1358$, then the harvesting effort is chosen to be $E_{\max }=0.2667$ until the prey size reduces to $\widetilde{x}$. Once this happens, i.e., $x(t)=0.1358$, then we will adopt the singular optimal control $\widetilde{E}$, given in this case by $\widetilde{E}=\frac{1}{q}\left( 1-\widetilde{x}-\frac{c}{b}(b-1)\right) =0.1308$. When $x(t)<\widetilde{x}$, the harvesting is stopped, i.e., $E=0$ and remains so until the prey population density is restored at least to the level of $\widetilde{x}$ again. The optimal trajectory for system (4) with initial population densities $(x_{0},y_{0})=(0.9,0.4)$ along with the optimal strategy is shown in Fig. 6. The optimal trajectory is a combination of two trajectories, one (dashed) corresponding to the maximum harvesting effort $E_{\max }=0.2667$, while the second one corresponds to the singular effort $\widetilde{E}=0.1308$. The switch from maximum harvesting effort $E_{\max }$ to singular effort $\widetilde{E}$ happens at time $t=5.3$.

Fig. 6

The left hand figure shows the optimal path emanating from point $(0.9,0.4)$ subject to the system (4) with parameter values $c=1.1,m=1,b=3,q=1,p=1$ and $c_{1}=0.005$. The right hand figure shows the corresponding optimal strategy (which is a combination of bang-bang and singular control), and it illustrates that the harvesting should start with maximum effort $E_{\max }=0.2667$ and continue up to 5.3 time units, and after that harvesting effort must be switched to $\widetilde{E}=0.1308$

The optimal harvesting policy will thus be

$$\begin{aligned} E^{~\text {RD}}(t)= {\left\{ \begin{array}{ll} E_{\max }=0.2667&{}~\text {if}~t\le 5.3,\\ \widetilde{E} =0.1308&{}~\text {if}~t>5.3. \end{array}\right. } \end{aligned}$$

7 Optimal harvesting policy for the modified ratio-dependent model

For the modified ratio-dependent model, the problem of optimal harvesting policy is formulated as follows:

$$\begin{aligned} \max _{0\le E\le E_{\max }}\int \limits _{0}^{\infty } \mathrm{e}^{-\delta t}\left[ \left( pqx-c_{1}\right) E-c_{2}\xi \right] \mathrm{d}t \end{aligned}$$

(11)

subject to the system (6)

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}&= x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi }-qEx,\\ \frac{\mathrm{d}y}{\mathrm{d}t}&= m\left( \frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1\right) y. \end{aligned}$$

and the effort constraint

$$\begin{aligned} E \in \left[ 0, E_{\max }\right] \end{aligned}$$

with the initial and terminal conditions $(x(0),y(0))=(x_{0},y_{0})$ and $(x(\infty ),y(\infty ))=(x_{2},y_{2})$, respectively. The parameters $p$, $c_{1}$, $E_{\max }$ and $\delta$ have the same interpretation as in the case of harvesting for classical ratio-dependent model discussed in the previous section. The new parameter $c_{2}$ is the cost per unit quantity biomass of additional food with some fixed nutrition value. As before, the objective of the problem is to find the optimal harvesting effort, i.e., $E(t)\in [0, E_{\max }]$ for $t\ge 0$ so as to achieve the bioeconomic objective of maximizing the profits from harvesting while ensuring population conservation. The Hamiltonian for this control problem is defined as

$$\begin{aligned} \mathcal {H}&= \mathrm{e}^{-\delta t}\left[ \left( pqx-c_{1}\right) E-c_{2}\xi \right] \\&\quad +\,\lambda _{1}\left[ x\left( 1-x\right) -\frac{cxy}{x+y+\alpha \xi }-qEx\right] \\&\quad +\,\lambda _{2}\left[ m\left( \frac{b\left[ x+\xi \right] }{x+y+\alpha \xi }-1\right) y\right] . \end{aligned}$$

Using Pontryagin’s maximum principle results in the state equations for this problem being given by (6) while the co-state equations are given by,

$$\begin{aligned} \frac{\mathrm{d}\lambda _{1}}{\mathrm{d}t}&= -\frac{\partial \mathcal {H}}{\partial x} =-\mathrm{e}^{-\delta t}pqE\nonumber \\&\quad {}-\lambda _{1}\left( 1-2x-\frac{cy(y+\alpha \xi )}{(x+y+\alpha \xi )^{2}}-qE\right) \nonumber \\&\quad {}-\lambda _{2}\frac{bmy(y+\alpha \xi -\xi )}{(x+y+\alpha \xi )^2}\nonumber ,\\ \frac{\mathrm{d}\lambda _{2}}{\mathrm{d}t}&= -\frac{\partial \mathcal {H}}{\partial y} =\lambda _{1}\frac{cx(x+\alpha \xi )}{(x+y+\alpha \xi )^2}\nonumber \\&\quad {}-m\lambda _{2}\left( \frac{b\left( x+\xi \right) (x+\alpha \xi )}{(x+y+\alpha \xi )^2}-1\right) . \end{aligned}$$

(12)

Note that, here $\mathcal {H}$ is linear in control $E$. Therefore, the optimal control will be a combination of bang-bang and singular control [13]. The optimal control follows from the condition,

$$\begin{aligned} \frac{\partial \mathcal {H}}{\partial E}=\mathrm{e}^{-\delta t}(pqx-c_{1})-\lambda _{1}qx=0. \end{aligned}$$

To determine the singular optimal equilibrium solution $(x^{*},y^{*})$, we take $\delta =0$ and substitute the interior equilibrium points of the systems (6) and (12) into $\frac{\partial \mathcal {H}}{\partial E}=0$ which results in the following cubic equation,

$$\begin{aligned}&(-2bpq)x^{3}+(bc_{1}+(-4b\xi +b+c-bc)pq)x^{2}\nonumber \\&\quad +\,2(bc_{1}+pq(b+c-bc-b\xi ))\xi )x\nonumber \\&\quad +\,\xi (-c(1-\alpha )c_{1}\!+\!bc_{1}\xi \!+\! pq(b-c(b-\alpha ))\xi )=0.\nonumber \\ \end{aligned}$$

(13)

When sign of the coefficient of $x^{3}$ and constant term in a cubic equation are opposite, then the equation has atleast one positive root. Thus, in the above case, if $(\frac{c\alpha }{b}-\frac{c}{b}+\xi )c_{1}+pq\xi (1-c+\frac{c\alpha }{b})>0$, then above cubic equation has at least one positive root. Let $x^{*}$ be the positive root of this cubic equation. Then, $x^{*}$ is called the singular optimal equilibrium prey population level. The necessary conditions for the singular control to be optimal are that the generalized Legendre condition [13]

$$\begin{aligned}&(2\lambda _{1}-p)\left( 1-\frac{cy}{(x+y+\alpha \xi )^{2}}\right) \\&\quad +\,(\lambda _{1}cx+\lambda _{2}bm(y+\alpha \xi -\xi ))\frac{y}{(x+y+\alpha \xi )^{3}}\ge 0 \end{aligned}$$

is satisfied along singular solution. Hence, the optimal harvesting policy will be

$$\begin{aligned} E^{~\text {MRD}}(t)= {\left\{ \begin{array}{ll} E_{\max }&{}~\text {if}~x>x^{*}\\ E^{*} &{}~\text {if}~x=x^{*}\\ 0 &{}~\text {if}~x<x^{*}. \end{array}\right. } \end{aligned}$$

Note that, in order to ensure an economically better harvesting policy with the additional food as compared to harvesting without additional food being supplied to the predators in the system, the integrand in (11) must be greater than the integrand in (8). This can be ensured as long as the cost per unit quantity biomass of additional food satisfies

$$\begin{aligned} c_{2}<\frac{1}{\xi }\left( pqx-c_{1}\right) \left( E^{~\text {MRD}}-E^{~\text {RD}}\right) . \end{aligned}$$

It can be shown that Eq. (13) reduces to

$$\begin{aligned} 2bpq(x^{*}+\xi )^{2}(x^{*}-\widetilde{x})=c\xi (c_{1}+pq\xi )(\alpha -1). \end{aligned}$$

Consequently, $x^{*}<(>)\widetilde{x} \iff \alpha <(>)1$. This means that in order to undertake prey harvesting with additional food at a level, $x^{*}$ below (above) $\widetilde{x}$ (the level without additional food), the predators need to be supplied with good (poor) quality of additional food. There is no benefit in terms of harvesting stock level, by providing same quality of additional food relative to the prey, i.e., $\alpha =1$, since this results in $x^{*}=\widetilde{x}$ and $E^{*}=\widetilde{E}$. Apart from this, there is added financial burden arising from supply of additional food in this case. The harvesting strategy for the additional food provided harvested system (6) can be seen in Fig. 7.

Fig. 7

Figure illustrates how effort $E$ must be chosen (in the additional food provided harvested system) once we know the singular optimal equilibrium level $x^{*}$ for the prey population. If prey size is above this threshold value (i.e., $x>x^{*}$), then one can choose the maximum harvest effort, while at the threshold value (i.e., $x=x^{*}$), harvest effort will be the singular optimal harvest effort. When the prey size falls below this threshold value (i.e., $x<x^{*}$), then there will be no harvesting effort. The threshold value $x^{*}$, here, can be controlled by the quality of additional food. When $\alpha <1$, then we have $x^{*}<\widetilde{x}$, while by taking $\alpha >1$, we have $x^{*}>\widetilde{x}$

One can observe from the cubic equation (13) that the singular optimal prey-equilibrium level $x^{*}$ is dependent on the biological control parameters $\alpha$ and $\xi$. We will now illustrate through numerical examples, that for the modified model with additional food, the optimal harvesting policy can be more effectively decided by an appropriate choice of $\alpha$ and $\xi$. For this purpose, we refer to the example on prey harvesting without additional food case, as given in the previous section. Recall that for the parameter values $b=3, c=1.1, m=1, p=1, q=1$ and $c_{1}=0.005$, no prey harvesting can be done until the prey size reaches a level of $\widetilde{x}=0.1358$. However, for this set of parameter values, the system supported by additional food to the predators results in bioeconomically sustainable harvesting policy for some $x(t)<\widetilde{x}$. In fact, in this case, the harvesting effort can be more than the corresponding harvesting effort for the system without additional food.

To begin with, we set $x^{*}=0.0001$. Then, in this case, $\alpha$ and $\xi$ have to satisfy the relation $(-0.2856+1.1\alpha )\xi ^{2}+(-0.00533712+0.0055\alpha )\xi +0.8144\times 10^{-8}=0$. By choosing $\alpha =0.94$ and $\xi = 0.0001515$ (which satisfies this relation), one can harvest at the maximum effort level $E_{\max }= 0.2447$, for all time, provided $x(0)>x^{*}$. Clearly, the economic returns here is better than the returns without the additional food. Now, choosing $\alpha =0.9,0.8,0.7$ with corresponding $\xi =0.0005277, 0.001569, 0.003065$, respectively, one can prey harvest at the maximum harvest rate of $0.23, 0.1933, 0.1567$, respectively, provided $x(0)>x^{*}$. These numerical values of $\alpha$ suggest that, as we decrease the $\alpha$ value (improvement in the quality of additional food), maximum harvest rate keeps decreasing. This phenomenon is possibly due to the increase in the predator population level (resulting from better quality of additional food) but the quantity being fixed, thereby resulting in more predation of prey by the predators. This can also be mathematically justified, by recalling that $y_{2}=(b-1)x_{2}+(b-\alpha )\xi$. As we decrease the value of $\alpha$ (for fixed $\xi$), $y_{2}$ (predator equilibrium level) will increase, while prey-equilibrium level $x_{2}$ will decrease. For the parameter values $\alpha =0.94$ and $\xi = 0.0001515$, the optimal trajectory for system (6) with initial population densities $(x_{0},y_{0})=(0.9,0.4)$ along with the optimal strategy is shown in Fig. 8.

Fig. 8

The left hand figure shows the optimal path emanating from point $(0.9,0.4)$ subject to the system (6) with parameter values $c=1.1,m=1,b=3,q=1,p=1, c_{1}=0.005,~\alpha =0.94$ and $\xi =0.0001515$. The right hand figure shows the corresponding optimal strategy (which is bang-bang control only), and it illustrates that harvesting should start with maximum effort $E_{\max }=0.2447$ and continue with it

We now consider a second example, when $\widetilde{x}<x^{*}$, with same parameters values chosen earlier, namely $b=3, c=1.1, m=1, p=1, q=1$ and $c_{1}=0.005$. In this case, for some $x(t)>\widetilde{x}$, harvesting cannot be undertaken till the prey population reaches a level of atleast $x^{*}$. But, whenever harvesting is possible, $E_{\max }$ and $E^{*}$ can be increased by increasing the value of $\alpha$ and $\xi$. This may be possible from an ecological point of view, since supply of poor quality additional food could result in the predators being distracted, thereby easing the predation pressure on the prey, whose size consequently increases. Thus, the harvest effort can be increased in such a scenario. We set $x^{*}=0.2$, in which case $\alpha$ and $\xi$ have to satisfy the relation $(-1.485+1.1\alpha )\xi ^{2}+(-0.1595+0.0055\alpha )\xi -0.0154=0$. By choosing $\alpha =2$ and $\xi =0.2836$ and if $x(0)>x^{*}$, one can start harvesting at the maximum effort level $E_{\max }=0.6333$, till $x$ reduces to $x^{*}=0.2$. After reaching $x^{*}=0.2$, we switch to the singular effort level $E^{*}=0.2817$.

For the parameter values $\alpha =2$ and $\xi =0.2836$, the optimal trajectory for system (6) with initial population densities $(x_{0},y_{0})=(0.9,0.4)$ along with the optimal strategy is shown in Fig. 9. The optimal trajectory is a combination of two trajectories, one (dashed) corresponding to the maximum harvesting effort $E_{\max }=0.6333$ while the second one corresponds to the singular effort $E^{*}=0.2817$. The switch from maximum harvesting effort $E_{\max }$ to singular effort $\widetilde{E}$ happens at time $t=2.9$.

$$\begin{aligned} E^{~\text {MRD}}(t)= {\left\{ \begin{array}{ll} E_{\max }=0.6333&{}~\text {if}~~t\le 2.9,\\ E^{*}~~~~=0.2817&{}~\text {if}~~t>2.9. \end{array}\right. } \end{aligned}$$

Note that, in this case also, we get an improved harvesting policy, even with the low-quality additional food as compared to prey nutrients, since $\alpha =2>1$ and while keeping prey population level at a level higher than the level without the additional food case. This is illustrative of how the supply of additional food can play a critical role in formulating an efficient harvesting policy along with population conservation.

Table 6 Possibilities of ecologically sustainable harvesting effort with and without additional food supply under all the three cases

Fig. 9

The left hand figure shows the optimal path emanating from point $(0.9,0.4)$ subject to the system (6) with parameter values $c=1.1,m=1,b=3,q=1,p=1,c_{1}=0.005,\alpha =2$ and $\xi =0.2836$. The right hand figure shows the corresponding optimal strategy (which is a combination of bang-bang and singular control), and it illustrates that harvesting should start with maximum effort $E_{\max }=0.6333$ and continue up to 2.9 time units, and after that harvesting effort must be switched to $E^{*}=0.2817$

8 Discussion and conclusion

We undertake a comparative study between classical ratio-dependent and modified ratio-dependent predator–prey model by incorporating prey harvesting into both the models. While the classical ratio-dependent model has a ratio-dependent functional response, the modified model also has ratio-dependent functional response but with the additional food being made available to predators. In this paper, we have assumed that the predator–prey system follows the ratio-dependent model prior to harvesting. The comparison of the models is done from the perspective of how the additional food supply to the predators plays a role in deciding the range of bioeconomically sustainable prey harvesting effort. This was accomplished by (1) stability analysis of both the models, and (2) determination of the optimal harvesting policy using the Pontryagin’s maximum principle for both the models.

We analyzed the stability results of both the bioeconomic models (to determine the extent of ecologically sustainable harvesting effort) under the three natural conditions (i.e., Case 1, Case 2 and Case 3) which arise from the stability results of the interior equilibrium of the ratio-dependent model (3). In particular, the conditions for existence and stability of the interior equilibrium point were studied since a stable interior equilibrium point represents the coexistence of both the species for all time. The various possibilities with regards to ecologically sustainable harvesting effort for systems (4) and (6) under all the three cases (defined in Table 2) are summarized in Table 6.

The results in Table 6 suggest that harvesting in the absence of additional food supply is meaningful (i.e., harvesting with conservation of both species) only under Case 3. This means that if both the prey and predator have coexisted prior to harvesting, only then harvesting (with population conservation) is possible, provided the harvesting effort does not exceed the allowable limit of $\frac{1}{q}(1-c+\frac{c}{b})$. On the other hand, in the presence of additional food supply, meaningful harvesting is possible under all the three cases. Also, here, the maximum sustainable effort level can be made greater than the corresponding maximum sustainable effort level without additional food, by providing additional food with quality $\alpha >1$. In other words, if we supply inferior (relative to prey) quality of additional food to predators, then ecologically sustainable harvesting effort level can be increased. This is plausible, because a supply of better quality additional food in limited quantity results in the increase in the predator population. Consequently, the predators intensify the predation of their natural prey, resulting in reduced harvesting. Instead, if additional food of inferior quality is supplied, it helps in the distraction of the predator population from their natural prey and consequently the prey population increases leading to more harvesting.

A harvesting exercise with random effort (keeping the effort level within the allowable range obtained by stability analysis of both the bioeconomic models) may not necessarily result in the best net profit. Thus, in order to determine the most economically and ecologically viable harvesting effort, we formulated a bioeconomic control problem with the goal of maximizing the net profit from harvesting while ensuring population conservation. In the absence of additional food being supplied, we calculated prey threshold level $\widetilde{x}=\frac{1}{2}\left[ \frac{c_{1}}{pq}+\left( 1-c+\frac{c}{b}\right) \right]$, beyond which harvesting is not allowed. We found that this threshold level can be made flexible as desired, by providing additional food to predators with appropriate quality. In other words, if we undertake harvesting with additional food provided predator–prey system, then the threshold level can be made less or more than $\widetilde{x}$, depending upon the quality of additional food. If the quality $\alpha$ is less than (more than) $1$, then the new threshold level $x^{*}$ is less than (greater than) $\widetilde{x}$.

We also showed that the singular optimal control with additional food can be increased to a level which is more than that of the system without additional food, provided the additional food parameters $\alpha$ and $\xi$ are chosen such that $\frac{c(\alpha -1)\xi }{b(x^{*}+\xi )}>x^{*}-\widetilde{x}$. Overall, our study found that we can achieve better harvesting policy (which gives higher returns as well as better population conservation), if we consider additional food supply to predators to be a part of the total harvest effort.