Free vibration analysis of a spinning piezoelectric beam with geometric nonlinearities

Abstract

The linear and non-linear free vibrations of a spinning piezoelectric beam are studied by considering geometric nonlinearities and electromechanical coupling effect. The non-linear differential equations of the spinning piezoelectric beam governing two transverse vibrations are derived by using transformation of two Euler angles and the extended Hamilton principle, wherein an additional piezoelectric coupling term and different linear terms are present in contrast to the traditional shaft model. Linear frequencies are obtained by solving the standard eigenvalues of the linearized system directly, and the non-linear frequencies and non-linear complex modes are achieved by using the method of multiple scales. For free vibrations analysis of a spinning piezoelectric beam, the non-linear modal motions are investigated as forward and backward precession with different spinning speeds. The responses to the initial conditions for this gyroscopic system are studied and a beat phenomenon is found, which are then validated by numerical simulation. The influences of some parameters such as electrical resistance, rotary inertia and spinning speeds to the non-linear dynamics of a spinning piezoelectric beam are investigated.

1 Introduction

A spinning piezoelectric beam can often be used to make a piezoelectric vibratory gyroscope, which has several applications such as in mobile phones, high-grade cars, intelligent robotics, military weapons and aerospace systems. In the past, the piezoelectric vibratory gyroscope has become one of the best essential electromechanical system sensors, especially in the field of inertial navigation systems [1]. To simplify the analysis of the piezoelectric gyroscope, traditionally, most investigations are confined to the linear system with piezoelectric excitation and piezoelectric detection [2, 3]. Based on the linear approximation and non-linear “slow” system, Lajimi et al. [4] investigated the non-linear estimate of the mechanical thermal noise for an electrostatic gyroscope. The applications of non-linear analysis are also significant for flexible components, and the characteristics of the non-linear gyroscopic system have attracted much attention in a field of rotating shaft [5, 6]. By using the fractional calculus and the Gurtin–Murdoch theory, Oskouie et al. [7] investigated the nonlinear vibration of viscoelastic Euler–Bernoulli nanobeam. By considering three types of boundary conditions, Zhao et al. [8] studied the natural frequencies of the Timoshenko beam with surface effects. Recently, there has been a growing research interest to investigate piezoelectric materials on energy harvesters [9,10,11] and microstructures [12,13,14,15] for rotational motion. As a conclusion, the non-linear characteristics of gyroscopes modeled by a spinning piezoelectric beam should be investigated, so that the guidance to improve the performance of piezoelectric vibratory gyroscope can be proposed.

Modal analysis of gyroscopic system is an effective tool to investigate the dynamic responses and mode interactions [16, 17]. However, when coping with the gyroscopic continuum, the modal theories become difficult because the complex modes should be considered [18, 19]. To this end, Rosenburg [20] firstly presented the non-linear normal modes, which expanded the modal motions from the linear non-gyroscopic systems to non-linear non-gyroscopic systems. The non-linear normal mode concept is utilized in the field of non-linear systems by many researchers. By using the multiple scales method, Nayfeh and Nayfeh [21, 22] studied the non-linear normal modes with internal resonance and geometric non-linearity of a one-dimensional continuous system. To solve the modal motions of gyroscopic systems, Shaw and Pierre [23, 24] used the invariant manifold method to expand the non-linear normal modes to the gyroscope coupling systems. The work of Carlos et al. [25] made a comparison for the non-linear normal modes of an axially loaded beam by both the invariant manifold method and multiple scales method. For a linear system, Uspensky and Avramov [26] studied the non-linear normal mode under a forced excitation by using the invariant manifold method and Rauscher method. To analyze the free vibration of a gyroscopic system, Arvin and Nejad [27] described the complex dynamical characteristics of non-linear normal modes. In their work, Qian et al. [28] studied parametric instability analysis of a linear gyroscopic system based on the traditional coupled gyroscopic system and decoupled gyroscopic modes decoupling method. Recently, there are several valuable research towards non-linear normal modes of undamped systems [29,30,31] and damped systems [32, 33] by using numerical calculation. The study by Pan et al. [34] used the complex modal technique to evaluate the natural frequencies and complex modes of serpentine belt drives.

The gyroscopic effect caused by spinning motion appears comprehensively in the rotor dynamics systems [35, 36]. By deriving the closed polynomial of frequency equations and integral forms under an ordinary forcing function, Sturla and Argento [37] studied the free and forced vibrations of a viscoelastic rotating Rayleigh beam. The work Ishida and Inoue [38] considered the effect of internal resonance of a non-linear rotor. It is always hard to gain the physical model of nonlinear rotor-bearing system, thus Ma et al. [39] identified a data-driven non-linear auto-regressive network with exogenous inputs (NARX) model to solve this problem. By considering random excitations, Hosseini and Khadem [40] investigated the vibration and stability of a spinning beam with random characteristics subject to white noise by using the finite element method. In order to guide the design of distorted model, Luo et al. [41] provided a new dynamic scaling law of geometrically distorted model in predicting the dynamic characteristics. Moreover, many researchers analyzed the free vibrations dynamic properties of shafts by different methods [5, 6, 42, 43].

In this paper, the piezoelectric coupling governing differential expressions with non-linearities in curvature and inertia of a spinning piezoelectric beam are obtained, and the natural frequencies, as well as gyroscopic complex modes, are analyzed. By using the multiple scales method, the non-linear modal motions and non-linear frequencies are investigated. The responses to the initial values are discussed for the gyroscopic system by multiple scales method, and numerical simulation validates the results. The piezoelectric coupling effect and non-linear features of the gyroscopic continuum are also investigated in detail. The contribution of the electrical resistance, rotary inertia, electromechanical coupling coefficient and spinning speeds to the forward and backward natural frequencies of the spinning piezoelectric beam are studied, which prompts possible optimizations in the design of piezoelectric vibratory gyroscopes.

2 Governing equations of a spinning piezoelectric beam

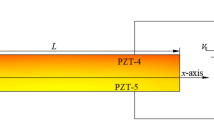
Figure 1 shows the structure of a spinning beam which is surrounded with four piezoelectric films. The length (L₁, L₂, L) and width (w_b, w_p) of the beam and piezoelectric films are shown in the figure. The beam displacement is made of three components, u(s, t), v(s, t), and w(s, t), along the inertial frame x, y, and z directions, respectively, where s denotes the undeformed arclength along the x-axis from the root of the beam to the observed reference point, t denotes time. The x–y–z coordinate system denotes the inertial frame.

Fig. 1

Spinning beam with surrounded four piezoelectric films

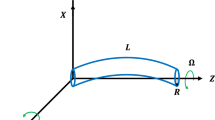
The transformation of two Euler angles by which an arbitrary beam cross section can be expressed with three coordinate systems is shown in Fig. 2. The x₀–y₀–z₀ system is a spinning frame around the x-axis with constant speed Ω of the undeformed beam; the x₁–y₁–z₁ and x₂–y₂–z₂ systems are orthogonal coordinate frames associated with Euler angle transformation. Moreover, we let (i_x, i_y, i_z), ($\varvec{i}_{{\hat{1}}}$,$\varvec{i}_{{\hat{2}}}$,$\varvec{i}_{{\hat{3}}}$), and (i₁, i₂, i₃) represent the unit vectors of the x₀–y₀–z₀, x₁–y₁–z₁, and x₂–y₂–z₂ coordinate frames, respectively.

Fig. 2

Sequence of Euler angle transformation

From the undeformed plane, the cross section first spins by α degree about n axis from x₀–y₀–z₀ to x₁–y₁–z₁

$$\left\{{\begin{array}{*{20}c} {\varvec{i}_{{{\hat{\text{1}}}}}} \\ {\varvec{i}_{{{\hat{\text{2}}}}}} \\ {\varvec{i}_{{{\hat{\text{3}}}}}} \\ \end{array}} \right\} = \varvec{B}(\alpha)\left\{{\begin{array}{*{20}c} {\varvec{i}_{\varvec{x}}} \\ {\varvec{i}_{\varvec{y}}} \\ {\varvec{i}_{\varvec{z}}} \\ \end{array}} \right\}.$$

(1)

The transformation matrix B(α) can be expressed by the displacements [44]

$$\varvec{B}(\alpha) = \left[{\begin{array}{*{20}c} {1 + u^{\prime}} & {v^{\prime}} & {w^{\prime}} \\ {- \,v^{\prime}} & {1 + u^{\prime} + \frac{{w^{\prime 2}}}{{2 + u^{\prime}}}} & {- \frac{{v^{\prime} w^{\prime}}}{{2 + u^{\prime}}}} \\ {- \,w^{\prime}} & {- \,\frac{{v^{\prime} w^{\prime}}}{{2 + u^{\prime}}}} & {1 + u^{\prime} + \frac{{v^{\prime 2}}}{{2 + u^{\prime}}}} \\ \end{array}} \right].$$

(2)

Here, the primes of (u, v, w) denote the derivatives with respect to s, respectively.

Further, the cross-section spins ϕ by about x₁ axis from x₁–y₁–z₁ to x₂–y₂–z₂, thus the transformation from x₀–y₀–z₀ to x₂–y₂–z₂ is

$$\left\{{\begin{array}{*{20}c} {\varvec{i}_{ 1}} \\ {\varvec{i}_{ 2}} \\ {\varvec{i}_{ 3}} \\ \end{array}} \right\} = \varvec{P}\left\{{\begin{array}{*{20}c} {\varvec{i}_{\varvec{x}}} \\ {\varvec{i}_{\varvec{y}}} \\ {\varvec{i}_{\varvec{z}}} \\ \end{array}} \right\},\quad \varvec{P} = \left[{\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos \phi} & {\sin \phi} \\ 0 & {- \,\sin \phi} & {\cos \phi} \\ \end{array}} \right]\varvec{B}(\alpha).$$

(3)

For an in-extensional beam, u′ ≅ − (v′² + w′²)/2, expanding ϕ with a Taylor series, cosϕ = 1 − ϕ²/2, sinϕ = ϕ − ϕ³/6, the transformation matrix P can be attained as

$$\varvec{P} = \left[{\begin{array}{*{20}c} {1 - \frac{1}{2}v^{\prime 2} - \frac{1}{2}w^{\prime 2}} & {v^{\prime}} & {w^{\prime}} \\ {- \,v^{\prime} - w^{\prime} \phi + \frac{1}{2}v^{\prime} \phi^{2}} & {1 - \frac{1}{2}v^{\prime 2} - \frac{1}{2}\phi^{2} - \frac{1}{2}\phi v^{\prime} w^{\prime}} & {\phi - \frac{1}{2}v^{\prime} w^{\prime} - \frac{1}{2}w^{\prime 2} \phi - \frac{1}{6}\phi^{3}} \\ {- \,w^{\prime} + v^{\prime} \phi + \frac{1}{2}w^{\prime} \phi^{2}} & {- \,\phi - \frac{1}{2}v^{\prime} w^{\prime} + \frac{1}{2}v^{\prime 2} \phi + \frac{1}{6}\phi^{3}} & {1 - \frac{1}{2}w^{\prime 2} - \frac{1}{2}\phi^{2} + \frac{1}{2}v^{\prime} w^{\prime} \phi} \\ \end{array}} \right].$$

(4)

Using the concept of continuity, one can obtain the deformed curvatures ρ_i (i = 1, 2, 3)

$$\begin{aligned} \rho_{1} \equiv \varvec{i}_{{\mathbf{2}}}^{\prime} \cdot \varvec{i}_{{\mathbf{3}}} = \sum\limits_{i = 1}^{3} {P_{2i}^{\prime}} P_{3i} = \phi^{\prime} + \frac{1}{2}v^{{\prime \prime}} w^{\prime} - \frac{1}{2}v^{\prime} w^{{\prime \prime}}, \hfill \\ \rho_{2} \equiv - \,\varvec{i}_{{\mathbf{1}}}^{\prime} \cdot \varvec{i}_{{\mathbf{3}}} = - \sum\limits_{i = 1}^{3} {P_{1i}^{\prime}} P_{3i} = - \,w^{{\prime \prime}} + v^{{\prime \prime}} \phi - \frac{1}{2}v^{\prime} v^{{\prime \prime}} w^{\prime} - \frac{1}{2}w^{{\prime \prime}} w^{\prime 2} + \frac{1}{2}\phi^{2} w^{{\prime \prime}}, \hfill \\ \rho_{3} \equiv \varvec{i}_{{\mathbf{1}}}^{\prime} \cdot \varvec{i}_{{\mathbf{2}}} = \sum\limits_{i = 1}^{3} {P_{1i}^{\prime}} P_{2i} = v^{{\prime \prime}} + w^{{\prime \prime}} \phi + \frac{1}{2}v^{{\prime \prime}} v^{\prime 2} + \frac{1}{2}v^{\prime} w^{\prime} w^{{\prime \prime}} - \frac{1}{2}\phi^{2} v^{{\prime \prime}}. \hfill \\ \end{aligned}$$

(5)

The relative angular velocity vector ω to the inertial frame are then obtained as

$$\begin{aligned} \omega_{1} \equiv \dot{\varvec{i}}_{{\mathbf{2}}} \cdot \varvec{i}_{{\mathbf{3}}} = \sum\limits_{i = 1}^{3} {(\dot{P}_{2i} P_{3i} + \varOmega P_{1i})} = \varOmega + \dot{\phi} + \frac{1}{2}\dot{v}^{\prime} w^{\prime} - \frac{1}{2}v^{\prime} \dot{w}^{\prime} - \frac{1}{2}\varOmega v^{\prime 2} - \frac{1}{2}\varOmega w^{\prime 2}, \hfill \\ \omega_{2} \equiv - \,\dot{\varvec{i}}_{{\mathbf{1}}} \cdot \varvec{i}_{{\mathbf{3}}} = - \sum\limits_{i = 1}^{3} {\dot{P}_{1i}} P_{3i} = - \,\varOmega v^{\prime} - \varOmega w^{\prime} \phi + \dot{v}^{\prime} \phi - \dot{w}^{\prime}, \hfill \\ \omega_{3} \equiv \dot{\varvec{i}}_{{\mathbf{1}}} \cdot \varvec{i}_{{\mathbf{2}}} = \sum\limits_{i = 1}^{3} {\dot{P}_{1i}} P_{2i} = - \,\varOmega w^{\prime} + \varOmega v^{\prime} \phi + \dot{w}^{\prime} \phi + \dot{v}^{\prime}. \hfill \\ \end{aligned}$$

(6)

Here, the dots of (u, v, w) denote the derivatives with respect to t, respectively.

The deformation of any point on the beam can be denoted by the position vector R as

$$\varvec{R} = u\varvec{i}_{x} + v\varvec{i}_{y} + w\varvec{i}_{z} + y\varvec{i}_{2} + z\varvec{i}_{{_{3}}}.$$

(7)

Using directional time derivatives, $\dot{\varvec{R}}$ in the coordinate system of x₀–y₀–z₀ is expressed as

$$\dot{\varvec{R}} = \dot{u}\varvec{i}_{\varvec{x}} + \left({\dot{v} - w\varOmega} \right)\varvec{i}_{y} + \left({\dot{w} + v\varOmega} \right)\varvec{i}_{z} + \left({\begin{array}{*{20}c} {\varvec{i}_{x}} & {\varvec{i}_{y}} & {\varvec{i}_{z}} \\ \end{array}} \right)\varvec{P}^{\text{T}} \varvec{r\omega},$$

(8)

with

$$\varvec{r} = \left[{\begin{array}{*{20}c} 0 & z & {- \,y} \\ {- \,z} & 0 & 0 \\ y & 0 & 0 \\ \end{array}} \right],\;\varvec{\omega}= \left\{{\begin{array}{*{20}c} {\omega_{1}} \\ {\omega_{2}} \\ {\omega_{3}} \\ \end{array}} \right\}.$$

(9)

The kinetic energy of a spinning Rayleigh beam can be obtained by substituting Eqs. (6), (8), and (9) into the following expression

$$T = \frac{1}{2}\int_{0}^{L} {\int_{A} {\rho \dot{\varvec{R}} \cdot \dot{\varvec{R}}\text{d}A}} \text{d}s.$$

(10)

According to the assumption of an inextensional beam and using the geometric boundary condition u(0,t) = 0, one can obtain

$$u = - \frac{1}{2}\int_{0}^{s} {\left({w^{\prime 2} + v^{\prime 2}} \right)} \text{d}s.$$

(11)

Hence, the kinetic energy can be obtained as

$$\begin{aligned} T & = \frac{1}{2}\int_{0}^{L} {\left\{{m\left \{{\dot{w}^{2} + \dot{v}^{2} + \left[{- \frac{1}{2}\int_{0}^{s} {\frac{\partial}{\partial t}\left({w^{\prime 2} + v^{\prime 2}} \right)\text{d}s}} \right]^{2}} \right \} + m\varOmega^{2} \left({w^{2} + v^{2}} \right) + 2m\varOmega \left({v\dot{w} - w\dot{v}} \right)} \right \}} \text{d}s \\ & \quad +\frac{1}{2}\int_{0}^{L} {\left[{j\left({\dot{v}^{\prime 2} + \dot{w}^{\prime 2}} \right) + j\varOmega^{2} \left({v^{\prime 2} + w^{\prime 2}} \right) + 2j\varOmega \left({v^{\prime}\dot{w}^{\prime} + w^{\prime}\dot{v}^{\prime}} \right)} \right]} \text{d}s + jL\varOmega^{2}, \\ \end{aligned}$$

(12)

with

$$\begin{aligned} & m = w_{b} \rho_{b} h_{b} + 4S(s)w_{p} \rho_{p} h_{p},\quad j = \int_{A} {\rho (s)z^{2}} {\text{d}}A = \int_{A} {\rho (s)} y^{2} {\text{d}}A, \\ & \rho (s) = \rho_{b} + S(s)\rho_{p},\quad S(s) = H(s - L_{1}) - H(s - L_{2}). \\ \end{aligned}$$

(13)

In Eq. (13), H(s) is the Heaviside function, A is the cross-sectional area of the beam, m, ρ(s), and j are the total mass, total density, and total rotary inertia of the beam and the piezoelectric films, respectively, and ρ_b,p, w_b,p, and h_b,p (w_b/h_b= 1) are the volumetric mass density, width and thickness of the beam and the piezoelectric film, respectively. For all the parameters used in this paper, subscript b denotes the beam material and p denotes piezoelectric film.

The mechanical properties of piezoelectric films are coupled with their electric properties. For the configuration and non-linear strain considered here, the electrical displacement is one dimensional and the stress–strain relations for these materials are known as follows [45, 46]

$$\begin{aligned} & T_{p} = E_{p} S - e_{31} E_{3},\quad D = e_{31} S + \varepsilon_{33}^{{}} E_{3}, \\ & S = - \,y\rho_{3} + z\rho_{2},\quad E_{3} = \frac{{V_{v,w}}}{h}, \\ \end{aligned}$$

(14)

where E_p is the stiffness coefficient, ε₃₃ is the dielectric permittivity, T_p is the stress, S is the strain, e₃₁ is the piezoelectric strain constant, D is the electrical displacement, E₃ is the electrical field, and V_v,w is the voltage. The relation between voltage and current is

$$V_{w} = Z\dot{Q}_{w},V_{v} = Z\dot{Q}_{v},$$

(15)

where Z is electrical resistance, Q is charge quantity.

An isotropic beam is considered, and the stress–strain satisfies the relation

$$T_{b} = E_{b} S,$$

(16)

where E_b stands for stiffness coefficient.

The total potential energy for spinning beam can be derived as follows

$$U = \frac{1}{2}\int_{{V_{b}}} {T_{b} S\text{d}V_{b}} + \frac{1}{2}\int_{{V_{p}}} {(T_{p} S - DE_{3})\text{d}V_{p}}.$$

(17)

Substituting Eq. (15) into Eq. (14), then further inserting the results and Eq. (16) into Eq. (17), we can obtain

$$\begin{aligned} U & = \frac{EI}{2}\int_{0}^{L} {\left({\rho_{2}^{2} + \rho_{3}^{2}} \right)\text{d}s} + \frac{\theta}{2}\int_{{L_{1}}}^{{L_{2}}} {(- \rho_{2}Z\dot{Q}_{w} + \rho_{3} Z\dot{Q}_{v})} \text{d}s \\ & \quad - \,\frac{{C_{p}}}{2}\int_{{L_{1}}}^{{L_{2}}} {\left[{(Z\dot{Q}_{w})^{2} + (Z\dot{Q}_{v})^{2}} \right]} \text{d}s, \\ \end{aligned}$$

(18)

where $EI = E_{b} I_{b} + S(s)E_{p} I_{p}$ is bending stiffness, $C_{p} = w_{p} \varepsilon_{33}^{{}}/h_{p}$ is piezoelectric film capacitor, $\theta = w_{p} e_{31} (h_{b}/2 + h_{p})$ is electromechanical coupling coefficient, and

$$I_{b} = \frac{1}{12}w_{b} h_{b}^{3},\quad I_{p} = 2\left[{\frac{1}{12}w_{p} h_{p}^{3} + w_{p} h_{p} \left({\frac{{h_{p}}}{2} + \frac{{h_{b}}}{2}} \right)^{2} + \frac{1}{12}h_{p} w_{p}^{3}} \right].$$

(19)

The virtual work done by mechanical damping and electrical resistance is

$$\delta W = - \frac{1}{2}\int_{0}^{L} {(c\dot{v}\delta v + c\dot{w}\delta w + Z\dot{Q}_{w} \delta Q_{w} + Z\dot{Q}_{v} \delta Q_{v})\text{d}s}.$$

(20)

The next step is to substitute the results of kinetic, potential energy and virtual work into the Hamilton principle

$$\int_{{t_{1}}}^{{t_{2}}} {\left({\delta T - \delta U + \delta W} \right)\text{d}t = 0}.$$

(21)

Because the torsional frequency is larger than the flexural frequency, so the twist angle ϕ can be neglected [42]. By using voltage and current relation and expanding the results up to three orders, we can obtain the following four partial governing equations with electromechanical coupling

$$\begin{aligned} & m(\ddot{v} - \dot{\varOmega}w - 2\varOmega \dot{w} - \varOmega^{2} v) - j(\varOmega^{2} v^{{\prime \prime}} + \ddot{v}^{{\prime \prime}}) + EI[v^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + v^{{\prime {\prime \prime}}}]^{\prime} + c\dot{v} \\ & \quad + \,\frac{1}{2}\left\{{v^{\prime} \int_{L}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2}){\text{d}}s}} \right]\text{d}s}} \right\}^{\prime} - \theta V_{v} (t)S(s)^{{\prime \prime}} = 0, \\ & m(\ddot{w} + \dot{\varOmega}v + 2\varOmega \dot{v} - \varOmega^{2} w) - j(\varOmega^{2} w^{{\prime \prime}} + \ddot{w}^{{\prime \prime}}) + EI[w^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + w^{{\prime {\prime \prime}}}]^{\prime} + c\dot{w} \\ & \quad + \,\frac{1}{2}\left\{{w^{\prime} \int_{L}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2}){\text{d}}s}} \right]\text{d}s}} \right\}^{\prime} - \theta V_{w} (t)S(s)^{{\prime \prime}} = 0, \\ & C_{p} \dot{V}_{v} (t) + \frac{{V_{v} (t)}}{Z} + \theta S(s)^{{\prime \prime}} \dot{v} = 0, \\ & C_{p} \dot{V}_{w} (t) + \frac{{V_{w} (t)}}{Z} + \theta S(s)^{{\prime \prime}} \dot{w} = 0. \\ \end{aligned}$$

(22)

Substituting periodic voltages $\left\{{v,w,V_{v},V_{w}} \right\} = \left\{{\bar{v},\bar{w},\bar{V}_{v},\bar{V}_{w}} \right\}\text{e}^{{\text{i}\omega t}}$ into the last two equations of Eq. (22), removing the overbar above the displacements and voltages for simplification, we obtain

$$\begin{aligned} &\left({1 + \frac{{Z_{0}}}{Z}} \right)V_{v} + \frac{\theta}{{C_{p}}}S(s)^{\prime\prime}v = 0, \hfill \\ &\left({1 + \frac{{Z_{0}}}{Z}} \right)V_{w} + \frac{\theta}{{C_{p}}}S(s)^{\prime\prime}w = 0, \hfill \\ \end{aligned}$$

(23)

with Z₀ = 1/(iωC_p).

Hence, substituting Eq. (23) into Eq. (22), the last two equations of (22) can be eliminated by using displacements to replace voltages [47], and then the equations can be reduced to partial differential equations of two degrees of freedom

$$\begin{aligned} & m(\ddot{v} - \dot{\varOmega}w - 2\varOmega \dot{w} - \varOmega^{2} v) - j(\varOmega^{2} v^{{\prime \prime}} + \ddot{v}^{{\prime \prime}}) + EI[v^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + v^{{\prime {\prime \prime}}}]^{\prime} + c\dot{v} \\ & \quad + \,\frac{1}{2}m\left\{{v^{\prime} \int_{L}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2})\text{d}s}} \right]\text{d}s}} \right\}^{\prime} + \frac{{\theta^{2} S(s)^{{{\prime \prime}2}} v}}{{C_{p} (1 + Z_{0}/Z)}} = 0, \\ & m(\ddot{w} + \dot{\varOmega}v + 2\varOmega \dot{v} - \varOmega^{2} w) - j(\varOmega^{2} w^{{\prime \prime}} + \ddot{w}^{{\prime \prime}}) + EI[w^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + w^{{\prime {\prime \prime}}}]^{\prime} + c\dot{w} \\ & \quad + \,\frac{1}{2}m\left\{{w^{\prime} \int_{L}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2})\text{d}s}} \right]\text{d}s}} \right\}^{\prime} + \frac{{\theta^{2} S(s)^{{{\prime \prime}2}} w}}{{C_{p} (1 + Z_{0}/Z)}} = 0. \\ \end{aligned}$$

(24)

Introducing dimensionless variables and parameters

$$\begin{aligned} & s^{*} = \frac{s}{L},\quad v^{*} = \frac{v}{L},\quad w^{*} = \frac{w}{L},\quad t^{*} = \tau t,\quad J = \frac{j}{{mL^{2}}},\quad \tau = \sqrt {\frac{EI}{{mL^{4}}}},\quad \varOmega^{*} = \frac{\varOmega}{\tau}, \\ & c^{*} = \frac{c}{m\tau},\quad \kappa = \frac{{\theta^{2}}}{{mC_{p} L^{4} \tau^{2}}}. \\ \end{aligned}$$

(25)

Substituting Eq. (25) into Eq. (24), the dimensionless form of the governing equations becomes

$$\begin{aligned} & \ddot{v} - \dot{\varOmega}w - 2\varOmega \dot{w} - \varOmega^{2} v - J\varOmega^{2} v^{{\prime \prime}} - J\ddot{v}^{{\prime \prime}} + [v^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + v^{{\prime {\prime \prime}}}]^{\prime} + c\dot{v} \\ & \quad + \,\frac{1}{2}\left\{{v^{\prime} \int_{1}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2})\text{d}s}} \right]\text{d}s}} \right\}^{\prime} + \frac{{\kappa S(s)^{{{\prime \prime}2}} v}}{{1 + Z_{0}/Z}} = 0, \\ & \ddot{w} + \dot{\varOmega}v + 2\varOmega \dot{v} - \varOmega^{2} w - J\varOmega^{2} w^{{\prime \prime}} - J\ddot{w}^{{\prime \prime}} + [w^{\prime} (v^{\prime} v^{{\prime \prime}} + w^{\prime} w^{{\prime \prime}})^{\prime} + w^{{\prime {\prime \prime}}}]^{\prime} + c\dot{w} \\ & \quad + \,\frac{1}{2}\left\{{w^{\prime} \int_{1}^{s} {\frac{{\partial^{2}}}{{\partial t^{2}}}\left[{\int_{0}^{s} {(v^{\prime 2} + w^{\prime 2})\text{d}s}} \right]\text{d}s}} \right\}^{\prime} + \frac{{\kappa S(s)^{{{\prime \prime}2}} w}}{{1 + Z_{0}/Z}} = 0. \\ \end{aligned}$$

(26)

By neglecting the terms of the rotary inertia and geometric non-linearity, our governing Eq. (26) can recover those equations in Refs. [1, 2] that focused on the linear counterpart of the piezoelectric gyroscope. In contrast to the non-linear shaft models [42, 48], which studied only a rotating beam without piezoelectric materials, two additional piezoelectric coupling terms (κS(s)″²v/(1 + Z₀/Z) and κS(s)″²w/(1 + Z₀/Z)) and different linear terms such as gyroscopic coupling terms and centrifugal force terms are presented in the current formulation for an investigation.

In this study, considering the simply-supported boundary condition (v = w=0 and v″ = w″ = 0) at both ends, we use Galerkin method and the appropriate sine function

$$\begin{aligned} v(s,t) & = q(t)\sin (n\uppi s), \\ w(s,t) & = p(t)\sin (n\uppi s), \\ \end{aligned}$$

(27)

where n is the mode number, p and q are generalized temporal coordinates and coupled to each other. Substituting Eq. (27) into Eq. (26), letting L₁ = 0, L₂ = L, and assuming a constant base angular speed Ω, we can obtain two non-linear ordinary differential equations

$$\begin{aligned} & (1 + Jn^{2} {\uppi}^{2})\ddot{q} - 2\varOmega \dot{p} + cn^{4} {\uppi}^{4} \dot{q} + \left({n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \frac{{\kappa n^{4} {\uppi}^{4}}}{{1 + Z_{0}/Z}}} \right)q + n^{6} {\uppi}^{6} q^{3} \\ & \quad + \,n^{6} {\uppi}^{6} qp^{2} - \left({\frac{3}{8}n^{2} {\uppi}^{2} - \frac{1}{3}n^{4} {\uppi}^{4}} \right)(q\dot{q}^{2} + q\dot{p}^{2} + qp\ddot{p} + q^{2} \ddot{q}) = 0, \\ & (1 + Jn^{2} {\uppi}^{2})\ddot{p} + 2\varOmega \dot{q} + cn^{4} {\uppi}^{4} \dot{p} + \left({n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \frac{{\kappa n^{4} {\uppi}^{4}}}{{1 + Z_{0}/Z}}} \right)p + n^{6} {\uppi}^{6} p^{3} \\ & \quad + \,n^{6} {\uppi}^{6} pq^{2} - \left({\frac{3}{8}n^{2} {\uppi}^{2} - \frac{1}{3}n^{4} {\uppi}^{4}} \right)(p\dot{p}^{2} + p\dot{q}^{2} + qp\ddot{q} + p^{2} \ddot{p}) = 0. \\ \end{aligned}$$

(28)

3 Analysis of the linear frequency and responses to initial conditions

In this section, the free vibration of the linear part of Eq. (28) is studied first. Neglecting damping and non-linear terms, one can obtain two second-order linear ordinary differential equations with respect to t

$$\varvec{M\ddot{Q}} + \varvec{G\dot{Q}} + \varvec{KQ} = 0,$$

(29)

with

$$\begin{aligned} &\varvec{Q} = \left[{\begin{array}{*{20}c} q & p \\ \end{array}} \right]^{\text{T}},\;\varvec{M} =\left[{\begin{array}{*{20}c} {1 + Jn^{2} {\uppi}^{2}} & {0} \\ {0} & {1 + Jn^{2} {\uppi}^{2}} \\ \end{array}} \right],\;\varvec{G} = \left[{\begin{array}{*{20}c} 0 & {- \,2\varOmega} \\ {2\varOmega} & 0 \\ \end{array}} \right], \hfill \\ &\varvec{K} =\left[{\begin{array}{*{20}c} {n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \frac{{\kappa n^{4} {\uppi}^{4}}}{{1 + Z/Z_{0}}}} & 0 \\ 0 & {n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \frac{{\kappa n^{4} {\uppi}^{4}}}{{1 + Z/Z_{0}}}} \\ \end{array}} \right]. \hfill \\ \end{aligned}$$

(30)

Substituting Q = μe^iωt into Eq. (29), and according to the boundary conditions, the natural frequencies based on the linear system can be obtained as

$$\omega_{f,\,b} = \frac{{\pm \,\varOmega + \sqrt {(1 + Jn^{2} {\uppi}^{2})\left[{n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right] + \varOmega^{2}}}}{{1 + Jn^{2} {\uppi}^{2}}}.$$

(31)

Then, the corresponding column vector μ can be obtained by substituting ω_f and ω_b of Eq. (31) back into Eq. (29). The column vector μ is different when Ω greater or smaller than a critical value

$$\varvec{\mu}= \left\{\begin{aligned} \left[{\begin{array}{*{20}c} {- \,\text{i}} & \text{i} \\ 1 & 1 \\ \end{array}} \right],\quad {\text{when}}\quad \varOmega < n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}, \hfill \\ \left[{\begin{array}{*{20}c} {- \,\text{i}} & {- \,\text{i}} \\ 1 & 1 \\ \end{array}} \right],\quad {\text{when}}\quad \varOmega > n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}, \hfill \\ \end{aligned} \right.$$

(32)

where the first column [−i 1]^T corresponding to ω_f represents forward precession and the second column [i 1]^T corresponding to ω_b represents backward precession in the sub-critical case. On the critical value there exists a switch point of the first mode from backward precession to forward precession. Beyond the critical point, both modes are forward precession.

The two scalar equations of Eq. (29) are only linearly gyroscopic coupled by neglecting the non-linear terms and damping. In Fig. 3, the first two natural frequencies versus spinning speeds are plotted for electrical resistance Z₀/Z = 10 and Z₀/Z = ∞ with parameters J = 0.002, n = 1, κ = 0.5, and c = 0. For each value of Z, two natural frequencies correspond to the two gyroscopic modes of the spinning piezoelectric beam. Figure 3 shows that the forward frequency ω_f increases and the backward frequency ω_b decreases, followed by an increase after the critical point. In the local amplified plot, there are no electric fields in both directions for the case of shortened electrodes (Z₀/Z = ∞). In this case, the piezoelectric coupling effect related to electric fields does not exist. When the electrodes are not shortened (Z₀/Z = 10), as presented in Fig. 3, there are electric energy transfers in the two directions, which causes stiffening of the spinning piezoelectric beam, and higher frequencies are found. Figure 3 also shows that the frequency ω_b is decreasing first, and then increasing, and there exists a critical switch value. When the electrodes are not shortened (Z₀/Z = 10), the point of critical value is pushed back compared with the shortened case (Z₀/Z = ∞), although the effect of the electrodes is weak. Similarly, Fig. 4 shows the second two natural frequencies versus spinning speeds, which are plotted for Z₀/Z = 10 and Z₀/Z = ∞ with parameters J = 0.002, n = 2, κ = 0.5, and c = 0. When shortened electrodes (Z₀/Z = ∞) are considered, there exist neither electric fields nor piezoelectric coupling effect. When the electrodes are not shortened (Z₀/Z = 10), electric field appears causing higher frequencies. We will further explain the dynamics of the four typical points A_f,b, B_f,b, C_f,b, and D_f,b on Figs. 3 and 4 in the analysis of modal motions in the next section.

Fig. 3

Natural frequencies versus spinning speed (J = 0.002, n = 1, κ = 0.5, and c = 0)

Fig. 4

Natural frequencies versus spinning speed (J = 0.002, n = 2, κ = 0.5, and c = 0)

4 Application of multiple scales method for the non-linear system

The method of multiple scales is extensively used in this study of gyroscopic system. Now we treat the non-linear gyroscopic system Eq. (28) by using the procedure of the multiple scales method. Then, the solutions of Eq. (28) are assumed as

$$\begin{aligned} q & = \varepsilon q_{1} (T_{0},T_{2}) + \varepsilon^{3} q_{3} (T_{0},T_{2}) + \cdots, \\ p & = \varepsilon p_{1} (T_{0},T_{2}) + \varepsilon^{3} p_{3} (T_{0},T_{2}) + \cdots, \\ \end{aligned}$$

(33)

where ε is a bookkeeping device denoting small parameter, and the fast and slow time scale T₀= t and T₂= ε²t are introduced. Damping c is scaled with cε² since it is usually very weak. The time derivatives can be written as

$$\frac{\partial}{\partial t} = D_{0} + \varepsilon^{2} D_{2} + \cdots,\quad \frac{\partial}{{\partial t^{2}}} = D_{0}^{2} + 2\varepsilon^{2} D_{2} D_{0} + \cdots,$$

(34)

with D₀ = ∂/∂T₀, D₂ = ∂/∂T₂.

Substituting Eqs. (33) and (34) into Eq. (28) and equating the coefficient of different orders of ε yields

$$\begin{aligned} & (1 + Jn^{2} {\uppi}^{2})D_{0}^{2} q_{1} - 2\varOmega D_{0} p_{1} + [n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)]q_{1} = 0, \\ & (1 + Jn^{2} {\uppi}^{2})D_{0}^{2} p_{1} + 2\varOmega D_{0} q_{1} + [n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)]p_{1} = 0, \\ \end{aligned}$$

(35)

$$(1 + Jn^{2} {\uppi}^{2})D_{0}^{2} q_{3} - 2\varOmega D_{0} p_{3} + \left[{n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]q_{3} = - \,cD_{0} q_{1} + 2\varOmega D_{2} p_{1} - 2(1 + Jn^{2} {\uppi}^{2})D_{0} D_{2} q_{1} - n^{6} {\uppi}^{6} (q_{1}^{3} + q_{1} p_{1}^{2}) + \left({\frac{3}{8}n^{2} {\uppi}^{2} - \frac{1}{3}n^{4} {\uppi}^{4}} \right)\left[{q_{1}^{2} D_{0}^{2} q_{1} + q_{1} (D_{0} q_{1})^{2} + q_{1} (D_{0} p_{1})^{2} + q_{1} p_{1} D_{0}^{2} p_{1}} \right], (1 + Jn^{2} {\uppi}^{2})D_{0}^{2} p_{3} + 2\varOmega D_{0} q_{3} + \left[{n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]p_{3} = - \,cD_{0} p_{1} - 2\varOmega D_{2} q_{1} - 2(1 + Jn^{2} {\uppi}^{2})D_{0} D_{2} p_{1} - n^{6} {\uppi}^{6} (p_{1}^{3} + p_{1} q_{1}^{2}) + \left({\frac{3}{8}n^{2} {\uppi}^{2} - \frac{1}{3}n^{4} {\uppi}^{4}} \right)\left[{p_{1}^{2} D_{0}^{2} p_{1} + p_{1} (D_{0} q_{1})^{2} + p_{1} (D_{0} p_{1})^{2} + q_{1} p_{1} D_{0}^{2} q_{1}} \right].$$

(36)

For the sub-critical case, $\varOmega < n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}$, the solutions to Eq. (35) are assumed as

$$\begin{aligned} & {\text{q}}_{1} (T_{0},T_{2}) = - \,\text{i}A_{1} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} + \text{i}A_{2} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}} + \text{i}\bar{A}_{1} (T_{2})\text{e}^{{- \text{i}\omega_{f} T_{0}}} - \text{i}\bar{A}_{2} (T_{2})\text{e}^{{- \text{i}\omega_{b} T_{0}}}, \\ p_{1} (T_{0},T_{2}) &= A_{1} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} + A_{2} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}} + \bar{A}_{1} (T_{2})\text{e}^{{- \text{i}\omega_{f} T_{0}}} + \bar{A}_{2} (T_{2})\text{e}^{{- \text{i}\omega_{b} T_{0}}}. \\ \end{aligned}$$

(37)

Substituting Eq. (37) into Eq. (36), one can obtain

$$\begin{aligned} & (1 + Jn^{2} {\uppi}^{2})D_{0}^{2} q_{3} - 2\varOmega D_{0} p_{3} + \left[{n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]q_{3} \\ & \quad = F_{1} (T_{2}){\text{e}}^{{\text{i}\omega_{f} T_{0}}} + B_{1} (T_{2}){\text{e}}^{{\text{i}\omega_{b} T_{0}}} + cc + nst, \\ & (1 + Jn^{2} {\uppi}^{2})D_{0}^{2} p_{3} + 2\varOmega D_{0} q_{3} + \left[{n^{4} {\uppi}^{4} - \varOmega^{2} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]p_{3} \\ & \quad = F_{2} (T_{2}){\text{e}}^{{\text{i}\omega_{f} T_{0}}} + B_{2} (T_{2}){\text{e}}^{{\text{i}\omega_{b} T_{0}}} + cc + nst, \\ \end{aligned}$$

(38)

where “nst” denotes non-secular terms, “cc” denotes the conjugate of the proceeding terms, and

$$\begin{aligned} & F_{1} (T_{2}) = - 2(\omega_{f} + Jn^{2} {\uppi}^{2} \omega_{f} - \varOmega)D_{2} A_{1} (T_{2}) - c\omega_{f} A_{1} (T_{2}) + 4\text{i}n^{6} {\uppi}^{6} \bar{A}_{1} (T_{2})A_{1}^{2} (T_{2}) \\ & \quad + \,\frac{1}{2}\text{i}(\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})\bar{A}_{2} (T_{2})A_{2} (T_{2}), \\ &B_{1} (T_{2}) = 2(\omega_{b} + Jn^{2} {\uppi}^{2} \omega_{b} + \varOmega)D_{2} A_{2} (T_{2}) + c\omega_{b} A_{2} (T_{2}) - 4\text{i}n^{6} {\uppi}^{6} \bar{A}_{2} (T_{2})A_{2}^{2} (T_{2}) \\ & \quad - \,\frac{1}{2}\text{i}(\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})A_{2} (T_{2})\bar{A}_{1} (T_{2}), \\ &F_{2} (T_{2}) = - 2\text{i}(\omega_{f} + Jn^{2} {\uppi}^{2} \omega_{f} - \varOmega)D_{2} A_{1} (T_{2}) - c\text{i}\omega_{f} A_{1} (T_{2}) - 4n^{6} {\uppi}^{6} \bar{A}_{1} (T_{2})A_{1}^{2} (T_{2}) \\ & \quad - \,\frac{1}{2}(\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})A_{2} (T_{2})\bar{A}_{2} (T_{2}), \\ &B_{2} (T_{2}) = - 2\text{i}(\omega_{b} + Jn^{2} {\uppi}^{2} \omega_{b} + \varOmega)D_{2} A_{2} (T_{2}) - c\text{i}\omega_{b} A_{2} (T_{2}) - 4n^{6} {\uppi}^{6} \bar{A}_{2} (T_{2})A_{2}^{2} (T_{2}) \\ & \quad - \,\frac{1}{2}(\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})A_{2} (T_{2})\bar{A}_{1} (T_{2}), \\ &\varGamma_{1} = \left({\frac{3}{2}n^{2} {\uppi}^{2} - \frac{4}{3}n^{4} {\uppi}^{4}} \right)(\omega_{f} + \omega_{b})^{2}. \\ \end{aligned}$$

(39)

To determine the solvability conditions of gyroscopic ordinary differential Eq. (38), q₃ and p₃ are expressed as

$$\begin{aligned} & q_{3} (T_{0},T_{2}) = A_{11} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} + A_{12} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}}, \\ & {\text{p}}_{3} (T_{0},T_{2}) = A_{21} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} + A_{22} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}}. \\ \end{aligned}$$

(40)

Substituting Eq. (40) into Eq. (39) and equating the coefficient of $\text{e}^{{\text{i}\omega_{f} T_{0}}}$, we obtain

$$\begin{aligned} & \left[{- \,\omega_{f}^{2} - Jn^{2} {\uppi}^{2} \omega_{f}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]A_{11} (T_{2}) \\ & \quad - \,2\text{i}\omega_{f} \varOmega A_{21} (T_{2}) = F_{1} (T_{2}), \\ & \left[{- \,\omega_{f}^{2} - Jn^{2} {\uppi}^{2} \omega_{f}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]A_{21} (T_{2}) \\ & \quad + \,2\text{i}\omega_{f} \varOmega A_{11} (T_{2}) = F_{2} (T_{2}). \\ \end{aligned}$$

(41)

Similarly, for coefficient of $\text{e}^{{\text{i}\omega_{b} T_{0}}}$, the following equations are obtained

$$\begin{aligned} & \left[{- \omega_{b}^{2} - Jn^{2} {\uppi}^{2} \omega_{b}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]A_{12} (T_{2}) \\ & \quad - \,2\text{i}\omega_{b} \varOmega A_{22} (T_{2}) = B_{1} (T_{2}), \\ & \left[{- \omega_{b}^{2} - Jn^{2} {\uppi}^{2} \omega_{b}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} \right]A_{22} (T_{2}) \\ & \quad + \,2\text{i}\omega_{b} \varOmega A_{12} (T_{2}) = B_{2} (T_{2}). \\ \end{aligned}$$

(42)

Equations (41) and (42) are composed of algebraic equations with respect to A₁₁(T₂), A₂₁(T₂) and A₁₂(T₂), A₂₂(T₂). The nontrivial condition can be expressed as [42]

$$\begin{aligned} \left| {\begin{array}{*{20}c} {- \,\omega_{f}^{2} - Jn^{2} {\uppi}^{2} \omega_{f}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} & {F_{1} (T_{2})} \\ {2\text{i}\omega_{f} \varOmega} & {F_{2} (T_{2})} \\ \end{array}} \right| = 0, \hfill \\ \left| {\begin{array}{*{20}c} {- \,\omega_{b}^{2} - Jn^{2} {\uppi}^{2} \omega_{b}^{2} - \varOmega^{2} + n^{4} {\uppi}^{4} + J\varOmega^{2} n^{2} {\uppi}^{2} + \kappa n^{4} {\uppi}^{4}/(1 + Z_{0}/Z)} & {B_{1} (T_{2})} \\ {2\text{i}\omega_{b} \varOmega} & {B_{2} (T_{2})} \\ \end{array}} \right| = 0. \hfill \\ \end{aligned}$$

(43)

After some mathematical manipulations, the solvability conditions can be written as

$$\begin{aligned} & \text{i}\varLambda_{1} D_{2} A_{1} (T_{2}) + 2\text{i}c\omega_{f} A_{1} (T_{2}) + (\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})\bar{A}_{2} (T_{2})A_{2} (T_{2}) \\ & \quad + \,8n^{6} {\uppi}^{6} \bar{A}_{1} (T_{2})A_{1} (T_{2})^{2} = 0, \\ & \text{i}\varLambda_{2} D_{2} A_{2} (T_{2}) + 2\text{i}c\omega_{b} A_{2} (T_{2}) + (\varGamma_{1} + 16n^{6} {\uppi}^{6})A_{2} (T_{2})\bar{A}_{1} (T_{2})A_{1} (T_{2}) \\ & \quad + \,8n^{6} {\uppi}^{6} \bar{A}_{2} (T_{2})A_{2} (T_{2})^{2} = 0, \\ \end{aligned}$$

(44)

with

$$\varLambda_{1} = 4(\omega_{f} + Jn^{2} {\uppi}^{2} \omega_{f} - \varOmega),\quad \varLambda_{2} = 4(\omega_{b} + Jn^{2} {\uppi}^{2} \omega_{b} + \varOmega).$$

(45)

For the super-critical case, $\varOmega > n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}$, the solutions of Eq. (35) are assumed

$$\begin{aligned} {\text{q}}_{1} (T_{0},T_{2}) & = - \,\text{i}A_{1} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} - \text{i}A_{2} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}} + \text{i}\bar{A}_{1} (T_{2})\text{e}^{{- \text{i}\omega_{f} T_{0}}} + \text{i}\bar{A}_{2} (T_{2})\text{e}^{{- \text{i}\omega_{b} T_{0}}}, \\ p_{1} (T_{0},T_{2}) & = A_{1} (T_{2})\text{e}^{{\text{i}\omega_{f} T_{0}}} + A_{2} (T_{2})\text{e}^{{\text{i}\omega_{b} T_{0}}} + \bar{A}_{1} (T_{2})\text{e}^{{- \text{i}\omega_{f} T_{0}}} + \bar{A}_{2} (T_{2})\text{e}^{{- \text{i}\omega_{b} T_{0}}}. \\ \end{aligned}$$

(46)

Similarly, the solvability conditions are derived as

$$\begin{aligned} & \text{i}\varLambda_{1} D_{2} A_{1} (T_{2}) + 2\text{i}c\omega_{f} A_{1} (T_{2}) + (\varGamma_{2} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})\bar{A}_{2} (T_{2})A_{2} (T_{2}) \\ & \quad + \,8n^{6} {\uppi}^{6} \bar{A}_{1} (T_{2})A_{1} (T_{2})^{2} = 0, \\ & \text{i}\varLambda_{3} D_{2} A_{2} (T_{2}) + 2\text{i}c\omega_{b} A_{2} (T_{2}) + (\varGamma_{2} + 16n^{6} {\uppi}^{6})A_{1} (T_{2})\bar{A}_{1} (T_{2})A_{2} (T_{2}) \\ & \quad + \,8n^{6} {\uppi}^{6} \bar{A}_{2} (T_{2})A_{2} (T_{2})^{2} = 0, \\ \end{aligned}$$

(47)

where

$$\varGamma_{2} = \left({\frac{3}{2}n^{2} {\uppi}^{2} - \frac{4}{3}n^{4} {\uppi}^{4}} \right)(\omega_{f} - \omega_{b})^{2},\quad \varLambda_{3} = 4(\omega_{b} + Jn^{2} {\uppi}^{2} \omega_{b} - \varOmega).$$

(48)

For both the sub-critical and super-critical cases, slow-varying complex amplitudes A₁ and A₂ are expressed in polar form

$$A_{1} (T_{2}) = \frac{1}{2}a_{1} (T_{2})\text{e}^{{\text{i}\gamma_{1} (T_{2})}},\quad A_{2} (T_{2}) = \frac{1}{2}a_{2} (T_{2})\text{e}^{{\text{i}\gamma_{2} (T_{2})}},$$

(49)

where a₁(T₂), a₂(T₂) and γ₁(T₂), γ₂(T₂) are real amplitudes and phases of the response, respectively.

When $\varOmega < n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}$, substituting Eq. (49) into Eq. (44), and separating real part and imaginary part, the slow-varying amplitudes and phases can be obtained as

$$\begin{aligned} & \frac{1}{2}\varLambda_{1} D_{2} a_{1} (T_{2}) + c\omega_{f} a_{1} (T_{2}) = 0, \\ & \frac{1}{2}\varLambda_{2} D_{2} a_{2} (T_{2}) + c\omega_{b} a_{2} (T_{2}) = 0, \\ & - \,\frac{1}{2}\varLambda_{1} a_{1} (T_{2})D_{2} \gamma_{1} (T_{2}) + \frac{1}{8}(\varGamma_{1} + 16n^{6} {\uppi}^{6})a_{1} (T_{2})a_{2}^{2} (T_{2}) + n^{6} {\uppi}^{6} a_{1}^{3} (T_{2}) = 0, \\ & - \,\frac{1}{2}\varLambda_{2} a_{2} (T_{2})D_{2} \gamma_{2} (T_{2}) + \frac{1}{8}(\varGamma_{1} + 16n^{6} {\uppi}^{6})a_{2} (T_{2})a_{1}^{2} (T_{2}) + n^{6} {\uppi}^{6} a_{2}^{3} (T_{2}) = 0. \\ \end{aligned}$$

(50)

Substituting the first two equations of Eq. (50) for a₁(T₂) and a₂(T₂)

$$a_{1} (T_{2}) = C_{1} \text{e}^{{- 2c\omega_{f} T_{2}/\varLambda_{1}}},\quad a_{2} (T_{2}) = C_{2} \text{e}^{{- 2c\omega_{b} T_{2}/\varLambda_{2}}},$$

(51)

into the last two equations of Eq. (50), γ₁(T₂) and γ₂(T₂) can be obtained as

$$\begin{aligned} \gamma_{1} (T_{2}) & = - \,\frac{{C_{2}^{2} (\varGamma_{1} + 16n^{6} {\uppi}^{6})\varLambda_{2} \text{e}^{{- 4c\omega_{b} T_{2}/\varLambda_{2}}}}}{{16\varLambda_{1} c\omega_{b}}} - \frac{{C_{1}^{2} n^{2} {\uppi}^{2} \text{e}^{{- 4c\omega_{f} T_{2}/\varLambda_{1}}}}}{{2c\omega_{f}}} + C_{4}, \\ \gamma_{2} (T_{2}) & = - \,\frac{{C_{1}^{2} (\varGamma_{1} + 16n^{6} {\uppi}^{6})\varLambda_{1} \text{e}^{{- 4c\omega_{f} T_{2}/\varLambda_{1}}}}}{{16\varLambda_{2} c\omega_{f}}} - \frac{{C_{2}^{2} n^{2} {\uppi}^{2} \text{e}^{{- 4c\omega_{b} T_{2}/\varLambda_{2}}}}}{{2c\omega_{b}}} + C_{3}. \\ \end{aligned}$$

(52)

where C₁–C₄ are constants determined by initial conditions. Substituting Eqs. (51) and (52) into Eq. (49), and using the results into Eq. (37), we obtain the approximate analytical solutions

$$\begin{aligned} v(s,t) & = \sin (n{\uppi}s)[B_{f} \sin (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) - \text{i}B_{f} \cos (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) \\ & \quad - \,B_{b} \sin (B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3}) + \text{i}B_{b} \cos(B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3})], \\ w(s,t) & = \,\sin (n{\uppi}s)[B_{f} \cos (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) + \text{i}B_{f} \sin (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) \\ & \quad + B_{b} \cos (B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3}) + \text{i}B_{b} \sin(B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3})], \\ \end{aligned}$$

(53)

with

$$\begin{aligned} & B_{f} = C_{1} {\text{e}}^{{\frac{{- 2c\omega_{f} T_{0}}}{{\varLambda_{1}}}}},\quad B_{b} = C_{2} {\text{e}}^{{\frac{{- 2c\omega_{b} T_{0}}}{{\varLambda_{2}}}}}, \\ & B_{1} = - \,\frac{{(\varGamma_{1} + 16n^{6} {\uppi}^{6})\varLambda_{2}}}{{16\varLambda_{1} c\omega_{b}}},\quad B_{2} = - \,\frac{{n^{6} {\uppi}^{6}}}{{2c\omega_{f}}},\quad B_{3} = - \,\frac{{(\varGamma_{1} + 16n^{6} {\uppi}^{6})\varLambda_{1}}}{{16\varLambda_{2} c\omega_{f}}},\quad B_{4} = - \,\frac{{n^{6} {\uppi}^{6}}}{{2c\omega_{b}}}. \\ \end{aligned}$$

(54)

When $\varOmega > n^{2} {\uppi}^{2} \sqrt {\frac{{1 + \kappa/(1 + Z_{0}/Z)}}{{1 - Jn^{2} {\uppi}^{2}}}}$, similarly, the approximate analytical solutions can be obtained as

$$\begin{aligned} v(s,t) & = \sin (n{\uppi}s)[B_{f} \sin (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) - \text{i}B_{f} \cos (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) \\ & \quad +\,B_{b} \sin (B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3}) - \text{i}B_{b} \cos(B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3})], \\ w(s,t) & = \sin (n{\uppi}s)[B_{f} \cos (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) + \text{i}B_{f} \sin (B_{1} B_{b}^{2} + B_{2} B_{f}^{2} + \omega_{f} T_{0} + C_{4}) \\ & \quad +\,B_{b} \cos (B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3}) + \text{i}B_{b} \sin(B_{3} B_{f}^{2} + B_{4} B_{b}^{2} + \omega_{b} T_{0} + C_{3})], \\ \end{aligned}$$

(55)

where

$$\begin{aligned} & B_{f} = C_{1} {\text{e}}^{{\frac{{- 2c\omega_{f} T_{0}}}{{\varLambda_{1}}}}},\quad B_{b} = C_{2} {\text{e}}^{{\frac{{- 2c\omega_{b} T_{0}}}{{\varLambda_{3}}}}}, \\ & B_{1} = - \,\frac{{(\varGamma_{2} + 16n^{6} {\uppi}^{6})\varLambda_{3}}}{{16\varLambda_{1} c\omega_{b}}},\quad B_{2} = - \,\frac{{n^{6} {\uppi}^{6}}}{{2c\omega_{f}}},\quad B_{3} = - \,\frac{{(\varGamma_{2} + 16n^{6} {\uppi}^{6})\varLambda_{1}}}{{16\varLambda_{3} c\omega_{f}}},\quad B_{4} = - \,\frac{{n^{6} {\uppi}^{6}}}{{2c\omega_{b}}}. \\ \end{aligned}$$

(56)

4.1 Numerical analysis

In this subsection, the numerical simulation will be employed to validate the results by the method of multiple scales [49, 50]. The displacement time histories of the spinning piezoelectric beam based on the gyroscopically coupled non-linear system have been illustrated in Figs. 5 and 6 by both analytical and numerical simulation. The two figures share the same parameters J = 0.002, κ = 0.5, Z₀/Z = 10, and c = 0.005, where only the first mode is excited. An initial condition of v(0) = 0.01, w(0) = 0, $\dot{v}(0) = 0$, and $\dot{w}(0) = 0$ in the plane v is used in Fig. 5, by which responses occur in plane w due to the gyroscopic effect. Since the spinning speed is not high, Ω = 0.5, the results of two natural frequencies are close. Hence a beat phenomenon can be located. The displacements of both directions are gradually attenuated until zero because of damping. During the vibration process, the transfer of energy from one direction to another can locate the working mechanism of the piezoelectric vibratory gyroscope. Figure 6 shows the non-spinning case, Ω = 0.5: an initial displacement in the plane v is given, where there is no oscillation in plane w because of there is no gyroscope coupling, which is the key role to make the vibratory gyroscopes work.

Fig. 5

Time history for Ω = 0.5, J = 0.002, κ = 0.5, Z₀/Z = 10, and c = 0.005

Fig. 6

Time history for Ω = 0, J = 0.002, κ = 0.5, Z₀/Z = 10, and c = 0.005

4.2 Non-linear modal analysis

In this subsection, the modal motions will be discussed. Using the parameters J = 0.002, κ = 0.5, and Z₀/Z = ∞, the non-linear complex mode functions in Eqs. (53) and (55) based on the multiple scales method are shown in Fig. 7. The snapshots for different spinning cases (Ω = 5 and Ω = 15) in a period of the non-linear spinning piezoelectric beam for the first two orders modal motions are shown in Fig. 7. The modal motions are corresponding to the four typical points A_f,b, B_f,b, C_f,b, and D_f,b in Figs. 3 and 4. The first-order modal motions exhibited in Fig. 7a, e are all forward whirling in the sub-critical and supercritical regions, respectively. However, the first-order modal motion exhibited in Fig. 7c is backward whirling in the sub-critical region where the first-order modal motion exhibited in Fig. 7g is forward whirling in the supercritical region. The second-order modal motions of the spinning piezoelectric beam are forward whirling motions as presented in Fig. 7b, f where the second-order modal motions presented in Fig. 7d, h are backward whirling in the sub-critical and supercritical regions.

Fig. 7

Complex mode functions derived by the non-linear systems. a The first mode (ω_f) when Ω = 5, at A_f. b The second mode (ω_f) when Ω = 5, at C_f. c The first mode (ω_b) when Ω = 5, at A_b. d The second mode (ω_b) when Ω = 5, at C_b. e The first mode (ω_f) when Ω = 15, at B_f. f The second mode (ω_f) when Ω = 15, at D_f. g The first mode (ω_b) when Ω = 15, at B_b. h The second mode (ω_b) when Ω = 15, at D_b

4.3 Non-linear frequency analysis

It is found that the non-linear frequencies involve two parts in Eqs. (53) and (55). The first part is linear natural frequencies of constants ω_f and ω_b and the second part depends on the slow-varying amplitude $(C_{1} B_{b}^{2} + C_{2} B_{f}^{2})/T_{0}$ and $(C_{3} B_{f}^{2} + C_{4} B_{b}^{2})/T_{0}$. Therefore, the non-linear natural frequency is a function of J, c, κ, Z₀/Z, and Ω as well as time. Hence, the effect of rotary inertia J, electrical resistance Z₀/Z and spinning speed Ω on the non-linear natural frequencies can be discussed for a specified instant of time (for example T₀ = 1). We can make a definition regarding forward and backward non-linear frequency

$$\omega_{fnl} = C_{1} B_{b}^{2} + C_{2} B_{f}^{2} + \omega_{f},\omega_{bnl} = C_{3} B_{f}^{2} + C_{4} B_{b}^{2} + \omega_{b},$$

(57)

where C_i (i = 1–4) are coefficients which determined by initial conditions v(0) = 0.01, w(0) = 0, $\dot{v}(0) = 0$, and $\dot{w}(0) = 0 .$

The first order amplitude-dependent non-linear frequency is presented in Fig. 8 by using the parameters J = 0.002, κ = 0.5, c = 0.005, and Z₀/Z = 10. The dotted line represents linear frequencies, and the solid line represents non-linear frequencies. It is found that with an increase of the initial amplitudes, the non-linear natural frequencies increase. It is also found that with the increase of the spinning speed, the forward and backward non-linear frequencies all increase.

Fig. 8

Non-linear frequencies versus the amplitude (κ = 0.5, Z₀/Z = 10, c = 0.005, and J = 0.002)

In Figs. 9 and 10, ω_fnl and ω_bnl are plotted versus spinning speed Ω for different values of electrical resistance Z₀/Z by using the parameters J = 0.002, κ = 0.5, and c = 0.005. In Fig. 9, the first mode (n = 1) of the forward non-linear frequencies ω_fnl increase and the backward frequencies ω_bnl decrease first, then increase with the increase of spinning speed for all the values of Z₀/Z. In the local enlarged view, the reduction of electrical resistance causes the higher ω_fnl. It is seen that for ω_bnl, there exists a local minimum point, the reduction of electrical resistance (Z₀/Z = ∞, 10, and 5) causes the higher ω_bnl before the minimum point, but the reduction of Z₀/Z causes the lower ω_bnl after the minimum point. In Fig. 10, the second mode (n = 2) of ω_fnl increase and ω_bnl decrease for all the values of Z₀/Z. From all the figures, we can see the values of ω_fnl are larger than ω_bnl by using the same parameters.

Fig. 9

Non-linear frequencies versus spinning speed (n = 1, c = 0.005, κ = 0.5, and J = 0.002)

Fig. 10

Non-linear frequencies versus spinning speed (n = 2, c = 0.005, κ = 0.5, and J = 0.002)

The non-linear frequencies ω_fnl and ω_bnl of the first two modes as functions of spinning speed Ω for different rotary inertia J are shown in Figs. 11 and 12 by using the parameters Z₀/Z = 10, κ = 0.5, and c = 0.005. It is observed from Figs. 11 and 12 that the essential properties of curves are similar with Figs. 9 and 10 for different rotary inertia J. Figure 11 shows that the reduction of rotary inertia (J = 0.02, 0.002, and 0.0002) causes the higher ω_fnl of the first mode (n = 1). It is seen that for ω_bnl, there exists a local minimum point. Before the local minimum point, the reduction of J causes the higher ω_bnl from Ω = 0 to Ω = 5, and the reduction of J causes the lower ω_bnl from Ω = 5 to the minimum point. After the minimum point, the reduction of J causes the higher ω_bnl. The reduction of rotary inertia (J = 0.02, 0.002, and 0.0002) causes the higher ω_fnl of the second mode (n = 2) are shown in Fig. 12. It is found that for ω_bnl, there exists a cross-over point. Before the cross-over point, the reduction of J causes the higher ω_bnl from Ω = 0 to Ω = 20, and the reduction of J causes the lower ω_bnl from Ω = 20 to Ω = 25.

Fig. 11

Non-linear frequencies versus spinning speed (n = 1, c = 0.005, κ = 0.5, and Z₀/Z = 10)

Fig. 12

Non-linear frequencies versus spinning speed (n = 2, c = 0.005, κ = 0.5, and Z₀/Z = 10)

The relation of the linear and non-linear frequencies versus Z₀/Z are plotted in Figs. 13 and 14 for Ω = 1, 3 by using the parameters J = 0.002, κ = 0.5, and c = 0.005. The two figures illustrate that the linear and non-linear frequencies become further apart as the Ω increases. Moreover, the value of linear frequency (e.g. Ω = 1, ω_f) is lower than the value of non-linear frequency (e.g. Ω = 1, ω_fnl) due to the effect of geometric nonlinearities as depicted in Figs. 13 and 14. Further, Fig. 13 shows that the linear and non-linear frequencies vary rapidly according to the small electrical resistance and then become smoothly for the first mode (n = 1). Together with the dependence of the linear and non-linear frequencies on the spinning speed as shown in Figs. 3 and 9, respectively, the electrical resistance Z₀/Z dependence of non-linear frequencies further complicates the design of the piezoelectric gyroscopes. Figure 14 shows that the linear and non-linear frequencies vary more rapidly than that in Fig. 13 according to the small Z₀/Z and then become smoothly for the second mode (n = 2). The effect of Z₀/Z for ω_b and ω_bnl is greater than ω_f and ω_fnl, respectively.

Fig. 13

Linear and non-linear frequencies versus electrical resistance (n = 1, c = 0.005, κ = 0.5, and J = 0.002)

Fig. 14

Linear and non-linear frequencies versus electrical resistance (n = 2, c = 0.005, κ = 0.5, and J = 0.002)

Large vibration of flexible structures leads to high sensitivity of the gyroscopes. However, the non-linear effects should reconsidered in the engineering field of gyroscopes. The clear understanding of varying rules on non-linear frequencies and non-linear normal modes may provide possible optimizations in the vibrating beam gyroscope design, especially for the ones with very flexible structures.

5 Conclusions

The linear and non-linear free vibrations of a spinning piezoelectric beam are investigated by both analytical and numerical simulation. The additional piezoelectric coupling terms and symmetrical governing equations with non-linearities in curvature and inertia of a spinning piezoelectric beam are derived by using extended Hamilton principle and the transformation of two Euler angles. The non-linear frequencies and complex modes are obtained by the multiple scales method. The initial value responses are studied by the analytical method and then validated by numerical method. The main conclusions are highlighted as follows.

• 1. In the linear and non-linear free vibration analysis of a spinning piezoelectric beam, forward and backward frequencies are studied. The switch of the forward precession and backward precession of the gyroscopic system have been located.

• 2. The whirling motions of the non-linear complex modes have been illustrated.

• 3. The electrical resistance (including electromechanical coupling coefficient) should be considered in the field of the piezoelectric spinning beam. The rules of non-linear frequencies varying with electrical resistance, amplitude, and other parameters have been discussed in detail.

• 4. The investigations of non-linear frequencies and non-linear normal modes provide basic theories needed in the high flexible vibratory gyroscope design.