1 Introduction

Harvesting energy from ambient vibrations by using the direct piezoelectric effect has received significant attention over the last two decades [1,2,3]. This focus is due to the need for low-power consumption devices, such as micro-electromechanical systems and sensors [4]. Many review papers have summarized the literature of piezoelectric energy harvesting [5,6,7,8]. The most common configuration for piezoelectric energy harvesting has been either a unimorph or a bimorph piezoelectric cantilever beam. Many researchers have focused on the mathematical modeling of this harvester. A reliable mathematical model may allow studying different aspects of energy harvesting, predicting the electrical outputs, moreover, optimizing the harvester in order to obtain the maximum electrical output for a given input. The linear models of piezoelectric energy harvesters are available in many papers. For example, Erturk and Inman [3] presented a distributed parameter electromechanical model of cantilevered piezoelectric energy harvester with the Euler–Bernoulli beam assumptions. Closed-form expressions of the voltage, current, and power outputs, as well as the mechanical response were obtained under the base excitation. Some linear models have been validated experimentally and show good agreement between theory and experiment [9,10,11]. The study of Tang and Wang [12] presented a modified model of cantilevered piezoelectric energy harvester with tip mass offset and a dynamic magnifier by using the generalized Hamilton’s principle. The modified model was demonstrated by parametric studies. The results show that the harvesting power can be dramatically enhanced with proper selection of the design parameters of the dynamic magnifier and tip mass offset. However, these validations are very low levels of excitation and not necessarily valid in all applications. In practical application, it is likely that linear models of the energy harvester will be unable to predict accurately the resonance frequency, leading to inaccurate prediction for the performance of the harvester due to frequency shift. It is advisable to take into account the nonlinear behavior of energy harvesters in the design, particularly if the energy harvester is subjected to high levels of excitation. The paper by Daqaq et al. [13] identified the primary limitations associated with linear vibration harvesters and presented a critical review of recent research focused on the use of nonlinearity to improve the performance of vibration harvesters.

Fig. 1
figure 1

Configuration of the cantilevered piezoelectric beam for an energy harvester

Full size image

A work by Mahmoodi et al. [14,15,16] presented an analytical model of nonlinear vibration response for cantilevered piezoelectric beams. The Galerkin decomposition method was used to derive the equations of motion. The multiple scales method was utilized to obtain analytical solutions of the system. Also, Stanton et al. [17] studied the influence of piezoelectric material nonlinearities on the dynamic response of a geometrically linear piezoelectric energy harvester using a theoretical model and experimental validation. Work by Abdelkefi et al. [18] presented a nonlinear distributed-parameter model of cantilevered piezoelectric beam energy harvesters with tip mass under direct excitation. The presented model included geometric, inertia, and piezoelectric nonlinearities. The Galerkin decomposition method and the multiple scales method were used to determine analytical expressions of the harvester. In their study, Triplett and Quinn [19] investigated the effect of nonlinear piezoelectric coupling on a vibration energy harvester, which included mechanical damping, stiffness nonlinearities, and the nonlinear piezoelectric constitutive relationship. The response of the harvesting system was approximated using Poincare–Lindstedt perturbation analysis. Work by Neiss et al. [20] provided analytical solutions of the output power and bandwidth of nonlinear energy harvester based on a lumped-parameter model of cantilevered piezoelectric beam. The results were verified by numerical simulations. The stability of the simply supported piezoelectric laminated rectangular plate under simultaneous transverse and inplane excitations was studied by Mousa et al. [21]. The multiple scales method was used to achieve the second-order approximation. The work by Mahmoudi et al. [22] investigated the performance of a novel hybrid nonlinear vibration energy harvester based on piezoelectric and electromagnetic transductions. Furthermore, Friswell et al. [23] derived the electromechanical equations of nonlinear piezoelectric vibration energy harvesting from a vertical cantilever beam with tip mass. The presented equations were investigated using the method of numerical simulation and experimental validation. The bistable piezoelectric inertial generators, which can produce large-amplitude motions under ambient excitations, have attracted more attention of researchers [24,25,26,27,28,29]. Thus, Karami and Inman [26] presented a unified approximation method to study the performance of linear, softly nonlinear, and bi-stable nonlinear energy harvesters. Then Stanton et al. [27] used the harmonic balance method to investigate analytically the influence of parameter variations on the intrawell and interwell oscillations of bistable piezoelectric inertial generator. A mathematical model of the multi-stable magnetic attraction energy harvester, which was composed of a bimorph cantilever beam with soft magnetic tip and two external permanent magnets, was developed based on the nonlinear Euler–Bernoulli beam theory and linear piezoelectricity [28]. Based on arrays of coupled levitated magnets, Abed et al. [29] proposed a multi-modal vibration energy harvesting method. The presented differential equations of motion were solved using the harmonic balance method combined with the asymptotic numerical method.

The parametric resonance theory predicts that the vibration energy harvesters using parametric resonance will obtain significant performance enhancement. One of the key problems of parametric resonance is the presence of a certain initiation threshold, which must be overcome prior to reaching parametric resonance. Therefore, Daqaq et al. [30] studied the energy harvester of parametric excitation. In their approach, a lumped-parameter nonlinear model was presented to study the nonlinear dynamics of a parametrically excited cantilever-type harvester. Then Jia et al. [31,32,33,34] used a novel design and working mechanism in order to overcome the limitation of initiation threshold amplitude and reduce the shortcomings of a parametrically excited vibration energy harvester. The study by Abdelkefi et al. [35] presented a global nonlinear distributed-parameter model for a piezoelectric energy harvester under parametric excitation. Also, Bitar et al. [36] presented a discrete model for the collective dynamics of periodic nonlinear oscillators under simultaneous parametric and external excitations, which was suitable for several physical applications. The study by Chiba et al. [37] investigated the dynamic stability of a vertically standing cantilever beam under simultaneous horizontal and vertical excitations. To the best knowledge of the authors, few research has been reported for the nonlinear vibration response of a cantilevered piezoelectric beam under parametric and external excitations. In their work, Kacem et al. [38, 39] and Jallouli et al. [40] investigated the benefits and applications of the nonlinear resonator simultaneously subjected to external and parametric excitations.

In this paper, the nonlinear dynamics of a cantilevered piezoelectric beam is investigated under simultaneous parametric and external excitations. The beam is composed of a substrate and two piezoelectric layers and assumed as the Euler–Bernoulli model with inextensible deformation. A nonlinear distributed-parameter model of the cantilevered piezoelectric beam is developed by use of the generalized Hamilton principle. The derived model accounts for geometric nonlinearities, but neglects the material nonlinearities by assuming linear constitutive equations. The Galerkin decomposition method is employed to transform nonlinear partial differential equations of motion into a set of nonlinear ordinary differential equations in the time domain. We focus on the first mode of the beam. The harmonic balance method is used to obtain analytical solutions for the vertical displacement, output voltage, and power output amplitude. The influences of the damping, load resistance, and electro-mechanical coupling coefficient on the frequency–response curves are investigated.

2 Mathematical model of energy harvester system

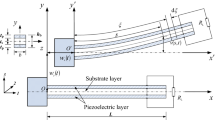
We consider a uniform bimorph cantilever beam with length L under its base horizontal and vertical excitations as shown in Fig. 1.

The beam is composed of a substrate and two piezoelectric layers. The piezoelectric layers are bounded by two in-plane electrodes of negligible thickness connected to the load resistance \(R_\mathrm{L} \). The beam is treated as the Euler–Bernoulli beam with length L, width b, and height \(h_\mathrm{b} =t_\mathrm{s} +2t_\mathrm{p} \), and shearing deformation and rotatory motion are neglected. \(t_\mathrm{s} \) is the thickness of the substrate layer and \(t_\mathrm{p}\) is the thickness of each piezoelectric layer. Setting the oxy as the inertia coordinate system, the clamped end displacements of the beam are \(w_{x} (t)\) and \(w_{y} (t)\) in the horizontal and vertical direction, respectively. The \({o'}{x'}{y'}\) is the base-fixed coordinate system (moving with the base). s is the coordinate along the middle plane of the beam. u(s, t) and v(s, t) are the displacements of the beam relative to the \({o'}{x'}{y'}\) coordinate system. u(s, t) is in the \({x'}\) direction and v(s, t) in the \({y'}\) direction. We assume that the beam is inextensible [35]

$$\begin{aligned} \left( {1+{u'}} \right) ^{2}+{v}^{\prime 2}=1, \end{aligned}$$
(1)

where prime \((^{\prime })\) indicates the derivative with respect to the arc length, s. Using Taylor’s expansion, there are

$$\begin{aligned} {u'}\approx -\frac{1}{2}{v}^{\prime 2}, \quad u=-\frac{1}{2}\int _{0}^{s} {{v}^{\prime 2}} \hbox {d}\eta . \end{aligned}$$
(2)

The constitutive relations of the substrate and piezoelectric layers of the beam can be expressed as

$$\begin{aligned} T_1^\mathrm{s}= & {} Y_\mathrm{s} S_1^\mathrm{s}, \nonumber \\ T_1^\mathrm{p}= & {} Y_\mathrm{p} \left( {S_1^\mathrm{p} -d_{31} E_3 } \right) , \nonumber \\ D_3= & {} d_{31} T_1^\mathrm{p} +\varepsilon _{33}^\mathrm{T} E_3, \end{aligned}$$
(3)

where Y is Young’s modulus, \(S_1 \) is the strain, \(T_1 \) is the stress, \(d_{31} \) is the piezoelectric strain constant, \(D_3 \) is the electric displacement and \(\varepsilon _{33}^\mathrm{T} \) is the permittivity and superscript T represents constant stress, subscript/superscript p and s stand for the piezoelectric and substrate layers, respectively; the 1 and 3 directions are coincident with the x and y directions, respectively (where 1 is the direction of axial strain and 3 is the direction of polarization). \(E_3 (t)=-V(t)/\hbox {(}2t_\mathrm{p} )\) is the electric field for series connection of piezoelectric layers. \(V(t)=R_\mathrm{L} \hbox {d}q/\hbox {d}t\) is the electric voltage. q is the electric charge.

In what follows, a nonlinear distributed parameter mathematical model of cantilevered piezoelectric vibration energy harvesting system will be derived by using the generalized Hamilton variational principle. Considering the inextensible beam condition in Eq. (1) and the Lagrange’s multiplier \(\lambda \), the modified energy functional can be expressed as

$$\begin{aligned} \varPi =T-U_\mathrm{e} +W_\mathrm{e} +\int _{0}^{L} {\lambda [1-{v'}^{2}} -(1+{u'})^{2}]\hbox {d}s, \end{aligned}$$
(4)

where T is the kinetic energy, \(U_\mathrm{e} \) is the potential energy, \(W_\mathrm{e} \) is the electrical energy.

The kinetic energy of the beam is

$$\begin{aligned} T&=\frac{1}{2}\int _{0}^{L} m \left\{ \left[ {\left( {\dot{v}(s,t)+\dot{w}_{y} (t)} \right) } \right] ^{2}\right. \nonumber \\&\quad \ +\left. \left[ {\left( {\dot{u}(s,t)+\dot{w}_{x} (t)} \right) } \right] ^{2} \right\} \hbox {d}s, \end{aligned}$$
(5)

where dot (\(\cdot \)) indicates the derivative with respect to time, \(t, m=2\rho _\mathrm{p} t_\mathrm{p} b+\rho _\mathrm{s} t_\mathrm{s} b, \rho _\mathrm{p} \) and \(\rho _\mathrm{s} \) are the density of the piezoelectric and substrate layers, respectively.

The total potential energy of the substrate and piezoelectric layers is

$$\begin{aligned} U_\mathrm{e} =\frac{1}{2}\int _{V_\mathrm{s} } {T_1^\mathrm{s} } S_1^\mathrm{s} \hbox {d}V_\mathrm{s} +\frac{1}{2}\int _{V_\mathrm{p} } {T_1^\mathrm{p} } S_1^\mathrm{p} \hbox {d}V_\mathrm{p}, \end{aligned}$$
(6)

where \(V_\mathrm{s} \) and \(V_\mathrm{p} \) are the volumes of the substrate and piezoelectric layers, respectively.

Considering the geometric nonlinearities, the strain of the beam can be expressed as follows [35]

$$\begin{aligned} S_1^\mathrm{s} =S_1^\mathrm{p} =-y\left( {{v''}+\frac{1}{2}{v''}{v}^{\prime 2}} \right) . \end{aligned}$$
(7)

Substituting Eqs. (3) and (7) into Eq. (6), we obtained

$$\begin{aligned} U_\mathrm{e}= & {} \frac{1}{2}\int _{0}^{L} \left\{ YI\left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] ^{2}\right. \nonumber \\&\left. -\,Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) {v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) \frac{\hbox {d}q}{\hbox {d}t} \right\} \hbox {d}s, \end{aligned}$$
(8)

where \(YI=Y_\mathrm{s} I_\mathrm{s} +\frac{2}{3}Y_\mathrm{p} b\left( {3h^{2}t_\mathrm{p} +3ht_\mathrm{p} ^{2}+t_\mathrm{p} ^{3}} \right) , Y_\mathrm{s} I_\mathrm{s} \) is the bending stiffness of the substrate layer, \(h=t_\mathrm{s} /2\).

The electric energy of the piezoelectric layers is given by

$$\begin{aligned} W_\mathrm{e} =\frac{1}{2}\int _{V_\mathrm{p} } {E_3 } D_3 \hbox {d}V_\mathrm{p}. \end{aligned}$$
(9)

The permittivity component at constant strain is replaced by the permittivity component at constant stress. The electric field is replaced by the electric charge. There are

$$\begin{aligned} \varepsilon _{33}^\mathrm{S} =\varepsilon _{33}^\mathrm{T} -d_{31}^2 Y_\mathrm{p},\quad E_3 =-\frac{R_\mathrm{L} }{2t_\mathrm{p} }\frac{\hbox {d}q}{\hbox {d}t}. \end{aligned}$$
(10)

Substituting Eqs. (3) and (10) into Eq. (9), the following expression is obtained

$$\begin{aligned} W_\mathrm{e}= & {} \frac{1}{2}Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) \int _{0}^{L} {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \frac{\hbox {d}q}{\hbox {d}t}\hbox {d}s \nonumber \\&+\,\frac{1}{2}bL\varepsilon _{33}^\mathrm{S} \left( {\frac{R_\mathrm{L}^2 }{2t_\mathrm{p} }} \right) \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) ^{2}. \end{aligned}$$
(11)

The generalized Hamilton variational principle of the electromechanical coupling beam can be expressed as

$$\begin{aligned}&\delta \int _{t_0 }^{t_1 } \left\{ \left( {T-U_\mathrm{e} +W_\mathrm{e} +W} \right) \right. \nonumber \\&\quad \left. +\int _{0}^{L} {\lambda \left[ {1-{v}^{\prime 2}-(1+{u'})^{2}} \right] } \hbox {d}s \right\} \hbox {d}t=0, \nonumber \\&\delta u(x,t)=\delta v(x,t)=0,\nonumber \\&\delta q(t)=0,\quad 0\leqslant x\leqslant L, \ t=t_0, t_1, \end{aligned}$$
(12)

where W is the electrically extracted work and the work done by the damping force. \(\delta W\) is given by

$$\begin{aligned} \delta W=-\int _{0}^{L} c \dot{v}\,\delta v\hbox {d}s-R_\mathrm{L} \frac{\hbox {d}q}{\hbox {d}t}\delta q, \end{aligned}$$
(13)

where c is linear viscous air damping coefficient.

The variations of the kinetic energy, the potential energy, and the electrical energy can be expressed as

$$\begin{aligned}&\delta \int _{t_0 }^{t_1 } T \hbox {d}t\nonumber \\&\quad =-\,m\int _{t_0 }^{t_1 } {\int _{0}^L {\left\{ {(\ddot{v}+\ddot{w}_{y} )\delta v+(\ddot{u}+\ddot{w}_{x} )\delta u} \right\} \hbox {d}s\hbox {d}t} }, \end{aligned}$$
(14)
$$\begin{aligned}&\delta \int _{t_0 }^{t_1 } {U_\mathrm{e} \hbox {d}t}\nonumber \\&\quad =\int _{t_0 }^{t_1 } {\int _0^L {YI\left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] \delta \left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] } \hbox {d}s\hbox {d}t} \nonumber \\&\qquad -\,\frac{1}{2}Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) \int _{t_0 }^{t_1 } {\int _0^L {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) \delta \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) } \hbox {d}s} \hbox {d}t \nonumber \\&\qquad -\,\frac{1}{2}Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) \int _{t_0 }^{t_1 } \int _0^L \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) \left[ {H\left( s \right) -H\left( {s-L} \right) } \right] \delta \nonumber \\&\qquad \times \left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] \hbox {d}s\hbox {d}t, \end{aligned}$$
(15)
$$\begin{aligned}&\delta \int _{t_0 }^{t_1 } {W_\mathrm{e} \hbox {d}t}\nonumber \\&\quad =\frac{1}{2}Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) \int _{t_0 }^{t_1 } {\int _0^L {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) \delta \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) } \hbox {d}s} \hbox {d}t \nonumber \\&\qquad \ +\,\,\frac{1}{2}Y_\mathrm{p} bd_{31} R_\mathrm{L} \left( {h+\frac{t_\mathrm{p} }{2}} \right) \int _{t_0 }^{t_1 } \int _0^L \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) \left[ {H\left( s \right) -H\left( {s-L} \right) } \right] \delta \nonumber \\&\qquad \times \,\left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] \hbox {d}s\hbox {d}t \nonumber \\&\qquad +\,\,bL\varepsilon _{33}^\mathrm{S} \left( {\frac{R_\mathrm{L}^2 }{2t_\mathrm{p} }} \right) \int _{t_0 }^{t_1 } {\left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) \delta \left( {\frac{\hbox {d}q}{\hbox {d}t}} \right) \hbox {d}t}. \end{aligned}$$
(16)

In Eqs. (15) and (16), H(s) is the Heaviside step function which is related to the Dirac delta function. They have the following relation

$$\begin{aligned}&\frac{\hbox {d}H(s)}{\hbox {d}s}=\delta (s), \nonumber \\&\int _{-\infty }^\infty {\frac{\hbox {d}^{n}\delta (s-s_0 )}{\hbox {d}s^{n}}} f(s)\hbox {d}s =(-1)^{n}\frac{\hbox {d}f^{n}(s_0 )}{\hbox {d}x^{n}}. \end{aligned}$$
(17)

Applying Eq. (10) and the generalized Hamilton principle of Eq. (12), performing a series of variational manipulations and taking up to the cubic order of v, the governing differential equations of motion can be obtained as follows

$$\begin{aligned}&m[v+w_{y} ]_{,tt} +cv_{,t} \nonumber \\&\quad \quad +YI\left( {{{v}''''}+{v}'^{2}{{v}''''}+4{v'}{v''}{v'''}+{v''}^{3}} \right) \nonumber \\&\qquad +\,\left[ {{v''}(L-s)-{v'}} \right] mw_{{x},tt} \nonumber \\&\qquad +\,\frac{1}{2}m\left[ {{v'}\int _{0}^{s} {\left( {{v}^{\prime 2}} \right) _{,tt} \hbox {d}\eta } -{v}''\int _{s}^{L} {\int _{0}^{\xi } {\left( {{v}^{\prime 2}} \right) _{,tt} \hbox {d}\eta \hbox {d}\xi } } } \right] \nonumber \\&\qquad -\,\alpha V\left\{ \left( 1+\frac{1}{2}{v}^{\prime 2}\right) \left[ {\frac{\hbox {d}\delta (s)}{\hbox {d}s}-\frac{\hbox {d}\delta (s-L)}{\hbox {d}s}} \right] \right. \nonumber \\&\qquad \left. +\,{v''}{v'}\left[ {\delta \left( s \right) -\delta \left( {s-L} \right) } \right] \right\} =0, \end{aligned}$$
(18)
$$\begin{aligned}&\alpha \int _{0}^{L} {\left[ {{v''}\left( {1+\frac{1}{2}{v}^{\prime 2}} \right) } \right] } _{,t} \hbox {d}s+C_\mathrm{p} V_{,t} +\frac{V}{R_\mathrm{L} }=0, \end{aligned}$$
(19)

where \(\alpha =Y_\mathrm{p} bd_{31} \left( {h+\frac{t_\mathrm{p} }{2}} \right) , \bar{{C}}_\mathrm{p} =\frac{b\varepsilon _{33}^\mathrm{S} }{2t_\mathrm{p} },C_\mathrm{p} =\bar{{C}}_\mathrm{p} L\). \(\alpha \) is the electromechanical coupling coefficient. \(C_\mathrm{p}\) is the capacitance of the piezoelectric layers. The above equations are a mathematical model of nonlinear distributed-parameter cantilevered piezoelectric energy harvesting system under simultaneous parametric and external excitations. The horizontal external excitation is transformed into parametric excitation. By removing the nonlinear terms and the base horizontal excitation, the direct excited linear model is recovered [3]. Without considering electromechanical coupling, Eq. (18) is similar to the governing equation of motion of the slender beam presented by Chiba et al. [37].

For the purpose of generality, the following dimensionless quantities are introduced into Eqs. (18) and (19)

$$\begin{aligned}&\bar{{s}}=s/L,\quad \bar{{\xi }}=\xi /L,\quad \bar{{\eta }}=\eta /L,\quad \bar{{v}}=v/L,\nonumber \\&\bar{{w}}_{x} =w_{x} /L,\quad \bar{{w}}_{y} =w_{y} /L, \nonumber \\&\omega _0 =\sqrt{YI/mL^{4}},\quad \tau =\omega _0 t,\quad \bar{{c}}=c/(m\omega _0 ),\nonumber \\&\omega _\mathrm{v} =\varOmega _\mathrm{v} /\omega _0,\quad \omega _\mathrm{h} =\varOmega _\mathrm{h} /\omega _0, \nonumber \\&V=\omega _0 L\sqrt{m/\bar{{C}}_\mathrm{p} }\bar{{V}},\quad \alpha =\omega _0 L^{2}\sqrt{m\bar{{C}}_\mathrm{p} }\bar{{\alpha }}, \end{aligned}$$
(20)

where \(\varOmega _\mathrm{h}\) and \(\varOmega _\mathrm{v}\) are the horizontal and vertical excited frequencies, respectively.

Equations (18) and (19) can be represented in non-dimensional form as

$$\begin{aligned}&\ddot{\bar{v}}+\bar{c}\dot{\bar{v}}+{\bar{v}''''}+\bar{v}'^{2} {\bar{v}''''}+4{\bar{v}'}{\bar{v}''}{\bar{v}'''}+\bar{v}''^{3} \nonumber \\&\quad +\,\left[ {{\bar{{v}}}''\left( {1-\bar{{s}}} \right) -{\bar{{v}}}'} \right] \ddot{\bar{{w}}}_{x} +\,{\bar{{v}}}'\int _0^{\bar{{s}}} {\left( \dot{{\bar{v}}}' {\dot{\bar{v}}'}+{\bar{{v}}}'\ddot{{\bar{{v}}}}'\right) \hbox {d}\bar{{\eta }}}- {\bar{{v}}}''\nonumber \\&\int _{\bar{{s}}}^1 {\left[ \int _0^{\bar{{\xi }}} {\left( \dot{{\bar{{v}}}}'{\dot{\bar{v}}'}+{\bar{{v}}}'\ddot{{\bar{{v}}}}'\right) \hbox {d}\bar{{\eta }}} \right] } \hbox {d}\bar{{\xi }} \end{aligned}$$
(21)
$$\begin{aligned}&\quad -\,\bar{{\alpha }}\bar{{V}}\left\{ \left( {1+\frac{1}{2}{\bar{{v}}}'^{2}} \right) \left[ {\frac{\hbox {d}\delta (\bar{{s}})}{\hbox {d}\bar{{s}}}-\frac{\hbox {d}\delta (\bar{{s}}-1)}{\hbox {d}\bar{{s}}}} \right] \nonumber \right. \\&\quad \left. +\,{\bar{{v}}}''{\bar{{v}}}'\left[ {\delta (\bar{{s}})-\delta (\bar{{s}}-1)} \right] \right\} =-\ddot{\bar{{w}}}_{y},\nonumber \\&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\int _0^1 \left[ {\dot{{\bar{{v}}}}''+\frac{1}{2}{\bar{{v}}}'^{2}\dot{{\bar{{v}}}}''+{\bar{{v}}}''{\bar{{v}}}'{\dot{\bar{{v}}}'}} \right] \hbox {d}\bar{{s}}=0, \end{aligned}$$
(22)

where \(\mu =\frac{1}{R_\mathrm{L} \omega _0 C_\mathrm{p} }\), (\(\cdot \)) indicates the derivative with respect to the time variable, \(\tau \).

3 Reduced-order model

To develop a reduced-order model of cantilevered piezoelectric energy harvesting system, the modal Galerkin decomposition method is used to transform the nonlinear partial differential equations (21) and (22) into a set of coupled second order nonlinear ordinary differential equations. The transverse deflection \(\bar{{v}}(\bar{{s}},\tau )\) is decomposed into a summation of N generalized displacement amplitude \(A_m (\tau )\) and orthogonal basis function \(X_m (\bar{{s}})\) as follows

$$\begin{aligned} \bar{{v}}(\bar{{s}},\tau )=\sum _{m=1}^N {A_m \left( \tau \right) X_m \left( {\bar{{s}}} \right) }. \end{aligned}$$
(23)

The orthogonal basis functions utilized in this analysis are the linear mode shape functions for the Euler–Bernoulli beam with fixed-free boundary conditions. The normalized mode shape function is given as follows:

$$\begin{aligned}&X_m \left( {\bar{{s}}} \right) =\cosh \bar{{\beta }}_m \bar{{s}}-\cos \bar{{\beta }}_m \bar{{s}}+\,\bar{{\alpha }}_m \left( {\sin \bar{{\beta }}_m \bar{{s}}-\sinh \bar{{\beta }}_m \bar{{s}}} \right) ,\nonumber \\\end{aligned}$$
(24)
$$\begin{aligned}&\bar{{\alpha }}_m =\frac{\cos \bar{{\beta }}_m +\cosh \bar{{\beta }}_m }{\sin \bar{{\beta }}_m +\sinh \bar{{\beta }}_m }, \end{aligned}$$
(25)

where \(\bar{{\beta }}_m^2 =\bar{{\omega }}_m , \bar{{\omega }}_m =\omega _m /\omega _0 , \omega _m\) is the mth eigenfrequency of a cantilever beam, \(\bar{{\beta }}_m \) satisfies the following frequency equation

$$\begin{aligned} 1+\cosh \bar{{\beta }}_m \cos \bar{{\beta }}_m =0. \end{aligned}$$
(26)

Inserting Eq. (23) into Eqs. (21) and (22), multiplying Eq. (21) by \(X_n (\bar{{s}})\), considering the orthogonality conditions of the mode shape functions and subsequently integrating over the length of the beam, we yield a set of nonlinear ordinary differential equations of motion (for \(m=1,2,\ldots ,N)\).

$$\begin{aligned}&\ddot{A}_m +2\tilde{c}\dot{A}_m +\bar{{\omega }}_m^2 A_m +\sum _{m=1}^N {2\bar{{\sigma }}_{nm} \ddot{\bar{{w}}}_{x} } A_m \nonumber \\&\quad \ +\,\sum _{m,k,\ell =1}^N {\beta _{nmk\ell } } A_m A_k A_\ell \nonumber \\&\quad \ +\sum _{m,k,\ell =1}^N {\kappa _{nmk\ell } } A_m (\dot{A}_k \dot{A}_\ell +A_k \ddot{A}_\ell )\nonumber \\&\quad \ -\,\bar{{\alpha }}\left( {\zeta _{nm} +\sum _{m,k=1}^N {\gamma _{nmk} A_m A_k } } \right) \bar{{V}}=-\bar{{\lambda }}_{nm} \ddot{\bar{{w}}}_{y}, \end{aligned}$$
(27)
$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}\nonumber \\&\quad \ +\,\,\bar{{\alpha }}\sum _{m=1}^N {\left( {\eta _m +\sum _{k,\ell =1}^N {\chi _{mk\ell } A_k A_\ell } } \right) } \dot{A}_m =0, \end{aligned}$$
(28)

where

$$\begin{aligned}&\tilde{c}=\frac{1}{2}\bar{{c}}, \ \bar{{\sigma }}_{nm} =\frac{{b}_{3nm}-{b}_{4nm}-b_{6nm}}{2b_{1nn}}, \nonumber \\&\beta _{nmk\ell }=\frac{b_{2nmk\ell }}{b_{1nn}}, \ \kappa _{nmk\ell } =\frac{b_{7nmk\ell }-b_{5nmk\ell }}{b_{1nn}}, \nonumber \\&\zeta _{nm} =\frac{b_{9n}}{b_{1nn}}, \ \gamma _{nmk} =\frac{{b}_{10nmk}-2b_{11nmk}}{2b_{1nn}}, \nonumber \\&\bar{{\lambda }}_{nn}=\frac{b_{8n} }{b_{1nn} }, \ \eta _m =b_{12m}, \ \chi _{mk\ell }=\frac{3}{2}b_{13mk\ell } , \nonumber \\&a_{1k\ell } (\bar{{s}})=\sum _{k,\ell =1}^N {\int _{\bar{{s}}}^{1} {\left( {\int _{0}^{\bar{{\xi }}} {{X}'_k {X}'_\ell \hbox {d}\bar{{\eta }}} } \right) } } \hbox {d}\bar{{\xi }},\nonumber \\&a_{2k\ell } (\bar{{s}})=\sum _{k,\ell =1}^N {\int _{0}^{\bar{{s}}} {{X}'_k {X}'_\ell \hbox {d}\bar{{\eta }}} } , \nonumber \\&b_{1nm} =\int _0^{1} {X_m } X_n \hbox {d}\bar{{s}}, \nonumber \\&b_{2nmk\ell }=\!\!\int _{0}^{1} \!\!\left( \bar{{\beta }}_\ell ^4 X_m {X}'_k {X}'_\ell +4 {X}'_m {X}''_k {X}'''_\ell +{X}''_m {X}''_k {X}''_\ell \right) X_n \hbox {d}\bar{{s}}, \nonumber \\&b_{3nm} =\int _{0}^{1} {{X}''_m } X_n \hbox {d}\bar{{s}}, \nonumber \\&b_{4nm}=\int _{0}^{1} {\bar{{s}}{X}''_m } X_n \hbox {d}\bar{{s}}, \ b_{5nmk\ell } =\int _{0}^{1} {a_{1k\ell } } (\bar{{s}}){X}''_m X_n \hbox {d}\bar{{s}}, \nonumber \\&b_{6nm} =\int _{0}^{1} {{X}'_m } X_n \hbox {d}\bar{{s}}, \ b_{7nmk\ell } =\int _{0}^{1} {a_{2k\ell } } (\bar{{s}}){X}'_m X_n \hbox {d}\bar{{s}}, \nonumber \\&b_{8n}=\int _{0}^{1} {X_n } \hbox {d}\bar{{s}}, \ b_{9n}=\left. {\frac{\hbox {d}X_n (\bar{{s}})}{\hbox {d}\bar{{s}}}} \right| _{\bar{{s}}=1} \nonumber \\&b_{10nmk} =\left. {\frac{\hbox {d}\left[ {{X}'_m (\bar{{s}}){X}'_k (\bar{{s}})X_n (\bar{{s}})} \right] }{\hbox {d}\bar{{s}}}} \right| _{\bar{{s}}=1} \nonumber \\&b_{11nmk}={X}'_m (1){X}''_k (1)X_n (1), \nonumber \\&b_{12m} =\int _{0}^{1} {{X}''_m } \hbox {d}\bar{{s}}, \ b_{13mk\ell } =\int _{0}^{1} {{X}'_m } {X}'_k {X}''_\ell \hbox {d}\bar{{s}}. \end{aligned}$$
(29)

Assuming the excitation frequency is very close to the nth modal frequency, we focus on the nth vibration mode of the beam and neglect the interactions with any of the other modes. Considering only the nth term of the orthogonal basis functions and \(m=k=\ell =n\), there are

$$\begin{aligned}&b_{1nn} =\int _0^1 {X_n } X_n \hbox {d}\bar{{s}}=1,\nonumber \\&b_{12n} =\int _0^1 {{X}''_n \hbox {d}\bar{{s}}=\left. {\frac{\hbox {d}X_n (\bar{{s}})}{\hbox {d}\bar{{s}}}} \right| } _{\bar{{s}}=1} \nonumber \\&=b_{9n} , \nonumber \\&b_{13nnn} =\int _0^1 {{X}'_n {X}'_n {X}''_n } \hbox {d}\bar{{s}}=\frac{1}{3}{X'}_n^3 (1), \nonumber \\&b_{10nnn} =\left. \frac{\hbox {d}\left[ {{X'}_n (\bar{{s}}){X'}_n (\bar{{s}})X_n (\bar{{s}})} \right] }{\hbox {d}\bar{{s}}} \right| _{\bar{{s}}=1} \nonumber \\&=2X_n (1){X'}_n (1){X''}_n (1)+{X'}_n^3 (1), \nonumber \\&\eta _n =\zeta _{nn} ,\quad \chi _{nnn} =\gamma _{nnn} . \end{aligned}$$
(30)

For the nth mode, Eqs. (27) and (28) can be rewritten as follows

$$\begin{aligned}&\ddot{A}_n +2\tilde{c}\dot{A}_n +\left( {\bar{{\omega }}_n^2 +2\bar{{\sigma }}_n \ddot{\bar{{w}}}_{x} } \right) A_n +\beta _n A_n^3 \nonumber \\&\quad +\,\kappa _n \left( {\dot{A}_n^2 +A_n \ddot{A}_n } \right) A_n -\bar{{\alpha }}\left( {\zeta _n +\gamma _n A_n^2 } \right) \bar{{V}}=-\,\bar{{\lambda }}_n \ddot{\bar{{w}}}_{y},\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\left( {\zeta _n +\gamma _n A_n^2 } \right) \dot{A}_n =0, \end{aligned}$$
(32)

where \(\bar{{\sigma }}_n =\bar{{\sigma }}_{nn},\beta _n =\beta _{nnnn},\kappa _n =\kappa _{nnnn},\gamma _n =\gamma _{nnn} ,\bar{{\lambda }}_n =\bar{{\lambda }}_{nn},\zeta _n =\zeta _{nn} \).

The term \(\beta _n A_n^3 \) is used to describe cubic geometric nonlinearity, \(\kappa _n (\dot{A}_n^2 +A_n \ddot{A}_n )A_n \) represents inertia nonlinearity. \(2\bar{{\sigma }}_n \ddot{\bar{{w}}}_{x} \) and \(\bar{{\lambda }}_n \ddot{\bar{{w}}}_{y} \) are parametric and external excitations, respectively. Equation (31) is the Mathieu equation with non-linear stiffness and inertia terms as well as with the external force term and voltage. It describes the nonlinear dynamics of cantilevered piezoelectric beams of a single mode approximation under simultaneous parametric and external excitations. Equations (31) and (32) are similar to the nonlinear lumped parameter model presented by Daqaq et al. [30]. But the electromechanical coupling terms include nonlinearity, which is different from the nonlinear lumped-parameter model.

4 Harmonic balance analysis

The harmonic balance method has been extensively used to analyze periodic solutions of nonlinear differential equations. Using Fourier series, the nonlinear differential equations in the time variables are transformed into a set of nonlinear algebraic equations in the frequency variables. The number of Fourier series terms dictates the accuracy of the intended solution. The resulting algebraic equations are solved iteratively. When nonlinearities are complicated, the derivation of the algebraic system becomes very cumbersome. Works by Souayeh and Kacem [41], Kacem et al. [42], and Jallouli et al. [43] used the harmonic balance combined with the asymptotic numerical method to analyze the nonlinear problem of resonant sensors at large amplitudes. For a low level of nonlinearity, a single-term harmonic balance solution is sufficient to approximate the steady state response to harmonic excitation. Stanton et al. [27] applied the harmonic balance method to analyze the existence, stability, and influence of parameter variations of bistable piezoelectric inertial generator.

For an analytical solution of the presented problem, harmonic excitations are considered

$$\begin{aligned} \ddot{\bar{{w}}}_{x} \left( \tau \right) =\varepsilon \cos \omega _\mathrm{h} \tau , \quad \ddot{\bar{{w}}}_{y} \left( \tau \right) =\delta \cos \left( {\omega _\mathrm{v} \tau +\psi } \right) , \end{aligned}$$
(33)

where \(\varepsilon \) and \(\delta \) are the non-dimensional amplitudes, respectively.

In the present analysis, assuming that the first bending mode of the beam should be the dominant mode of the system, only one mode (\(n=1\)) is retained and the other modes are neglected. A single-term harmonic balance solution is sufficient to approximate the steady state response to harmonic excitation for a low level of nonlinearity.

In what follows, the subscripts on the different variables will be omitted for the sake of simplicity. Using Eq. (33), Eqs. (31) and (32) can be rewritten as follows

$$\begin{aligned}&\ddot{A}+2\tilde{c}\dot{A}+\left( {\bar{{\omega }}^{2}+2\bar{{\varepsilon }}\cos \omega _\mathrm{h} \tau } \right) A+\beta A^{3} \nonumber \\&\qquad \ \ +\,\kappa \left( {\dot{A}^{2}+A\ddot{A}} \right) A-\bar{{\alpha }}\left( {\zeta +\gamma A^{2}} \right) \bar{{V}}\nonumber \\&\quad =\ -\,\bar{{\delta }}\cos (\omega _\mathrm{v} \tau +\psi ), \end{aligned}$$
(34)
$$\begin{aligned}&\dot{\bar{{V}}}+\mu \bar{{V}}+\bar{{\alpha }}\left( {\zeta +\gamma A^{2}} \right) \dot{A}=0, \end{aligned}$$
(35)

where \(\bar{{\varepsilon }}=\bar{{\sigma }}\varepsilon ,\bar{{\delta }}=\bar{{\lambda }}\delta \).

In order to achieve parametric resonance, it has been shown that the first-order (principal) parametric resonance can be attained when the parametric excited frequency is twice the natural frequency [30, 31, 37]. Introducing the non-dimensional excitation frequency \(\omega , \omega _\mathrm{h} \), and \(\omega _\mathrm{v} \) are presented as

$$\begin{aligned} \omega _\mathrm{h} =2\omega , \quad \omega _\mathrm{v} =\omega . \end{aligned}$$
(36)

The steady-state displacement and voltage responses are assumed as

$$\begin{aligned}&A(\tau )=a_1 \sin \omega \tau +b_1 \cos \omega \tau =\bar{{w}}\cos \left( {\omega \tau +\varphi _1 } \right) , \nonumber \\&\bar{{w}}=\sqrt{a_1^2 +b_1^2 }, \end{aligned}$$
(37)
$$\begin{aligned}&\bar{{V}}(\tau )=a_2 \sin \omega \tau +b_2 \cos \omega \tau =\bar{{V}}\cos \left( {\omega \tau +\varphi _2 } \right) , \nonumber \\&\bar{{V}}=\sqrt{a_2^2 +b_2^2 }. \end{aligned}$$
(38)

Substituting Eqs. (37) and (38) into Eqs. (34) and (35), and applying the harmonic balance method, the resulting algebraic equations can be written as

$$\begin{aligned}&{{\begin{array}{l} a_1 \left( {Z+\bar{{\varepsilon }}} \right) +2\tilde{c}\omega b_1 +\bar{{\alpha }}\zeta a_2 \\ \quad +\,\bar{{\alpha }}\gamma \left( {\frac{3}{4}a_2 a_1^2 +\frac{1}{4}a_2 b_1^2 +\frac{1}{2}a_1 b_1 b_2} \right) =-\,\bar{{\delta }}\sin \psi , \\ b_1 \left( {Z-\bar{{\varepsilon }}} \right) -2\tilde{c}\omega a_1 +\bar{{\alpha }}\zeta b_2\\ \quad +\,\bar{{\alpha }}\gamma \left( {\frac{3}{4}b_2 b_1^2 +\frac{1}{4}b_2 a_1^2 +\frac{1}{2}a_1 a_2 b_1 } \right) =\bar{{\delta }}\cos \psi , \\ \end{array} }} \end{aligned}$$
(39)
$$\begin{aligned}&{\begin{array}{l} \omega b_2 -\mu a_2 +\omega \bar{{\alpha }}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) b_1 =0, \\ \omega a_2 +\mu b_2 +\omega \bar{{\alpha }}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) a_1 =0, \\ \end{array}} \end{aligned}$$
(40)

where

$$\begin{aligned} Z=\left( {1+\frac{1}{2}\kappa \bar{{w}}^{2}} \right) \omega ^{2}-\bar{{\omega }}^{2}-\frac{3}{4}\beta \bar{{w}}^{2}. \end{aligned}$$
(41)

Solutions of Eq. (40) can be obtained as follows

$$\begin{aligned} {\begin{array}{l} a_2 =\frac{\bar{{\alpha }}\omega }{\mu ^{2}+\omega ^{2}}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) \left( {\mu b_1 -\omega a_1 } \right) , \\ b_2 =-\frac{\bar{{\alpha }}\omega }{\mu ^{2}+\omega ^{2}}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) \left( {\omega b_1 +\mu a_1 } \right) \hbox {.} \\ \end{array}} \end{aligned}$$
(42)

Substituting Eq. (42) into Eq. (39), Eq. (39) can be rewritten as

$$\begin{aligned} {{\begin{array}{l} {\varDelta _\mathrm{a} a_1 +\varDelta _\mathrm{b} b_1 =-\,\bar{{\delta }}\sin \psi ,} \\ {\varDelta _\mathrm{c} b_1 -\varDelta _\mathrm{b} a_1 =\bar{{\delta }}\cos \psi ,} \\ \end{array} }} \end{aligned}$$
(43)

where

$$\begin{aligned}&\varDelta _1 =Z-\omega \tilde{\zeta }-\frac{3}{4}\omega \tilde{\gamma },\quad \varDelta _\mathrm{a} =\varDelta _1 +\bar{{\varepsilon }}, \nonumber \\&\varDelta _\mathrm{b} =2\tilde{c}\omega +\mu \tilde{\zeta }+\frac{1}{4}\mu \tilde{\gamma },\quad \varDelta _\mathrm{c} =\varDelta _1 -\bar{{\varepsilon }}, \nonumber \\&\tilde{\zeta }=\zeta \frac{\bar{{\alpha }}^{2}\omega }{\mu ^{2}+\omega ^{2}}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) , \nonumber \\&\tilde{\gamma }=\gamma \frac{\bar{{\alpha }}^{2}\omega }{\mu ^{2}+\omega ^{2}}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) \bar{{w}}^{2}. \end{aligned}$$
(44)

Solution of Eq. (43) can be expressed as follows

$$\begin{aligned} a_1= & {} \frac{-\left( {\varDelta _\mathrm{c} \sin \psi +\varDelta _\mathrm{b} \cos \psi } \right) \bar{{\delta }}}{\varDelta _\mathrm{a} \varDelta _\mathrm{c} +\varDelta _\mathrm{b}^2 }, \nonumber \\ b_1= & {} \frac{\left( {-\varDelta _\mathrm{b} \sin \psi +\varDelta _\mathrm{a} \cos \psi } \right) \bar{{\delta }}}{\varDelta _\mathrm{a} \varDelta _\mathrm{c} +\varDelta _\mathrm{b}^2 }. \end{aligned}$$
(45)

The nonlinear algebraic equation of the frequency–response curves can be expressed in terms of the displacement amplitude and excitation frequency as

$$\begin{aligned}&\bar{{w}}^{2}\left( {\varDelta _\mathrm{a} \varDelta _\mathrm{c} +\varDelta _\mathrm{b}^2 } \right) ^{2}\nonumber \\&\quad =\bar{{\delta }}^{2}\left( {\varDelta _\mathrm{b}^2 +\varDelta _1^2 +\bar{{\varepsilon }}^{2}+2\bar{{\varepsilon }}\varDelta _1 \cos 2\psi -2\varDelta _\mathrm{b} \bar{{\varepsilon }}\sin 2\psi } \right) .\nonumber \\ \end{aligned}$$
(46)

The frequency–response curves can be determined by numerically finding the positive real roots of the above equation in a range of excitation frequencies. The dimensionless response voltage can be written in terms of the mechanical amplitude as follows

$$\begin{aligned} \bar{{V}}=\sqrt{a_2^2 +b_2^2 }=\frac{\bar{{\alpha }}\omega }{\sqrt{\mu ^{2}+\omega ^{2}}}\left( {\zeta +\frac{1}{4}\gamma \bar{{w}}^{2}} \right) \bar{{w}}. \end{aligned}$$
(47)

The power amplitude frequency–response is given as

$$\begin{aligned} P=\frac{V^{2}}{R_\mathrm{L} }=\frac{m\omega _0^2 L^{3}}{C_\mathrm{p} R_\mathrm{L} }\frac{\bar{{\alpha }}^{2}\omega ^{2}}{\mu ^{2}+\omega ^{2}}\left( {\zeta \bar{{w}}+\frac{1}{4}\gamma \bar{{w}}^{3}} \right) ^{2}. \end{aligned}$$
(48)

Substituting the solution of Eq. (46) into Eqs. (47) and (48), the frequency–response curve of the voltage and power amplitude can be obtained.

5 Results and discussion

In the previous section, the theoretical model and analytical method have been described for determining the harmonic solutions of the cantilevered piezoelectric energy harvesters under simultaneous parametric and external excitations. In this section, the frequency–response curves of the energy harvesting system will be given and discussed in detail.

Table 1 Geometric and material properties of the energy harvester
Full size table

Using \(n=m=1\), the influence of the model parameter variations on the performance of the energy harvester is investigated. These parameters are parametric and external excitation amplitudes \(\varepsilon \) and \(\delta \), damping coefficient \(\bar{{c}}\), load resistance parameter \(R_\mathrm{L}\) and electro-mechanical coupling coefficient \(\bar{{\alpha }}\). The base excitations are considered as harmonic excitation. \(\psi =0\) is assumed. In the absence of specified cases, the results presented in this paper are calculated with the geometric and material parameters given in Table 1. Using the geometric and material coefficients defined in Table 1, all parameters of Eqs. (34) and (35) are as follows

$$\begin{aligned}&\bar{{\sigma }}=-\,0.7854, \ \beta =40.4407,\ \kappa =4.5968,\\&\zeta =2.7530,\ \gamma =10.4326,\ \bar{{\lambda }}=0.7830,\\&\bar{{\alpha }}=-\,0.4119,\ \bar{{\omega }}=3.5160,\\&\omega _0 =188.9150,\ C_\mathrm{p} =8.3884\times 10^{-8}. \end{aligned}$$

5.1 Only under parametric excitation

In this section, using the presented analytical expression, the numerical results under parametric excitation are obtained. Figure 2 gives the frequency–response curves of the deflection and output power amplitude in the case of different parametric excited amplitude \(\varepsilon \) when \(\delta =0, \bar{{c}}=0.01\), and \(R_\mathrm{L} =500\, \ \Omega \). Figure 2 shows that when \(\delta =0\) (only parametric excitation), electrical energy can only be harvested within a certain range of excitation frequencies where the non-trivial solutions exist. Outside of this range, only the trivial solution \(\bar{{w}}=0\) exists and no electrical energy can be harvested.

Fig. 2
figure 2

Frequency–response curves of the deflection and output power for different parameters \(\varepsilon \) when \(R_\mathrm{L} =500 \ \Omega , \delta =0\), and \(\bar{{c}}=0.01\)

Full size image
Fig. 3
figure 3

The steady-state resonant peak curves of the deflection and output voltage under parametric excitation at various excitation levels for different parameters \(\bar{{c}}\) and \(R_\mathrm{L} \). a, b \(R_\mathrm{L} =500 \ \Omega \), and c, d \(R_\mathrm{L} =500\) k\( \Omega \) when \(\delta =0\)

Full size image
Fig. 4
figure 4

The steady-state resonant peak curves of the deflection and output power at various parametric excitation levels for different external excited amplitude \(\delta \) when \(\bar{{c}}=0.01, R_\mathrm{L} =500 \ \Omega \)

Full size image

Figure 2 shows the nonlinear hardening effect. The frequency–response peak curves are hysteretic and shifted to the high frequencies. The nonlinear hardening effect results in an enhancement of the bandwidth of the energy harvester. The bandwidth enhancement can be reachable when the energy harvester is excited beyond its critical amplitude [44,45,46]. The critical electrical resistance characterizes the upper bound limit of the linear dynamic range of the harvester.

Figure 3 gives the steady-state resonant peak curves of the deflection and output voltage under parametric excitation at various excitation levels for different parameters \(\bar{{c}}\) when \(R_\mathrm{L} =500 \ \Omega , R_\mathrm{L} =500\) k\(\Omega \), and \(\delta =0\). \(\bar{{w}}_{\max } \) is the dimensionless peak deflection, \(\bar{{V}}_{\max }\) is the dimensionless peak voltage. Figure 3 shows that only in the case of the parametric excitation, the energy harvesting system has an initiation threshold. When the excited amplitude \(\varepsilon \) exceeds the initiation threshold, a rapid growth of the resonant peak deflection and peak output voltage is obtained. The mechanical damping and load resistance have significant influence on the initiation threshold, which must be overcome prior to accessing parametric resonance.

A steep jump of the nonlinear peak response curves is observed at high parametric excited amplitude \(\varepsilon \) in Fig. 3. For this behavior, a reasonable theoretical explanation can be obtained from the view of mechanics. When parametric excited amplitude \(\varepsilon \) is very small, the beam is in the state of axial deformation and the state of stable equilibrium, the beam deflection is equal to zero and no energy is harvested. When parametric excited amplitude \(\varepsilon \) reaches a certain critical value, the state of axial deformation of the beam is transformed to the bending deformation and the state of the beam buckling. The beam deflection increases rapidly and the harvested power is raised dramatically. Buckling of the beam results in significant stresses and produces large output power. However, if the beam’s buckling is not controlled, the beam will be damaged. To prevent the beam’s damage, the bending deformations of the beam must be constrained within a limited range in practical application.

Parametric resonance converges to a zero steady-state response below the initiation threshold. With excitation amplitudes increasing beyond this threshold barrier, it is able ultimately to obtain higher response amplitude. Figure 3 shows that this initiation threshold is relatively larger value, whereas the ambient vibration available for energy harvester is usually very small. Accordingly, this initiation threshold must be minimized in order to use the advantages of parametric resonance in practical application.

5.2 Simultaneous parametric and external excitations

Figure 4 gives the steady-state resonant peak curves of the deflection and output power at varying parametric excitation levels for different external excited amplitude \(\delta \) when \(\bar{{c}}=0.01, R_\mathrm{L} =500 \ \Omega \). \(\bar{{w}}_{\max }\) is the dimensionless resonant peak deflection, \(\bar{{V}}_{\max } \) is the dimensionless resonant peak output voltage. In the case that the excited amplitude \(\varepsilon \) is below the initiation threshold, Fig. 4 shows that when \(\delta \) equals constant, the frequency–response curves rapidly enlarge with the parametric excited acceleration level increasing.

Figure 5 gives the frequency–response curves of the deflection and output power for different parameter \(\varepsilon \) and \(R_L\) when \(\delta =0.22\) and \(\bar{{c}}=0.01\). Figures 4 and 5 also show that although parameter \(\varepsilon \) is below the initiation threshold, the peak deflection and peak output voltage increase with the parameter \(\varepsilon \) increasing. This is because the external excitation (\(\delta \ne 0)\) pushes the system out of axial stable equilibrium and an initial non-zero displacement is obtained. When parameter \(\varepsilon \) exceeds the initiation threshold, a rapid growth of the peak deflection and peak output voltage is obtained.

Fig. 5
figure 5

Frequency–response curves of the deflection and output voltage for different parameters \(\varepsilon \) and \(R_\mathrm{L} \). a, b \(R_\mathrm{L} =500 \ \Omega \) and c, d \(R_\mathrm{L} =500\) k\(\Omega \) when \(\delta =0.0055\) and \(\bar{{c}}=0.01\)

Full size image

In the case of simultaneous parametric and external excitations, the external excitation pushes the system out of axial stable equilibrium, the initial non-zero deflection is obtained. Accordingly, the deflection, the harvested power and frequency bandwidth increase dramatically along with parametric excited amplitude increasing when the excited amplitude \(\varepsilon \) is below the initiation threshold.

Figure 6 gives the effect of damping coefficient on the amplitude of the steady-state deflection, output voltage. When damping coefficient is relatively small, the response curves bend to a higher frequency direction corresponding to the hardening behavior. The larger damping will weaken the effect of nonlinearity.

Fig. 6
figure 6

Frequency–response curves of the deflection and output voltage for different parameters \(\bar{{c}}\). a, c \(R_\mathrm{L} =500 \ \Omega \) and b, d \(R_\mathrm{L} =500\) k\(\Omega \) when \(\delta =\varepsilon =0.022\)

Full size image
Fig. 7
figure 7

Frequency–response curves of the deflection and output power for different \(\bar{{\alpha }}\). a, b \(R_\mathrm{L} =500 \ \Omega \) and c, d \(R_\mathrm{L} =500\) k\(\Omega \) when \(\delta =\varepsilon =0.0165, \bar{{c}}=0.01\)

Full size image
Fig. 8
figure 8

Frequency–response curves of the deflection and output power for different load resistance \(R_\mathrm{L}\) when \(\delta =\varepsilon =0.0165\) and \(\bar{{c}}=0.01\)

Full size image
Fig. 9
figure 9

Comparison of frequency–response curves of the deflection and output power between distributed-parameter and lumped-parameter models for different load resistance \(R_\mathrm{L} \). a, b \(R_\mathrm{L} =500 \ \Omega \) and c, d \(R_\mathrm{L} =500\) k\(\Omega \) when \(\delta =\varepsilon =0.022\) and \(\bar{{c}}=0.01\)

Full size image

In what follows, we will investigate the effect of the electro-mechanical coupling coefficient change on energy harvesting performance. Electro-mechanical coupling coefficient is related to the piezoelectric strain constant \(d_{31} \), the width of the piezo-layer, the thickness of the piezo-layer and the Young’s modulus of the piezo-layer. Different piezoelectric materials have different piezoelectric strain constants. Assuming that the piezoelectric strain constant is changed and the other parameters remain the constant, electro-mechanical coupling coefficient \(\bar{{\alpha }}\) will be changed.

Figure 7 gives the frequency–response curves for different electro-mechanical coupling \(\bar{{\alpha }}\) when \(\varepsilon =\delta =0.0165, R_\mathrm{L} =500 \ \Omega , R_\mathrm{L} =500\) k\(\Omega \), and \(\bar{{c}}=0.01\). The peak value of the deflection amplitudes, with increasing electro-mechanical coupling \(\bar{{\alpha }}\), decreases because some of the harvesting energy suppresses the deformation of the beam. The peak values of the output power amplitude do not increase as one would expect. This can be explained by examining Eq. (48). For a given load resistance, the output power is affected by three major parameters which are the electromechanical coupling, the excited frequency and the deflection amplitude. If the electromechanical coupling increases and the deflection amplitude holds constant, then the output power will increase. However, Fig. 7a, c clearly indicate that when the electromechanical coupling increases, the deflection amplitude reduces. Obviously, there is an optimal electromechanical coupling which makes the harvested energy maximization. This result agrees with the previous findings of Daqaq et al. [30]. Figure 7 describes that the output power increases initially as electromechanical coupling increases, exhibits a maximum at an optimal electromechanical coupling and drops again beyond the optimal value. In the short-circuit resonance, Fig. 7a, b shows that the shift of the resonance frequency is relatively small. In the open-circuit resonance, Fig. 7c, d shows that the resonance frequency has a slightly larger shift to the right side along with the electric–mechanical coupling \(\bar{{\alpha }}\) increasing.

The effect of the load resistance \(R_\mathrm{L} \) on the displacement and power frequency–response curves, with \(\varepsilon =\delta =0.0165\) and \(\bar{{c}}=0.01\), is shown in Fig. 8. The load resistance affects the performance of the energy harvester when the base excitation, the damping and the electro-mechanical coupling remain constant. Figure 8a shows that the frequency–response curves have the two resonant ranges which are the open-circuit resonance and the short-circuit resonance. When \(R_\mathrm{L} \) is between 100 and 10 k\(\Omega \), the electrical net work approaches the short-circuit resonance. For \(R_\mathrm{L} \) is greater than 50 k\(\Omega \), the electrical net work approaches the open-circuit resonance. The change of the load resistance is similar to the change of the damping and the frequency of the given system. The electro-mechanical coupled damping and resonance frequency can be shown as a function of the load resistance. In the case of near the short-circuit resonance, the peak of the deflection frequency–response curves decreases with the increasing load resistance. In the case near the open-circuit resonance, the peak of the deflection frequency–response curves increases with increasing load resistance. In these two cases, Fig. 8b demonstrates that the power increases initially as the load resistance increases, exhibits a maximum at an optimal load resistance and drops again beyond the optimal value. It can be inferred that there exists an optimal load resistance to extract maximum power for a certain set of excitation, damping and electro-mechanical parameter.

5.3 Comparison of distributed-parameter and lumped-parameter models

In this section, we study the difference between the distributed-parameter and lumped-parameter models. Equations (31) and (32) of nonlinear distributed-parameter model of cantilevered piezoelectric energy harvesting system are similar to the nonlinear lumped parameter model presented by Daqaq et al. [30]. But the electromechanical coupling terms include nonlinearity, which is different from the nonlinear lumped-parameter model. The electromechanical terms of Eq. (31) are proportional to the voltage, as well as the square of the generalized displacement amplitude. The electromechanical terms of Eq. (32) are proportional to the rate of the generalized displacement amplitude and the square of the generalized displacement amplitude. \(\gamma =0\) corresponds to the nonlinear lumped-parameter model [30]. \(\gamma \ne 0\) indicates the nonlinear distributed-parametric model. Figure 9 shows the effect of nonlinear electro-mechanical coupling term on the frequency–response curves. For \(R_\mathrm{L} =500 \ \Omega \) (the short-circuit resonance), Fig. 9a, b shows that for these two models, the hardening characteristics of the frequency–response curves are not changed. For \(R_\mathrm{L} =500\) k\(\Omega \) (the open-circuit resonance), Fig. 9c, d illustrates that for the nonlinear distributed-parametric model, the frequency–response curves bend to the higher frequency direction, which reflects the effect of the nonlinear electro-mechanical coupling term on the hardening behavior. Compared with the nonlinear lumped parameter model, the nonlinear distributed-parametric model reduces slightly the amplitude of the deflection and the output power of energy harvester, but enhances the frequency bandwidth of the energy harvester.

Figures 9 and 10 compare with the resonant peak curves of the deflection and output voltage between the lumped-parameter model presented by Daqaq et al. [30] and the proposed distributed-parameter model. For varying excited acceleration level \(\varepsilon \), Fig. 10 shows that in the short-circuit resonance (\(R_\mathrm{L} =500 \ \Omega )\), there are small differences between the resonant peak curves of two models. In the open-circuit resonance (\(R_\mathrm{L} =500\) k\(\Omega )\), there are larger differences between the resonant peak curves of the two models. This physical phenomenon can be explained as the damping of the electro-mechanical coupling system increases with the load resistance increasing. The initiation thresholds of the two models are not changed. This phenomenon can be explained as when the energy harvester is the state of axial stable equilibrium there is no bending deformation and geometric nonlinearity.

Fig. 10
figure 10

Comparison of resonant peak curves of the deflection and output voltage between distributed-parameter and lumped-parameter models for different load resistance \(R_\mathrm{L} \). a, b \(R_\mathrm{L} =500 \ \Omega \) and c, d \(R_\mathrm{L} =500\) k\(\Omega \) when \(\delta =0\) and \(\bar{{c}}=0.01\)

Full size image

6 Conclusions

In this study, a nonlinear distributed parameter model of piezoelectric cantilevered beam harvesters under external and parametric excitations has been developed by the generalized Hamilton principle. Analytical expressions of the frequency–response curves have been presented by use of the Galerkin method and harmonic balance method. Utilizing the resulting expressions, we have discussed the effects of the damping, load resistance, electromechanical coupling, and excitation amplitude on the frequency–response curves. We have also studied the difference between the nonlinear lumped-parameter and nonlinear distributed-parameter model for predicting the performance of the energy harvesting system. Several main conclusions are as follows:

  1. (1)

    The presented nonlinear distributed parameter model, which includes the nonlinear electro-mechanical coupling term, is different from the nonlinear lumped-parameter model. In the case of the short-circuit resonance, the nonlinear electromechanical coupling term does not affect the hardening characteristics of the frequency–response curves. In the case of the open-circuit resonance, the frequency–response curves bend to the higher frequency direction, which reflects the effect of the nonlinear electro-mechanical coupling term on the hardening behavior.

  2. (2)

    The peak of the deflection frequency–response curves, in the case of the short-circuit resonance, decreases with the load resistance increasing. The peak of the deflection frequency–response curves, at the case of the open-circuit resonance, increases with the load resistance increasing. In these two cases, the output power increases initially as the load resistance increases, exhibiting a maximum at an optimal load resistance and dropping again beyond the optimal value. For a certain set of excitation and electro-mechanical coupling, there exists an optimal load impedance to extract maximum power.

  3. (3)

    The peak of the deflection frequency–response curves decreases with the electromechanical coupling coefficient increasing. The peak of power frequency–response curves increases initially with electromechanical coupling coefficient increasing, reaches a maximum at an optimal electromechanical coupling and drops again beyond the optimal value.

  4. (4)

    In the case of parametric resonance, the energy harvesting system has an initiation excitation threshold below this threshold no energy can be harvested. The mechanical damping and load resistance have significant influence on the initiation threshold.

  5. (5)

    In the case of simultaneous parametric and external excitations, the external excitation pushes the system out of axial stable equilibrium, the initial non-zero deflection is obtained. Accordingly, the deflection, harvested power and frequency bandwidth increase dramatically along with parametric excitation amplitudes increasing although the parametric excitation amplitude is below the initiation threshold.