Introduction

In recent years, due to the superior performance of nanotechnology, it plays an important role in the field of machinery, and has been widely concerned by researchers [1,2,3,4,5,6,7]. With the rapid development of current nanotechnology, some new mechanical devices are used in the fields of biology, medicine, engineering, etc., such as wireless sensors, transistors, biological probes, micro-motors and other mechanical structures. However, some nano-mechanical structures are affected by complex chemical and physical environments during work, which causes difficulties such as work failure and structural fatigue. Therefore, studying the mechanical behavior of nano-machines is crucial to the design of nanodevices.

Studies have shown that the mechanical properties of objects at a small scale are very different from those at a macro-scale, or even completely opposite. Since the classical elastic theory at the macro-scale cannot explain the microscopic phenomena when dealing with small-scale problems, various new constitutive relations have been constructed, such as nonlocal theory [8], strain gradient theory [9] and nonlocal strain gradient theory [10]. The nonlocal theory is obtained by introducing a nonlocal parameter and writing the internal forces as nonlocal expressions to replace the relevant variables in the traditional continuum medium. In 1972, Eringen and Edelen pointed out that the theory of nonlocal continuum mechanics is to explain the small-scale effect by the stress at a given point depending on the strain at all points. The strain gradient theory is based on accurate energy variation method, it regards the object as a coordinated continuum of deformation composed of macroscopic and microscopic matter, and treats each material point in the continuum as a cell containing high-order strain. However, some different or even completely opposite conclusions have been obtained in applications of these theories. Li and his collaborators [11,12,13,14,15,16,17] resolved those puzzling problems. The nonlocal strain gradient theory considers both nonlocal effects and strain gradient effects, and resolves the confusion and controversy caused by other theories. When studying the mechanical behaviors at the micro/nanoscale, some physical phenomena also need to be considered. This is because the physical phenomena play significant roles in the physical parameters and deformation potential of the structure. Such as surface effects, flexoelectric effects and so on. The surface effects, containing the surface energy, the surface tension, and the surface relaxation, should not be ignored where the overall elastic attributes of nanostructures are studied. The surface energy plays an important role due to the high surface-to-volume ratio. In the surface energy theory, the energy saved in the surfaces is due to the surface elasticity, the surface stress, and the surface density. The flexoelectric effect has a major role on responses of piezoelectric materials when their dimensions become submicron. The flexo-electricity is associated with a specific electrical–mechanical coupling phenomena among polarizations and strains gradients. Actually, inflicting the strain gradients to a dielectric may exert special electric polarizations via changing the inversion symmetries. This paper is based on the nonlocal theory to study the micro-nano-mechanical behavior, which is a modified classical elastic theory. In the classical local continuous medium mechanics, it is assumed that the stress state at a point depends only on the strain at that point. In 1972, Eringen and Edelen pointed out that the theory of nonlocal continuum mechanics is to explain the small-scale effect by the stress at a given point depending on the strain at all points. Applying the nonlocal elastic theory to study the deformation, buckling and vibration of nanostructures have attracted a lot of research interest [18,19,20,21,22,23,24]. Yang [25] proposed a new analytical solution for free vibration of thick nanostructures based on the nonlocal elastic stress field theory and the Timoshenko shear deformable nanobeam model, and studied the effects of nonlocal parameter on vibration frequencies. Rahmani [26] et al. studied the torsional vibration of cracked nanobeam based on nonlocal elasticity theory. Li [27] et al. analyzed the free vibration of circular cross-section nanocone and solved the problem of how to determine the values of small-scale parameter. Lim et al. [28,29,30,31,32,33,34,35] have reported plenty of research work in the fields of the nonlocal theory and nano-mechanics, and obtained many meaningful results.

With the demand and development of intelligentization, miniaturization and nanometerization, it has been a development trend to shrink rotating mechanical parts to micrometer or even nanoscale [36,37,38,39,40,41], therefore, many researchers have conducted research on rotating nanodevices. Azimi [42] et al. analyzed the vibration behavior of rotating functionally graded nano-Timoshenko beam in a thermal environment and explored the effect of changes in rotational angular velocity on vibration characteristics. Mahinzare [43] et al. studied the free vibration of a rotating smart circular nanoplate made of bidirectional functionally gradient piezoelectric materials, and explored the effect of voltage and angular velocity on the natural frequencies. Ghadiri M [44] et al. studied the free vibration of a nano-turbine blade based on the Kirchhoff plate theory, and explored the effect of small-scale parameter and angular velocity on the natural frequencies. Farzad E [45] et al. studied wave propagation responses of smart rotating magneto-electro-elastic graded nanoscale plates.

There have been few reports on the vibration behavior of rotating piezoelectric nanobeams by referring to the data. In this paper, the free vibration behaviors of the nanosheets are studied using the rotating functional gradient piezoelectric nanobeam as a model. To more accurately predict the mechanical behavior of the beam, this paper analyzes the free vibration behavior of the rotating functionally graded piezoelectric nanobeam based on the nonlocal elastic theory and the Timoshenko beam model. The influence of rotational velocity, nonlocal parameter, gradient index, aspect ratio and external voltage on the vibration frequencies were investigated.

Rotating Piezoelectric Nano-Model

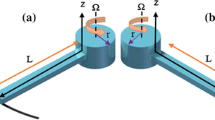
Consider a rotating functionally graded piezoelectric nanobeam with rectangular cross-section. The length, width and height of the beam are \(L\),\(h\) and \(b\), respectively. The beam is fixed on a rigid rotor of radius \(r\) and rotates around the z axis at an angular velocity \(\omega\), as shown in Fig. 1. The materials of the beam are composed of piezoelectric materials. Assuming that the material properties are distributed in a gradient along the thickness direction, which can be expressed as [46]

$$P\left( z \right) = P_{5} + \left( {P_{4} - P_{5} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{k} ,$$
(1)
Fig. 1
figure 1

A rotating piezoelectric nanobeam

Full size image

where \(P_{4}\) and \(P_{5}\) represent material properties of the bottom surface and top surface of the beam, respectively, and the \(k\) is gradient index of the material.

Taking the end of the beam fixing point as the coordinate origin \(o\), the \(x\) and \(y\) coordinates are established in the physical midplane of the beam and along the length and width directions, and the \(z\) coordinate is perpendicular to the physical midplane of the beam, as shown in Fig. 1. Assuming that the physical midplane of the beam is at \(z = z_{0}\), according to the concept of the physical midplane proposed in [47], the calculation formula is

$$z_{0} = \frac{{\int_{ - h/2}^{h/2} {zP\left( z \right){\text{d}} z} }}{{\int_{ - h/2}^{h/2} {P\left( z \right){\text{d}} z} }} = \frac{{(E_{{({\text{PZT}} - 4)}} - E_{{({\text{PZT}} - 5)}} )kh}}{{2\left( {2 + k} \right)(E_{{({\text{PZT}} - 4)}} + kE_{{({\text{PZT}} - 5)}} )}},$$
(2)

where \(E_{{({\text{PZT}} - 4)}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} E_{{({\text{PZT}} - 5)}} {\kern 1pt}\), respectively, represent the elastic modulus of the \({\text{PZT}} - 4\) material and the \({\text{PZT}} - 5\) material.

Since the thickness and width of the beam are much smaller than its length, only considering the movements of the beam in the \(x - z\) plane, the nonlocal elastic constitutive relationship can be approximated as a one-dimensional form, which can be expressed as follows [48]:

$$\sigma_{x} - (e_{0} a)^{2} \frac{{\partial^{2} \sigma_{x} }}{{\partial x^{2} }} = C_{11} \varepsilon_{x} - e_{31} E_{z} ,$$
(3)
$$\sigma_{xz} - (e_{0} a)^{2} \frac{{\partial^{2} \sigma_{xz} }}{{\partial x^{2} }} = C_{44} \gamma_{xz} - e_{15} E_{x} ,$$
(4)
$$D_{x} - (e_{0} a)^{2} \frac{{\partial^{2} D_{x} }}{{\partial x^{2} }} = e_{15} \gamma_{xz} + \Xi_{11} E_{x} ,$$
(5)
$$D_{z} - (e_{0} a)^{2} \frac{{\partial^{2} D_{z} }}{{\partial z^{2} }} = e_{31} \varepsilon_{x} + \Xi_{33} E_{z} ,$$
(6)

where \(\sigma_{x}\) represent nonlocal stress and strain in the \(x\) direction; \(\sigma_{xz} ,\gamma_{xz}\) represent nonlocal shear stress and shear strain in the cross-section; \(D_{x} ,D_{z}\) are the nonlocal electrical displacement in the \(x\) and \(z\) directions, respectively;\(E_{x} ,E_{z}\) are the electric field in the \(x\) and \(z\) directions;\(C_{11} ,C_{44}\) are the elastic constants;\(e_{31} ,e_{15}\) are the piezoelectric constants; \(\Xi_{11} ,\Xi_{33}\) are the dielectric constants, \(e_{0}\) is the nonlocal constant of material, and a is the internal characteristic scale. In all the size-dependent mechanical behavior studies based on the nonlocal elastic method, researchers explored the effects of small-scale parameter on the mechanical behaviors of the research objects by changing the values of \(e_{0} a\). It is worth mentioning that there is a critical size for deciding whether to take the nonlocal effect into account or not. It can be determined by molecular dynamics simulations, theoretical analyses and experiments. However, this is not the point of the present work. Moreover, previous literature (e.g., [49]) has presented useful analysis and discussion on such an aspect, including the critical internal sizes in one-dimensional and two-dimensional nanostructural dynamics. The present work is concerned on the free vibration of one-dimensional nanostructures. Hence, the critical value range of \(e_{0} a\), generally 0 ~ 2.5 nm can be adopted directly.

Assuming that the displacements of the nanobeam along the \(x\), \(y\), and \(z\) directions are \(u_{1}\), \(u_{2}\) and \(u_{3}\), the expressions obtained by Timoshenko beam theory are

$$\left\{ {\begin{array}{*{20}l} {u_{1} (x,z,t) = u_{0} (x){ + }\left( {z - z_{0} } \right)\varphi (x,t)} \hfill \\ {u_{2} (x,z,t) = 0} \hfill \\ {u_{3} (x,z,t) = w(x,t)} \hfill \\ \end{array} } \right.,$$
(7)

where \(u_{0}\) represents the axial displacement of the nanobeam caused by the centrifugal force and external static voltage in the process of constant speed rotation, regardless of the time \(t\). \(\varphi \left( {x,t} \right)\) is the angular displacement of the cross-section of the nanobeam, and \(w\left( {x,t} \right)\) is the lateral displacement of the nanobeam.

From the geometric relationship, the relationships between the strain and displacement of the piezoelectric nanobeam are

$$\varepsilon_{x} = \frac{{\partial u_{0} }}{\partial x}{ + }\left( {z - z_{0} } \right)\frac{\partial \varphi }{{\partial x}},$$
(8)
$$\gamma_{xz} = \frac{\partial w}{{\partial x}} + \varphi .$$
(9)

The rotating nanobeam has the characteristics of electromechanical coupling during the movements, and its potential distribution meets Maxwell formula, and can be set as a combination of cosine function and linear variable, and its specific expression is [50]

$$\Phi (x,z,t) = - \cos (\beta z)\phi (x,t) + \frac{{zV_{0} }}{h},$$
(10)

where \(\beta = \frac{\pi }{h}\), \(\phi (x,t)\) is the potential distribution in the \(x\) direction, and \(V_{0}\) is the external static voltage applied to the top and bottom surfaces of the beam. According to the relationships between the electric potential and the electrostatic field, the electrostatic fields in the \(x\) and \(z\) directions are obtained from Eq. (10):

$$\left\{ \begin{gathered} E_{x} = - \frac{\partial \Phi }{{\partial x}} = \cos (\beta z)\frac{\partial \phi }{{\partial x}} \hfill \\ E_{z} = - \frac{\partial \Phi }{{\partial z}} = - \beta \sin (\beta z)\phi - \frac{{V_{0} }}{h} \hfill \\ \end{gathered} \right..$$
(11)

From Eqs. (8), (9) and (11), the deformation energy of the piezoelectric nanobeam is

$$\begin{gathered} U_{b} = \frac{1}{2}\int_{0}^{L} {\int_{A} {(\sigma_{x} \varepsilon_{x} + \sigma_{xz} \gamma_{xz} - D_{x} E_{x} - D_{z} E_{z} )} {\mathbf{d}}A{\mathbf{d}}x} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{2}\int_{0}^{L} {\left[ {N\frac{\partial u}{{\partial x}} + M\frac{\partial \varphi }{{\partial x}} + Q\left( {\frac{\partial w}{{\partial x}} + \varphi } \right)} \right]} {\mathbf{d}}x + \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\int_{0}^{L} {\int_{A} {\left[ { - D_{x} \cos \left( {\beta z} \right)\frac{\partial \phi }{{\partial x}} + D_{z} \left( {\beta \sin \left( {\beta z} \right)\phi + \frac{{V_{0} }}{h}} \right)} \right]} } {\mathbf{d}}A, \hfill \\ \end{gathered}$$
(12)

where the nonlocal axial force \(N\), bending moment \(M\) and shear force \(Q\) are expressed as

$$N = \int_{A} {\sigma_{x} } {\text{d}} A{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} M = \int_{A} {\sigma_{x} } \left( {z - z_{0} } \right){\text{d}} A{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q = \int_{A} {\sigma_{xz} } {\text{d}} A.$$
(13)

The potential energy of the axial tension \(N_{F}\) is

$$U_{F} = \frac{1}{2}\int_{0}^{L} {\left[ {\left( {\frac{\partial w}{{\partial x}}} \right)^{2} N_{F} } \right]{\mathbf{d}}x} ,$$
(14)

where the axial force \(N_{F}\) received at each point on the beam is composed of the centrifugal force \(N_{r}\) generated by the beam due to the rotation and the axial force \(N_{e}\) generated by the external voltage

$$N_{F} = N_{e} + N_{r} .$$
(15)

The centrifugal force \(N_{r}\) at each point along the direction of the x-axis is

$$N_{r} = \int_{A} {\int_{r + x}^{r + L} {\rho (z)\omega^{2} (\zeta + r){\text{d}}A{\mathbf{d}}\zeta } } = I_{0} \omega^{2} \left( {L - x} \right)\left( {\frac{L + x}{2} + 2r} \right),$$
(16)

where \(I_{0} = \int_{A} {\rho (z)} {\mathbf{d}}A{\kern 1pt} {\kern 1pt}\).

The axial force \(N_{e}\) generated by the external voltage \(V_{0}\) is

$$N_{e} { = }\int_{A} {\frac{{e_{31} V_{0} }}{h}} {\mathbf{d}}A = \frac{{V_{0} b}}{h}\int_{ - h/2}^{h/2} {e_{31} (z)} {\mathbf{d}}z.$$
(17)

During the rotation of the piezoelectric nanobeam at a constant velocity \(\omega\), it vibrates freely in the \(xoz\) plane, and its kinetic energy is

$$\begin{array}{*{20}l} {T = \frac{1}{2}\int_{0}^{L} {\int_{A} {\rho \left( z \right)\left[ {\left( {\frac{\partial w}{{\partial t}}} \right)^{2} + \left( {\frac{{\partial u_{0} }}{\partial t} + \left( {z - z_{0} } \right)\frac{\partial \varphi }{{\partial t}}} \right)^{2} + \omega^{2} \left( {u_{0} + (z - z_{0} )\varphi } \right)^{2} } \right]} } {\mathbf{d}}A{\mathbf{d}}x} \hfill \\ { \, \,\,\,\,\,{ = }\frac{1}{2}\int_{0}^{L} {\left[ {I_{0} \left( {\frac{\partial w}{{\partial t}}} \right)^{2} + I_{0} \left( {\frac{{\partial u_{0} }}{\partial t}} \right)^{2} + 2I_{1} \frac{{\partial u_{0} }}{\partial t}\frac{\partial \varphi }{{\partial t}} + I_{2} \left( {\frac{\partial \varphi }{{\partial t}}} \right)^{2} + I_{0} \omega^{2} u_{0}^{2} + 2I_{1} \omega^{2} u_{0} \varphi + I_{2} \omega^{2} \varphi^{2} } \right]} {\mathbf{d}}x} \hfill \\ \end{array}$$
(18)

where the equivalent mass \(I_{i}\) is expressed as

$$I_{i} = \int_{A} {\rho (z) \cdot \left( {z - z_{0} } \right)^{i} } {\mathbf{d}}A{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} (i = {\kern 1pt} {\kern 1pt} 1,{\kern 1pt} {\kern 1pt} 2).$$
(19)

According to the Hamilton principle, the variation of the total energy is zero, that is

$$\int_{0}^{t} {\delta (U_{b} + U_{F} - T)} {\mathbf{d}}t = 0.$$
(20)

Substituting Eqs. (12), (14) and (18) into Eq. (20), the governing equations of the rotating piezoelectric nanobeam are

$$\left\{ \begin{gathered} I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} = \frac{\partial Q}{{\partial x}} + \frac{\partial }{\partial x}\left( {N_{F} \frac{\partial w}{{\partial x}}} \right) \hfill \\ I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }} = I_{1} \omega^{2} u_{0} + I_{2} \omega^{2} \varphi + \frac{\partial M}{{\partial x}} - Q \hfill \\ \int_{A} {\left( {D_{z} \beta \sin (\beta z) + \frac{{\partial D_{x} }}{\partial x}\cos (\beta z)} \right){\mathbf{d}}A} = 0 \hfill \\ \end{gathered} \right.$$
(21)

and the mechanical boundary conditions are

Hinged end

$$w = M = 0$$
(22)

Clamped end

$$w = \varphi = 0$$
(23)

Free end

$$Q = M = 0$$
(24)

as well as the electrical boundary conditions are

$$\int_{{{ - }h/2}}^{h/2} {D_{x} \cos (\beta z)} {\mathbf{d}}z = 0{\kern 1pt} {\kern 1pt} {\text{or}}\phi = 0\,\,x = 0,L.$$
(25)

Integrating the expressions (3, 4, 5, 6) one can get

$$M - (e_{0} a)^{2} \frac{{\partial^{2} M}}{{\partial x^{2} }} = A_{11} \frac{{\partial u_{0} }}{\partial x} + A_{12} \frac{\partial \varphi }{{\partial x}} + F_{31} \phi + M_{e} ,$$
(26)
$$Q - (e_{0} a)^{2} \frac{{\partial^{2} Q}}{{\partial x^{2} }} = K_{s} A_{44} \left( {\frac{\partial w}{{\partial x}} + \varphi } \right) - K_{s} E_{15} \frac{\partial \phi }{{\partial x}},$$
(27)
$$\int_{A} {\left( {\left( {D_{x} - (e_{0} a)^{2} \frac{{\partial^{2} D_{x} }}{{\partial x^{2} }}} \right)\cos (\beta z)} \right){\mathbf{d}}A} = E_{15} \left( {\frac{\partial w}{{\partial x}} + \varphi } \right) + X_{11} \frac{\partial \phi }{{\partial x}},$$
(28)
$$\int_{A} {\left( {\left( {D_{z} - (e_{0} a)^{2} \frac{{\partial^{2} D_{z} }}{{\partial x^{2} }}} \right)\beta \sin (\beta z)} \right){\mathbf{d}}A} = T_{31} \frac{{\partial u_{0} }}{\partial x} + F_{31} \frac{\partial \varphi }{{\partial x}} - X_{33} \phi - V_{e} ,$$
(29)

where \(K_{s}\) is the shear correction factor, which depends on the cross-sectional shape of the beam. In this paper, the value of the \(K_{s}\) is 5/6, and other coefficients are expressed as follows:

$$\left\{ \begin{gathered} A_{11} = \int\limits_{A} {C_{11} (z)(z - z_{0} )} {\text{d}} A{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} A_{44} = \int\limits_{A} {C_{44} (z){\text{d}} A} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} A_{12} = \int\limits_{A} {C_{11} (z)(z - z_{0} )^{2} } {\text{d}} A \hfill \\ E_{15} = \int\limits_{A} {e_{15} (z)\cos (\beta z)} {\mathbf{d}}A{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} F_{31} = \int\limits_{A} {e_{31} (z)\beta \sin (\beta z)(z - z_{0} )} {\mathbf{d}}A{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} X_{11} = \int\limits_{A} {\Xi_{11} (z)\cos^{2} (\beta z){\mathbf{d}}A} \hfill \\ X_{33} = \int\limits_{A} {\Xi_{33} (z)\left[ {\beta \sin (\beta z)} \right]^{2} {\mathbf{d}}A{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,T_{31} = \int\limits_{A} {e_{31} (z)\beta \sin (\beta z)} {\mathbf{d}}A{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} M_{e} = \int\limits_{A} {\frac{{\left( {z - z_{0} } \right)V_{0} }}{h}} {\mathbf{d}}A} \hfill \\ {\kern 1pt} {\kern 1pt} V_{e} = \int\limits_{A} {\frac{{V_{0} }}{h}} \Xi_{33} (z)\left[ {\beta \sin (\beta z)} \right]{\mathbf{d}}A{\kern 1pt} {\kern 1pt} \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} .$$
(30)

Equations (21), (26) and (27) can be used to derive nonlocal bending moment and nonlocal shear force expressions:

$$M = A_{11} \frac{{\partial u_{0} }}{\partial x}{\text{ + A}}_{12} \frac{\partial \varphi }{{\partial x}}{ + }F_{31} \phi { + }M_{e} { + }(e_{0} a)^{2} \left( {I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{3} \varphi }}{{\partial x\partial t^{2} }} - I_{1} \omega^{2} \frac{{\partial u_{0} }}{\partial x} - I_{2} \omega^{2} \frac{\partial \varphi }{{\partial x}} - \frac{\partial }{\partial x}\left( {N_{F} \frac{\partial w}{{\partial x}}} \right)} \right),$$
(31)
$$Q = K_{s} A_{44} \left( {\frac{\partial w}{{\partial x}} + \varphi } \right) - K_{s} E_{15} \frac{\partial \phi }{{\partial x}}{ + }(e_{0} a)^{2} \left( {I_{0} \frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} - \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {N_{F} \frac{\partial w}{{\partial x}}} \right)} \right).$$
(32)

Substituting the nonlocal bending moment and shear force into the governing Eqs. (21) and parallel vertical Eqs. (28) and (29) can derive the equations of motion of the rotating functional gradient piezoelectric nanobeam:

$$\left\{ \begin{gathered} I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} = K_{s} A_{44} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \varphi }{{\partial x}}} \right) - K_{s} E_{15} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} + (e_{0} a)^{2} \left[ {I_{0} \frac{{\partial^{4} w}}{{\partial x^{2} \partial t^{2} }} - \frac{{\partial^{3} }}{{\partial x^{3} }}\left( {N_{F} \frac{\partial w}{{\partial x}}} \right)} \right] + \frac{\partial }{\partial x}\left( {N_{F} \frac{\partial w}{{\partial x}}} \right) \hfill \\ \hfill \\ I_{2} \frac{{\partial^{2} \varphi }}{{\partial t^{2} }} = I_{2} \omega^{2} \varphi + I_{1} \omega^{2} u_{0} + A_{11} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} + A_{12} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + F_{31} \frac{\partial \phi }{{\partial x}}{\kern 1pt} - K_{s} A_{44} \left( {\frac{\partial w}{{\partial x}} + \varphi } \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + K_{s} E_{15} \frac{\partial \phi }{{\partial x}} + (e_{0} a)^{2} \left[ {I_{2} \frac{{\partial^{4} \varphi }}{{\partial x^{2} \partial t^{2} }} - I_{1} \omega^{2} \frac{{\partial^{2} u_{0} }}{{\partial x^{2} }} - I_{2} \omega^{2} \frac{{\partial^{2} \varphi }}{{\partial x^{2} }}} \right] \hfill \\ \hfill \\ T_{31} \frac{{\partial u_{0} }}{\partial x} + E_{15} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{\partial \varphi }{{\partial x}}} \right) + F_{31} \frac{\partial \varphi }{{\partial x}} + X_{11} \frac{{\partial^{2} \phi }}{{\partial x^{2} }} - X_{33} \phi - V_{e} = 0 \hfill \\ \end{gathered} \right..$$
(33)

To make the Eq. (33) have universal applicabilities, they can be transformed into a non-dimensional form. Let \(A_{10} = C_{11(PZT - 4)} bh{\kern 1pt}\), we define the following dimensionless expressions as

$$\left\{ \begin{gathered} \overline{x} = \frac{x}{L}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} \overline{w} = \frac{w}{h},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{u}_{0} = \frac{{u_{0} }}{h}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\varphi } = \varphi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = \frac{{e_{0} a}}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta = \frac{L}{h},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta = \frac{r}{L},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{A}_{11} = \frac{{A_{11} }}{{A_{10} h}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{A}_{12} = \frac{{A_{12} }}{{A_{10} h^{2} }} \hfill \\ \overline{A}_{44} = \frac{{A_{44} }}{{A_{10} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{N}_{F} = \frac{{N_{F} }}{{A_{10} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} \overline{M}_{e} = \frac{{M_{e} L}}{{A_{10} h^{2} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{V}_{e} = \frac{{V_{e} L^{2} }}{{h^{2} \sqrt {A_{10} X_{{33\left( {{\text{PZT}} - 4} \right)}} } }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\phi } = \phi \sqrt {\frac{{X_{{33\left( {{\text{PZT}} - 4} \right)}} }}{{A_{10} }}} {\kern 1pt} \hfill \\ \overline{X}_{11} = \frac{{X_{11} }}{{X_{{33\left( {{\text{PZT}} - 4} \right)}} h^{2} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} \overline{X}_{33} = \frac{{X_{33} }}{{X_{{33\left( {{\text{PZT}} - 4} \right)}} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{E}_{15} = \frac{{E_{15} }}{{h\sqrt {A_{10} X_{{33\left( {{\text{PZT}} - 4} \right)}} } }}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{F}_{31} = \frac{{F_{31} }}{{h\sqrt {A_{10} X_{{33\left( {{\text{PZT}} - 4} \right)}} } }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{T}_{31} = \frac{{T_{31} }}{{\sqrt {A_{10} X_{{33\left( {{\text{PZT}} - 4} \right)}} } }}{\kern 1pt} {\kern 1pt} \hfill \\ (\overline{I}_{0} ,\overline{I}_{1} ,\overline{I}_{2} ) = (\frac{{I_{0} }}{{I_{0(PZT - 4)} }},\frac{{I_{1} }}{{hI_{0(PZT - 4)} }},\frac{{I_{2} }}{{h^{2} I_{0(PZT - 4)} }}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \tau = \frac{t}{L}\sqrt {\frac{{A_{10} }}{{I_{0(PZT - 4)} }}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\omega } = \omega \eta L\sqrt {\frac{{I_{0(PZT - 4)} }}{{A_{10} }}} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\Omega } = \Omega L\sqrt {\frac{{I_{0(PZT - 4)} }}{{A_{10} }}} \hfill \\ \end{gathered} \right.{\kern 1pt} {\kern 1pt} .$$
(34)

Accordingly, the governing equations can be transformed into dimensionless forms

$$\left\{ \begin{gathered} K_{s} \overline{A}_{44} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }} - \mu^{2} \frac{{\partial^{3} }}{{\partial \overline{x}^{3} }}\left( {\overline{N}_{F} \frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{x}}}\left( {\overline{N}_{F} \frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right) + K_{s} \overline{A}_{44} \eta \frac{{\partial \overline{\varphi }}}{{\partial \overline{x}}} - K_{s} \overline{E}_{15} \frac{{\partial^{2} \overline{\phi }}}{{\partial \overline{x}^{2} }} = \overline{I}_{0} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{t}^{2} }} - \mu^{2} \overline{I}_{0} \frac{{\partial^{4} \overline{w}}}{{\partial \overline{x}^{2} \partial \overline{t}^{2} }} \hfill \\ \hfill \\ - \overline{I}_{1} \mu^{2} \frac{{\overline{\omega }^{2} }}{\eta }\frac{{\partial^{2} \overline{u}_{0} }}{{\partial \overline{x}^{2} }} + \overline{A}_{11} \frac{{\partial^{2} \overline{u}_{0} }}{{\partial \overline{x}^{2} }} + \overline{I}_{1} \frac{{\overline{\omega }^{2} }}{\eta }\overline{u}_{0} - K_{s} \overline{A}_{44} \eta \frac{{\partial \overline{w}}}{{\partial \overline{x}}} + \left( {\overline{A}_{12} - \mu^{2} \overline{I}_{2} \frac{{\overline{\omega }^{2} }}{{\eta^{2} }}} \right)\frac{{\partial^{2} \overline{\varphi }}}{{\partial \overline{x}^{2} }} + \left( {\overline{F}_{31} \eta + K_{s} \eta \overline{E}_{15} } \right)\frac{{\partial \overline{\phi }}}{{\partial \overline{x}}} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} + \left( {\overline{I}_{2} \frac{{\overline{\omega }^{2} }}{{\eta^{2} }} - K_{s} \overline{A}_{44} \eta^{2} } \right)\overline{\varphi } = I_{2} \frac{{\partial^{2} \overline{\varphi }}}{{\partial \overline{t}^{2} }} - \mu^{2} \overline{I}_{2} \frac{{\partial^{4} \overline{\varphi }}}{{\partial \overline{x}^{2} \partial \overline{t}^{2} }} \hfill \\ \hfill \\ \overline{T}_{31} \eta \frac{{\partial \overline{u}_{0} }}{{\partial \overline{x}}} + \overline{E}_{15} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }} + \left( {\overline{E}_{15} \eta + \overline{F}_{31} \eta } \right)\frac{\partial \varphi }{{\partial \overline{x}}} + \overline{X}_{11} \frac{{\partial^{2} \overline{\phi }}}{{\partial \overline{x}^{2} }} - X_{33} \overline{\phi } - \overline{V}_{e} = 0 \hfill \\ \end{gathered} \right..$$
(35)

The boundary conditions of the hinged end, the fixed end and the free end are expressed in dimensionless forms as follows:

Hinged end

$$\overline{w} = \overline{M} = \overline{\phi } = 0$$
(36)

Clamped end

$$\overline{w} = \overline{\varphi } = \overline{\phi } = 0$$
(37)

Free end

$$\overline{Q} = \overline{M} = \overline{\phi } = 0$$
(38)

The nonlocal expressions of the bending moment \(M\) and shear force \(Q\) at the free end can be derived from Eqs. (31) and (32), respectively, as follows:

$$\begin{gathered} \overline{A}_{11} \frac{{\partial \overline{u}_{0} }}{{\partial \overline{x}}} - \frac{{\mu^{2} \overline{I}_{1} \overline{\omega }^{2} }}{\eta }\frac{{\partial \overline{u}_{0} }}{{\partial \overline{x}}} - \mu^{2} \eta \frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\frac{{\partial \overline{w}}}{{\partial \overline{x}}} - \mu^{2} \eta \overline{N}_{F} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }}{ + }\overline{A}_{12} \frac{{\partial \overline{\varphi }}}{{\partial \overline{x}}} \hfill \\ - \frac{{\mu^{2} \overline{I}_{2} \overline{\omega }^{2} }}{{\eta^{2} }}\frac{{\partial \overline{\varphi }}}{{\partial \overline{x}}} + \overline{F}_{31} \eta \overline{\phi } + \overline{M}_{e} = - \mu^{2} \overline{I}_{0} \eta \frac{{\partial^{2} \overline{w}}}{{\partial \tau^{2} }} - \overline{I}_{2} \mu^{2} \frac{{\partial^{3} \overline{\varphi }}}{{\partial \overline{x}\partial \tau^{2} }}, \hfill \\ \end{gathered}$$
(39)
$$K_{s} \overline{A}_{44} \frac{{\partial \overline{w}}}{{\partial \overline{x}}} - \mu^{2} \frac{{\partial^{2} }}{{\partial \overline{x}^{2} }}\left( {\overline{N}_{F} \frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right) + K_{s} \overline{A}_{44} \eta \overline{\varphi } - K_{s} \overline{E}_{15} \frac{{\partial \overline{\phi }}}{{\partial \overline{x}}} = - \mu^{2} \overline{I}_{0} \frac{{\partial^{3} \overline{w}}}{{\partial \overline{x}\partial^{2} \tau }}.$$
(40)

To study the characteristics of the free vibration of the nanobeam, the differential equations can be obtained from the Eqs. (35) as follows:

$$\left\{ \begin{gathered} K_{s} \overline{A}_{44} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }} - \mu^{2} \frac{{\partial^{3} }}{{\partial \overline{x}^{3} }}\left( {\overline{N}_{F} \frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right) + \frac{\partial }{{\partial \overline{x}}}\left( {\overline{N}_{F} \frac{{\partial \overline{w}}}{{\partial \overline{x}}}} \right) + K_{s} \overline{A}_{44} \eta \frac{{\partial \overline{\varphi }}}{{\partial \overline{x}}} - K_{s} \overline{E}_{15} \frac{{\partial^{2} \overline{\phi }}}{{\partial \overline{x}^{2} }} = \overline{I}_{0} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{t}^{2} }} - \mu^{2} \overline{I}_{0} \frac{{\partial^{4} \overline{w}}}{{\partial \overline{x}^{2} \partial \overline{t}^{2} }} \hfill \\ \hfill \\ - K_{s} \overline{A}_{44} \eta \frac{{\partial \overline{w}}}{{\partial \overline{x}}} + \left( {\overline{A}_{12} - \mu^{2} \overline{I}_{2} \frac{{\overline{\omega }^{2} }}{{\eta^{2} }}} \right)\frac{{\partial^{2} \overline{\varphi }}}{{\partial \overline{x}^{2} }} + \left( {\overline{I}_{2} \frac{{\overline{\omega }^{2} }}{{\eta^{2} }} - K_{s} \overline{A}_{44} \eta^{2} } \right)\overline{\varphi } + \left( {\overline{F}_{31} \eta + K_{s} \overline{E}_{15} \eta } \right)\frac{{\partial \overline{\phi }}}{{\partial \overline{x}}} = I_{2} \frac{{\partial^{2} \overline{\varphi }}}{{\partial \overline{t}^{2} }} - \mu^{2} \overline{I}_{2} \frac{{\partial^{4} \overline{\varphi }}}{{\partial \overline{x}^{2} \partial \overline{t}^{2} }} \hfill \\ \hfill \\ \overline{E}_{15} \frac{{\partial^{2} \overline{w}}}{{\partial \overline{x}^{2} }} + \left( {\overline{E}_{15} \eta + \overline{F}_{31} \eta } \right)\frac{{\partial \overline{\varphi }}}{{\partial \overline{x}}} + \overline{X}_{11} \frac{{\partial^{2} \overline{\phi }}}{{\partial \overline{x}^{2} }} - X_{33} \eta^{2} \overline{\phi } = 0 \hfill \\ \end{gathered} \right..$$
(41)

Therefore, the governing equations and boundary conditions of the mechanical model are derived from the Hamilton principle. The partial differential equations can be converted into linear algebraic equations by a differential quadrature method, and then calculated and analyzed in detail.

Characteristic Equations

In this paper, the differential quadrature method is used to transform the governing Eqs. (41) into a set of algebraic equations. The differential quadrature method is a common numerical method to solve partial differential equations. According to the differential quadrature method, the coefficients of the interpolation points are calculated, so that the governing Eqs. (41) are transformed into

$$\left\{ \begin{gathered} K_{s} \overline{A}_{44} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{w}_{j} } - \mu^{2} \left( {\frac{{\partial^{3} \overline{N}_{F} }}{{\partial \overline{x}^{3} }}\sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{w}_{j} } + 3\frac{{\partial^{2} \overline{N}_{F} }}{{\partial \overline{x}^{2} }}\sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{w}_{j} } + 3\frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\sum\limits_{j = 1}^{n} {c_{ij}^{3} \overline{w}_{j} } + \overline{N}_{F} \sum\limits_{j = 1}^{n} {c_{ij}^{4} \overline{w}_{j} } } \right) \hfill \\ {\kern 1pt} + \frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{w}_{j} } + \overline{N}_{F} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{w}_{j} } + K_{s} \overline{A}_{44} \eta \sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{\varphi }_{j} } {\kern 1pt} - K_{s} \overline{E}_{15} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{\phi }_{j} } = \overline{I}_{0} \ddot{\overline{w}}_{i} - \mu^{2} \overline{N}_{F} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \ddot{\overline{w}}_{j} } \hfill \\ - K_{s} \overline{A}_{44} \eta \sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{w}_{j} } + \left( {\overline{A}_{12} - \frac{{\mu^{2} \overline{I}_{2} \overline{\omega }^{2} }}{{\eta^{2} }}} \right)\sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{\varphi }_{j} } + \left( {\frac{{\overline{I}_{2} \overline{\omega }^{2} }}{{\eta^{2} }} - K_{s} \overline{A}_{44} \eta^{2} } \right)\overline{\varphi }_{i} {\kern 1pt} \hfill \\ + \left( {\overline{F}_{31} \eta + K_{s} \overline{E}_{15} \eta } \right)\sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{\phi }_{j} } = \overline{I}_{2} \ddot{\overline{\varphi }}_{i} - \mu^{2} \overline{I}_{2} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \ddot{\overline{\varphi }}_{j} } \hfill \\ \overline{E}_{15} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{w}_{j} } + \left( {\overline{F}_{31} \eta + \overline{E}_{15} \eta } \right)\sum\limits_{j = 1}^{n} {c_{ij}^{1} \overline{\varphi }_{j} } + \overline{X}_{11} \sum\limits_{j = 1}^{n} {c_{ij}^{2} \overline{\phi }_{j} } - \overline{X}_{33} \eta^{2} \overline{\phi }_{i} = 0 \hfill \\ \end{gathered} \right.$$
(42)

where \(i = 2, \ldots ,N - 1\),\(N\) is the total number of sampling points on the piezoelectric nanobeam, and \(c_{ij}^{k}\) is the \(j\)-th weighting coefficient of the \(k\)-th differential in the \(i\) equation and the expressions of the correlation coefficients are as follows:

$$c_{ij}^{k} = k\left[ {c_{ii}^{k - 1} c_{ij}^{1} - \frac{{c_{ij}^{k - 1} }}{{\left( {x_{i} - x_{j} } \right)}}} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i,j = 1,2,...,n{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \ne j{\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{and}} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2 \le k \le n - 1} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,$$
(43)
$$\left\{ \begin{gathered} c_{ij}^{1} = \frac{{M\left( {x_{i} } \right)}}{{\left( {x_{i} - x_{j} } \right)M\left( {x_{j} } \right)}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i,j = 1,2,...,n{\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \ne j{\kern 1pt} {\kern 1pt} } \right) \hfill \\ c_{ii}^{k} = - \sum\limits_{j = 1,i \ne j}^{n} {c_{ij}^{k} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = 1,2,...,n{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,k = 1,2,...,n - 1} \right){\kern 1pt} \hfill \\ M\left( {x_{i} } \right) = \prod\limits_{j = 1,i \ne j}^{n} {\left( {x_{i} - x_{j} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = 1,2,...,n{\kern 1pt} {\kern 1pt} {\kern 1pt} } \right)} \hfill \\ x_{i} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\pi \left( {i - 1} \right)}}{n - 1}} \right]} \right\}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {i = 1,2,...,n} \right) \hfill \\ \end{gathered} \right.{\kern 1pt} .$$
(44)

The boundary conditions of the nanobeam clamped at both ends are expressed as follows:

$$\overline{w}_{1} = \overline{\varphi }_{1} = \overline{\phi }_{1} = 0,\overline{x} = 0,$$
(45)
$$\overline{w}_{N} = \overline{\varphi }_{N} = \overline{\phi }_{N} = 0,\overline{x} = 1.$$
(46)

The boundary conditions of the clamped-hinged supported nanobeam are expressed as follows:

$$\overline{w}_{1} = \overline{\varphi }_{1} = \overline{\phi }_{1} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{x} = 0,$$
(47)
$$\mathop { - \mu^{2} \eta \frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\sum\limits_{{m{ = }1}}^{N} {c_{Nm}^{1} \overline{w}_{m} } - \mu^{2} \eta \overline{N}_{F} \sum\limits_{{m{ = }1}}^{N} {c_{Nm}^{2} \overline{w}_{m} } { + }A_{12} \sum\limits_{{m{ = }1}}^{N} {c_{Nm}^{1} \overline{\varphi }_{m} } - \frac{{\mu^{2} \overline{I}_{2} \overline{\omega }^{2} }}{{\eta^{2} }}\sum\limits_{{m{ = }1}}^{N} {c_{Nm}^{1} \overline{\varphi }_{m} } { + }\overline{F}_{31} \overline{\phi }_{N} { = } - \mu^{2} \overline{I}_{0} \eta \ddot{\overline{w}}_{N} - \mu^{2} \overline{I}_{2} \sum\limits_{m = 1}^{N} {c_{Nm}^{1} \ddot{\overline{\varphi }}_{m} } }\limits_{{\overline{w}_{N} = \overline{\phi }_{N} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{x} = 1}} .$$
(48)

The boundary conditions of the clamped-free end nanobeam are expressed as follows:

$$\begin{gathered} K_{s} \overline{A}_{44} \sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{1} \overline{w}_{j} } - \mu^{2} \left( {\frac{{\partial^{2} \overline{N}_{F} }}{{\partial \overline{x}^{2} }}\sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{1} \overline{w}_{j} + 2\frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{2} \overline{w}_{j} + \overline{N}_{F} \sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{3} \overline{w}_{j} } } } } \right){ + }\eta \overline{\varphi }_{N} - K_{s} \overline{E}_{15} \sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{1} \overline{\phi }_{j} } { = } - \mu^{2} \overline{I}_{0} \sum\limits_{j = 1}^{N} {c_{Nj}^{1} \ddot{\overline{w}}_{j} } \hfill \\ - \mu^{2} \eta \frac{{\partial \overline{N}_{F} }}{{\partial \overline{x}}}\sum\limits_{j = 1}^{N} {c_{Nj}^{1} \overline{w}_{j} } - \mu^{2} \eta \overline{N}_{F} \sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{2} \overline{w}_{j} } { + }A_{12} \sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{1} \overline{\varphi }_{j} } - \frac{{\mu^{2} \overline{I}_{2} \overline{\omega }^{2} }}{{\eta^{2} }}\sum\limits_{{j{ = }1}}^{N} {c_{Nj}^{1} \overline{\varphi }_{j} } { + }\overline{F}_{31} \overline{\phi }_{N} { = } - \mu^{2} \overline{I}_{0} \eta \ddot{\overline{w}}_{N} - \mu^{2} \overline{I}_{2} \sum\limits_{j = 1}^{N} {c_{{N_{j} }}^{1} \ddot{\overline{\varphi }}_{j} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\phi }_{N} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{x} = 1. \hfill \\ \end{gathered}$$
(49)

Define the generalized displacement vector as

$${\text{d}} = \left\{ {\left. {\overline{w}_{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{w}_{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot \cdot \cdot ,\overline{w}_{N} ,\overline{\varphi }_{1} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \overline{\varphi }_{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot \cdot \cdot ,\overline{\varphi }_{N} {\kern 1pt} ,\overline{\phi }_{1} ,{\kern 1pt} {\kern 1pt} \overline{\phi }_{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \cdot \cdot \cdot ,\overline{\phi }_{N} {\kern 1pt} } \right\}} \right.^{T} ,$$
(50)

where \(\overline{w}_{i}\),\(\overline{\varphi }_{i}\) and \(\overline{\phi }_{i}\), respectively, represent the vibration lateral displacement value, rotation angle value and electric potential value of each selected point. The governing equations and boundary conditions can be expressed as a matrix

$${\text{M}} \ddot{d} + Kd = 0$$
(51)

where \({\text{M}}\) and \({\text{K}}\) are the equivalent mass matrix and equivalent stiffness matrix composed of dimensionless coefficients, respectively.

Let the form of its equation solution be

$${\text{d}} = {\text{d}}^{{\mathbf{*}}} e^{i\Omega \tau }$$
(52)

where \(\Omega\) represents the vibration frequencies of the nanobeam, and \({\text{d}}^{{\mathbf{*}}}\) are the modal vectors. Substituting Eq. (52) into Eq. (51), we can get

$$({\text{K}} - \Omega^{2} {\text{M}} ){\text{d}}^{*} = 0$$
(53)

The frequencies and modes can be obtained by solving the matrix Eq. (53).

Calculation Results and Analysis

In this paper, we use the examples in [51] to analyze the vibration characteristics of the rotating functional gradient piezoelectric nanobeam. When simulating the mechanics of nanoturbine or molecular motor, the length range of the model is described in detail in [52] and [53]. The length \(L = 10\,{\text{nm}}\) and height \(h\) of the beam is changed. The material parameters are shown in Table 1. To verify the validity of the model in this paper and the accuracy of the calculation, first consider the comparison between the results of the functionally graded piezoelectric nanobeam and the analytical method in [54] without rotation. The results in Table 2 show a good agreement.

Table 1 Properties of materials
Full size table
Table 2 Comparison of the results of natural frequencies for piezoelectric nanobeam
Full size table

When rotating piezoelectric nanobeam vibrates freely, its energy is mainly concentrated in the low order, so the first three-order vibrations are mainly studied in the following analysis.

Tables 3, 4 and 5 explore the effects of the nonlocal parameter \(\mu\) and the functional gradient index \(k\) on the first three dimensionless natural frequencies of the nanobeam under the three boundary conditions without rotation. It can be seen from the table that when the functional gradient index is determined under three boundary conditions, as the small-scale parameter increases, the first three dimensionless natural frequencies of the nanobeam gradually decrease, which indicates that when the nanobeam does not rotate, the increase of small-scale parameter weaken the equivalent stiffness of nanobeam and reduce its natural frequencies. For the cantilever beam, the increase of the small-scale parameter makes the fundamental frequency gradually increases, which is opposite to the change trend of the second and third-order frequencies. In summary, without rotation, the influence of small-scale parameter on the fundamental frequency of the nanobeam is related to the boundary conditions. In addition, the data in Tables 3, 4, and 5 show that during the gradual change of the material from pzt-4 to pzt-5, the change trend of the first three-order dimensionless natural frequencies of the nanobeam first decrease and then increase. The frequencies range of change are not large, that is, when the composition ratio of the two piezoelectric materials change exponentially, the change of physical parameters have little effect on the equivalent stiffness of the nanobeam. This is because the specific gravity of the two materials is the same, and the change of other material parameters has little effects on the stiffness.

Table 3 The effect of small-scale parameter and gradient index on dimensionless natural frequencies (C–C)
Full size table
Table 4 The effect of small-scale parameter and gradient index on dimensionless natural frequencies (C–H)
Full size table
Table 5 The effect of small-scale parameter and gradient index on dimensionless natural frequencies (C–F)
Full size table

The first three natural frequencies of the rotating nanobeam are calculated and compared using two beam models including Euler and Timoshenko in Table 6. It is shown that with the increase of the aspect ratio, the numerical results calculated by the two models gradually approach when the model changing from a thick beam to a thin one. Since the Timoshenko beam theory considers the effects of shear deformation and cross-section rotation around the neutral axis, the calculated values are less than the results of Euler beam theory. From the numerical data, it can also be analyzed that as the parameter \(\eta\) becomes larger, the flexibility of beam model becomes larger, resulting in a decrease in the stiffness and the natural frequencies.

Table 6 Comparison of the first three-order dimensionless natural frequencies of the two nanobeam models (\(\overline{\omega } = 1\), \(\overline{r} = 0.25\), \(\mu = 0.1\), \(k = 0\), \(V_{0} = 0\))
Full size table

Figures 2, 3 and 4 mainly explore the influence of the dimensionless rotational velocity \(\overline{\omega }\) on the first third-order dimensionless natural frequencies of the nanobeam under three boundary conditions. Taking, \(\overline{r} = 0.25\), \(\mu = 0.1\), \(k = 0\), \(V_{0} = 0\).When the geometric sizes of the nanobeam are determined, the first three dimensional dimensionless natural frequencies of the nanobeam increase with the increase of the dimensionless rotational velocity. This is due to the centrifugal force at each point change with the increase of the rotational velocity, and the stiffness of the beam gradually increase, which leads to the increase of dimensionless natural frequencies. It can be seen from the figures that the effects of the aspect ratio \(\eta\) on the first three dimensionless natural frequencies of the nanobeam are independent of the rotational velocity. As the parameter \(\eta\) becomes larger, the flexibility of the beam becomes larger, resulting in a decrease in the rigidity and the natural frequencies of the beam.

Fig. 2
figure 2

The relationship between dimensionless natural frequencies and rotational velocity for a beam clamped at both ends

Full size image
Fig. 3
figure 3

The relationship between dimensionless natural frequencies and rotational velocity for a clamped-hinged beam

Full size image
Fig. 4
figure 4

The relationship between dimensionless natural frequencies and rotational velocity for a cantilever beam

Full size image

Figure 5 shows the relationship between the first three dimensional dimensionless natural frequencies and the external voltage \(V_{0}\), when the nanobeam rotates at a constant speed under three conditions. Taking \(\overline{\omega } = 1\), \(\overline{r} = 0.25\), \(\mu = 0.1\), \(k = 3\), and \(\eta = 8\), it can be seen from the figures that when the voltage value \(V_{0}\) gradually increases, the first three-order dimensionless natural frequencies of the nanobeam gradually increase. From the change trend of the curve, it can be analyzed that, under the influence of the piezoelectric coefficient, the voltage leads to uniformly distributed physical forces in the axis direction of the nanobeam, so that each micro-segment of the beam is axially stretched, which enhances the stiffness of beam. The enhancements of effective stiffness increase its natural frequencies, so such a trend becomes more obvious as the positive voltage value increases. During the rotation of the piezoelectric nanobeam, the effects of the external voltage value on its natural frequencies are consistent with the law of change of the nanobeam without rotation in [55]. This is because the axial force generated under the actions of the voltage and the centrifugal force during rotation is linearly superimposed, and with the increases of the positive voltage value, the equivalent stiffness of the beam is further enhanced, so the natural frequencies increase. From Eq. (15), it can be seen that the axial force is linearly superposed by the centrifugal force and the pre-tightening force generated by the external voltage, so the influence of the axial force on the natural frequencies can be a linear combination of these two parts.

Fig. 5
figure 5

The relationship between dimensionless natural frequencies and external voltage

Full size image

Figure 6 studies the change of the first two-order dimensionless natural frequencies of the nanobeam clamped at both ends under the influence of small-scale parameter. Taking, \(\overline{r} = 0.25\), \(V_{0} = 0\), \(\eta = 8\), and k = 3, it can be seen from Fig. 6 that with the increases of the small-scale parameter, the dimensionless fundamental frequencies of the nanobeam gradually increase, and with the increase of the rotational velocity, the influence of the small-scale parameter on the frequencies are obviously nonlinear. When the dimensionless velocity is low, as the small-scale parameter increase, the second-order dimensionless natural frequencies of the nanobeam gradually decreases, but as the velocity increases, the increase of the small-scale parameter makes the second-order dimensionless frequencies change obviously. In this state, the increase of the small-scale parameter enhances the equivalent stiffness of the beam and thus, increases natural frequencies, which is contrary to the influence of small-scale parameter without rotation. In fact, this is the additional effect of the rotational motion of the nanobeam. The dynamic responses of rotating functionally graded nanobeams are influenced by both external kinematic factor and internal scale effect, both of which are independent and coupled with each other.

Fig. 6
figure 6

The effect of small-scale parameter on the first two-order dimensionless natural frequencies for a beam clamped at both ends

Full size image

Figure 7 studies the change law of the first two-order dimensionless natural frequencies of the nanobeam with the fixed-hinged boundary condition under the influence of small-scale parameters. Figure 7a shows that during the rotation of the piezoelectric nanobeam, the increase of small-scale parameter gradually increases the dimensionless fundamental frequencies of the nanobeam, and with the increase of the rotational velocity, this change law becomes more and more obvious. Figure 7b shows that when the dimensionless velocity is low, the increase of the small-scale parameter reduces the second-order dimensionless natural frequencies of the piezoelectric nanobeam. When the dimensionless velocity increases to a certain extent, the increase of small-scale parameter makes the second-order dimensionless natural frequencies of the nanobeam larger.

Fig. 7
figure 7

The effect of small-scale parameter on the first two-order dimensionless natural frequencies for a clamped-hinged beam

Full size image

Figure 8 studies the change law of the first two-order dimensionless natural frequencies of the cantilever beam under the influence of small-scale parameter. Figure 8a shows that during the rotation of the piezoelectric nanobeam, the increase of small-scale parameter gradually increases the dimensionless fundamental frequencies of the nanobeam, and with the increase of the rotational velocity, this change law becomes more and more obvious. Figure 8b shows that the increase of small-scale parameter increases the second-order dimensionless natural frequencies of the nanobeam, and the change law is obvious with the increase of the velocity.

Fig. 8
figure 8

The effect of small-scale parameter on the first two-order dimensionless natural frequencies for a cantilever beam

Full size image

It can be seen from Figs. 6, 7, and 8 that with the increases of the small-scale parameter, the dimensionless fundamental frequencies of the nanobeam gradually increase, and with the increase of the rotational velocity, the influence of the small-scale parameter on the frequencies are obviously nonlinear. This is because small-scale parameter has an important influence on the inherent properties of micro-scale structures, and this change becomes more obvious with the increase of small-scale parameter, and it has a nonlinear coupling effect with other parameters such as rotational velocity.

Figures 9, 10, and 11 depict the first three-order vibration mode diagrams of the nanobeam with three boundary conditions under the influence of different rotational velocity. Taking \(\overline{r} = 0.25\), \(\mu = 0.1\), \(k = 3\), \(V_{0} = 0\), and \(\eta = 8\), it can be seen from the figures that the change of the dimensionless velocity has effects on the modal shape of the nanobeam, and the modal shape change of the piezoelectric nanobeam with fixed-hinged boundary condition become more obvious. Under the three boundary conditions, the change of the velocity affects the positions of the amplitude point in the modal curves. As the dimensionless velocity increases, the coordinate positions of the amplitude point shift to the right.

Fig. 9
figure 9

The vibration mode for a nanobeam clamped at both ends

Full size image
Fig. 10
figure 10

The vibration mode for a clamped-hinged nanobeam

Full size image
Fig. 11
figure 11

The vibration mode for a cantilever nanobeam

Full size image

Conclusion

Based on the nonlocal theory, the free vibration behaviors of rotating functionally graded piezoelectric nanobeams are studied. The Timoshenko beam model is adopted, and the governing equations and boundary conditions are derived through the Hamilton principle. The natural frequencies are determined by the differential quadrature method. The influences of angular rotational velocity, nonlocal parameter, functional gradient index, slenderness ratio and external voltage on the natural frequencies are examined. The effects of rotational angular velocity on the structural modal are also analyzed. It is concluded that: (i) during the rotation of the piezoelectric nanobeam, the change of the rotational angular velocity has a great influence on the natural frequencies, and the change trend of the natural frequencies is proportional to the change of the rotational angular velocity. Essentially, the variation in rotational velocity changes the centrifugal forces at the cross-section of each point on the beam, causing an axial tensile deformation at the micro-segment of each point of the piezoelectric nanobeam, and it affects the equivalent stiffness of the beam. (ii) The relationship between the external positive voltage and the natural frequencies under three kinds of boundary conditions is not affected by the magnitude of the rotational angular velocity, and the axial force generated by the positive voltage at each micro-segment of the nanobeam is stretched and deformed, so that the rigidity of the piezoelectric nanobeam is enhanced and the natural frequencies increase. (iii) When the dimensionless rotational angular velocity increases to a certain value during the rotation of the piezoelectric nanobeam, the increase of the small-scale parameter enhances the equivalent stiffness of the nanobeam, and makes the frequencies increase. (iv) The influence of the rotational angular velocity on the vibrational mode shape is related to specific boundary conditions. Compared with the clamped–clamped and fixed-free boundary conditions, the shape of the first three vibration modes of the nanobeam under the fixed-hinged boundary condition is significantly affected by the rotational angular velocity. In addition, the increase of the rotational angular velocity shifts the amplitude point of the vibration mode to the right.