Application of the Green function method to flow-thermoelastic forced vibration analysis of viscoelastic carbon nanotubes

Abstract

In this paper, the Green function method (GFM) is implemented for forced vibration analysis of carbon nanotubes (CNTs) conveying fluid in thermal environment. The Eringen’s nonlocal elasticity theory is used to take into account the size effect of CNT with modeling the CNT wall–fluid flow interaction by means of slip boundary condition and Knudsen number (Kn). The derived governing differential equations are solved by GFM which demonstrated to have high precision and computational efficiency in the vibration analysis of CNTs. The validity of the present analytical solution is confirmed by comparing the results with those reported in other literature, and good agreement is observed. The analytical examinations are accomplished, while the emphasis is placed on considering the influences of nonlocal parameter, boundary conditions, temperature change, structural damping of the CNT, Knudsen number, fluid velocity and visco-Pasternak foundation on the dynamic deflection response of the fluid-conveying CNTs in detail.

1 Introduction

CNTs conveying fluid due to their outstanding mechanical, chemical and electrical properties have attracted worldwide attention in different applications such as fluid storages (Che et al. 1998), microfluidic and nanofluidic devices (Mattia and Gogotsi 2008), molecular and biological sensors (Yang et al. 2007) and drug-delivery devices (Bianco et al. 2005). Furthermore, it is one of the top subjects which are received great deal of attention by many researchers. For instance, Ghavanloo and Fazelzadeh (2011) investigated thermovibration and instability analysis of fluid-conveying CNT embedded in viscous fluid by using Galerkin method. Their examination determined that the eigenvalues and the related critical flow velocity could be affected by the nonlocal parameter, temperature change and structural damping of the CNT. Kiani (2013) studied vibration of embedded single-walled carbon nanotubes (SWCNTs) conveying viscous fluid based on the nonlocal elasticity theory. By using Galerkin method, he reported the effects of the small-scale parameter, inclination angle, speed and density of the fluid flow on the maximum dynamic amplitude of longitudinal and transverse displacements of the CNT. Bahaadini and Hosseini (2016a) inspected the influences of nonlocal parameter, Knudsen number, structural damping of the CNT and mass ratio on the eigenvalues and flutter flow velocity of a fluid-conveying CNT. In another study, Bahaadini and Hosseini (2016b) also scrutinized the nonlocal divergence and flutter instability analysis within CNTs conveying fluid flow. The obtained results by employed Galerkin method revealed the effects of nonlocal parameter, internal fluid flow, magnetic field and elastic foundation on the frequency and critical flow velocity of CNT. The forced vibration of CNTs containing fluid flow resting on nonlinear foundation and subjected to thermal environment has been studied by Askari and Esmailzadeh (2017) based on the nonlocal elasticity theory and surface effects. Wang et al. (2016) have investigated the dynamics of cantilevered CNTs conveying fluid subjected to longitudinal magnetic field using the differential quadrature method. Acoustic nanowave absorption through clustered fluid-conveying CNT has been studied by Zhang et al. (2016). The quantum effect on the microfluid-induced vibration of a nanotube in thermal environment has been performed by Zhang et al. (2017). The influences of nonlocal parameter, fluid velocity, mass ratio, visco-Pasternak medium, follower forces and surface effects on flow-induced flutter instability of CNTs have been performed by Bahaadini et al. (2017b). The various researchers modified flow velocity of nanoflow to analyze the slip boundary conditions between the flow and wall of nanotube (Bahaadini et al. 2017a; Hosseini et al. 2014; Mirramezani and Mirdamadi 2012; Rashidi et al. 2012; Sadeghi-Goughari and Hosseini 2015). Furthermore, some works regarding vibration analysis of CNTs could be found in the literature (Habibi et al. 2016; Hosseini et al. 2014, 2016a; Mohammadimehr et al. 2017; SafarPour and Ghadiri 2017; Zeighampour et al. 2017).

In many studies, various methods have been implemented to solve the mechanical problem, such as Galerkin method (Askari et al. 2013; Jafari et al. 2017), Ritz method (Lei et al. 2013; Mirzaei and Kiani 2016), Levy-type solution method (Hosseini et al. 2016b, c, d; Jamalpoor et al. 2017a, b), boundary element method (BEM) (Liu and Chen 2003; Liu et al. 2005, 2008), finite element method (FEM) (Husson et al. 2011; Tserpes and Papanikos 2005), Adomian decomposition method (Sweilam and Khader 2010), differential quadrature method (DQM) (Ansari et al. 2016; Ghorbanpour Arani et al. 2013; Hosseini et al. 2017a, b; Xia and Wang 2010), differential transfer method (DTM) (Hosseini and Sadeghi-Goughari 2016) and Green function method (GFM) (Li and Yang 2014).

In current study, the GFM is used to examine the dynamic deflection of viscoelastic CNTs conveying fluid subjected to different boundary conditions and thermal environments. The Green function method is a powerful tool for theoretical studies of various types of problems, but there are very limited studies in the literature that use this effective method to analysis the mechanical behavior of nano-/microscale structures. Based on the GFM, the third-harmonic susceptibility of zigzag CNTs was studied by Rezania and Daneshfar (2012). Yan et al. (2013) described the linear hydrodynamic nonlocal response of arbitrarily shaped nanowires in arbitrary inhomogeneous backgrounds via Green’s function surface-integral method. Mehdipour et al. (2012) determined the Green’s function for an infinitesimal horizontal electric dipole on a dielectric slab over a carbon-fiber composite ground plane having anisotropic conductivity. The GFM was applied to investigate the coefficient of thermal expansion in single-walled CNT and graphene by Jiang et al. (2009). In a related work in macroscale, Kukla and Zamojska (2007) examined free vibration of axially loaded stepped beam by using GFM. Based on the Laplace transform method and GFM, the Timoshenko beam model with various boundary conditions, Li et al. (2014) examined the forced vibration of beams with damping effects. Combination effects of frequency of harmonic force and internal moving fluid flow on the forced vibration of pipes conveying fluid under different boundary conditions were studied by Li and Yang (2014). In their study, by exploiting the Euler–Bernoulli beam theory, the problem was examined in the context of classical continuum theory via GFM. Zhao et al. (2015) analyzed the coupling effects between temperature and displacement fields through analytical solutions. For this purpose, the GFM and superposition principle is employed to solve the coupled thermoelastic vibration equations of a beam. Zhao et al. (2016) proposed a GFM to obtain closed-form expressions for the mechanical behavior of cracked Euler–Bernoulli beams. Chen et al. (2016) investigated forced vibration of Timoshenko beam model under axial forces. To this end, the GFM was implemented to solve a generalized equation of motion and the dynamic deflection and rotating angle for a beam with different supported ends. According to the classical circular plate theory and GFM, Ghannadiasl and Mofid (2016) studied free vibration of stepped plates embedded in a Winkler medium by consideration of internal elastic ring support.

A scrutiny of the literature reveals that the vibration and dynamic deflection of CNTs conveying fluid flow have been fairly well studied in the context of various numerical solutions. Some of investigation has been performed on the forced vibration analysis of various beam models using GFM. However, no inclusive study on the exact solution for flow-thermoelastic forced vibration analysis of CNTs with various boundary conditions by means of GFM has been covered so far. To this end, the CNT is modeled according to the nonlocal viscoelastic Euler–Bernoulli beam theory under various boundary conditions. By considering the interaction forces of the fluid flow on the CNT, the equation of motion is obtained in the framework of the Eringen’s nonlocal elasticity theory and slip boundary conditions and then is solved by using GFM. The influences of nonlocal parameter, fluid velocity, Knudsen number, temperature change, structural damping of the CNT, elastic foundations and boundary conditions on the maximum values of dynamic displacements of system are discussed.

2 Preliminary

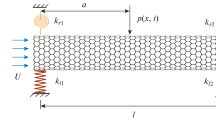
Figure 1 shows a schematic view of a fluid-conveying CNT of thickness h, outer radius R _o, inner radius R _i, length L and flexural rigidity EI. The CNT is supported by a visco-Pasternak medium which is assumed to be continuously connected to the CNT and is subjected to a harmonic force p at position l. Consider the Cartesian coordinate system (x, y, z) with the x-axis along the length of the deflected CNT, the z-axis along the neutral axis and the y-axis along the transverse direction. The transverse CNT displacement at the axial coordinate x and time t is shown by w(x, t). The governing equations of motion (Eq. (1)) and the related boundary conditions (Eq. (2a–2b)) based on viscoelastic CNTs conveying fluid using nonlocal Euler–Bernoulli beam theory and considering visco-Pasternak foundation will be attained as (Arani and Amir 2013; Bahaadini and Hosseini 2016a; Ghavanloo and Fazelzadeh 2011):

$${\text{EI}}\left( {1 + g\frac{\partial }{\partial t}} \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} + \left( {1 - \left( {e_{0} a} \right)^{2} \frac{{\partial^{2} }}{{\partial x^{2} }}} \right)\left[ {\left( {MU_{\text{avg,slip}}^{2} - N^{\text{T}} - K_{\text{G}} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2MU_{\text{avg,slip}} \frac{{\partial^{2} w}}{\partial x\partial t} + \left( {M + m} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t} + K_{\text{w}} w - p\left( {x,t} \right)} \right] = 0$$

(1)

$${\text{EI}}\left( {1 + g\frac{\partial }{\partial t}} \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} - \left( {e_{0} a} \right)^{2} \left[ {\left( {MU_{\text{avg,slip}}^{2} - N^{\text{T}} - K_{\text{G}} } \right)\frac{{\partial^{2} w}}{{\partial x^{2} }} + 2MU_{\text{avg,slip}} \frac{{\partial^{2} w}}{\partial x\partial t} + \left( {M + m} \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + C\frac{\partial w}{\partial t} + K_{\text{w}} w - p\left( {x,t} \right)} \right] = 0\;{\text{or}}\;\frac{\partial \delta w}{\partial x} = 0$$

(2a)

$$- \,{\text{EI}}\left( {1 + g\frac{\partial }{\partial t}} \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} + \left( {e_{0} a} \right)^{2} \left[ {\left( {MU_{\text{avg,slip}}^{2} - N^{\text{T}} - K_{\text{G}} } \right)\frac{{\partial^{3} w}}{{\partial x^{3} }} + 2MU_{\text{avg,slip}} \frac{{\partial^{3} w}}{{\partial x^{2} \partial t}} + \left( {M + m} \right)\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }} + C\frac{{\partial^{2} w}}{\partial x\partial t} + K_{\text{w}} \frac{\partial w}{\partial x} - \frac{{\partial p\left( {x,t} \right)}}{\partial x}} \right] + \left( {N^{\text{T}} + K_{\text{G}} } \right)\frac{\partial w}{\partial x} = 0\,{\text{or}}\;\delta w = 0$$

(2b)

where M and m are the mass per unit length of fluid and the CNT, respectively, and K _w, K _G and C denote the Winkler, Pasternak and damping of visco-Pasternak foundation, respectively. Also, e ₀ is a material constant, and a is the internal characteristic length. Therefore, e ₀ a shows the nonlocal parameter that includes the small-scale effects into the constitutive equations for forced vibration of CNT. As indicated in Eqs. (1) and (2a), nonlocal elasticity theory is strongly dependent on the proper value of the nonlocal parameter. However, it was found that various parameters such as crystal structure in lattice dynamics, mode shapes, aspect ratio and boundary conditions have a considerable effect on the appropriate values of nonlocal parameter (Ansari and Sahmani 2012; Duan et al. 2007; Hu et al. 2011; Narendar and Gopalakrishnan 2011). Therefore, choice of the optimized value for nonlocal parameter is crucial to calibrate the non-locality effect, whereas there are no experiments conducted to obtain the value of nonlocal parameter. Details of the various values of nonlocal parameter as described by various researchers can be found in Ansari and Sahmani (2012), Duan et al. (2007), Ghavanloo and Fazelzadeh (2016) and Narendar and Gopalakrishnan (2011). For CNTs and graphene sheets, the range of e ₀ a = 0–2 nm has been widely used because the exact value of the nonlocal parameter is not known (Karlicic et al. 2015; Tiwari 2013; Wang et al. 2006).

Fig. 1

Viscoelastic CNTs conveying fluid embedded in visco-Pasternak foundation

In addition, g is viscoelastic structural damping coefficient of Kelvin’s model on elastic material. This viscoelastic properties, as reported by Xu et al. (2010), may be due to zipping–unzipping mechanism between CNT and CNT contacts which lead to energy dissipation. Some additional mechanism of energy dissipation may also be happen and causes viscoelastic damping properties in CNTs (Gogotsi 2010).Viscoelastic damping may also denote certain polymer matrix, van der Waals forces or other external damping effects. So, the vibration of CNTs conveying fluid can be repressed by counting viscoelastic damping properties. Thus, the size-dependent effect and viscoelastic behavior of CNT structure may be more realistic due to the presence of energy dissipation problem at nanoscales.

There are very limited direct experimental data on the viscoelastic properties of the CNT. However, a number of researchers have reported the quality factor Q (the inverse of the energy dissipation) in CNT (Lassagne et al. 2008; Qian and Zhou 2011; Sazonova et al. 2004). Based on the viscoelasticity model represented by Kelvin model, the Q factor can be defined as ratio between the storage and loss modulus in a viscoelastic material which is related to a measure of structural damping (Zhou et al. 2011). The CNT with high-quality factors has lower rate of energy loss relative to the stored energy so that they have low damping. It was found that chirality had no noticeable effect on the CNT viscoelastic properties, while they are strongly dependent on the tube radius of CNTs in which Q factor is reduced with increase in CNT radius (Qian and Zhou 2011; Zhou et al. 2011). For CNT with tube diameters in range of 1–4 nm, Sazonova et al. (2004) reported that Q factor is in the range of 40–200 for a resonant frequency 55 MHz.

While the CNT ends are restrained both axially, a thermal axial force N ^T will be induced in the structure due to temperature changes as:

$$N^{\text{T}} = - \frac{EA}{1 - 2v}\alpha_{x} \Delta T$$

(3)

where A is the cross-sectional area, v is Poisson’s ratio, α _x denotes the coefficient of thermal expansion in the direction of the x-axis and ΔT is temperature change. Based on the thermal elasticity mechanics theory, the Young’s modulus of CNT is insensitive to temperature change in the tube when the temperature is lower than approximately 1100 K (Hsieh et al. 2006). Furthermore, it is apparent that Poisson’s ratio increases with temperature although the augmentation is limited and can be measured constant at temperatures between 300 and 1200 K (Scarpa et al. 2010). Moreover, the temperature dependence of radial and axial coefficient of thermal expansion has been studied by Hwang (2004) and it was concluded that coefficients are negative at low or room temperature and become positive at high temperature.

In addition, it should be mentioned that in nanoscale, Rashidi et al. (2012) developed a modified nanotube that incorporates nanoflow viscosity and slip boundary condition. With considering the Knudsen number, one can model the slip boundary conditions between the nanoflow and walls of nanotube properly. It should be noted that Knudsen number, i.e., the ratio of the molecular mean free path length to a representative physical length scale, can be used to identify flow regime: (1) 0 < Kn < 10⁻² for continuum flow regime; (2) 10⁻² < Kn < 10⁻¹for slip flow regime; (3) $10^{ - 1} < Kn < 10$ for transition flow regime; and (4) Kn > 10 for free molecular flow regime (Karniadakis et al. 2005). For CNTs conveying fluid, it could be possible that Kn be larger than 10⁻². Therefore, by considering Knudsen number, the flow velocity can be expressed as U _avg,slip = VCF × U _{avg,(no-slip)} where U _avg,slip and U _{avg,(no-slip)} are the average fluid velocities through nanotube with slip boundary conditions and without slip boundary conditions, respectively. Also, VCF is the average velocity correction factor, which is described in more detail in “Appendix 1”.

Hereafter, for simplicity, the following dimensionless quantities are defined:

$$\begin{aligned} & \xi = \frac{x}{L},\quad \eta = \frac{w}{L},\quad \mu = \frac{{e_{0} a}}{L},\quad \ell = \frac{l}{L},\quad \tau = \sqrt {\frac{\text{EI}}{{\left( {M + m} \right)}}} \frac{t}{{L^{2} }},\quad u = \sqrt {\frac{M}{\text{EI}}} v_{{{\text{avg}}\left( {\text{no - slip}} \right)}}^{{}} L,\quad \beta = \frac{M}{M + m}, \\ & N = \frac{{N^{\text{T}} L^{2} }}{\text{EI}},\quad c = \frac{{CL^{2} }}{{\sqrt {{\text{EI}}\left( {M + m} \right)} }},\quad \alpha = \sqrt {\frac{EI}{{\left( {M + m} \right)}}} \frac{g}{{L^{2} }},\quad \omega = \sqrt {\frac{{\left( {M + m} \right)}}{\text{EI}}} \varOmega L^{2} , \\ & q\left( {\xi ,\tau } \right) = \frac{{p\left( {x,t} \right)L^{3} }}{\text{EI}},\quad k_{\text{w}} = \frac{{K_{\text{w}} L^{4} }}{\text{EI}},\quad k_{\text{G}} = \frac{{K_{\text{G}} L^{2} }}{\text{EI}} \\ \end{aligned}$$

(4)

Therefore, the non-dimensional governing equations of motion and the associated boundary conditions of the CNT with considering velocity correction factor VCF can be stated as:

$$\left( {1 + \alpha \frac{\partial }{\partial \tau }} \right)\frac{{\partial^{4} \eta }}{{\partial \xi^{4} }} + \left( {1 - \mu^{2} \frac{{\partial^{2} }}{{\partial \xi^{2} }}} \right)\left[ {\left( {\left( {{\text{VCF}} \times u} \right)^{2} - N - k_{\text{G}} } \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} +\,2\left( {{\text{VCF}} \times u} \right)\sqrt \beta \frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } +\,\frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} + c\frac{\partial \eta }{\partial \tau } + k_{\text{w}} \eta - q\left( {\xi ,\tau } \right)} \right] = 0$$

(5)

For pinned–pinned (P–P) boundary condition

at ξ = 0, 1

$$\eta = 0,$$

$$- \,\left( {1 + \alpha \frac{\partial }{\partial \tau }} \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + \mu^{2} \left[ {\left( {\left( {{\text{VCF}} \times u} \right)^{2} - N - k_{\text{G}} } \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + 2\left( {{\text{VCF}} \times u} \right)\sqrt \beta \frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } + \frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} + c\frac{\partial \eta }{\partial \tau } + k_{\text{w}} \eta - q\left( {\xi ,\tau } \right)} \right] = 0$$

(6)

For clamped–pinned (C–P) boundary condition

at ξ = 0

$$\eta = \frac{\partial \eta }{\partial \xi } = 0$$

at ξ = 1

$$\eta = 0,$$

$$- \,\left( {1 + \alpha \frac{\partial }{\partial \tau }} \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + \mu^{2} \left[ {\left( {\left( {{\text{VCF}} \times u} \right)^{2} - N - k_{\text{G}} } \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} +\,2\left( {{\text{VCF}} \times u} \right)\sqrt \beta \frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } + \frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} + c\frac{\partial \eta }{\partial \tau } + k_{\text{w}} \eta - q\left( {\xi ,\tau } \right)} \right] = 0$$

For clamped–clamped (C–C) boundary condition

at ξ = 0, 1

$$\eta = \frac{\partial \eta }{\partial \xi } = 0$$

Let us define harmonic concentrate force, q, as:

$$q\left( {\xi ,\tau } \right) = F_{0} \delta \left( {\xi - l} \right)e^{\omega \tau i}$$

(7)

where δ (·) is the Dirac delta function, ω is the excitation frequency and ℓ is non-dimensional position of the concentrated force.

3 Application of GFM to solve the forced vibration of CNT conveying fluid

Different analytical techniques can be implemented to solve the governing equation and related boundary conditions. Among them, the GFM has revealed a great potential in solving complicated partial differential equations and has been successfully applied in many examinations. In current study, the size-dependent thermomechanical dynamic deflection of CNTs conveying fluid resting on visco-Pasternak medium with different boundary conditions is studied using analytical GFM. Thus, the results obtained by the present solution are accurate than those in previous results. In order to eliminate time variable from Eq. (5), substitute the expression η(ξ, τ) = X(ξ)e ^ωτi and Eq. (7) into Eq. (5). Consequently, the steady-state vibration equation of CNT conveying fluid is recasted to

$$\lambda_{1} \frac{{\partial^{4} X\left( \xi \right)}}{{\partial \xi^{4} }} + \lambda_{2} \frac{{\partial^{3} X\left( \xi \right)}}{{\partial \xi^{3} }} + \lambda_{3} \frac{{\partial^{2} X\left( \xi \right)}}{{\partial \xi^{2} }} + \lambda_{4} \frac{\partial X\left( \xi \right)}{\partial \xi } + \lambda_{5} X\left( \xi \right) = \left( {1 - \mu^{2} \frac{{\partial^{2} }}{{\partial \xi^{2} }}} \right)f\left( \xi \right)$$

(8)

where

$$\begin{aligned} \lambda_{1} & = 1 + \omega \alpha i - \mu^{2} \left( {\left( {{\text{VCF}} - u} \right)^{2} - N - k_{\text{G}} } \right) \\ \lambda_{2} & = - 2\omega \mu^{2} \left( {{\text{VCF}} \times u} \right)\sqrt \beta i \\ \lambda_{3} & = \left( {{\text{VCF}} \times u} \right)^{2} - N - k_{\text{G}} - \mu^{2} \left( {k_{\text{w}} + \omega ci - \omega^{2} } \right) \\ \lambda_{4} & = 2\omega \left( {{\text{VCF}} \times u} \right)\sqrt \beta i \\ \lambda_{5} & = k_{\text{w}} + \omega ci - \omega^{2} \\ \end{aligned}$$

(9)

According to superposition principle, the solution of Eq. (8) can be written in the following form (Nicholson and Bergman 1986):

$$X\left( \xi \right) = \int_{0}^{1} {f\left( {\xi_{0} } \right)G\left( {\xi ,\xi_{0} } \right){\text{d}}\xi_{0} }$$

(10)

where G(ξ, ξ ₀) denotes the Green’s function. Physically, a Green’s function of the steady-state vibration equation of the beam is the deflection of its steady-state response due to a unit concentrated harmonic stimulus acting at an arbitrary position. Therefore, to obtain the Green function, we first consider f(ξ) = δ(ξ − ξ ₀) in Eq. (8) and then take Laplace transform on both sides of the equation in terms of the variable ξ which lead to the following equation:

$$\begin{aligned} \bar{X}\left( {s,\xi_{0} } \right) & = \frac{1}{{\varLambda_{1} }}\left[ {\left( {1 - \mu^{2} s^{2} } \right)e^{{ - s\xi_{0} }} + \varLambda_{2} X\left( 0 \right) + \varLambda_{3} X^{\prime } \left( 0 \right) + \varLambda_{4} X^{\prime \prime } \left( 0 \right) + \lambda_{1} X^{\prime \prime \prime } \left( 0 \right)} \right], \\ \varLambda_{1} & = \lambda_{1} s^{4} + \lambda_{2} s^{3} + \lambda_{3} s^{2} + \lambda_{4} s + \lambda_{5} \\ \varLambda_{2} & = \lambda_{1} s^{3} + \lambda_{2} s^{2} + \lambda_{3} s + \lambda_{4} \\ \varLambda_{3} & = \lambda_{1} s^{2} + \lambda_{2} s + \lambda_{3} \\ \varLambda_{4} & = \lambda_{1} s + \lambda_{2} \\ \end{aligned}$$

(11)

where s is a complex Laplace variable and $\bar{X}\left( {s,\xi_{0} } \right)$ is Laplace transform of X(s, ξ ₀); further, X(0), X′(0), X′′(0) and X′′′(0) are constants to be determined from the boundary conditions. To obtain Green function, by performing the inverse Laplace transform of Eq. (11), we arrive at

$$G\left( {\xi ,\xi_{0} } \right) = X\left( {\xi ,\xi_{0} } \right) = L^{ - 1} \left[ {\bar{X}\left( {s,\xi_{0} } \right)} \right] = \phi_{1} \left( \xi \right)X\left( 0 \right) + \phi_{2} \left( \xi \right)X^{\prime } \left( 0 \right) + \phi_{3} \left( \xi \right)X^{\prime \prime } \left( 0 \right) + \lambda_{1} \phi_{4} \left( \xi \right)X^{\prime \prime \prime } \left( 0 \right) + \phi_{4} \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) - \mu^{2} \phi_{5} \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right)$$

(12)

where H(·) is the Heaviside function and ϕ _i (ξ) (i = 1, 2, …, 5) are

$$\begin{aligned} \phi_{1} (\zeta ) & = \sum\limits_{i = 1}^{4} {R_{i} (\zeta )} \left( {\lambda_{1} s_{i}^{3} + \lambda_{2} s_{i}^{2} + \lambda_{3} s_{i} + \lambda_{4} } \right),\quad \phi_{2} \left( \zeta \right) = \sum\limits_{i = 1}^{4} {R_{i} \left( \zeta \right)\left( {\lambda_{1} s_{i}^{2} + \lambda_{2} s_{i} + \lambda_{3} } \right),} \\ \phi_{3} \left( \zeta \right) & = \sum\limits_{i = 1}^{4} {R_{i} \left( \zeta \right)\left( {\lambda_{1} s_{i} + \lambda_{2} } \right),} \quad \phi_{4} \left( \zeta \right) = \sum\limits_{i = 1}^{4} {R_{i} \left( \zeta \right),} \quad \phi_{5} \left( \zeta \right) = \sum\limits_{i = 1}^{4} {R_{i} \left( \zeta \right)s_{i}^{2} } \\ \end{aligned}$$

(13)

with

$$\begin{aligned} R_{1} (\zeta ) & =\,\frac{{e^{{s_{1} \zeta }} }}{{(s_{1} - s_{2} )(s_{1} - s_{3} )(s_{1} - s_{4} )}},\quad R_{2} (\zeta ) = \frac{{e^{{s_{2} \zeta }} }}{{(s_{2} - s_{1} )(s_{2} - s_{3} )(s_{2} - s_{4} )}}, \\ R_{3} (\zeta ) & = \frac{{e^{{s_{3} \zeta }} }}{{(s_{3} - s_{1} )(s_{3} - s_{2} )(s_{3} - s_{4} )}},\quad R_{4} (\zeta ) = \frac{{e^{{s_{4} \zeta }} }}{{(s_{4} - s_{1} )(s_{4} - s_{2} )(s_{4} - s_{3} )}}. \\ \end{aligned}$$

(14)

Also, s _i (i = 1, …, 4) are roots of the left-hand term of equation $\varLambda_{1} = 0$. The first, second and third derivatives of X(ξ, ξ ₀) in terms of ξ for $\xi \ge \xi_{0}$ are given by:

$$\begin{aligned} X^{\prime } \left( {\xi ,\xi_{0} } \right) & = \phi_{1}^{\prime } \left( \xi \right)X\left( 0 \right) + \phi_{2}^{\prime } \left( \xi \right)X^{\prime } \left( 0 \right) + \phi_{3}^{\prime } \left( \xi \right)X^{\prime \prime } \left( 0 \right) + \lambda_{1} \phi_{4}^{\prime } \left( \xi \right)X^{\prime \prime \prime } \left( 0 \right) \\ & \quad + \phi_{4}^{\prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) - \mu^{2} \phi_{5}^{\prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) \\ \end{aligned}$$

(15)

$$\begin{aligned} X^{\prime \prime } \left( {\xi ,\xi_{0} } \right) & = \phi_{1}^{\prime \prime } \left( \xi \right)X\left( 0 \right) + \phi_{2}^{\prime \prime } \left( \xi \right)X^{\prime } \left( 0 \right) + \phi_{3}^{\prime \prime } \left( \xi \right)X^{\prime \prime } \left( 0 \right) + \lambda_{1} \phi_{4}^{\prime \prime } \left( \xi \right)X^{\prime \prime \prime } \left( 0 \right) \\ & \quad + \phi_{4}^{\prime \prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) - \mu^{2} \phi_{5}^{\prime \prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) \\ \end{aligned}$$

(16)

$$\begin{aligned} X^{\prime \prime \prime } \left( {\xi ,\xi_{0} } \right) & = \phi_{1}^{\prime \prime \prime } \left( \xi \right)X\left( 0 \right) + \phi_{2}^{\prime \prime \prime } \left( \xi \right)X^{\prime } \left( 0 \right) + \phi_{3}^{\prime \prime \prime } \left( \xi \right)X^{\prime \prime } \left( 0 \right) + \lambda_{1} \phi_{4}^{\prime \prime \prime } \left( \xi \right)X^{\prime \prime \prime } \left( 0 \right) \\ & \quad + \phi_{4}^{\prime \prime \prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) - \mu^{2} \phi_{5}^{\prime \prime \prime } \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) \\ \end{aligned}$$

(17)

Inserting ξ = 1 into Eqs. (12), (15–17) and substituting them into boundary conditions where it is needed and with further manipulations, the following relation in matrix form can be expressed as:

$$\left[ {\begin{array}{*{20}l} {A_{11} } \hfill & {A_{12} } \hfill & {A_{13} } \hfill & {A_{14} } \hfill \\ {A_{21} } \hfill & {A_{22} } \hfill & {A_{23} } \hfill & {A_{24} } \hfill \\ {A_{31} } \hfill & {A_{32} } \hfill & {A_{33} } \hfill & {A_{34} } \hfill \\ {A_{41} } \hfill & {A_{42} } \hfill & {A_{43} } \hfill & {A_{44} } \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} {X(0)} \hfill \\ {X^{\prime } (0)} \hfill \\ {X^{\prime \prime } (0)} \hfill \\ {X^{\prime \prime \prime } (0)} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {B_{11} } \hfill \\ {B_{21} } \hfill \\ {B_{31} } \hfill \\ {B_{41} } \hfill \\ \end{array} } \right]$$

(18)

For fluid-conveying CNT, “Appendix 2” lists the coefficient matrix elements A _ij and B _ij from which the constants X(0), X ^′(0), X ^′′(0) and X ^′′′(0) can be determined completely for each boundary conditions. Then, by substituting these constants into Eq. (12) the Green function is determined. Thus, inserting Green function and f(ξ ₀) = F ₀ δ(ξ ₀ − ℓ) into Eq. (10) yields the following equation

$$X\left( \xi \right) = \int_{0}^{1} {F_{0} \delta \left( {\xi_{0} - \ell } \right)\left[ {\phi_{1} \left( \xi \right)X\left( 0 \right) + \phi_{2} \left( \xi \right)X^{\prime } \left( 0 \right) + \phi_{3} \left( \xi \right)X^{\prime \prime } \left( 0 \right) + \lambda_{1} \phi_{4} \left( \xi \right)X^{\prime \prime \prime } \left( 0 \right)} \right]{\text{d}}\xi_{0} } + \int_{0}^{1} {F_{0} \delta \left( {\xi_{0} - \ell } \right)\left[ {\phi_{4} \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right) - \mu^{2} \phi_{5} \left( {\xi - \xi_{0} } \right)H\left( {\xi - \xi_{0} } \right)} \right]{\text{d}}\xi_{0} }$$

(19)

The relation of delta function can be expressed as:

$$\int_{{\alpha_{0} }}^{{\beta_{0} }} {\phi_{i} \left( \xi \right)\delta \left( {\xi - \xi_{0} } \right){\text{d}}\xi = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\xi_{0} < \alpha_{0} } \hfill \\ {\phi_{i} \left( {\xi_{0} } \right)} \hfill & {\alpha_{0} < \xi_{0} < \beta_{0} } \hfill \\ 0 \hfill & {\xi_{0} > \beta_{0} } \hfill \\ \end{array} } \right.}$$

(20)

Therefore, the first and second integrations are given by:

$$I_{1} \left( \xi \right) = F_{0} \left\{ {\phi_{1} \left( \xi \right)\left[ {X\left( 0 \right)} \right]_{{\xi_{0} = \ell }} + \phi_{2} \left( \xi \right)\left[ {X^{\prime } \left( 0 \right)} \right]_{{\xi_{0} = \ell }} + \phi_{3} \left( \xi \right)\left[ {X^{\prime \prime } \left( 0 \right)} \right]_{{\xi_{0} = \ell }} + \lambda_{1} \phi_{4} \left( \xi \right)\left[ {X^{\prime \prime \prime } \left( 0 \right)} \right]_{{\xi_{0} = \ell }} } \right\}$$

(21a)

$$I_{2} \left( \xi \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {0 < \xi < l} \hfill \\ {F_{0} \left\{ {\phi_{4} \left( {\xi - \ell } \right) - \mu^{2} \phi_{5} \left( {\xi - \ell } \right)} \right\}} \hfill & {l < \xi < 1} \hfill \\ \end{array} } \right.$$

(21b)

Thus, the dynamic response of the CNT conveying fluid is written as:

$$X\left( \xi \right) = I_{1} \left( \xi \right) + I_{2} \left( \xi \right)$$

(22)

The dynamic response obtained from Eq. (22) is in general complex. Therefore, the real form of dynamic response of the CNT conveying fluid can be written as:

$$\eta \left( {\xi ,\tau } \right) = Re \left[ {X\left( \xi \right)} \right]\cos \left( {\omega \tau } \right) - Im \left[ {X\left( \xi \right)} \right]\sin \left( {\omega \tau } \right)$$

(23)

4 Results and discussion

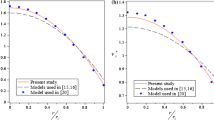
In all numerical calculations in this section, it was assumed that CNT carries a harmonic concentrated force at the mid-span (ℓ = 0.5). In order to justify the validity of the present analysis, the natural frequency and maximum deflection of CNT conveying fluid obtained by the present solution are compared with those in previous results. For this purpose, Fig. 2 depicts the variation of maximum dynamic deflection for the pinned–pinned CNT versus excitation frequency. It can be seen that with increase in excitation frequency, the maximum dynamic deflection of the system first increases and then tends to decrease. Also, the excitation frequency at which the maximum dynamic deflection is reached is related to the natural frequency. Therefore, the achieved first four dimensionless natural frequencies which are obtained by this method are compared with those reported by Wang et al. (2007) and good agreement is observed. The calculation of maximum dynamic deflection for clamped–clamped boundary conditions is similar to that for P–P boundary condition, but not shown here. Also, the results of natural frequencies are tabulated in Table 1. It should be mentioned that to compare the results with those proposed by Wang et al. (2007), the effects of the Knudsen number, temperature change and visco-Pasternak foundation are assumed to be neglected. Moreover, the natural frequencies predicted by using the nonlocal theory (μ ≠ 0) are always lower than those obtained by the classical theory (μ = 0). This means that the effect of nonlocal parameter softens the CNTs and consequently causes to increase in maximum dynamic deflections. Furthermore, the comparison of the maximum dynamic deflections of CNT without considering the nonlocal effect, Knudsen number and viscoelastic Pasternak medium is presented in Table 2, for different values of fluid velocities against results presented by Li and Yang (2014). It is observed from Table 2 that the current model is actually in good agreement with previous models. After this verification, it was discussed on the numerical results concerned with the forced vibration response of viscoelastic CNTs conveying fluid subjected to thermal field and resting on visco-Pasternak foundation with various boundary conditions. Therefore, this section assigned to show the effects of nonlocal parameter, fluid velocity, visco-Pasternak foundation, Knudsen number, structural damping of CNT, temperature change and various boundary conditions on the dynamic deflections of CNT in several numerical examples. In this regard, the values for several physical parameters of the system are with the following data (Ávila and Lacerda 2008; Mirramezani and Mirdamadi 2012; Yakobson et al. 1996; Yao and Han 2008):

Fig. 2

Dimensionless maximum dynamic deflection of pinned–pinned CNT versus dimensionless excitation frequency for α = 0, $\Delta T = 0$, u = 0, $\beta = 0.5$, Kn = 0, F = 2, ξ = 0.3, k _w = 0, k _G = 0, c = 2: a near ω ₁, b near ω ₂, c near ω ₃, d near ω ₄

Table 1 Comparison of the four first frequency parameters $\sqrt \omega$ obtained from the present model with the results reported by Wang et al. (2007) for α = 0, $\Delta T = 0$, u = 0, $\beta = 0.5$, Kn = 0, F = 2, k _w = 0, k _G = 0, c = 2

Table 2 Comparison of the maximum deflections obtained from the present study with the results obtained by Li and Yang (2014) for a clamped–clamped pipe conveying fluid at position ξ = 0.8536

$$E = 5.5\;{\text{TPa}},\quad v = 0.2,\quad \rho_{\text{CNT}} = 2300\,{\text{kg/m}}^{3} ,\quad \rho_{\text{f}} = 790\,{\text{kg/m}}^{3} ,\quad 2R_{\text{o}} = 1\,{\text{nm}},\quad h = 0.066\,{\text{nm}},\quad L /2R_{\text{o}} = 10$$

On the basis of the reported results by Sazonova et al. (2004), the viscoelastic structural damping coefficient (g) may vary from 0 to 1.45 × 10⁻¹¹ s for the problem under investigation. So, we will use a conservative range of dimensionless viscoelastic damping coefficient α from 0 to 1. Also, in this paper, the nonlocal and material length scale parameter $e_{0} a$ will vary from 0 to 2 nm (μ = 0–0.2).

Figures 3 and 4 illustrate the dimensionless maximum dynamic deflection versus nonlocal parameter for different boundary conditions and various values of fluid velocities, respectively. Figure 3 reveals that by increasing the value of nonlocal parameter, the dimensionless maximum dynamic deflection of CNT conveying fluid increases. In other words, with the increase in nonlocal parameter, the CNT stiffness decreases and dimensionless maximum dynamic deflection increases. Figure 4 shows that by increasing the value of fluid velocity, the dimensionless maximum dynamic deflection of clamped–clamped CNT conveying fluid increases.

Fig. 3

Effects of the boundary conditions on the dimensionless maximum dynamic deflection versus dimensionless nonlocal parameter for α = 0, $\Delta T = 0$, β = 0.5, Kn = 0.01, ω = 4, F = 2, u = 2, k _w = 0, k _G = 0, c = 0

Fig. 4

Effects of the fluid velocities on the dimensionless maximum dynamic deflection versus dimensionless nonlocal parameter for α = 0, $\Delta T = 0$, β = 0.5, Kn = 0.01, ω = 4, F = 2, ξ = 0.3, k _w = 0, k _G = 0, c = 0 and clamped–clamped boundary conditions

The structural damping coefficient of CNT on the dimensionless maximum dynamic deflection of a clamped-pinned CNT conveying fluid is studied as shown in Fig. 5. As seen in these figures, by increasing the structural damping coefficient, the dimensionless maximum dynamic deflection of the system decreases. In Fig. 5a, b, the influences of nonlocal parameter and mass ratio on the variation of dimensionless maximum dynamic deflection versus structural damping coefficient of CNT are shown. With the increase in nonlocal parameter and mass ratio, dimensionless maximum dynamic deflection decreases. As shown in Fig. 5c, by increasing the fluid velocity, the dimensionless maximum dynamic deflection increases. It can be seen that for α > 0.8, the fluid velocity has not more significant effect on dimensionless maximum dynamic deflection.

Fig. 5

Maximum dimensionless dynamic deflection in terms of structural damping coefficient of clamped-pinned CNT for ΔT = 0, Kn = 0.01, ω = 4, F = 2, ξ = 0.3, k _w = 0, k _G = 0, $c = 0$ and different values of: a μ (β = 0.5 and u = 2), b β (μ = 0.1 and u = 2), c u (μ = 0.1 and $\beta = 0.5$)

Figure 6 indicates effect of elastic foundation, including Winkler, Pasternak and visco-Pasternak mediums on dimensionless maximum dynamic deflection of clamped–clamped CNT as a function of ξ. It is seen that dimensionless maximum dynamic deflection is dependent on the spring, shear and damping modulus of the surrounding foundation. Also, it is observed from the figure that the dimensionless maximum dynamic deflection predicted by visco-Pasternak foundation is smaller than that predicted by Winkler foundation, and it is due to the more elastic foundation stiffness that predicted in visco-Pasternak medium model in comparison with other models.

Fig. 6

Effects of the elastic foundation on the dimensionless maximum dynamic deflection versus dimensionless ξ for α = 0.001, ΔT = 0, β = 0.5, μ = 0.05, Kn = 0.01, ω = 4, F = 2 and clamped–clamped boundary conditions

Effect of the temperature change on dimensionless maximum dynamic deflection of the clamped–clamped CNT conveying fluid is presented in Fig. 7. The results are shown in two coefficients of thermal expansion corresponding to room or low temperature (α _x  = − 1.6 × 10⁻⁶1/K) and high temperature (α _x  = 1.1 × 10⁻⁶1/K). For the case of room or low temperature, the dimensionless maximum dynamic deflection decreases with increasing the temperature change, whereas resonance frequency of forced vibration shifts rightwards. For the case of high temperature, it is observed that the dimensionless maximum dynamic deflection incorporating thermal effect is larger than those excluding the influence of temperature change. Indeed, increase in temperature change of the negative/positive coefficients of thermal expansion increases/decreases the stiffness and natural frequency of the CNT conveying fluid.

Fig. 7

Effects of the temperature changes on the dimensionless maximum dynamic deflection versus dimensionless excitation frequency for α = 0.001, β = 0.5, μ = 0.1, Kn = 0, ω = 4, F = 2, ξ = 0.3, k _w = 0, k _G = 0, c = 0 and clamped–clamped boundary conditions

Figure 8 indicates the influences of Knudsen number on the variation of dimensionless maximum dynamic deflection in terms of excitation frequency for the case of low temperature. It can be observed that by increasing the Knudsen number, which is the ratio of mean free path of the fluid molecules to the length of flow property, the dimensionless maximum dynamic deflection increases, whereas the natural frequency of clamped–clamped CNT conveying fluid reduces. As shown, at low excitation frequencies away from the natural frequency the increase in Kn causes an increase in maximum dynamic deflection, but as the excitation frequency increases the opposite behavior is observed. Furthermore, by increasing Kn from 0 to 0.01 there is no noticeable change in maximum dynamic deflection.

Fig. 8

Effects of the Knudsen number on the dimensionless maximum dynamic deflection versus dimensionless excitation frequency for α = 0.001, ΔT = 15 (low temperature), β = 0.5, μ = 0.1, ω = 4, F = 2, ξ = 0.3, k _w = 200, k _G = 20, c = 5 and clamped–clamped boundary conditions

Figure 9 shows the dimensionless maximum dynamic deflection versus excitation frequency for the case of low temperature and different boundary conditions. As expected, pinned–pinned CNT has a bigger maximum dynamic deflection than clamped–clamped CNT, whereas structural stiffness of clamped–clamped CNT conveying fluid is higher than other boundary conditions.

Fig. 9

Effects of the boundary conditions on the dimensionless maximum dynamic deflection versus dimensionless excitation frequency for α = 0.001, ΔT = 15 (low temperature), β = 0.5, μ = 0.1, Kn = 0.1, ω = 4, F = 2, ξ = 0.3, k _w = 200, k _G = 20, c = 5

5 Conclusions

This research addressed the flow-thermoelastic forced vibration of viscoelastic CNT resting on visco-Pasternak foundation and subjected to various boundary conditions. To consider the slip boundary condition between the wall of CNT and fluid, the Knudsen-dependent flow velocity is employed. Due to incapability of classical elasticity theory to demonstration the small-scale effects, Eringen’s nonlocal theory was employed to capture the size effects. The GFM was implemented for solving the governing differential equation to achieve the dynamic deflections of CNTs. It was found that the increase in nonlocal parameters leads to increasing non-dimension maximum dynamic deflections of CNTs conveying fluid. Furthermore, it was seen that by the increase in structural damping coefficient of CNT, the dimensionless maximum dynamic deflections decrease. In addition, it was shown that the temperature change has significant effect on the dimensionless maximum dynamic deflections of CNTs. Moreover, the results indicated that dimensionless maximum dynamic deflection of visco-Pasternak and Winkler mediums is minimum and maximum, respectively, while Pasternak type is between of them.

Appendices

Appendix 1

1.1 Viscosity in nanoflows

For the effective viscosity of fluid in terms of Kn number, relation between effective viscosity μ _e and bulk viscosity μ ₀ is formulated as (Beskok and Karniadakis 1999):

$$\mu_{\text{e}} = \mu_{0} \left( {\frac{1}{{1 + \bar{a}Kn}}} \right)$$

(24)

where $\bar{a}$ is a coefficient which is dependent to Knudsen number, as follows (Karniadakis et al. 2005):

$$\bar{a} = a_{0} \frac{2}{\pi }\left[ {\tan^{ - 1} \left( {a_{1} Kn^{B} } \right)} \right]$$

(25)

here a ₁ = 4 and B = 0.4 represent empirical parameters and a ₀ is defined as (Karniadakis et al. 2005):

$$\mathop {\lim }\limits_{Kn \to \infty } \bar{a} = a_{0} = \frac{64}{{3\pi \left( {1 - \frac{4}{b}} \right)}}$$

(26)

where b represent a general slip coefficient. By choosing b = − 1, we reach a second-order term of slip boundary condition equation.

1.2 Slip boundary conditions

The slip velocity model to consider the slip boundary conditions in nanoflow field as (Beskok and Karniadakis 1999)

$$V_{\text{s}} - V_{\text{w}} = \left( {\frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}} \right)\left( {\frac{Kn}{1 - bKn}} \right)\left( {\frac{{\partial v_{x} }}{\partial n}} \right)$$

(27)

where V _s, V _w and σ _v are slip velocity of the flow near nanotube’s wall, axial velocity of wall velocity and tangential moment accommodation coefficient, respectively. Furthermore, v _x denote the axial flow velocity, n is the normal vector, and σ _v is expressed as below (Beskok and Karniadakis 1999):

$$\sigma_{\text{v}} = \frac{{\left( {\tau_{\text{i}} - \tau_{\text{r}} } \right)}}{{\left( {\tau_{\text{i}} - \tau_{\text{w}} } \right)}}$$

(28)

where τ _i, τ _r and τ _w denote, respectively, tangential momentum of incoming, reflected and reemitted molecules. The value of σ _v is equal to 0.7 (Shokouhmand et al. 2010).

1.3 Derivation of the average velocity correction factor

For investigating the effect of flow passing through a CNT, we consider a homogeneous fluid, isothermal isotropic, fully developed laminar, incompressible, parallel and viscous fluid flow of constant density and viscosity. For a Newtonian fluid, considering a constant pressure gradient along CNT length, and neglecting the effects of gravitational and electromagnetic body forces, the well-known Navier–Stokes equations are stated as follows (Shames and Shames 1982)

$$\rho \frac{{d\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V} }}{dt} = - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\nabla } P + \mu_{\text{e}} \nabla^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {V}$$

(29)

where ρ, V and P are the fluid density, flow velocity vector and pressure, respectively. By these assumptions, the fluid velocity distribution by solving Navier–Stokes equation can be expressed as (Shames and Shames 1982)

$$v_{x} = \frac{1}{{4\mu_{\text{e}} }}\left( {\frac{\partial P}{\partial x}} \right)r^{2} + C_{3} \ln \left( r \right) + C_{4}$$

(30)

where r and x, respectively, represent the CNT radius and longitudinal coordinate of CNT elastic axis and axial flow. The boundary conditions enforce C ₃ = 0. In order to obtain C ₄, the slip boundary conditions at the CNT wall can be applied:

$$v_{{x\left( {r = R_{\text{i}} } \right)}} = R_{\text{i}} \left( {\frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}} \right)\left( {\frac{Kn}{1 - bKn}} \right)\left( {\frac{{\partial v_{x} }}{\partial r}} \right)_{{r = R_{\text{i}} }}$$

(31)

where R _i denote the inner radius of the CNT. Thus, Eq. (30) may be written as:

$$V_{\text{slip}} \left( r \right) = \frac{1}{{4\mu_{0} \left( {\frac{1}{1 + aKn}} \right)}}\left( {\frac{\partial P}{\partial x}} \right)\left[ {r^{2} - R^{2} - 2R^{2} \left( {\frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}} \right)\left( {\frac{Kn}{1 + Kn}} \right)} \right]$$

(32)

Therefore, the average fluid velocities through nanotube with slip boundary conditions can be obtained as:

$$U_{\text{ave, slip}} = \frac{1}{A}\mathop \int \limits_{A}^{{}} V_{\text{slip}} \left( r \right){\text{d}}A = \frac{2}{{R^{2} }}\mathop \int \limits_{0}^{{R_{\text{i}} }} V_{\text{slip}} \left( r \right)r{\text{d}}r = \frac{{R^{2} }}{{8\mu_{0} \left( {\frac{1}{1 + aKn}} \right)}}\left( { - \frac{\partial P}{\partial x}} \right)\left( {4\left( {\frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}} \right)\left( {\frac{Kn}{1 + Kn}} \right) + 1} \right)$$

(33)

For no-slip boundary conditions, the Kn approaches to zero in Eqs. (32, 33). Finally, the dimensionless average velocity correction is represented as:

$${\text{VCF}} \equiv \frac{{U_{\text{avg,slip}} }}{{U_{{{\text{avg,}}\left( {\text{no - slip}} \right)}} }} = \left( {1 + aKn} \right)\left[ {4\left( {\frac{{2 - \sigma_{\text{v}} }}{{\sigma_{\text{v}} }}} \right)\left( {\frac{Kn}{1 + Kn}} \right) + 1} \right]$$

(34)

where U _avg,slip and U _{avg,(no-slip)} are the average fluid velocities through nanotube with slip boundary conditions and without slip boundary conditions, respectively. With considering the average velocity correction factor, the flow velocity can be expressed as U _avg,slip = VCF × U _{avg,(no-slip)}.

Appendix 2

The coefficient matrix elements A _ij and B _ij are derived for various boundary conditions.

• For P–P boundary condition

Symbol	Value	Symbol	Value
A 11	1	A 31	ϕ 1(1)
A 12	0	A 32	ϕ 2(1)
A 13	0	A 33	ϕ 3(1)
A 14	0	A 34	λ 1 ϕ 4(1)
A 21	μ 2λ5	A 41	− λ 1 ϕ ′′1 (1) − λ 2 ϕ ′1 (1) + μ 2 λ 5 ϕ 1(1)
A 22	− λ2	A 42	− λ 1 ϕ ′′2 (1) − λ 2 ϕ ′2 (1) + μ 2 λ 5 ϕ 2(1)
A 23	− λ1	A 43	− λ 1 ϕ ′′3 (1) − λ 2 ϕ ′3 (1) + μ 2 λ 5 ϕ 3(1)
A 24	0	A 44	− λ 21 ϕ ′′4 (1) − λ 2 λ 1 ϕ ′4 (1) + μ 2 λ 5 λ 1 ϕ 4(1)
B 11	0	B 31	μ 2 ϕ 5(1 − ξ 0)H(1 − ξ 0) − ϕ 4(1 − ξ 0)H(1 − ξ 0)
B 21	0	B 41	λ 1[ϕ ′′4 (1 − ξ 0)H(1 − ξ 0) − μ 2 ϕ ′′5 (1 − ξ 0)H(1 − ξ 0)] + λ 2[ϕ ′4 (1 − ξ 0)H(1 − ξ 0) − μ 2 ϕ ′5 (1 − ξ 0)H(1 − ξ 0)] − μ 2 λ 5[ϕ 4(1 − ξ 0)H(1 − ξ 0)− μ 2 ϕ 5(1 − ξ 0)H(1 − ξ 0)]

• For C–P boundary condition

Symbol	Value	Symbol	Value
A 11	1	A 31	ϕ 1(1)
A 12	0	A 32	ϕ 2(1)
A 13	0	A 33	ϕ 3(1)
A 14	0	A 34	λ 1 ϕ 4(1)
A 21	0	A 41	−λ 1 ϕ ′′1 (1) − λ 2 ϕ ′1 (1) + μ 2 λ 5 ϕ 1(1)
A 22	1	A 42	− λ 1 ϕ ′′2 (1) − λ 2 ϕ ′2 (1) + μ 2 λ 5 ϕ 2(1)
A 23	0	A 43	− λ 1 ϕ ′′3 (1) − λ 2 ϕ ′3 (1) + μ 2 λ 5 ϕ 3(1)
A 24	0	A 44	− λ 21 ϕ ′′4 (1) − λ 2 λ 1 ϕ ′4 (1) + μ 2 λ 5 λ 1 ϕ 4(1)
B 11	0	B 31	μ 2 ϕ 5(1 − ξ 0)H(1 − ξ 0) − ϕ 4(1 − ξ 0)H(1 − ξ 0)
B 21	0	B 41	λ 1[ϕ ′′4 (1 − ξ 0)H(1 − ξ 0) − μ 2 ϕ ′′5 (1 − ξ 0)H(1 − ξ 0)] + λ 2[ϕ ′4 (1 − ξ 0)H(1 − ξ 0) − μ 2 ϕ ′5 (1 − ξ 0)H(1 − ξ 0)] − μ 2 λ 5[ϕ 4(1 − ξ 0)H(1 − ξ 0) − μ 2 ϕ 5(1 − ξ 0)H(1 − ξ 0)]

• For C–C boundary condition

Symbol	Value	Symbol	Value
A 11	1	A 31	ϕ 1(1)
A 12	0	A 32	ϕ 2(1)
A 13	0	A 33	ϕ 3(1)
A 14	0	A 34	λ 1 ϕ 4(1)
A 21	0	A 41	ϕ ′1 (1)
A 22	1	A 42	ϕ ′2 (1)
A 23	0	A 43	ϕ ′3 (1)
A 24	0	A 44	λ 1 ϕ ′4 (1)
B 11	0	B 31	μ 2 ϕ 5(1 − ξ 0)H(1 − ξ 0) − ϕ 4(1 − ξ 0)H(1 − ξ 0)
B 21	0	B 41	μ 2 ϕ ′5 (1 − ξ 0)H(1 − ξ 0) − ϕ ′4 (1 − ξ 0)H(1 − ξ 0)