1 Introduction

The superior applications of microstructures in the area of microelectromechanical systems (MEMS) have inspired scientists to comprehend all mechanical features associated with these mechanical systems (Ghayesh et al. 2013c; Ghayesh and Farokhi 2013). Among them, electrically actuated microstructures have received a considerable attention in development of MEMS. Electrically excited microstructures (e.g., the deformable electrode of a MEMS resonator) undergo both DC and AC voltages in two steps; first, under the electrostatic actuation (i.e., the DC voltage), the microstructure (i.e., the deformable electrode in this paper) is deflected to a new non-trivial equilibrium configuration. Then, by applying the AC excitation, it oscillates around the new non-trivial configuration. One of the concerns associated with electrically actuated microstructures is pull-in instability phenomenon, i.e., a discontinuity related to the interaction of the mechanical restoring force of the microstructure and the electric forces; when the applied electric potential difference exceeds a critical value known as the pull-in voltage, the microstructure fails to establish a force balance between the elastic force and the electric force. Hence, the microstructure is pulled into the fixed electrode.

Another important mechanical aspect that might considerably influence the mechanical response of a microstructure is the small-size-dependent behaviour. The small-size-dependent mechanical behaviour in microstructures has been demonstrably approved by experiments; the interested reader is referred to Lam et al. (2003). Inasmuch as classical continuum mechanics is not capable of capturing small-size effects, developing size-dependent elasticity theories is of great importance. In this regard, one can mention the use of the following non-classical continuum theories: couple stress elasticity; nonlocal elasticity; the strain gradient elasticity (Gurtin and Murdoch 1978; Aifantis 1999). These non-classical theories have been frequently employed in different studies to investigate the mechanical characteristics of micro and nanostructures (Ansari et al. 2011, 2012a, b, c; Ghayesh et al. 2013c; Farokhi et al. 2013c). The modified couple stress theory (MCST), proposed by Yang et al. (2002), is a widely used non-classical theory. They facilitated the application of the classical couple stress theory by considering only one material length-scale parameter together with two classical material constants (Ghayesh et al. 2013d, 2014; Ghayesh and Amabili 2014; Gholipour et al. 2014; Farokhi and Ghayesh 2015; Ghayesh and Farokhi 2015).

There are several studies in the literature which have investigated the pull-in instability of microbeams (i.e., the simplified model of the deformable electrode in a MEMS device). One can categorize these studies into two groups; the first one investigated the microbeams actuated by a DC voltage, leading to static pull-in behaviour; the second category considered both the DC (static) and AC (dynamic) components of the electric load, resulting in dynamic response of the system around the deflected configuration.

Regarding the studies on the static pull-in behaviour of microbeams incorporating size-dependence, one can mention, for example, Baghani (2012), who studied the size-dependent response of cantilever microbeams actuated electrostatically via an analytical technique. Rokni et al. (2013) presented an analytical closed-form solution for the size-dependent static pull-in behaviour of cantilevered and clamped–clamped microbeams, based on a non-classical Euler–Bernoulli beam theory possessing one material length-scale parameter.

Regarding the studies which considered both the DC and AC components of the electric load, some valuable papers can be found in the literature (Ghayesh et al. 2013e), for instance, Younis and Nayfeh (2003), who examined the response of a resonant microbeam due to an electric actuation. In another effort, Nayfeh and Younis (2005) analyzed the dynamics of microbeams actuated electrically; as they found, the dynamic pull-in occurs when the slope of the frequency–response curve reaches infinity and the Floquet multipliers approach unity; however, the response of the system after infinite slope was not the subject of their study. A nonlinear model was developed by Mestrom et al. (2008) in order to examine the dynamics of MEMS resonators and capture the experimentally observed behavior. Abdel-Rahman and Nayfeh (2003) contributed to the field by investigating the behaviour of a resonant sensor under superharmonic and subharmonic actuations by incorporating the nonlinearities related to fairly large displacements and electric forces. Younis et al. (2003) presented an analytical approach and a reduced-order model to examine the static and dynamic behaviours of electrically actuated MEMS devices. Jia et al. (2012) employed an analytical technique to study the nonlinear dynamics of electrically actuated micro-switches in the vicinity of a resonance region. In another analytical study, Kim et al. (2012) investigated the resonant behaviour of a nonlinear cantilevered microbeam containing a tip mass and undergoing an axial force and an electrostatic excitation. Meguid et al. (2013b) contributed to the field by examining the nonlinear quasistatic and dynamic behavior of a MEMS switch employing the Euler–Bernoulli beam theory along with the modified couple stress-based strain gradient theory; they discretized the equations employing the Galerkin scheme and solved the resultant equations using Newmark’s integration scheme. In another effort (Li et al. 2013a), they performed a nonlinear analysis on thermally and electrically actuated functionally graded material microbeams; they examined the effect of the size of the beam, the electrostatic gap, the temperature field and material property on the pull-in voltage of the microbeam. The studies were continued by Ouakad and Younis (2014), who examined the possibility of using the dynamic snap-through motion of initially curved MEMS resonators for filtering applications via numerical and experimental investigations.

Both the mid-plane stretching and the electric load cause nonlinear terms that can profoundly affect the response of electrically actuated microbeams. As shown by Younis (2011), in order to perform a static analysis on a clamped-free system actuated electrostatically, at least seven modes are required to guarantee the convergence of the results. Accordingly, for dynamic analysis, higher numbers of modes are required, especially in the presence of modal interactions; nevertheless, most of the above-mentioned valuable studies are limited to analytical analysis with a single-mode approximation.

As concluded from the previous paragraphs, in the study of dynamic behaviour of MEMS resonators, the effect of size seems to have been neglected. In this study, a cantilevered deformable electrode (i.e., a microcantilever) subjected to electrical loads is considered; the MCST and the Euler–Bernoulli beam theory are employed to derive the size-dependent nonlinear equation of motion. A 16-mode Galerkin scheme is then used to discretize the equation of motion, leading to a high-dimensional reduced-order model of the system. Afterwards, the pseudo-arclength continuation technique is utilized to solve the discretized equations numerically. In order to investigate the static pull-in instability, the microcantilever subject to only the electrostatic actuation (DC voltage) is considered. The nonlinear dynamic behaviour of the microcantilever due to both the DC and AC actuations is then investigated for both primary and superharmonic excitations.

2 Modified couple stress theory

Based on the MCST (Yang et al. 2002), the stored strain energy in a continuum made of a linear elastic material occupying region Ω can be written as a function of the strain tensor and gradient of the rotation vector as

$$ U = \frac{1}{2}\int_{\varOmega } {\left( {{\varvec{\upsigma}}\text{:}{\varvec{\upvarepsilon}} + {\mathbf{m}}\text{:}{\varvec{\upchi}}} \right)dv} , $$
(1)

where \( {\varvec{\upsigma}} \) and \( {\varvec{\upvarepsilon}} \) represent the stress and strain tensors, respectively; \( {\varvec{\upchi}} \) is the symmetric curvature tensor and m stands for the deviatoric part of the couple stress tensor defined for a linear isotropic elastic material (Timoshenko and Goodier 1970). m and \( {\varvec{\upchi}} \) are defined as follows:

$$ {\mathbf{m}} = 2\mu l^{2} {\varvec{\upchi}}\,, $$
(2a)
$$ {\varvec{\upchi}} = \frac{1}{2}\left( {\nabla {\varvec{\uptheta}} + \left( {\nabla {\varvec{\uptheta}}} \right)^{\text{T}} } \right) ,\quad {\text{with}}\quad {\varvec{\uptheta}} = \frac{1}{2}\nabla \times {\mathbf{u}}, $$
(2b)

where \( {\varvec{\uptheta}} \) denotes the rotation vector and l is a material length scale parameter whose value can be specified through micro-torsion tests of slim cylinders or micro-bending tests of thin beams. Also, \( \lambda \) and \( \mu \) are Lame’s constants defined as \( \lambda = \frac{E\nu }{(1 + \nu )(1 - 2\nu )} \) and \( \mu = \frac{E}{2(1 + \nu )} \) (Reddy and Kim 2012), where \( \nu \) and E stand for Poisson’s ratio and Young’s modulus, respectively; u is the displacement vector.

3 Governing equation of motion

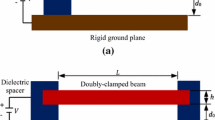
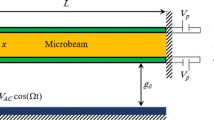
As shown in Fig. 1, a micro resonator is considered consisting of a cantilevered deformable electrode (i.e., modelled here as an Euler–Bernoulli microbeam) with length L, width b, and thickness h, separated by a dielectric space with an initial gap d from the fixed electrode. The microcantilever undergoes an electric load \( V_{\text{DC}} + V_{\text{AC}} \cos (\omega t) \), where V DC is the polarization voltage or static loading and V AC represents the amplitude of the AC voltage—ω shows the frequency of the AC voltage. EI denotes the flexural stiffness and EA represents the axial stiffness of the microcantilever. The equation governing the motion of the deformable electrode is derived in the following.

Fig. 1
figure 1

Schematic representation of a simplified microcantilever under an electric actuation

Full size image

Based on the Euler–Bernoulli beam theory, the components of the displacement vector (u) are given by (Ghayesh et al. 2011, 2012b)

$$ u_{x} = - z\frac{\partial w(x,t)}{\partial x},\quad u_{y} = 0,\quad u_{z} = w(x,t). $$
(3)

where w(x, t) represent the transverse displacement of the centerline of the deformable electrode.

Inserting Eq. (3) into Eqs. (2a, 2b), one can obtain the non-zero components of the symmetric curvature tensor and hence the couple stress tensor as

$$ \chi_{xy} = \chi_{yx} = - \frac{1}{2}\frac{{\partial^{2} w}}{{\partial x^{2} }}, $$
(4a)
$$ m_{xy} = m_{yx} = - \mu l^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }}. $$
(4b)

The nonlinear strain–displacement relation for an Euler–Bernoulli microbeam can be expressed as (Asghari et al. 2012; Farokhi et al. 2013a; Kazemirad et al. 2013; Ghayesh and Amabili 2012a, 2013c; Ghayesh 2012d)

$$ \varepsilon_{xx} = \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} - z\frac{{\partial^{2} w}}{{\partial x^{2} }}. $$
(5)

Accordingly, from Eqs. (1–5), one can formulate the total strain energy of the system as

$$ U = \frac{1}{2}\int_{0}^{L} {\left( {EI + \mu Al^{2} } \right)\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)^{2} \text{d} x} +\, \frac{1}{2}EA\int_{0}^{L} {\left( {\frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} } \right)^{2} \text{d} x} . $$
(6)

The kinetic energy of the system can be expressed as (Ghayesh and Amabili 2013d; Ghayesh 2010)

$$ T = \frac{1}{2}\rho A\int_{0}^{L} {\left( {\frac{\partial w}{\partial t}} \right)^{2} \text{d} x} . $$
(7)

The variation of the work done by the electric force and damping are given, respectively, by

$$ \delta W_{D} = - c_{d} \int_{0}^{L} {\left( {\frac{\partial w}{\partial t}\delta w} \right)\text{d} x} , $$
(8a)
$$ \delta W_{F} = \int_{0}^{L} {q\left( {x,t} \right)\,} \delta w\,\text{d} x, $$
(8b)

where c d denotes the coefficient of the viscous damping; the electrical force exerted on the deformable electrode is given by

$$ q\left( {x,t} \right) = \frac{{\varepsilon b\left[ {V_{\text{DC}} + V_{\text{AC}} \cos \left( {\omega t} \right)} \right]^{2} }}{{2\left( {d - w} \right)^{2} }}, $$
(9)

in which \( \varepsilon \) is the dielectric constant of the gap medium.

Inserting Eqs. (6–9) into Hamilton’s principle, the equation of motion can be obtained as

$$ \rho A\frac{{\partial^{2} w}}{{\partial t^{2} }} + c_{d} \frac{\partial w}{\partial t} + \left( {EI + \mu Al^{2} } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} = \frac{3}{2}EA\frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} + \frac{{\varepsilon b\left[ {V_{\text{DC}} + V_{\text{AC}} \cos \left( {\omega t} \right)} \right]^{2} }}{{2\left( {d - w} \right)^{2} }}, $$
(10)

where the corresponding boundary conditions for the clamped-free supports are

$$ \left. w \right|_{x = 0} = \left. {\frac{\partial w}{\partial x}} \right|_{x = 0} = 0,\quad \left. {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right|_{x = L} = \left. {\frac{{\partial^{3} w}}{{\partial x^{3} }}} \right|_{x = L} = 0. $$
(11)

Introducing the following non-dimensional parameters:

$$ \begin{gathered} x^{*} = \frac{x}{L},\quad w^{*} = \frac{w}{d},\quad \alpha_{1} = 6\left( \frac{d}{h} \right)^{2} ,\quad t^{*} = t\sqrt {\frac{EI}{{\rho AL^{4} }}} ,\quad \alpha_{2} = \frac{{6\varepsilon L^{4} }}{{Eh^{3} d^{3} }}, \hfill \\ \eta = 12\frac{\mu }{E}\left( \frac{l}{h} \right)^{2} ,\quad \varOmega = \omega \sqrt {\frac{{\rho AL^{4} }}{EI}} ,\quad c_{d}^{*} = \frac{{c_{d} L^{4} }}{EI}\sqrt {\frac{EI}{{\rho AL^{4} }}} , \hfill \\ \end{gathered} $$
(12)

one can express the size-dependent equation governing the transverse motion of the electrically actuated microbeam in the non-dimensional form as

$$ \frac{{\partial^{2} w}}{{\partial t^{2} }} + c_{d} \frac{\partial w}{\partial t} + \left( {1 + \eta } \right)\frac{{\partial^{4} w}}{{\partial x^{4} }} - 3\alpha_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }}\left( {\frac{\partial w}{\partial x}} \right)^{2} \qquad- \frac{{\alpha_{2} \left[ {V_{\text{DC}} + V_{\text{AC}} \cos (\varOmega t)} \right]^{2} }}{{(1 - w)^{2} }} = 0. $$
(13)

For the sake of accuracy the term \( 1/(1 - w)^{2} \) in Eq. (13) is not approximated by the Taylor expansion; instead, we consider this term as it is in the numerical simulations to ensure accurate results.

4 Solution procedure

Equation (13) describes a continuous system with infinite degrees of freedom. In order to discretize the system, a high-dimensional Galerkin scheme is used to achieve the reduced-order model of the system with finite degrees of freedom. Based on this scheme, the solution of Eq. (13) can be approximated by the following series expansion (Ghayesh 2012a, b, c; Ghayesh et al. 2012a, 2013b)

$$ w(x,t) = \sum\limits_{r = 1}^{N} {\phi_{r} (x)q_{r} (t),} $$
(14)

in which \( q_{r} (t) \) denotes the rth generalized coordinate for the transverse displacement and \( \phi_{r} (x) \) shows the rth mode shape for the transverse motion of a linear cantilever which satisfies the boundary conditions (Rao 2007). Inserting the expression given in Eq. (14) into Eq. (13) and applying the Galerkin method, one can obtain the discretized model of the system as

$$ \begin{aligned} & \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\phi_{i} \phi_{j} \text{d} x} } \right)} \textit{\"{q}}_{j} + \left( {1 + \eta } \right)\sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\phi_{i} \phi_{j}^{{{\prime \prime \prime \prime }}} \text{d} x} } \right)} q_{j} - 3\alpha_{1} \sum\limits_{j = 1}^{N} {\sum\limits_{k = 1}^{N} {\sum\limits_{l = 1}^{N} {\left[ {\int_{0}^{1} {\phi_{i} \phi_{j}^{{\prime \prime }} \phi_{k}^{{\prime }} \phi_{l}^{{\prime }} \text{d} x} } \right]} q_{j} q_{k} q_{l} } } \\ & \quad + \,c_{d} \sum\limits_{j = 1}^{N} {\left( {\int_{0}^{1} {\phi_{i} \phi_{j} \text{d} x} } \right)} \dot{q}_{j} - \alpha_{2} \left[ {V_{\text{DC}} + V_{\text{AC}} \cos \left( {\varOmega t} \right)} \right]^{2} \int_{0}^{1} {\left[ {\left( {1 - \sum\limits_{j = 1}^{N} {\phi_{j} q_{j} } } \right)^{ - 2} \phi_{i} } \right]} \text{d} x = 0,\quad i = 1 , { 2, } \ldots , {N} .\\ \end{aligned} $$
(15)

The overdot and prime notations denote the differentiations with respect to the dimensionless time and axial coordinate, respectively. Equation (15) represents a set of N second-order nonlinear ordinary differential equations (ODEs); this set is transformed into a new set of 2N first-order nonlinear ODEs via a change of variables (Farokhi et al. 2013b; Ghayesh et al. 2013a; Ghayesh and Amabili 2012b, 2013a, b). It should be noted that in case of a microcantilever resonator, at least seven modes are required to be able to obtain reliable results. In this study, N = 16 is selected; this high number of modes in the Galerkin scheme ensures convergence and accuracy—the analysis is numerically expensive and the computer codes should be well-optimized for accuracy and run-time. The pseudo-arclength method (Doedel et al. 2007) is employed to obtain the solution of the system.

5 Results and discussion

5.1 Linear analysis

In this section, the first linear natural frequency of the deformable electrode, i.e., ω 1, is obtained as a function of the DC voltage for different values of the dimensionless length-scale parameter η. In particular, as shown in Fig. 2, ω 1 is obtained for η = 0, 0.5, and 0.75. It is seen that, as the DC voltage is increased, the natural frequency of the system decreases for different values of η until reaching the zero value at a critical DC voltage, known as the pull-in voltage. The figure shows that the qualitative response trend is similar for different values of η; nevertheless, for higher values of η, the natural frequency of the system reaches the zero value at higher DC voltages. It is worthwhile noting that for V DC far below the critical value, the natural frequency decreases gradually with increasing V DC; however, as V DC approaches the pull-in voltage, there is a sudden decrease in the natural frequency of the system.

Fig. 2
figure 2

The variation of the first linear natural frequency of the system, i.e., ω 1, as a function of V DC, for different values of η

Full size image

5.2 Nonlinear static analysis

In the absence of the AC voltage, i.e., \( V_{\text{AC}} = 0 \), the deflected configuration of the deformable electrode due to the electrostatic actuation is shown in Fig. 3; the DC voltage is varied in this figure and the corresponding amplitude of the deformable electrode is plotted. The figure is depicted for a system with the following parameters: c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, and η = 0.75. The solution curves include a stable branch indicated with solid lines and an unstable branch shown by dashed lines. With an increase in the DC voltage, the amplitude of the transverse deformation grows until the point where a pull-in instability occurs and the slope of the solution curve tends to infinity; the DC voltage corresponding to this point is known as the static pull-in voltage; i.e., the maximum DC voltage that a system can withstand to avoid collapse, which for the current system is V DC = 0.8303. The amplitude of the transverse deformation at the static pull-in voltage is roughly w max = 0.4 for the free end (tip) of the microcantilever. The amplitude of the unstable solution branch corresponding to \( V_{\text{DC}} = 0 \) is equal to 1.0 for the tip; this value is more than two times the amplitude at the static pull-in voltage. Accordingly, the unstable and stable branches are not symmetric.

Fig. 3
figure 3

The static deflection of the deformable electrode actuated by an electrostatic excitation: a amplitude of the transverse displacement at the tip (x = 1.0); b amplitude of the first generalized coordinate. Solid and dashed lines represent the stable and unstable solutions; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, and η = 0.75

Full size image

Figure 4 shows the nonlinear static deflection of the deformable electrode undergoing electrostatic actuation predicted by both the modified couple stress and classical theories. The following parameters are selected for this figure: c d  = 0.0239, α 1 = 3.7, and α 2 = 3.9; η = 0.75 for the MCST and η = 0.0 for the classical continuum mechanics theory. The figure clearly highlights that for a certain DC voltage, the classical theory overestimates the stable amplitude of the transverse displacement, especially at higher DC voltages until the static pull-in voltage is hit. In other words, the size-dependent behaviour gets more prominent at higher voltages. Also, the static pull-in voltage is significantly underestimated by the classical continuum mechanics theory.

Fig. 4
figure 4

The static deflection of the deformable electrode actuated by an electrostatic excitation predicted by both the MCST and classical theories: a amplitude of the transverse displacement at the tip (x = 1.0); b amplitude of the first generalized coordinate. c d  = 0.0239, α 1 = 3.7, and α 2 = 3.9; η = 0.75 for the MCST and η = 0.0 for the classical theory

Full size image

Figure 5 shows how the variation of \( \alpha_{1} \) affects the amplitude of the transverse deflection (Fig. 5a) and the first generalized coordinate (Fig. 5b) when the DC voltage is varied. As seen in the figure, the system with a lower \( \alpha_{1} \) resists a higher DC voltage and gets pulled-in at higher voltages. Additionally, the amplitude corresponding to the static pull-in voltage decreases with increasing \( \alpha_{1} \).

Fig. 5
figure 5

The effect of α 1 (denoted on the curves) on the static deflection of the deformable electrode actuated by an electrostatic excitation: a amplitude of the transverse displacement at the tip (x = 1.0); b amplitude of the first generalized coordinate. c d  = 0.0239, α 2 = 3.9, and η = 0.75

Full size image

The effect of \( \alpha_{2} \) on the static deflection of the deformable electrode is shown in Fig. 6. As seen in this figure, for a lower value of \( \alpha_{2} \), the system displays a lower stable amplitude and the pull-in instability is delayed to higher voltages. Unlike the effect of \( \alpha_{1} \), variations in \( \alpha_{2} \) do not affect the amplitude corresponding to the static pull-in voltage.

Fig. 6
figure 6

The effect of α 2 (denoted on the curves) on the static deflection of the deformable electrode actuated by an electrostatic excitation: a amplitude of the transverse displacement at the tip (x = 1.0); b amplitude of the first generalized coordinate. c d  = 0.0239, α 1 = 3.7, and η = 0.75

Full size image

5.3 Nonlinear size-dependent resonant behaviour

In order to investigate the nonlinear size-dependent dynamical behaviour of the deformable electrode (i.e., the microcantilever), first, it is actuated by a certain DC voltage and the corresponding non-trivial deflected configuration is obtained numerically. Then, the oscillations over the deflected state, due to the AC voltage, are obtained numerically. The size-dependent resonant behaviour of the system is studied under primary and superharmonic excitations and results are presented in the form of AC frequency-amplitudes and AC voltage-amplitudes. The numerical calculations are performed for a system with the following parameters: c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, and η = 0.75. Moreover, the first linear natural frequency of the microbeam is obtained, by means of an eigenvalue analysis, as ω 1 = 4.4884.

5.3.1 Primary excitation

The size-dependent resonant behaviour of the system under the primary actuation is discussed in this subsection. According to the definition of the primary resonance, the frequency of the AC voltage, \( \varOmega \), is varied around the first linear natural frequency of the deformable electrode, ω 1.

Shown in Fig. 7 are the AC actuation frequency-amplitude curves of the deformable electrode under an electric actuation with V DC = 0.4006 and V DC = 0.0080. The figure shows the maximum amplitude of the transverse displacement at the tip (x = 1.0), maximum amplitude of the q 1 motion, and the minimum amplitude of the q 1 motion, in sub-figures (a), (b) and (c), respectively. At first glance, it is seen that the system displays a softening-type nonlinear behaviour as opposed to the case of a clamped–clamped microbeam where the response is a hardening type (Nayfeh and Younis 2005); as a result, the response of the system depends on both current and history of the input (hysteresis). In particular, by increasing the excitation frequency from Ω = 0.9 ω 1, the maximum amplitude of the oscillations grows until reaching point A. At this point, corresponding to Ω = 0.9882 ω 1, an instability occurs at via a limit point bifurcation, causing the system to jump to a new state, i.e., the upper stable solution branch. It is seen that the response amplitude decreases thereafter by increasing the excitation frequency. Another scenario is observed for the case when the excitation frequency is decreased from Ω = 1.05 ω 1. In this case, decreasing the frequency ratio causes the maximum amplitude of the transverse deflection to increase. This growth continues until point B (Ω = 0.9400 ω 1) is hit, where the system loses stability once again via the second limit point bifurcation, and jumps to the lower-amplitude stable branch. The details of the dynamic response of the system at Ω = 0.9610 ω 1 are represented in Fig. 8, through time histories and phase-plane portraits of the tip of the microbeam as well as the q 1 and q 3 generalized coordinates.

Fig. 7
figure 7

AC frequency–response curves of the deformable electrode near the primary resonance over the deflected configuration: a maximum amplitude of the transverse displacement at the tip (x = 1.0); b, c maximum and minimum amplitudes of the first generalized coordinate, respectively. Solid and dashed lines represent the stable and unstable solutions, respectively; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, η = 0.75, V DC = 0.4006, and V AC = 0.0080

Full size image
Fig. 8
figure 8

Periodic motion for the microcantilever of Fig. 7 at Ω = 0.9601 ω 1: a, b time history and phase-plane portrait of the tip of the microcantilever (x = 1.0), respectively; c, d time history and phase-plane portrait of the q 1 motion, respectively; e, f time history and phase-plane portrait of the q 2 motion, respectively

Full size image

The AC voltage-response curves of the system, when the frequency of the AC voltage is set near the primary resonance, are depicted in Fig. 9. The numerical calculations are performed for a system with V DC = 0.4006 and Ω = 0.95 ω 1. As seen in Fig. 9a, with increasing AC voltage, the maximum amplitude of system increases from 0.05 at V AC = 0.0 to around 0.3 at point A corresponding to V AC = 0.0571. At this point, the response becomes unstable, due to occurrence of a limit point bifurcation, causing the system to jump to the larger-amplitude stable branch, where the amplitude is increased with increasing AC voltage. A decrease in the AC voltage from 0.3 leads to a gradual decrease in the maximum amplitude of the system. This trend continues until point B (V AC = 0.0076), where through a limit point bifurcation, the system jumps down to the lower-amplitude stable solution branch; the maximum amplitude declines thereafter with decreasing V AC.

Fig. 9
figure 9

V AC-response curves of the deformable electrode when the frequency of the AC voltage is set near the primary resonance (Ω = 0.95 ω 1): a maximum amplitude of the transverse displacement at the tip (x = 1.0); b, c maximum and minimum amplitudes of the first generalized coordinate, respectively. Solid and dashed lines represent the stable and unstable solutions, respectively; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, η = 0.75, and V DC = 0.4006

Full size image

5.3.2 Superharmonic excitation

The numerical results obtained for a superharmonically excited deformable electrode (i.e., microcantilever) are discussed in this subsection, while the frequency of the excitation varies in the neighbourhood of the half of the first linear natural frequency of the transverse motion (0.5 ω 1).

The AC frequency–response curves of the system excited superharmonically are depicted in Fig. 10. The numerical results are performed for the system under V DC = 0.4006 and V AC = 0.0768. A similar qualitative trend as for the primary excitation can be observed in this figure. The system displays softening behaviour with two stable solution branches and an unstable one. As the frequency increases, the maximum amplitude of the tip increases accordingly until point A (Ω = 0.9894(0.5 ω 1)) is reached where the slope of the response curve approaches infinity. In other words, a limit point bifurcation occurs at this point which renders the system unstable and causes it to jump to the upper stable solution branch; the maximum amplitude then decreases with further increase in the excitation frequency. When the frequency is decreased from Ω = 1.0200(0.5 ω 1), the maximum amplitude of the tip ascends reaching the top at point B Ω = 0.9737(0.5 ω 1), where a limit point bifurcation occurs and the system jumps to the lower-amplitude stable solution branch; the amplitude declines steadily thereafter with decreasing frequency.

Fig. 10
figure 10

AC frequency–response curves of the deformable electrode at the superharmonic resonance: a maximum amplitude of the transverse displacement at the tip (x = 1.0); b, c maximum and minimum amplitudes of the first generalized coordinate, respectively. Solid and dashed lines represent the stable and unstable solutions, respectively; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, η = 0.75, V DC = 0.4006, and V AC = 0.0768

Full size image

Figure 11 depicts the V AC-response curves of the deformable electrode under the superharmonic excitation with Ω = 0.95 × 0.5 ω 1. According to subfigure (a), with an increase in V AC, the transverse amplitude of the tip of the deformable electrode grows until reaching point A (V AC = 0.1941), where the slope of the response tends to infinity and a limit point bifurcation occurs. At this point, the maximum amplitude jumps to an upper stable solution branch; beyond that, the amplitude grows mildly. With a decrease in V AC from 0.3, the maximum amplitude declines and follows the upper stable solution branch until point B V AC = 0.0838 is hit. At this point, the system jumps to the lower stable solution branch; with further reduction in V AC, the maximum amplitude diminishes steadily.

Fig. 11
figure 11

V AC-response curves of the deformable electrode under superharmonic excitation at Ω = 0.95(0.5 ω 1): a maximum amplitude of the transverse displacement at the tip (x = 1.0); b, c maximum and minimum amplitudes of the first generalized coordinate, respectively. Solid and dashed lines represent the stable and unstable solutions, respectively; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, η = 0.75, and V DC = 0.4006

Full size image

The V AC-response curves of the deformable electrode excited superharmonically with Ω = 1.05 × 0.5 ω 1 are plotted in Fig. 12; the Ω/0.5 ω 1 ratio for this case is higher than unity, as opposed to the case of Fig. 11. It is clearly seen that the maximum amplitude of the deformable electrode increases with increasing V AC. The response curves are seen to follow a stable solution branch without any bifurcations for the ranges studied here. Comparing Figs. 11 and 12 reveals that, depending on the value of the excitation frequency of superharmonically excited microcantilever, the V AC-response curves show completely different qualitative behaviour.

Fig. 12
figure 12

V AC-response curves of the deformable electrode under superharmonic excitation at Ω = 1.05(0.5 ω 1): a maximum amplitude of the transverse displacement at the tip (x = 1.0); b, c maximum and minimum amplitudes of the first generalized coordinate, respectively; c d  = 0.0239, α 1 = 3.7, α 2 = 3.9, η = 0.75, and V DC = 0.4006

Full size image

6 Conclusions

A comprehensive study has been performed on the nonlinear size-dependent static and dynamic behaviours of an electrically actuated microcantilever of a MEMS resonator. The nonlinear partial differential equation of motion was discretized into a set of nonlinear ordinary differential equations by means of a high-dimensional Galerkin scheme. The resultant set of equations was solved numerically via the pseudo-arclength continuation technique, for both static and dynamic cases.

The most important outcomes are listed as follows: (1) for the cantilevered deformable electrode under consideration, the pull-in static voltage is obtained as VDC = 0.8303 with the approximate corresponding amplitude of 0.4. Moreover, it was seen that the stable and unstable solutions of the nonlinear static response of the system are not symmetric counterparts; (2) the classical theory overestimates the amplitude of the transverse displacement and predicts a lower static pull-in voltage; (3) the static pull-in instability occurs at higher DC voltages for a deformable electrode with lower values of α1 and α2 parameters; (4) examining the AC frequency–response curves of the deformable electrode under primary excitation revealed that the system exhibits a softening-type nonlinear behaviour; (5) the AC frequency–response trend for the case of superharmonic excitation was similar to that of the case of primary resonance; (6) the VAC-response curves for a superharmonically excited microcantilever showed that the system displays two limit point bifurcations for the excitation frequencies lower than unity, while showing no limit point bifurcations for those higher than unity, for the ranges studied here.