Nonlinear forced vibrations of a slightly curved nanotube conveying fluid based on the nonlocal strain gradient elasticity theory

Abstract

Advances in miniaturization of medical and engineering equipment made nanotubes and nanopipes to be very important components for these devices. A nonlinear mechanical behaviour of nonlocal strain gradient of a slightly curved tube conveying pressurized fluid under thermal loading subjected to forced vibration is investigated in this study. The microtube’s viscoelasticity of the material is assumed using the Kelvin–Voigt model. First the effects of scale due to fluid and solid are considered. Then using Hamilton’s principle, and the nonlocal strain gradient elasticity, the nonlinear size-dependent governing partial integro-differential equation (PDE) is derived. Two different methods are used to solve this problem. These are; (1) finite difference method (FDM), is used to solve the PDE, and (2) the Eigenfunction expansion methods was combined using Runge–Kutta and Heun schemes to solve the resulting ODE in time. The results of pipe’s midpoint displacement and frequency are almost indistinguishable with Runge–Kutta and Heun schemes. However, comparing FDM with RK, the displacement is within 16% while frequency is within 2% respectively. Results show that particularly the effect of initial curvature have profound effects on the resonance of the system. For the linear analysis, the slip, nonlocal and thermal parameters degraded the natural frequency of the nanotube. For forced vibration, when initial curvature is zero, one distinct resonant frequency was obtained. However, for slightly curved pipe, two distinct resonant frequencies were obtained for flow velocity between 3.7 and 4.5 respectively. Slightly curved nanopipes with slip boundary condition behave very differently from those without slip boundary condition. There are no comparable results in the study of micropipes conveying fluids in the oil and gas industry.

1 Introduction

Fluid–solid interactions at nano/small scales in micro and nanofluids, are vital since these interactions can change the mechanical characteristics/behaviour of the system. For example, it has been observed that flow in carbon nanotube (CNT) differs in vibration response and its stability behaviour is quite different from conventional tube or pipe Li et al. (2016). Indeed, less work has been done on fluid solid interactions of macropipes and macrotubes (Gholipour and Ghayesh 2020; Adebusoye and Oyediran 2016; Orolu et al. 2019; Owoseni et al. 2017; Oyelade et al. 2020; Liu and Mote 1974; Zhong-min et al. 2005; Li and Yi-ren 2017; Oyelade and Oyediran 2020). However, in the last few years, attention has been on nanotubes and pipes due to brilliant mechanical and electrical properties of these nanostructures which find wide applications in engineering and medicine. Therefore, for better understanding and production of these small scale systems, their fluid structure interactions should be investigated comprehensively.

In mechanics of nanotubes, it has been observed that the mechanics of microscale structures is greatly determined by size effects which are usually expressed in terms of strain gradient and couple stress models (Farajpour et al. 2018; Ghayesh et al. 2018, 2019a, b; Ghayesh and Farajpour 2008; Ghayesh et al. 2016, 2020). In these works, modified elasticity theory was developed from the classical continuum mechanics to incorporate microscale structures. In the work of Ghayesh et al. (2020), size effects in both solid and fluid nanoscale parts are taken into consideration with the slip boundary conditions, however the authors investigated straight nanotube without thermal load. The effects of slip boundary conditions and initial curvature will be addressed in this paper. In a similar work by Ghayesh’s group, the effect of slip boundary conditions was shown to overestimate the critical speed of the fluid (Farajpour et al. 2018). Furthermore, nonlinear dynamics of a geometrically imperfect microbeam without fluid has been studied by Ghayesh’s group (Farokhi et al. 2013), and the frequency-response curves for the system with different initial imperfections were investigated. In another study, fluttering and divergence instability of viscoelastic nanotubes conveying fluid were investigated by Nematollahi et al. (2019). The pipe was analysed with continuous variations of the material properties through the thickness of the nanotube, the elastic modulus and the density. The linear analysis was presented up to six modes. The effects of structural damping, nonlocal parameter, and power-law parameter were investigated. A functionally graded material (FGM) pipes conveying fluid using power law was studied using a hybrid method which combines reverberation-ray matrix method and wave propagation method (Deng et al. 2017). The effects of fluid velocity, volume fraction exponent, internal pressure and internal damping on free vibration and stability of multi-span pipes conveying fluid were studied numerically.

Oyelade and Oyediran (2020) explored the cusp bifurcation due to the initial curvature on the temperature, pressure, and tension. However, in many studies, the size dependent due to strain gradient was neglected. Nonlinear vibration of a single walled carbon nanotube was shown to exhibit different characteristics under high levels of mass weight and velocity (Kiani 2014; Mohammadi et al. 2014; Ansari et al. 2012). The nanotube was modeled using only nonlocal parameter which has been discovered to be insufficient in modelling the characteristics behaviour of nanotubes (Farajpour et al. 2020). Recently, the nonlinear strain incorporating the initial curvature was used in the work of Farajpour et al. (2020) in investigating dynamics of nanotube conveying fluid. Beskok-Karniadakis approach was utilized for relative motions at the nanotube wall, and there was a coupling of the transverse and longitudinal motion of the microtube. This work omitted the effects of cusp bifurcation due to initial curvature and thermal, pressure or tension load on the nanotube.

All previous contributions are restricted to one parameter size-dependent models, straight nanotube or linear models, or frequency response of each mode of vibration via a frequency-continuation method, to the best of our knowledge no work has extensively dealt with all the variables in nanopipe. In this work, a comprehensive analysis of nonlocal strain gradient theory (both the nonlocal stresses and the strain gradient) is presented for a slightly curved viscoelastic nanopipe conveying hot pressurized fluid under forced vibration with both ends clamped. To better describe the nanopipe which normally are not perfectly straight, the pipe is assumed to have an initial curvature modeled as trigonometric function of cosine. Then the size effect of the solid part is accounted for by the nonlocal strain gradient theory while that of the nanofluid by the slip parameter. The nanopipe ends are assumed as clamped-clamped which models a gyroscopic nanosystem (Farajpour et al. 2018). The Euler–Bernoulli beam and Hamilton’s principle were used to derive the nonlinear equation of motion of the size-dependent motion of the nanotube. The nonlinear partial integro-differential equation of motion is solved using two different methods. In the first instance, the eigenfunction of the nanopipe was used to change the PDE to ODE in time. Four modes were considered. This was used to solve the linear and nonlinear analyses (Runge–Kutta and Heun). In the second method, the PDE was discretized and finite difference method (FDM) was used to solve for the deflection. The results of the FDM and Eigenfunction expansions were compared and is found that deflections are within 16% of each other. The results using the Eigenfunction expansion were used exclusively for other cases reported here. The linear analysis results show that the natural frequencies decrease as the slip, and nonlocal parameters increases. When the nanopipe is straight, one distinct resonant frequency was obtained while for the slightly curve nanotube, two resonants frequencies were observed. The behaviour of nanopipe with slip boundary condition behaves quite differently from the pipe with no slip boundary condition. Thermal and viscoelastic parameters significantly affected the dynamics response of the nanotube. The paper is organized as follows. Firstly, the nonlinear governing equation of size dependent pipe is introduced using Hamilton’s principle and the semi analytical solution are presented in Sect. 2. The stability analysis is conducted for the system to show the effect of various parameters such as initial curvature, non local, strain gradients and slip boundary to guarantee stability. Secondly, the nonlinear effect of the system is systematically analysed by showing the frequency versus midpoint displacement of the nanotube for various forcing frequencies and initial curvature in Sect. 3. Conclusion is presented in Sect. 4 of this paper.

Fig. 1

A slightly curved nanoscale tube conveying hot pressurized fluid flow subject to external loading

2 Mathematical formulation and method of solution

2.1 Effect of slip boundary condition

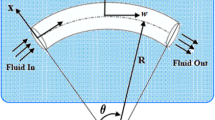
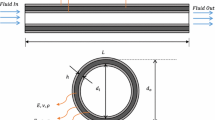
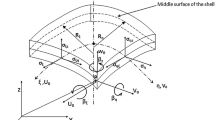
Figure 1 shows the schematic representation of a micropipe, subjected to a transverse harmonic excitation force per unit length $F(x)\cos (xt)$. The no-slip boundary condition is assumed at a solid surface, where the fluid velocity assumes the velocity of the solid surface. No slip boundary condition assumption works well in marcoscales levels for fluid in pipes and tubes. However, when the characteristics length scale is of manometers, the assumption of no-slip boundary conditions is not valid any longer. Hence, the effect of slip boundary conditions will be included based on the earlier work done by Karniadakis et al. (2006). The deviation of the state of the fluid from continuum is measured by the Knedsen number’s Kn, which is defined as the ratio of the mean free path of the molecules to external characteristics length scale of a fluid conveying system. Karniadakis et al. (2006) proposed for generalized diffusion coefficient as a function of Kn:

$$\begin{aligned} \mu _{nf}(Kn)=\mu _{nf0}\left[ \dfrac{1}{1+\lambda Kn}\right] , \end{aligned}$$

(1)

where $\mu _{nf0}$ is the dynamic bulk viscosity of the gas at a specified temperature and $\lambda$ is the generalized diffusion coefficient. Diffusion coefficient $\lambda$ as presented in Farajpour et al. (2018) is obtained by

$$\begin{aligned}&\begin{array}{l} \lambda =\dfrac{2 \lambda _0}{\pi } \tan ^{-1}\left[ \alpha _0 (Kn)^{\alpha _1}\right] , \end{array} \end{aligned}$$

(2)

$$\begin{aligned}&\begin{array}{l} \lambda _0=\underset{Kn \rightarrow \infty }{\lim }=\dfrac{64 \beta _0}{3 \pi (\beta _0-4)}=\dfrac{64}{15 \pi }. \end{array} \end{aligned}$$

(3)

In Eqs. (2) and (3), the coefficients $\alpha _0$, $\alpha _1$ and $\beta _0$ which are determined as $\alpha _0$ = 4, $\alpha _1$ = 0.4, and $\beta _0$ = -1 Farajpour et al. (2018). Based on the Beskok–Karniadaki model, the slip speed can be written as Karniadakis et al. (2006)

$$\begin{aligned} \begin{array}{l} v_x=\dfrac{1}{4 \mu _{nf}} P' r^2+\dfrac{R_i^2}{4 \mu _{nf}}P'\left[ 2 \left( \dfrac{\sigma _v-2}{\sigma _v}\right) \left( \dfrac{Kn}{1-\beta _0 Kn}\right) -1\right] . \end{array} \end{aligned}$$

(4)

Now, a correction factor for the average speed of the flowing fluid inside the nanoscale tube is defined as

$$\begin{aligned} \begin{array}{l} \kappa _{nf1}=\dfrac{v^s}{v^{ns}} \end{array} \end{aligned}$$

(5)

where $v^s$ and $v^{ns}$ are the average fluid velocity for slip and no slip boundary conditions respectively. In view of the above relations Eqs. (4) and (5), the fluid speed correction factor is obtained as

$$\begin{aligned} \begin{array}{l} \kappa _{nf1}=(1+ \lambda Kn)\bigg [1+\dfrac{4 Kn}{1+Kn}\bigg (\dfrac{2-\sigma _v}{\sigma _v}\bigg )\bigg ]. \end{array} \end{aligned}$$

(6)

2.2 Non local strain gradient theory

The classical continuum mechanics cannot describe physical phenomena in which the long-range interactions play a major role. It fails to observe many of the micro-/nano-scale phenomena. Therefore, the properties and behaviour of materials captured by the classical continuum mechanics are invariant with respect to time and length scales, and more notably size effects cannot be captured by this classical mechanics (Eringen and Edelen 1973; Eringen and Wegner 2003). The physics of nonlocal elasticity continuum theory is to characterize the material body whose behavior (stress field) at a material point is not only a function of the strain at the point of application of stress but of all points of the body. This implies that the stress at a given point within a body depends on the strain over the entire material body (Eringen and Wegner 2003). For homogeneous and isotropic elastic solids, the nonlocal stress tensor at point x is given by

$$\begin{aligned}&\begin{array}{l} t_{xx}=\sigma _{xx}-\dfrac{\mathrm{d}}{\mathrm{d}x}\sigma _{xx}^{(1)} \end{array} \end{aligned}$$

(7)

$$\begin{aligned}& \sigma _{xx}=\int \limits _{0}^L E \alpha _0(x,x',e_0a)\varepsilon _{xx}'(x')\mathrm{d}x' \end{aligned}$$

(8)

$$\begin{aligned}& \sigma _{xx}^{(1)}=l^2\int \limits _{0}^L E \alpha _1(x,x',e_0a)\varepsilon _{xx}'(x')\mathrm{d}x' \end{aligned}$$

(9)

where E is the elastic modulus of the pipe, $\alpha _0(x',x,e_0a)$ and $\alpha _1(x',x,e_1a)$ are the nonlocal attenuation functions associated with the strain $\varepsilon _{xx}$ and the first-order strain gradient $\varepsilon _{xx,x}=\dfrac{\mathrm{d} \varepsilon _{xx}}{\mathrm{d}x}$ , respectively, and l is the strain gradient length scale parameter. It is noted that the higher order strain gradient attenuation function $\alpha _1(x',x,e_1a)$ and the strain gradient length scale l are not present in Eringen’s nonlocal elasticity theory. The linear nonlocal differential operator can be given by Eringen and Edelen (1973)

$$\begin{aligned} \begin{array}{l} {\mathcal {L}}_i=1-(e_ia)^2\nabla ^2 \qquad i=0,1. \end{array} \end{aligned}$$

(10)

By applying Eq. (10) into Eq. (7), a general constitutive model in a differential form can be given by Li and Hu (2016)

$$\begin{aligned} \begin{array}{rl} &{}\left[ 1-(e_1a)^2\nabla ^2\right] \left[ 1-(e_0a)^2\nabla ^2\right] t_{xx}=E\left[ 1-(e_1a)^2\nabla ^2\right] \varepsilon _{xx}\\ &{}\quad -El^2\left[ 1-(e_0a)^2\nabla ^2\right] \nabla ^2\varepsilon _{xx}, \end{array} \end{aligned}$$

(11)

where $\nabla ^2=\dfrac{\mathrm{d}^2}{\mathrm{d}x^2}$ is defined as the one dimensional differential operator. Equation (11) is the generalized nonlocal constitutive relation based on the new higher-order nonlocal strain gradient theory for the Euler–Bernoulli beam model. It contains three length scale parameters; two of which represent the nonlocal size effect, one of them for the lower-order nonlocal stress and the other the higher-order nonlocal stress; and the third one accounts for the size effect induced by higher-order deformation or strain gradients. The nonlocal strain gradient constitutive relation Eq. (11) could be easily reduced to the lower order nonlocal stress model

$$\begin{aligned} \begin{array}{l} \sigma _{xx}-(ea)^2\nabla ^2\sigma _{xx} =E \big (1-l_{sg}^2\nabla ^2\big )\varepsilon _{xx}. \end{array} \end{aligned}$$

(12)

The strain gradient and nonlocal parameters are, respectively, denoted by $l_{sg}$ and $e_oa$ in which $e_o$ and a represent the nonlocal calibration coefficient and the internal characteristic length, respectively. Also, nanotubes resting on the polymer matrix can be considered as viscoelastic systems. In this research, we use the Kelvin–Voigt viscoelastic model in order to capture the damping effects in fluid-conveying hot pressurized nanotubes as Farajpour et al. (2018)

$$\begin{aligned} \begin{array}{l} \sigma _{xx} =E\left( 1+\eta \dfrac{\partial }{\partial t}\right) \varepsilon _{xx}. \end{array} \end{aligned}$$

(13)

Therefore, the size-dependent constitutive equation based on the nonlocal strain gradient theory associated with the Kelvin–Voigt viscoelastic model may be defined as

$$\begin{aligned}&\begin{array}{l} \left( 1-(ea)^2\nabla ^2\right) \sigma _{x} =\left( 1-l_{sg}^2 \nabla ^2 \right) \left( E+\eta \dfrac{\partial }{\partial t}\right) \varepsilon _{xx} \end{array}\end{aligned}$$

(14)

$$\begin{aligned}&\begin{array}{l} \bigg (1-(ea)^2\nabla ^2\bigg )M_x =-I\bigg (1-l_{sg}^2 \nabla ^2\bigg )\bigg (E+\eta \dfrac{\partial }{\partial t}\bigg )w'' \end{array} \end{aligned}$$

(15)

2.3 Equations of motion of size-dependent nonlinear pipe

Consider a clamped-clamped slightly curved viscoelastic nanotube (SCVN) conveying hot pressurized fluid resting on linear and nonlinear foundations under an external loading (see Fig. 1). The total strain and elastic energy of the beam can be expressed as

$$\begin{aligned} U =\int \limits _{0}^L \int \limits _{A} \sigma _x \varepsilon _{xx}\mathrm{d}A\mathrm{d}x. \end{aligned}$$

(16)

The total strain due to bending and slightly curved differential element in transverse direction together with the temperature changes, tension and pressure is given as

$$\begin{aligned} \begin{array}{l} \varepsilon _{xx}=\dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }}+\bigg (\dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\bigg )-z{\bar{w}}'', \end{array} \end{aligned}$$

(17)

where ${\bar{w}}$, ${\bar{a}}_0$, ${\bar{T}}$, ${\bar{P}}$, ${\bar{\theta }}$ are the transverse displacement, initial curvature, tension, pressure and temperature respectively. $\alpha$ is the coefficient of thermal expansion, E is the Young modulus of the tube and A is the nanotube’s cross-sectional area. The strain energy can be expressed as

$$\begin{aligned} U=\int \limits _{0}^L \int \limits _{0} \sigma _x\left[ \dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }}+\left( \dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\right) -z{\bar{w}}''\right] \mathrm{d}A\mathrm{d}x. \end{aligned}$$

(18)

Adding the strain energy function for the damping (c), linear stiffness $(k_1)$ and nonlinear stiffness $(k_3)$ to the tube gives:

$$\begin{aligned} U&=\displaystyle \int \limits _{0}^L \left[ N_x \bigg \{\dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }}+\bigg (\dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\bigg )\bigg \}-M_x{\bar{w}}''\right] \mathrm{d}x\\ &\quad +\dfrac{1}{2}c\dot{{\bar{w}}}+\dfrac{1}{2}{\bar{k}}_1{\bar{w}}^2+\dfrac{1}{4}{\bar{k}}_3{\bar{w}}^4. \end{aligned}$$

(19)

In this study, the stress resultants $(N_x,M_x )$ are defined by integration over the cross-section of the nanotube with area A as follows

$$\begin{aligned} M_x=\int _{A}\sigma _x z\,\mathrm{d}A \qquad N_x=\int _{A}\sigma _x\,\mathrm{d}A. \end{aligned}$$

(20)

The kinetic energy of the pipe in the transverse direction is given by

$$\begin{aligned} \begin{array}{l} T=\dfrac{1}{2} m_p \displaystyle \int \limits _{0}^L \dot{{\bar{w}}}^2\mathrm{d}x+ \dfrac{1}{2} m_f\displaystyle \int \limits _{0}^L (\dot{{\bar{w}}}+\kappa _{nf1}{\bar{v}}{\bar{w}}')^2 \mathrm{d}x. \end{array} \end{aligned}$$

(21)

Here, $m_p$ ,$m_f$ and ${\bar{v}}$ represent the mass of the nanopipe, mass of the nanofluid and the velocity of the flow, respectively. The external harmonic excitation force is obtained as:

$$\begin{aligned} W_F=\int _{0}^L{\bar{F}}(x)cos({\bar{\omega }}_n{\bar{t}})\mathrm{d}x, \end{aligned}$$

(22)

in which ${\bar{\omega }}_n$ and ${\bar{F}}$ denote the excitation frequency and the force amplitude. Applying the variational methods to Eqs (19),(21) and (22), and evaluating the Lagrangian for the equation of motion as $L=T-U$. Using

$$\begin{aligned} \begin{array}{l} \dfrac{\partial L}{\partial {\bar{w}}}-\dfrac{\partial }{\partial t}\left( \dfrac{\partial L}{\partial \dot{{\bar{w}}}}\right) + \dfrac{\partial ^2}{\partial x^2}\left( \dfrac{\partial L}{\partial {\bar{w}}''}\right) +\dfrac{\partial ^2}{\partial x \partial t} \left( \dfrac{\partial L}{\partial \dot{{\bar{w}}}'}\right) -\dfrac{\partial }{\partial x}\dfrac{\partial L}{\partial {\bar{w}}'} = 0 \end{array} \end{aligned}$$

(23)

the equations of motion in transverse direction with external force is given by

$$\begin{aligned} \begin{array}{l} (m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}+m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}'+\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'')+\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3\\ -\dfrac{\partial }{\partial x} N_x({\bar{w}}'+\bar{a_0}') -\dfrac{\partial ^2 M_x}{\partial x^2}-{\bar{F}}(x)cos({\bar{\omega }}_n{\bar{t}}) = 0. \end{array} \end{aligned}$$

(24)

Inserting Eq. (17) in Eq. (14) yields

$$\begin{aligned} &\big [1-(ea)^2\nabla ^2\big ]\sigma _{x} =\big [1-l_{sg}^2 \nabla ^2\big ]\big [E+\eta \dfrac{\partial }{\partial t}\big ] \\ &\quad \times \bigg [\dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }} +\bigg (\dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\bigg )-z{\bar{w}}''\bigg ]. \end{aligned}$$

(25)

Integrating both sides of Eq. (25) over the pipe area A gives

$$\begin{aligned} & N_x-(e_0a)^2 N_x''=EA\bigg [\bigg (\dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }}+\bigg (\dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\bigg )\bigg )\\ &\quad -l_{sg}^2 \nabla ^2\bigg (\dfrac{1}{2}{\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'-\alpha {\bar{\theta }}+\bigg (\dfrac{{\bar{T}}}{EA}-\dfrac{{\bar{P}}}{E}\bigg )\bigg )\bigg ]\\ &\quad +\eta A\big [\big (\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}'\big )-l_{sg}^2 \nabla ^2\big (\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}'\big )\big ]. \end{aligned}$$

(26)

From Eq. (24), one obtains

$$\begin{aligned} \begin{array}{rl} \dfrac{\partial ^2 M_x}{\partial x^2}=(m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}+m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}'+\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'') \\ +\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3-\dfrac{\partial }{\partial x} N_x({\bar{w}}'+{\bar{a}}')-{\bar{F}}(x)\mathrm{cos} ({\bar{\omega }}_n{\bar{t}}) . \end{array} \end{aligned}$$

(27)

Then the transverse equation of motion becomes

$$\begin{aligned} \begin{array}{l} (m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}+m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}'+\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'')+\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3 \\ -\dfrac{\partial }{\partial x} N_x({\bar{w}}'+\bar{a_0}')\\ +EI {\bar{w}}^{IV}-l_{sg}^2\nabla ^2 EI {\bar{w}}^{IV}+\eta I \dfrac{\partial }{\partial t}{\bar{w}}^{IV}-l_{sg}^2\nabla ^2 \eta I \dfrac{\partial }{\partial t}{\bar{w}}^{IV} \\ -{\bar{F}}(x)\mathrm{cos}({\bar{\omega }}_n{\bar{t}})-(ea)^2 \nabla ^2\bigg [(m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}+m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}' \\ +\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'')+\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3-\dfrac{\partial }{\partial x} N_x({\bar{w}}'+\bar{a_0}')-{\bar{F}}(x) \mathrm{cos}({\bar{\omega }}_n{\bar{t}})\bigg ]= 0. \end{array} \end{aligned}$$

(28)

Using Eq. (26), it can be easily shown that;

$$\begin{aligned} N_x&=\dfrac{EA}{L}\displaystyle \int \limits _{0}^L\bigg [\bigg (\dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'\bigg )-l_s^2 \nabla ^2\bigg (\dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'\bigg )\bigg ]\mathrm{d}x\\ &\quad +\dfrac{\eta A}{L}\displaystyle \int \limits _{0}^L\bigg [(\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}')-l_{sg}^2 \nabla ^2(\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}')\bigg ]\mathrm{d}x\\ &\quad +({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }})-l_{sg}^2 \nabla ^2({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }}). \end{aligned}$$

(29)

while Eq .(28) becomes

$$\begin{aligned}&(m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}+m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}'+\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'')+\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3\nonumber \\&\quad +EI {\bar{w}}^{IV}-l_{sg}^2\nabla ^2 EI {\bar{w}}^{IV}+\eta I \dfrac{\partial }{\partial t}{\bar{w}}^{IV} -l_{sg}^2\nabla ^2 \eta I \dfrac{\partial }{\partial t}{\bar{w}}^{IV}\nonumber \\&\quad -\dfrac{EA}{L}\displaystyle \int \limits _{0}^L\bigg [\left( \dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}')-l_{sg}^2 \nabla ^2(\dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'\right) \bigg ]\mathrm{d}x ({\bar{w}}''+{\bar{a}}'')\nonumber \\&\quad -\dfrac{\eta A}{L}\displaystyle \int \limits _{0}^L\bigg [(\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}') -l_{sg}^2 \nabla ^2(\dot{{\bar{w}}}'{\bar{w}}'+\dot{{\bar{a}}}_0'{\bar{w}}')\bigg ]\mathrm{d}x ({\bar{w}}''+{\bar{a}}'') \\&\quad -{\bar{F}}(x)cos({\bar{\omega }}_n{\bar{t}})-({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }}) ({\bar{w}}''+{\bar{a}}'')\nonumber \\&\quad +l_{sg}^2 \nabla ^2({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }})({\bar{w}}''+{\bar{a}}'')-(ea)^2 \nabla ^2\bigg [(m_p+m_f)\ddot{{\bar{w}}}+c \dot{{\bar{w}}}\nonumber \\&\quad +m_f(2 \kappa _{nf1}{\bar{v}}\dot{{\bar{w}}}'+\kappa _{nf1}^2{\bar{v}}^2{\bar{w}}'')+\bar{k_1}{\bar{w}}+\bar{k_3}{\bar{w}}^3\nonumber \\&\quad -\dfrac{EA}{L}\displaystyle \int \limits _{0}^L\big [\left( \dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'\right) -l_{sg}^2 \nabla ^2\left( \dfrac{1}{2} {\bar{w}}'^2+{\bar{a}}_0'{\bar{w}}'\right) \big ]\mathrm{d}x ({\bar{w}}''+{\bar{a}}'')\nonumber \\&\quad -\dfrac{\eta A}{L}\displaystyle \int \limits _{0}^L\big [(\dot{{\bar{w}}}'{\bar{w}}'+{\bar{a}}_0'\dot{{\bar{w}}}')-l_{sg}^2 \nabla ^2(\dot{{\bar{w}}}'{\bar{w}}'+\dot{{\bar{a}}}_0'{\bar{w}}')\big ]\mathrm{d}x ({\bar{w}}''+{\bar{a}}'')\nonumber \\&\quad -({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }}) ({\bar{w}}''+{\bar{a}}'')+l_s^2 \nabla ^2({\bar{T}}-{\bar{P}}A-EA\alpha {\bar{\theta }})({\bar{w}}''+{\bar{a}}'')\nonumber \\ {}&\quad -{\bar{F}}(x)\mathrm{cos}({\bar{\omega }}_n{\bar{t}})\bigg ]= 0.\nonumber \end{aligned}$$

(30)

For convenience of numerical solution, the following dimensionless parameters and operators are considered

$$\begin{aligned} {\bar{w}} &= wr, \quad {\bar{x}}=xL, \quad {\bar{a}}_0=a_0r, \quad {\bar{t}}=t\sqrt{\dfrac{(m_p+m_f)}{EI}}L^2, \quad \chi _{sg}=\dfrac{l_{sg}}{L}\nonumber \\ {\bar{T}} &= T \dfrac{EI}{L^2}, \quad {\bar{P}}=P \dfrac{EI}{A L^2},\quad {\bar{\theta }}=\theta \dfrac{I}{\alpha A L^2},\quad {\bar{v}}=v \sqrt{\dfrac{EI}{m_f}}\dfrac{1}{L}, \nonumber \\ \bar{k_1} &= k_1 \dfrac{EI}{L^4}, \quad \bar{k_3}=k_3 \dfrac{EI}{L^4 r^2}, \quad \beta =\sqrt{\dfrac{m_f}{m_p+m_f}}, \nonumber \\ \chi _{nl} &= \dfrac{e_0a}{L}, \quad \eta _1=\dfrac{\eta I}{L^2 \sqrt{(m_p+m_f)}},\quad {\bar{F}}=F \dfrac{EI r}{L^4},\nonumber \\ {\bar{\omega }}_n&= \dfrac{1}{L^2}\sqrt{\dfrac{EI}{(m_p+m_f)}}\Omega ,\quad \mu =\dfrac{c L^2}{\sqrt{EI(m_p+m_f)}}. \end{aligned}$$

(31)

Using these dimensionless parameters, Eq. (30) yields a partial integro-differential equation given by

$$\begin{aligned} \begin{aligned}&\ddot{w}+\mu {\dot{w}}+2 \kappa _{nf1}v\sqrt{\beta }{\dot{w}}'+(\kappa _{nf1}^2 v^2-T\\&\quad +P+\theta )w''+k_1 w+k_3 w^3+w^{IV} \\&\quad -\chi _{sg}^2 w^{VI}+\eta _1 {\dot{w}}^{IV}-\chi _{sg}^2 \eta _1 {\dot{w}}^{VI}\\&\quad -\displaystyle \int \limits _{0}^L\Bigg [\Bigg (\dfrac{1}{2} w'^2+a_0' w'\Bigg ) -\chi _{sg}^2 (w''+a_0''' w'+2 a_0'' w''+a_0' w''')\Bigg ] \mathrm{d}x (w''+a_0'')\\&\quad - F_1 \mathrm{cos}(\Omega t)-\eta _1 \displaystyle \int \limits _{0}^L \big [ {\dot{w}}'w'-\chi _{sg}^2 ({\dot{w}}''' w'\\&\quad +2{\dot{w}}'' w''+{\dot{w}}'w''')\big ]\mathrm{d}x (w''+a_0'')\\&\quad -(T-P-\theta )a_0''+\chi _{sg}^2 (T-P-\theta ) \left( w^{IV}+a_0^{IV}\right) \\&\quad -\chi _{nl}^2 \bigg [ \ddot{w}''+\mu {\dot{w}}'' +2\kappa _{nf1}v\sqrt{\beta }{\dot{w}}'''\\&\quad +(\kappa _{nf1}^2 v^2-T+P+\theta )w^{IV}+k_1 w''+6k_3 ww''\\&\quad -\displaystyle \int \limits _{0}^L\Bigg [\Bigg (\dfrac{1}{2} w'^2+a_0' w'\Bigg )-\chi _{sg}^2(w''+a_0''' w'\\&\quad +2 a_0'' w''+a_0' w''')\Bigg ] \mathrm{d}x (w^{IV}+a_0^{IV})\\&\quad -\eta _1 \displaystyle \int \limits _{0}^L \big [ {\dot{w}}'w'-\chi _{sg}^2 ({\dot{w}}''' w'+2{\dot{w}}'' w''\\&\quad +{\dot{w}}'w''')\big ]\mathrm{d}x (w^{IV}+a_0^{IV}) -(T-P-\theta )a_0^{IV}\\&\quad +\chi _{sg}^2 (T-P-\theta ) (w^{VI}+a_0^{VI})\bigg ]=0, \end{aligned} \end{aligned}$$

(32)

with the following boundary conditions for a clamped-clamped microbeam

$$\begin{aligned} \begin{array}{l} w(0,t)=w(1,t)=w'(0,t)=w'(1,t)=0 \end{array} \end{aligned}$$

(33)

2.4 Method of solutions

In this subsection, both the Eigenfunction expansion method and FDM will be considered. The former method was previously explained in Oyelade and Oyediran (2020), where PDE was reduced to a set of ODE in time. The ODE was solved using Runge–Kutta and Heun methods. The second method discretizes the PDE directly and solved for the deflection. These two methods are described below:

2.4.1 Eigenfunction expansion technique

The nonlinear partial integro-differential equation of motion (Eq. (32)) is discretized into a set of second-order nonlinear ordinary differential equations (ODEs) by means of the Eigenfunctions expansion technique. The eigenfunctions for the transverse motion of a linear clamped-clamped beam is assumed as the appropriate basis functions for the transverse motion of the system. The trial function for the transverse displacement is taken as

$$\begin{aligned} \begin{array}{l} w(x,t)= \sum \limits _{i=1}^{N} q_i(t) \varphi _i(x), \end{array} \end{aligned}$$

(34)

where $q_i$ is function to be determined. $\varphi _i$ is the eigenfunction of the clamped-clamped boundary condition. N is the number of modes to consider, and for this work, four-mode expansion will be used for satisfactory precision. The eigenfunction of clamped-clamped case is

$$\begin{aligned} \begin{array}{l} \varphi _i(x)= \cosh {\lambda _i x}- \cos {\lambda _i x}-\dfrac{\cosh { \lambda _i }- \cos {\lambda _i}}{\sinh {\lambda _i} - \sin { \lambda _i}}(\sinh {\lambda _i x} -\sin {\lambda _i x}) \end{array} \end{aligned}$$

(35)

Considering the initial curvature as a sinusoidal function of the spatial coordinates of amplitude b, the initial curvature that satisfies the clamped-clamped boundary condition can be expressed as

$$\begin{aligned} \begin{array}{l} a_0= \dfrac{b}{2}(1- \cos {2 \pi x}). \end{array} \end{aligned}$$

(36)

The required partial derivatives of Eq. (34) is substituted in Eq. (32) and a system of ordinary differential equations resulting from Eigenvalue expansion are numerically solved by using the Runge–Kutta method.

2.4.2 Numerical validation by FDM

In this subsection, the numerical procedures for validation of the results above are described. The above system (32) of non-linear partial integro-differential equations is solved under the relevant initial and boundary conditions using central difference schemes as approximations to the partial derivatives (Mattheij et al. 2005). The integral terms in the equation are approximated by the well-known trapezoidal rule for numerical integration (Burden and Faires 2011). Numerical analysis for partial integro-differential equations have been studied in Sloan and Thomée (1986), Sanz-Serna (1988), Kauthen (1992), and Soliman et al. (2012), while the numerical modelling of applied problems with partial intgero-differntial equations using the finite-difference approach has been explored in Dehghan (2006) and Ding and Chen (2019). The basic idea of the finite difference method is to approximate the derivative and integral terms in the model problem (32). The partial integro-differential equations will then be transformed to a sequential sets of algebraic equations for the time-dependent problems. The approach taken here follows the recent work of Ding and Chen (2019).

Equation (32) are solved by finite difference method. Taking the uniform mesh of step k and time step h, the grid points generated are

$$\begin{aligned} (t_i,x_j)=(ih,jk), \qquad j=0,1,2,\ldots ,M, i=1,2,\ldots ,N \end{aligned}$$

Partial derivatives are approximated with the following finite difference schemes using the notations in the form $w_{i,j}$, where $w_{i,j}$ approximates the exact solution w(x, t) of Eq. (32). To discretize the space derivatives, the following second order symmetric difference approximation schemes are adopted

$$\begin{aligned} \begin{array}{l} w'(ih,jk)=\dfrac{w_{i,j+1}-w_{i,j-1}}{2k}, \\[2ex] w''(ih,jk)=\dfrac{w_{i,j+1}-2w_{i,j}+w_{i,j-1}}{k^2}, \\[2ex] w'''(ih,jk)=\dfrac{2(w_{i,j-1}-w_{i,j+1})+w_{i,j+2}-w_{i,j-2}}{2k^3}, \\[2ex] w^{IV}(ih,jk)=\dfrac{w_{i,j+2}+w_{i,j-2}+6w_{i,j}-4(w_{i,j+1}+w_{i,j-1})}{k^4},\\[2ex] w^{VI}(ih,jk)=\dfrac{w_{i,j+3}+w_{i,j-3}-6(w_{i,j+2}+w_{i,j-2})+15(w_{i,j+1}+w_{i,j-1})-20w_{i,j}}{k^6}. \end{array} \end{aligned}$$

(37)

The temporal derivatives are similarly approximated by the central difference scheme

$$\begin{aligned} \begin{array}{l} {\dot{w}}(ih,jk)=\dfrac{w_{i+1,j}-w_{i-1,j}}{2h}, \\[2ex] \ddot{w}(ih,jk)=\dfrac{w_{i+1,j}-2w_{i,j}+w_{i-1,j}}{h^2}. \end{array} \end{aligned}$$

(38)

The integral terms are approximated using the composite trapezoidal rule

$$\begin{aligned} \begin{array}{ll} \int \limits _0^L w(t,x)\mathrm{d}x &{} =\dfrac{k}{2}\left( w(t,0)+2\sum \limits _{j=1}^{M-1}w(t,jk)+w(t,L)\right) \\[2ex] &{} =\dfrac{k}{2}\left( w_{i,0}+2\sum \limits _{j=1}^{M-1}w_{i,j}+w_{i,M}\right) . \end{array} \end{aligned}$$

(39)

The clamped boundary conditions are equally resolved in discretized form as follows:

$$\begin{aligned} w_{0,j} &= 0.0001, j=1,2,\ldots ,(M-1) \Leftrightarrow w(0,x)=0.0001\nonumber \\[2ex] w_{i,0} &= 0 \Leftrightarrow w(t,0)=0\nonumber \\[2ex] w_{i,M} &= 0 \Leftrightarrow w(t,L)=0\\[2ex] w_{i,-1} &= w_{i,1} \Leftrightarrow w'(t,0)=0\nonumber \\[2ex] w_{i,M+1} &=w_{i,M-1} \Leftrightarrow w'(t,L)=0\nonumber \end{aligned}$$

(40)

With the implementation of the finite difference approximations (37) and (38), integral approximations (39) and clamped boundary conditions (40), Eq. (32) takes a very cumbersome $(N-1)\times (M-1)$ nonlinear equations of the form

$$\begin{aligned} F(W_{i+1}) &\equiv f_{i+1,j}(w_{i+1,1},w_{i+1,2},\ldots ,\nonumber \\ w_{i+1,M-1}) &= 0 \quad j=1,2,\ldots ,(M-1), \nonumber \\i&=1,2,\ldots ,(N-1). \end{aligned}$$

(41)

From (41), a system of decoupled $(M-1)$ nonlinear equations is generated for $j=1,2,\ldots ,(M-1$), which is solved sequentially by Newton’s method to compute the grid displacement $\{w_{i+1,1},w_{i+1,2},\ldots ,w_{i+1,(M-1)}\}$ for time grids $i=0,1,2, \ldots , (N-1)$. The iterative formula takes the vector form

$$\begin{aligned} W_{i+1}^{(k+1)}=W_{i+1}^{(k)}-J^{-1}F(W_{i+1}^{(k)})F(W_{i+1}^{(k)}) \end{aligned}$$

(42)

where, $W_{i+1}^{(k)}=\{w_{i+1,1},w_{i+1,2},\ldots ,w_{i+1,(M-1)}\}$ generated at the kth iteration, $F(W_{i+1}^{(k)})$ is the vector function consisting of $f_{i+1,j}(w_{i+1,1},w_{i+1,2},\ldots ,w_{i+1,M-1}), j=1,2,\ldots ,(M-1)$ evaluated at $W_{i+1}^{(k)}$, while $J^{-1}F(W_{i+1}^{(k)})$ is the inverse of the Jacobian of the vector function $F(W_{i+1})$ evaluated at $W_{i+1}^{(k)}$. This procedure is halted when the norm $\Vert W_{i+1}^{(k+1)}-W_{i+1}^{(k)} \Vert \le \mathrm{tol}$, where $\mathrm{tol}$ is specified tolerance to break the iterative procedure. The iterative procedure is repeated sequentially for $i=0,1,2, \ldots , (N-1)$. See Burden and Faires (2011) for more exposition.

The Newton’s procedure is implemented using the $\mathtt {FindRoot}$ command in $\mathtt {Mathematica}$. Consequently, to validate the Eigen function expansion via Runge-methods presented in Sect. 2.4.1, the graphical results are presented in Sect. 3

3 Results and discussion

In this section, results of the dynamics are presented. The dynamical behaviour of the system, frequency versus fluid velocity diagrams of the nanotube conveying hot pressurized fluids are presented for clamped-clamped boundary condition.

3.1 Verifications

To demonstrate the accuracy of the linear model, the dimensionless linear critical velocities are compared with those calculated in Ghayesh et al. (2019b).The governing equation in the static form can be achieved by dropping the time-dependent terms from Eq. (32) (Dehrouyeh-Semnani et al. 2017a, b). Figure 2 shows a very good agreement between the calculated results and those reported in Ref Ghayesh et al. (2019b).

Fig. 2

Verification study for the size-dependent modelling; reported result is from Ghayesh et al. (2019b)

In order to obtain the amplitude of the steady-state response of the slightly curved pipe, the local maximum and minimum values of the vibration of last period are taken, then the amplitude-frequency response of the middle point of the pipe is shown in Fig. 3. The steady-state response amplitude plot is defined as the half of the difference between the maximum and minimum values of the displacement for each forcing frequency. Results obtained from the Eigen expansion solutions using Runge–Kutta–Fehlberg and Heun are then compared with the solution via FDM, as shown in Fig. 4. It is seen in Fig. 4 that as far as the displacement tendency with varying frequency is concerned, the numerical results obtained by the Runge–Kutta–Fehlberg, Heun method and FDM methods are in good agreement. The discernible discrepancies between the FDM and the ODE results can be attributed to a number of factors, such as order of the methods, space grids and stepsize in the numerical integration of the resulting ODEs. Hence, the three numerical methods for solving the nonlinear forced vibration of the slightly curved nanotube conveying fluid are accurate and credible. The results of the Galerkin method using Runge–Kutta are presented.

Fig. 3

Time-domain response of the mid-point of the slighlty curved tube. a response in 20 s and b steady-state response in a time interval of 10–10.5 s $v = 4$.$F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.0001$, $\chi _{nl} = 0.0005$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$, $\Omega =6$

Fig. 4

Comparisons between the Eigenvalue expansion method (with Runge–Kutta) and the FDM with velocity. a Initial amplitude varies for $v = 4$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.0001$, $\chi _{nl} = 0.0005$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$, b Slip parameter varies for $v = 4$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=0.5$, $\chi _{sg} = 0.0001$, $\chi _{nl} = 0.0005$, $k_1=10$, $k_3=10^5$, $\eta _1 = 0.005$

3.2 Free vibration: natural frequency

In order to determine the influence of the initial curvature on the natural frequency of the nanotube pipe, Fig.5 depicts the initial curve amplitude effects on the stability of the nanotube conveying hot pressurized nanofluid. The real parts of the frequencies decrease as the velocity increases between zero and first critical velocity for all initial curvatures. However, the critical velocity changes from 4.5 for straight pipe to 4.6 and 4.8 for initial curvature of 0.5 and 1.0, respectively. Between the first critical velocity and the second, the eigen frequency of the nanotube is mainly imaginary, while the real part is zero as the velocity increases. There are two branches of the imaginary part which represents the positive and negative damping effect. The negative parts causes the instability in the nanotube. Coupled mode fluttering can be observed at the second, third and fourth modes where we have mode 1 and 2, 2 and 3 and 3 and 4 being coupled together. Imperfect nanotube due to initial curvature can be seen to delay the divergence instability of the nanotube at the first critical velocity but have no significant difference at higher modes as we have in classical pipes where the effect of the initial curvature affect all the critical velocities significantly (Yi-Min et al. 2012; Ni et al. 2011) .

Fig. 5

Plot of natural frequency against fluid velocity for various initial curvature. a real part, b imaginary parts. $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0$, $\chi _{nl} = 0.001$, $k_1=0$, $k_3=0$, $\eta _1 = 0$

Figure 6 presents the plots of the slip boundary effects on the natural frequencies of the nanotube conveying nanofluid flow. The speed correction factor is set to $\kappa _{nf1}$ = 1.2 and 1.4 for slip boundary conditions while it is set to $\kappa _{nf1}$ = 1 for no-slip boundary conditions (classical pipe). The slip boundary parameter has a decreasing influence on the stiffness of nanotubes. This effect is noticed for all the critical velocities unlike the initial curvature that has effect on the fundamental critical velocity only. For example, for classical pipe, the first critical velocity is 6.40 while when slip parameter is 1.2 and 1.4 the critical velocity is 5.35 and 4.6, respectively. Likewise, for the second critical velocity for the classical is 9.0 and for slip parameter 1.2 and 1.4 is 7.5 and 6.4, respectively. At low fluid velocity the frequency is almost the same, but as the velocity increases the effect of slip ratio on the frequency becomes pronounced in the system.

Fig. 6

Plot of natural frequency against fluid velocity for various slip boundary parameter. a real part, b imaginary parts. $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=0.5$, $\chi _{sg} = 0.01$, $\chi _{nl} = 0.01$, $k_1=0$, $k_3=0$, $\eta _1 = 0$

Figure 7 shows the dynamical behaviour of a clamped-clamped nanotube conveying fluid under the influence of three different non-local parameters. The properties of the system are considered as $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.2$, $\chi _{sg} = 0.01$, and $b = 1$. It is observed that the nonlocal parameters soften the total stiffness for the nanotube system. As the value of non-local parameter increases, the critical velocity tends to decrease. This result is consistent with other published literature on non-local parameters (Nematollahi et al. 2019; Farajpour et al. 2018). However, instead of the corresponding decrease in frequency as the velocity increases for increase in non-local parameters, it is seen that the fourth mode has increase for high non-local parameter. For illustration, the frequency at velocity 4 for first mode is 15, 13.5 and 8.7 for non local parameter 0, 0.1 and 0.2, respectively. While for the fourth mode, the frequency is 201.8, 202.8 and 204, respectively. Hence, at some point as the velocity increases the frequency of the nanotube can be higher than that of the classical tube.

Fig. 7

Plot of natural frequency against fluid velocity for various nonlocal parameters. a real part, b imaginary parts. $P = 0$, $\theta = 0$, $T = 0$,$\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.2$, $\chi _{sg} = 0.01$, $b = 1$, $k_1=0$, $k_3=0$, $\eta _1 = 0$

Fig. 8

Plot of natural frequency against fluid velocity for various initial curvature and viscoelastic parameters. bf a, b real part, c, d corresponding imaginary parts. $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.01$, $\chi _{nl} = 0.1$, $k_1=0$, $k_3=0$, $b = 0.5$

Fig. 9

Plot of natural frequency against fluid velocity for various temperature parameters. a real part, b imaginary parts. $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.01$, $\chi _{nl} = 0.1$, $k_1=0$, $k_3=0$, $\eta _1 = 0$

Strain gradient causes an increase in both the critical velocity and natural frequency of the fluid. The first critical velocity is almost the same for all strain gradient parameters, however, there are differences in the second, third and fourth modes. This can be seen in Fig. 10. The frequency for the first two modes are similar for the three strain gradient at the low fluid velocity. Though the difference becomes pronounced at the 3rd and 4th modes. For example at strain gradient $\chi _{sg}$=0, 0.01, and 0.03, the frequency is 200, 202, and 218 respectively at fluid velocity 2 for the 4th modes, whereas at 3rd modes the frequency is 60, 60.1 and 61.6, respectively at the same fluid velocity. The effect of strain gradient on frequency at first two modes is quite different in terms of the magnitude from the third and the fourth mode.

Fig. 10

Plot of natural frequency against fluid velocity for various strain gradient parameter a real part, b imaginary parts. $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.2$, $b=0.5$, $\chi _{nl} = 0.1$, $k_1=0$, $k_3=0$, $\eta _1 = 0$

The effect of viscoelastic parameter is studied in two ways; the influence of the inital curvature on elastic nanotube and viscoelastic parameter. It is observed that the initial geometry imperfection of the pipe only affect the first critical velcoity for elastic and viscoelastic pipe. The presence of damping parameter decoupled the third and fourth mode as can be seen in Fig 8b, d (Oyelade et al. 2020). Therefore. the higher frequencies are affected by damping more than the lower mode (Nematollahi et al. 2019).

Figure 9 shows the effect of thermal load on the critical velocity of the slightly curved nanotube. Here, as temperature increases, the critical velocity and the natural frequencies decrease. Thus, thermal load causes a softening effect on the pipe which collaborated the work of Ashley and Haviland (1950) and Qian et al. (2009). When the flow velocity is lower than the critical, the first natural frequency decreases with the increase of the temperature change. This result is at variance with nanotube at low or room temperature, in which case thermal coefficient is negative.

3.3 Forced vibration: steady state

The effects of the initial curvature on the dynamics of nanotubes before and after critical velocity are shown in Figs. 11 and  12, respectively. The geometric imperfection of the tube is varied between zero and 1. When $b=0$, the tube is straight. However when $b\ne 0$ then the tube is slightly curved. It can be seen in Fig. 11 that straight tube and tube with geometric imperfection up to 0.2 display only one resonant frequency while tube with geometric imperfection greater than 0.2 show two resonants frequencies. Furthermore, the first resonant peak tends to be higher than the second peak when the system displays two resonant peaks. Hence, the geometric imperfection has significant effect on the forced nanotube. The works of Farajpour et al. (2018, 2019) did not capture this phenomenon because the work is based on the straight pipe. From Fig. 12, where the fluid velocity is chosen as 10, there is only one resonant for all values of initial curvature. Though amplitude value has reduced for all frequencies compared to the plots before bifurcation as shown in Fig.11. Furthermore, the two resonants observed when $b\ge 0.2$, has turned to one. Hence, there is need to further probe the effect of fluid velocity on the dynamics of the pipe. According to Figs. 13a, and c when the initial curvature of the pipe is zero and the excitation frequency increases from 0 to 30, there is only one resonance frequency for all vibration. However, when the initial curvature $b\ne 0$, the response of the slightly curved pipe becomes more complex with two different resonance frequency Fig. 13b. This can be observed when the flow velocity is between 3.7 and 4.5. The contour plot in Fig. 13d clearly shows the two resonants around these velocities. Therefore, in general, dynamics of the tube is significantly affected by the initial curvature of the pipe and the velocity of the fluid.

The resonance frequency is overestimated when the slip boundary condition is not incorporated. Moreover, the fluid–structure interaction model with no-slip boundary conditions cannot predict modal interactions in the size-dependent frequency-amplitude behaviour of fluid-conveying viscoelastic nanotubes

Fig. 11

Midpoint displacement of the system as a function of frequency and initial curvature amplitude before critical velocity. $v = 5$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.05$, $\chi _{nl} = 0.1$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$

Fig. 12

Midpoint displacement of the system as a function of frequency and initial curvature amplitude after critical velocity. $v = 10$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{sg} = 0.05$, $\chi _{nl} = 0.1$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$

Fig. 13

Midpoint displacement of the system as a function of frequency and fluid velocity. a $b = 0$, b $b = 1$, c, d corresponding contour map, for $\kappa _{nf1}=1.5$, $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\chi _{sg} = 0.05$, $\chi _{nl} = 0.2$, $k_1=0$, $k_3=0$, $\eta _1 = 0.0005$

Fig. 14

Midpoint displacement of the system as a function of frequency and slip parameters $v=4$, $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=0.5$, $\chi _{sg} = 0.05$, $\chi _{nl} = 0.1$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$

Fig. 15

Midpoint displacement of the system as a function of frequency and nonlocal parameters $v = 4$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $b=0.5$, $\chi _{sg} = 0.05$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$

Fig. 16

Midpoint displacement of the system as a function of frequency and strain gradient parameters $v = 4$.$F = 1$, $P = 0$, $\theta = 0$, $T = 0$,$\beta = 0.5$, $\mu = 0.5$, $\kappa _{nf1}=1.4$, $\chi _{nl} = 0.1$, $b = 1$, $k_1=100$, $k_3=10^5$, $\eta _1 = 0.0005$

Fig. 17

Midpoint displacement of the system as a function of frequency and thermal parameters $v = 4$. $F = 1$, $P = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=1$, $\chi _{sg} = 0.05$, $\kappa _{nf1}=1.4$, $\chi _{nl} = 0.2$, $k_1=100$, $k_3=100$, $\eta _1 = 0.0005$

Fig. 18

Midpoint displacement of the system as a function of frequency and thermal parameters $v = 4$. $F = 1$, $P = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=1$, $\chi _{sg} = 0.01$, $\kappa _{nf1}=1.0$, $\chi _{nl} = 0.01$, $k_1=100$, $k_3=100$, $\eta _1 = 0.0005$

Fig. 19

Midpoint displacement of the system as a function of frequency for a pressure and b tension with parameters $v = 5$. $F = 1$, $\beta = 0.5$, $\mu = 0.5$, $b=1$, $\chi _{sg} = 0.05$, $\kappa _{nf1}=1.0$, $\chi _{nl} = 0.2$, $k_1=10$, $k_3=10$, $\eta _1 = 0.0005$

Fig. 20

Midpoint displacement of the system as a function of frequency and viscoelastic parameters $v = 4$. $F = 1$, $P = 0$, $\theta = 0$, $T = 0$, $\beta = 0.5$, $\mu = 0.5$, $b=0.5$, $\chi _{sg} = 0.05$, $\chi _{nl} = 0.1$, $k_1=100$, $k_3=100$, $\kappa _{nf1}=1.2$

Figure 14 illustrates the effects of fluid slip boundary condition on the frequency and midpoint displacement of the slightly curved viscoelastic nanotube conveying fluid. An interesting phenomenon is found in this system by the variation of the slip boundary conditions; there is a reduction in resonant frequency as the slip boundary parameters increases up to 1.4, then the dynamics of the system changes from when the slip parameter becomes 1.5. The resonant frequency tends to increases and there is evolution of another resonant peak, making two resonant peaks for slip parameters greater than 1.5. For example, when $\kappa _{nf1}=1.4$ ,and $\kappa _{nf1}=1.2$, the resonant frequency are 5 and 12, respectively. This is lower compared to nanotube with no slip boundary condition. In addition, the peak displacements values are within range when $\kappa _{nf1}=1.3$ and $\kappa _{nf1}=1.6$. Hence, no slip boundary parameter normally assumed for pipe can not actually capture the dynamics of nanotube systems. Therefore, the internal wall of the tube has effect on the dynamics of the nanotube.

The midpoint displacement of the pipe system as a function of nonlocal parameters and frequency is shown in Fig.15. By inspecting Fig.15, three remarkable features can be found; (i) As the nonlocal parameter increases, the resonant frequency shift towards the lower frequency up till a point where $\chi _{nl} = 0.15$; (ii) two resonant peaks are formed at range $\chi _{nl} = 0.15$ to $\chi _{nl} = 0.2$; and (iii) after $\chi _{nl} = 0.3$, the resonant peaks reduce drastically and the resonant frequency goes beyond the 30.

It is observed that increase in strain gradient parameter causes an increase in the resonant frequency. This can be easily seen in Fig. 16. Furthermore, larger strain gradient parameters lead to lower peak mid displacement of the pipe transverse motions (Farajpour et al. 2020). For illustration when $\chi _{sg} = 0.01$, the displacement is around 0.05, while at $\chi _{sg} = 0.3$, the displacement is 0.03.

Figure 17 shows that the midpoint displacement of the pipe system as a function of frequency and thermal load. First, it is obvious that the peak value of the midpoint displacement of the pipe reduces with the increase of thermal load. Second, the resonance point of the pipe system increases as the $\theta$ increases. This effect is due to the slip parameter. The slip boundary condition tends to drag the displacement of the pipe. To better understand this, we remove the effect of the slip parameter in Fig. 18. In Fig. 18 slip parameter was set as zero, and the frequency and temperature variation shows that as the frequency is increasing the resonant decreases. The behaviour of nanopipe with slip boundary condition behaves quite differently from the pipe with no slip boundary condition. Figure 19a highlights the influences of pressure and tension on nanotubes frequency diagrams for P =0,2 and 4. A larger pressure parameter gives a lower peak amplitude for the midpoint displacement accompanied by a resonance-region shift to the right. Conversely,the tension parameter increase tends to increase the amplitude of the displacement and shift the resonant region to the left Fig. 19b.

It can be concluded that viscoelastic parameters does not significantly alter the resonant frequency of the nanosystem. However, it has an important effect on the midpoint displacement of the transverse motion of the nanotube (Fig. 20). The resonant frequency for all the forcing frequency occurs at 12, and the maximum displacement at when there is no damping which is expected from basic physics.

4 Conclusion

In this paper, the initial curvature of the curved nanotube has been considered with thermal load in studying the transverse vibration of tube considering the effects of scale due to fluid and solid. To the best of our knowledge, this is one of few papers on forced vibration. The Eigenfunction expansion method and fourth order Runge–Kutta method were combined to analyze the vibration of the initially nanotube under slip boundary conditions,nonlocal effect, strain gradient, viscoelastic and thermal load parameters. The dynamic equation of the nanotube was derived using the generalized Hamilton’s principle. Eigenfunction expanson was used to analyze the natural frequencies of the nanotube. The steady-state response under harmonic excitation was obtained by the numerical methods. The effects of key parameters on the steady-state response were examined. Based on the obtained results, the following conclusions can be drawn:

• 1. The vibration features of a slightly curved nanotube, including its linear frequency and the nonlinear response are greatly prone to the initial curvature of the tube.

• 2. An increase in fluid slip parameter degrades both the linear natural frequency and the critical velocity of the tube. The resonant frequency tends to reduce as the slip parameter increases. However, for slip boundary conditions, the amplitude of the vibration are higher than no slip boundary condition.

• 3. With an increase of the nonlocal parameter, there is a decrease in the total stiffness of the nanotube while an increase in strain gradient causes an increase in the stiffness of the tube. For the steady state, there is reduction of the resonant frequency as the nonlocal parameter increases. While strain gradient increase produces an increase resonant frequency.

• 4. For forced vibration, when initial curvature is zero, one distinct resonant frequency was obtained. However, for slightly curved pipe, two distinct resonant frequencies were obtained for flow velocity between 3.7 and 4.5 respectively. One resonant frequency is obtained for velocities below 3.7 and above 4.5 respectively.

• 5. Changes in the thermal load and viscoelastic parameters significantly affect the dyanmic response of the nanotube in linear and nonlinear state.

Consequently, the initial curvature of the nanotube and thermal load demonstrate complex dynamic features. Therefore, initial curvature with other scale dependents effects should be considered in the study of vibration of nanotubes.