1 Introduction

Various rotating systems have been reported in the literature based on a wide range of mechanical structures. The vast majority of rotating systems have an asymmetrical rotating shaft. The common goal of all rotating structures is to realize instability sources. The common instability sources are induced on the system due to nonlinearities of the system. Thus, analysis of the nonlinear system when the system is near the resonances is required. Ganesan [1] considered the stability of an asymmetrical rotor supported on the asymmetric bearings when the system is near the major critical speeds. It was shown that in the absence of damping the amplitude of the system could be limited to finite values using a proper combination of bearing and shaft asymmetries. Wettergren et al. [2] investigated instability of an asymmetrical rotor with internal damping. The asymmetry of rotor was due to asymmetry of stiffness of the shaft. It was shown that the instabilities could be removed with the suitable combination of the internal damping, external damping, shaft asymmetry and asymmetry of the bearings stiffness. Verichev et al. [3] considered damping vibration of a rotary system without change in the visco-elastic properties of the system. They used a harmonic addition to the constant speed of the system for reduction of vibration. They showed that damping vibration could be achieved by selection of the best parameters for harmonic addition. Shahgholi et al. [4, 5] studied the primary and parametric resonances of an asymmetrical rotating shaft. The nonlinearities were due to extensionality or in-extensionality of shaft and large amplitudes. It was shown that the stationary points of asymmetrical shaft are of spiral or node type but for symmetrical shaft are of spiral type. Sabuncu et al. [6] investigated dynamic stability of pre-twisted Timoshenko beam having asymmetric aerofoil cross section subject to lateral parametric excitation. They showed that pre-twist angle has an influence on coupling and shear coefficient. Vakakis [7] investigated the main and subharmonic resonances of a nonlinear system with cubic nonlinearity. The system was in a 1-1 internal resonances. It was shown that the number of resonance branches before and after the mode bifurcation is different. Carrella et al. [8] investigated the reduction of vibration response of rotor using nonlinear springs. It was shown that the nonlinear supports have considerable effect on the system response. Zhang and Meng [9] studied stability, chaotic dynamics and bifurcations in the micro rotor system. It was shown that damping coefficient could restrict chaotic motion and reduce amplitude of vibration. Mcdonald et al. [10] investigated the global bifurcations in two degrees of freedom conservative nonlinear gyroscopic systems which are periodically perturbed. They studied the effect of periodic perturbations near a double zero eigenvalue of the linear system in the presence of symmetry breaking. It was shown that the chaotic motion occurs in the system. Badlani et al. [11] studied the stability of asymmetrical linear shafts with unequal bending stiffness in the direction of principal axes. They found new instability region by considering Timoshenko beam theory. Parkinson [12] investigated linear vibration of a rigid rotor supported by anisotropic flexible bearings of negligible mass. The effect of large and small asymmetry of bearings and internal damping on the response of the system was studied. The stability and self-excited vibration of a rotating shaft with elastic and viscous nonlinearities and transverse load were investigated by Kurnik [13]. The effect of cubic nonlinearities, transverse load and dimensionless stress relaxation time were investigated. In addition, it was found that the system has a transition from super- to subcritical bifurcation due to interaction between nonlinearities and transverse load. Al-Nassar et al. [14] investigated nonlinear vibration of a rotating blade on a torsionally flexible shaft. They obtained instability regions of the blades vibrations when the torsional excitation frequency is lower than the blade bending natural frequency. Legrand et al. [15] considered nonlinear vibrations of a rotating shaft supported by two journal bearings. The nonlinearities of the model were due to hydraulic bearings. The nonlinear normal mode invariant manifold approach was used to describe the vibration behavior of nonlinear mechanical systems with general damping, gyroscopic, and stiffness matrices. Rajalingham et al. [16] investigated vibrations of an asymmetrical rotor and showed that instability of the rotor could be removed using suitable parameters for supports. Khadem et al. [17] studied two-mode combinational resonances of a nonlinear rotating shaft. The effect of eccentricities and damping coefficient on the stability and bifurcation points were investigated. The same authors [18] investigated the primary resonances of a nonlinear in-extensional rotating shaft. They showed the effect of damping and eccentricity on the system response, and loci of bifurcation points. Luczko [19] developed a geometrically nonlinear model of a rotating shaft. Their model was included the Von-Karman nonlinearity, nonlinear curvature, large displacements and rotations as well as gyroscopic and shear deformation effects. He investigated internal resonances. Karpenko et al. [20] considered nonlinear dynamics of a rotor system with bearing clearance effects. They showed that periodic, quasi-periodic and chaotic motions occur in the system. Wang et al. [21] investigated the nonlinear-coupled dynamic of the blade-rotor-bearing systems and studied influence of nonlinear vibrations of rotor on the blade vibrations. It was shown that the system has a various kind of phenomenon such as period-doubling bifurcation, the multi-period and quasi-period motions. Pei [22] studied stability boundaries of a spinning linear rotor with parametric excitation. It was shown that the instability region obtained by Bolotin method was larger than that of the Floquet method. Sinou [23] probed nonlinear vibrations of a rotor supported by ball bearings. It was shown that amplitude of vibrations in the critical and sub-critical resonances is dependent on the radial clearance and imbalances. Fan et al. [24] considered the linear vibration control of a horizontal rotor with an asymmetrical mass moments of inertia. The shaft was rigid, and the bending stiffness was neglected. They investigated the effect of asymmetrical mass moments of inertia on the system performance. Turhan et al. [25] considered dynamic stability of a linear rotating beam with a periodically fluctuating speed. It was shown that a speed fluctuation might have a stabilizing effect on statically unstable inward-oriented beams. Kamel and Bauomy [26] considered the nonlinear vibrations of a rotor with active magnetic bearings under multi-parametric excitations. They showed that in the system various phenomena such as chaotic, hardening nonlinearities, softening nonlinearities and jump occur. Sheu [27] investigated parametric instability of a cantilever shaft-disk system subjected to axial and follower loads, respectively. It was shown that instability due to periodic axial load was more than periodic follower force in the same static load factor. Chang-Jian and Chen [28] investigated nonlinear vibrations of a rotor-bearing system with rub impact effect. They showed that system has quasi-periodic, periodic and 2T-periodic responses for various values of speed ratio. Shahgholi and Khadem [29] investigated the Hopf and double Hopf bifurcations of an asymmetrical rotating shaft. They obtained the standard normal form for the above-mentioned bifurcations for symmetrical and asymmetrical rotating shafts. Also, the effect of various parameters of the system on the over-mentioned resonances was studied.

A linear model of a rotating system is an ideal model for representation of the actual behavior of the system. However, in many cases, the achieved results may be an unsatisfactory approximation. In addition, when the deflections of the rotating system become large (especially, when the system is near resonances) the nonlinearities of the system appear. Consequently, in the system, interesting phenomena such as jump phenomena, internal resonances, combinational resonances, sub-harmonic resonances etc may occur. Furthermore, most of the rotating systems are asymmetrical and investigation of these nonlinear phenomena in the asymmetrical rotating system is complicated compared to symmetrical rotating system. Accordingly, by considering the above works, it can be concluded that investigation of the above-mentioned resonances using analytical method for an asymmetrical rotating shaft provide remarkable results. For this purpose, the above-mentioned resonances for a simply supported asymmetrical rotating shaft with extensional effect and large amplitudes are investigated. For this rotating system, rotary inertia and gyroscopic effects are included; however, shear deformation is neglected. The excitation terms are due to shaft asymmetry and dynamics imbalances of the shaft. In this paper, the excitation term due to shaft asymmetry, called parametric excitation, is, in turn, due to inequality between mass moments of inertia and bending stiffness in the direction of principal axes. However, mostly in the literature, the parametric excitation is due to lateral force, speed fluctuations or stiffness anisotropy. The equations of the motion are derived with the aid of extended Hamilton principle with the extensionality assumption in the complex plane. The system is analyzed by the harmonic balance method. The frequency response curves are plotted for the first two modes. The effect of inequality between eccentricities in the direction of principal axes and external damping on the steady-state responses and bifurcation points of the rotating asymmetrical shaft are investigated. The characteristics of the steady-state solutions are studied and the imaginary part of the eigenvalues corresponding to the steady-state solutions is plotted versus detuning parameter. It is shown that the characteristics of the stable steady-state solution are a stable node or a stable spiral. To validate the perturbation results, numerical computations are utilized and a good agreement is achieved.

2 Modeling and equations of motion

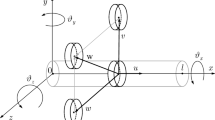
An asymmetrical rotating shaft with arbitrary cross section and length \(l\) is shown in Fig. 1. In order to investigate the dynamics of the system two frames are used as illustrated in Fig. 1. A global frame XYZ, and a local frame xyz, which is attached to the shaft centroid. The components of the deformation of the shaft with respect to the global frame in the directions of \(X\), \(Y\), and \(Z\) are denoted by \(u(x,t)\), \(v(x,t) \) and \(w(x,t)\), respectively.

Fig. 1
figure 1

The global and local frames of an asymmetrical rotating shaft with arbitrary cross section

Full size image

To obtain the equations of motion the extended Hamilton principle is used as:

$$\begin{aligned} \delta \int _0^l {(T-V)} dt=0 \end{aligned}$$
(1)

where \(T\) is the kinetic energy, \(V\) is the potential energy, \(\delta \) is variation operator and \(t\) is time.

The kinetic and potential energies of the system can be obtained as [4]:

$$\begin{aligned}&T=\frac{1}{2}\int _0^l \{m(\dot{u}^{2}+\dot{v}^{2}+\dot{w}^{2})\nonumber \\&\quad +\,\,I_{xx} \omega _x^2 +I_{xx} \omega _y^2 +I_{xx} \omega _z^2 \} \mathrm{d}x \nonumber \\&\quad +\,\,\frac{1}{2}\int _0^l m\varOmega ^{2}[e_y^2 (x)+e_z^2 (x)]-2m\varOmega \{[e_z (x)\dot{v}\nonumber \\&\quad +\,\,e_y (x)\dot{w}]\sin \varOmega t+[e_y (x)\dot{v}-e_z (x)\dot{w}]\cos \varOmega t\} \mathrm{d}x\end{aligned}$$
(2)
$$\begin{aligned}&V=\frac{1}{2}\int _0^l {(N_{xx} \xi ^{2}+D_{xx} } k_{_x }^2 +D_{yy} k_{_y }^2 +D_{zz} k_{_z }^2 ) \mathrm{d}x\nonumber \\ \end{aligned}$$
(3)

where \(m, I_{xx} , I_{yy} , I_{zz} , N_{xx} ,D_{xx} , D_{yy} \) and \(D_{zz} \) are the mass per unit length, polar mass moment of inertia, mass moment of inertia about \(y\) axis, mass moment of inertia about \(z\) axis, longitudinal stiffness, torsional stiffness, flexural stiffness about \(y\) axis, and flexural stiffness about \(z\) axis, respectively, which can be computed as:

$$\begin{aligned}&m=\int {\rho \mathrm{d}A ,\quad I_{xx} =\int {\rho (y^{2}+z^{2}) \mathrm{d}A} } ,\nonumber \\&I_{yy} = \int {\rho z^{2} \mathrm{d}A} ,\quad I_{zz} =\int {\rho y^{2} \mathrm{d}A}\nonumber \\&N_{xx} =\int _A {E\mathrm{d}A} ,\quad D_{xx} =\int _A {G(y^{2}+z^{2})\mathrm{d}A} , \nonumber \\&D_{yy} =\int _A {Ez^{2}\mathrm{d}A},\quad D_{zz} =\int _A {Ey^{2}\mathrm{d}A} \end{aligned}$$
(4)

where \(\rho , A, E\) and \(G\) are mass density, cross-sectional area, Young and shear modulus, respectively. The second integral in Eq. (2) is due to dynamic imbalances of the shaft and \(e_y (x) \) and \(e_z (x) \) are eccentricity distributions with respect to the \(y\) and \(z\) axes, respectively.

In Eqs. (2–3), \(\omega _x , \omega _y ,\omega _z \) are the components of angular velocities and \(k_x ,k_y ,k_z \) are components of curvatures of the rotating shaft which can be determined as [4]:

$$\begin{aligned}&\omega _x \!=\!(\varOmega \!-\!\dot{\psi }\sin \theta ) , \omega _y \!=\!\dot{\psi }\cos \theta \sin (\varOmega t)+\dot{\theta }\cos (\varOmega t)\! ,\nonumber \\&\omega _z =\dot{\psi }\cos \theta \cos (\varOmega t)-\dot{\theta }\sin (\varOmega t)\end{aligned}$$
(5)
$$\begin{aligned}&k_x \!=\!(-{\psi }'\sin \theta ) , k_y \!=\!{\psi }'\cos \theta \sin (\varOmega t)+{\theta }'\cos (\varOmega t) , \nonumber \\&k_z ={\psi }'\cos \theta \cos (\varOmega t)-{\theta }'\sin (\varOmega t) \end{aligned}$$
(6)

where \(\varOmega \) is the rotational speed, \(\psi (x,t)\) and \(\theta (x,t)\) are the Euler angles which for slender shaft, these angles satisfy the following relation [4]:

$$\begin{aligned} \psi&= \sin ^{-1}\frac{{v}'}{\sqrt{(1+{u}')^{2}+{v}'^{2}}} ,\nonumber \\ \theta&= \sin ^{-1}\frac{-{w}'}{\sqrt{(1+{u}')^{2}+{v}'^{2}+{w}'^{2}}} \end{aligned}$$
(7)

Also, in Eq. (3) \(\xi \) is the strain along the neutral axis of the shaft, which can be obtained as:

$$\begin{aligned} \xi =\sqrt{(1+{u}')^{2}+{v}'^{2}+{w}'^{2}}-1 \end{aligned}$$
(8)

Substituting Eq. (7) into Eqs. (5–6) and expanding the results up to the third order, consequently, the potential and kinetic energies can be computed up to the third order. Substituting reduced form of the kinetic and potential energies into Eq. (1) and equating the coefficients of \(\delta u\), \(\delta v\) and \(\delta w\) the equations of motion are obtained. It is noted that the longitudinal stiffness is much higher than the flexural stiffness. So, in the equations of motion, the nonlinear coefficients of the flexural stiffness are negligible [30]. In addition, for slender shafts, the longitudinal inertia \(m\ddot{u}\) may be negligible [31]. Hence, the longitudinal equation of motion and the corresponding boundary conditions \(u(0)=u(l)=0\) are obtained as:

$$\begin{aligned} {u}'=-\frac{1}{2}[{v}'^{2}+{w}'^{2}-\frac{1}{l}\int _0^l {({v}'^{2}+{w}'^{2})\mathrm{d}x} ]+\cdots \end{aligned}$$
(9)

To simplify the notation, the following parameters are used:

$$\begin{aligned}&\varDelta _\mathrm{D} =\frac{D_{zz} -D_{yy} }{2} ,\quad D=\frac{D_{zz} +D_{yy} }{2} ,\nonumber \\&\varDelta _\mathrm{I} =\frac{I_{zz} -I_{yy} }{2} ,\quad I=\frac{I_{zz} +I_{yy} }{2} \end{aligned}$$
(10)

Using Eq. (9) and the following dimensionless quantities, the flexural equations of the motion in the complex form are obtained as:

$$\begin{aligned}&v^{*}=\frac{v}{e_0 } ,\quad w^{*}=\frac{w}{e_0 } ,\quad x^{*}=\frac{x}{l} ,\nonumber \\&I^{*}=\frac{I\pi ^{2}}{ml^{2}} ,\quad I_1^*=\frac{I_{xx} \pi ^{2}}{ml^{2}} ,\quad \varDelta _\mathrm{I}^*=\frac{\varDelta _\mathrm{I} \pi ^{2}}{ml^{2}} ,\nonumber \\&e_{_z }^*=\frac{e_z }{e_0 } ,\quad e_{_y }^*=\frac{e_y }{e_0 } , \quad \varDelta _\mathrm{D}^*=\frac{\varDelta _\mathrm{D} }{D} ,\nonumber \\&\varOmega ^{*}=\sqrt{\frac{ml^{4}}{D\pi ^{4}}}\varOmega ,\quad \alpha =\frac{N_{xx} e_0^2 }{2D} , \nonumber \\&t^{*}=\sqrt{\frac{D\pi ^{4}}{ml^{4}}}t ,\quad c^{*}=\frac{cl^{2}}{\pi ^{2}\sqrt{mD}} ,\nonumber \\&q^{*}=v^{*}+iw^{*},\quad \bar{{q}}^{*}=v^{*}-iw^{*}\end{aligned}$$
(11)
$$\begin{aligned}&\frac{q^{(IV)}}{\pi ^{4}}+\ddot{q}+c\dot{q}-\frac{\alpha }{\pi ^{4}}{q}''\int _0^1 {{q}' {\bar{{q}}}'} \mathrm{d}x+i\varOmega \frac{I_1 }{\pi ^{2}}{\dot{q}}''\nonumber \\&\quad -\frac{I}{\pi ^{2}} {\ddot{q}}'' \!-\!\frac{\varDelta _\mathrm{I} }{\pi ^{2}}({\ddot{\bar{{q}}}}'' \!+\! 2i\varOmega {\dot{\bar{{q}}}}'')e^{2i\varOmega t}\!+\!\varDelta _\mathrm{D} \frac{\bar{{q}}^{(IV)}}{\pi ^{4}}e^{2i\varOmega t} \nonumber \\&\quad =\varOmega ^{2}(ie_z (x)+e_y (x))e^{i\varOmega t}\end{aligned}$$
(12)
$$\begin{aligned}&z={z}''=0 \hbox { at } x=0 \hbox { and } x=1 \end{aligned}$$
(13)

where \(e_0\) is a quantity which has same order with the rotor imbalance. It should be noted that, since, shear deformation effects are ignored, rotational deformations are only due to \({v}'\) and \({w}'\) and any other rotational deformations are neglected. Hence, if \(v\) and \(w\) are of \(O(\varepsilon )\), the rotary inertia would be of \(O(\varepsilon ^{2})\). Therefore, the nonlinear coefficients of the rotary inertia in Eq. (12) are negligible and have been omitted. The viscous damping force acts in the direction opposite to the velocity of the rotating shaft; hence, the damping force \(c\dot{z}\) is added to Eq. (12) where \(c\) is a damping coefficient. For ease of notation, the stars are dropped.

3 Descretized the equations of motion by Galerkin method

The partial differential equations of motion can be converted to the ordinary ones by the Galerkin approach as:

$$\begin{aligned} q(x,t)=\phi _n (x)Q(t) \end{aligned}$$
(14)

where \(n,\) is the mode number, and \(\phi _n (x)\) is the linear mode shape of the shaft which for simply support conditions is:

$$\begin{aligned} \phi _n (x)=2\sqrt{2}\sin n\pi x \end{aligned}$$
(15)

Considering Eqs. (15), (12) and using the mode’s orthogonality; it can be obtained:

$$\begin{aligned}&\varGamma _1^{(n)} \ddot{Q}+K_{11}^{(3n)} Q+cK_{11}^{(1n)} \dot{Q}\nonumber \\&\quad +\,\,i\varOmega \varGamma _3^{(n)} \dot{Z}-\varGamma _5^{(n)} (\ddot{\bar{{Q}}}+2i\varOmega \dot{\bar{{Q}}})e^{2i\varOmega t}\nonumber \\&\quad +\,\,\varDelta _\mathrm{D} {K}_{11}^{(3n)} \bar{{Q}}e^{2i\varOmega t}+\varGamma _4^{(n)} Q^{2}\bar{{Q}}=\vartheta _t \varOmega ^{2}e^{i(\varOmega t+\theta )}\nonumber \\ \end{aligned}$$
(16)

where the coefficients of Eq. (16) are presented in “Appendix”. In Eq. (16) for bookkeeping, a transformation is defined as follows [32]:

$$\begin{aligned} \begin{array}{l} Q(t)=\varepsilon ^{\lambda }Z(t) \\ \vartheta _t =\varepsilon ^{\lambda }e_t \\ \end{array} \end{aligned}$$
(17)

where \(\lambda >0\) and \(\varepsilon \) is small dimensionless parameter to measure the system deflection. Therefore, substituting Eq. (17) into Eq. (16), and letting \(\lambda =1/2\) the following equation is obtained:

$$\begin{aligned}&\varGamma _1^{(n)} \ddot{Z}+K_{11}^{(3n)} Z+cK_{11}^{(1n)} \dot{Z}+i\varOmega \varGamma _3^{(n)} \dot{Z}\nonumber \\&\quad -\,\,\varGamma _5^{(n)} (\ddot{\bar{{Z}}}+2i\varOmega \dot{\bar{{Z}}})e^{2i\varOmega t}+\varDelta _\mathrm{D} K_{11}^{(3n)} \bar{{Z}}e^{2i\varOmega t}\nonumber \\&\quad +\,\,\varepsilon \varGamma _4^{(n)} Z^{2}\bar{{Z}}=e_t \varOmega ^{2}e^{i(\varOmega t+\theta )} \end{aligned}$$
(18)

It is noted that the small parameter \(\varepsilon \) would be set equal to unity, as a bookkeeping parameter, after solution of equation of motion.

3.1 Analysis of linear homogeneous part of equation of motion

The linear homogeneous part of Eq. (18) is as:

$$\begin{aligned}&\varGamma _1^{(n)} \ddot{Z}+K_{11}^{(3n)} Z+cK_{11}^{(1n)} \dot{Z}+i\varOmega \varGamma _3^{(n)} \dot{Z}\nonumber \\&\quad -\,\,\varGamma _5^{(n)} (\ddot{\bar{{Z}}}+2i\varOmega \dot{\bar{{Z}}})e^{2i\varOmega t}+\varDelta _\mathrm{D} K_{11}^{(3n)} \bar{{Z}}e^{2i\varOmega t}=0\nonumber \\ \end{aligned}$$
(19)

Considering the general solution of \(Z\) as:

$$\begin{aligned} Z=ae^{i\lambda t}+be^{i(2\varOmega -\bar{{\lambda }})t} \end{aligned}$$
(20)

where \(a, b\) and the frequency \(\lambda \) may become complex, and \(\bar{{\lambda }}\) is complex conjugate of \(\lambda \).

Substituting Eq. (20) into Eq. (19), equating the coefficients of \(e^{i\lambda t}\) and \(e^{i(2\varOmega -\bar{{\lambda }})t}\) in both sides and equating the coefficients of \(a/{\bar{{b}}}\) in the achieved results gives:

$$\begin{aligned} G(p)G(2\varOmega -p)-F(p)F(2\varOmega -p)=0 \end{aligned}$$
(21)

where:

$$\begin{aligned}&G(p)=-\varGamma _1^{(n)} p^{2}+K_{11}^{(3n)} -\varOmega \varGamma _3^{(n)} p ,\nonumber \\&F(p)=\varDelta _\mathrm{D} K_{11}^{(3n)} -\varGamma _5^{(n)} p(2\varOmega -p) \end{aligned}$$
(22)

Using Eqs. (21) and (20), it can be written:

$$\begin{aligned}&Z=R_1 e^{i(\omega _\mathrm{f} t+\varphi _1 )}+r_1 e^{i((2\varOmega -\omega _\mathrm{f} )t-\varphi _1 )}\nonumber \\&\quad +\,\,R_2 e^{i(\omega _\mathrm{b} t+\varphi _2 )}+r_2 e^{i((2\varOmega -\omega _\mathrm{b} )t-\varphi _2 )} \end{aligned}$$
(23)

where \(\omega _\mathrm{f} \) and \(\omega _\mathrm{b} \) are forward and backward frequencies of the linear system. Also, between the coefficients of Eq. (23) the following relation holds:

$$\begin{aligned}&\frac{r_1 }{R_1 }=\left. {-\frac{G(p)}{F(2\varOmega -p)}} \right| _{p=\omega _\mathrm{f} } , \nonumber \\&\frac{r_2 }{R_2 }=\left. {-\frac{G(p)}{F(2\varOmega -p)}} \right| _{p=\omega _\mathrm{b} } \end{aligned}$$
(24)

3.2 Nonlinear analysis of the equation of motion using the harmonic balance method

The equation of motion [Eq. (16)] is nonlinear; hence, various kinds of resonances such as combinational, internal, primary and sub-harmonic resonances occur in the system. In this study, an asymmetrical rotating shaft with internal resonances is considered. When the asymmetrical rotating shaft is in the one-to-one internal resonance condition as \(\omega _\mathrm{f} =-\omega _\mathrm{b} \), the following resonances may occur simultaneously:

  1. (i)

    Forward sub-harmonic resonances as \(\varOmega =3\omega _\mathrm{f} \)

  2. (ii)

    Backward sub-harmonic resonances as \(\varOmega =-3\omega _\mathrm{b} \)

  3. (iii)

    Combinational resonances as \(\varOmega =2\omega _\mathrm{f} -\omega _\mathrm{b} \)

  4. (iv)

    Combinational resonances as \(\varOmega =\omega _\mathrm{f} -2\omega _\mathrm{b} \)

Consequently, the terms with frequencies \(\varOmega /3\), \(-\varOmega /3\), \(2\varOmega -\varOmega /3={5\varOmega }/3\) and \(2\varOmega -({-\varOmega }/3)={7\varOmega }/3\) may exist in the response of the system where two last cases are due to asymmetry of the shaft. In addition, a constant term exists in the solution. Consequently, frequency \(2\varOmega -0=2\varOmega \) occurs in the system due to shaft asymmetry. Therefore, the solution of the equations of motion is as:

$$\begin{aligned}&Z(t)=R_\mathrm{f} e^{i\left( \frac{\varOmega }{3}t+\delta _\mathrm{f} \right) }+r_\mathrm{f} e^{i\left( \frac{5\varOmega }{3}t-\delta _\mathrm{f} \right) }+R_\mathrm{b} e^{i\left( -\frac{\varOmega }{3}t+\delta _\mathrm{b} \right) }\nonumber \\&\quad +\,\,r_\mathrm{b} e^{i\left( \frac{7\varOmega }{3}t-\delta _\mathrm{b} \right) }+Pe^{i(\varOmega t+\beta )}+S e^{i(2\varOmega t+\delta )}+A\nonumber \\ \end{aligned}$$
(25)

It is noted that the term with frequency \(\varOmega \) is due to the excitation force, which is due to dynamic imbalances of the shaft. To analyze the steady-state response of the system, the harmonic balance method is used. For this purpose, Eq. (25) is substituted into Eq. (18) and by considering the order of magnitude terms the coefficients of \(e^{i\frac{\varOmega }{3}t}\), \(e^{i\frac{5\varOmega }{3}t}\), \(e^{-i\frac{\varOmega }{3}t}\), and \(e^{i\frac{7\varOmega }{3}t}\) on both sides of Eq. (16) are equated. Consequently, equations for forward amplitudes \(R_\mathrm{f} \) and \(r_\mathrm{f} \), backward amplitudes \(R_\mathrm{b} \) and \(r_\mathrm{b} \), phase angles \(\delta _\mathrm{f} \) and \(\delta _\mathrm{b} \), and constant values \(A\) can be obtained. Also, using Eq. (24), the relationship between \(R_\mathrm{f} \), \(r_\mathrm{f} \), \(R_\mathrm{b} \) and \(r_\mathrm{b} \) from zero order of the harmonic balance equations are as:

$$\begin{aligned} \frac{r_\mathrm{f} }{R_\mathrm{f} }=\frac{-G_1 }{F_5 } ,\quad \frac{r_\mathrm{b} }{R_\mathrm{b} }=\frac{-G_{-1} }{F_7 } \end{aligned}$$
(26)

where:

$$\begin{aligned} G_j \!=\! G\left( j\frac{\varOmega }{3}\right) ,\quad \! F_j \!=\!F\left( j\frac{\varOmega }{3} \right) , \quad j=-1,1,5,7\nonumber \\ \end{aligned}$$
(27)

The amplitude \(P\) and associated phase angle \(\beta \) can be obtained by equating the coefficients of \(e^{i\varOmega t}\) on the both sides of the zero order of harmonic balance equations as:

$$\begin{aligned} P&= \frac{e_t \varOmega ^{2}\cos \theta }{(G(\varOmega )+F(\varOmega ))\cos \beta }\nonumber \\&= \frac{e_t \varOmega ^{2}\sin \theta }{(G(\varOmega )-F(\varOmega ))\sin \beta } ,\nonumber \\ \beta&= \tan ^{-1}\left[ \frac{\tan \theta (G(\varOmega )+F(\varOmega ))}{(G(\varOmega )-F(\varOmega ))}\right] \end{aligned}$$
(28)

In addition, the amplitude \(S\) and the associated phase angle \(\delta \) are obtained by equating the coefficients of \(e^{i2\varOmega t}\) on the both sides of the zero order of harmonic balance equations as:

$$\begin{aligned}&S\cos \delta =\frac{-\varDelta _\mathrm{D} K_{11}^{(3n)} a\cos \beta _A }{G(2\varOmega )} , \nonumber \\&S\sin \delta =\frac{\varDelta _\mathrm{D} K_{11}^{(3n)} a\cos \beta _A }{G(2\varOmega )} \end{aligned}$$
(29)

From Eq. (29), it can be concluded:

$$\begin{aligned} \delta =-\beta _A, \quad S=Qa,\quad Q=\frac{-\varDelta _\mathrm{D} K_{11}^{(3n)} }{G(2\varOmega )} \end{aligned}$$
(30)

where:

$$\begin{aligned} A=ae^{i\beta _A } \end{aligned}$$
(31)

Considering Eqs. (25–30) the following equations are obtained:

$$\begin{aligned}&\varTheta _\mathrm{f} \dot{R}_\mathrm{f} =\varOmega cK_{11}^{(n)} (5G_1 -G_5 )R_\mathrm{f}\nonumber \\&\quad +3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \sin (\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A ) \nonumber \\&\varTheta _\mathrm{f} R_\mathrm{f} \dot{\delta }_\mathrm{f} =3(G_1 G_5 -F_1 F_5 )R_\mathrm{f}\nonumber \\&\quad +3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \cos (\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A ) \nonumber \\&\quad + 3\varGamma _4^{(n)} (G_1 +G_5 )(2R_\mathrm{f} P^{2}+2R_\mathrm{f} S^{2}+2R_\mathrm{f} a^{2}) \nonumber \\&\varTheta _\mathrm{b} \dot{R}_\mathrm{b} =\varOmega cK_{11}^{(n)} (7G_{-1} +G_7 )R_\mathrm{b}\nonumber \\&\quad +3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \sin (\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A ) \nonumber \\&\varTheta _\mathrm{b} R_\mathrm{b} \dot{\delta }_\mathrm{b} =3(G_{-1} G_7 -F_{-1} F_7 )R_\mathrm{b}\nonumber \\&\quad +3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \cos (\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A )\nonumber \\&\quad +3\varGamma _4^{(n)} (G_{-1} +G_7 )\left( 2R_\mathrm{b} P^{2}+2R_\mathrm{b} S^{2}+2R_\mathrm{b} a^{2}\right) \nonumber \\&\quad 2\left( 1-\frac{G_{-1} }{F_7 }Q-\frac{G_1 }{F_5 }Q\right) R_\mathrm{b} R_\mathrm{f} \sin (\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A )\nonumber \\&\quad +P^{2}Q\sin (2\beta )=0 \nonumber \\&\quad 2\left( R_\mathrm{b}^2 +R_\mathrm{f}^2 +P^{2}+S^{2}+\frac{1}{2}a^{2}\right. \nonumber \\&\quad \left. +\left( \frac{G_1 }{F_5 }\right) ^{2}R_\mathrm{f}^2 +\left( \frac{G_{-1} }{F_7 }\right) ^{2}R_\mathrm{b}^2 \right) \nonumber \\&\quad +2\left( 1\!-\!\frac{G_{-1} }{F_7 }Q\!-\!\frac{G_1 }{F_5 }Q\right) R_\mathrm{f} R_\mathrm{b} \cos (\delta _\mathrm{b} \!+\!\delta _\mathrm{f} -2\beta _A )\nonumber \\&\quad +2(r_\mathrm{f} R_\mathrm{f} Q+r_\mathrm{b} R_\mathrm{b} Q) \nonumber \\&\quad +P^{2}Q\cos (2\beta )-K_{11}^{(3n)} -\varDelta _\mathrm{D} K_{11}^{(3n)} Q=0 \end{aligned}$$
(32)

To simplify Eq. (32), the following transformation is introduced:

$$\begin{aligned} \phi =\delta _\mathrm{b} +\delta _\mathrm{f} -2\beta _A \end{aligned}$$
(33)

Hence, using Eqs. (32–33), it can be written:

$$\begin{aligned}&\varTheta _\mathrm{f} \dot{R}_\mathrm{f} =\varOmega cK_{11}^{(n)} (5G_1 -G_5 )R_\mathrm{f} \nonumber \\&\quad +3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \sin \phi \nonumber \\&\varTheta _\mathrm{b} \dot{R}_\mathrm{b} =\varOmega cK_{11}^{(n)} (7G_{-1} +G_7 )R_\mathrm{b} \nonumber \\&\quad +3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \sin \phi \nonumber \\&\dot{\phi }\!=\!\frac{1}{\varTheta _\mathrm{f} R_\mathrm{f} }\left[ 3(G_1 G_5\! -\!F_1 F_5 )R_\mathrm{f} \!+\!3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \cos \phi \right. \nonumber \\&\quad \left. +3\varGamma _4^{(n)} (G_1 +G_5 )\left( 2R_\mathrm{f} P^{2}+2R_\mathrm{f} S^{2}+2R_\mathrm{f} a^{2}\right) \right] \nonumber \\&\quad +\frac{1}{\varTheta _\mathrm{b} R_\mathrm{b} }\left[ 3(G_{-1} G_7 \!-\!F_{-1} F_7 )R_\mathrm{b}\right. \nonumber \\&\quad \left. + 3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \cos \phi \right. \nonumber \\&\quad \left. +\,\,3\varGamma _4^{(n)} (G_{-1} +G_7 )\left( 2R_\mathrm{b} P^{2}+2R_\mathrm{b} S^{2}+2R_\mathrm{b} a^{2}\right) \right] \nonumber \\&\quad 2\left( 1-\frac{G_{-1} }{F_7 }Q-\frac{G_1 }{F_5 }Q\right) R_\mathrm{b} R_\mathrm{f} \sin \phi \nonumber \\&\quad +\,\,P^{2}Q\sin (2\beta )=0 \nonumber \\&\quad 2\left( R_\mathrm{b}^2 +R_\mathrm{f}^2 +P^{2}+S^{2}+\frac{1}{2}a^{2}\right. \nonumber \\&\quad \left. +\left( \frac{G_1 }{F_5 }\right) ^{2}R_\mathrm{f}^2 +\left( \frac{G_{-1} }{F_7 }\right) ^{2}R_\mathrm{b}^2 \right) \nonumber \\&\quad +\,\,2\left( 1-\frac{G_{-1} }{F_7 }Q-\frac{G_1 }{F_5 }Q\right) R_\mathrm{f} R_\mathrm{b} \cos \phi \nonumber \\&\quad +\,\,2\left( r_\mathrm{f} R_\mathrm{f} Q+r_\mathrm{b} R_\mathrm{b} Q\right) \nonumber \\&\quad +\,\,P^{2}Q\cos (2\beta )-K_{11}^{(3n)} -\varDelta _\mathrm{D} K_{11}^{(3n)} Q=0 \end{aligned}$$
(34)

The fact that \(R_\mathrm{f} ,R_\mathrm{b} \) , and \(\phi \) are constants in the steady state can be used in determination of the steady-state responses of the system. Therefore, it can be written \(\dot{R}_\mathrm{f} =0\), \(\dot{R}_\mathrm{b} =0\), and \(\dot{\phi }=0\) [31]. Consequently, the steady-state responses of the system are the solution of the following equations:

$$\begin{aligned}&\varOmega cK_{11}^{(n)} (5G_1 -G_5 )R_\mathrm{f} +3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \sin \phi =0 \nonumber \\&\varOmega cK_{11}^{(n)} (7G_{-1} +G_7 )R_\mathrm{b} +3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \sin \phi =0 \nonumber \\&\frac{1}{\varTheta _\mathrm{f} R_\mathrm{f} }\left[ 3(G_1 G_5 -F_1 F_5 )R_\mathrm{f}+3G_5 \varGamma _4^{(n)} a^{2}R_\mathrm{b} \cos \phi \right. \nonumber \\&\quad \left. +3\varGamma _4^{(n)} (G_1 +G_5 )\left( 2R_\mathrm{f} P^{2}+2R_\mathrm{f} S^{2}+2R_\mathrm{f} a^{2}\right) \right] \nonumber \\&\quad +\,\,\frac{1}{\varTheta _\mathrm{b} R_\mathrm{b} }\left[ 3(G_{-1} G_7 -F_{-1} F_7 )R_\mathrm{b}\right. \nonumber \\&\quad +\,\,3G_7 \varGamma _4^{(n)} a^{2}R_\mathrm{f} \cos \phi +3\varGamma _4^{(n)} (G_{-1} +G_7 )\nonumber \\&\quad \times \left. \left( 2R_\mathrm{b} P^{2}+2R_\mathrm{b} S^{2}+2R_\mathrm{b} a^{2}\right) \right] =0 \nonumber \\&2\left( 1\!-\!\frac{G_{-1} }{F_7 }Q\!-\!\frac{G_1 }{F_5 }Q\right) R_\mathrm{b} R_\mathrm{f} \sin \phi \!+\! P^{2}Q\sin (2\beta )\!=\!0 \nonumber \\&2\left( R_\mathrm{b}^2 +R_\mathrm{f}^2 +P^{2}+S^{2}+\frac{1}{2}a^{2}\right. \nonumber \\&\quad \left. +\left( \frac{G_1 }{F_5 }\right) ^{2}R_\mathrm{f}^2 +\left( \frac{G_{-1} }{F_7 }\right) ^{2}R_\mathrm{b}^2 \right) \nonumber \\&\quad +\,\,2\left( 1-\frac{G_{-1} }{F_7 }Q-\frac{G_1 }{F_5 }Q\right) R_\mathrm{f} R_\mathrm{b} \cos \phi \nonumber \\&\quad +\,\,2\left( r_\mathrm{f} R_\mathrm{f} Q+r_\mathrm{b} R_\mathrm{b} Q\right) \nonumber \\&\quad +\,\,P^{2}Q\cos (2\beta )-K_{11}^{(3n)} -\varDelta _\mathrm{D} K_{11}^{(3n)} Q=0 \end{aligned}$$
(35)

Equation (35) indicates the analytical form of steady-state response of the system for aforementioned resonance case. It is noted that the stationary points of Eq. (34) are associated with the steady-state responses of the system. In addition, to investigate the stability of steady-state response, the eigenvalues of Jacobian matrix of Eq. (34) is used.

4 Numerical results and discussion

In this section, the numerical results are represented in order to investigate the analytical results, which are obtained in the preceding section. Figures 2 and 3 represent frequency response curves for the first and the second forward whirling modes of the asymmetrical shaft for the various values of eccentricities when the system is near the aforementioned resonances. It is noted that \(\sigma =O(1)\) is a detuning parameter, which is used to express the nearness of the system to each of the resonance case. It is seen that the system has three types of solutions as: (1) two nontrivial unstable solutions, (2) four nontrivial solutions, two of which are unstable, (3) four nontrivial solution, one of which is unstable. These figures show that by decreasing values of eccentricity, the number of stable solutions at the lower speeds increases. Consequently, in the absence of adequate damping, the vibration response of the system may be harmful to the rotating system and may even prevent the safe and reliable operation of the system. In addition, such resonances must be located outside of the operating speed range unless the resonances are critically damped. Furthermore, due to existence of the nontrivial solutions, the rotor cannot be operated near these resonances without the occurrence of resonance even though a weak disturbance is applied to the system. One of the nonlinear phenomena is jump phenomenon. This phenomenon occurs due to bifurcations in the system. Bifurcation, in turn, is due to multivalued solutions in the system. Bifurcations occur in the intersection of stable and unstable solutions. Accordingly, when the system is near the bifurcation point a jump phenomenon occurs. Therefore, Figs. 2 and 3 show that the jump phenomenon occurs in the system. In fact, it can be assumed that the system response is on the stable resonance curve with low amplitude. Therefore, by decreasing detuning parameter, the system response moves along this resonance curve. When the response reaches bifurcation point, a jump phenomenon occurs in the system and the response of the system jumps to nearest stable resonance curve. It is noted that the location of the bifurcation point is dependent on the various parameters such as: eccentricities and damping coefficient. Also, by increasing eccentricity, the bifurcation point occurs in the lower speeds. As can be seen the bifurcation occurs for the speeds lower than the linear forward frequency. To verify the harmonic balance method results, numerical computations are utilized in Figs. 2 and 3. In order to compute numerical solutions, the Rung–Kutta method has been used. The system is exposed to various initial conditions. Then, the steady-state solutions are obtained after a long time. Each initial condition is attracted to a periodic solution. The results of the harmonic balance method are in accordance with those of numerical computations.

Fig. 2
figure 2

Frequency response curves, the first forward whirling mode

Full size image
Fig. 3
figure 3

Frequency response curves, the second forward whirling mode

Full size image

Figures 4 and 5 show the amplitude of the forward and backward modes versus damping coefficient for various values of detuning parameter. It is seen that for the lower values of damping coefficient, system at the low speeds is stable. For example, for \( \sigma =-0.6\), and \(c<0.065\), system has two unstable solutions and for \(c>0.065\), system has two stable solutions. However, for \(\sigma =-0.2\), and \(c<0.14\), system has four solutions two of which are unstable, and for \(c>0.14\), system has two stable solutions. Also, with an increase of damping coefficient, the steady-state amplitudes of forward and backward modes are decreased. It is worthy to note a jump phenomenon may be seen in these figures.

Fig. 4
figure 4

The amplitude of forward mode versus damping coefficient, the first mode

Full size image
Fig. 5
figure 5

The amplitude of backward mode versus damping coefficient, the first mode

Full size image

Figures 6 and 7 represent the phase of solution versus detuning parameter for the various values of eccentricities for the first two modes. As it can be seen, for \(\phi <1.5\), system in the first mode has stable solutions. However, in the second mode, for \(\phi <1.5\), system has stable and unstable solutions. In addition, it is seen that the unstable region of the system in the second mode is wider than stable region. Furthermore, in the higher values of eccentricity, for most values of detuning parameter, system has a lower phase. Also, the stability and number of solutions in these figures are in agreement with those of frequency response curves. In addition, a jump phenomenon occurs which can be seen in these figures.

Fig. 6
figure 6

The phase versus detuning parameter, the first mode

Full size image
Fig. 7
figure 7

The phase versus detuning parameter, the second mode

Full size image

The imaginary part of stable eigenvalues versus detuning parameter is plotted in Fig. 8. It is seen that the type of stationary points for various values of detuning parameters are stable spiral or stable node.

Fig. 8
figure 8

Imaginary part of the stable eigenvalues versus detuning parameter; the first mode

Full size image

To investigate the one-to-one internal resonances in the asymmetrical system, the imaginary part of the eigenvalues versus the real part of eigenvalues are plotted in Fig. 9. In this figure, the detuning parameter is as variable parameter of the system. It is seen that when three eigenvalues reach to each other the one-to-one internal resonance occurs.

Figure 10 shows the effect of damping coefficient on the frequency response curves for the first forward mode. As can be seen with an increase of the damping coefficient, the range of unstable solutions is reduced and the bifurcation occurs in the lower speeds. For large values of the damping coefficient, two unstable solutions and bifurcation point are eliminated. Consequently, for large values of damping coefficient, system has two stable solutions.

Fig. 9
figure 9

The imaginary part of eigenvalues versus the real part of eigenvalues

Full size image
Fig. 10
figure 10

Frequency response curves for various values of damping coefficient; forward amplitude

Full size image

For symmetrical shaft \(F(\varOmega )=0\), Eq. (28) indicates that for this shaft \(\beta =\theta \) and for any values of \(e_1 \) and \(e_2 \) which gives a same \( e_t \), system has same solutions. However, for asymmetrical shaft \(F(\varOmega )\ne 0\), hence, Eq. (28) implies that for any values of \(e_1 \) and \(e_2 \) which gives a same \( e_t \), system has different solutions. Figure 11 shows frequency response curves of asymmetrical shaft for the first mode for equal and unequal values of eccentricities, which gives the same \( e_t \). This figure shows that due to inequality between eccentricities, the range of unstable solutions increases and bifurcations occur in the lower speeds. Hence, the effect of inequality between eccentricities for the asymmetrical shaft is significant. Accordingly, since in the bifurcation point the stability of the system is changed, existence of bifurcation in the operating speed range is harmful to system and complete balancing of the rotating asymmetrical shaft is recommended.

Fig. 11
figure 11

Frequency response curves for equal and unequal values of eccentricities; the first mode

Full size image

5 Conclusions

Simultaneous internal, combinational and sub-harmonic resonances of asymmetrical rotating shafts with extensionality effect are investigated. Rotary inertia and gyroscopic effects are considered, but shear deformation is neglected. Harmonic balance method is applied to the ordinary differential equations of the motion. It is shown that the effect of difference between two eccentricities on the stability and bifurcations of the asymmetrical shaft is considerable. In the asymmetrical shaft for the aforementioned resonances by increasing eccentricity or damping coefficient, the bifurcation point occurs in the lower speeds. For large values of damping coefficient, system has two stable solutions. In addition, bifurcations occur for the speeds lower than the linear forward frequency. The results achieved from harmonic balance method show a good agreement with those of numerical computations.