Introduction

Integer ambiguity resolution (AR) can significantly shorten the convergence time and improve the accuracy of precise point positioning (PPP). Phase fractional cycle biases (FCBs) originating from satellites and receivers destroy the integer nature of PPP carrier phase ambiguities. The receiver FCB can be eliminated by single differencing across satellites or assimilated into the receiver clock parameter by forcing one zero difference ambiguity to its nearest integer, while the satellite FCBs must be estimated from a network of reference stations (Gabor and Nerem 1999). With the additional satellite FCB estimates, PPP users are able to remove satellite FCBs and recover the integer nature of ambiguities.

The fact that double-differenced ambiguities in global or regional networks can be resolved to integer values lays the foundation of integer ambiguity resolution for PPP. The resolved double-differenced ambiguity implies that the fractional parts of two single-differenced ambiguities (across satellites) must agree well with each other. By estimating the fractional parts at the server end and applying them to single-differencing PPP at the user end, PPP integer ambiguity resolution can be achieved. In this sense, PPP integer ambiguities are in fact equivalent to double-differenced ambiguities (Teunissen and Khodabandeh 2015). Ge et al. (2008) proposed to estimate the common fractional parts of the single-differenced ambiguities in a wide lane (WL) and narrow lane (NL) form. The fractional parts, denoted as single-differenced FCB (SD-FCB), were estimated by averaging the fractional parts of all-involved float single-differenced WL and NL ambiguity estimates. Based on the same principle but instead of the averaging process, a least squares method (LSM) in an integrated adjustment was adopted to enhance the estimates (Li and Zhang 2012; Zhang and Li 2013). Since January 1, 2015, the School of Geodesy and Geomatics at Wuhan University (WHU-SGG) routinely releases GPS WL and NL FCB products with open access (Li et al. 2015). Similar approaches have also been applied to BDS (Li et al. 2017; Wang et al. 2017), Galileo (Tegedor et al. 2016) and GLONASS (Geng and Shi 2016). To exploit the ionosphere characteristics, the model has been extended to deal with GPS L1 and L2 raw observables (Gu et al. 2015b; Li et al. 2013) and BDS triple-frequency observables (Gu et al. 2015a).

Different from the above approaches, Collins et al. (2008) developed a decoupled clock model by separating satellite clocks for code and phase observations. Similarly, Laurichesse et al. (2009) developed an integer phase clock model in which the NL FCBs were assimilated into receiver and satellite clock estimates of a network solution. This model has been employed to generate the precise satellite clock products by Groupe de Recherche de Géodésie Spatiale of the Centre National d’Etudes Spatiales (CNES-GRG) (Loyer et al. 2012). The only difference between the decoupled clock model and the integer phase clock model is the approach for determining the WL ambiguity. The integer phase clock model utilizes WL FCB corrections and a satellite-averaging process to fix the integer WL ambiguity, whereas the decoupled clock model directly estimates the integer WL ambiguity along with other unknowns through the functional model. The difference between the WL/NL FCB model and the integer phase clock model is the strategy of separating NL FCBs from integer ambiguities. NL FCBs are directly estimated in the WL/NL FCB model, whereas they are assimilated into the clock estimates in the integer phase clock model.

These PPP AR techniques are proven to be equivalent in theory (Shi and Gao 2014). The systematic biases between position estimates have been demonstrated to be minimal and negligible with data from a global network of reference stations (Geng et al. 2010). The WL/NL FCB model can conveniently supplement current network solutions as an additional software module, as the FCB determination is compatible with current official clock-generation methods. In contrast, the integer phase clock products are incompatible with current clock products although they may perform slightly better in practice.

Based on the review of existing work, we find that the LSM is routinely utilized for FCB estimation. However, the LSM can be extremely time consuming concerning the large number of observations from hundreds of reference stations and thousands of epochs during the FCB estimation. This is unfavorable for the more and more popular real-time applications. In addition, iterations are required to deal with the one-cycle inconsistency among FCB measurements. Since the FCB estimates are limited in the range of one cycle, e.g., [− 0.5, 0.5] and [0, 1] for WHU-SGG and CNES-GRG products, respectively, the one-cycle inconsistency arises whenever the superposition of receiver FCB and satellite FCB exceeds the boundary. The additional iterations of LSM and computation of a large matrix demand a long time to finish. Therefore, a fast and efficient estimation method is desirable.

In this contribution, a Kalman filter is employed to speed up the computation. The large number of observations are handled epoch by epoch, which significantly reduces the dimension of the involved matrix and accelerates the computation. The recursive computation of the Kalman filter allows real-time applications. As for the one-cycle inconsistency, a pre-elimination method is developed to avoid the posterior adjustments and iterations of the whole process. The following section describes the theoretical background of FCB estimations and Kalman filter. Then, a pre-elimination method of one-cycle inconsistency is proposed following the analysis of temporal stabilities of satellite FCBs. A set of FCB products is determined and evaluated by comparing with those of CNES and WHU. With the estimated FCBs, the improvements from PPP AR are assessed. Finally, the methodology is summarized, and an outlook for future research is presented.

Methodology

We start with the basic PPP float mode followed by a description of FCB estimation strategy. The pre-elimination method of one-cycle inconsistency is elaborated as well as an introduction to Kalman filter.

PPP float mode

In GNSS dual-frequency PPP, the ionospheric-free (IF) combination is routinely employed to eliminate the effect of the first-order ionospheric delay. For a satellite s observed by receiver r, the corresponding pseudorange and carrier phase observation equation can be expressed as:

$$\left\{ {\begin{array}{*{20}{l}} {P_{{r,{\text{IF}}}}^{s}=\rho _{r}^{s}+d{t_r} - d{t^s}+dT+{D_{r,{\text{IF}}}} - D_{{{\text{IF}}}}^{s}+{\varepsilon _{{P_{{\text{IF}}}}}}~~~~~~~~~~~~~~~~~~~~~~~~} \\ {\varPhi _{{r,{\text{IF}}}}^{s}=\rho _{r}^{s}+d{t_r} - d{t^s}+dT+{\lambda _{{\text{IF}}}}(N_{{r,{\text{IF}}}}^{s}+{B_{r,{\text{IF}}}} - B_{{{\text{IF}}}}^{s})+{\varepsilon _{{\varPhi _{{\text{IF}}}}}}} \end{array}} \right.$$
(1)

where \(\rho _{r}^{s}\) indicates the geometric distance between satellite and receiver; dtr and dts are the clock errors of receiver and satellite; dT is the slant tropospheric delay; Dr,IF and \(D_{{{\text{IF}}}}^{s}\) are the receiver and satellite-specific code hardware delays; λIF and \(N_{{r,{\text{IF}}}}^{s}\) are the wavelength in meters and ambiguity in cycles; Br,IF and \(B_{{{\text{IF}}}}^{s}\) are the receiver-dependent and satellite-dependent uncalibrated phase delays; \({\varepsilon _{{P_{{\text{IF}}}}}}\), \({\varepsilon _{{\varPhi _{{\text{IF}}}}}}\) are the pseudorange and carrier phase measurement noise.

Conventionally, precise orbit and clock products from the IGS analysis center are used to remove satellite orbit and clock errors. During the generation of IGS precise products, the pseudorange ionospheric-free hardware delay bias \(D_{{{\text{IF}}}}^{s}\) is assimilated into the clock offset dts in accordance with the IGS analysis convention. Due to the fact that pseudorange measurements provide the reference to clock parameters, the actual receiver clock estimate would absorb the ionospheric-free combination of the receiver pseudorange hardware delay Dr,IF. After applying the GNSS precise satellite clock products, Eq. (1) can be rewritten as:

$$\left\{ {\begin{array}{ll} {P_{{r,{\text{IF}}}}^{s}=\rho _{r}^{s}+dT+\bar {d}{t_r}+{\varepsilon _{{P_{{\text{IF}}}}}}~~~~~~~~~~~~~~~~~~~~~} \\ {\varPhi _{{r,{\text{IF}}}}^{s}=\rho _{r}^{s}+dT+\bar {d}{t_r}+{\lambda _{IF}}\bar {N}_{{r,{\text{IF}}}}^{s}+{\varepsilon _{{\Phi _{{\text{IF}}}}}}} \end{array}} \right.$$
(2)

where the receiver clock and ambiguity can be re-parameterized as:

$$\bar {d}{t_r}=(d{t_r}+{D_{r,{\text{IF}}}})$$
(3)
$$\bar {N}_{{r,{\text{IF}}}}^{s}=N_{{r,{\text{IF}}}}^{s}+{b_{r,{\text{IF}}}} - b_{{{\text{IF}}}}^{s}$$
(4)
$${b_{r,{\text{IF}}}}={B_{r,{\text{IF}}}} - {D_{r,{\text{IF}}}}/{\lambda _{{\text{IF}}}}$$
(5)
$$b_{{{\text{IF}}}}^{s}=B_{{{\text{IF}}}}^{s} - D_{{{\text{IF}}}}^{s}/{\lambda _{{\text{IF}}}}$$
(6)

For ambiguity float PPP solutions, the ionospheric-free ambiguity parameter \(\bar {N}_{{r,{\text{IF}}}}^{s}\) is estimated as a real-value constant. Since the estimated ambiguity parameter is a combination of the integer ambiguity, the corresponding code hardware delays, and the uncalibrated carrier phase delays at both receiver and satellite ends, the integer property is lost.

FCB estimation

For an ambiguity-fixed PPP solution, \(\bar {N}_{{r,{\text{IF}}}}^{s}\) is usually decomposed into the following combination of integer WL and float NL ambiguities for ambiguity fixing

$$\bar{N}_{{r,{\text{IF}}}}^{s} = {{\left( {\frac{{cf_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{{r,{\text{WL}}}}^{s} + \frac{c}{{f_{1} + f_{2} }}\bar{N}_{{r,{\text{NL}}}}^{s} } \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{cf_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{{r,{\text{WL}}}}^{s} + \frac{c}{{f_{1} + f_{2} }}\bar{N}_{{r,{\text{NL}}}}^{s} } \right)} {\lambda _{{{\text{IF}}}} }}} \right. \kern-\nulldelimiterspace} {\lambda _{{{\text{IF}}}} }}$$
(7)

Note that, \(N_{{r,{\text{WL}}}}^{s}\) is an integer WL ambiguity, which implies that WL FCB will not directly contribute to PPP. The WL ambiguity can be resolved by the Hatch–Melbourne–Wübbena (HMW) combination observable (Hatch 1982; Melbourne 1985; Wübbena 1985),

$$\begin{aligned}{\text{HMW}}&=\frac{{{f_1}\varPhi _{{r,1}}^{s} - {f_2}\varPhi _{{r,2}}^{s}}}{{{f_1} - {f_2}}} - \frac{{{f_1}P_{{r,1}}^{s}+{f_2}P_{{r,2}}^{s}}}{{{f_1}+{f_2}}}\\ &=\lambda _{{r,{\text{WL}}}}^{s}\left( {N_{{r,{\text{WL}}}}^{s}+{d_{r,{\text{WL}}}} - d_{{{\text{WL}}}}^{s}} \right) \end{aligned}$$
(8)

where

$${d_{r,{\text{WL}}}}={B_{r,1}} - {B_{r,2}} - \frac{{{f_1}{D_{r,1}}+{f_2}{D_{r,2}}}}{{\lambda _{{r,{\text{WL}}}}^{s}({f_1}+{f_2})}}$$
(9)
$$d_{{{\text{WL}}}}^{s}=B_{1}^{s} - B_{2}^{s} - \frac{{{f_1}D_{1}^{s}+{f_2}D_{2}^{s}}}{{\lambda _{{r,{\text{WL}}}}^{s}({f_1}+{f_2})}}$$
(10)
$$\bar {N}_{{r,{\text{WL}}}}^{s}=N_{{r,{\text{WL}}}}^{s}+{d_{r,{\text{WL}}}} - d_{{{\text{WL}}}}^{s}$$
(11)

If the WL ambiguity is correctly resolved to an integer value based on (8), the NL ambiguity observable can be derived,

$$\bar {N}_{{r,{\text{NL}}}}^{s}=N_{{r,1}}^{s}+{d_{r,{\text{NL}}}} - d_{{{\text{NL}}}}^{s}$$
(12)

where

$${d_{r,{\text{NL}}}}=\frac{{{f_1}+{f_2}}}{c}\left( {{\lambda _{{\text{IF}}}}{B_{r,{\text{IF}}}} - {D_{r,{\text{IF}}}}} \right)$$
(13)
$$d_{{{\text{NL}}}}^{s}=\frac{{{f_1}+{f_2}}}{c}\left( {{\lambda _{{\text{IF}}}}B_{{{\text{IF}}}}^{s} - D_{{{\text{IF}}}}^{s}} \right)$$
(14)

Equations (11) and (12) serve as the basic model for estimating FCBs. Since they have the same structure, a general expression can be formulated as:

$$R_{r}^{s}=\bar {N}_{r}^{s} - N_{r}^{s}={d_r} - {d^s}$$
(15)

for WL and NL linear combinations, respectively. \(R_{r}^{s}\) represents the FCB measurements; \(\bar {N}_{r}^{s}\) denotes the float undifferenced ambiguities; \(N_{r}^{s}\) denotes the integer part of \(\bar {N}_{r}^{s}\), which is the sum of the original integer ambiguity and the integer part of the combined code hardware delays and uncalibrated phase delays from both receiver r and satellite s; dr and ds denote the receiver and satellite FCBs.

A set of equations in the form of (15) can be integrated based on a network of reference stations. Suppose that there are n satellites tracked at m reference stations, the system of equations can be expressed as:

$$\left[ {\begin{array}{*{20}{c}} {R_{{r,1}}^{{s,1}}} \\ \vdots \\ {R_{{r,1}}^{{s,n}}} \\ \vdots \\ {R_{{r,m}}^{{s,1}}} \\ \vdots \\ {R_{{r,m}}^{{s,n}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} {\bar {N}_{{r,1}}^{{s,1}} - N_{{r,1}}^{{s,1}}} \\ \vdots \\ {\bar {N}_{{r,1}}^{{s,n}} - N_{{r,1}}^{{s,n}}} \\ \vdots \\ {\bar {N}_{{r,m}}^{{s,1}} - N_{{r,m}}^{{s,1}}} \\ \vdots \\ {\bar {N}_{{r,m}}^{{s,n}} - N_{{r,m}}^{{s,n}}} \end{array}} \right]=\left[ {\begin{array}{*{20}{c}} 1& \cdots &0&{ - \;1}& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1& \cdots &0&0& \cdots &{ - \;1} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0& \cdots &1&{ - \;1}& \cdots &0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0& \cdots &1&0& \cdots &{ - \;1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{d_{r,1}}} \\ \vdots \\ {{d_{r,m}}} \\ {{d^{s,1}}} \\ \vdots \\ {{d^{s,n}}} \end{array}} \right].$$
(16)

The obtained system of equations is singular. The integer ambiguities \(N_{r}^{s}\) need to be determined for each equation on the left side, while one arbitrarily selected FCB should be set to zero on the right side. Assuming the float ambiguities \(\bar {N}_{r}^{s}\) are precisely estimated, \(N_{r}^{s}\) can be determined by rounding \(\bar {N}_{r}^{s}\). In this way, the system of equations can be resolved. However, the rounding approach may introduce one cycle inconsistencies.

One-cycle inconsistency

Since the FCB estimates are limited in the range of one cycle, e.g., [− 0.5, 0.5] and [0, 1] for WHU-SGG and CNES-GRGS products, respectively, the one-cycle inconsistency arises whenever the superposition of receiver FCB and satellite FCB exceeds the boundary. A simple example is presented to depict the situation. Assuming there is one satellite (ds = 0.2) tracked at two stations (dr,1 = 0.6 and dr,2 = 0.8), the superposition of FCBs should be \((R_{{r,1}}^{s}= - \;0.4\;{\text{~and}}\;~R_{{r,2}}^{s}= - \;0.6)\). However, the \(R_{{r,2}}^{s}\) would be 0.4 due to the rounding approach. As a consequence, the corresponding satellite FCB derived from the two stations differs one cycle. The one-cycle inconsistency can be detected by examining the posterior residuals, as employed in former works. The posterior adjustments are inefficient as iterations of the whole process are required. In contrast, we propose to eliminate the inconsistency in advance, which shows a clear advantage over posterior adjustment. The proposed method consists of the following steps:

  1. 1.

    For all the FCB measurements at a single station, the satellite FCBs are eliminated using previous estimates. The underlying assumption is that satellite FCBs are stable over successive epochs and can be eliminated to a large extent by previous estimates, which will be proved in the next section.

  2. 2.

    The residual of each FCB measurement after the subtraction of the satellite FCB yields an initial estimate of the receiver FCB. A set of initial receiver FCB estimates could be obtained from all simultaneously observed satellites.

  3. 3.

    In theory, the receiver FCBs obtained from all simultaneously observed satellites are expected to be consistent. Therefore, a one-cycle inconsistency can be detected by examining the group of initial receiver FCBs. If an inconsistency exists, the corresponding receiver FCB will differ by ± 1 cycle.

  4. 4.

    To compensate the one-cycle inconsistency in receiver FCBs, the corresponding integer ambiguity \(N_{r}^{s}\) is adjusted by ± 1 cycle.

  5. 5.

    The procedures described above can be performed in an iterative way until a consistent receiver FCB is obtained from all satellite measurements.

In addition, stations can also be handled individually to obtain clean FCB measurements. After the pre-elimination of the one-cycle inconsistency, the clean FCB measurements are fed to the Kalman filter.

Kalman filter

The Kalman filter addresses the general problem of state estimates of discrete time-controlled processes that are governed by a linear stochastic difference equation (Kalman 1960). The theory has been well studied and widely applied (Yang 2006; Yang et al. 2010). Since the Kalman filter is based upon the theory of least squares, it is theoretically possible to calculate the same solution as LSM and vice versa. However, the design and normal equation matrix will be huge in LSM, considering the large number of observations from hundreds of reference stations and thousands of epochs. Computation of the large matrix is time consuming, which is inefficient and unfavorable for real-time applications. In contrast, the large number of observations are handled epoch-by-epoch in a Kalman filter, which significantly reduces the dimension of the involved matrix and accelerates the computation. One additional advantage of Kalman filter is its real-time capability. This is of particular interest for real-time PPP AR and its applications. Therefore, a Kalman filter is employed in this work. The design and flowchart of a Kalman filter are depicted in Fig. 1. In our case, \(R_{r}^{s}\) is the input FCB measurement for the Kalman filter, while dr and ds are the output estimates.

Fig. 1
figure 1

Flow chart of the proposed Kalman filter. The dashed blocks represent additional steps adopted in this study

Full size image

Two additional steps are added to the standard Kalman filter. The first step aims at establishing the dynamic model and determining the state transition matrix by analyzing the temporal stability of existing FCB products. Satellite WL FCBs are stable over several days, which can be characterized as a constant parameter on a daily basis. Satellite NL FCBs are considered as constant within 15 min but exhibit small variations over 15-min intervals. Therefore, NL FCBs are characterized as random walk processes. The second step is introduced to eliminate the one-cycle inconsistency of FCB measurements. Only clean measurements are sent to the Kalman filter to avoid iterations. Note that, a constraint is imposed on the Kalman filter to eliminate the rank deficiency. A satellite FCB is selected and set to zero, which is accomplished by adding a pseudo-observational error equation with zero variance (Yang et al. 2010).

Results, comparison, and analysis

In this section, the temporal stability of FCB is first analyzed based on existing products. Then, the proposed pre-elimination method of one-cycle inconsistency is demonstrated. Ten sets of FCBs are computed and evaluated with respect to existing products. At last, with the estimated FCBs, the improvements from PPP AR are assessed.

Temporal stability of FCB

To study the characteristics of satellite FCBs, products from CNES GRG and WHU SGG are employed. Both organizations provide WL FCBs derived from the same strategy, while NL FCBs are only available for SGG products since they are absorbed by satellite phase clock offsets in GRG products. The products for the entire 2016 are downloaded and analyzed in this study. Due to the rank deficiency of FCB equations, a receiver FCB for GRG products and a satellite FCB for SGG products are selected as references. Therefore, a single-differencing process across satellites is performed to remove the datum before comparison. The single-differenced WL FCBs are presented in Fig. 2. Note that, the two products have opposite signs.

Fig. 2
figure 2

Single-differenced WL FCBs of CNES GRG (top) and WHU SGG (bottom) products in 2016. The lines represent individual satellite WL FCBs with respect to that of G01

Full size image

The WL FCBs of satellites are remarkably stable over days with standard deviations (STDs) of less than 0.08 cycles for both products. An exception is observed for G32 satellite. The STD of G32 is significantly larger than the others with 0.2 cycles. The reason is that a new Block IIF satellite (G32) was launched on 5 February 2016 and activated since 10 February. After the replacement, the WL FCB exhibits a similar temporal stability as the other satellites. The statistics further confirm the conclusion that the satellite WL FCB is stable over at least several days. Therefore, WL FCBs are estimated as constant on a daily basis in the proposed Kalman filter.

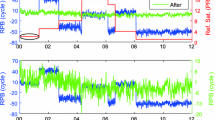
NL FCB products are estimated with respect to specific IGS precise clock products in the WL/NL FCB-based method. Due to the daily boundaries of precise clock products, NL FCB estimates are only continuous within 1 day. The single-differenced SGG NL FCBs on day of year (DoY) 001, 2016, are presented in Fig. 3. The top panel shows the raw SD NL FCBs for each satellite while G01 is selected as reference. It can be seen that the datum changes frequently, which introduces a difference of one cycle between two consecutive epochs. After adjustments, the NL FCB series are continuous, as presented in the middle panel.

Fig. 3
figure 3

Raw (top) and adjusted (middle) Single-differenced NL FCBs of SGG products on DoY 001. The bottom panel presents the histogram of all daily STDs in 2016

Full size image

One can easily discern that satellite NL FCBs are also stable. The STDs of all single-differenced satellite NL FCBs are within ± 0.05 cycles for DoY 001. In addition, daily STDs of all satellite NL FCBs for the whole year 2016 are calculated. The bottom panel depicts the distribution of daily STDs. 98.37% of the daily STDs are below 0.15 cycles while 97.02% are below 0.1 cycles. These results show that satellite NL FCBs may be more stable than reported in former research. Note that, a small number of daily STDs may reach 0.5 cycles. These abnormal STDs may be caused by maneuvers during satellite eclipse or unmodeled errors. And we could not exclude the possibility that there may be blunders. Nevertheless, satellite NL FCBs are modeled as random walk processes in the proposed Kalman filter. In addition, note that the characteristics of receiver NL FCB depend on the receiver type, environment, and other factors. It is hard to characterize receiver NL FCBs with a general model. Therefore, they are modeled as white noise. The temporal stability of satellite FCBs also implies that it can be utilized for pre-elimination of the one-cycle inconsistency.

Pre-elimination of the one-cycle inconsistency

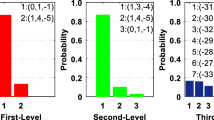
For a successful pre-elimination of the one-cycle inconsistency, the satellite FCBs should be removed in advance. The key issue is if or at what extent the satellite FCBs of the current epoch can be counteracted by the previous estimation. In the proposed pre-elimination method, the differences of satellite FCBs between two successive epochs will be absorbed by receiver FCB. Therefore, epoch differences of satellite FCBs should be small enough to avoid impacts on the detection of the one-cycle inconsistency. To validate the hypothesis, an additional epoch differencing process is performed on the single-differenced FCBs. The histograms of epoch differences for WL FCBs in 2016 are presented in Fig. 4.

Fig. 4
figure 4

Histograms of epoch-differenced WL FCBs of GRG (top) and SGG (bottom) products in 2016

Full size image

99.78 and 95.81% of the differences are within ± 0.05 cycles for GRG and SGG products, respectively. The max differences, with a magnitude of 0.386 cycles, are found in SGG products. Since these values are much smaller than one cycle, it will scarcely affect the detection and elimination of the one-cycle inconsistency. Note that, the distribution of epoch differences for GRG products is more concentrated around zero than that of SGG, which may indicate better quality.

The epoch differencing process is also conducted for NL FCB products, as shown in Fig. 5. 99.73% of the differences are within ± 0.05 cycles for SGG products. The result is even better than that of WL FCB. This can be attributed to the fact that the intervals (15 min) of NL FCB are much shorter than those of WL FCB (24 h).

Fig. 5
figure 5

Histogram of epoch-differenced NL FCBs of SGG products

Full size image

According to the above analysis of satellite FCB products, it can be concluded that the major parts of both WL and NL satellite FCBs can be mitigated by previous estimations. After the removal of satellite FCBs, the one-cycle inconsistency among FCB measurements can be detected by examining the residuals. After the detection of inconsistency, it is eliminated by adjusting the corresponding integer ambiguity. An example of the process is shown in Fig. 6. One can easily observe that the one-cycle inconsistencies occur on several satellite measurements and can be effectively eliminated by the proposed method. It should be noted that elimination of the one-cycle inconsistency will not improve the precision of FCB estimation as the fractional part remains the same. In this sense, the magnitude of the epoch difference is less of concern as long as it is sufficient to detect potential inconsistencies. In addition, note that this can be accomplished by posterior residual adjustments. However, pre-elimination shows a clear advantage over posterior adjustment in terms of efficiency.

Fig. 6
figure 6

Pre-elimination of the one-cycle inconsistency for station IQQE on 2016/02/26. The top panels represent receiver WL FCB adjustment, while the bottom ones represent that of the receiver NL FCB. The left and right panels represent the raw and adjusted measurements, respectively

Full size image

In this way, all epochs and all station data can be processed individually to obtain clean FCB measurements. For post-processing, the above procedure can be simplified. Daily WL FCB measurements can be adjusted simultaneously as the receiver WL FCBs are also constant within one day. For the initialization of the Kalman filter, a preliminary set of satellite FCBs should be provided for the first epoch. The initial satellite WL FCBs are taken from the estimations of the last day, while the initial satellite NL FCBs are determined with the route method (Li et al. 2015).

Comparison of FCB products

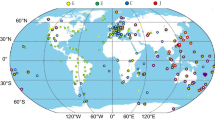
A globally distributed network consisting of about 200 stations is selected from IGS network, as shown in Fig. 7. Observations from DoY 52 to 61 (2016/02/21–2016/03/01) are processed to determine GPS satellite FCBs. GFZ final precise products are applied to remove satellite orbit and clock errors. The other errors are corrected according to the IGS standard error models (Kouba 2009). FCB estimations are conducted in three sequential steps. First, float ambiguities containing FCBs are obtained by HMW combinations and PPP processing from the network of reference stations. Second, FCB measurements are generated from the float ambiguities. Third, the proposed Kalman filter is adopted to estimate FCBs from all FCB measurements.

Fig. 7
figure 7

Geographical distribution of the selected reference stations

Full size image

The quality of FCB estimation can be indicated by the posterior residuals of FCB measurements. In general, a highly consistent FCB estimation is expected if the residuals are close to zero. Figure 8 shows the distribution of the residuals of FCB estimations for the 10 days. It can be seen that both histograms are symmetric and nearly centered at zero. The root mean square (RMS) of WL residuals is 0.09 cycles while the RMS of NL residuals is about 0.05 cycles, which indicates a good consistency between the estimated FCBs and the input float ambiguities. The total number of input float ambiguities is 934,908. Figure 9 shows the usage rates of WL and NL float ambiguities for each satellite. The averaged usage rate for WL is 96.66%, while that for NL is 98.17%. We find that the quality of NL FCBs is better than that of WL. The possible reason is that, WL FCBs are estimated as daily invariants and easily affected by pseudorange noise, while the NL FCBs are updated every 15 min and derived from much more precise carrier phase measurements.

Fig. 8
figure 8

Distributions of posterior residuals after WL (top) and NL (bottom) FCB estimation

Full size image
Fig. 9
figure 9

Usage rates of the float WL and NL ambiguities

Full size image

For better visualization, the derived satellite FCBs are shifted with integer cycles, as presented in Fig. 10. It can be seen that the derived satellite FCBs show similar temporal stability as in the above analysis. Satellite WL FCBs exhibit extremely small variations over the 10-day period, while NL FCB shows a larger variation over tens of minutes.

Fig. 10
figure 10

Time series of satellite WL (top) and NL (bottom) FCBs for all the other 31 satellites while G01 is selected as reference

Full size image

To validate the external accuracy of our estimation, the derived satellite FCBs are also compared with those of SGG and GRG. As discussed before, WL FCB measurements are obtained from HMW combinations and are relatively independent of PPP processing. The determined WL FCBs should be consistent across all products. Figure 11 presents the comparison of the derived satellite WL FCBs with those of GRG and SGG products.

Fig. 11
figure 11

Histograms of the differences between our WL FCB estimation and SGG (top) and GRG products (bottom)

Full size image

It can be seen that our WL FCB estimates show good consistency with those of SGG and GRG. All of the differences are within ± 0.1 cycles. Compared with SGG products, 76.7% of the differences are within ± 0.05 cycles with an RMS of 0.05 cycles. Compared with GRG products, 91.0% of the differences are within ± 0.05 cycles with an RMS of differences of 0.03 cycles. Based on the above analysis, we can safely conclude that there is no systematic bias between our WL FCB estimates and those of SGG and GRG. The differences are actually minimal and negligible. However, one can realize that our WL FCB estimates agree better with GRG products than those of SGG. Note that, the RMS of differences between SGG and GRG is 0.03 cycles. We suspect that the GRG products may perform slightly better in practice.

NL FCBs are only available for SGG products. The derived satellite NL FCBs are compared with SGG products, as shown in Fig. 12. It can be seen that our NL FCBs agree well with SGG NL FCB products. 97.9% of the differences are within ± 0.1 cycles while 70.4% of the differences are within ± 0.05 cycles. The RMS of the differences is 0.05 cycles, corresponding to 5.1 mm. The discrepancy between the two results may be ascribed to different PPP processing strategies. Since NL FCB measurements are directly derived from PPP float ambiguities, discrepancies between error correction models, such as tropospheric models, may introduce small systematic biases. Another possible reason could be the different distributions of reference stations. Since FCB estimates are contaminated by unknown temporally and spatially correlated errors, these unknown errors may change with the distribution of reference stations. GRG products should be employed for comparison in further investigations. Note that, the discrepancy will not affect PPP AR at user end if the same error model as at the server end is used.

Fig. 12
figure 12

Histogram of the differences between our NL FCB estimation and SGG products

Full size image

PPP AR solution

To validate our FCB estimates and to assess the improvement by ambiguity resolution, all IGS network stations are processed in PPP float and AR mode with the obtained satellite FCB estimates. The 24-h observations from over 500 stations in the 10 days are divided into 3-h sessions. The solutions with data integrity less than 80%, wrongly fixed, and incomplete convergence are removed. After the pre-processing, there are 22,953 sessions. The performance in terms of convergence time and positional accuracy is evaluated under different confidence levels for the sake of reliability (Lou et al. 2016).

Figure 13 presents the positional errors of GPS PPP float and AR solutions based on the statistics over all the sessions. It can be seen that the convergence time is significantly shortened by ambiguity resolutions, especially for the east and up components. It takes 64 min for float solutions to converge to three-dimensional 10 cm accuracy, while that for AR solutions is only 48.5 min, corresponding to an improvement of 24%. To assess the improvements with respect to time length, the positional errors are calculated for 1-, 2-, and 3-h solutions, as presented in Table 1. It can be seen that PPP ambiguity resolutions are able to enhance the accuracy for all the schemes. The most significant improvement is found for the east component. Due to the design of satellite navigation systems, the accuracy of the east component is worse than that of north component in mid-latitude because of weaker model strength. Ambiguity resolutions can improve this situation by imposing tight constraints on ambiguity parameters. However, the improvements decrease as the time length increases. The improvements of ENU components for 1-h solutions are (70, 45, 28%), while that for 2-h solutions and 3-h solutions are (62, 32, 21%) and (51, 22, 20%), respectively. The reason is that the model strength of the float solution is improved with more observations. In addition, note that the improvements differ with respect to the confidence level. They are less significant under 95% level, which implies the PPP AR is not effective for some stations. Since FCB estimates are contaminated by temporally and spatially correlated errors, a small and dense network is preferred for better performance.

Fig. 13
figure 13

Convergence performance of GPS PPP float and AR solutions based on 22,953 3-h sessions under 95% confidence levels

Full size image
Table 1 Accuracy comparison of GPS PPP float and AR solutions based on 22,953 3-h sessions under different confidence level (unit: cm)
Full size table

Conclusions

In this contribution, estimating satellite FCBs based on the Kalman filter is proposed and demonstrated. Since the Kalman filter is based upon LSM, it is theoretically possible to calculate the same solution as for the commonly used LSM. In the proposed Kalman filter, the large number of observations is handled epoch-by-epoch, which significantly reduces the dimension of the involved matrix and accelerates the computation. Hence, it outperforms the commonly used LSM in terms of efficiency. To avoid iterations caused by the one-cycle inconsistency among FCB measurements, a pre-elimination method is developed based on the temporal stability of satellite FCBs. The pre-elimination method shows a clear advantage over post-residual adjustment, which further improves the efficiency.

A globally distributed network consisting of about 200 IGS stations has been selected to determine GPS satellite FCBs. The estimated WL FCBs have a good consistency with existing WL FCB products (e.g., CNES-GRG, WHU-SGG). The RMS of differences with respect to GRG and SGG products are 0.03 and 0.05 cycles, which indicates the consistency of the proposed approach. For satellite NL FCB estimates, 97.9% of the differences with respect to SGG products are within ± 0.1 cycles. The RMS of the differences is 0.05 cycles. These results prove the efficiency of the proposed approach.

The state-based approach of the Kalman filter also allows for more realistic modeling of stochastic parameters, which will be investigated in future research.