1 Introduction

Over the past years, precise point positioning (PPP) has proven efficient in providing real-time precise positions because of its cost-effectiveness, global coverage and high accuracy (Zumberge et al. 1997; Bisnath and Gao 2008; Kouba and Héroux 2001). Since only one station is employed in PPP processing, the uncalibrated phase delays (UPDs) caused by initial phase biases together with the signal-dependent hardware effects destroy the integer property of the zero-difference (ZD) ambiguities, and thus integer ambiguity resolution cannot be achieved straightforwardly (Geng et al. 2010a).

The work by Gabor and Nerem (1999) was the first attempt to perform ambiguity resolution for point positioning, in which single difference (SD) is utilized to remove the receiver UPD, and the satellite pair UPDs of wide lane (WL) and narrow lane (NL) are estimated using the Melbourne–Wübbena (MW) and ionosphere-free (IF) combination measurements, respectively. Though the WL UPD shows favorable temporal behavior, the NL UPD seems unstable with an arbitrary day-by-day variation. It is only until recently that PPP with integer ambiguity resolution is achieved due to improved satellite ephemeris and state-of-the-art receivers. Despite the temporal instability, the SD NL UPD of satellite updated every 15 min shows good consistency among different receivers as evidenced by user positioning with an improvement of 30 % for the east component (Ge et al. 2008). Collins (2008) and Laurichesse et al. (2009) redefined the satellite clock products, denoted as integer-recovery clocks (IRCs) to guarantee the integer properties of the NL ambiguities by assimilating the corresponding UPD into the clock estimates, while leaving the WL UPD the same as that of Ge et al. (2008). Geng et al. (2010a) theoretically proved the equivalence of integer ambiguity resolution by methods of UPD isolation and IRCs estimation with an extensive data set. Those studies reveal the potential of a combination technique PPP-RTK as a key solution for the high accuracy GNSS applications (Wübbena et al. 2005; Bertiger et al. 2010; Geng et al. 2010b; Teunissen et al. 2010).

Although there is no between-station or between-satellite difference involved, PPP cannot be regarded as ZD data processing strictly, since the between-frequency “difference” known as IF is usually employed due to the limited knowledge in separating the ionospheric delays. However, on the one hand, the modernization of GPS and GLONASS, together with the deployment of BDS and Galileo, is featured by various types (P-code, C-code, etc.) of multi-frequency observable and, hence, the choice of optimum combination will become practically difficult given the diversity of terminal equipments (Schönemann et al. 2011; Geng and Bock 2013). On the other hand, the progress in ionosphere environment study offers various a priori knowledge on ionosphere delay, notably the precise ionosphere correction models, e.g., global ionosphere map (GIM) (Mannucci et al. 1998; Schaer 1999); the sophisticated ionosphere parameterization methods for a single station, e.g., the work by Yuan and Ou (2004) and Shi et al. (2012). This information cannot be employed due to the elimination of ionosphere delay in IF combination. As a result, a uniform solution in which the individual signal of each frequency is treated as independent observable has drawn increasing interest in the GPS community (Schönemann et al. 2011; Gu et al. 2013; Gu 2013).

The efficiency of raw signal processing has already been confirmed in terms of convergence and precision with single-frequency PPP (Le and Tiberius 2007; Bock et al. 2009; Shi et al. 2012) as well as dual-frequency PPP (Keshin et al. 2006). However, only float ambiguities are considered in these studies. Regarding the PPP-RTK based on raw observable, the generation of UPD on individual frequency is a great challenge since the reliable UPD separation depends on the ionosphere delay estimation with an extremely high precision. It is usually not a problem for a dense network with a typical inter-station distance of 60 km as demonstrated by Teunissen et al. (2010), Zhang et al. (2011) and Feng et al. (2013), in which PPP is inevitably downgraded to a regional service.

Regarding the wide area PPP-RTK, though its feasibility has been verified by Li et al. (2013) and Gu et al. (2013), there is little in-depth analysis on UPD generation with respect to the ionosphere effect. Theoretically, the quality of UPD measurements of the raw-observable approach is rather sensitive to the efficiency of ionosphere corrections. However, depending on the coverage area, normal and disturbed ionosphere condition, the performance of ionosphere correction varies. Thus, can we always expect that the performance of UPD as well as PPP-RTK should benefit from the new approach? If not, which is the best strategy in UPD generation and PPP ambiguity resolution?

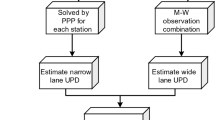
In this contribution, the COM model based on MW/IF combination and the RAW model based on L1/L2 observable with ionosphere constraints are compared in both theoretical analysis and numerical demonstration. This paper is organized as follows: firstly, a mathematical framework of these two models are presented, based on which the ambiguities are addressed by concentrating on the ionosphere residual effect. Secondly, to evaluate the precision of GNSS-based ionosphere corrections, over 1 year of data set is collected in the ionosphere modeling with both global and regional stations. Constrained by these ionosphere models, WL/NL UPDs are then generated and assessed in terms of stability and consistency. Finally, these UPD products are utilized as corrections in the ambiguity-fixed PPP to demonstrate the performance of the RAW model.

2 Methods

2.1 Basic observable

The raw observables of the dual-frequency GNSS pseudo-range and carrier phase are generally expressed as

$$\begin{aligned}&{\left. \begin{array}{lll} P_{r,f}^s &{} =&{}\rho _r^s+t_r-t^s+\alpha _r^s\cdot T_z+b_{r,f}-b_f^s \\ &{}&{} +\beta _f \cdot I_{r}^s+\varepsilon _P \\ \Phi _{r,f}^s&{} =&{}\rho _r^s+t_r-t^s+\alpha _r^s\cdot T_z+b_{r,f}-b_f^s \\ &{}&{} -\lambda _f\cdot (N_{r,f}^s-\varphi )-\beta _f \cdot I_{r}^s+\varepsilon _\Phi , \end{array} \right\} } \end{aligned}$$
(1)

in which \(P_{r,f}^s\), \(\Phi _{r,f}^s\) are pseudo-range and carrier phase on frequency \(f\) from satellite \(s\) to receiver \(r\) in length units, respectively; \(\rho \) is the geometric distance, while antenna phase center corrections should be applied to \(P\), \(\Phi \) before \(\rho \) becomes unassociated with the frequency; \(t(_r^s)\) is the receiver and satellite clock error, respectively; \(T_z\) is the zenith tropospheric delay that can be converted to slant with the mapping function \(\alpha \); \(b\) is the frequency-dependent signal delay for receiver and satellite, respectively; \(N\) is the float ambiguity and \(\varphi \) is the phase windup error in cycle, together with the corresponding wavelength \(\lambda \); \(I\) denotes the line-of-sight total electron content with the frequency-dependent factor \(\beta _f=40.3/f^2\).

In the case that integer ambiguities \(n\) are considered, UPD \(d\) of both receiver and satellite should be separated from \(N\), i.e.,

$$\begin{aligned} N=n-d_r+d^s. \end{aligned}$$
(2)

Furthermore, since \(b_{r,1}\) and \(b_{r,2}\), and \(b_1^s\) and \(b_2^s\) are linear dependent, it is assumed that

$$\begin{aligned}&\left. \begin{array}{l} b_{r,1} =0 \\ b_1^s =0 \end{array} \right\} \end{aligned}$$
(3)

to make it uniquely solvable; thus, \(-b_2^s\) is actually known as \(DCB_{P1P2}\) and can be corrected precisely (Schaer and Dach 2010).

A few notations are now defined for future reference:

$$\begin{aligned}&{z_s=\left( \begin{array}{llll} 0&0&\cdots&0 \end{array} \right) ^T }\end{aligned}$$
(4)
$$\begin{aligned}&{u_s=\left( \begin{array}{llll} 1&1&\cdots&1\end{array} \right) ^T}\end{aligned}$$
(5)
$$\begin{aligned}&{Z_{s}=\left( \begin{array}{lll} 0 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} 0 \\ 0 &{} \cdots &{} 0 \\ \end{array} \right) }\end{aligned}$$
(6)
$$\begin{aligned}&{U_s=\left( \begin{array}{lll} 1 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} 0 \\ 0 &{} \cdots &{} 1 \\ \end{array}\right) } \end{aligned}$$
(7)
$$\begin{aligned}&\left. \begin{array}{l} J_1 =\left( \begin{array}{ll}\dfrac{-f_1}{f_1+f_2} &{} \dfrac{-f_2}{f_1+f_2}\end{array}\right) \\ J_2 =\left( \begin{array}{ll}\dfrac{ f_1}{f_1-f_2} &{} \dfrac{-f_2}{f_1-f_2}\end{array}\right) \\ J_3 =\left( \begin{array}{ll}\dfrac{f_1^2}{f_1^2-f_2^2} &{} \dfrac{-f_2^2}{f_1^2-f_2^2}\end{array}\right) \\ \end{array} \right\} . \end{aligned}$$
(8)

As defined, \(z_s\) is a \(s\times 1\) vector with zero entries and \(u_s\) is a \(s\times 1\) vector with one entry, while \(Z_s\) is a \(s\times s\) matrix with zero entries and \(U_s\) is a \(s\times s\) identity matrix; \(J_1\) and \(J_2\) are the coefficients of MW combination, and \(J_3\) is the coefficient of IF combination.

Without loss of generality, it is assumed that the terms \(\rho \), \(t^s\), \(T_z\), \(b_{r,1}\), \(b^s\) and \(\varphi \) are exactly known and have been applied to \(\widetilde{P}\), \(\widetilde{\Phi }\) in the following discussion. Consequently, the observation equations based on Eq. (1) for a dual-frequency receiver observing \(j\) satellites read

$$\begin{aligned}&\left. \begin{array}{l} E \left( l\right) =A\cdot \left( \begin{array}{l} t_r b_{r,2} \bar{N} \bar{I} \end{array} \right) ^T \\ D \left( l\right) =\sigma _0^2 \cdot \left( \begin{array}{l} U_{2\cdot j} \\ 1\mathrm{e}^{-4} \cdot U_{2\cdot j} \end{array} \right) \end{array} \right\} \end{aligned}$$
(9)

with

$$\begin{aligned}&l=\left( \begin{array}{llllllll} \widetilde{P}_{r,1}^1&\widetilde{P}_{r,2}^1&\ldots&\widetilde{P}_{r,2}^j&\widetilde{\Phi }_{r,1}^1&\widetilde{\Phi }_{r,2}^1&\ldots&\widetilde{\Phi }_{r,2}^j \end{array} \right) ^T\end{aligned}$$
(10)
$$\begin{aligned}&A=\left( \begin{array}{ccccccc} u_{2\cdot j} &{} u_j \otimes \left( \begin{array}{l} 0 \\ 1 \end{array} \right) &{} Z_{2\cdot j} &{} U_j \otimes \left( \begin{array}{l} \beta _1 \\ \beta _2 \end{array} \right) \\ u_{2\cdot j} &{} u_j \otimes \left( \begin{array}{l} 0 \\ 1 \end{array} \right) &{} -U_j \otimes \left( \begin{array}{ll} \lambda _1 &{} 0 \\ 0 &{} \lambda _2 \end{array} \right) &{} -U_j \otimes \left( \begin{array}{l} \beta _1 \\ \beta _2 \end{array} \right) \end{array} \right) \nonumber \\\end{aligned}$$
(11)
$$\begin{aligned}&\left. \begin{array}{l} \bar{N}=\left( \begin{array}{lllll}N_1^1 &{} N_2^1 &{} \ldots &{} N_1^j &{} N_2^j\end{array}\right) \\ \bar{I}=\left( \begin{array}{lllll}I^1 &{} \ldots &{} I^j\end{array}\right) , \end{array} \right\} \end{aligned}$$
(12)

where \(\otimes \) is the Kronecker product (Teunissen 1997), \(1\mathrm{e}^{-4}\) comes from the fact that the precision of phase is 100 times better then that of pseudo-range and \(\sigma _0^2\) is the unit weight variance, e.g., \((0.2\,\mathrm{m})^2\) for IGS receivers.

2.2 COM model: model based on MW and IF combination

Denote the linear transformation \(\mathbb P\) as

$$\begin{aligned} \mathbb P= \left( \begin{array}{cc} U_j \otimes J_1 &{} U_j \otimes J_2 \\ U_j \otimes J_3 &{} 0 \\ 0 &{} U_j \otimes J_3 \end{array} \right) . \end{aligned}$$
(13)

Then from Eqs. (9) and (13), the models based on MW and IF observable \(l_{\mathrm{com}}\) are expressed as

$$\begin{aligned} \left. \begin{array}{l} E\left( l_{\mathrm{com}}\right) =\mathbb P A\cdot \left( \begin{array}{lllll} \Delta t_r &{} b_{r,2} &{} \bar{b_2^s} &{} \bar{\widetilde{N}} &{} \bar{I} \end{array} \right) ^T \\ D\left( l_{\mathrm{com}}\right) =\sigma _0^2 \cdot \mathbb P \left( \begin{array}{llll} U_{2\cdot j} &{} \\ &{} 1\mathrm{e}^{-4} \cdot U_{2\cdot j} \end{array} \right) \mathbb P^T \end{array} \right\} . \end{aligned}$$
(14)

Substituting Eqs. (8) and (13) into (14), we get the design matrix

$$\begin{aligned} A_{\mathrm{com}}&= \mathbb P A \nonumber \\&= \begin{array}{l} \left( \begin{array}{ccccc} 0 &{} \dfrac{-2f_1f_2}{f_1^2\!-\!f_2^2}\cdot u_j &{} -\lambda _w \cdot U_j \otimes \left( \begin{array}{ll}1 &{} -1\end{array}\right) &{} 0 \\ u_j &{} \dfrac{-f_2^2}{f_1^2\!-\!f_2^2}\cdot u_j &{} 0 &{} 0 \\ u_j &{} \dfrac{-f_2^2}{f_1^2\!-\!f_2^2}\cdot u_j &{} -\lambda _1 \cdot U_j\otimes \left( \begin{array}{ll}\dfrac{f_1^2}{f_1^2\!-\!f_2^2} &{} \dfrac{-f_1f_2}{f_1^2\!-\!f_2^2}\end{array}\right) &{} 0 \\ \end{array} \right) \end{array}\nonumber \\ \end{aligned}$$
(15)

and the stochastic model

$$\begin{aligned}&\begin{array}{l} D\left( l_{\mathrm{com}}\right) \\ \quad =\sigma _0^2\cdot \left( \begin{array}{ccc} U_j\otimes \left( J_1\cdot J_1^T+1\mathrm{e}^{-4}J_2\cdot J_2^T\right) &{} U_j\otimes J_1\cdot J_3^T &{} 1\mathrm{e}^{-4}U_j\otimes J_2\cdot J_3^T \\ U_j\otimes J_3\cdot J_1^T &{} U_j\otimes J_3\cdot J_3^T &{} 0 \\ 1\mathrm{e}^{-4}U_j\otimes J_3\cdot J_2^T &{} 0 &{} 1\mathrm{e}^{-4}U_j\otimes J_3\cdot J_3^T \end{array} \right) . \end{array}\nonumber \\ \end{aligned}$$
(16)

Different from the traditional approach (Ge et al. 2008) based on a stepwise processing procedures, model (14) processes MW and IF combination in one filter to ensure their consistency. Additionally, it is noted that the MW observable is actually a measurement of the joint effect of WL ambiguity and code bias \(b_{r,2}\).

2.3 RAW model: model based on raw observable with ionosphere constraints

The model expressed as Eq. (9) is addressed now along with ionosphere constraints, including the constraints from its temporal and spatial behavior; the constraints are from a priori ionosphere correction model which can be described with the following equations respectively:

$$\begin{aligned}&\left. \begin{array}{l} I_r^s=\gamma _r^s \cdot I(z)_r^s \\ I(z)_r^s=a_0+a_1\mathrm{dL}+a_2\mathrm{dL}^2+a_3\mathrm{dB}+a_4\mathrm{dB}^2+r_r^s \end{array} \right\} \end{aligned}$$
(17)
$$\begin{aligned} \widetilde{I}(z)_r^s&= a_0+a_1\mathrm{dL}+a_2\mathrm{dL}^2+a_3\mathrm{dB}+a_4\mathrm{dB}^2\nonumber \\&+r_r^s+\varepsilon _{\widetilde{I}(z)_r^s}, \end{aligned}$$
(18)

where \(I(z)_r^s\) is the vertical total electron content of the ionosphere pierce point (IPP); \(\gamma \) is the mapping function as proposed by Schaer (1999); \(a_0\) is the average value of ionosphere delay over the station; \(a_1\), \(a_2\) and \(a_3\), \(a_4\) are the coefficients of the two second-order polynomials which are used to fit the horizontal gradients in east–west and south–north direction, respectively, and \(a_i\) together describes the deterministic behavior of the ionosphere delay; while the scalar field \(r_r^s\) represents the stochastic component from a second-order stationary process, \(\mathrm{dL}(_r^s), \mathrm{dB}(_r^s)\) are the longitude and latitude difference between the IPP and the approximate location of station, respectively, and for more details concerning Eq. (17) we refer to Shi et al. (2012); \(\widetilde{I}(z)_r^s\) is the vertical ionosphere delay correction interpolated from GIM or an available regional ionosphere model (Yao et al. 2013) with the corresponding noise \(\varepsilon _{\widetilde{I}(z)_r^s}\).

We define the ionosphere delay coefficient matrices

$$\begin{aligned} A_I&= \widetilde{\gamma }\cdot A(z)_I\nonumber \\&= \begin{array}{l}\left( \begin{array}{lll}\gamma _r^1 &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \gamma _r^j \end{array}\right) \cdot \left( \begin{array}{llllllll} 1 &{} \mathrm{dL} &{} \mathrm{dL}^2 &{} \mathrm{dB} &{} \mathrm{dB}^2 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} \mathrm{dL} &{} \mathrm{dL}^2 &{} \mathrm{dB} &{} \mathrm{dB}^2 &{} 0 &{} \cdots &{} 1 \end{array} \right) , \end{array} \end{aligned}$$
(19)

in which the subscript \(_r^s\) is omitted for simplification. Substituting Eqs. (19) into (9), and applying the corrections \(\widetilde{I}(z)_r^s\) as pseudo-observable, the RAW model with ionosphere constraints is then denoted by its design matrix and the stochastic model

$$\begin{aligned}&A_{\mathrm{raw}}=\begin{array}{l} \left( \begin{array}{lllllll} u_{2\cdot j} &{} u_j \otimes \left( \begin{array}{l} 0 \\ 1 \end{array} \right) &{} Z_{2\cdot j} &{} A_I \otimes \left( \begin{array}{l} \beta _1 \\ \beta _2 \end{array} \right) \\ u_{2\cdot j} &{} u_j \otimes \left( \begin{array}{l} 0 \\ 1 \end{array} \right) &{} -U_j \otimes \left( \begin{array}{ll} \lambda _1 &{} 0 \\ 0 &{} \lambda _2 \end{array} \right) &{} -A_I \otimes \left( \begin{array}{l} \beta _1 \\ \beta _2 \end{array} \right) \\ z_j &{} z_j &{} Z_j &{} A(z)_I \end{array} \right) \end{array}\nonumber \\\end{aligned}$$
(20)
$$\begin{aligned}&D\left( l_{\mathrm{raw}} \right) =\sigma _0^2 \cdot \left( \begin{array}{lll} U_{2\cdot j} &{} &{}\\ &{} 1\mathrm{e}^{-4} \cdot U_{2\cdot j} &{} \\ &{} &{} D_I/\sigma _0^2 \end{array} \right) . \end{aligned}$$
(21)

This approach was originally developed by Shi et al. (2012) for single-frequency PPP with a great effort to optimize the parameterization strategy.

The COM model (14) eliminates the ionosphere terms as well as the a priori ionosphere constraints; in contrast, the RAW model (20) reveals an alternative solution, in which ionosphere spatial and temporal characteristics are represented by a set of parameters, and its priori corrections that are usually recovered from a monitoring network are used as pseudo-observable.

2.4 UPD separation

By solving either COM or RAW model, float ambiguities on L1 and L2 frequencies for each satellite can be derived over a network, from which the phase bias \((-d_r+d^s)\) can be extracted by removing the integer parts. Suppose \(j\) satellites are tracked by \(i\) dual-frequency receivers, then it can be written in the following form:

$$\begin{aligned}&\left( \begin{array}{l} \bar{N}_1-\bar{n}_1 \\ \bar{N}_2-\bar{n}_2 \\ \vdots \\ \bar{N}_i-\bar{n}_i \end{array} \right) = \left( \begin{array}{lllllll} -U_i \otimes u_j&u_i \otimes U_j \end{array} \right) \left( \begin{array}{l} \bar{d}_r \\ \bar{d}^s \end{array}\right) \end{aligned}$$
(22)

where \(\bar{N}_r\) and \(\bar{n}_r\) are the float and integer ambiguity vectors for station \(r\); \(\bar{d}_r\) and \(\bar{d}^s\) are the UPD vectors for receiver \(r\) and satellite \(s\), respectively. To solve Eq. (22), extra condition

$$\begin{aligned} 0=\sum _{s=1}^{j} d^s \end{aligned}$$
(23)

should be applied to eliminate the rank deficiency and then \(d_r\) and \(d^s\) are finally estimated epoch by epoch.

2.5 Ionosphere residual effect on UPD

Besides proper quality control, \(d_r\) and \(d^s\) are highly sensitive to the the quality of float ambiguity. In this section, comparison of different float solutions is carried out to investigate ionosphere residual effect.

Zero entries of the last column in design matrix \(A_{\mathrm{com}}\) as presented in Eq. (15) imply that the float ambiguities \(N_1\) and \(N_2\) are free of ionosphere delay, but only subject to the observable noise; however, the float ambiguities estimated with the RAW model are highly sensitive to the unmodeled ionosphere effects. Since the parameters \(t_r\) and \(b_{r,2}\) are unassociated with either satellite or frequency, the offset of ionosphere estimate from its true value is most likely to be compensated by the float ambiguity terms \(N_1\) and \(N_2\) that can be written as

$$\begin{aligned}&\left. \begin{array}{l} \Delta N_1=\dfrac{-1}{\lambda _1}\Delta I \\ \Delta N_2=\dfrac{-f_1}{\lambda _1f_2}\Delta I \end{array} \right\} , \end{aligned}$$
(24)

where \(\Delta I\) is the ionosphere residual effect in unit of L1 distance; \(\Delta N_1\) and \(\Delta N_2\) are the corresponding bias on each frequency due to \(\Delta I\) in unit of cycle. To extract UPD from these float ambiguities over a network, an efficient way is to first retrieve the WL ambiguities following the rounding procedure to identify the UPD for WL; then NL ambiguities are fixed with the assistance of fixed WL ambiguities.

$$\begin{aligned}&\left. \begin{array}{l} N_{\mathrm{WL}}=N_1-N_2 \\ N_{\mathrm{NL}}=\dfrac{f_1\cdot N_1}{f_1-f_2}-\dfrac{f_2\cdot N_2}{f_1-f_2}-\dfrac{f_2\cdot n_{\mathrm{WL}}}{f_1-f_2} \end{array} \right\} , \end{aligned}$$
(25)

where \(n_{\mathrm{WL}}\) is the fixed WL ambiguity. Substituting Eq. (24) into Eq. (25), we get the ionosphere residual effect on WL and NL ambiguities \(\Delta N_{\mathrm{WL}}\), \(\Delta N_{\mathrm{NL}}\) based on raw observable

$$\begin{aligned}&\left. \begin{array}{l} \Delta N_{\mathrm{WL}} = \dfrac{1}{\lambda _w}\cdot \dfrac{f_1}{f_2}\Delta I = \dfrac{1}{\lambda _w}\cdot (1.28\Delta I) \\ \Delta N_{\mathrm{NL}} = 0. \end{array} \right\} \end{aligned}$$
(26)

As presented, though the NL ambiguity is free of ionosphere delay, the WL ambiguity based on raw observable amplifies the ionosphere residual effect. On the contrary, the WL ambiguity based on COM model is only subject to the observable noise which is about \(0.166\) cycle as inferred from Eq. (16). For the WL ambiguity based on RAW model performs better than based on COM model, it should satisfy

$$\begin{aligned} \dfrac{1}{\lambda _w}\cdot (1.28\Delta I) < 0.166, \end{aligned}$$
(27)

It implies that the precision of ionosphere should be better than 0.7 total electron content unit (TECU).

Ors et al. (2002) summarized that the best performance of global-scale ionosphere model is the GPS data-driven models which present an error of \(24\,\%\) of the RMS. With a typical slant ionosphere delay of \(5\) m, the residual effect on WL ambiguity is about \(5\times 24\,\% \times 1.28/\lambda _w=1.786\) cycle. Though it is expected that the residual effect will maintain at centermeter level after the convergence of ionosphere parameters, an important argument is how long it takes for this initialization.

3 Experimental validation

To confirm the above analysis with numerical experiment, we have adopted both COM and RAW model in the Position and Navigation System Data Analyst software package (Liu and Ge 2003; Shi et al. 2008). The following demonstration consists of three parts: firstly, the ionosphere model are generated and evaluated for both global and regional network. Based on these ionosphere products, UPD are then extracted from the RAW model and compared to the COM model. Finally, PPP is carried out in both RAW and COM model to assess the reliability of different UPD products as well as the PPP-RTK performance.

The processing strategy and observable for ION, UPD and PPP are summarized in Table 1. One year of data collected at about 360 IGS stations in 2010 are utilized in the global-scale experimental validation, while 39 CORS stations from days 061 to 062 2011 are utilized for regional data processing. The distribution of the corresponding network is presented in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Distribution of nearly 360 global tracking stations with 210 for ionosphere modeling in red and 100 for UPD estimation in green, while all these stations are included in positioning

Full size image
Fig. 2
figure 2

Distribution of 39 regional tracking stations with 14 for ionosphere modeling in red and 14 for UPD estimation in green, while all these stations are included in positioning

Full size image
Table 1 Summary of strategy and observable
Full size table

3.1 Ionosphere model

In Sect. 2.5, we have concluded that if the WL UPD based on the RAW model performs better then the COM model, the precision of ionosphere correction should be better than \(0.7\) TECU. Thus, this section derived the ionospheric measurements along the line of sight with the observable collected at all the stations and scaled to the vertical direction. Those vertical ionosphere delays from the red stations are then utilized in modeling, while those from the remaining stations are regarded as true value to evaluate the precision of ionosphere corrections.

In the global-scale ionosphere modeling, the vertical delays are usually attributed to an infinitesimally thin shell with a typical height of 350–400 km and then fitted by the sphere harmonic function in a Sun-fixed geomagnetic reference frame (Schaer 1999). We adopt this approach in the global ionosphere model with 210 IGS stations (red stations in Fig. 1). However, this strategy does not capture small-scale and high-frequency ionospheric disturbances; thus, when the regional network with dense stations is involved, e.g., network shown in Fig. 2, a more efficient modeling method is employed as described in detail in the work by Rocken et al. (2000) and Yao et al. (2013). Generally speaking, based on the fact that, for a dense regional network, the ionosphere effect of a specific satellite is highly correlated with each other among different stations, the ionosphere correction of a rover station to the same satellite can be interpolated simply by inverse distance weight.

In place of the IGS GIM products with a precision of 2–8 TECU, ionosphere delays of rover stations (green and blue stations in Figs. 1, 2) are extracted as reference to better evaluate the precision of ionosphere models. Regarding these estimates as true value, Fig. 3 shows the difference of vertical ionosphere delay interpolated from the reference stations. As presented, the precision of global ionosphere model based on IGS tracking network is only 3.9 TECU. It implies that based on raw observable, the WL UPD products generated from a global network may suffer a lot from the poor precision of the ionosphere model. For the regional model of a high temporal–spatial resolution, though the RMS is about 0.636 TECU which satisfies the criteria (27), it has to be converted to slant in UPD processing which will amplify the noise.

Fig. 3
figure 3

Difference of vertical ionosphere delay between rover station extracted and model interpolated values with the increase of elevation angle in unit of TECU

Full size image

3.2 UPD comparison

As introduced in Sect. 2.4, no matter which model is involved, the UPD separation procedure stays the same once the float ambiguities are readily available. Hence, the fundamental difference between the COM model and RAW model in UPD extraction is the float ambiguity estimates. As a result, the UPD comparison can be also regarded as the comparison of float ambiguity.

Since no reference ambiguity is available, the temporal stability of float ambiguity estimates is employed as an indicator to assess its quality. Firstly, ambiguities are generated with the rover stations in green for both global and regional network during the experiment. In the case that RAW model is involved, the ionosphere models described in Sect. 3.1 are introduced as constraints. Then the temporal stability of ambiguity is measured by standard deviation (STD) which is calculated for each continuous tracking arc. To ensure the reliability of these statistics, additional requirements are applied: firstly, for each tracking arc, the first 30 min of ambiguities are removed; secondly, only those arcs involved with more than 20 samples are included.

Averaging over all the tracking arcs for each satellite, the mean STD of WL/NL ambiguity series is shown in Fig. 4 for both global network and regional network. There are typically 65,000 arcs involved in the global statistic for each satellite; however, the satellite PRN1 seems abnormal during the global experiment with less than 4,000 arcs, and thus it is removed in the global statistic. It is observed that the stability of NL ambiguity based on RAW model is improved significantly by about \(17.6\,\%\) on average. However, for WL ambiguity estimation, the COM model is preferable for global network experiment. Furthermore, only slight improvement can be achieved even when the regional network is involved. We can thus infer that for the WL to be benefited from this RAW model, high-precision ionosphere correction is essential, while improvement of NL estimation can be expected regardless of the quality of the a priori ionosphere model.

Fig. 4
figure 4

Mean standard deviation of WL and NL ambiguity for each satellite estimated from all the rover stations in green during the experiment with global and regional ionosphere model constraints. The results based on the COM model are denoted with black bar, while those based on RAW model are denoted with red bar

Full size image

Besides the ambiguity stability, the UPD consistency among float ambiguities of different stations also plays a key role. As introduced in Sect. 2.4, the solution residual of model (22) can be regarded as a measurement of UPD consistency. The residual distribution of the global UPD solution as well as the regional UPD solution is shown in Fig. 5. Obviously, the regional solution performs better than the global case due to the high correlation of un-modeled errors in space. In addition, it is observed that in both cases, the better strategy is to generate WL UPD from the COM mode and NL UPD from the RAW mode.

Fig. 5
figure 5

Residual distribution of the global UPD solution (left panel) and the regional UPD solution (right panel)

Full size image

3.3 PPP

In this section, observables from all these stations are collected in PPP processing in simulated real-time kinematic mode. For the ambiguity-fixed PPP, the corresponding UPD products are included and the threshold for ratio test is set as 5 in ambiguity resolution. The position accuracy of global experiment is measured by the differences between the estimates and the coordinates from the IGS weekly combination, while, for the regional experiment, the post-estimated coordinates in static mode are set as reference.

Table 2 shows the overall statistics of the ambiguity-fixed solution, from which it can be inferred that the contribution of ambiguity resolution to the convergence is rather limited as observed by the long period of time to first fix (TTFF). The TTFF is rather long compared to the results of other authors, e.g., Geng et al. (2010b). Besides the different sampling rate and station location of the observable collected, it is most likely due to the real-time processing mode of both UPD and PPP solution, and the stricter threshold for ratio test compared to 3 in other works. Moreover, the mean times spent on ambiguity-fixed solution based on RAW model are almost twice that of the COM model. One possible reason for this result is that the ionosphere parameterization reduces the model strength as compared to the COM model; as a result, the ratio test is more difficult to pass (Li et al. 2014). The comparison between the global and regional experiment demonstrated that both the reliability and efficiency of ambiguity resolution decrease with the increase of the inter-station distance, while once the ambiguity is fixed correctly the accuracy of PPP is improved by a factor of 18.1–31.3 % in three dimension (3D) for both COM and RAW models.

Table 2 Statistics of the ambiguity-fixed solution
Full size table

Since the positioning RMS of Table  2 is based on different samples due to different TTFF, it cannot be used directly for the accuracy comparison of the COM and RAW models. To illustrate this argument, Figs. 6 and 7 present the positioning statistics of the common samples for global and regional experiments, respectively. It is demonstrated that the float solution is expected to be benefited with the RAW model by 15.5, 12.8, 13.6 % in the north, east and up directions on average. For the ambiguity-fixed solution, though the WL ambiguity solution based on COM filter may perform better as discussed in Sect. 3.2, slight improvement of \(7.9\,\%\) in 3D is still achievable by the RAW model. This result confirms that the key factor in high-precision ambiguity-fixed PPP is the efficient solution of NL rather than WL.

3.4 Discussion

To achieve instantaneous centimeter-level positioning with a stand-alone receiver, great efforts have been focused on PPP over the past years. There are typically two promising approaches: on the one hand, the RAW signal processing method constrained with the a priori ionosphere model has already been demonstrated as an efficient way for the multi-frequency float PPP; on the other hand, exploiting the integer property and the application of ambiguity resolution to PPP have the potential to improve the positioning performance. It is natural to expect that the PPP AR based on the RAW GNSS data processing model should absorb both advantages. Unfortunately, the comparison in both theory and practice reveals that to fully unleash the potential of the RAW model, the physics-based ionosphere models have to be very accurate, beyond the ordinary level. Since the advances in atmospheric research looks unlikely in the short term, it is suggested to perform WL (and EWL for triple-frequency signal) resolution with the traditional approach and the NL resolution with the RAW model for a compromise.

4 Conclusions

Raw observable processing strategy provides a possible solution to future GNSS data analysis with multi-frequency signals. Thereby, we adopt this RAW model into the ZD ambiguity resolution and compare it with the COM model based on MW and IF combinations. Numerical demonstrations are also carried out with over 1 year observables collected at about 360 globally distributed as well as 39 regionally distributed stations.

Fig. 6
figure 6

Daily RMS distribution of COM float (black bar), COM fixed (red bar), RAW float (green bar) and RAW fixed (blue bar) PPP for 360 sites from 001 to 031 in year 2010

Full size image
Fig. 7
figure 7

Average RMS of COM float (black bar), COM fixed (red bar), RAW float (green bar) and RAW fixed (blue bar) PPP for 39 sites from 060 to 061 in year 2011

Full size image

This study begins with the formulation of a mathematical framework for both COM and RAW GNSS data processing model. Based on this formulation, the ionosphere effect on WL/NL ambiguity estimates is analyzed theoretically. It is revealed that NL ambiguities are insensitive to the ionosphere delay for both COM and RAW model, while for the estimates of WL ambiguity performs better than the COM model, the precision of the a priori ionosphere correction should be better than 0.7 TECU. Thus, to evaluate the GNSS-based ionosphere model, both global- and regional-scale ionosphere models are generated. The RMS of the vertical ionosphere correction is 3.9 TECU for global-scale model and 0.636 TECU for the regional model. Then, WL/NL UPDs are extracted with both approaches, it is concluded that the RAW approach can evidently improve the NL estimation by \(17.6\,\%\). However, the COM model is more suitable for the WL estimation, since the ionosphere model is still not precise enough in its current stage. Based on these UPD products, ambiguity-fixed PPP are finally carried out with the corresponding approach. The results suggest that TTFF of the RAW model PPP is almost twice that of the COM model due to the reduction of model strength, while the positioning accuracy of the RAW model outperforms COM PPP contributed to the efficient NL ambiguity resolution.

In conclusion, concerning the ZD ambiguity resolution of dual-frequency observables, the COM model and RAW model have merits and demerits, respectively. To fully explore the potential of raw observable processing strategy, sustained efforts should focus on ionosphere modeling.