Introduction

In the past few decades, the American Global Positioning System (GPS) has been the primary positioning tool for many applications. The integration with the emerging Global Navigation Satellite Systems (GNSSs), such as the Chinese BeiDou Navigation Satellite System (BDS), can give improved precise real-time kinematic (RTK) positioning. Some first results using BDS outside of China are reported in Montenbruck et al. (2013) and Nadarajah et al. (2013). When BDS is combined with GPS about double the number of satellites will be visible in the Asia-pacific region, which can make single-frequency RTK (Verhagen et al. 2012; He et al. 2014; Teunissen et al. 2014; Odolinski et al. 2015) and low-cost receiver RTK positioning possible (Odolinski and Teunissen 2016; Mongredien et al. 2016). Other studies on GPS RTK positioning and ambiguity resolution using low-cost receivers can be found in Takasu and Yasuda (2008, 2009), Wisniewski et al. (2013) and Pesyna et al. (2014). We will analyze the performance of L1 GPS + B1 BDS in Dunedin, New Zealand, using low-cost ublox receivers. We will compare the performance to that of dual-frequency GPS survey-grade receivers.

We describe first the GPS + BDS functional/stochastic model and then the real data used for our evaluations. Least-squares variance component estimation (LS-VCE) results are then presented as a way to determine the code and phase (co)variances and formulate a realistic stochastic model. An incorrect stochastic model deteriorates the ambiguity resolution performance and consequently impacts the achievable positioning precisions. For that same reasons, receiver-induced time correlation will also be investigated. Once the stochastic model has been correctly defined, the ambiguity resolution and positioning performance is investigated. The performance is evaluated formally and empirically, for customary and high elevation cut-off angles. The high cut-off angles are used to mimic situations when low-elevation multipath is to be avoided. All results will be compared between using low-cost and survey-grade antennas. We then further extend our short-baseline analysis and investigate the performance for a baseline where small residual ionospheric delays are present. A summary with conclusions is finally given.

GPS + BDS model

The model that will be used for the LS-VCE, as introduced in Teunissen (1988), is given as follows. Assume that s G  + 1 GPS satellites are tracked on f G frequencies and s B  + 1 BDS satellites on f B frequencies. As we apply system-specific double differencing (DD), one pivot satellite is used per system. The total number of DD phase and code observations per epoch equals then 2f G s G  + 2f B s B . We assume for now that cross-correlation between frequencies and code and phase is absent. Following Teunissen et al. (2014), the combined multi-frequency short-baseline GPS + BDS model is then defined as follows.

The system-specific DD phase and code observation vectors are denoted as ϕ * and p *, respectively, with * = {G, B} where \( G = {\text{GPS}}\, {\text{and}}\,B = {\text{BDS}} \). The single-epoch GNSS model of the combined system is given as

$$ \left[ {\begin{array}{*{20}c} \phi \\ p \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} \varLambda & I \\ 0 & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}l} a \hfill \\ \rho \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} \varepsilon \hfill \\ e \hfill \\ \end{array} } \right] $$
(1)

and

$$ D\left[ {\begin{array}{*{20}c} \phi \\ p \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{\phi \phi } } & 0 \\ 0 & {Q_{pp} } \\ \end{array} } \right] $$
(2)

in which \( \phi = [\phi_{G}^{T} ,\phi_{B}^{T} ]^{T} \in {\mathbb{R}}^{{f_{G} s_{G} + f_{B} s_{B} }} \) is the combined phase vector, \( p = [p_{G}^{T} ,p_{B}^{T} ]^{T} \in {\mathbb{R}}^{{f_{G} s_{G} + f_{B} s_{B} }} \) is the combined code vector, \( a = [a_{G}^{T} ,a_{B}^{T} ]^{T} \in {\mathbb{Z}}^{{f_{G} s_{G} + f_{B} s_{B} }} \) is the combined integer ambiguity vector, \( \rho = [\rho_{G}^{T} ,\rho_{B}^{T} ]^{T} \in {\mathbb{R}}^{{s_{G} + s_{B} }} \) is the receiver-satellite range, \( \varepsilon = \left[ {\varepsilon_{G}^{T} ,\varepsilon_{B}^{T} } \right]^{T} \in {\mathbb{R}}^{{f_{G} s_{G} + f_{B} s_{B} }} \) is the combined phase random observation noise vector, \( e = \left[ {e_{G}^{T} ,e_{B}^{T} } \right]^{T} \in {\mathbb{R}}^{{f_{G} s_{G} + f_{B} s_{B} }} \) is the combined code random observation noise vector, D[·] denotes the dispersion operator, and with the entries of the wavelength matrix given as

$$ \varLambda = {\text{blkdiag}}\left[ {\varLambda_{G} ,\varLambda_{B} } \right],\quad \varLambda_{*} = {\text{diag}}\left[ {\lambda_{{1_{*} }} , \ldots ,\lambda_{{f_{*} }} } \right] \otimes I_{{s_{*} }} $$

where \( \lambda_{{j_{*} }} \) is the wavelength of frequency j *, ⊗  denotes the Kronecker product, \( I_{{s_{*} }} \) is the s * × s * unit matrix, and ‘diag’ is a diagonal and ‘blkdiag’ a block diagonal matrix, respectively. The entries of the positive definite variance matrices are given as

$$ \begin{aligned} Q_{\phi \phi } & = {\text{blkdiag}}\left[ {Q_{{\phi_{G} \phi_{G} }} ,Q_{{\phi_{B} \phi_{B} }} } \right],\quad Q_{{\phi_{ *} \phi_{ *} }} = C_{{\phi_{ *} \phi_{ *} }} \otimes 2Q_{ *} \\ Q_{pp} & = {\text{blkdiag}}\left[ {Q_{{p_{G} p_{G} }} ,Q_{{p_{B} p_{B} }} } \right],\quad Q_{{p_{ *} p_{ *} }} = C_{{p_{ *} p_{ *} }} \otimes 2Q_{ *} \\ C_{{\phi_{ *} \phi_{ *} }} & = {\text{diag}}\left[ {\sigma_{{\phi_{{1_{ *} }} }}^{2} , \ldots ,\sigma_{{\phi_{{f_{ *} }} }}^{2} \left] {,\quad C_{{p_{ *} p_{ *} }} = {\text{diag}}} \right[\sigma_{{p_{{1_{ *} }} }}^{2} , \ldots ,\sigma_{{p_{{f_{ *} }} }}^{2} } \right] \\ Q_{ *} & = D_{{s_{ *} }}^{T} W_{ *}^{ - 1} D_{{s_{ *} }} ,\quad W_{ *} = {\text{diag}}\left[ {w_{{1_{ *} }} , \ldots ,w_{{s_{ *} + 1}} } \right] \\ \end{aligned} $$
(3)

where \( D_{{s_{*} }}^{T} = \left[ { - e_{{s_{*} }} ,I_{{s_{*} }} } \right] \) is the s * × (s * + 1) differencing matrix, \( e_{{s_{*} }} \) is the s * × 1 vector of \( {\text{values of}} 1 \), \( \sigma_{{\phi_{{j_{*} }} }} \), \( \sigma_{{p_{{j_{*} }} }} \) is the phase and code standard deviation, respectively, and \( w_{{i_{*} }} \) denotes the satellite elevation-dependent weight.

The model (1) applies to short baselines, and thus, the ionospheric and tropospheric delays are assumed absent. The broadcast ephemerides are used to obtain the satellite coordinates, and the baseline is precisely known. Hence, the receiver-satellite range ρ is known, which is referred to as the “geometry-fixed” model. The Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) (Teunissen 1995) is furthermore used to estimate the integer ambiguities a and we treat them as time-constant parameters over a large observation time span, so that their uncertainty can be assumed to be negligible, which is referred to as the “ambiguity-fixed” model. The observation noise vectors ɛ and e, respectively, are zero-mean vectors provided that no multipath is present in (1).

Experiment setup

The GNSS receivers used to collect GNSS data are depicted in Fig. 1. Two ublox EVK-M8T receivers were setup to collect L1 + B1 GPS + BDS data for two days with a measurement interval of 1 s. These low-cost receivers cost a few hundred USDs. Since patch antennas have been shown to have less effective signal reception and multipath suppression in comparison with survey-grade antennas (Pesyna et al. 2014), the receivers that collected data for two days were also connected to Trimble Zephyr 2 antennas. These antennas have a cost of slightly more than one thousand USDs per antenna. To compare the low-cost solution to a survey-grade solution, two Trimble NetRS receivers, which cost several thousand USDs, were connected to the same Zephyr antennas through a splitter and collected L1 + L2 GPS data. Another receiver setup, with Zephyr antennas, was also analyzed with a baseline length of 7 km, so as to evaluate the low-cost receiver performance when small residual ionospheric delays are present. The detection, identification, and adaption (DIA) procedure (Teunissen 1990) was furthermore used to eliminate any outliers.

Fig. 1
figure 1

GNSS ublox EVK-M8T receivers collecting data for GPS + BDS single-baseline RTK, with patch antennas (top, left) and Trimble Zephyr 2 antennas (top, right) in January 4–6 and January 6–8, 2016, respectively. Survey-grade Trimble NetRS dual-frequency GPS receivers have been connected to the same Zephyr 2 antennas to truly track the same GPS constellation. A 7-km baseline setup (January 18–19, 2016) also used to assess the positioning performance is shown at bottom

Full size image

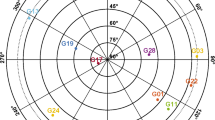
The model we will use for positioning is obtained by linearizing the observation equations in (1) with respect to the unknown receiver coordinates. Figure 2 depicts the corresponding redundancy of the two models when also including ambiguities as unknown parameters, together with the number of satellites over 48 h with a 30-s epoch interval.

Fig. 2
figure 2

Number (#) of satellites (bottom) and redundancy (top) of L1 + B1 GPS + BDS and L1 + L2 GPS in January 6–8, 2016, (48 h) for an elevation cut-off angle of 10°

Full size image

While the number of BDS satellites (magenta lines) is overall smaller than when compared to GPS (blue lines) in Dunedin, Fig. 2 shows that the redundancy of L1 + B1 GPS + BDS is almost similar to that of L1 + L2 GPS except for some hours at the middle of the two days. This implies, for instance, that the two models can potentially give competitive RTK ambiguity resolution and positioning performance, see the extensive overviews in Teunissen et al. (2014) and Odolinski and Teunissen (2016). This is, however, only true if the receiver-satellite geometry strength and receiver code and phase observation noise would be of similar magnitude between the receivers used, hence the need for an analysis of the observation precision.

In the following receiver evaluations, a set of reference ambiguities were determined using a known baseline and treated as time-constant parameters over the two days in a dynamic model. Note also that the geostationary orbit (GEO) C03 BDS satellite had to be excluded from all the results as it yielded many incorrectly fixed instances caused by low-elevation multipath (Wang et al. 2015a, b), due to it being almost stationary and having a low elevation angle of around 12° with respect to the receivers (Odolinski and Teunissen 2016).

Least-squares variance component estimation for low-cost receivers

We make use of the LS-VCE procedure (Teunissen 1988; Teunissen and Amiri-Simkooei 2008) to determine the code and phase precision of the low-cost receivers. The estimated (co)variances are needed to formulate a realistic stochastic model for precise RTK positioning. The ambiguity resolution performance would otherwise deteriorate and hence the achievable positioning precisions as well.

The noise vectors for phase ɛ and code e in (1) serve as an input into the LS-VCE. To capture the elevation dependency, an exponential weighting function (Euler and Goad 1991) is used in (3) as follows

$$ w_{{i_{*} }} = \left[ {1 + 10\exp \left( { - \frac{{\theta^{{i_{*} }} }}{10}} \right)} \right]^{ - 2} $$
(4)

where \( \theta^{{i_{*} }} \) is the elevation of the satellite i * in degrees. This formulation allows us to estimate zenith-referenced standard deviations (STDs) of the undifferenced phase and code observations, \( \sigma_{{\phi_{{j_{*} }} }} \) and \( \sigma_{{p_{{j_{*} }} }} \), respectively. Table 1 depicts the corresponding code and phase STDs for the short-baseline setups at top of Fig. 1 for instantaneous, i.e., epoch-by-epoch, RTK. The presented STDs are the mean of the single-epoch STDs over the entire observation time span. The STDs within parentheses are based on single-epoch multipath (MP)-corrected DD residuals. These residuals were obtained by subtracting the DD residuals (1) from the previous day of data (January 6 minus January 5 for patch and January 9 minus January 8 for Zephyr antennas), while taking into account the approximate satellite constellation repeatability of 23 h and 56 min and using the elevation weighting (4) similar to Zaminpardaz et al. (2016). This procedure was applied since the code e and phase ɛ vectors in (1) are believed to be contaminated by multipath effects. The MP correction was only applied to the GPS Medium Earth Orbit (MEO) and BDS GEO/inclined geosynchronous satellite orbit (IGSO), since these satellites have a constellation repeatability of about one sidereal day (Axelrad et al. 2005; Jiang et al. 2011), and the GEO satellites are almost stationary (Montenbruck et al. 2013). One should, however, also be aware of that different satellites can have different repeatability periods that differ several seconds from each other, as was shown for GPS (Axelrad et al. 2005). We use the same time separation between days for all satellites when applying the MP corrections, which consequently can result in some residual multipath effects to remain in the presented results. The doubling in noise that enters through the epoch-by-epoch MP correction has been accounted for in all the results presented by dividing the day-differenced residuals by square root of two.

Table 1 LS-VCE of zenith-referenced and undifferenced code \( \hat{\sigma }_{{p_{{j_{*} }} }} \) and phase \( \hat{\sigma }_{{\phi_{{j_{*} }} }} \) STDs for Dunedin
Full size table

In support of understanding Table 1 better, Fig. 3 shows the single-epoch B1 BDS code and phase STDs (left two columns) corresponding to a period of two hours. The code and phase DD residuals are also shown for two consecutive days (right two columns), where elevation weighting (4) is applied since the observations are highly dependent on the elevation of the satellites. The patch antenna residuals and corresponding single-epoch estimated STDs show very large fluctuations at times likely due to multipath or poor signal reception since it repeats over both days. The code and phase STDs based on elevation-weighted day-differenced DD residuals are thus depicted as well at the second and fourth row, respectively.

Fig. 3
figure 3

Single-epoch LS-VCE of zenith-referenced and undifferenced B1 BDS code and phase STDs (left two columns) for day 1 [2 h (1 s)] using ublox EVK-M8T receivers and L1 + B1 GPS + BDS. The elevation-weighted code/phase DD residuals are also shown (right two columns), all in the first and third row. The corresponding STDs and code and phase DD residuals when applying MP corrections are shown in the second and fourth row, using a repeatability period of approximately one sidereal day for the GPS MEO and BDS GEO + IGSO satellites. In the first two rows, results are given for patch on January 5 at 18:00 and January 6 at 17:56 (hh:mm) UTC, and in the last two rows when Zephyr antennas are used on January 8 at 17:48 and January 9, 2016 at 17:44 (hh:mm) UTC

Full size image

Figure 3 shows the significant improved patch antenna STDs when the MP corrections have been applied (second row left), which is also reflected by the corresponding much smaller residuals (second row right). Table 1 shows consequently the more similar magnitude of STDs between using Zephyr and patch antennas for the ublox receivers when MP corrections have been applied. For example, the B1 code STD decreases from 74 cm for the patch antenna model to 22 cm when day differencing has been applied. Corresponding values for the Zephyr-antenna model are 33 cm, which decreases to 20 cm. Since the non-differenced STDs for the patch antenna model are much larger than the corresponding Zephyr ones, this indicates the potentially better multipath suppression by the Zephyr antennas which is also reflected by the much smaller code and phase residuals in the figure. We also note in Table 1 that the Trimble NetRS non-differenced L1 and L2 code STDs of 18 and 20 cm, respectively, decrease to 15 cm for both frequencies when day differencing has been applied.

The covariances between code and phase, and frequencies, were also estimated. Table 2 shows the corresponding cross-correlations together with the STDs based on the 2-h (1 s) data in Table 1, whereas the patch antenna model is based on 24 h (30 s) due to the earlier-referenced possibility of multipath so that these effects are more likely to average out over time.

Table 2 LS-VCE of zenith-referenced cross-correlations, which are the non-diagonal values, and undifferenced code \( \hat{\sigma }_{{p_{{j_{ *} }} }} \) and phase \( \hat{\sigma }_{{\phi_{{j_{ *} }} }} \) STDs, which are the diagonal values
Full size table

Table 2 shows that the Trimble NetRS receivers have an estimated correlation coefficient of 0.35 between L1C and L2W phase, which is significant since the corresponding STD is 0.007 that is not explicitly shown herein. That the GPS L1 and L2 phase observables can be highly correlated for some receivers has also been found in Teunissen et al. (1998), Bona and Tiberius (2000), Amiri-Simkooei and Tiberius (2007) and Amiri-Simkooei et al. (2009), and specifically for a Trimble NetRS receiver in Amiri-Simkooei et al. (2016). More importantly, the ublox receivers show close to zero cross-correlation between GPS C1C code and L1C phase, as well as BDS C2I code and L2I phase.

Time correlation of low-cost RTK positioning

In this section, we examine the time correlation of the low-cost receivers, which, if neglected in a multi-epoch model, could negatively influence the ambiguity resolution and hence positioning performance. Time correlation can be caused by internal effects in the receivers, for instance filtering to reduce the observation noise level (Bona 2000). External effects can also cause time correlation, which include atmospheric delays and multipath. We use a short-baseline (SB) setup (Fig. 1, top), and thus, multipath is the main external source herein that can cause time correlation in addition to the internal effects within the receivers. We will also compare the results to a zero-baseline (ZB) setup, where two receivers are connected to the same antenna at the same location as the setups shown at the top of Fig. 1. As a result of the zero-baseline setup, the contributions of multipath are largely eliminated. The remaining small effects would mainly be due to the non-simultaneity of sampling between the receivers. One should finally be aware that internal errors due to the noise from the common low-noise amplifier (LNA) between the receivers largely extent cancel when a zero-baseline is used (Amiri-Simkooei and Tiberius 2007). This is the reason that the receiver noise thus far has only been assessed based on the short-baseline setups in Fig. 1, where the receivers are connected to their own antenna and LNA and thus give more realistic noise estimates.

Time correlation without reducing multipath

The model we will now use is obtained by linearizing the observation equations in (1) with respect to the unknown receiver coordinates. In this step, the code and phase variances that were estimated by LS-VCE in Table 2 are fixed. We consider estimating a functionally known quantity, like local North/East/Up ambiguity-float or ambiguity-fixed components, respectively, and m is the number of times. These positioning errors were obtained by comparing the estimated positions to precise benchmark coordinates. The autocovariance function can then be determined by (Teunissen and Amiri-Simkooei 2008)

$$ \hat{\sigma }_{\tau } = \frac{{\sum\nolimits_{i = 1}^{m - \tau } {\hat{e}_{i} } \hat{e}_{i + \tau } }}{m - \tau },\quad \tau = 1,2, \ldots ,m - 1 $$
(5)

where τ is the time lag and \( \hat{e}_{i} \) is the least-squares positioning errors. The variance of the noise process follows as,

$$ \hat{\sigma }^{2} = \frac{{\sum\nolimits_{i = 1}^{m} {\hat{e}_{i} } \hat{e}_{i} }}{m} $$
(6)

The autocorrelation function can then be defined by,

$$ \hat{\rho }_{\tau } = \frac{{\hat{\sigma }_{\tau } }}{{\hat{\sigma }^{2} }},\quad \tau = 1,2, \ldots ,m - 1 $$
(7)

where \( \hat{\rho }_{\tau = 0} = 1 \) by definition. An approximation of the STD of the autocorrelation function is given through linearization and the error propagation law of (7) as follows under the assumption of white noise, i.e., that consecutive observations are uncorrelated (Amiri-Simkooei and Tiberius 2007),

$$ \sigma_{{\hat{\rho }_{\tau } }} \approx \sqrt {\frac{1}{m - \tau } + \frac{{2\hat{\rho }_{\tau }^{2} }}{m}} ,\quad \tau = 1,2, \ldots ,m - 1 $$
(8)

Equation (8) shows that with increasing time lags τ the precision of the estimated time correlation (7) becomes poorer, which makes sense since the number of positions used to estimate the autocovariance \( \hat{\sigma }_{\tau } \) (5) is m − τ. To see this at work, Fig. 4 depicts the autocorrelation function (7) in green for instantaneous ambiguity-fixed L1 + B1 GPS + BDS RTK positioning for the local Up component. This is based on 1 h (1 s) of data for ublox + patch at top and ublox + Zephyr at bottom for the short baselines in Fig. 1. In order to separate the contribution of multipath on the time correlation estimates, we depict in black color the corresponding autocorrelation for a zero-baseline ublox + patch antenna setup, which collects independent data with approximately the same satellite configuration to the short baselines but about 100 days later. This is given together with the 95% confidence interval (CI) in red as computed from the STD of the autocorrelation in (8).

Fig. 4
figure 4

Autocorrelation coefficients (green) for L1 + B1 GPS + BDS instantaneous short-baseline ambiguity-fixed positioning errors during 1 h (1 s). The results are based on data on January 5 at 02:50 for ublox + patch at top and January 8, 2016, at 02:38 (hh:mm) UTC for ublox + Zephyr at bottom. Autocorrelation coefficients are also depicted for a ublox + patch zero-baseline setup in black color, on April 15, 2016, at 19:39 (hh:mm) UTC. Their corresponding 95% confidence intervals are depicted as dashed red lines

Full size image

Figure 4 shows that the precision gets poorer with increasing time lags since the autocorrelation function is then based on less data. We can also see time correlation estimates with a periodic behavior that differ significantly from zero for the short-baseline setups, which indicates that multipath might be present. The short-baseline patch antenna setup (top) experiences time correlation estimates that take several hundreds of seconds to reach about zero, with a reduction in time to reach zero when the Zephyr antenna is used (bottom). These decorrelaton times are similar to the phase-multipath time correlation results found in Ray and Cannon (1999), Miller et al. (2012) and Pesyna et al. (2014). However, the zero-baseline time correlation estimates in black color, without multipath, fall reasonably well within the 95% CI and quickly drop to about zero after a time lag of one second. This can also be seen in the zoom-in depicted in Fig. 5.

Fig. 5
figure 5

Autocorrelation coefficients for ublox L1 + B1 GPS + BDS instantaneous short-baseline ambiguity-fixed (left) and ambiguity-float (right) positioning errors based on 1 h (1 s). Day 1 is January 5, at 02:50 (hh:mm) UTC for patch in the top three rows and January 8, 2016, at 02:38 (hh:mm) UTC for Zephyr in bottom three rows. The corresponding autocorrelation coefficients for day-differenced, January 6–January 5 for patch and January 9–January 8 for Zephyr, and zero-baseline, ublox + patch at April 15 of 2016 at 19:39 (hh:mm) UTC, positioning are also shown. Their corresponding 95% confidence intervals are depicted as dashed red lines. A zoom-in is given for the first 300 and 30 s, respectively

Full size image

Time correlation when reducing multipath

We will now further compare the zero-baseline results, based on independent data, to the short baselines that were likely influenced by multipath effects (Fig. 4). We will attempt to reduce multipath for the short baselines by performing day differences on the estimated positions while taking into account the satellite repeatability period of approximately 23 h and 56 min, similar to the DD residuals used to compute the code and phase STDs in Table 1.

Figure 5 depicts the autocorrelation functions for instantaneous short-baseline ambiguity-fixed (left) and ambiguity-float (right) North/East/Up positioning, for the ublox + patch (top three rows) and ublox + Zephyr (bottom three rows) models based on 1 h (1 s) of data. The corresponding estimates based on ublox + patch zero-baseline data are depicted in black color. This is given together with the 95% confidence interval (CI) for the autocorrelation function. A zoom-in is used to depict the first five minutes (300 s) and 30 s only.

Figure 5 shows the overall larger time correlation estimates for the short-baseline patch antenna model over the 300 s in comparison with the Zephyr antenna. There is a relatively similar magnitude of time correlation estimates for the zero-baseline (black color) and the day-differenced short-baseline (cyan) positioning time series between the Zephyr and patch antenna (shown at bottom three rows), particularly after a time lag of about 10 s. The differences to the zero-baseline are, however, larger when the patch antenna model is used for the short baseline (top), which is likely due to larger magnitudes of residual multipath that remain in the day-differenced positioning solutions. Most importantly, the zero-baseline L1 + B1 phase-driven instantaneous ambiguity-fixed positioning shows time correlation estimates that drop down close to zero after a time lag of one second. The code-driven ambiguity-float positioning, however, shows time correlation coefficients for time lags up to a few seconds that exceed values of about 0.2 (c.f. Table 3). This can, for instance, be caused by receiver-related filtering to bring down the code observation noise level, see also Bona (2000) and Li et al. (2008, 2016).

Table 3 Time correlation estimates (\( \hat{\rho }_{\tau } \)) for different time lags τ = 0, …, 4 s of the day-differenced N/E/U ambiguity-float short-baseline (day-differenced) positioning for Trimble NetRS L1 + L2 GPS, and zero-baseline for the L1 + B1 GPS + BDS ublox receivers with patch antennas
Full size table

Table 3 summarizes the zero-baseline time correlation estimates for different time lags between τ = 0, …, 4 s, where the Trimble NetRS L1 + L2 GPS time correlation estimates are based on day-differenced short-baseline data. In support of Table 3, Fig. 6 shows the corresponding survey-grade Trimble NetRS receiver L1 + L2 GPS results. For both L1 and L2 code and phase, one can see that the time correlation drops down to close to zero after one second for the day-differenced positions, where multipath has been largely reduced.

Fig. 6
figure 6

Autocorrelation coefficients for Trimble NetRS + Zephyr L1 + L2 GPS instantaneous short-baseline ambiguity-fixed (left) and ambiguity-float (right) positioning errors, based 1 h (1 s). Day 1 is January 8, 2016, at 02:38 (hh:mm) UTC. The corresponding autocorrelation coefficients for day-differenced (January 9–January 8, 2016) positioning are also shown. Their corresponding 95% confidence intervals are depicted as dashed red lines. A zoom-in window is given for the first 300 and 30 s, respectively

Full size image

Low-cost RTK positioning

We are now in the position to test our (co)variances that were estimated by LS-VCE. For this purpose, we will use data that is independent of data used to estimate the STDs in Tables 1 and 2. The positioning stochastic models will be based on STDs estimated from 2 h (1 s) data for the Zephyr-antenna models, whereas for the patch antenna model a 24-h period is used so that any multipath effects are more likely to average out over time (Table 1). In the evaluations, we neglect the cross-correlation coefficients. To avoid the earlier-referenced receiver-induced time correlation, a 30-s measurement interval will also be used.

Positioning performance

The instantaneous RTK positioning results for 24 h data are shown in Fig. 7. The 95% empirical and formal confidence ellipse and interval are shown in green and red, respectively. They were computed from the empirical and formal position variance matrices. The empirical variance matrix was estimated from the positioning errors as obtained from comparing the estimated positions to precise benchmark coordinates. The formal variance matrix used is determined from the mean of all single-epoch formal variance matrices.

Fig. 7
figure 7

Few-meter baseline horizontal (N, E) position scatter and corresponding vertical (U) time series of the float (top) and correctly fixed (bottom) ublox L1 + B1 GPS + BDS single-epoch RTK solutions for an elevation cut-off angle of 10°. The 95% empirical and formal confidence ellipse and interval are shown in green and red, respectively. The 24-h (30 s) period is 22:00–22:00 UTC January 5–6 for patch in the left two columns and 21:48–21:48 (hh:mm) UTC January 8–9, 2016, for Zephyr in the right two columns, which are periods independent of the periods used to determine the stochastic model through the code/phase STDs in Table 2

Full size image

Figure 7 shows a good fit between the formal and empirical confidence ellipses and intervals, which thus illustrates realistic LS-VCE STDs in Table 2 that were used in the stochastic model. Note the improvement by two orders of magnitude when going from float to fixed solutions and that the ublox + Zephyr-antenna model has significantly more precise ambiguity-float positioning solutions in comparison with when patch antennas are used.

Ambiguity resolution and positioning performance for higher cut-off angles

We will investigate the low-cost L1 + B1 GPS + BDS positioning performance for high elevation cut-off angles to mimic situations in urban canyon environments or when low-elevation multipath is to be avoided. Comparisons will be made to the survey-grade Trimble NetRS L1 + L2 GPS receivers. In Teunissen et al. (2014) and Odolinski and Teunissen (2016), it was shown that a good ambiguity resolution performance does not necessarily imply a good positioning performance; hence, we will also investigate what effect this will have on our models at hand.

To investigate the ambiguity resolution performance, we consider the ambiguity success rates (SRs). We can make use of the SR formula of Teunissen (1998),

$$ P\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{{{\text{I}}B}} = z} \right] = \prod\limits_{i = 1}^{n} {\left[ {2\varPhi \left( {\frac{1}{{2\sigma_{{\hat{z}_{i|I} }} }}} \right) - 1} \right]} $$
(9)

where \( P\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{{{\text{I}}B}} = z} \right] \) denotes the probability of correct integer estimation of the integer bootstrapped (IB) estimator \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z}_{{{\text{I}}B}} \) and \( \sigma_{{\hat{z}_{i|I} }} \), i = 1, …, n, I = {1, …, (i − 1)}, denote the conditional STDs of the LAMBDA-decorrelated ambiguities. The bootstrapped SR (9) is easy to compute and is also a sharp lower bound of the integer least-squares (ILS) SR (Teunissen 1999).

Figure 8 depicts the single-epoch SRs of the two RTK models over two days of data. The SRs are computed based on epochs with the condition of positional dilution of precision (PDOP) ≤ 10 and averaged over all epochs. By including and excluding epochs with large PDOPs, we will show how the positioning performance of the different models is affected by poor receiver-satellite geometries. The results reveal that the L1 + B1 ublox + Zephyr (full black lines) has similar PDOP-conditioned formal ambiguity SRs for cut-off angles up to 25° when compared to the Trimble NetRS L1 + L2 GPS model (blue lines). The L1 + B1 ublox + patch model (dotted black lines) has also a similar performance to the two other models for a cut-off angle of 10°, whereas the performance gets worse with increasing cut-off angles.

Fig. 8
figure 8

Single-epoch bootstrapped (BS) success rate (SR) for L1 + L2 GPS and L1 + B1 GPS + BDS, as function of the elevation cut-off angle. The results are based on data in January 4–6 and January 6–8, 2016, for the patch and Zephyr-antenna models, respectively. The BS SRs are taken as a mean of all single-epoch SRs over two days, and conditioned on PDOP ≤ 10

Full size image

The formal results in Fig. 8 are very promising. Hence in the next step, we will investigate the corresponding empirical performance of the different models. To better understand how this exclusion of epochs with large PDOPs influences the empirical ambiguity-fixed and ambiguity-float positioning performance, Table 4 shows the corresponding positioning STDs for two days of data. These STDs were computed by comparing the estimated positions to very precise benchmarks. In addition to the positioning performance, we depict in Table 4 the corresponding empirical ILS SRs for full ambiguity resolution, which is given by,

$$ P_{{s_{E} }} = \frac{{\# {\text{of correctly fixed epochs}}}}{{{\text{total }}\# {\text{of epochs}}}} $$
(10)
Table 4 Single-epoch empirical STDs (N, E, U) of correctly ambiguity-fixed positions for Trimble NetRS L1 + L2 GPS, L1 + B1 ublox + Zephyr and ublox + patch, respectively, together with their ILS SR, for 20°–35° elevation cut-off and 48 h of data in January 4–6 and January 6–8, 2016, respectively
Full size table

In addition and within parentheses, the corresponding bootstrapped SRs are given.

Table 4 shows that all PDOP-conditioned ILS SRs are consistent with the BS SRs, which again shows that the STDs in Table 2 used for the stochastic models are realistic. It also shows that the L1 + B1 ublox + patch model has, as expected, smaller SRs in comparison with when the survey-grade Zephyr antenna is used. Moreover, this latter ublox + Zephyr model has comparable SRs to the PDOP-conditioned SRs of the Trimble NetRS L1 + L2 GPS model for cut-off angles up to 25°, similar to what we showed in the previous formal analysis (Fig. 8).

In support of a better understanding Table 4, Figs. 9 and 10 show typical positioning examples of the different models for an elevation cut-off angle of 10° and 25°, respectively. The first row shows the local horizontal (N, E) positioning scatterplots and the second row the vertical (U) time series over two days of data. The float solutions are depicted in gray and incorrectly and correctly fixed solutions in red and green, respectively. The zoomed-in is given to better show the spread of the correctly fixed solutions with millimeter-centimeter-level precisions. The formal ambiguity-float STDs are also shown under the Up time series as to reflect consistency between the empirical and formal positioning results. In addition, we depict in Fig. 9 the ambiguity dilution of precision (ADOP) as introduced by Teunissen (1997), as an easy-to-compute scalar diagnostic to measure the intrinsic model strength for successful ambiguity resolution. The ADOP is defined as

$$ {\text{ADOP}} = \sqrt {\left| {Q_{{\hat{a}\hat{a}}} } \right|}^{{\frac{1}{n}}} \quad ({\text{cycle}}) $$
(11)

with n the dimension of the ambiguity vector, \( Q_{{\hat{a}\hat{a}}} \) is the ambiguity variance matrix, and |·| denotes the determinant. ADOP gives a good approximation to the average precision of the ambiguities, and it also provides for a good approximation to the ILS SR (Verhagen 2005). The rule of thumb is that an ADOP smaller than about 0.12 cycles corresponds to an ambiguity SR larger than 99.9% (Odijk and Teunissen 2008).

Fig. 9
figure 9

Few-meter baseline horizontal (N, E) scatterplots and vertical (U) time series for L1 + B1 ublox + patch (first column) with 99.5% ILS SR, L1 + B1 ublox + Zephyr (second column) with 100% ILS SR, and Trimble L1 + L2 GPS (third column) with 100% ILS SR, using 10° cut-off. The results are based on data in January 4–6 for ublox + patch and January 7–8, 2016, for ublox/Trimble + Zephyr. The SRs are conditioned on PDOP ≤ 10 and computed based on all epochs. The correctly fixed solutions are depicted in green, incorrectly fixed in red, and ambiguity float in gray. Below the vertical time series, the ADOP is depicted in blue color and the 0.12 cycles level as red, and ambiguity-float Up formal STDs are shown in gray

Full size image
Fig. 10
figure 10

Few-meter baseline horizontal (N, E) scatterplots and vertical (U) time series for L1 + B1 ublox + patch (first column) with 89.8% ILS SR, L1 + B1 ublox + Zephyr (second column) with 97.8% ILS SR, and Trimble L1 + L2 GPS (third column) with 94.1% ILS SR, using 25° cut-off. The results are based on data in January 4–6 for ublox + patch and January 7–8, 2016, for ublox/Trimble + Zephyr. The SRs are conditioned on PDOP ≤ 10 and computed based on all epochs. The correctly fixed solutions are depicted in green, incorrectly fixed in red, and ambiguity float in gray. Below the vertical time series, the ADOP is depicted in blue color and the 0.12 cycles level as red, and ambiguity-float Up formal STDs are shown in gray

Full size image

Figures 9 and 10 reveal that more solutions are likely to be incorrectly fixed (red dots) when the ADOPs (blue lines) are larger than the 0.12 cycle level (red dashed lines). Figure 9 also shows that the L1 + B1 ublox + patch model achieves an ILS SR similar to that of the survey-grade L1 + L2 GPS model for the cut-off angle of 10°. The SR is namely 99.5% for the L1 + B1 ublox + patch model and 100% for the L1 + L2 GPS model. This ILS SR corresponds to the availability of correctly fixed solutions (green dots) with millimeter- to centimeter-level positioning precision over the two days.

Figure 10 shows that the L1 + B1 ublox patch antenna model has some instances with significantly different ADOPs in comparison with the corresponding Zephyr-antenna model for the cut-off angle of 25°, for example just before epochs 1440 and 4320, respectively. This is mainly because the two models are based on different days of data where the BDS MEO satellite constellation does not repeat each day, and thus, the patch antenna model has a smaller number of satellites for some epochs that result in larger ADOPs. The L1 + L2 GPS model has, moreover, large ambiguity-fixed positioning excursions at the same time as the formal STDs are large for the cut-off angle of 25°, due the poor GPS-only receiver-satellite geometry for this high cut-off angle. This is also reflected by the corresponding relatively large ambiguity-fixed STDs depicted in Table 4 that are improved from decimeter to millimeter level when the PDOP ≤ 10 condition is applied. Finally, Fig. 10 shows that L1 + B1 ublox + Zephyr has a larger SR of 97.8% when compared to the PDOP-conditioned SR for L1 + L2 GPS of 94.1% for the cut-off angle of 25° (Table 4), owing to the use of BDS that improves the receiver-satellite geometry.

Low-cost RTK positioning for a 7-km baseline

So far we have considered baseline lengths of a few meters only. One might wonder whether the low-cost L1 + B1 GPS + BDS ublox RTK solution would perform similarly well for baselines where small residual ionospheric delays are present. Hence in the following, we analyze the RTK positioning performance for a 7-km baseline in Dunedin for 24 h (30 s) during January 18–19, 2016 (Fig. 1). The Australian Space Forecast Centre (http://www.sws.bom.gov.au/Geophysical/2/1) warned for an increased geomagnetic disturbance during this period, which implies that residual ionospheric delays can indeed be present. We make use of the same stochastic model settings as in the previous section (Table 2), which is based on an independent baseline.

To deal with any residual ionospheric delays, we also add to our model (1) a vector with slant ionosphere pseudo-observations \( \iota = [\iota_{G}^{T} ,\iota_{B}^{T} ]^{T} \in {\mathbb{R}}^{{s_{G} + s_{B} }} \) and parameterize the ionospheric delays. The inclusions of these pseudo-observables can provide us with stochastic information of the ionospheric delays between stations, which is also referred to as the “ionosphere-weighted” model. The stochastic model settings of these observables are set by following the rule of thumb by Schaffrin and Bock (1988), where the double-differenced (DD) slant ionospheric delay zenith-referenced STD can be modeled as a function of the baseline length as 1.4 mm/km. For a baseline length of 7 km, this corresponds to a DD STD of almost 10 mm.

As to verify whether slant ionospheric delays are indeed present, we depict in Fig. 11 the DD slant ionospheric delays with the ionosphere-weighted stochastic model settings mentioned above, while making use of a L1 + B1 ublox + Zephyr geometry-fixed and ambiguity-fixed model. The DD slant ionospheric delays are shown for all satellites (GPS + BDS) with an elevation cut-off angle of 20°, as to avoid any low-elevation multipath on our estimates. At top of Fig. 11, the few-meter baseline setup is shown to illustrate the situation when ionospheric delays are not present, whereas at bottom the corresponding 7-km baseline results are depicted.

Fig. 11
figure 11

DD ambiguity-fixed slant ionospheric delays using L1 + B1 GPS + BDS ublox + Zephyr for a few-meter baseline (top) on January 7 and 7-km baseline (bottom) on January 18, 2016, for an elevation cut-off angle of 20°. The ionosphere-weighted model has been used with the DD slant ionospheric delay zenith-referenced STD set to approximately 10 mm for both models

Full size image

Figure 11 shows, as expected, that the magnitudes of the slant ionospheric delays for the few-meter baseline resemble that of the phase noise precision (Fig. 3). The 7-km baseline, however, shows significantly larger magnitudes of the slant ionospheric delays that exceeds the phase noise precision, which indicates that the slant ionospheric delays should indeed be modeled.

To investigate whether the stochastic model settings as determined from a few-meter baseline is also applicable to the 7-km baseline, we show in Fig. 12 the corresponding instantaneous RTK positioning results for ublox + Zephyr L1 + B1 GPS + BDS and Trimble NetRS + Zephyr L1 + L2 GPS, while making use of an elevation cut-off angle of 10°. There is a good fit between the formal and empirical positioning confidence ellipses and intervals, which thus again illustrates realistic LS-VCE STDs in Table 2 that were used in the stochastic model. This in addition to the STD used for the DD slant ionosphere pseudo-observations.

Fig. 12
figure 12

Seven-kilometer baseline horizontal (N, E) position scatter and corresponding vertical (U) time series of the float (top) and correctly fixed (bottom) ublox L1 + B1 GPS + BDS (left two columns) and Trimble L1 + L2 GPS (right two columns) single-epoch RTK solutions for an elevation cut-off angle of 10°. The 95% empirical and formal confidence ellipse and interval is shown in green and red, respectively. The 24-h (30 s) period is 23:00–23:00 UTC January 18–19, 2016, where the baseline is independent of the few-meter baseline used to determine the stochastic model through the code/phase STDs in Table 2

Full size image

Figure 13 depicts the corresponding float and incorrectly and correctly fixed positioning solutions at top, respectively, together with the ADOPs and ambiguity-float Up formal STDs at the bottom. The figure reveals that the L1 + B1 GPS + BDS model has some instances around and after epoch 720 when the ADOP (blue color) is relatively large which consequently yields incorrectly fixed solutions (red). The instantaneous ILS SR for the L1 + B1 ublox + Zephyr model is 97%, whereas the corresponding ILS SR for the Trimble NetRS L1 + L2 model is 99.8%. We have thus illustrated that the low-cost receiver solution still has the potential to perform very well even for a baseline length of 7 km, where small residual ionospheric delays are present.

Fig. 13
figure 13

Seven-kilometer baseline horizontal (N, E) scatterplots and vertical (U) time series for L1 + B1 ublox + Zephyr (first column) with 97.0% ILS SR, and Trimble L1 + L2 GPS (second column) with 99.8% ILS SR, using 10° cut-off during January 18–19, 2016. The correctly fixed solutions are depicted in green, incorrectly fixed in red, and ambiguity float in gray. Below the vertical time series, the ADOP is depicted in blue color and the 0.12 cycles level as red, and ambiguity-float Up formal STDs are shown in gray

Full size image

Conclusions

We evaluated a low-cost ublox L1 + B1 GPS + BDS RTK model and compared its ambiguity resolution and positioning performance to a survey-grade receiver L1 + L2 GPS solution, in Dunedin, New Zealand. The least-squares variance component estimation (LS-VCE) procedure was initially used to determine the (co)variances of the low-cost receivers. The estimated (co)variances are needed so as to formulate a realistic stochastic model. Otherwise, the ambiguity resolution performance and hence the achievable positioning precisions would deteriorate. For the same reasons, we also investigated the presence of receiver-induced time correlation. Since we analyzed a short baseline, the LS-VCE and time correlation estimates were shown to likely be affected by multipath. To mitigate multipath, we connected the low-cost receivers to survey-grade antennas and compared the performance to a zero-baseline setup.

It was shown that the survey-grade antennas can significantly improve the performance for the low-cost receivers so that the code and phase noise estimates more resemble that of survey-grade receivers. The cross-correlations between GPS L1 code and phase and BDS B1 code and phase were all shown to be close to zero for the low-cost receivers at hand, whereas significant cross-correlation was present for the L1 and L2 phase observables of the survey-grade receivers. The receiver-induced time correlation was also shown to be close to zero for phase in both receiver types, whereas some time correlation existed for the code observables in the low-cost receivers. The LS-VCE STDs were shown to be realistically estimated for both an independent period and baseline. We also demonstrated that the low-cost receivers, which cost a few hundred USDs, can give competitive instantaneous ambiguity resolution and positioning performance to the survey-grade receivers, which cost several thousand USDs. This was shown both formally and empirically and is particularly true when the low-cost receivers are connected to survey-grade antennas. It was finally shown that the low-cost receiver solution with survey-grade antennas still has the potential to achieve competitive ambiguity resolution and positioning performance to the survey-grade receiver solution for a baseline length of 7 km, where small residual slant ionospheric delays are present.