Single-frequency, dual-GNSS versus dual-frequency, single-GNSS: a low-cost and high-grade receivers GPS-BDS RTK analysis

Abstract

The concept of single-frequency, dual-system (SF-DS) real-time kinematic (RTK) positioning has become feasible since, for instance, the Chinese BeiDou Navigation Satellite System (BDS) has become operational in the Asia-Pacific region. The goal of the present contribution is to investigate the single-epoch RTK performance of such a dual-system and compare it to a dual-frequency, single-system (DF-SS). As the SF-DS we investigate the L1 GPS + B1 BDS model, and for DF-SS we take L1, L2 GPS and B1, B2 BDS, respectively. Two different locations in the Asia-Pacific region are analysed with varying visibility of the BDS constellation, namely Perth in Australia and Dunedin in New Zealand. To emphasize the benefits of such a model we also look into using low-cost ublox single-frequency receivers and compare such SF-DS RTK performance to that of a DF-SS, based on much more expensive survey-grade receivers. In this contribution a formal and empirical analysis is given. It will be shown that with the SF-DS higher elevation cut-off angles than the conventional $10^{\circ }$ or $15^{\circ }$ can be used. The experiment with low-cost receivers for the SF-DS reveals (for the first time) that it has the potential to achieve comparable ambiguity resolution performance to that of a DF-SS (L1, L2 GPS), based on the survey-grade receivers.

1 Introduction

Global Navigation Satellite Systems (GNSSs) can provide for precise millimetre to centimetre level positioning provided that the phase ambiguities are determined to their correct integer number of cycles. This is also referred to as real-time kinematic (RTK). The Chinese BeiDou Navigation Satellite System (BDS) attained its initial regional operational status in 2011. Making use of BDS can give double the number of visible satellites when combined with the US-American Global Positioning System (GPS) in the Asia-Pacific region. The global BDS constellation is expected to be operational in 2020 and will consist of five Geostationary Earth Orbit (GEO), three Inclined Geo-Synchronous Orbit (IGSO) and 27 Medium Earth Orbit (MEO) satellites (CSNO 2013).

Some first simulation positioning results using BDS can be found in Grelier et al. (2007), Chen et al. (2009), Yang et al. (2011), Verhagen and Teunissen (2014). The BDS ambiguity resolution performance was investigated by simulation in Cao et al. (2008), and some real data results were presented in Shi et al. (2012, (2013), Li et al. (2013b) on BDS single point positioning, orbit determination and GPS + BDS Precise Point Positioning (PPP). Some GPS + BDS RTK results can be found in Li et al. (2013a), He et al. (2014), Deng et al. (2014). First results using BDS outside of China are reported in Montenbruck et al. (2013), Steigenberger et al. (2013), Nadarajah et al. (2013) and combined GPS + BDS RTK in Odolinski et al. (2014b, (2015b), Teunissen et al. (2014).

In Teunissen et al. (2014) the single-frequency dual-system (SF-DS) GPS + BDS model in Perth was shown to achieve better RTK positioning performance than a dual-frequency single-system (DF-SS), provided that higher than customary elevation cut-off angles were used. Therefore, in this contribution we will further explore the capabilities of such a SF-DS both in Perth (Australia) and Dunedin (New Zealand), respectively. The SF-DS we will focus on is L1 GPS + B1 BDS and its performance will be compared to that of DF-SS, L1, L2 GPS and B1, B2 BDS, respectively. Some comparisons to the single-frequency single-systems (SF-SSs) and dual-frequency dual-system (DF-DS) will also be made. See Table 1 for all the single-baseline RTK models that will be analysed.

Table 1 Single-baseline RTK models that will be analysed

The Dunedin location is chosen since it is of interest to see what BDS can bring in New Zealand despite the smaller number of visible regional BDS satellites in comparison to Perth. As a proof-of-concept we will also investigate the SF-DS (L1 + B1) when making use of low-cost ublox single-frequency receivers and compare the performance to that of a DF-SS (L1, L2 GPS) based on much more expensive survey-grade receivers. Other studies on ambiguity resolution and RTK positioning using low-cost receivers and antennas can be found in, e.g., Takasu and Yasuda (2009), Wisniewski et al. (2013), Pesyna et al. (2014). Our analyses will furthermore focus on the single-epoch model with the added advantage that it will become insensitive to cycle-slips.

Fig. 1

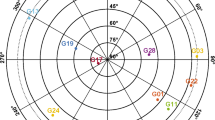
BDS ground tracks with satellite locations (dots) (May 14, 2015, UTC 08:00 a.m.); Number ($\#$) of GPS, BDS and GPS + BDS satellites that can be tracked with $10^{\circ }$ cut-off elevation angle in a Perth (May 14, 2015) and b Dunedin (September 11, 2015). Note that fewer BDS satellites can be tracked in Dunedin

This contribution is organized as follows: In Sect. 2 we describe the GPS + BDS visibility in the Asia-Pacific region, followed by Sect. 3 where the combined GPS + BDS model is given. Section 4 introduces the formal analysis of the SF-DS and DF-SS. It provides for comparisons of Ambiguity Dilution of Precisions (ADOPs), integer bootstrapped (IB) success rates and positioning precisions. This analysis is based on elevation cut-off angles ranging from $10^{\circ }$ to $40^{\circ }$. Making use of high cut-off angles can be of benefit in urban-canyons or when low-elevation multipath is present. It will be demonstrated that good ambiguity resolution performance does not always indicate a good positioning performance. Section 5 introduces the empirical results to verify the formal claims using high-grade receivers. This analysis is based on empirically determined success rates and positioning precisions. In Sect. 6 we conduct an experiment of the SF-DS with low-cost ublox receivers, with comparisons to the DF-SS based on the more expensive high-grade receivers. It will be shown that the low-cost SF-DS has the potential to achieve similar ambiguity resolution performance to that of a DF-SS. Summary and conclusions are given in Sect. 7.

2 GPS + BDS in the Asia-Pacific region

The American GPS consists of 32 MEO satellites available for positioning. The Chinese regional BDS consists of five GEO, five IGSO and four MEO satellites. In Fig. 1 the 24-h ground tracks are depicted of the current regional BDS satellites available for positioning as of May 14, 2015. The positions of the satellites are given at UTC 08:00 am and are indicated with dots. The full global BDS constellation is expected to consist of 35 satellites being 5 GEO, 3 IGSO and 27 MEO satellites (CSNO 2013).

The regional BDS satellites transmit on B1, B2 and B3 and GPS on the L1, L2 and L5 frequencies, as shown in Table 2. The BDS signals are based on the Code Division Multiple Access (CDMA) technique similar to GPS, European Galileo, Indian Regional Navigation Satellite System (IRNSS) and the Japanese Quasi-Zenith Satellite System (QZSS). In this contribution we compare the SF-DS (L1 + B1) RTK performance with that of a DF-SS, namely L1, L2 GPS and B1, B2 BDS, respectively. This since, as of December 2015, only eleven Block IIF GPS satellites have been launched with the L5 signal that has a more precise code observable in comparison to the L1 and L2 signals (Nadarajah et al. 2015). Four modernized global BDS satellites have also been launched since March 2015 that transmit a L1 frequency similar to the one of GPS (GPS World 2015), which allows for inter-system bias calibration to further strengthen the underlying RTK model (Odijk and Teunissen 2013; Odolinski et al. 2014a, 2015a; Paziewski et al. 2015; Paziewski and Wielgosz 2015). This implies that in the double-differencing (DD) functional model to be presented, one common reference satellite between the systems could have been taken. In this contribution, however, we will focus on the integration of the current regional BDS constellation (Fig. 1) with GPS, since the model can still give around double the number of GPS satellites in the Asia-Pacific region.

Table 2 GPS and regional BDS frequencies

For the current BDS situation (Fig. 1), we have chosen Perth (Australia) and Dunedin (New Zealand) as tracking stations for our evaluations. This since Perth has a close to optimal location with respect to the regional BDS, whereas Dunedin has a challenging location since it is close to the boundary of the regional BDS system. The figure also shows the time-series of the number of GPS (blue) and BDS (magenta) satellites that can be tracked in Perth (Fig. 1a) and Dunedin (Fig. 1b), respectively, for an elevation cut-off angle of $10^{\circ }$.

Figure 1 shows that the number of satellites for a combined GPS + BDS model (black) becomes overall double to the number of GPS satellites in Perth and that in Dunedin fewer BDS satellites can be tracked. The Dunedin station can only track three out of five GEOs (C01, C03, C04) and a smaller part of the tracks of the five IGSO satellites when compared to Perth. Thus the RTK performance improvement, when including the regional BDS system, is expected to be less significant in Dunedin as compared to Perth.

3 SF-DS model vs DF-SS model

In this section we compare the SF-DS model with the DF-SS model.

3.1 The two GNSS models

As both models, SF-DS and DF-SS, can be considered special cases of the more general multi-frequency combined GNSS model, we first describe this latter model. Therefore, assume that $s_{G}+1$ GPS satellites are tracked on $f_{G}$ frequencies and $s_{B}+1$ BDS satellites on $f_{B}$ frequencies. As we apply system-specific double-differencing (DD), we have one reference (or pivot) satellite per system. The total number of DD phase and code observations per epoch equals, therefore, $2f_{G}s_{G} + 2f_{B}s_{B}$. We assume that cross-correlation between code and phase, and between frequencies, is absent. Following (Teunissen et al. 2014), the combined multi-frequency short-baseline GPS + BDS model is then defined as follows:

Definition

(Combined multi-frequency GPS + BDS model) Let the system-specific DD phase and code observation vectors be denoted as $\phi _{*}$ and $p_{*}$, respectively, with $*=\{G, B\}$ $(G=\mathrm{GPS}, B=\mathrm{BDS})$. Then the single-epoch linear(ized) GNSS model of the combined system is given as

$$\begin{aligned} E \left[ \begin{array}{lll} \phi \\ p \end{array} \right] = \left[ \begin{array}{l@{\quad }l} \varLambda &{} A \\ 0 &{} A \end{array} \right] \left[ \begin{array}{l} a \\ b \end{array} \right] ,\quad D \left[ \begin{array}{l} \phi \\ p \end{array} \right] = \left[ \begin{array}{l@{\quad }l} Q_{\phi \phi } &{} 0 \\ 0 &{} Q_{pp} \end{array} \right] \end{aligned}$$

(1)

in which $E [.]$ and $D [.]$ denote the expectation and dispersion operator, respectively, $\phi =[\phi _{G}^{\mathrm{T}}, \phi _{B}^{\mathrm{T}}]^{\mathrm{T}} \in \mathbb {R}^{f_{G}s_{G}+f_{B}s_{B}}$ the combined phase vector, $p=[p_{G}^{\mathrm{T}}, p_{B}^{\mathrm{T}}]^{\mathrm{T}} \in \mathbb {R}^{f_{G}s_{G}+f_{B}s_{B}}$ the combined code vector, $a=[a_{G}^{\mathrm{T}}, a_{B}^{\mathrm{T}}]^{\mathrm{T}} \in \mathbb {Z}^{f_{G}s_{G}+f_{B}s_{B}}$ the combined integer ambiguity vector, $b \in \mathbb {R}^{\nu }$ the real-valued baseline vector and with the entries of the design matrix given as

$$\begin{aligned} \varLambda= & {} \mathrm{blkdiag}[\varLambda _{G}, \varLambda _{B}],\quad \varLambda _{*}=\mathrm{diag}[\lambda _{1_{*}}, \ldots , \lambda _{f_{*}}] \otimes I_{s_{*}}\\ A= & {} [A_{G}^{\mathrm{T}}, A_{B}^{\mathrm{T}}]^{\mathrm{T}},\quad A_{*}=[e_{f_{*}} \otimes D_{s_{*}}^{\mathrm{T}}G_{*}], \end{aligned}$$

where $I_{s_{*}}$ is the $s_{*} \times s_{*}$ unit matrix, $e_{f_{*}}$ is the $f_{*} \times 1$ vector of 1’s and $D_{s_{*}}^{\mathrm{T}}=[-e_{s_{*}}, I_{s_{*}}]$ is the $s_{*} \times (s_{*}+1)$ differencing matrix and with the entries of the positive definite variance matrix given as

$$\begin{aligned}&Q_{\phi \phi } = \mathrm{blkdiag}[Q_{\phi _{G}\phi _{G}}, Q_{\phi _{B}\phi _{B}}],\quad Q_{\phi _{*}\phi _{*}}= C_{\phi _{*}\phi _{*}} \otimes 2 Q_{*}\\&Q_{pp} = \mathrm{blkdiag}[Q_{p_{G}p_{G}}, Q_{p_{B}p_{B}}], \quad Q_{p_{*}p_{*}}= C_{p_{*}p_{*}} \otimes 2 Q_{*}\\&C_{\phi _{*}\phi _{*}} = \mathrm{diag}[\sigma _{\phi _{1_{*}}}^{2}, \ldots , \sigma _{\phi _{f_{*}}}^{2}],\quad C_{p_{*}p_{*}} = \mathrm{diag}[\sigma _{p_{1_{*}}}^{2}, \ldots , \sigma _{p_{f_{*}}}^{2}] \\&Q_{*}=D_{s_{*}}^{\mathrm{T}}W_{*}^{-1}D_{s_{*}},\quad W_{*}=\mathrm{diag}[w_{1_{*}}, \ldots , w_{s_{*}+1}], \end{aligned}$$

where $w_{i_{*}}$ denotes the satellite elevation-dependent weight. $\diamondsuit$

In the above definition, $\otimes$ denotes the Kronecker product. The diagonal matrix $\varLambda$ contains the wavelengths of the observed frequencies and the geometry-matrices $G_{G}$ and $G_{B}$ contain the undifferenced receiver-satellite unit direction vectors for GPS and BDS, respectively. As the above model applies to short baselines, the ionospheric delays are assumed absent (Goad 1998). The zenith tropospheric delay (ZTD), however, may be present. If it is included, then $\nu =4$ instead of 3, and $G_{G}$ and $G_{B}$ will have a fourth column containing the ZTD mapping functions.

From the above general formulation, we obtain our two specific models by using the following settings:

$$\begin{aligned} \begin{array}{lllll} \text {SF-DS}: &{} f_{G}=1, &{}f_{B}=1 &{} \;\;\; (\mathrm{GPS}+\mathrm{BDS})\\ \text {DF-SS}: &{} f_{G}=2, &{}f_{B}=0 &{}\;\;\; (\mathrm{GPS})\\ \text {DF-SS}: &{} f_{G}=0, &{}f_{B}=2 &{}\;\;\;(\mathrm{BDS}) \end{array} \end{aligned}$$

(2)

3.2 Redundancy and availability

The design matrix of (1) is assumed to be of full column rank. Its redundancy is then equal to the number of DD observables minus the number of unknowns. For the multi-frequency combined system this results in a redundancy of $s_{G}f_{G}+s_{B}f_{B} - \nu$. It is the sum of the redundancies of the single systems plus $\nu$, the number of parameters the two systems have in common. Hence, the redundancy increases by $s_{*}f_{*}$ if one goes from a single system to a combined system. For our specific two type of models the redundancy thus works out as follows:

$$\begin{aligned} \begin{array}{lll} \text {SF-DS}:&{} \mathrm{redundancy}= s_{G}+s_{B} - \nu &{}\quad (\mathrm{GPS}+\mathrm{BDS})\\ \text {DF-SS}:&{} \mathrm{redundancy}= 2s_{G} - \nu &{}\quad (\mathrm{GPS})\\ \text {DF-SS}:&{} \mathrm{redundancy}= 2s_{B} - \nu &{}\quad (\mathrm{BDS}) \end{array} \end{aligned}$$

(3)

The redundancy time series for Perth and Dunedin are shown in Fig. 2. It compares the redundancies for L1 + L2, B1 + B2 and L1 + B1. In Fig. 2 top, the redundancies are shown using a $10^{\circ }$ elevation cut-off angle, while in Fig. 2 middle they are shown for $40^{\circ }$ (Perth) and $30^{\circ }$ (Dunedin). These latter cut-off values are the largest values for which one still has $100~\%$ GPS + BDS positioning availability in Perth and Dunedin, respectively. The redundancy decreases of course when higher cut-off elevations are chosen.

Fig. 2

Redundancy (L1 + L2, B1 + B2, L1 + B1) and availability at Perth (AU) (May 14, 2015) and Dunedin (NZ) (September 11, 2015). a Redundancy: Perth (left) and Dunedin (right) for $10^{\circ }$ elevation cut-off angle. b Redundancy: Perth (left) for $40^{\circ }$ and Dunedin (right) for $30^{\circ }$ elevation cut-off angle respectively. c Availability: Perth (left) for $40^{\circ }$ and Dunedin (right) for $30^{\circ }$ elevation cut-off angle respectively

For Perth, the SF-DS model shows a comparable redundancy to that of the two DF-SSs. This can be explained by the fact that the combined model overall doubles the number of satellites for Perth (see Fig. 1). In case of Dunedin, however, the SF-DS model shows a somewhat larger redundancy than the DF-SS (BDS) model. This is due to the fact that fewer BDS satellites can be tracked in Dunedin (see Fig. 1).

Next to the redundancy, we consider the solvability condition for the two types of models:

$$\begin{aligned} \begin{array}{lll} \text {SF-DS}:&{} \mathrm{solvability}= s_{G}+s_{B} \ge \nu &{}\quad (\mathrm{GPS}+\mathrm{BDS})\\ \text {DF-SS}:&{} \mathrm{solvability}= s_{G} \ge \nu &{}\quad (\mathrm{GPS})\\ \text {DF-SS}:&{} \mathrm{solvability}= s_{B} \ge \nu &{}\quad (\mathrm{BDS}) \end{array} \end{aligned}$$

(4)

Equation (4) demonstrates the increase in availability that a combination of the two systems brings. For a single system, the system is only solvable if $s_{*} \ge \nu$ (at least four satellites are needed if $\nu =3$). For the combined system, however, this single-system condition can be relaxed as now also the satellites of the second system contribute. Instead of a minimum of four satellites when $\nu =3$, the combined system only requires the total number of satellites to be not smaller than five. Hence, where three GPS satellites ($s_{G}=2$) and three BDS satellites ($s_{B}=2$) would not be sufficient for single-system solvability when $\nu =3$, it does suffice for the combined case.

Table 3 Zenith-referenced undifferenced code and phase STDs for Perth (Dunedin within brackets) for $j_{*}=1_{*},\ldots ,f_{*}$

Figure 2 bottom shows the availability over Perth and Dunedin for $40^{\circ }$ and $30^{\circ }$ cut-off angles, respectively. Note that although the BDS-availability is rather poor over Dunedin (only $37~\%$), one can still benefit significantly from the BDS presence. By combining BDS with GPS, the $89~\%$ GPS-only availability is increased to an L1 + B1 availability of $100~\%$ for up to a high cut-off elevation angle of $30^{\circ }$.

Fig. 3

$P_\mathrm{ADOP}$ vs ADOP for varying number of DD ambiguities n

In the next sections we show, first formally and then empirically, how in case of GPS and BDS, the RTK performance of the SF-DS model compares to that of the DF-SS model. For our numerical and empirical analyses, the weights $w_{i_{*}}$ are taken as the elevation-dependent function of Euler and Goad (1991). For the zenith-referenced undifferenced phase- and code standard deviations, $\sigma _{\phi _{j_{*}}}$ and $\sigma _{p_{j_{*}}}$ ($j_{*}=1_{*}, \ldots , f_{*}$), we use the values of Table 3. They were estimated using data that are independent from the data used in the following sections. The method of estimation is described in Odolinski et al. (2013). Furthermore we have taken $\nu =3$.

4 Ambiguity resolution and positioning: a formal analysis

4.1 ADOP-theory

The Ambiguity Dilution of Precision (ADOP) was introduced in Teunissen (1997a, (1997b, (1997c, (1997d) as an easy-to-compute scalar diagnostic to measure the intrinsic model strength for successful ambiguity resolution. The ADOP is defined as

$$\begin{aligned} \mathrm{ADOP}= \sqrt{|Q_{\hat{a}\hat{a}}|}^{\frac{1}{n}}\quad (\mathrm{cycle}), \end{aligned}$$

(5)

with n being the dimension of the ambiguity vector, $Q_{\hat{a}\hat{a}}$ is the ambiguity variance matrix and |.| denotes the determinant. The ADOP has several important properties. First, it is invariant against the choice of ambiguity parametrization. Since all admissible ambiguity transformations can be shown to have a determinant of one, the ADOP does not change when one changes the definition of the ambiguities. Second, it is also a measure of the volume of the ambiguity confidence ellipsoid (Teunissen et al. 1996). And third, the ADOP equals the geometric mean of the standard deviations of the ambiguities, in case the ambiguities are completely decorrelated. This follows from $|Q_{\hat{a}\hat{a}}| = \prod _{i=1}^{n} \sigma _{\hat{a}_{i}}^{2}|R_{\hat{a}\hat{a}}|$, with $\sigma _{\hat{a}_{i}}$ the ambiguity standard deviation and $R_{\hat{a}\hat{a}}$ the ambiguity correlation matrix. Since the LAMBDA method (Teunissen 1995) produces ambiguities that are largely decorrelated, the ADOP approximates the average precision of the transformed ambiguities. Since the ADOP gives a good approximation to the average precision of the ambiguities, it also provides for a good approximation to the integer least-squares (ILS) ambiguity success rate (Verhagen 2005; Ji et al. 2007). We, therefore, have the following approximation:

$$\begin{aligned} P(\check{a}_\mathrm{LS} =a) = P(\check{z}_\mathrm{LS} =z)\approx \underbrace{\left[ 2\varPhi \left( \frac{1}{2 \mathrm ADOP} \right) -1 \right] ^{n}}_{P_\mathrm{ADOP}} \end{aligned}$$

(6)

in which $\check{a}_\mathrm{LS}$ and $\check{z}_\mathrm{LS}$ are the ILS ambiguity estimators of the original and transformed ambiguities, respectively, and where $\varPhi (\cdot )$ is the standard normal cumulative distribution function.

Figure 3 shows $P_\mathrm{ADOP}$ as a function of ADOP for varying levels of n. It can be seen that the ADOP-based success rate decreases for increasing ADOP and this decrease is steeper the more ambiguities are involved. In general, Fig. 3 shows that if ADOP is smaller than about 0.12 cycles, $P_\mathrm{ADOP}$ becomes larger than 0.999, while for ADOP smaller than 0.14 cycles, $P_\mathrm{ADOP}$ is always better than 0.99. In the following we will use as a rule-of-thumb that an ADOP smaller than about 0.12 cycle corresponds to an ambiguity success-rate larger than 0.999.

4.2 From single-frequency to dual-frequency system

We now show analytically how the ADOP changes when one goes from a single-frequency system to a dual-frequency system. The single-system ADOP can be obtained from Odijk and Teunissen (2008) as

$$\begin{aligned} \text {ADOP}_{\mathrm{SF}\text {-}\mathrm{SS}}= w \left[ \frac{\sigma _{\phi }}{\lambda }\right] \left[ 1+\frac{1}{\varepsilon ^{2}}\right] ^{\frac{v}{2s}} \approx w \left[ \frac{\sigma _{\phi }}{\lambda }\right] \left[ \frac{\sigma _{p}}{\sigma _{\phi }}\right] ^{\frac{v}{s}} \end{aligned}$$

(7)

with the small phase-code variance ratio $\varepsilon ^{2}= (\sigma _{\phi }/\sigma _{p})^{2}$ (${\approx } 10^{-4})$ and the satellite-elevation weighting factor $w=\sqrt{2}[\sum _{i=1}^{s+1}w_{i}/\prod _{i=1}^{s+1}w_{i}]^{\frac{1}{2s}}$. This result shows that the ADOP is dominated by the relatively poor code precision in case redundancy is absent, i.e. when $s=v$. Only in the presence of redundancy ($s>v$) will the very precise phase measurements start contributing in bringing the ADOP down to lower values.

From (ibid) we obtain the DF-SS ADOP as

$$\begin{aligned} \text {ADOP}_{\mathrm{DF}\text {-}\mathrm{SS}}= w \left[ \frac{\bar{\sigma }_{\phi }}{\bar{\lambda }}\right] \left[ 1+\frac{1}{\bar{\varepsilon }^{2}}\right] ^{\frac{v}{4s}} \approx w \left[ \frac{\sigma _{\phi }}{\lambda }\right] \left[ \frac{\sigma _{p}}{\sigma _{\phi }}\right] ^{\frac{v}{2s}} \end{aligned}$$

(8)

with $\bar{\sigma }_{\phi } = |C_{\phi \phi }|^{\frac{1}{4}}$, $\bar{\lambda } = \prod _{i=1}^{2}\lambda _{i}^{\frac{1}{2}}$ and $\bar{\varepsilon }^{2}= \frac{e_{2}^{\mathrm{T}}C_{pp}^{-1}e_{2}}{e_{2}^{\mathrm{T}}C_{\phi \phi }^{-1}e_{2}}$. The approximation follows from taking $\lambda = \bar{\lambda }$, $C_{\phi \phi }=\sigma _{\phi }^{2}I_{2}$, $C_{pp}=\sigma _{p}^{2}I_{2}$. By combining (7) and (8), we obtain the important result

$$\begin{aligned} \text {ADOP}_{\mathrm{DF}\text {-}\mathrm{SS}} \approx \text {ADOP}_{\mathrm{SF}\text {-}\mathrm{SS}} \times \left[ \frac{\sigma _{\phi }}{\sigma _{p}}\right] ^{\frac{v}{2s}} \end{aligned}$$

(9)

This shows that the inclusion of a second frequency reduces the ADOP by a factor of approximately $(0.01)^{v/(2s)}$. This factor gets smaller the weaker the model is, i.e. for larger v and/or smaller s. With more parameters and/or fewer satellites, the inclusion of a second frequency will have a greater impact on improving the ADOP.

Fig. 4

Single-frequency and dual-frequency ADOP: single-epoch time-series for Perth with $10^{\circ }$ elevation cut-off (May 14–15, 2015). The red line indicates the 0.12 cycle level. a L1. b L1 + L2

Figure 4 sees formula (9) at work when going from L1 GPS to L1 + L2 GPS. This figure makes the difference between the single-frequency case and dual-frequency case very clear. The single-frequency ADOP values vary a lot and are generally too large to expect successful ambiguity resolution. The dual-frequency ADOPs are much smaller and also less variable, thus giving a better and more constant performance.

4.3 From single-system to dual-system

From the results of Teunissen et al. (2014), we can determine the single-system to dual-system ADOP relation as

$$\begin{aligned} \text {ADOP}_{f, \mathrm{{DS}}} \approx \text {ADOP}_{f, \mathrm{{SS}}} \times \left[ \frac{\sigma _{\phi }}{\sigma _{p}}\right] ^{\frac{v}{2fs}} \end{aligned}$$

(10)

Again we see that it is the phase-code variance ratio that drives the improvement in the ADOP. When we now combine (9) with (10), we obtain the important result

$$\begin{aligned} \text {ADOP}_{{\mathrm{SF}\text {-}\mathrm{DS}}} \approx \text {ADOP}_{{\mathrm{DF}\text {-}\mathrm{SS}}} \end{aligned}$$

(11)

This shows that one can expect the SF-DS ADOP to be approximately the same as the DF-SS ADOP. This is indeed confirmed with the instantaneous ADOP time series as given in Fig. 5 for both Perth and Dunedin. For both locations, the SF-DS (L1 + B1) gives ADOPs that are approximately the same as that of the DF-SS (L1 + L2). As the ADOP values remain below or close to the 0.12 cycle level at all times, one can expect to have an ambiguity success rate larger than or close to $99.9~\%$ over the whole day with both models.

Fig. 5

Single-epoch ADOP time-series (blue) and number of visible satellites (in red when less than 8) for L1 + L2 and L1 + B1 at a Perth (May 14–15, 2015) and b Dunedin (September 11–12, 2015), using $10^{\circ }$ elevation cut-off

Fig. 6

Single-epoch bootstrapped (BS) success-rates (SR) for L1 + L2, B1 + B2 and L1 + B1, as function of the cut-off elevation angle (May 14–15, 2015 in Perth and September 11–12, 2015 in Dunedin). In a + b, the BS SRs are taken as a mean of all single-epoch SRs over 2 days, while in c + d the averaging is only done over the epochs when positioning is available. a BS SR (all epochs): L1 + L2, B1 + B2, L1 + B1 (Perth). b BS SR (all epochs): L1 + L2, B1 + B2, L1 + B1 (Dunedin). c BS SR (if available): L1 + L2, B1 + B2, L1 + B1 (Perth). d BS SR (if available): L1 + L2, B1 + B2, L1 + B1 (Dunedin)

4.4 The SF-DS and DF-SS bootstrapped success-rates

To further analyse the ambiguity resolution performance, we now consider the ambiguity success rates. For our formal analyses, we make use of the success rate formula of Teunissen (1998),

$$\begin{aligned} \textsc {P}[\check{z}_\mathrm{IB}=z] = \prod _{i=1}^{n} \left[ 2\varPhi \left( \frac{1}{2 \sigma _{\hat{z}_{i|I}}} \right) -1 \right] , \end{aligned}$$

(12)

where $\textsc {P}[\check{z}_\mathrm{IB}=z]$ denotes the probability of correct integer estimation of the integer bootstrapped (IB) estimator $\check{z}_{\mathrm{IB}}$ and $\sigma _{\hat{z}_{i|I}}$, $i=1, \ldots , n$, $I=\{1, \ldots , (i-1)\}$, denote the conditional standard deviations of the LAMBDA decorrelated ambiguities.

We use here the bootstrapped success rate (12), instead of the approximate $P_\mathrm{ADOP}$, not only because it is easy to compute, but also since it is a sharp lower bound of the ILS success rate (Teunissen 1999). In fact, the bootstrapped success rate is currently the sharpest lower bound available to the ILS success rate (Verhagen et al. 2013).

It is important that the bootstrapped success rate is computed for the decorrelated ambiguities and not for the original DD ambiguities. As the DD ambiguities have a rather poor precision, their corresponding bootstrapped success rate would be low as well. In Teunissen (1995) it is shown how the required $\sigma _{\hat{z}_{i|I}}$ can be obtained from the triangular decomposition of the decorrelated ambiguity variance matrix $Q_{\hat{z}\hat{z}}= Z^{\mathrm{T}}Q_{\hat{a}\hat{a}}Z$.

In Fig. 6, the mean single-epoch success rates are shown for Perth and Dunedin as function of the cut-off elevation. The figure allows for a direct comparison between the SF-DS success rates and the DF-SS success rates. In order to show the impact of positioning availability, the mean success rates are shown when averaged over all epochs (Fig. 6a + b) as well as when only averaged of those epochs when positioning is available (Fig. 6c + d). The L1 + B1 success rate curves are the same in both cases for Perth as the availability is at $100~\%$ for the dual-system (cf. Fig. 2). As Fig. 6 top shows, the mean success rates get smaller for higher cut-off elevation angles. This is primarily due to the reduction in positioning availability for increasing cut-off angles. That the BDS success rates of Dunedin are smaller than those of Perth is due to the fewer BDS satellites that can be tracked from Dunedin.

Fig. 7

ADOP and PDOP at Dunedin (NZ). Top ADOP and PDOP time series for L1, L2 + B1, B2 over a 2-day period with $25^{\circ }$ elevation cut-off (September 11–12, 2015); Bottom ADOP and PDOP time series for L1 + L2 over a particular short time span ($25^{\circ }$ elevation cut-off). a L1,L2 + B1,B2. b L1 + L2 snapshot

Figure 6 bottom shows that where the SF-DS success rate drops off for high cut-off elevation angles, the DF-SS success rate remains reasonably stable. This is due to the fact that the dual-frequency success rate is generally less dependent on the number of satellites than the single-frequency success rate. For both Perth and Dunedin, however, the L1 + B1 performance is still very good as its success rates remain large and close to the best performing dual-system for high cut-off elevation angles.

4.5 Ambiguity resolution and positioning

The above results are very promising; however, one should be aware of the fact that a good ambiguity resolution performance not necessarily implies a good positioning performance (Teunissen 1997a, b, c, d). Ambiguity resolution and positioning are namely driven by different contributing factors of the GNSS model and can, therefore, show quite a different behaviour (Teunissen et al. 2014). Figure 7 shows two Dunedin examples of ADOP and Positional Dilution of Precision (PDOP) time series for the same period and same satellites. The PDOP is a measure of the receiver-satellite geometry strength. Figure 7 (top) shows results for the dual-frequency GPS + BDS model. It shows, while the ADOPs remain reasonably stable well below 0.12 cycles over the 2 days, that the PDOPs have several excursions in that period. That the ADOP behaviour can be quite different from that of the PDOP is also clear from Fig. 7 (bottom) for L1 + L2 GPS. Here we see that the ADOP remains practically unchanged over the period, while the PDOP chances dramatically over this period of time.

4.6 SF-DS and DF-SS positioning

Ambiguity resolution is not a goal in itself. The goal is to have positioning profit from the integer ambiguity constraints through successful ambiguity resolution. Tables 4 and 5 provide information on the expected positioning precision. They provide the formal standard deviations (North, East, Up) of float and fixed single-epoch positioning for SF-DS and the two DF-SS models. The results clearly show the two orders of magnitude improvement when going from ambiguity-float positioning to ambiguity-fixed positioning. They also show the improvement, both for float and fixed, that a combined system achieves. Since the fixed solutions are already driven by the very-precise carrier-phase data, their improvement from combining the two systems is of course less spectacular.

When we compare the BDS-only results between the two Tables 4 and 5, we also note the poorer positioning precision for Dunedin, with float standard deviations that range up to several metres. Nevertheless, the dual-frequency BDS-only success-rate performance of Dunedin is still quite good (cf. Fig. 6). This again shows that positioning and ambiguity resolution performance do not always go hand in hand. In case of Dunedin, the good ambiguity resolution performance still manages to bring the poor float precision of several metres down to only a few centimetres.

Table 4 Perth: Formal standard deviations (STD) for float/fixed single-epoch positioning (North, East, Up)

Table 5 Dunedin: Formal standard deviations (STD) for float/fixed single-epoch positioning (North, East, Up)

Fig. 8

PDOPs as function of cut-off elevation angle for Perth (top; mean over May 14–15, 2015) and Dunedin (bottom; mean over September 11–12, 2015). PDOPs are shown for L1 + L2, B1 + B2 and L1 + B1

The results of Tables 4 and 5 hold true for a $10^{\circ }$ cut-off elevation angle. Since the ambiguity resolution results of the previous section predict that much higher cut-off elevations are possible when combining GPS and BDS, it is of interest to see what high cut-off elevations do to the PDOP. Figure 8 shows the Perth and Dunedin PDOPs as function of the cut-off elevation angle for the DF-SSs and the SF-DS. For Perth, B1 + B2 has the poorest PDOP for cut-off angles of $10^{\circ }{-}20^{\circ }$, whereas the L1 + L2 PDOP gets significantly worse at $25^{\circ }{-}40^{\circ }$, and the L1 + B1 PDOP remains at a level slightly above five even for a cut-off of $40^{\circ }$. For Dunedin, B1 + B2 has the largest PDOPs for cut-off angles $10^{\circ }{-}30^{\circ }$ due to the poor BDS-only receiver-satellite geometry. The L1 + B1 PDOP, however, remains at a level slightly below five even for a cut-off angle up to $30^{\circ }$.

5 Ambiguity resolution and positioning: empirical analysis with high-grade receivers

5.1 The SF-DS and DF-SS success-rates and positioning

A 4-day instantaneous single-baseline multiple-frequency GPS + BDS campaign was conducted as to verify the formal claims in the previous sections. Two days were collected in Perth, Australia (May 14–15, 2015) and 2 days in Dunedin, New Zealand (September 11–12, 2015) with Trimble NetR9 receivers and 30-s sampling. The detection, identification and adaption (DIA) procedure (Teunissen 1990) was used to eliminate any outliers and the LAMBDA method for ambiguity resolution. The receiver setup can be found in Fig. 9, where the baseline distance in Perth is 350 m and in Dunedin 6.9 km. Standard broadcast ephemerides were used to provide satellite orbits and clocks for GPS and BDS. All the estimated receiver positions were compared to very precise benchmark coordinates.

Fig. 9

GNSS Trimble NetR9 receivers collecting data for GPS + BDS single-baseline (ionosphere-fixed) RTK, involving CUTA-SPA5 (350 m baseline, May 14–15, 2015) in Perth (left) obtained through Map data ©Google, and OTAG-DUND (6.9 km baseline, September 11–12, 2015) in Dunedin (middle and right)

The empirical success-rates (SRs) were computed by comparing the estimated ambiguities to a set of reference ambiguities. The reference ambiguities were determined by a known baseline, multiple-frequencies and assuming the ambiguities to be time-constant over the 2 days in a dynamic model. The ILS SRs for full ambiguity-resolution were then computed by

(13)

The repeatability of the empirical ILS SRs between 2 days is given in Table 6 for Perth, based on an elevation cut-off angle of $10^{\circ }$ for the DF-SS and SF-DS models. The SRs of $100~\%$ are given in bold, and all models have positioning availabilities of $100~\%$.

Table 6 Perth: Single-epoch, empirical ILS and formal BS SRs repeatability, for single- and dual-frequency, single and combined GPS and BDS (May 14–15, 2015, $10^{\circ }$ elevation cut-off)

The SF-DS models in Perth (Table 6) are shown to have a similar ambiguity resolution performance to the DF-SSs. Moreover, the repeatability of SRs is good, with all bootstrapped SRs smaller than the ILS SRs except for the L1 + B1 model. The incorrectly fixed instances were all due to low-elevation multipath caused by newly risen satellites (G20 and G21) near an elevation angle of $10^{\circ }$ that causes the empirical SRs to differ from the predicted one hundred per cent. The results of Table 6 also show that the SF-SS all fail to achieve successful instantaneous ambiguity resolution, where BDS with the larger number of satellites gives the better performance.

The corresponding SR repeatability for Dunedin is given in Table 7. Note that the GEO C03 BDS satellite has been excluded since it caused approximately $3~\%$ of incorrectly fixed instances for the SF-DS caused by low-elevation multipath due to it being almost stationary and having a low elevation angle of around $12^{\circ }$ with respect to the receivers (He and Zhang 2015; Wang et al. 2015a, b).

Table 7 Dunedin: Single-epoch, empirical ILS and formal BS SRs repeatability, for single- and dual-frequency, single and combined GPS and BDS (September 11–12, 2015, $10^{\circ }$ elevation cut-off)

The SF-DS models in Dunedin (Table 7) are also shown to have a similar ambiguity resolution performance to dual-frequency GPS and better than the corresponding BDS-only model. The BDS performance is poorer than for Perth (Table 6) since in Dunedin there are fewer visible BDS satellites (Fig. 1).

A positioning example corresponding to Table 7 is depicted in Fig. 10 for the DF-SS models and the SF-DS (L1 + B1) in Dunedin. The top row shows the local horizontal (N, E) positioning scatterplots and the second row the vertical (U) time-series over 2 days of data. The float solutions are depicted in grey, incorrectly and correctly fixed solutions in red and green, respectively. The zoom-in is given to better show the spread of the correctly fixed solutions with millimetre–centimetre level precisions. Below each vertical time-series the number of satellites is depicted in green, whereas instances with below eight satellites are given in red. To illustrate how poor receiver-satellite geometries can cause excursions in the positioning errors, the PDOP time-series are given in cyan as well.

Fig. 10

Dunedin: Horizontal (N, E) scatterplots and vertical (U) time series for B1 + B2 (1st column), L1 + L2 (2nd column), L1 + B1 (3rd column) with $10^{\circ }$ cut-off (September 11–12, 2015). The correctly fixed solutions are depicted in green, incorrectly fixed solutions in red and float solutions in grey. A zoom-in window is given to depict the spread of the correctly fixed horizontal (N, E) and vertical (U) time-series. The total number of satellites below 8 is depicted in red colour (otherwise green), the $\#$ of BDS satellites in the last column is shown in magenta and PDOP is shown in cyan. Note the scale difference in PDOPs between BDS and GPS + BDS, respectively

The BDS-only model has many instances with PDOP above five and GPS-only a few instances with PDOP close to five (at the beginning of the 2 days) that causes some positioning excursions. When GPS and BDS are combined, however, the PDOPs are improved which thus results in better positioning performance.

Table 8 Perth: Empirical standard deviations (STD) for float/(correctly)-fixed single-epoch positioning (North, East, Up)

Table 9 Dunedin: Empirical standard deviations (STD) for float/(correctly)-fixed single-epoch positioning (North, East, Up)

Note particularly that SF-DS (L1 + B1) gives similar SRs (Table 7) and positioning performance (Fig. 10) to L1 + L2 GPS and better than the B1 + B2 BDS model. The elongated BDS-only horizontal positioning excursions are due to the poor receiver-satellite geometries in Dunedin, which is consistent with what we predicted by the formal STDs in Table 5.

Table 10 Perth: Single-epoch, empirical ILS/formal BS SRs and positioning availability (given if ${\ne }100~\%$) for cut-off angles of $10^{\circ }$ to $40^{\circ }$ (May 14–15, 2015)

To illustrate this further, we give in Tables 8 and 9 the empirical precision of the float and correctly fixed SF-DS and DF-SS positions for Perth and Dunedin, respectively. The precisions are in a reasonably good agreement with the formal STDs in Tables 4 and 5, respectively, which implies realistic stochastic model settings in Table 3. The differences in the GPS-only performance between Tables 8 and 9 are mainly due to the more precise code-only measurements for the receivers in Dunedin. Most importantly, the L1 + B1 model is also here shown to have a comparable positioning performance to the DF-SSs in Perth and to L1 + L2 GPS in Dunedin.

5.2 The SF-DS and DF-SS success-rates for higher-cut-off angles

The SRs in Tables 6 and 7 were given for an elevation cut-off angle of $10^{\circ }$. It is, however, also of our interest to analyse how the SRs vary as a function of the elevation cut-off angle in Perth and Dunedin, respectively. In the following analysis, we will distinguish between two types of SRs, one type based on averaging over all epochs (13) and the other type averaged over epochs when positioning is available according to (4), similar to the bootstrapped SRs in Fig. 6.

In Table 10 the ILS SRs are depicted for Perth, and in Table 11 the corresponding SRs for Dunedin with elevation cut-off angles ranging between $10^{\circ }$ to $40^{\circ }$. All SRs of one hundred per cent are given in bold, and the positioning availability, i.e. the percentage of all epochs that fulfill the solvability condition (4), is given as well.

Table 11 Dunedin: Single-epoch, empirical ILS/formal BS SRs and positioning availability (given if ${\ne }100~\%$) for cut-off angles of $10^{\circ }$ to $40^{\circ }$ (September 11–12, 2015)

As we would expect the SF-SSs have the poorest performance, particularly for increasing cut-off angles. The GPS performance is decreasing more rapidly than for BDS in Perth due to the fewer number of tracked GPS satellites at higher cut-off angles, whereas in Dunedin the performance for GPS is better than for BDS due to the fewer number of tracked BDS satellites.

In Table 10 one can note that the earlier discussed low-elevation multipath effect disappears for the L1 + B1 model once the cut-off angle is increased to $15^{\circ }$. The corresponding ILS SRs achieve a one hundred per cent level all the way up to the cut-off angle of $25^{\circ }$, as predicted by the bootstrapped SRs in Fig. 6. It is also shown that the L1 + B1 model has an overall better ambiguity resolution performance than L1 + L2 GPS when the SRs are based on all epochs, except for the cut-off angle of $10^{\circ }$ (due to the low-elevation multipath). This can be explained by the fact that the L1 + B1 model has a positioning availability of $100~\%$ for cut-off angles up to $40^{\circ }$, whereas the GPS-only model can only solve for positions $58~\%$ of the time for the same cut-off angle (Fig. 2). The dual-frequency GPS + BDS model achieves, as expected, the best ambiguity resolution performance.

In Dunedin in Table 11 the SF-DS models are shown to have an overall similar ambiguity resolution performance to L1 + L2 GPS for cut-off angles of $10^{\circ }{-}25^{\circ }$ and when the SRs are based on averaging over all epochs. This is an excellent outcome as it shows that by adding, e.g. B1 BDS to L1 GPS one can expect similar ambiguity resolution performance for the SF-DS to DF-SS also in New Zealand.

Table 12 Perth: Single-epoch, empirical FFRT SRs (probability of successful fixes within brackets) with user-defined failure-rate $P_{f}=0.1~\%$ for single- and dual-frequency, single and combined GPS and BDS (May 14–15, 2015, $10^{\circ }{-}40^{\circ }$ elevation cut-off)

5.3 The SF-DS and DF-SS ambiguity validation

In this analysis we focus on two different integer ambiguity validation techniques since a set of reference ambiguities is normally not available in real-time to decide upon whether the ambiguities are correct or not. The ambiguity validation test to be used is as follows:

(14)

where $\hat{a}$ is the least-squares solution of the float ambiguities, $\check{a}$ is the fixed integer ambiguities, $\check{a}^{'}$ is the integer vector that gives the next smallest value of the quadratic form, $\Vert .\Vert _{Q_{\hat{a}\hat{a}}}^{2}=\left( .\right) ^{\mathrm{T}}Q_{\hat{a}\hat{a}}^{-1}\left( .\right)$, $Q_{\hat{a}\hat{a}}$ is the variance matrix of the float ambiguities and c is the critical value. A practical assumption is to take c as constant, referred to as the Fixed Critical-value Ratio Test (FCRT). However, this is non-optimal (Teunissen and Verhagen 2009; Verhagen and Teunissen 2013) since doing so cannot guarantee a constant failure-rate. Instead c should be taken as a variable value based on a fixed user-defined failure rate. This is referred to as the Fixed Failure-rate Ratio Test (FFRT).

We compute the empirical FFRT SRs as follows,

$$\begin{aligned} P_{s,\mathrm{FFRT}} = \frac{\#~\hbox {of accepted and correctly fixed epochs}}{\hbox {total}~\#~\hbox {of epochs}}, \end{aligned}$$

(15)

where the corresponding failure-rate follows as

$$\begin{aligned} P_{f,\mathrm{FFRT}} = \frac{\#~\hbox {of accepted and incorrectly fixed epochs}}{\hbox {total}~\#~\hbox {of epochs}} \end{aligned}$$

(16)

Note that $P_{s,\mathrm{FFRT}}+P_{f,\mathrm{FFRT}}+P_{u,\mathrm{FFRT}}=1$ with $P_{u,\mathrm{FFRT}}$ being the undecided-rate, i.e. the number of rejected solutions divided by the total number of epochs. The empirical probability of successful fixing is given by

$$\begin{aligned} P_{sf,\mathrm{FFRT}} = \frac{P_{s,\mathrm{FFRT}}}{P_{s,\mathrm{FFRT}}+P_{f,\mathrm{FFRT}}} \end{aligned}$$

(17)

This implies that if the failure-rate $P_{f,\mathrm{FFRT}}$ is low $P_{sf,\mathrm{FFRT}}$ becomes high and one can be confident that the accepted integer ambiguities are correct. The empirical failure-rate $P_{f,\mathrm{FFRT}}$ should be smaller or at most equal to the user-defined failure-rate $P_{f}$.

In Table 12 the empirical FFRT SRs are given for Perth with a user-defined failure-rate of $P_{f}=0.1~\%$. The presented SRs are averaged over epochs when positioning is available, whereas the values given below the SRs and in bold are SRs based on averaging over all epochs (15).

Table 13 Perth: Single-epoch, empirical FCRT SRs (probability of successful fixes within brackets) with $c=\frac{1}{3}$ for single- and dual-frequency, single and combined GPS and BDS (May 14–15, 2015, $10^{\circ }{-}40^{\circ }$ elevation cut-off)

Table 12 reveals that the SF-DS (L1 + B1) achieves continuous successful ambiguity resolution for cut-off angles of $15^{\circ }{-}20^{\circ }$, whereas the DF-SS (L1 + L2) can only achieve this for cut-off angles of $10^{\circ }{-}15^{\circ }$. The SF-SSs all fail to give continuous successful ambiguity resolution and the performance becomes very poor for higher cut-off angles. However, the SF-DSs (L1 + B1 and L2 + B2) retain their very good ambiguity resolution performance for cut-off angles up to $25^{\circ }$ (compare also to the poorer performance for the dual-frequency GPS model). Note also that the GPS-only model has positioning availabilities different from $100~\%$ for higher cut-off angles (see Table 10) that gives GPS SRs based on all epochs smaller than that for the SF-DS models for all cut-off angles above $15^{\circ }$. Finally, we remark that the FFRT gives probabilities of successful fixes between 99.8 and 100 % for all cases (given within brackets), and the empirical failure rates (not shown herein) are all below or equal to the user-defined $P_{f}=0.1~\%$ (except for the SF-DS (L1 + B1) and the cut-off angle of $10^{\circ }$, which has an empirical failure rate of $0.3~\%$, due to the earlier referenced low-elevation multipath).

As to show the effect by using the non-optimal FCRT, we present in Table 13 the corresponding SRs for Perth where $c=\frac{1}{3}$ in (14) is taken as a standard value. Although some FCRT empirical SRs turn out higher than the FFRT SRs in Table 12, the FCRT probabilities of successful fixes are also overall lower than the corresponding FFRT probabilities (significantly lower for weaker models such as the SF-SSs and higher cut-off angles). This shows that the FCRT cannot guarantee the accepted solutions to be correct, which can be critical in safety-of-life applications such as precise aircraft navigation.

In Table 14 we show the corresponding FFRT SRs in Dunedin. The SF-DS models are shown to achieve comparable ambiguity resolution performance to the L1 + L2 GPS model for cut-off angles of $10^{\circ }{-}15^{\circ }$. The probability of successful fixes are between 99.7 and 100 % for all cases and the empirical failure rates are again all below or equal to the user-defined $P_{f}=0.1~\%$.

Table 14 Dunedin: Single-epoch, empirical FFRT SRs (probability of successful fixes within brackets) with user-defined failure-rate $P_{f}=0.1~\%$ for single- and dual-frequency, single and combined GPS and BDS (September 11–12, 2015, $10^{\circ }{-}40^{\circ }$ elevation cut-off)

5.4 SF-DS and DF-SS positioning for higher cut-off angles

The SRs in the previous analysis are very promising; however, as we demonstrated in Sect. 4.5 a good ambiguity resolution performance does not always imply a good positioning performance. Hence in the following analysis we will show how the different GNSS models are affected by different elevation cut-off angles.

In Table 15, the single- and dual-frequency GPS and GPS + BDS SRs and positioning results are shown in Perth for different elevation cut-off angles computed by averaging epochs when positioning is available. The SRs are also computed based on epochs with the condition $PDOP \le 10$, and within brackets and in bold the corresponding SRs are given when computed based on all epochs. By including and excluding epochs with large PDOPs, we show how the SRs and positioning performance of the different models are affected by poor receiver-satellite geometries. In support of Table 15 we also show in Fig. 11 typical positioning examples for the cut-off angle of $25^{\circ }$ for L1 GPS, L1 + L2 GPS and L1 + B1.

Table 15 Perth: Single-epoch empirical STDs (N, E, U) of correctly fixed positions (L1, L1 + L2, L1 + B1 and L1, L2 + B1, B2), together with their ILS SR, for $25^{\circ }{-}40^{\circ }$ elevation cut-off (May 14–15, 2015)

Fig. 11

Perth: Horizontal (N, E) scatterplots and vertical (U) time series for L1 (1st column), L1 + L2 (2nd column), L1 + B1 (3rd column) with $25^{\circ }$ cut-off (May 14–15, 2015). The total $\#$ of satellites below 8 is depicted in red colour (otherwise green), the $\#$ of BDS satellites in the last column is shown in magenta and PDOP is shown in cyan

Table 15 reveals the excellent performance of the SF-DS (L1 + B1) for the cut-off angle of $25^{\circ }$, which allows for continuously fixed solutions over the 2 days whereas the L1 GPS and L1 + L2 GPS models have corresponding SRs of approximately 30 and 98 %, respectively. The DF-SS (L1 + L2) also has epochs where ambiguity resolution is successful, whereas the receiver-satellite geometry is at the same time poor, which is reflected by the large PDOPs. This results in some correctly fixed positioning excursions at the level of several decimetres to metres, see Fig. 11 (and the corresponding STDs in Table 15). This illustrates as mentioned before that successful ambiguity resolution does not automatically imply correspondingly good positioning performance. The fixed solutions of the L1 GPS model is not as affected by poor PDOPs since the minimum number of satellites required to obtain a correctly fixed solution is then also higher. When imposing the $\hbox {PDOP}\le 10$ condition all correctly fixed solutions obtain millimetre–centimetre level precision. However, as a result of this condition the L1 + L2 GPS SR for the cut-off angle of $25^{\circ }$ decreases to $95~\%$, whereas the L1 + B1 SR at one hundred per cent remains unchanged since the model is not affected by large PDOPs.

By further inspecting Table 15 and the cut-off angle of $40^{\circ }$ when the $\hbox {PDOP}\le 10$ condition is imposed, the SR decreases significantly for GPS. The L1 + L2 GPS SR namely drops from $94~\%$ down to $75~\%$. The L1 + B1 model has fewer number of epochs with poor receiver-satellite geometry when ambiguity resolution is successful; thus its PDOP-conditioned corresponding SR of $78~\%$ is larger than for L1 + L2 GPS. This is particularly true when the L1 + L2 GPS SR is computed on the basis of all epochs (the SR is then $44~\%$), whereas the L1 + B1 SR remains unchanged since positioning is available throughout the 2 days. As expected, we can also conclude that the dual-frequency GPS + BDS model gives the best performance.

In Table 16, the corresponding Dunedin results are shown. Once again in support of understanding the table better we depict in Fig. 12 typical examples of positioning results for the cut-off angle of $25^{\circ }$ for L1 GPS, L1 + L2 GPS and L1 + B1.

Table 16 Dunedin: Single-epoch empirical STDs (N, E, U) of correctly fixed positions (L1, L1 + L2, L1 + B1 and L1, L2 + B1, B2), together with their ILS SR, for $25^{\circ }{-}40^{\circ }$ elevation cut-off (September 11–12, 2015)

Fig. 12

Dunedin: Horizontal (N, E) scatterplots and vertical (U) time series for L1 (1st column), L1 + L2 (2nd column), L1 + B1 (3rd column) with $25^{\circ }$ cut-off (September 11–12, 2015). The total $\#$ of satellites is depicted in green colour and when below 8 in red (below 9 satellites for GPS + BDS), the $\#$ of BDS satellites in the last column is shown in magenta, and PDOP is shown in cyan

Similar to what we found in Perth (Fig. 11), Fig. 12 reveals that the GPS-only model in Dunedin suffers from many instances with large PDOP excursions. When GPS and BDS are combined the PDOPs are improved which thus results in better (correctly fixed) positioning performance. Table 16 shows that the SF-DS (L1 + B1) for the cut-off angle of $25^{\circ }$ has a better SR ($94~\%$) than DF-SS (L1 + L2) when the SR is based on a $\hbox {PDOP}\le 10$ condition and averaged over all epochs ($93~\%$). This since the GPS + BDS model, in contrast to the GPS-only model, has no epochs with a PDOP above ten and also a $100~\%$ positioning availability over the 2 days. The dual-frequency GPS + BDS model gives, as expected, the best performance for all cut-off angles.

6 Ambiguity resolution and positioning: empirical analysis with low-grade receivers

So far we have illustrated that the SF-DS can achieve similar or better ambiguity resolution and positioning performance to the DF-SS when GPS and BDS are combined in Perth and Dunedin. This analysis was based on geodetic survey-grade receivers (Trimble NetR9s). In the following analysis we will make use of low-cost single-frequency L1/B1 receivers (which costs a few hundred USD) and compare the performance to DF-SS using survey-grade multiple-frequency receivers (which can cost tens of thousands of USD).

The experiment was conducted for 5.5 h between 09.24 and 14.54 Dunedin local time during November 25, 2015 with 10-s sampling. L1 GPS and B1 BDS data were collected by two ublox EVK-M8T receivers that were connected to low-cost ublox patch antennas (see Fig. 13). As to make a comparison to the DF-SS (L1 + L2) with survey-grade receivers, two stations OTAG (Trimble NetR9) and OUS3 (Septentrio PolarX4) connected to choke-ring antennas were also used to collect data at the same time instances at approximately the same location as the ublox receivers.

Four days later (November 29, 2015) another 5.5 h experiment was setup connecting the ublox receivers at the same locations with Trimble Zephyr 2 antenna (costing slightly more than one thousand USD), as to illustrate the performance improvement from better signal reception and multipath suppression in comparison to using the ublox patch antennas. The data were collected with a time separation to the first data set so that the GPS constellation repeatability period of approximately 23 h and 56 min (Axelrad et al. 2005) was also taken into account. The BDS IGSO satellites have a similar repeatability period to GPS (Jiang et al. 2011), and the GEO satellites are almost stationary. The ublox stochastic model settings are given in Table 17.

In Fig. 14 the L1 GPS (ublox patch-antenna), L1 + L2 GPS (Trimble-Septentrio) and L1 + B1 (ublox patch-antenna) positioning results are shown for an elevation cut-off angle of $10^{\circ }$ (top two rows) and $25^{\circ }$ (bottom two rows), respectively.

Fig. 13

Low-cost single-frequency ublox EVK-M8T GNSS receivers (top) with patch antennas (bottom left) collecting data for L1 GPS + B1 BDS single-baseline (ionosphere-fixed) RTK (November 25, 2015) in Dunedin. The survey-grade multiple-frequency receivers (top) OTAG (Trimble NetR9) and OUS3 (Septentrio PolarX4) are connected to choke-ring antennas. Four days later (November 29, 2015) the ublox receivers were collecting data with the same GPS and IGSO/GEO constellation repeated, but then connected to Trimble Zephyr 2 antenna (bottom right)

Table 17 Zenith-referenced undifferenced code and phase STDs for the ublox receivers with patch antennas (Trimble Zephyr 2 antenna within brackets) for $j_{*}=1_{*}$

The SF-SS (L1) in Fig. 14 (using two ublox receivers) gives, as expected, large ambiguity-float and incorrectly fixed positioning errors at the level of several metres. This is mainly due to that patch antennas have less effective signal reception and multipath suppression in comparison to survey-grade antennas (Pesyna et al. 2014), where multipath is larger for code than for phase. Moreover the L1 GPS model achieves an ILS SR of $50~\%$ and $16~\%$ for the cut-off angle of $10^{\circ }$ and $25^{\circ }$, respectively, which is a poorer performance to what was achievable in our previous analysis when using survey-grade receivers (see e.g. Table 11). Once the number of satellites increases (around epoch 1080), the number of incorrectly fixed solutions (in red) decreases. The DF-SS (L1 + L2), with the survey-grade receivers, achieve (as expected) much better ambiguity-float precisions and continuous successful ambiguity resolution for the cut-off angle of $10^{\circ }$. When combining L1 + B1 (using two ublox receivers) the ambiguity-float positioning errors become somewhat improved in comparison to L1 GPS.

Fig. 14

Ublox (SF-DS) and Trimble-Septentrio (DF-SS): Horizontal (N, E) scatterplots and vertical (U) time series for ublox L1 (1st column) with $50.3~\%$ ($16.3~\%$) ILS SR, Trimble-Septentrio L1 + L2 (2nd column) with $100~\%$ ($99.9~\%$) ILS SR, and ublox L1 + B1 (3rd column) with $100~\%$ ($92.2~\%$) ILS SR, using $10^{\circ }$ (top two rows) and $25^{\circ }$ (bottom two rows) cut-off, respectively (Dunedin, 5.5 h during November 25, 2015). The total $\#$ of satellites below 8 is depicted in red colour (otherwise green), the $\#$ of BDS satellites in the last column is shown in magenta and PDOP is shown in cyan. Note: The patch antennas are used for the ublox receivers

Most importantly though the ublox SF-DS (L1 + B1) in Fig. 14 succeeds in getting continuous instantaneous ambiguity-fixed positioning precisions at the millimetre level for the cut-off angle of $10^{\circ }$, similar to the L1 + L2 GPS model based on survey-grade receivers. These excellent results thus show that using low-cost ublox receivers with patch antennas can potentially achieve one hundred per cent SRs similar to traditional survey-grade receivers, provided that L1 GPS and B1 BDS are combined. The SF-DS ILS SR for the cut-off angle of $25^{\circ }$ becomes poorer ($92~\%$) in comparison to the L1 + L2 GPS model ($99.9~\%$). However, the GPS-only model also suffers from large PDOPs causing excursions in the correctly fixed positioning results. If one imposes a $\hbox {PDOP}\le 10$ condition the corresponding SR decreases to approximately $95~\%$, whereas the SF-DS SR remains unchanged.

As to show how the positioning performance is improved if the ublox receivers are connected to a Trimble Zephyr 2 antenna instead of the patch antenna, we depict in Fig. 15 the corresponding L1 GPS and L1 + B1 ublox positioning results. Note that although the constellation repeatability period has been taken into account, the BDS MEO satellites do not repeat approximately every 23 h and 56 min (similar to GPS and IGSO), and thus the number of BDS satellites is somewhat different to the data in Fig. 14. The ublox correctly fixed positioning STDs and corresponding bootstrapped/ILS SRs are summarized in Table 18. The consistency between the bootstrapped and ILS SRs indicates realistic stochastic model settings in Table 17.

Fig. 15

Ublox (SF-DS): Horizontal (N, E) scatterplots and vertical (U) time series for ublox L1 (1st column) with $89.3~\%$ ($45.8~\%$) ILS SR and ublox L1 + B1 (2nd column) with $100~\%$ ($98.7~\%$) ILS SR, using $10^{\circ }$ (top two rows) and $25^{\circ }$ (bottom two rows) cut-off, respectively (Dunedin, 5.5 h during November 29, 2015). The total $\#$ of satellites is depicted in green colour and when below 8 in red (below 9 satellites for GPS + BDS), the $\#$ of BDS satellites in the last column is shown in magenta and PDOP is shown in cyan. Note: The Trimble Zephyr 2 antenna is now used for the ublox receivers

Figure 15 reveals that the SF-DS (L1 + B1) again achieves the same excellent results of continuous successful ambiguity resolution over the entire time-span for the cut-off angle of $10^{\circ }$. Moreover, the ambiguity-float positioning precisions are significantly improved in comparison to Fig. 14 owing to the use of Zephyr antennas. For the cut-off angle of $25^{\circ }$ we also see a significant improvement in the SF-DS SRs, going from $92~\%$ with patch antennas to $98~\%$ when the Zephyr antennas are used (despite the somewhat smaller number of BDS satellites). The positioning precisions are now also of more similar magnitude to the survey-grade L1 + L2 GPS results in Fig. 14.

Table 18 Ublox (SF-DS) Single-epoch empirical STDs (N, E, U) of correctly fixed positions (L1 and L1 + B1), together with their bootstrapped and ILS SR, for $10^{\circ }$ and $25^{\circ }$ elevation cut-off angles, respectively

7 Summary and conclusions

In this contribution the single-frequency dual-system (SF-DS) capabilities of a GPS + BDS system was analysed and compared to that of a dual-frequency single-system (DF-SS) in Perth, Australia, and in Dunedin, New Zealand. It was shown that the SF-DS can give similar or better instantaneous ambiguity resolution and positioning performance than the DF-SS, particularly for higher cut-off angles. The SF-DS performance in Perth is better than that in Dunedin because of the larger number of visible BDS satellites. A low-cost single-frequency ublox receiver positioning experiment with patch antennas was also conducted in Dunedin. It was shown, for the first time, that the low-cost receiver SF-DS (L1 + B1) can give similar ambiguity resolution performance to when using survey-grade receivers and the DF-SS (L1 + L2 GPS).

The study consisted of a formal and an empirical analysis. In the formal analysis, the redundancy, positioning availability, ADOP, bootstrapped success-rate and the positioning precision were used to gain insight into the effect of combining the two systems at the two locations. It was shown that the SF-DS ADOP approximates the DF-SS in both Perth and Dunedin because of the about double number of satellites in a GPS + BDS model. The bootstrapped success-rates were also found consistent with the empirically determined success-rates computed from 2 days of GNSS data.

In our analysis of the positioning precisions we demonstrated that improved ambiguity resolution does not always go hand in hand with improved positioning. This was particularly obvious when looking into the dual-frequency BDS-only positioning performance in Dunedin with the poorer receiver-satellite geometry in comparison to Perth. We also found that the SF-DS positioning capability clearly outperforms that of the DF-SS in Perth for high elevation cut-off angles up to $40^{\circ }$. In Dunedin the positioning performance of the SF-DS is similar to that of the DF-SS (L1 + L2 GPS) up to a cut-off angle of $25^{\circ }$.

We then investigated the ambiguity validation techniques of the Fixed Failure-rate Ratio Test (FFRT) and compared it to the performance of the Fixed Critical-value Ratio Test (FCRT). It was concluded that the FFRT gives an empirical failure rate smaller than or equal to the user-defined failure rate of $0.1~\%$, whereas the FCRT cannot guarantee such constant and small failure rate. In this analysis it was also concluded that the SF-DS has a similar or better ambiguity-validated performance than the DF-SS, particularly in Perth.

Our low-cost receiver experiment in Dunedin showed that the ambiguity resolution and positioning performance is to a large extent dependent on the quality of the antennas used. By making use of low-cost ublox single-frequency receivers (which costs a few hundred USD) and patch antennas, it was, however, revealed that the SF-DS (L1 + B1) still can give $100~\%$ availability of instantaneous ambiguity-resolved positioning precisions at the millimetre-level similar to that of a DF-SS (L1 + L2 GPS), based on survey-grade receivers (which can cost tens of thousand of USD).